Some Interacting Dark Energy Models
Abstract
1. Introduction
- The differential age of old galaxies, given by .
- The peak position of baryonic acoustic oscillations (BAO).
- The SN Ia data.
- Strong Gravitation Lensing data.
2. Models and Observational Constraints
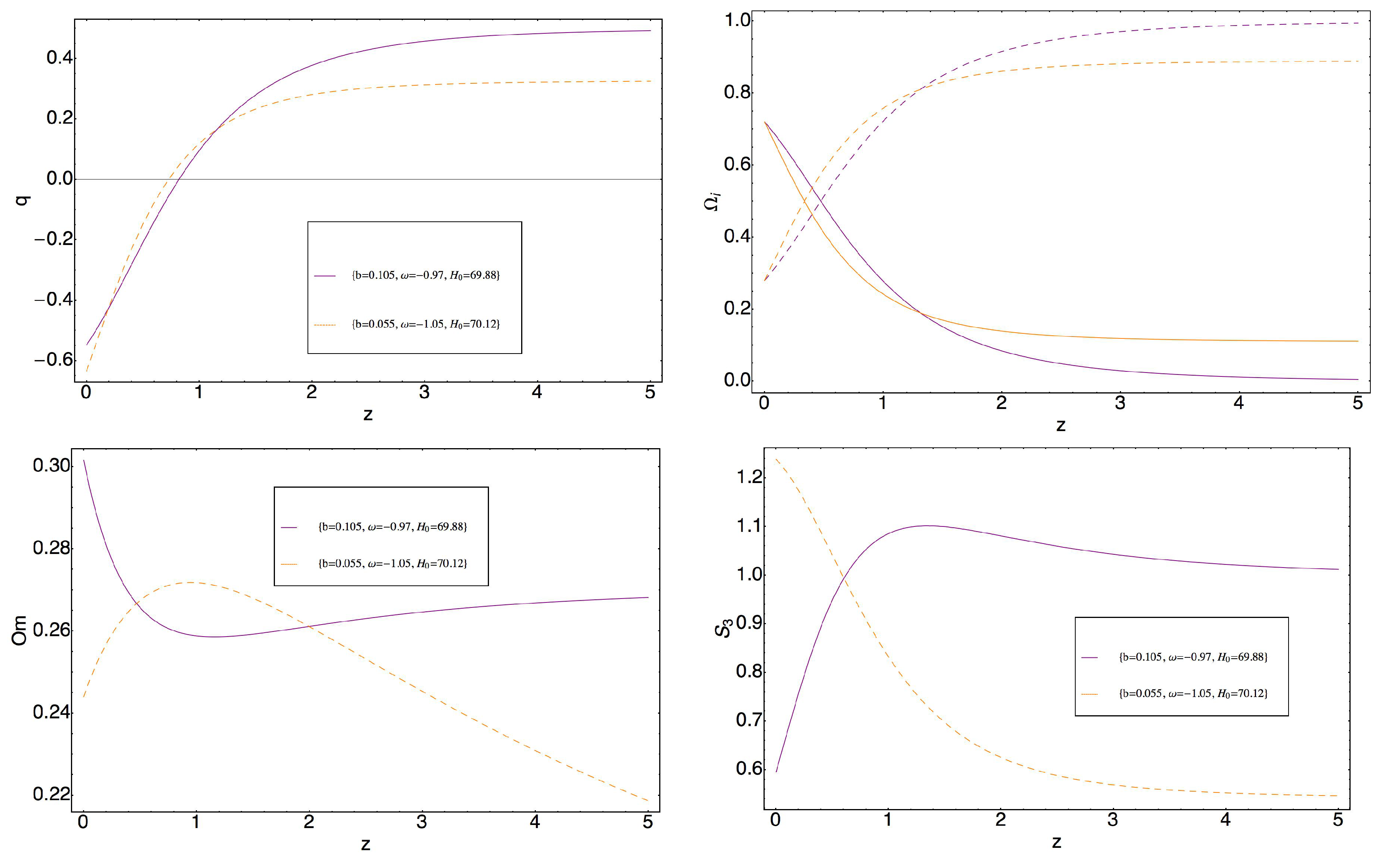
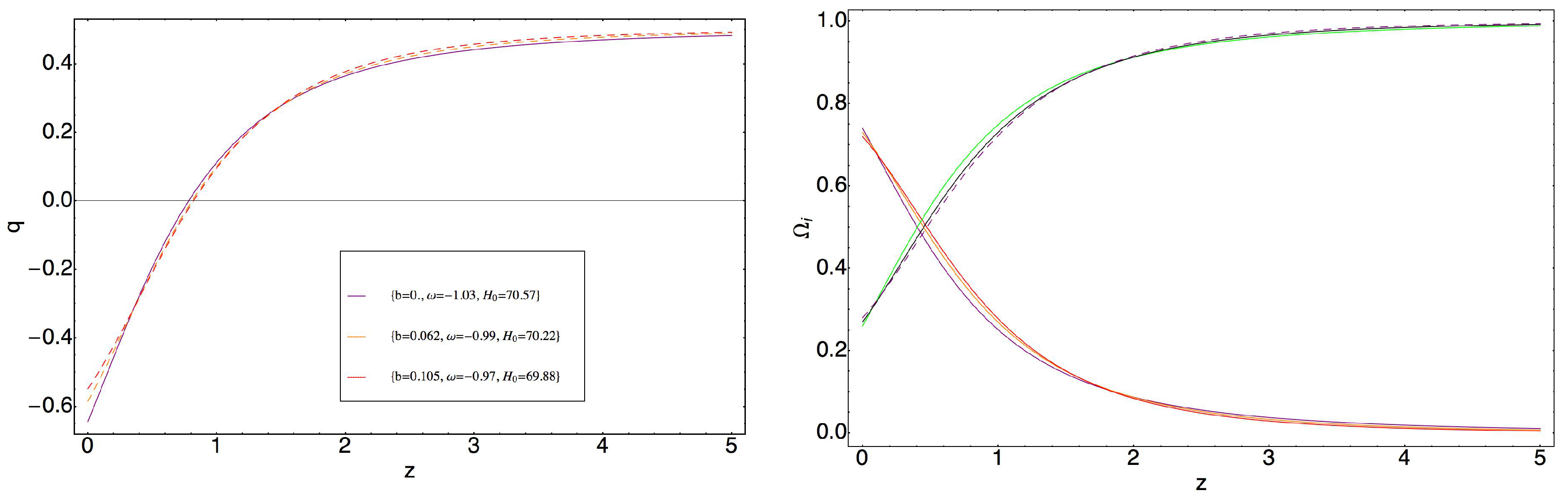
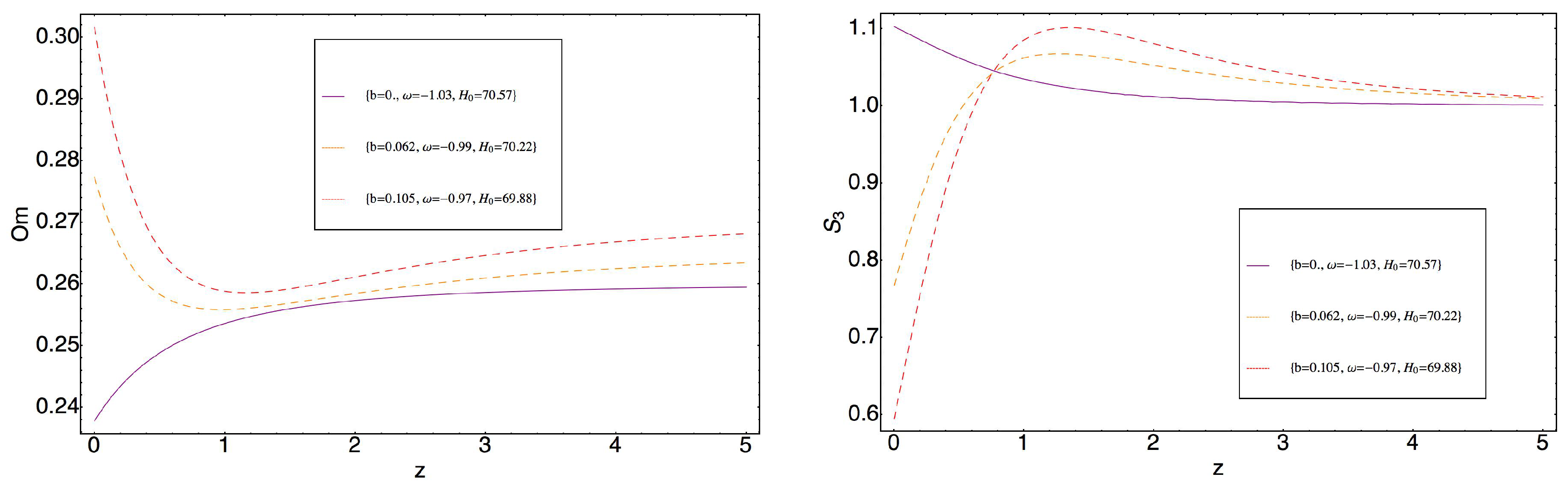
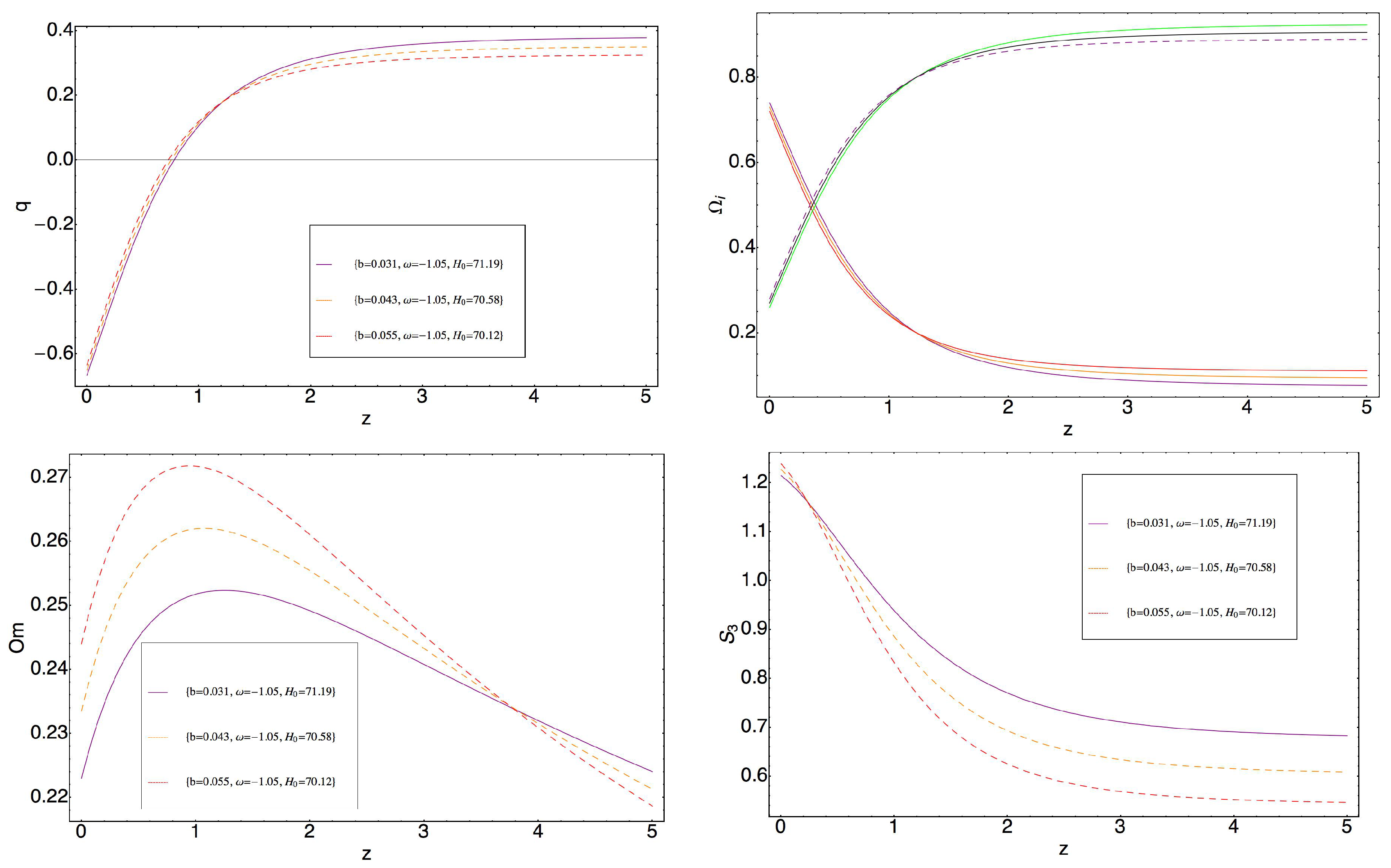
3. Model 1
3.1. Transition from Dark Energy to Dark Matter
3.2. Transition from Dark Matter to Dark Energy
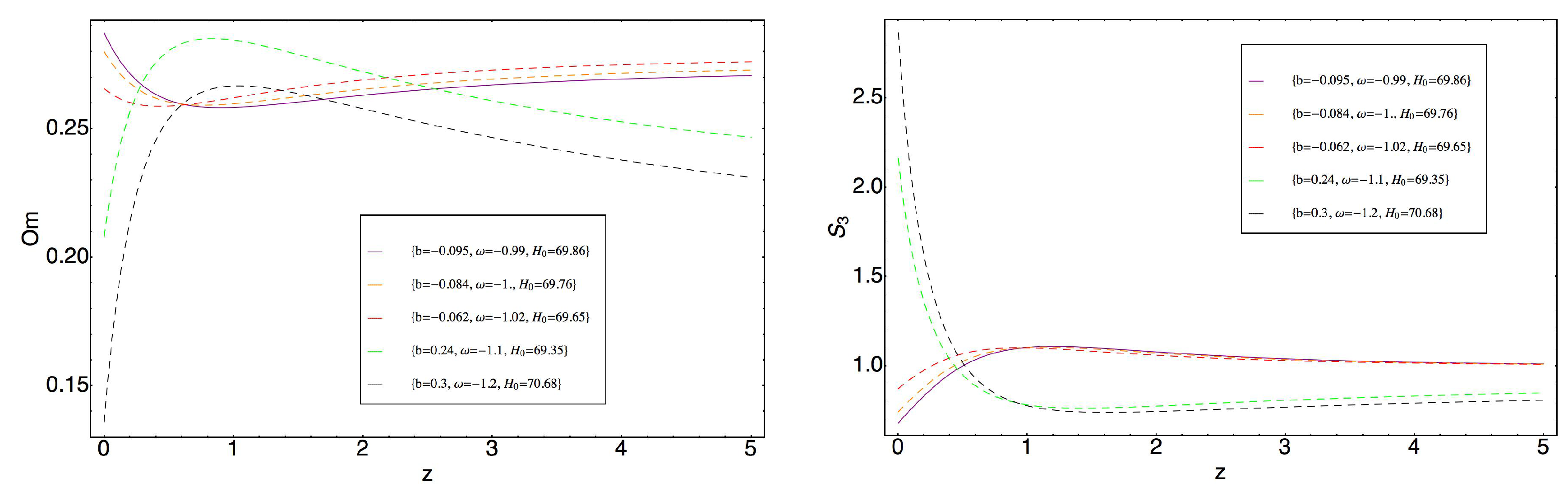
4. Model 2
5. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Velten, H.E.S.; vom Marttens, R.F.; Zimdahl, W. Aspects of the cosmological coincidence problem. Eur. Phys. J. C 2014, 74, 3160. [Google Scholar] [CrossRef]
- Sivanandam, N. Is the cosmological coincidence a problem? Phys. Rev. D 2013, 87, 083514. [Google Scholar] [CrossRef]
- Rowland, D.; Whittingham, I.B. Models of interacting dark energy. Mon. Not. R. Astron. Soc. 2008, 390, 1719–1726. [Google Scholar] [CrossRef]
- Cui, W.; Baldi, M.; Borgani, S. The halo mass function in interacting dark energy models. Mon. Not. R. Astron. Soc. 2002, 424, 993–1005. [Google Scholar] [CrossRef]
- Baldi, M. Clarifying the effects of interacting dark energy on linear and non-linear structure formation processes. Mon. Not. R. Astron. Soc. 2011, 414, 116–128. [Google Scholar] [CrossRef]
- Sadeghi, J.; Khurshudyan, M.; Movsisyan, A.; Farahani, H. Interacting ghost dark energy models with variable G and Λ. J. Cosmol. Astropart. Phys. 2013, 12, 031. [Google Scholar] [CrossRef]
- Sadeghi, J.; Khurshudyan, M.; Hakobyan, M.; Farahani, H. Phenomenological Fluids from Interacting Tachyonic Scalar Fields. Int. J. Theor. Phys. 2014, 53, 2246–2260. [Google Scholar] [CrossRef]
- Sadeghi, J.; Khurshudyan, M.; Hakobyan, M.; Farahani, H. Mutually interacting Tachyon dark energy with variable G and Λ. Res. Astron. Astrophys. 2015, 15, 175–190. [Google Scholar] [CrossRef]
- Sadeghi, J.; Khurshudyan, M.; Farahani, H. Interacting ghost dark energy models in the higher dimensional cosmology. Int. J. Mod. Phys. D 2016, 25, 1650108. [Google Scholar] [CrossRef]
- Sadeghi, J.; Khurshudyan, M.; Hakobyan, M.; Farahani, H. Hubble Parameter Corrected Interactions in Cosmology. Adv. High. Energy Phys. 2014, 2014, 129085. [Google Scholar] [CrossRef]
- Khurshudyan, M.; Chubaryan, E.; Pourhassan, B. Interacting Quintessence Models of Dark Energy. Int. J. Theor. Phys. 2014, 53, 2370–2378. [Google Scholar] [CrossRef]
- Khurshudyan, M.; Khurshudyan, A.; Myrzakulov, R. Interacting varying ghost dark energy models in general relativity. Astrophys. Space Sci. 2015, 357, 113. [Google Scholar] [CrossRef]
- Khurshudyan, M.; Myrzakulov, R. Phase space analysis of some interacting Chaplygin gas models. Eur. Phys. J. C 2017, 77, 65. [Google Scholar] [CrossRef]
- Khurshudyan, M. Some non-linear interactions in polytropic gas cosmology: Phase space analysis. Astrophys. Space Sci. 2015, 360, 33. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, X. Revisit of the interacting holographic dark energy model after Planck 2015. J. Cosmol. Astropart. Phys. 2016, 08, 072. [Google Scholar] [CrossRef]
- Cataldo, M.; Chimento, L.P.; Richarte, M.G. Finite time future singularities in the interacting dark sector. Phys. Rev. D 2017, 95, 063510. [Google Scholar] [CrossRef]
- Jimenez, J.B.; Rubiera-Garcia, D.; Sáez-Gómez, D.; Salzano, V. Cosmological future singularities in interacting dark energy models. Phys. Rev. D 2016, 94, 123520. [Google Scholar] [CrossRef]
- Elizalde, E.; Khurshudyan, M.; Nojiri, S. Cosmological singularities in interacting dark energy models with an ω(q) parameterization. arXiv, 2018; arXiv:1809.01961. [Google Scholar]
- Elizalde, E.; Khurshudyan, M. Cosmology with an interacting van der Waals fluid. Int. J. Mod. Phys. D 2018, 27, 1850037. [Google Scholar] [CrossRef]
- Khurshudyan, M. On a holographic dark energy model with a Nojiri-Odintsov cut-off in general relativity. Astrophys. Space Sci. 2016, 361, 232. [Google Scholar] [CrossRef]
- Bolotin, Y.L.; Kostenko, A.; Lemets, O.A.; Yerokhin, D.A. Cosmological evolution with interaction between dark energy and dark matter. Int. J. Mod. Phys. D 2015, 24, 1530007. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2018 results. VI. Cosmological parameters. arXiv, 2018; arXiv:1807.06209. [Google Scholar]
- Mortsell, E.; Dhawan, S. Does the Hubble constant tension call for new physics? arXiv 2018, arXiv:1801.07260. [Google Scholar]
- Verde, L.; Protopapas, P.; Jimenez, R. Planck and the local Universe: Quantifying the tension. Phys. Dark Universe 2013, 2, 166–175. [Google Scholar] [CrossRef]
- Roos, M. Introduction to Cosmology, 4th ed.; John Wiley & Sons: New York, NY, USA, 2015. [Google Scholar]
- Yoo, J.; Watanabe, Y. Theoretical models of dark energy. Int. J. Mod. Phys. D 2012, 21, 1230002. [Google Scholar] [CrossRef]
- Brevik, I.; Gron, O.; de Haro, J.; Odintsov, S.D.; Saridakis, E.N. Viscous Cosmology for Early- and Late-Time Universe. Int. J. Mod. Phys. D 2017, 26, 1730024. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1935. [Google Scholar] [CrossRef]
- Miao, L.; Miao, X.D.; Wang, S.; Wang, Y. Dark energy. Commun. Theor. Phys. 2011, 56, 525. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Khurshudyan, M.Z.; Makarenko, A.N. On a phenomenology of the accelerated expansion with a varying ghost dark energy. Astrophys. Space Sci. 2016, 361, 187. [Google Scholar] [CrossRef]
- Khurshudyan, M. Varying ghost dark energy and particle creation. Eur. Phys. J. Plus. 2016, 131, 25. [Google Scholar] [CrossRef]
- Khurshudyan, M. Low redshift Universe and a varying ghost dark energy. Mod. Phys. Lett. A 2016, 31, 1650055. [Google Scholar] [CrossRef]
- Khurshudyan, M. A varying polytropic gas Universe and phase space analysis. Mod. Phys. Lett. A 2016, 31, 1650097. [Google Scholar] [CrossRef]
- Khurshudyan, M. On the Phenomenology of an Accelerated Large-Scale Universe. Symmetry 2016, 8, 110. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S. Unifying phantom inflation with late-time acceleration: Scalar phantom–non-phantom transition model and generalized holographic dark energy. Gen. Relativ. Gravit. 2006, 38, 1285–1304. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Covariant Generalized Holographic Dark Energy and Accelerating Universe. Eur. Phys. J. C 2017, 77, 528. [Google Scholar] [CrossRef]
- Saridakis, E.N. Theoretical limits on the equation-of-state parameter of phantom cosmology. Phys. Lett. B 2009, 676, 7–11. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Methods Mod. Phys. 2007, 4, 115–145. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified gravity with negative and positive powers of curvature: Unification of inflation and cosmic acceleration. Phys. Rev. D 2003, 68, 123512. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified f(R) gravity consistent with realistic cosmology: From a matter dominated epoch to a dark energy universe. Phys. Rev. D 2006, 74, 086005. [Google Scholar] [CrossRef]
- Capozziello, S.; Nojiri, S.; Odintsov, S.D.; Troisia, A. Cosmological viability of f(R)-gravity as an ideal fluid and its compatibility with a matter dominated phase. Phys. Lett. B 2006, 639, 135–143. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. Class of viable modified f (R) gravities describing inflation and the onset of accelerated expansion. Phys. Rev. D 2008, 77, 046009. [Google Scholar] [CrossRef]
- Cai, Y.F.; Capozziello, S.; De Laurentis, M.; Saridakis, E.N. f (T) teleparallel gravity and cosmology. Rept. Prog. Phys. 2016, 79, 106901. [Google Scholar] [CrossRef] [PubMed]
- Dent, J.B.; Contaldi, C.R. Testing model independent modified gravity with future large scale surveys. J. Cosmol. Astropart. Phys. 2011, 013. [Google Scholar] [CrossRef]
- Nesseris, S.; Basilakos, S.; Saridakis, E.N.; Perivolaropoulos, L. Viable f (T) models are practically indistinguishable from ΛCDM. Phys. Rev. D 2013, 88, 103010. [Google Scholar] [CrossRef]
- Kofinas, G.; Saridakis, E.N. Teleparallel equivalent of Gauss-Bonnet gravity and its modifications. Phys. Rev. D 2014, 90, 084044. [Google Scholar] [CrossRef]
- Skugoreva, M.A.; Saridakis, E.N.; Toporensky, A.V. Dynamical features of scalar-torsion theories. Phys. Rev. D 2015, 91, 044023. [Google Scholar] [CrossRef]
- Oikonomou, V.K.; Saridakis, E.N. f (T) gravitational baryogenesis. Phys. Rev. D 2016, 94, 124005. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified gravity and cosmology. Phys. Rept. 2012, 513, 1–189. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rept. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D. Inflationary Cosmology in Modified Gravity Theories. Symmetry 2015, 7, 220–240. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rep. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Pasqua, A.; Khurshudyan, M. New holographic reconstruction of scalar-field dark-energy models in the framework of chameleon Brans–Dicke cosmology. Eur. Phys. J. C 2014, 74, 3080. [Google Scholar] [CrossRef]
- Lima, J.A.S.; Singleton, D. The impact of particle production on gravitational baryogenesis. Phys. Lett. B 2016, 762, 506–511. [Google Scholar] [CrossRef]
- Jesus, J.F.; Pereira, S.H. CCDM model from quantum particle creation: Constraints on dark matter mass. J. Cosmol. Astropart. Phys. 2014, 40. [Google Scholar] [CrossRef]
- Paliathanasis, A.; Barrow, J.D.; Pan, S. Cosmological solutions with gravitational particle production and nonzero curvature. Phys. Rev. D 2017, 95, 103516. [Google Scholar] [CrossRef]
- Chen, J.; Wu, P.; Yu, H.; Li, Z. Age problem in the creation cold dark matter cosmology model. Eur. Phys. J. C 2012, 72, 1861. [Google Scholar] [CrossRef]
- Nunes, R.C.; Pan, S. Cosmological consequences of an adiabatic matter creation process. Mon. Not. R. Astron. Soc. 2016, 459, 673–682. [Google Scholar] [CrossRef]
- Paul, B.C.; Thakur, P. Observational constraints on EoS parameters of emergent Universe. Astrophys. Space Sci. 2017, 362, 73. [Google Scholar] [CrossRef]
- Wang, N.; Xu, L. Strong gravitational lensing and its cosmic constraints. Mod. Phys. Lett. A 2013, 28, 1350057. [Google Scholar] [CrossRef]
- Zimdahl, W.; Pavón, D.; Chimento, L.P. Interacting quintessence. Phys. Lett. B 2001, 521, 133–138. [Google Scholar] [CrossRef]
- Sahni, V.; Shafieloo, A.; Starobinsky, A.A. Two new diagnostics of dark energy. Phys. Rev. D 2008, 78, 103502. [Google Scholar] [CrossRef]
- Sahni, V.; Shafieloo, A.; Starobinsky, A.A. Model-independent evidence for dark energy evolution from baryon acoustic oscillations. Astrophys. J. Lett. 2014, 793, L40. [Google Scholar] [CrossRef]
- Arabsalmani, M.; Sahni, V. Statefinder hierarchy: An extended null diagnostic for concordance cosmology. Phys. Rev. D 2011, 83, 043501. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khurshudyan, M.; Khurshudyan, A.Z. Some Interacting Dark Energy Models. Symmetry 2018, 10, 577. https://doi.org/10.3390/sym10110577
Khurshudyan M, Khurshudyan AZ. Some Interacting Dark Energy Models. Symmetry. 2018; 10(11):577. https://doi.org/10.3390/sym10110577
Chicago/Turabian StyleKhurshudyan, Martiros, and Asatur Zh. Khurshudyan. 2018. "Some Interacting Dark Energy Models" Symmetry 10, no. 11: 577. https://doi.org/10.3390/sym10110577
APA StyleKhurshudyan, M., & Khurshudyan, A. Z. (2018). Some Interacting Dark Energy Models. Symmetry, 10(11), 577. https://doi.org/10.3390/sym10110577