Charged and Non-Charged Black Hole Solutions in Mimetic Gravitational Theory

Abstract

In this study, we derive, in the framework of mimetic theory, charged and non-charged black hole solutions for spherically symmetric as well as flat horizon spacetimes. The asymptotic behavior of those black holes behave as flat or (A)dS spacetimes and coincide with the solutions derived before in general relativity theory. Using the field equations of non-linear electrodynamics mimetic theory we derive new black hole solutions with monopole and quadrupole terms. The quadruple term of those black holes is related by a constant so that its vanishing makes the solutions coincide with the linear Maxwell black holes. We study the singularities of those solutions and show that they possess stronger singularity than the ones known in general relativity. Among many things, we study the horizons as well as the heat capacity to see if the black holes derived in this study have thermodynamical stability or not.

1. Introduction

General Relativity (GR) is believed to be an interesting theory which permits the construction of black holes [1,2,3]. Regarding this fact, the field equations of GR, which are non-linear, can be solved exactly by postulating a specific symmetry on the geometry of the spacetime. For instant, assuming the space to be spherically symmetric then one can obtain the Schwarzschild spacetime as an analytic vacuum solution to Einstein theory of GR. Moreover, and from our experience of astrophysics, we realize that at the final stage of the development of a stellar object with sufficiently large mass, nothing can stop it from falling and finally one gets a black hole [4,5].

It is well known that Einstein’s GR foretells the existence of singularities which are responsible for the formation of black holes [6]. At the singularity, the invariants formulated from the curvature, Kretschmann, Ricci tensors square and the Ricci scalars, diverge and the curvature of the spacetime and geodesics become incomplete. From the philosophy of GR, a falling body takes a finite time to pass into the event horizon and after that, the body continues in falling until it reaches the singularity. From our knowledge of GR, this body would be smashed before reaching the singularity due to the huge forces act on it [3].

One of the defects that makes the theory incomplete is the occurrence of singularities. It is well known that GR is a classical theory, thus, it is expected that quantum effects or viable quantum theory of gravity are necessary near singularities. Therefore, those singularities could be improved if we take into consideration the quantum gravity effects. Despite this, up to this moment, no viable quantum gravity theory formulated [7].

There are may trials to resolve the problem of singularity in GR. Among these trails $f\left(R\right)$ gravity [8,9,10,11,12,13,14,15,16,17,18,19,20] and the torsion-based $f\left(T\right)$ gravity [21,22,23,24,25,26]. In this study, we use another trial which is the conformal invariant gravitational theories [27,28,29,30,31,32,33,34,35]. It is well known that Einstein’s GR is invariant under general diffeomorphisms however, it is not invariant under the conformal transformation. Mimetic gravity theories are presented to solve the problems of singularity as well as to supply other alternative description of dark matter theories [36]. There are many amendments of the original mimetic gravity formulated in the literature [37]. The mimetic gravity theory which depends on a Proca-like vector field has been used to discuss the caustic instabilities [38]. One more variant is the “tensor-vector-scalar theory”, that has been constructed to discuss the ghost instabilities [39]. Other modified theory which take into account the potential of the mimetic scalar field [40,41] has been presented to discuss the cosmological evolutions. Moreover, the effect of the quantum corrections can be considered if one takes into account the higher-order curvature invariants to the action of mimetic gravitation theory, like mimetic $f\left(R\right)$ gravity [42,43]. Many modified mimetic theories have been constructed to taking into consideration the quantum corrections, like mimetic $f\left(G\right)$ [44], mimetic $f(R,T)$ [45], mimetic covariant Horava-like gravity [46], mimetic $f(R,\varphi )$ [47], mimetic Galileon gravity [48,49], mimetic Horndeski gravity [50], unimodular-mimetic $f\left(R\right)$ gravity [51], mimetic Born-Infeld gravity [52] and non-local mimetic $f\left(R\right)$ gravity [53]. The motivation and importance of the higher-derivative invariants of the Lagrangian of the mimetic theory have been discussed [54,55,56,57,58,59,60]. Other modifications of the mimetic theory have been constructed, for example by involving the vector-tensor mimetic gravity [61], bi-scalar mimetic models [62], the one that considers the limiting curvature hypothesis to solve the problems of the cosmological singularity [63,64] and the braneworld mimetic gravity [65]. Moreover, the theories in which the mimetic field is non-minimally coupled with matter [66]. The effective theory of cosmological perturbations, in mimetic theories, has been developed to overcome the problem of gradient instability [56]. Curiously, the mimetic $f\left(R\right)$ theory suffers from ghosts [67] and despite this, it has been shown that such problem could be overcome by using an appropriate gravitational Lagrangian multiplier [67]. The latest developments in mimetic gravitational theory in addition to other modified theories are displayed in [68].

The non-linear effect of the magnetic dipole and quadrupole fields on the propagation of electromagnetic waves in the eikonal approximation of the parameterized post-Maxwell electrodynamics of the vacuum is calculated [69]. The regular multi-horizon black holes in the Einstein gravity, $f\left(R\right)$ gravity coupled with non-linear electrodynamics have been investigated [70]. In non-linear electrodynamics coupled to gravity, regular spherically symmetric electrically charged solutions satisfy the weak energy condition and have obligatory de Sitter center have been investigated in [71]. Later, many different regular black hole solutions in the non-linear electrodynamics have been derived [72,73,74,75,76,77,78,79,80,81,82].

The constructions of this study are as follows: In Section 2, a fundamental process of the mimetic gravitational theory is presented. In Section 3, non-charged and charged spherically symmetric black holes are derived in the frame of linear Maxwell case. In Section 4, non-charged and charged cylindrical horizon black holes are also presented in the frame of linear Maxwell electrodynamics. In Section 5, we study the singularities of those black holes derived in Section 3 and Section 4. In Section 6, we apply the field equations of the non-linear electrodynamic mimetic theory to the spherically symmetric and flat horizon spacetimes, presented in Section 3 and Section 4, and derived new black holes include monopole as well as quadrupole terms. In Section 7, the features of the non-linear electrodynamics black hole solutions are studied. In Section 8, we study the thermodynamical properties of the black holes derived in Section 3, Section 4 and Section 6. In the final section, we discuss the main results.

2. Preliminaries of Mimetic Gravitational Theory

The mimetic gravity was constructed in GR to discuss the dark matter in cosmology [83]. The formulation of the mimetic theory of the physical metric $g_{\mu \nu }$ is defined as [83]:

$$g_{\alpha \beta }=-{\overline{g}}_{\alpha \beta }\left({\overline{g}}^{\mu \beta }{\partial }_{\mu }\psi {\partial }_{\nu }\psi \right),$$

(1)

with ${\overline{g}}_{\alpha \beta }$ being the conformal auxiliary metric, $\psi$ is the mimetic scalar field and ${\overline{g}}^{\alpha \beta }$ is the inverse of ${\overline{g}}_{\alpha \beta }$. From Equation (1) one can show that GR theory is invariant under the transformation, i.e., ${\overline{g}}_{\alpha \beta }\to \omega \left(x_{\mu }\right){\overline{g}}_{\alpha \beta }$ where $\omega \left(x_{\mu }\right)$ is an arbitrary function of the coordinates. Equation (1) shows that the mimetic field should satisfy:

$$g^{\mu \nu }{\partial }_{\mu }\psi {\partial }_{\nu }\psi =-1.$$

(2)

Considering the mimetic Maxwell theory which includes the cosmological constant $\Lambda$ in the form

$$\mathcal{S}:=\frac{1}{2\chi }\int d^{4}x\sqrt{-g({\overline{g}}_{\mu \nu },\psi )}\left\{R({\overline{g}}_{\mu \nu },\psi )-\Lambda -{\mathcal{S}}_{M.F.}\right\},$$

(3)

with $\chi$ being the 4-dimensional gravitational constant, $\chi =8\pi$ and $g\equiv g({\overline{g}}_{\mu \nu },\psi )$ is the determinant of the physical metric given by Equation (1). The Maxwell filed action is defined as [84,85] S_M.F. = F Λ^∗ F, where F = dV, and V = V_μdx^μ, being the gauge potential 1-form.

Varying the action (3) with respect to the physical metric we get the gravitational field equation in the form

$$I_{\mu }{}^{\nu }=G_{\mu }{}^{\nu }+\frac{1}{2}{\delta }_{\mu }^{\nu }\Lambda -{\stackrel{\mathrm{em}}{\mathcal{T}}}_{\mu }{}^{\nu }-{\tilde{\mathcal{T}}}_{\mu }{}^{\nu }\equiv 0$$

(4)

where $G_{\mu \nu }$ is the Einstein tensor with $G=-R$ is its trace and the energy momentum-tensor of Maxwell field $\stackrel{\mathrm{em}}{\mathcal{T}}{}_{\mu }{}^{\nu }$, is given by

$$\stackrel{\mathrm{em}}{\mathcal{T}}{}_{\mu }{}^{\nu }=F_{\mu \alpha }{F}^{\nu \alpha }-\frac{1}{4}{\delta }_{\mu }^{\nu }{F}_{\alpha \beta }{F}^{\alpha \beta },$$

(5)

which has a vanishing trace. Remarkably, the auxiliary metric does not appear in the field equations, however it implicitly does through the physical metric of Equation (2) and the mimetic field $\psi$. The presence of the mimetic field can be written as

$${\tilde{\mathcal{T}}}_{\mu \nu }=-(G+2\Lambda ){\partial }_{\mu }\psi {\partial }_{\nu }\psi .$$

(6)

Finally, the variation of the action (3) with respect to the 1-form gauge potential gives [84]

$${\partial }_{\nu }\left(\sqrt{-g}{F}^{\mu \nu }\right)=0.$$

(7)

It is worth mentioning that the energy-momentum tensors, ${\stackrel{\mathrm{em}}{\mathcal{T}}}_{\mu \nu }$ and ${\tilde{\mathcal{T}}}_{\mu \nu }$, are conserved, i.e., they satisfy the continuity equations ${\nabla }^{\mu }{\stackrel{\mathrm{em}}{\mathcal{T}}}_{\mu \nu }=0={\nabla }^{\mu }{\tilde{\mathcal{T}}}_{\mu \nu }$, where ∇ is the covariant derivative with respect to the symmetric affine connection. Using the mimetic field condition given by Equation (2) and the energy-momentum tensor (6), the corresponding continuity gives

$${\nabla }^{\nu }\left([G+2\Lambda ]{\partial }_{\nu }\psi \right)=\frac{1}{\sqrt{-g}}{\partial }_{\nu }\left(\sqrt{-g}[G+2\Lambda ]g^{\nu \sigma }{\partial }_{\sigma }\psi \right)=0.$$

(8)

On the other hand, one can show that Equation (2) is satisfied when Equation (8) is used. It is simple to show that the trace of Equation (4) has the form

$$[G+2\Lambda ](1+g^{\mu \nu }{\partial }_{\mu }\psi {\partial }_{\nu }\psi )=0.$$

(9)

Finally, one can note that the conformal degree of freedom provides a dynamical quantity, i.e., ($G\ne 0$), and thence the mimetic theory has non-trivial solutions [83]. For many physical applications of the mimetic gravity, we refer to [51,86,87] and references therein.

3. Spherically Symmetric Black Holes in Mimetic Gravity

Using the following spherically symmetric spacetime

$$d{s}^2=-f\left(r\right)d{t}^2+\frac{1}{f\left(r\right)}d{r}^2+r^2(d{\theta }^2+{\sin }^2\theta d{\varphi }^2),$$

(10)

with $f\left(r\right)$ being an unknown function of r we get the Ricci scalar in the form

$$R=-\frac{r^2{f}^{″}+4r{f}^{\prime }+2f-2}{r^2}.$$

(11)

Applying the field Equation (4) when $\stackrel{\mathrm{em}}{\mathcal{T}}{}_{\mu }{}^{\nu }=0$ to the metric (10) we get:

$$\begin{array}{c}{I}^t{}_t=\frac{r{f}^{\prime }-1+f}{r^2}\equiv 0,\hfill \\ I^r{}_r=\frac{r{f}^{\prime }-1+f-2{\psi }^{\prime }{}^2[2rf{f}^{\prime }-f+f^2]-f{r}^2{\psi }^{\prime }{}^2{f}^{″}}{r^2}\equiv 0,\hfill \\ I^{\theta }{}_{\theta }=I^{\varphi }{}_{\varphi }=\frac{2f^{\prime }+r{f}^{″}}{2r}\equiv 0,\hfill \end{array}$$

(12)

where $f^{\prime }=\frac{df\left(r\right)}{dr}$, $f^{″}=\frac{d^{2}f\left(r\right)}{d{r}^2}$ and ${\psi }^{\prime }=\frac{d\psi \left(r\right)}{dr}$. Equation (12) shows clearly that one cannot control the value of the mimetic field, therefore we are going to assume certain value of it (This result i.e., the field equations of the mimetic theory are not able to fix the mimetic field, is valid through the whole of the present study). The exact solution of the differential Equation (12) takes the form

$$\begin{array}{c}\hfill f\left(r\right):=1+\frac{c}{r},\psi \left(r\right):=\frac{c_1}{r}.\end{array}$$

(13)

Using Equation (13) in (10) we get the metric spacetime in the form

$$d{s}^2=-\left(1-\frac{2m}{r}\right)d{t}^2+{\left(1-\frac{2m}{r}\right)}^{-1}d{r}^2+r^2(d{\theta }^2+{\sin }^2\theta d{\varphi }^2),\mathrm{where}c=-2m.$$

(14)

Equation (14) indicates that the metric behaves asymptotically as a flat spacetime and has an event horizon at $r=2m$. Equation (13) is an exact solution to the field Equation (4) in addition to Equation (9) since the Ricci scalar of this solution has a nil value.

Now, we are going to use the following metric

$$d{s}^2=-f\left(r\right)d{t}^2+\frac{1}{f_1\left(r\right)}d{r}^2+r^2(d{\theta }^2+{\sin }^2\theta d{\varphi }^2),$$

(15)

where $f\left(r\right)$ and $f_1\left(r\right)$ are two unknown functions of the radial coordinate r to calculate the Ricci scalar and get

$$R=-\frac{r^{2}f{f}^{\prime }{f}_1^{\prime }+2r^{2}f{f}_1{f}^{″}-r^2{f}^{\prime }{}^2{f}_1+4rf{f}_1{f}_1^{\prime }+4f^{2}r{f}_1^{\prime }-4f^2+4f^2{f}_1}{2r^2{f}^2}.$$

(16)

Equation (16) coincides with (11) when the unknown functions $f\left(r\right)=f_1\left(r\right)$. Using the metric (15) into (4) when $\stackrel{\mathrm{em}}{\mathcal{T}}{}_{\mu }{}^{\nu }=0$ we get:

$$\begin{array}{c}{I}^t{}_t\equiv \frac{2r{f}_1^{\prime }-2+2f_1+r^2\Lambda }{2r^2}=0,\hfill \\ I^r{}_r\equiv \frac{2rf{f}_1{f}^{\prime }-f^2(2-2f_1+r^2\Lambda )-4f{f}_1{\psi }^{\prime }{}^2[r{\left(f{f}_1\right)}^{\prime }+f{f}_1-f+r^{2}f\Lambda ]-f_1{r}^2{\psi }^{\prime }{}^2[f{f}_1^{\prime }{f}^{\prime }+2f{f}_1{f}^{″}-f_1{f}^{\prime }{}^2]}{2r^2{f}^2}=0,\hfill \\ I^{\theta }{}_{\theta }\equiv I^{\varphi }{}_{\varphi }=\frac{2f{\left(f{f}_1\right)}^{\prime }+r[f{f}^{\prime }{f}_1^{\prime }+2f{f}_1{f}^{″}-f_1{f}^{\prime }{}^2]+2r^2\Lambda }{4r{f}^2}=0.\hfill \end{array}$$

(17)

The exact solution of the differential Equation (17) has the form

$$\begin{array}{c}f\left(r\right)=f1\left(r\right):=1-\frac{r^2\Lambda }{6}+\frac{c}{r},\psi \left(r\right):=\pm \left[b_1\left(r\right)+c\ln \sqrt{r-c/2+b_1\left(r\right)}\right],\mathrm{with}{b}_1\left(r\right)=\sqrt{r^2-cr}.\end{array}$$

(18)

Equation (18) coincides with (13) when the cosmological constant vanishing. To write the metric spacetime of Equation (18) we use Equation (15) and get

$$\begin{array}{cc}\hfill & d{s}^2=-\left\{1-\frac{r^2\Lambda }{6}-\frac{2m}{r}\right\}d{t}^2+{\left(1-\frac{r^2\Lambda }{6}-\frac{2m}{r}\right)}^{-1}d{r}^2+r^2(d{\theta }^2+{\sin }^2\theta d{\varphi }^2).\hfill \end{array}$$

(19)

Equation (19) shows that the metric behaves asymptotically as (A)dS spacetime.

Now we are going to study the effect of the electromagnetic field on the mimetic theory, i.e., when $\stackrel{\mathrm{em}}{\mathcal{T}}{}_{\mu }{}^{\nu }\ne 0$. Applying the field Equation (4) to the metric (10) we get:

$f\left(r\right)=f1\left(r\right):=1-\frac{r^2\Lambda }{6}+\frac{c}{r},\psi \left(r\right):=\pm \left[b_1\left(r\right)+c\ln \sqrt{r-c/2+b_1\left(r\right)}\right],\mathrm{with}{b}_1\left(r\right)=\sqrt{r^2-cr}.$

$$\begin{array}{c}{I}^t{}_t=\frac{2r{f}^{\prime }-2+2f+r^2{q}^{\prime }{}^2}{2r^2}\equiv 0,\hfill \\ I^r{}_r=\frac{2r{f}^{\prime }-2(1-f)-4{\psi }^{\prime }{}^2[2rf{f}^{\prime }-f+f^2]-2f{r}^2{\psi }^{\prime }{}^2{f}^{″}+r^2{q}^{\prime }{}^2}{2r^2}\equiv 0,\hfill \\ I^{\theta }{}_{\theta }=I^{\varphi }{}_{\varphi }=\frac{2f^{\prime }+r{f}^{″}-r{q}^{\prime }{}^2}{2r}\equiv 0,\hfill \end{array}$$

(20)

where the unknown function $q\left(r\right)$ is given from the vector potential which has the form

$$V:=q\left(r\right)dt.$$

(21)

Equation (20) reduces to Equation (12) when $q\left(r\right)=0$. The exact solution of the differential Equation (20) takes the form

$$\begin{array}{c}\hfill f\left(r\right):=1+\frac{c}{r}+\frac{c_2{}^2}{2r^2},\psi \left(r\right):=\frac{c_1}{r},q\left(r\right):=\frac{c_2}{r}.\end{array}$$

(22)

Equation (22) reduces to (13) when $c_2=0$.

Using Equation (22) in (10) we get the metric spacetime in the form

$$d{s}^2=-\left(1-\frac{2m}{r}+\frac{q^2}{r^2}\right)d{t}^2+{\left(1-\frac{2m}{r}+\frac{q^2}{r^2}\right)}^{-1}d{r}^2+r^2(d{\theta }^2+{\sin }^2\theta d{\varphi }^2),\mathrm{where}{c}_2=\sqrt{2}q.$$

(23)

Equation (23) indicates that the metric behaves asymptotically as a flat spacetime and coincides with Reissner-Nordström which has an event horizon at $r=m\pm \sqrt{4m^2-2q^2}$ [88,89,90].

Now we are going to apply the field Equation (4) to the metric (15) when $\stackrel{\mathrm{em}}{\mathcal{T}}{}_{\mu }{}^{\nu }\ne 0$ and get:

$$\begin{array}{c}{I}^t{}_t={\displaystyle \frac{2rf{f}_1^{\prime }-2f+2f{f}_1+r^2{f}_1{q}^{\prime }{}^2}{2r^{2}f}}\equiv 0,\hfill \\ I^r{}_r=\frac{1}{2r^2{f}^2}\left(f[2r{f}_1{f}^{\prime }-2f(1-f_1)+r^2{f}_1{q}^{\prime }{}^2]-4f{f}_1{\psi }^{\prime }{}^2[r{\left(f{f}_1\right)}^{\prime }+f{f}_1-f]-r^2{f}_1{\psi }^{\prime }{}^2[f{f}_1^{\prime }{f}^{\prime }+2f{f}_1{f}^{″}-f_1{f}^{\prime }{}^2]\right)\equiv 0,\hfill \\ I^{\theta }{}_{\theta }=I^{\varphi }{}_{\varphi }={\displaystyle \frac{2f{\left(f{f}_1\right)}^{\prime }+r[f{f}^{\prime }{f}_1^{\prime }+2f{f}_1{f}^{″}-f_1{f}^{\prime }{}^2]-2rf{f}_1{q}^{\prime }{}^2}{4r{f}^2}}\equiv 0.\hfill \end{array}$$

(24)

The physical solution (Physical solution is the one that has a well behave asymptote at infinity, i.e., when $r\to \infty$ the solution has well asymptote.) of the differential Equation (24) has the same form given by (22).

4. Cylindrical Black Holes in Mimetic Gravity

Now, we are going to study the cylindrical spacetime. For this purpose we suppose the spacetime configuration to have the form

$$d{s}^2=-f\left(r\right)d{t}^2+\frac{1}{f\left(r\right)}d{r}^2+r^2(d{\theta }^2+d{z}^2),$$

(25)

where $0\le r<\infty$, $-\infty <t<\infty$, $0\le \theta <2\pi$ and $-\infty <z<\infty$. For the spacetime (25), the Ricci scalar takes the form

$$R=-\frac{r^2{f}^{″}+4r{f}^{\prime }+2f}{r^2}.$$

(26)

Then, the non-vanishing components of Equations (4) and (7) are:

$$\begin{array}{c}{I}_t{}^t={\displaystyle \frac{2r{f}^{\prime }+2f+\Lambda r^2+q^{\prime }{}^2{r}^2}{2r^2}}\equiv 0,\hfill \\ I_r{}^r={\displaystyle \frac{2r{f}^{\prime }+2f+\Lambda r^2-2{\psi }^{\prime }{}^{2}f[4f^{\prime }r+2f+2f^{″}{r}^2+\Lambda r^2]+q^{\prime }{}^2{r}^2}{2r^2}}\equiv 0,\hfill \\ I_{\theta }{}^{\theta }=E_z{}^z={\displaystyle \frac{2f^{\prime }+r{f}^{″}+\Lambda r-r{q}^{\prime }{}^2}{2r}}\equiv 0.\hfill \end{array}$$

(27)

We solve the field Equation (27) and get

$$\begin{array}{c}q\left(r\right)=\frac{c_2}{r},f\left(r\right)=\frac{c}{r}-\frac{\Lambda r^2}{6}+\frac{c_1{}^2}{2r^2},\psi \left(r\right)=\left[\sqrt{r^2-c_{3}r}+c_3\ln \sqrt{r-c_3/2+\sqrt{r^2-c_{3}r}}\right],\end{array}$$

(28)

where $c_3$ is constant. It is worth mentioning that Equation (28) is an exact solution of Maxwell-mimetic gravitational theory given by Equations (4) and (7). Plugging solution (28) into the spacetime metric (25), we get

$$d{s}^2=-\left(-\frac{\Lambda r^2}{6}-\frac{2m}{r}+\frac{q^2}{r^2}\right)d{t}^2+{\left(-\frac{\Lambda r^2}{6}-\frac{2m}{r}+\frac{q^2}{r^2}\right)}^{-1}d{r}^2+r^2(d{\theta }^2+d{z}^2),\mathrm{where}c=-2m,c_2=\sqrt{2}q.$$

(29)

As is clear the spacetime (29) is asymptotically (A)dS and coincides with Reissner-Nordström (A)dS. If we repeat our calculations using the following metric

$$d{s}^2=-f\left(r\right)d{t}^2+\frac{1}{f_1\left(r\right)}d{r}^2+r^2(d{\theta }^2+d{z}^2),$$

(30)

the solution of the resulting differential equation will be the same as that given by (28) in which $f\left(r\right)=f_1\left(r\right)$.

5. Features of the Black Hole Solutions

In this section, we are going to discuss the physical features of solutions (18), (22) and (28) derived in the previous sections. To achieve this we are going to study their singularities.

Singularities of the black holes:

To derive the physical singularities one must calculate the invariants of curvature. Calculating all the invariants of curvature of solutions (18), (22) and (28) we get

$$\begin{array}{c}\mathrm{solution}\left(18\right)R^{\mu \nu \lambda \rho }{R}_{\mu \nu \lambda \rho }=\frac{2({\Lambda }^2{r}^2+72m^2)}{3r^6},R^{\mu \nu }{R}_{\mu \nu }={\Lambda }^2,R=2\Lambda ,\hfill \\ \mathrm{solution}\left(22\right)R^{\mu \nu \lambda \rho }{R}_{\mu \nu \lambda \rho }=\frac{48m^2{r}^2-96rm{q}^2+56q^4}{r^8},R^{\mu \nu }{R}_{\mu \nu }=\frac{4q^4}{r^8},R=0,\hfill \\ \mathrm{solution}\left(28\right)R^{\mu \nu \lambda \rho }{R}_{\mu \nu \lambda \rho }=\frac{2({\Lambda }^2{r}^8+168q^2-144\sqrt{2}rmq+72m^2{r}^2)}{3r^8},R^{\mu \nu }{R}_{\mu \nu }=\frac{{\Lambda }^2{r}^8+8q^4}{r^8},R=2\Lambda ,\hfill \end{array}$$

(31)

where $R^{\mu \nu \lambda \rho }{R}_{\mu \nu \lambda \rho }$, $R^{\mu \nu }{R}_{\mu \nu }$, R are the Kretschmann scalar, the Ricci tensor square and the Ricci scalar. Equation (31) shows that:

(i)

There is a singularity at $r=0$ which is a true singularity for all the derived solutions.

(ii)

The Ricci scalar has a vanishing value for solutions (22) and constant value for solutions (18) and (28). As is clear from our previous discussion that all the non-charged and charged solutions in the frame of mimetic theory have no shift from GR. Therefore, in the next section, we are going to study the effect of the non-linear electrodynamics of the mimetic gravitational theory on the previous two spacetimes given by Equations (10) and (25).

6. New Black Holes with Non-Linear Electrodynamics in Mimetic Gravity

In this section, we consider the mimetic theory with non-linear electrodynamics in the presence of a cosmological constant.

Therefore, we take the following action

$${\mathcal{L}}_{\mathcal{NL}}:=\frac{1}{2\chi }\int d^{4}x\sqrt{-g({\overline{g}}_{\mu \nu },\psi )}\left[R({\overline{g}}_{\mu \nu },\psi )-\Lambda -\mathcal{L}\left(\mathcal{F}\right)\right],$$

(32)

where $\mathcal{L}\left(\mathcal{F}\right)$ is a gauge-invariant electromagnetic Lagrangian that depends on a single invariant F defined as $F=\frac{1}{4}{F}_{\alpha \beta }{F}^{\alpha \beta }$ [91].

The electromagnetic field F is the antisymmetric Faraday tensor

$$F_{\alpha \beta }=E_{\alpha ,\beta }-E_{\beta ,\alpha },$$

where $E_{\mu }$ is its gauge potential 1-form. The Lagrangian $\mathcal{L}\left(\mathcal{F}\right)$ in the Maxwell theory has the form $\mathcal{L}\left(\mathcal{F}\right)=4F$.

In this study, we will be considering more general choices of the electromagnetic Lagrangians. As Equation (32) informs us that the nonlinear electrodynamics is described by terms of a nonlinear electrodynamic field, $F_{\alpha \beta }$, and its invariants. However, we can provide a dual representation in terms of an auxiliary field $P_{\alpha \beta }$. This method is proved to be highly benefit to derive an exact solution in GR, specifically for the electric case [92,93]. The dual formalism can be obtained by using the following Legendre transformation:

$$\mathcal{H}=2F{\mathcal{L}}_F-\mathcal{L},\mathrm{where}{\mathcal{L}}_F=\frac{\partial \mathcal{L}}{\partial F},$$

(33)

with $\mathcal{H}$ being an arbitrary function which depends on the invariant P that is defined as $P=\frac{1}{4}{P}_{\alpha \beta }{P}^{\alpha \beta }$. Using Equation (33) then the theory of the non-linear electrodynamics can be recast in terms of P formalism by using the following relations

$$P_{\mu \nu }={\mathcal{L}}_F{F}_{\mu \nu },F_{\mu \nu }={\mathcal{H}}_P{P}_{\mu \nu },\mathcal{L}=2P{\mathcal{H}}_P-\mathcal{H},$$

(34)

where the linear Maxwell field can be obtained by setting ${\mathcal{L}}_F=1$. As is clear from the above equations that $\mathcal{H}$ is a function of P, where [92,93]

$${\mathcal{H}}_P=\frac{\partial \mathcal{H}}{\partial P}.$$

Varying the action of Equation (32) with respect to the physical metric, one can write the gravitational field equations as

$$I_{\mu }{}^{\nu }=G_{\mu }{}^{\nu }+\frac{1}{2}{\delta }_{\mu }^{\nu }\Lambda -\stackrel{\mathrm{NL}}{\mathrm{T}}-\tilde{\mathrm{T}}{}_{\mu }{}^{\nu }\equiv 0,$$

(35)

and the Maxwell field equations of the nonlinear electrodynamics take the form [93]

$${\partial }_{\nu }\left(\sqrt{-g}{P}^{\mu \nu }\right)=0.$$

(36)

The energy-momentum tensor of the electrodynamic is defined as,

$$\stackrel{\mathrm{NL}}{\mathrm{T}}{}_{\mu }{}^{\nu }:=2({\mathcal{H}}_P{P}_{\mu \alpha }{P}^{\nu \alpha }-{\delta }_{\mu }^{\nu }[2P{\mathcal{H}}_P-\mathcal{H}]).$$

(37)

It is important to mention that Equation (37) has a non-vanishing value of the trace. In addition, the mimetic field contributes in the field equations as

$${\tilde{\mathrm{T}}}_{\mu \nu }=-(G+2\Lambda -\stackrel{\mathrm{NL}}{\mathrm{T}}){\partial }_{\mu }\psi {\partial }_{\nu }\psi .$$

(38)

Similar to the linear electrodynamics case, the energy-momentum tensors, ${\stackrel{\mathrm{NL}}{\mathrm{T}}}_{\mu \nu }$ and ${\tilde{\mathrm{T}}}_{\mu \nu }$ are conserved, i.e., ${\nabla }^{\mu }{\stackrel{\mathrm{NL}}{\mathrm{T}}}_{\mu \nu }=0={\nabla }^{\mu }{\tilde{\mathrm{T}}}_{\mu \nu }$. Using Equations (2) and (38), we write the continuity equation of the mimetic field

$${\nabla }^{\nu }([G+2\Lambda -\stackrel{\mathrm{NL}}{\mathrm{T}}]{\partial }_{\nu }\psi )\equiv \frac{1}{\sqrt{-g}}{\partial }_{\nu }\left(\sqrt{-g}[G+2\Lambda -\stackrel{\mathrm{NL}}{\mathrm{T}}]g^{\nu \sigma }{\partial }_{\sigma }\psi \right)=0.$$

(39)

It is useful to give the trace of Equation (35) which has the form

$$(G+2\Lambda -\stackrel{\mathrm{NL}}{\mathrm{T}})(1+g^{\mu \nu }{\partial }_{\mu }\psi {\partial }_{\nu }\psi )=0.$$

(40)

As is clear, Equation (40) is satisfied identically, if Equation (2) is used. Since $G\ne 0$ or $\stackrel{\mathrm{NL}}{\mathrm{T}}\ne 0$, the mimetic theory at hand has non-trivial solutions and the conformal degree of freedom, remarkably, provides a dynamical quantity [83].

Now, we are going to apply the field Equations (35) and (36) to the spacetime metric (10) and get the following non-vanishing components:

$$\begin{array}{c}{I}_t{}^t=\frac{r{f}^{\prime }-2+f-r^2\mathcal{H}}{r^2}\equiv 0,\hfill \\ I_r{}^r=\frac{1}{{\varphi }^{\prime }{}^2{r}^2}\left\{[r{f}^{\prime }-1+f-r^2\mathcal{H}-r^{2}f{\psi }^{\prime }{}^2{f}^{″}+2f{\psi }^{\prime }{}^2\{2r^2\mathcal{H}+1-f-r{f}^{\prime }\}]{\varphi }^{″}-2r^{2}f{\varphi }^{\prime }{\psi }^{\prime }{}^2{\mathcal{H}}^{\prime }\right\}\equiv 0,\hfill \\ I_{\theta }{}^{\theta }=I_{\varphi }{}^{\varphi }=\frac{1}{2r{\varphi }^{″}}\left\{2{\varphi }^{″}{f}^{\prime }+r{f}^{″}{\varphi }^{″}+2r{\varphi }^{\prime }{\mathcal{H}}^{\prime }-2r{\varphi }^{″}\mathcal{H}\right\}\equiv 0.\hfill \end{array}$$

(41)

In Equation (41), $\mathcal{H}\left(r\right)$ is the arbitrary function that represents the effect of the non-linear electrodynamics and $\varphi \left(r\right)$ (Please note that in the non-linear electrodynamics case the electromagnetic field is defined as $P_{\mu \nu }=A_{\mu ,\nu }-A_{\nu ,\mu }$ where A is the gauge potential which in this study has the form $A_{\mu }=\varphi \left(r\right)dt$) is an unknown function reproducing the electric charge of the of the electromagnetic field $P_{\mu \nu }$.

It is straightforward to show that the above system reduces to Equation (27) by setting $\mathcal{H}\left(r\right)=-{{\varphi }^{\prime }}^2/2$. The above system of differential equation has the following solution:

$$\mathcal{H}\left(r\right)=\frac{c_6}{r^4}-\frac{c_7{}^2}{r^6},\psi \left(r\right)=\frac{c_1}{r},\varphi \left(r\right)=\frac{c_8}{r},f\left(r\right)=\frac{3r^4+3c_9{r}^3-3c_6{r}^2+c_7{}^2}{3r^4},$$

(42)

where $c_i$, $i=6\cdots 9$ are constants. From the above solution, we can conclude that the non-linear electrodynamics consists of monopole and quadruple terms. Interestingly, the constant associated with the monopole is different from that appears in the quadrupole term. In this sense, one can get the form of the linear electrodynamics by setting the constant $c_7=0$. This can be seen from the calculation of the electric field

$$\begin{array}{c}\hfill E=F_{tr}={\mathcal{H}}_p{P}_{tr}.\end{array}$$

(43)

Using Equation (48) in Equation (43) one can get the electric field in the form

$$\begin{array}{c}\hfill E=\frac{4c_6}{c_{1}r}-\frac{2c_7{}^2}{c_1{r}^3},\end{array}$$

(44)

from which one can see that if the constant of the non linearity vanishing, i.e., $c_7=0$ we get the usual linear Maxwell field after some re-parametrization.

It is of interest to note that Equation (42) satisfies Equation (40). Moreover, it is worth mentioning that Equation (42) is an exact solution of the non-linear Maxwell-mimetic gravitational theory that is given by Equations (35) and (36). The line element corresponding to solution (42) has the form:

$$\begin{array}{c}d{s}^2=-\left\{\frac{3r^4+3c_9{r}^3-3c_6{r}^2+c_7{}^2}{3r^4}\right\}d{t}^2+\left\{\frac{3r^4}{3r^4+3c_9{r}^3-3c_6{r}^2+c_7{}^2}\right\}d{r}^2+r^2\left(d{\theta }^2+{\sin }^2\theta d{\varphi }^2\right).\end{array}$$

(45)

One can easily recognize that the spacetime (45) is asymptotically flat spacetime.

Now, we are going to apply the field Equations (35) and (36) to the spacetime metric (15) and the following non-vanishing components are obtained

$$\begin{array}{ccc}\hfill I_t{}^t& \equiv & {\displaystyle \frac{r{f}_1^{\prime }-1+f_1-r^2\mathcal{H}}{r^2}}=0,\hfill \\ \hfill I_r{}^r& \equiv & \frac{1}{2r^2{f}^2(f{\varphi }^{\prime }{f}_1^{\prime }-f_1{f}^{\prime }{\varphi }^{\prime }+2{\varphi }^{″}f{f}_1)}\{2r{f}_1{f}^{\prime }{f}_1^{\prime }{\varphi }^{\prime }+4r{f}_1{}^2{f}^{\prime }{\varphi }^{″}-2f_1^{\prime }{\varphi }^{\prime }-4f_1{\varphi }^{″}+2f{f}_1{f}_1^{\prime }{\varphi }^{\prime }+4f{f}_1{}^2{\varphi }^{″}-4{\psi }^{\prime }{}^{2}rf{f}_1{}^2[2f^{\prime }{f}_1^{\prime }{\varphi }^{\prime }\hfill \\ & & +4f_1{f}^{\prime }{\varphi }^{″}+f_1^{\prime }{}^2{\varphi }^{\prime }+2f{f}_1^{\prime }{\varphi }^{″}]+4{\psi }^{\prime }{}^{2}f{f}_1\left[f_1^{\prime }{\varphi }^{\prime }+2f_1{\varphi }^{″}-f{f}_1{f}_1^{\prime }{\varphi }^{\prime }-2rf{f}_1{f}_1^{\prime }{\varphi }^{″}+f_1^{\prime }{\varphi }^{\prime }+2f{f}_1{\varphi }^{″}-f{f}_1{f}_1^{\prime }{\varphi }^{\prime }-2f{f}_1{}^2{\varphi }^{″}\right]\hfill \\ & & -{\psi }^{\prime }{}^2{r}^{2}f{f}_1[f_1{}^2{f}^{\prime }{}^2{\varphi }^{″}+2f{f}_1{f}^{\prime }{f}_1^{\prime }{\varphi }^{″}+2f_1{f}_1^{\prime }{f}^{″}{\varphi }^{\prime }+4f_1{}^2{f}^{″}{\varphi }^{″}]+8{\psi }^{\prime }{}^2{r}^{2}f{f}_1[r\mathcal{H}{f}_1^{\prime }{\varphi }^{\prime }+2r{f}_1\mathcal{H}{\varphi }^{″}-r{f}_1{\varphi }^{\prime }{\mathcal{H}}^{\prime }]-2r^2\mathcal{H}{f}_1^{\prime }{\varphi }^{\prime }\hfill \\ & & -4r^2{f}_1\mathcal{H}{\varphi }^{″}\}=0,\hfill \\ \hfill I_{\theta }{}^{\theta }& \equiv & I_{\varphi }{}^{\varphi }={\displaystyle \frac{1}{2r^2{f}^2(f{\varphi }^{\prime }{f}_1^{\prime }-f_1{f}^{\prime }{\varphi }^{\prime }+2{\varphi }^{″}f{f}_1)}}\{4f^2{f}_1{f}^{\prime }{f}_1^{\prime }{\varphi }^{\prime }+8f_1{}^2{f}^{\prime }{\varphi }^{″}+2f{f}_1{}^2{f}^{\prime }{}^2{\varphi }^{″}+4f{f}_1{f}_1^{\prime }{\varphi }^{″}+r{f}^{\prime }{f}_1^{\prime }{}^2{\varphi }^{\prime }+2f_1{f}^{\prime }{f}_1^{\prime }{\varphi }^{″}\hfill \\ & & +2r{f}_1{f}_1^{\prime }{f}^{″}{\varphi }^{\prime }+4r{f}_1{}^2{f}^{″}{\varphi }^{″}+8r{f}_1{\varphi }^{\prime }{\mathcal{H}}^{\prime }-4r\mathcal{H}{f}_1^{\prime }{\varphi }^{\prime }-8r{f}_1\mathcal{H}{\varphi }^{″}\}=0.\hfill \end{array}$$

(46)

It is straightforward to show that the above system reduces to (24) by setting $\mathcal{H}\left(r\right)=-{{\varphi }^{\prime }}^2{f}_1/2f$. The solution of Equation (46) has the same form given by Equation (42) in which $f\left(r\right)=f_1\left(r\right)$.

Now we are going to apply the field Equations (35) and (36) to the spacetime metric (25) and get the non-vanishing components:

$$\begin{array}{c}{I}_t{}^t\equiv {\displaystyle \frac{2r{f}^{\prime }+2f+r^2\Lambda -2r^2\mathcal{H}}{2r^2}}=0,\hfill \\ I_r{}^r\equiv {\displaystyle \frac{1}{2{\varphi }^{\prime }{}^2{r}^2}}\left\{[2r{f}^{\prime }+2f+r^2\Lambda -2r^2\mathcal{H}-2r^{2}f{\psi }^{\prime }{}^2{f}^{″}+4f{\psi }^{\prime }{}^2\{2r^2\mathcal{H}-f-2r{f}^{\prime }-r^2\Lambda \}]{\varphi }^{″}-4r^{2}f{\varphi }^{\prime }{\psi }^{\prime }{}^2{\mathcal{H}}^{\prime }\right\}=0,\hfill \\ I_{\theta }{}^{\theta }=I_{\varphi }{}^{\varphi }={\displaystyle \frac{1}{2r{\varphi }^{″}}}\left\{2{\varphi }^{″}{f}^{\prime }+r{f}^{″}{\varphi }^{″}+2r{\varphi }^{\prime }{\mathcal{H}}^{\prime }-2r{\varphi }^{″}\mathcal{H}+r{\varphi }^{″}\Lambda \right\}=0.\hfill \end{array}$$

(47)

It is straightforward to show that the above system reduces to Equation (27) by setting $\mathcal{H}\left(r\right)=-{{\varphi }^{\prime }}^2/2$. Equation (47) has the following solution:

$$\mathcal{H}\left(r\right)=\frac{c_6}{r^4}-\frac{c_7{}^2}{r^6},\psi \left(r\right)=\frac{c_1}{r},\varphi \left(r\right)=\frac{c_8}{r},f\left(r\right)=\frac{6c_9{r}^3-6c_6{r}^2-\Lambda r^6+2c_7{}^2}{6r^4},$$

(48)

where $c_6$ and $c_7$ are constants. From the above solutions, we can conclude that the non-linear electrodynamics consists also of monopole, and quadrupole terms. Interestingly, the constant associated with the monopole is different from that appears in the quadrupole terms. In this sense, one can get the form of the linear electrodynamics by setting the constant $c_7=0$. The form of the Maxwell field in this case is given by Equation (44).

On the other hand, the mimetic field $\psi \left(r\right)$ is not constant in this case. It is of interest to note that Equation (48) is an exact solution to the non-linear Maxwell-mimetic gravitational theory that is given by Equations (35) and (36) as well as to the trace given by Equation (40). The line element corresponding to the solution (48) is given by

$$\begin{array}{c}d{s}^2=-\left\{\frac{6c_9{r}^3-6c_6{r}^2-\Lambda r^6+2c_7{}^2}{6r^4}\right\}d{t}^2+\left\{\frac{6r^4}{6c_9{r}^3-6c_6{r}^2-\Lambda r^6+2c_7{}^2}\right\}d{r}^2+r^2\left(d{\theta }^2+d{z}^2\right),\end{array}$$

(49)

which behaves asymptotically as (A)dS spacetime.

Now we are going to apply the field Equations (35) and (36) to the spacetime metric (30) and get the following non-vanishing components

$$\begin{array}{ccc}\hfill I_t{}^t& \equiv & \frac{2r{f}_1^{\prime }-1+2f_1+r^2\Lambda -2r^2\mathcal{H}}{r^2}=0,\hfill \\ \hfill I_r{}^r& \equiv & {\displaystyle \frac{1}{2r^2{f}^2(f{\varphi }^{\prime }{f}_1^{\prime }-f_1{f}^{\prime }{\varphi }^{\prime }+2{\varphi }^{″}f{f}_1)}}\{8r^2{f}_1{}^2{f}^3{\mathcal{H}}^{\prime }{\varphi }^{\prime }{\psi }^{\prime }{}^2-2r{f}^2{f}_1{f}^{\prime }{f}_1^{\prime }{\varphi }^{\prime }+4r{f}^3{f}_1{\psi }^{\prime }{}^2{f}_1^{\prime }{}^2{\varphi }^{\prime }-4rf{f}_1{}^3{\psi }^{\prime }{}^2{f}^{\prime }{}^2{\varphi }^{\prime }+8r{f}^2{f}_1{}^3{\psi }^{\prime }{}^2{f}^{\prime }{\varphi }^{″}\hfill \\ & & +4r^2{f}^2{f}_1{}^3{\psi }^{\prime }{}^2{f}^{″}{\varphi }^{″}-2r^{2}f{f}_1{}^3{\psi }^{\prime }{}^2{f}^{\prime }{\varphi }^{″}+8{\psi }^{\prime }{}^2{r}^2{f}_1{}^2{f}^3\Lambda {\varphi }^{″}-16{\psi }^{\prime }{}^2{r}^2{f}_1{}^2{f}^3\mathcal{H}{\varphi }^{″}+8{\psi }^{\prime }{}^{2}r{f}_1{}^2{f}^3{f}_1^{\prime }{\varphi }^{″}-4r{f}_1{}^2{f}^2{f}^{\prime }{\varphi }^{″}\hfill \\ & & +4{\psi }^{\prime }{}^2{f}_1{}^2{f}^3{f}_1^{\prime }{\varphi }^{\prime }-4{\psi }^{\prime }{}^2{f}_1{}^3{f}^2{f}^{\prime }{\varphi }^{\prime }+r^2{f}_1{}^3{f}^{\prime }{}^3{\varphi }^{\prime }{\psi }^{\prime }{}^2+8{\psi }^{\prime }{}^2{f}_1{}^3{f}^3{\varphi }^{″}+4r^2{f}^3{f}_1\mathcal{H}{\varphi }^{″}-2r^2{f}^3{f}_1\Lambda {\varphi }^{″}+{\psi }^{\prime }{}^2{r}^2{f}_1{f}^2{f}^{\prime }{f}_1^{\prime }{\varphi }^{\prime }\hfill \\ & & -2{\psi }^{\prime }{}^2{r}^2{f}_1{}^{2}f{f}^{\prime }{}^2{f}_1^{\prime }{\varphi }^{\prime }+4{\psi }^{\prime }{}^2{r}^2{f}_1{f}^3\Lambda f_1^{\prime }{\varphi }^{\prime }-4{\psi }^{\prime }{}^2{r}^2{f}_1{}^2{f}^2\Lambda f^{\prime }{\varphi }^{\prime }-8{\psi }^{\prime }{}^2{r}^2{f}_1{f}^3\mathcal{H}{f}_1^{\prime }{\varphi }^{\prime }+8{\psi }^{\prime }2r^2{f}^2{f}_1{}^2\mathcal{H}{f}^{\prime }{\varphi }^{\prime }\hfill \\ & & +2{\psi }^{\prime }{}^2{r}^2{f}^2{f}_1{}^2{f}^{\prime }{f}_1^{\prime }{\varphi }^{″}+2{\psi }^{\prime }{}^2{r}^2{f}^2{f}_1{}^2{f}^{″}{f}_1^{\prime }{\varphi }^{\prime }-2{\psi }^{\prime }{}^2{r}^2{f}_1{}^{3}f{f}^{″}{f}^{\prime }{\varphi }^{\prime }-4f^3{f}_1{}^2{\xi }^{″}+r^2\Lambda f^2{f}_1{f}^{\prime }{\varphi }^{\prime }-2r^2{f}^2{f}_1\mathcal{H}{f}^{\prime }{\varphi }^{\prime }+2r^2{f}^3\mathcal{H}{f}_1^{\prime }{\varphi }^{\prime }\hfill \\ & & -r^2\Lambda f^3{f}_1^{\prime }{\varphi }^{\prime }+2rf{f}_1{}^2{f}^{\prime }{}^2{\varphi }^{\prime }-2f^3{f}_1{f}_1^{\prime }{\varphi }^{\prime }+2f^2{f}_1{}^2{f}^{\prime }{\varphi }^{\prime }\}=0,\hfill \\ \hfill I_{\theta }{}^{\theta }& \equiv & I_{\varphi }{}^{\varphi }={\displaystyle \frac{1}{2r{f}^2(f_1{\varphi }^{\prime }{f}^{\prime }-f_1^{\prime }f{\varphi }^{\prime }-2{\varphi }^{″}f{f}_1)}}\{2f{f}_1{}^2{f}^{\prime }{}^2{\varphi }^{\prime }-4f^2{f}_1{}^2{f}^{\prime }{\varphi }^{″}-2f^3{f}_1^{\prime }{}^2{\varphi }^{\prime }-4f^3{f}_1{f}_1^{\prime }{\varphi }^{″}-r{f}^2{f}^{\prime }{f}_1{}^2{\varphi }^{\prime }+2rf{f}_1{f}^{\prime }{}^2{f}_1^{\prime }{\varphi }^{\prime }\hfill \\ & & -2r{f}^2{f}_1{f}^{\prime }{f}_1^{\prime }{\varphi }^{″}-2r{f}^2{f}_1{f}^{″}{f}_1^{\prime }{\varphi }^{\prime }+2r{f}_1{}^{2}f{f}^{″}{f}^{\prime }{\varphi }^{\prime }-4r{f}^2{f}_1{}^2{f}^{″}{\varphi }^{″}-r{f}_1{}^2{f}^{\prime }{}^3{\varphi }^{\prime }+2r{f}_1{}^2{f}^{\prime }{}^2{\varphi }^{″}-2r{f}^3\Lambda f_1^{\prime }{\varphi }^{\prime }+2r{f}^2{f}_1{f}^{\prime }{\varphi }^{\prime }\hfill \\ & & -4r{f}^3{f}_1\Lambda {\varphi }^{″}-8r{f}^3{f}_1{\mathcal{H}}^{\prime }+4r{f}^3\mathcal{H}{f}_1^{\prime }{\varphi }^{\prime }-4r{f}^2{f}_1\mathcal{H}{f}^{\prime }{\varphi }^{\prime }+8r{f}^3{f}_1\mathcal{H}{\varphi }^{″}\}=0.\hfill \end{array}$$

(50)

The solution of the system of differential Equation (50) coincides with (48) in which $f\left(r\right)=f_1\left(r\right)$.

7. Features of the Non-Linear Electrodynamics Black Hole Solutions

Now we are going to discuss some relevant features of the charged black hole solutions presented in the previous section of the non-linear case.

Firstly, for the spherically symmetric spacetime the metric of solution (42) takes the form

$$d{s}^2=-\left\{\frac{r^4-2m{r}^3+q^2{r}^2+q_1{}^2}{r^4}\right\}d{t}^2+\left\{\frac{r^4}{r^4-2m{r}^3+q^2{r}^2+q_1{}^2}\right\}d{r}^2+r^2\left(d{\theta }^2+{\sin }^2\theta d{\varphi }^2\right).$$

(51)

where we have put $c_6=-q^2$, $c_7=\sqrt{3}{q}_1$ and $c_9=-2m$. Equation (51) shows clearly that the metric besides the Reissner-Nordström term, which represented by the monopole which proportional to $O\left(\frac{1}{r^2}\right)$, there is another term which is the quadruple term that is proportional to $O\left(\frac{1}{r^4}\right)$. It is important to note that Equation (51) is asymptotically behaves as a flat spacetime. By taking the limit $q\to 0$ and $q_1\to 0$ we get the Schwarzschild black hole and when $q_1\to 0$ we get Reissner-Nordström spacetime. The horizons of the metric (51) are given by the real positive roots of $\Gamma \left(r\right)=0$, where $\Gamma \left(r\right)=r^4-2m{r}^3+q{r}^2-q_1{}^2$, see [94]. For the model at hand, namely the spacetime metric (51), taking $x=r^2$, we find that the constraint $\Gamma \left(x\right)=0$ gives two positive real roots.

Secondly, in the flat horizon case, the spacetime metric of the black hole solution (48), takes the form

$$d{s}^2=-\left\{\frac{6q^2{r}^2-12m{r}^3-\Lambda r^6+6q_1{}^2}{6r^4}\right\}d{t}^2+\left\{\frac{6r^4}{6q^2{r}^2-12m{r}^3-\Lambda r^6+6q_1{}^2}\right\}d{r}^2+r^2\left(d{\theta }^2+d{z}^2\right).$$

(52)

where we have put $c_9=-2m$, $c_6=-q^2$ and $c_7=\sqrt{3}{q}_1$. Equation (52) indicates that the metric of the charged black hole in the non-linear Maxwell case is different from Reissner-Nordström black hole. This difference is due to the existence of the quadruple term which is related to the constant $q_1$. When $q_1=0$, Equation (52) reduces to Reissner-Nordström case. It is of interest to note that the quadruple charged terms that appear in Equations (51) and (52) are reproduced from the arbitrary function, $\mathcal{H}$(r), which characterizes the non-linear electrodynamics. By taking the limit $q_1\to 0$, the solution goes to the (A)dS charged black hole of the linear case. Additionally by taking $x=r^3$, similar to the spherically symmetric case, we find that the constraint $\Gamma \left(x\right)=0$ has three positive real roots.

Next, we discuss some physical properties of the solutions (42) and (48) by investigating the singularity behaviors and their stabilities.

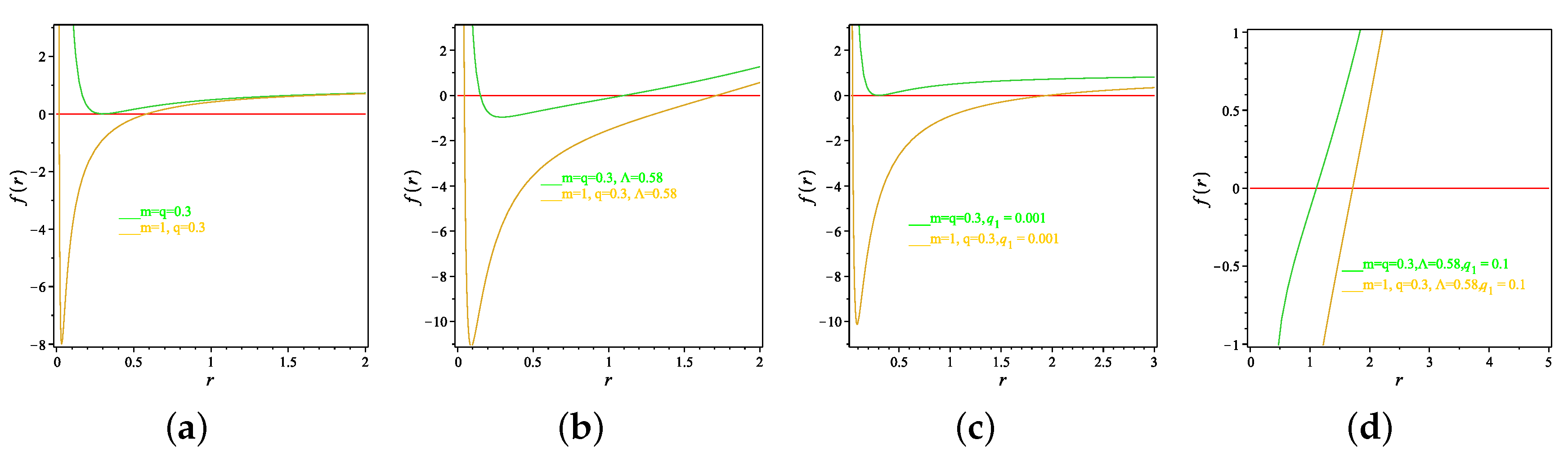
7.1. Visualization of Black Holes Singularities

We investigate the physical singularities by calculating some of the curvature invariants in the non-linear electrodynamics, see (42) and (48). For those solutions we evaluate the scalar invariants and get

$$\begin{array}{cc}\mathrm{solution}\left(42\right)& R^{\mu \nu \lambda \rho }{R}_{\mu \nu \lambda \rho }=\frac{96q^2{r}^{5}m-312r^2{q}^2{q}_1{}^2-240m{r}^3{q}_1+48m^2{r}^6+56q^4{r}^4+468q_1{}^2}{r^{12}},\hfill \\ & R^{\mu \nu }{R}_{\mu \nu }=\frac{4r^4{q}^4-36r^2{q}^2{q}_1+90q_1{}^2}{r^{12}},R=-\frac{6q_1}{r^6},\hfill \\ \mathrm{solution}\left(48\right)& R^{\mu \nu \lambda \rho }{R}_{\mu \nu \lambda \rho }=\frac{2(72m^2{r}^6+84r^4{q}^4+r^2{\Lambda }^2-468r^2{q}^2{q}_1+144r^{5}m{q}^2-360r^{3}m{q}_1-6r^6{q}_1\Lambda +702q_1{}^2)}{r^{12}},\hfill \\ & R^{\mu \nu }{R}_{\mu \nu }=\frac{4r^4{q}^4+{\Lambda }^2{r}^{12}-36r^2{q}^2{q}_1{}^2-6r^6{q}_1\Lambda +90q_1{}^2}{r^{12}},R=\frac{2(\Lambda r^6-3q_1)}{r^6}.\hfill \end{array}$$

(53)

As is clear that all invariants have true singularities at $r=0$. Remarkably, at the limit $r\to 0$, the behaviours of the Kretschmann scalars, the Ricci tensor square and the Ricci scalars of the non-linear charged black hole solutions are given as $K=R_{\mu \nu }{R}^{\mu \nu }\sim r^{-12}$, $R\sim r^{-6}$ in contrast with the solutions, (18), (22) and (28), of the linear Maxwell mimetic theory which have $K=R_{\mu \nu }{R}^{\mu \nu }\sim r^{-8}$ and $R\sim r^0$. This shows clearly that the singularities in the non-linear electrodynamics case are stronger than that obtained in the linear Maxwell mimetic gravity case. Notably, one may check if geodesics are extendible beyond these regions. According to Tipler and Krolak [95,96], this indicates the strength of the singularity. This topic will be discussed in forthcoming studies.

7.2. Energy Conditions

Energy conditions are critical tools to understand cosmological models and/or strong gravitational fields. We are interested in this study to investigate the energy conditions of the non-linear electrodynamics case, since the linear case is well known in the GR theory. The Energy conditions are arranged into four categories: The strong energy (SEC), the weak energy (WEC), the null energy (NEC) and the dominant energy conditions [1,97]. To satisfy these conditions, the inequalities below must be fulfilled

$$\begin{array}{c}\mathrm{SEC}:\rho +p_r\ge 0,\rho +p_r+2p_t\ge 0,\hfill \\ \mathrm{WEC}:\rho \ge 0,\rho +p_r\ge 0,\rho +p_t\ge 0,\hfill \\ \mathrm{NEC}:\rho +p_r\ge 0,\rho +p_t\ge 0,\hfill \\ \mathrm{DEC}:\rho \ge |p_r|,\rho \ge |p_t|,\hfill \end{array}$$

(54)

where $\stackrel{\mathrm{NL}}{\mathrm{T}}{}_0{}^0=\rho$, $\stackrel{\mathrm{NL}}{\mathrm{T}}{}_1{}^1=p_r$ and $\stackrel{\mathrm{NL}}{\mathrm{T}}{}_2{}^2=\stackrel{\mathrm{NL}}{\mathrm{T}}{}_3{}^3=p_t$ are the density, radial and tangential pressures, respectively. Using Equations (42) and (48) in Equation (54) we get

$$\begin{array}{c}\mathrm{SEC}:\rho +p_r=\frac{r^2{q}^2-3q_1{}^2}{r^6}>0,\rho +p_r+2p_t=\frac{3q_1{}^2}{r^6}>0,\hfill \\ \mathrm{WEC}:\rho =\frac{r^2{q}^2-3q_1{}^2}{2r^6}>0,\rho +p_r=\frac{r^2{q}^2-3q_1{}^2}{r^6}>0,\rho +p_t=\frac{3q_1{}^2}{2r^6}>0,\hfill \\ \mathrm{NEC}:\rho +p_r=\frac{r^2{q}^2-3q_1{}^2}{r^6}>0,\rho +p_t=\frac{3q_1{}^2}{2r^6}>0,\hfill \\ \mathrm{DEC}:\rho \ge |p_r|\left(\mathrm{satisfied}\right),\rho \ge |p_t|\left(\mathrm{satisfied}\right).\hfill \end{array}$$

(55)

From this we see that all the energy conditions can be satisfied, given $\varphi >{\varphi }_1$.

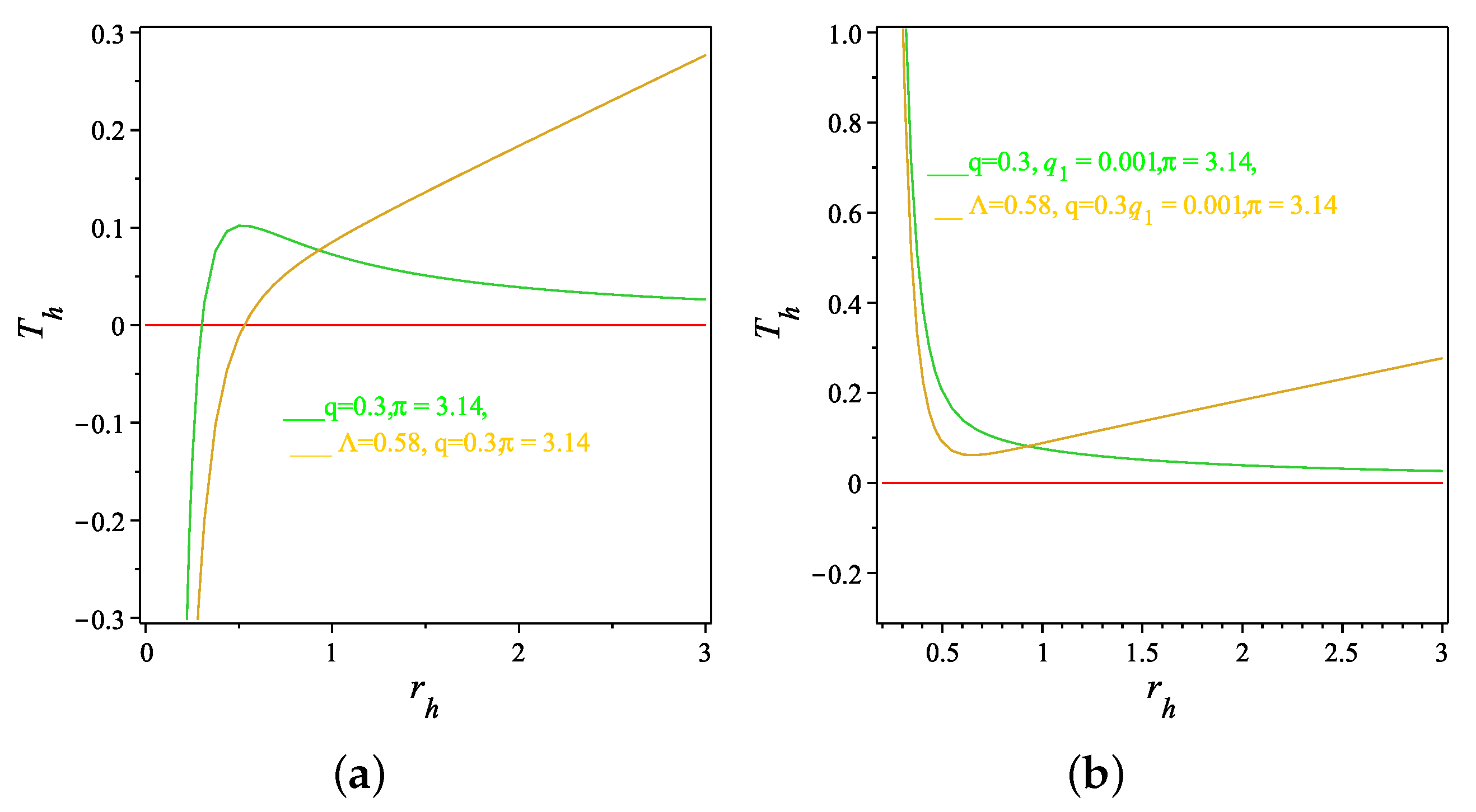
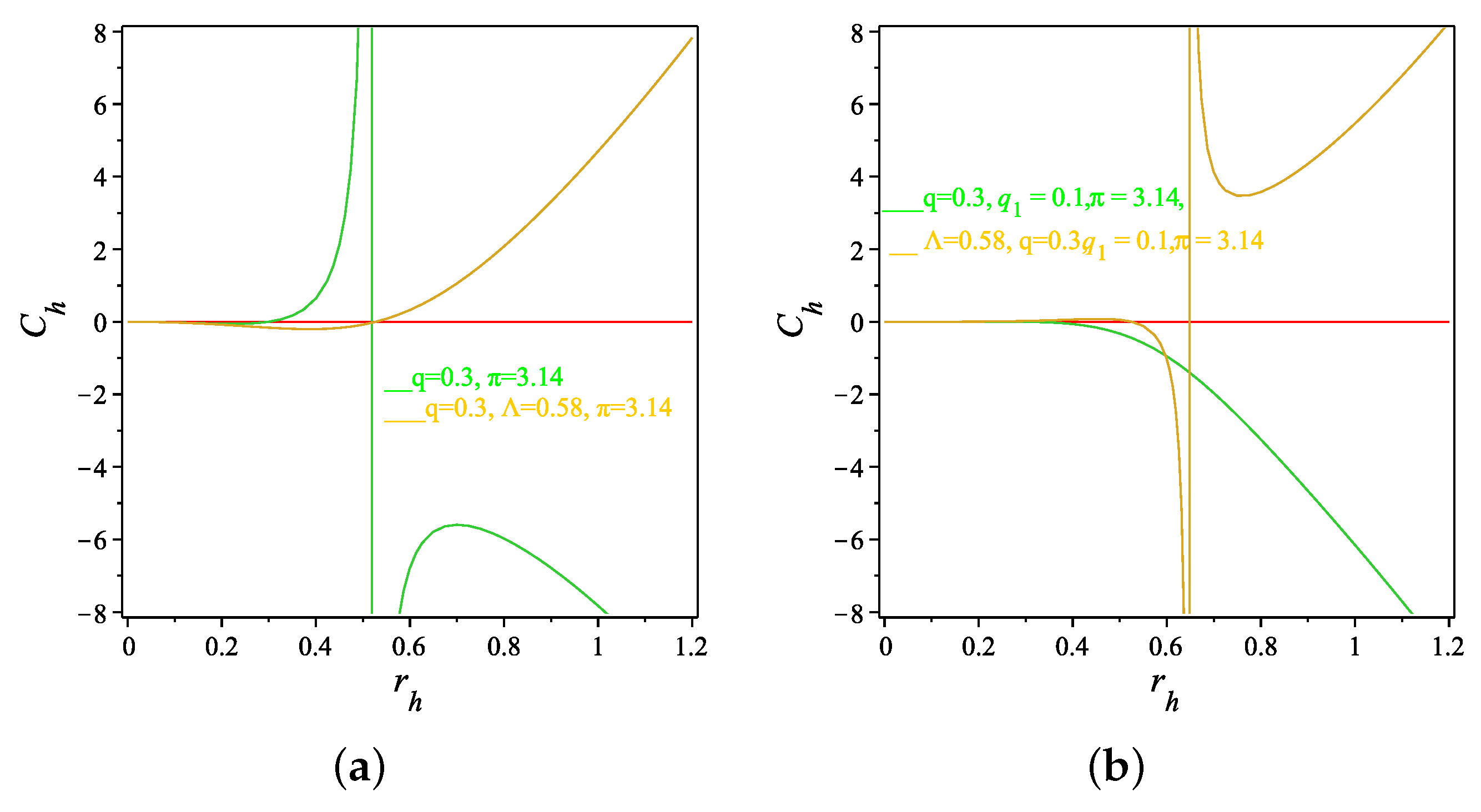
8. Thermodynamical Stability and Phase Transition

One of the most exciting topics in physics is the black hole thermodynamics. Two approaches have been constructed to extract the thermodynamical quantities of the black holes. The first approach, which was given by Gibbons and Hawking [98,99], was to study the thermal properties of the Schwarzschild black hole solution through the use of the Euclidean continuation. In the second approach one has to identify the horizon then define the temperature and finally study the thermodynamical stability of the black hole [100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124]. In this study, we will follow the second approach to study the thermodynamics of the black holes derived in Equations (22), (28), (42) and (48) then analyze their thermodynamical stability. It is of interest to mention here that these black holes are characterized by the mass, m, the charges (monopole, q and quadrupole, $q_1$) and also by the cosmological constant $\Lambda$.

The calculations of the horizons, of the Maxwell electrodynamics cases given by Equations (22) and (28) and the non-linear electrodynamics cases given by Equations (42) and (48), are carried out by finding the roots of the unknown function $f\left(r\right)=0$ which can be seen for specific values of the parameters which characterized the model. The plots of Figure 1 show that the two roots of $f\left(r\right)$ which determine the black hole are the inner $r_h$ and the cosmological $r_c$ horizons. It is of interest to note that, for solutions (22), (28), when $m>0$, $q>0$ and $\Lambda >0$, one can show that the two roots are possible when $m>m_{min}=q$ for solution (22), $m>m_{min}={(32q^6\Lambda /81)}^{1/4}$ for solution (28) and for the non-linear case $q_1>q_{min}=(1/6)\sqrt{(}3)q^2$ for solution (42). The most interesting thing is when $m=m_{min}$, or $q_1=q_{min}$ and one can determine the degenerate horizons $r_{dg}=q,{(32q^6\Lambda /81)}^{1/4},(1/6)\sqrt{3}{q}^2$ at which $r_h=r_c$, which is the Nariai black hole. When $m<m_{min}$ or $q_1<q_{min}$, there is no black hole formulation.

We define the Bekenstein-Hawking entropy as

$$S\left(r_h\right)=\frac{1}{4}A=\pi r_h{}^2,$$

(56)

where $r_h$ is the event horizon in units of the Planck area and A is the area of the event horizon. To check the thermodynamical stability of a black hole we have to know the sign of its heat capacity $C_h$. In the following, we investigate the thermal stability of the black hole solutions by means of the behavior of their heat capacities at fixed mass which is defined as [103,104,105,106,107].

$$C_h=\frac{\partial m}{\partial r_h}{\left(\frac{\partial r_h}{\partial T}\right)}_m.$$

(57)

In the event horizon, if the heat capacity has a positive value, i.e., $C_h>0$, then the black hole has a stable region and if ($C_h<0$) then the black hole has an unstable region.

To calculate Equation (57), we must derive analytical forms of $m_h\equiv m\left(r_h\right)$ and $T_h\equiv T\left(r_h\right)$. Let us begin with the calculations of the black hole mass inside the even horizon $r_h$. When we set $f\left(r_h\right)=0$, and get

$$\begin{array}{c}{m_h}_{{}_{{}_{{}_{{}_{Equation\left(22\right)}}}}}=\frac{r_h}{2}(1+\frac{q^2}{r_h{}^2}),\hfill \\ {m_h}_{{}_{{}_{{}_{{}_{Equation\left(28\right)}}}}}=\frac{r_h}{2}(\frac{q^2}{r_h{}^2}-\frac{\Lambda r_h{}^2}{6})\hfill \\ {m_h}_{{}_{{}_{{}_{{}_{Equation\left(42\right)}}}}}=\frac{r_h}{2}(1+\frac{q^2}{r_h{}^2}+\frac{q_1{}^2}{r_h{}^4})\hfill \\ {m_h}_{{}_{{}_{{}_{{}_{Equation\left(48\right)}}}}}=\frac{r_h}{2}(\frac{q^2}{r_h{}^2}+\frac{q_1{}^2}{r_h{}^4}-\frac{\Lambda r_h{}^2}{6}).\hfill \end{array}$$

(58)

The total mass as a function of the event horizon and charge is represented in Figure 2. As seen from Figure 2, the black hole mass curve in the horizon radius shows one common property

$$m(r_h\to 0)\to \infty ,m(r_h\to \infty )\to \infty .$$

(59)

The Hawking temperature of the black holes can be derived by demanding that the singularity at the horizon in the Euclidean sector of the black hole solutions disappears. Alternatively, we can obtain the associated temperature in the event horizon $r=r_h$ as [108]

$$T=\frac{\kappa }{2\pi },\mathrm{with}\kappa \mathrm{being}\mathrm{the}\mathrm{surface}\mathrm{gravity}\mathrm{defined}\mathrm{as}\kappa =\frac{f^{\prime }\left(r_h\right)}{2}.$$

(60)

The Hawking temperatures associated with the black hole solutions (22), (28), (42) and (48) are and get

$$\begin{array}{c}{T_h}_{{}_{{}_{{}_{{}_{Equation\left(22\right)}}}}}=\frac{1}{4r_h{}^3\pi }\left(r_h{}^2-q^2\right),\hfill \\ {T_h}_{{}_{{}_{{}_{{}_{Equation\left(28\right)}}}}}=-\frac{1}{8r_h{}^3\pi }\left(\Lambda r_h{}^4+2q^2\right),\hfill \\ {T_h}_{{}_{{}_{{}_{{}_{Equation\left(42\right)}}}}}=\frac{1}{4r_h{}^5\pi }\left(r^4-r_h{}^2{q}^2-3q_1{}^2\right),\hfill \\ {T_h}_{{}_{{}_{{}_{{}_{Equation\left(48\right)}}}}}=-\frac{1}{8r_h{}^5\pi }\left(\Lambda r_h{}^6+2r_h{}^2{q}^2+6q_1{}^2\right),\hfill \end{array}$$

(61)

where $T_h$ is the Hawking temperature at the event horizon. This show that there exists a radius $r_{min}$ at which $T_h$ vanishes, while the ultracold black holes are being characterized by the regions $r_h<r_{min}$ where $T_h$ goes below the absolute zero. Including the gravitational effect of thermal radiation, one can show that at some very high temperature $T_{max}$ the radiation would become unstable and collapse to a black hole [109]. Hence, the pure (A)dS solution is only stable at temperatures $T<T_{max}$ as is clear from Figure 3. Above $T_{max}$, only the heavy black holes would have stable configurations [109].

Next we evaluate the heat capacity by substituting Equations (58) and (61) into Equation (57) and get

$$\begin{array}{c}{C_h}_{{}_{{}_{{}_{{}_{Equation\left(22\right)}}}}}=\frac{2r_h{}^2\pi \left(r_h{}^2-q^2\right)}{3q^2-r_h{}^2},\hfill \\ {C_h}_{{}_{{}_{{}_{{}_{Equation\left(28\right)}}}}}=\frac{2r_h{}^2\pi \left(\Lambda r_h{}^4+q^2\right)}{\Lambda r_h{}^4-6q^2},\hfill \\ {C_h}_{{}_{{}_{{}_{{}_{Equation\left(42\right)}}}}}=\frac{4r_h{}^2\pi \left(r_h{}^4-q^2{r}_h{}^2-3q_1{}^2\right)}{3q^2{r}_h{}^2-r_h{}^4+15q_1{}^2},\hfill \\ {C_h}_{{}_{{}_{{}_{{}_{Equation\left(48\right)}}}}}=\frac{4r_h{}^2\pi \left(\Lambda r_h{}^6+2q^2{r}_h{}^2+6q_1{}^2\right)}{\Lambda r_h{}^6-6q^2{r}_h{}^2-30q_1{}^2}.\hfill \end{array}$$

(62)

It is not easy to extract information directly from Equation (62), therefore we plot them for particular values of the black hole parameters as shown in Figure 4. For solutions (22) and (28) a typical pattern of the heat capacity has been obtained in literature c.f. [110]. However, we find that the negative heat capacity region is associated with a positive temperature contrary to our case.

The free energy in the grand canonical ensemble which is called Gibbs free energy can be defined as [111]

$$G\left(r_h\right)=M\left(r_h\right)-T\left(r_h\right)S\left(r_h\right),$$

(63)

where $M\left(r_h\right)$, $T\left(r_h\right)$ and $S\left(r_h\right)$ are the mass of the black hole, the temperature and entropy at the event horizon, respectively. Using Equations (56), (58) and (61) in Equation (63) we get

$$\begin{array}{c}{G_h}_{{}_{{}_{{}_{{}_{Equation\left(22\right)}}}}}=\frac{r_h{}^2+3q^2}{4r_h},\hfill \\ {G_h}_{{}_{{}_{{}_{{}_{Equation\left(28\right)}}}}}=\frac{18q^2+\Lambda r_h{}^4}{24r_h},\hfill \\ {G_h}_{{}_{{}_{{}_{{}_{Equation\left(42\right)}}}}}=\frac{r_h{}^4+3r_h{}^2{q}^2+5q_1{}^2}{2r_h{}^3},\hfill \\ {G_h}_{{}_{{}_{{}_{{}_{Equation\left(48\right)}}}}}=\frac{\Lambda r_h{}^6+18r_h{}^2{q}^2+30q_1{}^2}{24r_h{}^3},.\hfill \end{array}$$

(64)

It is of interest to note that when the charge parameter $q\to 0$ the Gibb’s free energy of the spacetimes of Equations (22) and (28) will be coincident with that given in [112]. The behaviors of the Gibb’s energy of our black holes are presented in Figure 5a,b for particular values of the model parameters.

9. Discussion of the Main Results

In this research, we have studied the mimetic gravitational theory. We have applied a spherically symmetric spacetime with one unknown function to the field equations of the mimetic theory and have obtained a black hole solution which is not different from this obtained in orthodox general relativity, i.e., Schwarzschild spacetime. Then we have used another spherically symmetric spacetime with two unknown functions and have applied it to the mimetic theory including cosmological constant. We have derived a black hole solution that behaves like (A)dS spacetime. We repeated the same calculations to flat horizons spacetimes with one and two unknown functions and obtained the same well-known solutions derived in GR. All those solutions have dynamical mimetic field, i.e., $\psi \left(r\right)\ne constant$ because the field equations of the mimetic are not able to fix the mimetic field.

To go deep into these solutions we have investigated the singularity and have shown that all the invariants constructed from the curvature have a singularity at $r=0$. The asymptotic behavior of the Kretschmann invariant and the Ricci tensor squared and the Ricci scalar have the form $K=R_{\mu \nu }{R}^{\mu \nu }\sim r^{-8}$, $R\sim r^0$.

Next, we have derived the field equations of the mimetic field equations coupled with a non-linear electrodynamics. We have applied these field equations to the same spherically symmetric spacetimes used before. We derived a new charged spherically symmetric black hole that includes beside the monopole a quadrupole term. We repeated the same procedures to the flat horizon spacetime and also got a new black hole with monopole and quadrupole terms. To understand the physics of these black holes we studied the singularities. We have shown that the singularities of these black holes are stronger than those of GR. The deviation of singularities from GR is due to the presence of the quadrupole term whose non-linear arbitrary function is responsible for it. Are these strong singularities extendable? This will be studied elsewhere.

Also, we discussed some thermodynamical quantities of the non-linear black holes. We have shown that these black holes have two horizons, one is the inner horizon and the other is the cosmological one. We determine a minimum value of the black hole mass at which the two horizons coincide forming the degenerate horizon, above this minimum mass the black hole would have two horizons, below the minimum mass there is no black hole formation. Also, we have studied the thermodynamics of the black hole and analyzed its thermal phase transition based on the discontinuous change of the specific heat sign. As Figure 3b shows, in the non-linear case, the temperature drops below zero when $r_h<r_{min}$, while the black hole heat capacity is negative at these regions and so the black hole is unstable. Finally, we have studied the free energy of these spacetimes and have shown their pattern in Figure 5. As Figure 5b shows the non-linear charged black holes become more stable globally [113].