Monitoring the Variability in the Process Using Neutrosophic Statistical Interval Method
Abstract
:1. Introduction
2. Design of Proposed Control Chart
- For the fixed values of and , the range in indeterminacy interval of NARL increases as decreases from 300 to 370.
- For the fixed values of and , the range in indeterminacy interval of NARL decreases as increases.
- Step-1:
- Specify the indeterminacy interval of and .
- Step-2:
- Determine the indeterminacy interval of such that .
- Step-3:
- Find indeterminacy interval of using selected in Step-2.
3. Comparison Studies
3.1. Comparison by NARL
3.2. Comparison by Simulation
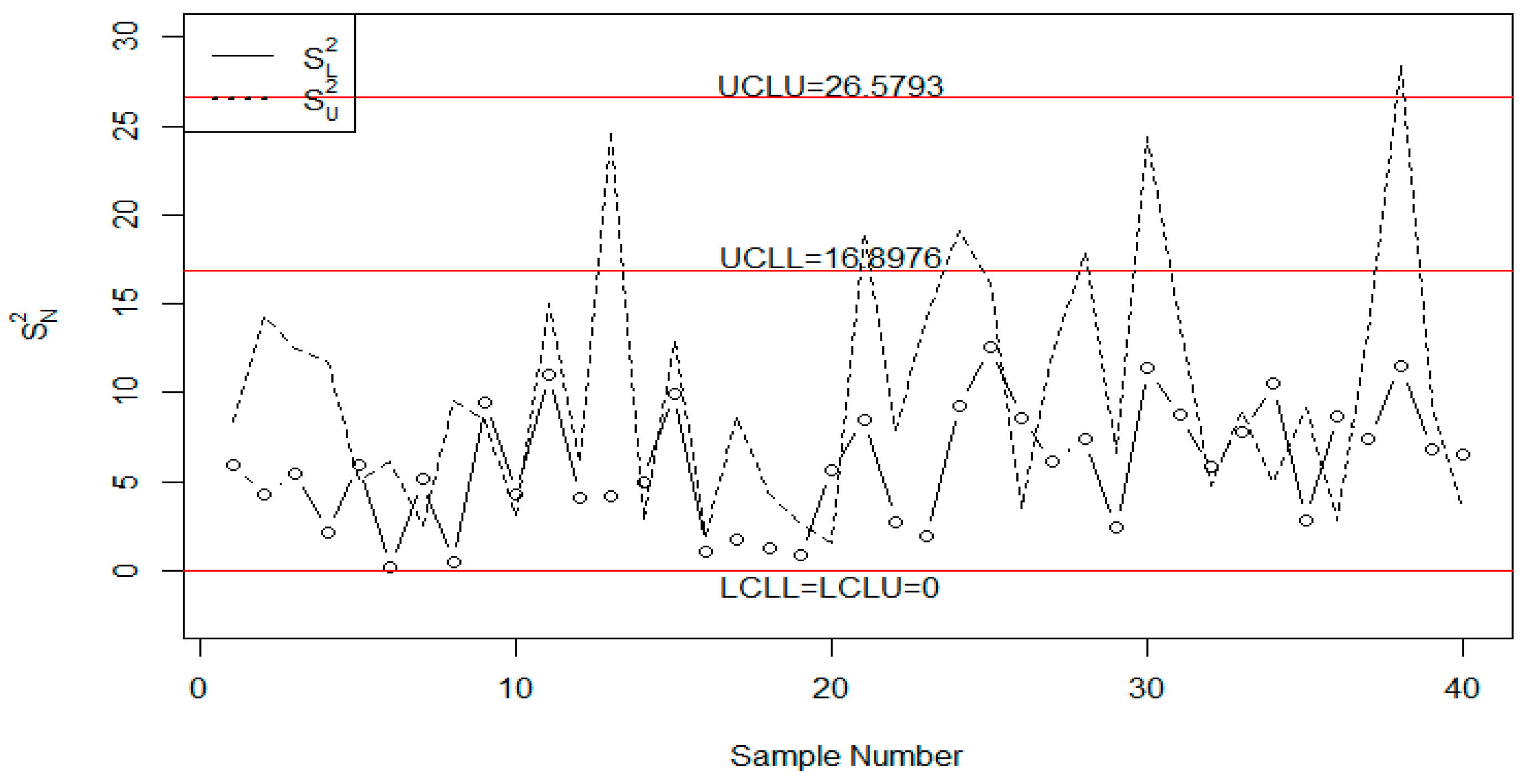
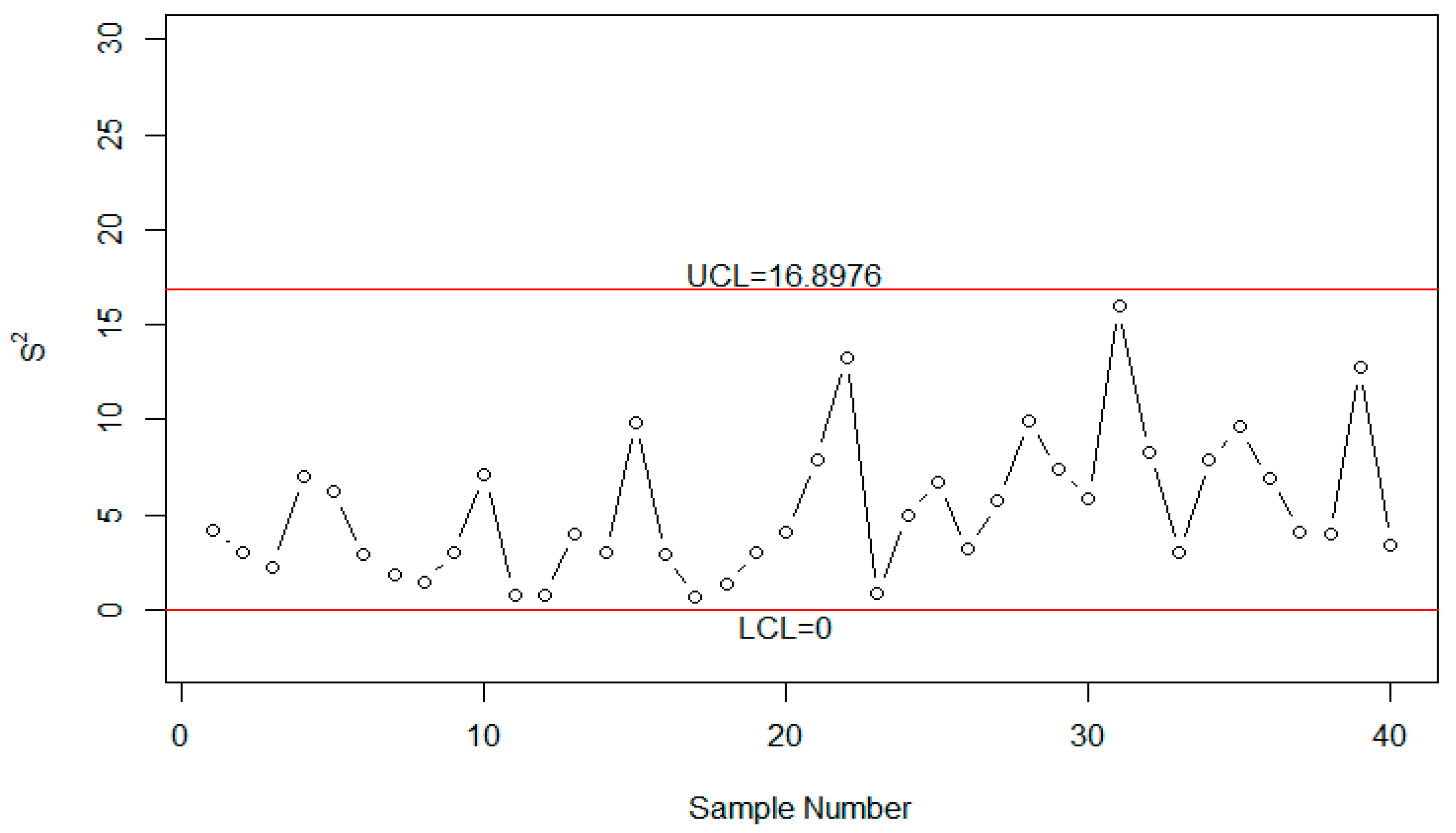
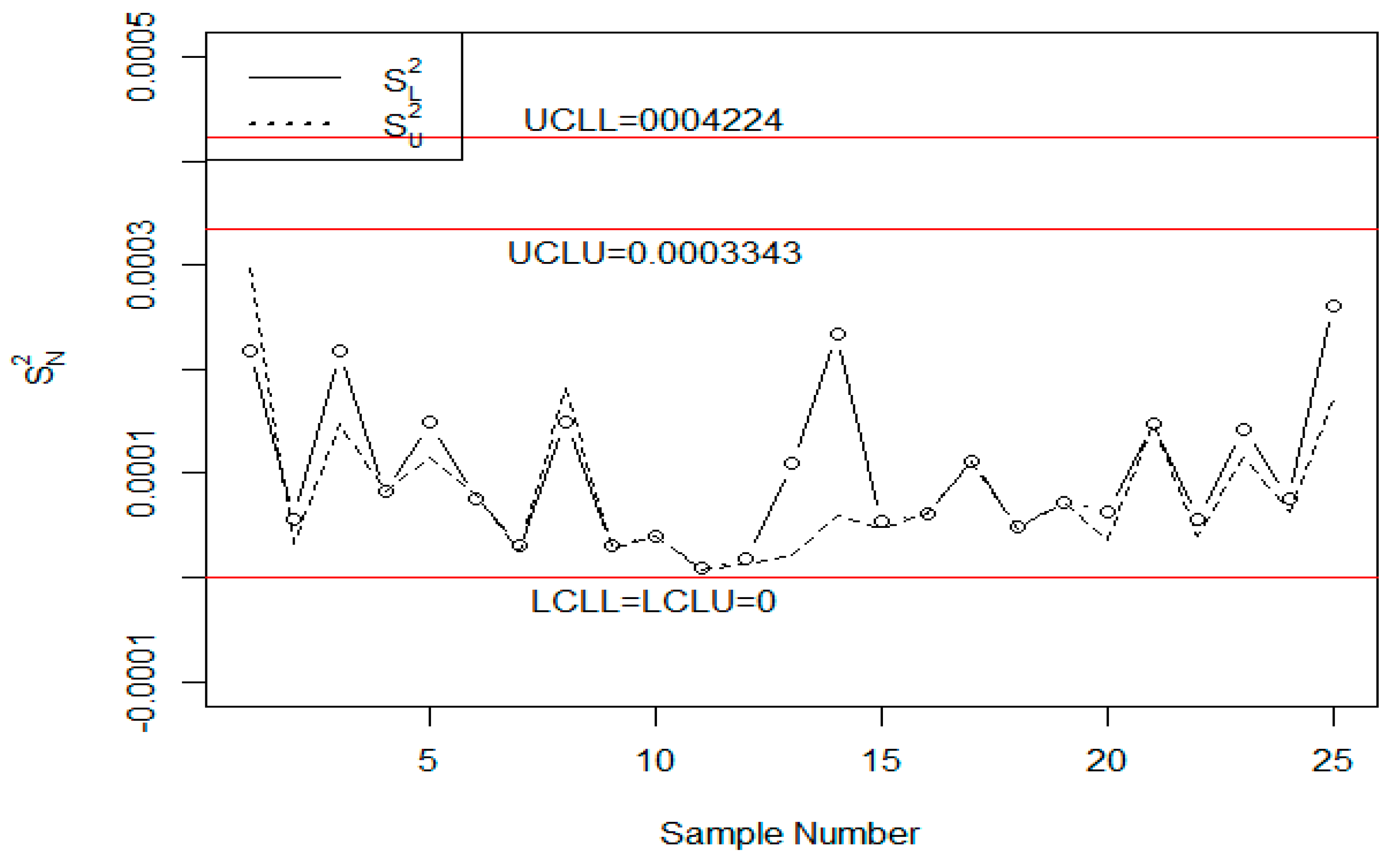
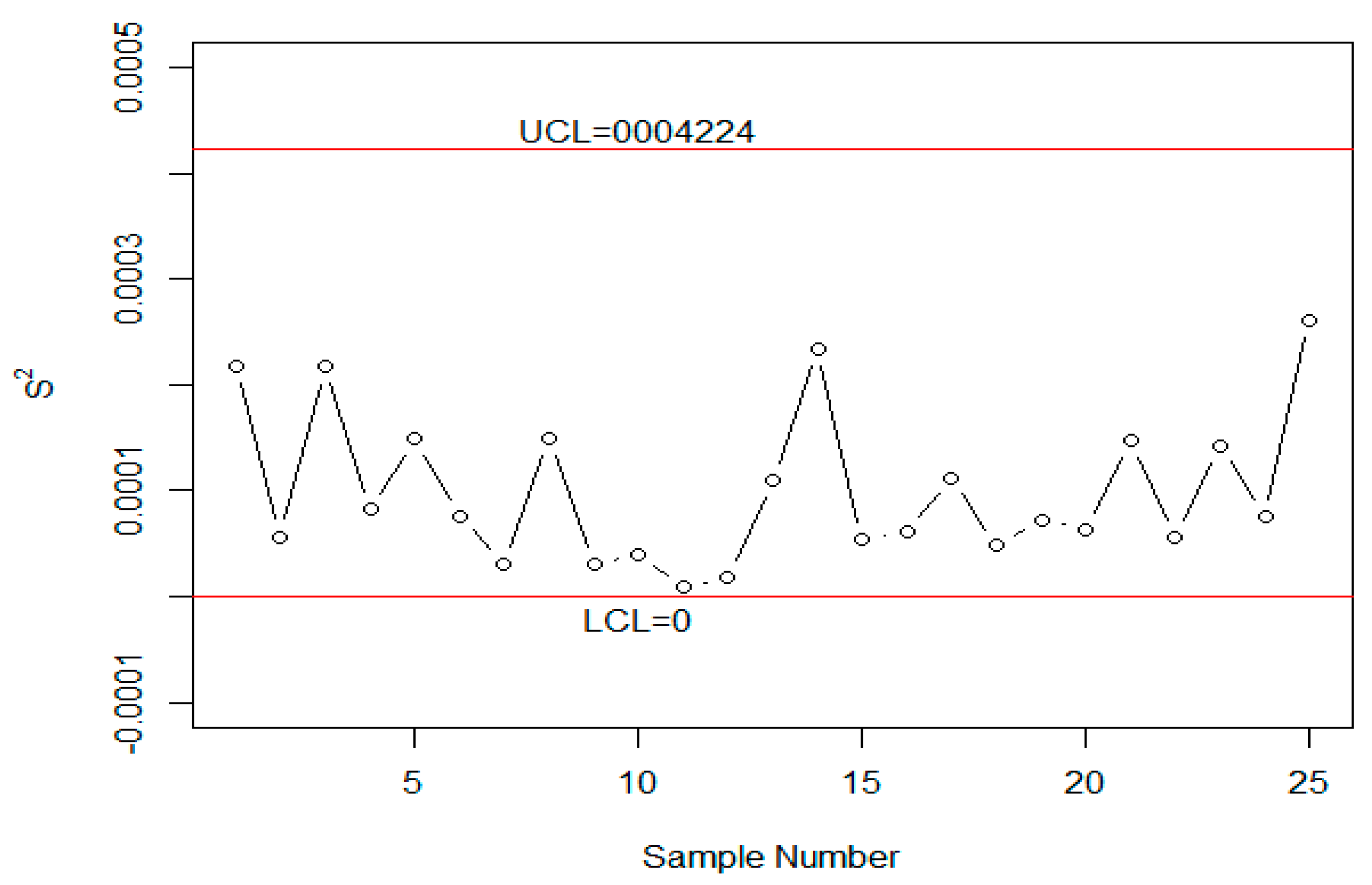
4. Case Study
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abbas, N.; Riaz, M.; Mahmood, T. An improved S2 control chart for cost and efficiency optimization. IEEE Access 2017, 5, 19486–19493. [Google Scholar] [CrossRef]
- RA, F. Statistical method from the viewpoint of quality control. Nature 1940, 146, 150. [Google Scholar]
- Khoo, M.B. S2 control chart based on double sampling. Int. J. Pure Appl. Math. 2004, 13, 249–258. [Google Scholar]
- Zhang, L.; Bebbington, M.; Lai, C.-D.; Govindaraju, K. On statistical design of the S2 control chart. Commun. Stat. Theory Methods 2005, 34, 229–244. [Google Scholar] [CrossRef]
- Khoo, M.B. A modified S chart for the process variance. Qual. Eng. 2005, 17, 567–577. [Google Scholar] [CrossRef]
- Lee, P.-H.; Chang, Y.-C.; Torng, C.-C. A design of S control charts with a combined double sampling and variable sampling interval scheme. Commun. Stat. Theory Methods 2012, 41, 153–165. [Google Scholar] [CrossRef]
- Riaz, M. A dispersion control chart. Commun. Stat. Simul. Comput. 2008, 37, 1239–1261. [Google Scholar] [CrossRef]
- Guo, B.; Wang, B.X. The design of the ARL-unbiased S2 chart when the in-control variance is estimated. Qual. Reliab. Eng. Int. 2015, 31, 501–511. [Google Scholar] [CrossRef]
- Zhang, G. Improved R and S control charts for monitoring the process variance. J. Appl. Stat. 2014, 41, 1260–1273. [Google Scholar] [CrossRef]
- Zadeh, L.A. Toward a generalized theory of uncertainty (GTU)––An outline. Inf. Sci. 2005, 172, 1–40. [Google Scholar] [CrossRef]
- Senturk, S.; Erginel, N. Development of fuzzy X¯~-R~ and X¯~-S~ control charts using α-cuts. Inf. Sci. 2009, 179, 1542–1551. [Google Scholar] [CrossRef]
- Rowlands, H.; Wang, L.R. An approach of fuzzy logic evaluation and control in SPC. Qual. Reliab. Eng. Int. 2000, 16, 91–98. [Google Scholar] [CrossRef]
- El-Shal, S.M.; Morris, A.S. A fuzzy rule-based algorithm to improve the performance of statistical process control in quality systems. J. Intell. Fuzzy Syst. 2000, 9, 207–223. [Google Scholar]
- Zabihinpour, M.; Tang, S.H.; Mohd ariffin, M.K.A.; Azfanizam, A.S. Construction of fuzzy −X-S control charts with an unbiased estimation of standard deviation for a triangular fuzzy random variable. J. Intell. Fuzzy Syst. 2015, 28, 2735–2747. [Google Scholar] [CrossRef]
- Shu, M.-H.; Dang, D.-C.; Nguyen, T.-L.; Hsu, B.-M.; Phan, N.C. Fuzzy and control charts: A data-adaptability and human-acceptance approach. Complexity 2017, 2017, 4376809. [Google Scholar] [CrossRef]
- Afshari, R.; Sadeghpour Gildeh, B. Designing a multiple deferred state attribute sampling plan in a fuzzy environment. Am. J. Math. Manag. Sci. 2017, 36, 328–345. [Google Scholar] [CrossRef]
- Fadaei, S.; Pooya, A. Fuzzy U control chart based on fuzzy rules and evaluating its performance using fuzzy OC curve. TQM J. 2018, 30, 232–247. [Google Scholar] [CrossRef]
- Ercan Teksen, H.; Anagun, A.S. Different methods to fuzzy X¯-R control charts used in production: Interval type-2 fuzzy set example. J. Enterp. Inf. Manag. 2018, 31, 848–866. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophic logic—A generalization of the intuitionistic fuzzy logic. arXiv, 2003; arXiv:math/0303009. [Google Scholar]
- Smarandache, F. Introduction to neutrosophic statistics. arXiv, 2014; arXiv:1406.2000. [Google Scholar]
- Chen, J.; Ye, J.; Du, S. Scale effect and anisotropy analyzed for neutrosophic numbers of rock joint roughness coefficient based on neutrosophic statistics. Symmetry 2017, 9, 208. [Google Scholar] [CrossRef]
- Chen, J.; Ye, J.; Du, S.; Yong, R. Expressions of rock joint roughness coefficient using neutrosophic interval statistical numbers. Symmetry 2017, 9, 123. [Google Scholar] [CrossRef]
- Aslam, M. A new sampling plan using neutrosophic process loss consideration. Symmetry 2018, 10, 132. [Google Scholar] [CrossRef]
- Aslam, M.; Arif, O. Testing of grouped product for the weibull distribution using neutrosophic statistics. Symmetry 2018, 10, 403. [Google Scholar] [CrossRef]
- Montgomery, D.C. Introduction to Statistical Quality Control; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
| Parameters | ||
|---|---|---|
| [3,4] | [3,4] | |
| [4.716,4.784] | [4.921,4.925] | |
| 1 | [303.571,482.268] | [372.916,567.398] |
| 1.1 | [180.551,257.614] | [217.685,298.395] |
| 1.2 | [117.098,153.218] | [138.998,175.183] |
| 1.3 | [81.177,98.952] | [95.096,111.902] |
| 1.4 | [59.298,68.163] | [68.685,76.363] |
| 1.5 | [45.169,49.433] | [51.809,54.931] |
| 1.6 | [35.597,37.374] | [40.482,41.237] |
| 1.7 | [28.85,29.239] | [32.562,32.06] |
| 1.8 | [23.935,23.534] | [26.833,25.662] |
| 1.9 | [20.251,19.399] | [22.567,21.048] |
| 2 | [17.423,16.317] | [19.311,17.625] |
| 3 | [6.721,5.593] | [7.198,5.874] |
| 4 | [4.174,3.353] | [4.394,3.474] |
| Parameters | ||
|---|---|---|
| [4,6] | [4,6] | |
| [4.37095,4.38408] | [4.56277,4.60236] | |
| 1 | [300.03049,490.72292] | [373.89462,521.39944] |
| 1.1 | [167.75455,236.62553] | [204.67051,261.86897] |
| 1.2 | [103.63777,130.01298] | [124.23386,148.39858] |
| 1.3 | [69.11578,78.91434] | [81.62574,92.2282] |
| 1.4 | [48.93744,51.76218] | [57.06262,61.60346] |
| 1.5 | [36.34426,36.10675] | [41.91335,43.57537] |
| 1.6 | [28.05528,26.46593] | [32.04372,32.28357] |
| 1.7 | [22.35463,20.20032] | [25.31664,24.84157] |
| 1.8 | [18.28768,15.94213] | [20.55525,19.72459] |
| 1.9 | [15.29499,12.93761] | [17.07608,16.07855] |
| 2 | [13.03379,10.74914] | [14.46377,13.40067] |
| 3 | [4.84897,3.5816] | [5.18032,4.44486] |
| 4 | [3.02663,2.21472] | [3.17374,2.68331] |
| Parameters | ||
|---|---|---|
| [9,10] | [9,10] | |
| [3.77774,3.87857] | [3.90143,3.92448] | |
| 1 | [310.11015,398.93766] | [374.85685,429.14801] |
| 1.1 | [140.42988,169.87263] | [166.07453,181.17044] |
| 1.2 | [73.89048,85.19126] | [85.81325,90.2116] |
| 1.3 | [43.56058,48.35266] | [49.82352,50.89613] |
| 1.4 | [28.04099,30.19755] | [31.65868,31.6243] |
| 1.5 | [19.345,20.33186] | [21.59801,21.19929] |
| 1.6 | [14.10561,14.53629] | [15.59629,15.09889] |
| 1.7 | [10.75721,10.90994] | [11.79341,11.29453] |
| 1.8 | [8.51099,8.52027] | [9.26122,8.79481] |
| 1.9 | [6.94206,6.87633] | [7.504,7.0795] |
| 2 | [5.80835,5.70385] | [6.24147,5.85883] |
| 3 | [2.16011,2.05723] | [2.24008,2.0842] |
| 4 | [1.48785,1.42243] | [1.51913,1.43261] |
| Proposed Chart | Existing Chart | |
|---|---|---|
| 1 | [300.03049,490.72292] | 300.0044 |
| 1.1 | [167.75455,236.62553] | 167.7414 |
| 1.2 | [103.63777,130.01298] | 103.6304 |
| 1.3 | [69.11578,78.91434] | 69.11124 |
| 1.4 | [48.93744,51.76218] | 48.93448 |
| 1.5 | [36.34426,36.10675] | 36.34222 |
| 1.6 | [28.05528,26.46593] | 28.05381 |
| 1.7 | [22.35463,20.20032] | 22.35353 |
| 1.8 | [18.28768,15.94213] | 18.28684 |
| 1.9 | [15.29499,12.93761] | 15.29432 |
| 2 | [13.03379,10.74914] | 13.03325 |
| 3 | [4.84897,3.5816] | 4.84884 |
| 4 | [3.02663,2.21472] | 3.02657 |
| Sample No. | Sample Observation | |||||
|---|---|---|---|---|---|---|
| 1 | [74.03,74.03] | [74.002,73.991] | [74.019,74.019] | [73.992,73.992] | [74.008,74.001] | [0.014772,0.017242] |
| 2 | [73.995,73.995] | [73.992,74.003] | [74.001,74.001] | [74.011,74.011] | [74.004,74.004] | [0.007503,0.005762] |
| 3 | [73.988,74.017] | [74.024,74.024] | [74.021,74.021] | [74.005,74.005] | [74.002,73.995] | [0.014748,0.012116] |
| 4 | [74.002,74.002] | [73.996,73.996] | [73.993,73.993] | [74.015,74.015] | [74.009,74.009] | [0.009083,0.009083] |
| 5 | [73.992,73.992] | [74.007,74.007] | [74.015,74.015] | [73.989,73.989] | [74.014,73.998] | [0.012219,0.010756] |
| 6 | [74.009,74.009] | [73.994,74.001] | [73.997,73.997] | [73.985,73.985] | [73.993,73.993] | [0.008706,0.008944] |
| 7 | [73.995,73.998] | [74.006,74.006] | [73.994,73.994] | [74,74] | [74.005,74.005] | [0.005523,0.00498] |
| 8 | [73.985,73.985] | [74.003,74.01] | [73.993,73.993] | [74.015,74.015] | [73.988,73.988] | [0.012256,0.01348] |
| 9 | [74.008,74.005] | [73.995,73.995] | [74.009,74.009] | [74.005,74.005] | [74.004,74.004] | [0.005541,0.005177] |
| 10 | [73.998,73.998] | [74,74] | [73.99,73.99] | [74.007,74.007] | [73.995,73.995] | [0.006285,0.006285] |
| 11 | [73.994,73.998] | [73.998,73.998] | [73.994,73.994] | [73.995,73.995] | [73.99,74.001] | [0.002864,0.002775] |
| 12 | [74.004,74.004] | [74,74.002] | [74.007,74.005] | [74,74.001] | [73.996,73.996] | [0.004219,0.003507] |
| 13 | [73.983,73.993] | [74.002,74.002] | [73.998,73.998] | [73.997,73.997] | [74.012,74.005] | [0.010455,0.004637] |
| 14 | [74.006,74.006] | [73.967,73.985] | [73.994,73.994] | [74,74] | [73.984,73.996] | [0.015304,0.007759] |
| 15 | [74.012,74.012] | [74.014,74.012] | [73.998,73.998] | [73.999,73.999] | [74.007,74.007] | [0.007314,0.006804] |
| 16 | [74,74] | [73.984,73.984] | [74.005,74.005] | [73.998,73.998] | [73.996,73.996] | [0.007797,0.007797] |
| 17 | [73.994,73.994] | [74.012,74.012] | [73.986,73.986] | [74.005,74.005] | [74.007,74.007] | [0.010569,0.010569] |
| 18 | [74.006,74.006] | [74.01,74.011] | [74.018,74.018] | [74.003,74.003] | [74,74.001] | [0.006986,0.006834] |
| 19 | [73.984,73.984] | [74.002,74.002] | [74.003,74.003] | [74.005,74.005] | [73.997,73.997] | [0.008468,0.008468] |
| 20 | [74,74] | [74.01,74.01] | [74.013,74.009] | [74.02,74.015] | [74.003,74.003] | [0.007981,0.005941] |
| 21 | [73.982,73.982] | [74.001,74.001] | [74.015,74.015] | [74.005,74.005] | [73.996,73.996] | [0.012153,0.012153] |
| 22 | [74.004,74.004] | [73.999,73.999] | [73.99,73.99] | [74.006,74.006] | [74.009,74.002] | [0.007436,0.006261] |
| 23 | [74.01,74.01] | [73.989,73.989] | [73.99,73.99] | [74.009,74.005] | [74.014,74.011] | [0.011929,0.010747] |
| 24 | [74.015,74.011] | [74.008,74.008] | [73.993,73.993] | [74,74] | [74.01,74.011] | [0.008701,0.007893] |
| 25 | [73.982,73.982] | [73.984,73.989] | [73.995,73.995] | [74.017,74.012] | [74.013,74.01] | [0.016177,0.013088] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aslam, M.; Khan, N.; Khan, M.Z. Monitoring the Variability in the Process Using Neutrosophic Statistical Interval Method. Symmetry 2018, 10, 562. https://doi.org/10.3390/sym10110562
Aslam M, Khan N, Khan MZ. Monitoring the Variability in the Process Using Neutrosophic Statistical Interval Method. Symmetry. 2018; 10(11):562. https://doi.org/10.3390/sym10110562
Chicago/Turabian StyleAslam, Muhammad, Nasrullah Khan, and Muhammad Zahir Khan. 2018. "Monitoring the Variability in the Process Using Neutrosophic Statistical Interval Method" Symmetry 10, no. 11: 562. https://doi.org/10.3390/sym10110562
APA StyleAslam, M., Khan, N., & Khan, M. Z. (2018). Monitoring the Variability in the Process Using Neutrosophic Statistical Interval Method. Symmetry, 10(11), 562. https://doi.org/10.3390/sym10110562





