Abstract
Due to scale and complexity of first-order formulas, simplifications play a very important role in first-order theorem proving, in which removal of clauses and literals identified as redundant is a significant component. In this paper, four types of clauses with the local redundancy property were proposed, separately called a set-blocked clause (SBC), extended set-blocked clause (E-SBC), equality-set-blocked clause (ESBC) and extended equality-set-blocked clause (E-ESBC). The former two are redundant clauses in first-order formulas without equality while the latter two are redundant clauses in first-order formulas with equality. In addition, to prove the correctness of the four proposals, the redundancy of the four kinds of clauses were proved. It was guaranteed eliminating clauses with the four forms has no effect on the satisfiability or the unsatisfiability of original formulas. In the end, effectiveness and confluence properties of corresponding clause elimination methods were analyzed and compared.
1. Introduction
Simplifications have been diffusely recognized as an indispensable component of both propositional SAT solving and first-order theorem proving. Clause elimination has always been crucial among simplification techniques. In 2010, blocked clause elimination in propositional logic was proposed for reducing the size of formulas and speeding up SAT solvers as a preprocessing technique [1]. After that, there have been published further research work related to blocked clause. Hidden blocked clause and asymmetric blocked clause were created by combining hidden literal addition and asymmetric literal addition with blocked clause at the same year [2,3]. Then, abcdSAT [4] based on blocked clause decomposition [5] won the SAT-Race 2015 competition. In 2016, the extension of blocked clause was widened further. Super-blocked clause and set-blocked clause in propositional logic were produced, in which super-blocked clause had the most general local redundancy property [6]. After that, Blocked clause was successfully lifted to first-order logic in 2017 [7], which as a preprocessing technique of Vampire boosted the efficiency of Vampire [8].
In the paper, we generalize the conception of blocked clause further in first-order logic. Set-blocked clause (SBC) and extended set-blocked clause (E-SBC) in first-order logic without equality are presented, which are generalizations of blocked clause in first-order logic. The evolution is that SBC is blocked by a subset of its literals while blocked clause (BC) is blocked by one of its literals. Similarly, E-SBC can be considered as a further generalization based on SBC. Informally, if a clause C is an E-SBC, for any assignment over the external ground atoms of the clause C, there exists a subset of literals of C, C is a SBC upon in . Assignments over the external ground atoms of C may transform resolution environment of C into a different one from the original resolution environment, in addition, the subset is able to be various along with the diversity of the assignment , which makes the requirement for a clause to be an extended set-blocked clause is quite flexible compared with the requirement for an SBC. To guarantee those clauses are capable to be eliminated from formulas without influencing the satisfiability or unsatisfiability, the redundancy of the two categories of clauses are proved. The proof is not given directly under the circumstance of first-order logic but lower it to propositional logic and connect with the variant of Herbrand’s Theorem: if a first-order formula F is satisfiable if and only if it is satisfiable for all the finite ground instances of F. After that, their abilities to simplify formulas are contrasted with blocked clause elimination (BCE) by comparing their effectiveness. Furthermore, set-blocked clause elimination (SBCE) and extended set-blocked clause elimination (E-SBCE) have the confluence properties just the same as blocked clause elimination.
The paper is not only relevant to first-order formulas without equality but also first-order formulas with equality. Because of the peculiarities of equality, there will be some mistakes if we remove clauses according to the definitions of SBC and E-SBC. The solution is to combine SBC and E-SBC with flattening and flat resolution, developing the new two categories of clauses: equality-set-blocked clause (ESBC) and extend equality-set-blocked clause (E-ESBC). The combination can erase the “confusion jamming” caused by the characteristics of equality that some different literals with distinct items have the same truth values under any assignment. Similarly, redundancy, effectiveness and confluence properties of ESBC and E-ESEB are also demonstrated, analyzed and compared.
The contribution of the paper mainly is: (1) Establish the concepts of SBC and E-SBC in formulas without equality and ESBC and E-ESBC in formulas with equality; (2) Prove all the four types of clauses are redundant; (3) Contrast the four corresponding clause elimination methods’ effectiveness; (4) Illuminate the confluence properties of the four clause elimination methods.
The rest of the paper is organized as follows. After some necessary preliminaries are introduced in Section 2, we propose SBC and E-SBC, and prove the redundancy of the two types of clauses in Section 3. In Section 4, we present ESBC and E-ESBC, show how they can deal with formulas with equality and prove the redundancy of the two types of clauses. Finally, we compare and analyze those clause elimination methods’ effectiveness and confluence properties in Section 5.
2. Preliminaries
In the section, we introduce some necessary notations, definitions and theorems for the paper.
Here we only consider first-order formulas in conjunctive normal form (CNF). A formula is a conjunction of clauses. A clause is a disjunction of literals. A literal is an atom or the negation of an atom. An atom is made up of a predicate symbol and items. Items can be the mixture of variables, constants and functions or just single variable, constant or function. Variables are usually represented by , constants are represented by and functions are represented by [9].
A propositional assignment is a mapping from ground atoms to the truth values 1 (true) and 0 (false). Accordingly, a set V of ground clause is propositionally satisfiable if there exists a propositional assignment which can assign every ground clause in V to the truth value 1. A clause is valid when it is true under any assignment, tautology is one case of valid clause. Let F be a formula and be an assignment, is defined as and does not satisfy . Two formulas F and are satisfiability equivalent if they are either both satisfiable or unsatisfiable. A clause C is redundant w.r.t. F if F and are satisfiability equivalent. A substitution is a mapping from variables to terms. A ground substitution is a mapping of which the range consists only of ground terms. For a literal, clause or formula F, denotes the atoms in F and denotes the ground atoms in F.
A clause is a blocked clause upon in a first-order formula F without equality, if all its L-resolvents are tautologies. L-resolvent is defined below [7]:
Definition 1.
Given two clausesandsuch that there exists a substitution σ which can unify, the clauseis called as the L-resolvent of C and D.
For a clause C in a formula F, the resolution environment, , of C in first-order formula F without equality is the set of all the clauses in which can be resolved with C: in such that and L and can be unified}
And for those atoms in but not appearing in C and not able to be unified with , they are called as the external atoms of C. The definition is: , and there is no unification between A and . The set of external ground atoms is defined as .
Since first-order CNF formulas with equality will be discussed in this paper, equality axioms is introduced here [10]: (1) ; (2) (3) (4) if f is a n-ary function symbol, ; (5) if P is a n-ary predicate symbol,
Flattening and flat resolution [11] are the constituent parts of E-SBC and E-ESBC. The definitions are showed below [7].
Definition 2.
After flattening the literal of the clause , the new flattened literal is and the new flattened clause is with being variables not occurring in C
Definition 3.
Supposeandandhave the same predicate symbol but the opposite polarity. After flattening L in C andin D, the new flattened clausesandare obtained. In addition, the resolventofandis called as a flat L-resolvent of C and D.
A clause C is an equality-blocked clause (EBC) upon in a formula F with equality, if all its flat L-resolvents are valid.
The resolution environment of a clause C in a formula F with equality is different from the definition in formulas without equality. The existence of equality makes the clauses own literals, which can be resolved with some literal in C, cannot consist of the whole resolution environment of C, but extend to clauses contain literals have the same predicate but the contrary polarity with some literal in C. such that and L and have the same predicate symbol}.
Meanwhile, the external atoms in , of C in first-order formulas with equality are also distinguished from the definition of external atom in first-order formulas without equality: and A has no same predicate symbol as , in which the set of ground external atoms is defined as .
In a formula F with equality, flipping the truth value of a ground literal under a propositional assignment , it should flip the truth value of all the ground literals with the form such that for all rather than simply flip the truth value of L [7].
Definition 4.
Given a propositional assignment β and a ground literalof which the predicate symbol is not equality symbol. The definition of a propositional assignmentis obtained from β by equivalence flipping the truth value of is below:
The following are two variants of Herbrand’s Theorm we adopt in the rest part of the paper. One is suitable for first-order CNF formulas without equality, while the other is suitable for first-order CNF formulas with equality [10].
Theorem 1.
For a first-order formula F without equality predicate, it is satisfiable if and only if every finite set of ground instances of clauses in F is propositionally satisfiable.
Theorem 2.
For a first-order formula F with equality predicate, it is satisfiable if and only if every finite set of ground instances of clauses inis propositionally satisfiable.
3. Set-Blocked Clause and Extended Set-Blocked Clause in First-Order Logic without Equality
In this section, we demonstrate set-blocked clause and extended set-blocked clause in formulas without equality. First, we give the definition of -resolvent as follows, which is different from the definition of L-resolvent of a clause C in the paper [7]. The former includes substituted literals from negations of some literals in the clause C while the latter has no such characteristics in it.
Definition 5.
Given two clauses,with the subsetsuch that and cannot be resolved with each other, and . If one of literals can be unified by an mgu σ, the clause is called -resolvent of C and D.
Example 1.
Let the clausewithand the clause.andcan be unified by the substitution. We can know thatand. Therefore,is the-resolvent of C and D.
Next is the definition of set-blocked clause, a generalization from blocked clause by extending one blocking literal of clause C to multiple blocking literals of clause C.
Definition 6.
A clause C is a set-blocked clause (SBC) in the formula F if there exists a setsuch thatandcannot be resolved with each other and all its-resolvent
Example 2.
Let the clauseand the formula. We can see that there is only one-resolvent and one-resolvent of C and D, separately obtained by resolving C withand resolving C with.-resolvent iswhich is a tautology and-resolvent iswhich is also a tautology. Then, all the-resolventsare tautologies. Therefore, C is set-blocked upon S w.r.t. F.
In Example 2, the clause C is an SBC; however, the clause C is not blocked no matter upon or .
To justify it has no impact on the satisfiability or unsatisfiability of formulas by removing SBCs in formulas, the redundancy property of SBC is proved subsequently.
Lemma 1.
Given a clause C is set-blocked uponin a formula F. Let α be an assignment that propositionally satisfies all the ground instances of clauses in but falsifies a ground instance of C. Then, the assignment , obtained from α by flipping all the truth values of ground literals in , still satisfies all the ground instances in .
Proof.
Let be a ground instance of D in . may be falsified according to the assignment by flipping all the truth values of ground literals in , only if contains a set of literals . Without loss of generality, assume that contains the literal (if contains more than one literal from , the proof process is the same) and let be all the literals in D such that for . Then, the substitution (note that C and D are variable disjoint by assumption) is a unifier of . Hence, , with an mgu of , is an -resolvent of C, which is a tautology due to the fact that the clause C is a set-blocked clause.
As the substitution is the most general unifier, there exists a substitution such that . We can obtain the following equation:
which is a ground instance of , so it is a tautology of which the truth value is 1. Because falsifies and is acquired by flipping all the truth values of to be true while the truth values of all the other ground literals are maintained. Therefore, falsifies and . Meanwhile, since the truth value of is 1, then the truth value of must be 1. Therefore, satisfies , and of course satisfies . Hence, flipping the truth values of ground literals will not falsify any ground instances in , so satisfies all the ground instances in .
Lemma 1 demonstrates that flipping the truth values of ground literals in S has no influence on the truth values of ground instances of clauses in . However, it may falsify other ground instances of C. Here is an example. □
Example 3.
Assumeis a SBC uponin a formula F. Consider two ground instances of C,and. The assignmentfalsifies, but we can satisfyby flipping the truth values of ground instancesandinand we can obtain the new assignment, apparently the new assignment satisfies; however, it falsifies the other ground instanceof C.
Even though flipping the truth values of ground literals of the set , one ground instance of S in a ground instance of C, may falsify other ground instances of C, it has no severe consequence. Assume that flipping the truth values of ground literals in falsifies another ground instances of C, then there are no identical ground literals in , one ground instance of S in the ground instance . Now that contains totally different ground literals from , and ground literals in are not capable to be resolved with ground literals in according to the definition of SBC, then it will not falsify by flipping the truth value of ground literals in . We can conclude that both and can keep their truth values as true, by flipping the truth values of ground literals as true in and .
Theorem 3.
If a clause C is set-blocked uponin a formula F, the clause C is redundant w.r.t. F.
Proof.
Given a clause C is set-blocked upon in a formula F. Assume that is satisfiable. Let and be finite sets of ground instances of clauses in and . Since is satisfiable, there exists a propositional assignment satisfies . Assume that it falsifies some ground instances of C which are contained in . Flipping all the truth value of ground literals of ground instance of S in , has no influence on ground instances in according to Lemma 1, but it may falsify some other ground instances of . Nevertheless, since is finite, we can satisfy those ground instances of by flipping orderly the truth value of ground literals of the ground instances of S in those falsified ground instances of C. Eventually, all the ground instances of are satisfied. According to Theorem 1, F is satisfiable, which means F and are satisfiability equivalent. Therefore, the clause C is redundant w.r.t. F. □
Apparently the redundancy property of set-blocked clause is local. A clause can be assessed whether it is an SBC, by only considering its resolution environment rather than the whole formula. If a clause C is an SBC in a formula F and the clause C has the same resolution environment in another formula , then the clause C is also an SBC in .
Next, we introduce extended set-blocked clause (E-SBC), a generalization of SBC. With respect to E-SBC, another factor, external ground atoms, is added into consideration. external ground atoms of a clause C are ground atoms in the resolution environment of C but not occurring in C and not able to be unified with atoms in , which means variations of truth values of external ground axioms and truth values of C are not relevant. In other words, if a clause is true because of the truth values of several external ground atoms of C in , then the clause will not be falsified under any change of the truth values of literals in C.
Definition 7.
A clause C is an extended set-blocked clause (E-SBC) in a formula F if, for every assignment β over the external ground atoms, there exists a subsetsuch that C is set-blocked uponin.
Example 4.
Supposeand the resolution environment of C:. Apparently, the clause C is not a set-blocked clause, because not all the-resovlentsare tautologies no matter which subset of C has been chosen to be S. The external ground atoms of C is. If an assignment α satisfiesand, thenandwill not be included inaccording to the definition of. Therefore, we only considerandas the resolution environment of C in. If we choose S as, C cannot be resolved with eitherorupon S, clause C is trivially set-blocked uponin. If another assignment λ satisfiesand, thenand it is not covered in. We only need to considerandas the resolution environment of C in. If we choose S as, the-resolventsand-resolventboth are tautologies by resolving C withand. Therefore, clause C is set-blocked uponin. Because α and λ cover all the possible assignments over, then we can conclude that C is set-blocked infor any assignment β over the external ground atoms. Therefore, the clause C is an E-SBC.
Evaluating whether a clause C is an E-SBC when there are no external ground atoms, it only needs to evaluate if the clause C is an SBC. No external ground atoms means no way to influence the resolution environment of C, therefore, is equal to F all the time for any assignment .
Lemma 2.
Given a clause C is an E-SBC in a formula F. Let α be an assignment that propositionally satisfies all the ground instances of clauses inbut falsifies a ground instanceof C. Then, there exist a subsetofsuch that the assignment, obtained from α by flipping all the truth values of ground literalsin, still satisfies all the ground instances in.
Proof.
Since flipping the truth values of ground literals of C can only affect the truth values of ground clauses in the resolution environment of C, we only consider the ground instances in the resolution environment of C whether they will be falsified by flipping the truth values of ground literals in C. It is analyzed in two cases:
Case 1: In the resolution environment of C, there are no external ground atoms. Since C is an E-SBC and there is no ground atoms in the resolution environment of C, it means that C is set-blocked in the formula F. Now that C is set-blocked in the formula F, there exists a subset of such that the assignment , obtained from by flipping all the truth values of ground literals in , still satisfies all the ground instances in according to Lemma 1.
Case 2: In the resolution environment of C, there exist external ground atoms . Since is an assignment which covers all the ground instances of clauses in , it also assigns the truth values of those external ground atoms to be true or false. Assume that the assignment to the external ground atoms make the truth values of clauses in the resolution environment of C are true. Since clause C is extended set-blocked in a formula F, there exist a subset of C, C is set-blocked upon S in , which means C is set-blocked upon S in the formula . Now that C is set-blocked upon S in the formula , flipping all the truth values of ground literals in will not falsify any ground instances of . Furthermore, already satisfies all the ground instances of by its assignment to those external ground atoms according to the assumption, flipping all the truth values of ground literals in will not falsify any ground instances of . Hence, flipping all the truth values of ground literals in will not falsify any ground instances of . Therefore, the assignment , obtained from by flipping all the truth values of ground literals in , still satisfies all the ground instances in . □
Theorem 4.
If a clause C is an E-SBC in a formula F, it is redundant w.r.t. F.
Proof.
Given finite ground instances and are sets of finite ground instances of and . Assume that is satisfiable, then there exists a propositional assignment satisfies all the ground instances of , but it may falsify some ground instances in . According to Lemma 2, there exists a subset of C, it will not affect the truth values of ground instances in by flipping the truth values of ground literals of S in those falsified ground instances of C. Even though flipping those truth values of ground literals in those falsified ground instances of C may falsify other ground instances of C in ; however, we can flip the truth values of ground literals in ground instances of S in those falsified ground instances successively, until all the truth values of falsified ground instances become true. According to Theorem 1, F is satisfiable. Therefore, the clause C is redundant w.r.t. F. □
4. Equality-Set-Blocked Clause and Extended Equality-Blocked Clause in First-Order Logic Formulas with Equality
In the last section, SBC and E-SBC in formulas without equality are discussed. In fact, the conceptions of SBC and E-SBC can only be adopted in first-order formulas without equality, if they are utilized in first-order formulas with equality, some clauses will be removed mistakenly. A counter-example is given as follows:
Example 5.
Letand the formula. According to the definition of SBC in Section 3, clause C is trivially set-blocked upon, because there is no clauses incan be directly resolved with clause C upon, which means clause C can be removed from formula F without influencing the satisfiability or unsatisfiability. However, F is unsatisfiable whileis satisfiable.
The reason why this situation happens is because the definitions of SBC and E-SBC are not involved with equality. For example, the truth values of R(a) and R(b) are always the same even though their forms are diverse in Example 5, nevertheless, this situation is not considered in the definitions of SBC and E-SBC. But if we combine the definitions of SBC and E-SBC in Section 3 with flattening and flat resolution, this problem can be solved.
The definition of flat -resolvent of clause C in first-order logic with equality is given below. It deletes a subset of substituted literals from literals in clause C but adds the subset of substituted literals from the negations of literals in clause C compared with flat L-resolvent of clause C.
Definition 8.
Given two clauses,withsuch thatdoes not contain the predicate symbol = andanddo not have the same predicate symbol but the opposite polarity, and. If a literalandhave the same predicate symbol and polarity, by flattening, new literalscan be obtained fromand new flattened clausesandcan be obtained from C and D. If the mgu ofis σ, the clauseis called the flat-resolvent of C and D.
Example 6.
Letand. After flatteningand, two new flattened clausesandcan be obtained from C and D. Then, the flat-resolvent of C and D isvia substitution.
Compared with equality-blocked clause, equality-set-blocked clause is obtained by generalizing one blocking literal in equality-blocked clause to multiple blocking literals.
Definition 9.
For a clause C in a formula F, if there exists a subsetsuch thatdoes not contain the predicate = andanddo not have the same predicate symbol but the opposite polarity. If all the flat-resolventsof C are valid, then the clause C is called as an equality-set-blocked clause (ESBC) upon S in the formula F.
Example 7.
Let, and the formula. About, there is only the clauseincontains the literalhas the same predicate symbol and the opposite polarity with the literalin S. Hence, the only flat-resolvent of C iswhich is valid. In addition, with respect to, there is only the clauseincontains the literalhas the same predicate symbol and the opposite polarity with the literalin the set S, then the only one flat-resolvent isand it is valid. According to Definition 9, the clause C is ESBC uponin the formula F.
ESBC is also redundant in first-order formulas with equality. Before proving its redundancy, a Lemma is introduced first.
Lemma 3.
Suppose a clause C is an ESBC uponin a formula F. β is a propositional assignment satisfying all the ground instances of equality axioms and all the ground instances of clauses in, but falsifies a ground instanceof C.is a propositional assignment obtained from β by equivalence flipping all the truth values of ground literalsin the set, thensatisfies all the ground instances of clauses inand all the ground instances of equality axioms.
Proof.
Let the clause and . Assume that equivalence flipping the truth values of ground literals in the set falsifies the truth value of a ground instance in , the form of the clause must be D with at least one literal in it and it has for all . Without loss of generality, we assume that the clause D with the literal .
Let the clause D be a clause with literals such that for . To simplify the presentation and without loss of generality, we assume that and are all such literals in the clause D, therefore .
Since C is equality-set-blocked upon S, then all the flat -resolvents are valid. Therefore, the flat -resolvent between C and D:
is valid, where is an mgu of the literals and , obtained by flattening and . Without loss of generality, we assume that , then the flat -resolvent can be written as:
Because R is valid, then the assignment must satisfy all the ground instances of R. A ground instance of R can be created by implementing the following substitution:
Then can be written as follows:
which must be satisfied by because it is valid. In , all the , all the , all the (according to the assumption) and are falsified by , we can conclude that all the , all the , all the and are also falsified by . In addition, because satisfies and is obtained by equivalence flipping the truth values of from , falsifies . As a result, must contain at least one literal which is satisfied by due to . Hence, is satisfied by . Therefore, satisfies not only but also all the ground instances of clauses in and all the ground instances of equality axioms. □
Theorem 5.
If a clause C is an ESBC uponin a formula F, it is redundant w.r.t. F.
Proof.
Given there are some finite ground instances and of and assume is a propositional assignment which satisfies and . Suppose the assignment falsifies some ground instances in , those ground instances can be satisfied by equivalence flipping the truth values of ground literals of ground instances of S in those ground instances without influencing the satisfiability of and according to Lemma 3. Even though it may falsify other ground instances in by equivalence flipping, those ground instances can be satisfied by equivalence flipping the truth values of ground literals of ground instances of S in those falsified ground instances of C in without affecting the satisfiability of the previous ground instances. Because those ground instances are finite in , all the ground instances in can be satisfied by orderly equivalence flipping the truth values of ground literals of ground instances of S in those ground instances which have been falsified. Therefore, for any satisfying propositional assignment of ground instances and of , there exists a satisfying propositional assignment , obtained by orderly equivalence flipping the truth values of ground literals of ground instances of S in those falsified ground instances of C from . Hence, is satisfiable according to Theorem 2. Therefore, and are satisfiable equivalent, then the clause C is redundant w.r.t. F. □
Similarly, there is a generalization of ESBC in first-order logic with equality, by adding a new factor, the assignments over the external ground atoms.
Definition 10.
A clause C is an extended equality-set-blocked clause (E-ESBC) in a formula F if, for every assignment β over the external ground atoms, there exists a subset, C is equality-set-blocked uponin.
Example 8.
Supposeand the resolution environment of C:. We can see that external ground atoms. If an assignment α satisfiesand, then. Therefore,andare the clauses in the resolution environment in C in. Since if the subsetis chosen as the,andcannot be resolved with the clause C, hence the clause C is trivially equality-set-blocked uponin. If the assignment λ satisfiesand, then.andconsist of the resolution environment of C in. When, two flat-resolventsandboth are valid. For, there is no -resolvents. As a result, the clause C is equality-set-blocked uponin. Hence, the clause C is an E-ESBC.
Lemma 4.
Suppose a clause C is an E-ESBC in a formula F. β is a propositional assignment satisfying all the ground instances of equality axioms and all the ground instances of clauses in, but falsifies a ground instanceof C. There exist a subsetsuch that, obtained from β by equivalence flipping all the truth values of ground literalsin the set, satisfies all the ground instances of clauses inand all the ground instances of equality axioms.
Proof.
We only consider whether the ground instances of clauses will be falsified in the resolution environment of C. It is analyzed in two cases.
Case 1: In the resolution environment of C, there is no external ground atoms. Since there are no external ground atoms in the resolution environment of C and C is an extended equality-set-blocked clause in the formula F, it means that C is equality-set-blocked in the formula F. In addition, because C is equality-set-blocked in the formula F, there must exist a subset of and the assignment , obtained from by flipping all the truth values of ground literals in , still satisfies all the ground instances in and all the ground instances of equality axioms according to Lemma 3.
Case 2: In the resolution environment of C, there exist external ground atoms . Since is an assignment which covers all the ground instances of clauses in , it also assigns the truth values of those external ground atoms . Assume that the assignment to the external ground atoms make the truth values of clauses in the resolution environment of C are true. Therefore, there exist a subset of C, C is equality-set-blocked upon S in the formula . Now that C is equality-set-blocked upon S in the formula , flipping all the truth values of ground literals in will not falsify any ground instances of . Furthermore, satisfies all the ground instances of by its assignment to those external ground atoms , as a result, equivalence flipping all the truth values of ground literals in will not falsify any ground instances of . Hence, equivalence flipping all the truth values of ground literals in will not falsify any ground instances of . Therefore, the assignment , obtained from by flipping all the truth values of ground literals in , still satisfies all the ground instances in and all the ground axioms of equality axioms. □
Theorem 6.
If a clause C is an E-ESBC in a formula F, it is redundant w.r.t. F.
Proof.
For every finite ground instances of and any assignment propositionally satisfies finite ground instances of , there exists a subset , equivalence flipping the truth values of ground literals of the subset S in some ground instances of C will not affect the truth values of those finite ground instances in according to Lemma 4. Besides, since the ground instances of C are finite, those falsified ground instances of C can become true by equivalence flipping the ground literals in ground instances of S in those falsified ground instances of C successively. Therefore, is satisfiable according to Theorem 2. Hence, the clause C is redundant w.r.t. F. □
5. Effectiveness and Confluence Property
In this section, we evaluate effectiveness and confluence properties of the four corresponding clause elimination methods set-blocked clause elimination, extended set-blocked clause elimination, equality-set-blocked clause elimination and extended equality-set-blocked clause elimination.
5.1. Comparison of Effectiveness
Effectiveness is a significant evaluation standard for a clause elimination method. It reflects the capability of clause elimination methods to simplify formulas. The more effective a kind of clause elimination method is, the more clauses can be removed from the formulas. Below is the definition of effectiveness [2].
Definition 11.
Given two clause elimination methodsand, and a CNF formula F. After the clause elimination methodoris implemented, the new formula isor. If, it is called thatis at least as effective as . In addition, if exists and there exists a formula , , then is more effective than .
First, we compare the effectiveness between blocked clause elimination (BCE) and set-blocked clause elimination (SBCE).
Theorem 7.
SBCE is more effective than BCE.
Proof.
If a clause C is a BC upon in a formula F, it must be a SBC upon . Assume that there is a clause in the formula and can be unified by an mgu , then -resolvent of C and D is , which is the same as the L-resolvent of C and D. Therefore, -resolvent of C and D is a tautology. This situation can generalize to all the -resolvent of C, so all the -resolvent of C are tautologies. Hence, the clause C is an SBC upon . On the contrary, the situation is not the same vice versa. For example, the clause C is an SBC but it is not a BC in Example 2. Therefore, we can conclude that SBCE is more effective than BCE. □
Next, effectiveness between extended set-blocked clause elimination (E-SBCE) and set-blocked clause (SBCE) is compared.
Theorem 8.
E-SBCE is more effective than SBCE.
Proof.
If a clause C is a set-blocked clause upon in a formula F, it must be an extended set-blocked clause. It is analyzed by two cases.
Case 1: There is no external ground atoms of the clause C. When there are no external ground atoms, the clause C is trivially an E-SBC when it is an SBC.
Case 2: Some external ground atoms exist in the resolution environment of C. For any assignment over , it may assign some clauses in as true and it only needs to consider as the resolution environment of C in . Since C is a SBC upon , all the -resovlents obtained by resolving C with clauses in are tautologies, then there is no doubt that all the -resovlents obtained by resolving C with clauses in are tautologies. Therefore, C is an SBC upon S in . As a result, C is an E-SBC.
However, if a clause C is an E-SBC, it may not be an SBC. For example, the clause C is an E-SBC but it is not an SBC in Example 4. □
Since effectiveness has the property of transitivity, then E-SBCE is more effective than BCE. Similarly, situation is analogous among those clause elimination methods dealing with first-order formulas with equality.
Theorem 9.
Equality-set-blocked clause elimination (ESBCE) is more effective than equality-blocked clause elimination (EBCE).
Proof.
If a clause is an EBC upon in a formula F, it must be an ESBC upon in the formula F. The reason is because all the flat -resolvents of C are the same as all the flat L-resolvents of C, then it is no doubt all the flat -resolvents of C are also valid. Therefore, the clause C is also an ESBC. However, if a clause is an EBC, it may not be an EBC. For example, in Example 7, the clause C is an ESBC but it is not an EBC. Hence, ESBC is more effective than EBCE. □
Theorem 10.
Extended equality-set-blocked clause elimination (E-ESBCE) is more effective than equality-set-blocked clause elimination (ESBCE).
Proof.
If a clause C is an ESBC upon in a formula F, then for all possible assignments over the external ground atoms of C, C must be an ESBC upon . Therefore, we can conclude that C is also an E-ESBC. Nevertheless, if a clause is an E-ESBC, it may not be an ESBC. For example, in Example 8, the clause C is an E-ESBC but it is not an ESBC. □
Figure 1 shows the effectiveness among those clause elimination methods, separately in the circumstance of first-order logic without equality and first-order logic with equality.
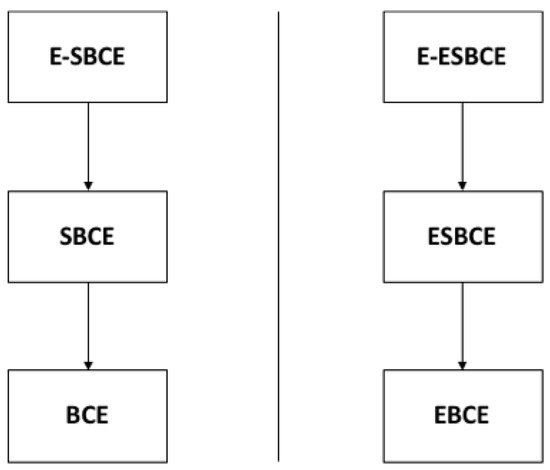
Figure 1.
Effectiveness among those clause elimination methods. A arrow from A to B means A is more effective than B.
5.2. Confluence Property
Confluence property is also a crucial evaluation standard for a clause elimination method. It illuminates whether the difference of the sequence of eliminating clauses in a formula will cause the final obtained new formula different. If a clause elimination method has the confluence property, the final obtained new formula is the same no matter what the elimination sequence is. However, the final obtained formula will vary according to the distinction of elimination sequence if the clause elimination method has no confluence property, as a result, making a good strategy for elimination sequence determines how much clauses can be removed. In this subsection, we discuss the four clause elimination methods’ confluence properties. Below is the definition of diamond property [12]:
Definition 12.
If a relation R has the diamond property, forwithand, there exists a v withand.
If a relation has the diamond property, it also has the confluence property [12]. Clause elimination methods can be seen as relations, which is between original formulas and new formulas after the elimination. Next, we prove all the four clause elimination methods have the confluence properties.
Theorem 11.
SBCE is confluent.
Proof.
Assume that there are two SBCs and in a formula F. Here we prove the other clause still can be removed no matter which clause will be removed first. Without loss of generality, assume that is removed earlier and is not an SBC in after that. Since is an SBC in the formula F, there exists such that all the -resovlents obtained by resolving with clauses in are tautologies. Now that is not an SBC after removing the clause , then there exists at least one -resovlents acquired by resolving with clauses in is not a tautology which is contradictory with the fact that is an SBC in the formula F. Therefore, is still a SBC after removing the clause . As a result, we can conclude that SBCE is confluent. □
Theorem 12.
E-SBCE is confluent.
Proof.
Here we prove E-SBC is confluent by proving a clause C is still an E-SBC in a subset of the formula F if it is an E-SBC in the formula F. Assume that the clause C is not an E-SBC in the subset , then there exists at least one assignment over the external ground atoms of C, satisfying that there exists a subset , such that C is not a set-blocked clause upon in , but C is a set-blocked clause upon in . Then there is at least one -resovlents is not a tautology by resolving C with the clauses in , which is a contradiction against the fact C is a set-blocked clause upon in . E-SBCE is confluent. □
Theorem 13.
ESBCE is confluent.
Proof.
Assume that there are two ESBCs and in a formula F. We prove that the order of eliminating clauses has no effect on the redundancy of ESBCs. Without loss of generality, we assume that the clause is removed first and is not an ESBC in after eliminating . Since is not an ESBC after removing , then for arbitrary subset , there exists at least one flat -resovlents is not valid obtained by resolving with clauses in , which is contradictory to the fact is an ESBC in F. Therefore, is also an ESBC in . Hence, equality-set-blocked clause is confluent. □
Theorem 14.
E-ESBCE is confluent.
Proof.
Assume that a clause C is an E-ESBC in a formula F, then the clause C must be an E-ESBC in any subset of F. Assume that C is not an E-ESBC in a subset of F, then there exists an assignment over the external ground atoms such that C is equality-set-blocked upon subset in while C is not equality-set-blocked upon S in , which means there exists a flat -resovlents is not valid obtained by resolving C with clauses in . Apparently it is a contradiction that C is an equality-set-blocked clause upon in . Therefore, C is also an E-ESBC in . Hence, E-ESBC is confluent. □
Table 1 shows that all the novel clause elimination methods have the confluence property.

Table 1.
Confluence properties of clause elimination methods.
6. Conclusions
In the paper, we generalized blocked clause in first-order logic further, proposing four types of redundant clauses set-blocked clause, extended set-blocked clause, equality-set-blocked clause and extended equality-set-blocked clause, of which the former two were suitable for formulas without equality while the latter two were suitable for formulas with equality. Besides, we proved the redundancies of the four types of clauses and they could be removed from formulas without influencing the satisfiability or unsatisfiability of the original formulas. Finally, we discussed and analyzed their effectiveness and confluence properties. It shows that the four clause elimination methods are more effective compared with blocked clause elimination and equality-blocked clause elimination, and all the four clause elimination methods have the confluence properties.
The paper is a theoretical work about the properties of the four types of clauses. Even though all the four clause elimination methods are more effective than blocked clause elimination and equality-blocked clause elimination, identification of the four types of clauses will be more complicated and more time-consuming in the specific implementation. In future work, we will implement those clause elimination methods as preprocessing techniques of first-order theorem provers by considering the balance between effectiveness and time consumption, expecting to improve the performance of first-order theorem provers.
Author Contributions
Conceptualization, X.N.; methodology, X.N.; validation, H.F., G.W. and Y.X.; writing—original draft preparation, X.N.; writing—review and editing, X.N.; supervision, Y.X.; funding acquisition, Y.X.
Funding
This research was funded by National Natural Science Foundation of China grant number 61673320 and Fundamental Research Funds for the Central Universities grant number 2682018ZT10.
Acknowledgments
This work is supported by the National Natural Science Foundation of China (Grant No. 61673320), and by the Fundamental Research Funds for the Central Universities (Grant No. 2682018ZT10).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Järvisalo, M.; Biere, A.; Heule, M. Blocked clause elimination. In International Conference on Tools and Algorithms for the Construction and Analysis of Systems (TACAS 2010); Lecture Notes in Computer Science (LNCS); Springer: Berlin/Heidelberg, Germany, 2010; pp. 129–144. [Google Scholar]
- Heule, M.J.H.; Järvisalo, M.; Biere, A. Clause elimination procedures for CNF formulas. In Proceedings of the 17th International Conference on Logic for Programming, Artificial Intelligence, and Reasoning (LPAR-17), LNCS; Springer: Berlin/Heidelberg, Germany, 2010; pp. 357–371. [Google Scholar]
- Järvisalo, M.; Heule, M.J.H.; Biere, A. Inprocessing rules. In International Joint Conference on Automated Reasoning (IJCAR-4); Springer: Berlin/Heidelberg, Germany, 2012; pp. 355–370. [Google Scholar]
- Chen, J. Fast Blocked Clause Decomposition with High Quality. arXiv, 2015; arXiv:1507.00459. [Google Scholar]
- Heule, M.; Biere, A. Blocked clause decomposition. In International Conference on Logic for Programming, Artificial Intelligence, and Reasoning (LPAR-19); Springer: Berlin/Heidelberg, Germany, 2013; pp. 423–438. [Google Scholar]
- Kiesl, B.; Seidl, M.; Tompits, H.; Biere, A. Super-Blocked Clauses. In International Joint Conference on Automated Reasoning (IJCAR); Springer: Cham, Switzerland, 2016; pp. 45–61. [Google Scholar]
- Kiesl, B.; Suda, M.; Seidl, M.; Tompits, H.; Biere, A. Blocked Clauses in First-Order Logic. arXiv, 2017; arXiv:1702.00847. [Google Scholar]
- Kovács, L.; Voronkov, A. First-order theorem proving and Vampire. In International Conference on Computer Aided Verification (CAV 2013); Lecture Notes in Computer Science (LNCS); Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–35. [Google Scholar]
- Kiesl, B.; Suda, M. A unifying principle for clause elimination in first-order logic. In International Conference on Automated Deduction (CADE 2017); Lecture Notes in Artificial Intelligence (LNAI 10395); Springer: Cham, Switzerland, 2017; pp. 274–290. [Google Scholar]
- Liu, X. Automated Reasoning based on Resolution; Science Press: Beijing, China, 1994. [Google Scholar]
- Khasidashvili, Z.; Korovin, K. Predicate elimination for preprocessing in first-order theorem proving. In International Conference on Theory and Applications of Satisfiability Testing; Springer: Cham, Switzerland, 2016; pp. 361–372. [Google Scholar]
- Baader, F.; Nipkow, T. Term Rewriting and All That; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).