An Emergency Decision Making Method for Different Situation Response Based on Game Theory and Prospect Theory
Abstract
:1. Introduction
2. Preliminaries
2.1. Game Theory in Emergency Decision Making
- Players: Players are always denoted by and at least ; this means that there are at least two players in one game. In EDM, there are two players, who are the decision maker (DM) and the EE. Thus, in the emergency game , , where 1 denotes the DM and 2 refers to EE.
- Strategies: Let be the set of action strategies of the i-th player who has strategies. In EDM, refers to the set of different alternatives of DM, in which denotes the -th alternatives, . refers to the set of different situations of EE, where denotes the -th possible situation of EE, .
- Payoffs: Let be the payoffs of the i-th player, where .
2.2. Prospect Theory in Emergency Decision Making
- An editing phase, in which the gains and losses can be calculated according to the RPs provided by DM.
- An evaluation phase: in this phase, the prospect values can be obtained by a value function, then the overall prospect values will be calculated on the foundation of prospect values and the weighting vector.
- A selection phase, in which the alternative with the highest overall prospect value will be selected as the best one to deal with the given decision problem.
2.3. Related Works
3. Emergency Decision Making Method Based on Game Theory and Prospect Theory
- Definition framework: this part introduces the basic notations and related terminology that are employed in this proposal.
- Computation of overall prospect values: in this part, the value function will be used to compute the overall prospect values according to gains and losses.
- Selecting the optimal alternative based on payoffs: the payoffs of DM including his/her psychological behavior and the payoffs of EE will be determined. Based on the payoffs, the optimal alternative will be selected to respond to corresponding emergency situation.
3.1. Definition Framework
- : refers to the set of different alternatives, in which denotes the -th alternative, .
- : refers to the set of different situations, in which denotes the -th situations, .
- : refers to the set of criteria, in which represents the m-th criterion, .
- : refers to the weighting vector, in which represents the weight of the m-th criterion. The weighting vector is usually provided by the DM satisfying , , .
- : refers to the cost of the -th available emergency alternative, .
- : refers to the values of RPs, in which and represent the lower and upper limits of RP provided by DM for the m-th criterion in the -th situation, respectively, , .
- : refers to the value of the pre-defined effective control scope [18], in which and represent the lower and upper limits of losses’ protection scope from EE with respect to the -th alternative concerning the m-th criteria, respectively. is usually determined by the local government, , .
3.2. Calculation of Gains and Losses
3.3. Computation of Overall Prospect Values
3.4. Selecting Optimal Alternative Based on Payoffs
3.4.1. Determining the Payoffs of the Players
3.4.2. Selection of the Optimal Alternative with Respect to Each Emergency Situation
- Based on the obtained payoffs of DM and EE, the DM can select the optimal strategies for dealing with all possible emergency situations according to Equation (7).
4. Case Study and Comparison
4.1. Case Study
4.2. Comparison with Other Methods
5. Conclusions and Future Works
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, B.S.; Zhao, X.; Li, Y. Review and Prospect of Studies on Emergency Management. Procedia Eng. 2016, 145, 1501–1508. [Google Scholar] [CrossRef]
- IFRC. Word Disaster Reprot 2016. Available online: http://media.ifrc.org/ifrc/publications/world-disasters-report-2016/ (accessed on 14 October 2016).
- Xia, L.; Xiao, Y. Generation Mechanism of Emergency Decision-making: Links, Elements and Serial Processing. J. Shanghai Adm. Inst. 2011, 4, 005. [Google Scholar]
- Domeneghetti, B.; Benamrane, Y.; Wybo, J.L. Analyzing nuclear expertise support to population protection decision making process during nuclear emergencies. Saf. Sci. 2018, 101, 155–163. [Google Scholar] [CrossRef]
- Levy, J.K.; Taji, K. Group decision support for hazards planning and emergency management: A Group Analytic Network Process (GANP) approach. Math. Comput. Model. 2007, 46, 906–917. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, Y.; Tang, Y.; Li, S.M. An incident information management framework based on data integration, data mining, and multi-criteria decision making. Decis. Support Syst. 2011, 51, 316–327. [Google Scholar] [CrossRef]
- Qu, J.H.; Meng, X.L.; You, H. Multi-stage ranking of emergency technology alternatives for water source pollution accidents using a fuzzy group decision making tool. J. Hazard. Mater. 2016, 310, 68–81. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.H.; Du, Z.J.; Chen, X.H. Consensus model for multi-criteria large-group emergency decision making considering non-cooperative behaviors and minority opinions. Decis. Support Syst. 2015, 79, 150–160. [Google Scholar] [CrossRef]
- Zhou, L.; Wu, X.H.; Xu, Z.S.; Fujita, H. Emergency Decision Making for Natural Disasters: An Overview. Int. J. Disaster Risk Reduction 2017, 27, 567–576. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica J. Econom. Soc. 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Bell, D.E. Regret in decision making under uncertainty. Oper. Res. 1982, 30, 961–981. [Google Scholar] [CrossRef]
- Bell, D.E. Disappointment in decision making under uncertainty. Oper. Res. 1985, 33, 1–27. [Google Scholar] [CrossRef]
- Schmidt, U.; Starmer, C.; Sugden, R. Third-generation prospect theory. J. Risk Uncertain. 2008, 36, 203. [Google Scholar] [CrossRef] [Green Version]
- Fan, Z.P.; Liu, Y.; Shen, R.J. Risk decision analysis method for emergency response based on prospect theory. Syst. Eng.-Theory Pract. 2012, 5, 011. [Google Scholar]
- Fan, Z.P.; Zhang, X.; Chen, F.D.; Liu, Y. Multiple attribute decision making considering aspiration-levels: A method based on prospect theory. Comput. Ind. Eng. 2013, 65, 341–350. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.M.; Hu, B.X. Dynamic adjusting method of emergency alternatives based on prospect theory. Control Decis. 2016, 1, 99–104. [Google Scholar]
- Wang, L.; Wang, Y.M.; Martínez, L. A group decision method based on prospect theory for emergency situations. Inf. Sci. 2017, 418, 119–135. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z.X.; Wang, Y.M. A prospect theory-based interval dynamic reference point method for emergency decision making. Expert Syst. Appl. 2015, 42, 9379–9388. [Google Scholar] [CrossRef]
- Camerer, C. Behavioral Game Theory: Experiments in Strategic Interaction; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Yang, J.J.; Xu, C.H. Emergency decision engineering model based on sequential games. Syst. Eng. Procedia 2012, 5, 276–282. [Google Scholar] [CrossRef]
- Chen, Y.M.; Wu, D.; Wu, C.K. A game theory approach for an emergency management security advisory system. In Proceedings of the 2008 IEEE International Conference on Intelligence and Security Informatics, Taipei, Taiwan, 17–20 June 2008; pp. 116–121. [Google Scholar]
- Coles, J.; Zhuang, J. Decisions in disaster recovery operations: a game theoretic perspective on organization cooperation. J. Homeland Secur. Emerg. Manag. 2011, 8. [Google Scholar] [CrossRef]
- Gupta, U.; Ranganathan, N. Multievent crisis management using noncooperative multistep games. IEEE Trans. Comput. 2007, 56, 577–589. [Google Scholar] [CrossRef]
- Yao, J.; Ji, L.; Chi, H. Dynamic games analysis of emergency management. Manag. Rev. 2005, 17, 46–50. [Google Scholar]
- Zhong, Q.; Li, Z.; Zhang, L. Analysis of the emergency procurement based on evolutionary game theory. In Proceedings of the KAM’09 Second International Symposium on Knowledge Acquisition and Modeling, Wuhan, China, 30 November–1 December 2009; Volume 2, pp. 261–264. [Google Scholar]
- Abdellaoui, M.; Bleichrodt, H.; Paraschiv, C. Loss aversion under prospect theory: A parameter-free measurement. Manag. Sci. 2007, 53, 1659–1674. [Google Scholar] [CrossRef] [Green Version]
- Camerer, C. Bounded rationality in individual decision making. Exp. Econ. 1998, 1, 163–183. [Google Scholar] [CrossRef]
- Limaei, S.M. Mixed strategy game theory, application in forest industry. For. Policy Econ. 2010, 12, 527–531. [Google Scholar] [CrossRef]
- Gibbons, R. Game Theory for Applied Economists; Princeton University Press: Princeton, NJ, USA, 1992. [Google Scholar]
- Tversky, A.; Kahneman, D. Advances in prospect theory: Cumulative representation of uncertainty. J. Risk Uncertain. 1992, 5, 297–323. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, U.; Zank, H. A genuine foundation for prospect theory. J. Risk Uncertain. 2012, 45, 97–113. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Loss aversion in riskless choice: A reference-dependent model. Q. J. Econ. 1991, 106, 1039–1061. [Google Scholar] [CrossRef]
- Bleichrodt, H.; Schmidt, U.; Zank, H. Additive utility in prospect theory. Manag. Sci. 2009, 55, 863–873. [Google Scholar] [CrossRef] [Green Version]
- Booij, A.S.; Van de Kuilen, G. A parameter-free analysis of the utility of money for the general population under prospect theory. J. Econ. Psychol. 2009, 30, 651–666. [Google Scholar] [CrossRef]
- Wakker, P.P. Prospect Theory: For Risk and Ambiguity; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Liu, Y.; Fan, Z.P.; Zhang, Y. Risk decision analysis in emergency response: A method based on cumulative prospect theory. Comput. Oper. Res. 2014, 42, 75–82. [Google Scholar] [CrossRef]
- Ju, Y.B.; Wang, A.H.; Liu, X.Y. Evaluating emergency response capacity by fuzzy AHP and 2-tuple fuzzy linguistic approach. Expert Syst. Appl. 2012, 39, 6972–6981. [Google Scholar] [CrossRef]
- Wang, L.; Labella, Á.; Rodríguez, R.M.; Wang, Y.M.; Martínez, L. Managing non-homogeneous information and experts’ psychological behavior in group emergency decision making. Symmetry 2017, 9, 234. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Wang, L.; Rodríguez, R.M.; Wang, Y.M.; Martínez, L. A hesitant group emergency decision making method based on prospect theory. Complex Intell. Syst. 2017, 3, 177–187. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Rodríguez, R.M.; Wang, Y.M. A dynamic multi-attribute group emergency decision making method considering experts’ hesitation. Int. J. Comput. Intell. Syst. 2018, 11, 163–182. [Google Scholar] [CrossRef]
- Chen, Y.M.; Wu, D.; Wu, C.K. A game theory approach for evaluating terrorist threats and deploying response agents in urban environments. J. Homeland Secur. Emerg. Manag. 2009, 6, 31. [Google Scholar] [CrossRef]
- Cheng, Y.; Zheng, X.P. Emergence of cooperation during an emergency evacuation. Appl. Math. Comput. 2018, 320, 485–494. [Google Scholar] [CrossRef]
- Rezazadeh, A.; Talarico, L.; Reniers, G.; Cozzani, V.; Zhang, L. Applying game theory for securing oil and gas pipelines against terrorism. Reliab. Eng. Syst. Saf. 2018. [Google Scholar] [CrossRef]
- Gao, Y.; Li, Z.W.; Wang, F.M.; Wang, F.; Tan, R.R.; Bi, J.; Jia, X.P. A game theory approach for corporate environmental risk mitigation. Resour. Conserv. Recycl. 2018, 130, 240–247. [Google Scholar] [CrossRef]
- Wu, C.K. A game theory approach for assessing risk value and deploying search-and-rescue resources after devastating tsunamis. Environ. Res. 2018, 162, 18–26. [Google Scholar] [CrossRef] [PubMed]
- Liu, X. Energy network dispatch optimization under emergency of local energy shortage with web tool for automatic large group decision-making. Energy 2017, 120, 740–750. [Google Scholar]



| EE | ||||||
|---|---|---|---|---|---|---|
| DM | … | … | ||||
| … | … | |||||
| ⋮ | ⋮ | … | ⋮ | … | ⋮ | |
| … | … | |||||
| ⋮ | ⋮ | … | ⋮ | … | ⋮ | |
| …… | …… | |||||
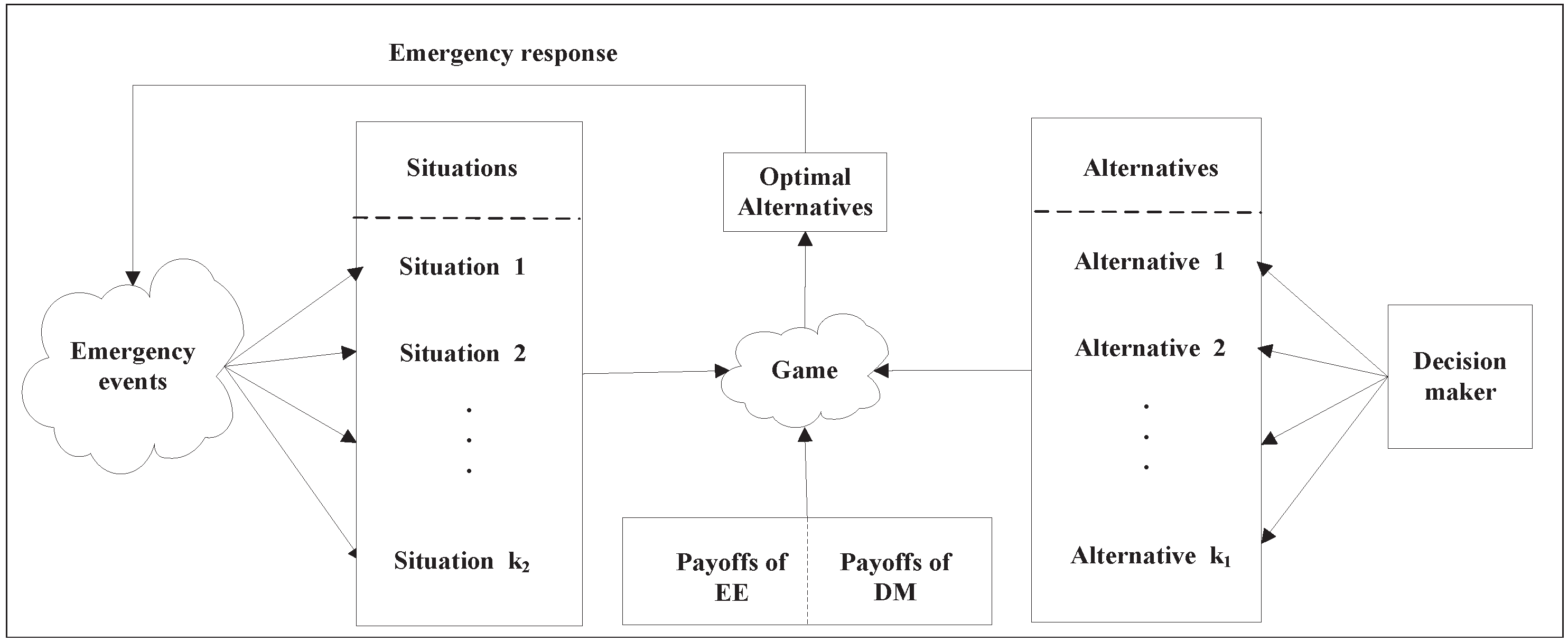
| Cases | Positional Relationship | |
|---|---|---|
| Case 1 | 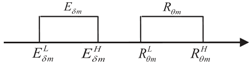 | |
| Case 2 | 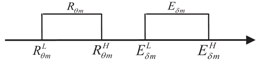 | |
| Case 3 |  | |
| Case 4 | 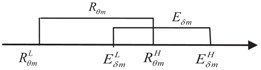 | |
| Case 5 | 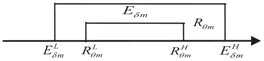 | |
| Case 6 | 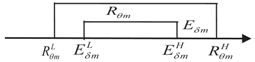 |
| Cases | Gain | Loss | |
|---|---|---|---|
| Case 1 | 0 | ||
| Case 2 | 0 | ||
| Case 3 | 0 | ||
| Case 4 | 0 | ||
| Case 5 | |||
| Case 6 | 0 | 0 |
| Cases | Gain | Loss | |
|---|---|---|---|
| Case 1 | 0 | ||
| Case 2 | 0 | ||
| Case 3 | 0 | ||
| Case 4 | 0 | ||
| Case 5 | |||
| Case 6 | 0 | 0 |
| Alternatives | Criteria | |||
|---|---|---|---|---|
| (0.5) | (0.25) | (0.25) | ||
| [3,5] | [200,400] | [40,50] | 10 | |
| [6,14] | [800,1200] | [50,60] | 30 | |
| [14,20] | [1200,1500] | [60,70] | 70 | |
| [18,25] | [1500,1800] | [70,80] | 130 | |
| Situations | Criteria | ||
|---|---|---|---|
| [5,8] | [100,300] | [20,35] | |
| [5,12] | [300,500] | [35,45] | |
| [12,18] | [600,800] | [45,55] | |
| [18,20] | [800,100] | [55,65] | |
| Situations | |||||
|---|---|---|---|---|---|
| Alternative | −0.0710 | −0.1927 | −0.8152 | −1.000 | |
| 0.4092 | 0.2841 | −0.1008 | −0.3524 | ||
| 0.7444 | 0.6508 | 0.3419 | 0.0238 | ||
| 1.000 | 1.000 | 0.6074 | 0.2511 | ||
| DM | EE | |||||
|---|---|---|---|---|---|---|
| DM | EE | |||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.-X.; Wang, L.; Wang, Y.-M. An Emergency Decision Making Method for Different Situation Response Based on Game Theory and Prospect Theory. Symmetry 2018, 10, 476. https://doi.org/10.3390/sym10100476
Zhang Z-X, Wang L, Wang Y-M. An Emergency Decision Making Method for Different Situation Response Based on Game Theory and Prospect Theory. Symmetry. 2018; 10(10):476. https://doi.org/10.3390/sym10100476
Chicago/Turabian StyleZhang, Zi-Xin, Liang Wang, and Ying-Ming Wang. 2018. "An Emergency Decision Making Method for Different Situation Response Based on Game Theory and Prospect Theory" Symmetry 10, no. 10: 476. https://doi.org/10.3390/sym10100476
APA StyleZhang, Z.-X., Wang, L., & Wang, Y.-M. (2018). An Emergency Decision Making Method for Different Situation Response Based on Game Theory and Prospect Theory. Symmetry, 10(10), 476. https://doi.org/10.3390/sym10100476





