Some q-Rung Dual Hesitant Fuzzy Heronian Mean Operators with Their Application to Multiple Attribute Group Decision-Making
Abstract
:1. Introduction
2. Basic Concepts
2.1. q-Rung Orthopair Fuzzy Set
- 1.
- .
- 2.
- .
- 3.
- .
- 4.
- .
- 1.
- If , then ;
- 2.
- If , thenif , then ;if , then .
2.2. q-Rung Dual Hesitant Fuzzy Set
- 1.
- If, thenis superior to, denoted by;
- 2.
- If, thenif , then is equivalent to , denoted by ;if , then is superior to , denoted by .In the following, we define some operations of the q-RDHFEs.
- 1.
- ;
- 2.
- ;
- 3.
- ;
- 4.
- .
2.3. Heronian Mean
3. The q-Rung Dual Hesitant Fuzzy Heronian Mean Operators
3.1. The q-Rung Dual Hesitant Fuzzy Heronian Mean Operator
- 1.
- If , then the q-RDHFHM reduces to a q-rung dual hesitant fuzzy generalized linear descending weighted mean operator, and we can obtain
- 2.
- If , then the q-RDHFHM reduces to a q-rung dual hesitant fuzzy generalized liner ascending weighted mean operator, and we can obtain
- 3.
- If , then the q-RDHFHM reduces to a q-rung dual hesitant fuzzy basic Heronian mean operator, and we can obtain
- 4.
- If , then the q-RDHFHM reduces to a q-rung dual hesitant fuzzy line Heronian mean operator. It follows that
- 5.
- If , then the q-RDHFHM reduces to a dual hesitant Pythagorean fuzzy Heronian mean operator. So, we can obtain
- 6.
- If , then the q-RDHFHM reduces to the dual hesitant fuzzy Heronian mean operator proposed by Yu et al. [47]. It follows that
3.2. The q-Rung Dual Hesitant Fuzzy Weighted Heronian Mean (q-RDHFWHM) Operator
3.3. The q-Rung Dual Hesitant Fuzzy Geometric Heronian Mean Operator
- If , then the q-RDHFGHM reduces to a q-rung dual hesitant fuzzy generalized geometric linear descending weighted mean operator, and we can obtain
- If , the q-RDHFGHM reduces to a q-rung dual hesitant fuzzy generalized geometric liner ascending weighted mean operator, and we can obtain
- If , the q-RDHFGHM reduces to a q-rung dual hesitant fuzzy basic geometric Heronian mean operator, and we can obtain
- If , the q-RDHFGHM reduces to a q-rung dual hesitant fuzzy line Heronian mean operator, and it follows that
- If , then the q-RDHFGHM reduces to the dual hesitant Pythagorean fuzzy Heronian mean operator, and can we can obtain
- If , then the q-RDHFGHM reduces to the dual hesitant fuzzy Heronian mean operator proposed by Yu et al. [47], and it follows that
3.4. The q-Rung Dual Hesitant Fuzzy Weighted Geometric Heronian Mean Operator
4. A Novel Approach to MAGDM with q-Rung Dual Hesitant Fuzzy Information
4.1. Description of a Typical MAGDM Problem with q-Rung Dual Hesitant Fuzzy Information
4.2. An Algorithm for q-Rung Dual Hesitant Fuzzy MAGDM Problems
5. Numerical Example
5.1. The Decision-Making Process
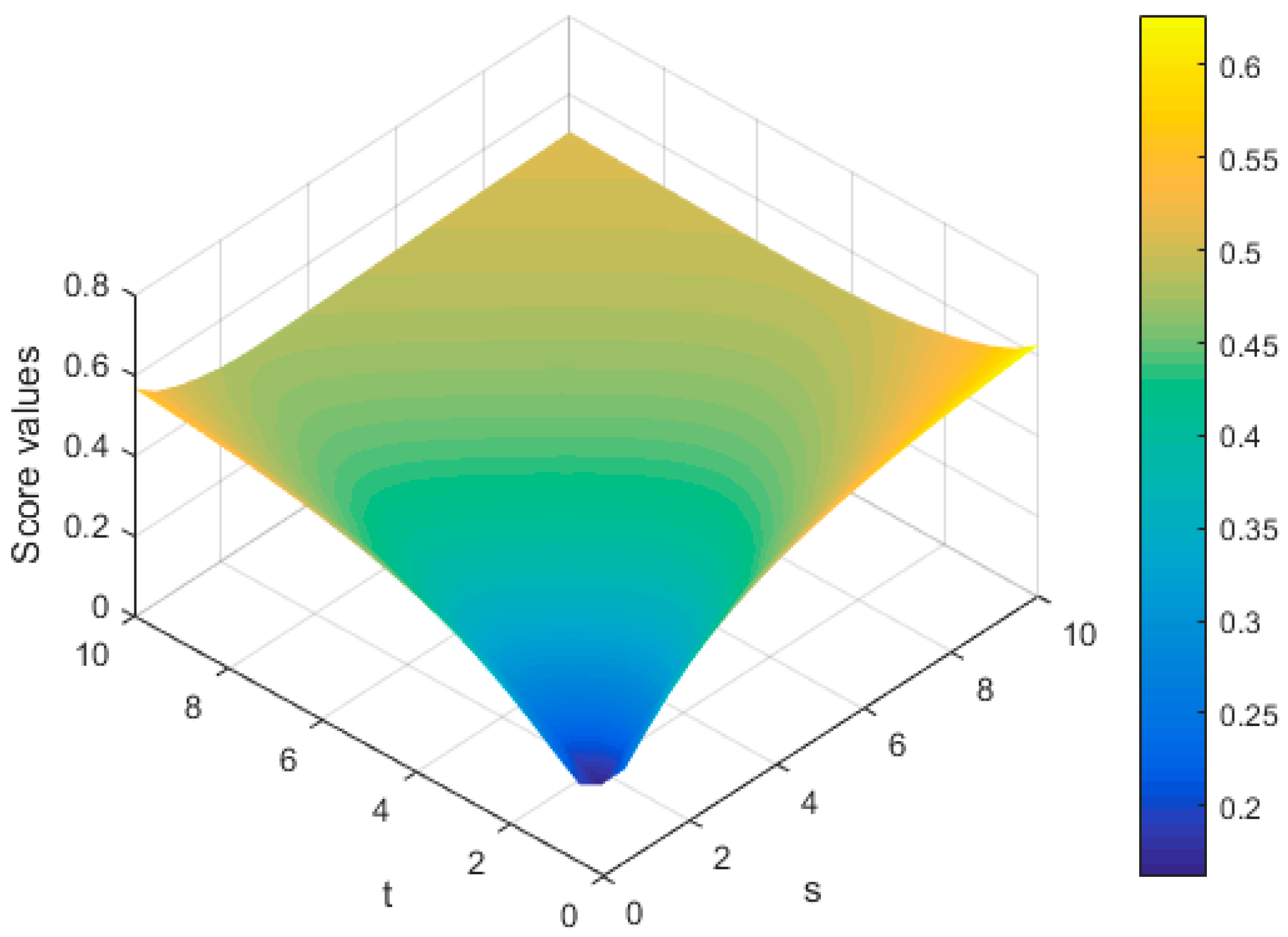
5.2. The Influence of the Parameters on the Results
5.3. Compared with Exiting MAGDM Methods
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–356. [Google Scholar] [CrossRef]
- Son, L.H.; Phong, P.H. On the performance evaluation of intuitionistic vector similarity measures for medical diagnosis 1. J. Intell. Fuzzy Syst. 2016, 31, 1597–1608. [Google Scholar] [CrossRef]
- Own, C.M. Switching between type-2 fuzzy sets and intuitionistic fuzzy sets: An application in medical diagnosis. Appl. Intell. 2009, 31, 283–291. [Google Scholar] [CrossRef]
- Chen, S.M.; Cheng, S.H.; Lan, T.C. A novel similarity measure between intuitionistic fuzzy sets based on the centroid points of transformed fuzzy numbers with applications to pattern recognition. Inf. Sci. 2016, 343–344, 15–40. [Google Scholar] [CrossRef]
- Hwang, C.M.; Yang, M.S.; Hung, W.L.; Lee, M.G. A similarity measure of intuitionistic fuzzy sets based on the Sugeno integral with its application to pattern recognition. Inf. Sci. 2012, 189, 93–109. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, Z.S.; Liu, S.S.; Tang, J. A netting clustering analysis method under intuitionistic fuzzy environment. Appl. Soft Comput. 2011, 11, 5558–5564. [Google Scholar] [CrossRef]
- Xu, D.W.; Xu, Z.S.; Liu, S.S.; Zhao, H. A spectral clustering algorithm based on intuitionistic fuzzy information. Knowl. Based Syst. 2013, 53, 20–26. [Google Scholar] [CrossRef]
- Liu, P.D. Multiple attribute decision-making methods based on normal intuitionistic fuzzy interaction aggregation operators. Symmetry 2017, 9, 261. [Google Scholar] [CrossRef]
- Wang, S.W.; Liu, J. Extension of the TODIM method to intuitionistic linguistic multiple attribute decision making. Symmetry 2017, 9, 95. [Google Scholar] [CrossRef]
- Liu, P.D.; Mahmood, T.; Khan, Q. Multi-attribute decision-making based on prioritized aggregation operator under hesitant intuitionistic fuzzy linguistic environment. Symmetry 2017, 9, 270. [Google Scholar] [CrossRef]
- Zhao, J.S.; You, X.Y.; Liu, H.C.; Wu, S.M. An extended VIKOR method using intuitionistic fuzzy sets and combination weights for supplier selection. Symmetry 2017, 9, 169. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean membership grades in multicriteria decision making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Z. Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. Int. J. Intell. Syst. 2014, 29, 1061–1078. [Google Scholar] [CrossRef]
- Sajjad, A.K.M.; Abdullah, S.; Yousaf, A.M.; Hussain, I.; Farooq, M. Extension of TOPSIS method base on Choquet integral under interval-valued Pythagorean fuzzy environment. J. Intell. Fuzzy Syst. 2018, 34, 267–282. [Google Scholar] [CrossRef]
- Ren, P.; Xu, Z.; Gou, X. Pythagorean fuzzy TODIM approach to multi-criteria decision making. Appl. Soft Comput. 2016, 42, 246–259. [Google Scholar] [CrossRef]
- Ma, Z.M.; Xu, Z.S. Symmetric Pythagorean fuzzy weighted geometric/averaging operators and their application in multi-criteria decision making problems. J. Intell. Fuzzy Syst. 2016, 31, 1198–1219. [Google Scholar]
- Xing, Y.P.; Zhang, R.T.; Wang, J.; Zhu, X.M. Some new Pythagorean fuzzy Choquet-Frank aggregation operators for multi-attribute decision making. Int. J. Intell. Syst. 2018. [Google Scholar] [CrossRef]
- Wei, G.W.; Lu, M. Pythagorean fuzzy Maclaurin symmetric mean operators in multiple attribute decision making. Int. J. Intell. Syst. 2017, 33, 1043–1070. [Google Scholar] [CrossRef]
- Liang, D.C.; Xu, Z.S.; Darko, A.P. Projection model for fusing the information of Pythagorean fuzzy multicriteria group decision making based on geometric Bonferroni mean. Int. J. Intell. Syst. 2017, 32, 966–987. [Google Scholar] [CrossRef]
- Zhang, R.T.; Wang, J.; Zhu, X.M.; Xia, M.M.; Yu, M. Some generalized Pythagorean fuzzy Bonferroni mean aggregation operators with their application to multi attribute group decision-making. Complexity 2017, 2017, 5937376. [Google Scholar] [CrossRef]
- Li, L.; Zhang, R.T.; Wang, J.; Zhu, X.M.; Xing, Y.P. Pythagorean fuzzy power Muirhead mean operators with their application to multi-attribute decision making. J. Intell. Fuzzy Syst. 2018, 35, 2035–2050. [Google Scholar] [CrossRef]
- Xu, Y.; Shang, X.P.; Wang, J. Pythagorean fuzzy interaction Muirhead means with their application to multi-attribute group decision making. Information 2018, 9, 7. [Google Scholar] [CrossRef]
- Teng, F.; Liu, Z.; Liu, P. Some power Maclaurin symmetric mean aggregation operators based on Pythagorean fuzzy linguistic numbers and their application to group decision making. Int. J. Intell. Syst. 2018, 33, 1949–1985. [Google Scholar] [CrossRef]
- Du, Y.; Hou, F.; Zafar, W.; Yu, Q.; Zhai, Y. A novel method for multiattribute decision making with interval-valued Pythagorean fuzzy linguistic information. Int. J. Intell. Syst. 2017, 32, 1085–1112. [Google Scholar] [CrossRef]
- Xian, S.; Xiao, Y.; Yang, Z.; Li, Y.; Han, Z. A new trapezoidal Pythagorean fuzzy linguistic entropic combined ordered weighted averaging operator and its application for enterprise location. Int. J. Intell. Syst. 2018, 33, 1880–1899. [Google Scholar] [CrossRef]
- Geng, Y.; Liu, P.; Teng, F.; Liu, Z. Pythagorean fuzzy uncertain linguistic TODIM method and their application to multiple criteria group decision making. J. Intell. Fuzzy Syst. 2017, 33, 3383–3395. [Google Scholar] [CrossRef]
- Liu, C.; Tang, G.; Liu, P. An approach to multicriteria group decision-making with unknown weight information based on Pythagorean fuzzy uncertain linguistic aggregation operators. Math. Probl. Eng. 2017. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, P.; Liu, W.; Pang, J. Pythagorean uncertain linguistic partitioned Bonferroni mean operators and their application in multi-attribute decision making. J. Intell. Fuzzy Syst. 2017, 32, 2779–2790. [Google Scholar] [CrossRef]
- Wei, G.; Lu, M.; Alsaadi, F.E.; Hayat, T.; Alsaedi, A. Pythagorean 2-tuple linguistic aggregation operators in multiple attribute decision making. J. Intell. Fuzzy Syst. 2017, 33, 1129–1142. [Google Scholar] [CrossRef]
- Huang, Y.H.; Wei, G.W. TODIM method for Pythagorean 2-tuple linguistic multiple attribute decision making. J. Intell. Fuzzy Syst. 2018, 35, 901–915. [Google Scholar] [CrossRef]
- Tang, X.; Wei, G. Models for green supplier selection in green supply chain management with Pythagorean 2-tuple linguistic information. IEEE Access 2018, 6, 18042–18060. [Google Scholar] [CrossRef]
- Yager, R.R. Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 2017, 25, 1222–1230. [Google Scholar] [CrossRef]
- Liu, P.D.; Wang, P. Some q-rung orthopair fuzzy aggregation operators and their applications to multiple-attribute decision making. Int. J. Intell. Syst. 2018, 33, 259–280. [Google Scholar] [CrossRef]
- Liu, P.D.; Liu, J.L. Some q-rung orthopair fuzzy Bonferroni mean operators and their application to multi-attribute group decision making. Int. J. Intell. Syst. 2018, 33, 315–347. [Google Scholar] [CrossRef]
- Liu, Z.M.; Liu, P.D.; Liang, X. Multiple attribute decision-making method for dealing with heterogeneous relationship among attributes and unknown attribute weight information under q-rung orthopair fuzzy environment. Int. J. Intell. Syst. 2018, 33, 1900–1928. [Google Scholar] [CrossRef]
- Bai, K.Y.; Zhu, X.M.; Wang, J.; Zhang, R.T. Some partitioned Maclaurin symmetric mean based on q-rung orthopair fuzzy information for dealing with multi-attribute group decision making. Symmetry 2018, 10, 383. [Google Scholar] [CrossRef]
- Li, L.; Zhang, R.T.; Wang, J.; Shang, X.P. Some q-rung orthopair linguistic Heronian mean operators with their application to multi-attribute group decision making. Arch. Control Sci. accepted.
- Li, L.; Zhang, R.T.; Wang, J.; Shang, X.P.; Bai, K.Y. A novel approach to multi-attribute group decision-making with q-rung picture linguistic information. Symmetry 2018, 10, 172. [Google Scholar] [CrossRef]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Zhu, B.; Xu, Z.S.; Xia, M.M. Dual hesitant fuzzy sets. J. Appl. Math. 2012, 2012, 879629. [Google Scholar] [CrossRef]
- Wei, G.; Lu, M. Dual hesitant Pythagorean fuzzy Hamacher aggregation operators in multiple attribute decision making. Arch. Control Sci. 2017, 27, 365–395. [Google Scholar] [CrossRef]
- Khan, M.S.A.; Abdullah, S.; Ali, A.; Siddiqui, N.; Amin, F. Pythagorean hesitant fuzzy sets and their application to group decision making with incomplete weight information. J. Intell. Fuzzy Syst. 2017, 33, 3971–3985. [Google Scholar] [CrossRef]
- Liang, D.C.; Xu, Z.S. The new extension of TOPSIS method for multiple criteria decision making with hesitant Pythagorean fuzzy sets. Appl. Soft Comput. 2017, 60, 167–179. [Google Scholar] [CrossRef]
- Sykora, S. Mathematical Means and Averages: Generalized Heronian Means; Stan’s Library: Castano Primo, Italy, 2009; Available online: http://www.ebyte.it/library/docs/math09/Means_Heronian.html (accessed on 9 October 2018).
- Yu, D.J. Intuitionistic fuzzy geometric Heronian mean aggregation operators. Appl. Soft Comput. 2013, 13, 1235–1246. [Google Scholar] [CrossRef]
- Yu, D.J.; Li, D.F.; Merigó, J.M. Dual hesitant fuzzy group decision making method and its application to supplier selection. Int. J. Mach. Learn. Cybern. 2016, 7, 819–831. [Google Scholar] [CrossRef]
- Wang, H.J.; Zhao, X.F.; Wei, G.W. Dual hesitant fuzzy aggregation operators in multiple attribute decision making. J. Intell. Fuzzy Syst. 2014, 26, 2281–2290. [Google Scholar]
- Tu, N.H.; Wang, C.Y.; Zhou, X.Q.; Tao, S.D. Dual hesitant fuzzy aggregation operators based on Bonferroni means and their applications to multiple attribute decision making. Annl. Fuzzy Math. Inform. 2017, 14, 265–278. [Google Scholar]














| G1 | G2 | G3 | G4 | |
|---|---|---|---|---|
| A1 | {{0.3, 0.4}, {0.6}} | {{0.7, 0.9}, {0.1}} | {{0.4}, {0.2,0.3}} | {{0.5, 0.6}, {0.2}} |
| A2 | {{0.2, 0.3}, {0.5}} | {{0.6, 0.7}, {0.2}} | {{0.7, 0.8}, {0.2}} | {{0.6}, {0.1, 0.2, 0.3}} |
| A3 | {{0.4}, {0.2,0.3}} | {{0.2,0.3,0.4}, {0.6}} | {{0.7,0.8}, {0.1}} | {{0.7}, {0.2,0.3}} |
| A4 | {{0.6,0.7}, {0.3}} | {{0.5}, {0.4}} | {{0.3,0.4}, {0.5}} | {{0.4, 0.6}, {0.1,0.2}} |
| Parameters | Score Function | Ranking Results |
|---|---|---|
| s = t = 1/2 | ||
| s = t = 1 | ||
| s = t = 2 | ||
| s = t = 5 | ||
| s = 1, t = 2 | ||
| s = 2, t = 1 | ||
| s = 1, t = 5 | ||
| s = 5, t = 1 |
| Parameters | Score Function | Ranking Results |
|---|---|---|
| s = t = 1/2 | ||
| s = t = 1 | ||
| s = t = 2 | ||
| s = t = 5 | ||
| s = 1, t = 2 | ||
| s = 2, t = 1 | ||
| s = 1, t = 5 | ||
| s = 5, t = 1 |
| Methods | Score Function | Ranking Results |
|---|---|---|
| Wang et al.’ [48] method based on the DHFWA operator | ||
| Yu et al.’ s [47] method based on the DHFWHM operator (s = t = 2) | ||
| Tu et al.’s [49] method based on the DHFWBM operator | ||
| Wei and Lu’s [42] method based on the DHPFHWA operator | ||
| The proposed method in this paper |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Shang, X.; Wang, J.; Wu, W.; Huang, H. Some q-Rung Dual Hesitant Fuzzy Heronian Mean Operators with Their Application to Multiple Attribute Group Decision-Making. Symmetry 2018, 10, 472. https://doi.org/10.3390/sym10100472
Xu Y, Shang X, Wang J, Wu W, Huang H. Some q-Rung Dual Hesitant Fuzzy Heronian Mean Operators with Their Application to Multiple Attribute Group Decision-Making. Symmetry. 2018; 10(10):472. https://doi.org/10.3390/sym10100472
Chicago/Turabian StyleXu, Yuan, Xiaopu Shang, Jun Wang, Wen Wu, and Huiqun Huang. 2018. "Some q-Rung Dual Hesitant Fuzzy Heronian Mean Operators with Their Application to Multiple Attribute Group Decision-Making" Symmetry 10, no. 10: 472. https://doi.org/10.3390/sym10100472
APA StyleXu, Y., Shang, X., Wang, J., Wu, W., & Huang, H. (2018). Some q-Rung Dual Hesitant Fuzzy Heronian Mean Operators with Their Application to Multiple Attribute Group Decision-Making. Symmetry, 10(10), 472. https://doi.org/10.3390/sym10100472





