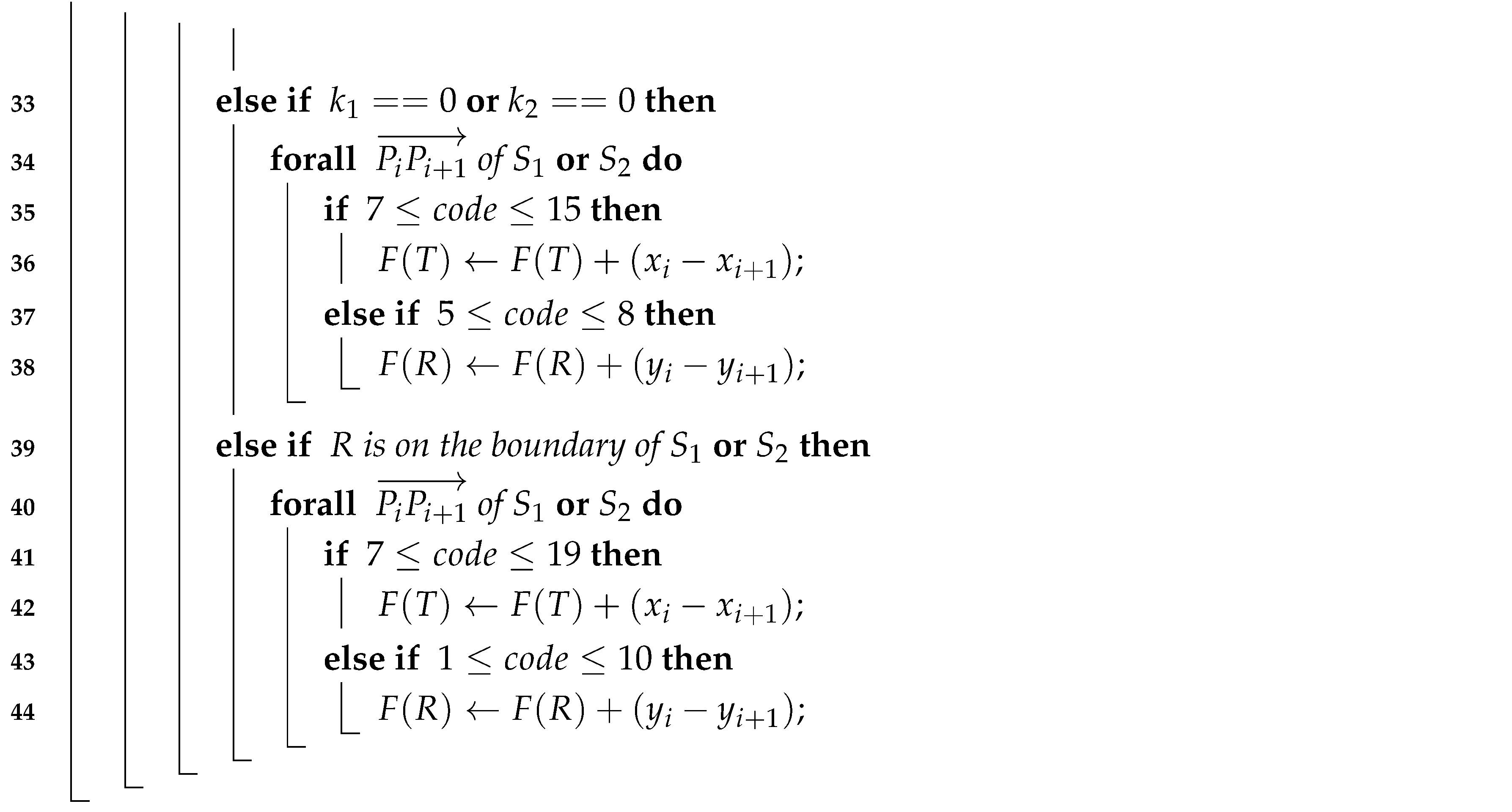3. The Point-in-Polygon Test Principle
Definition 1. A polygon S is composed of rings. A is a sequence of edges, which link together and form a closed circuit. A ring containing all other rings is the of S, while each of the remaining rings is the of S, also known as of S, and referred to as of S.
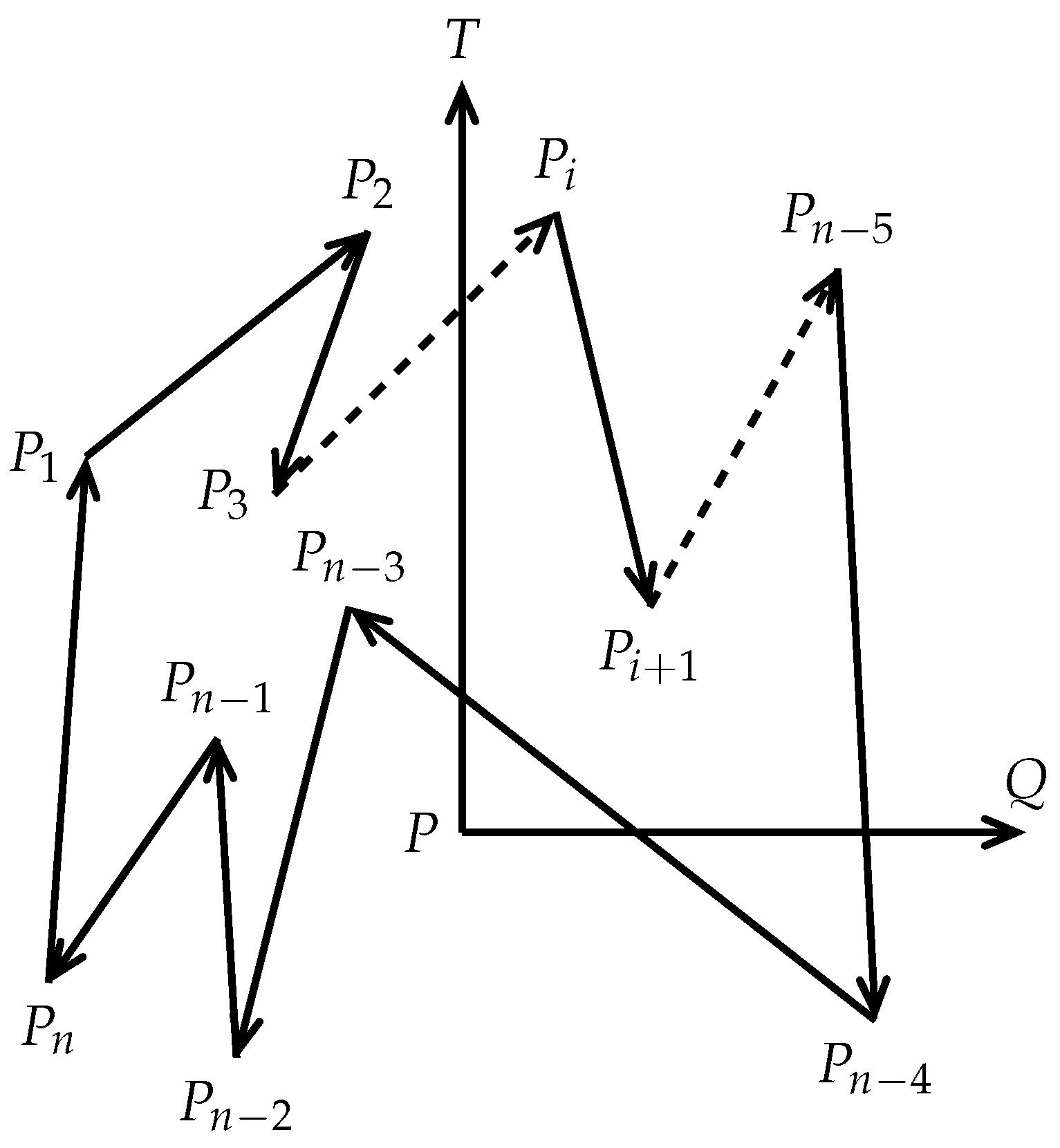
Let
S be a closed polygon on a plane with
n vertices
,
,
such that there exists an edge between
and
for all
and between
and
(see
Figure 5). Let
be an edge vector of
S. Let
be a point on the plane. We define a function
as follows:
Equation (
1) requires one addition, four subtractions, four multiplications, and a total of nine operations while Equation (
2) requires only five subtractions, two multiplications, and a total of seven operations. In addition, we know that multiplication takes more time than addition or subtraction. Therefore, to reduce the running times of our algorithms below, we always use Equation (
2).
Definition 2. Given an edge vector whose function with and .
satisfying the Jordan property means that the edge vector divides the plane into two half plane that are disconnected from each other (see Figure 6). Therefore, satisfying the Jordan property can also be called the vector satisfies Jordan property. Assume that
is a horizontal ray that starts at
, passes through
, and extends infinitely in the
direction (see
Figure 5). We define a variable
to accumulate the total number of intersections made by
and all edges of
S. By (
2) for
, it follows that
because
,
and
are either all positive or all negative. For
with
, if
, then
is on the left side of
(above). Otherwise, if
, then
is on the right side of
(below). If neither is true, then
is on the ray
. By substituting
into Equation (
2), we establish the following equation.
Starting from the point
, we traverse each edge vector
of
S exactly once and manage to determine the positional relationship between
and
. Thus, without calculating the intersection point, one can accurately determine whether
and
intersect each other. Furthermore, if
and
intersect each other, we set
. By carefully analyzing whether
and
intersect each other, and whether the point
P is on
, it can be seen that
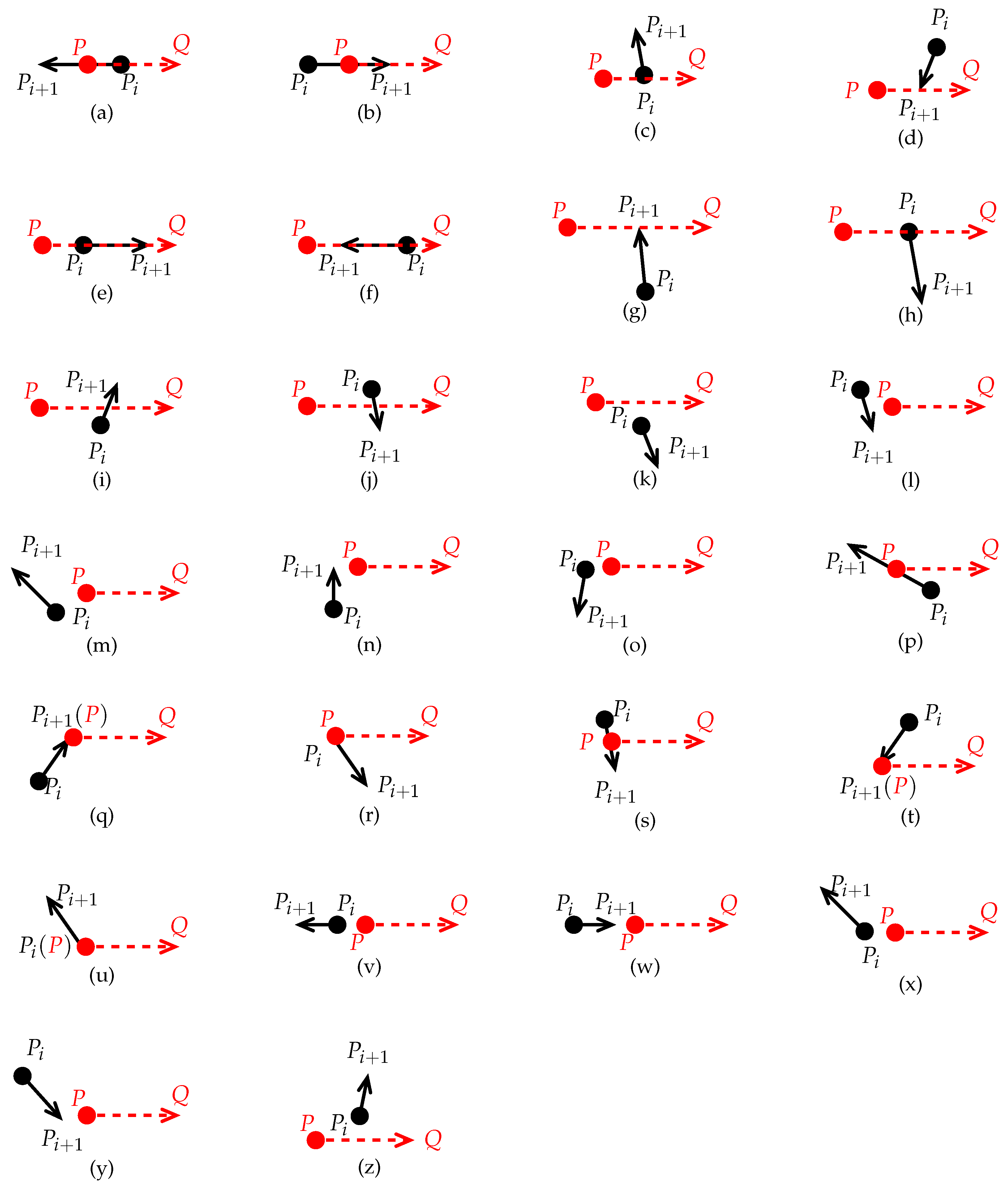
with
can have the following 26 different positional relationships (see
Figure 2).
,
P is on
(see
Figure 2a). Thus,
P is on
.
,
P is on
(see
Figure 2b. Thus,
P is on
.
,
P is on the back-left side of
( the viewing direction is along the direction of
, which is maintained below. see
Figure 2c). Thus,
intersects
and we set
.
,
P is on the front-right side of
(see
Figure 2d). Thus,
intersects
and we set
.
,
and
have the same direction, and the edge
is shorter than the edge
(see
Figure 2e). Although both overlap each other on
, we regard them as having no intersection, and
k remains unchanged.
,
overlaps
, and both have opposite directions (see
Figure 2f). Although both overlap on
, we regard them as having no intersection, and remain
k unchanged.
,
P is on the front-left side of
(see
Figure 2g). Although
intersects
at
, we regard them as having no intersection, and
k remains unchanged.
,
P is on the back-right side of
(see
Figure 2h). Although
intersects
at
, we regard them as having no intersection, and
k remains unchanged (similar to Case 7).
,
P is on the left-middle side of
(see
Figure 2i). Thus,
intersects
, and we set
.
,
P is on the right-middle side of
(see
Figure 2j). Thus,
intersects
, and we set
.
,
is on the right side of
(below) (see
Figure 2k). Thus, both are disjoint, and
k remains unchanged.
,
is also on the left side of
(see
Figure 2l). Thus, both are disjoint, and
k remains unchanged.
,
is on the right side of
(see
Figure 2m). Thus, both are disjoint, and
k remains unchanged.
,
is on the right side of
(see
Figure 2n). Thus, both are disjoint, and
k remains unchanged.
,
is on the left side of
(see
Figure 2o). Thus, both are disjoint, and
k remains unchanged.
,
P is on
(see
Figure 2p).
,
P is on
(see
Figure 2q).
,
P is on
(see
Figure 2r).
,
P is on
(see
Figure 2s).
,
P is on
(see
Figure 2t).
,
P is on
(see
Figure 2u).
,
and
are mutually separate, and both have opposite directions
(see
Figure 2v). Thus, they are disjoint, and
k remains unchanged.
,
and
are disjoint
(see
Figure 2w), and
k remains unchanged.
,
P is on the back-right side of
, and
and
are disjoint
(see
Figure 2x). Thus,
k remains unchanged.
,
P is on the front-left side of
, and
and
are disjoint
(see
Figure 2y). Thus,
k remains unchanged.
,
is on the left side of
(above), and
and
are disjoint
(see
Figure 2z). Thus,
k remains unchanged.
Further, we can classify and simplify the 26 positional relationships into three classes:
Class 1 includes Cases 3, 4, 9, and 10, for each of which intersects . Therefore, we set .
Class 2 includes Cases 1, 2, and 16–21, for each of which P is on .
Class 3 includes the remaining cases, for each of which and are disjoint. Therefore, k remains unchanged.
To facilitate the analysis and processing of the problem, we give each vector involved in these operations a number code of 1–26 such that each vector
in
Figure 2a–z has a number code of 1–26, which is one-to-one correspondence with Cases 1–26.
Definition 3. Let S consist of a set of closed polygons. The minimum bounding box of S, denoted by , is the smallest box that encloses the entire S and is axis-aligned rather than oriented-aligned.
For the point-in-polygon test and boolean operations, our methodology can be divided into two steps. The first step performs preprocessing to determine whether a point lies inside or outside the minimum bounding box of input polygons. If the point lies within the , we then perform the second step to determine whether the point is inside or outside the polygon.
Occasionally, a user may need to handle polygons with small sizes. Clearly, the occurrence probability of input polygons with limited sizes, involved in operations, is low. For example, let us consider the possibility of occurrence that the input polygon has vertices (0,0), (1,1), (1,) with small t. It is true that this probability is tiny. Furthermore, it follows that the probability of a point lying on the boundary of a polygon is approximately zero, since the actual width the edge of a polygon in use is not 0.
To optimize our algorithms, we can let the program automatically calculates the probabilities of a point lying within and outside a polygon. If the probability of the point lying within the polygon is greater than the probability of the point lying outside the polygon when the minimum bounding box has been calculated, we let the program first decide whether the point is within the polygon, and then decide whether the point is outside the polygon. Conversely, if the probability of the point lying outside the polygon is greater than the probability of the point lying within the polygon, we let the program first decide whether the point is outside the polygon, and then decide whether the point is within the polygon. Since the probability of the point lying on the boundary of the polygon is approximately zero, we let the program at last decide whether the point is on the polygon. In this paper, we assume that the probability of a point lying within a polygon is greater than the probability of the point lying outside the polygon.
Definition 4. Let S be a closed polygon and P a point on the plane. If P is on an edge of S, then we set . Otherwise, we set k equal to the number of intersections made by the ray and all edges of S. We define the variable k as the point P is odd-even number around S, referred to as the point P is odd-even number, denoted by .
In addition, when P is inside the of S (see Definition 1), if the k is even, then we call P outside S. On the contrary, if the k is odd, then we call P inside S.
Lemma 1. Let S be a closed polygon and P a point on the plane. By Definition 1, assume that Γ is a ring of S, which intersects with . Assume that are all intersections produced by and all edges of Γ with . Then, the P is outside Γ if and only if the t is an even.
Proof. By the conditions of Lemma 1, we have that
are the intersections produced by
and all edges of
. In
Figure 2a–z, it can be observed that
and just the
in
Figure 2c,d,i or
Figure 2j can have intersections.
Let us first prove the necessity. Suppose the P is outside S.
At first, we let and . For the intersections U, our proof is divided into the following two main steps.
From the intersection sequence , we remove and , and let and k = k + 1. Then, we repeat the above Steps 1 and 2 until there is no intersection in the intersection sequence . Finally, it can be seen that the conclusion of Lemma 1 holds.
Let us prove the sufficiency in Lemma 1. Suppose the t is even.
We use the induction for .
If
, by
Figure 2a–z, suppose the pair of intersections are
and
. Further, let us assume that
, then
must belong to an element of
(see the proof of the necessity of Lemma 1). Regardless of which element
belongs to
, eventually it can be seen that
P is outside
. Therefore, it is established that
P is outside
for
.
Suppose that P is outside for .
Let us prove that P is outside for .
Suppose that there exists a point that is outside for ; it can be asserted that there is always a point outside such that the number of pairs of intersection points of and is k.
Assume that only the x coordinate of the two intersections and is less than the x coordinate of any other intersection, and and meet condition .
Further, let us assume that , then must belong to an element of , , , , (see the proof of the necessity of Lemma 1). Regardless of which element belongs to , on the ray , there is only one pair of intersections and produced by and all edges of . Therefore, it can be inferred that P is outside .
Eventually, it can be seen that P is outside for . Therefore, it is established that P is outside for . □
Lemma 2. Let S be a closed polygon and P a point on the plane. By Definition 1, assume that Γ is a ring of S, which intersects with . Assume that are all intersections produced by and all edges of Γ with . Then, P is inside Γ if and only if the t is an odd.
Proof. Let us first prove the necessity. Suppose the P is inside . We now prove the necessity of Lemma 2 by contradiction. Assume by contradiction that the t is an even.
Then, by the sufficiency of Lemma 1, it follows that the P is outside , leading to a contradiction with the constraint that the P is inside . Therefore, the assumption that the t is an even does not hold. The necessity of Lemma 2 immediately follows.
Next, let us prove the sufficiency in Lemma 2. Suppose the t is an odd. We now prove the sufficiency of Lemma 2 by contradiction. Assume by contradiction that the P is outside .
Then, by the necessity of Lemma 1, it is clear that the t is an even, leading to a contradiction with the constraint that the t is an odd. Therefore, the assumption that the P is outside does not holds. The sufficiency of Lemma 2 immediately follows. □
Theorem 1. Let S be a closed polygon and P a point on the plane. If P is on the boundary of S, then the point P is odd-even number . Otherwise, if P is outside S, then is 0 or even. Otherwise, if P is inside S, is odd.
Proof. Our proof of Theorem 1 is divided into the following four main steps.
If P is on the boundary of S, then P is on an edge vector of S. Therefore, by Definition 4, it follows that the point P is odd-even number .
Otherwise, if P is outside S and does not intersect any edge of S, then by Definition 4.
Otherwise, if P is outside the of S (see Definition 1) and condition the number of intersections holds between and all edges of S, below let us prove that the number of intersections is even.
Let us assume that intersects with the , , ⋯, of S. By Lemma 1, it follows that the number of intersections produced by and all edges of is an even for . Therefore, the total number of intersections produced by and the , , ⋯, of S is an even and this conclusion that is even holds.
Otherwise, if P is inside the of S (see Definition 1). Let us assume that are all rings of S each of which the P is outside. Similarly, let us assume that are all rings of S each of which the P is within.
By the necessity of Lemma 1, it follows that the number of intersections between and is an even for . As a result, the total number of intersections produced by and is an even with .
Similarly, by the necessity of Lemma 2, it follows that the number of intersections between and is an odd(denoted by ) for . As a result, the total number of intersections produced by and with is whose parity is consistent with the parity of m.
Accordingly, if m is an even, then the k that denotes the number of intersections made by and all edges of S is also an even, and vice versa.
Eventually, when P is inside the of S, by Definition 4, it follows that
- (a)
If the k is even, then the P is outside S and is even.
- (b)
Conversely, if the k is odd, then the P is inside S and is odd.
□
| Algorithm 1: Determine whether P is inside, outside, or on . It cannot solve the problem of instability that can result from the comparison operations of floating-point numbers. |
![Symmetry 10 00477 i001 Symmetry 10 00477 i001]() |
4. A Serial Algorithm for the Point-in-Polygon Test
In this section, we show the serial Algorithm 1 for the point-in-polygon test that uses many comparison operations of floating-point numbers. One may worry that the comparison operations of floating-point numbers can lead to the floating point errors, which would cause the program to run incorrectly. The results of the experiment show that this worry is superfluous (see the conclusion of
Section 7).
Now, let us present the serial Algorithm 1 in detail. By using calculated values from previous Steps 4 and 7 in Algorithm 1, Steps 9, 15, 21, and 24 calculate the variable
f that corresponds to the function
F in Equation (
3). The for-loop in Steps 3–30 handles each edge
in turn and determines which case the positional relationship between
and
P belongs to, as shown in
Figure 2.
Steps 5–6 deal with Cases 11 and 26, as shown in
Figure 2k,z.
Steps 8–13 handle Cases 3, 9, 16, 21, 13, and 24 (see
Figure 2c,i,p,u,m,x). Furthermore, Step 11 corresponds to Case 3 or 9, while Step 13 corresponds to Case 16 or 21. The rest correspond to Case 13 or 24.
Steps 14–19 handle Cases 4, 10, 19, 20, 12, and 25 (see
Figure 2d,j,s,t,l,y). Furthermore, Step 17 corresponds to Case 4 or 10, while Step 19 corresponds to Case 19 or 20. The rest correspond to Case 12 or 25.
Steps 20–22 handle Cases 7, 14, and 17 (see
Figure 2g,n,q). Furthermore, Step 22 corresponds to Case 17. The rest correspond to Case 7 or 14.
Steps 23–25 handle Cases 8, 15, and 18 (see
Figure 2h,o,r). Furthermore, Step 25 corresponds to Case 18. The rest correspond to Case 8 or 15.
Steps 26–30 handle Cases 1, 2, 5, 6, 22, and 23 (see
Figure 2a,b,e,f,v,w). Furthermore, Step 28 corresponds to Case 1. Step 30 corresponds to Case 2. The rest correspond to Case 5, 6, 22, or 23.
Algorithm 1 does not clearly indicate how to deal with the remaining cases, including Cases 5–8, 12–15, and 22–25 (see
Figure 2e–h,l–o,v–y). However, no matter which of them appears,
k does not change and
P is not on
, therefore Algorithm 1 does not require any additional process step.
From the above discussion, it follows that Algorithm 1 can operate correctly under any condition and has been optimized for speed and robustness. Finally, using k, by Steps 31–32 Algorithm 1 can determine whether P is within, outside, or on S. Algorithm 1 is parallelizable because many of its operations can be done in parallel.
5. Boolean Operations Principle and Algorithm
In this section, we show the basic principle for boolean operations by deriving Theorems 2 and 3. Furthermore, we present a new Algorithm 2 for boolean operations. Let be a polygon with m vertices and m corresponding edges , . Let be a polygon with n vertices and n corresponding edges , , , . Let or .
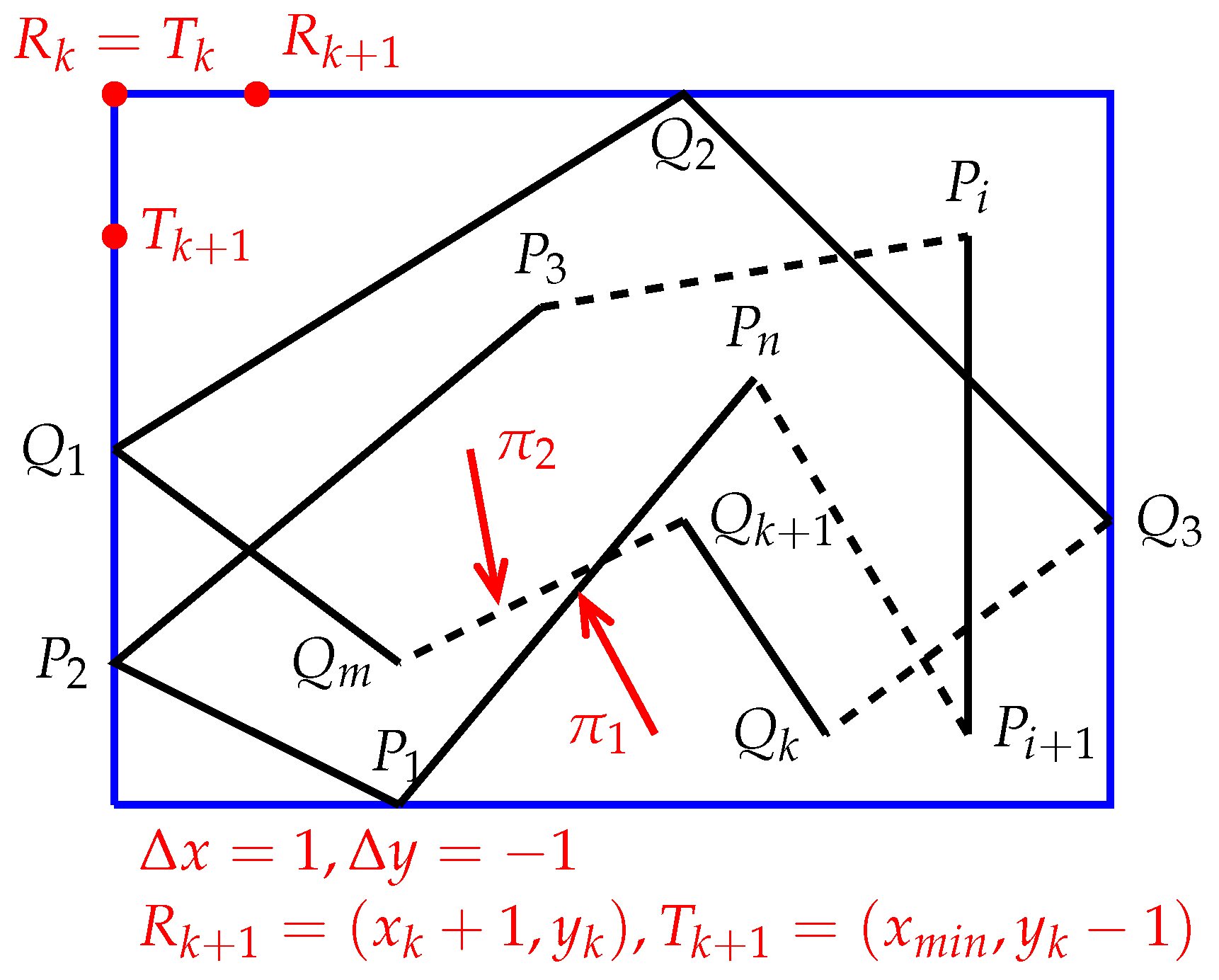
First, Algorithm 2 calculates the minimum bounding box of and denoted by . Then, starting from the top-left corner of the , Algorithm 2 scans the point by point, from left to right and from top to bottom until reaching the bottom-right corner. For each point involved, Algorithm 2 determines the positional relationship between P() and and between P() and .
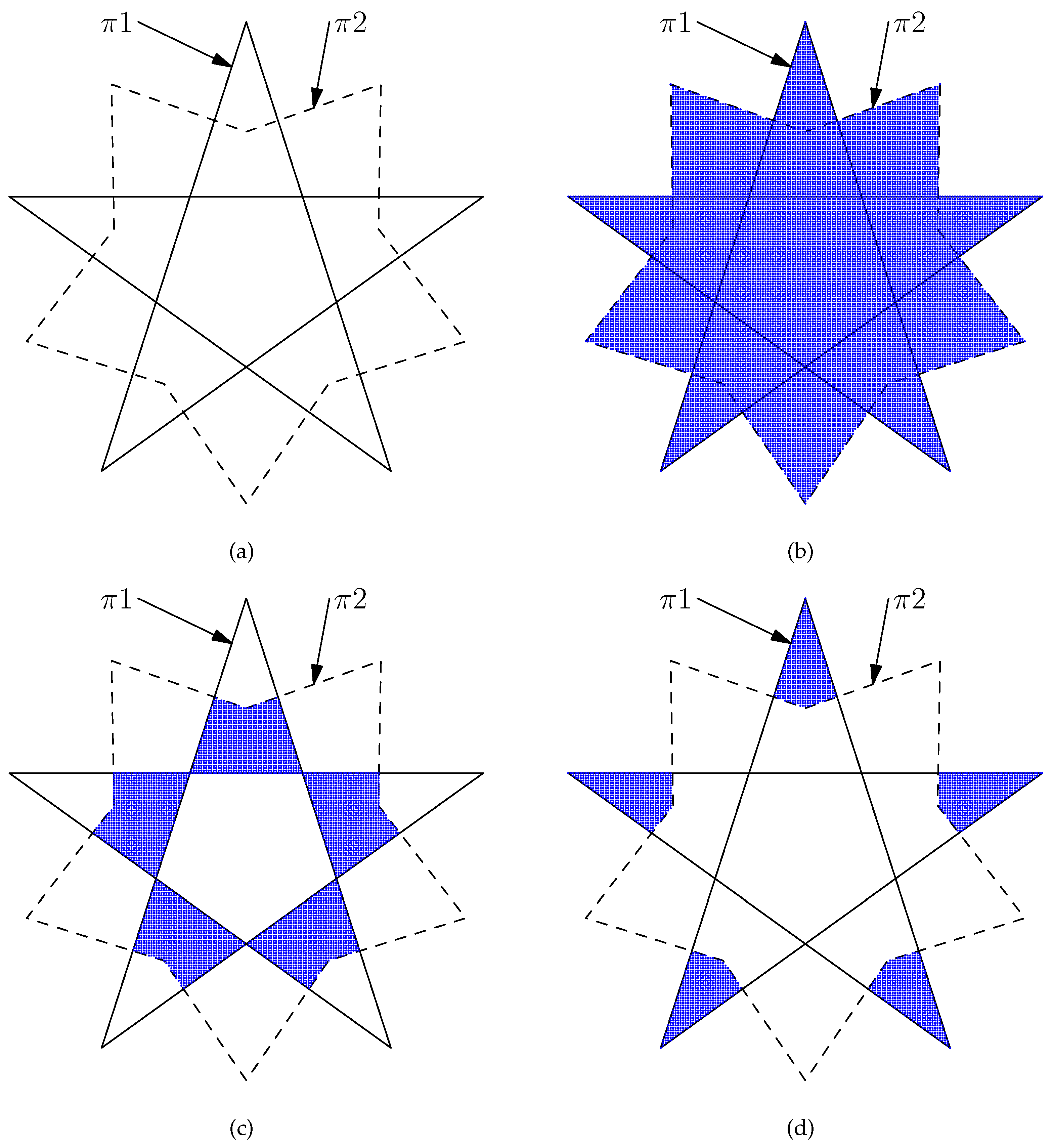
Using differential calculus, we will derive two iterative formulas by which Algorithm 2 can quickly determine the positional relationships between a set of points and a set of polygons. For this purpose, assume that Algorithm 2 sweeps across an intermediate point
(
and see
Figure 7), and the meaning of
Q (below) is the same as the previous definition of
Q. Suppose that Algorithm 2 already knows if
is inside, outside, or on the boundary of
S. Let
(
and see
Figure 7),
, and
where
is the smallest
x-coordinate of the
. For the point
, the following situations may occur:
is in the top-left corner of
(see
Figure 8).
is on the left border of
(see
Figure 9).
| Algorithm 2: Performing boolean operations on two polygons. |
![Symmetry 10 00477 i002 Symmetry 10 00477 i002]()
![Symmetry 10 00477 i003 Symmetry 10 00477 i003]() |
In Case 1, the equalities hold, where is the smallest x-coordinate of and is the largest y-coordinate of . Thus, we have , , and .
In Case 2, the equalities hold, where is the smallest x-coordinate of . Therefore, we have , , and .
In Case 3, with , , the condition holds, where is the smallest x-coordinate of . Therefore, we have , , and .
In
Figure 7, assume that
and
. Then,
and
. If
(
P in
Figure 2) is outside
S and the variable
k is 0, then
does not intersect
for any
,
m. Thus, the positional relationships between
and
belong to Cases 5–8, 11–15, or 22–26 (see
Figure 2). Therefore, to determine the positional relationships between
and
, Algorithm 2 only must recheck those edges whose positional relationships with
belong to Cases 5–8. Likewise, if
(
P in
Figure 2) is outside
S and the variable
k is 0, to determine the positional relationships between
and
, Algorithm 2 only must recheck those edges whose positional relationships with
belong to Cases 7–15.
If the variable
k is even or odd, then the positional relationships between
(
corresponds to
P in
Figure 2) and
do not belong to Cases 1, 2, and 16–21. Therefore, to determine the positional relationships between
and
, Algorithm 2 only must recheck those edges whose positional relationships with
belong to Cases 3–10. Likewise, if the variable
k is even or odd, the positional relationships between
(
corresponds to
P in
Figure 2) and
do not belong to Cases 1, 2, and 16–21, to determine the positional relationships between
(
corresponds to
P in
Figure 2) and
, Algorithm 2 only must recheck those edges whose positional relationships with
belong to Cases 7–15.
If
(
P in
Figure 2) is on the boundary of
S, then the positional relationships between
and
belong to Cases 1, 2, or 16–21. Therefore, to determine the positional relationships between
and
, Algorithm 2 only must recheck those edges whose positional relationships with
belong to Case 1–10. Likewise, if
(
P in
Figure 2) is on the boundary of
S, to determine the positional relationships between
and
, Algorithm 2 only must recheck those edges whose positional relationships with
belong to Cases 7–19.
From the above comparative analysis, it can be seen that to determine the positional relationship between and S, Algorithm 2 does not need to recheck all edges of S and usually needs only to recheck a small number of the edges whose number depends on the positional relationship between and S. Summarizing these findings, we get the following Theorem 2 by Definition 4.
Theorem 2. Suppose that and are two polygons. Assume that is the minimum bounding box of and . Let be a point inside or on the boundary of , and assume is a point on the left border of , where is the smallest x-coordinate of (see Figure 8). Let and , . Let or . Assume that , and . - 1.
If the odd-even number , to calculate one needs only to recheck the edges of S belonging to Cases 5–8 (see Figure 2). Likewise, if the odd-even number , to calculate , one needs only to recheck the edges of S belonging to Cases 7–15 (see Figure 2). - 2.
If the odd-even number is even or odd, to calculate one needs only to recheck the edges of S belonging to Cases 3–10 (see Figure 2). Likewise, if the odd-even number is even or odd, to calculate , one needs only to recheck the edges of S belonging to Cases 7–15 (see Figure 2). - 3.
If the odd-even number , to calculate , one needs only to recheck the edges of S belonging to Cases 1–10 (see Figure 2). Likewise, if the odd-even number , to calculate , one needs only to recheck the edges of S belonging to Cases 7–19 (see Figure 2).
Proof. 1. If the odd-even number
, then
(
P in
Figure 2) is outside
S and
does not intersect
for any
,
m. Thus, the positional relationships between
and
only belong to Cases 5–8, 11–15, or 22–26 (see
Figure 2). Therefore, to determine the positional relationships between
and
for calculating
, one needs only to recheck the edges of
S belonging to Cases 5–8 (see
Figure 2). Likewise, if the odd-even number
, then
(
P in
Figure 2) is outside
S. Thus, the positional relationships between
and
only belong to Cases 5–8, 11–15, or 22–26. Therefore, to determine the positional relationships between
and
for calculatint
, one needs only to recheck the edges of
S belonging to Cases 7–15 (see
Figure 2).
2. If the odd-even number
is even or odd, then the positional relationships between
(
corresponds to
P in
Figure 2) and
do not belong to Cases 1, 2, and 16–21. Therefore, to determine the positional relationships between
and
for calculating
, one needs only to recheck the edges of
S belonging to Cases 3–10 (see
Figure 2). Likewise, if the odd-even number
is even or odd, then the positional relationships between
(
corresponds to
P in
Figure 2) and
also do not belong to Cases 1, 2, and 16–21. Therefore, to determine the positional relationships between
(
corresponds to
P in
Figure 2) and
for calculating
, one needs only to recheck the edges of
S belonging to Cases 7–15 (see
Figure 2).
3. If the odd-even number
, then
(
P in
Figure 2) is on the boundary of
S, then the positional relationships between
and
only belong to Cases 1, 2, or 16–21. Therefore, to determine the positional relationships between
and
for calculating
, one needs only to recheck the edges of
S belonging to Cases 1–10 (see
Figure 2). Likewise, if the odd-even number
, then
(
P in
Figure 2) is on the boundary of
S. Thus, the positional relationships between
and
only belong to Cases 1, 2, or 16–21. Therefore, to determine the positional relationships between
and
for calculating
, one needs only to recheck the edges of
S belonging to Cases 7–19 (see
Figure 2). □
Theorem 3. Suppose that and are two polygons. Assume that is the minimum bounding box of and . Let be a point inside or on the edges of , and is a point on the left border of , where is the smallest x-coordinate of . Let and (see Figure 7, Figure 8 and Figure 9). Let or . Suppose that is an edge of or with and . Assume that and . If and satisfy Equation (1), then the following two iterative formulas hold. By Equations (
4) and (5), if Algorithm 2 already knows
and
, Algorithm 2 can quickly calculate
and
. Therefore, using Equations (
4) and (5), one can simplify the calculation and improve processing speed significantly.
By Theorems 2 and 3, and Algorithm 1, vertex by vertex, Algorithm 2 determines the positional relationship between and , yet between and . Furthermore, according to the types of boolean operations, if is simultaneously inside and (also including on their border), then . Otherwise, if is inside or (also including on their border), then . Otherwise, if is both inside (also including on its border) and outside , then . Otherwise, if is both outside and inside (also including on their border), then . Step-by-step, Algorithm 2 is well able to complete the corresponding boolean operations. Algorithm 2 is a comprehensive presentation and summary for all preceding discussion.
Proof. By Equation (
1), for
and
we have
□
6. Complexity Analysis of Algorithms
In this section, we analyze the time and space complexities of our algorithms. First, let us consider Algorithm 1. Assume that the number of edges of a polygon is n. The for-loop in Steps 3–30 determines the positional relationship between point P and the n edge vectors with . Steps 4 and 7 each perform two subtractions. One subtraction and two multiplication calculations are performed in function f in Steps 9, 15, 21, and 24. Step 5 performs at most seven operations, including four comparison operations and three logical operations. Steps 8, 14, 20, 23, 26, 27, and 29 each perform at most two comparison operations and one logical operation.
In the worst case, the for-loop must perform Steps 4–7, 8, 14, 20, 23, 26, 27, 29, and 30 simultaneously. Thus, the number of operations in the for-loop is equal to . Therefore, the total number of operations required is . Conversely, in the best case, the point P is on , and the for-loop must only perform Steps 4–10, 12, and 13 one time. As a result, the number of operations required is .
Furthermore, let us compute the average running time of Algorithm 1. Algorithm 1 includes many branch statements whose execution probabilities are all different. From the previous discussions, we know that the probability of a point lying on the boundary is far less than the probability of the point not lying on the boundary. Therefore, to calculate the average running time required by Algorithm 1, we only must consider the case in which the point is not on . Furthermore, we only must consider the paths that the for-loop most likely performs, 4→5→6, 4→5→7→8→9→10→11, or 4→5→7→8→14→15→16→17.
For an edge, the average number of operations required is
Because the number of polygon edges is n, the total average number of operations required is for Steps 3–30. Steps 31–32 require at most two logical operations, and one modulo operation. Therefore, the total average number of operations required is . Because Algorithm 1 uses an array to store the edge information, including the end nodes of each edge, its space complexity is also . The time and space complexities of Algorithm 1 are the same as Algorithm 1.
Second, let us consider Algorithm 2. Assume that the numbers of edges of two input polygons are
respectively. In addition, assume that execution probability of each branch is different for the for-loop in Algorithm 1. Step 5 requires at most 4
operations. For
R, on average, Step 10 requires
operations. Step 11 requires at most three operations. In the worst case, Steps 12–44 require at most
operations. Therefore, in the worst case, the time complexity of Algorithm 2 is
, where
Under normal circumstances, because the numbers of operations for Steps 10 and 12–44 are far less than
and
, the average time complexity of Algorithm 2 is far less than
. No matter how complex the input polygons are, it can be seen that
l is nearly constant. Thus, Algorithm 2 has an average time complexity of
, reconfirmed through the experimental results in
Section 7.
8. Results and Discussion
In
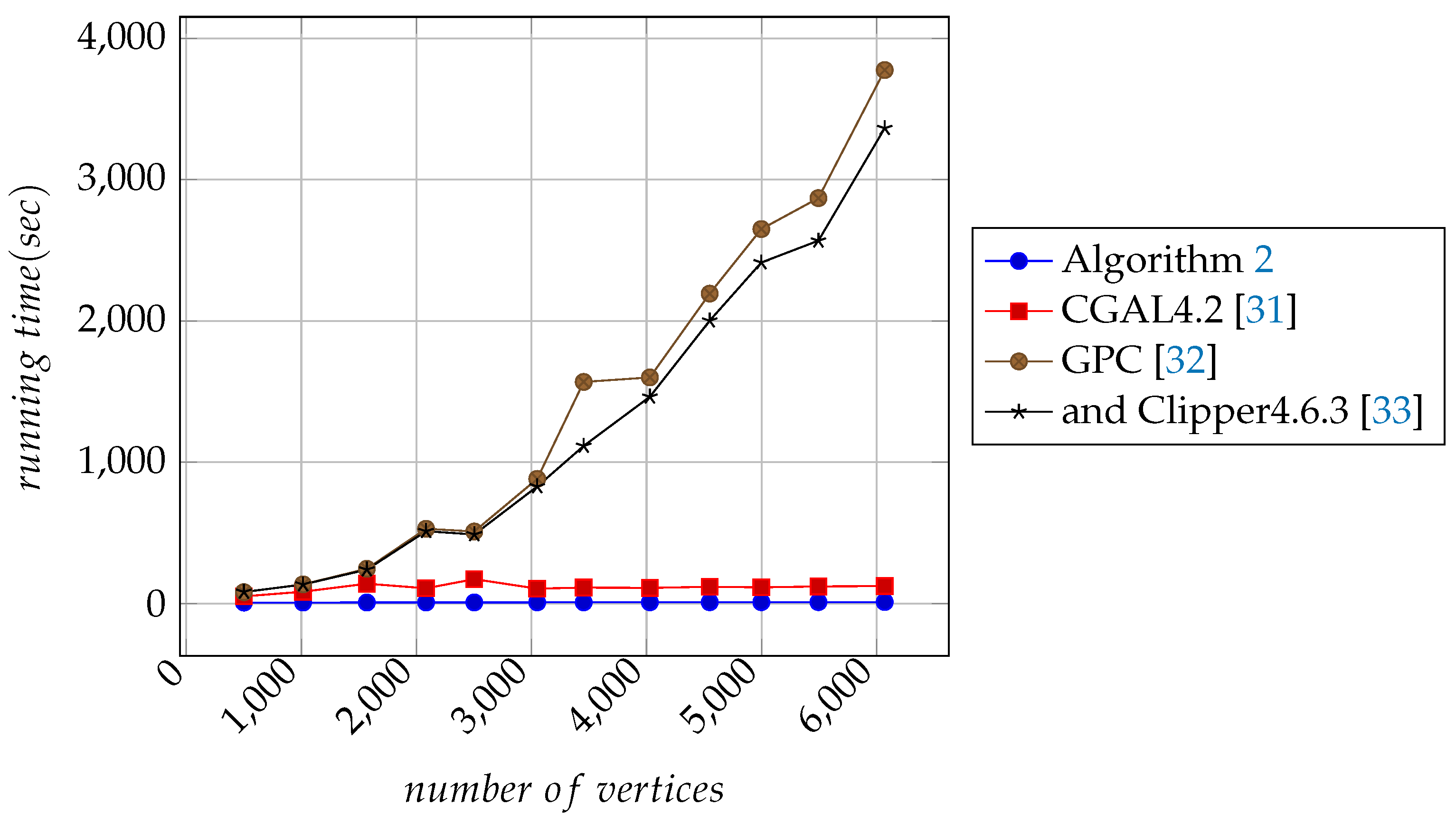
Figure 10, it can be seen that, with the increase of the number of vertices, the computation time of Algorithm 1 is getting less and less than the computational time of any other algorithm needed for the point-in-polygon test. This means that, with the increase of the number of points, the processing speed of Algorithm 1 is faster than any other algorithm.
Theorem 4. Let S be a closed polygon. The performance of Algorithm 1 is optimal for the point-in-polygon test on S.
Proof. By
Section 6, it follows that, because the total average number of operations required is
, the time complexity of Algorithm 1 is
where
n is the number of polygon edges. Clearly, the space complexity of Algorithm 1 is also
.
In
Figure 10, it can be seen that the run time of Algorithm 1 for the point-in-polygon test is minimal. Therefore, the computational performances of Algorithm 1 is better than that of the other algorithms. Observe that the related performances of Algorithms 1 described in
Table 1 go beyond that of the other algorithms except CGAL4.2 [
31].
Although the time and space complexities of Algorithm 1 are the same as the state-of-the-art methods for the point-in-polygon test, Algorithm 1 is optimal. Further, we present the following facts to support our view:
It handles all degenerate cases and simultaneously provides a corresponding solution to each degenerate case (see
Figure 2). These tactics both ensure its robustness and creates the prerequisites and basis for Algorithm 2.
It uses Equation (
3) to reduce the running time.
It uses the Jordan property of a vector to determine the positional relationship between a point and an edge, which avoids computing the intersection point and division operations.
It involves only addition, subtraction, multiplication, comparison, and logical operations such that it is unnecessary to compute any angle. In addition, It eliminates other time-consuming operations such as preprocessing.
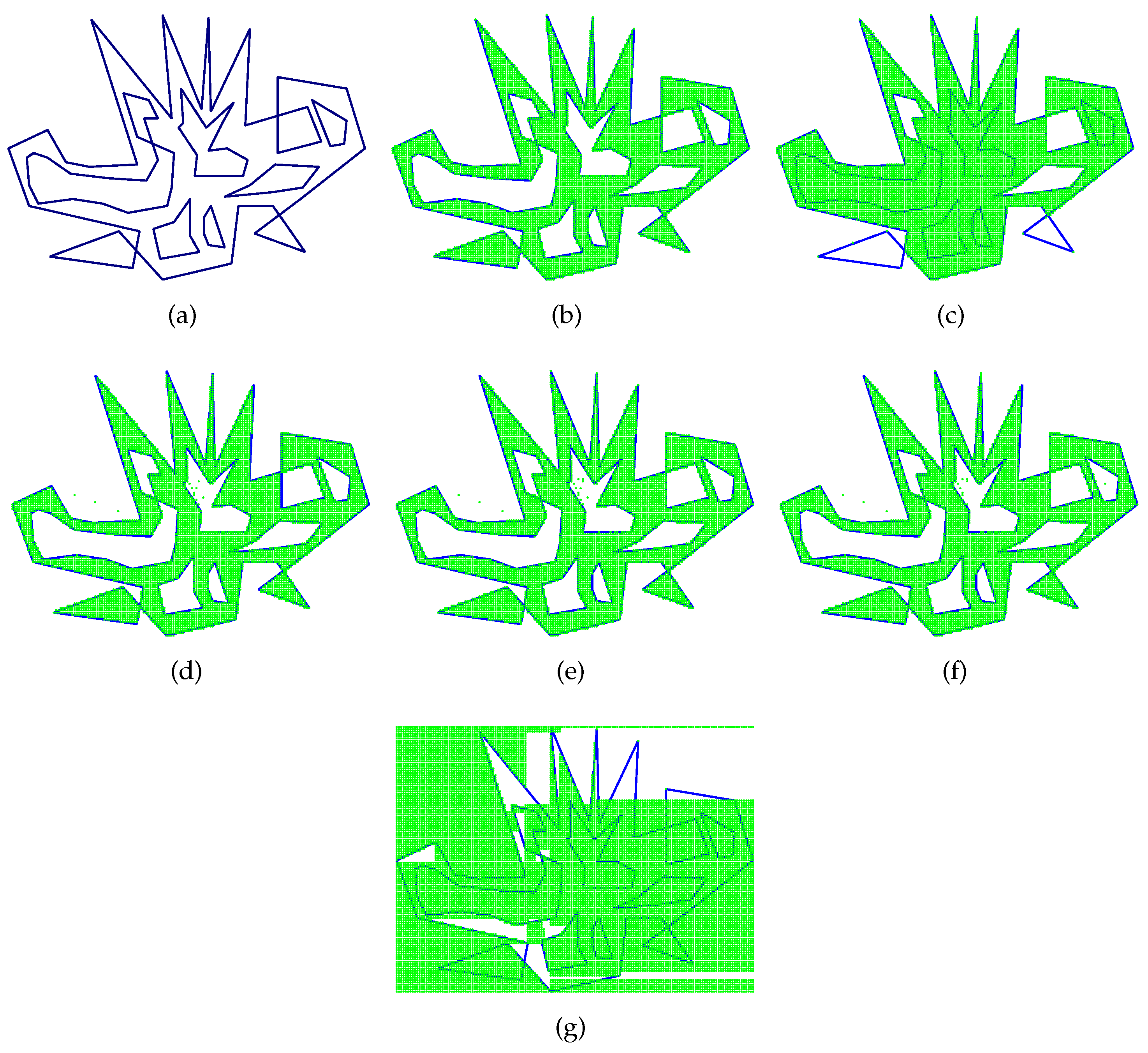
It does not impose any restrictions on the shape of input polygons, and is applicable to any polygons, including self-intersecting polygons or polygons with holes nested to any level of depth (see
Figure 3a). Therefore, It can both quickly determine whether a point is inside or outside a polygon and accurately determine the contours of input polygon (see
Figure 3b).
It does not need to sort the vertices clockwise or counterclockwise beforehand. Therefore, it processes all edges one by one in any order for each input polygon.
It is parallelizable because its many operations can be done in parallel.
A detailed theoretical analysis and the proof of the correctness of Algorithm 1 (see Theorems 1) for the point-in-polygon test are shown.
It considers the execution probability of each conditional branch and uses these probabilities to optimize the program flow.
Therefore, it follows that the conclusion of Theorem 4 holds. □
Although the comparison operations of floating point numbers introduced in Algorithm 1 increase the running time of the program and reduce its computing speed, the speed reduction is limited and would not cause the program significantly reduced operating speed. Although Algorithm 1 uses many comparison operations of floating-point numbers, this does not cause the program to run incorrectly. Performance of Algorithm 1 is only subjected to the number of vertices of tested polygon, rather than the number of floating point operations involved.
Based on Algorithm 1, Algorithm 2 inherits all of its advantages, including the simple data structure, low running time, high stability, and reliability. Algorithm 2 assigns each vector
in
Figure 2a–z a number code corresponding to Cases 1–26. In addition, Algorithm 2 uses two iterative formulas (Equations (
4) and (5)) to calculate
and
. Results from experiments show that the use of the two strategies increase processing speed and can accurately solve the given problem.
Our method can be applied to 3D printing [
8] to improve the 3D printing performance. The mechanism that we conceive for 3D printing is as follows: When performing 3D printing, we first use the planes
to intercept object in the size of the
z-axis from small to large, and then we apply Algorithm 2 on the plane
. This will enable 3D printing.