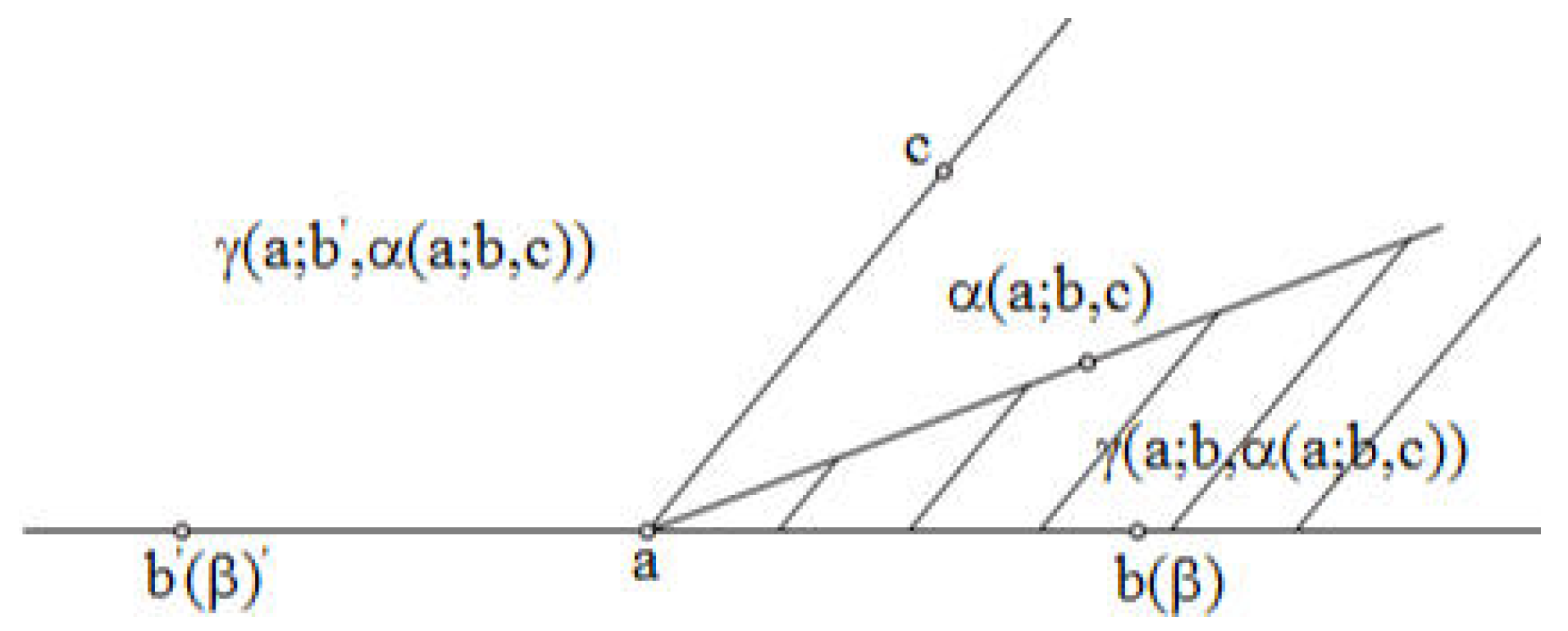
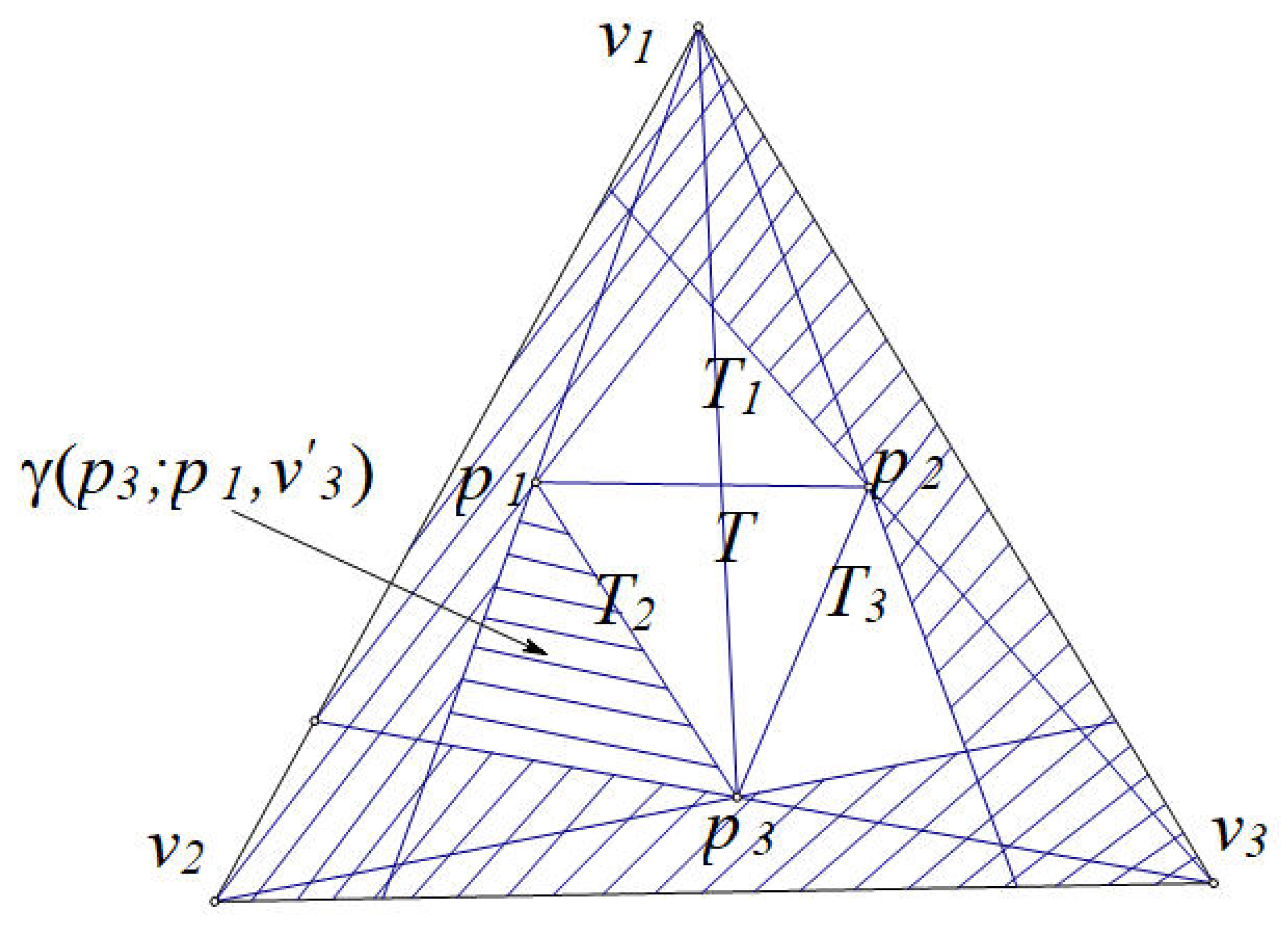
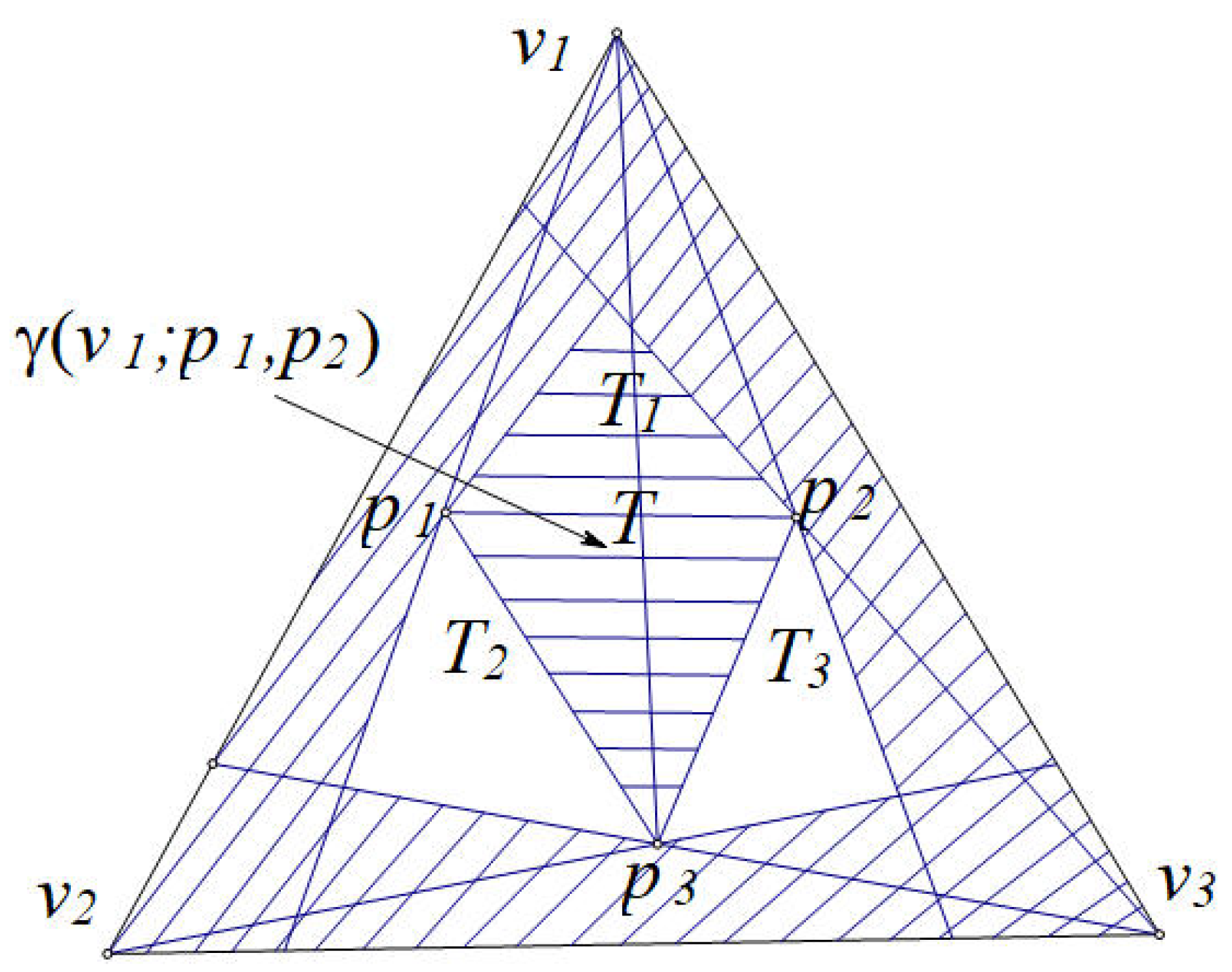
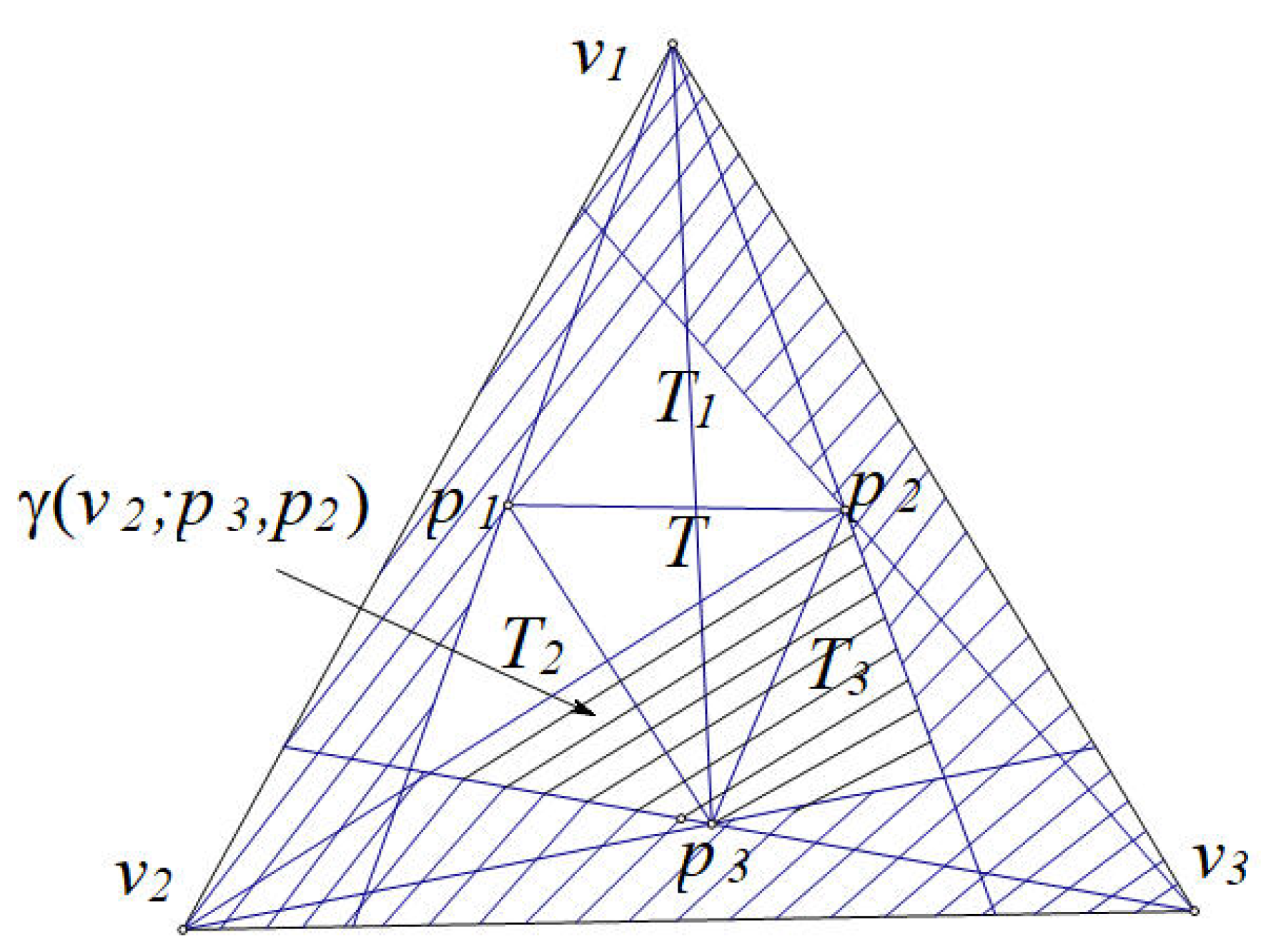
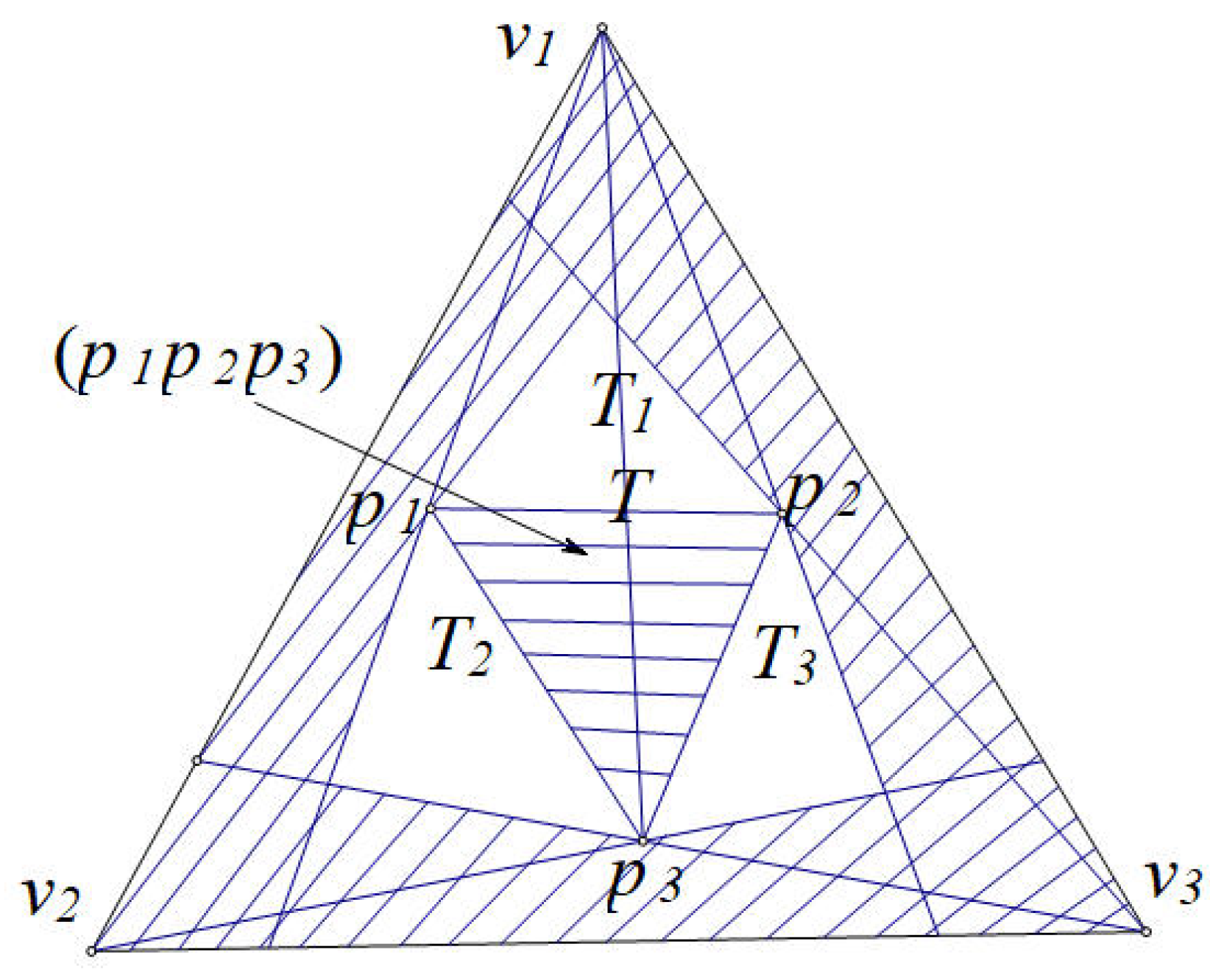
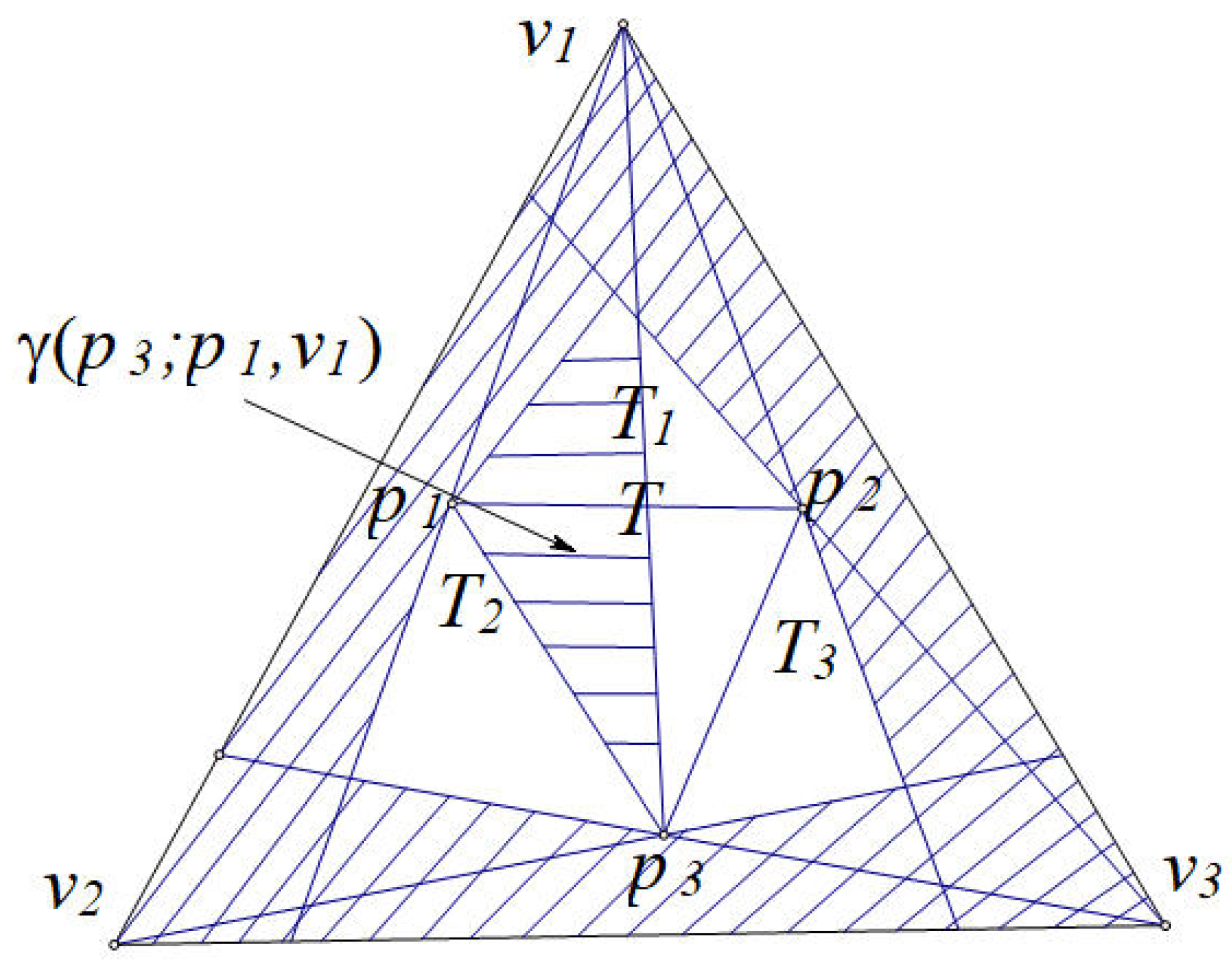
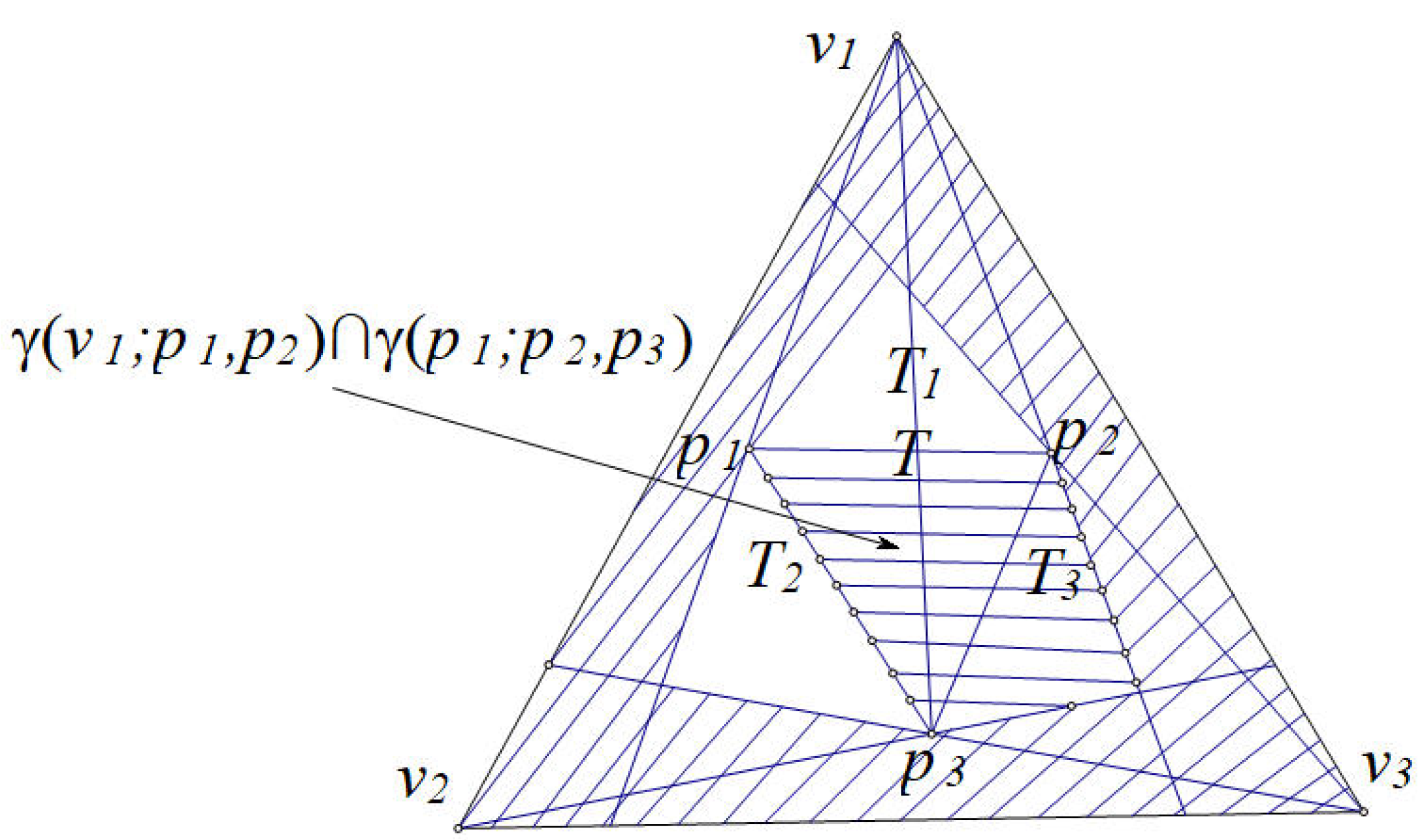
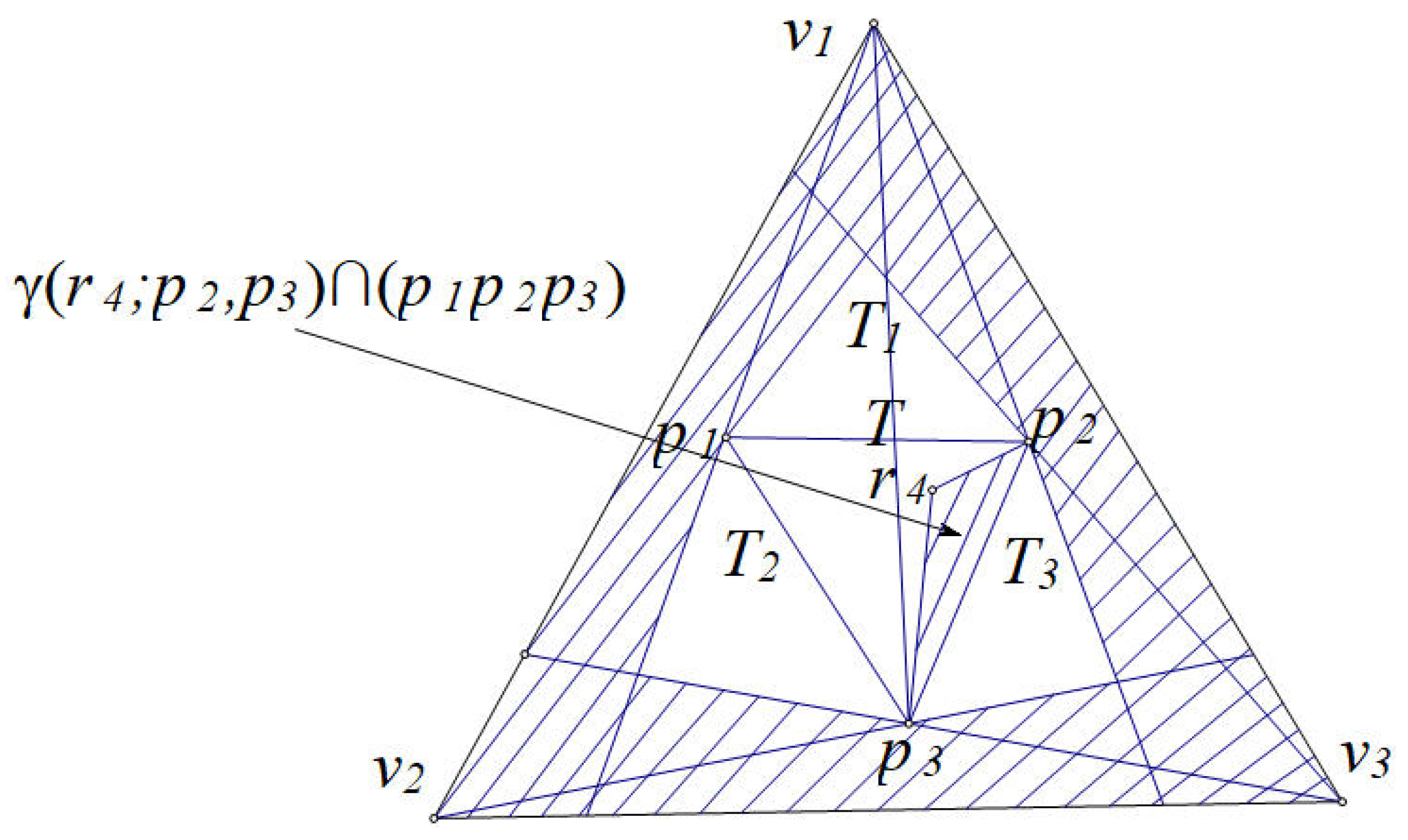
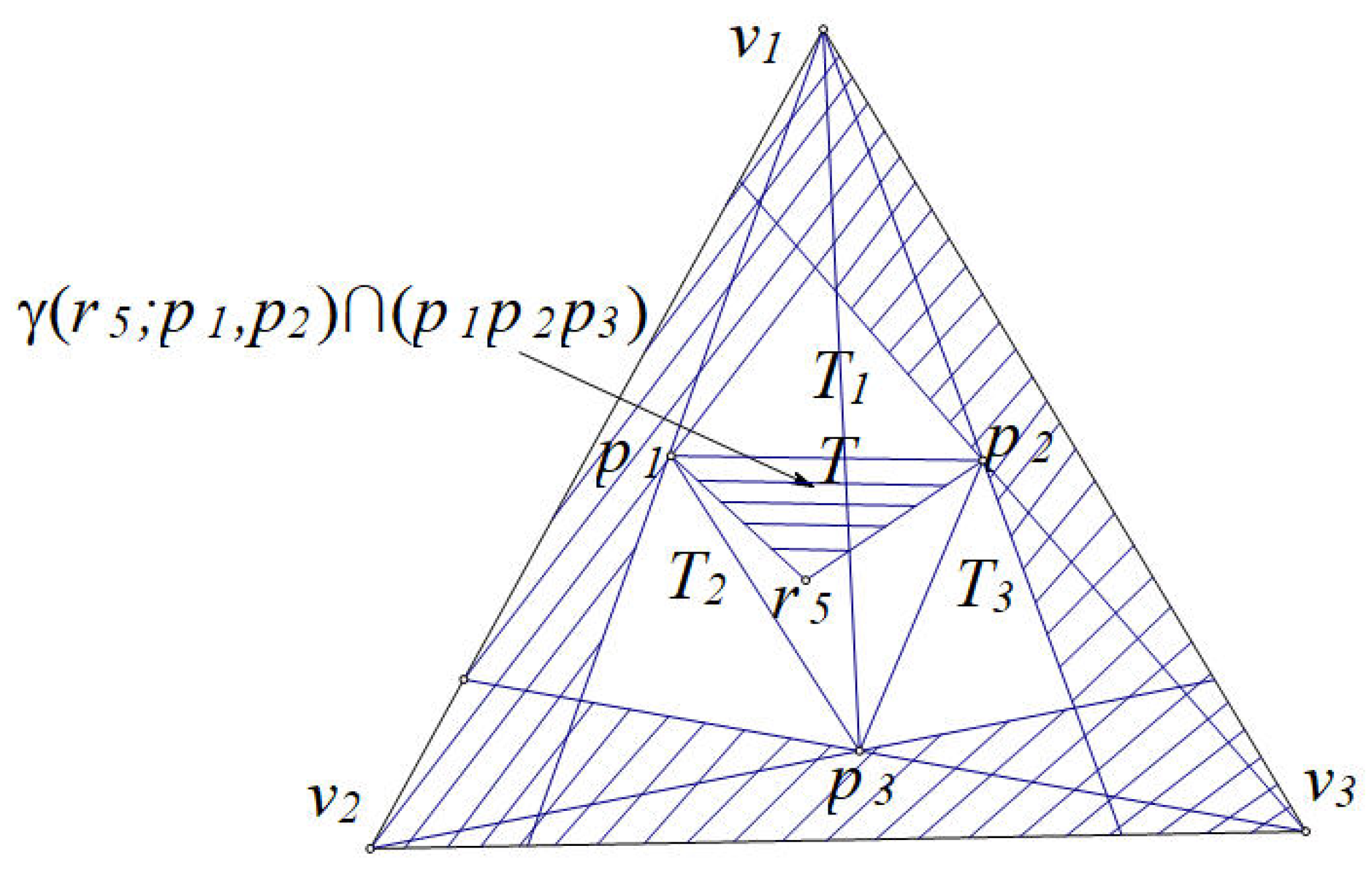
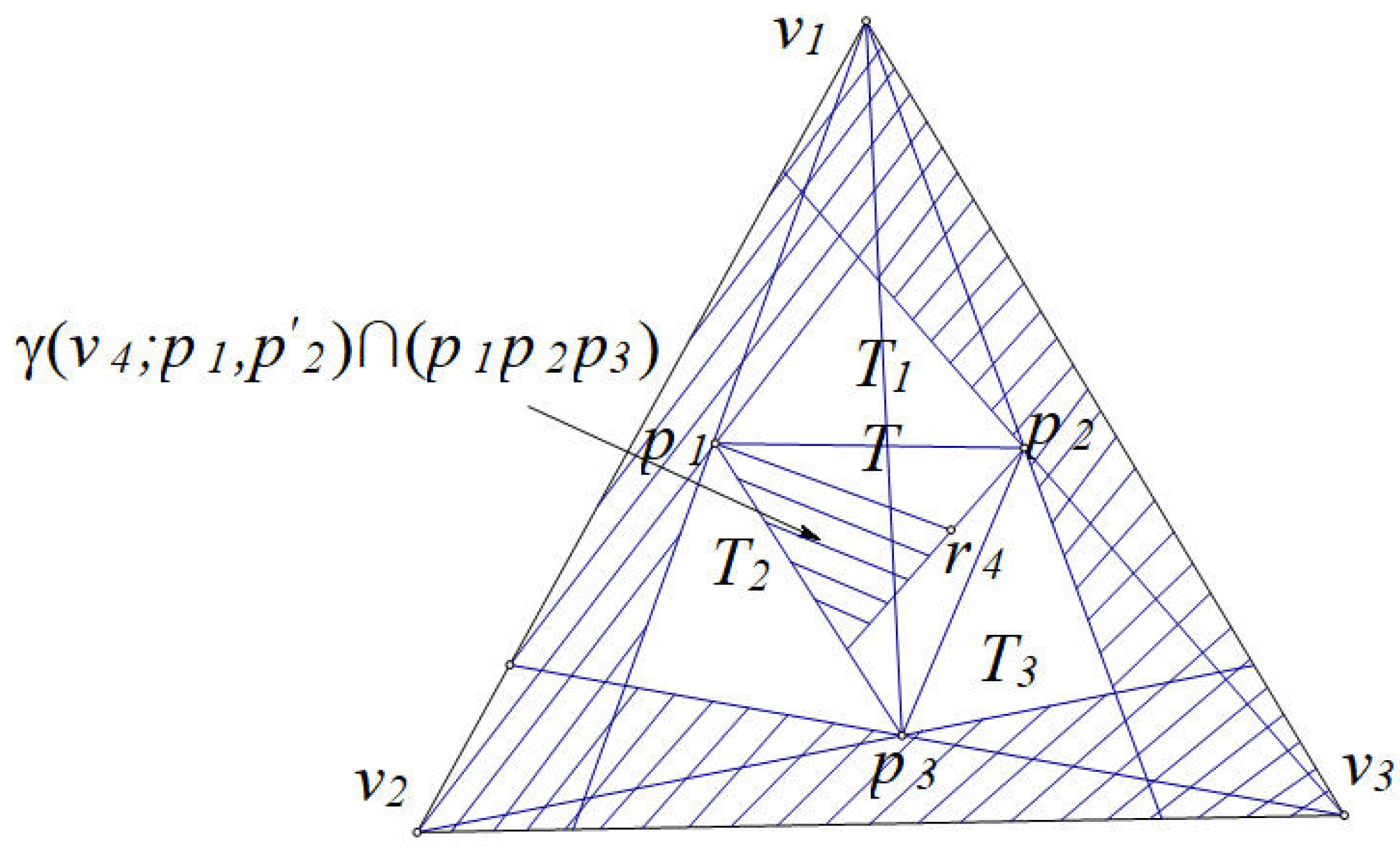
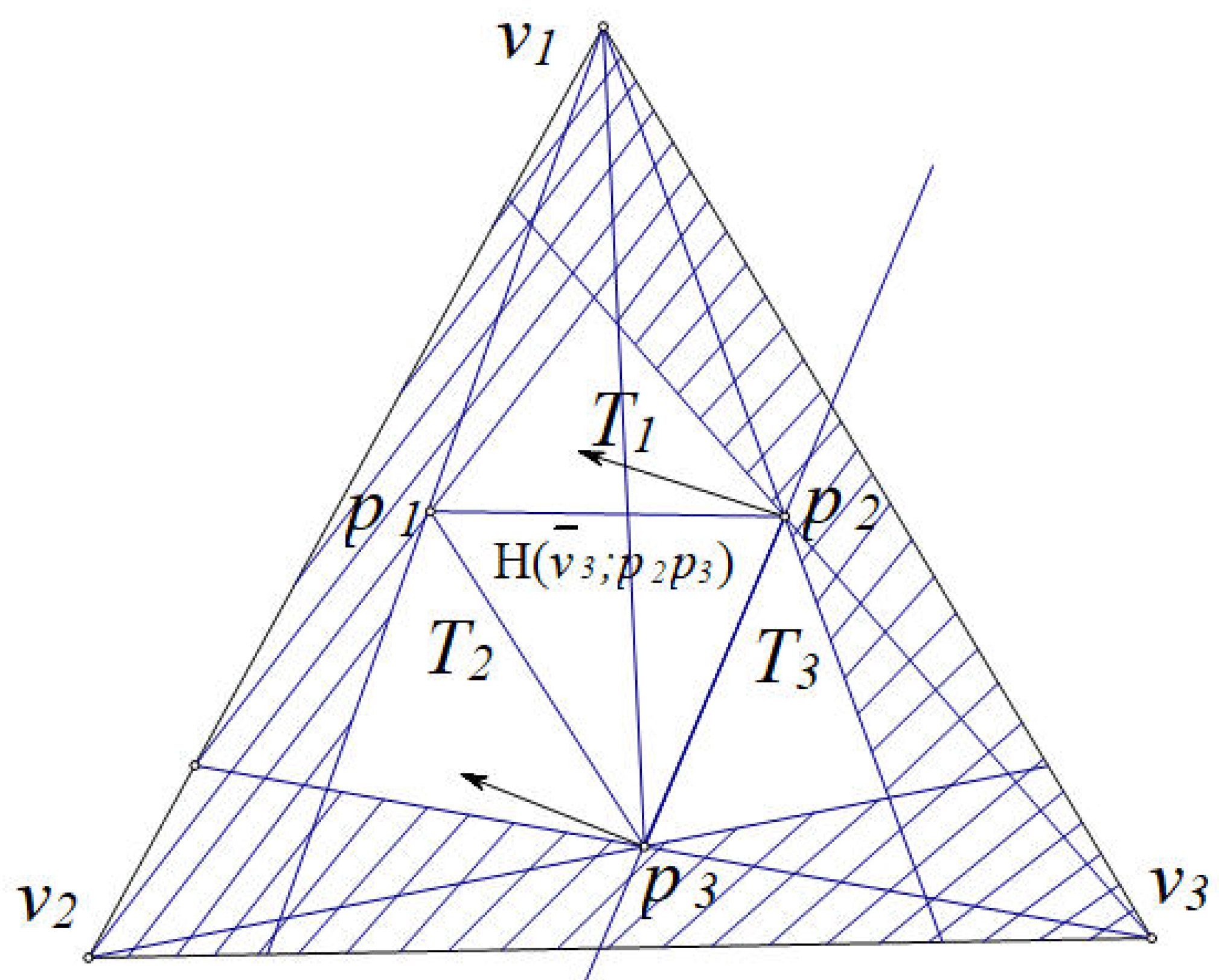
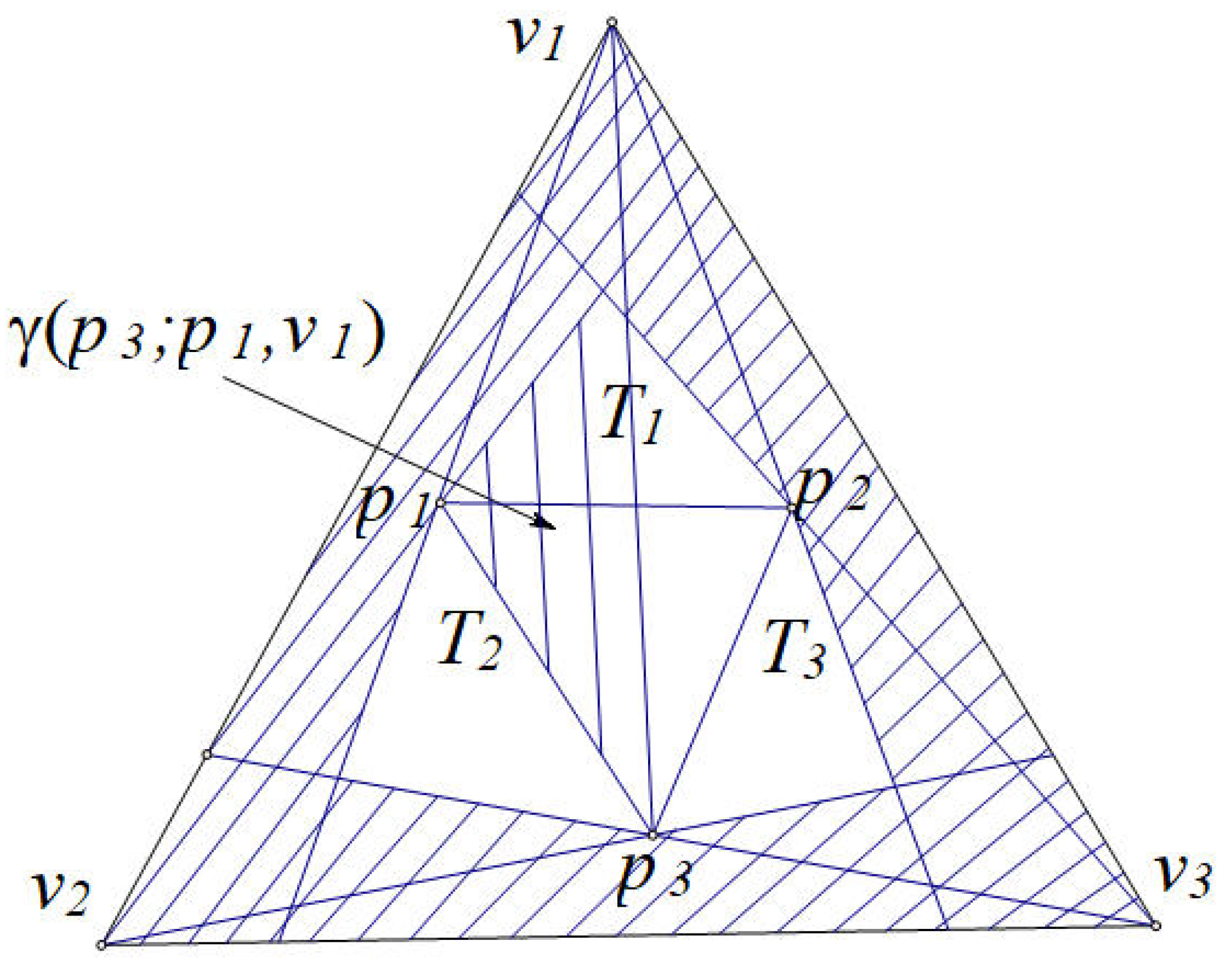
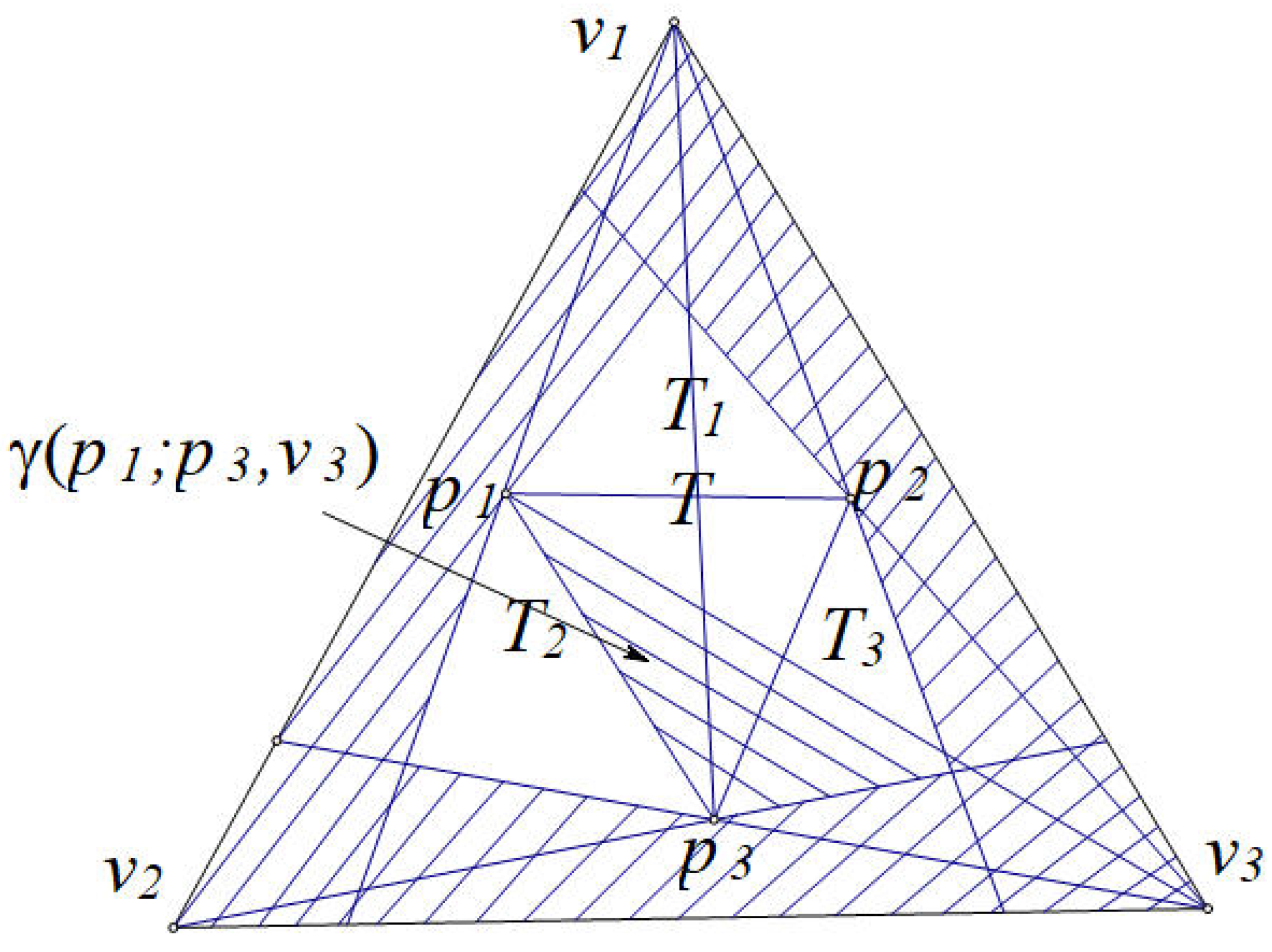
Proof. Let
P be a 13 points set.
. If we can find a 5-hole and a disjoint convex region with at least 7 points remained, we are done by
[
8]. That is to say, if we find a straight line which separates a 5-hole from at least 7 points remained, the result is correct. We call such a line a cutting line through two points
u and
v in
P, denoted by
. If we can find a 4-hole and the vertices number of the remaining points is more than 4, we are done by Theorem 1, where the two parts are disjoint. That is to say, if we can find such a cutting line through two points
m and
n in
P, denoted by
, our conclusion is correct. Therefore, in the following proof, if we can find a cutting line
or
, our conclusion must be true.
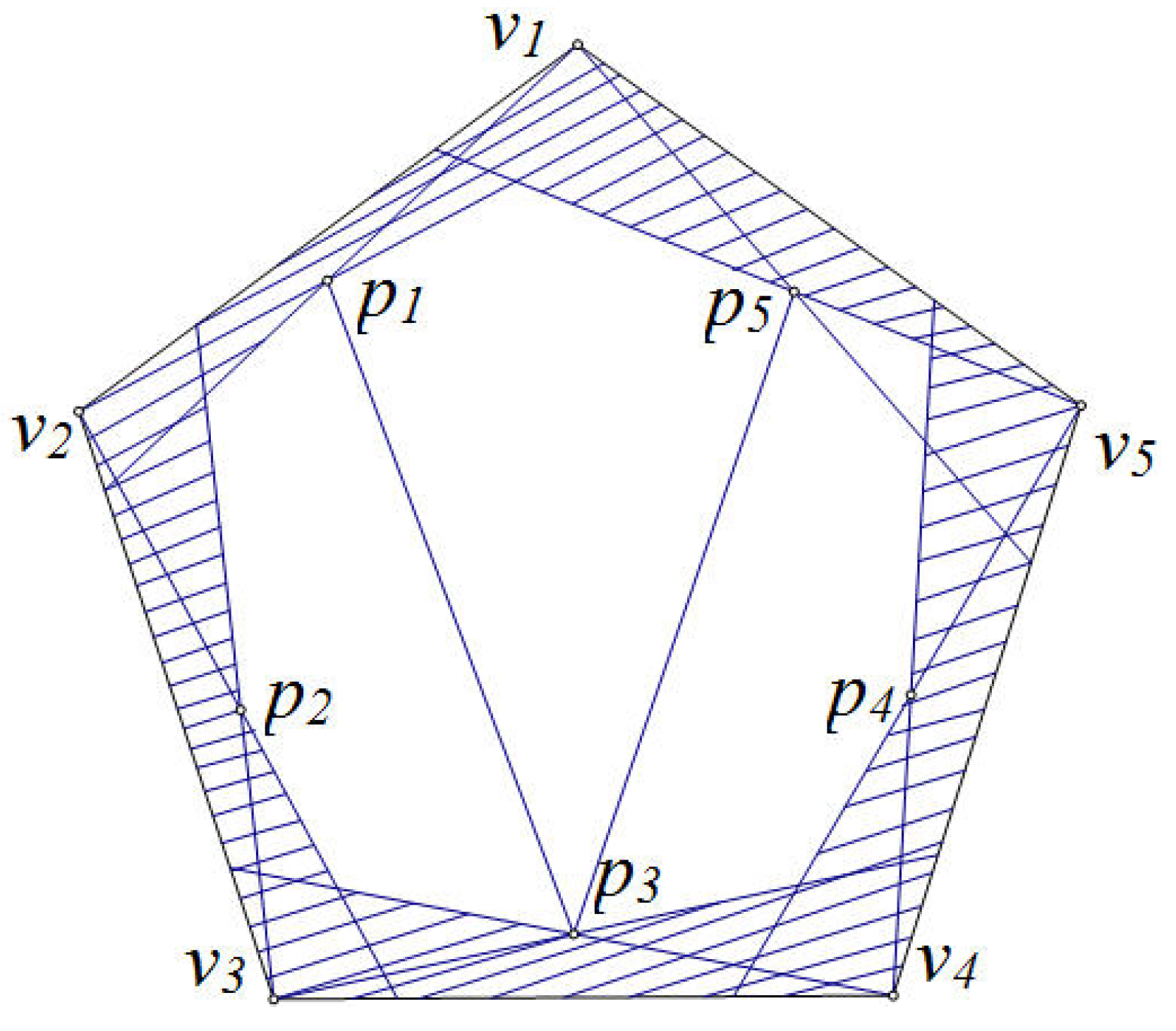
In the following, we will assume there does not exist a separating line
. Then there must exist a point
, such that
and
are empty, as shown in
Figure 3. Considering the 13 points, it is easy to know the conclusion is obvious right when
. Next, we discuss the considerations that
.
Case 1.
Let
for
. As shown in
Figure 4, we have the points
for
, such that the shaded region is empty and we have 1 point
remained.
As the isomorphism of geometry from
Figure 4, we only discuss one case. And the rest could be obtained in the same way.
Assume . We have a cutting line .
Assume . We have a cutting line .
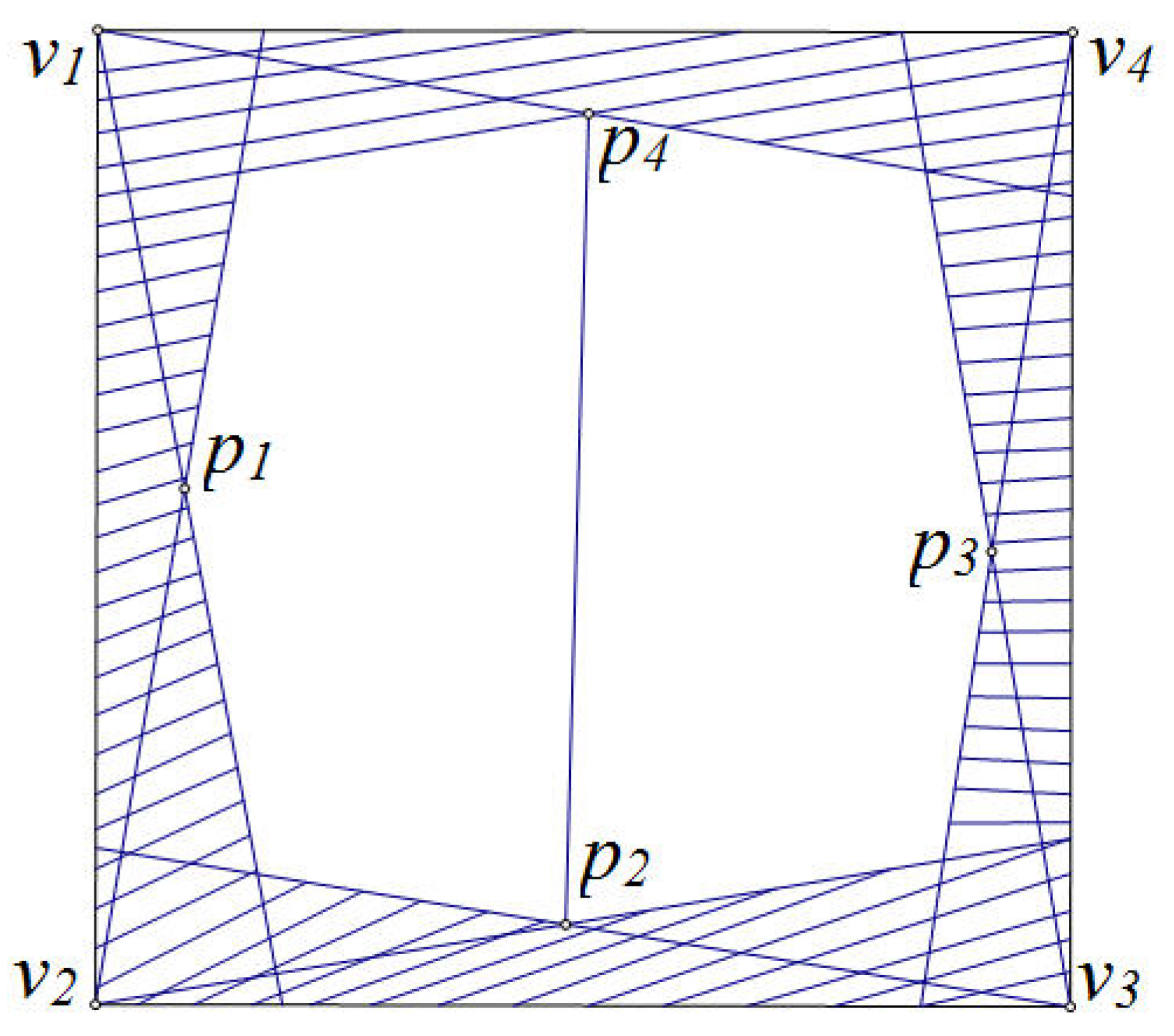
Case 2.
Let
for
. We have 5 friend points
for
as shown in
Figure 5. Then we have 3 points
remained.
Assume . We have a cutting line .
Assume . We have a cutting line .
Assume and . Suppose . If has two of the remaining points say , , let : and if , we have a cutting line ; and if , we have , and a 4-hole from the remaining points; and if , we have a cutting line . If has two of the remaining points, symmetrically, the conclusion is also right. Suppose . We may suppose , , . If , we have , and a 4-hole from the remaining points. If , we have , and a 4-hole from the remaining points. If and , we have , and a 4-hole from the remaining points.
Case 3.
Let
for
. We have 4 friend points
for
. Then we have 5 points
remained as shown in
Figure 6.
If or , we have a cutting line or . Then we will consider that and .
Assume one of the five points say and the remaining four say , . (If has four points and has one point, symmetrically, the conclusion is also right). Let .
Suppose or . We always have a cutting line . Suppose . We have , and a 4-hole from the remaining points. Suppose . We have , and a 4-hole from the remaining points.
Assume two of the five points, say and the remaining three say , . (If has three points and has two points, symmetrically, our conclusion is also right.)
Suppose . If , let , we have , and a 4-hole from the remaining points. If , we have , and a 4-hole from the remaining points. Suppose . Let . If , we have , and a 4-hole from the remaining points. If , we have , and a 4-hole from the remaining points. If , we have , and a 4-hole from the remaining points.
Case 4.
Let
. We have 3 friend points
and 7 points remained. As shown in
Figure 7, denote
,
,
.
Without loss of generality, we assume .
(1) .
We have a cutting line .
(2) .
Name the remaining one . If or , we have a cutting line . If : and if , we have a cutting line ; and if , we have , and a 4-hole from the remaining points.
(3) .
Name the remaining two points
. Then we will discuss the region
, as shown in
Figure 8.
Assume . (If , by the similar reason our conclusion is also right.) Let . Suppose .
If , we have a cutting line . If : and if , we have , and a 4-hole from the remaining points; and if , we have , and a 4-hole from the remaining points. Suppose . If , we have a cutting line . If , we have , and a 4-hole from the remaining points.
Assume and . Then we suppose has one point say and has one point say . If , we have a cutting line . If , we have a cutting line .
(4) .
Name the remaining three points
. Then we will discuss the region
, as shown in
Figure 9.
- (a)
Assume . Let . We have , and a 4-hole from the remaining points.
- (b)
Assume two of , say . Suppose . If : we have a 4-hole from , and a 3-hole from the remaining points. If , we have , and a 4-hole from the remaining points. If and , we have a cutting line .
- (c)
Assume one of , say .
Suppose . We have a cutting line .
Suppose . Let . If , we have a cutting line . Then we suppose . If : and if , we have a cutting line ; and if , we have , and a 4-hole from the remaining points; and if , we have , and a 4-hole from the remaining points; and if , we have a cutting line . If : and if , we have a cutting line ; and if , we have , and a 4-hole from the remaining points; and if , we have , and a 4-hole from the remaining points; and if , we have , and a 4-hole from the remaining points; and if , we have , and a 4-hole from the remaining points.
- (d)
Assume
. By the same reason, we also assume
. Then we will discuss the region
, as shown in
Figure 10.
- (d1)
Suppose . Let within .
If , we have , and a 4-hole from the remaining points.
If : and if , we have , and a 4-hole from the remaining points; and if , let within , we have , and a 4-hole from the remaining points when , we have , and a 3-hole from the remaining points when and , we have , and a 4-hole from the remaining points when and , we have , and a 4-hole from the remaining points when , we have , and a 4-hole from the remaining points when .
- (d2)
Suppose has one of the , say . Let .
If , we have , and a 4-hole from the remaining points.
If : and if , we have , and a 4-hole from the remaining points; and if , we have , and a 4-hole from the remaining points; and if , we have a cutting line when , we have , and a 4-hole from the remaining points when and , we have , and a 3-hole from the remaining points when and .
If , we have , and a 4-hole from the remaining points.
- (d3)
Suppose has two of the points , say . Let .
If , we have a cutting line .
If , let : and if , we have a cutting line when , we have , and a 4-hole from the remaining points when , we have , and a 4-hole from the remaining points when , we have , and a 4-hole from the remaining points when ; and if , we have , and a 3-hole from the remaining points when , we have a cutting line , when , we have , and a 4-hole from the remaining points when and .
- (d4)
Suppose has all of the three points . Let , .
If or , we always have a cutting line .
If and : and if , we have a cutting line ; and if , we have , and a 4-hole from the remaining points; and if , we have a cutting line ; and if , we have , and a 3-hole from the remaining points when , we have , and a 4-hole from the remaining points when .
(5) . Let .
- (a)
.
Let
. Name the remaining one point
. Assume
, as shown in
Figure 11.
Symmetrically, our conclusion is also right when . Let . We have , and a 4-hole from the remaining points.
- (b)
.
Let . Name the remaining two points .
- (b1)
. Let .
Assume . Let . Suppose . We have a cutting line . Suppose . If , we have a cutting line . If , we have a cutting line where . Suppose . We have , and a 4-hole from the remaining points.
Assume has one of . Let . Suppose . If , we have , and a 4-hole from the remaining points where . If , we have , and a 4-hole from the remaining points where .
Assume has . Let , . we have , and a 4-hole from the remaining points.
- (b2)
.
Let
and
, as shown in
Figure 12.
Assume . We have , and a 4-hole from the remaining points where . Assume . We have , and a 4-hole from the remaining points. Assume . If , we have , and a 4-hole from the remaining points where . If , we have , and a 4-hole from the remaining points where .
- (b3)
.
Let
. Then we will discuss the region
, as shown in
Figure 13.
Assume . Suppose . We have , and a 4-hole from the remaining points. Suppose . If , we have , and a 4-hole from the remaining points where . If , we have , and a 4-hole from the remaining points where within .
Assume . We have , and a 4-hole from the remaining points where and .
Assume and . We may assume and . Suppose . We have , and a 4-hole from the remaining points. Suppose . If , we have , and a 4-hole from the remaining points where . If : and if , we have , and a 4-hole from the remaining points where within ; and if , we have , and a 4-hole from the remaining points where .
- (c)
. Let .
- (c1)
. Let and .
Firstly, consider
, then we will discuss the region
, as shown in
Figure 14.
Assume . We have a cutting line . Assume . Let . If , we have a cutting line . Then we may assume .
Suppose . If , we have , and a 4-hole from the remaining points. If , we have a cutting line .
Suppose . If , we have , and a 4-hole from the remaining points. If : and if , we have , and a 4-hole from the remaining points; and if , we have , and a 4-hole from the remaining points. Suppose . If , we have , and a 4-hole from the remaining points. If , we have , and a 3-hole from the remaining points. If , we have , and a 4-hole from the remaining points. If , we have , and a 4-hole from the remaining points.
Secondly, consider
, then we will discuss the region
, as shown in
Figure 15.
Assume . We have , and a 4-hole from the remaining points where , . Assume . We have . Assume and . Then we may assume , . Suppose . If , we have , and where . If : and if , we have ; and if , we have ; and if , we have , and a 4-hole from the remaining points. Suppose . If , we have , and a 4-hole from the remaining points. If : and if , we have ; and if , we have , and a 4-hole from the remaining points.
- (c2)
.
Denote
,
,
. Let
within
. If
, we have
. Then we assume
, and we will discuss the region
, as hown in
Figure 16.
Assume , we have , and a 4-hole from the remaining points.
Assume . Let . Suppose . We have , and a 4-hole from the remaining points where . Suppose . We have , and a 4-hole from the remaining points where .
Assume and . Without loss of generality, we suppose , .
Firstly, we may assume . Suppose . We have . Suppose . We have a cutting line . Suppose . If , we have , and a 4-hole from the remaining points. If , we have , and where .
Secondly, we have may assume , we have , and a 4-hole from the remaining points.
- (d)
. .
Let
. And
,
,
. If
, we have
,
and a 4-hole from the remaining points. Assume
. If
, we have a cutting line
. Then we will discuss the region
and
, as shown in
Figure 17.
Assume . We have , and a 4-hole from the remaining points where .
Assume . Let . Suppose . We have , and a 4-hole from the remaining points. Suppose . We have , and . Suppose . We have , and . Suppose . We have , and a 4-hole from the remaining points. Suppose . We have a cutting line .
Assume and . Without loss of generality, assume , .
Suppose . We have a cutting line .
Suppose . If , we have , and a 4-hole from the remaining points. If , we have , and a 4-hole from the remaining points.
Suppose . If , we have , and . If , we have , and a 4-hole from the remaining points.
(6) .
Let
and
. Assume
. We have
and the remaining 9 points are in
, as shown in
Figure 18.
By the discussion of Part One, we know our conclusion is right. Assume . We have . By the discussion of Part One, we know our conclusion is also right. Assume . We have a cutting line .
(7) .
Let , , and . Let within .
Assume
, as shown in
Figure 19.
If , we have a cutting line . If , we have a cutting line . Assume . If , we have a cutting line . If , we have a cutting line . If and : and if , we have ; and if , we have . Then the remaining 9 points are all in . By the discussion of Part One, our conclusion is right.
(8) .
Then , and for . Let .
If
, as shown in
Figure 20.
We have and the remaining 9 points are all in . By the discussion of Part One, our conclusion is right. If : and if , we have and the remaining 9 points are all in ; and if , we have a cutting line . ☐