IgG Charge: Practical and Biological Implications
Abstract
1. Introduction
Theoretical Basics of Protein Charge
2. Materials and Methods
2.1. Monoclonal and Human Serum IgGs
2.2. IgG Fragmentation
2.3. Sample Preparation
2.4. Liquid Chromatography Mass Spectrometry (LC-MS)
2.5. Analytical Ultracentrifugation (AUC)
2.6. Imaged Capillary Isoelectric Focusing (icIEF)
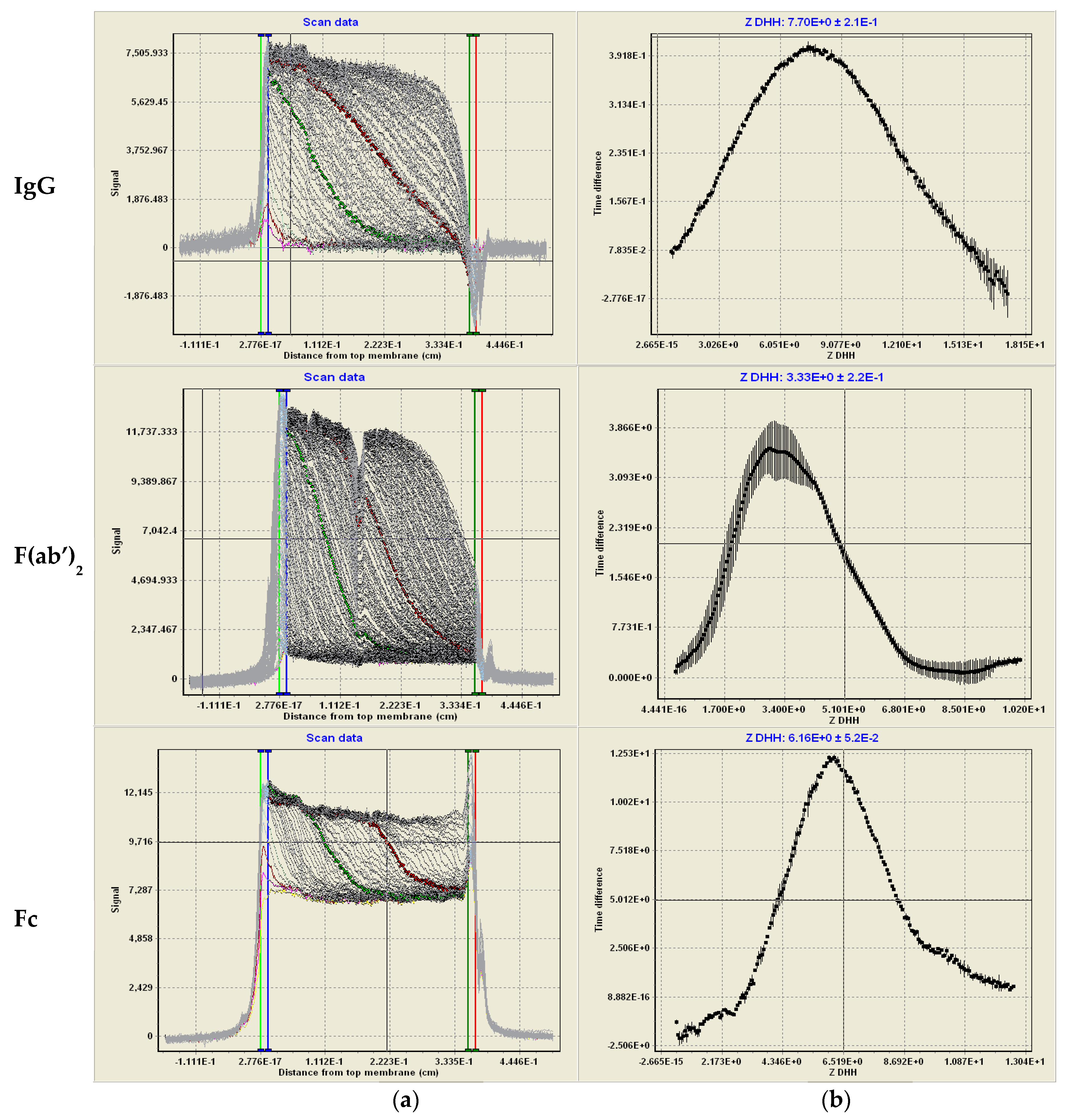
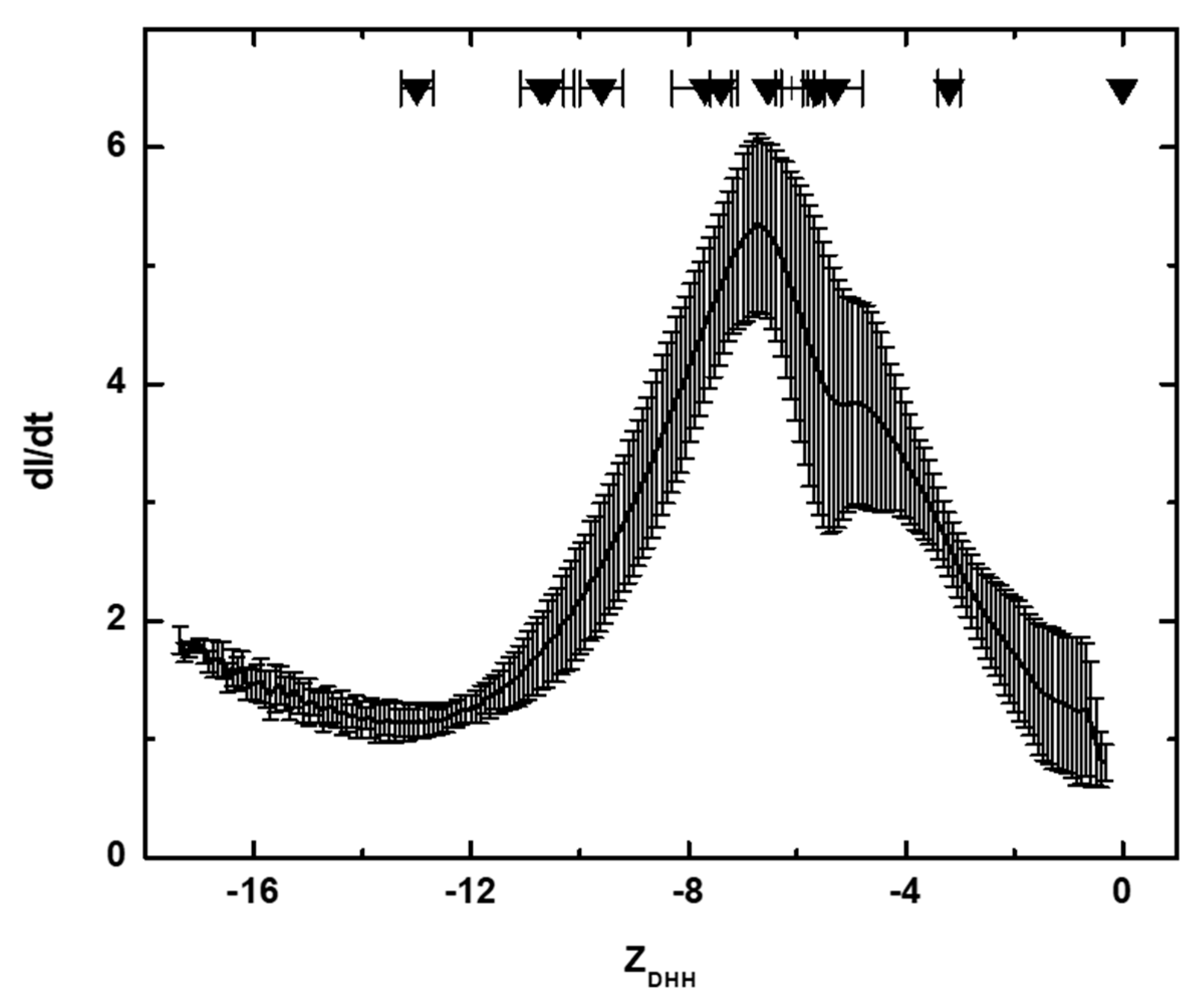
2.7. Membrane-Confined Electrophoresis (MCE) and ZDHH Determinations
2.8. Calculated Charge, Zcal, and Calculated Isoelectric pH, pICal
2.9. Dynamic Light Scattering (DLS) and kD Determinations
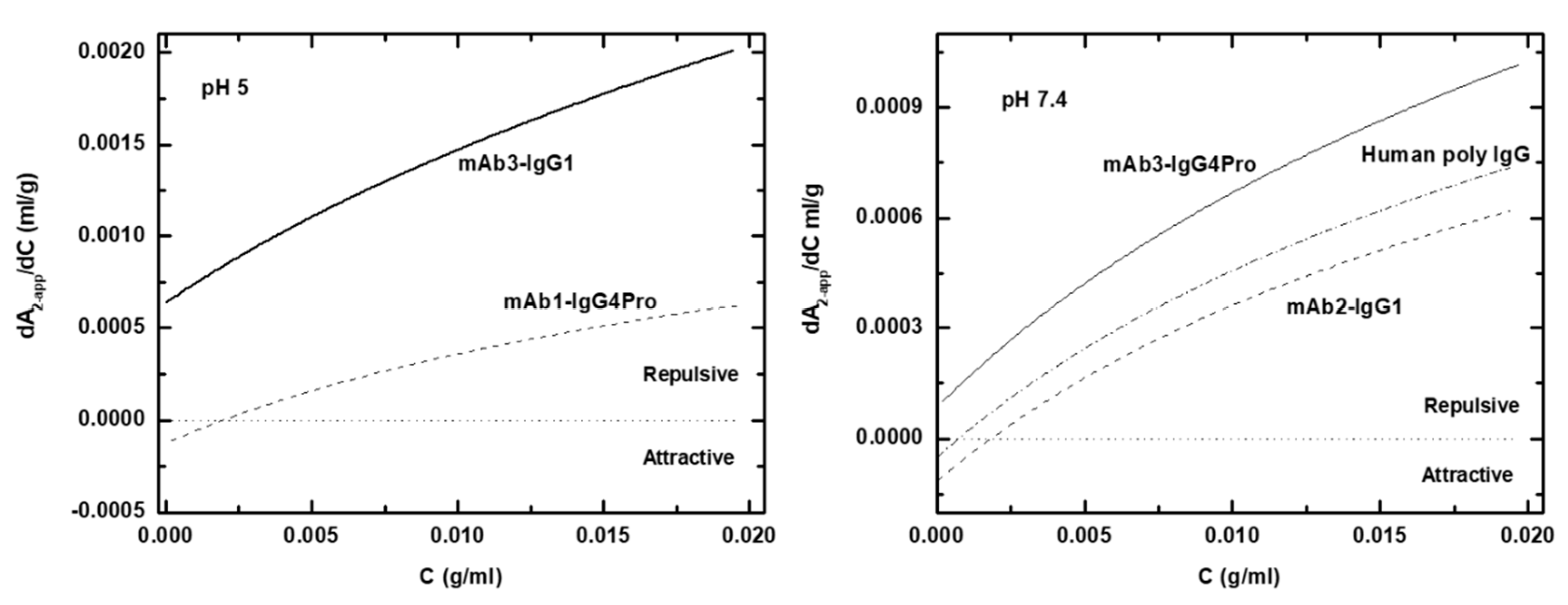
2.10. Calculation of the Protein–Protein Interaction Curve
3. Results
3.1. Solution Properties of IgGs and Their Fragments
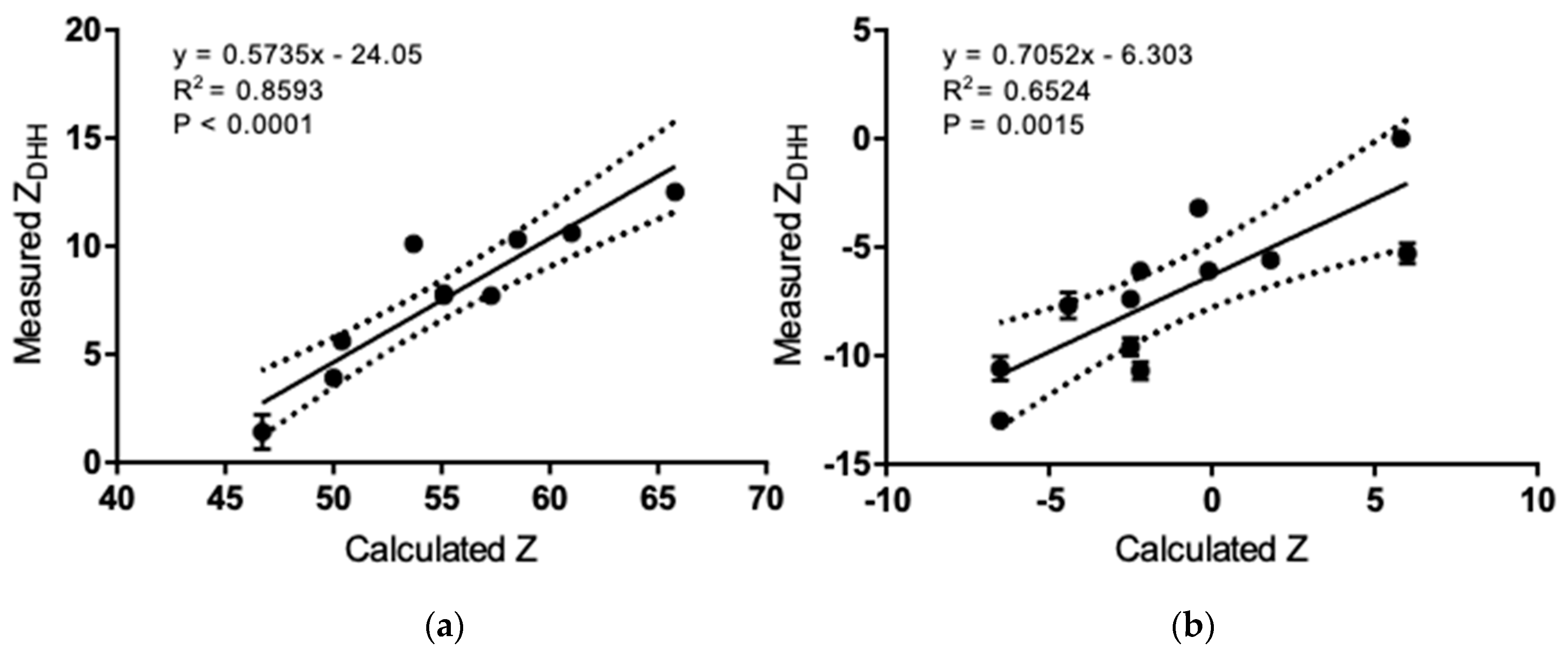
3.2. Isoelectric Point and Correlation to Calculated Values
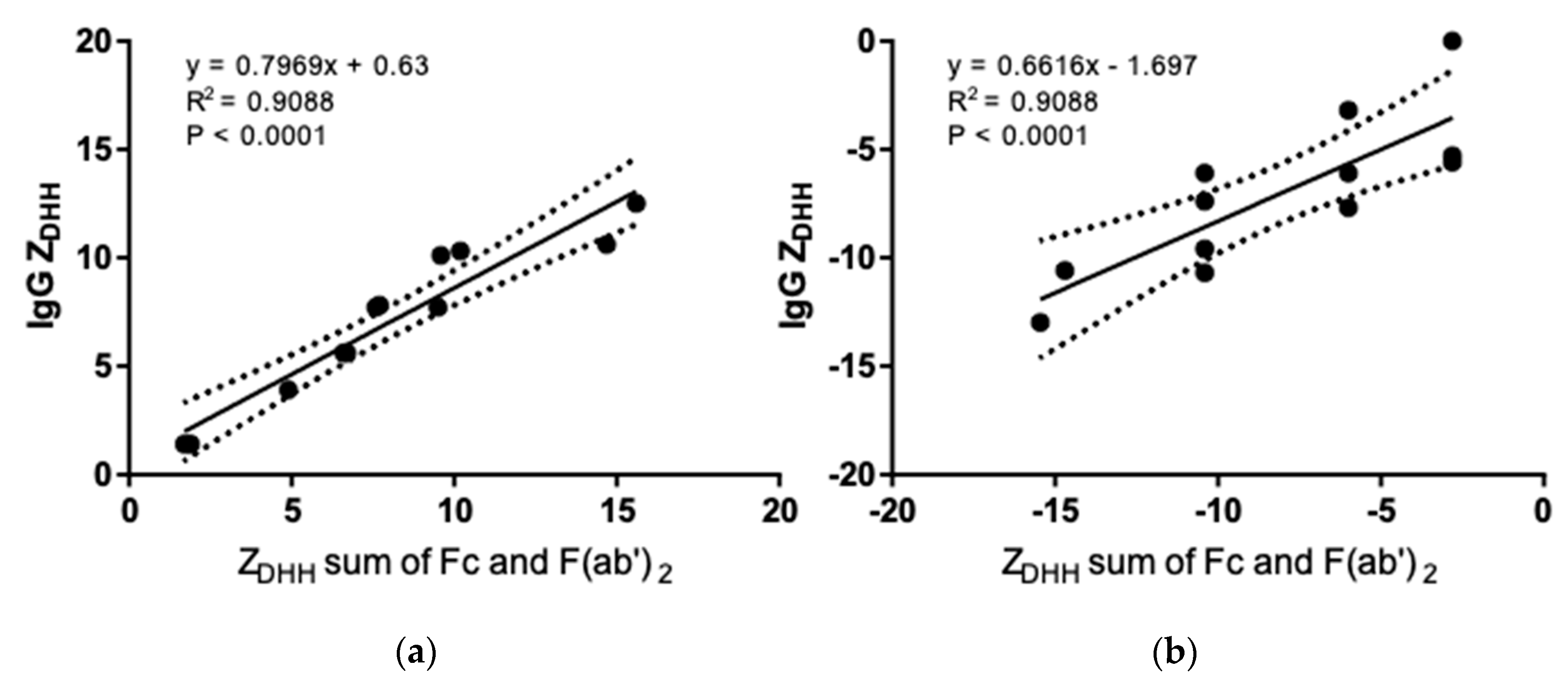
3.3. Net Charge of IgGs and Fragments in Formulation and Physiological Solutions
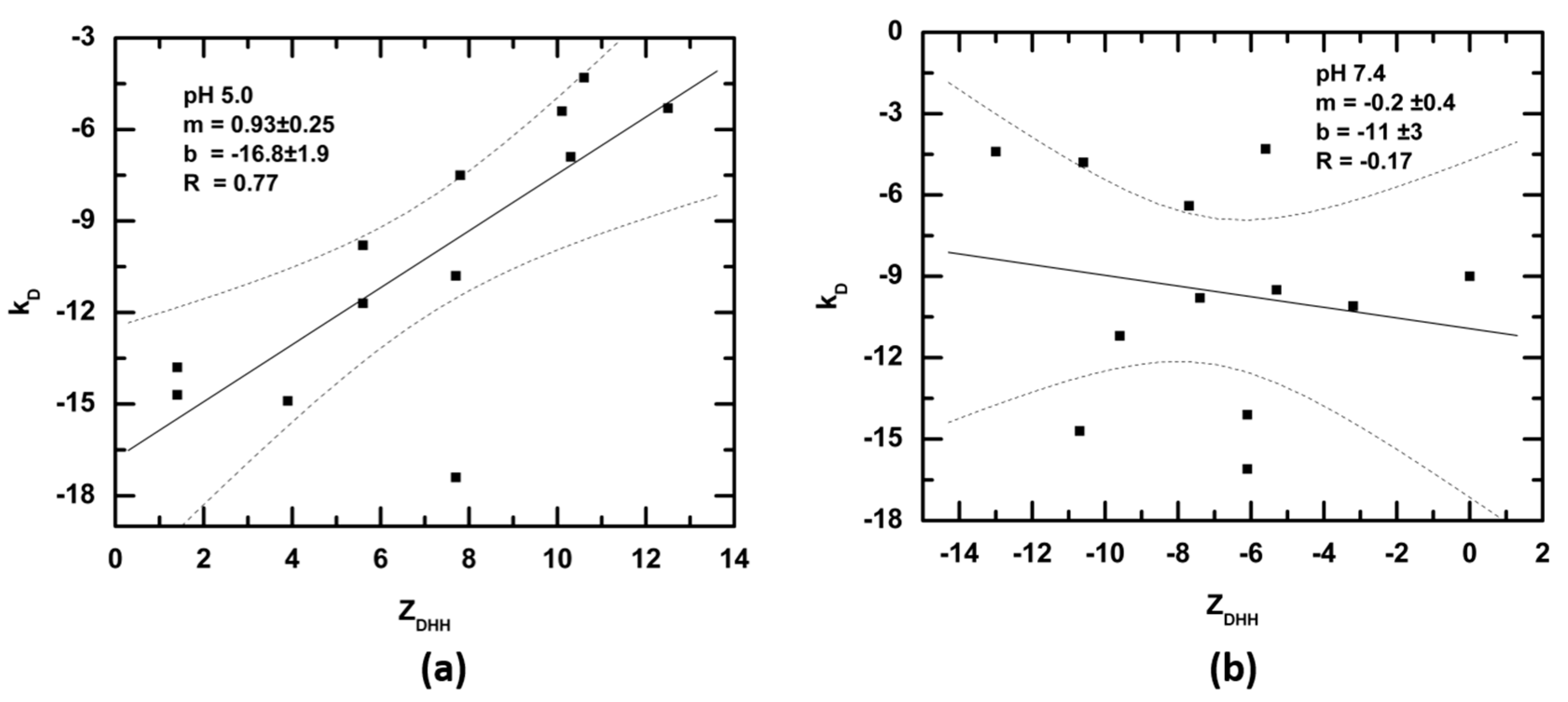
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cohn, E.J. Studies in the physical chemistry of the proteins: I. The solubility of certain proteins at their isoelectric points. J. Gen. Physiol. 1922, 4, 697–722. [Google Scholar] [CrossRef] [PubMed]
- Raut, A.S.; Kalonia, D.S. Opalescence in Monoclonal Antibody Solutions and Its Correlation with Intermolecular Interactions in Dilute and Concentrated Solutions. J. Pharm. Sci. 2015, 104, 1263–1274. [Google Scholar] [CrossRef]
- Shire, S.J.; Shahrokh, Z.; Liu, J. Challenges in the development of high protein concentration formulations. J. Pharm. Sci. 2004, 93, 1390–1402. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Kumar, S.; Buck, P.M.; Burns, C.; Lavoie, J.; Singh, S.K.; Warne, N.W.; Nichols, P.; Luksha, N.; Boardman, D. Concentration dependent viscosity of monoclonal antibody solutions: Explaining experimental behavior in terms of molecular properties. Pharm. Res. 2014, 31, 3161–3178. [Google Scholar] [CrossRef] [PubMed]
- Yadav, S.; Laue, T.M.; Kalonia, D.S.; Singh, S.N.; Shire, S.J. The Influence of Charge Distribution on Self-Association and Viscosity Behavior of Monoclonal Antibody Solutions. Mol. Pharm. 2012, 9, 791–802. [Google Scholar] [CrossRef] [PubMed]
- Chi, E.Y.; Krishnan, S.; Randolph, T.W.; Carpenter, J.F. Physical stability of proteins in aqueous solution: Mechanism and driving forces in nonnative protein aggregation. Pharm. Res. 2003, 20, 1325–1336. [Google Scholar] [CrossRef] [PubMed]
- Neergaard, M.S.; Kalonia, D.S.; Parshad, H.; Nielsen, A.D.; Møller, E.H.; van de Weert, M. Viscosity of high concentration protein formulations of monoclonal antibodies of the IgG1 and IgG4 subclass—Prediction of viscosity through protein–protein interaction measurements. Eur. J. Pharm. Sci. 2013, 49, 400–410. [Google Scholar] [CrossRef] [PubMed]
- Pindrus, M.A.; Shire, S.J.; Yadav, S.; Kalonia, D.S. The Effect of Low Ionic Strength on Diffusion and Viscosity of Monoclonal Antibodies. Mol. Pharm. 2018, 15, 3133–3142. [Google Scholar] [CrossRef]
- Singh, S.N.; Yadav, S.; Shire, S.J.; Kalonia, D.S. Dipole-Dipole Interaction in Antibody Solutions: Correlation with Viscosity Behavior at High Concentration. Pharm. Res. 2014, 31, 2549–2558. [Google Scholar] [CrossRef]
- Olsen, S.N.; Andersen, K.B.; Randolph, T.W.; Carpenter, J.F.; Westh, P. Role of electrostatic repulsion on colloidal stability of Bacillus halmapalus alpha-amylase. Biochim. Biophys. Acta 2009, 1794, 1058–1065. [Google Scholar] [CrossRef]
- Connolly, B.D.; Petry, C.; Yadav, S.; Demeule, B.; Ciaccio, N.; Moore, J.M.R.; Shire, S.J.; Gokarn, Y.R. Weak Interactions Govern the Viscosity of Concentrated Antibody Solutions: High-Throughput Analysis Using the Diffusion Interaction Parameter. Biophys. J. 2012, 103, 69–78. [Google Scholar] [CrossRef]
- Tanford, C. Physical Chemistry of Macromolecules, 1st ed.; John Wiley & Sons Inc.: New York, NY, USA, 1961; ISBN 978-0-471-84447-1. [Google Scholar]
- Wright, R.T.; Hayes, D.B.; Stafford, W.F.; Sherwood, P.J.; Correia, J.J. Characterization of therapeutic antibodies in the presence of human serum proteins by AU-FDS analytical ultracentrifugation. Anal. Biochem. 2018, 550, 72–83. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Correia, J.J.; Iii, W.F.S.; Roberts, C.J.; Singh, S.; Hayes, D.; Kroe-Barrett, R.; Nixon, A.; Laue, T.M. Weak IgG self- and hetero-association characterized by fluorescence analytical ultracentrifugation. Protein Sci. 2018, 27, 1334–1348. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, M.M.; Lambert, C.L.; Bee, J.S.; Parupudi, A.; Bain, D.L. Determination of Interaction Parameters for Reversibly Self-Associating Antibodies: A Comparative Analysis. J. Pharm. Sci. 2018, 107, 1820–1830. [Google Scholar] [CrossRef] [PubMed]
- Kelly, R.L.; Yu, Y.; Sun, T.; Caffry, I.; Lynaugh, H.; Brown, M.; Jain, T.; Xu, Y.; Wittrup, K.D. Target-independent variable region mediated effects on antibody clearance can be FcRn independent. mAbs 2016, 8, 1269–1275. [Google Scholar] [CrossRef] [PubMed]
- Leipold, D.; Prabhu, S. Pharmacokinetic and pharmacodynamic considerations in the design of therapeutic antibodies. Clin. Transl. Sci. 2018. [Google Scholar] [CrossRef]
- Bas, M.; Terrier, A.; Jacque, E.; Dehenne, A.; Pochet-Béghin, V.; Beghin, C.; Dezetter, A.-S.; Dupont, G.; Engrand, A.; Beaufils, B.; et al. Fc Sialylation Prolongs Serum Half-Life of Therapeutic Antibodies. J. Immunol. 2019, 202, 1582–1594. [Google Scholar] [CrossRef]
- Boswell, C.A.; Tesar, D.B.; Mukhyala, K.; Theil, F.-P.; Fielder, P.J.; Khawli, L.A. Effects of charge on antibody tissue distribution and pharmacokinetics. Bioconjug. Chem. 2010, 21, 2153–2163. [Google Scholar] [CrossRef]
- Igawa, T.; Tsunoda, H.; Tachibana, T.; Maeda, A.; Mimoto, F.; Moriyama, C.; Nanami, M.; Sekimori, Y.; Nabuchi, Y.; Aso, Y.; et al. Reduced elimination of IgG antibodies by engineering the variable region. Protein Eng. Des. Select. 2010, 23, 385–392. [Google Scholar] [CrossRef]
- Hintersteiner, B.; Lingg, N.; Janzek, E.; Mutschlechner, O.; Loibner, H.; Jungbauer, A. Microheterogeneity of therapeutic monoclonal antibodies is governed by changes in the surface charge of the protein. Biotechnol. J. 2016, 11, 1617–1627. [Google Scholar] [CrossRef]
- Hintersteiner, B.; Lingg, N.; Zhang, P.; Woen, S.; Hoi, K.M.; Stranner, S.; Wiederkum, S.; Mutschlechner, O.; Schuster, M.; Loibner, H.; et al. Charge heterogeneity: Basic antibody charge variants with increased binding to Fc receptors. mAbs 2016, 8, 1548–1560. [Google Scholar] [CrossRef]
- Zhang, G.; Massaad, C.A.; Gao, T.; Pillai, L.; Bogdanova, N.; Ghauri, S.; Sheikh, K.A. Sialylated intravenous immunoglobulin suppress anti-ganglioside antibody mediated nerve injury. Exp. Neurol. 2016, 282, 49–55. [Google Scholar] [CrossRef]
- Lardinois, O.M.; Deterding, L.J.; Hess, J.J.; Poulton, C.J.; Henderson, C.D.; Jennette, J.C.; Nachman, P.H.; Falk, R.J. Immunoglobulins G from patients with ANCA-associated vasculitis are atypically glycosylated in both the Fc and Fab regions and the relation to disease activity. PLoS ONE 2019, 14, e0213215. [Google Scholar] [CrossRef] [PubMed]
- Goyon, A.; Excoffier, M.; Janin-Bussat, M.-C.; Bobaly, B.; Fekete, S.; Guillarme, D.; Beck, A. Determination of isoelectric points and relative charge variants of 23 therapeutic monoclonal antibodies. J. Chromatogr. B 2017, 1065–1066, 119–128. [Google Scholar] [CrossRef]
- Filoti, D.I.; Shire, S.J.; Yadav, S.; Laue, T.M. Comparative study of analytical techniques for determining protein charge. J. Pharm. Sci. 2015, 104, 2123–2131. [Google Scholar] [CrossRef]
- Tiselius, A.; Kabat, E.A. An electrophoretic study of immune sera and purified antibody preparations. J. Exp. Med. 1939, 69, 119–131. [Google Scholar] [CrossRef]
- Tiselius, A.; Kabat, E.A. Electrophoresis of Immune Serum. Science 1938, 87, 416–417. [Google Scholar] [CrossRef]
- Mathews, C.K.; van Holde, K.E.; Appling, D.R.; Anthony-Cahill, S.J. Biochemistry, 4th ed.; Pearson: Toronto, ON, Canada, 2012; ISBN 978-0-13-800464-4. [Google Scholar]
- Moody, T.P.; Kingsbury, J.S.; Durant, J.A.; Wilson, T.J.; Chase, S.F.; Laue, T.M. Valence and anion binding of bovine ribonuclease A between pH 6 and 8. Anal. Biochem. 2005, 336, 243–252. [Google Scholar] [CrossRef]
- Her, C.; Filoti, D.I.; McLean, M.A.; Sligar, S.G.; Alexander Ross, J.B.; Steele, H.; Laue, T.M. The Charge Properties of Phospholipid Nanodiscs. Biophys. J. 2016, 111, 989–998. [Google Scholar] [CrossRef]
- Ridgeway, T.M.; Hayes, D.B.; Moody, T.P.; Wilson, T.J.; Anderson, A.L.; Levasseur, J.H.; Demaine, P.D.; Kenty, B.E.; Laue, T.M. An apparatus for membrane-confined analytical electrophoresis. Electrophoresis 1998, 19, 1611–1619. [Google Scholar] [CrossRef]
- Laue, T.M.; Shepard, H.K.; Ridgeway, T.M.; Moody, T.P.; Wilson, T.J. Membrane-confined analytical electrophoresis. Methods Enzymol. 1998, 295, 494–518. [Google Scholar] [PubMed]
- Kyne, C.; Jordon, K.; Filoti, D.I.; Laue, T.M.; Crowley, P.B. Protein charge determination and implications for interactions in cell extracts. Protein Sci. Publ. Protein Soc. 2017, 26, 258–267. [Google Scholar] [CrossRef] [PubMed]
- Moody, T.P.; Shepard, H.K. Nonequilibrium thermodynamics of membrane-confined electrophoresis. Biophys. Chem. 2004, 108, 51–76. [Google Scholar] [CrossRef]
- Edsall, J.T.; Wyman, J. Chapter 9—Polybasic Acids, Bases, and Ampholytes, Including Proteins. In Biophysical Chemistry; Edsall, J.T., Wyman, J., Eds.; Academic Press: Cambridge, MA, USA, 1958; pp. 477–549. ISBN 978-1-4832-2946-1. [Google Scholar]
- Pace, C.N.; Grimsley, G.R.; Scholtz, J.M. Protein ionizable groups: pK values and their contribution to protein stability and solubility. J. Biol. Chem. 2009, 284, 13285–13289. [Google Scholar] [CrossRef]
- Gokarn, Y.R.; Fesinmeyer, R.M.; Saluja, A.; Razinkov, V.; Chase, S.F.; Laue, T.M.; Brems, D.N. Effective charge measurements reveal selective and preferential accumulation of anions, but not cations, at the protein surface in dilute salt solutions: Effective Charge Measurements Reveal Direct Anion-Protein Interactions. Protein Sci. 2011, 20, 580–587. [Google Scholar] [CrossRef] [PubMed]
- Kukić, P.; Nielsen, J.E. Electrostatics in proteins and protein-ligand complexes. Future Med. Chem. 2010, 2, 647–666. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Nussinov, R. Close-range electrostatic interactions in proteins. Chembiochem 2002, 3, 604–617. [Google Scholar] [CrossRef]
- Shi, C.; Wallace, J.A.; Shen, J.K. Thermodynamic Coupling of Protonation and Conformational Equilibria in Proteins: Theory and Simulation. Biophys. J. 2012, 102, 1590–1597. [Google Scholar] [CrossRef]
- Swails, J.M.; York, D.M.; Roitberg, A.E. Constant pH Replica Exchange Molecular Dynamics in Explicit Solvent Using Discrete Protonation States: Implementation, Testing, and Validation. J. Chem. Theory Comput. 2014, 10, 1341–1352. [Google Scholar] [CrossRef]
- Oliveira, A.S.F.; Campos, S.R.R.; Baptista, A.M.; Soares, C.M. Coupling between protonation and conformation in cytochrome c oxidase: Insights from constant-pH MD simulations. Biochim. Biophys. Acta BBA Bioenergy 2016, 1857, 759–771. [Google Scholar] [CrossRef]
- Harding, S.E.; Horton, J.C.; Jones, S.; Thornton, J.M.; Winzor, D.J. COVOL: An Interactive Program for Evaluating Second Virial Coefficients from the Triaxial Shape or Dimensions of Rigid Macromolecules. Biophys. J. 1999, 76, 2432–2438. [Google Scholar] [CrossRef]
- Collins, K.D.; Neilson, G.W.; Enderby, J.E. Ions in water: Characterizing the forces that control chemical processes and biological structure. Biophys. Chem. 2007, 128, 95–104. [Google Scholar] [CrossRef] [PubMed]
- Miao, L.; Qin, H.; Koehl, P.; Song, J. Selective and specific ion binding on proteins at physiologically-relevant concentrations. FEBS Lett. 2011, 585, 3126–3132. [Google Scholar] [CrossRef] [PubMed]
- Harlow, E.; Lane, D.P. Antibodies: A Laboratory Manual, 1st ed.; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, USA, 1988; ISBN 978-0-87969-314-5. [Google Scholar]
- Stafford, W.F.; Braswell, E.H. Sedimentation velocity, multi-speed method for analyzing polydisperse solutions. Biophys. Chem. 2004, 108, 273–279. [Google Scholar] [CrossRef] [PubMed]
- Bjellqvist, B.; Ek, K.; Giorgio Righetti, P.; Gianazza, E.; Görg, A.; Westermeier, R.; Postel, W. Isoelectric focusing in immobilized pH gradients: Principle, methodology and some applications. J. Biochem. Biophys. Methods 1982, 6, 317–339. [Google Scholar] [CrossRef]
- Mao, Q.; Pawliszyn, J. Capillary isoelectric focusing with whole column imaging detection for analysis of proteins and peptides. J. Biochem. Biophys. Methods 1999, 39, 93–110. [Google Scholar] [CrossRef]
- Hayes, D.; Laue, T.; Philo, J. Program Sednterp: Sedimentation Interpretation Program, version 1.09; Alliance Protein Laboratories: Thousand Oaks, CA, USA, 1995. [Google Scholar]
- Edsall, J.T.; Wyman, J. Biophysical Chemistry; Academic Press: New York, NY, USA, 1958; ISBN 978-0-12-232201-3. [Google Scholar]
- Laue, T. Charge matters. Biophys. Rev. 2016, 8, 287–289. [Google Scholar] [CrossRef]
- Tomar, D.S.; Kumar, S.; Singh, S.K.; Goswami, S.; Li, L. Molecular basis of high viscosity in concentrated antibody solutions: Strategies for high concentration drug product development. mAbs 2016, 8, 216–228. [Google Scholar] [CrossRef]
- Saluja, A.; Fesinmeyer, R.M.; Hogan, S.; Brems, D.N.; Gokarn, Y.R. Diffusion and sedimentation interaction parameters for measuring the second virial coefficient and their utility as predictors of protein aggregation. Biophys. J. 2010, 99, 2657–2665. [Google Scholar] [CrossRef]
- Laue, T. Proximity energies: A framework for understanding concentrated solutions. J. Mol. Recognit. JMR 2012, 25, 165–173. [Google Scholar] [CrossRef]
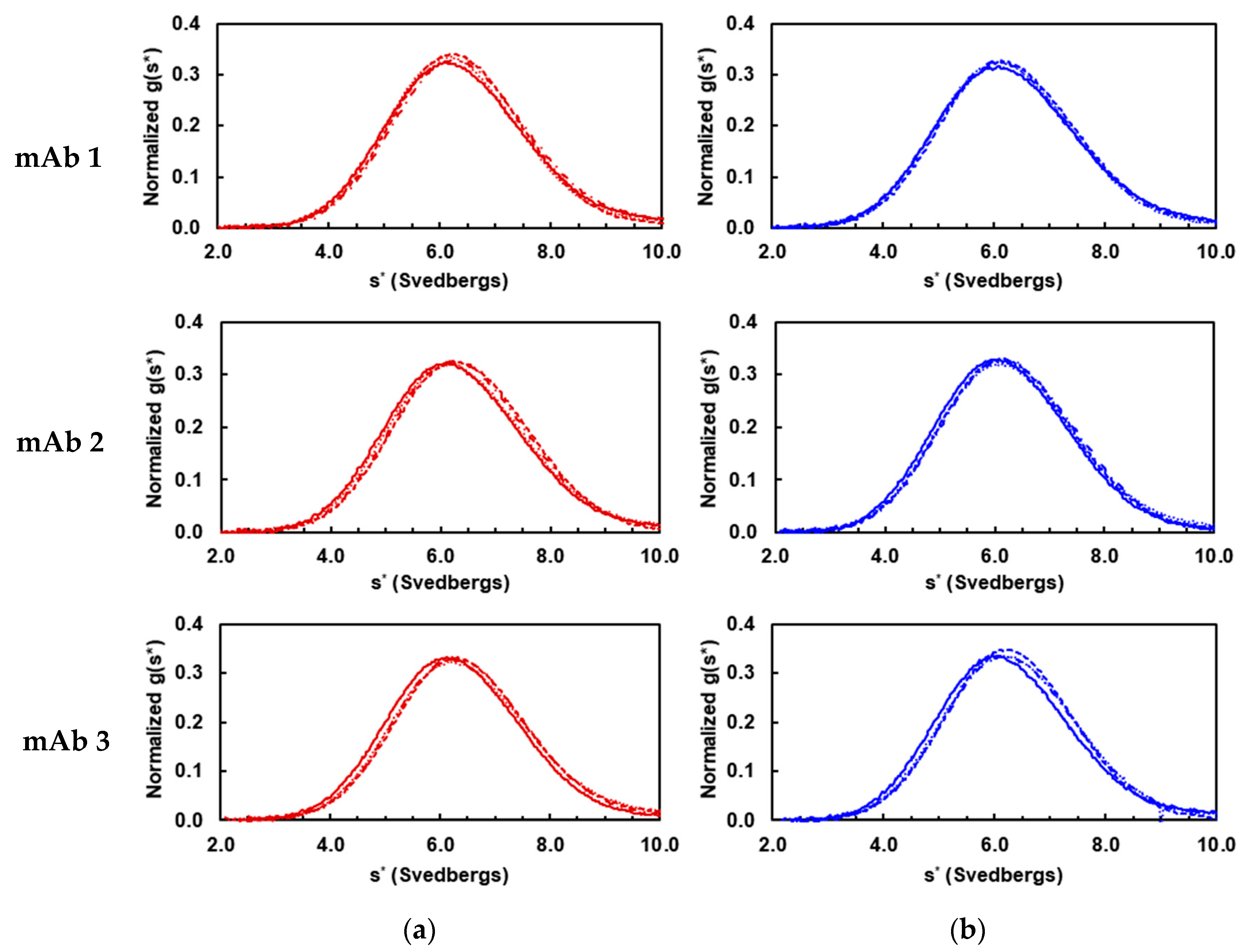
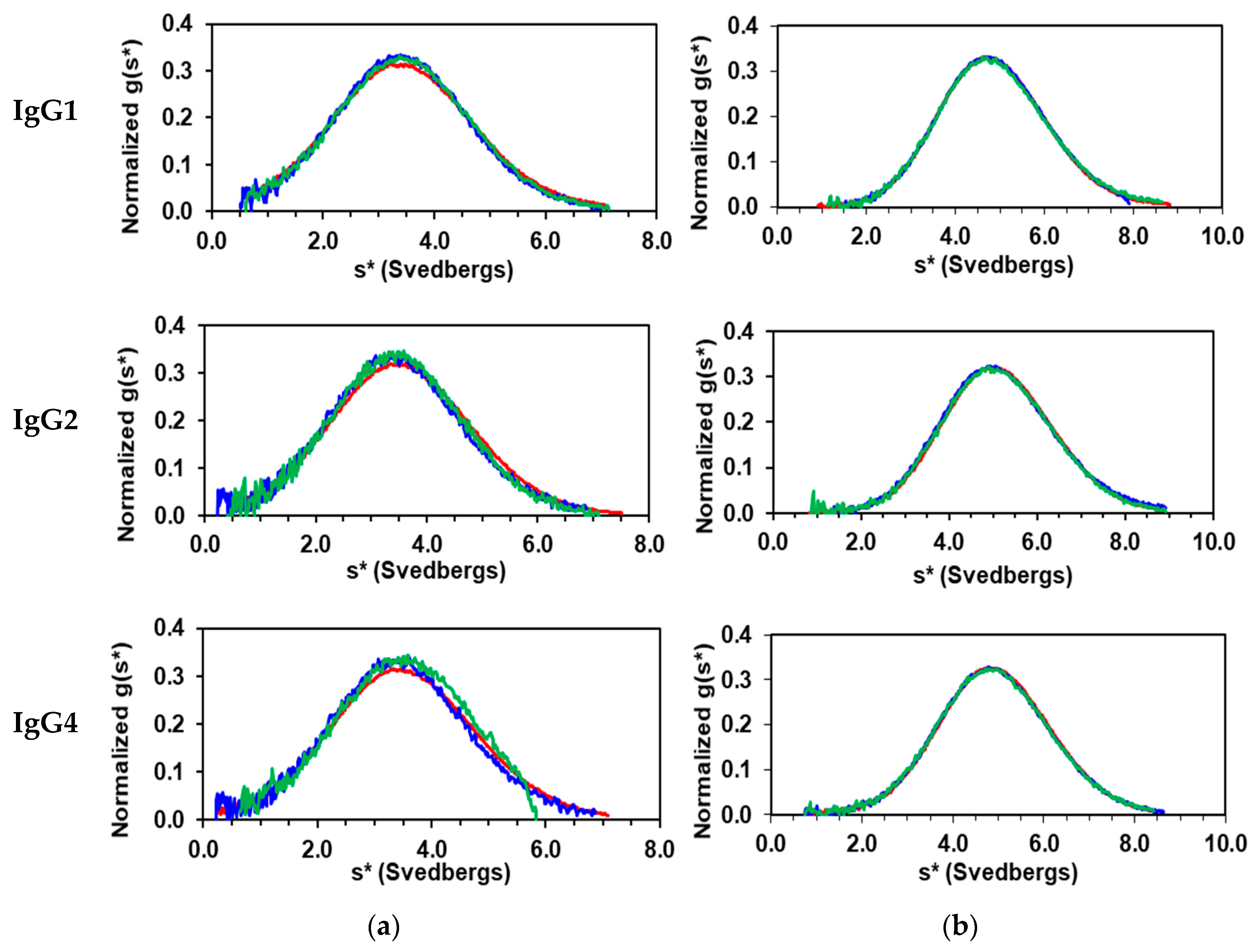
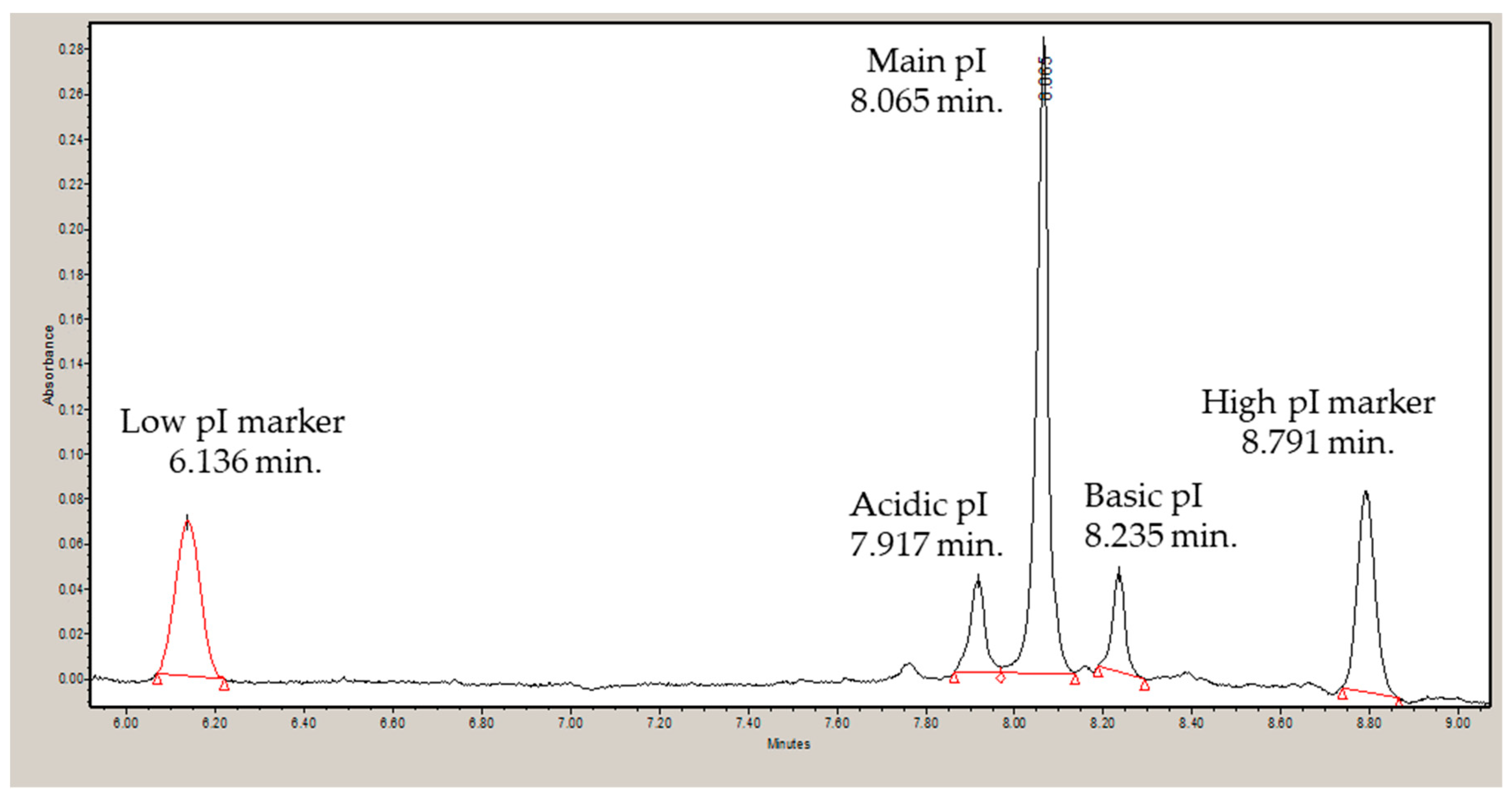
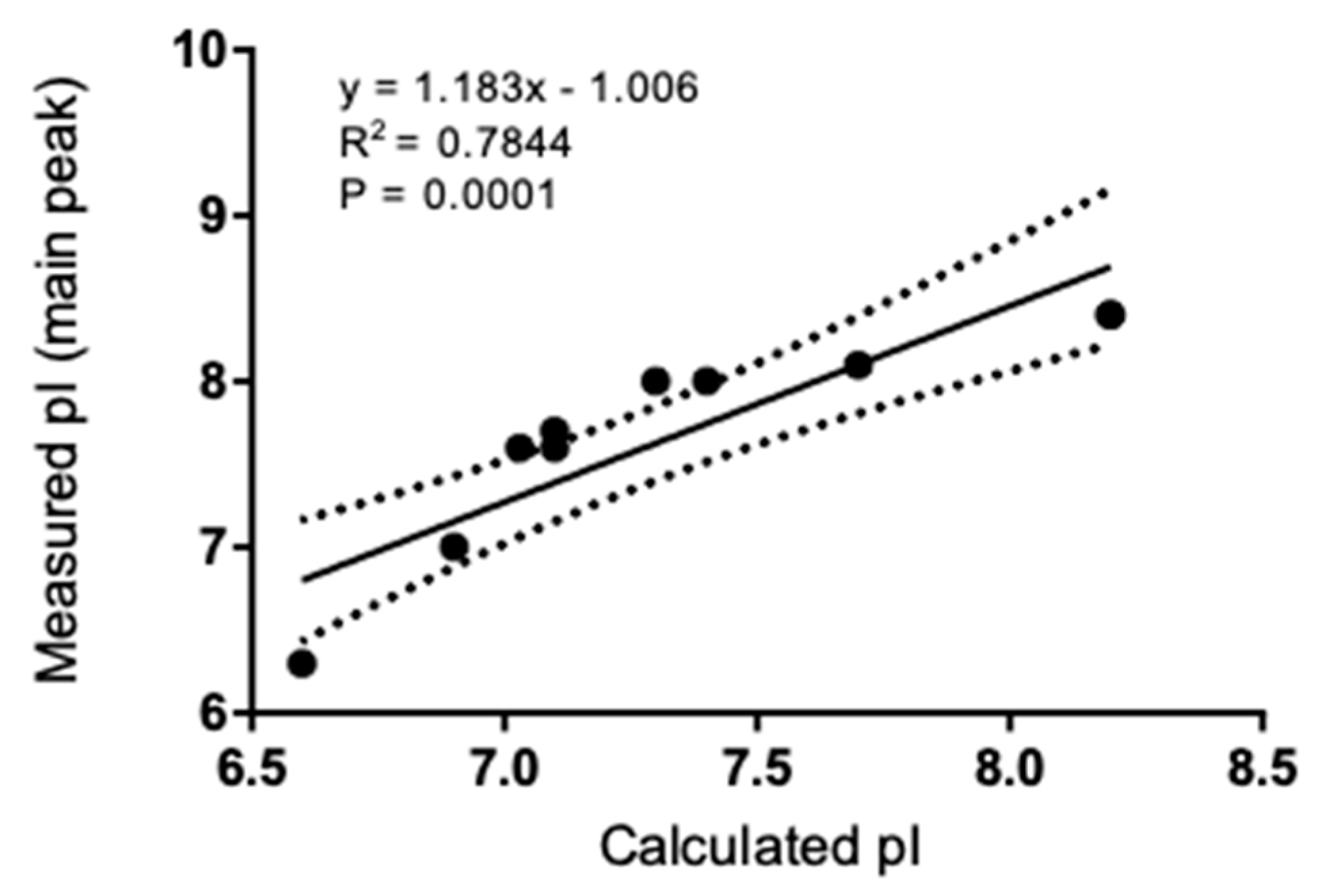
| ID | Subclass | Monomer (%) | Mass (Da) | Glycoform Level (%) * | ||
|---|---|---|---|---|---|---|
G0F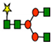 | G1F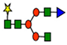 | G2F | ||||
| mAb 1 | IgG1 | >99 | 148,480 | 49 | 43 | 8 |
| IgG2 | >99 | 147,913 | 52 | 39 | 9 | |
| IgG4 | >99 | 148,190 | 45 | 39 | 16 | |
| IgG4Pro | >99 | 148,210 | 43 | 40 | 17 | |
| mAb 2 | IgG1 | >99 | 148,301 | 45 | 42 | 13 |
| IgG2 | >99 | 147,734 | 50 | 41 | 9 | |
| IgG4 | >99 | 148,012 | 43 | 43 | 14 | |
| IgG4Pro | >99 | 148,032 | 20 | 50 | 30 | |
| mAb 3 | IgG1 | >99 | 149,959 | 30 | 52 | 18 |
| IgG2 | >99 | 149,231 | 45 | 41 | 14 | |
| IgG4 | >99 | 149,507 | 49 | 43 | 8 | |
| IgG4Pro | >99 | 149,529 | 25 | 52 | 25 | |
 fucose.
fucose.| Subclass | V Region | Cleaved Site | F(ab’)2 Purity (%) | Fc Purity (%) |
|---|---|---|---|---|
| IgG1 | mAb 1 | CPPCPAPELLG/GPSVF | 95 | 100 |
| mAb 2 | 100 | |||
| mAb 3 | 100 | |||
| IgG2 | mAb 1 | CPPCPAPPVA/GPSVF | 100 | 98 |
| mAb 2 | 100 | |||
| mAb 3 | 100 | |||
| IgG4 | mAb 1 | CPSCPAPELLG/GPSVF | 95 | 97 * |
| mAb 2 | 95 | |||
| mAb 3 | 97 | |||
| IgG4Pro | mAb 1 | CPPCPAPELLG/GPSVF | 97 | |
| mAb 2 | 100 | 97 * | ||
| mAb 3 | 100 |
| ID | Subclass | pIcal | pIicIEF | ||
|---|---|---|---|---|---|
| Acidic Peak | Main Peak | Basic Peak | |||
| mAb 1 | IgG1 | 7.7 | 7.9 | 8.1 | 8.2 |
| IgG2 | 6.9 | 6.9 | 7.0 | 7.3 | |
| IgG4 | 6.6 | 6.2 | 6.3 | 6.5 | |
| IgG4Pro | 6.6 | 6.2 | 6.3 | 6.5 | |
| mAb 2 | IgG1 | 8.2 | 8.2 | 8.4 | 8.6 |
| IgG2 | 7.3 | 7.9 | 8.0 | 8.2 | |
| IgG4 | 7.0 | 7.4 | 7.6 | 7.7 | |
| IgG4Pro | 7.0 | 7.4 | 7.6 | 7.7 | |
| mAb 3 | IgG1 | 8.2 | 8.2 | 8.4 | 8.6 |
| IgG2 | 7.4 | 7.2 | 8.0 | 8.1 | |
| IgG4 | 7.1 | 7.5 | 7.7 | 7.8 | |
| IgG4Pro | 7.1 | 7.5 | 7.7 | 7.8 | |
| ID | Subclass | IgG | F(ab’)2 | Fc * | |||
|---|---|---|---|---|---|---|---|
| ZDHH | Zcal | ZDHH | Zcal | ZDHH | Zcal | ||
| mAb 1 | IgG1 | 7.7 ± 0.2 | 57.3 | 3.3 ± 0.2 | 31.2 | 6.2 ± 0.1 | 26.30 |
| IgG2 | 3.9 ± 0.1 | 50.0 | 0 | 25.9 | 4.9 ± 0.1 | 24.30 | |
| IgG4 | 1.4 ± 0.2 | 46.7 | 1.3 ± 0.1 | 27.9 | 0.45 ± 0.1 | 18.98 | |
| IgG4Pro | 1.4 ± 0.8 | 46.7 | 1.5 ± 0.2 | 27.9 | 0.45 ± 0.1 | 18.98 | |
| mAb 2 | IgG1 | 10.6 ± 0.1 | 61.0 | 8.6 ± 0.2 | 34.9 | 6.2 ± 0.1 | 26.30 |
| IgG2 | 10.1 ± 0.2 | 53.7 | 4.7 ± 0.1 | 29.6 | 4.9 ± 0.1 | 24.30 | |
| IgG4 | 5.6 ± 0.2 | 50.4 | 6.2 ± 0.1 | 31.6 | 0.45 ± 0.1 | 18.98 | |
| IgG4Pro | 5.6 ± 0.2 | 50.4 | 6.2 ± 0.1 | 31.6 | 0.45 ± 0.1 | 18.98 | |
| mAb 3 | IgG1 | 12.5 ± 0.1 | 65.8 | 9.4 ± 0.1 | 39.6 | 6.2 ± 0.1 | 26.30 |
| IgG2 | 10.3 ± 0.2 | 58.5 | 5.3 ± 0.2 | 34.3 | 4.9 ± 0.1 | 24.30 | |
| IgG4 | 7.7 ± 0.2 | 55.1 | 7.1 ± 0.1 | 36.3 | 0.45 ± 0.1 | 18.98 | |
| IgG4Pro | 7.8 ± 0.2 | 55.1 | 7.3 ± 0.1 | 36.3 | 0.45 ± 0.1 | 18.98 | |
| ID | Subclass | IgG | F(ab’)2 | Fc * | |||
|---|---|---|---|---|---|---|---|
| ZDHH | Zcal | ZDHH | Zcal | ZDHH | Zcal | ||
| mAb 1 | IgG1 | −5.6 ± 0.1 | 1.8 | 0 | −0.48 | −2.8 ± 0.1 | 1.50 |
| IgG2 | −7.7 ± 0.6 | −4.4 | 0 | −4.59 | −6.0 ± 0.6 | −0.48 | |
| IgG4 | −10.6 ± 0.5 | −6.5 | −4.3 ± 0.8 | −2.61 | −10.4 ± 0.3 | −4.60 | |
| IgG4Pro | −13 ± 0.3 | −6.5 | −5.05 ± 0.5 | −2.61 | −10.4 ± 0.3 | −4.60 | |
| mAb 2 | IgG1 | 0 | 5.8 | 0 | 3.5 | −2.8 ± 0.1 | 1.50 |
| IgG2 | −3.2 ± 0.2 | −0.4 | 0 | −0.61 | −6.0 ± 0.6 | −0.48 | |
| IgG4 | −7.4 ± 0.2 | −2.5 | 0 | 1.38 | −10.4 ± 0.3 | −4.60 | |
| IgG4Pro | −9.6 ± 0.4 | −2.5 | 0 | 1.38 | −10.4 ± 0.3 | −4.60 | |
| mAb 3 | IgG1 | −5.3 ± 0.5 | 6.0 | 0 | 3.45 | −2.8 ± 0.1 | 1.50 |
| IgG2 | −6.1 ± 0.3 | −0.1 | 0 | −0.36 | −6.0 ± 0.6 | −0.48 | |
| IgG4 | −6.1 ± 0.2 | −2.2 | 0 | 1.63 | −10.4 ± 0.3 | −4.60 | |
| IgG4Pro | −10.7 ± 0.4 | −2.2 | 0 | 1.63 | −10.4 ± 0.3 | −4.60 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, D.; Kroe-Barrett, R.; Singh, S.; Laue, T. IgG Charge: Practical and Biological Implications. Antibodies 2019, 8, 24. https://doi.org/10.3390/antib8010024
Yang D, Kroe-Barrett R, Singh S, Laue T. IgG Charge: Practical and Biological Implications. Antibodies. 2019; 8(1):24. https://doi.org/10.3390/antib8010024
Chicago/Turabian StyleYang, Danlin, Rachel Kroe-Barrett, Sanjaya Singh, and Thomas Laue. 2019. "IgG Charge: Practical and Biological Implications" Antibodies 8, no. 1: 24. https://doi.org/10.3390/antib8010024
APA StyleYang, D., Kroe-Barrett, R., Singh, S., & Laue, T. (2019). IgG Charge: Practical and Biological Implications. Antibodies, 8(1), 24. https://doi.org/10.3390/antib8010024





