Unsupervised Plot Morphology Classification via Graph Attention Networks: Evidence from Nanjing’s Walled City
Abstract
1. Introduction
- We introduce a framework that models each plot as a graph and applies GAT-based representation learning, thereby extending quantitative tools at the plot scale and effectively incorporating both parcel attributes and intra-plot building relations.
- By designing a loss function that jointly learns building attributes and inter-building spatial relations, the model fuses morphological and structural information into a unified graph-level embedding, yielding plot clusters that retain clear architectural interpretability.
- The resulting fine-grained typology offers planners a more nuanced basis for urban renewal, providing detailed spatial guidance for urban renewal. The framework also contributes a transferable toolset for scientific inquiry in land use management.
2. Literature Review
2.1. Urban Morphology at Plot Scale
2.1.1. Definitions of the Plot
2.1.2. Quantitative Approaches to Plots
2.2. Machine Learning Approaches to Plot Analysis
2.2.1. Machine Learning Techniques
2.2.2. Graph Neural Network Approaches
3. Methods
3.1. Methods Architecture
3.2. Graph Construction
3.2.1. Graph Using Delaunay Triangulation
3.2.2. Morphological Features
3.3. Multi-Dimensional Plot Vectors
3.3.1. Graph-Level Embeddings with Attention
3.3.2. Triple Loss Function
3.4. Clustering After Concatenation
4. Results
4.1. Dataset and Hyperparameter Tuning
4.1.1. Data Description
4.1.2. Hyperparameter Tuning
4.2. Results Interpretation
4.2.1. Morphological Types Identification
4.2.2. Classification Strengthened by Building Relation Features
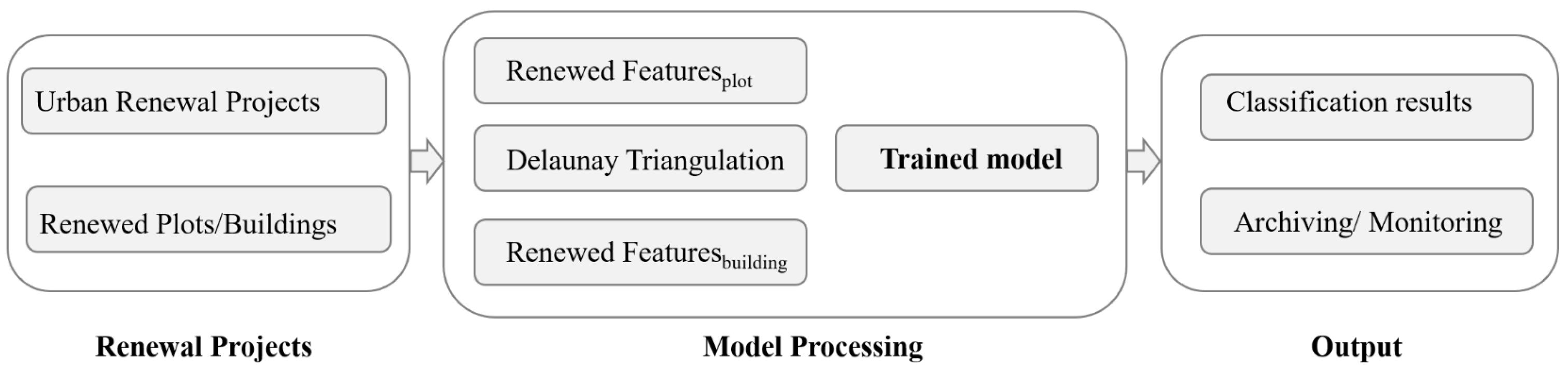
4.2.3. Urban Renewal Implications
5. Discussion
5.1. Triple Loss Function Validation
5.2. Theoretical Implications
5.3. From Genesis to Application
5.3.1. Historical Genesis of the Seven Types
5.3.2. Application Workflow in Design Practice
5.4. Research Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

| Metrics | Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 | Cluster 5 | Cluster 6 | Cluster 7 |
|---|---|---|---|---|---|---|---|
| plot_count | 202 | 259 | 15 | 1113 | 1263 | 3647 | 2474 |
| total_area | 9,044,316 | 1,641,203 | 4,543,404 | 6,101,306 | 6,852,669 | 4,344,258 | 2,250,693 |
| mean_area | 44,773.84 | 6336.69 | 302,893.6 | 5481.857 | 5425.708 | 1191.187 | 909.7383 |
| median_area | 36,191.13 | 4865.828 | 215,958.1 | 4122.018 | 3633.609 | 839.7579 | 599.6674 |
| max_area | 149,108.6 | 28,247.99 | 941,229 | 29,456.58 | 34,180.04 | 93,661.29 | 28,865.74 |
| plot_max_area | 1243 | 6642 | 2282 | 2792 | 2364 | 4536 | 8001 |
| min_area | 10,096.85 | 676.7026 | 180,580.6 | 227.4779 | 130.8906 | 42.82825 | 19.28698 |
| plot_min_area | 8674 | 2259 | 244 | 8391 | 415 | 3005 | 1755 |
| total_buildings | 4793 | 1290 | 1781 | 6228 | 7025 | 4798 | 3129 |
| mean_buildings | 23.72772 | 4.980695 | 118.7333 | 5.595687 | 5.562154 | 1.315602 | 1.264753 |
| median_buildings | 20 | 4 | 105 | 4 | 4 | 1 | 1 |
| max_buildings | 91 | 32 | 427 | 31 | 32 | 2 | 2 |
| plot_max_buildings | 7612 | 7681 | 2282 | 6946 | 7393 | 7 | 14 |
| min_buildings | 3 | 3 | 29 | 3 | 3 | 1 | 1 |
| plot_min_buildings | 1637 | 33 | 1225 | 5 | 36 | 1 | 2 |
| coverage_mean | 0.27465 | 0.484504 | 0.193145 | 0.367458 | 0.418382 | 0.338197 | 0.64935 |
| coverage_median | 0.271831 | 0.469069 | 0.2342 | 0.360743 | 0.398814 | 0.352608 | 0.61968 |
| coverage_max | 0.630115 | 1.577616 | 0.28901 | 0.926781 | 1.124933 | 0.584816 | 1 |
| coverage_min | 0.022058 | 0.150293 | 0.04755 | 0.039009 | 0.048126 | 0.000442 | 0.247814 |
| FAR_mean | 1.730994 | 8.60342 | 1.238802 | 2.221596 | 2.456136 | 1.801078 | 3.693972 |
| FAR_median | 1.712884 | 7.429124 | 1.064944 | 2.143638 | 2.336872 | 1.763918 | 3.362612 |
| FAR_max | 5.564863 | 33.86183 | 4.514469 | 6.678434 | 6.262421 | 8.232607 | 46.52596 |
| FAR_min | 0.039021 | 3.248306 | 0.11144 | 0.039009 | 0.237339 | 0.001767 | 0.587176 |



References
- Conzen, M.R.G. Alnwick, Northumberland: A Study in Town-Plan Analysis. Trans. Pap. (Inst. Br. Geogr.) 1960, iii–122. [Google Scholar] [CrossRef]
- Porta, S.; Romice, O. Plot-Based Urbanism: Towards Time-Consciousness in Place-Making; University of Strathclyde: Glasgow, UK, 2010; pp. 1–39. [Google Scholar]
- Kropf, K. Aspects of Urban Form. Urban Morphol. 2009, 13, 105–120. [Google Scholar] [CrossRef]
- Kropf, K. Ambiguity in the Definition of Built Form. JUM 2013, 18, 41–57. [Google Scholar] [CrossRef]
- Barbour, G.; Romice, O.; Porta, S. Sustainable Plot-Based Urban Regeneration and Traditional Master Planning Practice in Glasgow. Open House Int. 2016, 41, 15–22. [Google Scholar] [CrossRef]
- Feliciotti, A.; Romice, O.; Porta, S. Urban Regeneration, Masterplans and Resilience: The Case of Gorbals, Glasgow. Urban Morphol. 2017, 21, 61–79. [Google Scholar] [CrossRef]
- Caniggia, G.; Maffei, G.L. Composizione Architettonica e Tipologia Edilizia; FLORE: Marsilio, Venezia, 1979; Volume 1. [Google Scholar]
- Conzen, M.R.G.; Whitehand, J.W.R. The Urban Landscape: Historical Development and Management; Academic Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Caniggia, G.; Maffei, G.L. Architectural Composition and Building Typology: Interpreting Basic Building; Alinea Editrice: Firenze, Italy, 2001; Volume 176. [Google Scholar]
- Bobkova, E.; Berghauser Pont, M.; Marcus, L. Towards Analytical Typologies of Plot Systems: Quantitative Profile of Five European Cities. Environ. Plan. B Urban Anal. City Sci. 2021, 48, 604–620. [Google Scholar] [CrossRef]
- Dovey, K.; van Oostrum, M.; Chatterjee, I.; Shafique, T. Towards a Morphogenesis of Informal Settlements. Habitat Int. 2020, 104, 102240. [Google Scholar] [CrossRef]
- Simone, A. Cities of the Global South. Annu. Rev. Sociol. 2020, 46, 603–622. [Google Scholar] [CrossRef]
- Batty, M. The New Science of Cities; MIT Press: Cambridge, MA, USA, 2013; ISBN 978-0-262-01952-1. [Google Scholar]
- Ghosh, S.; Mallick, A.; Chowdhury, A.; De Sarkar, K.; Mukherjee, J. Graph Theory Applications for Advanced Geospatial Modelling and Decision-Making. Appl. Geomat. 2024, 16, 799–812. [Google Scholar] [CrossRef]
- Marshall, S.; Gil, J.; Kropf, K.; Tomko, M.; Figueiredo, L. Street Network Studies: From Networks to Models and Their Representations. Netw. Spat. Econ. 2018, 18, 735–749. [Google Scholar] [CrossRef]
- Wang, J.; Biljecki, F. Unsupervised Machine Learning in Urban Studies: A Systematic Review of Applications. Cities 2022, 129, 103925. [Google Scholar] [CrossRef]
- Panerai, P.; Castex, J.; Depaule, J.-C.; Samuels, I. Urban Forms: The Death and Life of the Urban Block; Routledge: London, UK, 2004; ISBN 978-0-7506-5607-8. [Google Scholar]
- Kropf, K. Plots, Property and Behaviour. JUM 2017, 22, 5–14. [Google Scholar] [CrossRef]
- Attilio, P. After Amnesia. Learning from the Islamic Mediterranean; Icar: Bari, Italy, 2007; ISBN 9788895006031. [Google Scholar]
- Song, Y.; Zhang, Y.; Han, D. Deciphering Built Form Complexity of Chinese Cities through Plot Recognition: A Case Study of Nanjing, China. Front. Archit. Res. 2022, 11, 795–805. [Google Scholar] [CrossRef]
- Whitehand, J.W.R.; Gu, K.; Conzen, M.P.; Whitehand, S.M. The Typological Process and the Morphological Period: A Cross-Cultural Assessment. Environ. Plann. B Plann. Des. 2014, 41, 512–533. [Google Scholar] [CrossRef]
- Elzeni, M.; Elmokadem, A.; Badawy, N.M. Classification of Urban Morphology Indicators towards Urban Generation. Port-Said Eng. Res. J. 2022, 26, 43–56. [Google Scholar] [CrossRef]
- Hermosilla, T.; Ruiz, L.A.; Recio, J.A.; Cambra-López, M. Assessing Contextual Descriptive Features for Plot-Based Classification of Urban Areas. Landsc. Urban Plan. 2012, 106, 124–137. [Google Scholar] [CrossRef]
- Berghauser Pont, M.; Marcus, L. Innovations in Measuring Density: From Area and Location Density to Accessible and Perceived Density. Nat. Astron. 2014, 26, 2–9. [Google Scholar]
- Berghauser Pont, M.; Haupt, P.A. Spacematrix: Space, Density and Urban Form; TU Delft OPEN: Municipality of Norrköping, Sweden, 2023. [Google Scholar]
- Marcus, L. Spatial Capital. A Proposal for an Extension of Space Syntax into a More General Urban Morphology. J. Space Syntax. 2010, 1, 30–40. [Google Scholar]
- Marcus, L.; Bobkova, E. Spatial Configuration of Plot Systems and Urban Diversity: Empirical Support for a Differentiation Variable in Spatial Morphology. In Proceedings of the 12th Space Syntax Symposium, Beijing, China, 8–13 July 2019; Volume 494, p. 1. [Google Scholar]
- Scoppa, M.D.; Peponis, J. Distributed Attraction: The Effects of Street Network Connectivity upon the Distribution of Retail Frontage in the City of Buenos Aires. Environ. Plann. B Plann. Des. 2015, 42, 354–378. [Google Scholar] [CrossRef]
- Porta, S.; Romice, O.; Strano, E.; Venerandi, A.; Morello, E.; Viana, M.; Da Fontoura Costa, L. Plot-Based Urbanism and Urban Morphometrics: Measuring the Evolution of Blocks, Street Fronts and Plots in Cities. 2011. Available online: https://strathprints.strath.ac.uk/35639/ (accessed on 13 July 2025).
- Bobkova, E. Towards a Theory of Natural Occupation: Developing Theoretical, Methodological and Empirical Support for the Relation between Plot Systems and Urban Processes. Ph.D. Thesis, Chalmers Tekniska Hogskola, Gothenburg, Sweden, 2019. [Google Scholar]
- Ye, Y.; van Nes, A. Quantitative Tools in Urban Morphology: Combining Space Syntax, Spacematrix and Mixed-Use Index in a GIS Framework. Urban Morphol. 2014, 18, 97–118. [Google Scholar] [CrossRef]
- Marshall, S. An Area Structure Approach to Morphological Representation and Analysis. JUM 2014, 19, 117–134. [Google Scholar] [CrossRef]
- Braun, A.; Warth, G.; Bachofer, F.; Schultz, M.; Hochschild, V. Mapping Urban Structure Types Based on Remote Sensing Data—A Universal and Adaptable Framework for Spatial Analyses of Cities. Land 2023, 12, 1885. [Google Scholar] [CrossRef]
- Li, R.; Sun, T.; Ghaffarian, S.; Tsamados, M.; Ni, G. GLAMOUR: GLobAl Building MOrphology Dataset for URban Hydroclimate Modelling. Sci. Data 2024, 11, 618. [Google Scholar] [CrossRef] [PubMed]
- Vanderhaegen, S.; Canters, F. Mapping Urban Form and Function at City Block Level Using Spatial Metrics. Landsc. Urban Plan. 2017, 167, 399–409. [Google Scholar] [CrossRef]
- Usui, H. Statistical Distribution of Building Lot Depth: Theoretical and Empirical Investigation of Downtown Districts in Tokyo. Environ. Plan. B Urban Anal. City Sci. 2019, 46, 1499–1516. [Google Scholar] [CrossRef]
- Fleischmann, M.; Feliciotti, A.; Romice, O.; Porta, S. Methodological Foundation of a Numerical Taxonomy of Urban Form. Environ. Plan. B Urban Anal. City Sci. 2022, 49, 1283–1299. [Google Scholar] [CrossRef]
- Karimi, F.; Sultana, S.; Shirzadi Babakan, A.; Suthaharan, S. An Enhanced Support Vector Machine Model for Urban Expansion Prediction. Comput. Environ. Urban Syst. 2019, 75, 61–75. [Google Scholar] [CrossRef]
- Ruiz Hernandez, I.E.; Shi, W. A Random Forests Classification Method for Urban Land-Use Mapping Integrating Spatial Metrics and Texture Analysis. Int. J. Remote Sens. 2018, 39, 1175–1198. [Google Scholar] [CrossRef]
- Liu, S.; Liu, R.; Tan, N. A Spatial Improved-kNN-Based Flood Inundation Risk Framework for Urban Tourism under Two Rainfall Scenarios. Sustainability 2021, 13, 2859. [Google Scholar] [CrossRef]
- Jun, M.-J. A Comparison of a Gradient Boosting Decision Tree, Random Forests, and Artificial Neural Networks to Model Urban Land Use Changes: The Case of the Seoul Metropolitan Area. Int. J. Geogr. Inf. Sci. 2021, 35, 2149–2167. [Google Scholar] [CrossRef]
- Zhang, P.; Ghosh, D.; Park, S. Spatial Measures and Methods in Sustainable Urban Morphology: A Systematic Review. Landsc. Urban Plan. 2023, 237, 104776. [Google Scholar] [CrossRef]
- Chen, C.-Y.; Koch, F.; Reicher, C. Developing a Two-Level Machine-Learning Approach for Classifying Urban Form for an East Asian Mega-City. Environ. Plan. B 2024, 51, 854–869. [Google Scholar] [CrossRef]
- Batty, M. Cities as Complex Systems: Scaling, Interaction, Networks, Dynamics and Urban Morphologies. In Encyclopedia of Complexity and Systems Science; Meyers, R.A., Ed.; Springer: New York, NY, USA, 2009; pp. 1041–1071. ISBN 978-0-387-30440-3. [Google Scholar]
- Caruso, G.; Hilal, M.; Thomas, I. Measuring Urban Forms from Inter-Building Distances: Combining MST Graphs with a Local Index of Spatial Association. Landsc. Urban Plan. 2017, 163, 80–89. [Google Scholar] [CrossRef]
- Fan, C.; Yang, Y.; Mostafavi, A. Neural Embeddings of Urban Big Data Reveal Spatial Structures in Cities. Humanit. Soc. Sci. Commun. 2024, 11, 409. [Google Scholar] [CrossRef]
- Lei, B.; Liu, P.; Milojevic-Dupont, N.; Biljecki, F. Predicting Building Characteristics at Urban Scale Using Graph Neural Networks and Street-Level Context. Comput. Environ. Urban Syst. 2024, 111, 102129. [Google Scholar] [CrossRef]
- Chen, D.; Feng, Y.; Li, X.; Qu, M.; Luo, P.; Meng, L. Interpreting Core Forms of Urban Morphology Linked to Urban Functions with Explainable Graph Neural Network. Comput. Environ. Urban Syst. 2025, 118, 102267. [Google Scholar] [CrossRef]
- You, Y.; Chen, T.; Sui, Y.; Chen, T.; Wang, Z.; Shen, Y. Graph Contrastive Learning with Augmentations. Advances in neural information Process. Systems. arXiv 2020, arXiv:2010.13902. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. arXiv 2018, arXiv:1710.10903. [Google Scholar]
- Wang, G.; Ying, R.; Huang, J.; Leskovec, J. Improving Graph Attention Networks with Large Margin-Based Constraints. arXiv 2019, arXiv:1910.11945. [Google Scholar] [CrossRef]
- Zhu, Y.; Xu, Y.; Liu, Q.; Wu, S. An Empirical Study of Graph Contrastive Learning. arXiv 2021, arXiv:2109.01116. [Google Scholar] [CrossRef]
- Fang, L.; Kou, Z.; Yang, Y.; Li, T. Representing Spatial Data with Graph Contrastive Learning. Remote Sens. 2023, 15, 880. [Google Scholar] [CrossRef]
- Lelo, K. Analysing Spatial Relationships through the Urban Cadastre of Nineteenth-Century Rome. Urban Hist. 2020, 47, 467–487. [Google Scholar] [CrossRef]
- Aurenhammer, F. Voronoi Diagrams—A Survey of a Fundamental Geometric Data Structure. ACM Comput. Surv. 1991, 23, 345–405. [Google Scholar] [CrossRef]
- Lee, D.T.; Schachter, B.J. Two Algorithms for Constructing a Delaunay Triangulation. Int. J. Comput. Inf. Sci. 1980, 9, 219–242. [Google Scholar] [CrossRef]
- Li, W.; Goodchild, M.F.; Church, R. An Efficient Measure of Compactness for Two-Dimensional Shapes and Its Application in Regionalization Problems. Int. J. Geogr. Inf. Sci. 2013, 27, 1227–1250. [Google Scholar] [CrossRef]
- Basaraner, M.; Cetinkaya, S. Performance of Shape Indices and Classification Schemes for Characterising Perceptual Shape Complexity of Building Footprints in GIS. Int. J. Geogr. Inf. Sci. 2017, 31, 1952–1977. [Google Scholar] [CrossRef]
- Gibbs, J.P. Urban Research Methods. In Van Nostrand Series in Sociology; University of Michigan: Ann Arbor, MI, USA, 1961. [Google Scholar]
- Sun, F.-Y.; Hoffmann, J.; Verma, V.; Tang, J. InfoGraph: Unsupervised and Semi-Supervised Graph-Level Representation Learning via Mutual Information Maximization. arXiv 2020, arXiv:1908.01000. [Google Scholar]
- Veličković, P.; Fedus, W.; Hamilton, W.L.; Liò, P.; Bengio, Y.; Hjelm, R.D. Deep Graph Infomax. arXiv 2018, arXiv:1809.10341. [Google Scholar] [CrossRef]
- Grover, A.; Leskovec, J. Node2vec: Scalable Feature Learning for Networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13 August 2016; pp. 855–864. [Google Scholar]
- Liu, P.; Neppl, M.; Dong, W. Smart Plot Division: Generating a Plot-Based Strategy for the Restoration of the Old South Historic Urban Area in Nanjing. Urban Des. Int. 2020, 25, 357–376. [Google Scholar] [CrossRef]
- Caldeira, T.P. Peripheral Urbanization: Autoconstruction, Transversal Logics, and Politics in Cities of the Global South. Environ. Plan. D 2017, 35, 3–20. [Google Scholar] [CrossRef]
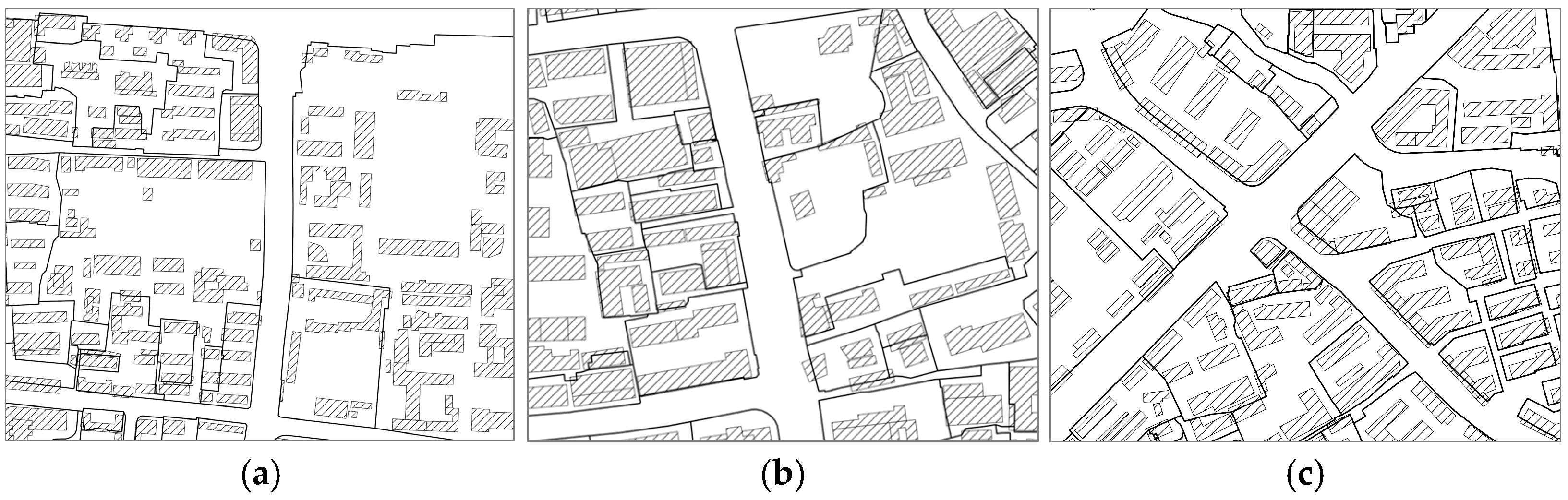






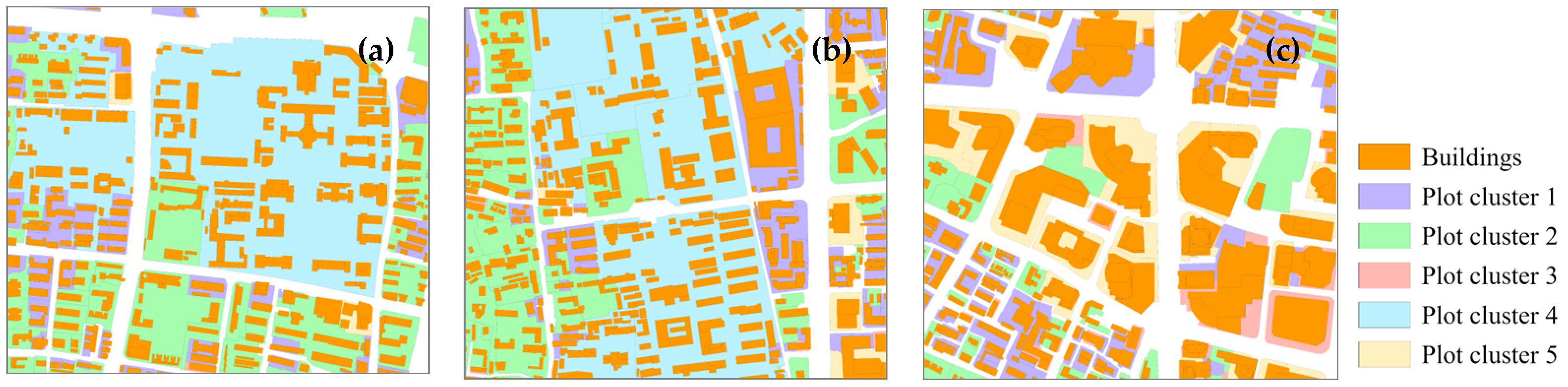


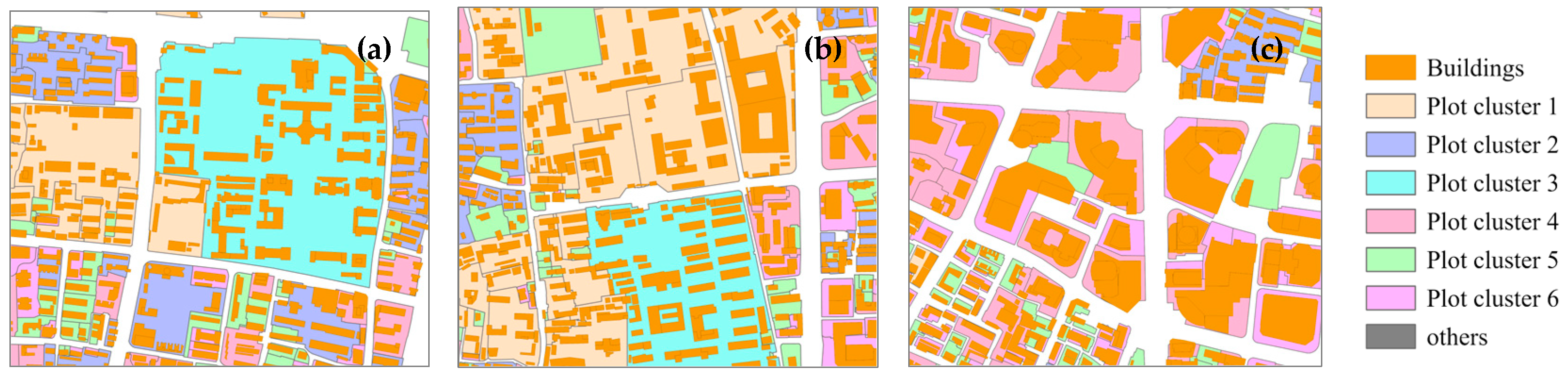
| Type | Features | Description | |
|---|---|---|---|
| Buildings | Size | Elevation | Height of building |
| Level | Number of stories | ||
| Area | Footprint area | ||
| Perimeter | Plan perimeter | ||
| Volume | Footprint area × height | ||
| Slenderness | Height divided by the square root of plan area | ||
| Height radius ratio | Height divided by mean radius of footprint shape | ||
| Shape | Complexity | Area divided by perimeter | |
| Isoperimetric quotient circularity | Quadratic relationship of building, between its area and the perimeter: | ||
| Fractality | Logarithmic relationship of building, between its area and the perimeter: | ||
| Max circularity | Relationship between radius of the equal area circle and the longest radius of a polygon: | ||
| Gibbs compactness | Ratio of a polygon to an ideal shape: | ||
| Plots | Plot area | Plot area | |
| Plot perimeter | Plot perimeter | ||
| GSI | Ground space index: describes the proportion of a plot’s horizontal surface covered by buildings | ||
| FAR | Floor area ratio: an index that reflects development intensity and land use density | ||
| Name | Label | Number | Explanation |
|---|---|---|---|
| Batch size | BS | 64 | number of plot graphs per training batch |
| Hidden layer representation dimension | Hidden Dim | 128 | size of the hidden representation in the GAT |
| Output channel dimension | Output Dim | 64 | dimensionality of the final embedding used for feature concatenation |
| Heads | H | 1 | number of heads in the GAT |
| Dropout rate | Dropout | 0.1 | prevents over-fitting |
| Decay constant | β | 0.1 | distance decay factor for Delaunay edges, giving higher weight to near neighbors |
| Learning rate | η | 1 × 10−3 | gradient descent step size |
| Proportion of link prediction loss | α | 0.2 | sets ratio between link prediction loss and node–graph loss |
| Diversity loss | λ | 0.35 | regularizes inter-graph distance to prevent collapse |
| Temperature value of diversity loss | τ | 0.7 | sensitivity parameter for the diversity term |
| Feature fusion factor | φ | 2 | scaling factor for plot attributes before concatenation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Song, Y. Unsupervised Plot Morphology Classification via Graph Attention Networks: Evidence from Nanjing’s Walled City. Land 2025, 14, 1469. https://doi.org/10.3390/land14071469
Liu Z, Song Y. Unsupervised Plot Morphology Classification via Graph Attention Networks: Evidence from Nanjing’s Walled City. Land. 2025; 14(7):1469. https://doi.org/10.3390/land14071469
Chicago/Turabian StyleLiu, Ziyu, and Yacheng Song. 2025. "Unsupervised Plot Morphology Classification via Graph Attention Networks: Evidence from Nanjing’s Walled City" Land 14, no. 7: 1469. https://doi.org/10.3390/land14071469
APA StyleLiu, Z., & Song, Y. (2025). Unsupervised Plot Morphology Classification via Graph Attention Networks: Evidence from Nanjing’s Walled City. Land, 14(7), 1469. https://doi.org/10.3390/land14071469







