Determination of Soil Thermal Properties Across Seasons in Alkaline–Nonalkaline Soils of Igdır, Türkiye

Abstract

Climate, which has important effects on pedogenesis, affects soils and its structure and mass transport through temperature and precipitation. Soil salinity or alkalinity, which is caused by the effects of climate, parent material, topography, and anthropogenic factors, is one of the important problems of arid and semi-arid regions and has negative effects on soil quality, requiring specific attention due to limited research. In this study, thermal properties were calculated using various classical and improved models in winter, spring, summer, and fall for alkaline and non-alkaline soil. For this purpose, temperature sensors were placed at depths of 0, 0.05, 0.10, 0.15, 0.20, and 0.40 m in non-alkaline and alkaline lands, and temperature data were collected from the sensors for 365 days. This study showed that (i) the thermal properties of both soils vary depending on the seasons of the year, and (ii) the thermal properties (thermal conductivity, thermal conductivity coefficient, thermal conductivity, attenuation depth, thermal conductivity coefficient, speed and length of the heat wave) were lower in the alkaline soil. These results could be used for consideration of climate change mitigation in similar semi-arid zones.

1. Introduction

In soil formation, climate, topography, parent material, and organisms are effective factors. Soil salinity or alkalinity, which is caused by the effects of climate, topography, and anthropogenic factors, is one of the important problems of arid–semi-arid regions and has negative effects on soil health [1,2].

Soil temperature, which is influenced by climate change and is itself an important climate factor, can affects various physical (soil thermal properties, water flow, etc.), chemical (mineralization, nutrients, etc.), and biological (microbial activity, microbial community, etc.) properties of soils [3,4,5]. Soil thermal properties have a close connection to temperature, moisture content, organic matter, bulk density, salt content, and porosity [5]. Some researchers have determined that in non-sodic soils, as the salt content of the soils increases, the thermal diffusivity decreases. In sodic soils, sodicity (ESP), which refers to the presence of excessive sodium ions (Na⁺) in the soil exchange complex, can significantly alter soil structure and behavior, which in turn influences how heat or water are stored and transferred through the soil [1,6,7,8].

Soil apparent thermal conductivity decreases as the salt concentration increases [8]. In refs [9,10], it was also found that increasing the amount of added salts at a given humidity reduces the thermal conductivity. Morozova [11] determined that the thermal conductivity increased with increasing KCl. A study by Tikhonravov [12,13] found that the salt and moisture contents of soil affect the thermal diffusivity coefficient.

Relevant research has shown that the field studies cost money, labor, time, etc. in determining the thermal properties of the soils. This shows that laboratory measurements under controlled conditions and in shorter periods are common [14,15,16,17,18].

Although the effects of salts on the thermal properties of soils have been studied, these studies were carried out under controlled conditions in the laboratory and may not reflect field conditions, particularly for sodic or alkaline soils [1]. In field conditions, it is important to calculate thermal properties with long-term temperature measurements of the main thermal characteristics of soil such as thermal diffusivity (κ), thermal conductivity (λ), thermal effusivity (e), volumetric heat capacity (C_v), depth of attenuation of temperature waves (d), heat wave velocity (ϑ), heat wave length (Λ), and heat flow (q).

Their identification is necessary in the formation of thermal processes in soils. The determination of these parameters is important in shaping the thermal regimes of soils. In this work, classical (amplitude, arctangent, logarithmic, and phase) methods are first used to determine the thermal conductivity coefficient [19,20,21,22,23,24,25,26,27,28,29,30,31]. Subsequently, a new “point” method was developed by our team [32,33,34,35,36,37,38], which, unlike classical approaches, also incorporates the amplitude of daily surface soil temperature (T_a)—a critical parameter that significantly influences thermal diffusivity in soils. Moreover, the proposed method accounts for the depth of the soil profile (i.e., z = L). Notably, in this approach, the thermal diffusivity parameter can be calculated at any investigation point (z_i) within the soil profile. Selecting the most suitable predictive model is essential for the effective monitoring and management of soil thermal dynamics.

The main novelties of this work, in contrast to the earlier works, are as follows:

• This paper presents analytical solutions to the heat transfer problem in soil of finite and semi-infinite thickness under boundary conditions of the first kind with infinite harmonics on the soil surface, as well as boundary conditions of the second kind at depth, i.e., T’_z(z = L, t) = 0 and T’_z(z → ∞, t) = 0.
• Based on these solutions, methods have been developed for determining the thermal conductivity coefficient from a point value of soil temperature of a given power based on the results of an analysis of temperature dynamics at one depth based on eight daily observations with an interval of 3 h.

Methods have been developed for determining the thermal diffusivity coefficient based on the point value of soil temperature of a given thickness based on the results of an analysis of temperature dynamics at one depth based on eight daily observations at 3 h intervals.

When applying this method, the temperature distribution in the soil layer is used for eight time points in the calculated time interval t₀ for each soil profile.

The proposed methods are based on solving (with two harmonics at the soil surface, i.e., z = 0) inverse problems of the heat transfer model.

3.

When using the second harmonic in boundary conditions on the soil surface (z = 0), the model allows for high-precision determination of the parameters of temperature distribution on the soil surface, as well as the thermal conductivity parameter using the proposed M8 method.

4.

The proposed methods, in addition to the amplitude of fluctuations (T_a) of the soil surface temperature, also take into account the depth of the soil profile (L).

The proposed methods make it possible to estimate the coefficient of thermal diffusivity in the soil under natural conditions, which should increase the adequacy of mathematical models of the movement of heat in soil.

Accurate models provide deeper insight into soil temperature fluctuations, which directly influence key processes such as irrigation scheduling, crop development, nutrient cycling, and microbial activity. Reliable predictions of soil thermal properties are particularly valuable for informed decision-making in areas such as precision agriculture, land reclamation, and environmental monitoring. Consequently, evaluating and selecting models based on their accuracy and performance under real field conditions is critical to promoting long-term sustainability and efficient resource use [3,4,5,9,10,32,33,34,35,36,37,38].

The objectives of this study were: (i) to calculate thermal diffusivity (κ) using both classical methods and the new “point” method developed by our team and to identify the most accurate method for the study area; (ii) to determine the thermal characteristic of soil—namely thermal diffusivity (κ), conductivity (λ), effusivity (e), volumetric heat capacity (C_v), depth of attenuation of temperature waves (d), heat wave velocity (ϑ), heat wavelength (Λ), and heat flow (q)—across different seasons; and (iii) to investigate the effects of soil alkalinity on these thermal properties.

2. Materials and Methods

2.1. Materials

2.1.1. Study Area

Our experiment was conducted at the Center for Agricultural Research and Application at Igdir University. The experimental site is located at 39°55′44.9″ N 44°05′36.4″ E. The climate is hot in summer and mild in winter in the region. According to Koppen-–Geiger climate classification, the climate is Bsh (hot, semi-arid climates).

The mean, maximum, and minimum temperature values from 1941 to 2021 were 12.2, 42, and −30.3 °C, respectively.

The climate of the region is microclimate, with the highest rainfall in May and the lowest in August. While the annual average precipitation is 254.2 mm, the evaporation is 1094.9 mm [39]. The soil of the region is calcareous alluvial material, which was formed as a result of floods of the Aras River. The horizons of the soil profile include Ap (0–35 cm), AB (35–55 cm), B (55–96 cm), BC (96–170 cm) in the region. According to the WRB system, the soil is a Calcaric Pantofluvic Fluvisol (Loamic, Aric, and Densic) [40]. The physicochemical properties of the soils are shown in

Table 1. Physicochemical soil properties.

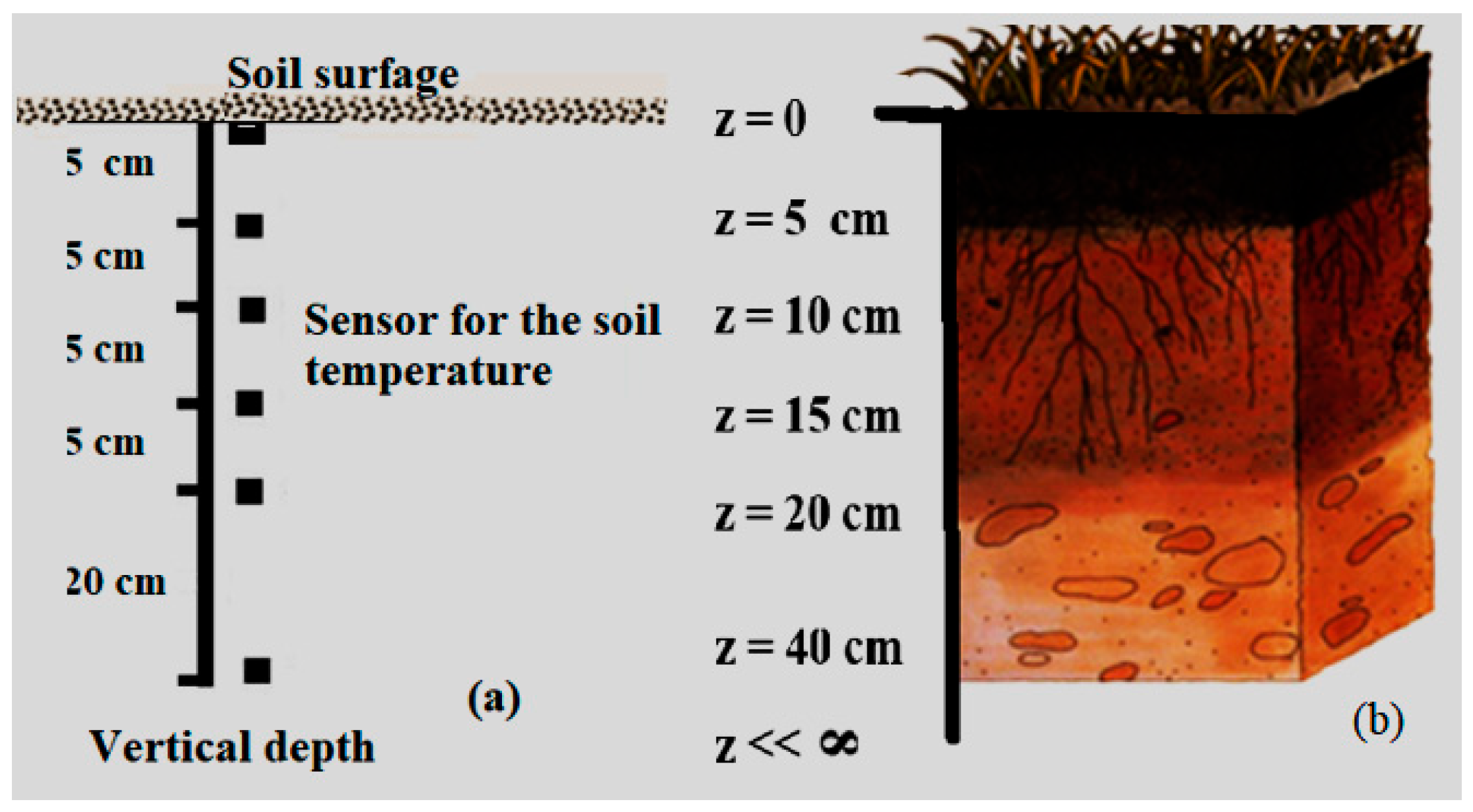
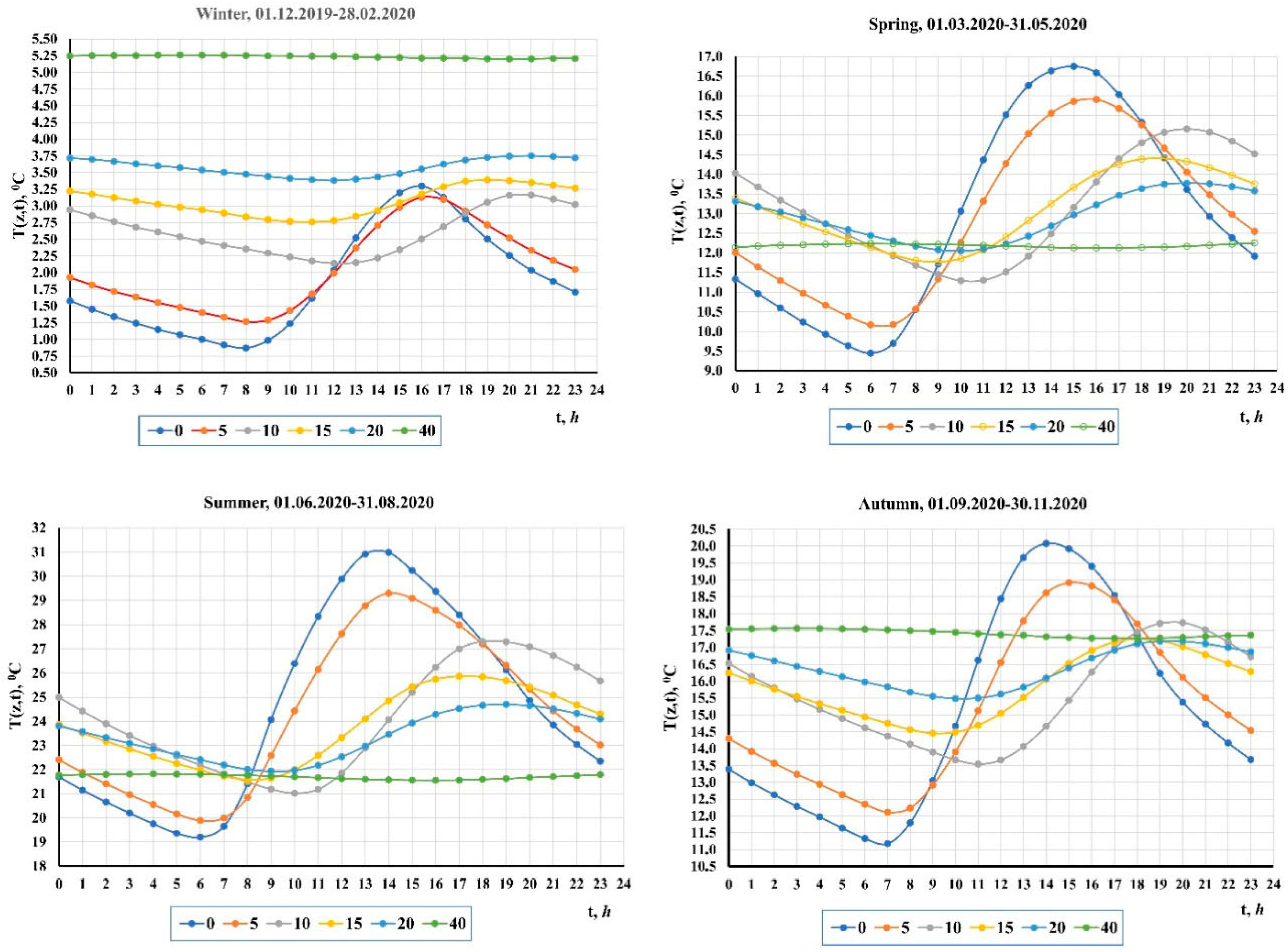
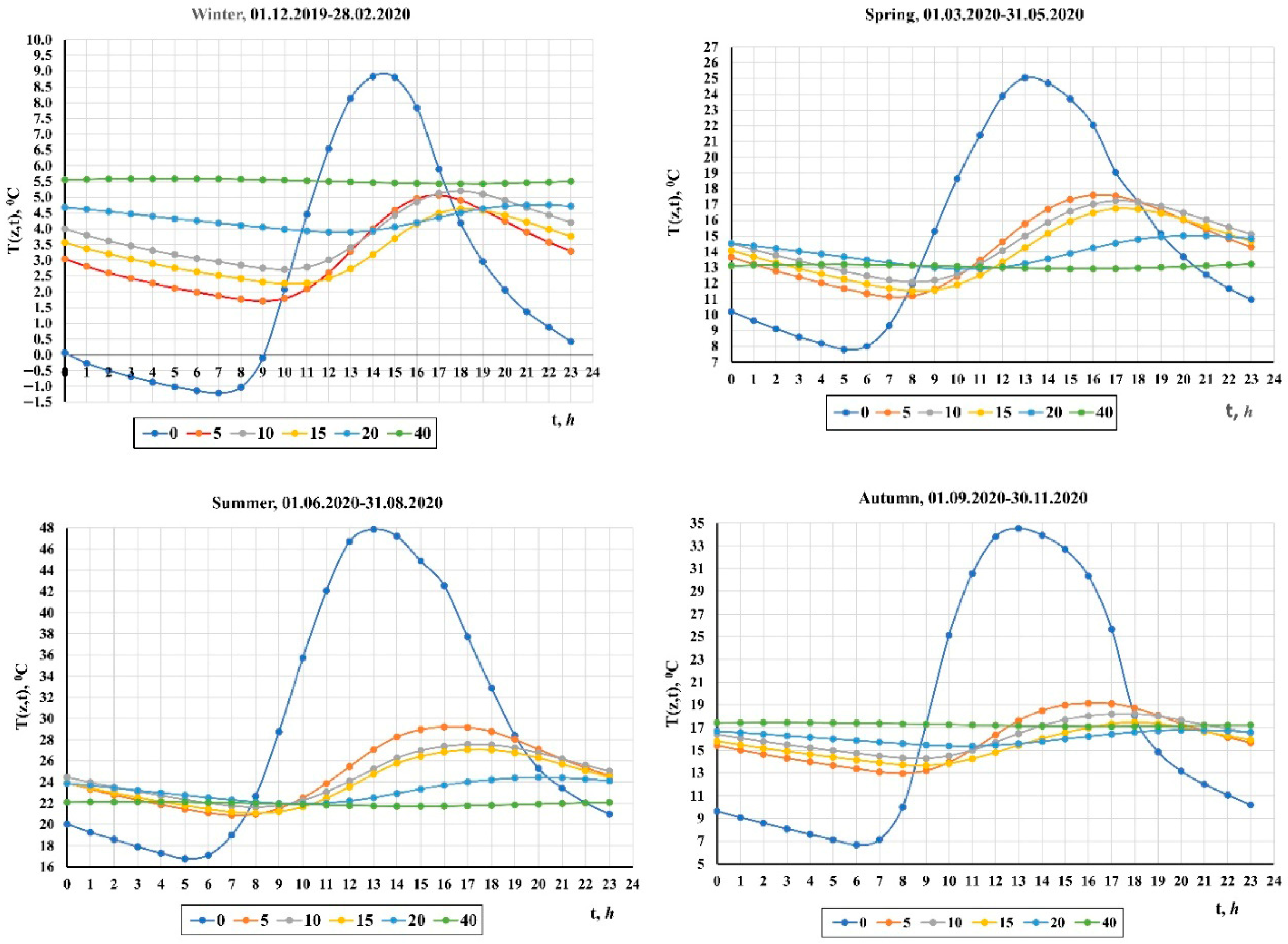
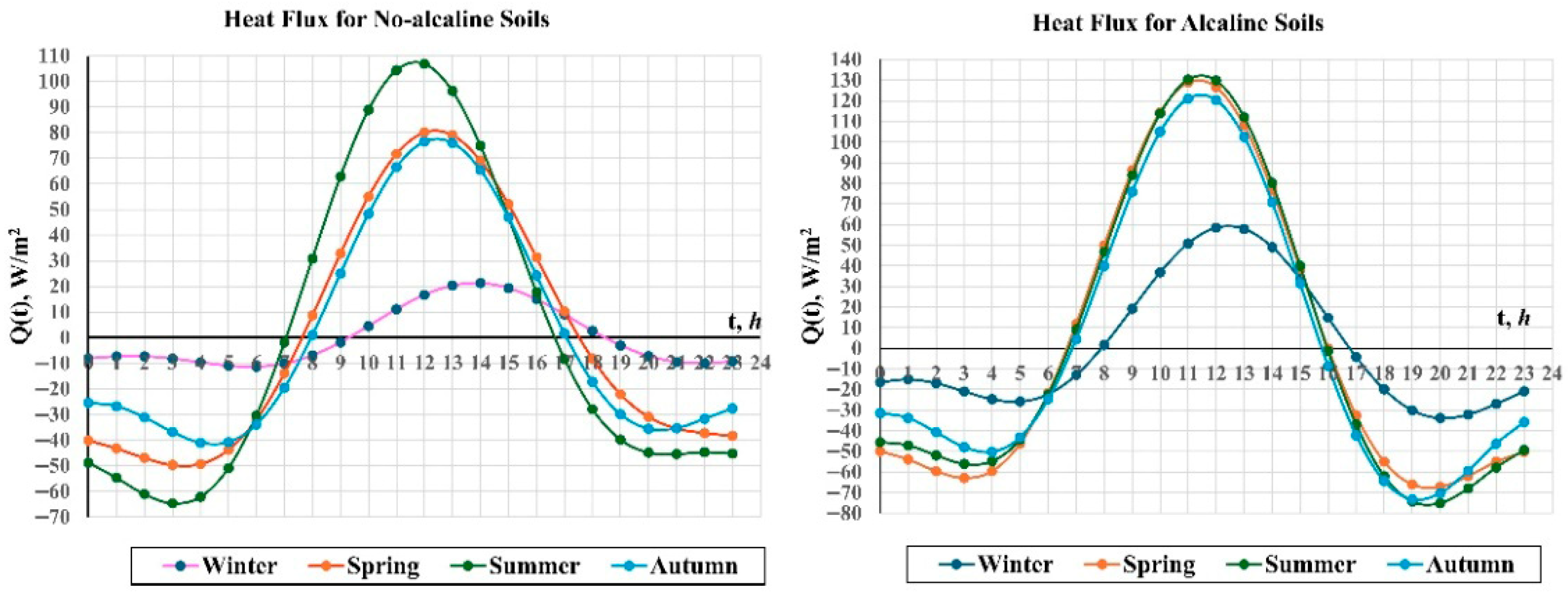
Soil	Depth	Texture	ρb	θ	OM	pH	EC	ESP
	cm		kg m−3	m3 m−3	%	01:01	dS m−1	%
Non-alkaline	0–10	CL	974.3	0.1449	1.40	8.42	0.3877	3.2
	10–20	CL	1023.3	0.1521	1.62	8.26	0.4126	3.4
	20–25	L	1105.4	0.1717	2.35	8.01	0.5417	3.1
	25–30	SCL	1245.7	0.1806	2.81	8.03	0.5524	3.5
	30–35	SL	1158.1	0.1907	3.07	8.05	0.5507	3.7
	35–40	SL	1216.5	0.1925	2.66	8.12	0.5121	3.6
	0–40		1120.6	0.1721	2.32	8.15	0.4929	3.4
Alkaline	0–10	CL	1072.7	0.1463	1.26	8.70	1.2724	17.9
	10–20	CL	1125.6	0.1628	1.24	8.56	1.2320	17.6
	20–25	L	1194.0	0.1738	0.91	8.54	0.9842	18.2
	25–30	SCL	1247.8	0.1874	1.12	9.45	0.8252	17.9
	30–35	SL	1160.4	0.1945	1.08	9.50	0.6945	17.5
	35–40	SL	1218.0	0.1948	1.55	9.68	0.5429	17.6
	0–40		1169.7	0.1766	1.19	9.07	0.9252	17.8

.

The meaning of the designations and symbols is given in Supplementary Materials S5.

Temperature sensors (Elitech RC-4, Elitech, Hengelo, The Netherlands) were used in this study [33]. The sensors were placed at depths of 0, 0.05, 0.10, 0.15, 0.20, and 0.40 m for both alkaline and non-alkaline soil. They were programmed to collect temperature data hourly, and data were received via computer. The sensors collected data for a year to determine the seasonal changes in the thermal properties of both non-alkaline and alkaline soils.

A basic diagram of the sensors’ placed positions is shown in Figure 1.

2.1.2. Soil Analysis

To determine soil properties, disturbed and undisturbed soil samples were collected from both non-alkaline and alkaline soils with three replicates. Additionally, disturbed soil samples were collected to determine soil moisture content for each season from both non-alkaline and alkaline soils with three replicates. Soil texture, soil organic carbon, pH, and electrical conductivity were determined in disturbed soil samples, while soil bulk density was determined in undisturbed soil samples [41,42,43,44,45,46]. Exchangeable sodium percentage (ESP) was calculated according to Shahid et al. [47]:

$$\mathrm{ESP}={\displaystyle \frac{\mathrm{Exch}.\mathrm{Na}}{\mathrm{CEC}}}\cdot 100$$

where $\mathrm{ESP}$ is the exchangeable sodium percentage, and CEC is the cation exchange capacity. CEC is the sum of exchangeable cations.

Saline and alkaline soils are formed by the accumulation of exchangeable cations on the soil surface or in layers near the surface. Determination of cation exchange capacity is important for determining the salinity and alkalinity of soils. Especially by determining the amount of exchangeable sodium in soils, it can be determined whether the soils are saline or alkaline as well as to assess its influence on soil biogeochemical processes.

2.2. Methods

2.2.1. Mathematical Formulation of the Problem

Further details on the mathematical formulation of the problem are given in Supplementary Materials S1 and S2.

It is known that one-dimensional distribution of the temperature field in an anisotropic medium is described by the following classical equation of heat conduction [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,48,49]:

$${\displaystyle \frac{\mathsf{\partial } T}{\mathsf{\partial } t}}=\mathsf{\kappa }{\displaystyle \frac{{\mathsf{\partial }}^{2}T}{\mathsf{\partial }{z}^2}} \left(\kappa ={\displaystyle \frac{\lambda }{C_v}}\right) , \left(z,t\right)\in \left(0,t\right)\times \left(0<z<L \mathrm{or} \infty \right)$$

(1)

The meanings of the designations and symbols are given in Supplementary Material S5.

In refs [19,21,23,24,25,26], solutions of the thermal conductivity in Equation (1) are considered under various boundary conditions. In this work, we will also consider Equation (1). In order to determine the change in soil temperature under the influence of various environmental factors depending on time and depth, Equation (1) must be solved analytically or numerically. For this purpose, Equation (1) must be defined and supplemented with initial and boundary conditions that account for the various factors influencing temperature variations in soils.

2.2.2. Direct Problem of Heat Transfer Model in Soil

The problems of thermal conductivity in soils with periodically changing temperatures on the soil surface are of great theoretical and practical interest.

Given the initial and boundary conditions, different solutions can be proposed for the direct problem of heat transfer, i.e., the determination of the temperature dynamics at a specific depth [21,23,25,26,33,34,35,36,37].

Problem-1. First, let us consider the heat transfer problem for a semi-infinite homogeneous soil region, i.e., [0 ≤ z < ∞):

$${\displaystyle \frac{\mathsf{\partial } T}{\mathsf{\partial } t}}=\kappa {\displaystyle \frac{{\mathsf{\partial }}^{2}T}{\mathsf{\partial }{z}^2}} \left(\kappa =\lambda /C_v\right) , \left(z,t\right)\in \left(0,t\right)\times \left(0<z< \infty \right),$$

(2)

$$T\left(z,0\right)=T_0$$

(3)

$$T\left(z=0,t\right)=T_0+{\displaystyle {\sum }_{j=1}^{j=m}{T}_j\cdot \cos \left(j\omega t+{\epsilon }_j\right)}, \left(t\ge 0\right)$$

(4)

$$\mathsf{\partial } T\left(z\to \infty ,t\right)/\mathsf{\partial }z=0, \left(t\ge 0\right).$$

(5)

The solution of Equation (2), with the initial (3) and boundary conditions (4) and (5) with dimensionless variables and parameters is as follows [33,34,35]:

$$T\left(y,\tau \right)=T_0+ {\displaystyle {\sum }_{j=1}^{j=m}{\Phi }_j\left(b_j,y\right)\cdot \cos \left[j\overline{\omega }\tau +{\alpha }_j\left(b_j,y\right)\right]}$$

(6)

$$\mathrm{Where}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}y={\displaystyle \frac{z}{L}}, \tau ={\displaystyle \frac{\kappa }{L^2}}t , b_j=\sqrt{j{\displaystyle \frac{\overline{\omega }}{2}}}=L\sqrt{j{\displaystyle \frac{\pi }{{\tau }_0\kappa }}} , \overline{\omega }=\omega {\displaystyle \frac{L^2}{\kappa }}$$

(7)

$${\Phi }_j\left(b_1,y\right)=T_j{e}^{-b_{j}y}, {\alpha }_j\left(b_j,y\right)={\epsilon }_j-b_{j}y$$

(8)

Φ_j is the amplitude of temperature fluctuations of the jth harmonic (°C), and α_j is the phase angle of the jth harmonic (radians).

This problem was studied by Fourier [19]. It was first used by Kelvin to determine the course of temperature in the soil of Edinburgh [23].

It is practically and theoretically impossible to set the given soil temperature values at infinity since they are unknown [32,33,34,35,36,37]. Moreover, it is impossible to measure it.

Therefore, instead of T(z → ∞, t), it is necessary to take the temperature at depth L, starting from which, at z > L, the value of T(z, t) is constant or the temperature gradient is zero, i.e., T′z(z = L, t) = 0. Thus, condition (S13) (T′_z(z = L, t)=0) is more consistent with real conditions than boundary condition (S12) (T(z → ∞, t) = const) [33,34,35,36,37].

Naturally, it also becomes necessary to consider the following boundary value problem for Equation (9).

Problem-2. Next, consider the boundary value problem for the thermal conductivity equation in a finite [0 ≤ z ≤ L] homogeneous soil region in the following form:

$${\displaystyle \frac{\mathsf{\partial } T}{\mathsf{\partial } t}}=\kappa {\displaystyle \frac{{\mathsf{\partial }}^{2}T}{\mathsf{\partial }{z}^2}} , \left(z,t\right)\in \left(0,t\right)\times \left(0<z< L\right),$$

(9)

$$T\left(0,t\right)=T_0+{\displaystyle {\sum }_{j=1}^{j=m}{T}_j\cdot \cos \left(j\omega t+{\epsilon }_j\right)},\left(t\ge 0\right)$$

(10)

$$\mathsf{\partial } T\left(z=L,t\right)/\mathsf{\partial }z=0 , \left( t\ge 0\right).$$

(11)

The solution of Problems (9)–(11) with dimensionless variables and parameters is as follows [33,34,35,36,37]:

$$T\left(y,\tau \right)=T_0+ {\displaystyle {\sum }_{j=1}^{j=m}{\Phi }_j\left(b_j,y\right)\cdot \cos \left[j\overline{\omega }\tau +{\alpha }_j\left(b_j,y\right)\right]}$$

(12)

where $y=z/L , \tau =\kappa t/L^2$ and

$$\begin{array}{l}{\Phi }_j\left(b_j,y\right)=T_j\cdot \sqrt{{\displaystyle \frac{\cosh \left(d_j\right)+\cos \left(d_j\right)}{\cosh \left(2b_j\right)+\cos \left(2b_j\right)}}} , d_j=2b_j\left(1-y\right), b_j=L\sqrt{j{\displaystyle \frac{\mathsf{\omega }}{2\kappa }}}\\ {\alpha }_j\left(b_j,y\right)={\epsilon }_j-\arctan \left[{\displaystyle \frac{\sinh \left(q_j\right)\sin \left(b_{j}y\right)+\sinh \left(b_{j}y\right)\sin \left(q_j\right)}{\cosh \left(q_j\right)\cos \left(b_{j}y\right)+\cosh \left(b_{j}y\right)\cos \left(q_j\right)}}\right] , q_j=b_j\left(2-y\right) \end{array}$$

(13)

where cosh(z) and sinh(z) are the hyperbolic cosine and sine, respectively.

In the analytical methods developed for the determination of the parameters of the heat and mass transport models, it has been shown that the data at any depth z = z_i of the soil profile are determined with statistically greater variation than the average data in the [0, L] layer of the soil. More precisely, the average temperature of a certain soil layer (for example, a layer of 0–20 or 0–40 cm) varies less than the temperature a certain depth z = z_i [50,51].

Consequently, it is advisable to use average soil layer temperatures to determine the thermal conductivity coefficient.

Using average temperature values to determine the thermal diffusivity parameter is called the average integral method.

For this purpose, at first, let us calculate the definite integral of the dimensionless solution (6) of Equation (2) in the interval 0 ≤ y ≤ 1 with respect to the variable y.

$$\overline{{\rm T}}\left(b_1,...,b_j,t\right)=T_0+{\displaystyle {\sum }_{j=1}^{j=m}{{\rm M}}_j\left(b_j\right)\cos \left[j\omega t+{\alpha }_j\left(b_j\right)\right]} , b_j=L\sqrt{j\pi /{\tau }_0\kappa }$$

(14)

$${{\rm M}}_j\left(b_j\right)=T_j\sqrt{{\displaystyle \frac{\cosh \left(b_j\right)-\cos \left(b_j\right)}{b_j^2{e}^{b_j}}}}, {\alpha }_j\left(b_j\right)={\epsilon }_j-\arctan \left\{{\displaystyle \frac{1-e^{-b_j }\left(\sin b_j+\cos b_j\right)}{1+e^{-b_j }\left(\sin b_j-\cos b_j\right)}}\right\}$$

(15)

Similarly, for the solution (12) with arbitrary harmonic m, the average temperature in layer 0 ≤ z ≤ L can be determined as follows:

$$\overline{{\rm T}}\left(b_1,...,b_j,t\right)={{\rm T}}_0+{\displaystyle {\sum }_{j=1}^{j=m}{\Phi }_j\left(b_j\right)\cdot \cos \left[j\omega t+{\gamma }_j\left(b_j\right)\right]}$$

(16)

$$\begin{array}{l} {\Phi }_j\left(b_j\right)=T_j\left[{\displaystyle \frac{\sqrt{{\sinh }^2\left(2b_j\right)+{\sin }^2\left(2b_j\right)}}{\sqrt{2 } b_j\Delta (b_j)}}\right], \Delta (b_j)=\cosh \left(2b_j\right)+\cos \left(2b_j\right)\\ {\gamma }_j\left(b_j\right)={\epsilon }_j-\arctan \left[{\displaystyle \frac{\sinh \left(2b_j\right)-\sin \left(2b_j\right)}{\sinh \left(2b_j\right)+\sin \left(2b_j\right)}}\right], b_j=L\sqrt{j{\displaystyle \frac{\pi }{{\tau }_0\kappa }}} . \end{array}$$

(17)

Solutions (6), (2), (14), and (16) are widely used in practice for two purposes: estimating the temperature values in the soil profile (direct tasks) and calculating the thermal conductivity coefficient (inverse tasks). Now, let us consider the inverse problem of heat transfer in the soil.

2.2.3. Inverse Problem of Heat Transfer Model in Soil

Methods for determining the coefficient of thermal diffusivity of soil are based on solving inverse problems of thermal conductivity, which are obtained under given boundary conditions. Depending on the boundary conditions, different methods are obtained.

A more detailed review of studies on the determination of the diffusion parameter in soils is given in many works [19,20,21,22,23,24,25,26,27,28,29,30,31,33,34,35,36,37,48,49,52,53,54,55,56,57,58,59,60].

This paper details methods for determining thermal diffusivity using analytical solutions (6) and (12) found by second-order boundary conditions at the lower boundary of the soil profile, i.e., T’_z(z → ∞, t) = 0 and T’_z(z = L, t) = 0.

Depending on the use of the measured temperature values of the soil profile, these methods are divided into three classes: layered, point, and numerical (harmonic) methods.

These methods are based on using 1) temperature values at two different depths of the soil profile, e.g., z = z_i and z = z_i+1, 2) temperature values at a certain depth z = zi, and 3) the value of the average temperature in the [0, L] layer of the soil.

Layered methods. These methods are based on temperature measurements at two different soil profile depths z = z_i and z = z_i+1 and are called layered methods. In addition, these layered methods will be denoted as algorithms M1, M2, M3, and M4 (See Supplementary Material S3).

Point methods. These methods are based on the use of measured temperature values at a certain depth z = zi soil profile and the amplitude (T_a) of the temperature wave at the soil surface (z = 0) [32,33,34,35,36,37,38]. These point (proposed) methods will be denoted as algorithms M5, M6, M7, and M8 (See Supplementary Material S3).

The following methods (M5 and M6) are developed on the basis of a boundary condition of the second kind in the infinity z → ∞, i.e., ∂T(z → ∞, t)/∂z = 0 when the diurnal temperature fluctuations at the soil surface is represented by one (m = 1) (M5) and two (m = 2) (M6) harmonics.

These methods, unlike the classical ones (M1–M4), include the amplitude of fluctuations (T_a) of the soil surface temperature.

The following methods (M7 and M8) are developed on the basis of the boundary condition of the second kind at a finite depth z = L, i.e., at ∂T(z = L, t)/∂z = 0 when the daily temperature fluctuation at the soil surface is represented by one (m = 1) (M7) and two (m = 2) (M8) harmonics.

These methods, in addition to the amplitude of fluctuations (T_a) of the soil surface temperature, also take into account the depth of the soil profile (L).

Numerical (Harmonic) methods. The value of heat diffusion (κ) is selected iteratively in a way that minimizes the sum of the differences between the measured temperature values T_mes(z_i, t_i) at the desired depth zi and the temperature values T_cal (z_i, t_i) estimated according to Solutions (6) or (12) [27,28,29,30,33,34]:

$$\underset{i,j}{\min }{\displaystyle {\sum }_{j=1}^{j=r}{\left[T_{mes}\left(z_i,t_j\right)-T_{cal}\left(z_i,t_j\right)\right]}^2}$$

(18)

For example, the iteration can be continued until the condition is met. The expression under the sum sign will consist of 24 integer (r = 0, 1, 2, ..., 24) or 48 half-hour (r = 0, 5, 1, 5, ..., 23, 5) differences between the measured and calculated temperature.

Supplementary Material S3 presents the existing [19,20,21,22,23,24] and our previously proposed methods [33,34,35,36,37] for calculating the thermal diffusivity parameter, developed for the lower boundary of the soil profile, i.e., T′_z(z → ∞, t)=0 and T’_z(z = L, t) = 0, respectively.

2.3. Calculation of Thermal Properties of Soil

Volumetric heat capacity was calculated using the following formula [32,33,34,46,52,59,60]:

$$C_v=C_{m, s}\cdot {\rho }_b+ C_{v,w}\cdot \theta , \mathrm{where} C_{m, s}=C_{m . org}\cdot {\displaystyle \frac{m_{org}}{m}}+C_{m . \min }\cdot \left(1-{\displaystyle \frac{m_{org}}{m}}\right)$$

(19)

The meaning of the designations and symbols is given in Supplementary Material S5.

The determination of the thermal diffusivity coefficient of the soil has been discussed in many experimental and theoretical works [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,46,48,49,53,54,55,56,57,58,59,60].

Thermal diffusivity will be determined first by existing (classical) layered methods using Formulas (S14)–(S17) and then by the proposed point methods using Formulas (S18)–(S21) (See Supplementary Material S3). These methods are developed based on the second-order boundary conditions at the lower boundary of the soil profile, i.e.,: T’_z(z → ∞, t) = 0 and T’_z(z = L, t) = 0.

Other thermal parameters such as thermal conductivity (λ), damping depth (d), thermal effusion (e), heat wave velocity (υ), and heat wave length (Λ) will be calculated using the following formulas, respectively [23,24,27,33,34,35,61,62]:

$$\lambda =\kappa C_v, d=\sqrt{{\displaystyle \frac{{\tau }_0\kappa }{\pi }}} , e=C_v\sqrt{\mathsf{\kappa }} , \vartheta =2\sqrt{{\displaystyle \frac{\pi \kappa }{{\tau }_0}}}, \Lambda =2\sqrt{\pi {\tau }_0\kappa }=2\pi d$$

(20)

Calculation of heat flux in soil is based on the use of values of known thermal properties. If these properties (C_v, κ, T₀, T_i and ε_i) are determined, it is possible to calculate the amount of heat and heat flux (J) passing through the soil surface and causing a certain temperature change.

The heat flux of a soil (J) is given by the Fourier law of heat conduction, expressed as follows [19,21,23,24]:

$$J\left(z,t\right)=-\mathsf{\lambda }{\displaystyle \frac{\mathsf{\partial } T\left(z,t\right)}{\mathsf{\partial }z}}$$

(21)

where ∂T/∂z is the temperature gradient. When referring to J at the soil surface (z = 0), it is denoted as q.

Existing methods for calculating heat flow based on the found solution for the boundary condition ∂T(z → ∞, t)/∂z = 0.

To calculate the heat flux from the soil surface to the depth, we first use the general solution (6) obtained for the boundary condition of the second kind, i.e., ∂T(z→∞, t)/∂z = 0 in Equation (21). Heat flux into the soil for any z = h and time t is of the following form [23,24]:

$$J\left(z,t\right)={\displaystyle {\sum }_{j=1}^m{T}_{\mathrm{j}}{C}_v\sqrt{j\mathsf{\omega }\kappa }\cdot \exp \left(-h\sqrt{j\frac{\mathsf{\omega }}{2k}}\right)\cdot \cos \left[\frac{\pi }{4}+\left(j\mathsf{\omega }\mathrm{t}+{\mathsf{\epsilon }}_j-h\sqrt{j\frac{\mathsf{\omega }}{2k}}\right)\right]}$$

(22)

Proposed methods for calculating heat flow based on the found solution for the boundary condition ∂T(z = L, t)/∂z = 0.

Similarly, using the general solution Equation (12) obtained for the boundary condition of the second kind, i.e., ∂T(z = L, t)/∂z = 0 in Equation (21), we have [33,34,35]:

$$J\left(z,t\right)=-\lambda {\left.{\displaystyle \frac{\mathsf{\partial } T\left(z,t\right)}{\mathsf{\partial }z}}\right|}_{z=h}=-{\displaystyle \frac{\lambda }{L}}{\displaystyle \sum _{j=1}^m\frac{T_j{b}_j}{\Delta \left(b_j\right)}\left\{\left[{\Pi }_{1j}\left(b_j,y_h\right)\cos \left(j\mathsf{\omega }t+{\mathsf{\epsilon }}_j\right)+{\Pi }_{2j}\left(b_j,y_h\right)\sin \left(j\mathsf{\omega }t+{\mathsf{\epsilon }}_j\right)\right]\right\}}$$

(23)

where

$$\begin{array}{l}{\Pi }_{1j}\left(b_j,y_h\right)=\sinh \left(b_j{y}_h\right)\cos \left[b_j\left(2-y_h\right)\right]-\sinh \left[b_j\left(2-y_h\right)\right]\cos \left(b_j{y}_h\right)\\ +\cosh \left(b{y}_h\right)\sin \left[b_j\left(2-y_h\right)\right]-\cosh \left[b_j\left(2-y_h\right)\right]\sin \left(b{y}_h\right)\\ {\Pi }_{2j}\left(b_j,y_h\right)=\sinh \left[b_j\left(2-y_h\right)\right]\cos \left(b_j{y}_h\right)-\cosh \left[b_j\left(2-y_h\right)\right]\sin (b_j{y}_h)\\ +\cosh \left(b_j{y}_h\right)\sin \left[b_j\left(2-y_h\right)\right]-\sinh \left(b_j{y}_h\right)\cos \left[b_j\left(2-y_h\right)\right] \\ \Delta \left(b_j\right)=\cosh \left(2b_j\right)+\cos \left(2 b_j\right), b_j=L\sqrt{j {\displaystyle \frac{\mathsf{\omega }}{2\kappa }}} , y_h={\displaystyle \frac{h}{L}}, 0\le h\le L\end{array}$$

(24)

Using Formula (22) found for the boundary condition T_z’(z → ∞, t) = 0 for m = 1 and m = 2 to calculate the heat flux q₁(z = 0, t) on the soil surface (z = 0) at time t, we have the following [23,24]:

$$q_1\left(z=0,t,m=1\right)=q_{1,z=0}^{m=1}\left(t\right)=B_1\cdot \cos \left[{\displaystyle \frac{\pi }{4}}+\left(\omega t+{\epsilon }_1\right)\right]$$

(25)

$$q_1\left(z=0,t,m=2\right)=q_{1,z=0}^{m=1}\left(t\right)=B_1\cos \left[{\displaystyle \frac{\pi }{4}}+\left(\omega t+{\epsilon }_1\right)\right]+ B_2\cos \left[{\displaystyle \frac{\pi }{4}}+\left(2\omega t+{\epsilon }_2\right)\right]$$

(26)

Similarly, using Formulas (23) and (24) found for the boundary condition ∂T(z = L, t)/∂z = 0 for m = 1 and m = 2 to calculate the heat flux q₂(z = 0,t) on the soil surface (z = 0) at time t, we have:

$$q_2\left(z=0,t,m=1\right)= q_{2,z=0}^{m=1}\left(t\right)= {\Gamma }_1\left\{\sinh \left(2b\right)\cos \left[{\displaystyle \frac{\pi }{4}}+\left(\omega t+{\epsilon }_1\right)\right]-\sin \left(2b\right)\cos \left[{\displaystyle \frac{\pi }{4}}-\left(\omega t+{\epsilon }_1\right)\right]\right\}$$

(27)

$$\begin{array}{l}{q}_2\left(z=0,t,m=2\right)= q_{2,z=0}^{m=2}\left(t\right)={\Gamma }_1\left\{\sin \mathrm{h}\left(2b_1\right)\cos \left[{\displaystyle \frac{\mathsf{\pi }}{4}}+\left(\omega t+{\epsilon }_1\right)\right]-\sin \left(2b_1\right)\cos \left[{\displaystyle \frac{\mathsf{\pi }}{4}}-\left(\omega t+{\epsilon }_1\right)\right]\right\}+\\ + {\Gamma }_2 \left\{\sin \mathrm{h}\left(2b_2\right)\cos \left[{\displaystyle \frac{\mathsf{\pi }}{4}}+\left(2\omega t+{\epsilon }_2\right)\right]-\sin \left(2b_2\right)\cos \left[{\displaystyle \frac{\mathsf{\pi }}{4}}-\left(2\omega t+{\epsilon }_2\right)\right]\right\}\end{array}$$

(28)

where

$${{\rm B}}_1={{\rm T}}_1{C}_v\sqrt{\mathsf{\omega }\mathsf{\kappa }} , {{\rm B}}_2={{\rm T}}_2{C}_v\sqrt{2\omega \kappa }$$

(29)

$$\begin{array}{l}{\Gamma }_1={\displaystyle \frac{{{\rm T}}_1 }{\mathsf{\Delta }\left(b_1\right)}}\left(\lambda \sqrt{{\displaystyle \frac{\omega }{\kappa }}}\right), {\Gamma }_2={\displaystyle \frac{{{\rm T}}_2 }{\mathsf{\Delta }\left(b_2\right)}}\left(\lambda \sqrt{2{\displaystyle \frac{\omega }{\kappa }}}\right), b_1=L\sqrt{{\displaystyle \frac{\omega }{2\kappa }}}, b_2=L\sqrt{2{\displaystyle \frac{\omega }{2\kappa }}} , \\ \mathsf{\Delta }\left(b_1\right)=\cosh \left(2b_1\right)+\cos \left(2b_1\right), \mathsf{\Delta }\left(b_2\right)=\cosh \left(2b_2\right)+\cos \left(2b_2\right), \omega =2\mathsf{\pi }/{\tau }_0\end{array}$$

(30)

The soil surface parameters (T₀, T_i, and ε_i) were calculated using Equations (S10) and (S11) (See Supplementary Material S2).

2.4. Comparison of Methods and Model Assessment

The performance of the classical (M1–M4) and proposed (M5–M8) methods will be evaluated using the most common model selection criteria, described below by Formulas (S23)–(S25) (See Supplementary Materials S4), namely coefficient of determination (R²) and root mean squared error (RMSE).

In determining the parameters (T₀, T₁, T₂, ε₁, and ε₂) and their statistical indicators, six indicators described by Formulas (S23)–(S28) were used, namely R², R²_adj, RMSE, D, UI, and AIC_c (see Supplementary Materials S5) [63,64,65].

3. Results and Discussion

Different soil temperature values were observed for non-alkaline and alkaline soil. Figure 2 and Figure 3 show the mean temperature values for the seasons. These figures show that the highest soil temperatures at the investigated soil depths and seasons were determined in the alkaline soils: 17.59 °C in alkaline soils at a 5 cm soil depth in the spring, and 15.91 °C in non-alkaline soils. This can be explained with the higher bulk density and higher volumetric heat capacity of alkaline soils.

Indeed, soil temperature increases as particle contact increases due to the decrease in air-filled pores between soil particles due to increased bulk density and solid particle agglomeration. Furthermore, soil alkalinity causes the disintegration of soil aggregates and an increase in microaggregates [66].

3.1. Calculations of the Parameters of the Soil Surface Zone

When determining the parameters T₀, T_i, and ε_i and their approximation statistics, we used one and two harmonics in Condition (S8) (see Supplementary Materials S2).

Based on the temperature measurement results for z = 0, i.e., T (z = 0, t_i), the parameters of the surface temperature distribution of the studied soils were calculated.

At the same time, six metrics (which are given in Supplementary Materials S4) were used in Formulas (S23)–(S28) i.e., R², R²_adj, RMSE, D, UI, and AIC_c.

Table 2. Parameter values for non-alkaline soil surfaces and model efficiency for all seasons.

Number of Harmonics in Equation (S8)
m = 1					m = 2
	Winter	Spring	Summer	Autumn		Winter	Spring	Summer	Autumn
n *	24	24	24	24	n	24	24	24	24
p	3	3	3	3	p	5	5	5	5
df	21	21	21	21	df	19	19	19	19
To	1.8643	12.9127	24.5478	15.0455	To	1.8643	12.9127	24.5478	15.0455
Ta1	1.0327	3.4375	5.4270	3.9363	Ta1	0.3598	0.7946	1.5067	1.3964
ε1	1.8468	2.1760	2.3607	2.2011	ε1	4.5802	−0.8483	−0.4932	−0.9846
Statistical parameters of approximation
R2	0.8862	0.9475	0.9227	0.8845	R2	0.9938	0.9981	0.9938	0.9958
R2adj	0.8810	0.9451	0.9192	0.8792	R2adj	0.9935	0.9980	0.9935	0.9956
D	0.9951	0.9991	0.9990	0.9979	D	0.9984	0.9995	0.9984	0.9989
UI	0.0466	0.0362	0.0405	0.0560	UI	0.0152	0.0041	0.0063	0.0063
RMSE	0.28	0.61	1.19	1.08	RMSE	0.07	0.12	0.35	0.22
AICc	−1.48	0.08	1.41	1.21	AICc	−2.25	−1.11	1.02	0.04

* n—number of observations, p—number of parameters, df—degrees of freedom.

and

Table 3. Parameter values for alkaline soil surfaces and model efficiency for all seasons.

Number of Harmonics in Equation (S8)
m = 1					m = 2
	Winter	Spring	Summer	Autumn		Winter	Spring	Summer	Autumn
n	24	24	24	24	n	24	24	24	24
p	3	3	3	3	p	5	5	5	5
df	21	21	21	21	df	19	19	19	19
To	2.4052	14.8979	28.9658	17.3838	To	2.4052	14.8979	28.9658	17.3838
Ta1	4.4773	7.9065	14.6342	13.1626	Ta2	1.8615	2.5074	4.9455	5.3725
ε1	2.3250	2.5422	2.5776	2.6118	ε2	−1.0822	−0.4765	−0.5980	−0.6023
Statistical parameters of approximation
R2	0.8424	0.9068	0.8943	0.8428	R2	0.9880	0.9980	0.9965	0.9846
R2adj	0.8352	0.9026	0.8895	0.8356	R2adj	0.9874	0.9979	0.9963	0.9839
D	0.9525	0.9938	0.9934	0.9801	D	0.9970	0.9995	0.9991	0.9961
UI	0.1922	0.0966	0.1068	0.1785	UI	0.0451	0.0081	0.0105	0.0311
RMSE	1.46	1.92	3.80	4.22	RMSE	0.43	0.29	0.73	1.39
AICc	1.83	2.37	3.74	3.95	AICc	1.39	0.64	2.47	3.76

give the results of the calculated parameters (T₀, T_i, and ε_i), and the statistical characteristics of the approximation between T_mes (0, t_i), the measurement initial data, and T_cal (0, t_i), the calculation data computed using Formula (S8) at m = 1 and m = 2 for non-alkaline and alkaline soils.

The results of the calculations of the parameters (T₀, T_i, and ε_i), as well as the statistical characteristics of the approximation between T_mes (0, t_i), the initial measurement data, and T_cal (0, t_i), the data calculated using Formula (S8) at m = 1 and m = 2 for non-alkaline and alkaline soils are shown in Table 2 and Table 3.

The soil surface parameters (T₀, T_i, and ε_i) were calculated using Formulas (S10) and (S11).

The calculation results show (see Table 2 and Table 3) that the introduction of the second harmonic makes it possible to determine with high accuracy the values of the parameters (T0, Ti, and ei) at the soil surface.

It was determined that the average temperature (T₀), amplitude (T_a), and phase (ε) of the soil surface were higher in the alkaline soils across all seasons (

Table 4. Parameters of non-alkaline and alkaline soil surfaces.

	Non-alkaline Soils					Alkaline Soils
	Winter	Spring	Summer	Autumn		Winter	Spring	Summer	Autumn
To	1.8643	12.9127	24.5478	15.0455	To	2.4052	14.8979	28.9658	17.3838
Ta1	1.0327	3.4375	5.4270	3.9363	Ta2	4.4773	7.9065	14.6342	13.1626
ε1	1.8468	2.1760	2.3607	2.2011	ε2	2.3250	2.5422	2.5776	2.6118
Cv	1878.49	2126.30	1596.04	1746.15	Cv	2014.11	2349.05	1637.30	1846.64

).

3.2. Calculation of Soil Thermal Parameters

The thermal parameters of the soil (C_v—volumetric heat capacity, κ—thermal diffusivity, λ—thermal conductivity, d—damping depth, e—thermal effusivity, ϑ—heat wave velocity, Λ—heat wave length, and q—heat flow) depending on the season, soil, and calculation models (M1–M8) are given in

Table 5. Thermal properties of non-alkaline soils.

Models	Harmoni	Season	10−6 κ	λ	d	e	V·10−5	Λ	Cv
			m2s−1	Wm−1 °C−1	cm	Ws0.5m−2 °C−1	m s−1	m	kJ m−3 °C−1
			Layered Methods with Boundary Conditions ∂T(∞.t)/∂z = 0
M1 *	m = 1	Winter	0.5376	1.0099	12.16	1377.35	0.8843	0.76	1878.49
		Spring	0.6972	1.4824	13.85	1775.39	1.0070	0.87	2126.30
		Summer	0.7422	1.1846	14.29	1375.01	1.0390	0.90	1596.04
		Autumn	0.6066	1.0591	12.92	1359.94	0.9393	0.81	1746.15
M2	m = 2	Winter	1.3235	2.4861	19.08	2161.05	1.3874	1.20	1878.49
		Spring	0.8752	1.8610	15.51	1989.24	1.1283	0.98	2126.30
		Summer	0.9287	1.4823	15.98	1538.12	1.1622	1.00	1596.04
		Autumn	0.8807	1.5378	15.56	1638.65	1.1318	0.98	1746.15
M3	m = 2	Winter	0.7050	1.3243	13.92	1577.22	1.0126	0.87	1878.49
		Spring	0.7202	1.5313	14.07	1804.43	1.0234	0.89	2126.30
		Summer	0.7643	1.2199	14.50	1395.33	1.0543	0.91	1596.04
		Autumn	0.6693	1.1688	13.57	1428.57	0.9867	0.85	1746.15
M4	m = 1	Winter	1.0292	1.9334	16.82	1905.73	1.2235	1.06	1878.49
		Spring	0.7969	1.6945	14.80	1898.17	1.0766	0.93	2126.30
		Summer	0.8174	1.3046	14.99	1442.97	1.0903	0.94	1596.04
		Autumn	0.6211	1.0845	13.07	1376.13	0.9504	0.82	1746.15
			Point Methodswith Boundary Conditions ∂T(∞.t)/∂z = 0
M5	m = 1	Winter	0.7550	1.4183	14.41	1632.27	1.0479	0.91	1878.49
		Spring	0.8756	1.8618	15.52	1989.67	1.1285	0.98	2126.30
		Summer	0.9325	1.4882	16.01	1541.20	1.1646	1.01	1596.04
		Autumn	0.6821	1.1911	13.70	1442.14	0.9960	0.86	1746.15
Μ6	m = 2	Winter	0.7164	1.3458	14.04	1590.02	1.0208	0.88	1878.49
		Spring	0.8843	1.8802	15.59	1999.48	1.1341	0.98	2126.30
		Summer	1.0022	1.5996	16.60	1597.80	1.2073	1.04	1596.04
		Autumn	0.7614	1.3295	14.47	1523.63	1.0523	0.91	1746.15
			Point Methodswith Boundary Conditions ∂T(L. t)/∂z = 0
Μ7	m = 1	Winter	0.8008	1.5042	14.84	1680.97	1.0792	0.93	1878.49
		Spring	0.9584	2.0379	16.24	2081.65	1.1807	1.02	2126.30
		Summer	1.0237	1.6339	16.78	1614.84	1.2202	1.05	1596.04
		Autumn	0.6766	1.1815	13.64	1436.31	0.9920	0.86	1746.15
Μ8	m = 2	Winter	0.7533	1.4151	14.39	1630.40	1.0467	0.90	1878.49
		Spring	0.9725	2.0678	16.35	2096.83	1.1893	1.03	2126.30
		Summer	1.1035	1.7613	17.42	1676.63	1.2669	1.09	1596.04
		Autumn	0.7854	1.3714	14.70	1547.45	1.0688	0.92	1746.15

* for M1–M8, see Supplementary Materials S3.

and

Table 6. Thermal properties of alkaline soils.

Models	Harmoni	Season	10−6 κ	λ	d	e	V·10−5	Λ	Cv
			m2s−1	Wm−1 °C−1	cm	Ws0.5 m−2 °C−1	m s−1	m	kJ m−3 °C−1
			Layered Methods with Boundary Conditions ∂T(∞.t)/∂z = 0
M1	m = 1	Winter	7.2882	14.6792	44.77	5437.41	3.2558	2.8130	2014.11
		Spring	92.7680	217.9169	159.73	22,625.17	3.2558	10.0360	2349.05
		Summer	209.4553	342.9403	240.01	23,695.88	17.4540	15.0802	1637.30
		Autumn	35.4889	65.5351	98.79	11,000.88	7.1845	6.2074	1846.64
M2	m = 2	Winter	3.6121	7.2751	31.52	3827.91	2.2921	1.9803	2014.11
		Spring	7.2158	16.9502	44.55	6310.06	2.2921	2.7990	2349.05
		Summer	349.4319	572.1234	310.00	30,606.13	22.5439	19.4779	1637.30
		Autumn	3.4077	6.2928	30.61	3408.88	2.2263	1.9235	1846.64
M3	m = 2	Winter	6.7248	13.5445	43.01	5223.03	3.1274	2.7021	2014.11
		Spring	24.9110	58.5173	82.77	11,724.34	3.1274	5.2006	2349.05
		Summer	143.4528	234.8747	198.63	19,610.19	14.4445	12.4801	1637.30
		Autumn	9.9721	18.4148	52.37	5831.42	3.8084	3.2904	1846.64
M4	m = 1	Winter	1.8315	3.6888	22.44	2725.74	1.6321	1.4101	2014.11
		Spring	7.0423	16.5427	44.01	6233.75	1.6321	2.7651	2349.05
		Summer	1399.3616	2291.1688	620.36	61,248.03	45.1142	38.9786	1637.30
		Autumn	1.7919	3.3090	22.20	2471.93	1.6144	1.3948	1846.64
			Point methodswith Boundary Conditions ∂T(∞.t)/∂z = 0
M5	m = 1	Winter	0.2669	0.5376	8,57	1040.56	0.6231	0.5383	2014.11
		Spring	0.3423	0.8041	9.70	1374.399	0.6231	0.6097	2349.05
		Summer	0.2085	0.3414	7.57	747.62	0.5507	0.4758	1637.30
		Autumn	0.1557	0.2876	6.54	728.77	0.4759	0.4112	1846.64
		Winter	0.2572	0.5181	8.41	1021.49	0.6116	0.5285	2014.11
Μ6	m = 2	Spring	0.3364	0.7903	9.62	1362.489	0.6116	0.6044	2349.05
		Summer	0.2106	0.3448	7.61	751.36	0.5534	0.4782	1637.30
		Autumn	0.1587	0.2931	6.61	735.75	0.4805	0.4152	1846.64
			Point methodswith Boundary Conditions ∂T(L. t)/∂z = 0
Μ7	m = 1	Winter	0.2477	0.4988	8.25	1002.33	0.6002	0.5185	2014.11
		Spring	0.3261	0.7661	9.47	1341.49	0.6887	0.5951	2349.05
		Summer	0.1912	0.3130	7.25	715.85	0.5273	0.4556	1637.30
		Autumn	0.1409	0.2601	6.22	693.09	0.4526	0.3911	1846.64
Μ8	m = 2	Winter	0.2371	0.4775	8.07	980.67	0.5872	0.5073	2014.11
		Spring	0.3214	0.7549	9.40	1331.69	0.6837	0.5907	2349.05
		Summer	0.1935	0.3168	7.29	720.16	0.5305	0.4583	1637.30
		Autumn	0.1431	0.2643	6.27	698.66	0.4563	0.3942	1846.64

.

The calculations of these parameters are described in more detail below.

Volumetric heat capacity. The calculated values of the volumetric heat capacity of the studied soils are shown in Table 5 and Table 6. Their values varied depending on the type of soil and the time of year.

For example, for the values we find are C_m,org = 1925.928 J kg^-1 °C⁻¹ or 0.46 cal g^-1 °C and C_m,min = 753.624 J kg^-1 °C⁻¹ or 0.18 cal g^-1 °C.

Using the results of the analysis of the studied soils in the site for layer 0.1–0.2 m, the mean bulk density of the non-alkaline soil ρ_b was 1023.3 kg m⁻³, the content of organic substance was m_org/m = 1.62%, and volumetric moisture content was θ = 0.1521 m³m⁻³ (Table 1).

$$\begin{array}{l}{C}_{m s}=C_{m org}\cdot {\displaystyle \frac{m_{org}}{m}}+C_{m \min }\cdot \left(1-{\displaystyle \frac{m_{org}}{m}}\right)=1925.928{\displaystyle \frac{\mathrm{J}}{\mathrm{kg} °C}}\cdot 0.0162+753.624{\displaystyle \frac{\mathrm{J}}{\mathrm{kg} °C}}\cdot \left(1-0.0162\right) =\\ 31.2000{\displaystyle \frac{\mathrm{J}}{\mathrm{kg}\cdot °C}}+741.4152912{\displaystyle \frac{\mathrm{J}}{\mathrm{kg}\cdot °C}}= 772.6153{\displaystyle \frac{\mathrm{J}}{\mathrm{kg}\cdot °C}}=0.772615{\displaystyle \frac{\mathrm{kJ}}{\mathrm{kg}\cdot °C}}\end{array}$$

Next, using the formulas for calculating C_v and considering that for the 0.1–0.2 m layer of our soil, θ = 0.1521 m³m⁻³, C_ms = 0.772615 kJ/(kg °C), and water C_v,w = 4186.8 kJ/(m °C), we calculate the volumetric heat capacity for the 0.1–0.2 m layer of the non-alkaline soil as follows:

$$\begin{array}{l}{C}_v=C_{ms}\cdot {\mathsf{\rho }}_b+C_{vw}\cdot \mathsf{\theta }=0.772615{\displaystyle \frac{\mathrm{kJ}}{\mathrm{kg}\cdot °C}}\cdot 1023.3 {\displaystyle \frac{\mathrm{kg}}{{\mathrm{m}}^3}}+4186.8{\displaystyle \frac{\mathrm{J}}{{\mathrm{m}}^3\cdot °C}}\cdot 0.1521{\displaystyle \frac{{\mathrm{m}}^3}{{\mathrm{m}}^3}}=\\ 790.627162{\displaystyle \frac{\mathrm{kJ}}{{\mathrm{m}}^3\cdot °C}}+636.81228\mathrm{}{\displaystyle \frac{\mathrm{kJ}}{{\mathrm{m}}^3\cdot °C}}=1427.44{\displaystyle \frac{\mathrm{kJ}}{{\mathrm{m}}^3\cdot °C}}\end{array}$$

Similarly, the volumetric heat capacity of the non-alkaline soil can be easily calculated for all soil layers and for all seasons.

For alkaline soil, ρ_b was 1125.6 kg m⁻³, organic matter content was m_org/m = 1.24%, and volumetric moisture content was θ = 0.1628 m³ m⁻³ (Table 1).

To give an example, the value of specific heat capacity (C_ms) for a 0.1–0.2 m layer of the solid part of non-alkaline soil calculated using Formula (19) would be as follows:

$$\begin{array}{l}{C}_{m s}\left(10 -20 cm\right)=C_{m org}\cdot {\displaystyle \frac{m_{org}}{m}}+C_{m \min }\cdot \left(1-{\displaystyle \frac{m_{org}}{m}}\right)=1925.928{\displaystyle \frac{\mathrm{J}}{\mathrm{kg}\cdot °C}}\cdot 0.0124+753.624{\displaystyle \frac{\mathrm{J}}{\mathrm{kg}\cdot °C}}\left(1-0.0124\right) =\\ 23.8815072{\displaystyle \frac{\mathrm{J}}{\mathrm{kg}\cdot °C}}+744.2790624{\displaystyle \frac{\mathrm{J}}{\mathrm{kg}\cdot °C}}= 768.16057{\displaystyle \frac{\mathrm{J}}{\mathrm{kg}\cdot °C}} =0.768161{\displaystyle \frac{\mathrm{kJ}}{\mathrm{kg}\cdot °C}}\end{array}$$

Next, using the formulas for calculating C_v and considering that for the 0.1–0.2 m layer of our soil, θ = 0.1628 m³m⁻³, C_ms = 0.768161 kJ/(kg °C), and C_v,w = 4186.8 kJ/(m °C), we calculate the value of volumetric heat capacity for the 0.1–0.2 m layer of non-alkaline soil as follows:

$$\begin{array}{l}{C}_v\left(10-20 cm\right)=C_{ms}\cdot {\mathsf{\rho }}_b+C_{vw}\cdot \mathsf{\theta }=768.16057{\displaystyle \frac{\mathrm{J}}{\mathrm{kg}\cdot °C}}\cdot 1125.6{\displaystyle \frac{\mathrm{kg}}{{\mathrm{m}}^3}}+4186.8{\displaystyle \frac{\mathrm{kJ}}{{\mathrm{m}}^3\cdot °C}}\cdot 0.1628{\displaystyle \frac{{\mathrm{m}}^3}{{\mathrm{m}}^3}}=\\ 864.664582{\displaystyle \frac{\mathrm{kJ}}{{\mathrm{m}}^3\cdot °C}}+681.5165021{\displaystyle \frac{\mathrm{kJ}}{{\mathrm{m}}^3\cdot °C}}=1546.181084{\displaystyle \frac{kJ}{{\mathrm{m}}^3\cdot °C}}\end{array}$$

The calculated C_v values for non-alkaline and alkaline soils for all seasons and for all soil layers are given in Table 5 and Table 6.

The values of the thermal diffusivity parameter of the studied soils for all seasons were calculated using Formulas (S14)–(S22) and are given in Table 5 and Table 6.

The estimated values of thermal diffusion calculated using the classical (M1–M4) and proposed (M5–M8) methods show that there are significant deviations between them.

All the considered thermal properties varied depending on the time of year, the models used, and the soils (Table 3 and Table 4). Tong et al. [55] also reported that the thermal diffusivity differed according to seasons.

Considering the differences between soils, higher thermal diffusivity was observed in non-alkaline soils, with the exception of the values calculated using methods M1–M4.

These values may be due to low values of the (T_o), the fluctuations (T_a), the phase shift (ε), and the volumetric heat capacity in non-alkaline soils (Table 2 and Table 3 or Table 4).

When the thermal diffusivity results of the soils are examined, there are quite high values in the classical models (Table 5).

However, more moderate results were obtained using the proposed models.

For example, the thermal diffusivity values calculated using the amplitude method (M1) were 7.2882 × 10⁻⁶ m s⁻¹ in winter, 92.768 × 10⁻⁶ m s⁻¹ in spring, 209.4553 × 10⁻⁶ m s⁻¹ in summer, and 35.4889 × 10⁻⁶ m s⁻¹ in autumn for alkaline soil.

Meanwhile, the thermal diffusivity values calculated using the (M8) method were 0.2371 × 10⁻⁶ m s⁻¹ in winter, 0.3214 × 10⁻⁶ m s⁻¹ in spring, 0.1935 × 10⁻⁶ m s⁻¹ in summer, and 0.1413 × 10⁻⁶ m s⁻¹ in autumn for alkaline soil.

This deviation shows that classical models are incorrect due to theoretical assumptions in setting boundary conditions at depth, i.e., z = L.

Consequently, T₀ and T_a also affect soil thermal diffusion.

The results of the thermal diffusivity values calculated using Methods 1–4 differ greatly depending on the time of year. This indicates the mathematical incompatibility of these methods. In contrast, the κ-values calculated using the improved method do not differ significantly.

The results of our studies (Table 5 and Table 6) showed that the soil thermal properties (temperature, thermal conductivity, etc.) decreased with increasing salt content at a given water content are consistent with previous findings [8].

Also, unlike the others, the improved method, in addition to the amplitude of fluctuations (Ta) of the soil surface temperature, also takes into account the depth of the soil profile (L); these are important parameters.

The values of the thermal conductivity coefficient of the studied soils were calculated using the formula λ = κC_v and are given in Table 5 and Table 6.

As in the case of thermal diffusivity, calculations using classical methods (M1–M4) give a spread of values for the thermal conductivity parameter λ.

When assessing the difference between soils, higher values of thermal conductivity calculated using the proposed methods (M5–M8) were observed in non-alkaline soils for all seasons.

Guo et al. [67] also reported that the thermal conductivity of the upper soil layers did not increase with a higher solid ratio in the solonchak and solonetz, as the salts in the upper layers contributed to a lower thermal conductivity. Some researchers have found that the effect of salts in the soil on thermal diffusivity differed depending on the water content [68,69].

Values of the damping depth of the soil temperature were calculated using Formula (20), i.e., d = √τ₀κ/π and varied depending on the models (M1–M8) used to calculate the κ parameter, as well as the season and soil (Table 5 and Table 6).

When analyzing the results of temperature measurements in both soils, it is evident that at depths z ≤ 15 cm, temperature waves attenuate (Figure 1 and Figure 2).

The estimated values of damping depth calculated using the classical (M1–M4) and proposed (M5–M8) methods show that there are significant deviations between them.

For example, the damping depth values calculated using the amplitude method (M1) were 44.77 cm in winter, 159.73 cm in spring, 240.01 cm in summer, and 31.52 cm in autumn for alkaline soil.

This situation is similar for the other methods (M2, M3, and M4). Excessive deviations between the obtained values reduce the reliability of these methods. These results are not consistent with measured temperatures in alkaline soils (Figure 2).

The damping depth (d) calculated using the values of κ obtained by Formulas (S15-S18) turned out to be greater than 10 cm, i.e., z >10.

However, the damping depth (d) calculated using the thermal diffusivity (κ) values obtained from Formulas (S19-S23) was calculated as ~15 cm on average across all seasons for non-alkaline soil (Table 5).

For alkaline soil, the results of calculations using classical (layered) methods (formulas (S15-S18)) showed that the depth of attenuation varied in the range of 14.77-620.36 cm for all seasons (Table 6). These results are inconsistent with the measured values of temperature in the soil layer (see Figure 3).

For alkaline soil, the results of calculations using to the point methods (Formulas (S19)–(S23)) showed that the damping depths were approximately equal to 8 cm on average for all seasons (Table 6).

At the same time, for alkaline soil, the results of calculations using point methods (formulas (S19-S23)) showed that the depth of damping was approximately 8 cm on average for all seasons (Table 6). The same results are in full agreement with the measured values of temperature in the soil layer for all seasons (see Figure 3).

These findings agree with the observed data. In line with these findings, it is seen that the most adequate model for this study is the point methods.

The values of the thermal effusivity parameter of the studied soils were calculated using the formula e = C_v√κ and varied depending on the models (M1–M8) used to calculate the κ parameter, season, and soil (Table 5 and Table 6).

The estimated values of thermal effusion calculated using the classical (M1–M4) and proposed (M5–M8) methods show that there are significant deviations between them.

For example, the thermal effusivity values calculated using the amplitude method (M1) were 5437.41 W·h^0.5∙m⁻²∙°C⁻¹ in winter, 22,625.17 W·h^0.5∙m⁻²∙°C⁻¹ in spring, 23,695.88 W·h^0.5∙m⁻²∙°C⁻¹ in summer, and 11,000.88 W·h^0.5∙m⁻² °C⁻¹ in autumn in alkaline soil.

This situation is similar for the other methods (M2, M3, and M4). Excessive deviations between the obtained values reduce the reliability of these methods.

Using the point method (M8), according to the seasons, the following values were obtained: 980.67 W·h^0.5∙m⁻²∙°C⁻¹ in winter, 1331.69 W·h^0.5∙m⁻² °C⁻¹ in spring, 720.16 W·h^0.5∙m⁻²∙°C⁻¹ in summer, and 698.66 W·h^0.5∙m^−2∙°C⁻¹ in autumn for alkaline soil (Table 4). A similar situation is observed for non-alkaline soils; 1630.40 W·h^0.5∙m⁻²∙°C⁻¹ in winter, 2096.83 W·h^0.5∙m⁻²∙°C⁻¹ in spring, 1676.63 W·h^0.5∙m⁻²∙°C⁻¹ in summer, and 1547.45 W·h^0.5∙m⁻²∙°C⁻¹ in autumn.

The highest thermal effusivity values were observed in non-alkaline soils. These results can be explained by the fact that the values of the thermal diffusivity coefficient are higher in non-alkaline soils. This is because the thermal effusion formula contains a diffusion parameter (see Formula (20)).

The values of the heat wave propagation velocity were calculated using Formula (20), i.e., ϑ = 2√πκ/τ₀ [23,61] and varied depending on the models (M1–M8) used to calculate the κ parameter, as well as the season and soil (Table 5 and Table 6).

Using the proposed method (model M8), the heat wave velocity values were found to be 1.0467 m s⁻¹ in winter, 1.1893 m s⁻¹ in spring, 1.2669 m s⁻¹ in summer, and 1.0688 m s⁻¹ in autumn for non-alkaline soil, and 0.5872 m s⁻¹ in winter, 0.6837 m s⁻¹ in spring, 0.5305 m s⁻¹ in summer, and 0.4563 m s⁻¹ in autumn for alkaline soil.

As can be understood from the text, the heat wave velocity was higher in non-alkaline soil for all seasons. The maximum heat wave velocity occurred in summer for non-alkaline soil.

The values of the heat wave length calculated using the formula Ʌ = 2πd varied depending on the models (M1–M8) used to calculate the κ parameter, as well as the season and soil (Table 5 and Table 6) [62].

The heat wave length was detected as 0.9 m in winter, 1.03 m in spring, 1.09 m in summer, and 0.92 m in autumn for non-alkaline soil, and 0.5 m in winter, 0.59 m in spring, 0.45 m in summer, and 0.39 m for autumn in alkaline soil.

It was concluded that the length between the two waves for non-alkaline soil was much greater than for the alkaline soil.

This difference can be explained by the fact that in non-alkaline soils, the values of the thermal diffusivity coefficient are higher, and the depth of temperature attenuation is lower than in alkaline soils.

3.3. Assessment of Soil Thermal Diffusivity Models

The measured (T_mes) and predicted temperature values (T_cal) (using Solutions (6) and (12) for one and two harmonics) were compared to evaluate the effectiveness of the eight methods (M1–M8).

To do this, we set up a linear regression equation, T_mes (z_i, t_j) = a + b⸳T_cal (z_i, t_j), between the measured and estimated values of the studied soil temperature for all four seasons.

The effectiveness of the eight methods (M1–M8) was assessed based on two criteria (see Supplementary Material S4): coefficient determination (R²) and root mean square error (RMSE), described in Equations (S24) and (S26).

The analysis of the calculation results (see

Table 7. Effectiveness of models (M1–M8) for predicting the temperature of non-alkaline soil at four depths, z = 5, 10, and 15 cm during the year (from 1 December 2019 to 20 November 2020) for four seasons.

	Depth	M1	M2	M3	M4	M5	M6	M7	M8
	z. m	Winter
R2	0.05	0.8523	0.8921	0.8705	0.8808	0.8740	0.9430	0.8783	0.9679
	0.10	0.6483	0.3788	0.5568	0.4886	0.5348	0.3959	0.5069	0.5035
	0.15	0.9180	0.8530	0.9368	0.9224	0.9347	0.7290	0.9305	0.9936
RMSE	0.05	0.3360	0.3003	0.3200	0.3106	0.3168	0.2631	0.3136	0.2494
	0.10	0.8321	0.8845	0.8450	0.8575	0.8487	0.8840	0.8523	0.8537
	0.15	1.2914	1.3009	1.2918	1.2937	1.2923	1.3087	1.2923	1.2907
	z. m	Spring
R2	0.05	0.9386	0.9477	0.9401	0.9444	0.9477	0.9761	0.9514	0.9912
	0.10	0.6140	0.5410	0.6033	0.5703	0.5408	0.4452	0.5075	0.4822
	0.15	0.9712	0.9708	0.9728	0.9742	0.9708	0.8453	0.9661	0.9853
RMSE	0.05	0.5680	0.5078	0.5584	0.5306	0.5077	0.3395	0.4885	0.2488
	0.10	0.9277	1.0431	0.9436	0.9946	1.0433	1.2158	1.0874	1.1292
	0.15	0.2607	0.2529	0.2539	0.2445	0.2529	0.5037	0.2613	0.2257
	z. m	Summer
R2	0.05	0.9143	0.9231	0.9157	0.9185	0.9233	0.9736	0.9270	0.9888
	0.10	0.6435	0.5762	0.6344	0.6140	0.5750	0.4494	0.5452	0.5037
	0.15	0.9469	0.9598	0.9500	0.9555	0.9598	0.8407	0.9592	0.9936
RMSE	0.05	1.0992	1.0228	1.0879	1.0636	1.0216	0.6347	0.9981	0.5228
	0.10	1.4630	1.6310	1.4840	1.5334	1.6341	2.0207	1.6962	1.8133
	0.15	0.9299	0.9086	0.9237	0.9133	0.9088	1.2002	0.9086	0.8647
	z. m	Autumn
R2	0.05	0.8857	0.8978	0.8898	0.8866	0.8906	0.9667	0.8909	0.9904
	0.10	0.5989	0.4780	0.5654	0.5907	0.5591	0.3783	0.5520	0.4829
	0.15	0.9266	0.9306	0.9351	0.9293	0.9361	0.7358	0.9366	0.9964
RMSE	0.05	0.8609	0.7911	0.8378	0.8550	0.8337	0.4593	0.8329	0.3279
	0.10	1.1172	1.3245	1.1691	1.1294	1.1794	1.5869	1.1842	1.3093
	0.15	0.8934	0.9085	0.8888	0.8918	0.8886	1.1820	0.8876	0.8570

and

Table 8. Effectiveness of models (M1–M8) for predicting the temperature of alkaline soil at four depths, z = 5, 10, and 15 cm during the year (from 1 December 2019 to 20 November 2020) for four seasons.

	Depth	M1	M2	M3	M4	M5	M6	M7	M8
	z. m	Winter
R2	0.05	0.5162	0.5580	0.5204	0.6134	0.8529	0.8223	0.8619	0.9460
	0.10	0.3464	0.4313	0.3545	0.5480	0.9139	0.6279	0.9092	0.9825
	0.15	0.3461	0.4736	0.3583	0.6435	0.6966	0.2732	0.6432	0.6508
RMSE	0.05	2.4549	2.2906	2.4384	2.0803	1.2065	1.5692	1.1705	1.1284
	0.10	2.7519	2.5047	2.7263	2.2188	1.5476	1.9136	1.5437	1.5220
	0.15	2.2593	1.9043	2.2218	1.5191	1.0836	1.6181	1.1023	1.1018
	z. m	Spring
R2	0.05	0.4672	0.5441	0.4949	0.5454	0.8636	0.8339	0.8707	0.9101
	0.10	0.2700	0.4180	0.3215	0.4207	0.9571	0.7420	0.9586	0.9988
	0.15	0.2514	0.4744	0.3281	0.4783	0.7991	0.4091	0.7746	0.7946
RMSE	0.05	4.5860	4.0131	4.3748	4.0038	1.7992	2.2409	1.7480	1.7239
	0.10	4.9233	3.8579	4.5224	3.8411	0.6147	1.5951	0.5871	0.4455
	0.15	4.8718	3.3972	4.3017	3.3750	1.3436	2.0376	1.3819	1.3620
	z. m	Summer
R2	0.05	0.4617	0.4572	0.4658	0.4496	0.9256	0.8564	0.9335	0.9807
	0.10	0.2548	0.2469	0.2622	0.2335	0.9008	0.5344	0.8709	0.9044
	0.15	0.2696	0.2575	0.2809	0.2372	0.3648	0.0714	0.2846	0.2916
RMSE	0.05	10.0685	10.1238	10.0178	10.2194	5.3090	6.1000	5.2119	5.2323
	0.10	10.7883	10.8938	10.6919	11.0775	4.8664	5.8961	4.8587	4.8479
	0.15	10.8287	10.9800	10.6913	11.2458	5.6042	6.6876	5.6402	5.6379
	z. m	Autumn
R2	0.05	0.4207	0.5235	0.4616	0.5788	0.9029	0.8192	0.9095	0.9908
	0.10	0.1886	0.3801	0.2601	0.4953	0.8424	0.3664	0.7937	0.8310
	0.15	0.1471	0.4343	0.2503	0.6087	0.2999	0.0223	0.2013	0.2078
RMSE	0.05	8.3498	7.1940	7.8738	6.6146	3.0722	4.5734	2.9157	2.9487
	0.10	8.5686	6.5279	7.7026	5.5862	1.6225	4.1208	1.5893	1.5858
	0.15	8.3795	5.6865	7.1937	4.5811	2.3271	4.6643	2.3667	2.3666

) showed that the proposed method (M8) (Formula (S23)) is the best, since it provides more accurate forecasts in soil layers z = 5, 10 and 15 cm for T(z, t) for both soils in all season compared to the other algorithms.

3.4. Heat Flux (q)

According to Table 7 and Table 8, M8 is a better model than the others. Therefore, the values of thermal diffusivity found using the proposed M8 were used to calculate the heat flow q(z = 0, t).

Using the thermal diffusivity values (Table 5 and Table 6) found using Formula (S23), the soil heat flow q(z = 0, t) was calculated for both soils (alkaline and non-alkaline).

These values varied depending on the season and soil (Figure 4). For non-alkaline soils, the highest value of heat flux was 21.29 W·m⁻² at 14 o’clock in winter, 80.12 W m⁻² at 12 o’clock in spring, 106.86 W m⁻² at 12 o’clock in summer, and 76.08 W m⁻² at 13 in autumn. The highest heat flux for non-alkaline soils was observed in summer (Figure 4).

The maximum heat flux was 58.48 W·m⁻² at 12 o’clock in winter, 128.90 W·m⁻² at 11 o’clock in spring, 130.35 W·m⁻² at 11 o’clock in summer, and 121.09 W·m⁻² at 11 o’clock in autumn. The highest heat flux was observed in summer (Figure 4).

The highest values of heat flow were observed in alkaline soils for all seasons. These values can be explained by the higher amplitude (T_a), phase shift (ε), and volumetric heat capacity of soils (C_v), which are included in the corresponding Formulas (25)–(30) and are the main factors influencing the heat flux of soils (Table 2 and Table 3 or Table 4).

4. Conclusions

In the study, the thermal properties of different soils (alkaline and non-alkaline) were investigated using various classical and proposed methods in different seasons from 1 December 2019 to 30 November 2020.

The considered thermal properties varied depending on the time of year, the model used, and the soil (Table 3 and Table 4).

Considering the differences between soils, higher thermal diffusivity was observed in non-alkaline soils, with the exception of the values calculated using Methods M1–M4.

The M8 model proved to be the best among the eight models in estimating soil temperature values due to the strong correlation between calculated and measured values.

For example, the correlation value (r) at a depth of z = 5 cm in non-alkaline soil was r = 0.9838 in winter, 0.9956 in spring, 0.9944 in summer, and 0.9952 in autumn.

For alkaline soil at a depth of z = 5 cm, we have r = 0.9726 in winter, 0.9540 in spring, 0.9903 in summer, and 0.9954 in autumn.

Accordingly, the following values were obtained for RMSE at a depth of z = 5 cm: 0.2494 °C in winter, 0.2488 °C in spring, 0.5228 °C in summer, and 0.3279 °C in autumn for non-alkaline soil. For alkaline soil at a depth of z = 5 cm, we have σ = 1.1284 in winter, 1.7239 in spring, 5.2323 in summer, and 2.9487 in autumn.

Therefore, the proposed method (M8) is the most effective, as it provides more accurate predictions of soil temperature values T(z, t) than the other methods for both soils across all seasons.

The proposed point method M8 is more informative and adequately reflects heat transfer in the soil since it includes, in addition to the values of the soil profile temperature, the amplitude of fluctuations (Ta) of the soil surface temperature as well as the depth of the soil profile (L), where there is no temperature gradient.

When comparing the attenuation depths that best reflect the attenuation of heat waves in soils, it was found that the best of the eight models used to calculate the soil thermal conductivity coefficient is the proposed M8 point method for both soils for the entire season.

The results of our studies (Table 4 and Table 5) showed that the thermal properties of soils decreased with increasing salt content, which is consistent with the conclusions given in the work [8].