Land Cover Classification from Hyperspectral Images via Weighted Spatial-Spectral Kernel Collaborative Representation with Tikhonov Regularization
Abstract
:1. Introduction
- (1)
- A correlation coefficient-weighted spatial filtering operation is proposed to mine spatial-spectral features, which effectively reduces the spectral shift of the reconstructed central pixel.
- (2)
- By introducing a weighted spatial filtering operation into the KCRT and DKCRT methods, weighted spatial-spectral KCRT (WSSKCRT) and weighted spatial-spectral DKCRT (WSSDKCRT) methods, respectively, are proposed for land cover classification.
- (3)
- By optimizing parameters, the proposed method can effectively classify land cover types using hyperspectral images in the case of small-size labeled samples.
2. Materials and Methods
2.1. Data Collection
2.2. Classification Methods
2.2.1. Principle of the Original KCRT Method
2.2.2. Principle of the Original DKCRT Method
2.2.3. Principle of the Original KCRT-CK and JDKCRT Method
2.2.4. Principle of the Proposed WSSKCRT and WSSDKCRT Method
3. Results and Discussion
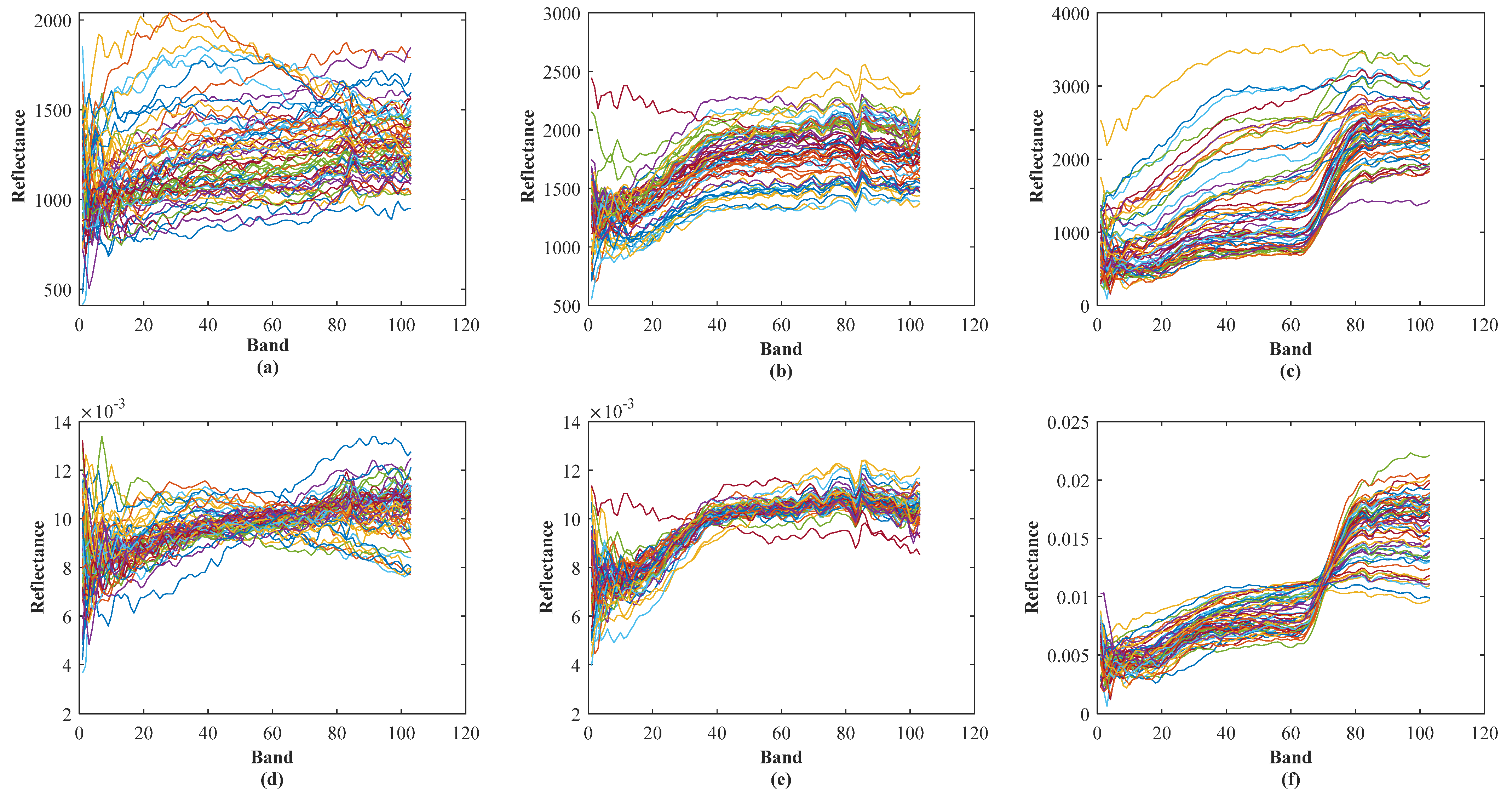
3.1. Hyperspectral Data Preprocessing
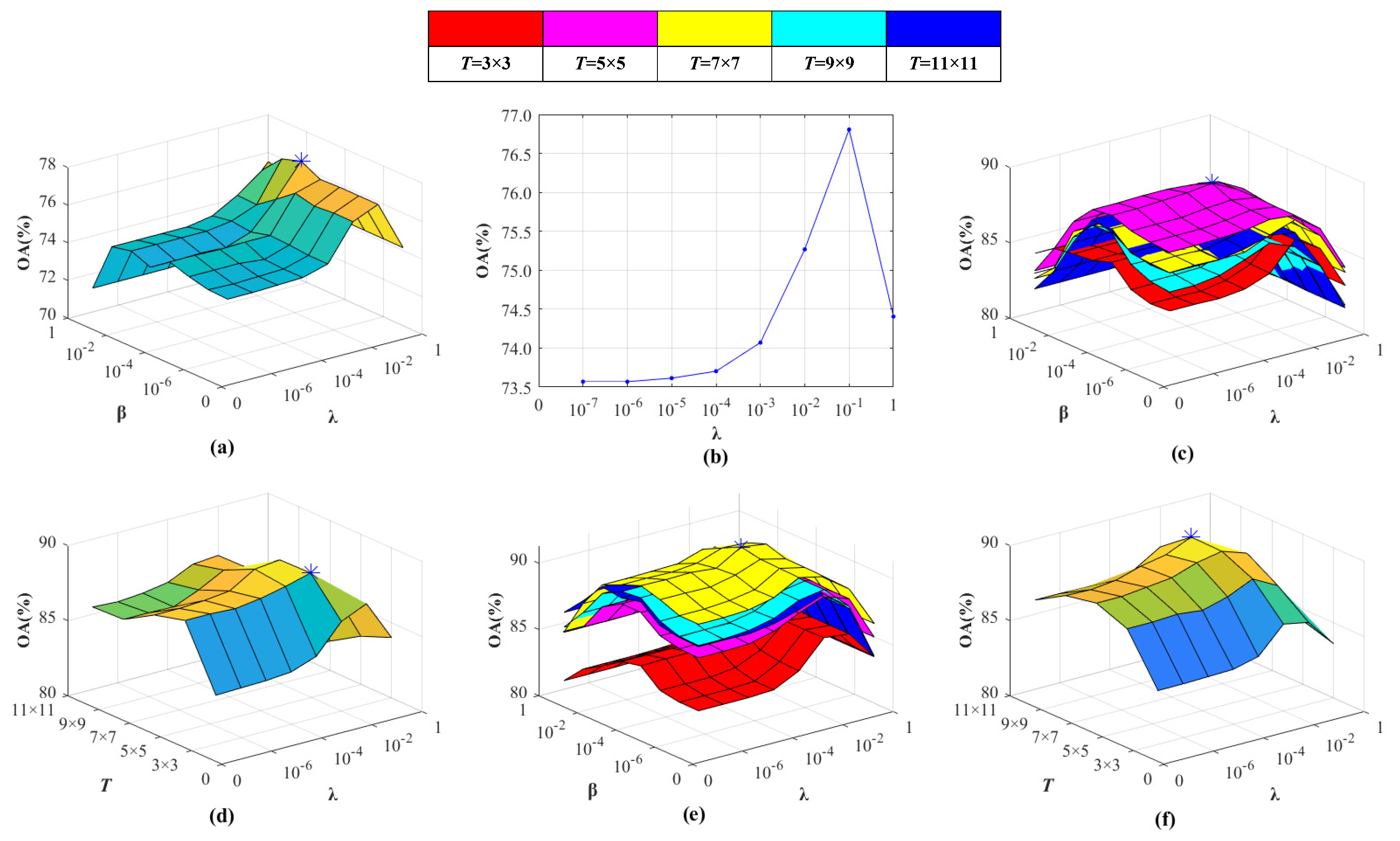
3.2. Parameter Optimization
3.3. Land Cover Classification
4. Conclusions
- (1)
- The proposed WSSKCRT method achieves the best classification result, in which OA, AA, and Kappa is 95.69%, 95.56%, and 0.9429, respectively.
- (2)
- WSSKCRT and WSSDKCRT outperform KCRT-CK and JDKCRT, respectively, which indicates that the proposed weighted spatial filtering operation can effectively alleviate the spectral shift caused by adjacency effect when mining the spatial-spectral features of hyperspectral images.
- (3)
- WSSKCRT and WSSDKCRT methods obtain the OA over 94% with only 540 labeled training samples, which indicates that the proposed methods can effectively classify land cover types under the situation of small-size labeled samples.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, Y.T.; Guan, H.Y.; Li, D.L.; Gu, T.N.; Wang, L.F.; Ma, L.F.; Li, J. A hybrid capsule network for land cover classification using multispectral LiDAR data. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1263–1267. [Google Scholar] [CrossRef]
- Kaplan, G. Semi-Automatic multi-segmentation classification for land cover change dynamics in North Macedonia from 1988 to 2014. Arab. J. Geosci. 2021, 14, 93. [Google Scholar] [CrossRef]
- Tong, X.Y.; Xia, G.S.; Lu, Q.K.; Shen, H.F.; Li, S.Y.; You, S.C.; Zhang, L.P. Land-Cover classification with high-resolution remote sensing images using transferable deep models. Remote Sens. Environ. 2020, 237, 111322. [Google Scholar] [CrossRef] [Green Version]
- Hong, D.F.; Hu, J.L.; Yao, J.; Chanussot, J.; Zhu, X.X. Multimodal remote sensing benchmark datasets for land cover classification with a shared and specific feature learning model. ISPRS-J. Photogramm. Remote Sens. 2021, 178, 68–80. [Google Scholar] [CrossRef]
- Phan, T.N.; Kuch, V.; Lehnert, L.W. Land cover classification using Google Earth Engine and random forest classifier-the role of image composition. Remote Sens. 2020, 12, 2411. [Google Scholar] [CrossRef]
- Ayhan, B.; Kwan, C. Tree, shrub, and grass classification using only RGB images. Remote Sens. 2020, 12, 1333. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z.C.; Wang, T.; Liu, S.L.; Kang, W.P.; Chen, X.; Feng, K.; Zhang, X.Q.; Zhi, Y. Biomass and vegetation coverage survey in the Mu Us sandy land-based on unmanned aerial vehicle RGB images. Int. J. Appl. Earth Obs. Geoinf. 2021, 94, 102239. [Google Scholar] [CrossRef]
- Bi, F.K.; Hou, J.Y.; Wang, Y.T.; Chen, J.; Wang, Y.P. Land cover classification of multispectral remote sensing images based on time-spectrum association features and multikernel boosting incremental learning. J. Appl. Remote Sens. 2019, 13, 044510. [Google Scholar] [CrossRef]
- Jenicka, S.; Suruliandi, A. Distributed texture-based land cover classification algorithm using hidden Markov model for multispectral data. Surv. Rev. 2016, 48, 430–437. [Google Scholar] [CrossRef]
- Mo, Y.; Zhong, R.F.; Cao, S.S. Orbita hyperspectral satellite image for land cover classification using random forest classifier. J. Appl. Remote Sens. 2021, 15, 014519. [Google Scholar] [CrossRef]
- Sun, H.; Zheng, X.T.; Lu, X.Q. A supervised segmentation network for hyperspectral image classification. IEEE Trans. Image Process. 2021, 30, 2810–2825. [Google Scholar] [CrossRef]
- Fang, Y.Y.; Zhang, H.Y.; Mao, Q.; Li, Z.F. Land cover classification with GF-3 polarimetric synthetic aperture radar data by random forest classifier and fast super-pixel segmentation. Sensors 2018, 18, 2014. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.T.; Xu, J.; Chen, Y.Y.; Xu, K.; Wang, D.M. Coastal wetland classification with GF-3 polarimetric SAR imagery by using object-oriented random forest algorithm. Sensors 2021, 21, 3395. [Google Scholar] [CrossRef]
- Liu, C.; Tao, R.; Li, W.; Zhang, M.M.; Sun, W.W.; Du, Q. Joint classification of hyperspectral and multispectral images for mapping coastal wetlands. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 982–996. [Google Scholar] [CrossRef]
- Hansch, R.; Hellwich, O. Fusion of multispectral LiDAR, hyperspectral, and RGB data for urban land cover classification. IEEE Geosci. Remote Sens. Lett. 2021, 18, 366–370. [Google Scholar] [CrossRef]
- Li, W.; Du, Q.; Zhang, F.; Hu, W. Hyperspectral image classification by fusing collaborative and sparse Representations. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 4178–4187. [Google Scholar] [CrossRef]
- Xie, M.L.; Ji, Z.X.; Zhang, G.Q.; Wang, T.; Sun, Q.S. Mutually exclusive-KSVD: Learning a discriminative dictionary for hyperspectral image classification. Neurocomputing 2018, 315, 177–189. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, M.; Feng, X.C. Sparse representation or collaborative representation: Which helps face recognition? In Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 471–478. [Google Scholar]
- Du, P.J.; Gan, L.; Xia, J.S.; Wang, D.M. Multikernel adaptive collaborative representation for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4664–4677. [Google Scholar] [CrossRef]
- Li, W.; Du, Q.; Zhang, F.; Hu, W. Collaborative-representation-based nearest neighbor classifier for hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2015, 12, 389–393. [Google Scholar] [CrossRef]
- Li, W.; Tramel, E.W.; Prasad, S.; Fowler, J.E. Nearest regularized subspace for hyperspectral classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 477–489. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Du, Q.; Xiong, M.M. Kernel collaborative representation with Tikhonov Regularization for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 48–52. [Google Scholar]
- Ma, Y.; Li, C.; Li, H.; Mei, X.G.; Ma, J.Y. Hyperspectral image classification with discriminative kernel collaborative representation and Tikhonov Regularization. IEEE Geosci. Remote Sens. Lett. 2018, 15, 587–591. [Google Scholar] [CrossRef]
- Su, H.J.; Zhao, B.; Du, Q.; Du, P.J. Kernel collaborative representation with local correlation features for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1230–1241. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. Joint within-class collaborative representation for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 2200–2208. [Google Scholar] [CrossRef]
- Yang, J.H.; Qian, J.X. Hyperspectral image classification via multiscale joint collaborative representation with locally adaptive dictionary. IEEE Geosci. Remote Sens. Lett. 2018, 15, 112–116. [Google Scholar] [CrossRef]
- Su, H.J.; Yu, Y.; Wu, Z.Y.; Du, Q. Random subspace-based k-nearest class collaborative representation for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6840–6853. [Google Scholar] [CrossRef]
- Shaw, G.A.; Burke, H. Spectral imaging for remote sensing. Lincoln Lab. J. 2003, 14, 3–28. [Google Scholar]
- Liu, H.; Li, W.; Xia, X.G.; Zhang, M.M.; Gao, C.Z.; Tao, R. Spectral shift mitigation for cross-scene hyperspectral imagery classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 6624–6638. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Li, W.; Tao, R.; Peng, J.T.; Du, Q.; Cai, Z.Q. Cross-Scene hyperspectral image classification with discriminative cooperative alignment. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9646–9660. [Google Scholar] [CrossRef]
- Chen, H.; Ye, M.C.; Lei, L.; Lu, H.J.; Qian, Y.T. Semisupervised dual-dictionary learning for heterogeneous transfer learning on cross-scene hyperspectral images. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 3164–3178. [Google Scholar] [CrossRef]

| No. | Class | Total Samples | Training Samples | Test Samples |
|---|---|---|---|---|
| 1 | Asphalt | 6631 | 60 | 6571 |
| 2 | Meadows | 18,649 | 60 | 18,589 |
| 3 | Gravel | 2099 | 60 | 2039 |
| 4 | Trees | 3064 | 60 | 3004 |
| 5 | Painted metal sheets | 1345 | 60 | 1285 |
| 6 | Bare Soil | 5029 | 60 | 4969 |
| 7 | Bitumen | 1330 | 60 | 1270 |
| 8 | Self-Blocking Bricks | 3682 | 60 | 3622 |
| 9 | Shadows | 947 | 60 | 887 |
| All classes | 42,776 | 540 | 42,236 | |
| Parameters | Methods | |||||
|---|---|---|---|---|---|---|
| DKCRT | KCRT | JDKCRT | KCRT-CK | WSSDKCRT | WSSKCRT | |
| 10−1 | 10−1 | 10−3 | 10−2 | 10−3 | 10−2 | |
| 10−3 | No application | 10−4 | No application | 10−4 | No application | |
| T | No application | No application | 5 × 5 | 5 × 5 | 7 × 7 | 9 × 9 |
| Class | DKCRT | KCRT | JDKCRT | KCRT-CK | WSSDKCRT | WSSKCRT |
|---|---|---|---|---|---|---|
| Asphalt | 74.47 | 71.71 | 92.34 | 92.22 | 91.54 | 91.56 |
| Meadows | 81.45 | 80.59 | 95.41 | 95.22 | 96.70 | 97.51 |
| Gravel | 85.85 | 77.78 | 94.77 | 90.32 | 95.70 | 91.48 |
| Trees | 94.00 | 94.41 | 96.32 | 96.43 | 96.81 | 96.66 |
| Painted metal sheets | 99.57 | 99.44 | 99.98 | 100.00 | 99.70 | 99.65 |
| Bare Soil | 80.56 | 78.03 | 94.01 | 94.07 | 96.27 | 97.13 |
| Bitumen | 92.61 | 90.86 | 98.38 | 96.83 | 99.35 | 97.50 |
| Self-Blocking Bricks | 61.65 | 77.03 | 69.80 | 88.21 | 73.34 | 90.92 |
| Shadows | 97.42 | 97.96 | 99.53 | 99.71 | 98.65 | 97.68 |
| OA (%) | 80.89 | 80.70 | 92.92 | 94.16 | 94.02 | 95.69 |
| AA (%) | 85.29 | 85.31 | 93.39 | 94.78 | 94.23 | 95.56 |
| Kappa | 0.7535 | 0.7512 | 0.9064 | 0.9228 | 0.9208 | 0.9429 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Fan, B.; Wei, R.; Wang, Y.; Zhou, Q. Land Cover Classification from Hyperspectral Images via Weighted Spatial-Spectral Kernel Collaborative Representation with Tikhonov Regularization. Land 2022, 11, 263. https://doi.org/10.3390/land11020263
Yang R, Fan B, Wei R, Wang Y, Zhou Q. Land Cover Classification from Hyperspectral Images via Weighted Spatial-Spectral Kernel Collaborative Representation with Tikhonov Regularization. Land. 2022; 11(2):263. https://doi.org/10.3390/land11020263
Chicago/Turabian StyleYang, Rongchao, Beilei Fan, Ren Wei, Yuting Wang, and Qingbo Zhou. 2022. "Land Cover Classification from Hyperspectral Images via Weighted Spatial-Spectral Kernel Collaborative Representation with Tikhonov Regularization" Land 11, no. 2: 263. https://doi.org/10.3390/land11020263
APA StyleYang, R., Fan, B., Wei, R., Wang, Y., & Zhou, Q. (2022). Land Cover Classification from Hyperspectral Images via Weighted Spatial-Spectral Kernel Collaborative Representation with Tikhonov Regularization. Land, 11(2), 263. https://doi.org/10.3390/land11020263






