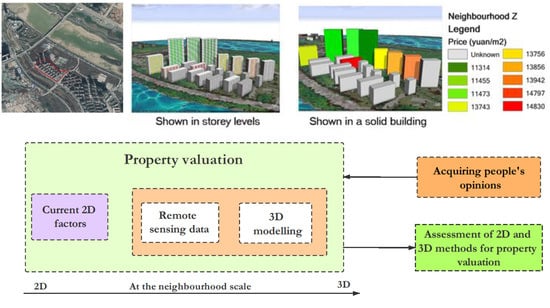
Making the Third Dimension (3D) Explicit in Hedonic Price Modelling: A Case Study of Xi’an, China
Abstract
1. Introduction
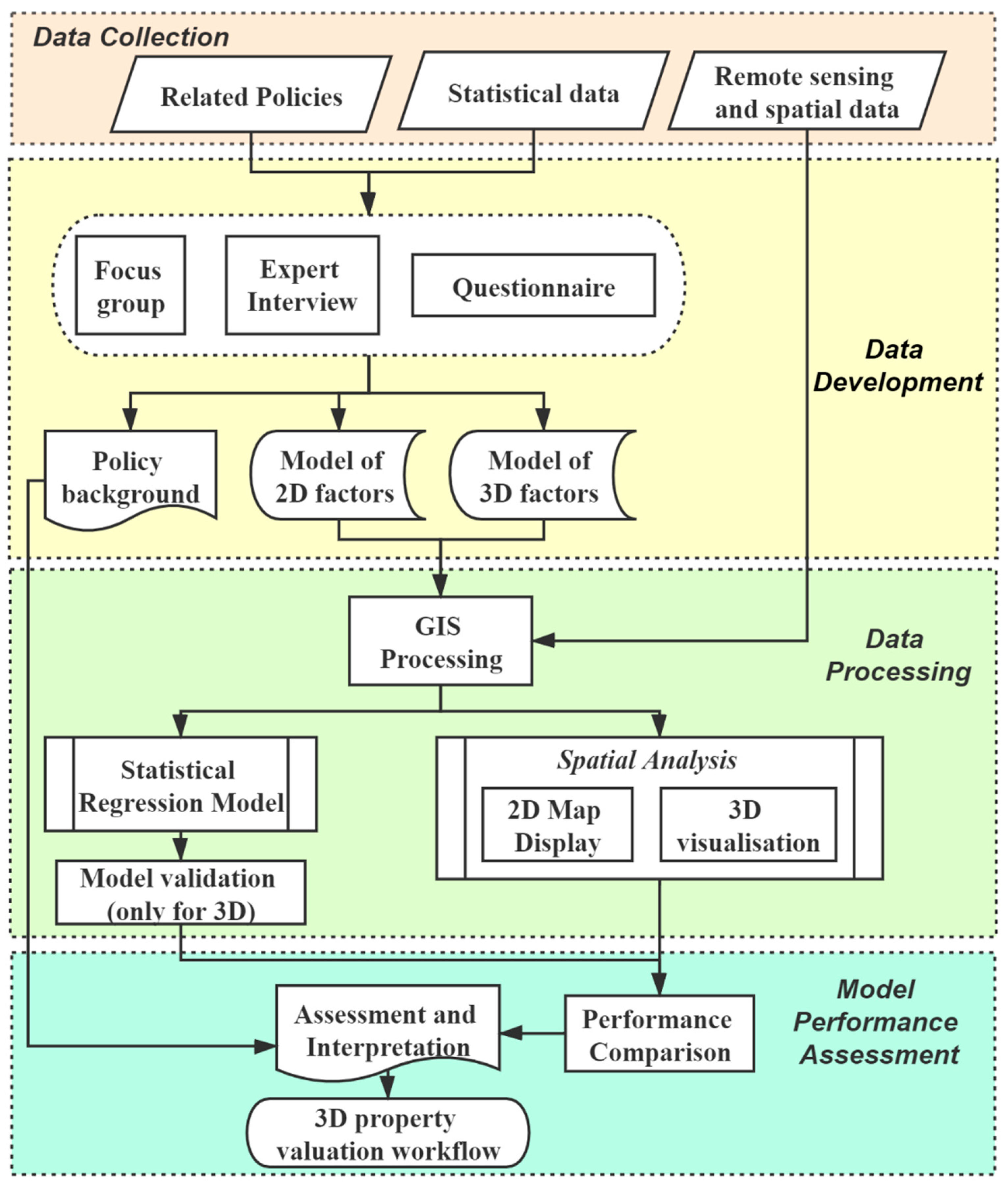
2. Materials and Methods
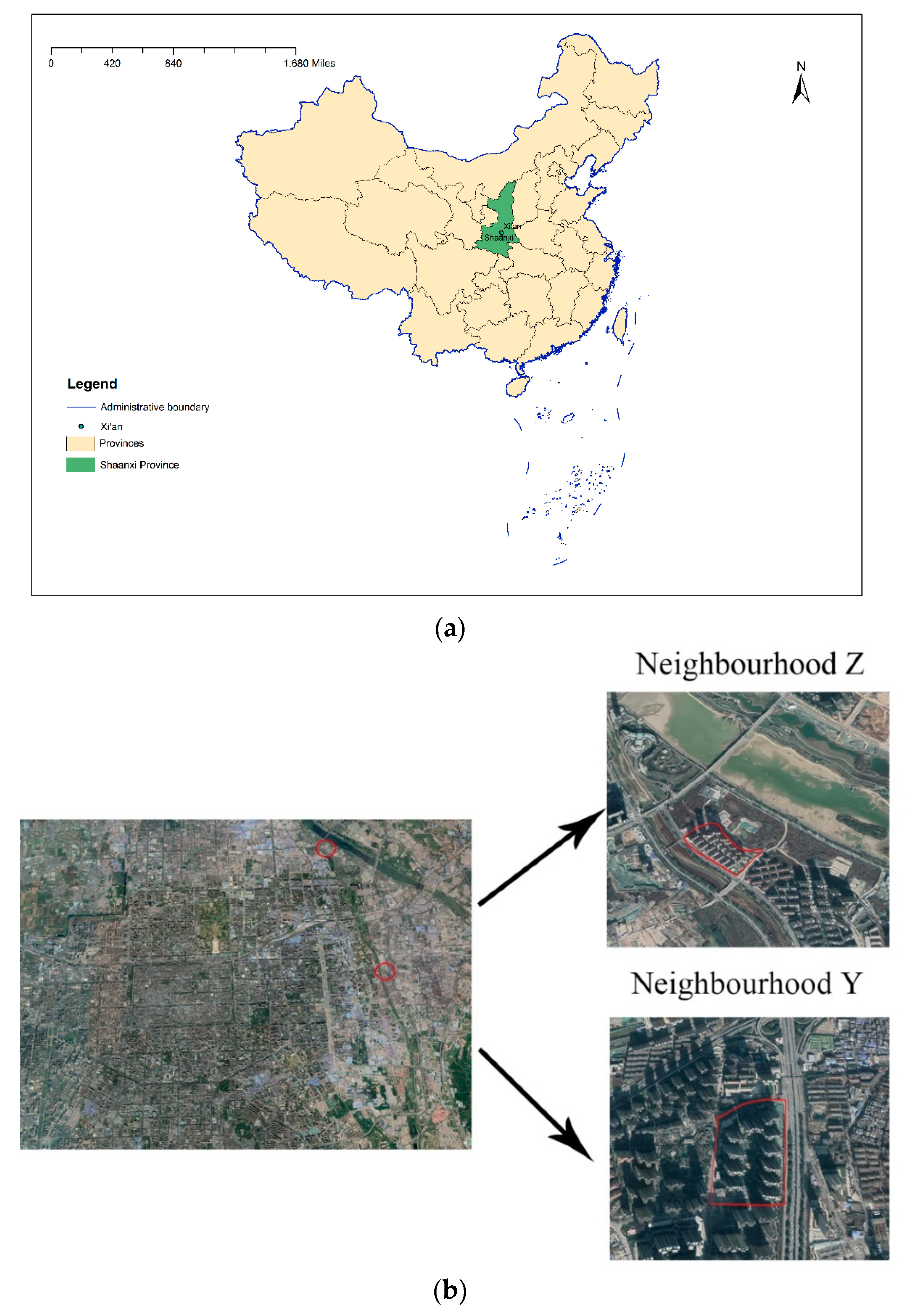
2.1. Study Area
2.2. Data Source
2.3. Expert Interview, Focus Group Discussion and Questionnaire
2.4. Factors for 2D and 3D Models
2.5. Statistical Models for 2D: OLS and GWR
2.6. Modelling 3D Factors
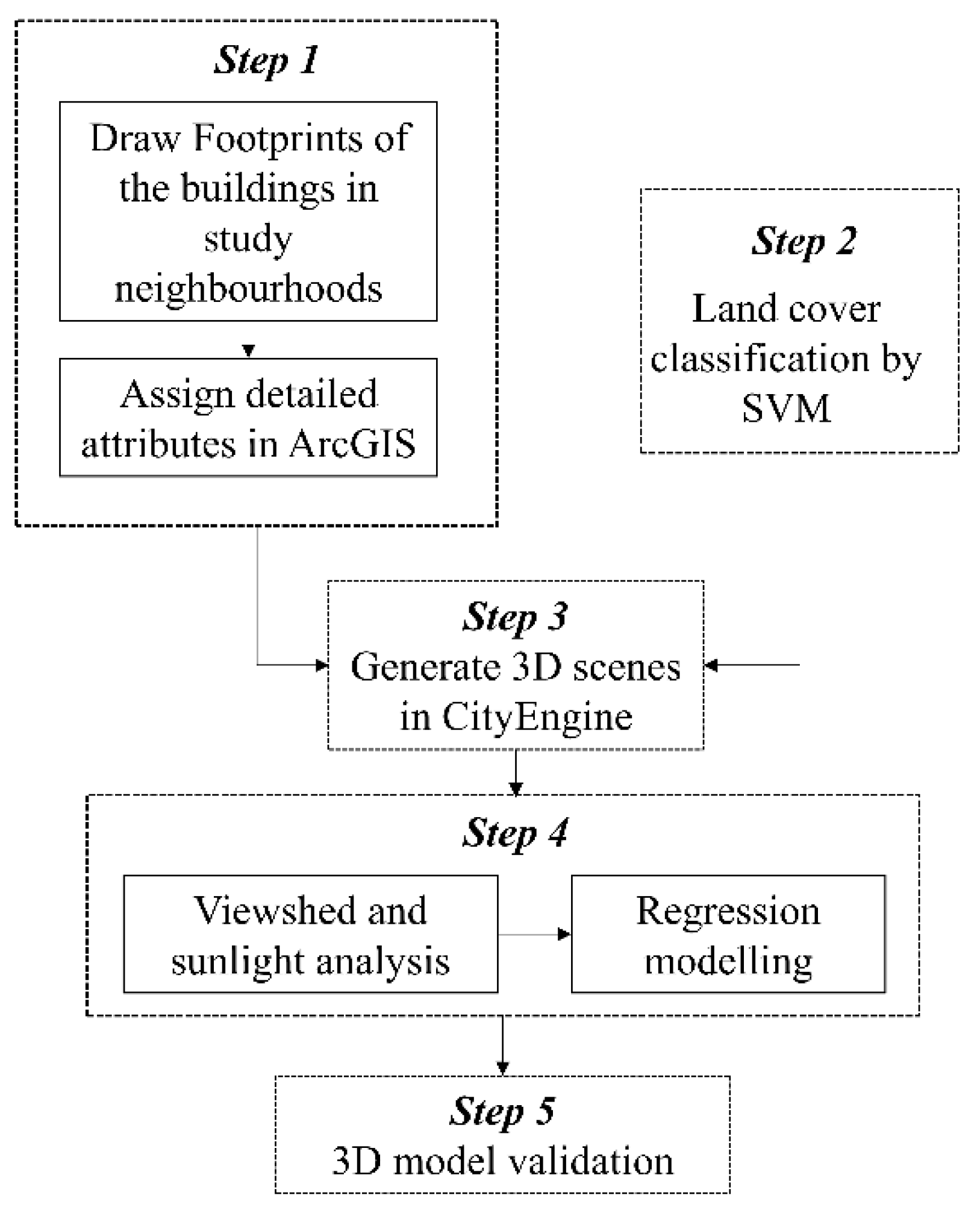
2.6.1. Workflow for 3D Modelling
2.6.2. 3D Analyses in CityEngine
- View quality and SVF
- 2.
- Sunlight
3. Results
3.1. 2D Models in OLS and GWR
3.1.1. The Comparison of OLS and GWR
3.1.2. GWR
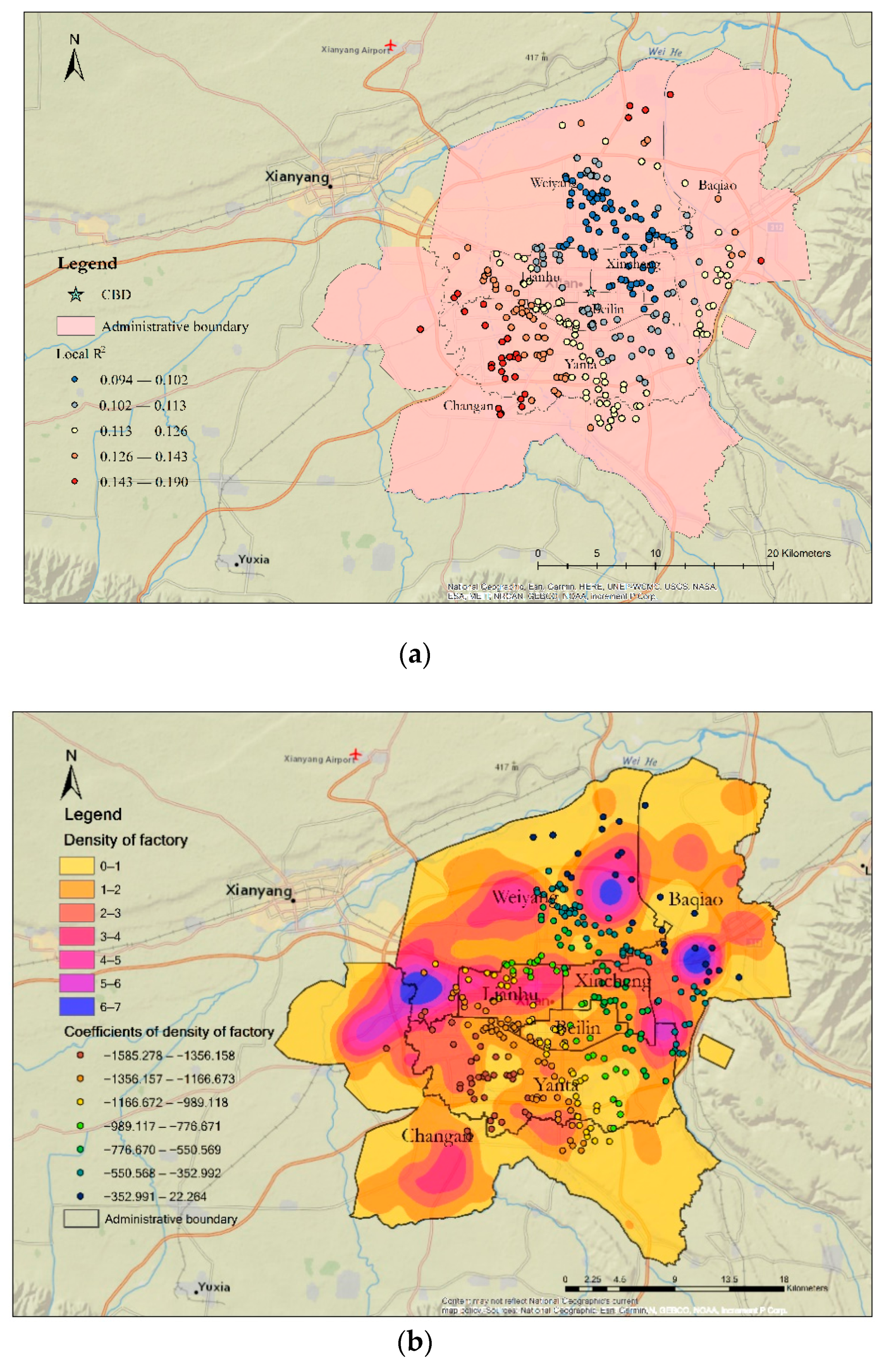
- Local R2
- 2.
- Factories
- 3.
- Food
- 4.
- Subway
- 5.
- CBD
- 6.
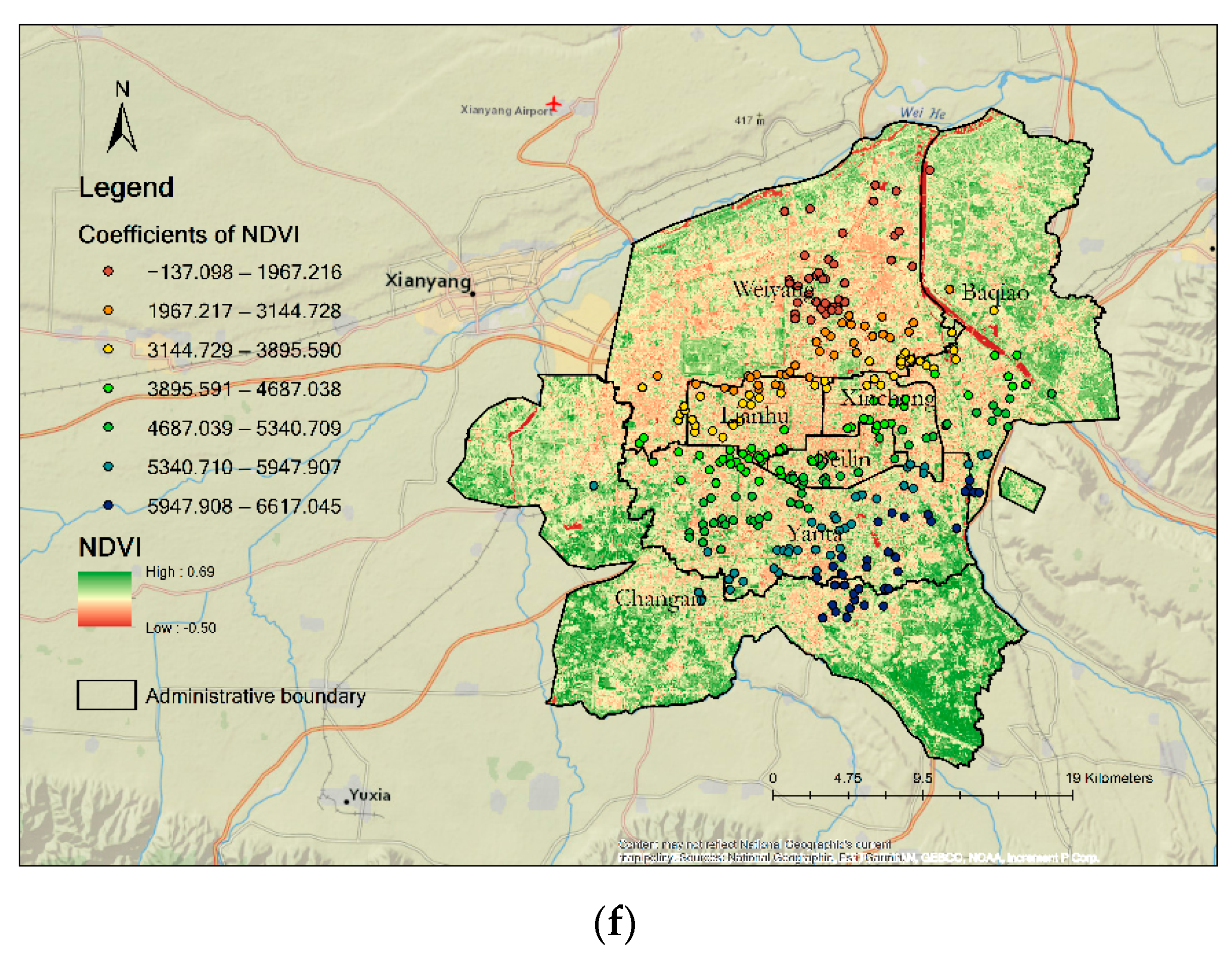
- NDVI
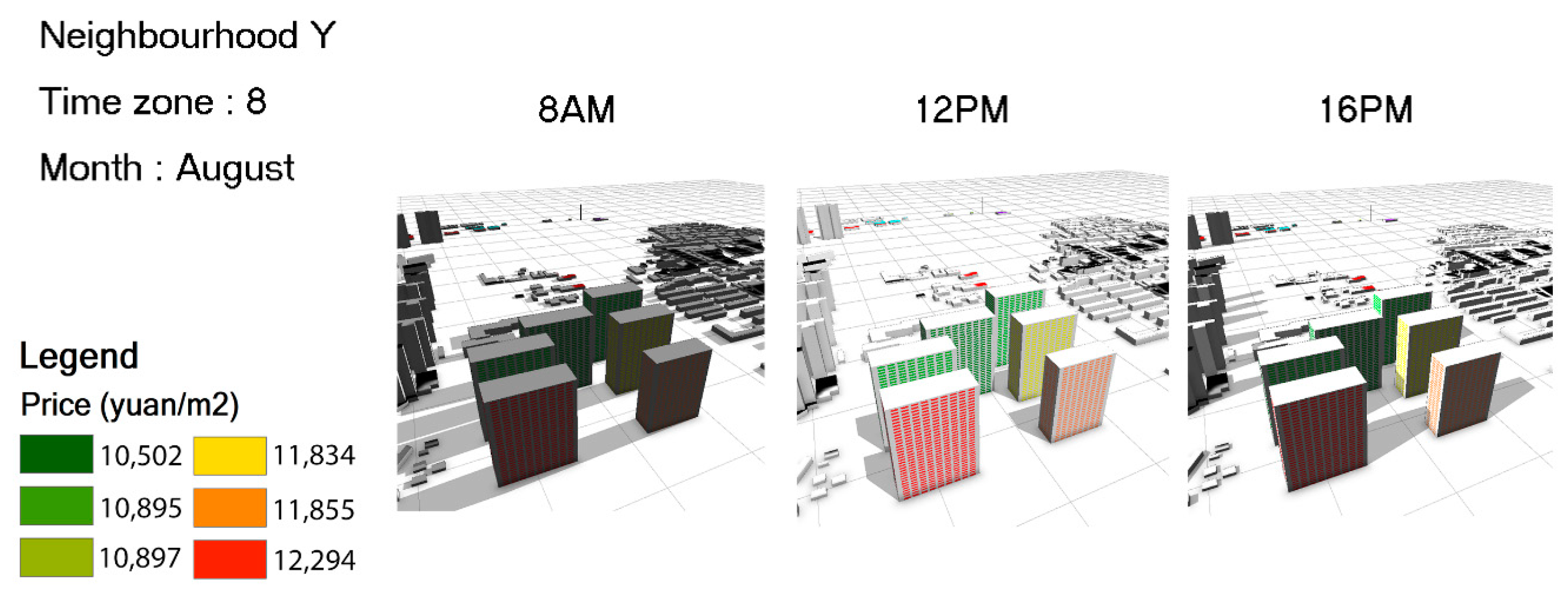
3.2. 3D Model and Visualisation
3.2.1. 3D Analysis
- View quality
- 2.
- SVF
- 3.
- Sunlight
- 4.
- Property orientation
3.2.2. Statistical Analysis of the 3D Model
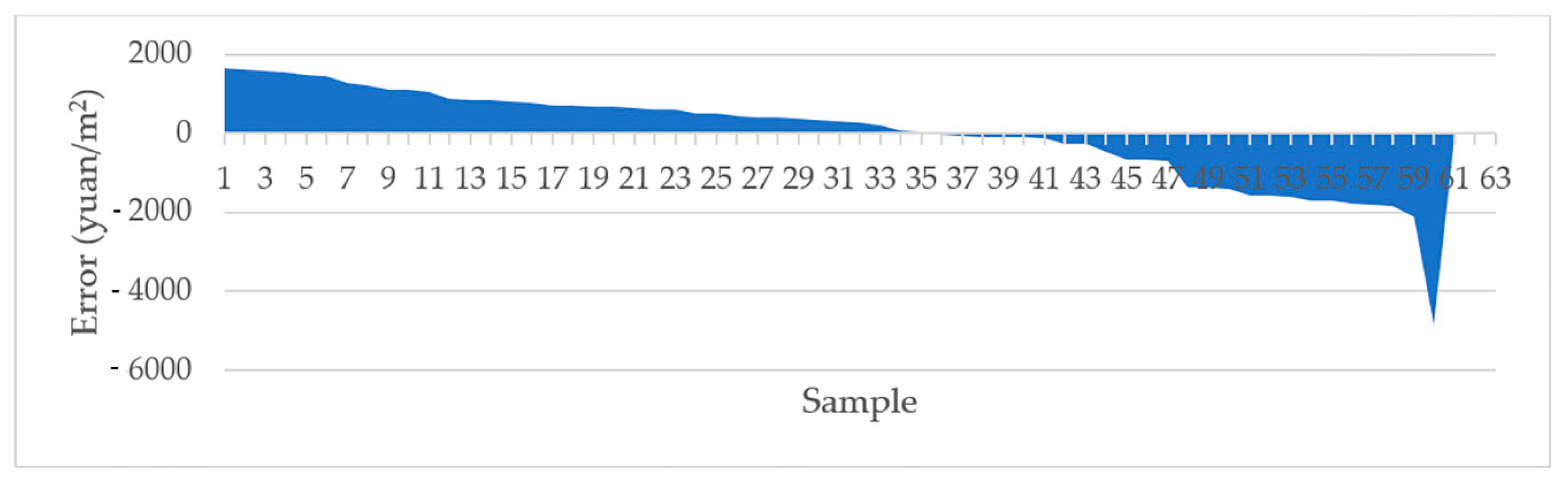
3.2.3. Model Validation
3.3. Model Performance Assessment
4. Discussions
4.1. Current Restricted Property Market and HPM with 2D Factors
4.2. Hedonic Price Model (HPM) with 3D Factors
5. Conclusions and Future Recommendations
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feng, Q.; Wu, G.L. Bubble or riddle? An asset-pricing approach evaluation on China’s housing market. Econ. Model. 2015, 46, 376–383. [Google Scholar] [CrossRef]
- Smith, K.; Liu, S.; Liu, Y.; Liu, Y.; Wu, Y. Reducing energy use for water supply to China’s high-rises. Energy Build. 2017, 135, 119–127. [Google Scholar] [CrossRef]
- Tavernor, R. Visual and cultural sustainability: The impact of tall buildings on London. Landsc. Urban Plan. 2007, 83, 2–12. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, X.; Jin, Y.; Jin, H.; Xu, X. Prediction of outdoor human thermal sensation at the pedestrian level in high-rise residential areas in severe cold regions of China. Energy Procedia 2019, 157, 51–58. [Google Scholar] [CrossRef]
- Ying, Y. Assessment of 2D and 3D Methods for Property Valuation Using Remote Sensing Data At the Neighbourhood Scale in Xi’an, China. Master’s Thesis, Faculty ITC, University of Twente, Enschede, The Netherlands, 2019. [Google Scholar]
- International Valuation Standards 2020; Page Bros: Norwich, UK, 2020.
- Rosen, S. Hedonic prices and implicit markets: Product differentiation in pure competition. J. Political Econ. 1974, 82, 34–55. [Google Scholar] [CrossRef]
- Lancaster, K.J. A new approach to consumer theory. J. Political Econ. 1966, 74, 132–157. [Google Scholar] [CrossRef]
- Wyatt, P.J. The development of a GIS-based property information system for real estate valuation. Int. J. Geogr. Inf. Sci. 1997, 11, 435–450. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Liu, B.; Liu, C. The application of GIS 3D modeling and analysis technology in real estate mass appraisal—Taking landscape and sunlight factors as the example. In Proceedings of the The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Suzhou, China, 14–16 May 2014; Volume XL, pp. 363–367. [Google Scholar]
- Zhu, Q.; Hu, M.; Zhang, Y.; Du, Z. Research and practice in three-dimensional city modeling. Geo Spat. Inf. Sci. 2009, 12, 18–24. [Google Scholar] [CrossRef]
- Jim, C.Y.; Chen, W.Y. Impacts of urban environmental elements on residential housing prices in Guangzhou (China). Landsc. Urban Plan. 2006, 78, 422–434. [Google Scholar] [CrossRef]
- Yu, S.-M.; Han, S.-S.; Chai, C.-H. Modeling the value of view in high-rise apartments: A 3D GIS approach. Environ. Plan. B Plan. Des. 2007, 34, 139–153. [Google Scholar] [CrossRef]
- Wen, H.; Xiao, Y.; Zhang, L. Spatial effect of river landscape on housing price: An empirical study on the Grand Canal in Hangzhou, China. Habitat Int. 2017, 63, 34–44. [Google Scholar] [CrossRef]
- Van Lammeren, R.; Houtkamp, J.; Colijn, S.; Hilferink, M.; Bouwman, A. Affective appraisal of 3D land use visualization. Comput. Environ. Urban Syst. 2010, 34, 465–475. [Google Scholar] [CrossRef]
- Onyimbi, J.R.; Koeva, M.; Flacke, J. Public participation using 3D city models. GIM Int. 2017, 31, 29–31. [Google Scholar]
- Biljecki, F.; Ledoux, H.; Stoter, J. An improved LOD specification for 3D building models. Comput. Environ. Urban Syst. 2016, 59, 25–37. [Google Scholar] [CrossRef]
- Gimenez, L.; Robert, S.; Suard, F.; Zreik, K. Automatic reconstruction of 3D building models from scanned 2D floor plans. Autom. Constr. 2016, 63, 48–56. [Google Scholar] [CrossRef]
- Ha, J.; Lee, S.; Park, C. Temporal effects of environmental characteristics on urban air temperature: The influence of the Sky View Factor. Sustainability 2016, 8, 895. [Google Scholar] [CrossRef]
- Yu, X.; Su, Y. Daylight availability assessment and its potential energy saving estimation-A literature review. Renew. Sustain. Energy Rev. 2015, 52, 494–503. [Google Scholar] [CrossRef]
- Isikdag, U.; Horhammer, M.; Zlatanova, S.; Kathmann, R.; van Oosterom, P. Utilizing 3D building and 3D cadastre geometries for better valuation of existing real estate. In Proceedings of the FIG Working Week 2015 ‘From the wisdom of the ages to the challenges of modern world’, Sofia, Bulgaria, 17 May 2015; pp. 17–21. [Google Scholar]
- Tomić, H.; Roić, M.; Ivić, S.M. Use of 3D cadastral data for real estate mass valuation in the urban areas. In Proceedings of the 3rd International Workshop on 3D Cadastres: Developments and Practices; van Oosterom, P., Ed.; International Federation of Surveyors, FIG: Copenhagen, Denmark, 2012; pp. 73–86. [Google Scholar]
- Kara, A.; van Oosterom, P.; Çağdaş, V.; Işıkdağ, Ü.; Lemmen, C. 3 Dimensional data research for property valuation in the context of the LADM Valuation Information Model. Land Use Policy 2020, 104179. [Google Scholar] [CrossRef]
- Hui, E.C.M.; Zhong, J.W.; Yu, K.H. The impact of landscape views and storey levels on property prices. Landsc. Urban Plan. 2012, 105, 86–93. [Google Scholar] [CrossRef]
- Yamagata, Y.; Murakami, D.; Yoshida, T.; Seya, H.; Kuroda, S. Value of urban views in a bay city: Hedonic analysis with the spatial multilevel additive regression (SMAR) model. Landsc. Urban Plan. 2016, 151, 89–102. [Google Scholar] [CrossRef]
- Sander, H.A.; Polasky, S. The value of views and open space: Estimates from a hedonic pricing model for Ramsey County, Minnesota, USA. Land Use Policy 2009, 26, 837–845. [Google Scholar] [CrossRef]
- Xi’an Municipal Bereau of Statistics. Xi’an Statistics Yearbook 2018; China Statistics Press: Xi’an, China, 2019.
- Lisi, G. Property valuation: The hedonic pricing model—location and housing submarkets. J. Prop. Invest. Financ. 2019, 37, 589–596. [Google Scholar] [CrossRef]
- Liang, X.; Liu, Y.; Qiu, T.; Jing, Y.; Fang, F. The effects of locational factors on the housing prices of residential communities: The case of Ningbo, China. Habitat Int. 2018, 81, 1–11. [Google Scholar] [CrossRef]
- Lei, J. The Operation Situation of Xi’an Property Market in 2018. Chinese Business View. 2018. Available online: http://news.hsw.cn/system/2018/1122/1042031.shtml (accessed on 10 November 2020).
- Hurun Global House Price Index was Released and Xi’an Enters Top Ten; Hurun Research Institute: Shanghai, China, 2018. Available online: http://www.hurun.net/CN/Article/Details?num=61C2A98F9932 (accessed on 10 November 2020).
- Hu, L.; He, S.; Han, Z.; Xiao, H.; Su, S.; Weng, M.; Cai, Z. Monitoring housing rental prices based on social media:An integrated approach of machine-learning algorithms and hedonic modeling to inform equitable housing policies. Land Use Policy 2019, 82, 657–673. [Google Scholar] [CrossRef]
- Field, A. Discovering Statistics Using SPSS, 3rd ed.; SAGE Publications Ltd.: London, UK, 2009; Volume 58, ISBN 9781847879073. [Google Scholar]
- Sander, E.; Libby, J.; Caza, A.; Jordan, P.J. Psychological perceptions matter: Developing the reactions to the physical work environment scale. Build. Environ. 2019, 148, 338–347. [Google Scholar] [CrossRef]
- Liu, F.; Kang, J. Relationship between street scale and subjective assessment of audio-visual environment comfort based on 3D virtual reality and dual-channel acoustic tests. Build. Environ. 2018, 129, 35–45. [Google Scholar] [CrossRef]
- Clifford, N.; Cope, M.; French, S.; Valentine, G. Key Methods in Geography; Sage: London, UK, 2010; ISBN 9781446298589. [Google Scholar]
- Zhang, L.; Zhou, J.; Hui, E.C. Man Which types of shopping malls affect housing prices? From the perspective of spatial accessibility. Habitat Int. 2020, 96, 102118. [Google Scholar] [CrossRef]
- Li, H.; Wei, Y.D.; Wu, Y.; Tian, G. Analyzing housing prices in Shanghai with open data: Amenity, accessibility and urban structure. Cities 2019, 91, 165–179. [Google Scholar] [CrossRef]
- Chen, W.Y.; Li, X. Cumulative impacts of polluted urban streams on property values: A 3-D spatial hedonic model at the micro-neighborhood level. Landsc. Urban Plan. 2017, 162, 1–12. [Google Scholar] [CrossRef]
- Bernard, J.; Musy, M.; Calmet, I.; Bocher, E.; Keravec, P. Urban heat island temporal and spatial variations: Empirical modeling from geographical and meteorological data. Build. Environ. 2017, 125, 423–438. [Google Scholar] [CrossRef]
- Mackey, C.W.; Lee, X.; Smith, R.B. Remotely sensing the cooling effects of city scale efforts to reduce urban heat island. Build. Environ. 2012, 49, 348–358. [Google Scholar] [CrossRef]
- Liang, J.; Gong, J.; Sun, J.; Liu, J. A customizable framework for computing sky view factor from large-scale 3D city models. Energy Build. 2017, 149, 38–44. [Google Scholar] [CrossRef]
- Czembrowski, P.; Kronenberg, J. Hedonic pricing and different urban green space types and sizes: Insights into the discussion on valuing ecosystem services. Landsc. Urban Plan. 2016, 146, 11–19. [Google Scholar] [CrossRef]
- Liu, G.; Wang, X.; Gu, J.; Liu, Y.; Zhou, T. Temporal and spatial effects of a ‘Shan Shui’ landscape on housing price: A case study of Chongqing, China. Habitat Int. 2019, 94, 102068. [Google Scholar] [CrossRef]
- Higgins, C.D. A 4D spatio-temporal approach to modelling land value uplift from rapid transit in high density and topographically-rich cities. Landsc. Urban Plan. 2019, 185, 68–82. [Google Scholar] [CrossRef]
- Yoo, S.; Im, J.; Wagner, J.E. Variable selection for hedonic model using machine learning approaches: A case study in Onondaga County, NY. Landsc. Urban Plan. 2012, 107, 293–306. [Google Scholar] [CrossRef]
- Schläpfer, F.; Waltert, F.; Segura, L.; Kienast, F. Valuation of landscape amenities: A hedonic pricing analysis of housing rents in urban, suburban and periurban Switzerland. Landsc. Urban Plan. 2015, 141, 24–40. [Google Scholar] [CrossRef]
- Wen, H.; Goodman, A.C. Relationship between urban land price and housing price: Evidence from 21 provincial capitals in China. Habitat Int. 2013, 40, 9–17. [Google Scholar] [CrossRef]
- Yuan, F.; Wei, Y.D.; Wu, J. Amenity effects of urban facilities on housing prices in China: Accessibility, scarcity, and urban spaces. Cities 2020, 96, 102433. [Google Scholar] [CrossRef]
- Mei, Y.; Gao, L.; Zhang, J.; Wang, J. Valuing urban air quality: A hedonic price analysis in Beijing, China. Environ. Sci. Pollut. Res. 2020, 27, 1373–1385. [Google Scholar] [CrossRef]
- Tian, G.; Wei, Y.D.; Li, H. Effects of accessibility and environmental health risk on housing prices: A case of Salt Lake County, Utah. Appl. Geogr. 2017, 89, 12–21. [Google Scholar] [CrossRef]
- Bitter, C.; Mulligan, G.F.; Dall’erba, S. Incorporating spatial variation in housing attribute prices: A comparison of geographically weighted regression and the spatial expansion method. J. Geogr. Syst. 2007, 9, 7–27. [Google Scholar] [CrossRef]
- Dziauddin, M.F.; Idris, Z. Use of geographically weighted regression (GWR) method to estimate the effects of location attributes on the residential property values. Indones. J. Geogr. 2017, 49, 97–110. [Google Scholar] [CrossRef][Green Version]
- Wen, H.; Xiao, Y.; Hui, E.C.M.; Zhang, L. Education quality, accessibility, and housing price: Does spatial heterogeneity exist in education capitalization? Habitat Int. 2018, 78, 68–82. [Google Scholar] [CrossRef]
- Lu, B.; Charlton, M.; Fotheringham, A.S. Geographically weighted regression using a non-Euclidean distance metric with a study on London house price data. Procedia Environ. Sci. 2011, 7, 92–97. [Google Scholar] [CrossRef]
- Mccluskey, W.J.; Mccord, M.; Davis, P.T.; Haran, M.; Mcilhatton, D. Prediction accuracy in mass appraisal: A comparison of modern approaches. J. Prop. Res. 2013, 30, 239–265. [Google Scholar] [CrossRef]
- Qu, S.; Hu, S.; Li, W.; Zhang, C.; Li, Q.; Wang, H. Temporal variation in the effects of impact factors on residential land prices. Appl. Geogr. 2020, 114, 102124. [Google Scholar] [CrossRef]
- Li, S.; Ye, X.; Lee, J.; Gong, J.; Qin, C. Spatiotemporal Analysis of Housing Prices in China: A Big Data Perspective. Appl. Spat. Anal. Policy 2017, 10, 421–433. [Google Scholar] [CrossRef]
- Singh, S.P.; Jain, K.; Mandla, V.R. Image based Virtual 3D Campus modeling by using CityEngine. Am. J. Eng. Sci. Technol. Res. 2014, 2, 1–10. [Google Scholar]
- Furey, T.S.; Cristianini, N.; Duffy, N.; Bednarski, D.W.; Schummer, M.; Haussler, D. Support vector machine classification and validation of cancer tissue samples using microarray expression data. Bioinformatics 2000, 16, 906–914. [Google Scholar] [CrossRef]
- Jin, S.; Li, D.; Wang, J. A comparison of support vector machine with maximum likelihood classification algorithms on texture features. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Seoul, Korea, 29 July 2020; IEEE: Piscataway Township, NJ, USA, 2005; Volume 5, pp. 3717–3720. [Google Scholar]
- Foody, G. Harshness in image classification accuracy assessment. Int. J. Remote Sens. 2008, 29, 3137–3158. [Google Scholar] [CrossRef]
- Xu, Z.; Coors, V. Combining system dynamics model, GIS and 3D visualization in sustainability assessment of urban residential development. Build. Environ. 2012, 47, 272–287. [Google Scholar] [CrossRef]
- Biljecki, F.; Stoter, J.; Ledoux, H.; Zlatanova, S.; Çöltekin, A. Applications of 3D City Models: State of the art review. ISPRS Int. J. Geo Inf. 2015, 4, 2842–2889. [Google Scholar] [CrossRef]
- Wong, T.T. Performance evaluation of classification algorithms by k-fold and leave-one-out cross validation. Pattern Recognit. 2015, 48, 2839–2846. [Google Scholar] [CrossRef]
- Standard for Urban Residential Area Planning and Design; Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Bejing, China, 2018.
- Kunming Medical University. A Suitable Viewing Distance Based on Spatial Cognition, Kunming Medical University. 2007. Available online: http://www.kmmu.edu.cn/Pages_560_2443.aspx (accessed on 10 November 2020).
- Breunig, R.; Hasan, S.; Whiteoak, K. Value of playgrounds relative to green spaces: Matching evidence from property prices in Australia. Landsc. Urban Plan. 2019, 190. [Google Scholar] [CrossRef]
- Jiao, L.; Liu, Y. Geographic Field Model based hedonic valuation of urban open spaces in Wuhan, China. Landsc. Urban Plan. 2010, 98, 47–55. [Google Scholar] [CrossRef]
- Dziauddin, M.F.; Powe, N.; Alvanides, S. Estimating the effects of Light Rail Transit (LRT) system on residential property values using geographically weighted regression (GWR). Appl. Spat. Anal. Policy 2015, 8, 1–25. [Google Scholar] [CrossRef]
- Jim, C.Y.; Chen, W.Y. External effects of neighbourhood parks and landscape elements on high-rise residential value. Land Use Policy 2010, 27, 662–670. [Google Scholar] [CrossRef]
- Yang, L.; Chen, Y.; Xu, N.; Zhao, R.; Chau, K.W.; Hong, S. Place-varying impacts of urban rail transit on property prices in Shenzhen, China: Insights for value capture. Sustain. Cities Soc. 2020, 58, 102140. [Google Scholar] [CrossRef]
- Tan, R.; He, Q.; Zhou, K.; Xie, P. The effect of new metro stations on local land use and housing prices: The case of Wuhan, China. J. Transp. Geogr. 2019, 79, 102488. [Google Scholar] [CrossRef]
- Renigier-Bilozor, M.; Janowski, A.; Walacik, M. Geoscience Methods in Real Estate Market Analyses Subjectivity Decrease. Geosciences 2019, 9, 130. [Google Scholar] [CrossRef]
- Panduro, T.E.; Veie, K.L. Classification and valuation of urban green spaces-A hedonic house price valuation. Landsc. Urban Plan. 2013, 120, 119–128. [Google Scholar] [CrossRef]
- Chen, W.Y.; Li, X. Impacts of urban stream pollution: A comparative spatial hedonic study of high-rise residential buildings in Guangzhou, south China. Geogr. J. 2018, 184, 283–297. [Google Scholar] [CrossRef]
- Fleming, D.; Grimes, A.; Lebreton, L.; Maré, D.; Nunns, P. Valuing sunshine. Reg. Sci. Urban Econ. 2018, 68, 268–276. [Google Scholar] [CrossRef]
- El-Mekawy, M.; Östman, A.; Hijazi, I. A unified building model for 3D Urban GIS. ISPRS Int. J. Geo Inf. 2012, 1, 120–145. [Google Scholar] [CrossRef]
- Xu, Z.; Li, Q. Integrating the empirical models of benchmark land price and GIS technology for sustainability analysis of urban residential development. Habitat Int. 2014, 44, 79–92. [Google Scholar] [CrossRef]
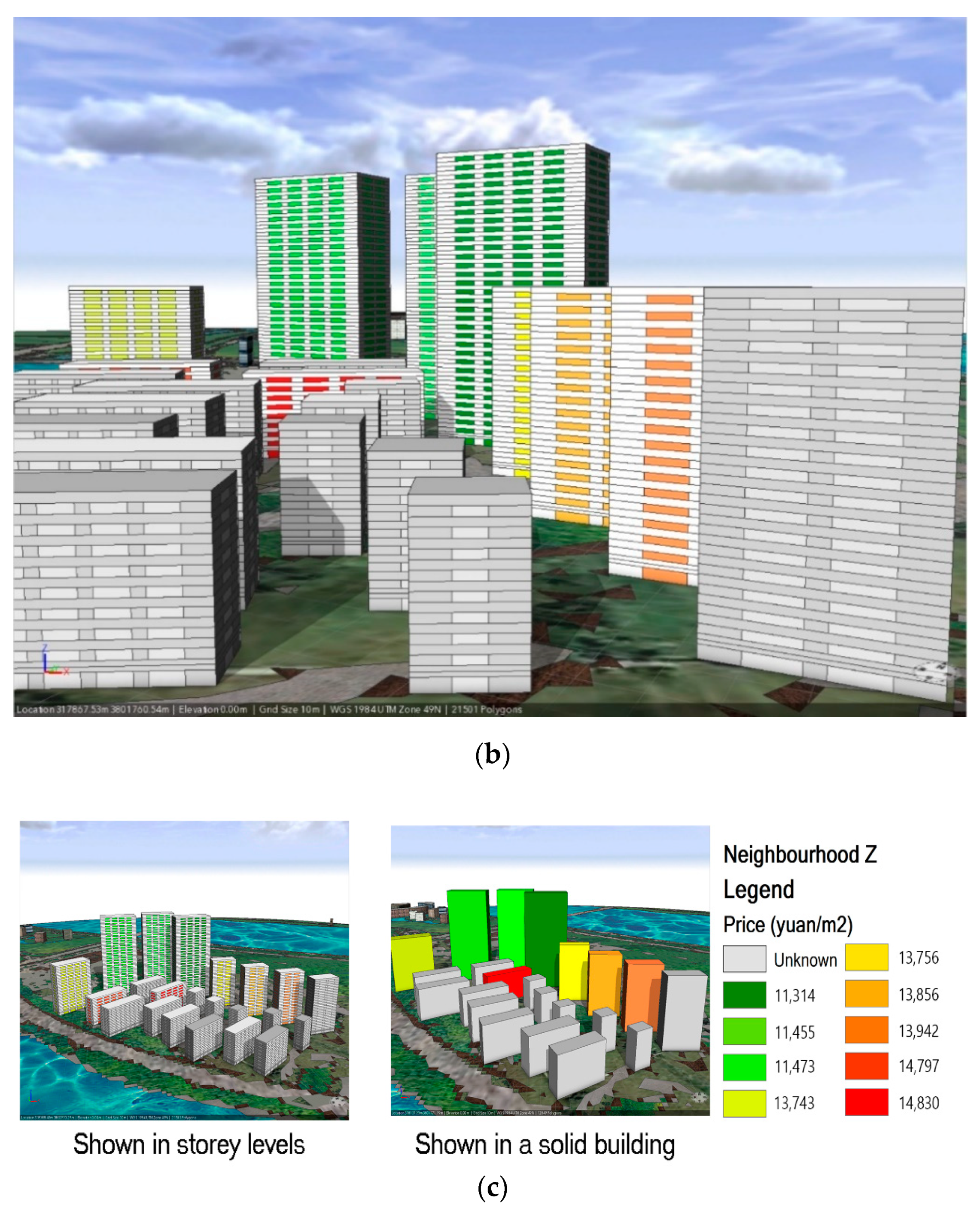
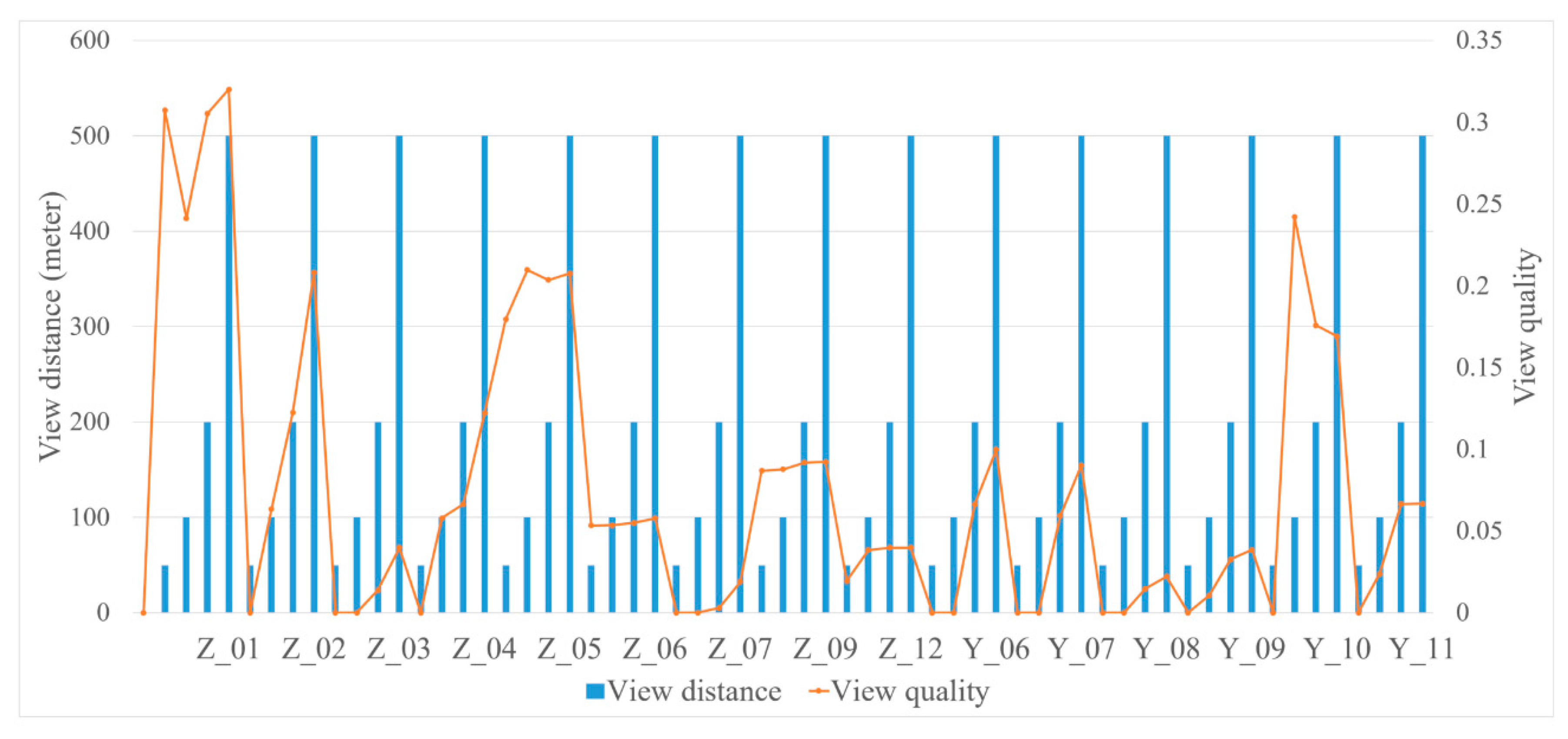
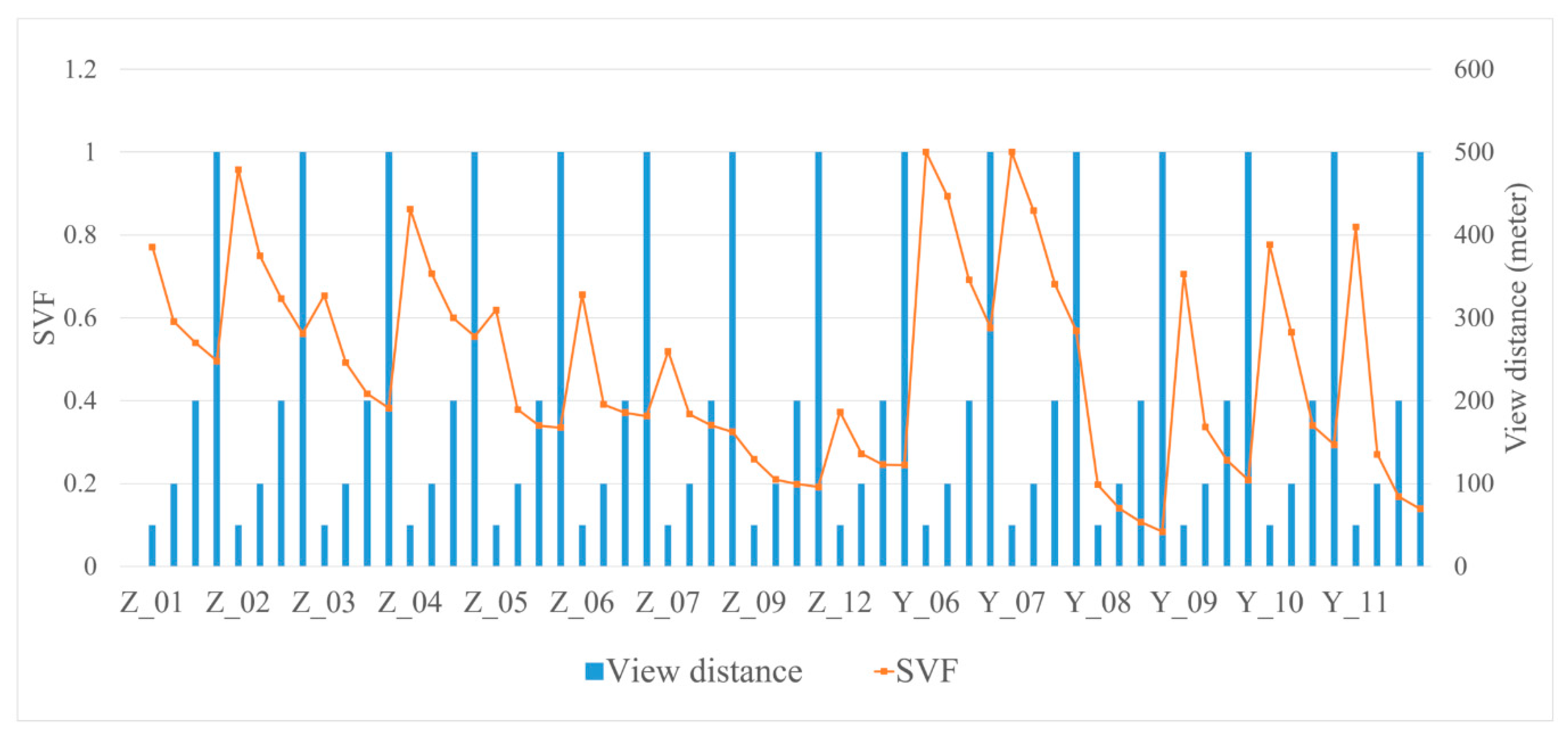
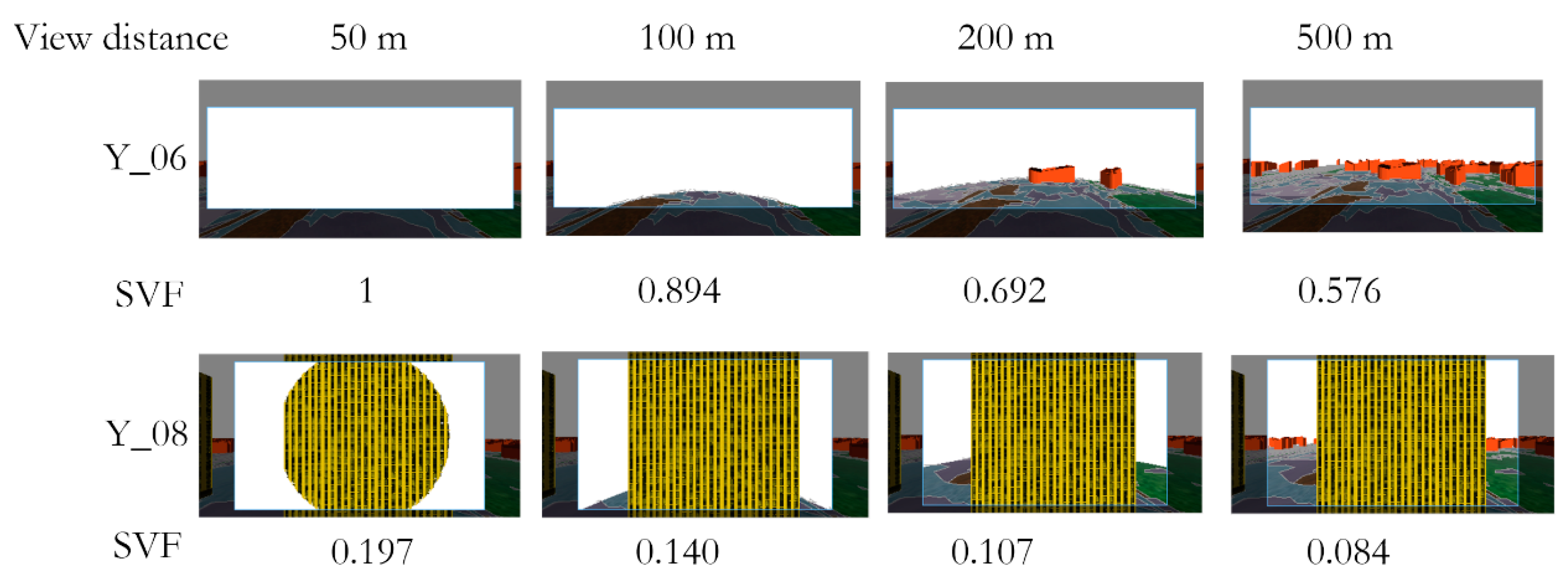
| Data | Unit | Source and Description | Purpose |
|---|---|---|---|
| Sentinel-2 satellite image | Tiff | Copernicus Open Access Hub, 10-m resolution, date 26-10-2018, cloud coverage 1.5% | Calculating the normalised difference vegetation index (NDVI). |
| Gaofen-2 satellite image | Tiff | Gaofen-2 Satellite, 4-m resolution, date 12-04-2017, cloud coverage 0.04% | Land cover classification for the 3D model. |
| Google Earth Image | Tiff | Pixel resolution 4800 × 2782, date 24-04-2017 | Land cover classification validation. |
| Floor numbers of the buildings in Xi’an | Vector | Baidu Map and Amap (AutoNavi) | Construct buildings for 3D analyses. |
| Point of interest (POI) of Xi’an | Point | Baidu Map | Creating 2D factors. |
| Footprints of the buildings in neighbourhoods Y and Z | Vector | Google Earth | 3D visualisation and spatial analysis. |
| Database of the average first-hand property values of Xi’an in 2018 | Yuan/m2 | China Index Academy | The dependent variable (regressions) of the 2D model. |
| First-hand property values of the neighbourhoods Y and Z in 2018 | Yuan/m2 | The Price Bureau of Xi’an (http://wjj.xa.gov.cn/) | The dependent variable (regression) of the 3D model. |
| Factor | Definition | Unit |
|---|---|---|
| Property value | The first-handed property value of high-rise neighbourhoods. | Yuan/m2 |
| Density of park | The density of the parks within 1 km. | Number |
| NDVI | The mean vegetation inside the neighbourhood within 50 m. | Number |
| Density of factory | The density of the factories within 1 km. | Number |
| Distance to food | Euclidean distance to restaurants, fast-food chains, and eateries. | Meter |
| Distance to college | Euclidean distance to colleges and universities. | Meter |
| Density of hospital | The density of major hospitals within 3 km. | Number |
| Density of supermarket | The density of supermarkets within 1 km. | Number |
| Distance to CBD | Euclidean distance to the central business district (CBD). | Meter |
| Distance to subway | Euclidean distance to subway stations. | Meter |
| Density of bus stop | The density of bus stops within 200 m. | Number |
| Distance to road | Euclidean distance to primary and secondary roads. | Meter |
| Factor | Definition | Unit |
|---|---|---|
| View quality | The proportion of the areas of positive view types to the total. | Percentage |
| SVF | The proportion of the visible sky from the observer point [42] | Percentage |
| Sunlight | The proportion of properties with direct sunlight to the total amount of properties at south orientation (per building) | Percentage |
| Property orientation | The preferred orientation of main rooms equals 1; otherwise, it equals 0. | Dummy variable |
| Parameter | Value | Reference | Description |
|---|---|---|---|
| The horizontal angle of view | 120° | The normal vision range of eyesight. | The horizontal angle of view in a 360° panorama from the observer. |
| The vertical angle of view | 90° | The normal vision range of eyesight. | The vertical angle of view in a 360° panorama from the observer. |
| Observer point of X | / | It changes with the building location. | X coordinate of the observer. |
| Observer point of Y | The middle of the building | It aims to represent the average value. | Y coordinate of the observer. |
| Observer point of Z | / | It changes with the building location. | Z coordinate of the observer. |
| Tilt angle | 0° | The observer looks straight ahead. | Vertical camera view angle. |
| Heading angle | 135° (southeast) or 180° (south) | The orientation from the main rooms. | Horizontal camera view angle. |
| View distance | 50 m, 100 m, 200 m, 500 m | Different view distances contain different view types and areas. | The distance from the observer to the point of interest. |
| Variable Name | β Mean | β Min | β Max | β Standardised | β Standard Deviation |
|---|---|---|---|---|---|
| NDVI | 4136.834 | −137.098 | 6617.045 | 2.630 * | 1572.973 |
| Density of bus stop | 2.037 | −26.437 | 21.607 | 0.231 | 8.829 |
| Density of supermarket | −11.377 | −29.688 | 4.423 | −1.441 | 7.896 |
| Density of factory | −870.293 | −1585.278 | 22.264 | −2.171 * | 400.941 |
| Density of hospital | −2880.989 | −5843.088 | 988.861 | −2.221 | 1297.092 |
| Distance to food | 5.455 | 1.488 | 9.706 | 2.695 * | 2.024 |
| Distance to college | 0.104 | −0.435 | 0.984 | 0.341 | 0.305 |
| Distance to road | −1.001 | −2.072 | 0.225 | −1.653 | 0.605 |
| Density of park | −173.801 | −810.403 | 434.060 | −0.680 | 255.686 |
| Distance to subway | −0.701 | −1.433 | −0.274 | −2.304 * | 0.304 |
| Distance to CBD | −0.230 | −0.381 | −0.175 | −4.880 * | 0.047 |
| Local R2 | 0.124 | 0.093 | 0.207 | / | 0.022 |
| Intercept | 11,531.725 | 8847.235 | 14,826.088 | 7.338 | 1571.418 |
| AICc | 5670.436 | ||||
| Adjusted R2 | 0.128 | ||||
| Name | Sunlight | Total | Mean | |||||
|---|---|---|---|---|---|---|---|---|
| 8 June (A.M.) | 12 June (A.M.) | 16 June (P.M.) | 8 Dec (A.M.) | 12 Dec (A.M.) | 16 Dec (P.M.) | |||
| Y_06 | 0.000 | 1.000 | 1.000 | 0.000 | 1.000 | 1.000 | 4.000 | 0.667 |
| Y_07 | 0.000 | 1.000 | 1.000 | 0.000 | 1.000 | 1.000 | 4.000 | 0.667 |
| Y_08 | 0.000 | 1.000 | 1.000 | 0.000 | 0.261 | 0.506 | 2.767 | 0.461 |
| Y_09 | 0.000 | 1.000 | 0.977 | 0.000 | 0.443 | 0.773 | 3.193 | 0.532 |
| Y_10 | 0.000 | 1.000 | 1.000 | 0.000 | 0.902 | 0.122 | 3.024 | 0.504 |
| Y_11 | 0.000 | 1.000 | 1.000 | 0.000 | 0.347 | 0.209 | 2.556 | 0.426 |
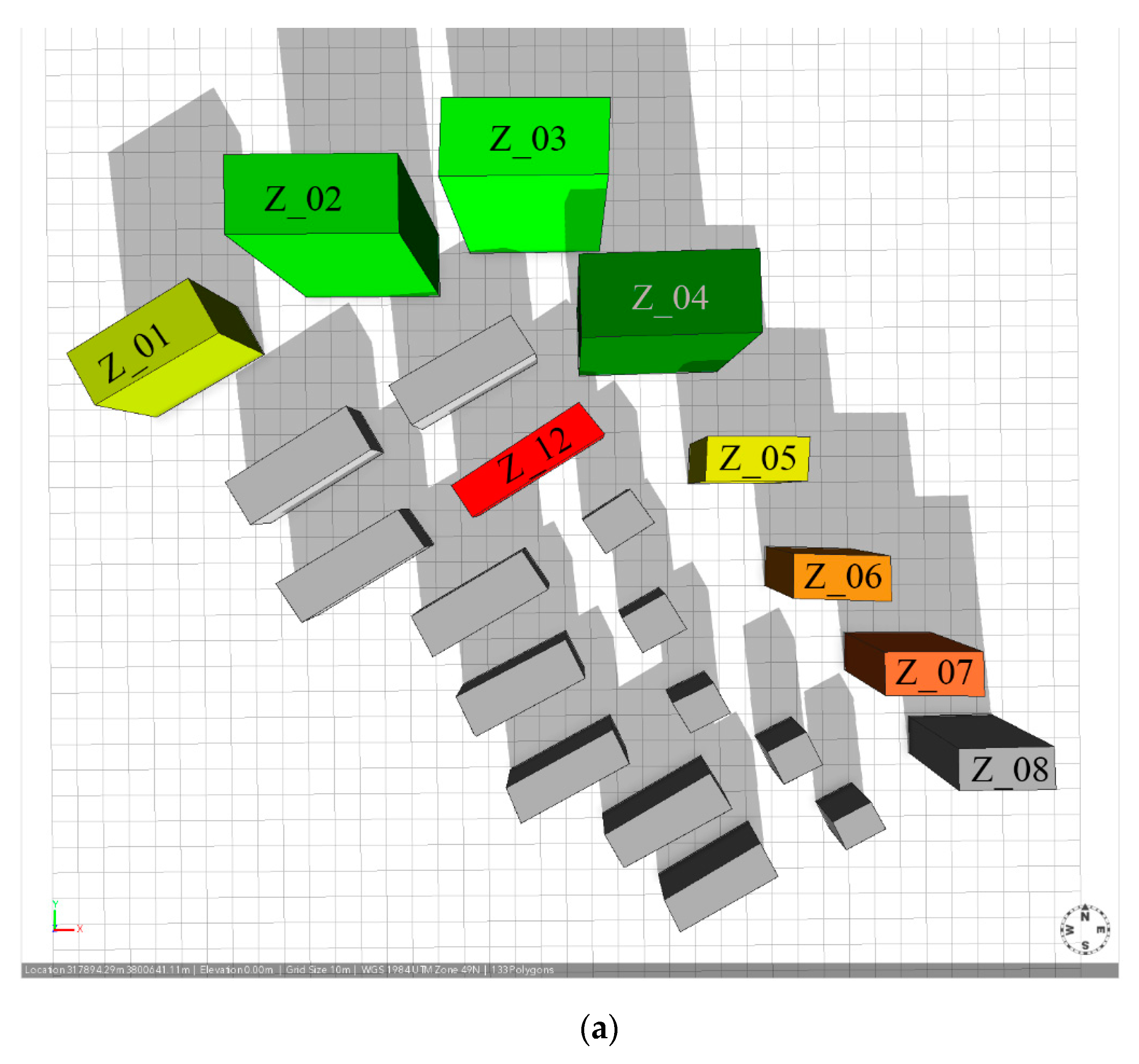
| Z_01 | 0.833 | 1.000 | 0.000 | 0.431 | 1.000 | 0.000 | 3.264 | 0.544 |
| Z_02 | 0.000 | 1.000 | 1.000 | 0.000 | 0.970 | 1.000 | 3.970 | 0.662 |
| Z_03 | 0.000 | 1.000 | 0.000 | 0.000 | 0.773 | 0.962 | 2.735 | 0.456 |
| Z_04 | 0.000 | 1.000 | 1.000 | 0.000 | 0.909 | 0.848 | 3.758 | 0.626 |
| Z_05 | 0.000 | 1.000 | 1.000 | 0.000 | 0.656 | 0.944 | 3.601 | 0.600 |
| Z_06 | 0.000 | 1.000 | 1.000 | 0.000 | 1.000 | 0.778 | 3.778 | 0.630 |
| Z_07 | 0.000 | 1.000 | 1.000 | 0.000 | 0.563 | 0.806 | 3.368 | 0.561 |
| Z_09 | 0.000 | 1.000 | 0.000 | 0.000 | 0.556 | 0.000 | 1.556 | 0.259 |
| Z_12 | 0.625 | 1.000 | 0.000 | 0.000 | 0.688 | 0.000 | 2.313 | 0.385 |
| Variable Name | Standardised Coefficient | t-Ratio | p-Value | Tolerance | VIF |
|---|---|---|---|---|---|
| View quality | −0.123 | −1.046 | 0.300 | 0.725 | 1.379 |
| SVF | −0.271 | −2.005 | 0.050 * | 0.547 | 1.828 |
| Property orientation | −0.792 | −5.747 | 0.000 ** | 0.526 | 1.901 |
| Sunlight | 0.327 | 2.000 | 0.050 * | 0.812 | 2.682 |
| Constant | 13,637.143 | 19.028 | / | / | / |
| Name | R2 | Adjusted R2 | SSR |
|---|---|---|---|
| OLS | 0.111 | 0.077 | 3,392,667,848 |
| GWR | 0.217 | 0.128 | 2,655,158,522 |
| 3D | 0.451 | 0.411 | 125,452,566 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ying, Y.; Koeva, M.; Kuffer, M.; Asiama, K.O.; Li, X.; Zevenbergen, J. Making the Third Dimension (3D) Explicit in Hedonic Price Modelling: A Case Study of Xi’an, China. Land 2021, 10, 24. https://doi.org/10.3390/land10010024
Ying Y, Koeva M, Kuffer M, Asiama KO, Li X, Zevenbergen J. Making the Third Dimension (3D) Explicit in Hedonic Price Modelling: A Case Study of Xi’an, China. Land. 2021; 10(1):24. https://doi.org/10.3390/land10010024
Chicago/Turabian StyleYing, Yue, Mila Koeva, Monika Kuffer, Kwabena Obeng Asiama, Xia Li, and Jaap Zevenbergen. 2021. "Making the Third Dimension (3D) Explicit in Hedonic Price Modelling: A Case Study of Xi’an, China" Land 10, no. 1: 24. https://doi.org/10.3390/land10010024
APA StyleYing, Y., Koeva, M., Kuffer, M., Asiama, K. O., Li, X., & Zevenbergen, J. (2021). Making the Third Dimension (3D) Explicit in Hedonic Price Modelling: A Case Study of Xi’an, China. Land, 10(1), 24. https://doi.org/10.3390/land10010024