The Influence of the Annual Number of Storms on the Derivation of the Flood Frequency Curve through Event-Based Simulation
Abstract
:1. Introduction
2. Materials and Methods
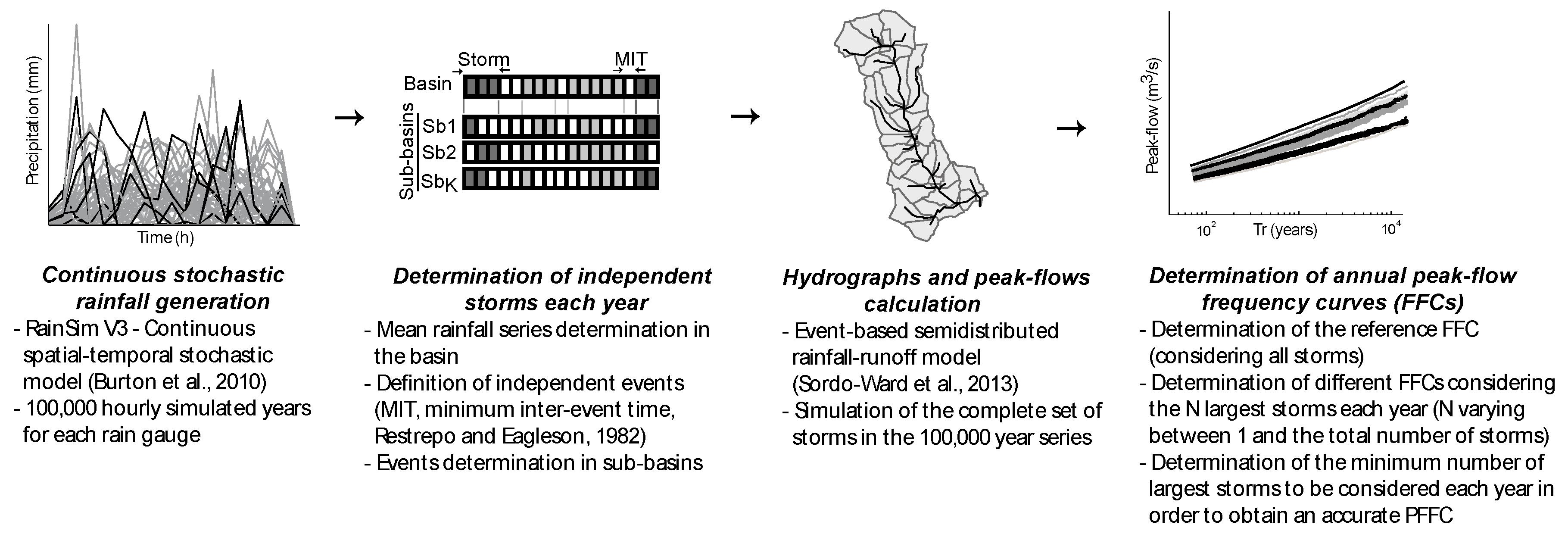
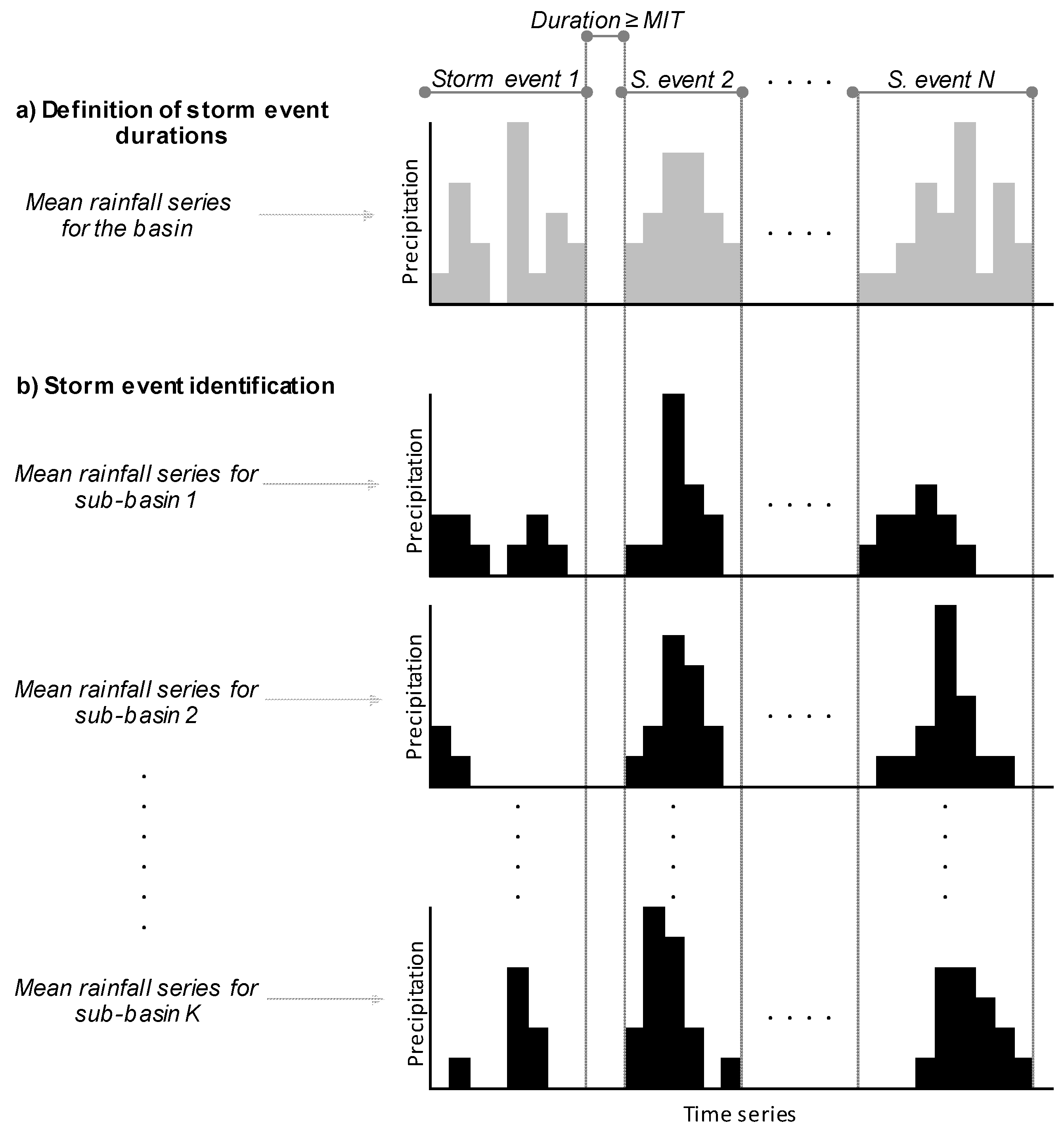
2.1. Stochastic Rainfall Series Generation and Storm Identification
2.2. Estimation of the Peak Flow Frequency Curves
2.3. Case Studies
2.4. Limitations of the Methodology
3. Results and Discussion
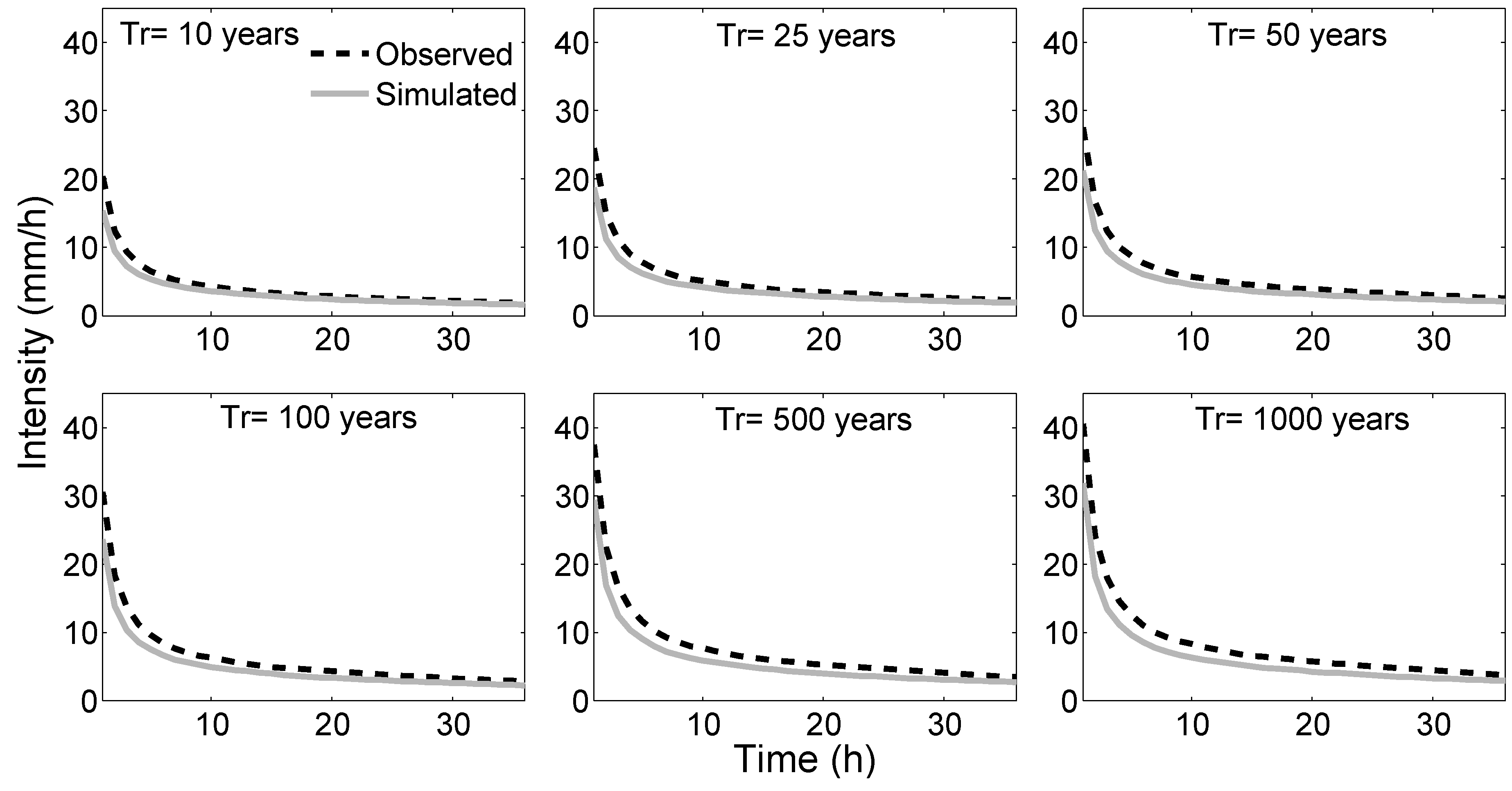
3.1. Rainfall Model Calibration/Validation and Rainfall Events Identification/Characterisation
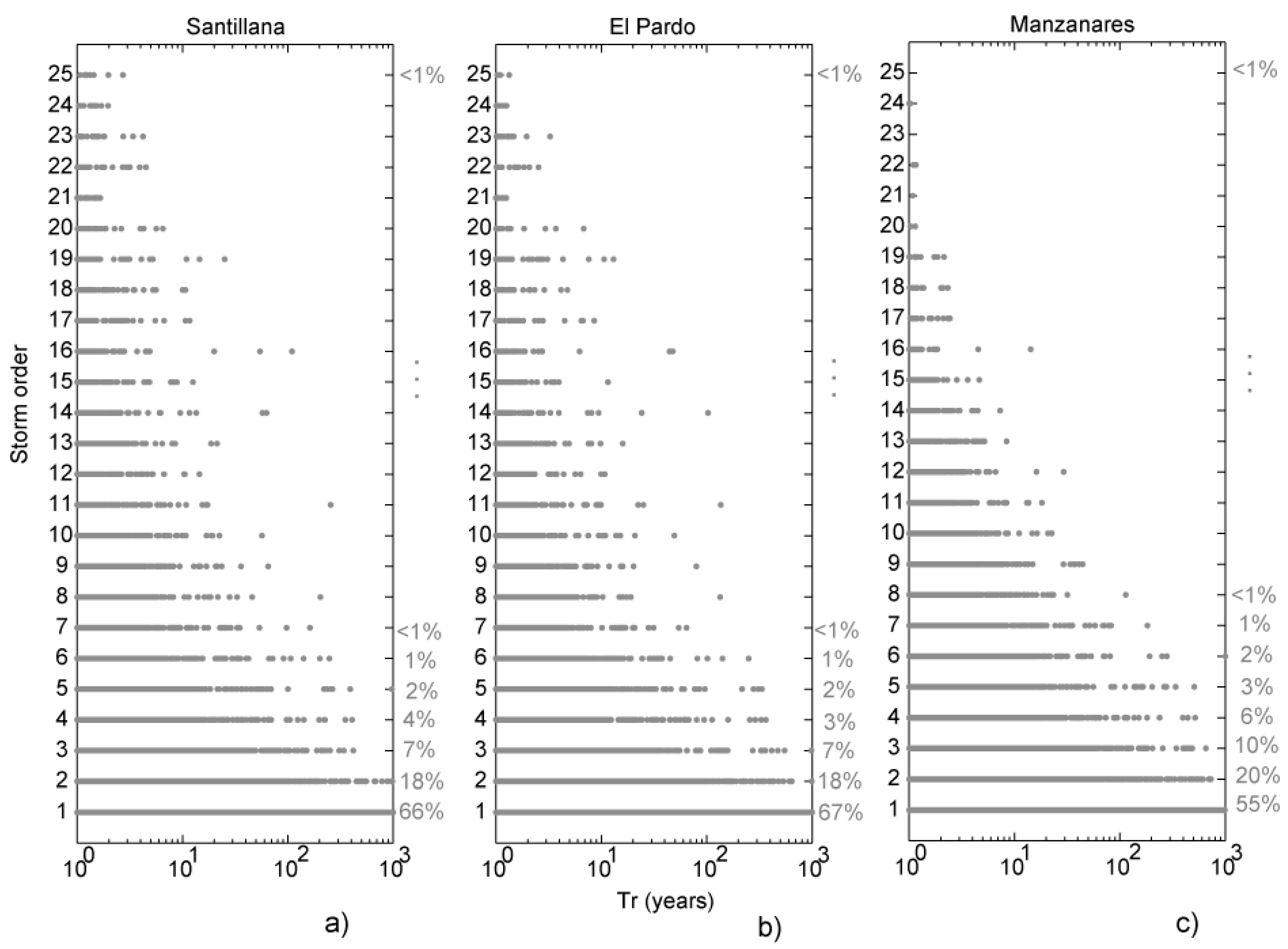
3.2. FFCs Estimation and Effect of Considering Different Number of Storms Each Year
3.3. Joint Analysis of Maximum Annual Peak Flow and Hydrograph Volume
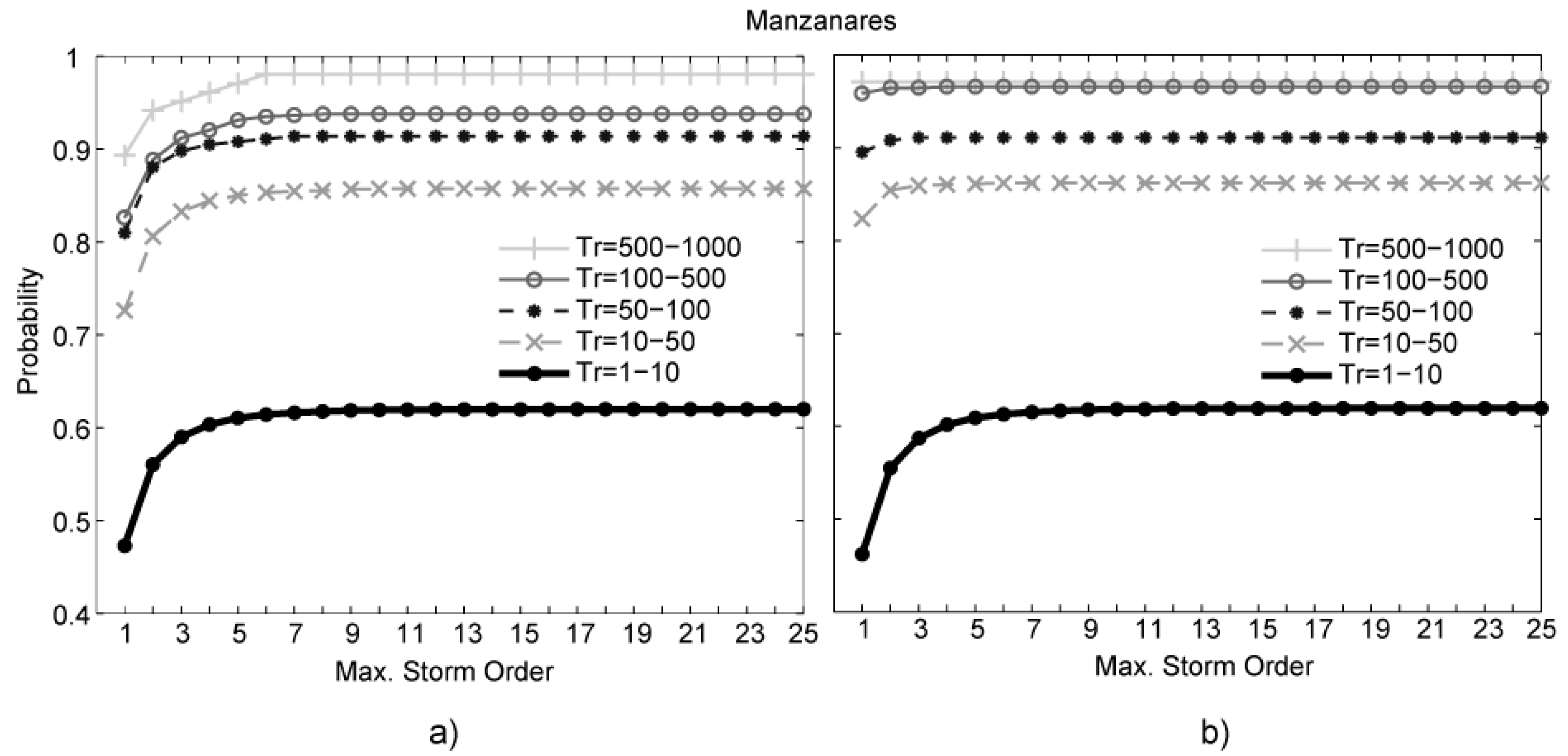
3.4. Sensitivity Analysis of Inter-Event Time Determination
4. Conclusions
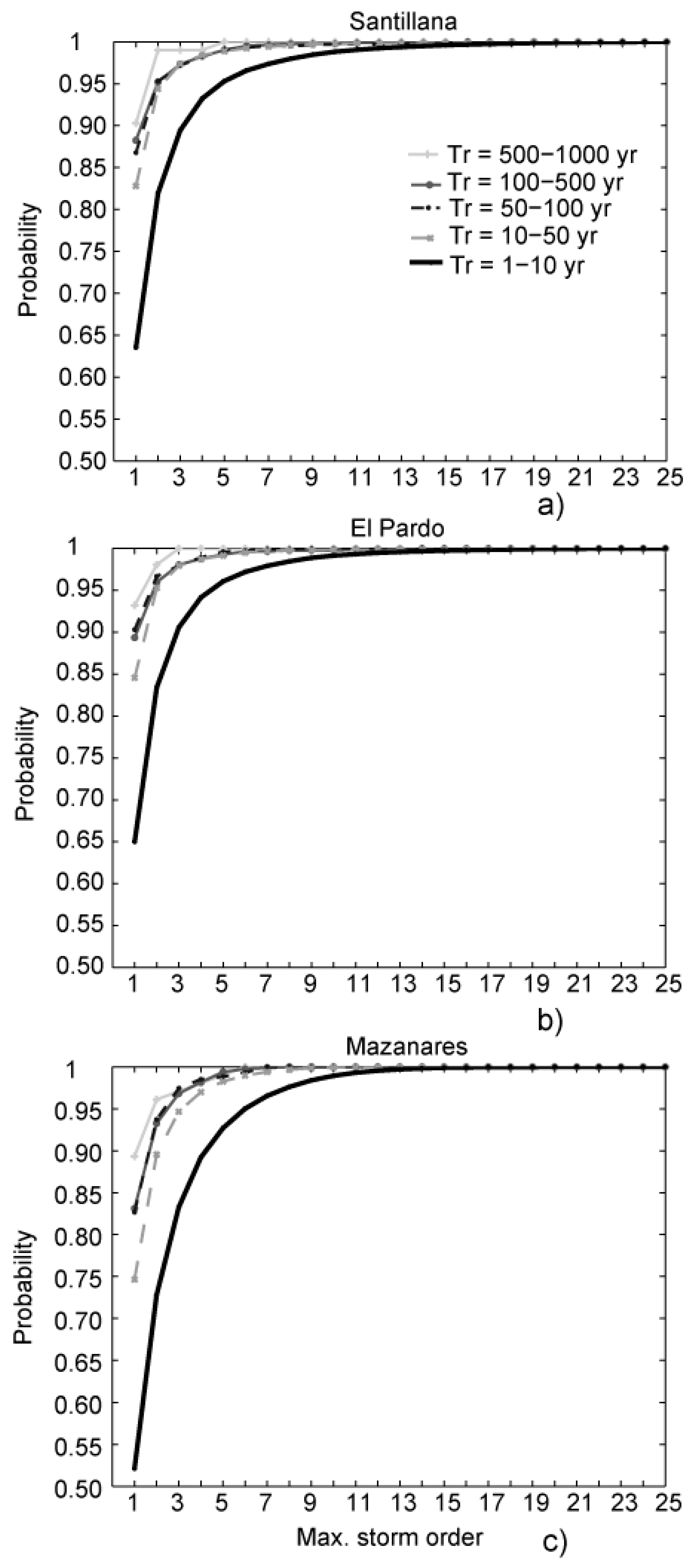
- The degree of alignment between the calculated flood frequency curves and the reference flood frequency curve depends on the return period of the peak flow considered.
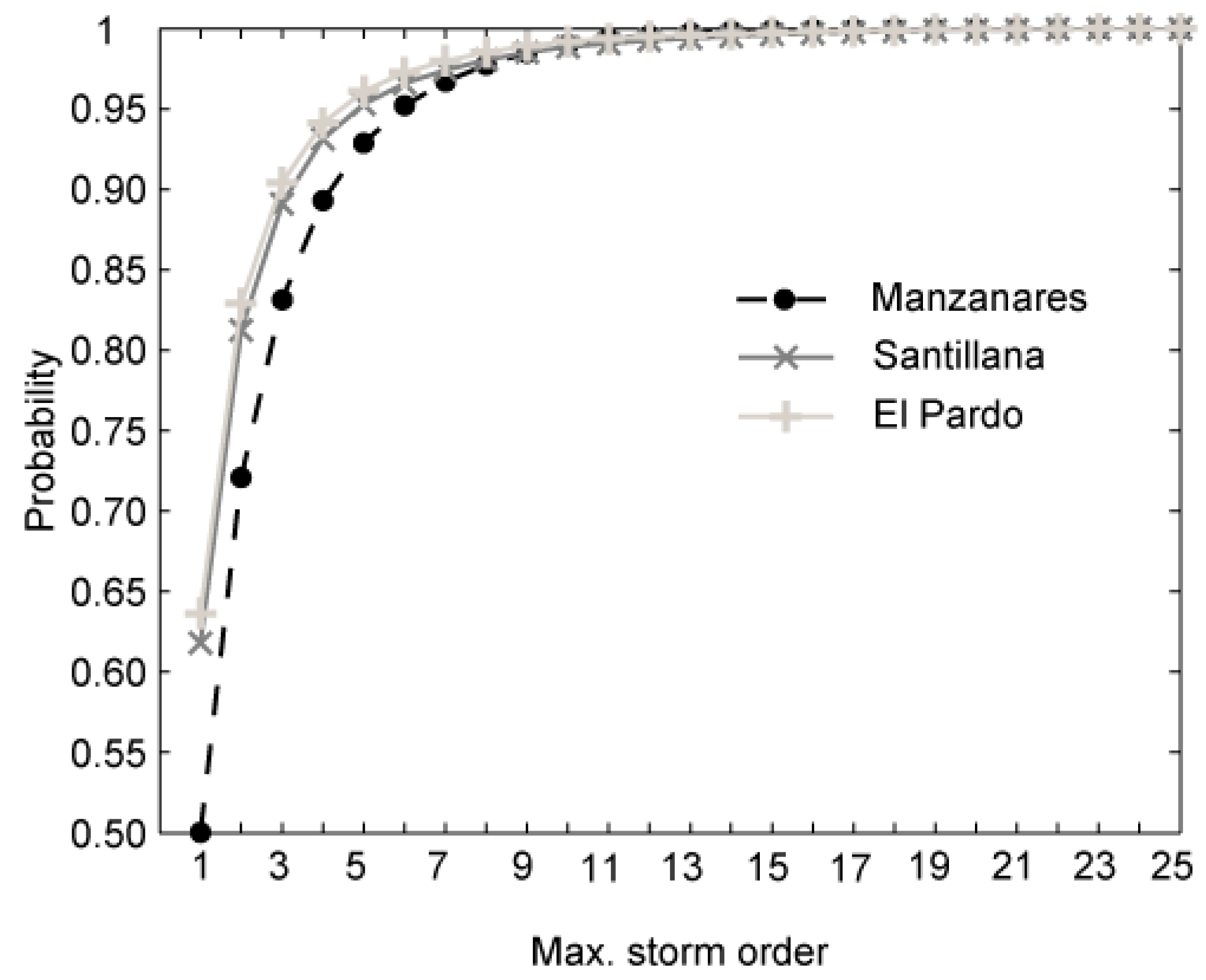
- Considering the criterion of the total rainfall depth to define when one storm is larger than another, a strong correlation was found between this criterion and the corresponding peak flow. Considering the three largest storms each year, the probability of achieving the maximum annual peak flow ranges between 83% and 92% depending on the analyzed basin.
- The flood frequency curve for high return period (50 ≤ return period ≤ 1000 years) generated by considering the three largest storms each year can be estimated with a difference lower than 3% regarding the reference flood frequency curve.
- By using the largest storm each year, for return periods higher than 10 years, the derived flood frequency curve determines which storms of order 1 show a difference lower than 10% regarding the reference flood frequency curve (considering all the identified storms).
- Basins with larger catchment areas would require more annual largest storms than in smaller basins in order to achieve the maximum peak flow each year.
- Considering the three largest storms each year, the probability of achieving simultaneously a hydrograph with the maximum annual peak flow and the maximum annual volume for a return period higher than 100 years is 94%, the return period being calculated from the maximum annual peak flows series. If we calculated the return period from the maximum annual hydrograph volume series, the probability would increase to 98%.
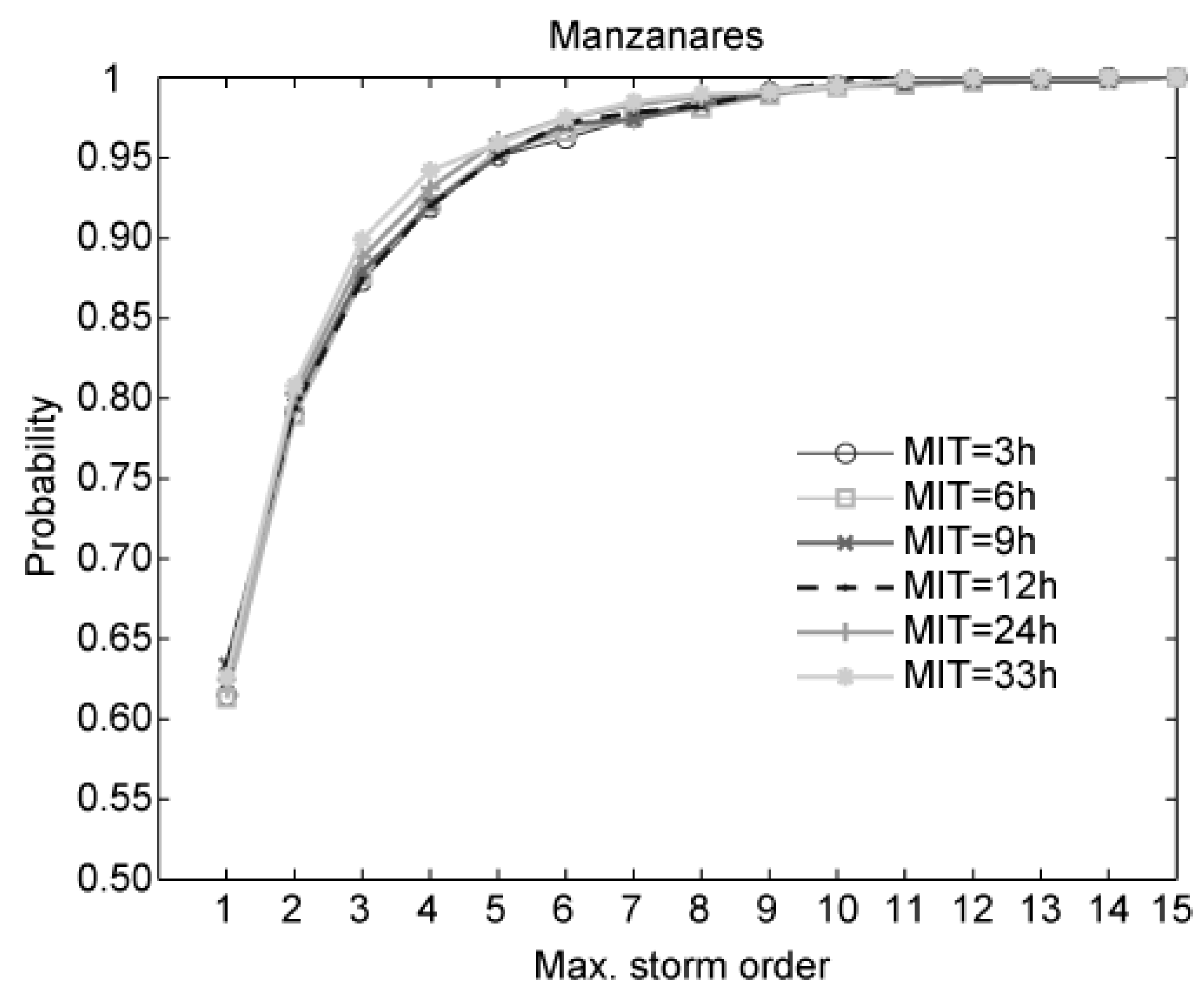
- The inter-storm time shows low influence on determining the minimum number of largest storms to be considered for achieving the maximum annually peak flow. Considering a wide range of inter-storm time (3 to 33 h) for the identification of storm events, the difference of the probability of including the maximum peak flow for a specific number of storms considered each year is lower than 3% in all cases.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CF | Cumulative frequency distribution |
| CV | Coefficient of variation |
| FFCi | Peak-flow frequency curve considering the i largest storms of each year |
| FFCR | Reference peak-flow frequency curve considering a maximum of 25 largest storms of each year |
| IDF | Intensity–Duration–Frequency curves |
| MIT | Minimum inter-event time (hours) |
| NS | Nash–Sutcliffe coefficient |
| RF | Relative frequency distribution |
| Rq | Ratio between the FFCs for different maximum storm orders and the reference FFCR |
| Tr | Return period (years) |
References
- Smith, A.; Sampson, C.; Bates, P. Regional flood frequency analysis at the global scale. Water Resour. Res. 2015, 51, 539–553. [Google Scholar]
- Botto, A.; Ganora, D.; Laio, F.; Claps, P. Uncertainty compliant design flood estimation. Water Resour. Res. 2014, 50, 4242–4253. [Google Scholar] [CrossRef]
- Nguyen, C.; Gaume, E.; Payrastre, O. Regional flood frequency analyses involving extraordinary flood events at ungauged sites: Further developments and validations. J. Hydrol. 2014, 508, 385–396. [Google Scholar] [CrossRef]
- Laio, F.; Ganora, D.; Claps, P.; Galeati, G. Spatially smooth regional estimation of the flood frequency curve (with uncertainty). J. Hydrol. 2011, 408, 67–77. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G. Flood frequency hydrology: 1. Temporal, spatial, and causal expansion of information. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Goñi, M.; López, J.J.; Gimena, F.N. Reservoir rainfall–runoff geomorphological model. I: Application and parameter analysis. Hydrol. Process. 2013, 27, 477–488. [Google Scholar] [CrossRef]
- Goñi, M.; López, J.J.; Gimena, F.N. Reservoir rainfall-runoff geomorphological model. II: Analysis, calibration and validation. Hydrol. Process. 2013, 27, 489–504. [Google Scholar] [CrossRef]
- Hadadin, N. Evaluation of several techniques for estimating storm water runoff in arid watersheds. Environ. Earth Sci. 2012, 69, 1773–1782. [Google Scholar] [CrossRef]
- Beven, K.J. Rainfall-Runoff Modelling: The Primer, 2nd ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2008; p. 488. [Google Scholar]
- Singh, V.P.; Frevert, D.K. Mathematical Models of Small Watershed Hydrology and Applications; Water Resources Publication: Highlands Ranch, CO, USA, 2002; p. 950. [Google Scholar]
- Singh, V.P.; Frevert, D.K. Mathematical Models of Large Watershed Hydrology; Water Resources Publication: Highlands Ranch, CO, USA, 2002; p. 891. [Google Scholar]
- Raines, T.; Valdés, J. Estimation of flood frequencies for ungaged catchments. J. Hydraul. Eng. 1993, 119, 1138–1154. [Google Scholar] [CrossRef]
- Hadadin, N. Modeling of Rainfall-Runoff Relationship in Semi-Arid Watershed in the Central Region of Jordan. Jordan J. Civ. Eng. 2016, 10, 209–218. [Google Scholar] [CrossRef]
- Blazkova, S.; Beven, K. A limits of acceptability approach to model evaluation and uncertainty estimation in flood frequency estimation by continuous simulation: Skalka catchment, Czech Republic. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Samuel, J.M.; Sivapalan, M. Effects of multiscale rainfall variability on flood frequency: Comparative multisite analysis of dominant runoff processes. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Aronica, G.; Candela, A. Derivation of flood frequency curves in poorly gauged Mediterranean catchments using a simple stochastic hydrological rainfall-runoff model. J. Hydrol. 2007, 347, 132–142. [Google Scholar] [CrossRef]
- Arnaud, P.; Lavabre, J. Coupled rainfall model and discharge model for flood frequency estimation. Water Resour. Res. 2002, 38. [Google Scholar] [CrossRef]
- Loukas, A. Flood frequency estimation by a derived distribution procedure. J. Hydrol. 2002, 255, 69–89. [Google Scholar] [CrossRef]
- Rahman, A.; Weinmann, P.E.; Hoang, T.M.T.; Laurenson, E.M. Monte Carlo simulation of flood frequency curves from rainfall. J. Hydrol. 2002, 256, 196–210. [Google Scholar] [CrossRef]
- Wagener, T.; Wheater, H.S.; Gupta, H.V. Rainfall-Runoff Modelling in Gauged and Ungauged Catchments; Imperial College Press: London, UK, 2004; p. 332. [Google Scholar]
- Berthet, L.; Andréassian, V.; Perrin, C.; Javelle, P. How crucial is it to account for the antecedent moisture conditions in flood forecasting? Comparison of event-based and continuous approaches on 178 catchments. Hydrol. Earth Syst. Sci. 2009, 13, 819–831. [Google Scholar] [CrossRef]
- Sivapalan, M.; Wood, E.; Beven, K. On hydrologic similarity: 3. A dimensionless flood frequency model using a generalized geomorphic unit hydrograph and partial area runoff generation. Water Resour. Res. 1990, 26, 43–58. [Google Scholar] [CrossRef]
- Natural Environment Research Council (NERC). Flood Studies Report; Natural Environment Research Council (NERC): London, UK, 1975. [Google Scholar]
- Flores-Montoya, I.; Sordo-Ward, A.; Mediero, L.; Garrote, L. Fully stochastic distributed methodology for multivariate flood frequency analysis. Water 2016, 8. [Google Scholar] [CrossRef]
- De Michele, C.; Salvadori, G. On the derived flood frequency distribution: Analytical formulation and the influence of antecedent soil moisture condition. J. Hydrol. 2002, 262, 245–258. [Google Scholar] [CrossRef]
- Silveira, L.; Charbonier, F.; Genta, J. The antecedent soil moisture condition of the curve number procedure. Hydrol. Sci. J. 2000, 45, 3–12. [Google Scholar] [CrossRef]
- Sordo-Ward, A.; Bianucci, P.; Garrote, L.; Granados, A. How safe is hydrologic infrastructure design? Analysis of factors affecting extreme flood estimation. J. Hydrol. Eng. 2014, 19. [Google Scholar] [CrossRef]
- Viglione, A.; Blöschl, G. On the role of storm duration in the mapping of rainfall to flood return periods. Hydrol. Earth Syst. Sci. 2009, 13, 205–216. [Google Scholar] [CrossRef]
- Alfieri, L.; Laio, F.; Claps, P. A simulation experiment for optimal design hyetograph selection. Hydrol. Process. 2008, 22, 813–820. [Google Scholar] [CrossRef]
- Blazkova, S.; Beven, K. Flood frequency estimation by continuous simulation of subcatchment rainfalls and discharges with the aim of improving dam safety assessment in a large basin in the Czech Republic. J. Hydrol. 2004, 292, 153–172. [Google Scholar] [CrossRef]
- Bocchiola, D.; Rosso, R. Use of a derived distribution approach for extreme floods design: A case study in Italy. Adv. Water Resour. 2009, 32, 1284–1296. [Google Scholar] [CrossRef]
- Andres-Domenech, I.; Montanari, A.; Marco, J.B. Stochastic rainfall analysis for storm tank performance evaluation. Hydrol. Earth Syst. Sci. 2010, 14, 1221–1232. [Google Scholar] [CrossRef]
- Arnaud, P.; Fine, J.; Lavabre, J. An hourly rainfall generation model applicable to all types of climate. Atmos. Res. 2007, 85, 230–242. [Google Scholar] [CrossRef]
- Wilks, D.; Wilby, R. The weather generation game: A stochastic weather models. Prog. Phys. Geogr. 1999, 23, 329–357. [Google Scholar] [CrossRef]
- Candela, A.; Brigandì, G.; Aronica, G.T. Estimation of synthetic flood design hydrographs using a distributed rainfall–runoff model coupled with a copula-based single storm rainfall generator. Nat. Hazards Earth Syst. Sci. 2014, 14, 1819–1833. [Google Scholar] [CrossRef]
- Vandenberghe, S.; Verhoest, N.E.C.; Buyse, E.; De Baets, B. A stochastic design rainfall generator based on copulas and mass curves. Hydrol. Earth Syst. Sci. 2010, 14, 2429–2442. [Google Scholar] [CrossRef]
- Kao, S.C.; Govindaraju, R.S. Trivariate statistical analysis of extreme rainfall events via the Plackett family of copulas. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Grimaldi, S.; Serinaldi, F. Design hyetograph analysis with 3-copula function. J. Sci. Hydrol. 2006, 51, 223–238. [Google Scholar] [CrossRef]
- Burton, A.; Fowler, H.J.; Kilsby, C.G.; O’Connell, P.E. A stochastic model for the spatial-temporal simulation of nonhomogeneous rainfall occurrence and amounts. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Burton, A.; Kilsby, C.G.; Fowler, H.J.; Cowpertwait, P.S.P.; O’Connell, P.E. RainSim: A spatial–temporal stochastic rainfall modelling system. Environ. Model. Softw. 2008, 23, 1356–1369. [Google Scholar] [CrossRef]
- Salsón, S.; García-Bartual, R. A space-time rainfall generator for highly convective Mediterranean rainstorms. Nat. Hazards Earth Syst. Sci. 2003, 3, 103–114. [Google Scholar] [CrossRef]
- Cowpertwait, P.; Kilsby, C.; O’Connell, P. A space-time Neyman-Scott model of rainfall: Empirical analysis of extremes. Water Resour. Res. 2002, 38. [Google Scholar] [CrossRef]
- Dunkerley, D. Identifying individual rain events from pluviograph records: A review with analysis of data from an Australian dryland site. J. Hydrol. Process. 2008, 22, 5024–5036. [Google Scholar] [CrossRef]
- Aryal, R.K.; Furumai, H.; Nakajima, F.; Jinadasa, H.K.P.K. The role of inter-event time definition and recovery of initial/depression loss for the accuracy in quantitative simulations of highway runoff. Urban Water J. 2007, 4, 53–58. [Google Scholar] [CrossRef]
- Bonta, J.V.; Rao, A.R. Factors affecting the identification of independent storm events. J. Hydrol. 1988, 98, 275–293. [Google Scholar] [CrossRef]
- Restrepo-Posada, P.J.; Eagleson, P.S. Identification of inde-pendent rainstorms. J. Hydrol. 1982, 55, 303–319. [Google Scholar] [CrossRef]
- Duan, Q.; Soorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Campo, M.A.; Sordo, A.; González-Zeas, D.; Cirauqui, D.; Garrote, L.; López, J. Application of a stochastic rainfall model in flood risk assessment. Geophys. Res. Abstr. 2009, 11. [Google Scholar] [CrossRef]
- Sordo-Ward, A.; Garrote, L.; Bejarano, M.D.; Castillo, L.G. Extreme flood abatement in large dams with gate-controlled spillways. J. Hydrol. 2013, 498, 113–123. [Google Scholar] [CrossRef]
- Sordo-Ward, A.; Garrote, L.; Martín-Carrasco, F.; Bejarano, M.D. Extreme flood abatement in large dams with fixed-crest spillways. J. Hydrol. 2012, 466–467, 60–72. [Google Scholar] [CrossRef]
- Bianucci, P.; Sordo-Ward, A.; Moralo, J.; Garrote, L. Probabilistic-Multi objective Comparison of User-Defined Operating Rules. Case Study: Hydropower Dam in Spain. Water 2015, 7, 956–974. [Google Scholar] [CrossRef]
- United States Soil Conservation Service. National Engineering Handbook, Section 4: Hydrology; U.S. Department of Agriculture: Washington, DC, USA, 1972; p. 127.
- McCarthy, G.T. The Unit Hydrograph and Flood Routing; US Army Corps of Engineers: Providence, RI, USA, 1939. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models, Part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Flores-Montoya, I.; Requena, A.; Sordo-Ward, A.; Mediero, L.; Garrote, L. Deriving bivariate flood frequency distributions for dam safety evaluation. In Proceedings of the 8th International Conference of European Water Resources Association (EWRA): Water Resources Management in an Interdisciplinary and Changing Context, Porto, Portugal, 26–29 June 2013.
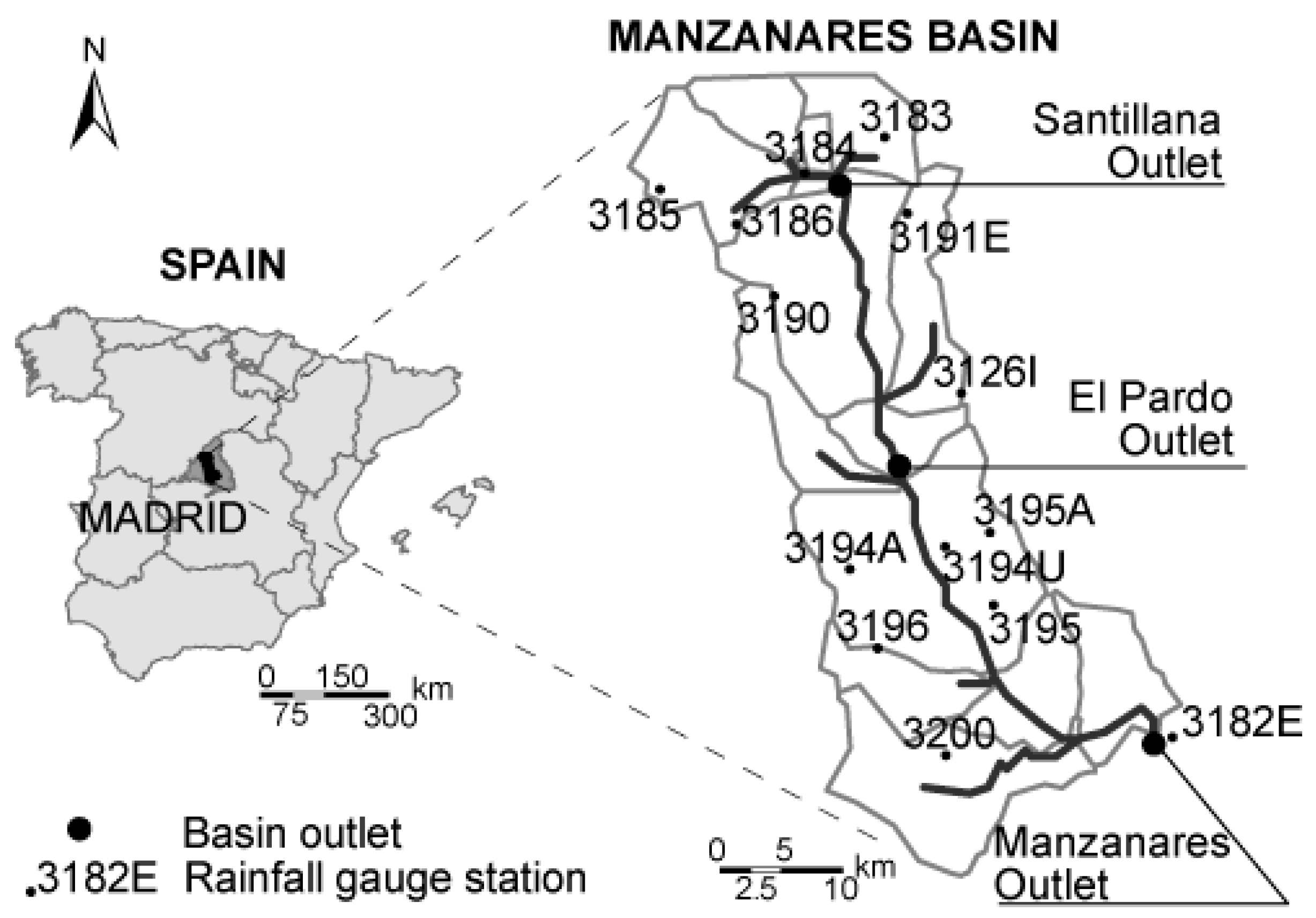

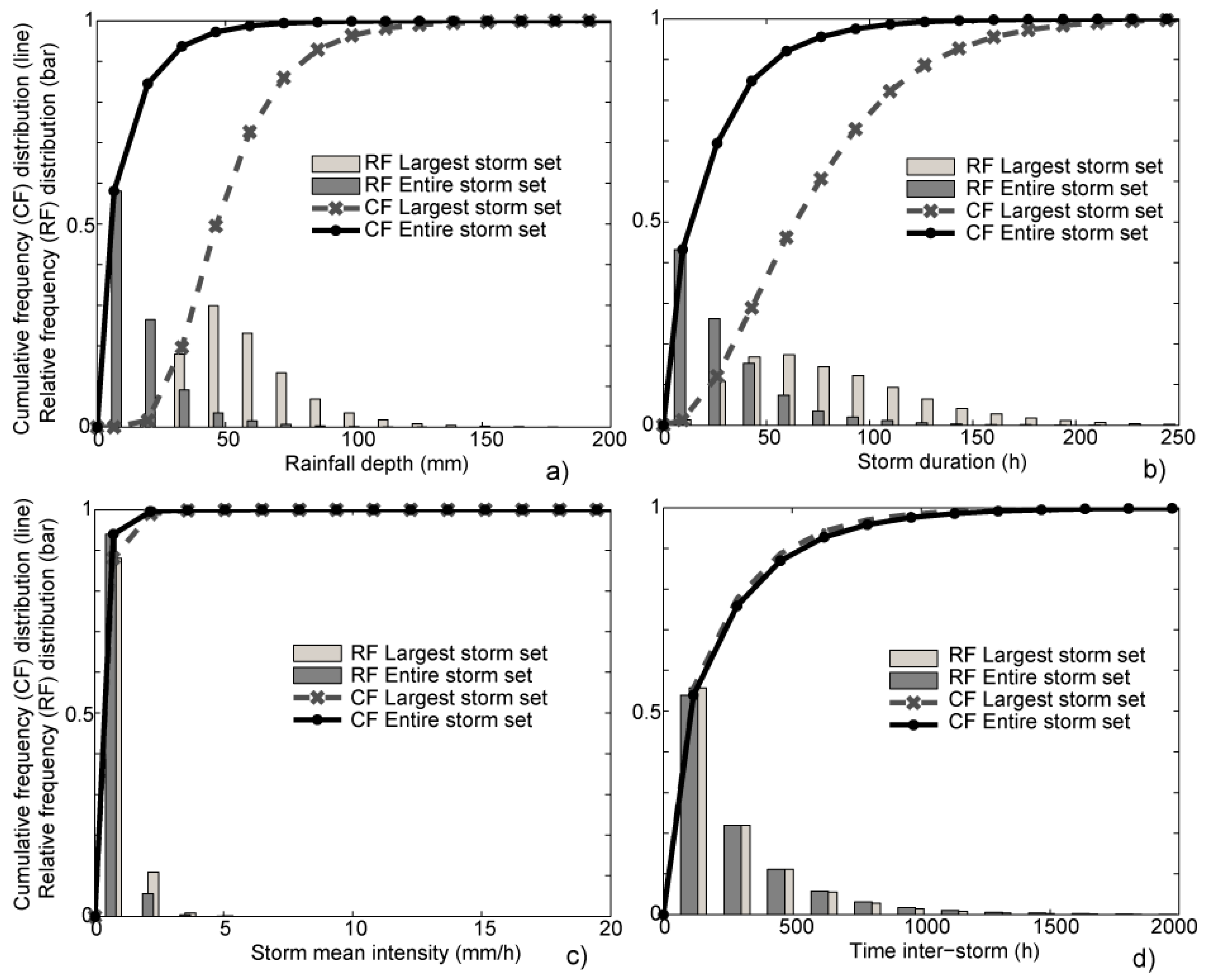
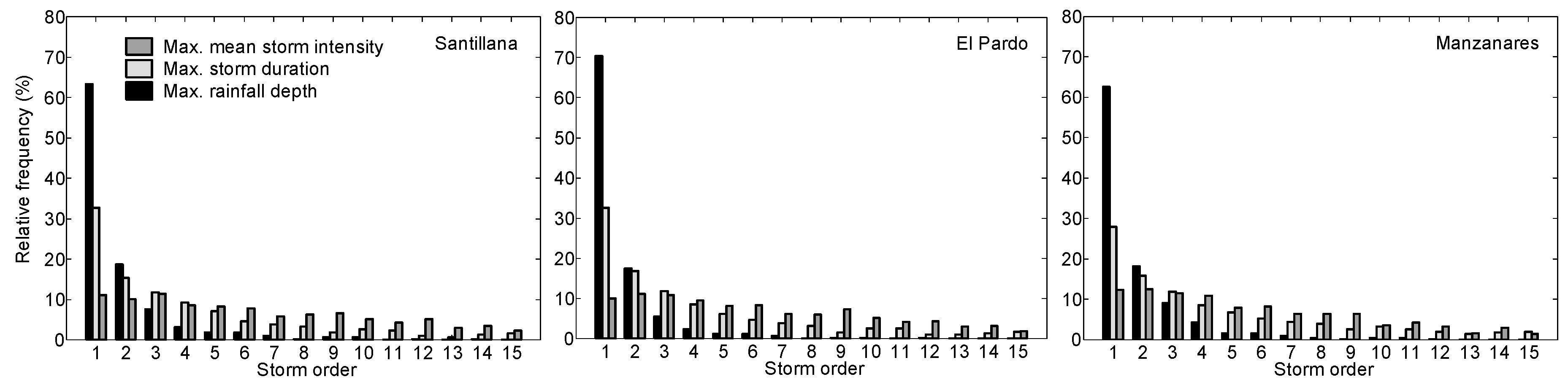
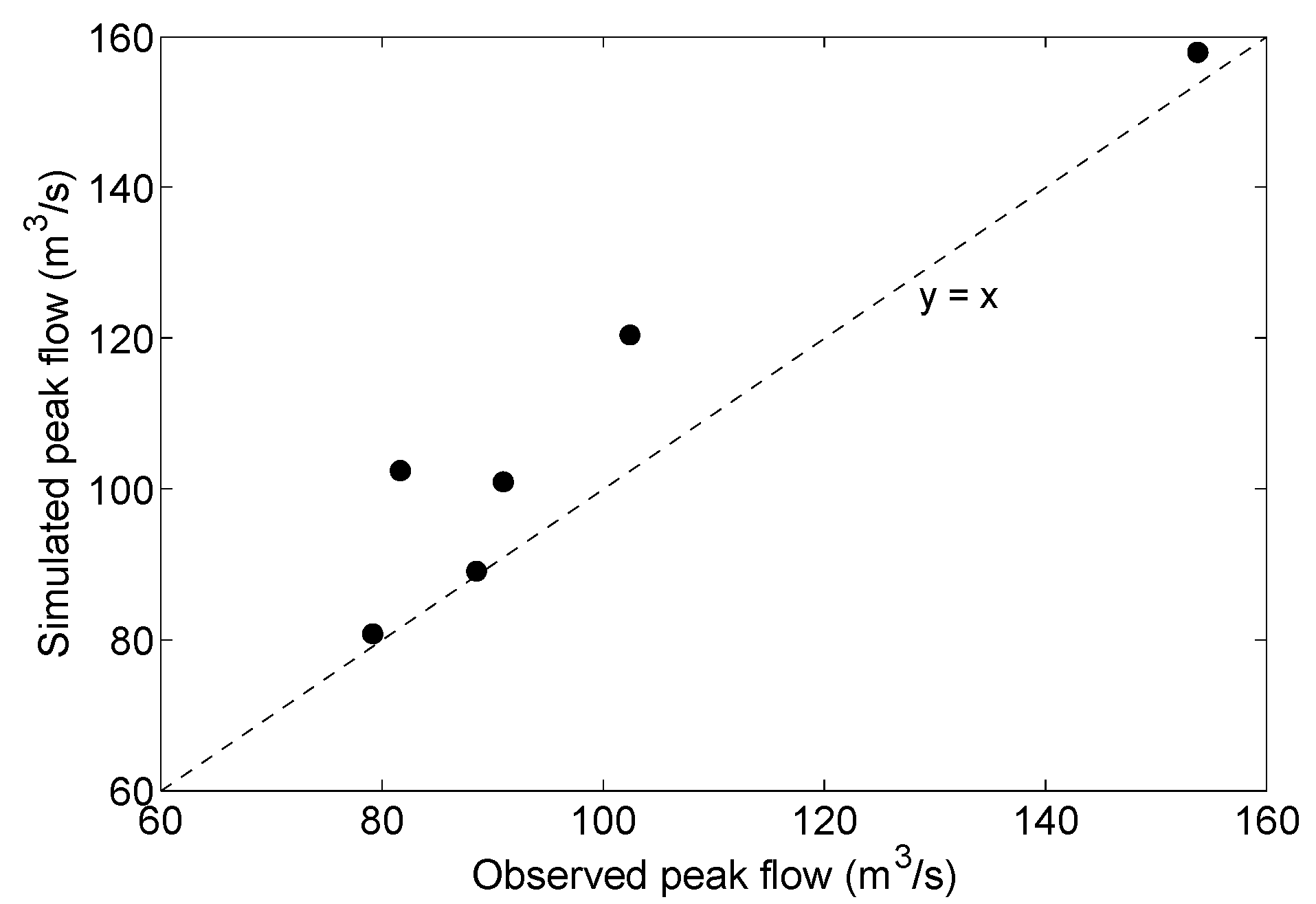
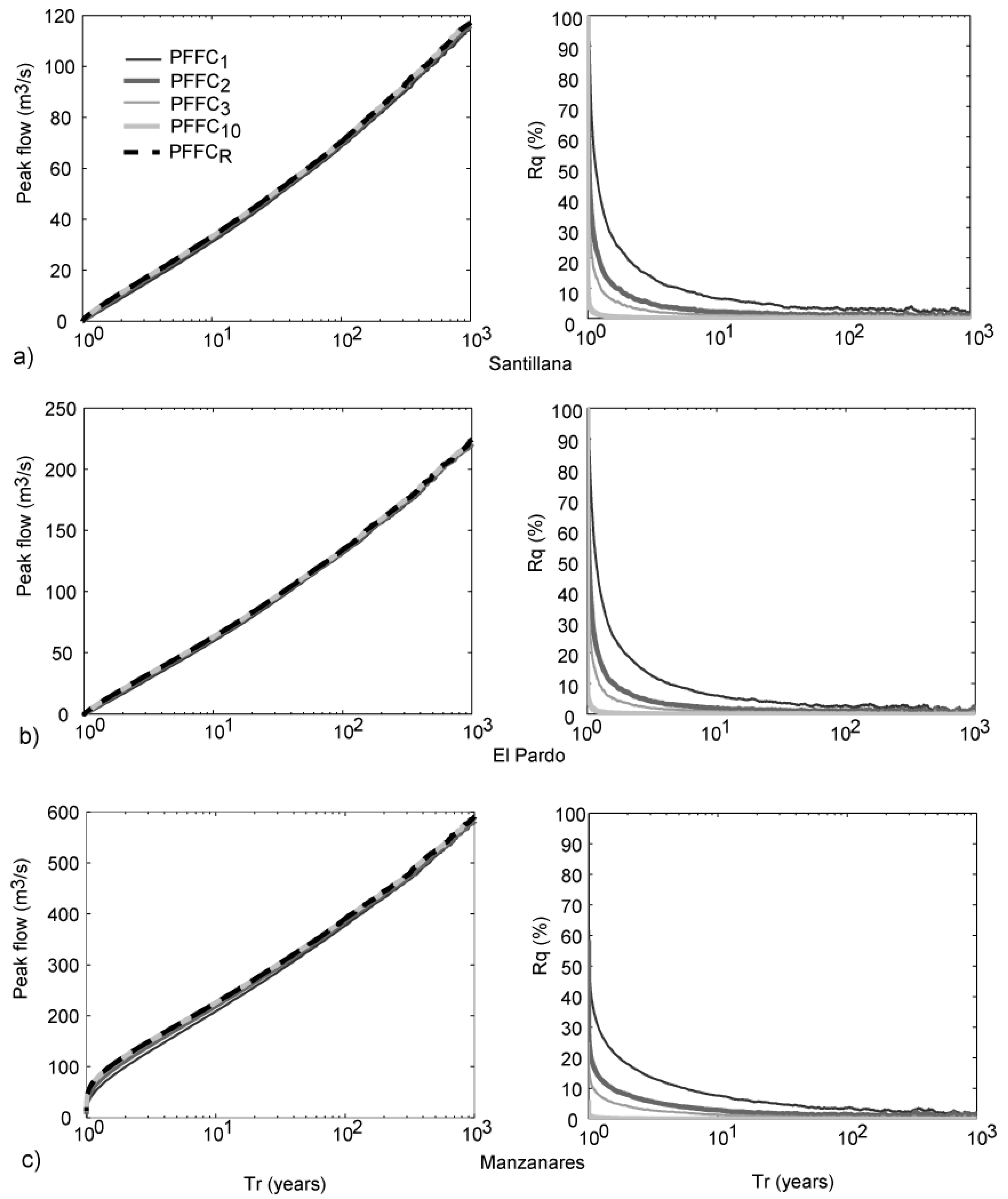
| Name | Area (km2) | N° Sub-Basins | Sub-Basin Area (km2) | |
|---|---|---|---|---|
| Average | Range | |||
| Santillana | 211 | 5 | 42 | 6.4/89 |
| Pardo | 495 | 7 | 71 | 6.4/196 |
| Manzanares | 1294 | 14 | 92 | 6.4/255 |
| Probability (%) | Tr (Years) | Maximum Storm Order to Be Considered | ||
|---|---|---|---|---|
| Santillana | Pardo | Manzanares | ||
| 95/99 | 1 ≤ Tr < 10 | 5/11 | 4/9 | 6/10 |
| 95/99 | 10 ≤ Tr < 50 | 2/5 | 2/5 | 3/6 |
| 95/99 | 50 ≤ Tr ≤ 100 | 2/5 | 2/5 | 3/6 |
| 95/99 | 100 ≤ Tr ≤ 500 | 2/5 | 2/5 | 2/5 |
| 95/99 | 500 ≤ Tr ≤ 1000 | 1/2 | 2/3 | 2/5 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sordo-Ward, A.; Bianucci, P.; Garrote, L.; Granados, A. The Influence of the Annual Number of Storms on the Derivation of the Flood Frequency Curve through Event-Based Simulation. Water 2016, 8, 335. https://doi.org/10.3390/w8080335
Sordo-Ward A, Bianucci P, Garrote L, Granados A. The Influence of the Annual Number of Storms on the Derivation of the Flood Frequency Curve through Event-Based Simulation. Water. 2016; 8(8):335. https://doi.org/10.3390/w8080335
Chicago/Turabian StyleSordo-Ward, Alvaro, Paola Bianucci, Luis Garrote, and Alfredo Granados. 2016. "The Influence of the Annual Number of Storms on the Derivation of the Flood Frequency Curve through Event-Based Simulation" Water 8, no. 8: 335. https://doi.org/10.3390/w8080335
APA StyleSordo-Ward, A., Bianucci, P., Garrote, L., & Granados, A. (2016). The Influence of the Annual Number of Storms on the Derivation of the Flood Frequency Curve through Event-Based Simulation. Water, 8(8), 335. https://doi.org/10.3390/w8080335








