1. Introduction
Recently, hydrological modelling has become more relevant, based on the technological advances that provide better spatial and temporal resolution. However, the ability to incorporate spatially distributed digital data is in turn hindered by the scarcity of datasets at the same scale. Alternatively, remote sensing techniques make it possible to rapidly obtain information for large areas by means of sensors operating in several spectral bands, mounted on aircraft or in satellites [
1,
2]. The above-described situation has opened the door to the use of big data [
3], applying it to hydrological models to make them more robust. Nevertheless, modelling spatially distributed hydrological processes can be challenging, particularly in strongly heterogeneous (soil use variation, slope, coverage) urbanised areas. Multiple interactions occur in urban areas between structures and the drainage system (for waste water and storm water) at various temporal and spatial scales, which in turn increase the data requirements and complexity [
4]. These complexities, in addition to the aforementioned data scarcity at the required level, make it difficult to define a universal methodology to reproduce urban flows at the catchment scale. Therefore, there is a growing need to assess the effect of uncertainty in results derived from hydrologic modelling approaches utilised in urban environments [
5,
6].
Models of hydrological processes produced by previous researchers incorporate uncertainty from a variety of sources. This uncertainty can lead to unrealistic results because of the interaction and aggregation of known and unknown errors within the modelling process [
7]. Research must be performed to estimate these errors [
8,
9]. It is acknowledged that knowing the factors that cause the uncertainty and its propagation in the final results will facilitate reliable hydrological modelling that can be used in decision making, structure design, flood warnings and emergency actions in urban environments, see [
10].
The sources of uncertainty can be categorised as either aleatory or epistemic [
11]. On one hand, aleatory uncertainty is caused by random or stochastic characteristics of natural processes that are variable over space and time (e.g., soil moisture); such uncertainty is not reducible. On the other hand, epistemic uncertainty is error caused by poor measurement, lack of knowledge, and exclusion of the processes by poor representation in a hydrologic model. Most of the epistemic uncertainty can be addressed by increasing information and improving data quality, except those that arise from the ‘unknown unknowns’, which are irreducible [
12].
Moreover, there is also uncertainty associated with input data in the models, for example rainfall, land cover, and soil hydraulic properties [
13]. The accurate representation of the spatio-temporal variability of these quantities in the field represents a particular challenge for catchments where the information of the gauge networks is sparse [
14]. In addition, there is uncertainty in the observed data that is used for model calibration, as possible errors could arise from the measurement of flow velocity and water depth, backwater effect, changes in river cross sections and fitting rating curve.
Model structure uncertainty (uncertainty in the parameter definition) is recognised as a main contributor to model prediction uncertainty; however, it is often ignored [
15]. Model structure uncertainty can be reduced if the dominant processes are sufficiently represented [
16]; however, it cannot be completely eliminated, even if the input data are error-free, because catchment responses are averaged over space and time [
17].
The influence of model structure uncertainty is exacerbated in catchments where knowledge of the dominant processes is limited and the choice of model structure is restricted by data availability. In data scarce catchments, model structure uncertainty is addressed by incorporating model structure into parameter uncertainty, which may be achieved by an analysis of the regression residuals between model predictions and observations [
18]. However, the problem of reducing model parameter uncertainty is further complicated by interactions between parameters, leading to difficulties in identifying optimal parameter values. Equifinality is considered as different combinations of parameter values that have performed equally well in terms of the selected objective functions [
19,
20,
21,
22].
Evaluation of the uncertainty in predictions from hydrological models applied to urban catchments has been limited [
23,
24]; as a consequence, such evaluations have not been widely used in engineering practice. In this sense, the transference between the knowledge fields of different uncertainty analysis approaches is required for the uncertainty characterisation in the hydrological modelling of urban basins [
25].
Among the most widely used uncertainty analysis techniques are the Generalised Likelihood Uncertainty Estimation (GLUE) approach [
11], the classical Bayesian Monte Carlo (i.e., Bayesian inference approach) [
23] and those that include the optimisation algorithms SCEM-UA [
26,
27] and AMALGAM [
28].
Following [
29], GLUE ‘‘represents an extension of Bayesian or fuzzy averaging procedures to less formal likelihood or fuzzy measures.” The concept of ‘‘the less formal likelihood” represents the main element of differentiation with the Bayesian inference. Although Bayesian methods present a formal statistical framework to the treatment of parameter distributions, they require a large amount of data, making their implementation difficult in data scarce applications. In comparison with Bayesian methods, the GLUE method is easy to implement. Some researchers have adopted these methodologies for performing the uncertainty analysis of model parameters. For example, in the case of [
30], the wetland design parameters for flooding control relating the hydrological and hydraulical parameters were analysed for a better model performance. Another example is the work of Fraga et al. [
31], in which the model parameter uncertainty and its propagation from a hydrological model 1D-2D was evaluated. Similarly, the work of Sun et al. [
32] focused on the hydrological parameters uncertainty behaviour regarding the model scale (surface study detail), and the work of Zhao et al. [
33] involved an uncertainty analysis for evaluating the capability of different likelihood measures in model parameter distribution.
Because data are scarce in much of the world (especially in developing countries), the focus of research should be on the reduction of the predictive uncertainty by achieving a better understanding of processes and the quantification of uncertainty itself [
34,
35]. This can be achieved through a comparison of the different approaches in data-scarce regions.
This investigation presents a comparison of two of the most common methods used for assessing hydrological model parameter uncertainties in an urban catchment in Mexico. The methods compared are (a) the Generalised Likelihood Uncertainty Estimation (GLUE) developed by [
11]; and (b) a multialgorithm, genetically adaptive multi-objective method (AMALGAM) developed by Vrugt and Robinson [
36]. The comparison aims to show the performance of both methods in implementing a well-known open-source model (Storm Water Management Model, SWMM) in a small urban catchment, using the index of agreements as the likelihood measure. In this case, the quantification of the uncertainty is estimated from the hydrologic parameters used in the setup of the rainfall-runoff model. This application will show the advantages of implementing such an analysis in applications with limited data.
The paper is organised as follows:
Section 2 illustrates the performance methodology implemented for the comparison;
Section 3 presents the case study along with the available data and the methods implemented; and
Section 4 summarises the results and discussions. Finally,
Section 5 introduces the main conclusions derived from this work.
2. Methodology
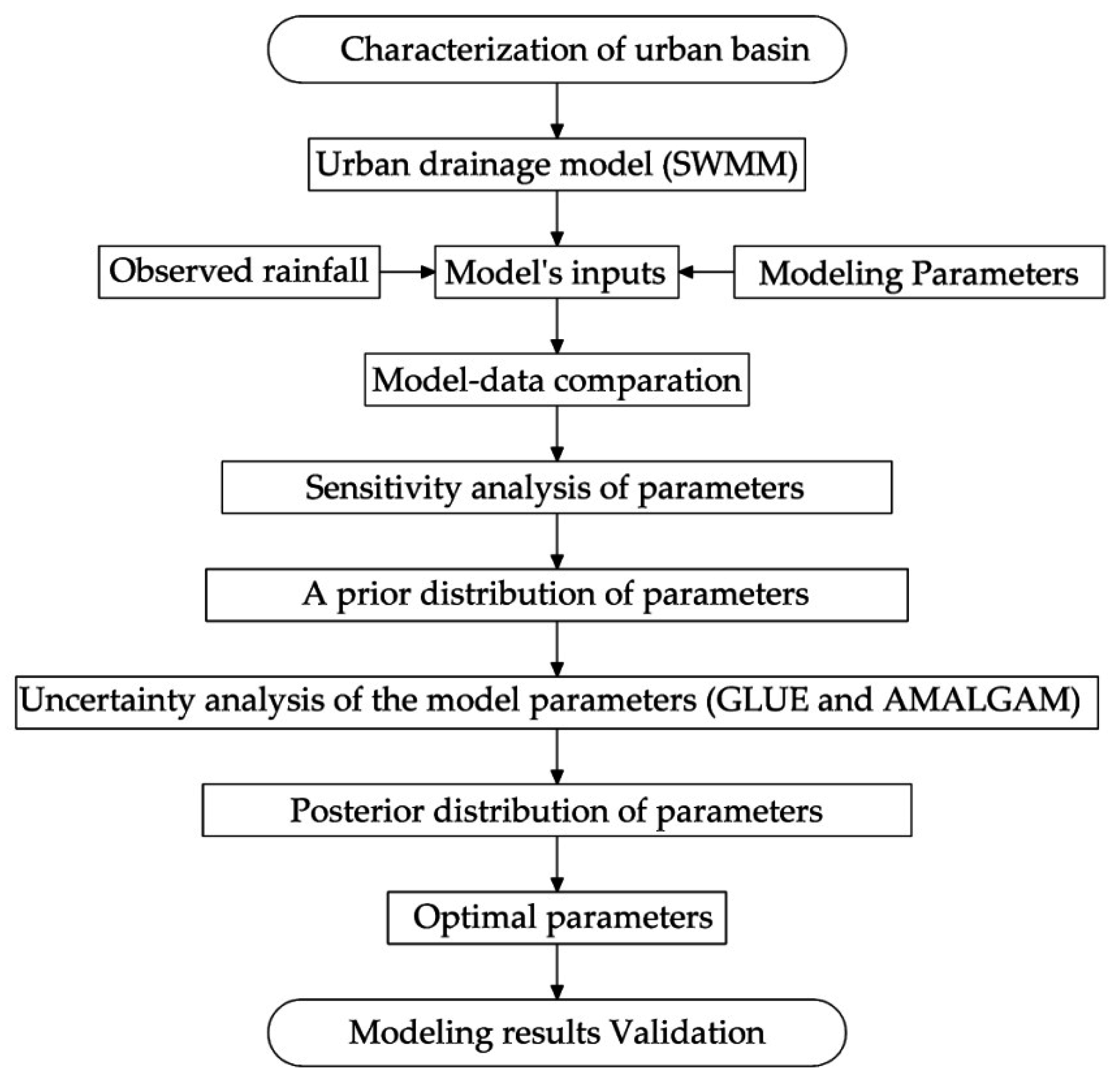
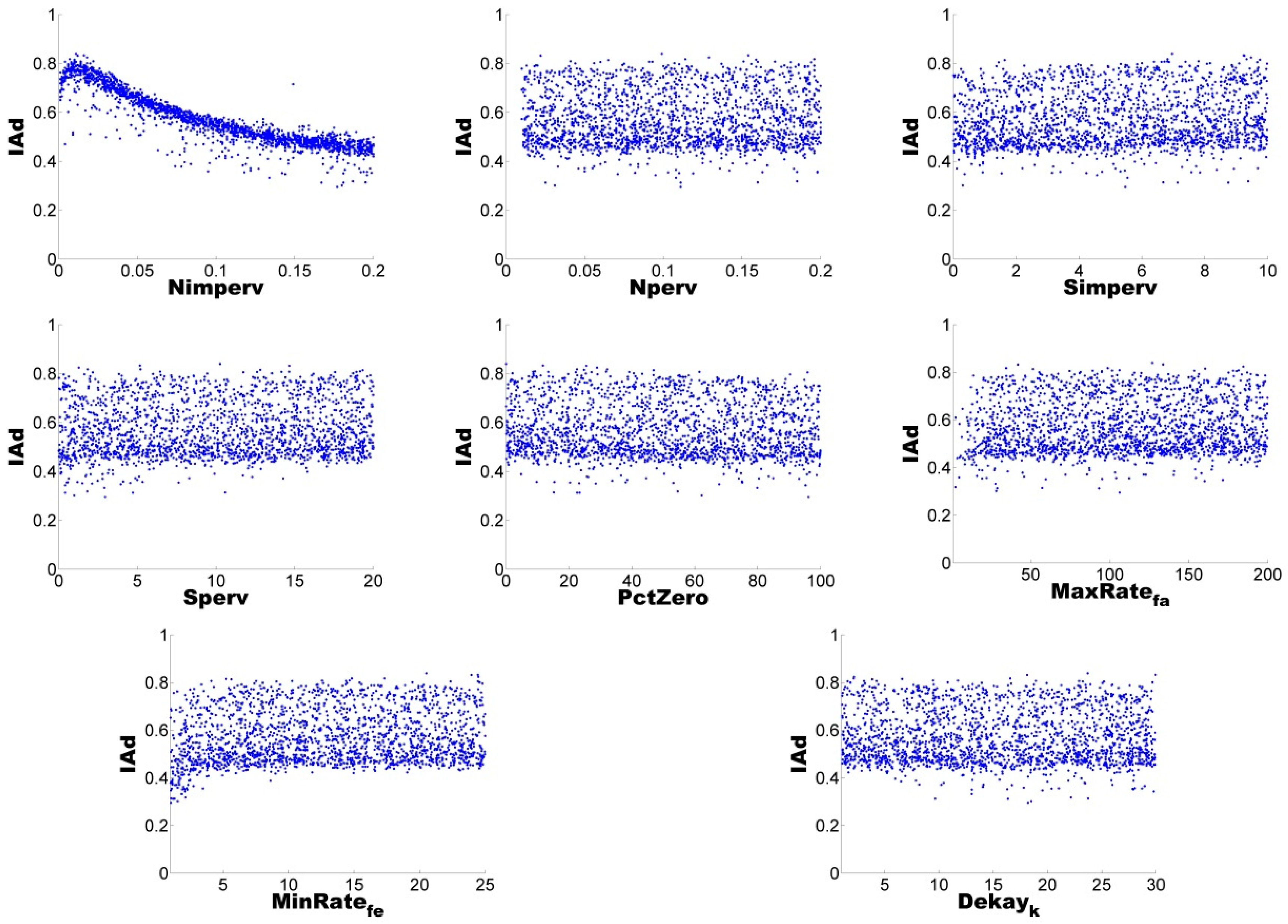
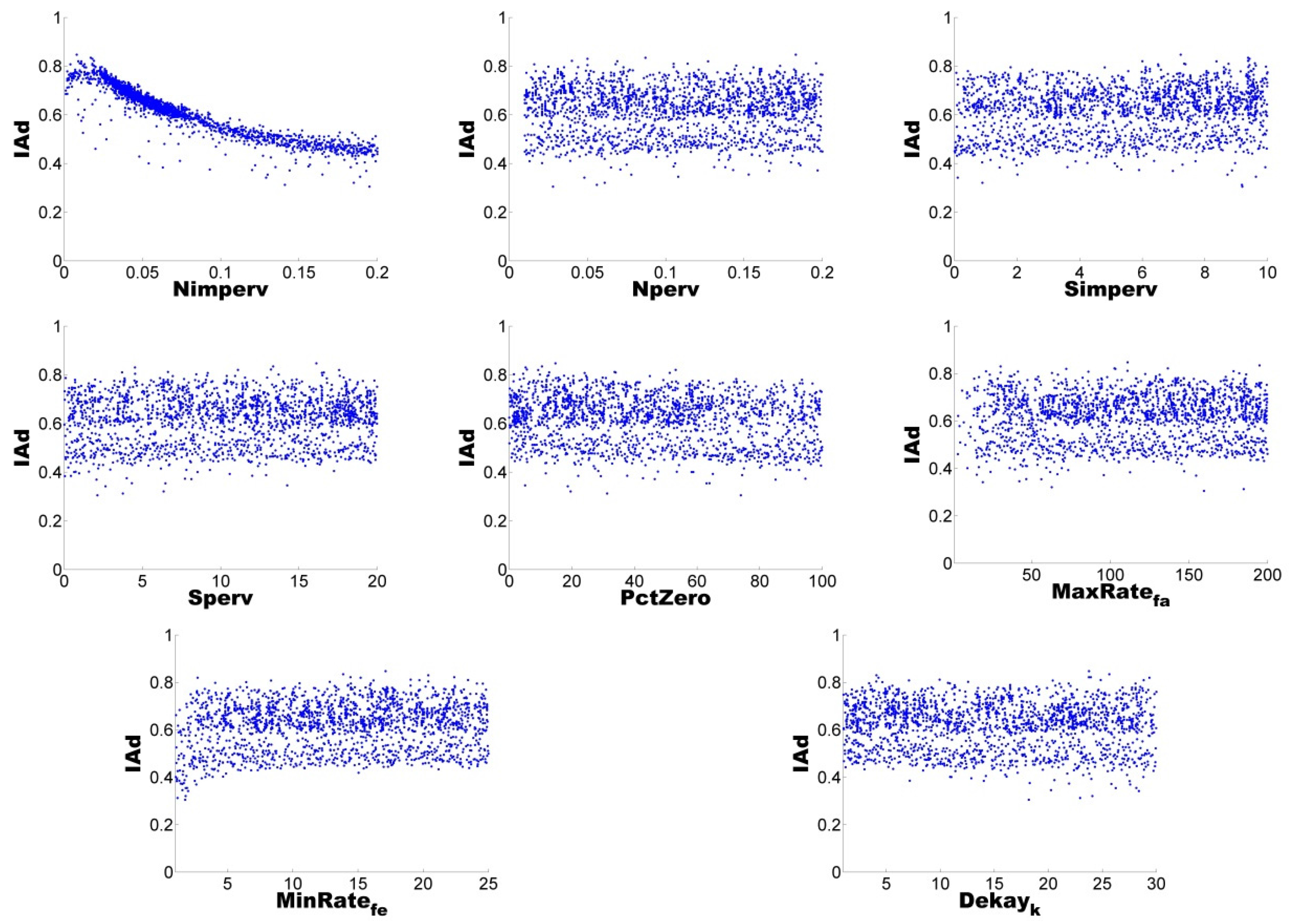
A flow chart of the methodology (shown in
Figure 1) illustrates the uncertainty analysis process, which involves the characterisation of the basin, followed by the hydrologic modelling and model-data comparison at the selected gauging station. Modelling errors for each run are evaluated and selected or discarded in relation to the defined confidence envelope. The uncertainty analysis techniques of GLUE and AMALGAM were used to quantify the uncertainties derived from the selected parameter sets. Following the work presented by Dotto et al. [
37], the results are evaluated through a measure of the model run performance through the index of agreement (IAd) and the Average Relative Interval Length (ARIL) [
38] (see Equation (1)), complemented with the evaluation of the Absolute Percentage Error (APE) (see Equation (2)). The set of “best” parameters is estimated based on the results that are within the range of 95% confidence. The ARIL coefficient is specified as follows:
where
is the number of results within the confidence band,
is the upper limit of the confidence band,
, is the lower limit of the confidence band, and
, is the observed value at the instant
i within the confidence band.
where
is the model result, and
, is the observed value at the same instant
i.
This comparison procedure between the two implemented uncertainty techniques was determined following the criteria proposed in previous investigations [
39,
40], where the performance of the model is assessed by the IAd proposed by Willmot [
41] and used by Krause et al. [
42] as a measure for the likelihood (Equation (3)), and the model prediction uncertainty is defined through the ARIL 95% probability bands (as proposed by Jin et al. [
38]).
where
is the modelling result in the instant
i,
, is the observed value in the instant
i and
is the observed average.
5. Conclusions
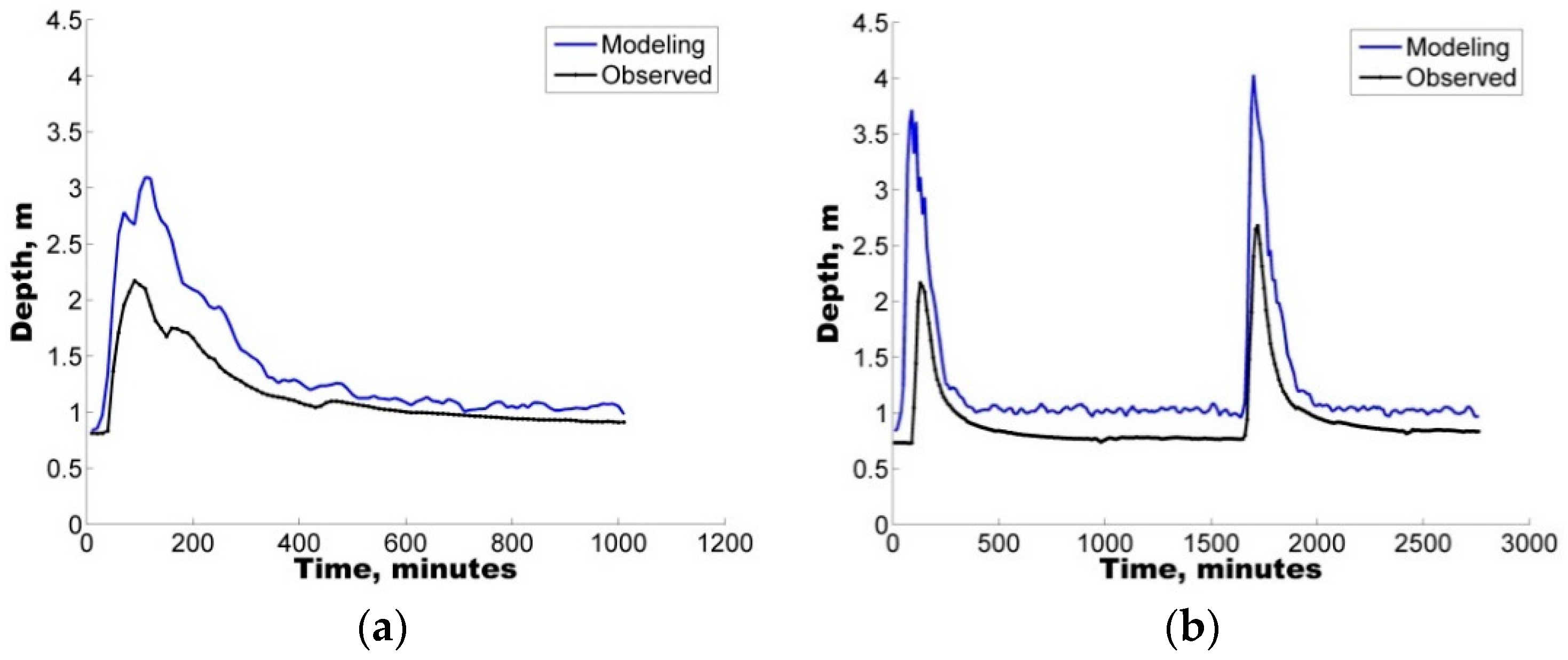
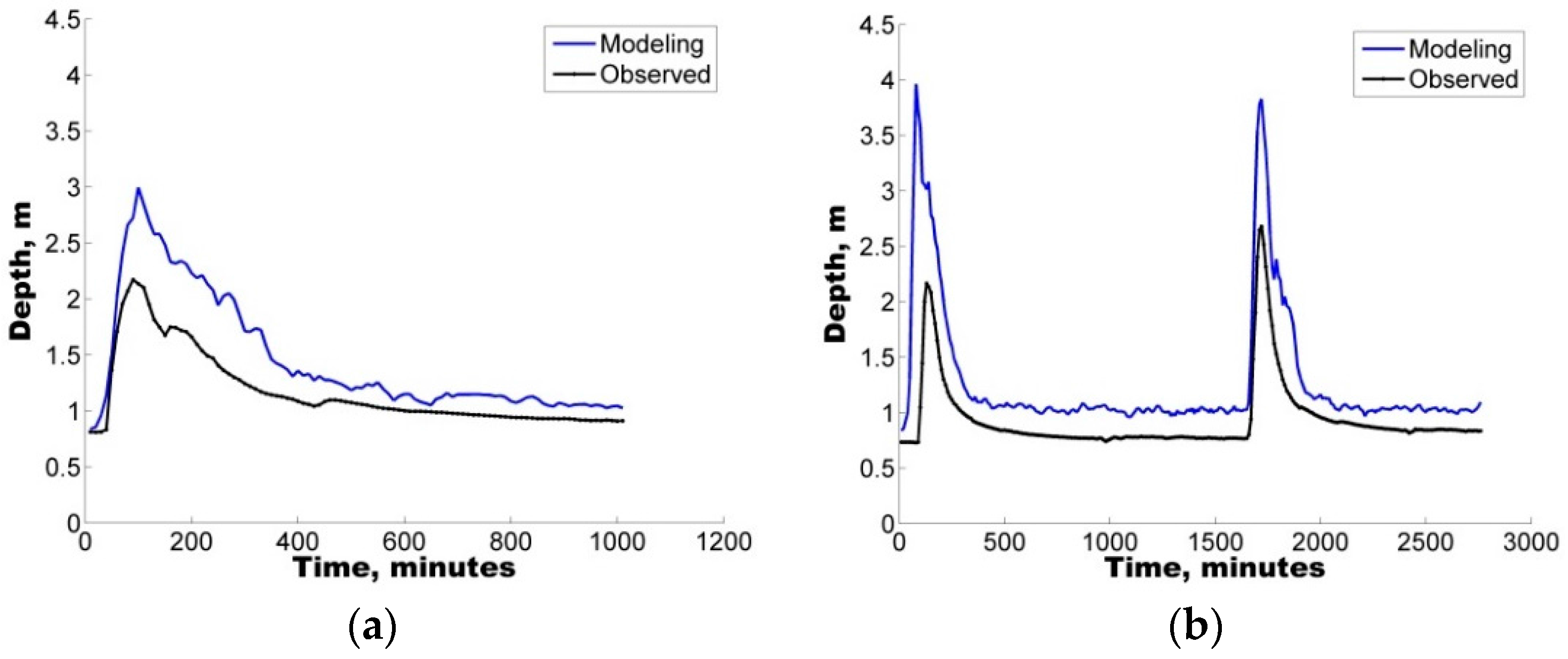
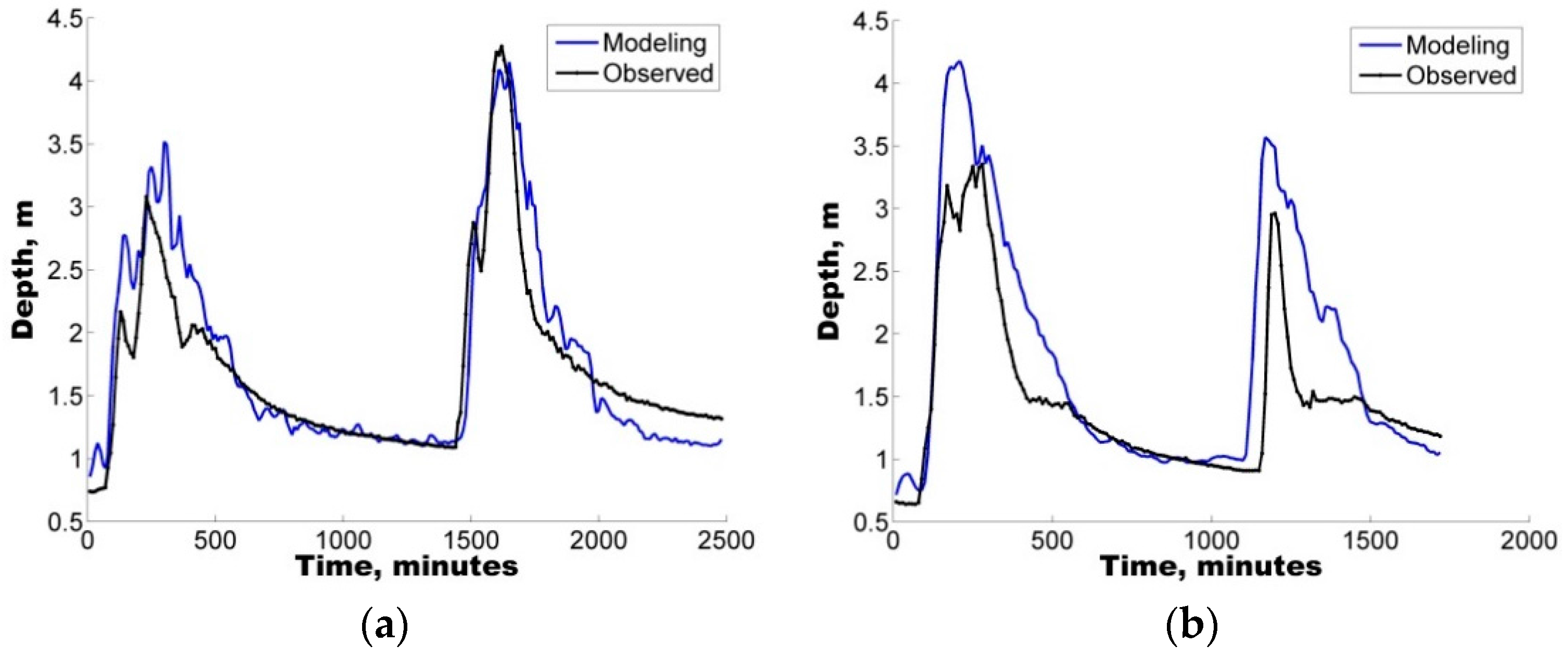
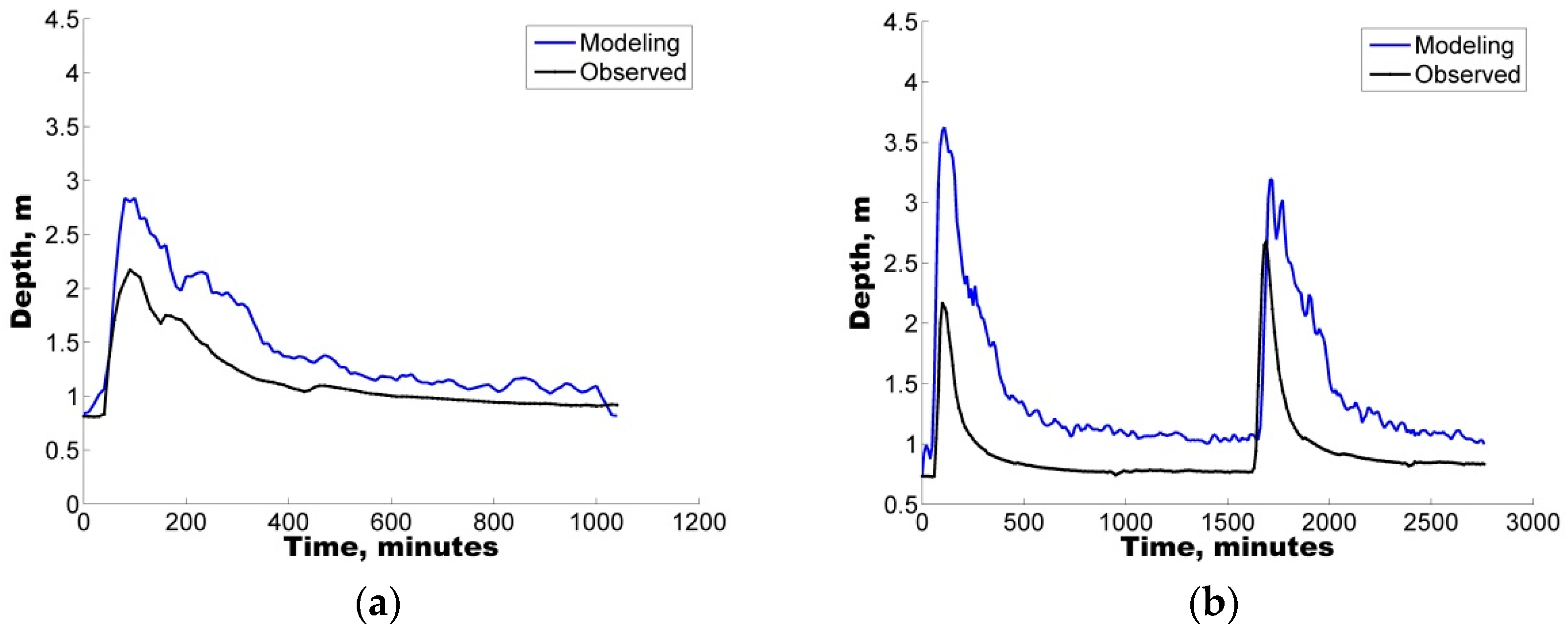
The present study represents the first effort in Mexico to highlight the significance of applying uncertainty analysis techniques to the hydrological prediction of flows in a small urban catchment by means of a well-known tool (SWMM).
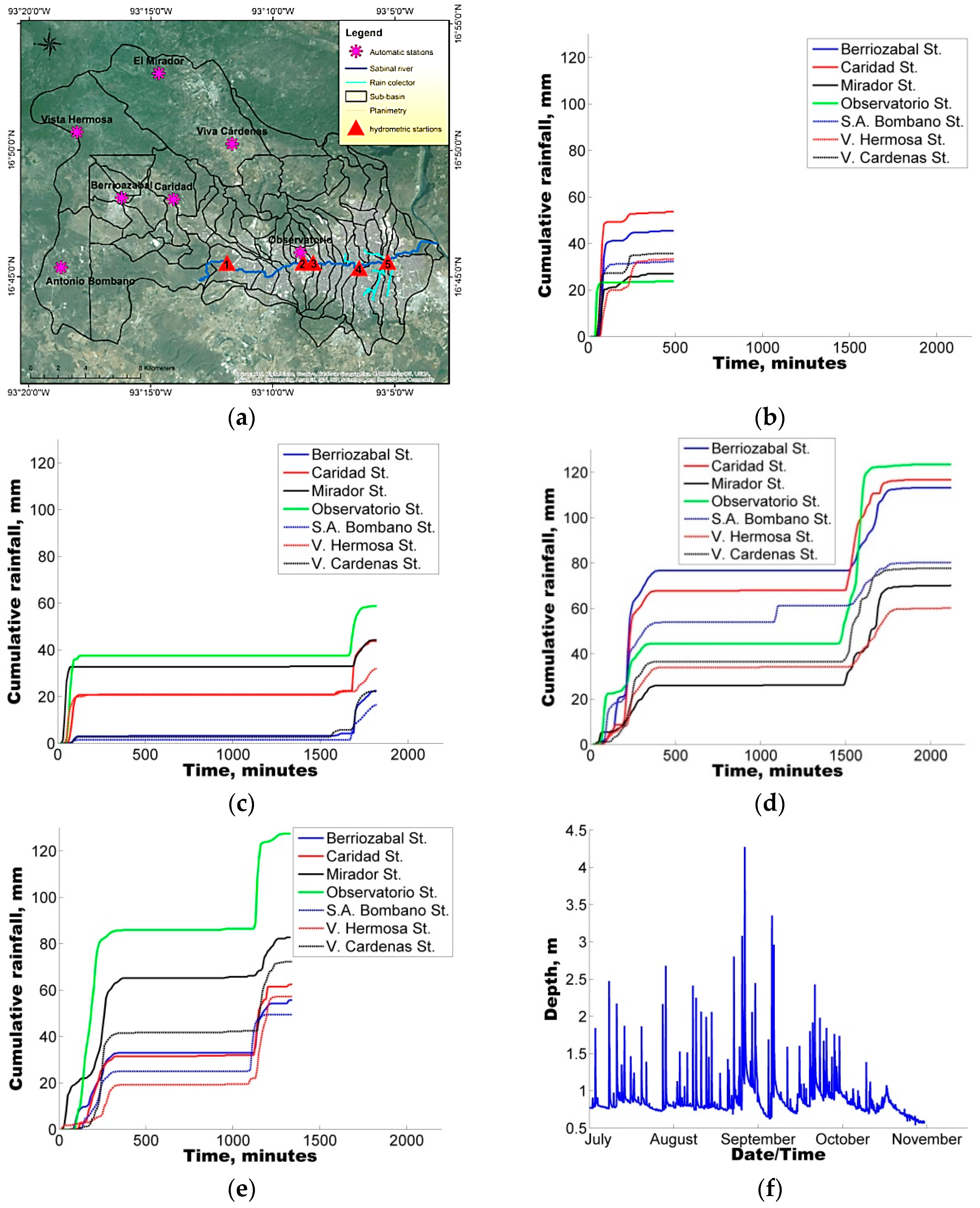
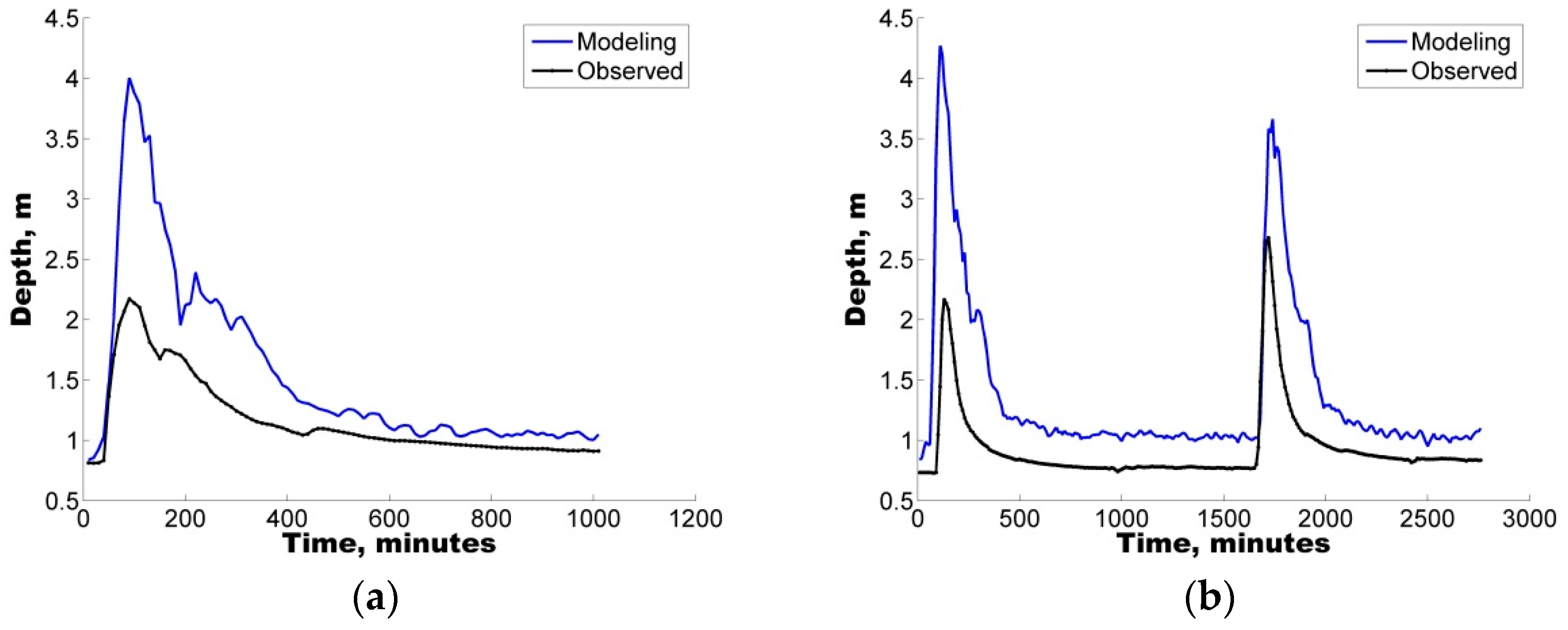
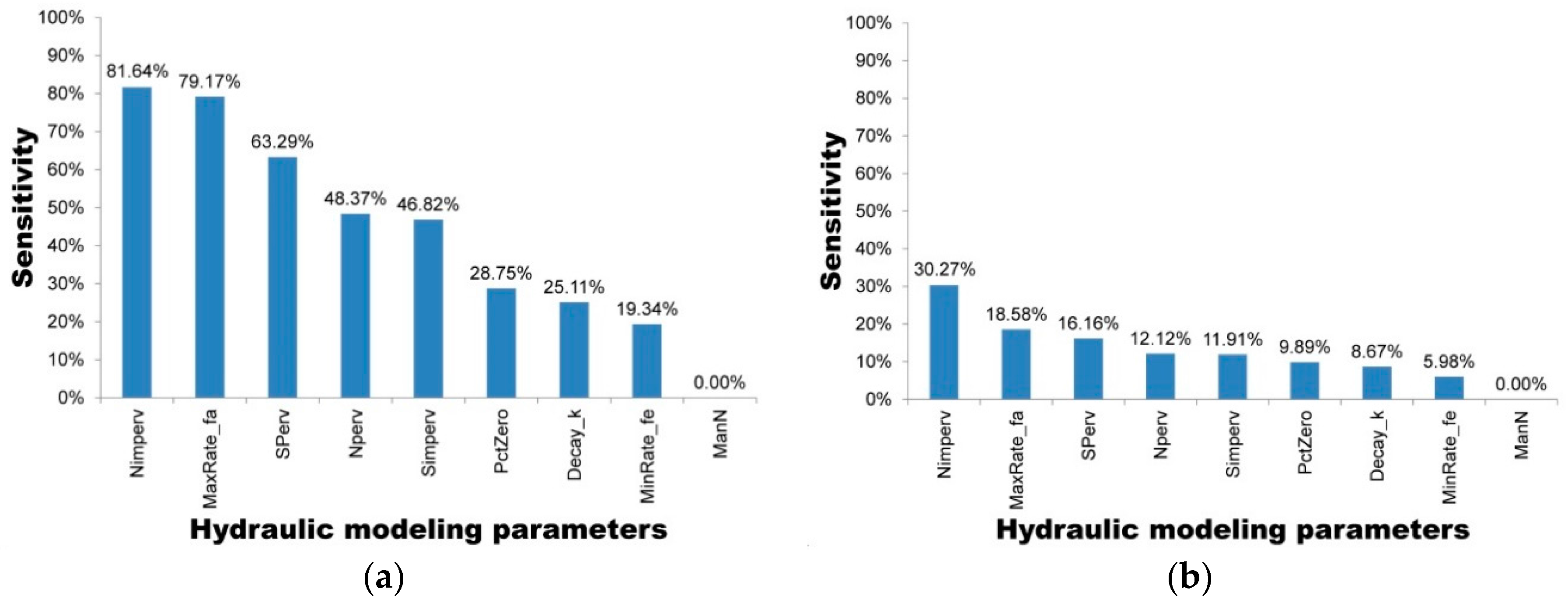
The model was first implemented in the study area followed by a sensitivity analysis of eight selected parameters. To identify the sets of parameters that allowed for a good representation of the rainfall-runoff response, four rainfall events varying from 20.0 mm to 120.2 mm were selected to ensure the applicability and reliability of the model for varying conditions from minor to major events.
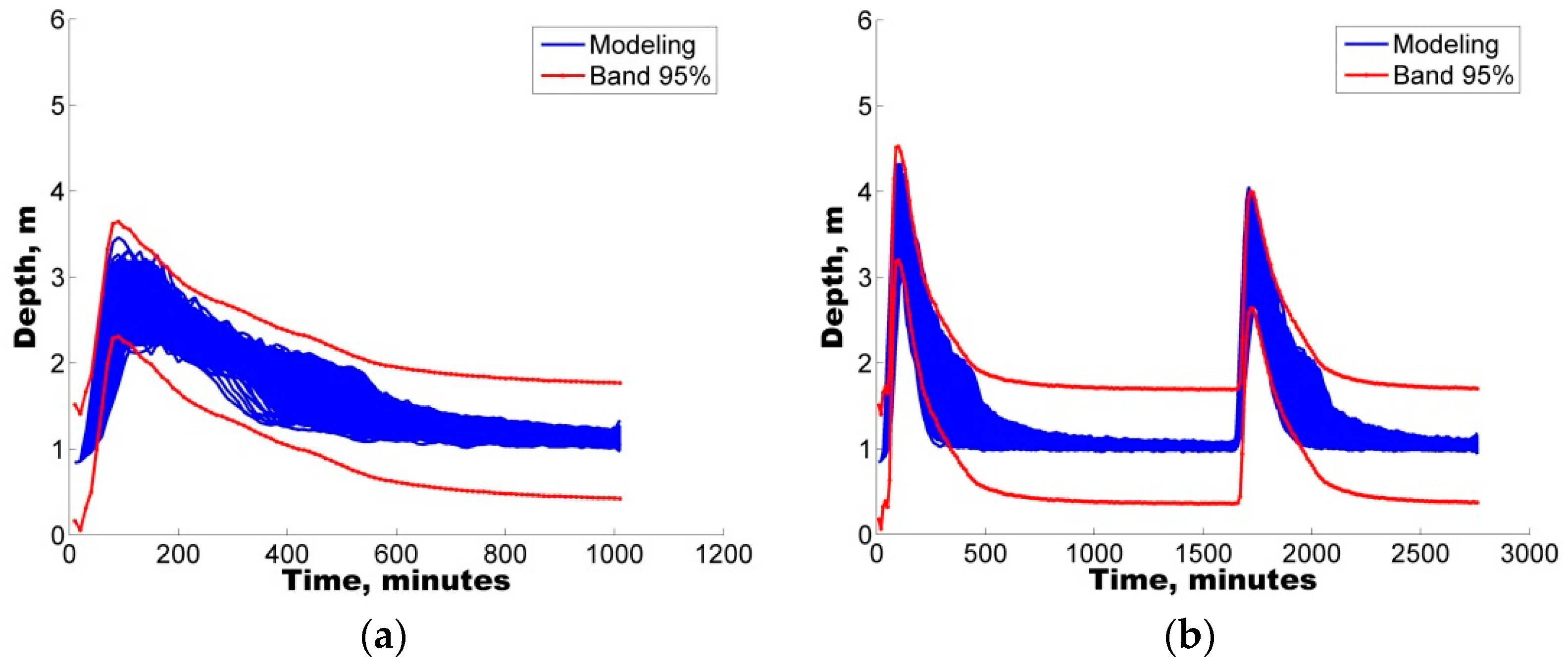
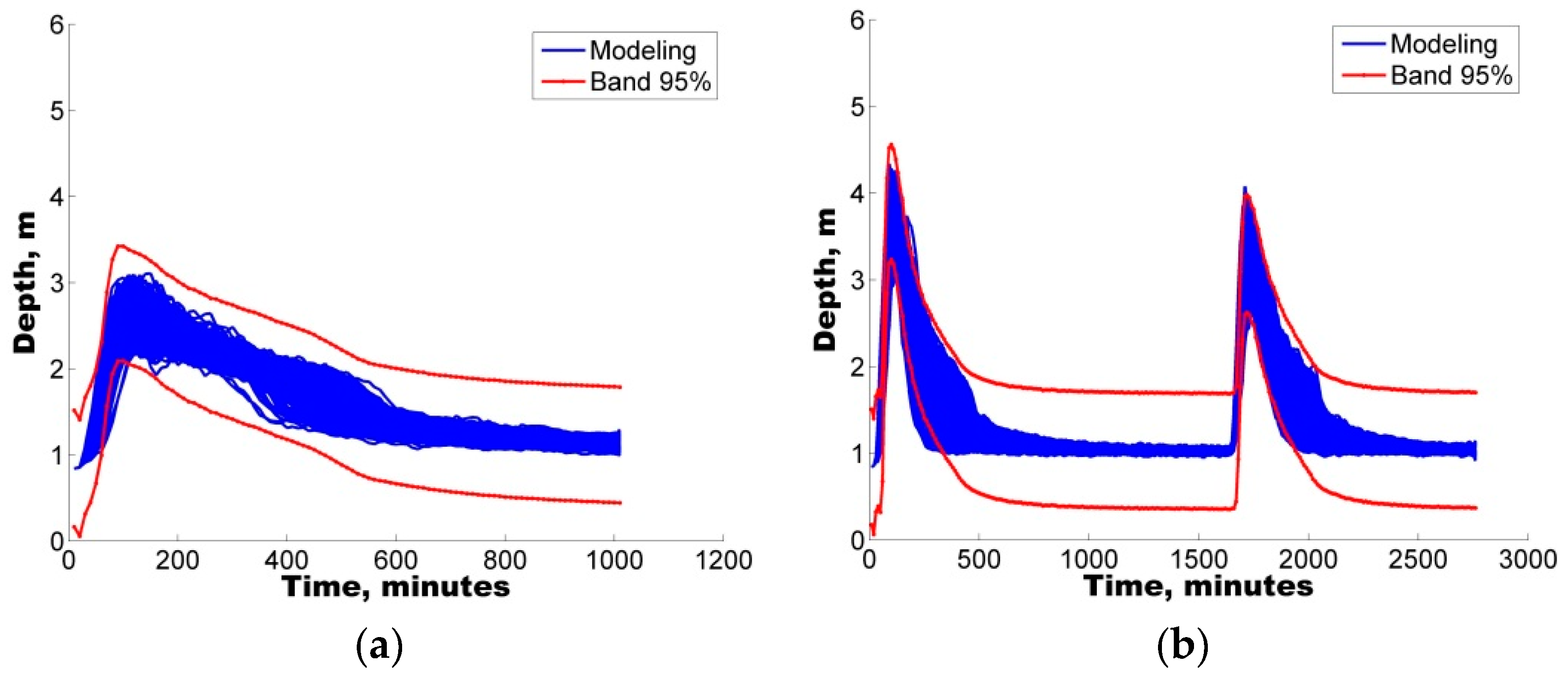
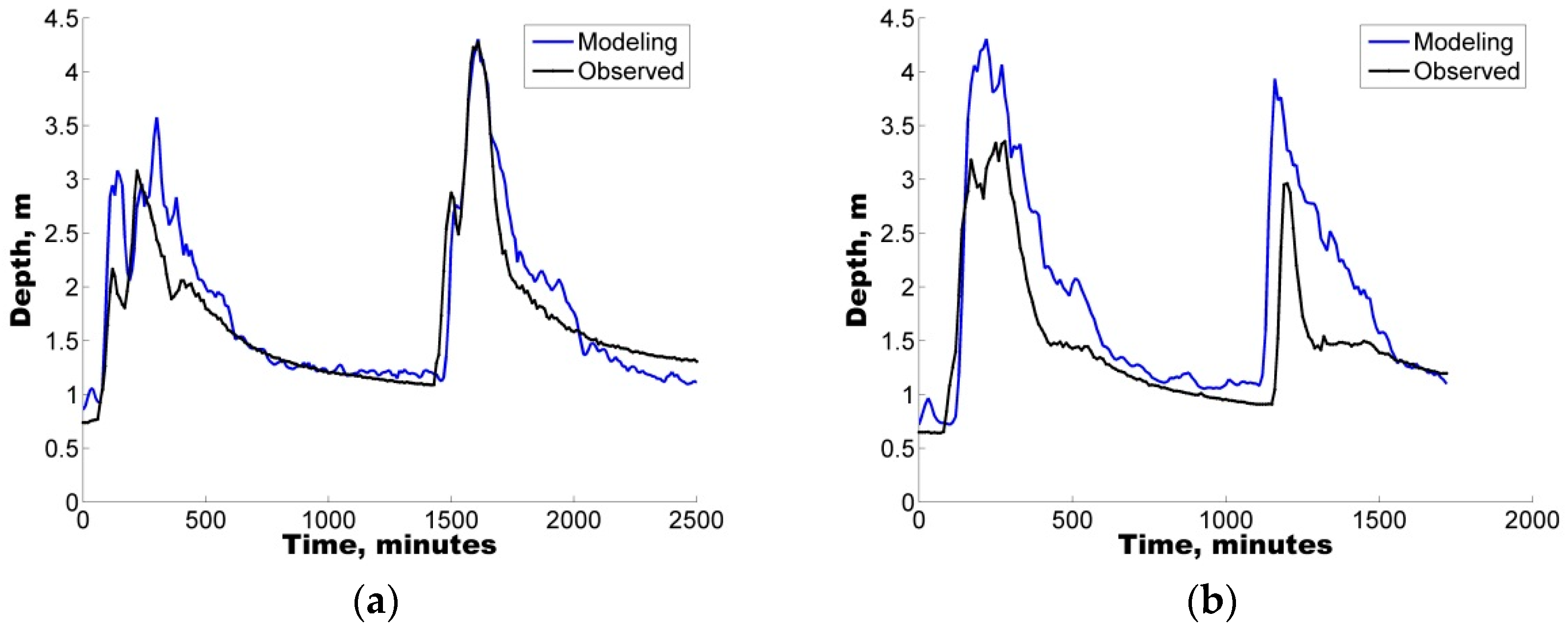
Additionally, with the purpose of quantifying the uncertainty ascribed to the definition of parameters in the hydrological model, two different uncertainty analysis techniques were also implemented, GLUE and AMALGAM. For the four selected storms, both techniques were found to generate results with similar skill (ARIL), both generating parameter sets with IAd greater than 60%, i.e., good model performance.
In all cases, the results show that hydrological predictions are more reliable when model deficiencies (e.g., parameter uncertainty) are considered. In addition to the use of the IAd, to complement the analysis, the APE values were used to select the optimal parameter sets for the calibration/validation of the study case.
Notably, an average EAP lower than 30% was observed in some of the depth sets, considering the parameter sets obtained from the uncertainty analysis. Therefore, the quantification of different error contributions enables the generation of more reliable flow predictions.
This investigation clearly shows the advantages of implementing a sensitivity analysis and uncertainty approach when modelling the rainfall-runoff response in data scarce countries. The selected approach seems to be promising with regards to the identification of the posterior parameter distributions and also elucidates the aggregation of errors within a modelling framework, suggesting the importance of parameter interaction.
Note that, in cases where data scarcity is high, the implementation of methods that enable the quantification of uncertainty in model predictions enables more transparent results that show the effects of aggregation of errors arising from different sources within a prediction. Both implemented techniques showed that there are several parameter sets that provide a good representation of the system. The ability to have an uncertainty band associated with the model predictions minimises the subjectivity associated with the predictions. Further work should be performed to investigate the impact of the initial parameter distribution on the posterior distribution generated with a Monte-Carlo procedure, particularly in cases where highly correlated parameters are present.