Evaluation of the Performance and the Predictive Capacity of Build-Up and Wash-Off Models on Different Temporal Scales
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Site and Monitoring Equipment
2.2. Data Set
2.3. Data Validation
2.3.1. Turbidity
- if the measurement is between the minimum and the maximum values given by the turbidity sensors, which are 0 and 3000, respectively;
- if the measurement is equal to the saturated value 3000;
- if the measurement is negative or equal to zero or recorded during intervention on site for maintenance operations.
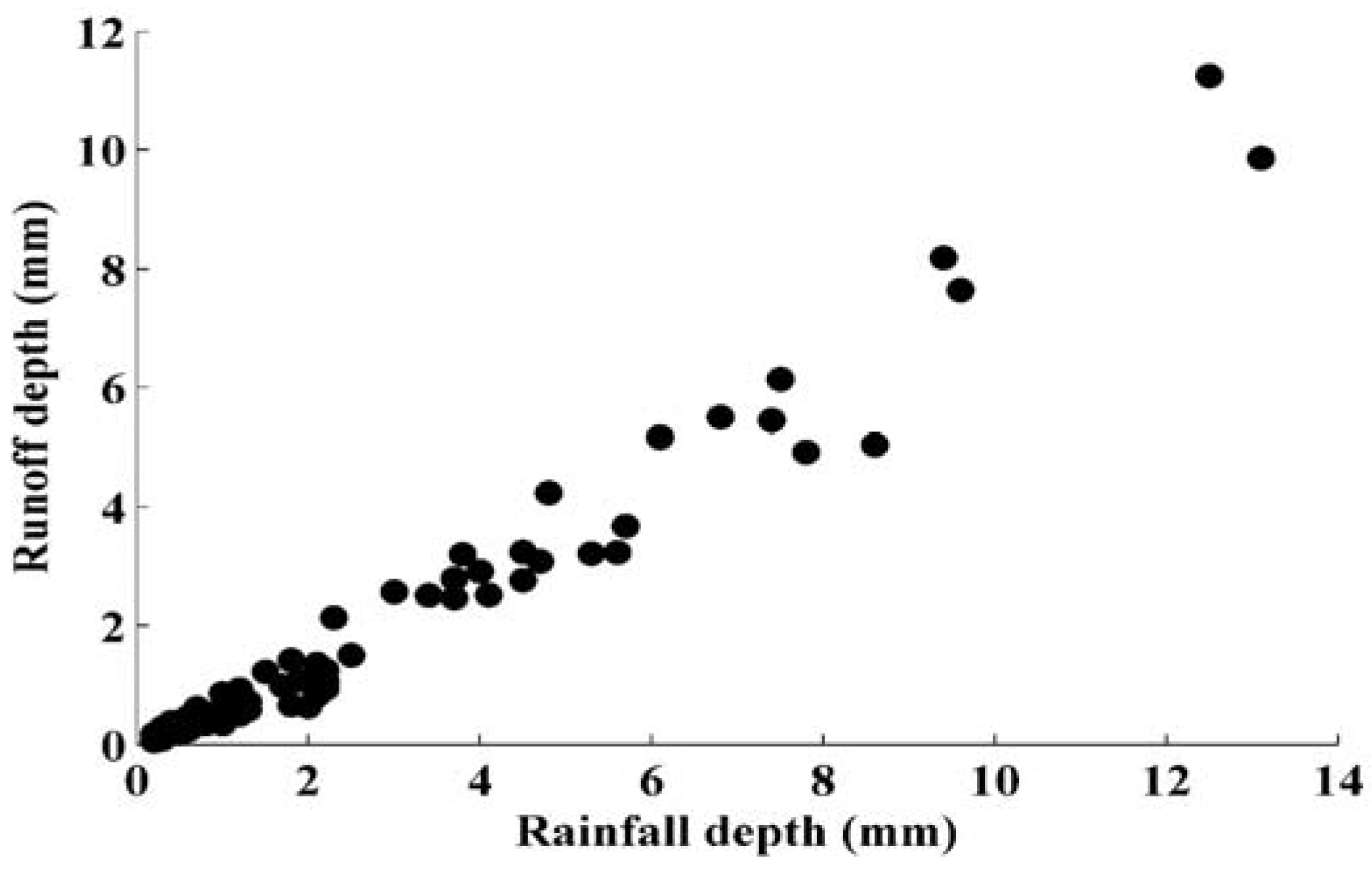
2.3.2. Hydrological Modeling
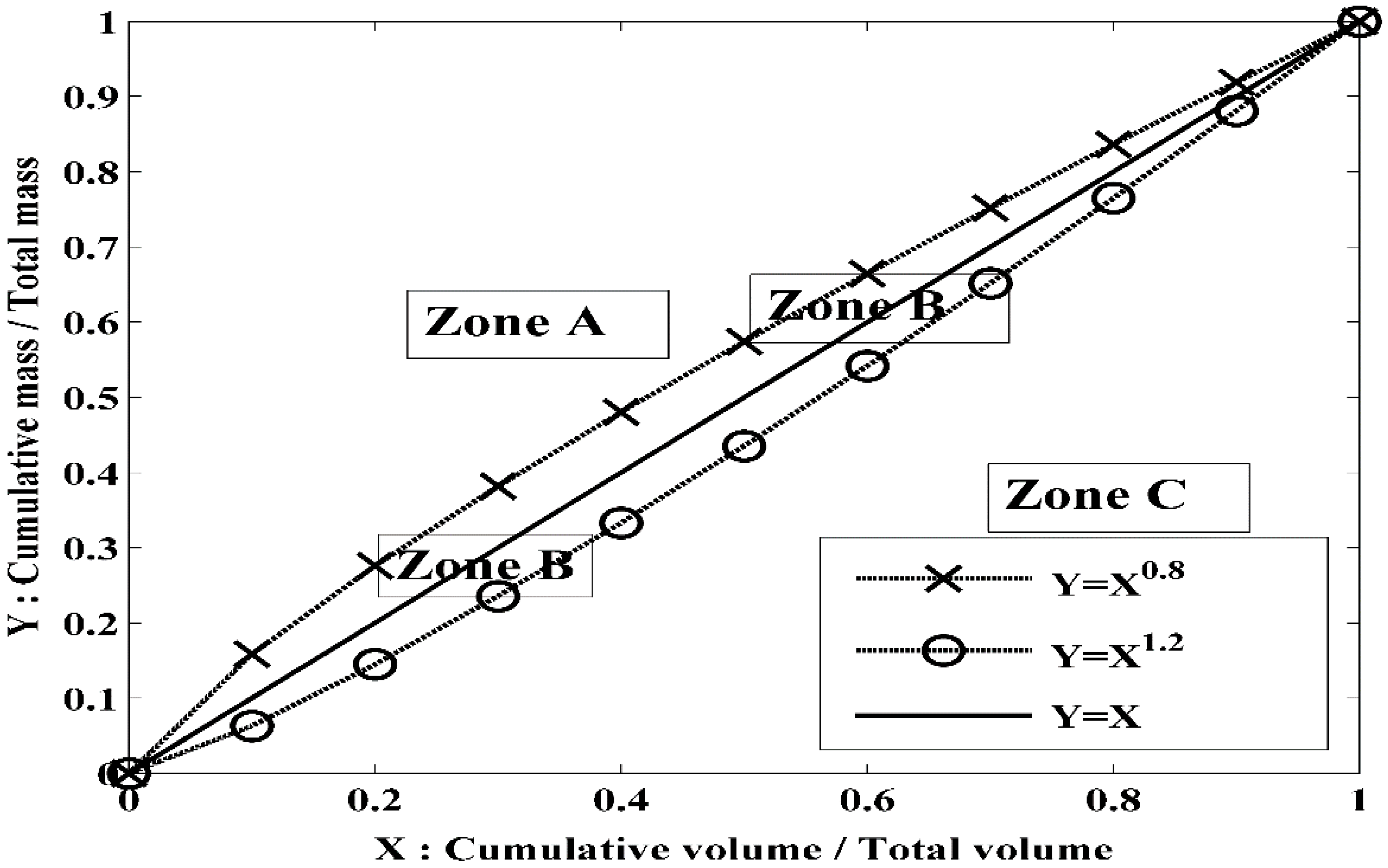
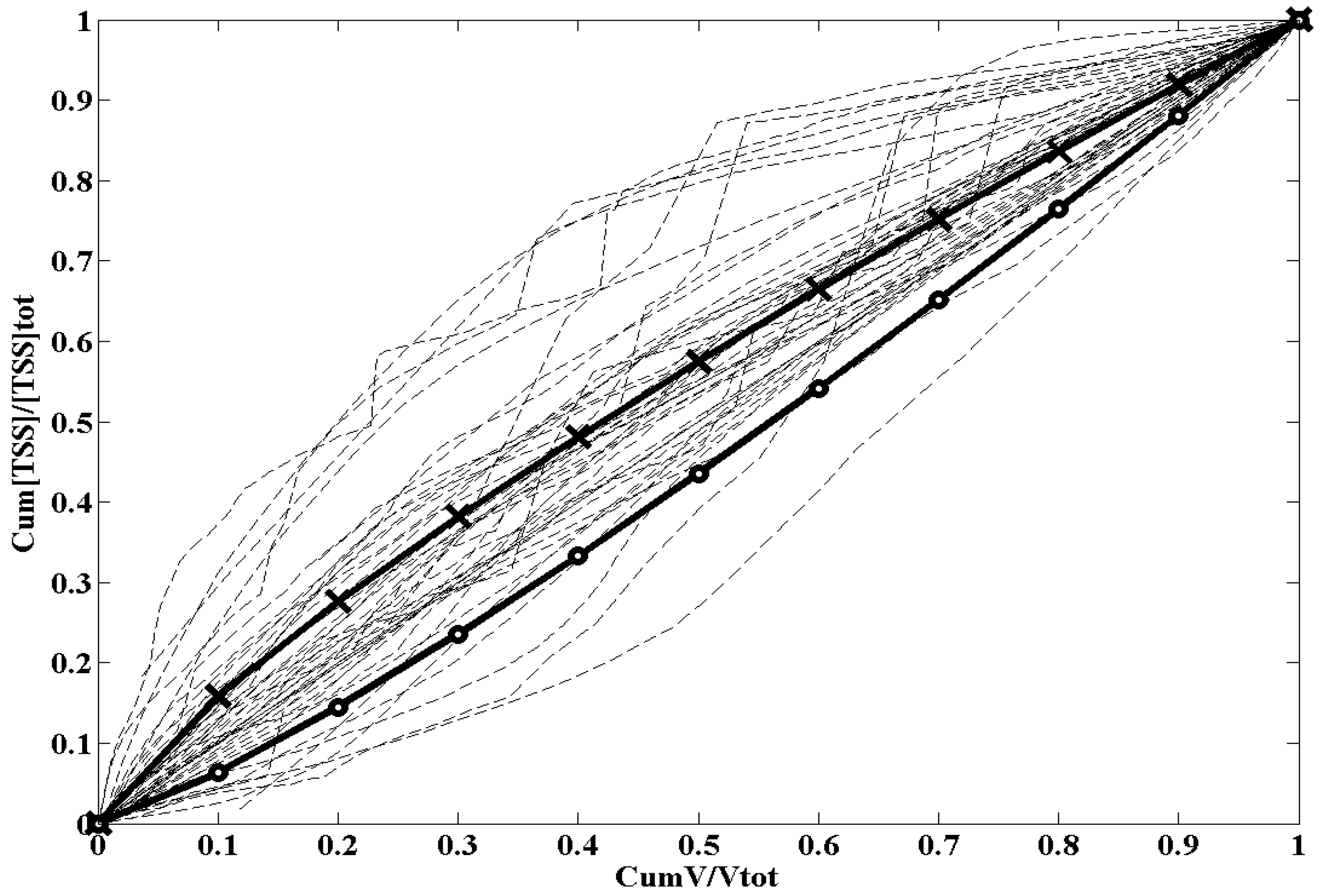
2.4. Intra-Event Dynamic of TSS Transport
2.5. Water Quality Modeling
2.5.1. The Models
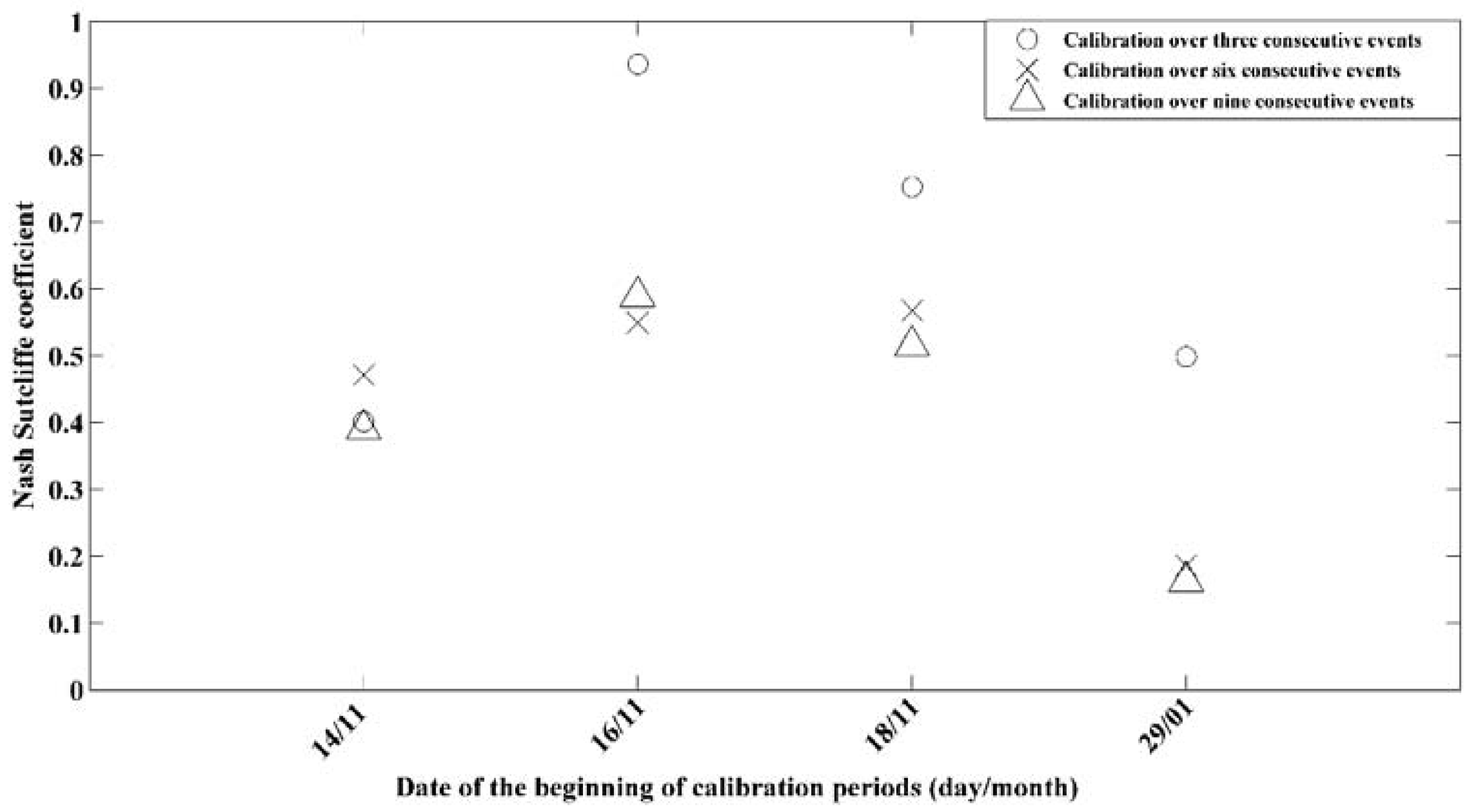
2.5.2. Calibration
2.5.3. Prediction on Short Term
3. Results and Discussion
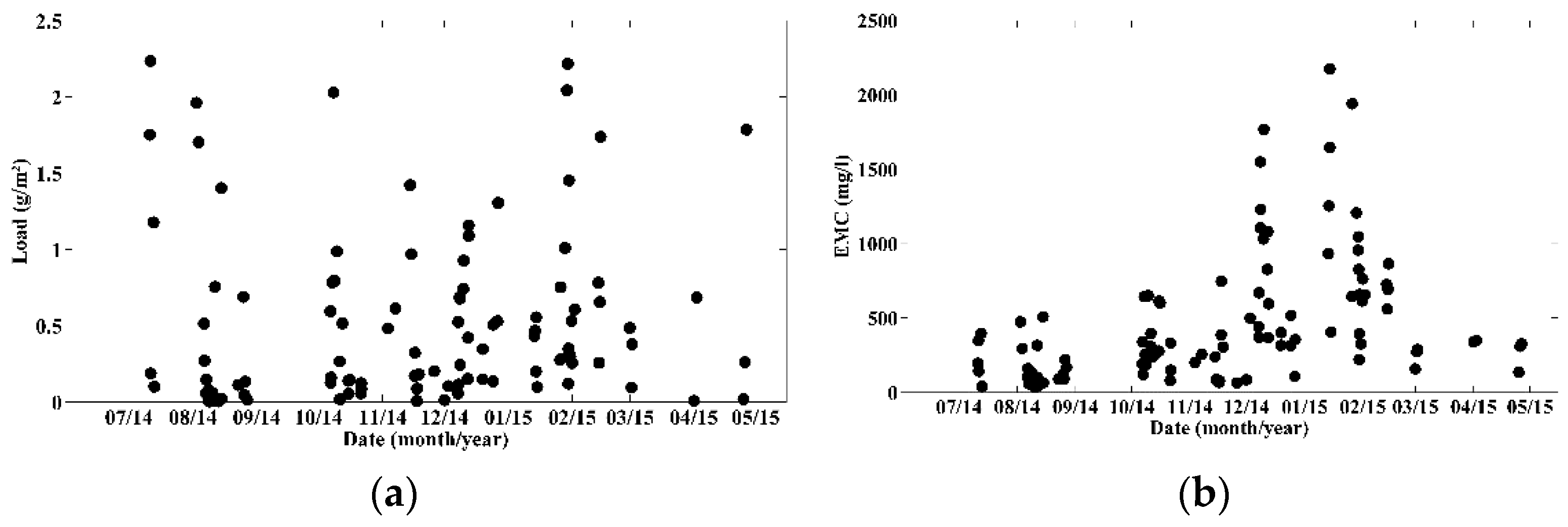
3.1. TSS Concentrations and Loads
3.2. Dynamic of Transport of TSS
3.3. Modeling
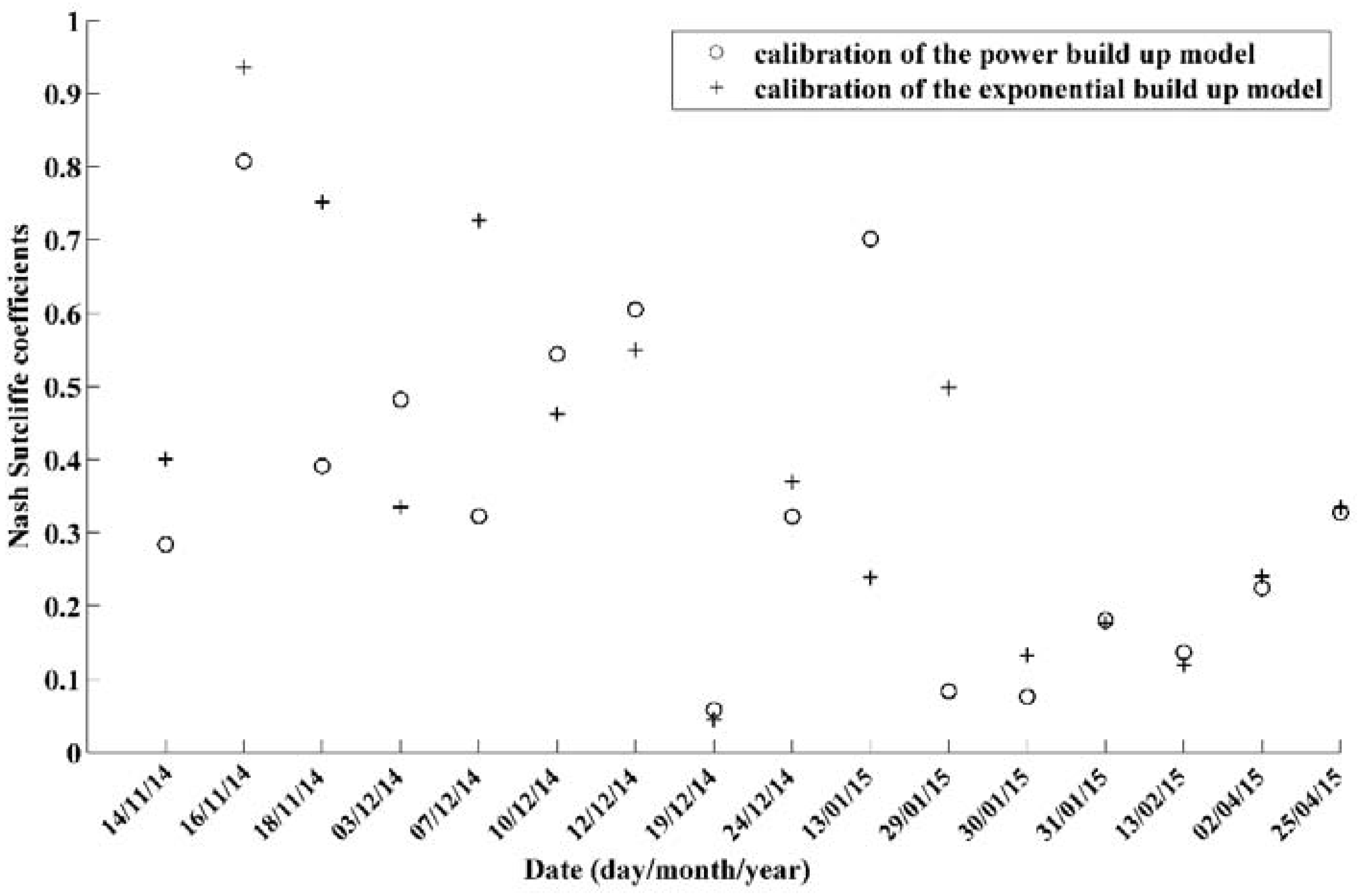
3.3.1. Wash-Off Assessment
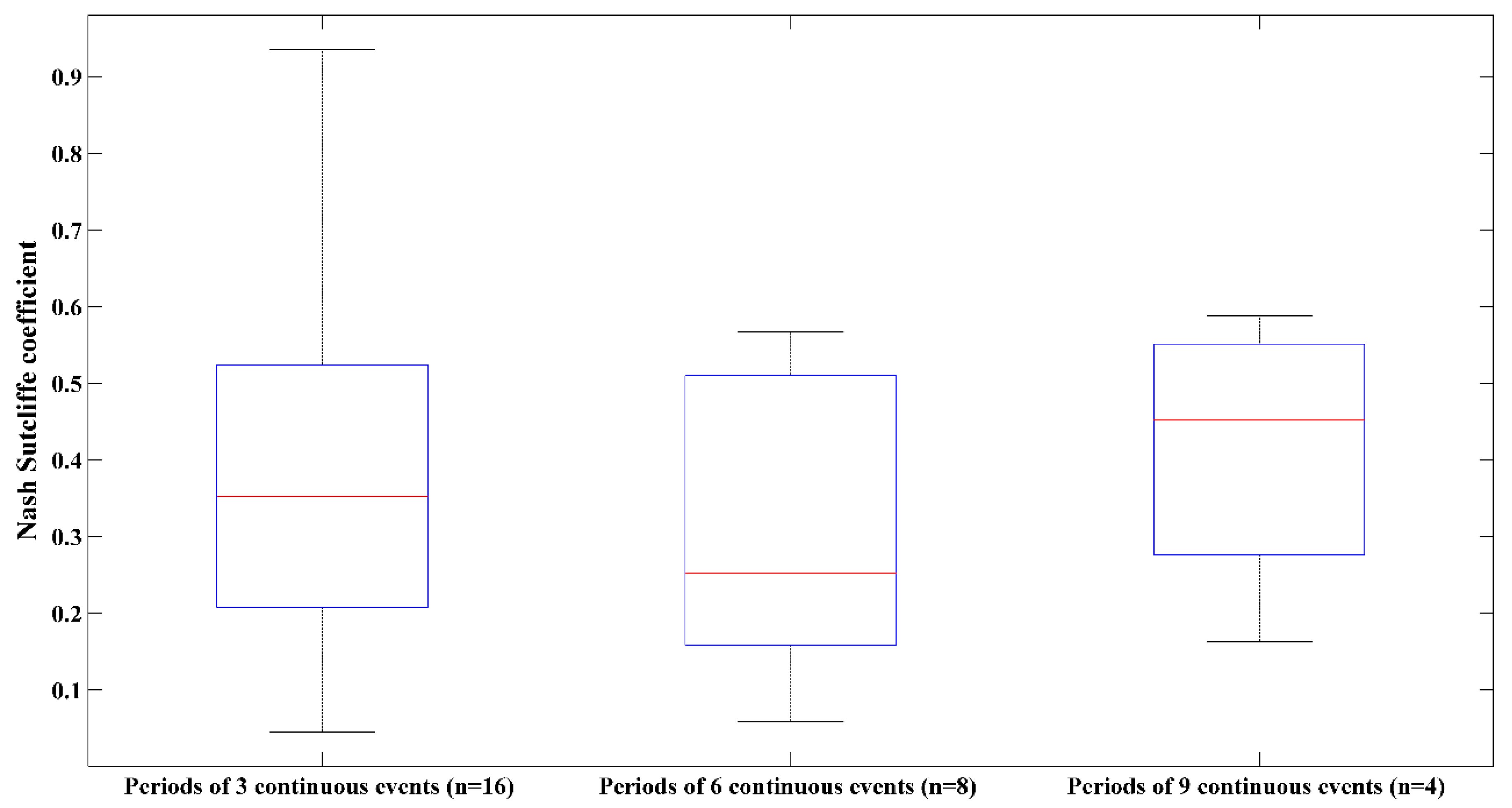
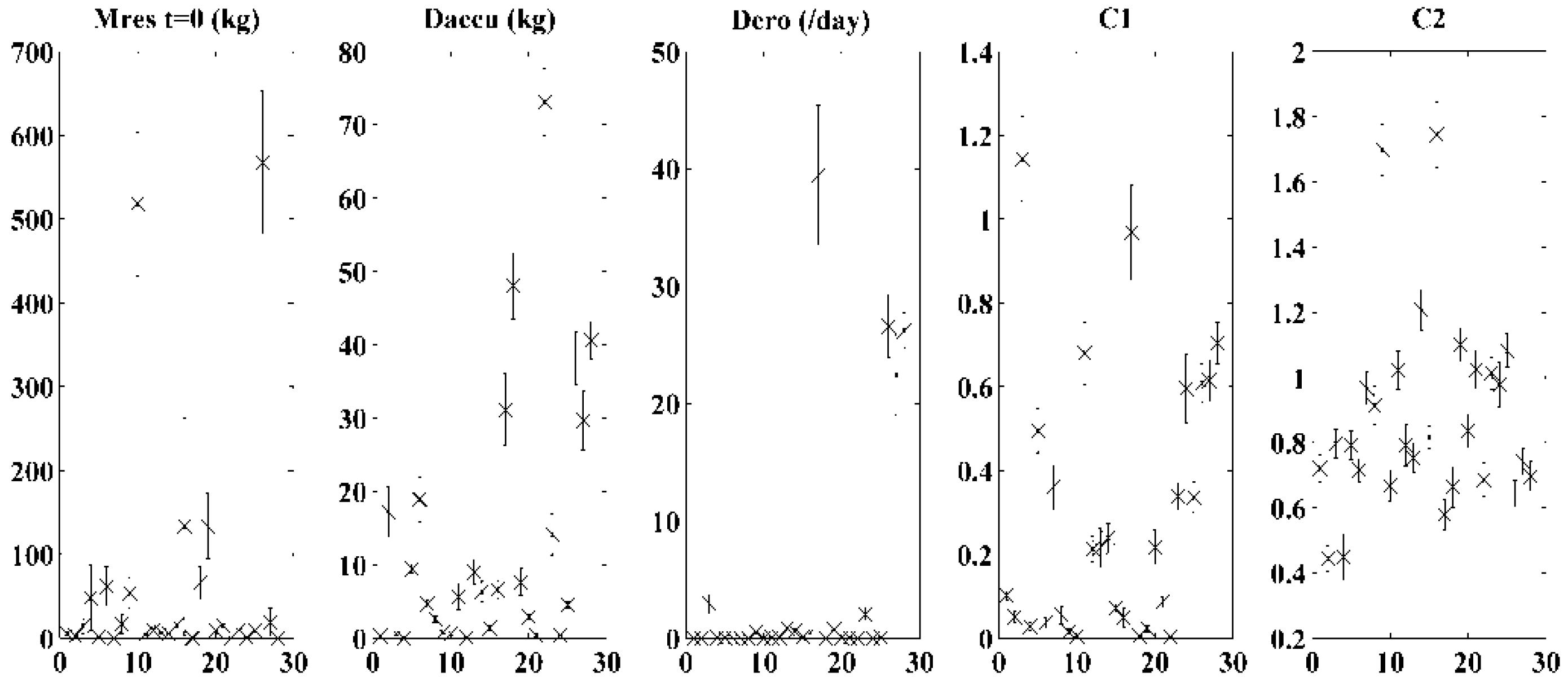
3.3.2. Build-Up Assessment
- Modified SWMM exponential build-up:
- Power build-up:
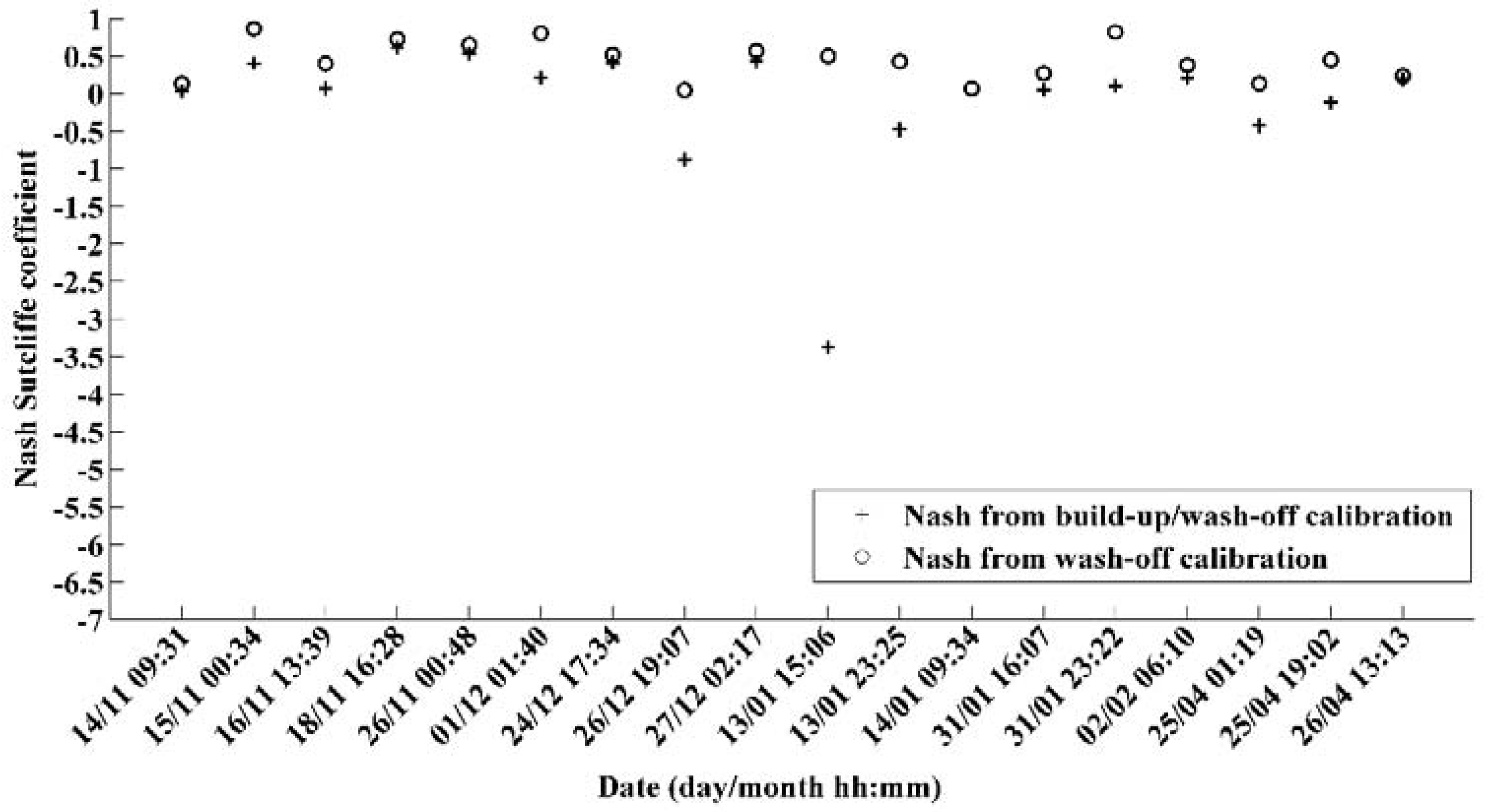
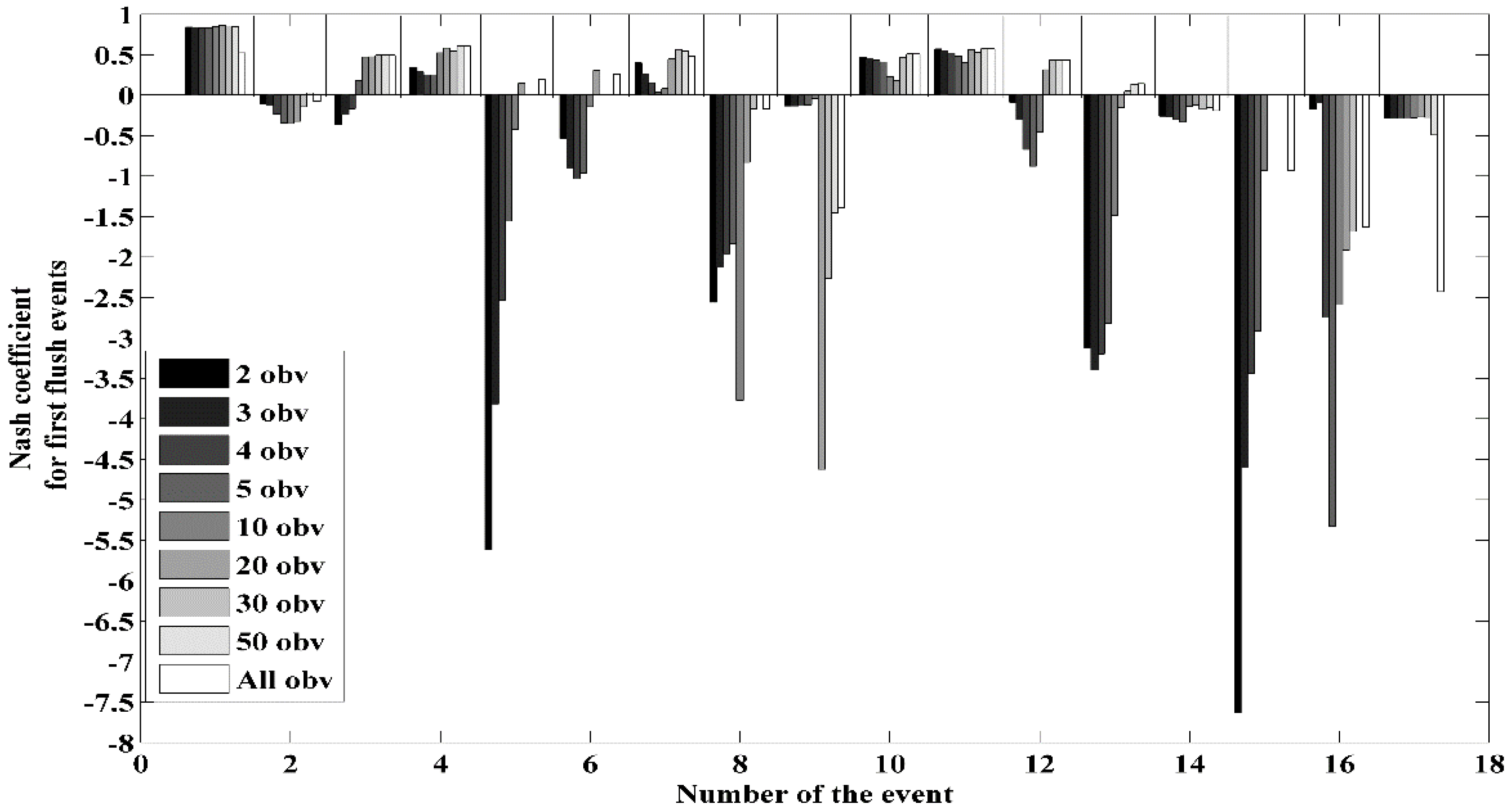
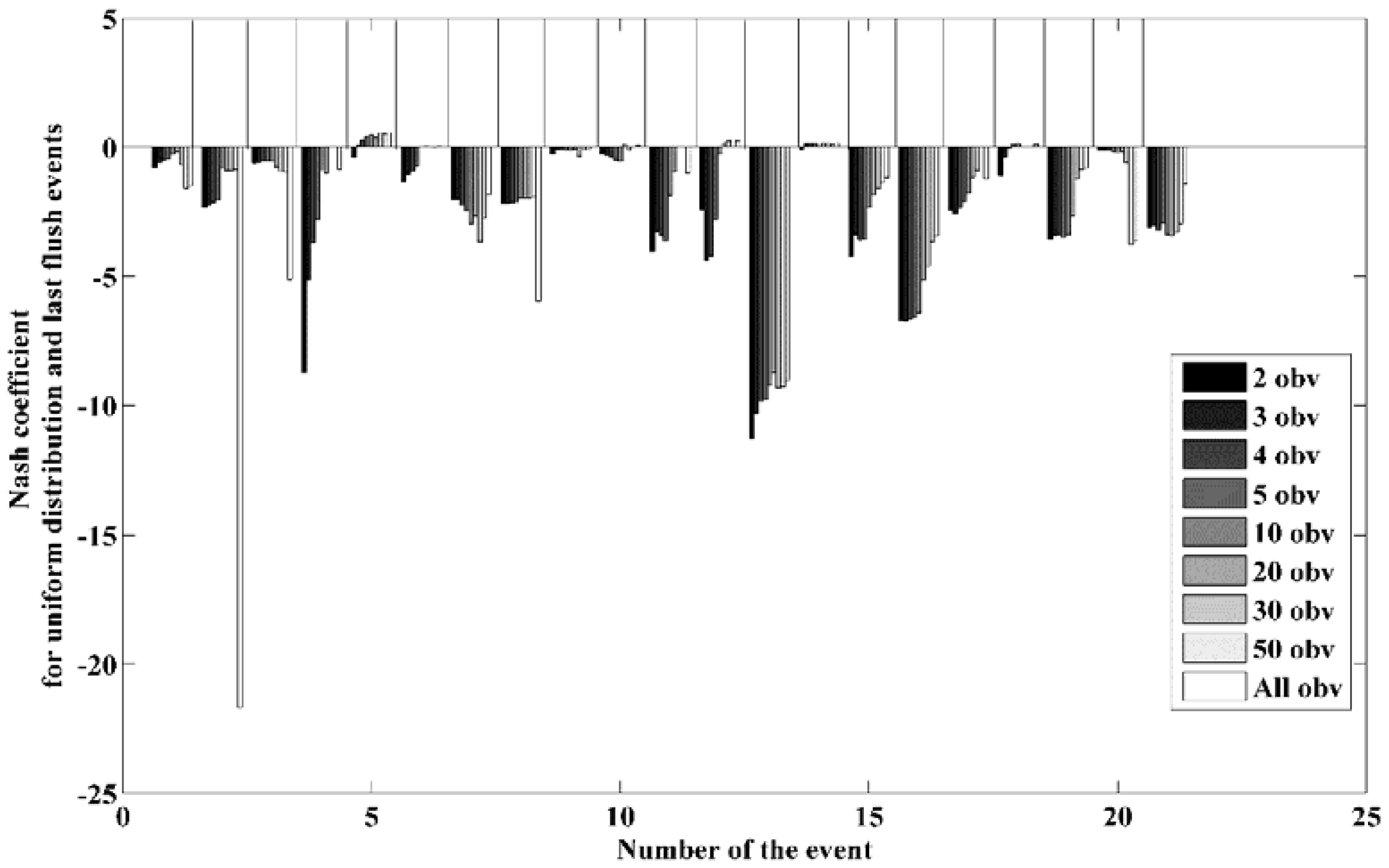
3.3.3. Short Term Predictive Capacity
- Inter-Event:
- Intra-Event:
4. Conclusions and Perspectives
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Initial Available Mass | ||||
| Parameters | R Linear | p-Value | R Spearman | p-Value |
| Hrain | −0.052 | 0.836 | 0.101 | 0.689 |
| Imax | 0.086 | 0.734 | −0.180 | 0.471 |
| Imax 5 | 0.122 | 0.628 | −0.015 | 0.954 |
| Imean | −0.056 | 0.824 | 0.032 | 0.901 |
| Duration | −0.106 | 0.675 | 0.120 | 0.632 |
| ADWP | −0.083 | 0.742 | −0.358 | 0.144 |
| Tmax | 0.509 | 0.031 | 0.106 | 0.674 |
| Tmin | 0.436 | 0.07 | 0.202 | 0.420 |
| Tmean | 0.491 | 0.038 | 0.16 | 0.525 |
| C1 | ||||
| Parameters | R Linear | p-Value | R Spearman | p-Value |
| Hrain | −0.184 | 0.463 | −0.597 | 0.008 |
| Imax | −0.034 | 0.890 | −0.275 | 0.267 |
| Imax 5 | 0.009 | 0.971 | −0.257 | 0.302 |
| Imean | 0.779 | <0.001 | 0.153 | 0.541 |
| Duration | −0.283 | 0.256 | −0.645 | 0.004 |
| ADWP | 0.212 | 0.398 | 0.279 | 0.260 |
| Tmax | 0.192 | 0.445 | −0.240 | 0.336 |
| Tmin | −0.051 | 0.838 | −0.297 | 0.230 |
| Tmean | 0.097 | 0.701 | −0.244 | 0.327 |
| C2 | ||||
| Parameters | R Linear | p-Value | R Spearman | p-Value |
| Hrain | 0.241 | 0.321 | 0.186 | 0.444 |
| Imax | 0.649 | 0.002 | 0.368 | 0.121 |
| Imax 5 | 0.846 | <0.001 | 0.340 | 0.154 |
| Imean | 0.382 | 0.106 | 0.431 | 0.066 |
| Duration | −0.114 | 0.642 | −0.184 | 0.448 |
| ADWP | −0.035 | 0.886 | 0.098 | 0.688 |
| Tmax | 0.237 | 0.327 | 0.136 | 0.578 |
| Tmin | −0.055 | 0.823 | −0.063 | 0.797 |
| Tmean | 0.067 | 0.785 | 0.053 | 0.827 |
References
- Elliott, A.; Trowsdale, S. A review of models for low impact urban stormwater drainage. Environ. Model. Softw. 2007, 22, 394–405. [Google Scholar] [CrossRef]
- Gromaire, M.-C. La Pollution des Eaux Pluviales Urbaines en Réseau d’Assainissement Unitaire. Caractéristiques et Origines; Ecole des Ponts ParisTech: Marne-la-Vallée, France, 1998. [Google Scholar]
- Bressy, A. Flux de Micropolluants Dans les Eaux de Ruissellement Urbaines: Effets de Différents Modes de Gestion à l’Amont; Université Paris-Est: Paris, France, 2010. [Google Scholar]
- Bai, S.; Li, J. Sediment Wash-Off from an Impervious Urban Land Surface. J. Hydrol. Eng. 2013, 18, 488–498. [Google Scholar] [CrossRef]
- Gunawardana, C.; Goonetilleke, A.; Egodawatta, P.; Dawes, L.; Kokot, S. Role of Solids in Heavy Metals Buildup on Urban Road Surfaces. J. Environ. Eng. 2012, 138, 490–498. [Google Scholar] [CrossRef] [Green Version]
- Herngren, L.; Goonetilleke, A.; Ayoko, G.A. Analysis of heavy metals in road-deposited sediments. Anal. Chim. Acta 2006, 571, 270–278. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mahbub, P.; Goonetilleke, A.; Ayoko, G.A.; Egodawatta, P.; Yigitcanlar, T. Analysis of build-up of heavy metals and volatile organics on urban roads in gold coast, Australia. Water Sci. Technol. 2011, 63, 2077–2085. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sabin, L.D.; Lim, J.H.; Stolzenbach, K.D.; Schiff, K.C. Contribution of trace metals from atmospheric deposition to stormwater runoff in a small impervious urban catchment. Water Res. 2005, 39, 3929–3937. [Google Scholar] [CrossRef] [PubMed]
- Shaw, S.B.; Walter, M.T.; Steenhuis, T.S. A physical model of particulate wash-off from rough impervious surfaces. J. Hydrol. 2006, 327, 618–626. [Google Scholar] [CrossRef]
- Vaze, J.; Chiew, F.H. Experimental study of pollutant accumulation on an urban road surface. Urban Water 2002, 4, 379–389. [Google Scholar] [CrossRef]
- Bertrand-Krajewski, J.-L.; Chebbo, G.; Saget, A. Distribution of pollutant mass vs volume in stormwater discharges and the first flush phenomenon. Water Res. 1998, 32, 2341–2356. [Google Scholar] [CrossRef]
- European Commission. Directive of the European Parliament and of the Council n 2000/60/EC establishing a framework for the community action in the field of water policy. Off. J. Eur. Communities 2000, 327, 1–72. [Google Scholar]
- Dotto, C.B.S.; Kleidorfer, M.; Deletic, A.; Rauch, W.; McCarthy, D.T.; Fletcher, T.D. Performance and sensitivity analysis of stormwater models using a Bayesian approach and long-term high resolution data. Environ. Model. Softw. 2011, 26, 1225–1239. [Google Scholar] [CrossRef]
- Sartor, J.D.; Boyd, G.B.; Agardy, F.J. Water Pollution Aspects of Street Surface Contaminants. J. Water Pollut. Control Fed. 1974, 46, 458–467. [Google Scholar] [PubMed]
- Francey, M.; Duncan, H.P.; Deletic, A.; Fletcher, T.D. Testing and Sensitivity of a Simple Method for Predicting Urban Pollutant Loads. J. Environ. Eng. 2011, 137, 782–789. [Google Scholar] [CrossRef]
- Vaze, J.; Chiew, F.H.S. Comparative evaluation of urban storm water quality models. Water Resour. Res. 2003, 39, 1280. [Google Scholar] [CrossRef]
- Alley, W.; Smith, P. Estimation of Accumulation Parameters for Urban Runoff Quality Modeling. Water Resour. Res. 1981, 17, 1657–1664. [Google Scholar] [CrossRef]
- Heng, B.C.P.; Sander, G.C.; Armstrong, A.; Quinton, J.N.; Chandler, J.H.; Scott, C.F. Modeling the dynamics of soil erosion and size-selective sediment transport over nonuniform topography in flume-scale experiments. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef] [Green Version]
- Massoudieh, A.; Abrishamchi, A.; Kayhanian, M. Mathematical modeling of first flush in highway storm runoff using genetic algorithm. Sci. Total Environ. 2008, 398, 107–121. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y.; Bonhomme, C.; Le, M.-H.; Chebbo, G. A new approach of monitoring and physically-based modelling to investigate urban wash-off process on a road catchment near Paris. Water Res. 2016, 102, 96–108. [Google Scholar] [CrossRef] [PubMed]
- Ball, J.E.; Jenks, R.; Aubourg, D. An assessment of the availability of pollutant constituents on road surfaces. Sci. Total Environ. 1998, 209, 243–254. [Google Scholar] [CrossRef]
- Huber, W.C.; Dickinson, R.E.; Barnwell, T.O., Jr.; Branch, A. Storm Water Management Model, Version 4; U.S. Environmental Protection Agency, Environmental Research Laboratory: Athens, GA, USA, 1988.
- Servat, E. Contribution à l’étude de la Pollution du Ruissellement Pluvial Urbain. Ph.D. Thesis, Université des Sciences et Techniques du Languedoc, Montpellier, France, 1987. [Google Scholar]
- Dembélé, A.; Bertrand-Krajewski, J.-L.; Becouze, C.; Barillon, B.; Dauthuille, P. TSS, COD and Priority Pollutants in Stormwater—Event Fluxes Modelling Using Conceptual Approach. 2013. Available online: http://hdl.handle.net/2042/51284 (accessed on 7 December 2015).
- Sage, J.; Bonhomme, C.; Al Ali, S.; Gromaire, M.-C. Performance assessment of a commonly used “accumulation and wash-off” model from long-term continuous road runoff turbidity measurements. Water Res. 2015, 78, 47–59. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.; Wei, J.; Huang, Y.; Wang, G.; Maqsood, I. Urban nonpoint source pollution buildup and washoff models for simulating storm runoff quality in the Los Angeles County. Environ. Pollut. 2011, 159, 1932–1940. [Google Scholar] [CrossRef] [PubMed]
- Kanso, A.; Tassin, B.; Chebbo, G. A benchmark methodology for managing uncertainties in urban runoff quality models. Water Sci. Technol. 2005, 51, 163–170. [Google Scholar] [PubMed]
- Métadier, M.; Bertrand-Krajewski, J.-L. From mess to mass: A methodology for calculating storm event pollutant loads with their uncertainties, from continuous raw data time series. Water Sci. Technol. 2011, 63, 369. [Google Scholar] [CrossRef] [PubMed]
- Mourad, M.; Bertrand-Krajewski, J.-L. A method for automatic validation of long time series of data in urban hydrology. Water Sci. Technol. 2002, 45, 263–270. [Google Scholar] [PubMed]
- Becouze-Lareure, C.; Invernon, N. EVOHE-Logiciel de Suivi des Capteurs—Validation de Données-Auto-Surveillance des Systèmes d’Assainissement; INSA Lyon ALISON: Lyon, France, 2014. [Google Scholar]
- Zoppou, C. Review of urban storm water models. Environ. Model. Softw. 2001, 16, 195–231. [Google Scholar] [CrossRef]
- Obropta, C.C.; Kardos, J.S. Review of Urban Stormwater Quality Models: Deterministic, Stochastic, and Hybrid Approaches JAWRA. J. Am. Water Resour. Assoc. 2007, 43, 1508–1523. [Google Scholar] [CrossRef]
- Egodawatta, P.; Thomas, E.; Goonetilleke, A. Mathematical interpretation of pollutant wash-off from urban road surfaces using simulated rainfall. Water Res. 2007, 41, 3025–3031. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Egodawatta, P. Translation of Small-Plot Scale Pollutant Build up and Wash off Measurements to Urban Catchment Scale. Ph.D. Thesis, Queensland University of Technology, Brisbane, Australia, 2007. [Google Scholar]
- Bonhomme, C.; Petrucci, G. Spatial Representation in semi-distributed modelling of water quantity and quality. In International Conference on Urban Drainage, Kuching, Malaysia; ICUD: Kuching, Malaysia, 2014; p. 2488399. [Google Scholar]
- Hasting, W.K. Monte carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Lee, J.H.; Bang, K.W.; Ketchum, L.H.; Choe, J.S.; Yu, M.J. First flush analysis of urban storm runoff. Sci. Total Environ. 2001, 293, 163–175. [Google Scholar] [CrossRef]
- Maniquiz, M.C.; Lee, S.; Kim, L.-H. Multiple linear regression models of urban runoff pollutant load and event mean concentration considering rainfall variables. J. Environ. Sci. 2010, 22, 946–952. [Google Scholar] [CrossRef]
- Gnecco, I.; Berretta, C.; Lanza, L.G.; La Barbera, P. Storm water pollution in the urban environment of Genoa, Italy. Atmos. Res. 2005, 77, 60–73. [Google Scholar] [CrossRef]
- Bechet, B.; Bonhomme, C.; Lamprea, K.; Campos, E.; Jean Soro, L.; Dubois, P.; Lherm, D. Towards a Modeling of Traffic Pollutant Flux at Local Scale—Chemical Analysis and Micro-Characterization of Road Dusts. Available online: http://hues.se/assets/Abstract_final_2015-05-27-final1.pdf (accessed on 22 March 2016).
- Spearman, C. The Proof and Measurement of Association between Two Things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Wijesiri, B.; Egodawatta, P.; McGree, J.; Goonetilleke, A. Influence of pollutant build-up on variability in wash-off from urban road surfaces. Sci. Total Environ. 2015, 527–528, 344–350. [Google Scholar] [CrossRef] [PubMed]
- Daly, E.; Bach, P.M.; Deletic, A. Stormwater pollutant runoff: A stochastic approach. Adv. Water Resour. 2014, 74, 148–155. [Google Scholar] [CrossRef]
- Wijesiri, B.; Egodawatta, P.; McGree, J.; Goonetilleke, A. Incorporating process variability into stormwater quality modelling. Sci. Total Environ. 2015, 533, 454–461. [Google Scholar] [CrossRef] [PubMed]

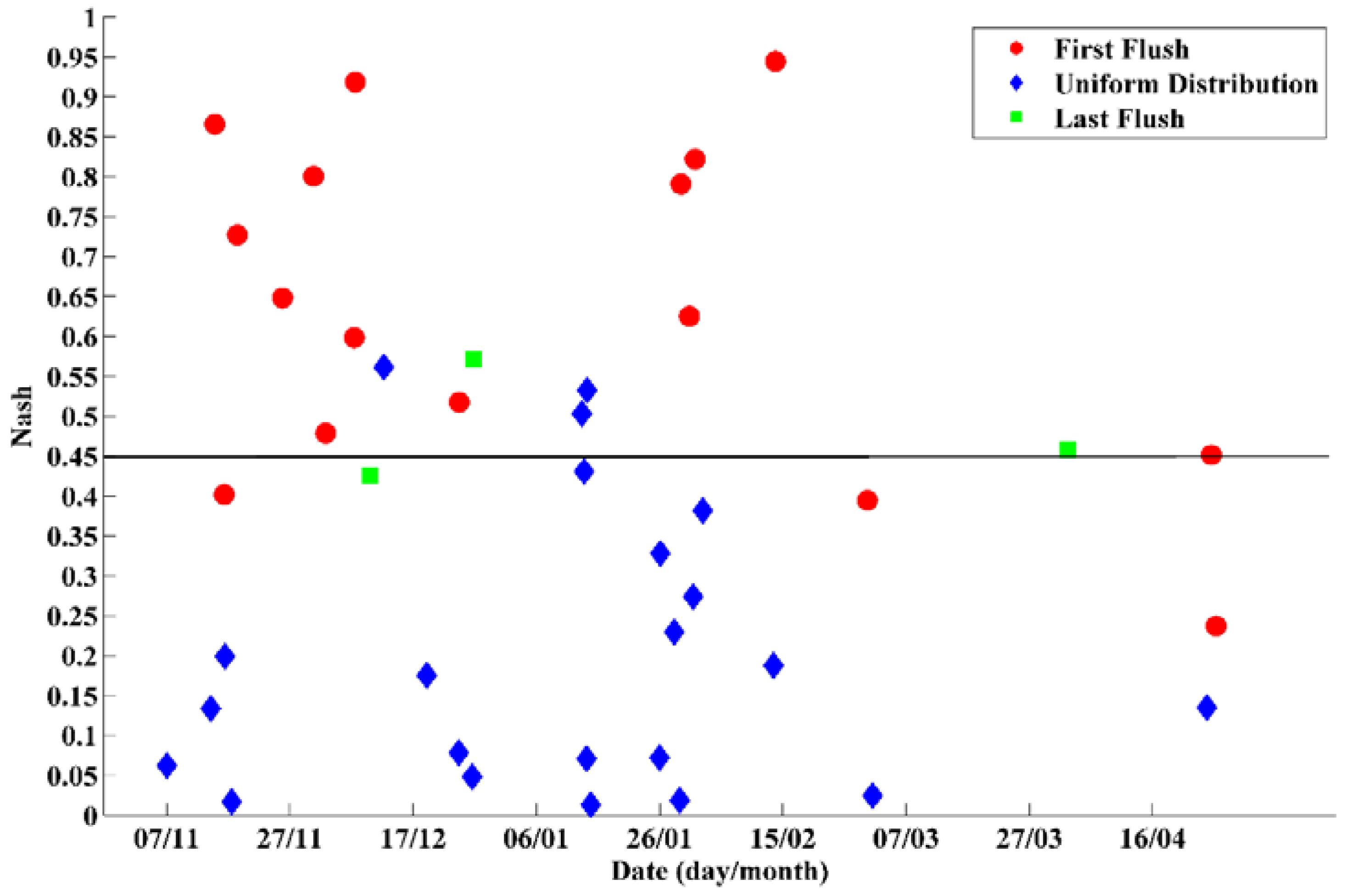
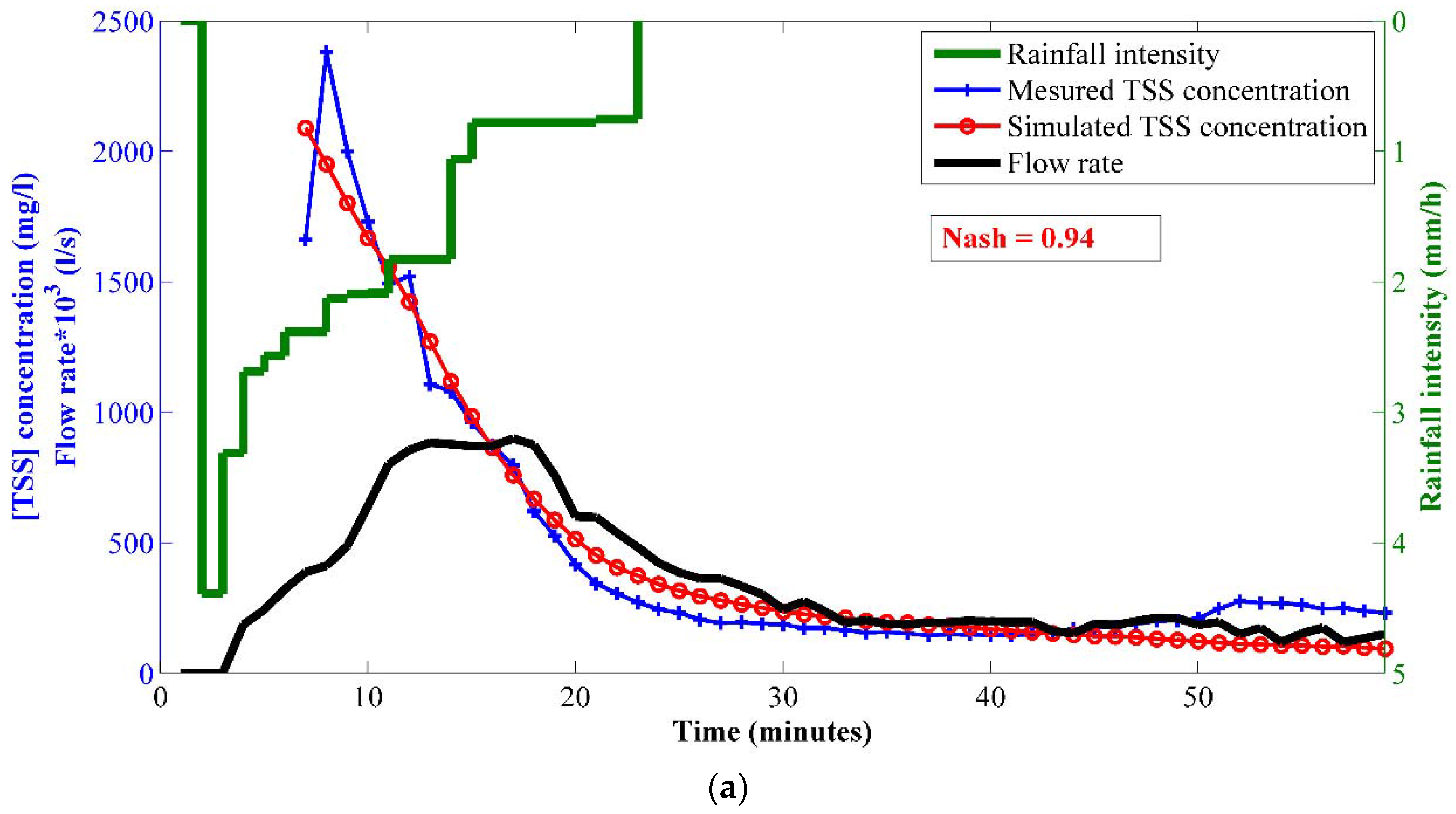
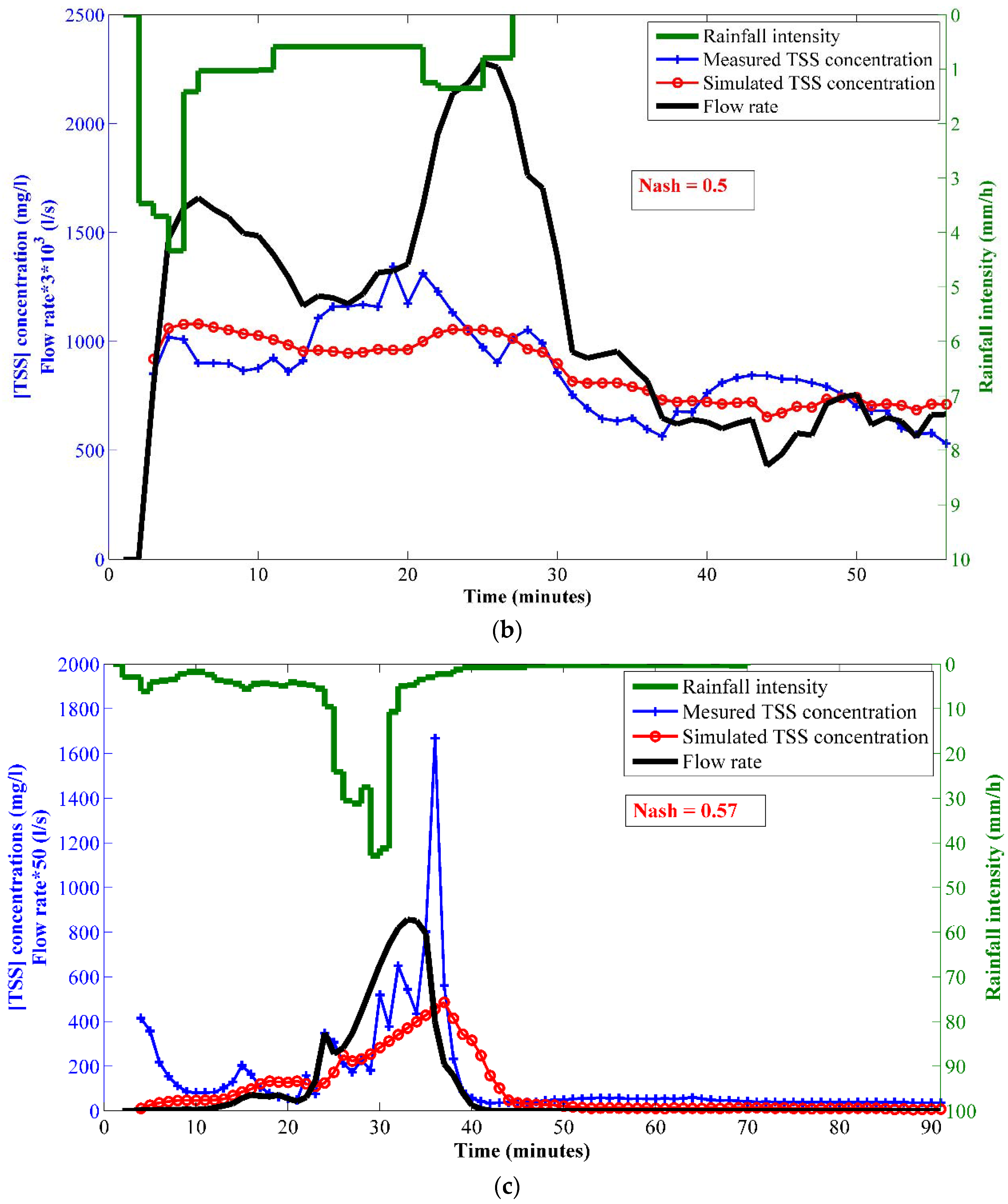
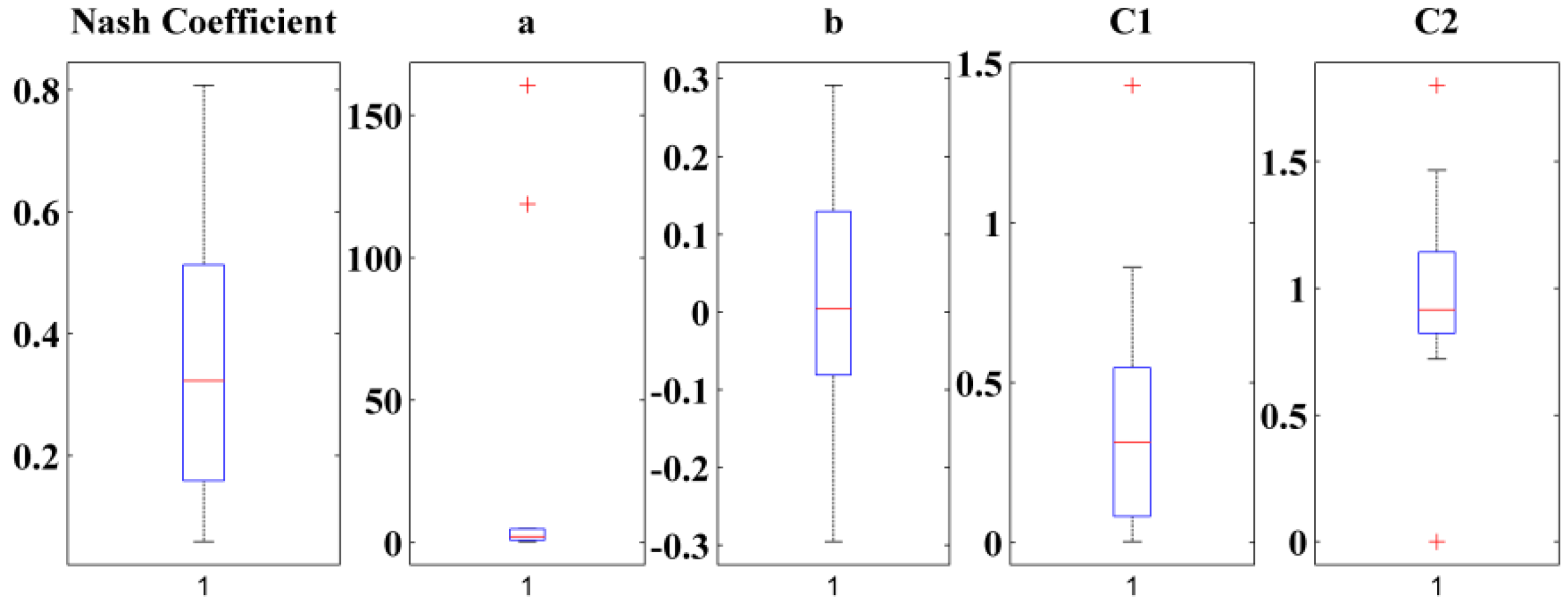
| Rainfall Characteristic | Rainfall Depth (mm) | Duration (min) | ADWP (DD HH:MM:SS) | Maximum 1 min Intensity (mm/h) | Maximum 5 min Intensity (mm/h) | Maximum Intensity (mm/h) | Average Intensity (mm/h) |
|---|---|---|---|---|---|---|---|
| Max | 21.3 | 641.1 | 21 05:28:19 | 131 | 100.2 | 360 | 53.9 |
| Min | 0.2 | 0.8 | 00 00:30:14 | 0.2 | 0.2 | 0.2 | 0.4 |
| Median | 0.7 | 34.78 | 00 06:47:05 | 3.03 | 2.31 | 2.94 | 1.36 |
| Mean | 2.128 | 75.2 | 01 06:14:24 | 9.19 | 6.61 | 14.09 | 3.25 |
| Criteria of Classification | Model Type | Description |
|---|---|---|
| Variable description | Deterministic | Variables properties are well known and do not include any randomness. The same input will yield the same output. |
| Stochastic | Variables have a probability distribution and its uncertainty is built into the model. The same input will yield different possible outputs. | |
| Process description | Empirical | Relations between inputs and outputs are established from observations only without any intervention of physical laws |
| Conceptual | Physical laws are applied in simple and simplified form | |
| Physically based | Logical structure based on physical laws governing the process | |
| Spatial scale | Global (lumped) | Catchment is described as a whole entity |
| Semi distributed | Catchment is divided into sub catchment | |
| Distributed | Catchment is divided into elementary unit using a grid | |
| Temporal scale | Event | Individual events are simulated |
| Continuous | Long period of time are simulated |
| Calibration | Wash-Off Assessment | Build-Up Assessment |
|---|---|---|
| Number of events | 42 | 16 periods of 3 successive events each |
| 8 periods of 6 successive events each | ||
| 4 periods of 9 successive events each | ||
| Model | MERO (t) = MB(t).C1.q(t)C2.dt | MB (i) = DACCU/DERO × [1 − e(−DERO × ADWP (i))] + MRES. e(−DERO × ADWP(i)) |
| MB (i) = a.ADWPb(i) |
| Prediction Approaches | Inter-Event Approach | Intra-Event Approach | |
|---|---|---|---|
| Number of events | 11 periods of 4 events each | 38 | |
| Model | Build-up | MB (i) = DACCU/DERO × [1 − e(−DERO × ADWP (i))] + MRES. e(−DERO × ADWP(i)) | - |
| MB (i) = a.ADWPb(i) | |||
| Wash-off | MERO (t) = MB(t).C1.q(t)C2.dt | ||
| Methodology | Calibration on the first two events of the period Validation on the third event of the corresponding period Validation on the third and the fourth events of the corresponding period | Calculation of the available mass prior to the storm event using an a incremental number of observations Simulation of the corresponding pollutograph | |
| Parameter | Maximum | Minimum | Mean | Median | Standard Deviation |
|---|---|---|---|---|---|
| EMC (mg/L) | 2174.37 | 35.39 | 452.09 | 320.97 | 432.42 |
| Load (g/m2) | 2.23 | 0.0035 | 0.51 | 0.27 | 0.56 |
| Season | Autumn | Winter | Spring | Summer |
|---|---|---|---|---|
| Beginning date | 6 October 2014 15:30 | 24 December 2014 15:30 | 01 April 2015 02:53 | 11 July 2014 02:16 |
| End date | 19 December 2014 13:53 | 2 March 2015 01:13 | 26 April 2015 12:56 | 27 August 2014 07:02 |
| Number of events | 42 | 29 | 5 | 30 |
| Average EMC (mg/L) | 270.35 | 550.82 | 326.43 | 228.37 |
| Total load (g/m2) | 18.75 | 18.83 | 2.75 | 13.62 |
| Maximum intensity (mm/h) (min–max) | 0.54–72 | 0.71–72 | 4.23–120 | 1.77–180 |
| Rainfall depth (mm) (min–max) | 0.2–14.2 | 0.3–7.8 | 0.3–6.8 | 0.4–21.3 |
| Total rainfall depth (mm) | 131.3 | 43.7 | 11.3 | 129.2 |
| Rainfall Characteristic | Pearson Correlation Coefficient R | |
|---|---|---|
| TSS | TSS Loads | |
| ADWP | −0.048 | 0.14 |
| Duration | −0.17 | 0.37 |
| Imean | −0.19 | 0.12 |
| Imax | −0.2 | 0.22 |
| Imax 5 | −0.18 | 0.28 |
| Hrain | −0.26 | 0.52 |
| Beginning of the Modeling Period | Nash Coefficient from Calibration over the First Two Events | Nash Coefficient from Validation over the Third Event |
|---|---|---|
| 14 November 2014 | 0.527 | −0.5714 |
| 17 November 2014 | 0.787 | −0.5981 |
| 7 December 2014 | 0.781 | 0.1643 |
| 13 January 2015 | 0.616 | −0.5890 |
| 30 January 2015 | 0.629 | −0.8874 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Ali, S.; Bonhomme, C.; Chebbo, G. Evaluation of the Performance and the Predictive Capacity of Build-Up and Wash-Off Models on Different Temporal Scales. Water 2016, 8, 312. https://doi.org/10.3390/w8080312
Al Ali S, Bonhomme C, Chebbo G. Evaluation of the Performance and the Predictive Capacity of Build-Up and Wash-Off Models on Different Temporal Scales. Water. 2016; 8(8):312. https://doi.org/10.3390/w8080312
Chicago/Turabian StyleAl Ali, Saja, Céline Bonhomme, and Ghassan Chebbo. 2016. "Evaluation of the Performance and the Predictive Capacity of Build-Up and Wash-Off Models on Different Temporal Scales" Water 8, no. 8: 312. https://doi.org/10.3390/w8080312
APA StyleAl Ali, S., Bonhomme, C., & Chebbo, G. (2016). Evaluation of the Performance and the Predictive Capacity of Build-Up and Wash-Off Models on Different Temporal Scales. Water, 8(8), 312. https://doi.org/10.3390/w8080312






