Next Article in Journal
Chinese State-Owned Enterprise Investment in Mekong Hydropower: Political and Economic Drivers and Their Implications across the Water, Energy, Food Nexus
Next Article in Special Issue
Obtaining the Thermal Structure of Lakes from the Air
Previous Article in Journal
Parameterization of Time-Averaged Suspended Sediment Concentration in the Nearshore
Previous Article in Special Issue
Spatial Modeling of Rainfall Patterns over the Ebro River Basin Using Multifractality and Non-Parametric Statistical Techniques
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 7
Issue 11
10.3390/w7116244
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Sensitivity Analysis of Flow and Temperature Distributions of Density Currents in a River-Reservoir System under Upstream Releases with Different Durations

by
Gang Chen
and
Xing Fang
*
Department of Civil Engineering, Auburn University, Auburn, AL 36849-5337, USA
*
Author to whom correspondence should be addressed.
Water 2015, 7(11), 6244-6268; https://doi.org/10.3390/w7116244
Submission received: 26 August 2015 / Revised: 30 September 2015 / Accepted: 2 November 2015 / Published: 6 November 2015
(This article belongs to the Special Issue New Developments in Methods for Hydrological Process Understanding)
Browse Figures
Versions Notes

Abstract

:
A calibrated three-dimensional Environmental Fluid Dynamics Code model was applied to simulate unsteady flow patterns and temperature distributions in the Bankhead river-reservoir system in Alabama, USA. A series of sensitivity model runs were performed under daily repeated large releases (DRLRs) with different durations (2, 4 and 6 h) from Smith Dam Tailrace (SDT) when other model input variables were kept unchanged. The density currents in the river-reservoir system form at different reaches, are destroyed at upstream locations due to the flow momentum of the releases, and form again due to solar heating. DRLRs (140 m3/s) with longer durations push the bottom cold water further downstream and maintain a cooler bottom water temperature. For the 6-h DRLR, the momentum effect definitely reaches Cordova (~43.7 km from SDT). Positive bottom velocity (density currents moving downstream) is achieved 48.4%, 69.0% and 91.1% of the time with an average velocity of 0.017, 0.042 and 0.053 m/s at Cordova for the 2-h, 4-h and 6-h DRLR, respectively. Results show that DRLRs lasting for at least 4 h maintain lower water temperatures at Cordova. When the 4-h and 6-h DRLRs repeat for more than 6 and 10 days, respectively, bottom temperatures at Cordova become lower than those for the constant small release (2.83 m3/s). These large releases overwhelm the mixing effects due to inflow momentum and maintain temperature stratification at Cordova.

1. Introduction

A density difference can exist between two fluids because of a difference in temperature, salinity, or concentration of suspended sediment. A density current is kept in motion by the force of gravity acting on differences in density. Density currents in nature such as turbidity currents typically flow along the bottom of oceans or lakes or reservoirs. Many laboratory and numerical model studies of density currents have been conducted in the last several decades. Density currents have been studied in situ [1,2,3,4,5,6]. Because it is quite challenging to study the density currents in the natural systems, the density currents are often investigated in the laboratory [7,8,9]. Most previous studies dealt with sloping channels and a rectangular cross section. Various simplifying assumptions were made to develop analytical models with laboratory data to understand density currents [10,11,12,13]. Fang and Stefan [14] developed an integral model for a discharge from a river channel over a horizontal or a sloping bottom into a reservoir or a lake to determine dilution up to plunging for density current computations. Using a series of laboratory experiments in a two-layered ambient stratification, Cortes and colleagues [15] developed a theory to predict the partition of the buoyancy flux into the interflow and underflow and how a gravity current splits in two upon reaching the sharp density step.
Two-dimensional hydrodynamic models were developed to study density current by assuming that the density current does not participate in the dynamics of heating and mixing; rather, the entrainment takes place from the ambient reservoir into the downflow [16,17,18]. Gu [19] used a validated two-dimensional (2D) simulation model CE-QUAL-W2 [20] to systematically quantify the effects of inflow and ambient parameters on the behavior of a density-induced contaminant current in various flow regimes in a stratified reservoir through numerical experiments. The k-ε turbulence model has been applied to study density currents plunging into reservoirs [21,22]. Bournet [23] developed the modified k-ε model with buoyancy effects to describe the characteristics of density currents in terms of plunge point and entrainment in an inclined channel of constant width and then in a diverging channel. Soliman and colleagues [24] developed a 2D multi-phase numerical model for incompressible, immiscible, and variable density fluids based on Navier-Stokes equations. Shlychkov and Krylova [25] proposed a numerical model for studying the dynamic mixing of sea and river waters in estuary areas, which is based on 2D longitudinal vertical stratified fluid mechanics equations and an equation of salt transport.
Several studies about three-dimensional (3D) gravity currents have been conducted recently using laboratory data and numerical models [26,27,28]. In the last several decades, 3D Environmental Fluid Dynamics Code (EFDC) (Hamrick 1992) has been widely used in modeling river, estuarine, and coastal hydrodynamics and transport processes. Hamrick and Mills [29] developed and used the EFDC model to simulate thermal transport and water temperature distributions in Conowingo Pond that were influenced by thermal discharges from the Peach Bottom atomic power plant. In order to quantify numerical and modeled entrainment, Kulis and Hodges [30] explored the grid resolution required in EFDC to capture gravity current motions in an idealized basin with and without a turbulence closure. Their study was based on the underflow from Oso Bay into Corpus Christi Bay in Texas, USA. Liu and Garcia [31] used a modified 3D EFDC model to simulate the density current and bi-directional flows in the Chicago River system. Xie et al. [32] used a calibrated 3D EFDC model developed for the Yangtze River estuary to study the migration behavior of the movement of fine silt particles in dumped silt. Lyubimova et al. [33] used 3D numerical simulations and in situ measurements to study the upstream propagation of vertical stratification of water mineralization, which is observed only under small (200 m3/s) or moderate (700 m3/s) seasonal flow rates but absent when flow rates in the rivers are larger than 1400 m3/s. Do An [34] used the Flow-3D [35] model to simulate the propagation dynamics of density currents under the same conditions as the laboratory experimental setup and focused on the intrusive density flows into a two-layer ambient fluid.
There are many studies about flow in natural systems such as flows from a river into a lake, a reservoir, an ocean, or an estuary. Fatih and Varcin [36] developed a mathematical model solving nonlinear, unsteady continuity, momentum, energy, and k-ε turbulence equations and applied the model to successfully simulate the formation of density currents and plunging flow in Eğrekkaya Dam Reservoir. Wells and Nadarajah [37] presented theoretical and laboratory experiments describing the intrusion depth of a density current into a linearly stratified water column. They concluded that, if the buoyancy flux of a dense current was to double while the stratification in ambient water remained constant, then the intrusion depth would only increase by 25%, whereas doubling the stratification would result in a 50% decrease of the intrusion depth. Soliman and colleagues [24] applied the 2D multi-phase numerical model to simulate the density current propagation and salinity intrusion into the Ohashi River, which connects the Nakaumi and Shinji coastal lakes, and concluded that further refinement of the model is needed for field study application. Biton and colleagues [38] studied density current formation and flow dynamics in the northern Gulf of Eilat, Red Sea, and demonstrated how the intrinsic nonlinearity of density currents, which is poorly represented in the general circulation model, affects properties of simulated density currents. Owens et al. [39] provided hourly measurements to study stream plunging and used the hydrodynamic and transport model ELCOM (Estuary Lake and Coastal Ocean Model) [40] to simulate the plunging behavior of two tributaries in Onondaga Lake, New York, USA. Cook and Richmond [41] conducted a field monitoring study and used the Flow-3D [35] model to simulate the complex 3D density currents at the Clearwater and Snake River confluence and discovered several predictable stratification patterns that would develop depending upon the discharge ratio and the thermal gradients between the two rivers. Jackson et al. [42] studied density currents in the Chicago River that mostly resulted from salinity differences between the North Branch and the main stem of the Chicago River, whereas temperature difference does not appreciably affect the creation of density currents.
In our previous study [43], preliminary simulation results using particle tracking show that particles of water released from Smith Dam could take several days to reach Cordova and Gorgas upstream cross section (GOUS); the momentum developed by the releases pushed the cooler water near the river bottom downstream. The momentum or pushing effect from the large release provides driving force for the density current movement along the river bottom in the river-reservoir system. In this study, we focus on understanding and analysis of formation and propagation of density currents under different short-duration (a few hours) large flow releases into a confined river-reservoir system. We studied constant small release (2.83 m3/s), single large releases (140 m3/s), and daily repeated large releases from an upstream reservoir. The primary objective of this study is to perform a series of model scenario runs and conduct in-depth result analysis to further investigate flow dynamics and temperature distributions in order to understand and quantify the formation and propagation of density currents caused by daily repeated upstream releases of different durations and solar heating. The model simulations include solar heating during the day and cooling during the night through the water surface. Both daily repeated intermittent releases and solar heating are different from other laboratory experimental studies and simple numerical experiments in which the density current only moves downstream under existing density stratification and due to inflow momentum from one constant release. The results of this study are important with regards to water quality modeling and management, habitat assessment in rivers, and management of thermal discharges from a power plant. The once-through cooling water system for the power plant in the study area is designed to withdraw cold water from the bottom layers at the river inlet to maintain high plant efficiency.

2. Study Area

The study deals with model simulations of flow and temperature in a river-reservoir system (124.2 river km) stretching from Smith Dam Tailrace (SDT) to Bankhead Lock & Dam (BLD, about 23.5 m height and 426.7 m long) in Alabama (AL), USA (Figure 1). The river reach from upstream to downstream includes Sipsey Fork (21.9 km), the lower Mulberry Fork (70.6 km), and a reservoir segment (31.7 km) of Bankhead Lake. Sipsey Fork and the lower Mulberry Fork are the riverine portions of Bankhead Lake. The Black Warrior River is formed about 40 km west of Birmingham, AL, by the confluence of the Mulberry Fork and the Locust Fork, which join as arms of Bankhead Lake, a narrow reservoir formed by constructing BLD in 1963. The study area is referred here as the Bankhead river-reservoir system (BRRS).
The bottom elevations along the centerline of BRRS in the upstream portion of BRRS (Figure 1b) ranged from about 65.8 to 77.2 m above mean sea level (using the 1998 North American Vertical Datum). The average bottom slope is 0.014% but there are local slope variations (ranging from −0.2% to 0.2% over each ~2 km distance). The water surface elevation in BRRS depends on water releases from Lewis Smith Dam, flows from its tributaries (Upper Mulberry, Locust Fork, Lost Creek and Blackwater Creek), and the water surface elevation in BLD, which is influenced by outflow through hydro turbines, spillage through gates of BLD, and loss of water through the Bankhead navigation lock. A typical water surface profile after a large release from Smith Dam (displayed in Figure 1b) depicts the response of water level increase in the upstream portion of BRRS from Smith Dam to the Gorgas upstream cross section (GOUS, Figure 1c).
The water release from Smith Dam to BRRS is normally 2.83 m3/s, but during late spring, summer, and early fall a large amount of intermittent water is released to meet peak electric generating demand. During normal water releases, water depths in Sipsey Fork range from 2.16 to 4.55 m, in the lower Mulberry Fork from 4.71 to 11.47 m, and in the Bankhead Lake from 12.12 to 17.73 m. The water surface elevation at Bankhead L&D is typically about 77.66 m (with relatively small variations) above mean sea level.
The monitoring stations and selected cross sections for result analysis are shown in Figure 1c and summarized in Table 1 including abbreviations used thereafter and descriptions. The middle cross section of Sipsey Fork (MSF) is located 11.1 km downstream from SDT. The cross section at a short distance (0.64 km) upstream of the junction of Sipsey Fork and the upper Mulberry Fork is called UPJ. The middle cross section between the junction and Cordova is called MJC. The monitoring station 5.58 km upstream of the power plant is called GOUS (Figure 1c).
Water 07 06244 g001 1024
Figure 1. (a) Geographic location of the study area—Bankhead river-reservoir system (BRRS); (b) Longitudinal bottom elevation along the centerline of BRRS and water surface elevation after a large release from the Smith Dam tailrace (SDT) to GOUS; (c) Color contours of the bottom elevation showing Sipsey Fork, the lower Mulberry Fork, and Black Warrior River as the model simulation domain; two monitoring stations (Cordova and GOUS); model upstream and downstream boundary locations: Smith Dam tailrace (SDT) and Bankhead Lock & Dam (BLD); three cross sections for reporting simulation results (MSF, UPJ and MJC).
Figure 1. (a) Geographic location of the study area—Bankhead river-reservoir system (BRRS); (b) Longitudinal bottom elevation along the centerline of BRRS and water surface elevation after a large release from the Smith Dam tailrace (SDT) to GOUS; (c) Color contours of the bottom elevation showing Sipsey Fork, the lower Mulberry Fork, and Black Warrior River as the model simulation domain; two monitoring stations (Cordova and GOUS); model upstream and downstream boundary locations: Smith Dam tailrace (SDT) and Bankhead Lock & Dam (BLD); three cross sections for reporting simulation results (MSF, UPJ and MJC).
Water 07 06244 g001
Table
Table 1. Abbreviations and descriptions of cross-sectional locations used in the study (Figure 1c).
Table 1. Abbreviations and descriptions of cross-sectional locations used in the study (Figure 1c).
AbbreviationDescription
BLDBankhead Lock & Dam (downstream boundary of EFDC model)
CordovaUSGS 1 monitoring station at Cordova on the lower Mulberry River
GOUSMonitoring station upstream the power plant
MSFMiddle cross section of Sipsey Fork
MJCMiddle cross section between the junction and Cordova
SDTSmith Dam tailrace (upstream boundary of EFDC model)
UPJJust upstream of the junction of Sipsey Fork and the upper Mulberry Fork
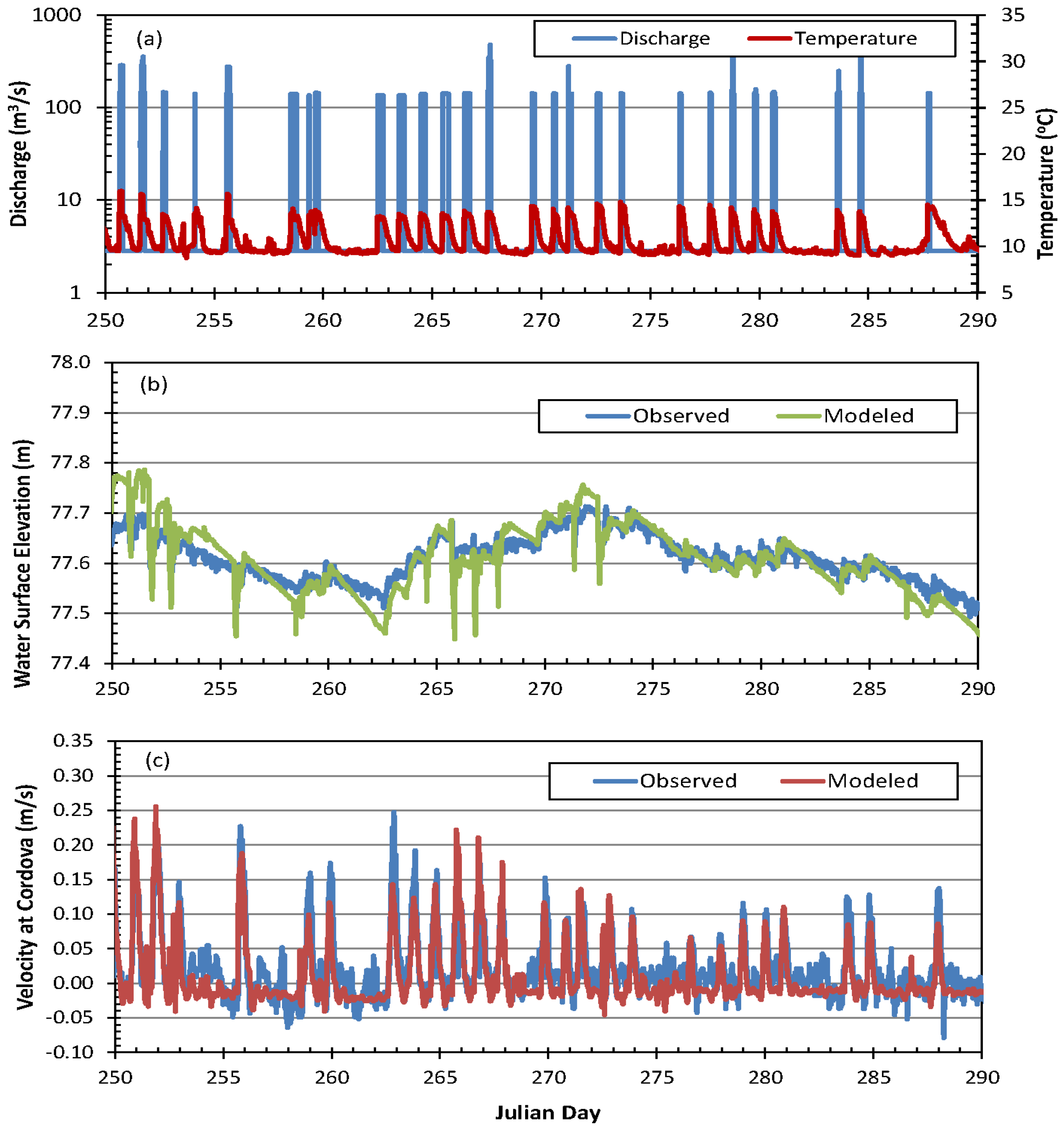
1 USGS stands for the U.S. Geological Survey.

3. Model Application, Boundary Conditions, and Calibration Results

In this study, a three-dimensional (3D) Environmental Fluid Dynamics Code (EFDC) model [44] configured for BRRS [43] was applied to simulate unsteady flow patterns and temperature distributions in BRRS including the intake canal and the discharge canal of a power plant (Figure 1c) near Parrish, AL. This study mainly focuses on the EFDC simulations and result analysis from SDT to GOUS, the upstream portion of BRRS, under different large releases from Smith Dam. The EFDC model is a general-purpose modeling package that can be configured to simulate 1D, 2D and 3D flow, transport, and biogeochemical processes in various surface water systems including rivers, lakes, estuaries, reservoirs, wetlands, and coastal regions [45,46,47,48,49,50]. The Mellor-Yamada level 2.5 turbulence closure scheme [51] is used in EFDC to calculate vertical turbulent diffusion coefficients of momentum and mass, which are linked to vertical turbulent intensity, turbulent length scale, and the Richardson number. Details of governing equations and numerical schemes for EFDC hydrodynamic model are given by Hamrick [44].
In addition to the hydrodynamic model, the EFDC temperature model component was activated to simulate unsteady water temperatures for each computation cell to understand density current movement. While using the EFDC temperature model we have four options for calculating the surface heat exchange. The CE-QUAL-W2 equilibrium method is the most robust method among the four options; therefore, it was used in this study for water temperature modeling. The surface heat exchange includes incident and reflected short and long wave solar radiations, back radiation, evaporative heat loss, and heat conduction from the water surface. The depth distribution of the solar heating (short-wave radiation) after penetrating the water surface is calculated by Beer’s law using a radiation or light attenuation coefficient as one of the model input parameters. Sediment heat exchange with overlying water is also included in the EFDC temperature model. Detailed information on the governing equations for the heat exchange processes in a water body is given in the CE-QUAL-W2 manual [20]. The EFDC hydrodynamic and temperature model applied to BRRS was previously calibrated and validated using extensive field data measured in 2010 and 2011 [43,52].
The upstream boundary of the EFDC model for BRRS is determined through one-minute time-series data of water releases (m3/s) at SDT. There are two types of water releases from Smith Dam: (1) More or less constant continuous release (2.83 m3/s) to support the downstream environment and ecosystem; (2) Intermittent releases from hydro-turbine units of Smith Dam in order to meet peak electric generation demand. Measured water temperatures used for upstream boundary condition at SDT from 8 September to 18 October 2010, were almost constant (9.6 °C) during the constant release, and water temperatures during the intermittent large releases were 10–15 °C, which were 4–5 °C higher than temperatures during the constant release only from Smith Dam (Figure 2a). This is because constant release occurred from a deep water depth and intermittent releases were from a shallower depth of Smith Dam; in addition, there was a lower water temperature in the hypolimnion due to thermal stratification in the summer.
The EFDC model applied for BRRS was calibrated for 2010 and 2011. In the previous study [43], the 3D hydrodynamic EFDC model was applied to simulate unsteady flow patterns and temperature distributions under various upstream releases and variable atmospheric forcing in BRRS in 2011. The calibrated EFDC model provided simulated water surface elevation, temperature, velocity, and discharge at different layers (depths) for all grids in different cross sections.
In addition to the calibration results previously presented [43], Figure 2b shows the time series plot of observed and modeled water surface elevation (WSE) at GOUS from 8 September to 18 October 2010. The agreement between observed and modeled WSEs at GOUS is very good, with a median difference of 0.008 m. The average difference between observed and modeled WSEs at GOUS is −0.020 m. Flow velocities at Cordova measured from 8 September to 18 October 2010 by USGS were compared with modeled results from the EFDC model. Negative velocity in Figure 2c indicates the flow direction from downstream towards upstream due to a backwater effect from BLD. Visually, modeled cross-sectional mean velocities matched reasonably well with observed mean velocities. After each large release from Smith Dam, the velocity at Cordova started to increase from ~0 to 0.12 m/s (depending on the release flow rate and duration), with a few hours of lag. Overall, the EFDC model was able to simulate the temporal and spatial distributions of flow and temperature in BRRS and reveal complex interactions and density currents due to dynamic upstream releases and solar heating from the atmosphere [43].
Water 07 06244 g002 1024
Figure 2. (a) Time-series plot of discharge and water temperature at the Smith Dam tailrace; (b) time-series plot of observed and modeled water surface elevation (m) at GOUS; and (c) time-series plot of modeled (depth averaged) and observed velocity at the USGS Cordova gauging station from 8 September to 18 October (Julian day 250 to 290) 2010.
Figure 2. (a) Time-series plot of discharge and water temperature at the Smith Dam tailrace; (b) time-series plot of observed and modeled water surface elevation (m) at GOUS; and (c) time-series plot of modeled (depth averaged) and observed velocity at the USGS Cordova gauging station from 8 September to 18 October (Julian day 250 to 290) 2010.
Water 07 06244 g002

4. Model Scenarios

In previous model simulations for BRRS [43,52], time series of observed upstream releases, observed or estimated discharges from rivers, observed water levels, and temperatures were used for model boundary conditions. For the scenario analysis performed in this study, various input data (boundary conditions) were modified into constant representative values excluding upstream boundary conditions. Therefore, we can focus on studying the effects of dynamic releases from the upstream reservoir only on density current formations and movement. The inflows from all tributaries and small streams (Figure 1) were set at average inflows calculated from time series of inflows used for model calibration. Average inflows from the Upper Mulberry Fork, Lost Creek, Blackwater Creek, and Locust Fork are 4.42, 5.54, 2.60 and 8.70 m3/s, respectively, for all scenario model runs. At BLD, water level was used as the downstream boundary condition. Observed water surface elevations ranged from 77.35 to 77.75 m from 4 May to 3 September 2011 with an average elevation of 77.60 m (standard deviation of 0.07 m). Therefore, water surface elevation at BLD was set at 77.60 m (constant) for the scenario runs. Based on the sensitivity analysis, the constant water level at BLD would not affect overall flow dynamics in the upstream portion of BRRS (from SDT to GOUS). For the atmospheric boundary conditions, weather data for a relatively warm day of the year were used to perform scenario model runs: hourly climate data from Birmingham, AL [43], on Julian day 140 (20 May 2011) were collected for each 24-h period. Because the diurnal effect (solar heating during the day and cooling during the night) is important, hourly climate variations were kept for model scenario runs but there is no warming and cooling trend over the simulation period (up to 18 days). Hourly air temperatures on 20 May ranged from 19.4 to 31.1 °C, and solar radiation from 57 to 888 watts/m2.
Flow releases from SDT vary during the summer based on power demand. Based on the 2011 release data, average flows during the intermittent release periods ranged from 104.0 to 273.5 m3/s, with average and median flows about 140 m3/s [43]. In 2011, 60.1% of the intermittent releases from SDT had a duration from 2 to 6 h, and most of the releases started around 1:00 p.m. [43]. The percentages of all 2011 releases with durations of about 2 h (from 1.8 to 2.2 h), 4 h (3.8 to 4.2 h), and 6 h (5.8 to 6.2 h) are 5.2%, 15.5% and 14.6%, respectively. Therefore, we used the intermittent daily large releases with these three durations (2, 4 and 6 h) for the sensitivity analysis.
The model scenario runs are distinguished as two groups. The first group of model scenario runs are to study the flow and temperature dynamics that resulted from one large release (LR): Smith Dam has constant small release (CSR, i.e., 2.83 m3/s) for six days, then one large release with different durations in the seventh day, and then CSR for another six days again. The model runs are restarted at the time of Julian day 142.53 (~1:00 p.m. on 22 May) using EFDC’s restart file [53], which was created from the calibration model run. The second group of scenario runs are similar to the actual releases that large flow release repeats day by day after Julian day 140 using EFDC’s restart file [53]. The large releases from Smith Dam have a flow rate of 140 m3/s, which is the average discharge of the intermittent releases from Smith Dam based on data analysis [43], and last for 2, 4 and 6 h for different cases, respectively. In the following discussions, the first group of scenario runs are called 2-, 4- and 6-h single large releases (SLRs), and the second group of scenario runs are called 2-, 4-, and 6-h daily repeated large releases (DRLRs).
The restart file created by the calibration model run starting from Julian Day 104 under actual flow releases in 2011 was used to set initial conditions for EFDC sensitivity model runs in this study. The model spin-up period is about 18 days. The initial conditions such as temperature stratification and water depth are representative environmental conditions in the BRRS in May. If we used initial conditions in June or other months, the specific results presented here might be somewhat different, but the overall conclusions of the study are the same.

5. Results and Discussion

5.1. Velocity Distributions

The density current formation and propagation in the natural system are complex and dynamic. Figure 3 shows simulated vertical velocity profiles at the centerlines of MSF, UPJ, MJC, Cordova and GOUS when DRLRs at SDT last 2, 4 and 6 h each day and at three different times: 1 h after the large release begins (left panels), 4 h after (middle), and 18 h after (right) the large release stops. When the large flow is released for 1 h from Smith Dam, the flow momentum begins to affect the velocities at MSF where water at all layers moves downstream (positive velocity) with a maximum velocity of ~0.15 m/s at the surface for all three duration releases. The velocities at UPJ indicate that the flow momentum effect has not yet reached UPJ at 1 h after release [43]. Flow dynamics at UPJ, MJC, Cordova and GOUS are more complex and may result from the release in previous days, as indicated by and discussed later for velocity profiles at 18 h after release. The density currents are clearly showed in the bottom layers moving downstream at UPJ and GOUS for all three duration DRLRs, and at Cordova for 6-h DRLR.
When the large flow release has stopped for 4 h, for the 2-h DRLR, vertical velocity profiles at Cordova and GOUS have steep gradients with near-zero velocity in the bottom layer. This indicates that the flow momentum for the 2-h DRLR is not strong enough to move/push bottom water and density current at Cordova and GOUS. For 4-h and 6-h DRLRs, the flow momentum reaches GOUS and is strong enough to affect whole velocity profiles because the surface and bottom velocities at GOUS begin to increase. The velocities at all five locations are all positive, which indicates that the flow is moving downstream. Therefore, the momentum effect resulted from the release creates adequate mixing to destroy or wipe out existing density currents at these locations, which are further discussed later using temperature distributions. Vertical velocity distributions at MSF, UPJ and MJC clearly show that longer release durations from Smith Dam result in larger velocities in all depths. The simulated velocities in the surface layer at MJC for 2-h, 4-h and 6-h DRLRs are 0.24, 0.27 and 0.29 m/s, respectively.
When the large flow release has stopped for 18 h, i.e., just before large release starts the next day, the velocities at MSF decrease to less than 0.07 m/s. At UPJ, MJC, Cordova and GOUS, the velocity profiles are similar to the profiles 1 h after the large release (Figure 3). The density current along the channel bottom at UPJ (indicated by positive velocities) can be due to low-discharge constant release with colder temperature. Small negative surface velocities at UPJ may indicate a certain backwater effect from BLD (downstream obstruction). The river-reservoir system in the study is relatively narrow and meandering (Figure 1), hence it is not the wind that changes the flow direction. At MJC and Cordova, flows in the surface layers move downstream with small velocities. At GOUS, the velocities are negative in the surface layers and positive in the bottom layers. These complex flow dynamics are also explained using time-series plots (Figure 4) and should be further studied using the particle tracking method [54,55,56,57] and other advanced analysis methods.
Water 07 06244 g003 1024
Figure 3. Simulated vertical velocity profiles at the centerlines of MSF, UPJ, MJC, Cordova, and GOUS when DRLRs at SDT last 2, 4 and 6 h each day and at three different times: 1 h after the large release begins (a), 4 h (b) and 18 h (c) after the large release stops.
Figure 3. Simulated vertical velocity profiles at the centerlines of MSF, UPJ, MJC, Cordova, and GOUS when DRLRs at SDT last 2, 4 and 6 h each day and at three different times: 1 h after the large release begins (a), 4 h (b) and 18 h (c) after the large release stops.
Water 07 06244 g003
Figure 4 shows time-series plots of simulated velocities in the surface and bottom layers at the centerlines of Cordova and GOUS when DRLRs at SDT last 2, 4 and 6 h each day. In the surface layer at Cordova, the flow moves downstream most of the time for the 2-h, 4-h and 6-h DRLRs (Figure 4a, 93.0%–97.4% in Table 2). There are short periods of time that have negative velocities, which may be due to the backwater effect from BLD. In Figure 4b, velocities in the bottom layer at Cordova start to increase ~4–6 h after each DRLR stops, have a maximum velocity greater than 0.1 m/s (maximum velocity is 0.139 m/s for the 6-h DRLR, Table 2), and have positive magnitude (density currents move downstream) most of the time for the 4-h and 6-h DRLRs. However, for the 2-h DRLR, flow in the bottom layer at Cordova has small velocities (absolute average velocity of 0.015 ± 0.015 m/s) and moves either downstream or upstream. There is a positive bottom velocity 48.4%, 69.0% and 91.1% of the time with average values of 0.017, 0.042 and 0.053 m/s at Cordova for the 2-h, 4-h and 6-h DRLR, respectively (Table 2). Therefore, the momentary effects created by the 2-h DRLR cannot have much impact on the bottom water at Cordova (Figure 4b). The repeated releases with longer durations push the bottom colder water from SDT downstream to form density currents and make the bottom water temperature in downstream locations cooler.
Water 07 06244 g004 1024
Figure 4. Time series of simulated velocities in the surface and bottom layers at the centerlines of Cordova and GOUS when DRLRs at SDT last 2, 4 and 6 h each day. (a): Surface layer at Cordova; (b): Bottom layer at Cordova; (c): Surface layer at GOUS; (d): Bottom layer at GOUS.
Figure 4. Time series of simulated velocities in the surface and bottom layers at the centerlines of Cordova and GOUS when DRLRs at SDT last 2, 4 and 6 h each day. (a): Surface layer at Cordova; (b): Bottom layer at Cordova; (c): Surface layer at GOUS; (d): Bottom layer at GOUS.
Water 07 06244 g004
At GOUS, the surface flow moving upstream is more obvious due to the backwater effect. For the 2-h DRLR, the surface flow mainly moves upstream (66.9% of the time, Table 2). For the 4-h DRLR, the surface flow (with an average velocity of 0.085 m/s) moves downstream when the large momentum from SDT reaches GOUS; the surface flow (with average velocity of 0.069 m/s) also moves upstream when there is a backwater effect from BLD. The durations moving downstream and upstream at GOUS are 140.5 and 99.5 h during the 10 days of simulation (240 h) for the 4-h DRLR (Table 2). For the 6-h DRLR, the surface flow dominantly moves downstream (Figure 4c). The durations moving downstream and upstream are 203.5 (84.8%) and 36.5 h, respectively, during the 10-day simulation period for the 6-h DRLR (Table 2). In the bottom layer at GOUS, it seems that the flow momentum still has a relatively strong impact at GOUS for 6-h DRLRs (Figure 4d), i.e., indication of the movement of density currents at GOUS.
Table
Table 2. Statistical information of simulated velocities (m/s) at Cordova and GOUS.
Table 2. Statistical information of simulated velocities (m/s) at Cordova and GOUS.
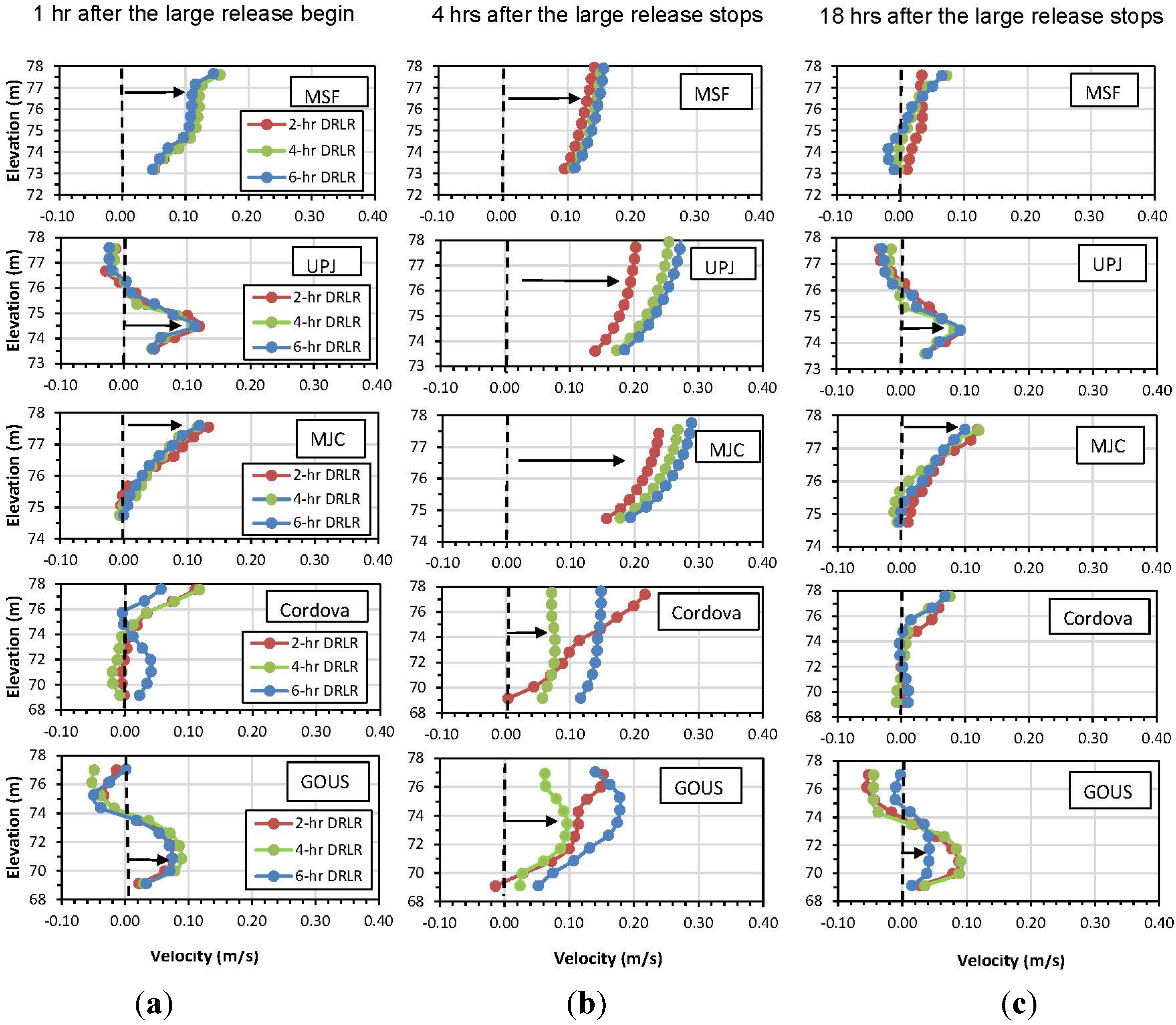
LocationReleaseLayerMaximumAverageDeviationPercent Hours 2
Cordova2-h DRLRSurface0.283 (−0.041) 10.085 (−0.010)0.055 (0.011)97.4% (2.6%)
Bottom0.135 (−0.064)0.017 (−0.013)0.018 (0.012)48.1% (51.9%)
4-h DRLRSurface0.282 (−0.053)0.093 (−0.017)0.060 (0.015)95.2% (4.8%)
Bottom0.142 (−0.052)0.042 (−0.012)0.033 (0.010)69.0% (31.0%)
6-h DRLRSurface0.266 (−0.057)0.104 (−0.021)0.061 (0.015)93.0% (7.0%)
Bottom0.139 (−0.028)0.053 (−0.011)0.038 (0.007)91.1% (8.9%)
GOUS2-h DRLRSurface0.325 (−0.176)0.072 (−0.065)0.066 (0.043)33.1% (66.9%)
Bottom0.172 (−0.104)0.029 (−0.021)0.023 (0.016)62.2% (37.8%)
4-h DRLRSurface0.326 (−0.212)0.085 (−0.069)0.057 (0.052)58.5% (41.5%)
Bottom0.174 (−0.103)0.034 (−0.022)0.027 (0.017)69.1% (30.9%)
6-h DRLRSurface0.285 (−0.164)0.106 (−0.037)0.068 (0.041)84.8% (15.2%)
Bottom0.151 (−0.081)0.038 (−0.015)0.027 (0.011)60.9% (39.1%)
Notes: 1 The first number in each cell is for positive velocities (moving downstream), and the number inside brackets is for negative velocities (moving upstream) for the simulation period: Julian day 140–150. 2 Percentage of hours with positive or negative velocities (numbers inside brackets) in the 10-day simulation period (240 h).

5.2. Temperature Distributions

5.2.1. Single Large Release

To understand how the density current moves under the CSR (2.83 m3/s) and one large release, simulated temperature distributions are calculated for the 4-h SLR simulation. Simulated water temperatures range from 10 °C (blue) to 30 °C (red), as shown by the color contours. Figure 5 shows simulated water temperature distributions from SDT (Distance = 0) to GOUS (~64 km) at six different times: model initial conditions at Day 142.573, after about three and six days of having CSR at SDT, when the 4-h SLR has just stopped in the seventh day, and about one and four days after the large release. Temperature stratification along the depth exists at most locations from SDT to GOUS under the model initial condition (Day 142.573), which was simulated from the calibrated EFDC model and resulted from actual flow releases and solar heating before 142 [43]. Surface temperatures near GOUS are higher because of solar heating effects and the backwater effect when warmer water near the power plant is pushed upstream to GOUS. Due to solar heating, temperature increases and stratification changes at most cross sections after three or six days having only CSR. Surface temperatures from MSF to GOUS are all greater than 25 °C at Julian Day 148.52 (six days). With the CSR only, the cold water current (blue) near SDT has moved downstream about 4 km in six days. With the 4-h SLR, the cold water can move from Smith Dam to UPJ (~22 km) in a few hours.
Water 07 06244 g005 1024
Figure 5. Simulated water temperature distributions from SDT to GOUS at six different times for the 4-h SLR simulation: at the beginning of the model run (initial conditions), after about three and six days with CSR, when the 4-h SLR stops (on the seventh day), and about one and four days after SLR.
Figure 5. Simulated water temperature distributions from SDT to GOUS at six different times for the 4-h SLR simulation: at the beginning of the model run (initial conditions), after about three and six days with CSR, when the 4-h SLR stops (on the seventh day), and about one and four days after SLR.
Water 07 06244 g005
The simulated water temperatures increase further due to the solar heating if there is no large release in the next few days. The CSR (2.83 m3/s) after the SLR still forms the cold water or density current and moves slowly downstream, but the density current near SDT without much momentum does not have much effect on downstream water movement. One day after SLR, density currents form in the bottom layers in different parts of BRRS from SDT to GOUS; two examples of density currents are shown by dashed-dark-line polygons (Figure 5). Density or temperature stratifications have developed due to solar heating when inflow momentum vanishes. Density currents are also discontinuous because some parts of BRRS have weak or no stratification after release. Due to the interaction of the large release and solar heating with ambient water in BRRS, the density current formation and propagation before and after a SLR are complex and dynamic.
Surface temperature warms up continuously in the surface layers due to solar heating in the 12 days of the simulation period (Figure 5). At four days after the large release, water temperatures at most depths become higher. These temperature increases are due to solar heating. Surface temperature increases may also be related to the backwater effect from the downstream boundary (BLD).
Figure 6 shows time-series plots of simulated water temperatures in the surface and bottom layers at MSF and Cordova for four sensitivity runs: CSR only, 2-h, 4-h and 6-h SLR. For CSR, surface and bottom temperatures gradually increase with time due to the solar heating.
Water 07 06244 g006 1024
Figure 6. Time series of simulated water temperatures in the surface and bottom layers at MSF and Cordova for four sensitivity runs: CSR only, 2-h, 4-h and 6-h SLRs. (a): MSF; (b): Cordova.
Figure 6. Time series of simulated water temperatures in the surface and bottom layers at MSF and Cordova for four sensitivity runs: CSR only, 2-h, 4-h and 6-h SLRs. (a): MSF; (b): Cordova.
Water 07 06244 g006
The typical water depth at MSF is 4.9 m, smaller than the depth at Cordova (9.2 m). At MSF after six days, the bottom temperatures have smaller variations, while the surface temperatures still fluctuate with air temperature. At Cordova, the bottom temperature has a smaller increase but the increase lasts for more days. The SLR starts at 1:00 p.m. on Julian day 148. Due to the momentum effect and mixing, both surface and bottom water temperatures at MSF have quickly dropped to ~12 °C shortly after the large release starts from SDT (Figure 6a). Surface and bottom temperatures begin to increase at a few hours after release, more or less continuously increase for about five days, and eventually reach the temperatures simulated under CSR. The 2-, 4- and 6-h SLRs have similar impacts on water temperature at MSF. When the flow momentum from an SLR comes to Cordova, longer-period SLR has more mixing and keeps the surface temperature lower (Figure 6b). The 2-h and 4-h SLRs have little effect on the bottom temperature at Cordova. The flow momentum from the 6-h SLR seems strong enough to mix or stir the bottom water, and its temperature fluctuates for a few hours then gradually increases with time (Figure 6b) due to solar heating. Figure 6 shows that one SLR does not have a long-term impact on downstream surface and bottom temperatures. Regular (daily repeated) large releases are required to maintain downstream temperature stratification, which will be discussed in the next section.

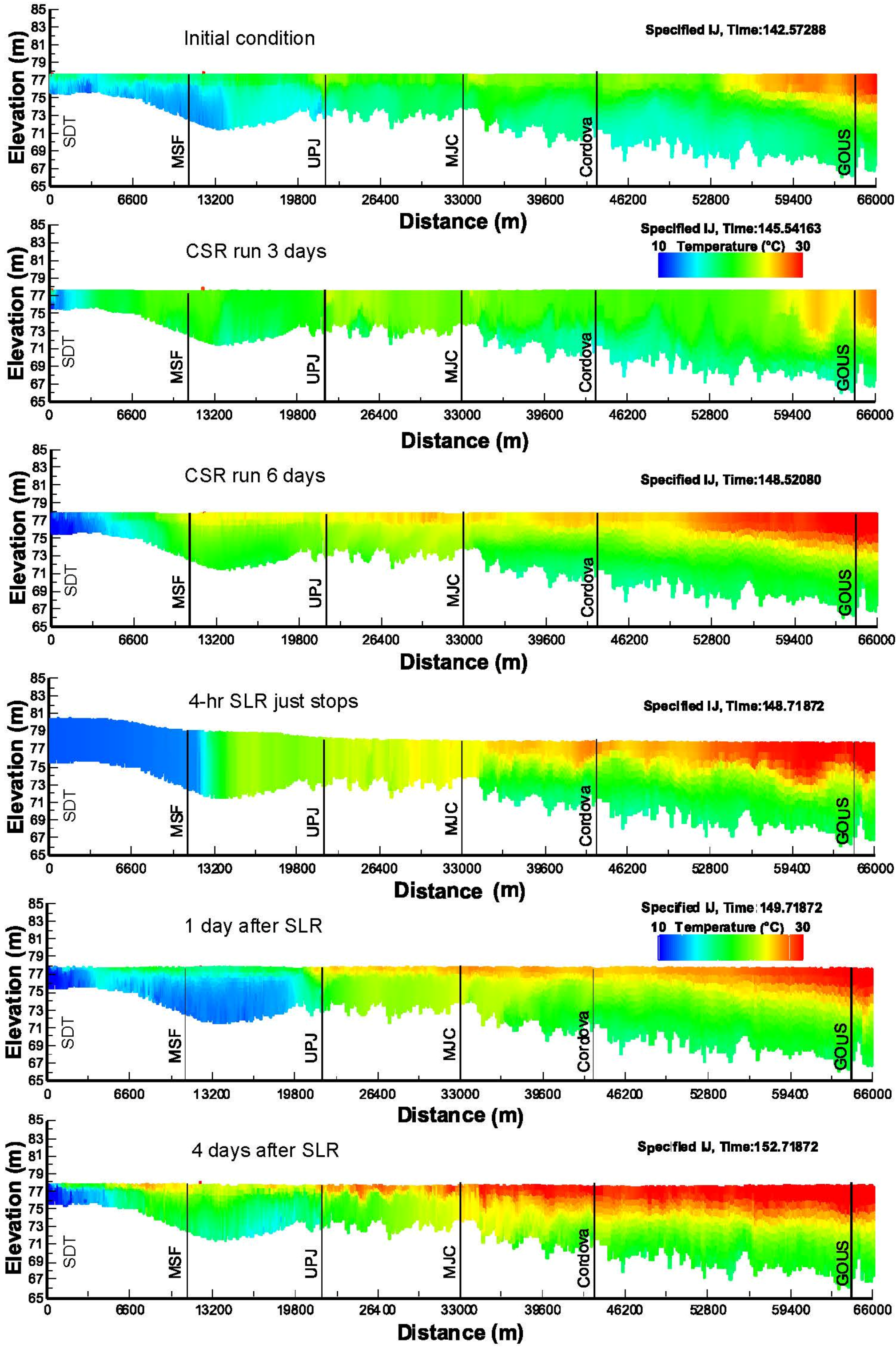
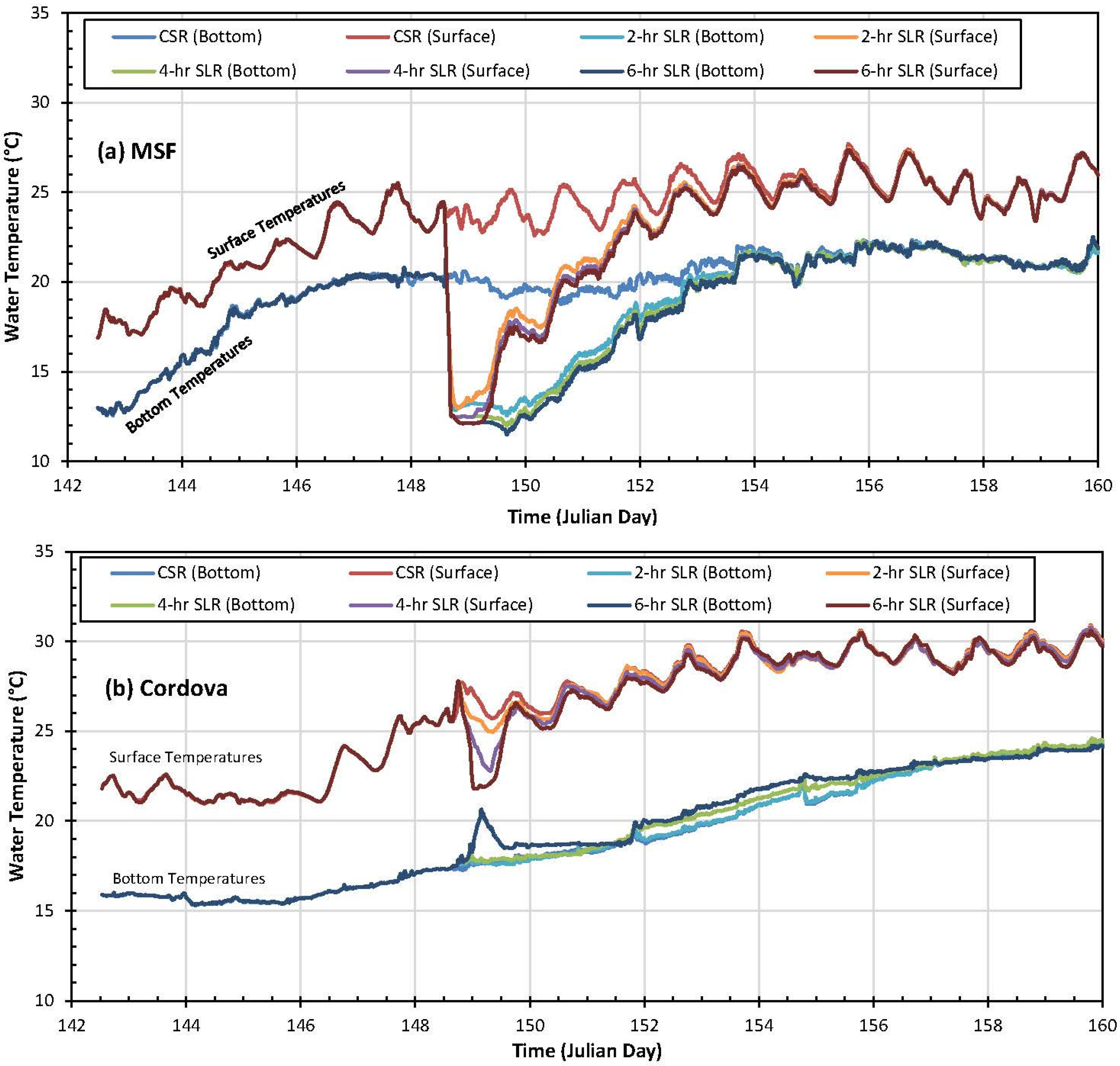
5.2.2. Daily Repeated Large Releases

In comparison to an SLR, DRLRs are closer to the actual releases to BRRS during the summer, which might have daily variations in discharge and duration; and occasionally there is no large release for one or two days [43]. Figure 7 shows the simulated water temperature distributions for 2-h, 4-h and 6-h DRLRs at three different times: (a) just before the large release on Day 142, (b) after the large release has just stopped, and (c) when SDT’s WSE decreases to the normal level. In comparison to 2-h and 4-h DRLRs, 6-h DRLR can push cold water further downstream and surface temperatures are less affected by the solar heating. Figure 7a shows that the bottom layer temperatures from SDT to GOUS after two days of 4-h and 6-h DRLRs are cooler than temperatures for 2-h DRLRs because large releases started on Julian Day 140 and were repeated every day. Without DRLR, the water temperature in BRRS increases gradually due to the warmer air temperature and solar heating. After the large release stops (Figure 7b), a relatively large longitudinal temperature gradient develops and is from ~10 °C at SDT to ~20 °C at GOUS when large flow momentum with colder water pushes relatively warmer water in BRRS downstream. Temperature stratification is very weak in the upstream part of BRRS due to the momentum mixing; for example, water has almost no vertical stratification from SDT to UPJ for 2-h DRLR, to MJC for 4-h DRLR, and to Cordova for 6-h DRLR (Figure 7b). This indicates that the momentum effect for the 6-h DRLR definitely reaches Cordova (~43.7 km from SDT). From Figure 6c, it seems that colder, denser water moves from downstream MSF to UPJ due to the remaining momentum of the 6-h DRLR. When the flow momentum pushes water downstream, it also mixes pre-existing water in rivers. The density currents moving downstream gradually form in the next day due to the remaining momentum along the bottom layers and solar heating. Before the next large release, density currents forming at different parts of BRRS are similar to ones shown in Figure 7a.
Figure 8 shows the simulated water temperature distributions at 12:45 on Julian day 146 for 2-h, 4-h and 6-h DRLRs since the first DRLR started on Julian Day 140 (21 May), i.e., DRLRs lasted for six days. By comparing with Figure 7a, which is only two days after 21 May, the 4- and 6-h DRLRs that lasted for six days can make the downstream temperature cooler, especially for the reach from Cordova to GOUS. The momentum effect can also make the surface warmer water downstream at GOUS when 6-h DRLRs were repeated for less than six days. The 4- and 6-h DRLRs lasting for six days result in temperature decreases from UPJ to GOUS for Julian day 142 and 143 (Figure 7). However, the 2-h DRLRs lasting for six days cannot override or compensate for the solar heating effect because water temperatures from UPJ to GOUS increase on Julian days 142 (Figure 7a) and 143 (Figure 7c). DRLRs with longer durations push colder density currents (highlighted by dashed-line polygons) further downstream from SDT.
Water 07 06244 g007a 1024Water 07 06244 g007b 1024
Figure 7. Simulated water temperature distributions for 2-h, 4-h and 6-h DRLRs at three different times: (a) just before the large release; (b) after the large release has just stopped; and (c) when SDT’s WSE decreases to normal levels.
Figure 7. Simulated water temperature distributions for 2-h, 4-h and 6-h DRLRs at three different times: (a) just before the large release; (b) after the large release has just stopped; and (c) when SDT’s WSE decreases to normal levels.
Water 07 06244 g007aWater 07 06244 g007b
Water 07 06244 g008 1024
Figure 8. Simulated water temperature distributions for 2-h, 4-h and 6-h DRLRs lasting for six days from Julian Day 140 (21 May).
Figure 8. Simulated water temperature distributions for 2-h, 4-h and 6-h DRLRs lasting for six days from Julian Day 140 (21 May).
Water 07 06244 g008
Results of sensitivity model runs for 2-h, 4-h and 6-h DRLRs are shown in Figure 9, including results for CSR only for comparison. At MSF, which is close to the release location (SDT), surface and bottom water temperatures are well mixed during each DRLR (Figure 9a). Simulated water temperatures remain constant for a few hours during the night. When the sun rises the next day, the surface water temperature gradually increases. For the longer repeated release, the water temperatures at MSF are a little bit cooler (Figure 9a). Compared with the simulated temperatures for SLRs (Figure 6), DRLRs can have a lasting impact on water temperatures in the surface (Figure 9b) and bottom (Figure 9c) layers at Cordova. Simulated surface temperatures at Cordova have certain daily variations due to solar heating and cooling (diurnal effects) but do not gradually increase with time instead of maintaining lower average temperatures during the simulation period.
Water 07 06244 g009 1024
Figure 9. Time series of simulated water temperatures in the surface and bottom layers at MSF and Cordova for CSR only, 2-, 4- and 6-h DRLRs. (a): MSF; (b): Cordova Surface; (c): Cordova Bottom.
Figure 9. Time series of simulated water temperatures in the surface and bottom layers at MSF and Cordova for CSR only, 2-, 4- and 6-h DRLRs. (a): MSF; (b): Cordova Surface; (c): Cordova Bottom.
Water 07 06244 g009
Overall average bottom temperatures at Cordova are lower for longer-duration DRLRs: 19.63 °C for the 4-h and 18.24 °C for the 6-h. For bottom temperatures at Cordova, the 4-h and 6-h DRLRs can maintain lower water temperatures with small daily variations, but for the 2-h DRLR temperatures still show a gradual increase with time. The bottom temperatures simulated with the 4-h and 6-h DRLRs are higher than temperatures under CSR for the first 6–8 days because cooler bottom water temperatures are mixed with warmer surface temperatures by the large flow momentum. Simulated bottom temperatures at Cordova under the 2-h DRLR are larger than ones under CSR in the first 14 days, but become lower afterwards, which eventually exhibits the effect of DRLR.

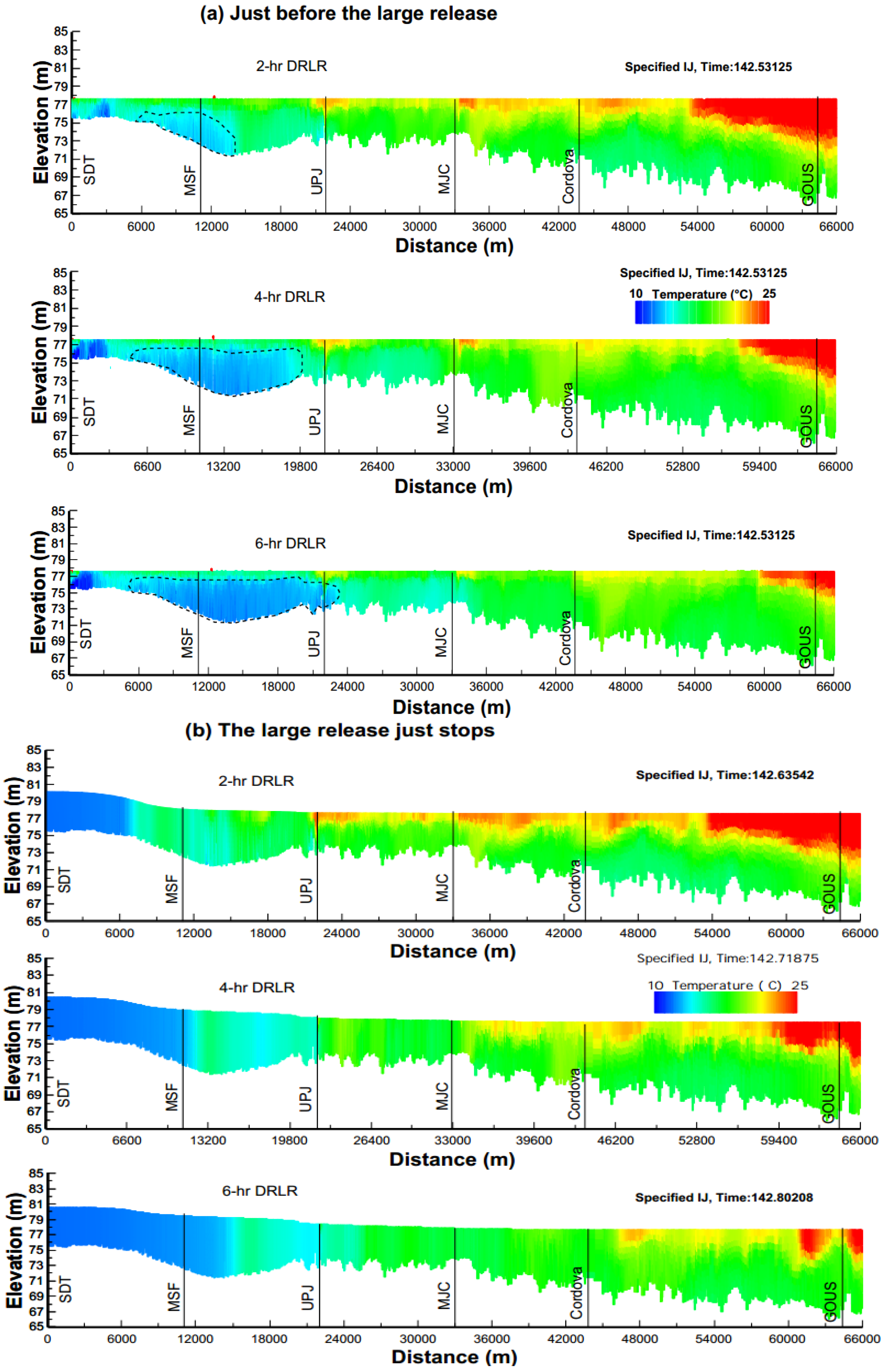
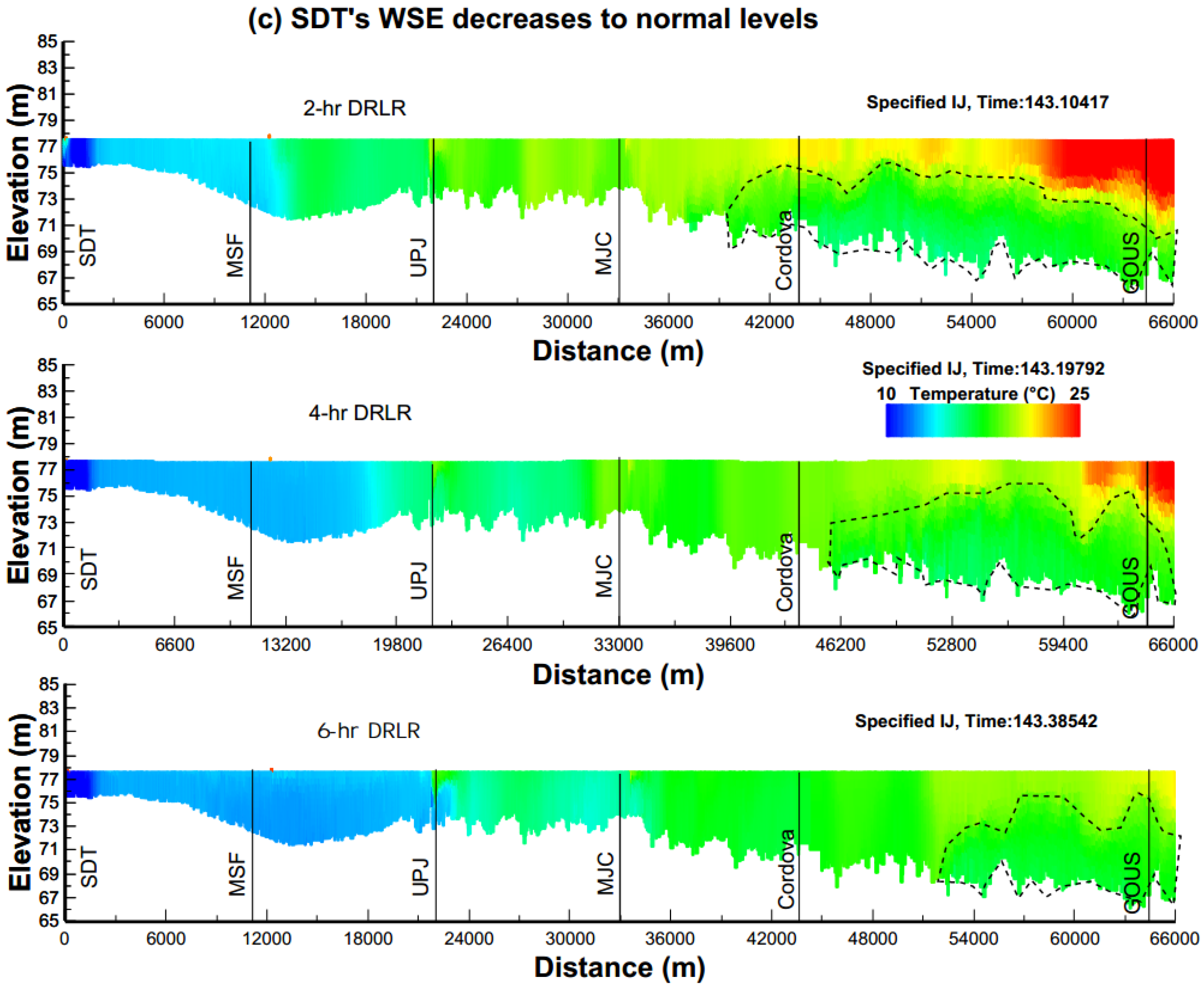
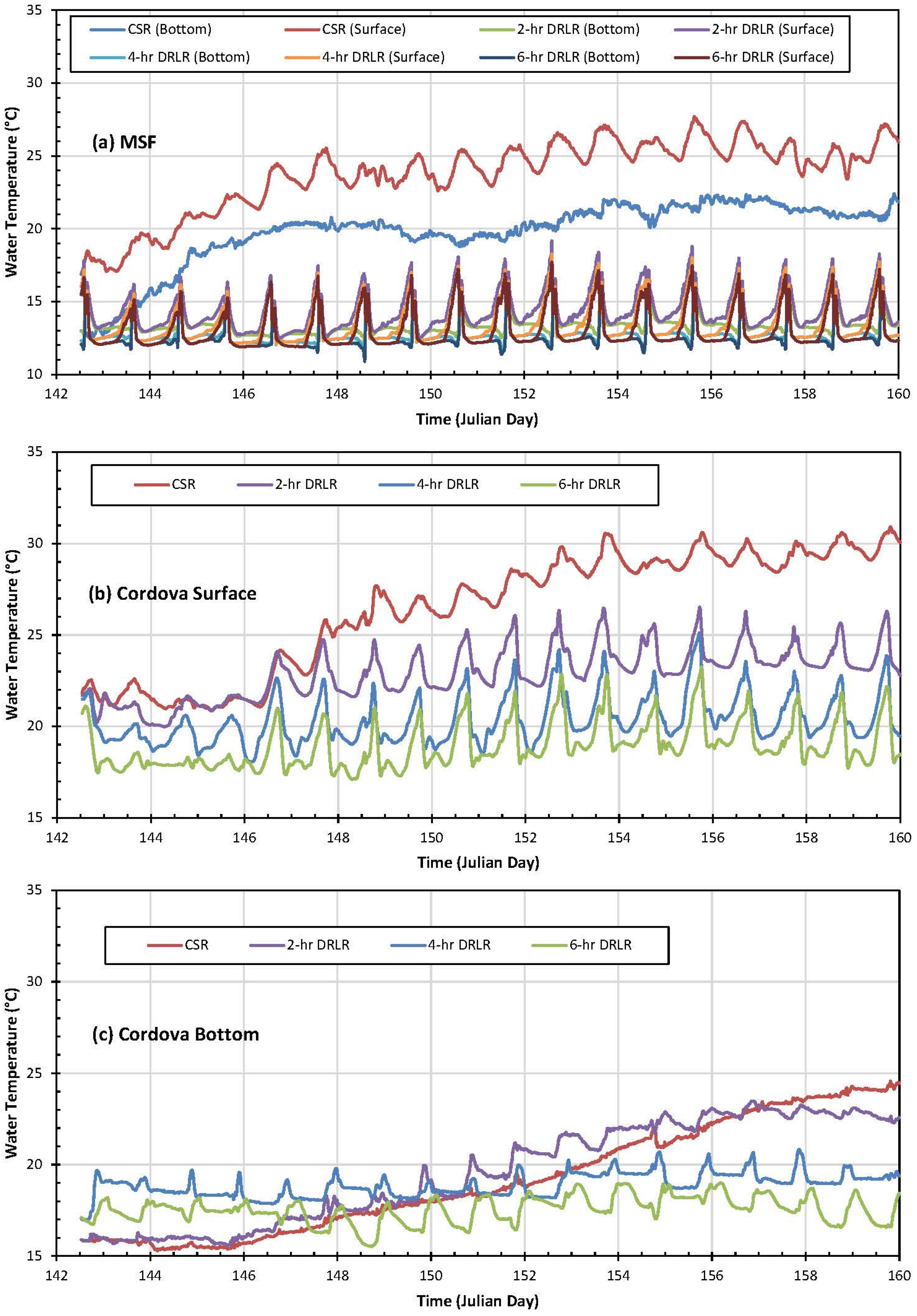
5.2.3. Comparison between CSR and DRLR

For CSR only, surface and bottom temperatures at Cordova increase by more than 8 °C over the 17 simulation days due to solar heating (Figure 9). The average differences between surface and bottom temperatures for CSR only are 3.99, 7.26 and 12.45 °C at MSF, Cordova, and GOUS (Table 3), respectively. The strength of the vertical temperature stratification increases from upstream to downstream, which is primarily due to the increase of the water depth. For DRLRs, the average differences between surface and bottom temperatures are much smaller (e.g., <1 °C at MSF) due to the large flow momentum to mix water (Table 3). For three DRLRs, the average temperature differences at Cordova are larger than ones at MSF (Table 3). The temperature differences between surface and bottom layers at GOUS (Table 3) indicate that DRLRs with longer duration (such as 6-h) result in stronger mixing downstream and can still have a strong impact on temperature dynamics and stratification at GOUS (~64 km from SDT).
Table
Table 3. Statistical summary of simulated differences (°C) between surface and bottom temperatures at MSF, Cordova, and GOUS for CSR only, 2-h, 4-h and 6-h DRLRs.
Table 3. Statistical summary of simulated differences (°C) between surface and bottom temperatures at MSF, Cordova, and GOUS for CSR only, 2-h, 4-h and 6-h DRLRs.
LocationRelease TypeDifference (Surface–Bottom) (°C)
MaximumMinimumAverageDeviation
MSFCSR6.601.713.991.08
2-h DRLR6.60−0.020.941.32
4-h DRLR6.35−0.010.761.32
6-h DRLR5.72−0.010.651.26
CordovaCSR10.444.967.261.43
2-h DRLR7.51−0.013.352.02
4-h DRLR6.07−0.011.471.37
6-h DRLR5.61−0.011.381.51
GOUSCSR14.629.2012.450.97
2-h DRLR13.636.6611.331.35
4-h DRLR12.241.888.532.40
6-h DRLR10.790.584.712.69
For time-series plots in Figure 9, the average differences of surface temperatures simulated under the 6-h DRLR and CSR only are −10.63 °C at MSF and −7.53 °C at Cordova (Table 4). The average differences of bottom temperature simulated under the 6-h DRLR and CSR only are −7.49, 1.64 and −1.10 °C at MSF, Cordova and GOUS, respectively (Table 4). The average difference of bottom temperatures at Cordova between 2-h DRLR and CSR is positive (0.38 °C) but negative (−0.30 or −16.4 °C) between 4-h or 6-h DRLR and CSR only (Table 4).
Time series of simulated water temperatures in the surface and bottom layers at GOUS have similar patterns as ones at Cordova under different releases, so they are not plotted in Figure 9. After 17 days of daily repeated releases (Julian day 142 to 160), bottom temperatures at GOUS simulated with 2-, 4- and 6-h DRLR are 1.64, 2.06 and 3.35 °C lower than from CSR only. Results in Figure 9 and Table 3 and Table 4 clearly show that DRLRs lasting for at least 4 h maintain lower water temperatures at Cordova and GOUS. When the 4-h and 6-h DRLRs repeat for more than 6 and 10 days, respectively, bottom temperatures at Cordova become lower than those for CSR. These releases overwhelm the mixing effects due to flow momentum and maintain downstream temperature stratification.
Table
Table 4. Statistical summary of differences (°C) of simulated temperatures between 2-h, 4-h and 6-h DRLRs and CSR only for surface and bottom layers at MSF, Cordova, and GOUS.
Table 4. Statistical summary of differences (°C) of simulated temperatures between 2-h, 4-h and 6-h DRLRs and CSR only for surface and bottom layers at MSF, Cordova, and GOUS.
LocationTemp DifferenceMaximumMinimumAverageDeviation
MSF (Surface)2-h DRLR-CSR0.23−13.72−9.352.49
4-h DRLR-CSR−0.41−14.65−10.252.56
6-h DRLR-CSR−0.92−14.67−10.632.53
Cordova (Surface)2-h DRLR-CSR0.36−7.35−3.532.24
4-h DRLR-CSR−0.33−10.82−6.102.84
6-h DRLR-CSR−1.01−12.63−7.532.76
GOUS (Surface)2-h DRLR-CSR0.67−3.90−1.490.70
4-h DRLR-CSR−0.55−9.43−4.291.65
6-h DRLR-CSR−1.56−12.91−8.842.20
MSF (Bottom)2-h DRLR-CSR3.53−9.23−6.302.39
4-h DRLR-CSR3.00−9.95−7.012.35
6-h DRLR-CSR2.75−10.23−7.292.34
Cordova (Bottom)2-h DRLR-CSR2.19−2.080.380.81
4-h DRLR-CSR3.98−5.11−0.302.63
6-h DRLR-CSR2.72−7.98−1.642.86
GOUS (Bottom)2-h DRLR-CSR1.20−2.88−0.380.70
4-h DRLR-CSR1.06−2.95−0.380.90
6-h DRLR-CSR0.54−4.48−1.101.17

6. Conclusions

The 3D EFDC model configured for BRRS was applied to simulate unsteady flow patterns and temperature distributions under large releases with different durations from SDT (upstream boundary). This study mainly focuses on result analyses of the EFDC simulations from SDT to GOUS, the upstream portion of BRRS. A series of model scenario or sensitivity runs were performed to understand and quantify the formation and propagation of density currents caused by upstream releases and solar heating when all other input variables were kept unchanged. The summaries of key findings from the study are as follows:
(a) The density current formation and propagation in the natural system under intermittent large releases are complex and dynamic. The density currents in BRRS form at different reaches, are destroyed at upstream locations due to the flow momentum of the releases, and form again due to solar heating. Both the duration of large releases and solar heating affect and control the formation and spread of density currents when the release flow rate is unchanged (140 m3/s).
(b) There is a positive bottom velocity (density currents moving downstream) 48.4%, 69.0% and 91.1% of the time, with an average positive velocity of 0.017, 0.042, and 0.053 m/s at Cordova for the 2-h, 4-h and 6-h DRLR, respectively (Table 2). The repeated releases with longer durations push the colder bottom water from SDT downstream and make the bottom water temperature in downstream locations cooler. For the 6-h DRLR, the momentum effect definitely reaches Cordova (~43.7 km from SDT).
(c) With CSR only, the cold water current (blue color) near SDT has moved downstream about 4 km in six days. With the 4-h SLR, the cold water density current can move from Smith Dam to UPJ (21 km) in a few hours (Figure 5). However, time-series plots of simulated surface and bottom temperatures at MSF and Cordova show that one SLR does not have a long-term impact on downstream surface and bottom temperatures (Figure 6). Regular (daily repeated) large releases are required to push density currents downstream and maintain temperature stratification in downstream locations (Figure 9).
(d) Overall average surface and bottom temperatures are lower for longer durations of DRLR. The average difference between surface and bottom temperatures for 6-h DRLR is 1.38 °C, while for 2-h DRLR it is 3.35 °C at Cordova (Table 3). Results in Figure 9 and Table 3 and Table 4 clearly show that DRLRs lasting for at least 4 h maintain lower water temperatures at Cordova and GOUS. When the 4-h and 6-h DRLRs repeat for more than 6 and 10 days, respectively, bottom temperatures at Cordova become lower than those for CSR only. These releases overwhelm the mixing effects due to flow momentum and maintain temperature stratification.

Acknowledgments

The authors wish to express their thanks to Jonathan B. Ponstein, P.E. (Professional Engineer), and Thomas B. Weems for providing necessary observation data, and Janesh Devkota for the EFDC model development and calibration for BRRS. Gang Chen wishes to express his gratitude to the Chinese Scholarship Council for financial support pursuing his graduate study at Auburn University. Thanks for the comments from two reviewers.

Author Contributions

Gang Chen planned the study, applied and configured the EFDC model for BRRS, ran the model for all sensitivity cases, performed data analyses of model results, and wrote the first draft of the manuscript. Xing Fang provided valuable instructions on study design, supervised the data analyses, and reviewed and revised the manuscript. Both authors contributed significantly in writing the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Serruya, S. The mixing patterns of the jordan river in lake kinneret. Limnol. Oceanogr. 1974, 19, 175–181. [Google Scholar] [CrossRef]
  2. Smith, P.C. A streamtube model for bottom boundary currents in the ocean. Deep Sea Res. Oceanogr. Abstr. 1975, 12, 853–873. [Google Scholar] [CrossRef]
  3. Carmack, E.C.; Gray, C.B.; Pharo, C.H.; Daley, R.J. Importance of lake-river interaction on seasonal patterns in the general circulation of kamloops lake, british columbia. Limnol. Oceanogr. 1979, 24, 634–644. [Google Scholar] [CrossRef]
  4. Fischer, H.B.; Smith, R.D. Observations of transport to surface waters from a plunging inflow to lake mead 1. Limnol. Oceanogr. 1983, 28, 253–272. [Google Scholar] [CrossRef]
  5. Alavian, V.; Ostrowski, P., Jr. Use of density current to modify thermal structure of tva reservoirs. J. Hydraul. Eng. 1992, 118, 688–706. [Google Scholar] [CrossRef]
  6. Chikita, K. The role of sediment-laden underflows in lake sedimentation: Glacier-fed peyto lake, canada. J. Fac. Sci. Hokkaido Univ. Ser. VII Geophys. 1992, 9, 211–224. [Google Scholar]
  7. Akiyama, J.; Stefan, H.G. Plunging flow into a reservoir: Theory. J. Hydraul. Eng. ASCE 1984, 110, 484–499. [Google Scholar] [CrossRef]
  8. Hauenstein, W.; Dracos, T. Investigation of plunging density currents generated by inflows in lakes. J. Hydraul. Res. 1984, 22, 157–179. [Google Scholar] [CrossRef]
  9. Alavian, V. Behavior of density currents on an incline. J. Hydraul. Eng. 1986, 112, 27–42. [Google Scholar] [CrossRef]
  10. Singh, B.; Shah, C. Plunging phenomenon of density currents in reservoirs. Houille Blanche 1971, 1, 59–64. [Google Scholar] [CrossRef]
  11. Savage, S.; Brimberg, J. Analysis of plunging phenomena in water reservoirs. J. Hydraul. Res. 1975, 13, 187–205. [Google Scholar] [CrossRef]
  12. Denton, R. Density current inflows to run of the river reservoirs. In Proceedings of the 21st IAHR World Congress, Melbourne, Australia, 13–18 August 1985.
  13. Kranenburg, C. Gravity current fronts advancing into horizontal ambient flow. J. Hydraul. Eng. 1993, 119, 369–379. [Google Scholar] [CrossRef]
  14. Fang, X.; Stefan, H.G. Dependence of dilution of a plunging discharge over a sloping bottom on inflow conditions and bottom friction. J. Hydraul. Res. 2000, 38, 15–25. [Google Scholar] [CrossRef]
  15. Cortés, A.; Rueda, F.; Wells, M. Experimental observations of the splitting of a gravity current at a density step in a stratified water body. J. Geophys. Res. Oceans 2014, 119, 1038–1053. [Google Scholar] [CrossRef]
  16. Imberger, J.; Patterson, J. Dynamic reservoir simulation model-dyresm: 5. In Transport Models for Inland and Coastal Waters; Academic Press: New York, NY, USA, 1981; pp. 310–361. [Google Scholar]
  17. Buchak, E.M. Simulation of a Density Underflow into Wellington Reservoir Using Longitudinal-Vertical Numerical Hydrodynamics; JE Edinger Associates: Washington, DC, USA, 1984. [Google Scholar]
  18. Jokela, J.; Patterson, J. Quasi-two-dimensional modelling of reservoir inflow. In Proceedings of the 21st Congress, International Association for Hydraulic Research, Melbourne, Australia, 19–23 August 1985.
  19. Gu, R.R. Impact of inflow and ambient conditions on density-induced current in a stratified reservoir. Mod. Phys. Lett. B 2009, 23, 429–432. [Google Scholar] [CrossRef]
  20. Cole, T.M.; Wells, S.A. CE-QUAL-W2: A Two-Dimensional, Laerally Averaged, Hydrodynamic and Water Quality Model; U.S. Army Engineering and Research Development Center: Vicksburg, MS, USA, 2010. [Google Scholar]
  21. Farrell, G.J.; Stefan, H.G. Buoyancy Induced Plunging Flow into Reservoirs and Costal Regions; Anthony Falls Hydraulics Laboratory: Minneapolis, MN, USA, 1986. [Google Scholar]
  22. Fukushima, Y.; Watanabe, M. Numerical simulation of density underflow by the k-ε turbulence model. J. Hydrosci. Hydr. Eng. 1990, 8, 31–40. [Google Scholar] [CrossRef]
  23. Bournet, P.; Dartus, D.; Tassin, B.; Vincon-Leite, B. Numerical investigation of plunging density current. J. Hydraul. Eng. 1999, 125, 584–594. [Google Scholar] [CrossRef]
  24. Soliman, M.; Ushijima, S.; Kantouch, S. Density current propagation in a tidal river. In River Flow 2014; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
  25. Shlychkov, V.A.; Krylova, A.I. A numerical model of density currents in estuaries of siberian rivers. Numer. Anal. Appl. 2014, 7, 255–261. [Google Scholar] [CrossRef]
  26. Imran, J.; Islam, M.A.; Huang, H.; Kassem, A.; Dickerson, J.; Pirmez, C.; Parker, G. Helical flow couplets in submarine gravity underflows. Geology 2007, 35, 659–662. [Google Scholar] [CrossRef]
  27. An, S.; Julien, P.Y. Three-dimensional modeling of turbid density currents in Imha Reservoir, South Korea. J. Hydraul. Eng. 2014, 140. [Google Scholar] [CrossRef]
  28. Firoozabadi, B.; Afshin, H.; Aram, E. Three-dimensional modeling of density current in a straight channel. J. Hydraul. Eng. 2009, 135, 393–402. [Google Scholar] [CrossRef]
  29. Hamrick, J.M.; Mills, W.B. Analysis of water temperatures in conowingo pond as influenced by the peach bottom atomic power plant thermal discharge. Environ. Sci. Policy 2000, 3, 197–209. [Google Scholar] [CrossRef]
  30. Kulis, P.; Hodges, B.R. Modeling gravity currents in shallow bays using a sigma coordinate model. In Proceedings of the 7th International Conference on Hydroscience ann Enginnering, Philadelphia, PA, USA, 10–13 September 2006.
  31. Liu, X.; Garcia, M.H. Numerical simulation of density current in Chicago river using environmental fluid dynamics code (EFDC). In Proceedings of World Environmental & Water Resource Congress, Honolulu, HI, USA, 12–16 May 2008.
  32. Xie, R.; Wu, D.-A.; Yan, Y.-X.; Zhou, H. Fine silt particle pathline of dredging sediment in the yangtze river deepwater navigation channel based on efdc model. J. Hydrodyn. Ser. B 2010, 22, 760–772. [Google Scholar] [CrossRef]
  33. Lyubimova, T.; Lepikhin, A.; Konovalov, V.; Parshakova, Y.; Tiunov, A. Formation of the density currents in the zone of confluence of two rivers. J. Hydrol. 2014, 508, 328–342. [Google Scholar] [CrossRef]
  34. Do An, S. Three-dimensional numerical simulation of intrusive density currents. J. Environ. Sci. Int. 2014, 23, 1223–1232. [Google Scholar] [CrossRef]
  35. Hirt, C.; Nichols, B. Flow-3D User’s Manual; Flow Science Inc.: Santa Fe, NM, USA, 1988. [Google Scholar]
  36. Fatih, Ü.; Varcin, H. Investigation of plunging depth and density currents in eğrekkaya dam reservoir. Teknik Dergi 2012, 23, 5725–5750. [Google Scholar]
  37. Wells, M.; Nadarajah, P. The intrusion depth of density currents flowing into stratified water bodies. J. Phys. Oceanogr. 2009, 39, 1935–1947. [Google Scholar] [CrossRef]
  38. Biton, E.; Silverman, J.; Gildor, H. Observations and modeling of a pulsating density current. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
  39. Owens, E.M.; Effler, S.W.; Prestigiacomo, A.R.; Matthews, D.A.; O’Donnell, S.M. Observations and modeling of stream plunging in an urban lake. J. Am. Water Resour. Assoc. 2012, 48, 707–721. [Google Scholar] [CrossRef]
  40. Hodges, B.; Dallimore, C. Estuary, Lake and Coastal Ocean Model: Elcom; Science Manual; Centre of Water Research, University of Western Australia: Perth, Australia, 2006. [Google Scholar]
  41. Cook, C.B.; Richmond, M.C. Monitoring and simulating 3-D density currents at the confluence of the snake and clearwater rivers. In Critical Transitions in Water And Environmental Resources Management; American Society of Civil Engineers (ASCE): Salt Lake City, UT, USA, 2004. [Google Scholar]
  42. Jackson, P.R.; García, C.M.; Oberg, K.A.; Johnson, K.K.; García, M.H. Density currents in the chicago river: Characterization, effects on water quality, and potential sources. Sci. Total Environ. 2008, 401, 130–143. [Google Scholar] [CrossRef] [PubMed]
  43. Chen, G.; Fang, X.; Devkota, J. Understanding Flow Dynamics and Density Currents in a River-Reservoir System under Upstream Reservoir Releases. Avaliable online: http://www.tandfonline.com/doi/abs/10.1080/02626667.2015.1112902 (accessed on 27 October 2015).
  44. Hamrick, J.M. A Three-dimensional Environmental Fluid Dynamics Code: Theoritical and Computational Aspects; Virginia Institute of Marine Science: Gloucester Point, VA, USA, 1992. [Google Scholar]
  45. Shen, J.; Lin, J. Modeling study of the influences of tide and stratification on age of water in the tidal james river. Estuar. Coast. Shelf Sci. 2006, 68, 101–112. [Google Scholar] [CrossRef]
  46. Jeong, S.; Yeon, K.; Hur, Y.; Oh, K. Salinity intrusion characteristics analysis using EFDC model in the downstream of geum river. J. Environ. Sci. 2010, 22, 934–939. [Google Scholar] [CrossRef]
  47. Kim, C.-K.; Park, K. A modeling study of water and salt exchange for a micro-tidal, stratified northern gulf of mexico estuary. J. Mar. Syst. 2012, 96–97, 103–115. [Google Scholar] [CrossRef]
  48. Devkota, J.; Fang, X. Numerical Simulation of Flow Dynamics in a Tidal River Under Various Upstream Hydrologic Conditions. Avaliable online: http://www.tandfonline.com/doi/pdf/10.1080/02626667.2014.947989 (accessed on 27 August 2015).
  49. Wang, Y.; Shen, J.; He, Q. A numerical model study of the transport timescale and change of estuarine circulation due to waterway constructions in the Changjiang estuary, China. J. Mar. Syst. 2010, 82, 154–170. [Google Scholar] [CrossRef]
  50. Caliskan, A.; Elci, S. Effects of selective withdrawal on hydrodynamics of a stratified reservoir. Water Resour. Manag. 2009, 23, 1257–1273. [Google Scholar] [CrossRef]
  51. Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. Space Phys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
  52. Fang, X.; Weems, T.B.; Devkota, J.; Chen, G. Watershed Modeling, Water Balance Analysis, Three-Dimensional Flow and Thermal Discharge Modeling for the William C. Gorgas Plant; Department of Civil Engineering: Auburn, AL, USA, 2013. [Google Scholar]
  53. Craig, P.M. User’s Manual for EFDC_Explorer 7: A Pre/Post Processor for the Environmental Fluid Dynamics Code; Dynamic Solutions-International, LLC: Edmonds, WA, USA, 2012. [Google Scholar]
  54. Harlow, F.H. The Particle-in-Cell Method for Numerical Solution of Problems in Fluid Dynamics; Los Alamos Scientific Lab.: Los Alamos, NM, USA, 1962. [Google Scholar]
  55. Ahlstrom, S.; Foote, H.; Arnett, R.; Cole, C.; Serne, R. Multicomponent Mass Transport Model: Theory and Numerical Implementation (Discrete-Parcel-Random-Walk Version); Battelle Pacific Northwest Labs.: Richland, WA, USA, 1977. [Google Scholar]
  56. Abrahams, A.D.; Parsons, A.J.; Luk, S.H. Field measurement of the velocity of overland flow using dye tracing. Earth Surf. Process. Landf. 1986, 11, 653–657. [Google Scholar] [CrossRef]
  57. Guo-Qing, H.; Yuan-Jie, D.; Hui, W.; Xian-Kui, Q.; Yan-Hua, W. Laboratory testing of magnetic tracers for soil erosion measurement. Pedosphere 2011, 21, 328–338. [Google Scholar] [CrossRef]

Share and Cite

MDPI and ACS Style

Chen, G.; Fang, X. Sensitivity Analysis of Flow and Temperature Distributions of Density Currents in a River-Reservoir System under Upstream Releases with Different Durations. Water 2015, 7, 6244-6268. https://doi.org/10.3390/w7116244

AMA Style

Chen G, Fang X. Sensitivity Analysis of Flow and Temperature Distributions of Density Currents in a River-Reservoir System under Upstream Releases with Different Durations. Water. 2015; 7(11):6244-6268. https://doi.org/10.3390/w7116244

Chicago/Turabian Style

Chen, Gang, and Xing Fang. 2015. "Sensitivity Analysis of Flow and Temperature Distributions of Density Currents in a River-Reservoir System under Upstream Releases with Different Durations" Water 7, no. 11: 6244-6268. https://doi.org/10.3390/w7116244

APA Style

Chen, G., & Fang, X. (2015). Sensitivity Analysis of Flow and Temperature Distributions of Density Currents in a River-Reservoir System under Upstream Releases with Different Durations. Water, 7(11), 6244-6268. https://doi.org/10.3390/w7116244

Article Metrics

Back to TopTop