Abstract
Rainfall, one of the most important climate variables, is commonly studied due to its great heterogeneity, which occasionally causes negative economic, social, and environmental consequences. Modeling the spatial distributions of rainfall patterns over watersheds has become a major challenge for water resources management. Multifractal analysis can be used to reproduce the scale invariance and intermittency of rainfall processes. To identify which factors are the most influential on the variability of multifractal parameters and, consequently, on the spatial distribution of rainfall patterns for different time scales in this study, universal multifractal (UM) analysis—C1, α, and γs UM parameters—was combined with non-parametric statistical techniques that allow spatial-temporal comparisons of distributions by gradients. The proposed combined approach was applied to a daily rainfall dataset of 132 time-series from 1931 to 2009, homogeneously spatially-distributed across a 25 km × 25 km grid covering the Ebro River Basin. A homogeneous increase in C1 over the watershed and a decrease in α mainly in the western regions, were detected, suggesting an increase in the frequency of dry periods at different scales and an increase in the occurrence of rainfall process variability over the last decades.
1. Introduction
Rainfall is one of the most important climate variables studied due to its non-homogenous behavior in terms of events and intensity, which creates drought, water runoff, and soil erosion with negative environmental and social consequences [1]. A change in the rainfall pattern will limit the storage of water that must occur during the winter to meet the heavy demands during the dry season [2].
Recently, several researchers have indicated that climate change will likely result in greater temperatures and lower rainfall in Mediterranean regions while increasing the intensity of extreme rainfall events [3,4,5]. These changes could have consequences for the rainfall regime [6], erosion [7], sediment transport and water quality [8], soil management [9], and the requirements of newly-designed diversion ditches [10]. Climate change is expected to result in increasingly unpredictable and variable rainfall, in both amount and timing, changing seasonal patterns, and increasing frequency of extreme weather events [11].
Water supplies in the Ebro River Basin, a Mediterranean area, present high seasonal fluctuations with extreme rainfall events during autumn and spring, and demands are increasingly stressed during the summer. Simultaneously, the repeated anomalous annual fluctuations in recent decades have become a serious concern for the regional hydrology, agriculture, and related industries in the region [12]. This scenario has resulted in devastating social and economic impacts and has led to debate over the changing seasonal patterns of rainfall and the increasing frequency of extreme rainfall events. Thus, it is extremely important to model rainfall events and trends in the Ebro River Basin.
To describe the precipitation in the Ebro River Basin, several authors have used different databases. Some authors have focused on data from specific meteorological stations and others have investigated irregularly distributed data networks, such as MOPREDAS [13]. Several techniques aim to statistically describe the precipitation pattern, but the results from these techniques applied to rainfall patterns in the study area show small variations between them. Consequently, these techniques do not always fulfill the predictions expressed by the models of the Intergovernmental Panel on Climate Change [14]. Significant increases in seasonal precipitation mainly occur in the Central Pyrenees and northeast of the Ebro Basin and are accompanied by a clear decrease in summer rainfall [15]. Additionally, De Luis et al. [16] used the MOPREDAS database from 1951 to 2000 and concluded that precipitation decreased by nearly 12% in the last period, mainly during winter. However, the conclusions made by these authors seem contradictory, which indicates the influences of the databases used. On the other hand, Valencia et al. [17] concluded that the extreme rainfall events did not increased in agreement with De Luis et al. [15].
The aims of this study are to (1) obtain more uniform results that are independent of the data base used by applying multiscaling techniques and to (2) detect and analyze significant rainfall patterns in the Ebro River Basin by modeling the spatial distributions that hydrologically characterize the watershed. To achieve these aims, an approach that combines multifractal techniques that allow for the reproduction of scale invariance and the intermittency of rainfall events, and non-parametric statistical techniques that allow for spatial-temporal comparisons of the distributions in the study area, was proposed in this paper. Multifractal analysis was developed to study turbulent intermittency and was adapted to provide a good description of the statistics at all orders and for a wide range of fields [18,19,20,21,22,23]. One of these fields consists of rainfall changes that result from climate change [24,25]. The statistical multifractal nature of rainfall has been intensively studied over the last two decades [18,19,20,21,22,23,24,25,26,27,28,29,30,31]. Among the different multifractal analyses, the multifractal analysis used by Lavallée et al. [32,33] and Royer et al. [24] was applied. These authors described and used the universal multifractal (UM) model and obtained two parameters, the intermittency (C1) and the Levy index (α), as well as a combination of them, the maximal probable singularity (γs). With these parameters, any conservative data field can be statistically characterized and used to analyze its scaling nature.
The combined approach proposed in this research applies as a first step time series analysis with non-parametric statistics to identify annual rainfall trends from 1931 to 2009. Then, multifractal analysis was used and UM parameters were estimated over the Ebro River Basin to compare two temporal periods. Finally, spatial and temporal analysis of the UM parameters based on non-parametric statistical techniques was applied to study the possible significant variations of the UM parameters based on geographical position, altitude and mean rainfall. Consequently, a homogeneous increase in the intermittency C1 over the Ebro River Basin and a decrease in the α index, mainly in the western areas of the watershed, were detected, which indicated that the frequency of dry periods at different scales increased over the last decades.
2. Materials and Methods
2.1. Study Area and Data
The Ebro River Basin covers an area of approximately 85,000 km2, is located in Northeast Spain, and is characterized by the high spatial heterogeneity of its geology, topography, climatology, and land use. The Ebro River is one of the most important rivers for Spanish water policy and supplies water through water transfer projects to other river basins affected by desertification in some areas of Spain [34]. This area is characterized by the presence of mountains that border the north (Pyrenees) and south (Iberian System and Catalan Mountains coastal chain), allowing the river to pass through a large depression to the southeast. For additional details, see [34] and the references therein.
Rainfall in this area is highly spatially variable. More than 1000 mm of rainfall occurs per year in the northern mountains, while semi-desert areas located in the interior of the depression experience average rainfall of up to 300 mm. Furthermore, the precipitation varies interannually and intermonthly. Rainfall is sparse throughout most of the basin, except in the north, and mainly occurs during the autumn and spring seasons.
The scaling behavior of precipitation in the area corresponding to the Ebro River Basin was evaluated using 132 complete and regular spatial rainfall daily data series elaborated by the “Servicio de Desarrollos Climatológicos” of the Spanish Meteorological Agency (AEMET) [35,36,37,38]. Each one of these time series was obtained using spatial interpolation by kriging and a grid of 25 km × 25 km. These daily rainfall series include 79 years, from 1931 to 2009, and cover the Ebro Basin with regular intervals, as shown in Figure 1, where each point represents the localization of the square center of the geographical area associated with each series. In order to obtain these spatially interpolated series, more than 1500 original rainfall series were used although with very irregular length. Some rainfall series have few years, while others have collected information from the 79 years under study but with some lags. The original gauges of weather stations are pluviometers or pluviographs that have not changed their location since were installed, although no changes are discarded in the vicinity of the stations due to human activity. AEMET ensures the reliability of these data, which have been compared with other databases on a global scale such as the ECMWF and NCEP, and other on a regional scale such as HIPOCAS, proving that they are more realistic [39]. In AEMET-gridded data, it is noteworthy that their extreme rainfall events are very close to the original ones and that the numbers of rainy days remain very close to the original ones [36]. Due to this minimization in the smoothing of rainfall series, the error that usually occurs in multifractal analysis when data are imputed in interpolation methods is reduced. Each series was subdivided into two overlapping periods, from 1931 to 1975 and from 1965 to 2009, to analyze the difference between both. Each period contains the same number of days, 16,834 (214), to achieve higher multifractal analysis efficiency.
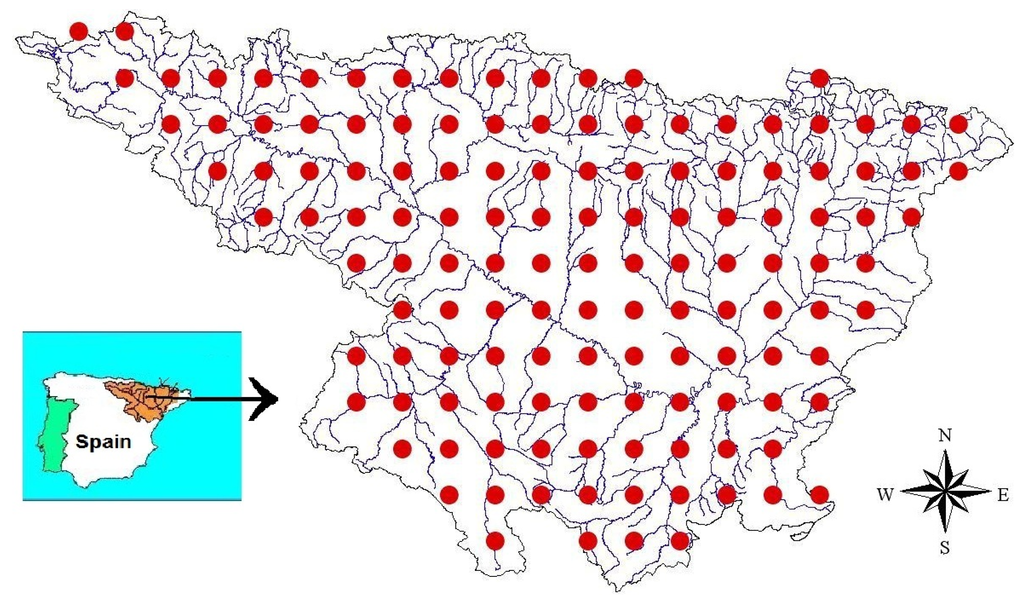
Figure 1.
Geographical areas in the Ebro River Basin. Each area has an associated daily rainfall time-series from 1931 to 2009.
2.2. Trend Test
Before evaluating the UM parameters, it is important to check for trends in the time-series. For this purpose, the Mann-Kendall test was used [40] because it has robust statistical properties. This test is valid for non-normal or cyclical data, such as rainfall data. The null hypothesis for this test is as follows H0: (no correlation between series and time) against Ha: (correlation between series and time). This test is very simple and calculates the difference, Dif, between the number of years i < j for which y(i) < y(j) and the number of years i < j for which y(i) > y(j), where y(k) represents the rainfall along the year k. Finally, because the data under study constitute a long time series, the Mann-Kendall statistic can be calculated as follows:
where n represents the number of years in each rainfall data series. The null hypothesis is rejected at a significance level of α if , where α represents the probability of concluding that there exists trend (increasing or decreasing) in the rainfall time series when such a trend does not really exists (probability of type I error in the test), Z is the standard normal distribution (Z ~ N (μ = 0, σ = 1)) and Zα/2 is the value that verifies Prob {Z > Zα/2} = α/2.
2.3. Spectral Analysis
Spectral methods, known as Fourier transform methods, were applied before performing a multifractal analysis. Spectral analysis is an approach for studying the statistical properties of a time series by using an intuitive frequency-based description [41,42]. The power spectrum, defined as the distribution of variance or power across the frequency, can be of intrinsic interest [43,44]. If a process contains periodic terms, the frequencies of these terms exhibit several high and sharp peaks in the spectrum. This result indicates that a significant amount of variance is contained in these frequencies [44]. Classical spectral analysis consists of interpreting the variance density distribution spectrum S(f) across different scales (frequencies in this case).
where f is the frequency, < > indicates the use of average values that vary with t, and is the autocorrelation function of the measurement process x(t).
The objective of this type of analysis is to determine the frequency intervals over which the spectrum follows the power law behavior (Equation (3)), at least for a certain frequency interval, because it is a necessary but not sufficient condition for guaranteeing statistical self-affinity and, therefore, fractal characterization [45].
The spectral exponent β in Equation (3) contains information regarding the degree of non-stationarity of the data. In the case β ≤ 1, the process is stationary; otherwise (β > 1), the process cannot be stationary. Daily rainfall datasets from the Ebro River Basin were examined to determine whether the spectral exponent was below a threshold of 1; if so, the evaluation of UM parameters can be carried out confidently. Otherwise (β > 1) the UM analysis should simply be carried out on the conservative part of the field obtained by fractionally integrating it [33].
2.4. UM Model
When there are no trends in the time series under study and the spectral exponents are below one, the multifractal behavior can be studied. Because the network of daily rainfall time series associated to Figure 1 is regular and extensive, the estimated values of the UM parameters will oscillate in a continuous way among neighboring geographical areas, offering a global realistic vision of the rainfall patterns within the Ebro River Basin, helping to posterior spatial analysis.
The UM model assumes that multifractals are generated from a random variable with an exponentiated extreme Levy distribution [18,24,26,32]. In UM analysis, the scaling exponent K(q) is highly relevant. K(q) relates the moment of order q of the field with the scale by the next expression <ελq> ≈ λK(q), where λ is the scale ratio, which is inversely proportional to the size of the measurement interval. The scaling exponent function K(q) for the moments q of a cascade conserved process is obtained according to [46] as follows:
where C1 and α are aforementioned UM parameters. Then, these multifractal functions can be characterized using the following three parameters, where the last one is a combination of the two previous:
- 1)
- C1 is the mean intermittency codimension, which estimates how concentrated the average of the measure is [45]. If the C1 value is low (near 0), the field (daily rainfall process in the present work) is similar to the average almost everywhere. However, when C1 is greater than 0.5, the field achieves very low values with respect to the average in most time series data, except in a few cases in which the measured value is much higher than the average value. This parameter can also be considered as an indicator of average fractality;
- 2)
- α is the Levy index and indicates the distance from a monofractality case [47]. The range of this parameter is [0, 2]. When the value of this parameter is two, a lognormal distribution case occurs; if 1 < α < 2, log Levy processes with unbounded singularities occur; if α = 1, the log-Cauchy distribution occurs; if 0 < α < 1, the Levy process with bounded singularities occurs; and when α = 0, the monofractal process occurs, which indicates the grade of variance of the measure [48]. Higher Levy index values represent extreme measurements that are more frequent (extreme rainfall events in the present work);
- 3)
- γs is the maximum probable singularity that can be observed from a unique sample of data and can be obtained from the other two parameters [24]. In addition, γs is directly related to the ratio of the range to the mean of the field. Here, the notion of singularity relates to an index used to characterize the variation of statistical behavior of data values as the measuring scale changes. Its distribution is consistent with the distribution of the anomalies of rainfall that result in anomalous amounts of energy releases at a fine (spatial and temporal) scale [46].
To obtain these multifractality parameters, the Double Trace Method (DTM) was applied. This method also evaluates estimations of the standard deviations of these parameters. For further details see Lavallée et al. [32] and Tessier et al. [18]. This technique was applied separately for each one of the 132 daily precipitation series relative to the square areas with similar amplitudes over the two selected periods of 1931–1975 and 1965–2009 by using previously described methods [49].
2.5. Temporal Comparison Test of the UM Parameters
According to the aim of this study to evaluate the UM parameters evolution between the two periods, a comparison statistical test was applied to each of the three multifractal parameters in each geographical area. To determine if the estimated values of the UM parameters were significantly different between each temporal period, these differences and their variances were evaluated. Then, based on the 95th percentile of the normal distribution, the UM parameter was assumed to change when the absolute value of the difference was greater than:
where li,j,s represents the estimated value of the j UM parameter in the i area and during the s period and V corresponds to the variance function, which was approximated by adding the variances of the two estimated values under comparison (different estimations of the UM parameters are generated by varying q in the final regression of the DTM method, allowing to obtain an estimation of the variance of each UM parameter in each period and geographical area).
Then, after comparing the UM parameters in the two temporal periods, each geographical area for each UM parameter can be classified as follows: areas with a statistically significant increase in the parameter (+), areas with a statistically significant decrease in the parameter (–), and areas that have non-significant statistical differences in the parameter (0).
2.6. Spatial Comparison Test of the Distributions of UM Parameter Evolutions
In combination with the UM model, statistical analysis was applied based on the Cramer-Von Mises non-parametric statistical test to compare the distributions of the UM parameter evolutions—increase (+), decrease (–), and stability (0)—along the different gradients in the Ebro River Basin. This method creates a dummy normalized variable for each of these three trend types (+, –, 0) and for each UM parameter (C1, α, γs). Therefore, nine variables were obtained, where the associated variables for each of the three UM parameters can be represented as follows:
Then, the density functions for the associated variables for each one of the UM parameters were defined as:
where i is a square geographical area, j is one of the UM parameters (C1, α or γs), n+,j is the number of square areas with a positive trend for parameter j, n−,j is the number of areas with a negative trend for parameter j, and n0,j is the number of areas without a trend for parameter j.
A generalization of the Cramer-Von Mises statistic was calculated as the squared difference between two cumulative distributions of f for opposite significant trends by adding values obtained from all sampling locations in the direction of the gradient [50,51,52]. Thus, this cumulative distribution was denoted as F as follows:
where represents the generalized Cramer-Von Mises statistic when comparing increasing trends distributions with decreasing trends distributions. The other two statistics, and , were calculated using a similar process.
When constructing the empirical distribution functions of Equation (8), the square geographical areas were selected based on an increasing gradient. The gradients used in this study were longitude, latitude, distance to the main river basin axis, distance to the river mouth, mean rainfall, and altitude. The order of the geographical areas is inherent to the gradient used, except for the longitude and the latitude gradients, for which this order must be specified due to its bivariate dimension.
To construct the empirical distribution functions to determine if a significant west–east effect occurred (longitude gradient), the square geographical areas were ordered from west to east in two different ways, as shown in Figure 2a. To eliminate the south–north effect, the areas were sorted with one beginning at the southern corner of the basin and the other beginning at the northern corner. Simultaneously, the watershed was covered from west to east. Similarly, to study the south–north effect (latitude gradient), the same technique was used (Figure 2b). The statistic used to test whether a west-east effect occurred was , and the statistic used to test whether a south-north effect occurred was . In these expressions, Ψ1, Ψ2, Ψ3, and Ψ4 represent the generalized Cramer-Von Mises statistics evaluated using different methods depending on the approach in which the square areas were sorted (see Figure 2a,b). Obviously, the rest of the gradients used in this work, which were univariates, did not require this type of average evaluation of the Ψ statistic. Figure 2c illustrates the case in which the gradient of the distance to the main river basin axis is considered. This is a simplified gradient, considering as principal axis of variation the general course of the river. Using this gradient, the geographical areas were shorted from the smallest to the largest projection on the main river basin axis.
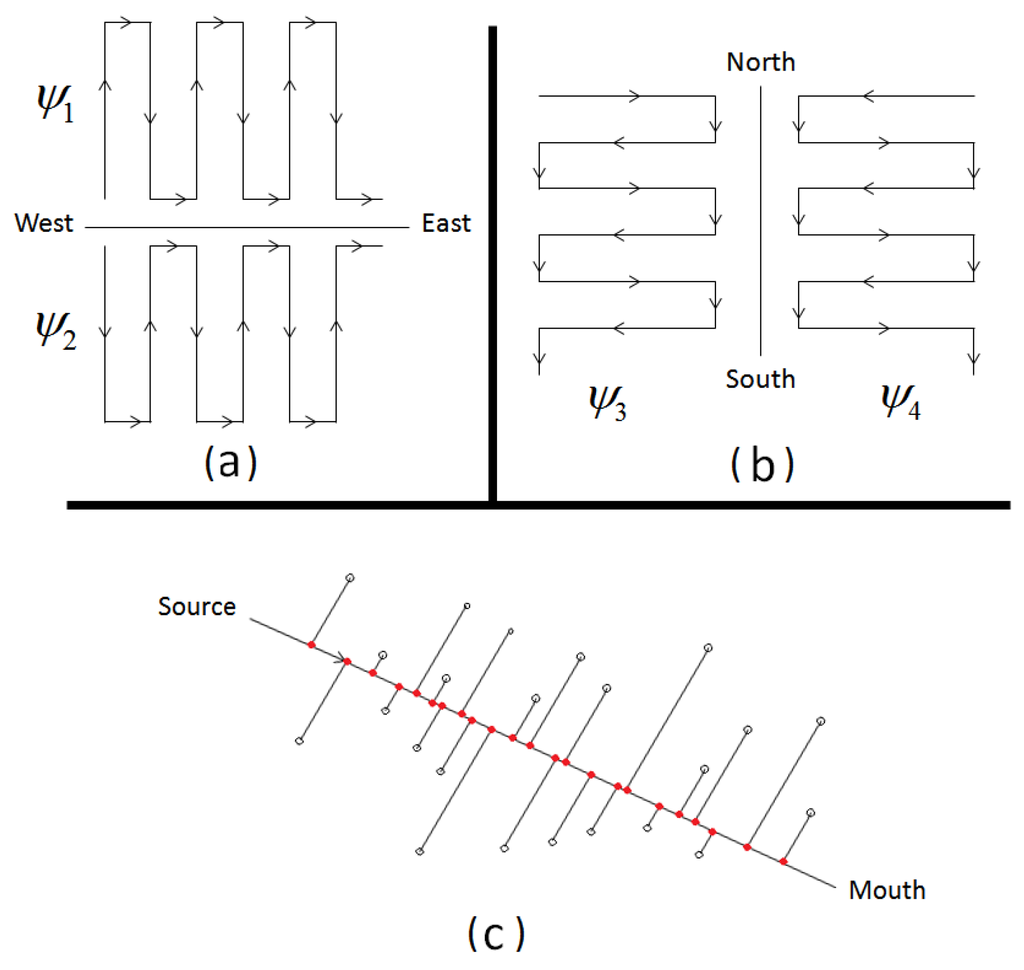
Figure 2.
The cumulative criterion used in the geographical characterization of universal multifractal (UM) parameter evolutions: (a) related to the spatial distribution of evolutions in an west–east gradient; (b) related to a south–north gradient; and (c) based on the geographical projection of the areas on the main river axis.
Finally, to determine the contrast significance level of the generalized Cramer-Von Mises statistic Ψ, the guidelines of Edgington [53] were followed. This method consists of simulating a larger number of random samples with the same number of positive trends, negative trends, and 0 values. For each sample, the value of the Ψ statistic was obtained. Then, the proportion of the random samples with values above the statistic obtained by the original data represents the p-value, which was determined according to the spatial gradient.
3. Results and Discussion
3.1. Annual Rainfall Trend Tests
The existence of trends in annual rainfall was examined for the 132 square areas of the region. The non-parametric Mann-Kendall test was applied fixing the significance level α = 0.05. If the Mann-Kendall statistic τ (Equation (1)) is lower than −Z0.025 = −1.96 then the rainfall series is statistically significantly decreasing, and if the statistic τ is bigger than Z0.025 = 1.96 then the rainfall series is statistically significantly increasing. It was found that most of the rainfall series did not show significant statistical trends, except in the case of the four series (areas), which showed a positive trend. Figure 3 shows a summary of these contrasts. Overall, it was concluded that no temporal trends exist in the Ebro River Basin, despite the four areas that exhibited significant trends in the northern watershed. Consequently, a stationary process was found and the spatial impact on trends in rainfall could not be determined in the watershed.
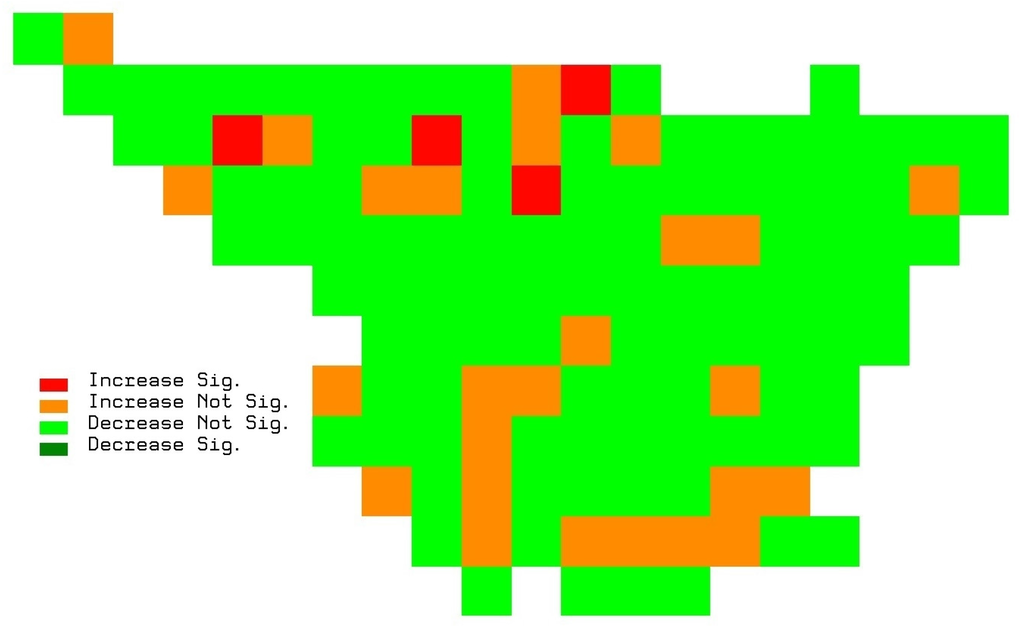
Figure 3.
Annual rainfall trends results using the Mann-Kendall test for a significance level α = 0.05, for each time series from 1931 to 2009.
3.2. Spectral Analysis
This analysis shows that only one area, corresponding to the first temporal period (1931–1975), exhibits a spectral exponent value greater than one for high frequencies. Figure 4 shows the evolution of this exponent for the 132 areas of the Ebro River Basin over the two periods. The exponents were computed for a scale lower than 32 days. The median and the minimum values of R2 in the performed regressions were 0.967 and 0.713, respectively. The mean of the β spectral exponent in the first period was 0.700, with a standard deviation of 0.128, while the mean of β in the second period decreased until 0.611, with a standard deviation of 0.119. Based on these results, the proposed methodology was used to obtain a multifractal characterization of the watershed, and after this characterization, the rainfall patterns were modeled spatially. For the problematic area with β > 1 in the first period, the DTM model was applied for homogeneity with the rest of the series. Furthermore, focusing on the information provided by these spectral exponents, a higher number of exponents with low values in the second period can be observed in Figure 4.
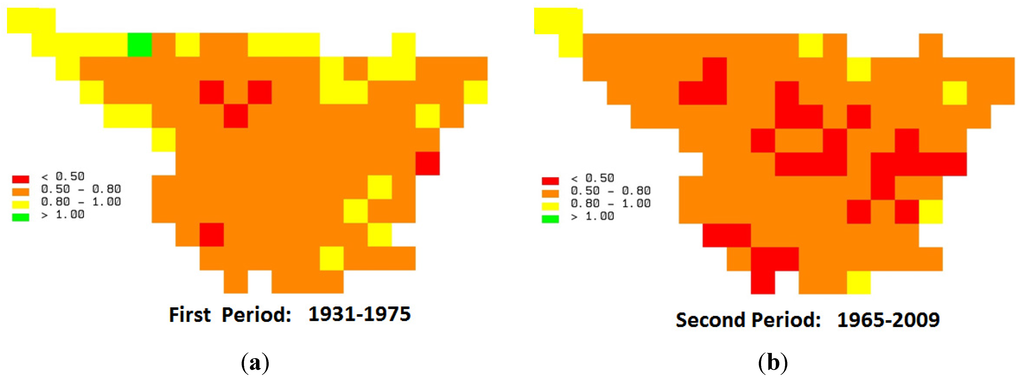
Figure 4.
Spectral slope (β) on the grid location and time period represented with different symbols, depending on their values. (a) First period; (b) Second period.
3.3. UM Model
The multifractal characterization of the Ebro River Basin is illustrated in Figure 5. This figure shows the values of the UM parameters (C1, α, γs) in the two temporal periods under study, 1931–1975 and 1965–2009, that were obtained using the DTM technique. For the first regression in DTM method, the scaling break was reached for a scale lower than 150 days. The median and the minimum of R2 were 0.967 and 0.901, respectively. On the other hand, the scaling break for the second regression used to estimate α parameter was 0.1 < μ < 2 and μq < 3.3 (where μ and q are the exponents of the field in the algorithm of DTM method). For these regressions the median and the minimum of R2 were 0.997 and 0.9232, respectively. Table 1 summarizes the descriptive statistics of the UM parameters throughout the watershed.
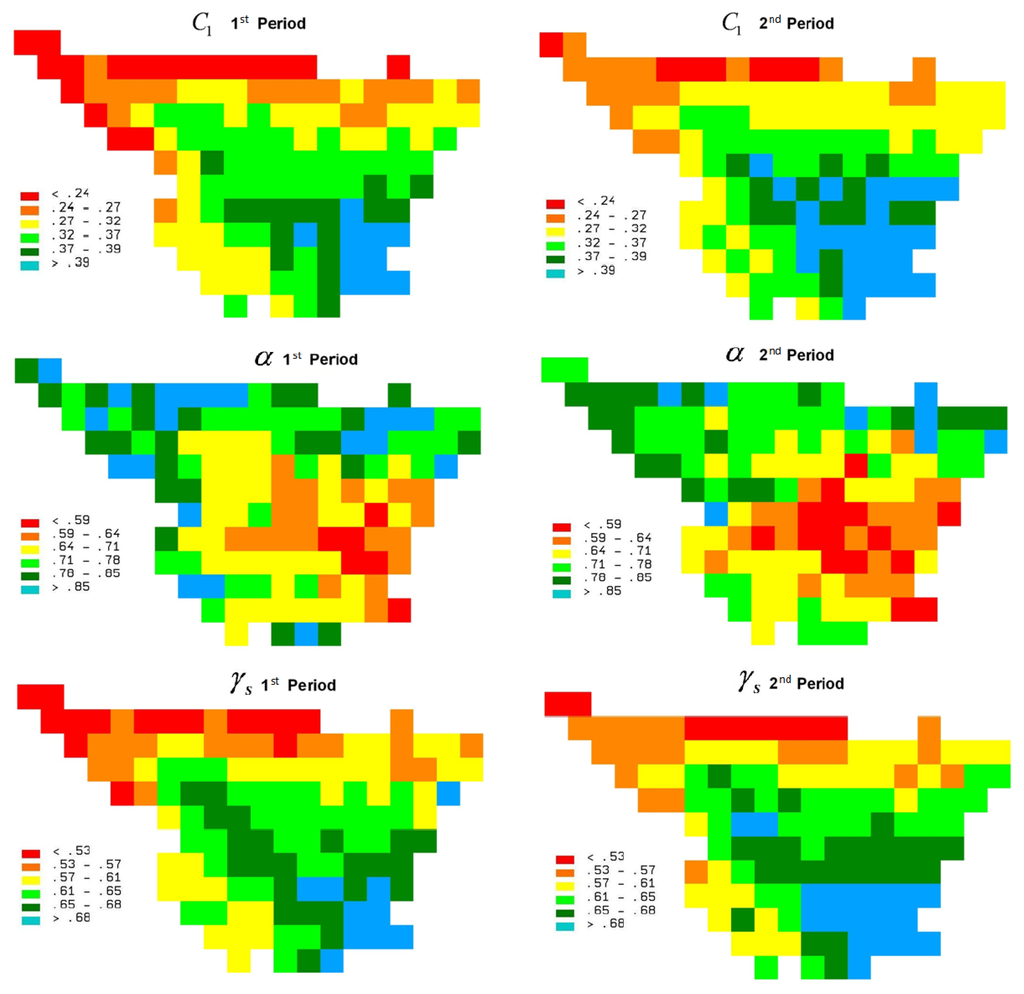
Figure 5.
UM parameters (C1, α and γs) for each spatial localization during the first period (left) and second period (right).
In Figure 5, the intermittency parameter C1 is the lowest in the northwest and increases towards the southeast, which is opposite of the trend indicated by the Levy index α. With respect to the maximal probable singularity γs, an increase from northwest to southeast is detected, which corresponds with the pattern observed in the intermittency. Therefore, it can be concluded that the effect of C1 dominates that of α in the Ebro River Basin because γs is graphically more strongly related to C1. The maps in Figure 5 show the spatial multifractal characterization of the watershed, which is symmetric with respect to the main river basin axis and increases in the direction of the river for the UM parameters C1 and γs.

Table 1.
Descriptive statistics of universal multifractal (UM) parameters in the Ebro River Basin for 1931–2009.
| Variable | Minimum | Median | Maximum | Mean | Std. Dev. | Coeff. of Variation |
|---|---|---|---|---|---|---|
| C1 1st period | 0.192 | 0.314 | 0.434 | 0.314 | 0.058 | 18.590 |
| C1 2nd period | 0.213 | 0.324 | 0.457 | 0.330 | 0.059 | 17.847 |
| α 1st period | 0.545 | 0.725 | 1.052 | 0.739 | 0.103 | 13.906 |
| α 2nd period | 0.523 | 0.706 | 0.917 | 0.705 | 0.088 | 12.495 |
| γs 1st period | 0.487 | 0.612 | 0.712 | 0.608 | 0.055 | 9.075 |
| γs 2nd period | 0.487 | 0.622 | 0.738 | 0.618 | 0.056 | 9.118 |
When comparing the two temporal periods, the results shown in Figure 5 clearly indicate an increase in the C1 values, which suggests a higher frequency of dry periods at several time scales. This increase seems especially important in the northwest region of the basin and, eventually, in the areas with higher annual average rainfall (in the north area of the basin) or with more frequent draught events (in the southeast area of the basin). In general, γs shows a much more moderate increase. However, the α index exhibits opposite behavior and decreases over most of the watershed. These graphical findings were further contrasted by conducting rigorous statistical tests.
3.4. Temporal Evolution of the UM Parameters
To determine if the differences between the temporal periods, which are found in the DTM estimations of the UM parameters and illustrated in Figure 5, were statistically significant, the test described in Section 2.5 was conducted. The results of this temporal comparison test on UM parameters over the 132 geographical areas of the Ebro River Basin are summarized in Figure 6.
Figure 6 shows that only 4 areas presented a statistically significant negative evolution (–) in the intermittency C1, and that 73 areas exhibited a significant positive evolution (+). The 55 remaining areas did not show any significant statistically evolution (0) of intermittency. The evolution of the α index was the opposite; that is, the α index generally decreased. However, this decrease was observed in fewer areas (34 in concrete) and was less intense (higher significant p-values). Only nine areas showed increasing α index values, and most of the basin areas (89 out of 132) did not show any statistically significant temporal evolution. Although Figure 5 suggests a slight increment in the γs parameter in most areas of the Ebro River Basin, the temporal comparison statistical test did not confirm this assumption because no single area of the watershed resulted in statistically significant evolution (increasing or decreasing).
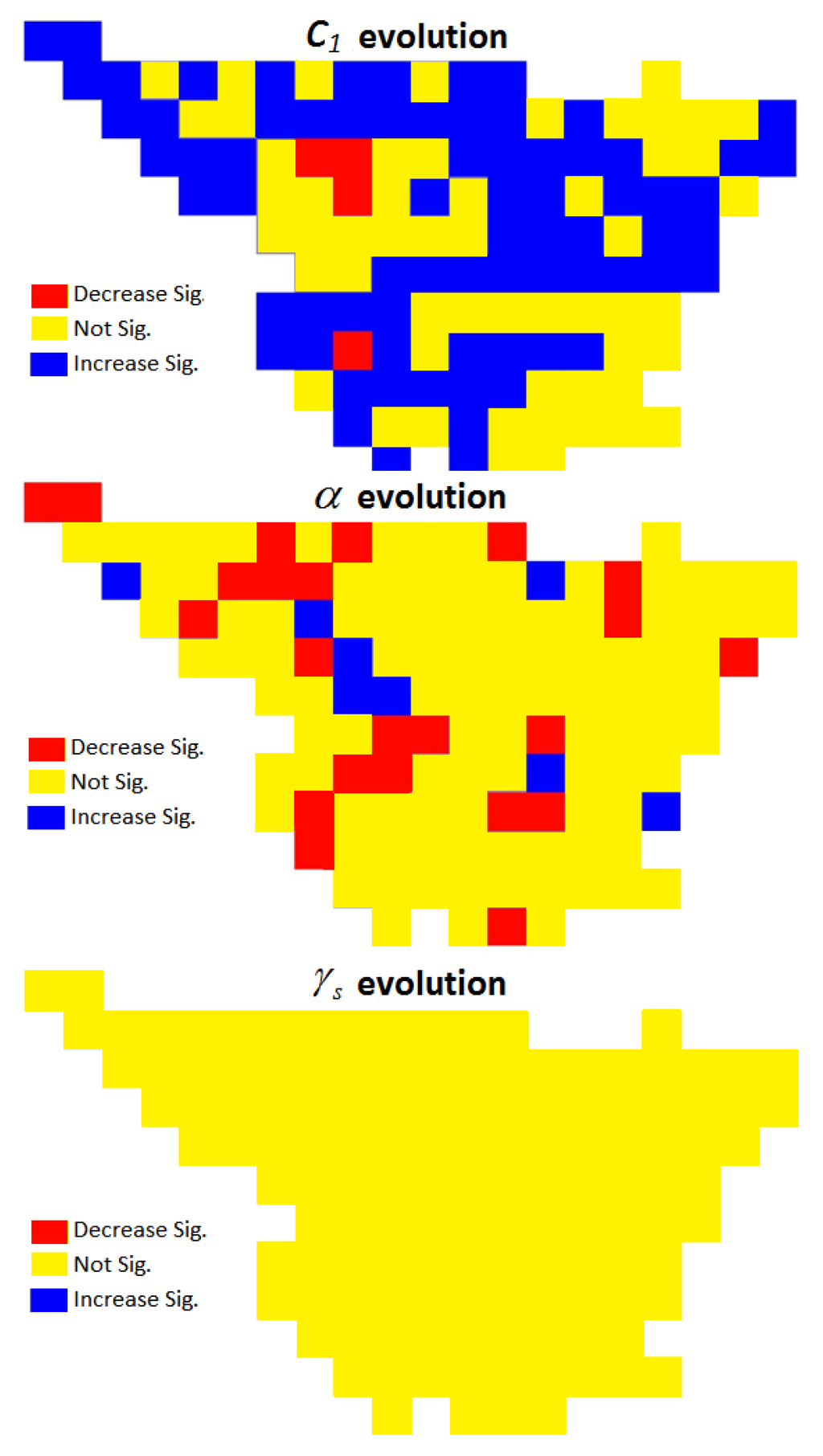
Figure 6.
Statistically significant variations, for a significance level α = 0.05, of the three UM parameters (C1, α, and γs) from the periods 1931–1975 to 1965–2009.
3.5. Spatial Analysis of Rainfall Patterns
The variations of the C1 and α UM parameters could result from the spatial distribution along the Ebro River Basin, with potential information about the rainfall patterns in the watershed. To discover such information, the generalized Cramer-Von Mises non-parametric statistical test was performed in the basin over six different gradients. The target was to look for spatial patterns that could explain the significant differences found in the evolution of both UM parameters on the watershed. The test was applied using three possible temporal evolutions of UM parameters for rainfall processes (increase (+), decrease (–), and not significant (0)) by comparing the spatial distributions of the possible evolutions two by two; i.e., + versus –, + versus 0, and 0 versus –. The results of each comparison were considered statistically significant when their p-values were below 0.05.
Table 2 summarizes the results of the twelve generalized Cramer-Von Mises tests that were conducted in the longitude (west–east) and latitude (south–north) gradients by considering the order for the geographical areas illustrated in Figure 2a,b, respectively. The tests were carried out in order to check whether each pair of types of trends (increasing, decreasing, or not significant) is equally distributed along longitude and latitude gradients. This table includes the Cramer-Von Mises statistic (Ψ) and the p-value used to study the UM parameters (C1 and α) using a cumulative criterion west–east (ΨW–E) and south–north (ΨS–N) gradients (see Section 2.6). A west–east component evolution was detected for the C1 and α UM parameters. Considering, i.e., the first row of the C1 UM parameter and west-east gradient, Table 2 shows that areas with decreasing evolution (–) for the intermittency C1 are distributed along the west–east axis in a different way compared with the areas with increasing evolution (+), at a p-value of 0.046 (<0.05); while considering i.e., the third row of such UM parameter and gradient, the areas with decreasing evolution (–) for C1 are distributed along the west–east axis in a different way compared with the areas with no significant evolution (0), at a p-value of 0.018 (<0.05). These results are consistent with the fact that the four areas with negative evolution are located at a very specific longitude in the midwest area of the watershed (see Figure 6) and in the Aragón River valley before reaching the Ebro River. When studying the spatial distribution of the α UM parameter, significant differences can be observed (as shown in Table 2) along the west–east axis between the areas with a negative evolution and the areas that did not show significant differences, which included most of the areas (p-value 0.033). Furthermore, the spatial cumulative distributions shown in Figure 7a graphically show that these significant differences are due to a larger number of areas with decreasing evolution in the west area of the watershed. Thus, it can be observed that among the 50 most western areas of the basin, more than 60 percent of areas with decreasing evolution were accumulated and only near 30 percent of the areas with no significant evolution were accumulated. In contrast, the south–north axis showed no significant differences in the distributions of the evolutions of the UM parameters. Figure 7b graphically illustrates the absence of significant differences along the south–north axis among the three spatial distributions for α.

Table 2.
Generalized Cramer-Von Mises statistic (Ψ) and the p-values used to study the UM parameters (C1 and α) using a cumulative criterion west–east (ΨW–E) and south–north (ΨS–N) gradient, as shown in Figure 2a,b.
| Pairwise Comparison | C1 | α | ||||||
|---|---|---|---|---|---|---|---|---|
| South–North | West–East | South–North | West–East | |||||
| ΨS–N | p-value | ΨW–E | p-value | ΨS–N | p-value | ΨW–E | p-value | |
| + versus – | 3.261 | 0.667 | 14.997 | 0.046 * | 2.155 | 0.606 | 0.895 | 0.930 |
| + versus 0 | 1.410 | 0.170 | 1.097 | 0.182 | 1.541 | 0.677 | 2.666 | 0.399 |
| 0 versus – | 4.796 | 0.491 | 20.867 | 0.018 * | 1.418 | 0.269 | 3.783 | 0.033 * |
Note: * Statistically significant temporal evolutions, for a significant level of 0.05.
The spatial localization of the UM parameters in Figure 5 suggested another gradient that could be appropriate for use when spatially analyzing rainfall patterns, the distance to the main river basin axis (the line in the north–west to south–east direction, joining the mouth and source of the river). To use this gradient, a projection of each geographical area on the axis was made, and these projections were sorted in increasing order. Figure 2c is helpful for understanding this procedure. Another gradient that also seemed adequate was the distance to the Ebro River mouth. Using this gradient, the geographical areas were sorted from the smallest to largest distance to the river mouth. Table 3 shows the results of the generalized Cramer-Von Mises tests that were conducted using these two gradients and the evolutions of the C1 and α UM parameters. With respect to the intermittency C1, this table indicates that the distribution of the areas with significant decreasing evolution (–) differs from the distribution of the areas that do not exhibited significant evolution (0) when considering the distance to the main river basin axis (p-value 0.030) as its proximity to the river mouth (p-value 0.049). These results correspond with the fact that only four areas with significant decreasing evolution were detected in the watershed and that these areas were located far from the river mouth and next to the main river basin axis. However, significant differences in the distributions of the areas regarding the evolutions of the α Levy index were not detected for either of these gradients.
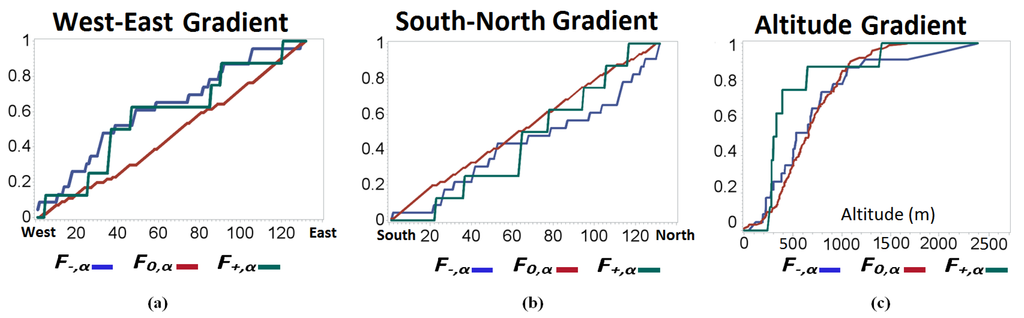
Figure 7.
Spatial cumulative distributions of statistically significant evolutions for the α UM parameter considering different gradients: (a) longitude gradient; (b) latitude gradient; and (c) altitude gradient.

Table 3.
Generalized Cramer-Von Mises statistic (Ψ) and the p-values used to study the UM parameters (C1 and α) using a cumulative criterion based on the progress of the main river basin (ΨP) and the distance to the main river mouth (ΨM) gradient, as shown in Figure 2c.
| Pairwise Comparison | C1 | α | ||||||
|---|---|---|---|---|---|---|---|---|
| Projection | Mouth | Projection | Mouth | |||||
| ΨP | p-value | ΨM | p-value | ΨP | p-value | ΨM | p-value | |
| + versus – | 11.349 | 0.111 | 10.428 | 0.139 | 9.299 | 0.062 | 1.328 | 0.828 |
| + versus 0 | 1.6248 | 0.077 | 1.566 | 0.089 | 5.533 | 0.124 | 3.389 | 0.292 |
| 0 versus – | 18.454 | 0.030 * | 15.893 | 0.049 * | 1.296 | 0.305 | 2.997 | 0.061 |
Note: * Statistically significant temporal evolutions, for a significant level of 0.05.
Finally, research has focused in on determining whether the mean rainfall or the altitude in the area have influenced the evolution of the UM parameters in the Ebro River Basin. Thus, the generalized Cramer-Von Mises non-parametric test was applied again, which orders the data according to the gradients of these variables. The results are summarized in Table 4. With respect to the parameter α, this table indicates that the distribution of the geographic areas with significant increasing evolution (+) is significantly different from the distribution of the areas that do not exhibited significant evolution (0) for the altitude of the areas (p-value 0.019). Furthermore, most of the geographical areas with increasing evolution (the 75 percent) were located below 400 meters, as shown in Figure 7c. On the other hand, significant differences in the distributions of the areas over the evolutions of intermittency C1 were not detected in either of the gradients.

Table 4.
Generalized Cramer-Von Mises statistic (Ψ) and the p-values used to study the UM parameters (C1 and α) using a cumulative criterion based on rainfall average (ΨR) and the altitude (ΨA) gradient of the river basin.
| Pairwise Comparison | C1 | α | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean Rainfall | Altitude | Mean Rainfall | Altitude | |||||
| ΨR | p-value | ΨA | p-value | ΨR | p-value | ΨA | p-value | |
| + versus – | 10.633 | 0.130 | 13.440 | 0.075 | 3.996 | 0.302 | 7.700 | 0.102 |
| + versus 0 | 0.235 | 0.846 | 0.629 | 0.392 | 3.791 | 0.234 | 10.982 | 0.019 * |
| 0 versus – | 8.529 | 0.201 | 10.503 | 0.142 | 1.976 | 0.155 | 0.540 | 0.723 |
Note: * Statistically significant temporal evolutions, for a significant level of 0.05.
3.6. Discussion
In this work a spatial study of the rainfall process has been carried out after multifractal analysis of the daily temporal series. Other authors have conducted a multifractal integrated spatial-temporal study, in order to reduce the loss of information resulting in not considering in detail the spatial heterogeneity. These include the work done by Pathirana et al. [54] who, instead of directly modeling rainfall by multifractal analysis for a small time scale—days—they modeled it after obtaining the product of filtering instantaneous rainfall with the own spatial heterogeneity based on the accumulation of mean monthly rainfall. Due to nature of data used in the research—daily rainfall in small geographic areas—it has been preferred to analyze the temporal behavior of each series through the UM model and then statistically analyze their spatial behavior. Therefore, comparison of these two approaches in the multifractal framework remains open to test whether greater efficiency in the results to be obtained by the method of Pathirana et al. could offset the increased complexity of such an approach.
Variations in the mean annual rainfall within watersheds constitute an important issue and must be considered for water resources management [55]. In this study, the results indicated that, in general, the mean annual rainfall in the Ebro River Basin did not significantly change during the period of 1931 to 2009 (Figure 3). However, previous studies of the Ebro River Basin [16] suggest a decrease in the mean annual rainfall, potentially because the time period considered by the authors (1951–2000) is shorter and does not include the 1940’s, which were extremely dry. A similar situation occurs when comparing the results from the northeastern Iberian Peninsula obtained by López-Moreno et al. [56], who investigated the period of 1955 to 2006. Furthermore, the data in this study are completely homogeneous in space and therefore more representative of the mean rainfall by geographic area than the aforementioned studies.
Regarding the results from the spectrum analysis (Figure 4), fewer spectral exponents β with values between 0.8 and 1 and a large number of exponents with values lower than 0.5, were observed in the second period. This result implies that the rainfall process evolved into a smaller number of convective rainfall events during the last half of the century [24].
Several previous studies have been conducted over different regions on rainfall processes based on multifractality. Among the studies conducted nearest the Ebro River Basin, the work of Labat et al. [28] focuses on small watersheds in the French Pyrenees. There is a good correspondence between the mean values of C1 and α UM parameters obtained by these authors (C1 = 0.25, α = 0.89) and the values of C1 and α found in the Pyrenees region of the Ebro River Basin in this study (most C1 values are less than 0.27 and most α values are between 0.79 and 1.05; Figure 5 and Table 1). Douglas et al. [57] found mean values for C1 and α of 0.48 and 0.5, respectively, in a wide region in the Midwestern and Southeastern United States by using 327 daily time-series. These differences, with respect to the resultant values in the Ebro River Basin, occurred because the region studied by these authors includes a greater number of arid areas. This result is also supported by the study of De Lima et al. [58], who studied a semi-arid region of Portugal and obtained values of C1 = 0.51 and α = 0.49, which were very similar to those of Douglas et al. [57]. Due to the results of the aforementioned references, it appears that the rainfall pattern in the Pyrenees region of the Ebro River Basin will be more similar to other semi-arid regions around the world if the value of C1 gradually increases and the value of α decreases.
Previously, one study has been conducted on the precipitation patterns of the Ebro River Basin by using multifractality, the study of Valencia et al. [49]. The data used for this previous study were directly obtained from a group of irregular rainfall stations scattered across the territory over the period of 1957 to 2002. By contrast, in the present study the data do not refer to specific points, but are weighted averages of data collected by the stations and represent the rainfall that occurred in small square areas across the watershed from 1931 to 2009. Thus, the series used in this study better reflects and provides more detail regarding the amount of rain that occurred in the Ebro River Basin at the expense of slightly altering some extreme values obtained by torrential storms acting over a very small area. In this sense, an improvement is achieved in the present study because the entire basin is present in the same proportion and relative evaluations can be made from the spatial point of view, i.e., by observing if there are special areas with higher or lower UM parameter values. In fact, this work involves the first research concerning rainfall data across the entire Ebro River Basin from a homogeneous geographic point of view and based on multifractality. Therefore, it is difficult to compare the absolute results obtained by these two studies. However, although Valencia et al. [49] observed that the value of α increased at some stations and the intermittency C1 increased at more than half of the stations (reaching values above those obtained in the present study), the parameter γs showed a general slightly increasing pattern at 12 of the 14 stations with values that were very similar to the values of the square geographical areas containing the analyzed stations. Thus, it seems that the γs parameter best reflects the evolution of the multifractal properties of rainfall distribution. However, this issue should be tested in further studies that consider different length in the time series.
The findings of this study indicate that the γs parameter reaches the higher values in the southeast of the Ebro River Basin (Figure 5) because this is the region of the watershed where major differences between the maximum values and the average values in rainfall events exist. Thus, the southeast region of the watershed has the greatest expected multifractality. This result indicates that the parameter γs could be used as an indicator for detecting climate change from a multifractal perspective [24,49].
Regarding the temporal evolution of the multifractal parameter γs, a slight increase in γs was found due to the temporal evolution of the C1 and α parameters and by considering the higher increase in C1 with respect to the decrease in α; however, this increase in γs was not statistically significant (Figure 6). That is, the hypotheses suggested graphically in Figure 5 regarding γs were not fully confirmed. Therefore, this result only provides a few small hints regarding the existence of climate change. On the other hand, the temporal evolution observed for the three UM parameters is in line with the results obtained by Royer et al. [24] on simulated data under a climate change scenario in France.
Once it was determined that significant increases in C1 occurred in nearly 2/3 of the areas in which the Ebro River Basin was divided and a significant decrease in α was shown in 1/3 of the areas, we attempted to explain why these changes occurred in specific areas rather than throughout the watershed. That is, the research focused on determining which gradients (factors) were more sensitive to substantial changes in the UM parameters. Using the available data, spatial patterns, which can explain such differences, were searched for based on six gradients. From the results (Table 2, Table 3 and Table 4, and Figure 6), it was concluded that the evolution of C1 is generally not influenced by any of the studied spatial factors because no spatial patterns were detected; in addition, the not significance in some areas may be explained by the typical deviations relatively large of the UM parameter estimations. The value of C1 only decreased in a very small region located in the midwest region of the Ebro River Basin, with some specific characteristics that have not yet been discovered. To explain this unusual fact, the microclimatic factors affecting this particular region, which is located in a depression of the Aragon River valley, should be controlled. In summary, regarding the C1 parameter, it is concluded that a generalized increase distributed throughout the watershed occurred that suggests an increase in the concentration of rainfall in the last decades over a smaller number of days in the Ebro River Basin [59]. On the other hand, regarding the α parameter, it was found evidence that the more easterly areas and the areas with more altitude appeared more resistant to significant changes (Table 2 and Table 4, Figure 6 and Figure 7a,c). Therefore, it is preferably in these areas in where it has remained so much the variability of rainfall at daily scale as the number of days with rainfall, because α is highly sensitive to this number and increases and decreases with such a number [59].
At this point, it is important to note that after the study of the UM parameters, and based on meteorological variables used in this research, it has been possible to predict the consequences of the UM parameters evolution on the rainfall pattern of the Ebro River Basin in the future. Such a prediction has been possible also taking into consideration the results in other regions of the Earth. Knowing the causes that have led to those changes in rainfall patterns, although exceeding the scope of this research, would also be of great interest. The causes of such changes observed in the Ebro River Basin may be multiple, because the precipitation process is very complex and there are many interrelated variables. In this sense, it is interesting to note that since the late 1970s the teleconnection pattern index NAO (North Atlantic Oscillation)—which measures the variation in the pressure difference between the Azores and Iceland—experienced a clear growth generally reaching positive values after that date, whereas in the preceding decades it usually took negative values. Several studies show that this index is negatively correlated with the intensity of the rainfall collected in the Ebro River Basin [17,60]. In addition, this relationship has been found using the mean monthly rainfall within the watershed with the data of the present study. This means that the growth in the NAO index, particularly intense in the second period of this analysis, increased droughts in the watershed. The result suggests that changes in pressure differences between the Azores and Iceland might be responsible for the observed changes in rainfall patterns within the Ebro River Basin.
The methodology offered in this work may be altered in some aspects according to the database available. In this sense, Gires et al. [61] have recently proposed a new method for estimating the UM parameters, particularly suitable for data series with very high resolution (i.e., hours in rainfall process), as an alternative to the DTM method. On the other hand, the advantages of using multifractal techniques in the study of rainfall processes at different scales have already been established in previous studies [18,25,26,27,29,46]. Combining non-parametric statistical techniques—the generalized Cramer-Von Mises tests—with multifractal techniques allows to determine additionally which factors (gradients) are the most influential on the variability of the multifractal parameters, and consequently, on the distribution of rainfall patterns for different time scales. Therefore, the proposed combined methodology allows determining the sensitivity of the significant statistically factors that characterize the study area in response to the effects of climate change in the rainfall process. The application of this methodological approach will be helpful for a more efficient management of hydrological resources in the watershed under study.
The next step in future research regarding the proposed methodology will be conducted by extending the temporal evolution to several periods throughout a time window; then, a sequence of UM parameters will be obtained for each one of the geographical areas that can be used to detect spatial rainfall patterns in a time continuous way. Furthermore, understanding of the rainfall process over the Ebro River Basin could be improved by using a seasonal scale in the methodology.
4. Conclusions
This study investigated the spatial rainfall patterns in the Ebro River Basin by using a method that combines the application of multifractal analysis—C1, α, and γs UM parameters—and non-parametric statistical techniques, such as the generalized Cramer-Von Mises test. This methodological approach allows for the reproduction of the scale invariance and intermittency of rainfall processes and allows spatial distribution comparisons to determine the sensitivity of statistically significant factors that hydrologically characterize the watershed in response to the effects of climate change in the rainfall process. To apply this method experimentally, a daily rainfall dataset of 132 time series dating from 1931 to 2009 that was subdivided (1931–1975 and 1965–2009), spatially and homogeneously distributed across a grid of 25 km × 25 km over the entire watershed, was used. The following main conclusions can be extracted from the analytical results:
- 1)
- Most of the geographical areas in the Ebro River Basin exhibited a slight decrease in the mean annual rainfall over the period 1931–2009, although such a decrease is not statistically significant;
- 2)
- The watershed shows a spatial characterization of the C1 and γs UM parameters that is symmetric with respect to the main river basin axis and increases in the river direction;
- 3)
- The evolution of the intermittency C1 over the last decades has preferably and homogeneously increased in the watershed, with a higher concentration of rainfall occurring over fewer days;
- 4)
- In several areas, especially those located in the western area of the watershed, the α index has decreased in recent decades; accordingly, dry periods and rainfall process variability have increased in this zone;
- 5)
- The γs UM parameter gradually, smoothly, and homogeneously increased in the watershed, although this temporal increase is not statistically significant. Since γs reacts positively to climate change effects in cases of increasing aridity, this result suggests that the effects of climate change have already begun to be perceived in the rain collected by the Ebro River Basin, although they are still very moderate.
The experimental results indicate that such a combined approach constitutes a modeling and analyzing method for rainfall patterns that is of practical value for managing hydrological resources in the Ebro River Basin. This method may be extended to other watersheds and their characteristic gradients to help predict changes in rainfall patterns and could be useful for making decisions regarding hydrological policies.
Acknowledgments
The authors wish to thank the reviewers for the time and effort dedicate to improve this work and also wish to thank the contribution of the Spanish Meteorological Agency (AEMET) in this research for sharing the analyzed rainfall data. In addition, funding provided by CEIGRAM (Research Centre for the Management of Agricultural and Environmental Risks) and the Spanish Ministry of Economy and Competitiveness through Project number CGL2014-58322-R, Project number MTM2013-46374-P and Project number CICYT PCIN-2014-080 is greatly appreciated.
Author Contributions
Each one of the authors contributed to this work, including the related research and writing. All authors read and approved the final version of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Walther, G.R.; Post, E.; Convey, P.; Menzel, A. Ecological responses to recent climate change. Nature 2002, 416, 389–395. [Google Scholar] [CrossRef] [PubMed]
- Batalla, R.J.; Gómez, C.M.; Kondolf, G.M. Reservoir induced hydrological changes in the Ebro River Basin (NE Spain). J. Hydrol. 2004, 290, 117–136. [Google Scholar] [CrossRef]
- Räisänen, J.; Hansson, U.; Ullerstig, A.; Döscher, R.; Graham, L.P.; Jones, C.; Meier, H.E.; Samuelsson, P.; Willén, U. European climate in the late twenty-first century: Regional simulations with two driving global models and two forcing scenarios. Clim. Dyn. 2004, 22, 13–31. [Google Scholar] [CrossRef]
- Golodets, C.; Sternberg, M.; Kigel, J.; Boeken, B.; Henkin, Z.; Seligman, N.G.; Ungar, E.D. From desert to Mediterranean rangelands: Will increasing drought and inter-annual rainfall variability affect herbaceous annual primary productivity? Clim. Chang. 2013, 119, 785–798. [Google Scholar] [CrossRef]
- Norrant-Romand, C.; Douguédroit, A. Significant rainfall decreases and variations of the atmospheric circulation in the Mediterranean (1950–2000). Reg. Environ. Chang. 2014, 14, 1725–1741. [Google Scholar] [CrossRef]
- Groisman, P.Y.; Knight, R.W.; Karl, T.R. Heavy precipitation and high stremflow in the contiguous United States: Trends in 20th century. Bull. Am. Meteorol. Soc. 2001, 82, 219–246. [Google Scholar] [CrossRef]
- Gonzalez-Hidalgo, J.C.; Peña-Monné, J.L.; de Luis, M.A. Review of daily soil erosion in Western Mediterranean areas. Catena 2007, 71, 193–199. [Google Scholar] [CrossRef]
- O’Neal, M.R.; Nearing, M.A.; Vining, R.C.; Southworth, J.; Pfeifer, R.A. Climate change impacts on soil erosion in Midwest United States with changes in crop management. Catena 2005, 61, 165–184. [Google Scholar] [CrossRef]
- Killham, K. Integrated soil management-moving towards globally sustainable agriculture. J. Agric. Sci. 2010, 149, 29–36. [Google Scholar] [CrossRef]
- Bryan, E.; Ringler, C.; Okoba, B.; Koo, J.; Herrero, M.; Silvestri, S. Agricultural Management for Climate Change Adaptation, Greenhouse Gas Mitigation, and Agricultural Productivity: Insights from Kenya; Discussion Paper 01098; International Food Police Research Institute (IFPRI): Washington, DC, USA, 2011. [Google Scholar]
- Tarquis, A.M.; Gobin, A.; Semenov, M. Preface: Agriculture in a changing climate. Clim. Res. 2010, 44, 1–2. [Google Scholar] [CrossRef] [Green Version]
- López-Moreno, J.I.; Morán-Tejeda, E.; Vicente Serrano, S.M.; Lorenzo-Lacruz, J.; García-Ruiz, J.M. Impact of climate evolution and land use changes on water yield in the Ebro basin. Hydrol. Earth Syst. Sci. 2011, 15, 311–322. [Google Scholar] [CrossRef]
- Gonzalez-Hidalgo, J.C.; Brunetti, M.; de Luis, M. A new tool for monthly precipitation analysis in Spain: MOPREDAS database (monthly precipitation trends December 1945–November 2005). Int. J. Climatol. 2011, 31, 715–731. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- De Luis, M.; González-Hidalgo, J.C.; Brunetti, M.; Longares, L.A. Precipitation concentration changes in Spain 1946–2005. Nat. Hazards Earth Syst. Sci. 2011, 11, 1259–1265. [Google Scholar] [CrossRef]
- De Luis, M.; González-Hidalgo, J.C.; Longares, L.A.; Stepanek, P. Seasonal precipitation trends in the Mediterranean Iberian Peninsula in second half of 20th century. Int. J. Climatol. 2009, 29, 1312–1323. [Google Scholar] [CrossRef]
- Valencia, J.L.; Saá-Requejo, A.; Gascó, J.M.; Tarquis, A.M. Change of extreme rainfall indexes at Ebro River Basin. Nat. Hazards Earth Syst. Sci. 2012, 12, 2127–2137. [Google Scholar] [CrossRef]
- Tessier, Y.; Schertzer, D.; Lovejoy, S. Universal Multifractal theory and observation for rain and clouds. J. Appl. Meteorol. 1993, 32, 223–250. [Google Scholar] [CrossRef]
- Hernandez-Martinez, E.; Perez-Muñoz, T.; Velasco-Hernandez, J.X.; Altamira-Areyan, A.; Velasquillo-Martinez, L. Facies recognition using multifractal Hurst analysis: Applications to well-log data. Math. Geosci. 2013, 45, 471–486. [Google Scholar] [CrossRef]
- Burgueño, A.; Lana, X.; Serra, C.; Martinez, M.D. Daily extreme temperature multifractals in Catalonia (NE Spain). Phys. Lett. A 2014, 378, 874–885. [Google Scholar] [CrossRef]
- Suarez-García, P.; Gomez-Ullate, D. Multifractality and long memory of a financial index. Phys. A 2014, 394, 226–234. [Google Scholar] [CrossRef]
- Li, E.; Mu, X.; Zhao, G.; Gao, P. Multifractal detrended fluctuation analysis of streamflow in the Yellow River Basin, China. Water 2015, 7, 1670–1686. [Google Scholar] [CrossRef]
- Xu, G.; Xu, X.; Liu, M.; Sun, A.Y.; Wang, K. Spatial downscaling of TRMM precipitation product using a combined multifractal and regression approach: Demonstration for South China. Water 2015, 7, 3083–3102. [Google Scholar] [CrossRef]
- Royer, J.F.; Biaou, A.; Chauvin, F.; Schertzer, D.; Lovejoy, S. Multifractal analysis of evolution of simulated precipitation over France in a climate scenario. Comptes Rendus Geosci. 2008, 340, 431–440. [Google Scholar] [CrossRef]
- Lovejoy, S.; Schertzer, D. The Weather and Climate: Emergent Laws and Multifractal Cascades; Cambrigde University Press: Cambridge, UK, 2013. [Google Scholar]
- Lovejoy, S.; Schertzer, D. Multifractals and rain. In New Uncertainty Concepts in Hydrology and Hydrological Modelling; Kundzewicz, A.W., Ed.; Cambridge Press: Cambridge, UK, 1995; pp. 62–103. [Google Scholar]
- Schertzer, D.; Lovejoy, S. From scalar cascades to Lie cascades: Joint multifractal analysis of rain and cloud processes. In Space/Time Variability and Interdependence for Various Hydrological Processes; Feddes, R.A., Ed.; Cambridge University Press: Cambridge, UK, 1995; pp. 153–173. [Google Scholar]
- Labat, D.; Mangin, A.; Ababou, R. Rainfall-runoff relations for karstic springs: Multifractal analyses. J. Hydrol. 2002, 256, 176–195. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Rybskia, D.; Zschiegnerb, S.A.; Braunc, P.; Koscielny-Bundea, E.; Livinae, V.; Havline, S.; Bundea, A. Multifractality of river runoff and precipitation: Comparison of fluctuation analysis and wavelet methods. Phys. A 2003, 330, 240–245. [Google Scholar] [CrossRef]
- García-Marín, A.P.; Jimenez-Hornero, F.J.; Ayuso, J.L. Applying multifractality and the self-organized criticality theory to describe the temporal rainfall regimes in Andalusia (southern Spain). Hydrol. Process. 2008, 22, 295–308. [Google Scholar] [CrossRef]
- Gires, A.; Onof, C.; Maksimovic, C.; Schertzer, D.; Tchiguirinskaia, I.; Simoes, N. Quantifying the impact of small scale unmeasured rainfall variability on urban runoff through multifractal downscaling: A case study. J. Hydrol. 2012, 442–443, 117–128. [Google Scholar] [CrossRef]
- Lavallée, D.; Schertzer, D.; Lovejoy, S. On the determination of the codimension function. In Non-Linear Variability in Geophysics; Schertzer, D., Lovejoy, S., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 1991; pp. 99–109. [Google Scholar]
- Lavallée, D.; Lovejoy, S.; Schertzer, D.; Schmitt, F. On the determination of universal multifractal parameters in turbulence. In Topological Aspects of the Dynamics of Fluids and Plasmas; Moffat, K., Zalslavsky, G.M., Comte, P., Tabor, M., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 1992; pp. 463–478. [Google Scholar]
- Valencia, J.L. Estudio Estadístico de la Calidad de las Aguas de la Cuenca Hidrográfica del Río Ebro. Ph.D. Thesis, Polytechnic University of Madrid, Madrid, Spain, March 2007. [Google Scholar]
- Sotillo, M.G.; Martín, M.L.; Valero, E.F.; Luna, M.Y. Validation of a homogeneous 41-year (1961–2001) winter precipitation hind casted dataset over the Iberian Peninsula: Assessment of the regional improvement of global reanalysis. Clim. Dyn. 2006, 27, 627–645. [Google Scholar] [CrossRef]
- Luna, M.Y.; Almarza, C. Interpolation of 1961–2002 daily climatic data in Spain. In Proceedings of the Conference on Spatial Interpolation in Climatology and Meteorology, Budapest, Hungary, 25–29 October 2004; Szalai, S., Bihari, Z., Szentimrey, T., Lakatos, M., Eds.; Office for Official Publications of the European Communities: Luxembourg, 2007; pp. 189–196. [Google Scholar]
- Luna, M.Y.; Morata, A.; Martín, M.L.; Santos-Muñoz, D.; de la Cruz, J. Validación de la base de datos reticular de la AEMet. Temperatura diaria máxima y mínima. In Cambio Climático General y Sus Impactos; Sigró, J., Brunet, M., Aguilar, E., Eds.; Asociación Española de Climatología (AEC): Tarragona, Spain, 2008; Volume 6, pp. 173–182. [Google Scholar]
- Valero, F.; Martín, M.L.; Sotillo, M.G.; Morata, A.; Luna, M.Y. Characterization of the Autumn Iberian precipitation from long-term datasets: Comparison between observed and hindcasted data. Int. J. Climatol. 2009, 29, 527–541. [Google Scholar] [CrossRef]
- Almarza, C.; Luna, M.Y. Homogeneidad y variabilidad de la precipitación y la temperatura en zonas climáticamente homogéneas de la Península Ibérica. In Proceedings of the XXIX Jornadas Científicas AME, Pamplona, Spain, 22–24 April 2006.
- Kendall, M.G. Rank Correlation Methods, 5th ed.; Charles Griffin Book Series; Oxford University Press: London, UK, 1990. [Google Scholar]
- De Lima, M.I.P.; de Lima, J.L.; Coelho, M.F. Spectral analysis of scale invariance in the temporal structure of precipitation in Mainland Portugal. Eng. Civil 2003, 16, 73–82. [Google Scholar]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications with R Examples, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Bendat, J.S.; Piersol, A.G. Engineering Applications of Correlation and Spectral Analysis; Wiley-Interscience: New York, NY, USA, 1980. [Google Scholar]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Davis, A.; Marshak, A.; Wiscombe, W.; Cahalan, R. Multifractal characterizations of nonstationarity and intermittency in geophysical fields: Observed, retrieved, or simulated. J. Geophys. Res. 1994, 99, 8055–8072. [Google Scholar] [CrossRef]
- Schertzer, D.; Lovejoy, S. Physical modeling and analysis of rain and clouds by anisotropic scaling multiplicative processes. J. Geophys. Res. 1987, 92, 9693–9714. [Google Scholar] [CrossRef]
- Schertzer, D.; Lovejoy, S.; Schmitt, F.; Chigirinskaya, Y.; Marsan, D. Multifractal cascade dynamics and turbulent intermittency. Fractals 1997, 5, 427–471. [Google Scholar] [CrossRef]
- Mandelbrot, B. Intermittent turbulence in self-similar cascades: Divergence of high moments and dimension of the carrier. J. Fluid Mech. 1974, 62, 331–350. [Google Scholar] [CrossRef]
- Valencia, J.L.; Saá-Requejo, A.; Gascó, J.M.; Tarquis, A.M. Universal Multifractal description applied to precipitation pattern in the Ebro River Basin. Clim. Res. 2010, 44, 17–25. [Google Scholar] [CrossRef]
- Syrjala, S.E. A statistical test for a difference between the spatial distributions of two populations. Ecology 1996, 77, 75–80. [Google Scholar] [CrossRef]
- De Luis, M.; Raventos, J.; Gonzalez-Hidalgo, J.C.; Sanchez, J.R.; Cortina, J. Spatial analysis of rainfall trends in the region of Valencia (East Spain). Int. J. Climatol. 2000, 20, 1451–1469. [Google Scholar] [CrossRef]
- Conover, W.J. Practical Nonparametric Statistics, 2nd ed.; Wiley: New York, NY, USA, 1980. [Google Scholar]
- Edgington, E.S. Randomization Test, 2nd ed.; Marcel Dekker: New York, NY, USA, 1980. [Google Scholar]
- Pathirana, A.; Herath, S. Multifractal modelling and simulation of rain fields exhibiting spatial heterogeneity. Hydrol. Earth Syst. Sci. 2002, 6, 695–708. [Google Scholar] [CrossRef]
- Gunkel, A.; Lange, J. New insights into the natural variability of water resources in the Lower Jordan River Basin. Water Resour. Manag. 2012, 26, 963–980. [Google Scholar] [CrossRef]
- López-Moreno, J.L.; Vicente-Serrano, S.M.; Beguería, S.; El Kenawy, A.M.; Angulo, M. Trends in daily precipitation on the north-eastern Iberian Peninsula, 1955–2006. Int. J. Climatol. 2010, 30, 1026–1041. [Google Scholar]
- Douglas, E.M.; Barros, A.P. Probable maximum precipitation estimation using multifractals: Application in the eastern United States. J. Hydrometeorol. 2003, 4, 1012–1024. [Google Scholar] [CrossRef]
- De Lima, M.I.P.; Grasman, J. Multifractal analysis of 15-min and daily rainfall from a semi-arid region in Portugal. J. Hydrol. 1999, 220, 1–11. [Google Scholar] [CrossRef]
- Portilla, F. Significado Empírico de la Multifractalidad en la Precipitación. Ph.D. Thesis, Polytechnic University of Madrid, Madrid, Spain, June 2012. [Google Scholar]
- Lopez-Bustins, J.-A.; Martin-Vide, J.; Sanchez-Lorenzo, A. Iberia winter rainfall trends based upon changes in teleconnection and circulation patterns. Glob. Planet. Chang. 2008, 63, 171–176. [Google Scholar] [CrossRef]
- Gires, A.; Tchiguirinskaia, I.; Schertzer, D.; Lovejoy, S. Influence of the zero-rainfall on the assessment of the multifractal parameters. Adv. Water Resour. 2012, 45, 13–25. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).