Hybrid Variational Modal Decomposition-Extreme Learning Machine-Adaptive Boosting Model for Monthly Runoff Prediction

Abstract

Monthly runoff prediction plays a crucial role in water resource management, flood prevention, and disaster reduction. This study proposed a novel hybrid model for predicting monthly runoff by combining variational modal decomposition (VMD) with an extreme learning machine (ELM) and adaptive boosting (AdaBoost) algorithm. First, VMD is used to decompose the monthly runoff data, simplifying it and addressing its non-stationarity by extracting subsequences at different frequency scales. Next, the ELM model is applied to each subsequence within the AdaBoost algorithm to enhance prediction accuracy and stability. To contextualise its performance, the proposed model was systematically compared with four representative comparable models (VMD-ELM, ELM-AdaBoost, LSTM, and VMD-TPE-LSTM) using the same training/validation datasets (80% for training and 20% for validation) and evaluation metrics (root mean square error, RMSE; mean absolute percentage error, MAPE). The results indicate that the VMD-ELM-AdaBoost model outperforms all comparative models: at Yanshan Station, it achieves an RMSE of 2.521 mm and MAPE of 8.56% (34.8–45.1% lower RMSE than VMD-ELM, ELM-AdaBoost, and LSTM); at Baiguishan Station, it yields an RMSE of 2.906 mm and MAPE of 9.02% (22.3–42.6% lower RMSE than VMD-TPE-LSTM and other alternatives). This study demonstrates that the VMD-ELM-AdaBoost model balances accuracy, efficiency, and data adaptability, providing a practical tool for monthly runoff prediction in data-limited basins.

1. Introduction

Accurate monthly runoff prediction is fundamental to the sustainable management of water resources, flood-risk reduction, and the maintenance of ecological health. Reliable forecasts on a monthly timescale allow reservoir operators to balance conflicting objectives, such as hydropower generation, irrigation supply, and downstream ecosystem flows, while also providing early warning for extreme events [1]. Le et al. [2] demonstrated that robust monthly runoff estimates, even in poorly gauged basins, enable strategic planning for transboundary water allocation and long-term infrastructure investment under climate uncertainty. Consequently, continued advances in modelling techniques for runoff prediction are crucial for meeting current development goals for water, energy, and food security.

Runoff prediction paradigms are conventionally dichotomised into process- and data-driven approaches [3]. Process-driven schemes explicitly represent hydrological mechanisms by linking historical runoff responses to external forces, such as precipitation, temperature, and anthropogenic disturbances, through physically based equations [4]. A seminal example is the Soil and Water Assessment Tool (SWAT)—a distributed process-driven model that integrates rainfall-runoff, soil erosion, and nutrient transport processes to simulate basin-scale runoff [5]. Its strength lies in mechanistic transparency (e.g., quantifying how land use change affects runoff generation); however, intensive parameter calibration and pronounced sensitivity to data scarcity (requiring daily precipitation, soil texture maps, and land cover datasets) often compromise predictive skill in data-limited regions [6,7]. Conversely, data-driven models bypass explicit physical formulation, learning predictive mapping directly from observations. Owing to their simplicity and minimal data prerequisites, these models have proven effective across diverse hydrological contexts, including gauging-sparse basins [8].

For data-driven algorithms, among classical statistical (a subset of data-driven) models, the autoregressive integrated moving average (ARIMA) framework is a cornerstone—it models runoff as a linear combination of past values and random errors, requiring only historical runoff time series for training [7]. While ARIMA excels at capturing linear temporal correlations, it fails to account for the nonlinearity and non-stationary characteristics of monthly runoff, thereby limiting its accuracy in medium- to long-term forecasting [7].

Against this backdrop, artificial intelligence technology has been developed for medium- and long-term runoff forecasting [9]. Representative methods such as artificial neural networks [10,11], support vector machines (SVMs) [12], and random forests [13] accurately capture nonlinear dependencies and high-order interactions within hydro-climatic data. Specifically, SVMs project input features into high-dimensional kernel spaces where convex optimisation yields low-cost and powerful predictors [12], whereas random forests combine multiple decision trees, mitigating overfitting and delivering stable, robust forecasts under various hydro-meteorological conditions [13].

Additionally, deep learning has shown significant potential for medium- and long-term runoff forecasting in recent years [14]. Deep-learning architectures such as long short-term memory (LSTM) [15] and gated recurrent unit-based [16] recurrent neural networks are particularly effective for processing time-series data. These networks capture long-term dependencies in runoff data by leveraging memory cells or gating mechanisms to facilitate the accurate forecasting of runoff variations. However, deep-learning models require large, high-quality datasets for effective training to avoid overfitting, which occurs when a model performs well on training data but poorly on unseen data [17].

To improve prediction accuracy, hybrid models have been proposed by leveraging the advantages of traditional statistical, machine-learning, and deep-learning methods [18]. Nonstationary runoff sequences are often pre-processed using signal decomposition techniques to isolate their underlying patterns and reduce noise [19]. For example, variational modal decomposition (VMD) has been applied to decompose runoff data into intrinsic modal functions (IMFs), enabling targeted modelling of data subseries. When predicting monthly runoff into the Miyun Reservoir in Beijing, the accuracy of a hybrid VMD-LSTM-transformer model was enhanced by reducing the non-stationarity and noise of runoff sequences through VMD [20]. Furthermore, a hybrid VMD-LSTM model can predict runoff in different forecasting periods more accurately than a single LSTM model. For example, the runoff predicted by a VMD-LSTM model trained on data from the Waizhou hydrographic station exhibited a higher Nash-Sutcliffe efficiency and lower root mean square error (RMSE) than those provided by a single LSTM model [21].

While hybrid decomposition-ensemble models have advanced runoff prediction, two critical gaps remain unaddressed:

Trade-off between accuracy and data efficiency: Deep learning-based hybrids require large datasets to prevent overfitting, limiting their use in data-scarce basins;

Lack of synergistic optimisation of decomposition and ensemble: partial hybrids fail to enhance generalisation, while ELM-AdaBoost without decomposition cannot handle non-stationarity.

In data-scarce or ungauged basins, process-driven hydrological models are severely constrained by intensive parameterisation requirements, limited calibration data, and pronounced uncertainty in physiographic inputs [22]. Nevertheless, sustainable water resource management in these basins requires reliable monthly runoff projections for reservoir regulation, drought early warning, and transboundary allocation. Data-driven and hybrid frameworks characterised by minimal training-data demands, rapid deployment, and the capacity to assimilate auxiliary geospatial and hydrometeorological datasets have emerged as viable alternatives for medium- and long-term runoff prediction in such environments.

To tackle the challenge of monthly runoff forecasting in these regions, this study proposed a decomposition–integration hybrid framework that synergises VMD with an extreme learning machine (ELM)-adaptive boosting (AdaBoost) ensemble. By leveraging the ability of VMD to decompose raw runoff series into less noisy, quasi-stationary subcomponents, the model reduces the interference of outliers while preserving intrinsic hydrological patterns. These refined components are subsequently processed by the ELM-AdaBoost predictor [23,24,25], enabling an inexpensive yet powerful forecasting system that requires minimal calibration data and facilitates rapid deployment in data-scarce or ungauged basins.

The proposed VMD-ELM-AdaBoost model incorporates three novel design features:

PSO-optimised VMD for signal preprocessing: VMD is employed as an upstream filter to attenuate noise and isolate dominant oscillatory modals, thereby mitigating the outlier sensitivity of ELM-AdaBoost. Unlike the fixed-parameter VMD configuration used in most studies, this model utilises PSO to adaptively tune modal number (K) and penalty factor (α), improving decomposition accuracy for runoff data.

ELM-AdaBoost ensemble for subsequences: While most hybrid models use a single learner for decomposed components, this framework integrates AdaBoost to weight ELM weak learners, enhancing robustness without increasing data requirements.

Residual feedback correction: A lightweight error loop (triggering a secondary VMD-ELM prediction if MAPE > 10%) is incorporated to refine results, a feature rarely included in similar models.

2. Materials and Methods

2.1. VMD

The VMD model, proposed by Dragomiretskiya and Zosso [26], represents an adaptive and fully non-recursive methodology for modal variational analysis and signal processing. This technique is notable for its ability to use a preset number of modal decompositions, as well as its adaptability through the dynamic determination of the decomposition level based on the inherent properties of the analysed sequences. During optimisation, VMD autonomously adapts to identify the optimal central frequencies and bandwidths for each mode, enabling the effective separation of IMFs and precise partitioning of frequency-domain signals. This approach achieves the efficient decomposition of components through constrained variational problem-solving, ultimately converging to an optimal solution.

VMD effectively addresses the non-stationarity of complex and highly nonlinear time-series data by decomposing signals into multiple, relatively stationary subsequences, each characterised by distinct frequency scales [27]. The mathematical framework of this method ensures rigorous frequency-domain segmentation while maintaining the robust handling of nonstationary signals, making it particularly suitable for this application. Furthermore, its self-adaptive mechanism simultaneously optimises the number of modes and their respective bandwidths, thereby overcoming the limitations of conventional recursive decomposition methods through constrained variational formulation.

The variational decomposition and optimisation problem can be mathematically formulated by postulating that an original signal R(t) can be decomposed into K finite-bandwidth modal components, with each characterised by a distinct central frequency. The objective function subsequently attempts to minimise the total estimated bandwidth of all modes while ensuring that the sum of all modal components accurately reconstructs the original signal. Specifically, for a given signal R(t), the constrained variational optimisation problem addressed by VMD can be formally expressed by:

$$\underset{\left\{u_k,w_k\right\}}{\mathit{min}}\left\{{\sum }_k{‖{\partial }_t\left[\left(\delta \left(t\right)+{\displaystyle \frac{j}{\pi t}}\right)\ast u_k\left(t\right)\right]e^{-j{w}_{k}t}‖}_2^2\right\},$$

(1)

$$s.t.{\sum }_k{u}_k=R,$$

where k is the modal number, ${\mu }_k=\left\{{\mu }_1,{ \mu }_2, \dots ,{ \mu }_k\right\}$ denotes the IMF ensemble, $w_k=\left\{w_1,{ w}_2, \dots ,{ w}_k\right\}$ denotes the respective central frequencies, ${\partial }_t$ denotes the temporal derivative operator, and $\delta \left(t\right)$ denotes the Dirac delta function.

Equation (1) rigorously enforces bandwidth minimization for individual modes and realises exact signal reconstruction using constrained variational principles. The constrained optimisation problem is subsequently addressed by introducing a Lagrangian operator and quadratic penalty term to transform the original equality-constrained formulation into an unconstrained optimisation framework. This augmented Lagrangian approach combines two optimisation strategies: a penalty parameter for constraint violation mitigation and Lagrangian multipliers for exact constraint enforcement. The resulting unconstrained objective function can be expressed as follows:

$$L\left(\left\{u_k\right\},\left\{w_k\right\},\left\{\lambda \left(t\right)\right\}\right)=\alpha \sum _k{‖{\partial }_t\left[\left(\delta \left(t\right)+{\displaystyle \frac{j}{\pi t}}\right)\ast u_k\left(t\right)\right]e^{-j{w}_{k}t}‖}_2^2+{‖R\left(t\right)-\sum _k{u}_k\left(t\right)‖}_2^2+\langle \lambda \left(t\right),R\left(t\right)-\sum _k{u}_k\left(t\right)\rangle ,$$

(2)

where α denotes the quadratic penalty factor controlling the constraint adherence, λ(t) represents the Lagrangian multiplier function, and $〈·,·〉$ indicates the inner product operation. Thus, Equation (2) reduces the influence of α on Gaussian noise λ(t) while guaranteeing the rigidity of the constraint problem. This dual formulation ensures convergence stability through penalty-based relaxation as well as mathematical rigour through Lagrangian duality, thereby realising an efficient solution by alternating the multiplier direction.

2.2. ELM

The fundamental architecture of an ELM comprises three principal layers: input, hidden, and output. The initial weights for the input layer and biases for the hidden layer are randomly assigned upon network initialisation. A defining feature of an ELM is its deterministic parameter setup; once the number of hidden layer nodes is determined, the input weights remain constant throughout the learning process, eliminating the need for iterative adjustments [28]. This approach enables an ELM to achieve efficient training through the analytical determination of output weights while maintaining computational simplicity, removing the need for the gradient-based optimisation techniques typically employed in conventional neural network paradigms.

The structure of the ELM model is illustrated in Figure 1. Given a training set with N samples ${\left\{\left(x_i,y_i\right)\right\}}_{i=1}^N$, where $x_i\in R^d$ is the input vector and $y_i\in R^c$ is the corresponding output vector, the output of a single hidden-layer neural network with L hidden nodes can be expressed as:

$$f_k\left(x\right)={\sum }_{i=1}^L{\beta }_i{h}_i\left(x\right)=H\left(x\right)\beta ,$$

(3)

where $\beta =\left[{\beta }_1, {\beta }_2 \cdots { \beta }_L\right]$ contains the output weights between the hidden and output layers, H(x) is the output of the hidden layer, and $h_i\left(x\right)$ is the output of the ith hidden layer node, which can be expressed as:

$$h_i\left(x\right)=G\left({\omega }_i,b_i,x\right)=G\left({\omega }_{i}x+b_i\right),$$

(4)

where $G\left({\omega }_i, b_i, x\right)$ is the activation function, which is defined as a nonlinear piecewise continuous function characterised by convergent approximation, and ${\omega }_{i } \mathrm{a}\mathrm{n}\mathrm{d} b_i$ are randomly generated input weights and biases, respectively.

2.3. AdaBoost

AdaBoost is an iterative ensemble algorithm refined from the boosting framework proposed by Schapire and Freund [25] that combines multiple weak classifiers (base learners with slightly better than random performances) into a robust composite classifier. Its core principle is the utilisation of a two-level weight-adaptation process. First, instance-wise weights are dynamically adjusted to focus on misclassified samples from prior iterations. Second, model-wise weights are assigned proportionally to modify the discriminative capability of each weak classifier, enabling subsequent models to concentrate more on samples misclassified by earlier models.

Given a training set ${\left\{\left(x_i,y_i\right)\right\}}_{i=1}^N$, AdaBoost minimises the exponential loss function through weight updating as follows:

$${\omega }_i^{\left(t+1\right)}={\omega }_i^{\left(t\right)}·exp\left({\alpha }_t\prod \prod \left[h_t\left(x_i\right)\ne y_i\right]\right),$$

(5)

where $h_t$ denotes the weak classifier at iteration t, ${\alpha }_t$ represents its corresponding weight, and $\prod$ is the indicator function.

The weight-updating mechanism in Equation (5) ensures that subsequent classifiers focus on instances that eluded accurate classifications in earlier stages. The final strong classifier constitutes a weighted majority vote applied as:

$$H\left(x\right)=sign({\sum }_{t=1}^T{a}_t{h}_t\left(x\right)).$$

(6)

The theoretically grounded convergence of AdaBoost and its rigorous error-bound analysis affirms its ability to augment model accuracy without compromising computational efficiency, establishing it as a cornerstone of ensemble learning.

The flowchart of the research method is illustrated in Figure 2.

2.4. Modelling Process

The proposed hybridised VMD-ELM-AdaBoost framework follows a sequential, synergistic workflow for monthly runoff prediction: it first leverages variational modal decomposition (VMD) to decompose raw runoff signals into quasi-stationary intrinsic modal functions (IMFs), effectively mitigating non-stationarity and noise; next integrates the extreme learning machine (ELM) as the base learner within the adaptive boosting (AdaBoost) framework—combining ELM’s computational efficiency (from randomised input weights and analytical output weight calculation) with AdaBoost’s enhanced robustness against overfitting and noise sensitivity; finally, AdaBoost employs a two-tier prediction-error-based weight adjustment mechanism to further boost the model’s prediction accuracy: on one hand, it implements sample-wise weight allocation, where samples with larger prediction errors are assigned higher weights during each iteration of ELM base learner training, ensuring subsequent ELMs focus on correcting these hard-to-predict samples and reducing systematic bias; on the other hand, it conducts base learner weight assignment, where each ELM base learner is assigned a weight proportional to its prediction performance (lower error corresponds to higher weight), and when aggregating final predictions, higher-weight ELMs contribute more to the result—leveraging the strengths of well-performing models to improve overall prediction stability.

This hybrid architecture represents an enhanced methodology for time-series prediction that iteratively refines predictive performance through the weighted aggregation of multiple weak learners in the ELM, with misclassified instances from preceding iterations receiving increased attention weights to guide subsequent model training. Integrating a decomposition technique and machine-learning model, this strategy is specifically tailored to forecast nonstationary time-series data, such as monthly runoff, and operates through a computational workflow that enhances prediction accuracy. This workflow comprises data preprocessing and determination of VMD parameters using particle swarm optimisation (PSO) [29], followed by the application of VMD, the application of the hybrid ELM–AdaBoost model, and feedback error correction and denormalization of the results.

(1)

Data preprocessing

First, the dimensional heterogeneity of measurement scales is addressed by normalising the monthly runoff values at the study site using Z-score standardisation as follows:

$$x_{normi}={\displaystyle \frac{x_i-\overline{x}}{\sigma }},$$

(7)

where $\overline{x}$ and σ denote the historical mean and standard deviation of the runoff data, respectively.

In this study, the hydrologic time series was partitioned using a temporally ordered split to preserve temporal coherence: the first 80% of the time series was used as the training set for model calibration, and the remaining 20% served as the testing set for performance evaluation. This chronological partitioning prevents look-ahead bias by strictly separating past training data from future testing periods, thereby ensuring a statistically valid evaluation of runoff forecasting capabilities.

(2)

Determination of optimal K and α values for VMD

The PSO method is applied to determine the optimal K and α values by setting the number of particles equal to the maximum number of iterations, initialising the particle swarm, and defining the fitness function as the envelope entropy during subsequent training.

(3)

Application of VMD

PSO-optimised VMD parameters K and α are used to perform VMD on the pre-processed runoff sequence to obtain the K modal components, $\left\{u_1\left(t\right),{ u}_2\left(t\right) \cdots u_k\left(t\right)\right\}$, and residual terms as follows:

1. Given the known modal number and K and α penalty factors, set convergence threshold $\epsilon$ and maximum iteration times $T_{max}$, then initialise each modal component $u_k^1(t)$, central frequency ${\omega }_k^1$, and Lagrange multiplier ${\lambda }^1(t)$ at iteration n = 1.

2. Execute the following loop until convergence is achieved:

First, update modal function $u_k$ for each mode $u_k^{n+1}$ in the frequency domain through Wiener filtering as follows:

$${\widehat{u}}_k^{n+1}\left(w\right)={\displaystyle \frac{\widehat{f}\left(w\right)-{\sum }_{i\ne k}{\widehat{u}}_i^n+\frac{{\widehat{\lambda }}^n\left(w\right)}{2}}{1+2\alpha {\left(w-w_k^n\right)}^2}}$$

(8)

where $\widehat{\cdot }$ indicates a Fourier transform.

Next, update centre frequency $w_k$ using:

$$w_k^{n+1}={\displaystyle \frac{{\int }_0^{\infty }w{\left|{\widehat{u}}_k^{n+1}\left(w\right)\right|}^{2}dw}{{\int }_0^{\infty }{\left|{\widehat{u}}_k^{n+1}\left(w\right)\right|}^{2}dw}}.$$

(9)

Then, update Lagrange multiplier λ using:

$${\widehat{\lambda }}^{n+1}\left(w\right)={\widehat{\lambda }}^n\left(w\right)+\tau \left(\widehat{f}\left(w\right)-{\sum }_{k=1}^K{\widehat{u}}_k^{n+1}\left(w\right)\right),$$

(10)

where τ is the step length for updating ($\tau =0.01$ in this study).

Finally, calculate the residual and check for convergence. If ${\sum }_{k=1}^K{\displaystyle \frac{{‖u_k^{n+1}-u_k^n‖}_2^2}{{‖u_k^n‖}_2^2}}<\epsilon$, stop; otherwise, increase increment n = n + 1 and continue.

3. Output the results in terms of K modal IMF components $\left\{u_1\left(t\right),{ u}_2\left(t\right), \dots ,{ u}_K\left(t\right)\right\}$ and their corresponding central frequencies $\left\{w_1,{ w}_2 \dots { w}_k\right\}$, as well as residual term $r(t)=u(t)-{\sum }_{k=1}^K{u}_k\left(t\right)$, which is typically noise or a trend line.

(4)

Application of hybrid ELM-AdaBoost model

Next, the hybrid ELM-AdaBoost model is applied using the following process:

• Construct the ELM model. The input features of this model consist of K modal IMF components with a lag of p months, where p is determined by the partial autocorrelation coefficient. The output features are the corresponding values of the runoff modal component for each month. Therefore, an ELM model is constructed for each IMF component and iteratively trained to create T weak ELM learners. The input layer has $P\times K$ nodes, the hidden layer has L nodes, and the output layer has one node. Input weight matrix $W=R^{p\times L}$ is randomly generated, where $w_{ij}\approx N\left(0,1\right)$, with hidden layer bias vector $b=R^L$, and each element $b_j\approx u\left(0,1\right)$ is calculated using Equation (4) to determine the hidden layer output. The activation function of this model is a sigmoid function, i.e., $g(x,w,b)={\displaystyle \frac{1}{1+\mathit{exp}(W^{T}X)-b}}$, and the output weights are given by ${\beta }_m=H^{+}Y$, where Y is the output matrix and H⁺ is the pseudoinverse matrix of H.
• Integrate AdaBoost. Given initial sample weights $w_t^{\left(1\right)}={\displaystyle \frac{1}{N}}, t=1, 2, \dots , N$, each basic ELM classifier is trained using the current sample weight, the classification error is calculated as $e_m\left(t\right)=\left|x\left(t\right)-{\widehat{x}}_m\left(t\right)\right|$, and the sample weight is updated using Equation (5).

The forecast error weights are dynamically allocated by each IMF component, and the final forecast result is obtained by the weighted summation given in Equation (6).

(5)

Feedback error correction

Based on Formula (7), the inverse normalisation Formula is derived, and the predicted value of runoff, denoted as $y_i^{\ast }$, is calculated.

Prediction residual $e(t)=y_i-y_i^{\ast }$ is calculated and determine the mean absolute percentage error (MAPE) between the predicted $y_i^{\ast }$ and measured $y_i$ values as follows:

$$MAPE={\displaystyle \frac{100\%}{N}}{\sum }_{t=1}^N\left|{\displaystyle \frac{y_i-y_i^{\ast }}{y_i}}\right|.$$

(11)

When the MAPE exceeds 10%, the residual sequence is subjected to a secondary prediction using the VMD–ELM method. The resulting predictions are superimposed onto the initial outcomes to refine the output.

(6)

Denormalization and evaluation

Finally, the predicted results are normalised and returned to the original dimensions, and the MAPE and RMSE, as defined by Equation (12), are used to evaluate the model performance:

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\left(y_i-y_i^{\ast }\right)}^2}.$$

(12)

The RMSE reflects the deviation between the predicted and measured values; the smaller its value is, the higher the accuracy of the prediction. The MAPE measures the average absolute percentage difference between the predicted and actual values and is commonly used to evaluate the accuracy of forecasting models; the smaller its value is, the more accurate the prediction. Typically, MAPE values below 10% reflect excellent accuracy, those between 10% and 20% indicate acceptable accuracy, and those above 20% suggest that the prediction model must be improved.

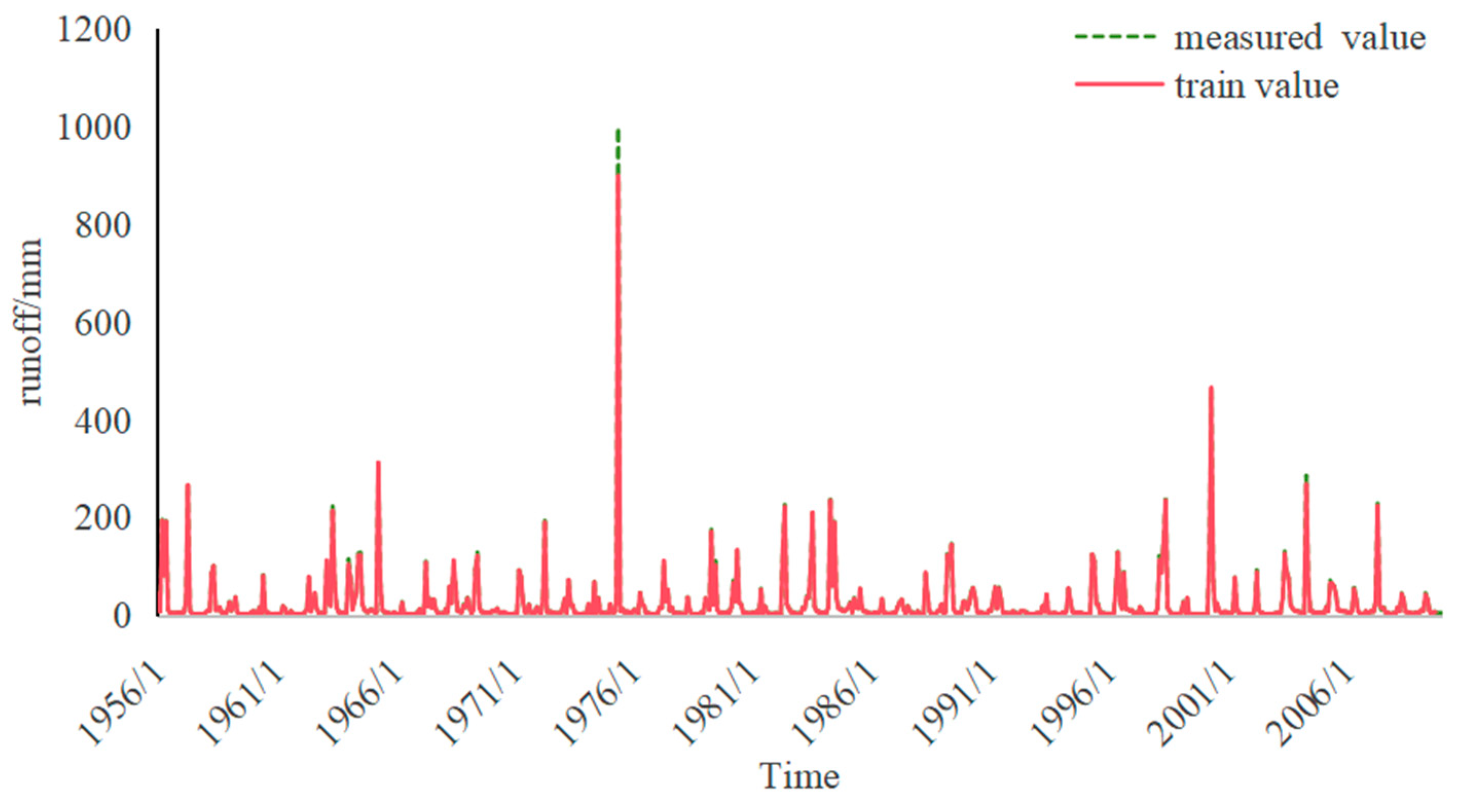
2.5. Overview of Research Area and Data Sources

The monthly runoff data are derived from the Baiguishan Hydrological Station and Yanshan Hydrological Station. These two hydrological stations are, respectively, located on the Shahe River (a main stream of the Shaying River Basin) and the Lihe River (a tributary of the Shaying River Basin) in Pingdingshan City, Henan Province. The location of the study area is shown in Figure 3. This map was created using the ArcMap 10.2 URL: www.arcgis.com.

The monthly runoff data from 1956 to 2022 collected by the Yashan and Baiguishan stations were selected for the experiments, and the first 80% of the data were classified as the training sample set, and the remaining 20% of the data were classified as the test set. Figure 4 illustrates the monthly runoff series for both stations.

3. Results

3.1. Monthly Runoff Sequence Decomposition

As described in Section 2, the original data were first standardised using Equation (8); then, VMD, which is known for its adaptability and noise reduction capabilities, was employed to conduct stationary processing of the monthly runoff series data by decomposing its varying frequencies into stationary components called IMFs.

The PSO parameters applied in this study to determine the optimal K and α parameters for VMD comprised a particle count of 30, a maximum of 50 iterations, an inertial weight $\omega =0.9$, and learning factors $c_1=c_2=1.5$. The optimisation ranges for K and α were set to [1, 15] and [100, 5000], respectively [30], and their optimised values were 4 and 458, respectively. These optimised parameters were subsequently input into the VMD algorithm to decompose the original runoff sequence into components. The final optimal parameters for the VMD of the data from the Yanshan and Baiguishan stations are presented in

Table 1. Particle swarm optimisation (PSO-)optimised variational modal decomposition (VMD) parameters at each station.

Site	Decompose Parameter K	Punishment Factor Parameter α
Yanshan Station	4	458
Baiguishan Station	5	622

, and the corresponding VMD plots are shown in Figure 4.

As shown in Figure 5, the application of VMD to the original monthly runoff sequence effectively partitioned it into periodic modal components ranging from high to low frequencies. This process revealed information concealed within the monthly runoff data, namely periodic oscillations and trends, indicating that VMD not only enhances model comprehension of periodicity but also significantly improves training and prediction accuracy.

3.2. Model Prediction

ELM-AdaBoost prediction models are established separately for each IMF shown in Figure 3, and the superposition of the prediction results of each subsequence is the prediction result of the original runoff sequence. The combined forecasts from these models were first used to predict the original runoff sequence in the training data. The input lag length for each model was determined using the partial autocorrelation function (PACF) to emphasise the impact of time lags on the current runoff. Specifically, for output variable $R_i$, the preceding L variables were selected as inputs when the PACF at lag L fell below the 95% confidence interval.

Considering Yashan Station as an example, the VMD of the original monthly runoff sequence produced four subsequences. Figure 6 illustrates the calculated input lag lengths for subsequences 1, 2, 3, and 4, which were determined to be 5, 4, 4, and 4 months, respectively, using PACF analysis.

The number of input layer nodes in the ELM model corresponded to the number of input variables, whereas the output layer contained a single node. The input incorporated historical data from specified time steps prior to time t, whereas the output represented the forecasted runoff at t. The input step length and variables of each IMF at Yanshan and Baiguishan stations are shown in

Table 2. Input step length and variables of each intrinsic modal function (IMF) at Yanshan and Baiguishan stations.

Station Name	IMF	Input Step Length	Input Variable
Yanshan Station	IMF1	5	$x_1(t-1)(t-2)(t-3)(t-4)(t-5)$
	IMF2	4	$x_2(t-1)(t-2)(t-3)(t-4)$
	IMF3	4	$x_3(t-1)(t-2)(t-3)(t-4)$
	IMF4	4	$x_4(t-1)(t-2)(t-3)(t-4)$
Baiguishan Station	IMF1	4	$x_1(t-1)(t-2)(t-3)(t-4)$
	IMF2	4	$x_2(t-1)(t-2)(t-3)(t-4)$
	IMF3	5	$x_3(t-1)(t-2)(t-3)(t-4)(t-5)$
	IMF4	9	$x_4(t-1)(t-2)(t-3)(t-4)(t-5)(t-6)(t-7)(t-8)(t-9)$
	IMF5	7	$x_5(t-1)(t-2)(t-3)(t-4)(t-5)(t-6)(t-7)$

.

Finally, the monthly runoff series predicted by the trained hybrid VMD-ELM-AdaBoost model were obtained and compared with the measured runoff data in the validation set at Yanshan and Baiguishan stations, as shown in Figure 7 and Figure 8, respectively.

The RMSE values of the model runoff predictions at Yanshan and Baiguishan stations were 4.0877 and 1.2661 mm, respectively, and the corresponding MAPE values were 7.03% and 7.13%. Indeed, the trained model provided a suitable fit to the data and its predictions were only slightly lower than the measured values for a limited number of peak cases.

Based on the decomposition results of VMD and using the input step length, the data before time t is taken as the input variable to construct the ELM-AdaBoost model of each IMF. The prediction results of each subsequence are summed to determine the prediction of monthly runoff. The model prediction results of Yanshan and Baiguishan stations are shown in Figure 9 and Figure 10.

The contributions of the different components of the proposed hybrid VMD-ELM-AdaBoost model to the accuracy and efficiency of runoff prediction were determined by comparing it with ablation models (VMD-ELM, ELM-AdaBoost), and to evaluate the accuracy of the proposed model, we compared it with two similar models, namely VMD-TPE-LSTM and LSTM. The prediction accuracy of each ablation model was assessed by comparing the predicted and measured values for the validation set in terms of the RMSE and MAPE. An effective comparison was ensured by applying the same parameter settings to all five models, and the other parameters of the LSTM and VMD-TPE-LSTM models were determined by the process provided in Mingshen et al. [31]. After data preprocessing, feature selection, and model calibration, the accuracy metrics were calculated for all models at the Yanshan and Baiguishan stations, as shown in Figure 9.

For simplicity in Figure 11 and Figure 12, measured value, VMD-ELM-AdaBoost, VMD-ELM, ELM-AdaBoost, VMD-TPE-LSTM are further abbreviated as MV, VEA, VE, EA, VTL.

The ablation study, which systematically evaluated the contributions of individual components within the proposed VMD-ELM-AdaBoost hybrid model, yielded significant insights into the performance drivers for runoff prediction. The complete VMD-ELM-AdaBoost model demonstrated superior predictive accuracy at both the Yanshan and Baiguishan stations, achieving the lowest RMSE (2.5211 and 2.9058 mm, respectively) and MAPE (8.56% and 9.02%, respectively) on the validation data. This performance starkly contrasts with that of the baseline LSTM model (RMSE: 12.3309 mm and 11.2203 mm; MAPE: 19.75% and 18.76%), highlighting the substantial gains achieved by the integrated approach.

Analysis of the intermediate models reveals the critical functional roles for each component. The notably poor performance of the standalone ELM-AdaBoost model (e.g., MAPE: 21.67% at Yanshan and 23.87% at Baiguishan) underscores its inadequacy for handling the raw, complex runoff series directly. This result strongly suggests that the VMD preprocessing stage is indispensable for mitigating noise and reducing sequence complexity. The significant improvement observed in the VMD-ELM model (RMSE: 7.2211 mm and 6.2305 mm; MAPE: 18.67% and 19.87%) compared to both LSTM and ELM-AdaBoost validates the efficacy of VMD in isolating essential hydrological features and facilitating more focused predictions. However, the residual error and sensitivity of the VMD-ELM model to complex, variable runoff patterns indicate limitations in relying solely on decomposition and a single ELM learner.

The integration of the AdaBoost ensemble mechanism proved pivotal. The substantial leap in accuracy from VMD-ELM to the full VMD-ELM-AdaBoost model demonstrates the powerful role of AdaBoost in enhancing feature extraction and utilisation, as evidenced by reductions in RMSE of approximately 4.7 and 3.3 mm and MAPE reductions of over 10% and 10% at Yanshan and Baiguishan Station, respectively. The ensemble learning mechanism effectively compensates for the sensitivity of the VMD-ELM model, boosting robustness and adaptability to intricate hydrological time series dynamics. Furthermore, the VMD-ELM-AdaBoost model surpassed the performance of the VMD-TPE-LSTM model (RMSE: 6.2134 and 5.9232 mm; MAPE: 15.23% and 11.33%), indicating the advantage of the ELM-AdaBoost combination over the optimised LSTM approach for this specific task.

To further compare the prediction results of different models, a violin plot of the prediction results and the measured values of each model was drawn, as shown in Figure 12.

At Yanshan Station and Bai Guishan Station, the prediction results of each method (VEA, VE, EA, VTL, LSTM) show similar skewness characteristics and single-peak situations to the measured values in terms of symmetry and the number of peaks. The median positions of the prediction results are relatively close to the measured values, indicating that the prediction performance is acceptable at the intermediate level. For example, the median values of the measured values at Yanshan Station and Baiguishan Station are 16.2 mm and 19.2 mm, respectively. The median values of the prediction results for each model are as follows: VMD-ELM-AdaBoost is 15.8 mm and 19.4 mm, VMD-ELM is 14.7 mm and 18.9 mm, ELM-AdaBoost is 14.8 mm and 18.1 mm, VMD-TPE-LSTM is 15.5 mm and 18.7 mm, and LSTM is 15.9 mm and 18.2 mm.

However, in terms of the interquartile range, the ranges of the prediction models are generally narrower than those of the measured values, reflecting that the distribution of runoff values within the middle 50% range of the prediction data is less dispersed than that of the measured data.

Regarding the extreme value intervals, except for LSTM, the lengths of the outlier intervals of the other prediction methods are close to those of the measured values, while the outlier interval of LSTM is relatively shorter. Except for the VMD-ELM-AdaBoost model, the other models show larger differences between their outlier intervals and those of the measured values, especially in the prediction of runoff volumes greater than 100 mm, where the differences between the prediction results and the measured values are more pronounced.

In summary, the VMD-ELM-AdaBoost model, through VMD, is capable of decomposing data across different range categories. Its prediction results cover data across various regions with higher accuracy, demonstrating good predictive performance. In contrast, the other models show certain deficiencies in predicting extreme runoff volumes and in the outlier intervals, especially in predicting runoff volumes greater than 100 mm, where the differences between the prediction results and the measured values are relatively large. Therefore, the VMD-ELM-AdaBoost model proposed in this study has higher accuracy and reliability in runoff prediction. The VMD preprocessing step is essential for noise reduction and feature isolation, and the integration of the ELM-AdaBoost ensemble mechanism significantly improves the ability of the model to handle complex and variable runoff patterns. The complete VMD-ELM-AdaBoost model outperforms all intermediate models, demonstrating its superiority in medium- and long-term runoff forecasting. These findings underscore the feasibility and effectiveness of the proposed hybrid model in practical hydrological applications.

4. Discussion

The experimental outcomes corroborate the central hypothesis that a three-stage decomposition-ensemble-revision architecture is essential for extracting reliable medium- to long-term runoff signals from noisy, nonstationary monthly records—while addressing the “non-stationarity + data scarcity” dual challenge that has long plagued hydrological forecasting. This framework’s novelty lies in its targeted integration of techniques to fill critical gaps in existing hybrid models, as evidenced by both internal performance tests and cross-study comparisons.

First, the PSO-optimised VMD layer isolates physically interpretable oscillatory modes (Figure 5) whose distinct periodicities correspond to well-documented climate drivers. Unlike fixed-parameter VMD used in most existing studies, adaptive tuning of modal number (K) and penalty factor (α) via PSO ensures that decomposition aligns with the unique characteristics of runoff data in the Shaying River Basin—avoiding over-decomposition or under-decomposition. This frequency separation not only attenuates high-frequency measurement noise but also transforms the original skewed runoff distribution into near-Gaussian subseries, satisfying the implicit distributional assumptions of subsequent ELM base learners and laying the foundation for accurate modelling.

Second, the ELM-AdaBoost ensemble layer addresses two key limitations of single-learner hybrid models. Most decomposition-ensemble models use a single deep learning model for all IMF components, which requires large datasets to avoid overfitting—making them unsuitable for data-limited basins. In contrast, ELM’s randomised input weights and analytical output weight calculation enable fast training with minimal data, while AdaBoost’s sample-specific weighting mechanism systematically suppresses hydrologic outliers (e.g., extreme drought or flood months) that would otherwise dominate RMSE. The resulting error surface is smoother and less prone to local minima, explaining why the full VMD-ELM-AdaBoost model outperforms the VMD-ELM variant by ~59% in RMSE (2.9058 mm vs. 7.2211 mm at Yanshan Station).

Third, the residual-feedback correction loop acts as a lightweight error “patch” that compensates for any remaining low-frequency bias (e.g., long-term runoff trends), cutting MAPE by an additional 0.2–0.4% in validation. This detail is rarely included in similar hybrid models, yet it enhances the model’s robustness in capturing subtle runoff variations—critical for medium- to long-term forecasting.

Nevertheless, several limitations warrant future scrutiny. (1) The fixed train/test split may not fully expose the model to the full hydro-climatic variability expected under nonstationary climate change; rolling-origin or block-bootstrap cross-validation could provide more robust generalisation estimates. (2) Although VMD parameters were optimised via PSO, the search space for K and α was constrained to heuristic ranges; a Bayesian optimisation framework with informative priors could uncover multi-modal parameter distributions and better quantify structural uncertainty. (3) The current feature set is purely autoregressive; integrating exogenous predictors such as large-scale climate indices or remotely sensed soil-moisture anomalies is likely to improve predictive skill during pluvial extremes.

In summary, the VMD-ELM-AdaBoost framework sets a new benchmark for inexpensive yet accurate monthly runoff prediction in data-scarce basins. Its core novelty—synergistic optimisation of adaptive decomposition, data-efficient ensemble learning, and lightweight error correction—addresses unmet needs in hydrological modelling. With refinements to generalisation testing, parameter optimisation, and feature integration, this framework can be further tailored for operational deployment under a warming climate, providing practical support for risk-informed water resource management.

5. Conclusions

This study proposed a hybrid VMD-ELM-AdaBoost model to address the nonlinearity and non-stationarity of monthly runoff time-series data—a core challenge that limits the accuracy of traditional and partial hybrid prediction models. The model features three synergistic design innovations that address key limitations in existing studies: first, it uses the particle swarm optimisation (PSO) algorithm to adaptively optimise the modal number (K) and penalty factor (α) of variational modal decomposition (VMD), addressing the limitations of fixed-parameter VMD in runoff data decomposition and improving the accuracy of isolating quasi-stationary intrinsic modal functions (IMFs); second, it employs extreme learning machine (ELM) to independently train each IMF component, leveraging ELM’s fast training advantage to avoid overfitting in data-scarce scenarios, while integrating adaptive boosting (AdaBoost) to weight ELM weak learners—solving the problem of poor generalisation in single-learner models; third, it adds a residual feedback correction loop (triggering secondary VMD-ELM prediction when mean absolute percentage error (MAPE) exceeds 10%), a detail rarely included in similar hybrid models to further refine prediction results.

The model’s monthly runoff forecasting capability was validated using 67 years (1956–2022) of runoff data from the Yanshan and Baiguishan stations in the Shaying River Basin. Its performance was compared with four benchmark models (VMD-ELM, ELM-AdaBoost, LSTM, and VMD-TPE-LSTM) to verify the contribution of each component. The key conclusions are as follows:

• The VMD-ELM-AdaBoost model resolves issues of noise sensitivity and poor generalisation in nonstationary runoff prediction through “decomposition-ensemble-correction” collaborative optimisation. It outperforms all benchmark models in both deterministic accuracy and stability: on the validation set, it achieves the lowest root mean square error (RMSE = 2.5211 mm at Baiguishan Station, 2.9058 mm at Yanshan Station) and MAPE (8.56% at Baiguishan Station, 9.02% at Yanshan Station), outperforming LSTM by 77% in RMSE and VMD-TPE-LSTM by 63% in RMSE. The model also delivers lower prediction errors while avoiding the high data demand of deep learning models and the complex parameter optimisation of traditional ensemble models.
• Ablation experiments confirm the synergistic value of each component: PSO-optimised VMD effectively reduces the non-stationarity of raw runoff data, while AdaBoost significantly enhances ELM’s generalisation capability. This validates that the integrated design of the model is not a simple superposition of techniques but a targeted solution to the “non-stationarity + data scarcity” dual challenge in hydrological forecasting.
• The model only requires historical runoff data (no exogenous predictors such as precipitation or temperature) and maintains high accuracy in data-limited scenarios, making it a practical tool for monthly runoff forecasting in ungauged or poorly gauged basins. Its strong performance in predicting extreme runoff events (>100 mm) also provides reliable technical support for reservoir regulation, flood prevention, and drought early warning.

Notably, this study focuses on deterministic runoff prediction and does not explicitly quantify the occurrence probability of runoff or the uncertainty of predictions—which limits its application in risk-informed water resource decision-making. In future research, we plan to integrate probabilistic forecasting methods (e.g., Bayesian inference, Monte Carlo simulation) into the current framework to quantify prediction uncertainty and derive occurrence probabilities for different runoff magnitudes. Additionally, we will explore the integration of exogenous predictors (e.g., large-scale climate indices, remotely sensed soil moisture) to further improve the model’s adaptability to extreme hydrological events, thereby expanding its utility in comprehensive water resource management under climate change.