1. Introduction
Water resources globally face mounting stress from climate change, population growth, urbanization, industrial discharge, and intensified agricultural inputs. Small reservoirs and irrigation ponds are particularly vulnerable due to their limited buffering capacity and low self-renewal ability. Issues such as eutrophication, nutrient enrichment, increased suspended solids, and chemical contamination can lead to rapid deterioration in the quality of small-scale water bodies [
1,
2].
Water quality (WQ) reflects the combined influence of multiple physicochemical and biological parameters that determine a water body’s suitability for drinking, irrigation, and supporting ecosystems. Indicators such as pH, electrical conductivity (EC), dissolved oxygen (DO), total phosphorus (TP), biochemical oxygen demand (BOD), and suspended solids (SS) are widely used to characterize water quality [
3]. Because interpreting all these parameters simultaneously is challenging for decision-makers, holistic indices such as the Water Quality Index (WQI) have been developed to facilitate this process. The WQI condenses multiple indicators into a single score, allowing for classification from “very good” to “poor” [
4,
5]. However, the choice of parameter thresholds, weighting schemes, and aggregation functions can introduce significant uncertainty and subjectivity into WQI assessments [
6,
7]. Recent efforts propose that machine learning can help optimize weights and aggregation rules, thereby reducing model uncertainty [
5,
8].
Traditional laboratory-based analyses provide high precision, but are often costly, labor-intensive, and may fail to capture abrupt events. These limitations have motivated a shift toward data-driven approaches, especially machine learning (ML) and deep learning (DL) techniques [
9,
10,
11,
12]. Data-driven modeling offers predictive capabilities by learning complex, nonlinear relationships within observational datasets [
13]. Such approaches can either supplement or replace process-based models, offering more flexible, scalable solutions [
14,
15,
16].
ML algorithms, such as Random Forest (RF), Extreme Gradient Boosting (XGBoost), Support Vector Machines (SVM), and k-Nearest Neighbors (k-NN), have demonstrated strong capabilities in predicting WQI classes by capturing hidden nonlinear interactions [
17,
18]. DL architectures, such as LSTM and CNN, can uncover spatial–temporal patterns in water quality dynamics [
19,
20]. Explainable AI (XAI) tools, such as SHAP and LIME, are increasingly being adopted to interpret model decisions and enhance policy relevance [
21]. In particular, optimizing WQI models with machine learning has been demonstrated to reduce uncertainties stemming from subjective choices in index construction [
5,
8].
The objective of this study is to evaluate water quality in the Taşçılar and Yumurtacılar ponds in Kastamonu, Türkiye, based on multiple physicochemical parameters; compare classification results using CCME-WQI and WA-WQI under both WHO and FAO thresholds; and assess the predictability of these results using ML algorithms (Logistic Regression, Decision Tree, Random Forest, XGBoost). By integrating index-based and data-driven approaches, this work proposes a scalable hybrid framework for small irrigation reservoirs in similar hydroclimatic settings. The proposed methodology aims not only for regional applicability but also for transferability to small water bodies under analogous environmental conditions.
2. Materials and Methods
2.1. Study Area
The study area consists of the Taşçılar (41°28′14″ N, 33°24′01″ E) and Yumurtacılar (41°28′51″ N, 33°26′29″ E) reservoirs, located within the administrative boundaries of Daday district, Kastamonu Province, in the Western Black Sea Region of Türkiye. Both reservoirs are located in the upper Kızılırmak Basin, characterized by complex topography and steep slopes.
Figure 1 illustrates the precise geographic location of the reservoirs, including basin boundaries, elevation gradients, and the surrounding drainage network.
The Daday district has a continental climate, with snowy winters, cool and rainy springs and autumns, and hot, dry summers [
22]. According to long-term meteorological data from the General Directorate of Meteorology [
23], the average annual temperature is 9.9 °C and the mean annual precipitation is 552.7 mm. The region’s geological formation dates back to the Triassic and Lower Jurassic periods [
24]. Soils are generally classified as chestnut-colored, medium-depth (50–90 cm) with moderate slopes (20–30%) and a medium risk of water erosion [
25].
The Taşçılar Reservoir was constructed for irrigation purposes, with a total capacity of 1,020,000 m
3, an irrigation area of 126 ha, and an annual water withdrawal of 280,000 m
3. It is an earthfill dam, and its basin is dominated by south-facing slopes, 83% of which are categorized as very steep and rugged, ranging in elevation from 671 m to 1652 m [
26].
The Yumurtacılar Reservoir also serves irrigation purposes, with a total capacity of 930,000 m
3, an irrigation area of 124 ha, and an annual water withdrawal of 230,000 m
3. Similar to Taşçılar, it is an earthfill dam, and 53% of its basin area consists of steep to very steep slopes, with elevations ranging from 860 m to 1243 m [
26].
2.2. Dataset and Data Analysis
Seven different sampling points were identified at each of the Taşçılar and Yumurtacılar Reservoirs located in Kastamonu. Water sampling was conducted over 12 consecutive months (May 2024–April 2025) to capture seasonal variability in hydrochemical conditions across the irrigation season, autumn rainfall period, winter low-temperature and low-flow conditions, and spring snowmelt transition. Previous studies on small ponds and reservoirs have shown that sampling in representative months (e.g., January, April, July, and October) can provide a general overview of seasonal variation [
27,
28,
29,
30,
31]. However, monthly sampling throughout an entire hydrological year allows for a more reliable evaluation of temporal dynamics and inter-seasonal transitions [
32,
33,
34,
35], which is consistent with recent international approaches that emphasize continuous temporal coverage for detecting hydrochemical responses to climatic and anthropogenic drivers [
36,
37,
38].
Before sampling, amber-colored glass bottles were thoroughly rinsed with distilled water to ensure that the chemical characteristics of the water samples remained unchanged and were not affected by external factors. To minimize temperature variations and diurnal effects, all samples were collected between 09:00 and 12:00 in each season under similar meteorological conditions. Immediately after collection, the samples were transported to the laboratory in insulated coolers at low temperature to prevent any chemical or biological alteration. All field measurements were performed using portable instruments that were calibrated before each sampling event in accordance with the manufacturers’ specifications.
A total of 336 water samples were collected twice per month from 14 different sampling points, and various measurements and analyses were performed.
The pH, electrical conductivity (EC), temperature, salinity, total dissolved solids (TDS), and dissolved oxygen (DO) parameters of the water samples were determined using the AZ Instrument 86031 Combo multi-parameter measurement device (AZ Instrument Corp., Taichung, Taiwan). Turbidity values were measured using the Milwaukee Mi415 turbidity meter (Milwaukee Instruments, Rocky Mount, NC, USA). Analyses for calcium, magnesium, sodium, potassium, copper, lead, phosphorus, chromium, nickel, and silver elements were performed using an ICP-OES device (Spectro Blue, Spectro Analytical Instruments GmbH, Kleve, Germany). Total suspended solids (TSS) analyses were performed using the gravimetric method [
39]. Nitrite and nitrate analyses were performed using the PhotoLab
® 7600 UV-VIS spectrophotometer with special photometric test kits (WTW—Xylem Analytics Germany GmbH, Weilheim, Germany). The Matriks Nitrate test kit used in nitrate analysis was 0.4–111 mg/L (Cat. No: 2.187.025), while the Matrix Nitrite test kit used in nitrite analysis has a measurement range of 0.03–2.3 mg/L (Cat. No: 1.214.323) (Matriks Kimya Analitik Sistemler Ltd. Şti., Ankara, Türkiye) [
40].
All analyses were performed in the laboratories of Kastamonu University, following the standard methods outlined in the “Water Pollution Control Regulation, Sampling and Analysis Methods Bulletin” [
41]. To ensure the accuracy and consistency of the analyses, all analytical instruments were calibrated according to the manufacturers’ instructions prior to each sampling session, and procedural blanks were used where applicable. All field and laboratory analyses were conducted by the same researcher, ensuring methodological consistency and minimizing external variability. Each measurement result was evaluated in conjunction with device logs and field observations. When verification was required, the retained water sample was re-analyzed to confirm the consistency of the measurement results. As a result, no missing or erroneous data were obtained during the study period.
2.3. Determination of Water Quality Classes
The data obtained from the parameters mentioned earlier, based on analyses conducted on samples taken from the reservoirs, were evaluated using different water quality determination indices commonly used in the literature, and water quality classes were determined. These indices are the Canadian Council of Ministers of the Environment Water Quality Index (CCME WQI) and the Weighted Arithmetic Water Quality Index (WA-WQI). The relevant water quality guidelines of the WHO and FAO were used to establish the classification threshold values for the water quality parameters required when applying these water quality determination methods [
42,
43].
To facilitate a direct comparison between drinking and irrigation water standards, the threshold limits adopted from the World Health Organization (WHO) [
42] and the Food and Agriculture Organization (FAO) [
43] guidelines are summarized in
Table 1.
These indices were chosen because they enable reservoirs to be examined in a multifaceted manner, both in terms of drinking water quality and agricultural irrigation [
44,
45,
46,
47].
2.3.1. Canadian Council of Ministers of the Environment Water Quality Index (CCME WQI)
This method is a comprehensive index that evaluates water quality in five classes based on comparing measured parameters with national or international standards. Three key factors are considered in calculating the index: coverage (F1), frequency (F2), and deviation (F3). These components are combined to produce a score ranging from 0 to 100, and the results are categorized as “Excellent,” “Good,” “Fair,” “Marginal,” and “Poor” [
45].
F1 (Coverage): Percentage of parameters not meeting standards,
F2 (Frequency): Ratio of the total number of measurements exceeding standards,
F3 (Deviation): Magnitude of deviation from standard values.
These three components are combined to obtain a quality score ranging from 0 to 100. The formula is given below [
48].
In the study, the Canadian Council of Ministers of the Environment—World Health Organization Water Quality Index (CCME WQI-WHO) version was calculated using the limit values set by the World Health Organization for drinking water, and the suitability of the ponds for human consumption was tested [
49].
In the study, the same methodological approach was also applied to the widely accepted criteria of the Food and Agriculture Organization (FAO) to determine the suitability of irrigation water [
43].
2.3.2. Weighted Arithmetic Water Quality Index (WA-WQI)
This method involves multiplying the normalized concentrations of the parameters by their standard values, using predefined weight coefficients, and then obtaining the index from the sum of these values [
50]. Thus, a more balanced evaluation has been made by considering the relative importance of the parameters. The general formula is given below:
In the formula;
The weight coefficient of the i-th parameter, indicating its relative importance in the water quality assessment.
The quality rating of the i-th parameter is calculated using the measured value (
), the ideal value (
), and the standard value (
) [
50].
In this study, the index was calculated according to both WHO standards (WA-WQI-WHO) and FAO irrigation criteria (WA-WQI-FAO).
The Friedman Test was used to evaluate whether the results obtained according to water quality indices differed from each other. The Nemenyi post hoc test was used to determine which methods differed significantly among groups [
51].
2.4. Machine Learning Approach for Determining Water Quality
In machine learning applications, four different algorithms—Logistic Regression (LR), Decision Tree (DT), Random Forest (RF), and Extreme Gradient Boosting (XGBoost)—were employed, and their comparative prediction performance was analyzed. The analyses were performed using the Python programming language (version 3.11.11). Specifically, the scikit-learn library was utilized for preprocessing, regression, and tree-based models; the XGBoost package was employed for gradient boosting; and supporting libraries, such as NumPy and Pandas were utilized for data handling. All algorithms were implemented as supervised learning methods, trained using input variables and corresponding target classes.
Logistic Regression (LR): Logistic Regression (LR) examines the probability of a specific outcome occurring based on explanatory variables. It models the log odds of occurrence using a linear combination of predictors [
52]. Detailed mathematical expressions are provided in the
Supplementary Information (Equation (S1)).
Decision Tree (DT): is a rule-based method that recursively divides data into non-linear subregions. The tree structure consists of root, decision, and leaf nodes representing data splits and predicted classes [
53]. The outputs obtained from leaf nodes generate classification or prediction results [
54].
Random Forest (RF): is an ensemble algorithm that combines multiple decision trees, where predictions are aggregated through majority voting to enhance accuracy and reduce overfitting [
55,
56].
Extreme Gradient Boosting Modeling (XGBoost): is an ensemble learning technique based on the gradient boosting approach and decision trees, offering high scalability and computational efficiency. It incrementally minimizes the loss function while regularizing tree complexity through gamma (γ) and lambda (λ) parameters to prevent overfitting [
57]. Detailed formulations for the objective and regularization functions are presented in the
Supplementary Information (Equations (S2) and (S3)).
2.5. Model Optimization
To minimize the effect of scale differences between variables, all features were standardized using the StandardScaler method in scikit-learn. This technique transforms variables to have a mean of zero and a standard deviation of one, ensuring consistent scaling before model training [
58]. The mathematical expression for this transformation is provided in the
Supplementary Information (Equation (S4)).
The tested hyperparameter ranges and their optimal values are summarized in
Table 2 and
Table 3. The ranges were selected based on values commonly reported in the literature to maintain an optimal balance between model complexity and generalization capability.
Tables present the hyperparameter ranges tested for each algorithm, along with the optimal values. The best results in logistic regression were obtained with an L2 penalty, the LBFGS solver, balanced class weights, and a high iteration limit. For the decision tree, the optimal configuration was mainly influenced by maximum depth and minimum sample thresholds. In the random forest, the number of trees and feature subset selection were key determinants of performance. The XGBoost algorithm achieved the highest predictive accuracy by jointly optimizing learning rate, depth, and regularization parameters.
Hyperparameters were optimized using the GridSearchCV method with 5-fold cross-validation. This approach systematically evaluates all possible parameter combinations, measures performance, and selects the configuration that yields the highest accuracy and lowest validation error [
59].
2.6. Model Evaluation Methods
The predictive performance of all classification models was assessed using multiple evaluation metrics to ensure a comprehensive and reliable comparison. These metrics included Accuracy, F1-macro score, Receiver Operating Characteristic–Area Under Curve (ROC–AUC), Balanced Accuracy, Cohen’s Kappa, Matthews Correlation Coefficient (MCC), Expected Calibration Error (ECE), and Brier Score.
This multi-metric approach enabled a detailed assessment of model performance in terms of classification success, robustness against class imbalance, and calibration quality.
Accuracy is the ratio of correctly classified examples to all examples. It is used to measure overall model performance [
60].
F1-macro represents the harmonic mean of precision and recall averaged across all classes, providing a balanced evaluation under imbalanced data conditions [
61].
Receiver Operating Characteristic–Area Under Curve (ROC–AUC) quantifies the model’s ability to distinguish between classes under varying thresholds; a higher AUC value indicates stronger discriminative power [
62].
Balanced Accuracy corrects for unequal class distributions by averaging recall scores across all classes [
63].
Cohen’s Kappa evaluates classification agreement while accounting for random chance [
64].
Matthews Correlation Coefficient (MCC) jointly considers true and false classifications, making it suitable for imbalanced datasets [
60].
Expected Calibration Error (ECE) assesses how closely predicted probabilities align with observed outcomes, reflecting the model’s calibration reliability [
65].
Finally, the Brier Score measures the mean squared difference between predicted probabilities and actual class labels, where lower scores indicate better-calibrated models [
66].
2.7. Relative Ranking Method
Comparing the performance of machine learning models is challenging because different metrics have varying scales and directions. In this study, the relative ranking method proposed by Poudel and Cao [
67] was applied to provide a holistic evaluation of the models [
68,
69,
70].
In this method, each performance metric (e.g., Accuracy, Macro-F1, ROC-AUC, Balanced Accuracy, Kappa, MCC, ECE, Brier) was considered, and models were ranked accordingly. For metrics in the “higher is better” category (e.g., Accuracy, F1, ROC-AUC), the model with the highest value was assigned rank 1, while the model with the lowest value was assigned rank k (where k = number of models). For metrics in the “lower is better” category (e.g., ECE, Brier), the ranking was reversed: the model with the lowest value received rank 1, and the one with the highest value received rank k.
The ranking values obtained for each model were then averaged using equal weighting, resulting in an average rank value for each model. This average rank represents the overall performance of the model, where a lower average indicates higher performance. Through this method, diverse performance indicators were consolidated under a single scale, enabling an objective ranking of model performance.
3. Results
Within the scope of the study, the descriptive statistical parameters of the dataset were first analyzed. For each variable, the number of observations, mean, minimum and maximum values, the 25th, 50th (median), and 75th percentiles, as well as the standard deviation, were calculated. The results are summarized in
Table 4.
Upon examining
Table 4, different distribution characteristics among the variables become evident. The pH values exhibit a narrow range (6.28–7.91) and are generally close to the neutral level. EC and TDS, on the other hand, display a wide range and high standard deviations, indicating variability in terms of conductivity and dissolved solids. While NO
2 remains at low levels, NO
3 shows a broader distribution. Turbidity and DO also demonstrate wide variability. Metal concentrations (e.g., Na, Ca, Pb, Ag) vary considerably, with Pb and Ag showing high mean values and large variances. These findings indicate heterogeneity, suggesting the presence of potential outliers in some cases.
To ensure data integrity and comparability before modeling, all physicochemical variables were subjected to a structured preprocessing and normalization procedure.
Boxplots and z-score analysis were employed to identify potential outliers; no extreme values requiring removal were found. Normality was evaluated using the Shapiro–Wilk test, and variables showing minor deviations from normality were standardized using the StandardScaler method (zero mean, unit variance).
These preprocessing steps enhanced numerical stability and ensured that all predictors contributed equally during model training, thereby improving the robustness and interpretability of subsequent analyses.
3.1. Water Quality Classification Results
The categories, counts, and percentages corresponding to the CCME-WQI-WHO, WA-WQI-WHO, and WA-WQI-FAO variables are presented in
Table 5.
Table 5 shows that the distribution of water quality indices varies significantly depending on the standard applied. In the CCME-WQI-WHO classification, most observations fall into the Fair (47.62%) and Marginal (46.73%) categories, suggesting that water quality is generally at acceptable levels. In contrast, under the WA-WQI-WHO classification, 80.6% of the samples fall into the Good category, indicating that the same water sources are evaluated as having higher quality according to WHO criteria. On the other hand, in the WA-WQI-FAO classification, more than half of the samples fall into the Poor category (51.79%), with only 41.37% classified as Good. This finding suggests that the FAO criteria provide a stricter assessment of water quality. Overall, these results demonstrate that different classification systems yield varying quality levels for the same dataset, highlighting that the chosen standard plays a decisive role in water quality interpretation.
To statistically validate these differences among the three water quality classification schemes (CCME-WQI-WHO, WA-WQI-WHO, and WA-WQI-FAO), a non-parametric Kruskal–Wallis H test was conducted. The analysis revealed a statistically significant difference among the schemes (H = 261.24, df = 2, p < 0.001). The calculated effect size (ε2 = 0.26) indicated a medium-to-strong magnitude of difference. Subsequently, a Bonferroni-adjusted Dunn post hoc test confirmed statistically significant pairwise differences across all comparisons (padj < 0.001). Examination of the mean rank values showed that the WA-WQI-WHO scheme yielded the highest mean rank, reflecting a more optimistic assessment of water quality, whereas the CCME-WQI-WHO scheme produced the lowest mean rank, suggesting a more conservative classification trend. The WA-WQI-FAO scheme fell between these two extremes, reflecting the influence of FAO’s stricter irrigation water quality thresholds. These findings indicate that, although all three indices rely on similar physicochemical parameters, variations in threshold values and weighting systems lead to statistically significant divergences in classification outcomes. Therefore, the selection of the reference standard (WHO or FAO) is crucial for the accurate interpretation of water quality indices and has significant implications for environmental management and policy decisions.
Since FAO standards define wider tolerance ranges compared to drinking water quality criteria, all observations were evaluated in the highest quality class (“Excellent”). This prevented the FAO-based CCME (CCME-WQI-FAO) results from capturing variation within the dataset; hence, the index was not suitable as a discriminating variable in the modeling phase.
3.2. Model Implementation and Optimal Model Selection
To predict water quality in the ponds, the designed models were tested using 6720 data records obtained from 19 parameters measured at 14 sampling points.
Table 6,
Table 7 and
Table 8 present the results of Accuracy, Macro-F1, ROC-AUC, Balanced Accuracy, Kappa, MCC, ECE, and Brier metrics for the four models across three different water quality classification schemes, prior to hyperparameter tuning and cross-validation. Although no independent external dataset was available for validation, model generalization was ensured through a 5-fold cross-validation scheme and independent test set evaluation, supported by multiple performance metrics (Balanced Accuracy, Macro-F1, ROC-AUC, ECE, and Brier scores).
3.2.1. Comparative Overview of Model Performance Across WQI Schemes
Across the three water quality index (WQI) classification schemes—CCME-WQI-WHO, WA-WQI-WHO, and WA-WQI-FAO—all machine learning models demonstrated high predictive capacity, with test accuracies generally exceeding 90%. The comparative rankings revealed that XGBoost achieved the highest overall predictive performance, leading in two out of three schemes (WA-WQI-WHO and WA-WQI-FAO). Meanwhile, Random Forest (RF) provided the most reliable calibration results (lowest ECE and Brier scores) and was identified as the top-performing model in the CCME-WQI-WHO classification. Logistic Regression (LR) consistently exhibited stable generalization, reflected by the smallest gap between training and test metrics, while Decision Tree (DT) models tended to overfit, as indicated by their near-perfect training scores (≈1.00) and slightly lower test performance.
Although all models maintained high ROC-AUC values (≥0.93), minor differences were observed in class-level sensitivities. Balanced Accuracy and Macro-F1 scores indicated that tree-based models were more sensitive to majority classes, whereas LR preserved better performance across minority classes. This outcome highlights the influence of class imbalance in the dataset, particularly for the “Poor” and “Excellent” water quality categories. However, no oversampling or resampling techniques (e.g., SMOTE or under-sampling) were applied in this study to preserve the natural class distribution. Instead, the imbalance effect was acknowledged and discussed through complementary metrics such as Balanced Accuracy and Macro-F1, which provided a fair assessment of model robustness under imbalanced conditions.
The variance analysis across k-fold validation folds confirmed that the models achieved stable generalization performance, despite overfitting tendencies observed in DT and RF. Among the models, XGBoost and RF consistently ranked highest across all evaluation metrics, while LR provided the most interpretable and computationally efficient alternative.
3.2.2. Performance Results of Machine Learning Models Based on the CCME-WQI-WHO Classification
The predictive performance of the four machine learning models was evaluated using the CCME-WQI-WHO classification scheme. The combined results, both pre- and post-hyperparameter optimization, are presented in
Table 6, which reports test performance metrics solely for clarity and conciseness.
Before optimization, all models achieved high predictive accuracy (≥0.95), with tree-based methods—particularly Random Forest (RF) and XGBoost—demonstrating strong discriminative ability (ROC-AUC ≥ 0.99). However, the near-perfect training scores (≈1.00) observed for DT, RF, and XGBoost indicated mild overfitting, whereas Logistic Regression (LR) provided more stable generalization, showing smaller gaps between training and test performance.
After hyperparameter optimization, all models maintained high predictive power. Ensemble-based approaches preserved their dominance: RF achieved the lowest calibration errors (ECE = 0.0095; Brier = 0.0139), and XGBoost retained the highest ROC-AUC (≈1.00). Despite these improvements, the Decision Tree (DT) still exhibited overfitting tendencies, while LR remained the most balanced and interpretable alternative across metrics.
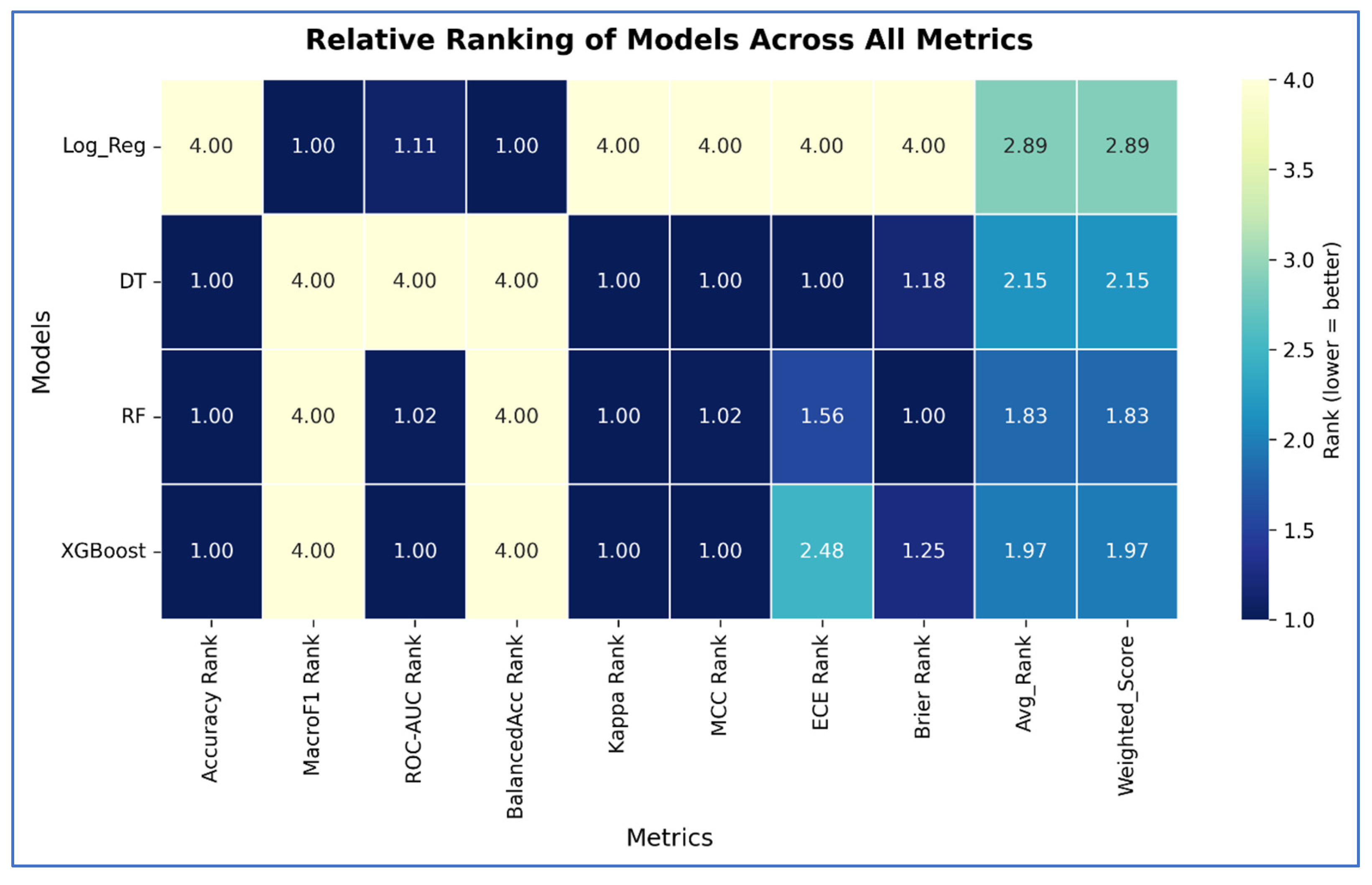
The relative ranking analysis (
Figure 2) confirmed RF as the best-performing model (average rank = 1.83), followed closely by XGBoost (1.97). Although both models performed comparably in accuracy and discrimination, RF’s superior calibration quality made it the preferred model under the CCME-WQI-WHO classification.
The Friedman test (Χ2 = 24.019, p = 0.001 < 0.05) revealed significant differences among the models, but the subsequent Nemenyi post hoc test found no statistically significant pairwise differences (p ≥ 0.05). Consequently, the final model selection was guided by secondary criteria—calibration reliability, sensitivity to class imbalance, and interpretability—highlighting RF as the most robust model for this classification.
3.2.3. Performance Results of Machine Learning Models Based on the WA-WQI-WHO Classification
The predictive performance of the four machine learning models was evaluated under the WA-WQI-WHO classification scheme. The pre- and post-optimization results are summarized in
Table 7, while the relative ranking of models is presented in
Figure 3.
Before optimization, all models achieved satisfactory accuracy levels (≥0.80) with ensemble-based approaches—particularly Random Forest (RF) and XGBoost—outperforming the others across most evaluation metrics. RF and XGBoost demonstrated the highest ROC-AUC values (≈1.00), reflecting strong discriminative ability. However, the tree-based methods exhibited nearly perfect training scores, suggesting a degree of overfitting. Logistic Regression (LR) showed the smallest discrepancy between training and test performance, indicating better generalization stability.
After hyperparameter optimization, the performance of all models slightly improved or remained stable across accuracy and calibration metrics. Among them, RF and XGBoost retained their superiority: RF achieved the lowest calibration errors (ECE = 0.1952; Brier = 0.1128), while XGBoost attained the highest ROC-AUC (≈0.9999). DT continued to display mild overfitting, and LR remained the most balanced yet comparatively less accurate model.
The comparative results highlight that although tree-based models achieved higher discriminative scores, they were more prone to overfitting than LR. This trade-off between interpretability and predictive strength underscores the importance of both calibration and class-level performance metrics when evaluating water-quality prediction models.
As shown in
Figure 3, the XGBoost model ranked first (average rank = 1.49), followed by RF (2.24), DT (2.61), and LR (3.44). Although RF showed slightly better calibration, XGBoost outperformed others in overall predictive ranking due to its superior ROC-AUC and Macro-F1 values. Hence, XGBoost was identified as the best model under the WA-WQI-WHO classification, offering both high accuracy and robust class discrimination.
3.2.4. Performance Results of Machine Learning Models Based on the WA-WQI-FAO Classification
The predictive performance of the four machine learning models was assessed under the WA-WQI-FAO classification scheme. The consolidated results before (Pre) and after (Post) hyperparameter optimization, along with the test metrics, are summarized in
Table 8. The relative ranking of the models is presented in
Figure 4.
Before optimization, all models achieved high predictive accuracy (≥0.88), with the ensemble-based models—particularly Random Forest (RF) and XGBoost—demonstrating strong discriminative ability (ROC-AUC ≈ 0.93−0.95). However, the nearly perfect training metrics (≈1.00) observed for the tree-based models indicated mild overfitting. Logistic Regression (LR) achieved lower overall accuracy but exhibited more stable generalization across folds.
The Macro-F1 results revealed notable class-imbalance effects: RF and XGBoost produced lower Macro-F1 scores (≈0.47−0.48), whereas LR achieved a more balanced performance (0.74). Balanced Accuracy followed a similar trend, showing that LR and XGBoost handled minority classes more consistently than RF or DT. All models maintained high ROC-AUC scores, confirming reliable discrimination between water-quality categories. In calibration metrics, XGBoost achieved the lowest Brier Score (0.068), while DT displayed the lowest ECE, though this value may reflect artificial improvement due to its discrete probability outputs.
After hyperparameter optimization, the general performance of all models improved or remained stable (
Table 8). RF achieved the highest test accuracy (0.94) and maintained strong discriminative power (ROC-AUC ≈ 0.97). Despite its slightly lower accuracy, LR remained the most balanced model in terms of class sensitivity (Balanced Accuracy ≈ 0.83) and calibration quality (Brier ≈ 0.076). DT continued to exhibit minor overfitting, while XGBoost demonstrated robust classification capability but showed a weaker balance across classes.
Overall, RF stood out for its combination of accuracy, discrimination, and calibration, whereas LR offered a more consistent and interpretable alternative. XGBoost achieved comparably high predictive strength but was more affected by class imbalance.
As shown in
Figure 4, the XGBoost model ranked first (average rank = 2.17), followed by Logistic Regression (2.53) and Random Forest (2.53), which performed at similar levels. Decision Tree (DT) ranked last (3.25). XGBoost excelled in key classification metrics such as Macro-F1, Kappa, and MCC, while RF delivered stronger calibration performance but fell slightly behind overall. Although LR provided the most balanced results, its lower accuracy placed it below the ensemble models.
According to the Friedman test (p = 0.266 ≥ 0.05), no statistically significant difference was found among the median model ranks. Consequently, final model selection relied on secondary criteria—calibration quality (ECE/Brier), ROC-AUC, Balanced Accuracy, MCC/Kappa, and interpretability—leading to the identification of RF as the most reliable model for practical deployment, while LR was favored in cases emphasizing class-balance sensitivity.
3.3. Feature Importance and Model Explainability
To enhance the interpretability of ensemble-based models and identify the contribution of individual variables to the classification process, a parameter importance analysis was conducted using the SHAP (Shapley Additive exPlanations) method. SHAP values quantify the influence of each physicochemical variable on the model’s prediction for a specific water quality class, providing a transparent understanding of model behavior.
Under the CCME-WQI-WHO classification, dissolved oxygen (DO) was found to be the most influential variable (
Figure 5), followed by pH and calcium (Ca). These parameters indicate that oxygen concentration, the balance of acidity and alkalinity, and hardness are key determinants of water quality. Ionic and metal parameters such as Ag, P, Ni, Na, and Mg contributed to a lesser extent, reflecting secondary hydrochemical variations among classes.
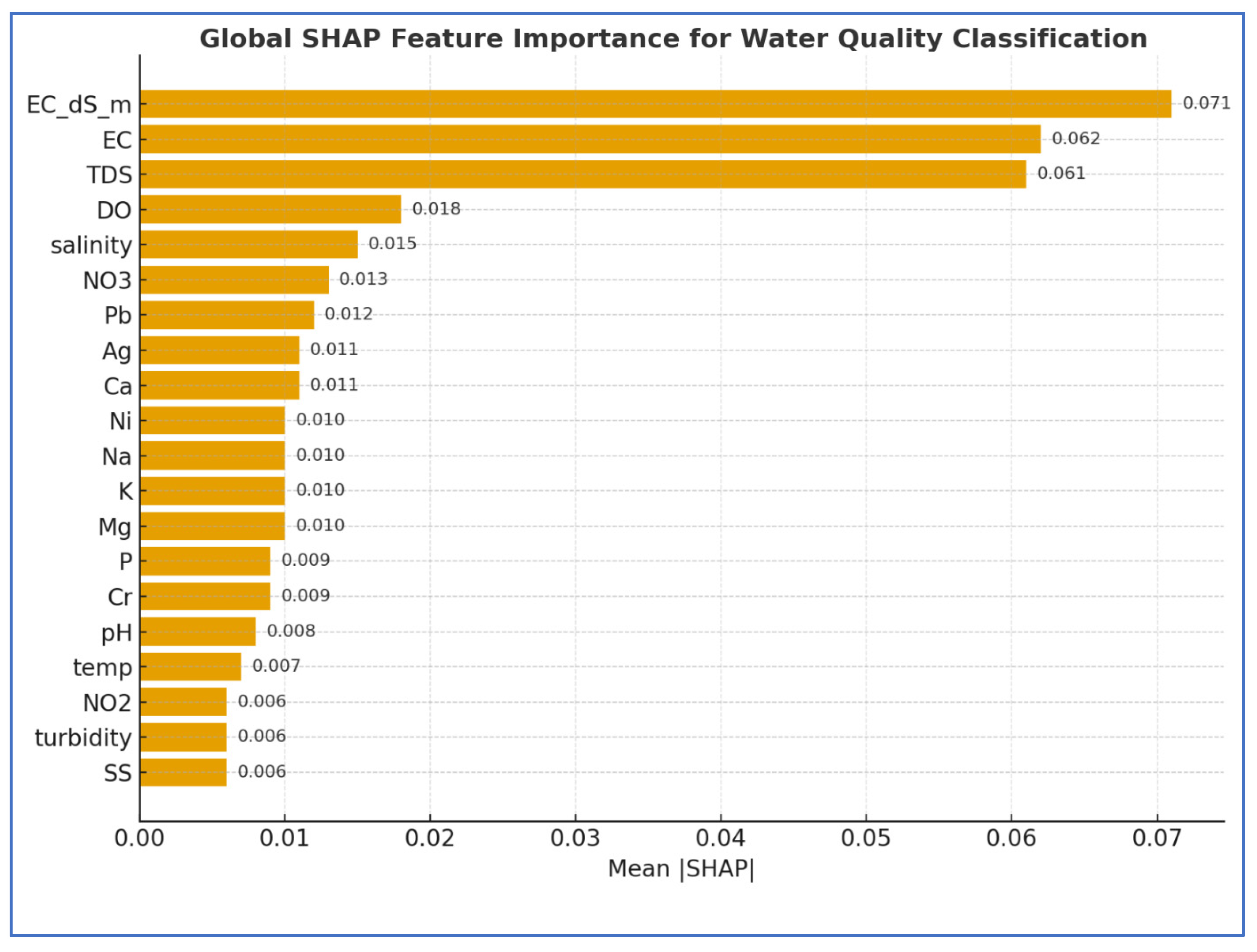
For the Weighted-WQI-WHO classification (
Figure 6), electrical conductivity (EC), and total dissolved solids (TDS) were identified as the most impactful predictors. This highlights the central role of ionic strength and dissolved matter in differentiating water quality classes, while DO, salinity, and NO
3− exhibited moderate importance consistent with their known effects on aquatic chemistry.
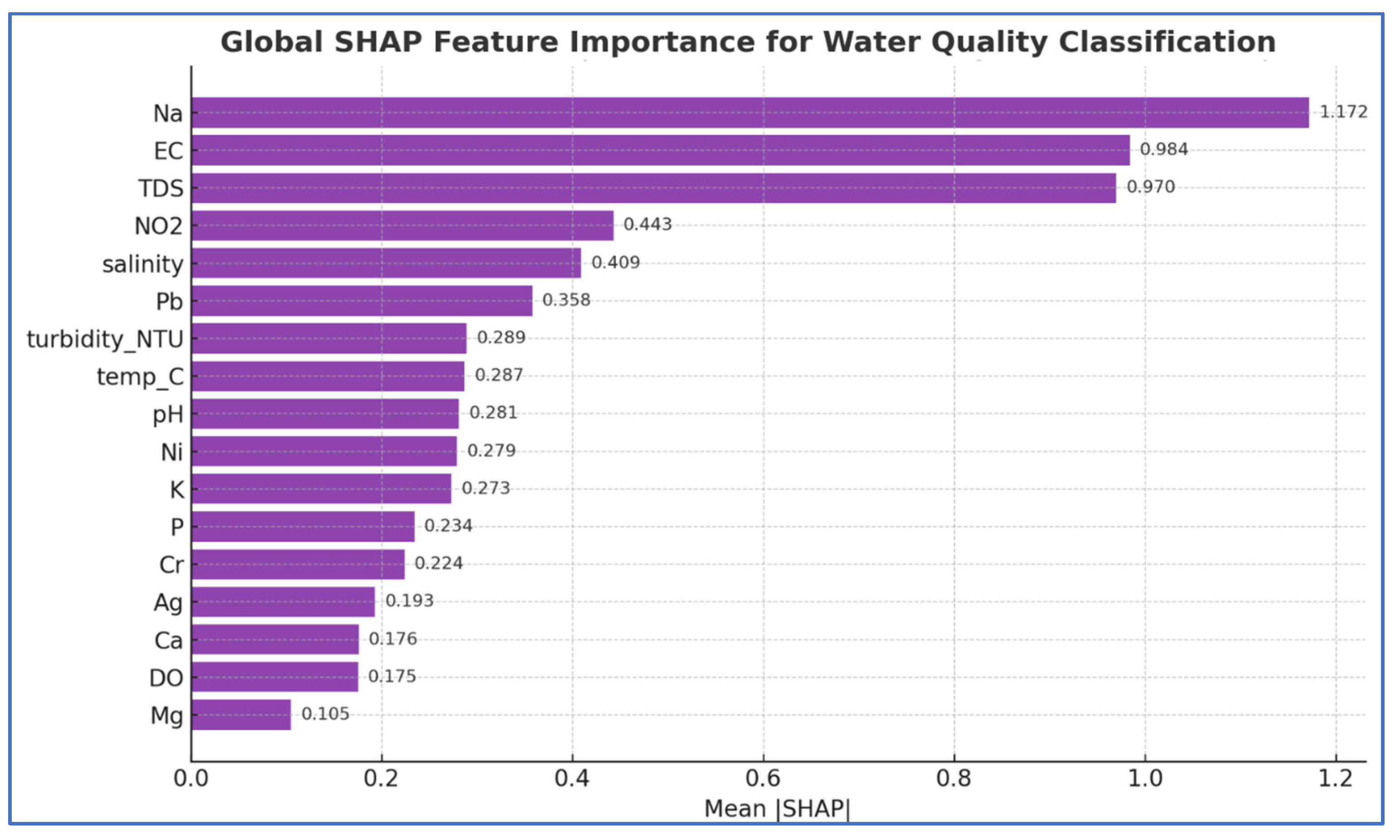
Under the Weighted-WQI-FAO scheme (
Figure 7), sodium (Na) emerged as the dominant predictor, followed by EC and TDS, confirming the strong link between sodium ion concentration, salinity, and water quality categorization. Parameters such as NO
2, Pb, and salinity exhibited intermediate effects, indicating supportive yet less dominant roles compared to the major ionic constituents. Other variables, including turbidity, temperature, pH, and trace metals, had lower SHAP values but still contributed to refining the classification boundaries.
Overall, the SHAP-based interpretability analysis revealed that the models successfully captured the dominant hydrochemical processes controlling water quality in the studied reservoirs. These results enhance the transparency and explainability of machine learning models, aligning them with best practices in environmental AI research.
4. Discussion
The findings of this study provide important insights into both the sensitivity of water quality indices (WQI) and the capacity of machine learning (ML) models to deliver reliable predictions. Notably, when CCME-WQI was applied using FAO threshold values, all samples were classified within a single Excellent category, indicating that the approach lost its discriminative power. By contrast, under the CCME-WQI-WHO classification, 64.3% of the samples were categorized as Fair or Marginal, while the WA-WQI-WHO classification placed 72.1% of the samples in the Good category. Meanwhile, the WA-WQI-FAO classification assigned 51.7% of the samples to the Poor category. These discrepancies clearly demonstrate the sensitivity of water quality interpretations to the choice of standards, particularly when considering irrigation and drinking water purposes. Previous studies similarly emphasize that WQI results vary depending on the threshold values used for water quality parameters [
46,
47].
The machine learning analyses further highlighted these differences. Prior to hyperparameter optimization, ensemble-based models such as Random Forest (RF) and Extreme Gradient Boosting (XGBoost) achieved accuracies above 95% and ROC-AUC scores in the range of 0.96–0.97. However, their Macro-F1 scores remained around 0.72, pointing to persistent class imbalance issues. Logistic Regression (LR), while yielding a lower accuracy (0.88), presented a more balanced error distribution across classes. After optimization, the Macro-F1 score of RF improved to 0.83, while XGBoost reached a ROC-AUC of approximately 0.99, indicating a marked improvement in the generalization capacity of the models. Although no resampling techniques, such as SMOTE or under-sampling, were applied, the evaluation using Balanced Accuracy and Macro-F1 metrics revealed that the models provided fair performance under imbalanced class distributions. This approach ensured the preservation of the natural class structure of the dataset while still maintaining a reliable assessment of model robustness.
These results underscore the importance of considering not only overall accuracy but also secondary metrics, such as calibration measures (e.g., Brier score) and performance on minority classes, in model selection. This aligns with prior literature, which highlights the significance of calibration and balanced classification performance for robust ML applications in environmental contexts [
53,
60,
65]. Moreover, the variance analysis across k-fold validation folds confirmed that the models exhibited stable generalization performance, despite minor overfitting tendencies observed in tree-based algorithms, which supports the reliability of their predictions.
Tree-based ensemble models maintained their superiority across different index classifications. For instance, under the CCME-WQI-WHO classification, RF achieved the highest performance. In contrast, under the WA-WQI-WHO and WA-WQI-FAO classifications, XGBoost outperformed other models, achieving an accuracy of 95% and ROC-AUC values of approximately 0.98–0.99. By contrast, Logistic Regression consistently showed the lowest performance, particularly under WHO-based classifications. This result indicates that linear models struggle to capture complex environmental relationships, whereas ensemble methods provide more generalizable and stable outcomes. Similar findings have been reported by Patel et al. [
50] in India and Hidayat et al. [
59] in Indonesia, where RF and XGBoost achieved ROC-AUC values ranging from 0.95 to 0.97. Likewise, Zhi et al. [
20] and Sajib et al. [
21] demonstrated that XGBoost outperforms linear and conventional algorithms in capturing nonlinear hydro-chemical interactions. The high ROC-AUC values obtained in this study (≈0.99) confirm that the models can capture the complex physicochemical dynamics of ponds in Kastamonu with remarkable accuracy.
Comparable ML-based WQI prediction studies from South Asia, West Asia, and the Mediterranean further validate these results. Nishat et al. [
71] analyzed fourteen ML algorithms for WQI prediction in the polluted rivers of Dhaka (Bangladesh) and reported that ensemble-based models such as XGBoost and Random Forest achieved R
2 ≈ 0.97, emphasizing the failure of linear models under tropical variability. Similarly, Shaheed et al. [
72] applied XGBoost, SVM, and Naïve Bayes to classify river water quality across Southeast, South, and West Asia and found XGBoost to be the most robust under diverse hydro-climatic pressures. Uddin et al. [
2] successfully predicted coastal WQI in the Bay of Bengal using ensemble learning (RF, XGBoost) with R
2 > 0.95, while Uddin et al. [
73] confirmed their superior interpretability in estuarine systems. In the Middle Eastern context, Mohammadpour et al. [
74] integrated ML-based WQI prediction with probabilistic health-risk analysis in southern Iran, demonstrating the method’s ability to identify contamination sources such as Pb, Cd, and Ni with high precision. In Egypt, Elshaarawy and Eltarabily [
75] optimized ML algorithms for groundwater quality prediction in El Moghra and found that Random Forest and Gradient Boosting achieved the highest performance. Collectively, these studies reveal that ensemble-based approaches consistently outperform linear and shallow models across diverse regions and environmental conditions, reinforcing the generalizability of the current study’s findings.
From a statistical perspective, the Friedman and Nemenyi tests confirmed that RF and XGBoost ranked highest overall. However, pairwise comparisons in the Nemenyi test did not yield statistically significant differences (
p ≥ 0.05). This suggests that model superiority may vary depending on the weighting of performance metrics. Muhammad et al. [
76] also emphasized that relying on a single performance indicator can be misleading, and that a multi-metric approach provides a more holistic assessment of model performance.
Although the physicochemical data used in this study were obtained through standardized field and laboratory protocols, minor uncertainties may still arise from temporal and environmental fluctuations inherent to hydrological systems. Throughout the irrigation year, variations in temperature, precipitation, and evaporation—particularly during transitional periods such as late summer and early spring—can influence the ionic composition and dissolved oxygen dynamics of small reservoirs. These seasonal differences may cause short-term fluctuations in parameters such as EC, NO3−, and TDS, reflecting the natural hydrochemical response to climatic variability. Nevertheless, the consistent sampling design, standardized measurement procedures, and full-year measurement coverage ensured that these temporal variations were clearly represented in the dataset, thereby strengthening its hydrological validity. Consequently, the model predictions reflect not only the physicochemical characteristics of the reservoirs but also their seasonal hydrodynamic behavior, providing a realistic representation of water quality dynamics under varying climatic conditions.
From a practical perspective, the inconsistencies between WQI classifications and ML predictions present both opportunities and risks for decision-makers. For example, while 72.1% of the water was classified as Good under the WA-WQI-WHO standard, nearly half of the same samples fell into the Poor category according to WA-WQI-FAO, highlighting the critical importance of standard selection in irrigation management. On the other hand, advanced models such as RF and XGBoost can account for such variability, offering more balanced and reliable predictions. This dual approach (index + ML) provides a more coherent decision-support framework for managing multipurpose ponds, bridging international standards with local conditions [
20,
47,
59]. In this context, the high concentrations of Pb (lead) and Ag (silver) observed in several samples (
Table 4) are of environmental concern. Pb, a persistent toxic metal, can accumulate in sediments and biota, impairing aquatic biodiversity and posing chronic health risks through bioaccumulation [
74]. Elevated Ag levels, although less common, can disrupt microbial activity and photosynthetic processes in aquatic systems, reducing self-purification capacity and ecosystem stability. These findings underscore the need for continuous monitoring and stricter control of trace metal inputs, particularly in small lentic systems used for irrigation and recreation.
From an operational standpoint, the combined WQI–ML workflow can be directly embedded into water-quality planning for small reservoirs. Routine, low-cost WQI screening can maintain continuity, while weekly or bi-weekly ML inference can flag degradation risk and trigger targeted sampling at specific sites or seasons (adaptive sampling). Threshold-aware reporting enables predictions to be mapped to FAO/WHO standards, facilitating actionable decisions in irrigation and drinking water use. Confusion matrices and class-specific metrics enable risk-tolerant operating points (e.g., prioritizing high recall for the “Poor” class to minimize false-safe decisions). Feature-importance/SHAP analyses identify controllable drivers (e.g., EC/TDS, NO3−), informing interventions such as aeration, optimized fertilizer timing, or blending strategies. The workflow is lightweight to maintain: models can be retrained quarterly as new data arrive, and calibration indicators (ECE/Brier) can be monitored as drift alarms to schedule re-training. In practice, this supports early warning for exceedances, reduces blanket sampling effort in favor of event-based campaigns, and prioritizes remedial actions across ponds with the highest predicted risk.
Conceptually, the hybrid framework proposed in this study also aligns with the hydrodynamic perspective presented by Piazza et al. [
77] which emphasizes that diffusion and dispersion processes play a crucial role in interpreting spatial and temporal variability in water quality data. Integrating these physical mechanisms with data-driven models, such as WQI and ML, can enhance both interpretability and predictive robustness, thereby bridging the gap between physical understanding and computational modeling in aquatic systems.
The SHAP-based feature importance analysis further confirmed that key physicochemical drivers such as dissolved oxygen, electrical conductivity, and sodium concentration play a decisive role in the classification process, aligning model predictions with established hydrochemical principles.
Overall, this study contributes to the growing body of literature advocating for the combined use of classical WQI-based approaches and advanced ML algorithms in water quality management. The findings demonstrate that WQI-based classifications are highly sensitive to threshold values, whereas models such as RF and XGBoost, with discriminative power reaching 0.99, provide more stable and generalizable predictions. When interpreted in conjunction with the referenced regional case studies, the present results confirm that ensemble-based ML models have high transferability and can support sustainable water governance in Mediterranean-type and semi-arid environments. Future research should expand datasets to capture seasonal and inter-annual variability, integrate satellite-derived indicators, and apply explainable AI (XAI) methods (e.g., SHAP, LIME) to enhance model interpretability and reliability for decision-makers [
21].
These findings align directly with the United Nations Sustainable Development Goals (SDGs). By enabling reliable monitoring of water resources (SDG 6: Clean Water and Sanitation), supporting climate-resilient water management systems (SDG 13: Climate Action), and protecting freshwater-dependent ecosystems (SDG 15: Life on Land), the combined use of index-based and machine-learning approaches provides applicable, reliable, and scalable tools for sustainable pond and reservoir management. Moreover, the quantitative outputs of ML models can be linked to global sustainability indicators, such as SDG 6.4.2 (Level of Water Stress) and SDG 6.5.1 (Implementation of Integrated Water Resources Management), facilitating international comparability of local water management practices. In this context, previous studies have demonstrated how ML-based modeling can support the monitoring of these indicators by improving freshwater withdrawal ratios, enhancing resilience to climate variability, and strengthening integrated management capacity [
69,
78,
79]. Consequently, the present study contributes not only methodologically but also strategically to aligning local-scale water governance in Türkiye with the global SDG framework.
5. Conclusions
This study integrated widely used water quality indices (CCME-WQI and WA-WQI) with supervised machine learning algorithms to comprehensively assess the water quality of two irrigation reservoirs (Taşçılar and Yumurtacılar) in Kastamonu. It represents one of the first comparative applications of WQI–ML integration for small inland reservoirs in Türkiye, bridging classical water assessment indices with data-driven modeling.
The findings revealed that the selection of the classification standard (WHO vs. FAO) strongly influences water quality interpretation, underscoring the need for context-specific index calibration in local management practices. Ensemble-based models (RF and XGBoost) consistently provided the highest predictive performance (ROC-AUC ≈ 0.99), while Logistic Regression demonstrated greater stability and interpretability under class imbalance conditions.
These results collectively suggest that combining WQI-based indices with machine learning improves the reliability and interpretability of water quality assessments, offering practical value for irrigation and ecosystem management.
However, this study has several limitations. The analysis was conducted using data from a single hydrological period and limited sampling points, which may constrain the temporal generalization of the models. Additionally, no external validation was performed across different basins, and the dataset did not include certain biological and heavy metal parameters that could influence long-term water quality trends.
Future research should expand its temporal coverage to include multi-seasonal data, incorporate remote sensing indicators (e.g., NDVI, LST) for dynamic monitoring, and employ explainable AI (XAI) frameworks, such as SHAP and LIME, to enhance interpretability. Cross-basin validation and integration with real-time monitoring systems will further increase the operational applicability of the proposed approach in sustainable water resource management.
In conclusion, this study highlights the importance of integrating classical WQI methods with modern ML tools to achieve transparent, scalable, and data-driven water management strategies under changing climatic and anthropogenic pressures.