Abstract
In the hydropower sector, accurate estimation of short-term reservoir inflows is an essential element to ensure efficient and safe management of water resources. Short-term forecasting supports the optimization of energy production, prevention of uncontrolled water discharges, planning of equipment maintenance, and adaption of operational strategies. In the absence of data on topography, vegetation, and basin characteristics (required in distributed or semi-distributed models), data-driven approaches can serve as effective alternatives for inflow prediction. This study proposes a novel hybrid approach that reverses the conventional LSTM (Long Short-Term Memory)—ARIMA (Autoregressive Integrated Moving Average) sequence: LSTM is first used to capture nonlinear hydrological patterns, followed by ARIMA to model residual linear trends.The model was calibrated using daily inflow data in the Izvorul Muntelui–Bicaz reservoir in Romania from 2012 to 2020, tested for prediction on the day ahead in a repetitive loop of 365 days corresponding to 2021 and further evaluated through multiple seven-day forecasts randomly selected to cover all 12 months of 2021. For the tested period, the proposed model significantly outperforms the standalone LSTM, increasing the R2 from 0.93 to 0.96 and reducing RMSE from 9.74 m3/s to 6.94 m3/s for one-day-ahead forecasting. For multistep forecasting (84 values, randomly selected, 7 per month), the model improves R2 from 0.75 to 0.89 and lowers RMSE from 18.56 m3/s to 12.74 m3/s. Thus, the hybrid model offers notable improvements in multi-step forecasting by capturing both seasonal patterns and nonlinear variations in hydrological data. The approach offers a replicable data-driven solution for inflow prediction in reservoirs with limited physical data.
1. Introduction
Prediction in hydrology plays an essential role in the management of water resources. In a context marked by climate uncertainties and increasingly frequent extreme events, the ability to predict the behaviour of hydrological systems is very important. Thus, classical methods, based on statistical and physical models, continue to provide a solid foundation, while methods based on artificial intelligence constitute new tools capable of learning from recorded chronological data and improving the accuracy of forecasts.
Traditional time series forecasting methods, such as autoregressive ones, are successfully used in short-term prediction provided that the time series is stationary [1,2,3]. One of the models that integrates a method of transforming time series from non-stationary to stationary by applying differentiation is the ARIMA (Autoregressive Integrated Moving Average) model. This model is successfully applied in forecasting in various fields, especially in the short term. With the increase of the forecast horizon, this method no longer provides good results. Hybrid and deep learning models, including LSTM and Bidirectional LSTM, have demonstrated improved capabilities compared to classical ARIMA approaches in time series forecasting [4].
Recently, AI-based methods have seen a significant expansion in the field of forecasting, demonstrating high potential in improving the accuracy of predictions through their ability to model nonlinear relationships between time series variables. Neural networks have successfully proven their applicability to different renewable energy sources: wind [5,6,7], solar [8,9], and hydraulic [10,11,12]. A comprehensive analysis of deep sequential models used in time series forecasting is performed in [13] highlighting the limitations of classical methods (ARIMA, Vector Machine Support) in capturing nonlinear relationships and long-term dependencies in complex time series compared to neural network-based models. Comparisons between artificial neural network and traditional statistical models are presented in many papers [14,15,16], highlighting the superiority of models belonging to artificial intelligence. A comprehensive review of the scientific literature on the comparison of ARIMA models with machine learning techniques applied to time series forecasting, including hybrid combinations between the two approaches, is carried out in [17]. Among AI-based methods, LSTM have proven to be suitable for time series with seasonal patterns, cyclicality, and trends hidden in long data series [18,19]. In [20] a dynamic classification-based LSTM model is developed for the forecasting of daily flows in different climatic regions, highlighting the importance of adapting the model according to dynamic flow patterns. Despite their flexibility and ability to model nonlinear patterns, LSTM networks often require large datasets and careful hyperparameter tuning, which can limit their practicality in data-scarce environments. In order to improve predictions, various approaches to combining and optimizing existing models have been developed over time. The integration of evolutionary algorithms allowed the optimization of model parameters, and the combination of different types of models led to the creation of hybrid models. These hybrid models provided superior accuracy in estimating the predicted values compared to classical autoregressive models [21,22,23].
Multi-step-ahead forecasting is essential for decision-making in time-dependent systems. However, multi-step prediction poses significant challenges compared to short-term prediction (one-step-ahead), mainly due to the propagation and accumulation of prediction errors from one step to the next as well as due to the stochastic nature of the forecasted variable.
In multi-step prediction, each future prediction is conditioned by previous values, either actual (open loop) or estimated (closed loop) [24]. Thus, an error introduced at the current time step (t + 1) is transported to the next step (t + 2), where it is combined with a new local error, and this process continues iteratively, generating a potential significant deviation from the trajectory of the real variable. This phenomenon leads to a rapid degradation of the model’s performance over longer prediction intervals (5–7 days or more), which causes the prediction’s “allure”, its shape or trend, to become completely unrealistic or even divergent.
This paper starts from the hypothesis that the accuracy of the prediction in the first timestep plays a critical role in the success of a multi-step prediction. The closer the first predicted value is to the real value, the lower the error transmitted to the subsequent steps, which contributes to increasing the accuracy of the forecast. Consequently, a well-calibrated model for one-step-ahead prediction can form the foundation of a robust short-term closed-loop prediction system.
This study proposes a hybrid approach combining LSTM and ARIMA models, applied to real-world hydrological data, namely discharge values. LSTM is used as the primary forecasting model, while ARIMA is applied to correct the residual errors. The method shows improved performance over standalone LSTM in both one-day and short-term multi-step forecasts, highlighting the robustness and effectiveness of the hybrid structure in inflow prediction. Notably, most existing studies adopt the reverse configuration, using ARIMA as the main predictor and LSTM for residual correction. Moreover, multi-step forecasts are generally prone to instability; however, the proposed hybrid model demonstrates consistent and reliable performance across multiple forecasting horizons.
2. Materials and Methods
Long short-term memory (LSTM) network is a special type of recurrent neural network that can process data sequences and retain information from the near and distant past of the time series, making them suitable for predicting data in hydrology. The neural network has the ability to retain patterns associated with variables, such as tributary flows, which exhibit complex behaviour, characterized by nonlinearity, seasonality, and stochastic components. This advantage of LSTM networks, together with the availability of subroutines for network training using various learning methods (Adam, Stochastic Gradient Descent with Momentum, Root Mean Square Propagation) already implemented in MATLAB programming languages, contributes to facilitating their application in forecasting practice. It is well known that setting the parameter characteristics of the model, such as number of epochs completed, learning rate, and mini-batch size, typically involves repeated experimentation. Even slight adjustments to these hyperparameters can lead to significantly different results. However, once properly tuned, the model is able to learn complex patterns and generate highly accurate predictions.
Each memory cell in the LSTM is updated by adding or removing information while the information is being transmitted through three gates: forget gate, input gate, and output gate.
In the simplest way, the day index can be implemented as a function composed of the sine and cosine functions to adjust the periodicity of inflows [25]:
where i is the day index; i = 1 corresponds to 1st of January and i = 365 corresponds to 31st of December.
In the proposed hybrid model, the LSTM network produces the baseline prediction for the time series. But no matter how well the model is trained, there are differences between the predictions and the expected values (target). To correct this component, an ARIMA model shall be fitted to the residual series obtained as the difference between the predicted values and the actual values corresponding to the data used during the training period.
The structure of the hybrid LSTM-ARIMA model used in this study is shown in Figure 1, illustrating the combination of the main forecast provided by LSTM and the error correction performed by ARIMA, applied for both open-loop (365 days) and closed-loop (7 days) predictions.

Figure 1.
LSTM-ARIMA hybrid model architecture for forecasting.
The residuals between the LSTM predictions and the observed values constituted a new time series, which generally shows autocorrelation. Based on this series of errors, an ARIMA model was calibrated to make additional predictions.
The time series model is estimated, and each forecast is recursively computed using the real values in an open loop (Figure 2a) or using previous forecasts in a closed loop (Figure 2b).

Figure 2.
Multi-step prediction scheme with LSTM + ARIMA model: (a) using open loop; (b) using closed loop.
In Figure 2, , , , …, are the observed (measured) values and , , , …, are the forecasted values. In Figure 2a it can be observed that the forecasted values at each time step are not used to forecast future values. In contrast, in Figure 2b it can be observed that, as they are forecasted, these values are added to the input sequence and used to forecast future values.
Performance evaluation criteria are an important aspect of validating the prediction model. The most used indicators are coefficient of determination (R2), root mean square error (RMSE), and Nash–Sutcliffe efficiency (NSE).
Coefficient of determination, R2, describes the proportion of the variance in measured data explained by the model. The relation for determining this coefficient is as follows:
where is the i-th observed value; is the i-th simulated value; is the average of observed values; is the average of simulated values; and N represents the total number of observations.
The relation for determining the root mean square error, RMSE, is as follows:
Nash–Sutcliffe efficiency, NSE, determines the relative magnitude of the residual variance compared to the measured data variance. This coefficient is calculated as follows:
In principle, for a day-ahead prediction, a model is considered good when R2 is higher than 0.85 [26] and RMSE is less than half of the standard deviation of the observations time series [27]. The coefficient NSE higher than 0.85 is considered very good and negative values indicate unacceptable performance [28].
3. Application of the Proposed Method on a Case Study
To validate the proposed methodology, the hybrid LSTM-ARIMA model was applied to a case study. The time series consists of daily inflows in Izvorul Muntelui-Bicaz reservoir, located in a mountainous area in the northeastern part of Romania (Figure 3). Being the first in a series of reservoirs located on the Bistrița River, it has the advantage that the flows entering the reservoir are natural inflows, not affected by the actions of the human factor, and follow a natural pattern, easiest to be forecasted.

Figure 3.
Izvorul Muntelui-Bicaz reservoir location [https://earth.google.com, accessed on 15 June 2025].
The average daily inflows in the reservoir in the period 2012–2021 were used. The data were divided in that corresponding to the period 2012–2019 for training, 2020 for validation, and the year 2021 was used for testing. For better precision of the model, the precipitation values downloaded from the https://open-meteo.com/ (accessed on 15 June 2025) were used along with the day index.
From the analysis of inflows data series, it can be observed that the inflows fall within the range 2.54–343.70 m3/s. The average inflow is 39.73 m3/s and the standard deviation is 35.98 m3/s.
Figure 4 presents the chronologically recorded daily inflows in the reservoir in the 2012–2020 period used for model calibration, providing an overview of the seasonal and interannual variability within the dataset.

Figure 4.
Inflows in Izvorul Muntelui-Bicaz reservoir in the period 2012–2020 used for the calibration of the model.
From Figure 4 it can be seen that the variation of flows has an important seasonality: in spring (March–May) the flows have increased values due to heavy rainfall and snow melting, and in summer (June–August) there may be sudden increases in flows following torrential rains and rapid runoff on the slopes. The main descriptive characteristics such as minimum (Min), maximum (Max), average (Mean), and multiannual standard deviation (Std) values are listed in Table 1.

Table 1.
Main descriptive characteristics of the multiannual monthly average values of the inflows for the period 2012–2020 used for the drive of the hybrid model LSTM + ARIMA.
In LSTM, the input sequence has a length of 30 values and is composed of inflows, day indices corresponding to the position within the year, and precipitation. The model architecture includes a LSTM layer with 150 hidden units. As for a learning algorithm, Adam was chosen, known for being robust and efficient in case of large data sets, working efficiently on small/medium minibatches, and accelerating training without degrading stability. During the training process, a mini-batch size of 32 was employed to balance computational efficiency and model convergence. Initial learning rate of 0.001 was set up, with a reduction factor of 0.9 after every 10 epochs, which helps to refine the adjustment of parameters throughout training. The maximum number of training epochs was set at 200. The data were kept in chronological order throughout the training process and were not shuffled, in order to preserve the temporal dependencies inherent in the time series.
The input data can be scaled using the Z-score (standardization) method [29]; however, for LSTM applications, the min–max normalization method [30] is often more suitable. For example, for daily inflows into the reservoir, Q, the normalization relation is as follows:
where is the normalized inflow and and are the minimum and the maximum values of the inflow time series, respectively.
In order to obtain a sufficiently long time series of residuals, both the residuals corresponding to the predictions of the neural network on the training set and those related to the validation set were used, the differences between the predicted and measured values being illustrated in Figure 5.

Figure 5.
Residuals between measured and predicted values, using LSTM model, for the training and validation period (2012–2020).
The errors in Figure 5 were obtained as differences between the values predicted by the LSTM and the actual values. These have higher values in the spring-summer periods, when there are rapid increases and decreases in flows, generally more difficult to forecast. To obtain an ARIMA forecast model, they were differenced and analyzed to determine the autoregressive order p and the moving average order q. The number of differences required (d) to achieve stationarity was found to be one. For this purpose, the autocorrelation function (ACF) and partial autocorrelation function (PACF) were graphically represented (Figure 6).

Figure 6.
(a) Partial autocorrelation function and (b) autocorrelation function plots for differentiated time series.
From Figure 6 one can see that the PACF suggests correlation between flows up to 7 lags, so that p = 2, 3, 4, …, 7 and the ACF suggests the choice of order for the MA, q = 2, 3, or 4. After testing different AR orders and MA orders, the variant leading to minimum RMSE and maximum R2 was chosen, as follows: p = 7, q = 2. Residual diagnostics, including the Ljung–Box test (p-value = 0.089), confirmed the absence of significant autocorrelation in the residuals, indicating that the selected parameters for the ARIMA model adequately captured the temporal structure of the data.
Figure 7 presents the values predicted using the LSTM network, the predictions obtained with the LSTM-ARIMA hybrid model, as well as the data measured for the analyzed period.

Figure 7.
Measured and one-day-ahead predicted inflows in reservoir for testing period 2021; (a) January–March; (b) April–June; (c) July–September; (d) October–December.
In Figure 7, the differences between the measured and predicted values are highlighted. These values were plotted on graphs for different time intervals (January–March, April–June, July–September, October–December).The values predicted with the LSTM model follow the general trends well but fail to accurately capture the daily oscillations and especially the extreme ones. However, these daily oscillations are better predicted by the ARIMA model.
Table 2 shows the values of the performance indicators of the prediction models with 1 day of anticipation, obtained in a repetitive open loop for 365 days corresponding to 2021 based on LSTM and the hybrid model LSTM-ARIMA, respectively.

Table 2.
Performance indicators for one-day-ahead prediction for training, validation, and testing period.
From Table 2 it can be seen that in the case of the one-day prediction, the coefficient of determination calculated for the 365 values of the year 2020 (in open loop) is higher in the case of using the hybrid model than in the case of LSTM. The same thing happens for the test period, 2021, when R2 is improved from 0.93 to 0.96, the increase being significant. The RMSE coefficient is also reduced, both in the case of predictions corresponding to the validation year and in the case of testing, in the case of using the hybrid model.
The validation of the hybrid model applied in a closed loop for 7 days was done for 2020. By randomly choosing a starting point from each month, for five independent simulations the results obtained on 7 consecutive days of each month and for the 12 months of the year (84 values), the performance indicators are presented in Table 3 (simulations 1 to 5). Simulation 6 contains the model’s performance indicators for predictions for 7 consecutive days obtained starting from January 1, every 7 days, to cover the entire year 2020 (365 values), and the last row of the table is the average of simulations 1 to 6 results.

Table 3.
Performance indicators for validation period, year 2020.
The values accurately forecasted for the 2020 validation year demonstrated the ability of the hybrid model to replicate the evolution of the time series. Consequently, the model was subsequently used to generate the forecast for 2021. The model has been updated by including the year 2020 in the training set, as well as in the calibration of the ARIMA model for residuals, thus expanding the history available for calibration. Predictions were made on windows of 7 consecutive days, randomly chosen from each month of 2021 with both the LSTM model and the hybrid model LSTM + ARIMA. Obtained values are graphically represented together with the real values and presented in Figure 8.
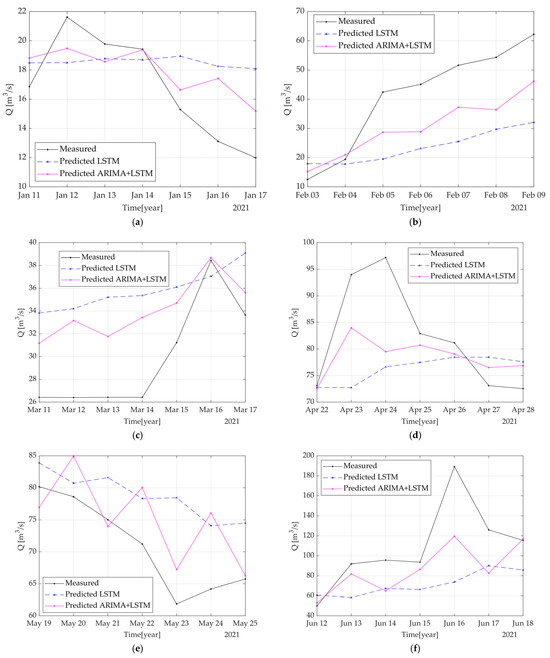

Figure 8.
Comparison between measured and predicted values over 7-day periods, for twelve different starting dates. Panels (a–l) correspond to twelve selected weeks during the testing period. (a) January: LSTM: RMSE = 3.60 m3/s, hybrid: RMSE = 2.40 m3/s (Std = 7.89 m3/s); (b) February: LSTM: RMSE = 21.49 m3/s, hybrid: RMSE= 13.35 m3/s (Std = 18.36 m3/s); (c) March: LSTM: RMSE = 6.84 m3/s, hybrid: RMSE = 4.80 m3/s (Std = 26.26 m3/s); (d) April: LSTM: RMSE = 11.75 m3/s, hybrid: RMSE = 8.04 m3/s (Std = 37.34 m3/s); (e) May: LSTM: RMSE = 8.95 m3/s, hybrid: RMSE = 6.53 m3/s (Std = 38.50 m3/s); (f) June: LSTM: RMSE = 51.08 m3/s, hybrid: RMSE = 33.41 m3/s (Std = 55.287 m3/s); (g) July: LSTM: RMSE = 4.66 m3/s, hybrid: RMSE = 4.98 m3/s (Std = 41.94 m3/s); (h) LSTM: RMSE = 8.63 m3/s, hybrid: RMSE = 5.36 m3/s (Std = 22.70 m3/s); (i) September: LSTM: RMSE = 6.24 m3/s, hybrid: RMSE = 4.84 m3/s (Std = 8.68 m3/s); (j) October: LSTM: RMSE = 2.78 m3/s, hybrid: RMSE = 2.19 m3/s (Std = 13.09 m3/s); (k) November: LSTM: RMSE = 4.06 m3/s, hybrid: RMSE = 3.52 m3/s (Std = 10.53 m3/s); (l) December: LSTM: RMSE = 5.20 m3/s, hybrid: RMSE = 3.70 m3/s (Std = 10.92 m3/s).
From Figure 8 it can be seen that the LSTM model generalizes well, managing to follow the general trend of the measured values over the periods of 7 consecutive days. However, daily fluctuations are not always accurately captured, which can lead to local differences between predictions and actual data. By adding the fluctuations predicted with the ARIMA model, the hybrid model’s predictions get closer to the curve of the measured values, improving short-term accuracy and better capturing rapid data variations.
The graphical analysis of Figure 8 shows that the values forecasted with the LSTM + ARIMA hybrid model are generally closer to the measured values compared to the predictions obtained with the simple LSTM network.
The same procedure for the validation of the hybrid model applied in a closed loop for 7 days for 2020 was also applied for 2021. The starting points for each month were randomly chosen. For five independent simulations, the results were obtained on 7 consecutive days of each month and for the 12 months of the year (84 values); the performance indicators are presented in Table 4 (simulations 1 to 5). Simulation 6 contains the model’s performance indicators for predictions for 7 consecutive days obtained starting from January 1, every 7 days, to cover the entire year 2021 (365 values), and the last row of the table is the average of simulations 1 to 6 results.

Table 4.
Performance indicators for testing period, year 2021.
From Table 4 it can be seen that the forecasted values obtained with the hybrid model are much more appropriate than those measured, which leads to a higher R2 than in the case of using LSTM. Considering simulation 6, the one that covers most of 2021, as the most significant, the forecasted RMSE values obtained with the hybrid model is 14.37 m3/s, compared to 20.15 m3/s obtained in the case of using simple LSTM. The average values of these indicators were then computed to provide an aggregated assessment of the model’s accuracy and robustness. The standard deviation of the analyzed series is 35.98 m3/s. It can be concluded that the hybrid model provides a satisfactory prediction.
To facilitate a clear and intuitive comparison between the two models, a boxplot was employed to visualize the distribution of relative prediction errors (%) (Figure 9). This graphical representation complements the numerical metrics by providing insights into the dispersion, central tendency, and presence of outliers, thereby contributing to a deeper understanding of model behaviour and robustness.

Figure 9.
Comparison of LSTM and LSTM + ARIMA model performance using boxplot of prediction errors; (a) for one-day-ahead prediction; (b) for seven-days-ahead prediction.
Figure 9a reveals that the standalone LSTM model produces a higher number of extreme negative outliers, with some errors exceeding −100%, indicating instability in certain predictions. In contrast, the LSTM + ARIMA hybrid shows fewer and milder outliers, suggesting enhanced robustness. The median error (red line) is also closer to zero, implying improved average accuracy. In the multi-step prediction scenario (Figure 9b), the LSTM + ARIMA model displays a narrower range of variation, reflecting more consistent performance across selected days. While LSTM continues to generate significantly negative outliers, those from the hybrid model remain closer to zero. The median error again indicates better performance for LSTM + ARIMA, highlighting its ability to reduce systematic bias and enhance predictive reliability.
To further assess model performance under extreme hydrological conditions, we analyzed prediction errors in the tails of the inflow distribution. Specifically, we focused on the right tail (high-flow events) and the left tail (low-flow events), which are operationally critical yet challenging to forecast. Figure 10 presents the error patterns for both models, LSTM and LSTM-ARIMA, across these extremes. The horizontal axis represents the observed inflow, while the vertical axis shows the prediction error. This visualization allows for a direct comparison of model behaviour in rare but impactful scenarios, with errors computed as the difference between measured and predicted flows within the 90th and 10th percentile ranges.

Figure 10.
Prediction Errors: (a) Right tail—high-flow conditions (≥98.05 m3/s); (b) left tail—low-flow conditions (≤13.02 m3/s).
Table 5 presents the error metrics for the right tail, highlighting model behaviour during extreme inflow events.

Table 5.
Tail prediction errors for LSTM and LSTM + ARIMA models.
As shown in Table 5, the analysis of prediction errors at the extremes of the inflow distribution highlights the differing behavior of the two tested models. In the case of high-flow conditions (≥90th percentile), the standalone LSTM model recorded significant errors, with a peak error of 99.67 m3/s and an RMSE of 29.23 m3/s, indicating a clear tendency to underestimate peak values. In contrast, the hybrid LSTM + ARIMA model substantially reduced these values (RMSE = 17.11 m3/s, Peak Error = 53.66 m3/s), demonstrating a better ability to adapt to extreme conditions. In the low-flow range (≤10th percentile), both models tend to overestimate the actual values; however, the LSTM + ARIMA model again shows superior performance, with a lower RMSE (2.38 vs. 3.81 m3/s) and a slightly reduced peak error. These results suggest that integrating the ARIMA component into the LSTM structure significantly enhances prediction accuracy under extreme hydrological conditions.
4. Discussion
In the case of the multi-day prediction in advance, using a closed loop, the forecasted values tend to gradually move away from the actual ones, and the calculated RMSE values increase compared to the prediction on a single time step, an aspect observed in other works [31,32]. For example, in [5], the coefficient of determination R2 decreases from 0.83 in the case of the prediction one step forward (one hour) to values between 0.48 and 0.58 when the prediction horizon increases to 24 h.
For each randomly chosen 7-day forecast from each month, represented in Figure 8, the RMSE for both the LSTM model and the hybrid LSTM + ARIMA model was calculated and displayed, together with the standard deviation of the measured multiannual monthly inflows. The aim was to compare the RMSE value with half of the standard deviation, and the results indicate that in most cases the RMSE remains below this threshold, suggesting a satisfactory accuracy of the predictions. Only in two months of the analyzed period it was observed that both models exceeded this threshold, namely in February and in June 2021, an aspect that could be associated with sudden variations in the data. At the same time, Table 3 shows that the RMSE calculated on a series of 7 selected values from each month (for all 12 months) is less than half of the standard deviation of the entire data series in all five simulations performed except for simulation 5. The year 2020 selected as the validation year included the period in which the maximum flow of the entire analyzed series was recorded. This peak flow could not be accurately predicted by either the LSTM network or the LSTM + ARIMA hybrid model, both models underestimating the extreme value recorded which resulted in a higher calculated RMSE value.
In general, the RMSE values obtained with the hybrid model are lower than those resulting from the predictions made only with the LSTM network, confirming the benefits of the hybrid approach. In fact, [33] presents a model in which an artificial neural network is trained on the residuals generated by the ARIMA model, making one-step forward predictions for three time series with distinct characteristics, and the results demonstrated improvement in the calculated Mean Absolute Error values.
In paper [34], a comparison of the performance of different predictive models for real-time series is made, analyzing how errors evolve as the prediction horizon increases to 1, 2, …, 10 steps ahead. The authors found that, for the Sunspot series, the best performance in the 5-, 8- and 10-step forward prediction is achieved by the bidirectional LSTM model, but the standard LSTM model also achieves similar performance, outperforming other methods tested in the study.
In a recent paper [35], the authors investigated the performance of multi-step forecasting of tributary flows in reservoirs using an encoder–decoder time-variant approach, applied to 12 different case studies. The results indicate that while the accuracy of the short-term forecast (one day ahead) is high, with NSE performance indicator values in the range of 0.6–0.97, this performance decreases as the forecast horizon expands. Thus, for the 2-day forecast, a decrease in performance is observed, and for the 7-day forecast, even using the best tested method (time-variant encoder–decoder), the indicator values can drop to 0.75 in some cases, and in others even below 0.2. Only the NSE was calculated. In eight of the cases, from the graphs presented it can be seen that the importance of flows was dominant (percentage of influence 80%) and in four of the cases the precipitation was the dominant factor (40–70%).
The boxplot analysis confirms the overall robustness of the hybrid LSTM + ARIMA model, showing lower errors, fewer outliers, and a median closer to zero compared to the standalone LSTM. These results are consistent with the model’s design, which aims to correct residual patterns in LSTM predictions. However, when focusing on extreme inflow conditions, particularly relevant for dam safety and operational decisions, the tail-based error analysis reveals limitations. The hybrid model, while improved, still struggles to accurately capture rare high-flow events. This suggests that dedicated modeling strategies, such as those using quantile regression to separate and target extreme cases [36], may offer more reliable solutions in such scenarios.
To strengthen the evaluation of the proposed LSTM + ARIMA model, three additional forecasting methods—Random Forest (RF), Gradient Boosting (GB), and Multilayer Perceptron (MLP)—were implemented and tested under identical conditions. These models were selected for their methodological diversity, representing tree-based, ensemble, and neural network approaches, respectively. The optimal parameters for each model were determined through grid search on the validation set. Specifically, for RF, the best configuration included a minimum leaf size of 5 and 100 decision trees; for GB, 50 learning cycles and a learning rate of 0.10; and for MLP, 20 neurons in the hidden layer. The configurations were selected by minimizing the RMSE on the validation set.
All models were trained and evaluated using identical 7-day forecasting windows randomly selected from each month to ensure consistency and fairness. A summary of the performance indicators obtained is provided in Table 6. Since the ARIMA component was trained exclusively on the residuals derived from the training phase, the final hybrid model was not applied to the training set. Instead, its performance was assessed on the validation and test sets, where both components were combined to generate multi-step forecasts. Consequently, performance metrics were reported only for the validation and test sets, as the hybrid LSTM + ARIMA model was not applied to the training data.

Table 6.
Performance indicators for training, validation, and testing.
The results, summarized in Table 6, indicate that although all models performed well on the training and validation sets (with R2 values exceeding 0.93 in most cases), their performance on the test set was considerably lower. The reduced performance highlights the inherent challenge of achieving generalization in multi-step time series forecasting.
In contrast, the hybrid LSTM + ARIMA model yielded superior results on the test set, with an RMSE of 12.74 m3/s, R2 of 0.89, and NSE of 0.87—outperforming all other models. These outcomes further demonstrate the robustness and predictive superiority of the hybrid approach, particularly under conditions characterized by high temporal variability and nonlinear dependencies. Such performance highlights the advantage of integrating statistical and deep learning components for capturing complex hydrological dynamics.
5. Conclusions
In the case of multi-step prediction (for example, on 5 to 7 consecutive days), prediction errors can accumulate progressively at each time step. This compounding effect often leads to a significant degradation in the accuracy of the prediction in the medium term, even if the model performs well in the short term. In this context, it is essential that the short-term prediction is as accurate as possible, as it serves as the basis for all subsequent predictions. A high-quality prediction at the initial time step significantly reduces the uncertainty propagated in the next steps, thus increasing the chances that the model will maintain a realistic and stable trajectory of the prediction in the multi-step forecasting horizon.
While other AI-based models, such as feedforward neural networks or other similar architectures, may provide higher accuracy for day-ahead prediction compared to LSTM, they have limited generalizability for forecasts over a seven-day horizon. Consequently, for the short-term forecast (seven days in advance) the use of LSTM networks was chosen, which allows the learning of long-term dependencies from the time series. Moreover, it was observed that the integration of the ARIMA model for adjusting LSTM errors leads to a high-performance combination for the seven-day forward forecast, in a closed-loop mode, without daily updating of the real values of the time series during the prediction horizon.
This study introduces a novel hybrid modeling approach that combines LSTM and ARIMA techniques, applied to real-world hydrological inflow data. Unlike most existing studies that use ARIMA as the primary predictor and LSTM for residual correction, our method reverses this configuration: LSTM serves as the main forecasting engine, capturing nonlinear patterns and seasonality (via sine and cosine encoding), while ARIMA is employed to refine predictions by modeling residual errors. This structure enhances both stability and accuracy, particularly in short-term multi-step forecasts such as seven-day predictions. The results demonstrate that the hybrid model consistently outperforms standalone LSTM, offering a robust and reliable solution for inflow forecasting across multiple horizons.
These findings highlight the potential of integrating deep learning with statistical methods to improve predictive performance in hydrological applications. Future research may explore specialized models for extreme events or real-time updating strategies to further enhance operational reliability.
Author Contributions
Conceptualization, A.N., B.P.; Methodology, A.N., E.-I.T.; Writing—original draft, A.N., E.-I.T.; Resources, O.N., B.P.; Supervision, L.-I.V., G.-E.D.; Writing—review & editing, L.-I.V., O.N., and G.-E.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a grant from the National Program for Research of the National Association of Technical Universities—GNAC ARUT 2023 (Contract no. 169).
Data Availability Statement
The data used in this study were provided by Hidroelectrica SA for research purposes only and are not publicly available.
Acknowledgments
The authors thank HIDROELECTRICA, the owner of the data for the inflows for agreeing with the use of the data. The authors used ChatGPT (OpenAI, GPT-5, 2025 version) only for language refinement and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LSTM | Long Short-Term Memory |
| ARIMA | Autoregressive integrated moving average |
| ACF | Autocorrelation function |
| PACF | Partial autocorrelation function |
| RMSE | Root mean square error |
| R2 | Coefficient of determination |
| NSE | Nash–Sutcliffe efficiency |
| mean | Average |
| std | Standard deviation |
| p | autoregressive order |
| d | degree of differencing (number of differences required to make the series stationary) |
| q | moving average order |
References
- Kaur, J.; Parmar, K.S.; Singh, S. Autoregressive models in environmental forecasting time series: A theoretical and application review. Environ. Sci. Pollut. Res. 2023, 30, 19617–19641. [Google Scholar] [CrossRef]
- Khazaeiathar, M.; Hadizadeh, R.; Fathollahzadeh Attar, N.; Schmalz, B. Daily Streamflow Time Series Modeling by Using a Periodic Autoregressive Model (ARMA) Based on Fuzzy Clustering. Water 2022, 14, 3932. [Google Scholar] [CrossRef]
- Gupta, A.; Kumar, A. Two-step daily reservoir inflow prediction using ARIMA-machine learning and ensemble models. J. Hydro-Environ. Res. 2022, 45, 39–52. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y. Multi-step ahead wind speed prediction based on optimal feature extraction, long short-term memory neural network and error correction strategy. Appl. Energy 2018, 230, 429–443. [Google Scholar] [CrossRef]
- Galarza-Chavez, A.A.; Martinez-Rodriguez, J.L.; Domínguez-Cruz, R.F.; López-Garza, E.; Rios-Alvarado, A.B. Multi-step wind energy forecasting in the Mexican Isthmus using machine and deep learning. Energy Rep. 2025, 13, 1–15. [Google Scholar] [CrossRef]
- Joseph, L.P.; Deo, R.C.; Casillas-Pérez, D.; Prasad, R.; Raj, N.; Salcedo-Sanz, S. Short-term wind speed forecasting using an optimized three-phase convolutional neural network fused with bidirectional long short-term memory network model. Appl. Energy 2024, 359, 122624. [Google Scholar] [CrossRef]
- Peng, T.; Zhou, J.; Zhang, C.; Zheng, Y. Multi-step ahead wind speed forecasting using a hybrid model based on two-stage decomposition technique and AdaBoost-extreme learning machine. Energy Convers. Manag. 2017, 153, 589–602. [Google Scholar] [CrossRef]
- Bai, R.; Li, J.; Liu, J.; Shi, Y.; He, S.; Wei, W. Day-ahead photovoltaic power generation forecasting with the HWGC-WPD-LSTM hybrid model assisted by wavelet packet decomposition and improved similar day method. Eng. Sci. Technol. Int. J. 2025, 61, 101889. [Google Scholar] [CrossRef]
- Salman, D.; Direkoglu, C.; Kusaf, M. Hybrid deep learning models for time series forecasting of solar power. Neural Comput. Appl. 2024, 36, 9095–9112. [Google Scholar] [CrossRef]
- Waqas, M.; Wannasingha Humphries, U. A critical review of RNN and LSTM variants in hydrological time series predictions. Methods 2024, 13, 102946. [Google Scholar] [CrossRef]
- Zemzami, M.; Benaabidate, L. Improvement of artificial neural networks to predict daily streamflow in a semi-arid area. Hydrol. Sci. J. 2016, 61, 1801–1812. [Google Scholar] [CrossRef]
- Ghimire, S.; Yaseen, Z.M.; Farooque, A.A.; Deo, R.C.; Zhang, J.; Tao, X. Streamflow prediction using an integrated methodology based on convolutional neural network and long short-term memory networks. Sci. Rep. 2021, 11, 17497. [Google Scholar] [CrossRef]
- Ahmed, D.M.; Hassan, M.M.; Mstafa, R.J. A Review on Deep Sequential Models for Forecasting Time Series Data. Appl. Comput. Intell. Soft Comput. 2022, 2022, 6596397. [Google Scholar] [CrossRef]
- Niknam, A.R.R.; Sabaghzadeh, M.; Barzkar, A.; Shishebori, D. Comparing ARIMA and various deep learning models for long-term water quality index forecasting in Dez River, Iran. Environ. Sci. Pollut. Res. 2025, 32, 10206–10222. [Google Scholar] [CrossRef]
- Wang, W.; Ma, B.; Guo, X.; Chen, Y.; Xu, Y. A Hybrid ARIMA-LSTM Model for Short-Term Vehicle Speed Prediction. Energies 2024, 17, 3736. [Google Scholar] [CrossRef]
- Kashif, K.; Ślepaczuk, R. LSTM-ARIMA as a hybrid approach in algorithmic investment strategies. Knowl.-Based Syst. 2025, 320, 113563. [Google Scholar] [CrossRef]
- Kontopoulou, V.I.; Panagopoulos, A.D.; Kakkos, I.; Matsopoulos, G.K. A Review of ARIMA vs. Machine Learning Approaches for Time Series Forecasting in Data Driven Networks. Future Internet 2023, 15, 255. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, W.; Wu, X.; Chen, P.C.Y.; Liu, J. LSTM network: A deep learning approach for short-term traffic forecast. IET Intell. Transp. Syst. 2017, 11, 68–75. [Google Scholar] [CrossRef]
- Neagoe, A.; Tică, E.I.; Popa, B.; Vafeidis, G. Daily inflow forecasting in Asomata reservoir, on Aliakmon River, using Long Short-Term Memory network. E3S Web Conf. 2025, 638, 02006. [Google Scholar] [CrossRef]
- Chu, H.B.; Wu, J.; Wu, W.Y.; Wei, J.H. A dynamic classification-based long short-term memory network model for daily streamflow forecasting in different climate regions. Ecol. Indic. 2023, 148, 110092. [Google Scholar] [CrossRef]
- Chu, H.; Wang, Z.; Nie, C. Monthly Streamflow Prediction of the Source Region of the Yellow River Based on Long Short-Term Memory Considering Different Lagged Months. Water 2024, 16, 593. [Google Scholar] [CrossRef]
- Dong, Z.; Zhou, Y. A Novel Hybrid Model for Financial Forecasting Based on CEEMDAN-SE and ARIMA-CNN-LSTM. Mathematics 2024, 12, 2434. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, Q.; Ding, Y.; Zhang, D. Application of a hybrid ARIMA-LSTM model based on the SPEI for drought forecasting. Environ. Sci. Pollut. Res. 2022, 29, 4128–4144. [Google Scholar] [CrossRef]
- Landassuri-Moreno, V.M.; Bustillo-Hernández, C.L.; Carbajal-Hernández, J.J.; Fernández, L.P.S. Single-Step-Ahead and Multi-Step-Ahead Prediction with Evolutionary Artificial Neural Networks. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8258, pp. 65–72. [Google Scholar]
- Taylor, S.J.; Letham, B. Forecasting at scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Am. Soc. Agric. Biol. Eng. 2015, 58, 1763–1785. [Google Scholar]
- Singh, J.; Knapp, H.V.; Demissie, M. Hydrologic modeling of the Iroquois River watershed using HSPF and SWAT. J. Am. Water Resour. Assoc. 2007, 41, 343–360. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models: Part 1. A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Prater, R.; Hanne, T.; Dornberger, R. Generalized Performance of LSTM in Time-Series Forecasting. App. Artif. Intell. 2024, 38, 2377510. [Google Scholar] [CrossRef]
- Pranolo, A.; Setyaputri, F.U.; Paramarta, A.K.I.; Triono, A.P.P.; Fadhilla, A.F.; Akbari, A.K.G.; Utama, A.B.P.; Wibawa, A.P.; Uriu, W. Enhanced Multivariate Time Series Analysis Using LSTM: A Comparative Study of Min-Max and Z-Score Normalization Techniques. Ilk. J. Ilm. 2024, 16, 210–220. [Google Scholar] [CrossRef]
- Liao, S.; Liu, Z.; Liu, B.; Cheng, C.; Jin, X.; Zhao, Z. Multistep-ahead daily inflow forecasting using the ERA-Interim reanalysis data set based on gradient-boosting regression trees. Hydrol. Earth Syst. Sci. 2020, 24, 2343–2363. [Google Scholar] [CrossRef]
- Luo, X.; Liu, P.; Dong, Q.; Zhang, Y.; Xie, K. Dongyang Han, Exploring the role of the long short-term memory model in improving multi-step ahead reservoir inflow forecasting. J. Flood Risk Manag. 2023, 16, 12854. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Chandra, R.; Goyal, S.; Gupta, R. Evaluation of Deep Learning Models for Multi-Step Ahead Time Series Prediction. IEEE Access 2021, 9, 83105–83124. [Google Scholar] [CrossRef]
- Fan, M.; Lu, D.; Gangrade, S. Enhancing Multi-Step Reservoir Inflow Forecasting: A Time-Variant Encoder–Decoder Approach. Geosciences 2025, 15, 279. [Google Scholar] [CrossRef]
- Weekaew, J.; Ditthakit, P.; Kittiphattanabawon, N.; Pham, Q.B. Quartile Regression and Ensemble Models for Extreme Events of Multi-Time Step-Ahead Monthly Reservoir Inflow Forecasting. Water 2024, 16, 3388. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).