High-Resolution Water Quality Monitoring of Small Reservoirs Using UAV-Based Multispectral Imaging
Abstract
:1. Introduction
2. Study Area and Methodology
2.1. Study Area
2.2. Field Measurement Data of the Reservoir
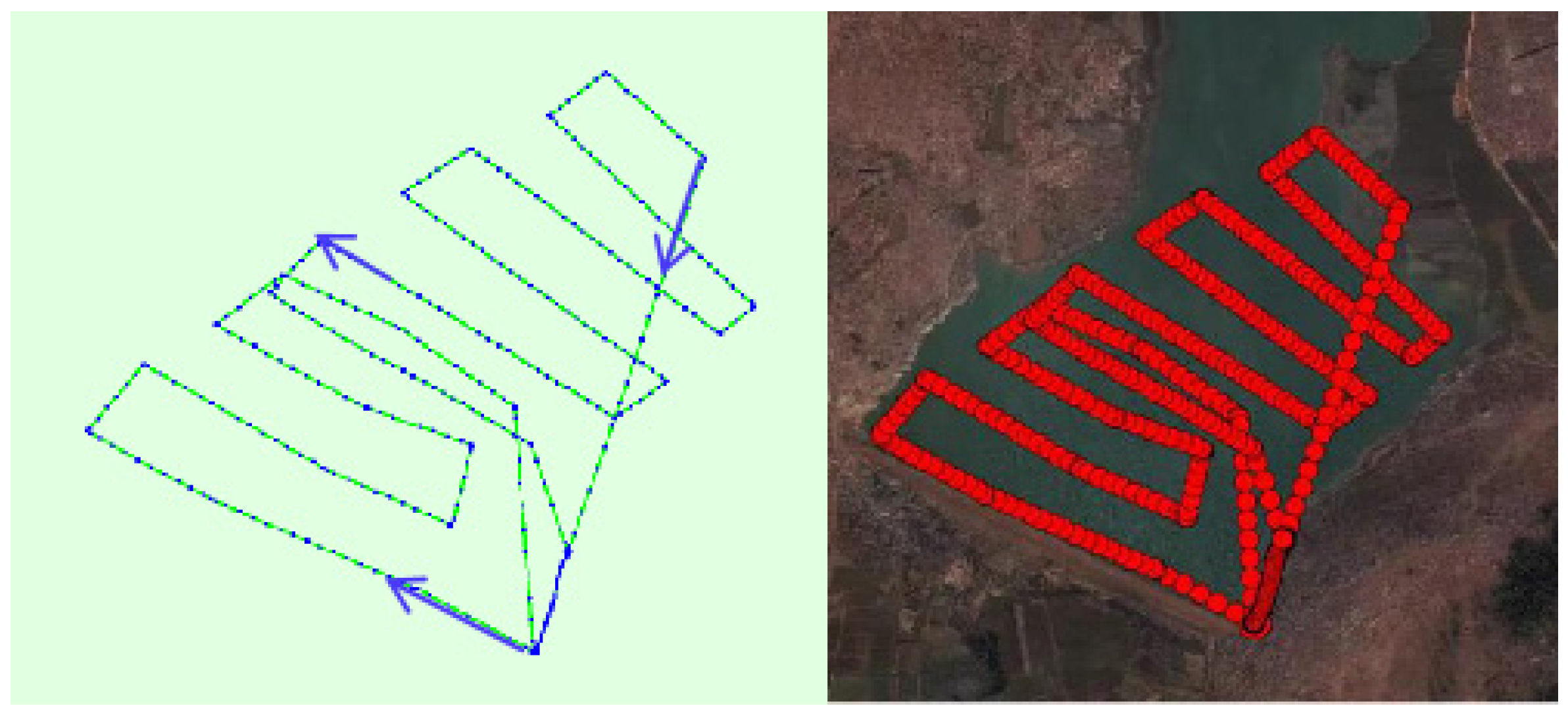
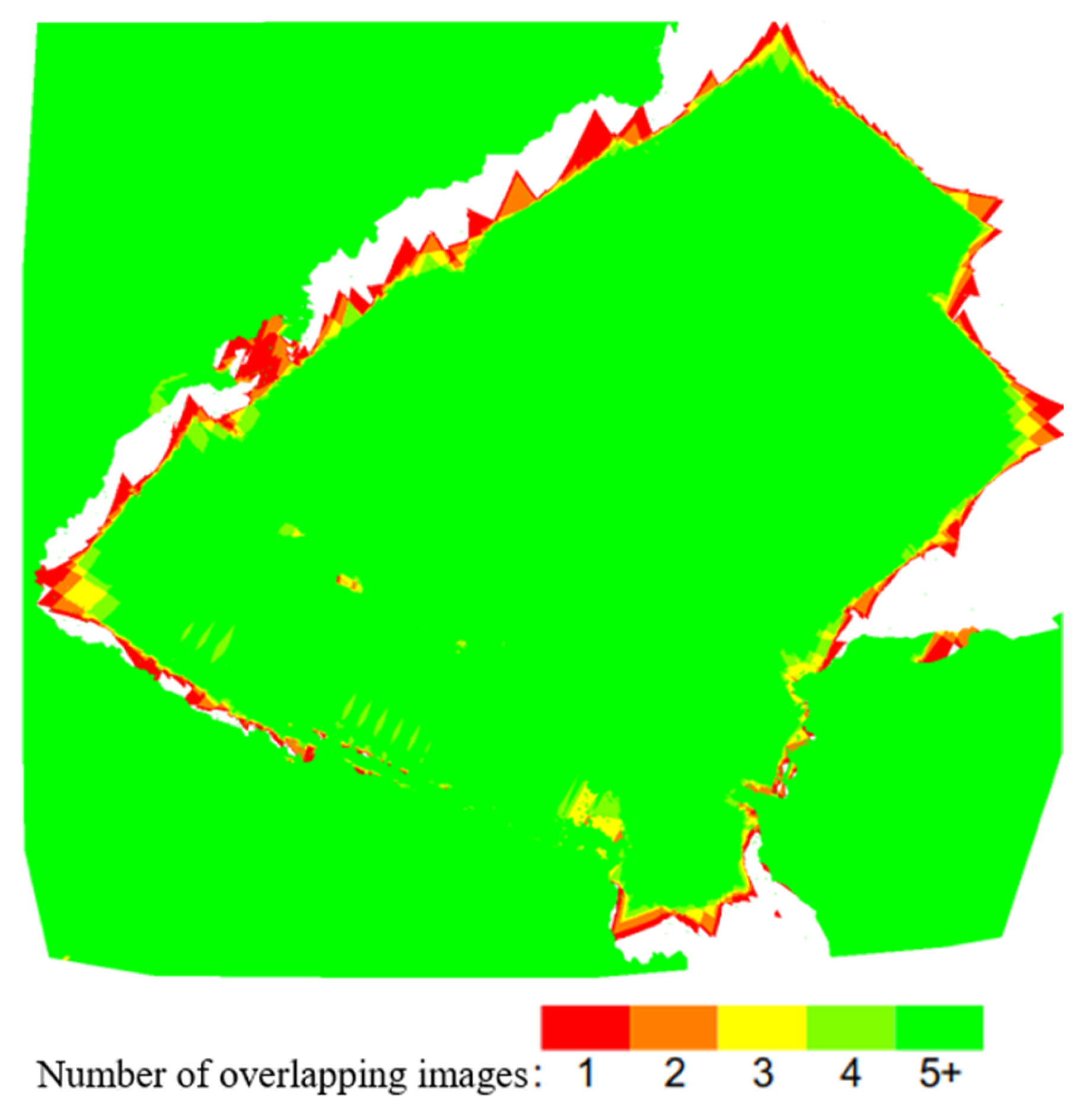
2.3. UAV System and Image Preprocessing
2.4. Image Preprocessing
- (1)
- Input camera calibration data and TIFF images of the study area, including images of the reference calibration target and the four spectral bands.
- (2)
- Use the SIFT algorithm to detect and match feature points.
- (3)
- Perform spatial block adjustment using the matched features and embedded GPS data to restore image orientation.
- (4)
- Apply aerial triangulation using the GCPs to generate a 3D point cloud.
- (5)
- Produce a digital surface model (DSM) and a digital orthophoto map (DOM) from the point cloud data.
2.5. Mapping Water Quality Parameters
- (1)
- MPP: directly links individual image pixels with field measurements.
- (2)
- Window Averaging Method (WAM): uses averaged values over a defined window to reduce noise and account for local variability.
2.5.1. MPP Algorithm—Fixed Window Size, Search for Matching Within the Window
2.5.2. WAM Algorithm—Changing Window Size to Search for the Best Match
2.5.3. Linear Regression Model
3. Results
3.1. Water Quality Parameters
3.2. WAM Algorithm Fitting Results
3.3. MPP Algorithm Fitting Results
3.4. Cross-Validation for the Estimation Performance of Regression Models
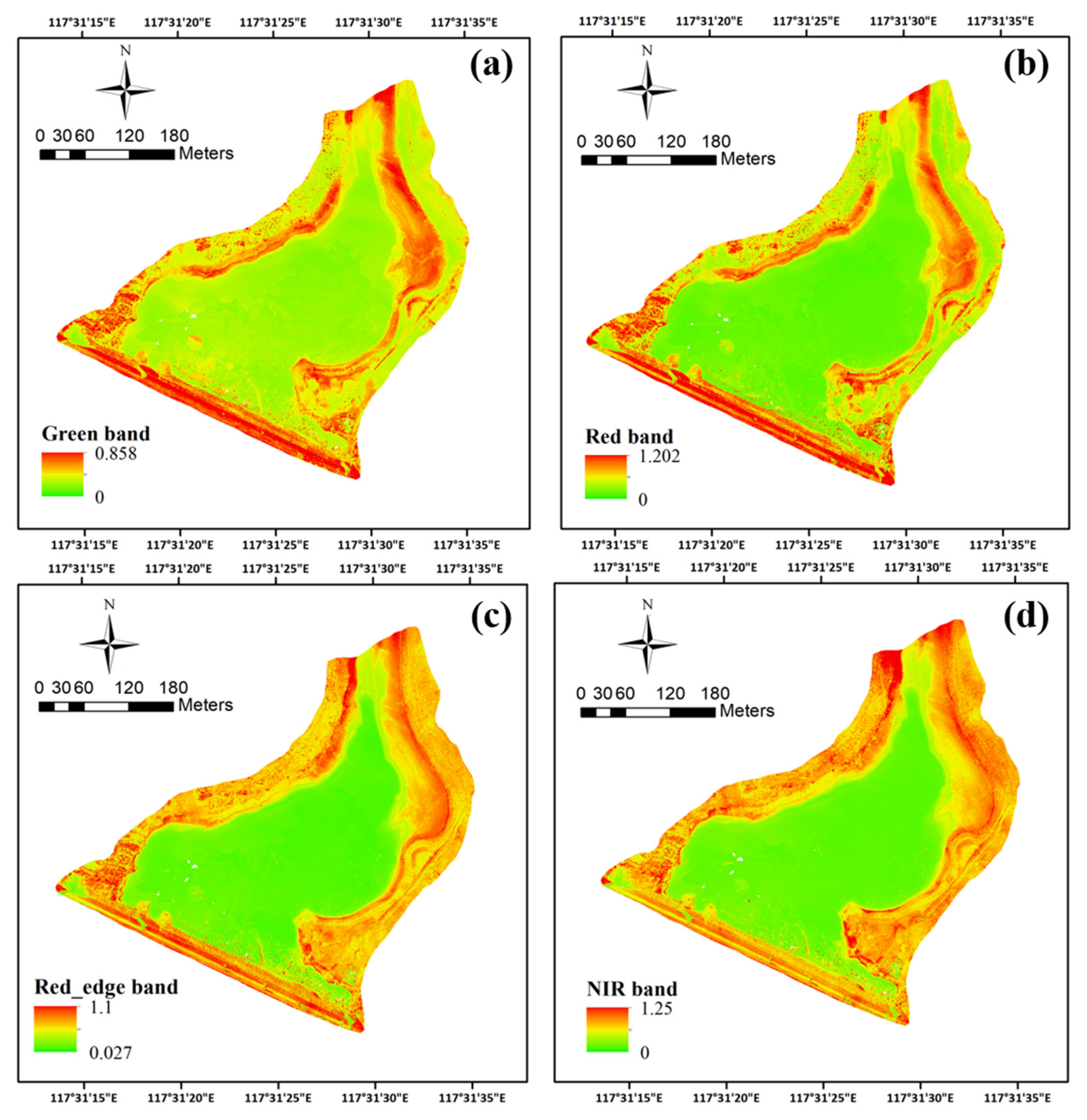
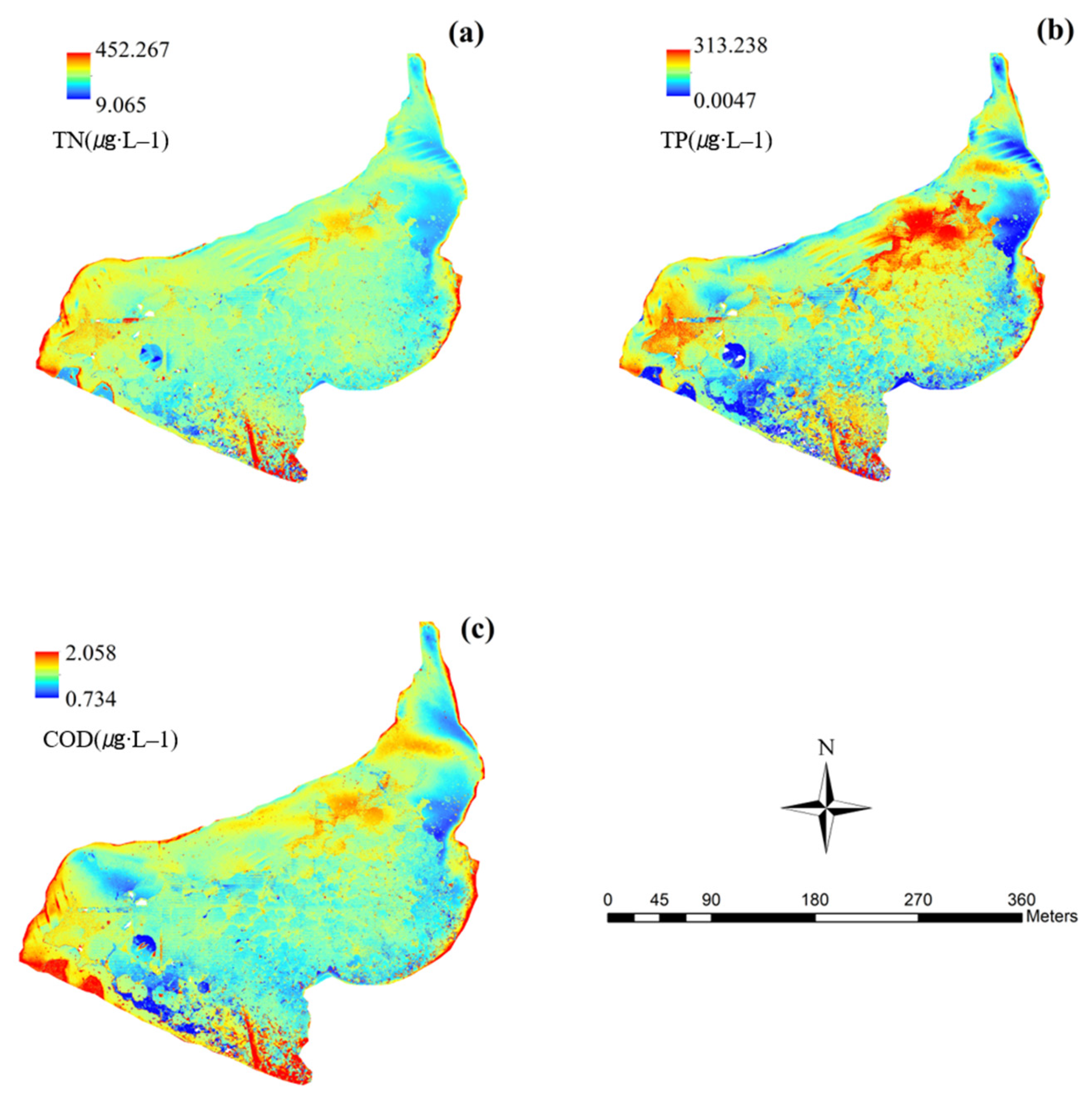
3.5. Water Quality Parameter Mapping
4. Discussion
4.1. Performance Comparison of WAM and MPP Algorithms
4.2. Sensitivity of Water Quality Parameters to Spectral Indices
4.3. Application Value and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, B.; Zhang, L.; Yang, L.; Zhang, F.; Norse, D.; Zhu, Z. Agricultural non-point source pollution in China: Causes and mitigation measures. Ambio 2012, 41, 370–379. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Wang, C.; Yang, R.; Sun, M.; Zhang, L.; Zhang, Y.; Li, X. Research on the progress of agricultural non-point source pollution management in China: A review. Sustainability 2023, 15, 13308. [Google Scholar] [CrossRef]
- Lo, Y.; Fu, L.; Lu, T.; Huang, H.; Kong, L.; Xu, Y.; Zhang, C. Medium-sized lake water quality parameters retrieval using multispectral uav image and machine learning algorithms: A case study of the yuandang lake, China. Drones 2023, 7, 244. [Google Scholar] [CrossRef]
- Kijowska-Strugala, M.; Wiejaczka, L.; Kozlowski, R. Influence of reservoirs on the concentration of nutrients in the water of mountain rivers. Ecol. Chem. Eng. 2016, 23, 413. [Google Scholar] [CrossRef]
- Yang, X.; Lu, X. Drastic change in China’s lakes and reservoirs over the past decades. Sci. Rep. 2014, 4, 6041. [Google Scholar] [CrossRef]
- Sani, S.A. Drawbacks of Traditional Environmental Monitoring Systems. TMP Univers. J. Res. Rev. Arch. 2023, 2, srep06041. [Google Scholar] [CrossRef]
- Bourouhou, I.; Salmoun, F. Sea water quality monitoring using remote sensing techniques: A case study in Tangier-Ksar Sghir coastline. Environ. Monit. Assess. 2021, 193, 557. [Google Scholar] [CrossRef]
- Tv, R. Remote sensing applications in water resources. J. Indian Inst. Sci. 2013, 93, 163–188. [Google Scholar]
- Wasehun, E.T.; Hashemi Beni, L.; Di Vittorio, C.A. UAV and satellite remote sensing for inland water quality assessments: A literature review. Environ. Monit. Assess. 2024, 196, 277. [Google Scholar] [CrossRef]
- Raghul, M.; Porchelvan, P. A Critical Review of Remote Sensing Methods for Inland Water Quality Monitoring: Progress, Limitations, and Future Perspectives. Water Air Soil Pollut. 2024, 235, 159. [Google Scholar] [CrossRef]
- Wong, M.S.; Zhu, X.; Abbas, S.; Kwok, C.Y.T.; Wang, M. Optical remote sensing. In Urban Informatics; Springer: Singapore, 2021; pp. 315–344. [Google Scholar]
- Dörnhöfer, K.; Oppelt, N. Remote sensing for lake research and monitoring–Recent advances. Ecol. Indic. 2016, 64, 105–122. [Google Scholar] [CrossRef]
- Lim, J.; Choi, M. Assessment of water quality based on Landsat 8 operational land imager associated with human activities in Korea. Environ. Monit. Assess. 2015, 187, 384. [Google Scholar] [CrossRef]
- Garg, V.; Aggarwal, S.P.; Chauhan, P. Changes in turbidity along Ganga River using Sentinel-2 satellite data during lockdown associated with COVID-19. Geomat. Nat. Hazards Risk 2020, 11, 1175–1195. [Google Scholar] [CrossRef]
- Baban, S.M.J. Detecting water quality parameters in the Norfolk Broads, UK, using Landsat imagery. Int. J. Remote Sens. 1993, 14, 1247–1267. [Google Scholar] [CrossRef]
- Kulkarni, A. Water quality retrieval from Landsat TM imagery. Procedia Comput. Sci. 2011, 6, 475–480. [Google Scholar] [CrossRef]
- Bonansea, M.; Ledesma, C.; Rodríguez, C.; Pinotti, L.; Antunes, M.H. Effects of atmospheric correction of Landsat imagery on lake water clarity assessment. Adv. Space Res. 2015, 56, 2345–2355. [Google Scholar] [CrossRef]
- Chen, L.; Tan, C.-H.; Kao, S.-J.; Wang, T.-S. Improvement of remote monitoring on water quality in a subtropical reservoir by incorporating grammatical evolution with parallel genetic algorithms into satellite imagery. Water Res. 2008, 42, 296–306. [Google Scholar] [CrossRef]
- Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A Comprehensive Review on Water Quality Parameters Estimation Using Remote Sensing Techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef]
- Song, K.; Li, L.; Li, S.; Tedesco, L.; Hall, B.; Li, L. Hyperspectral Remote Sensing of Total Phosphorus (TP) in Three Central Indiana Water Supply Reservoirs. Water Air Soil Pollut. 2012, 223, 1481–1502. [Google Scholar] [CrossRef]
- Singh, Y.; Walingo, T. Smart Water Quality Monitoring with IoT Wireless Sensor Networks. Sensors 2024, 24, 2871. [Google Scholar] [CrossRef]
- Reiners, P.; Sobrino, J.; Kuenzer, C. Satellite-Derived Land Surface Temperature Dynamics in the Context of Global Change—A Review. Remote Sens. 2023, 15, 1857. [Google Scholar] [CrossRef]
- Mansaray, A.S.; Dzialowski, A.R.; Martin, M.E.; Wagner, K.L.; Gholizadeh, H.; Stoodley, S.H. Comparing PlanetScope to Landsat-8 and Sentinel-2 for Sensing Water Quality in Reservoirs in Agricultural Watersheds. Remote Sens. 2021, 13, 1847. [Google Scholar] [CrossRef]
- Cheng, C.; Zhang, F.; Shi, J.; Kung, H.T. What is the relationship between land use and surface water quality? A review and prospects from remote sensing perspective. Environ. Sci. Pollut. Res. Int. 2022, 29, 56887–56907. [Google Scholar] [CrossRef]
- Yang, H.; Kong, J.; Hu, H.; Du, Y.; Gao, M.; Chen, F. A Review of Remote Sensing for Water Quality Retrieval: Progress and Challenges. Remote Sens. 2022, 14, 1770. [Google Scholar] [CrossRef]
- Mishra, V.; Avtar, R.; Prathiba, A.P.; Mishra, P.K.; Tiwari, A.; Sharma, S.K.; Singh, C.H.; Chandra Yadav, B.; Jain, K. Uncrewed aerial systems in water resource management and monitoring: A review of sensors, applications, software, and issues. Adv. Civ. Eng. 2023, 2023, 3544724. [Google Scholar] [CrossRef]
- Cillero Castro, C.; Domínguez Gómez, J.A.; Delgado Martín, J.; Hinojo Sánchez, B.A.; Cereijo Arango, J.L.; Cheda Tuya, F.A.; Díaz-Varela, R. An UAV and Satellite Multispectral Data Approach to Monitor Water Quality in Small Reservoirs. Remote Sens. 2020, 12, 1514. [Google Scholar] [CrossRef]
- Román, A.; Tovar-Sánchez, A.; Gauci, A.; Deidun, A.; Caballero, I.; Colica, E.; D’Amico, S.; Navarro, G. Water-Quality Monitoring with a UAV-Mounted Multispectral Camera in Coastal Waters. Remote Sens. 2023, 15, 237. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Chen, T.; Gu, X.; Zhang, L.; Li, X.; Tang, R.; He, Y.; Chen, G.; Zhang, B. Monitoring water quality parameters of freshwater aquaculture ponds using UAV-based multispectral images. Ecol. Indic. 2024, 167, 112644. [Google Scholar] [CrossRef]
- TungChing, S. A study of a matching pixel by pixel (MPP) algorithm to establish an empirical model of water quality mapping, as based on unmanned aerial vehicle (UAV) images. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 213–224. [Google Scholar] [CrossRef]
- Ying, H.; Xia, K.; Huang, X.; Feng, H.; Yang, Y.; Du, X.; Huang, L. Evaluation of water quality based on UAV images and the IMP-MPP algorithm. Ecol. Inform. 2021, 61, 101239. [Google Scholar] [CrossRef]
- Zhang, Y.; Jing, W.; Deng, Y.; Zhou, W.; Yang, J.; Li, Y.; Cai, Y.; Hu, Y.; Peng, X.; Lan, W. Water quality parameters retrieval of coastal mariculture ponds based on UAV multispectral remote sensing. Front. Environ. Sci. 2023, 11, 1079397. [Google Scholar] [CrossRef]
- Xiao, Y.; Guo, Y.; Yin, G.; Zhang, X.; Shi, Y.; Hao, F.; Fu, Y. UAV Multispectral Image-Based Urban River Water Quality Monitoring Using Stacked Ensemble Machine Learning Algorithms—A Case Study of the Zhanghe River, China. Remote Sens. 2022, 14, 3272. [Google Scholar] [CrossRef]
- Chen, B.; Mu, X.; Chen, P.; Wang, B.; Choi, J.; Park, H.; Xu, S.; Wu, Y.; Yang, H. Machine learning-based inversion of water quality parameters in typical reach of the urban river by UAV multispectral data. Ecol. Indic. 2021, 133, 108434. [Google Scholar] [CrossRef]
- Bureau, A.P.H. Real-Time Water Information of Zhangshan Reservoir. Available online: http://yc.wswj.net/ahsxx/LOL/?refer=upl&to=public_public (accessed on 23 October 2019).
- Wang, Z.; Hong, J.; Du, G. Use of satellite imagery to assess the trophic state of Miyun Reservoir, Beijing, China. Environ. Pollut. 2008, 155, 13–19. [Google Scholar]
- Michaelsen, E.; Meidow, J. Stochastic reasoning for structural pattern recognition: An example from image-based UAV navigation. Pattern Recognit. 2014, 47, 2732–2744. [Google Scholar] [CrossRef]
- Zaman, B.; Jensen, A.; Clemens, S.R.; McKee, M. Retrieval of spectral reflectance of high resolution multispectral imagery acquired with an autonomous unmanned aerial vehicle. Photogramm. Eng. Remote Sens. 2014, 80, 1139–1150. [Google Scholar]
- Sriwongsitanon, N.; Surakit, K.; Thianpopirug, S. Influence of atmospheric correction and number of sampling points on the accuracy of water clarity assessment using remote sensing application. J. Hydrol. 2011, 401, 203–220. [Google Scholar] [CrossRef]
- Su, T.-C.; Chou, H.-T. Application of multispectral sensors carried on unmanned aerial vehicle (UAV) to trophic state mapping of small reservoirs: A case study of Tain-Pu reservoir in Kinmen, Taiwan. Remote Sens. 2015, 7, 10078–10097. [Google Scholar] [CrossRef]
- Huang, X.-X.; Ying, H.-T.; Xia, K.; Feng, H.-L.; Yang, Y.-H.; Du, X.-C. Inversion of water quality parameters based on UAV multispectral images and the OPT-MPP algorithm. Huan Jing Ke Xue=Huanjing Kexue 2020, 41, 3591–3600. [Google Scholar]
- Saavedra-Ruiz, A.; Resto-Irizarry, P.J. A Portable UV-LED/RGB Sensor for Real-Time Bacteriological Water Quality Monitoring Using ML-Based MPN Estimation. Biosensors 2025, 15, 284. [Google Scholar] [CrossRef]
- Parra, L.; Ahmad, A.; Sendra, S.; Lloret, J.; Lorenz, P. Combination of Machine Learning and RGB Sensors to Quantify and Classify Water Turbidity. Chemosensors 2024, 12, 34. [Google Scholar] [CrossRef]
- Paepae, T.; Bokoro, P.N.; Kyamakya, K. From Fully Physical to Virtual Sensing for Water Quality Assessment: A Comprehensive Review of the Relevant State-of-the-Art. Sensors 2021, 21, 6971. [Google Scholar] [CrossRef]
- Guo, Y.; Deng, R.; Li, J.; Hua, Z.; Wang, J.; Zhang, R.; Liang, Y.; Tang, Y. Remote Sensing Retrieval of Total Nitrogen in the Pearl River Delta Based on Landsat8. Remote Sens. 2022, 14, 3710. [Google Scholar] [CrossRef]
- Zhang, D.; Zeng, S.; He, W. Selection and Quantification of Best Water Quality Indicators Using UAV-Mounted Hyperspectral Data: A Case Focusing on a Local River Network in Suzhou City, China. Sustainability 2022, 14, 16226. [Google Scholar] [CrossRef]
- Muhoyi, H.; Gumindoga, W.; Mhizha, A.; Misi, S.N.; Nondo, N. Water quality monitoring using remote sensing, Lower Manyame Sub-catchment, Zimbabwe. Water Pract. Technol. 2022, 17, 1347–1357. [Google Scholar] [CrossRef]
- Gao, Y.; Gao, J.; Yin, H.; Liu, C.; Xia, T.; Wang, J.; Huang, Q. Remote sensing estimation of the total phosphorus concentration in a large lake using band combinations and regional multivariate statistical modeling techniques. J. Environ. Manag. 2015, 151, 33–43. [Google Scholar] [CrossRef]
- Komas, J.M. Measuring Optical Water Quality Parameters Using an Unmanned Aerial Vehicle (UAV)-Based Multispectral Sensor, Lake Bloomington and Evergreen Lake; Illinois State University: Normal, IL, USA, 2022. [Google Scholar]
- Yang, Y.; Zhang, D.; Li, X.; Wang, D.; Yang, C.; Wang, J. Winter Water Quality Modeling in Xiong’an New Area Supported by Hyperspectral Observation. Sensors 2023, 23, 4089. [Google Scholar] [CrossRef]
- Carlson, R.E. A trophic state index for lakes 1. Limnol. Oceanogr. 1977, 22, 361–369. [Google Scholar] [CrossRef]
- Wang, S.; Li, J.; Zhang, B.; Lee, Z.; Spyrakos, E.; Feng, L.; Liu, C.; Zhao, H.; Wu, Y.; Zhu, L. Changes of water clarity in large lakes and reservoirs across China observed from long-term MODIS. Remote Sens. Environ. 2020, 247, 111949. [Google Scholar] [CrossRef]
- Prior, E.M.; O’Donnell, F.C.; Brodbeck, C.; Runion, G.B.; Shepherd, S.L. Investigating small unoccupied aerial systems (sUAS) multispectral imagery for total suspended solids and turbidity monitoring in small streams. Int. J. Remote Sens. 2021, 42, 39–64. [Google Scholar] [CrossRef]
- Feng, L.; Hu, C.; Han, X.; Chen, X.; Qi, L. Long-Term Distribution Patterns of Chlorophyll-a Concentration in China’s Largest Freshwater Lake: MERIS Full-Resolution Observations with a Practical Approach. Remote Sens. 2015, 7, 275–299. [Google Scholar] [CrossRef]
- Gai, Y.; Yu, D.; Zhou, Y.; Yang, L.; Chen, C.; Chen, J. An improved model for chlorophyll-a concentration retrieval in coastal waters based on UAV-Borne hyperspectral imagery: A case study in Qingdao, China. Water 2020, 12, 2769. [Google Scholar] [CrossRef]




| Sampling Point | Water Quality Parameters | Location Information | Sampling Time | |||||
|---|---|---|---|---|---|---|---|---|
| TN (mg·L−1) | srp (mg·L−1) | TP (mg·L−1) | COD | Longitude | Latitude | |||
| A | Range | 3.058–3.8 | 0.076–0.101 | 0.182–0.57 | 6.99–7.61 | 117°31′27″ | 32°37′2″ | 10:13 |
| Mean | 3.5453 | 0.09 | 0.2806 | 7.13 | ||||
| Standard Deviation | 0.2668 | 0.01 | 0.109 | 0.255 | ||||
| B | Range | 4.749–6.361 | 0.098–0.188 | 0.176–0.608 | 7.53–7.84 | 117°31′25″ | 32°37′4″ | 10:20 |
| Mean | 5.5081 | 0.116 | 0.3308 | 7.702 | ||||
| Standard Deviation | 0.5591 | 0.026 | 0.115 | 0.13 | ||||
| C | Range | 4.116–5.68 | 0.086–0.145 | 0.224–0.468 | 7.38–7.84 | 117°31′23″ | 32°37′7″ | 10:25 |
| Mean | 4.7828 | 0.104 | 0.3156 | 7.642 | ||||
| Standard Deviation | 0.6203 | 0.017 | 0.08 | 0.158 | ||||
| D | Range | 4.384–5.835 | 0.079–0.11 | 0.228–0.358 | 7.61–7.92 | 117°31′25″ | 32°37′9″ | 10:28 |
| Mean | 4.9991 | 0.088 | 0.2884 | 7.75 | ||||
| Standard Deviation | 0.5355 | 0.009 | 0.044 | 0.119 | ||||
| E | Range | 4.244–5.683 | 0.076–0.83 | 0.178–0.3 | 6.83–7.46 | 117°31′28″ | 32°37′11″ | 10:32 |
| Mean | 4.7256 | 0.159 | 0.2484 | 7.082 | ||||
| Standard Deviation | 0.5258 | 0.235 | 0.037 | 0.269 | ||||
| F | Range | 3.928–4.578 | 0.069–0.107 | 0.17–0.292 | 6.6–7.53 | 117°31′28″ | 32°37′7″ | 10:36 |
| Mean | 4.3619 | 0.084 | 0.219 | 7.238 | ||||
| Standard Deviation | 0.1997 | 0.01 | 0.038 | 0.349 | ||||
| Unit: mg·L−1 | TN | srp | TP | COD |
|---|---|---|---|---|
| TN | 1 | 0.342 | 0.392 | 0.586 ×× |
| srp | 1 | 0.228 | 0.33 | |
| TP | 1 | 0.484 | ||
| COD | 1 |
| n | Y = TN, X = NIR/R | ||
|---|---|---|---|
| r | r2 | p-Value | |
| 5 | 0.9678 | 0.9367 | 0.0068 |
| 9 | 0.9727 | 0.9463 | 0.0053 |
| 19 | 0.9974 | 0.995 | 0.0001 |
| 49 | 0.9467 | 0.8964 | 0.0146 |
| 99 | 0.9526 | 0.9076 | 0.0123 |
| n | Y = TP, X = NIR/R | Y = TP, X = Red_edge/G | Y = COD, X = NIR/R | ||||||
|---|---|---|---|---|---|---|---|---|---|
| r | r2 | p-Value | r | r2 | p-Value | r | r2 | p-Value | |
| 5 | 0.06 | 0.0036 | 0.9228 | 0.3 | 0.09 | 0.6229 | −0.561 | 0.3146 | 0.3253 |
| 9 | 0.2696 | 0.0727 | 0.6608 | 0.2603 | 0.0678 | 0.6722 | −0.702 | 0.4935 | 0.1859 |
| 19 | 0.0624 | 0.0039 | 0.92 | 0.3228 | 0.1042 | 0.5962 | −0.575 | 0.3306 | 0.3105 |
| 49 | 0.1403 | 0.0197 | 0.8219 | 0.2727 | 0.0744 | 0.657 | −0.46 | 0.2122 | 0.435 |
| 99 | 0.1224 | 0.015 | 0.844 | 0.2698 | 0.0728 | 0.6606 | −0.476 | 0.2263 | 0.418 |
| X | Y | Correlation Coefficient | Regression Coefficient | |||
|---|---|---|---|---|---|---|
| r | r2 | p-Value | a | b | ||
| NIR/R | TN | 1.000 ×× | 1.000 | 0.000 | 1.0726 | 5.0089 |
| NIR/G | TP | 0.978 ×× | 0.956 | 0.005 | 0.7235 | 3.5681 |
| Red_edge/G | COD | 0.803 ×× | 0.644 | 0.096 | 0.2005 | 0.1756 |
| Regression Model | Xij(l) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| l = 1 | l = 2 | l = 3 | l = 4 | l = 5 | ||||||
| i | j | i | j | i | j | i | j | i | j | |
| ln(TN) = 1.0726 ln(NIR/R) + 5.0089 | 1 | 3 | 1 | 4 | 2 | 2 | 3 5 | 1 2 | 1 4 | 4 3 |
| 2 | 3 | |||||||||
| 2 | 4 | |||||||||
| ln(TP) = 0.7235 ln(NIR/G) + 3.5681 | 3 | 3 | 1 | 1 | 4 5 | 2 3 | 3 4 | 1 1 | 2 4 | 2 2 |
| 3 | 1 | |||||||||
| 3 | 4 | |||||||||
| 5 | 1 | |||||||||
| 5 | 4 | |||||||||
| ln(COD) = 0.2005 ln(Red_edge/G) + 0.1756 | 4 | 1 | 5 | 5 | 3 | 2 | 1 | 4 | 2 3 4 | 2 1 5 |
| 2 | 5 | |||||||||
| 3 | 1 | |||||||||
| 4 | 4 | |||||||||
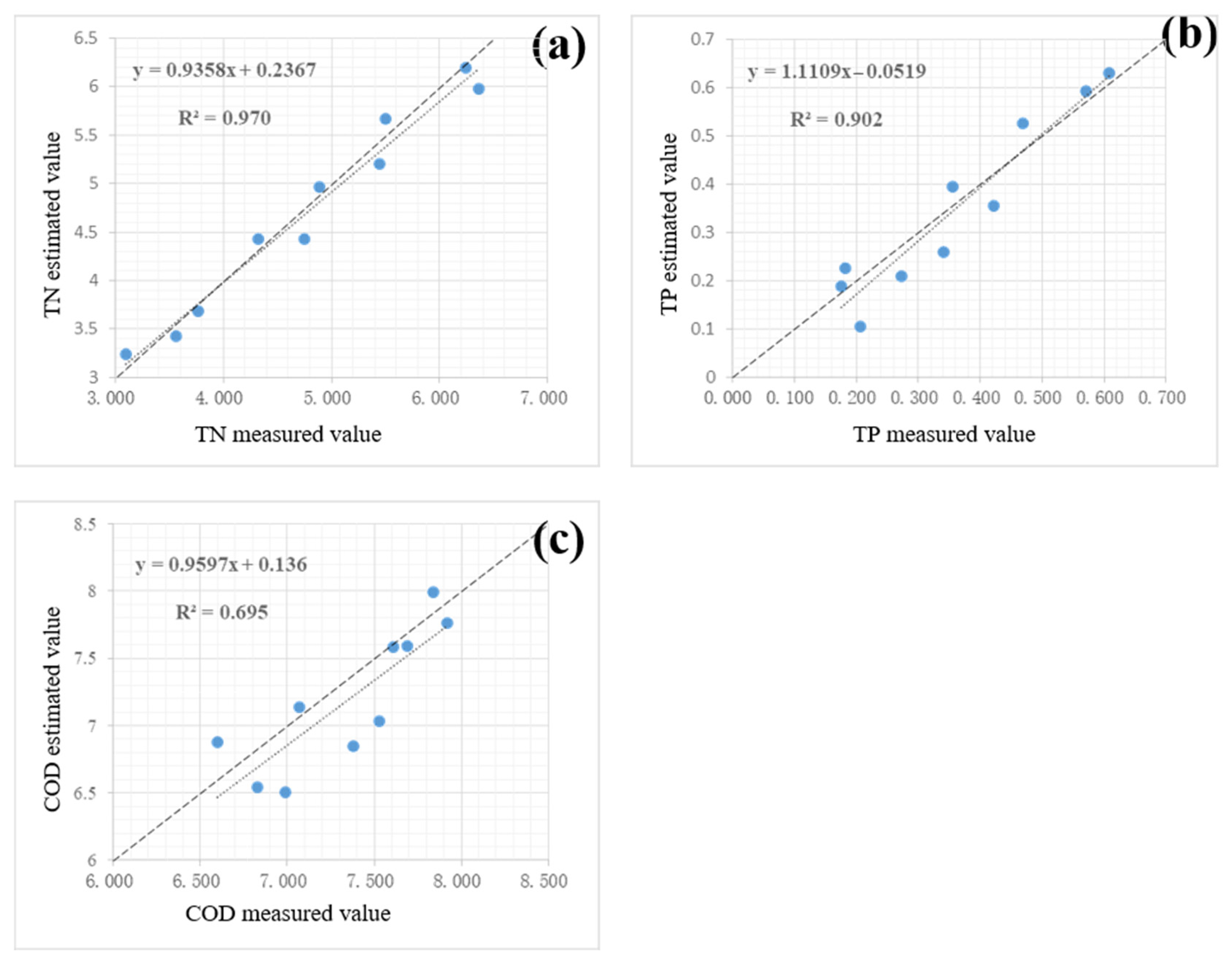
| Parameter | Estimation Model | R2 | RMSE | Regression Slope |
|---|---|---|---|---|
| TN | ln(TN) = 1.0726 ln(NIR/R) + 5.0089 | 0.970 | 0.198 | 0.9358 |
| TP | ln(TP) = 0.7235 ln(NIR/G) + 3.5681 | 0.902 | 0.057 | 1.1109 |
| COD | ln(COD) = 0.2005 ln(Red_edge/G) + 0.1756 | 0.695 | 0.315 | 0.9597 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, C.; Zhang, J.; Xia, X.; Liu, D.; Chen, L.; Yan, X. High-Resolution Water Quality Monitoring of Small Reservoirs Using UAV-Based Multispectral Imaging. Water 2025, 17, 1566. https://doi.org/10.3390/w17111566
Long C, Zhang J, Xia X, Liu D, Chen L, Yan X. High-Resolution Water Quality Monitoring of Small Reservoirs Using UAV-Based Multispectral Imaging. Water. 2025; 17(11):1566. https://doi.org/10.3390/w17111566
Chicago/Turabian StyleLong, Changyu, Jingyu Zhang, Xiaolin Xia, Dandan Liu, Lei Chen, and Xiqin Yan. 2025. "High-Resolution Water Quality Monitoring of Small Reservoirs Using UAV-Based Multispectral Imaging" Water 17, no. 11: 1566. https://doi.org/10.3390/w17111566
APA StyleLong, C., Zhang, J., Xia, X., Liu, D., Chen, L., & Yan, X. (2025). High-Resolution Water Quality Monitoring of Small Reservoirs Using UAV-Based Multispectral Imaging. Water, 17(11), 1566. https://doi.org/10.3390/w17111566






