A Numerical Study on the Pullback Process of a Submarine Cable Based on Trenchless Directional Drilling Technology
Abstract
1. Introduction
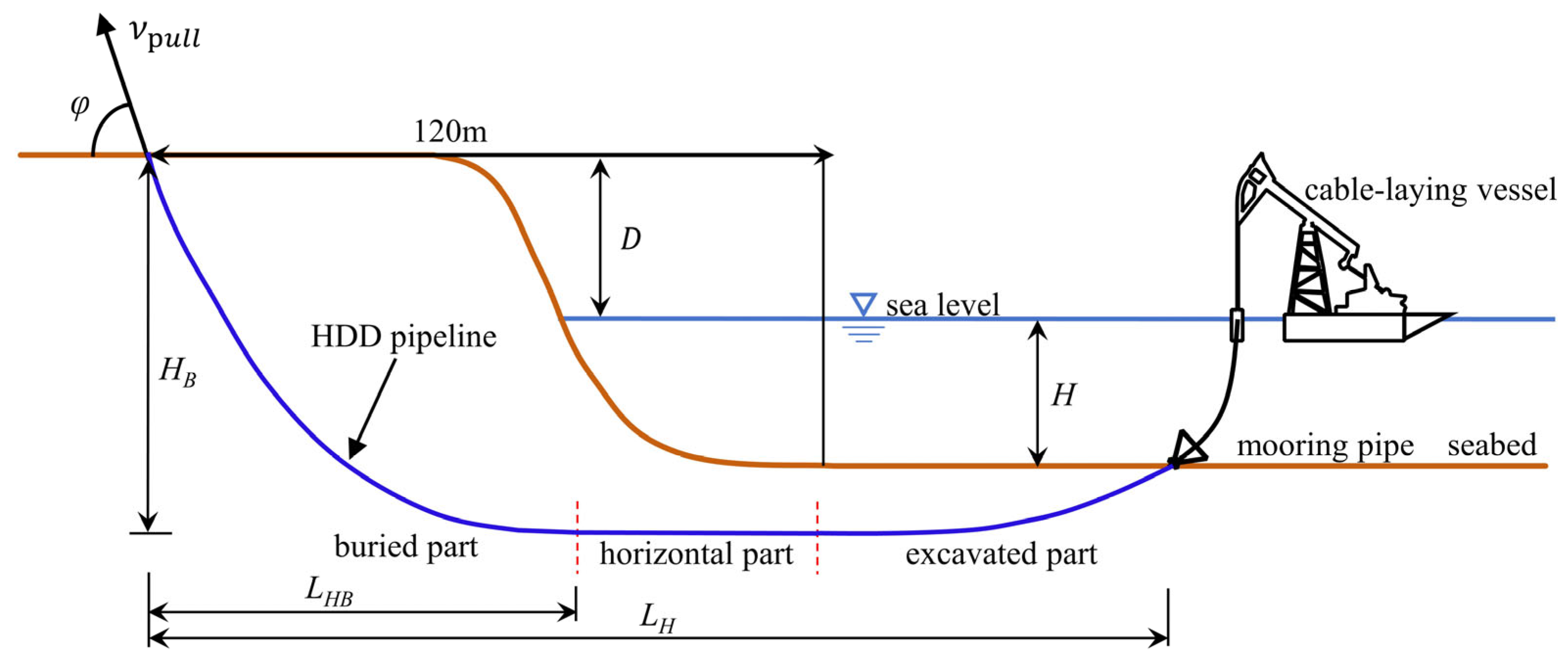
2. Problem Description
3. Numerical Model
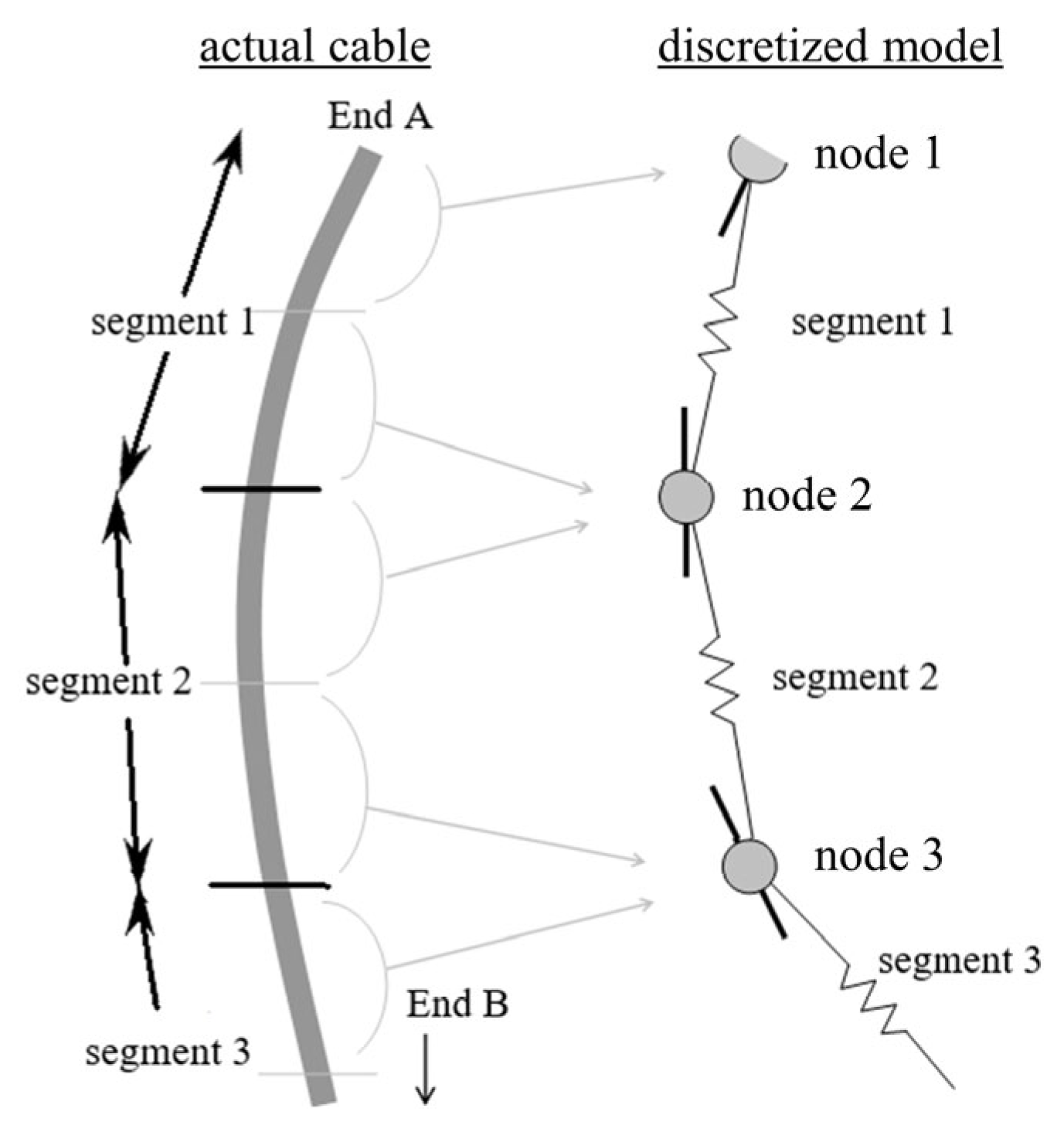
3.1. Fundamental Theory of FEM Cable Modeling
3.2. Numerical Model Setup
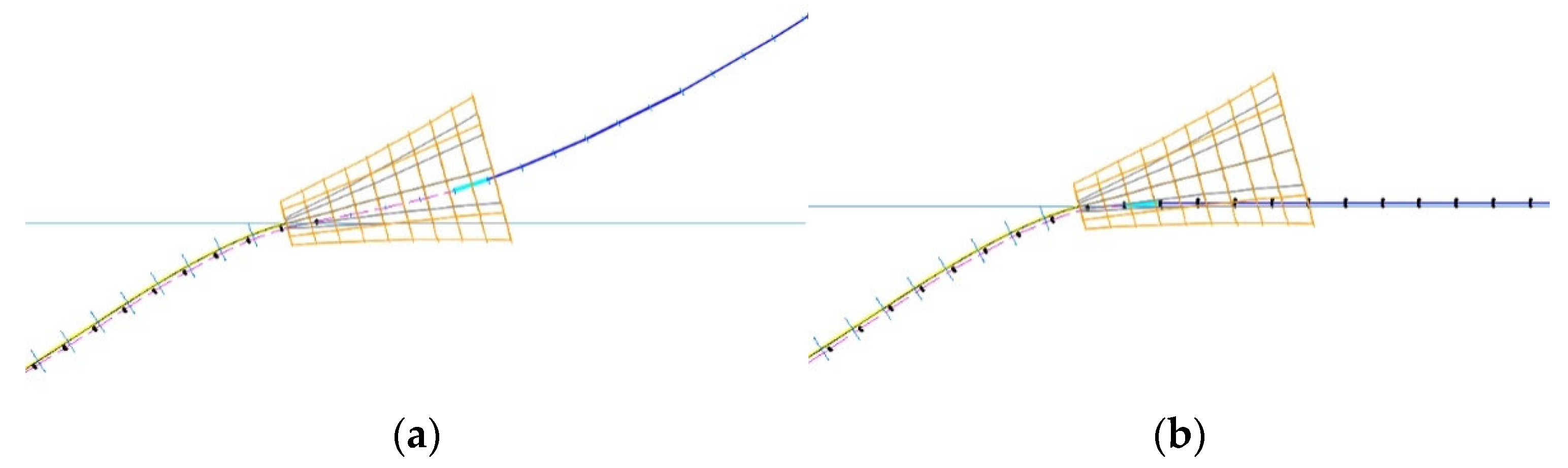
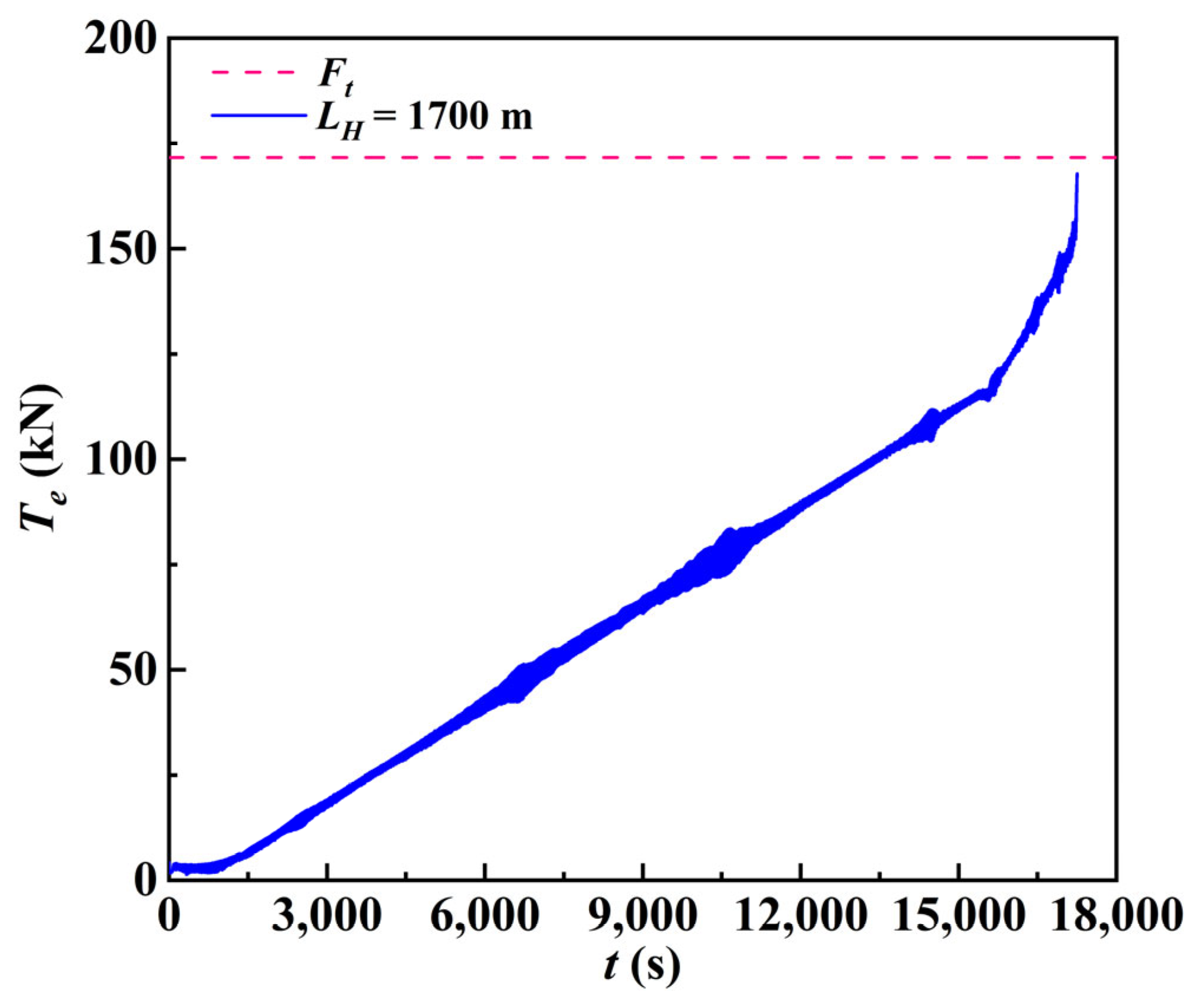
3.3. Numerical Model Validation
4. Results and Discussion
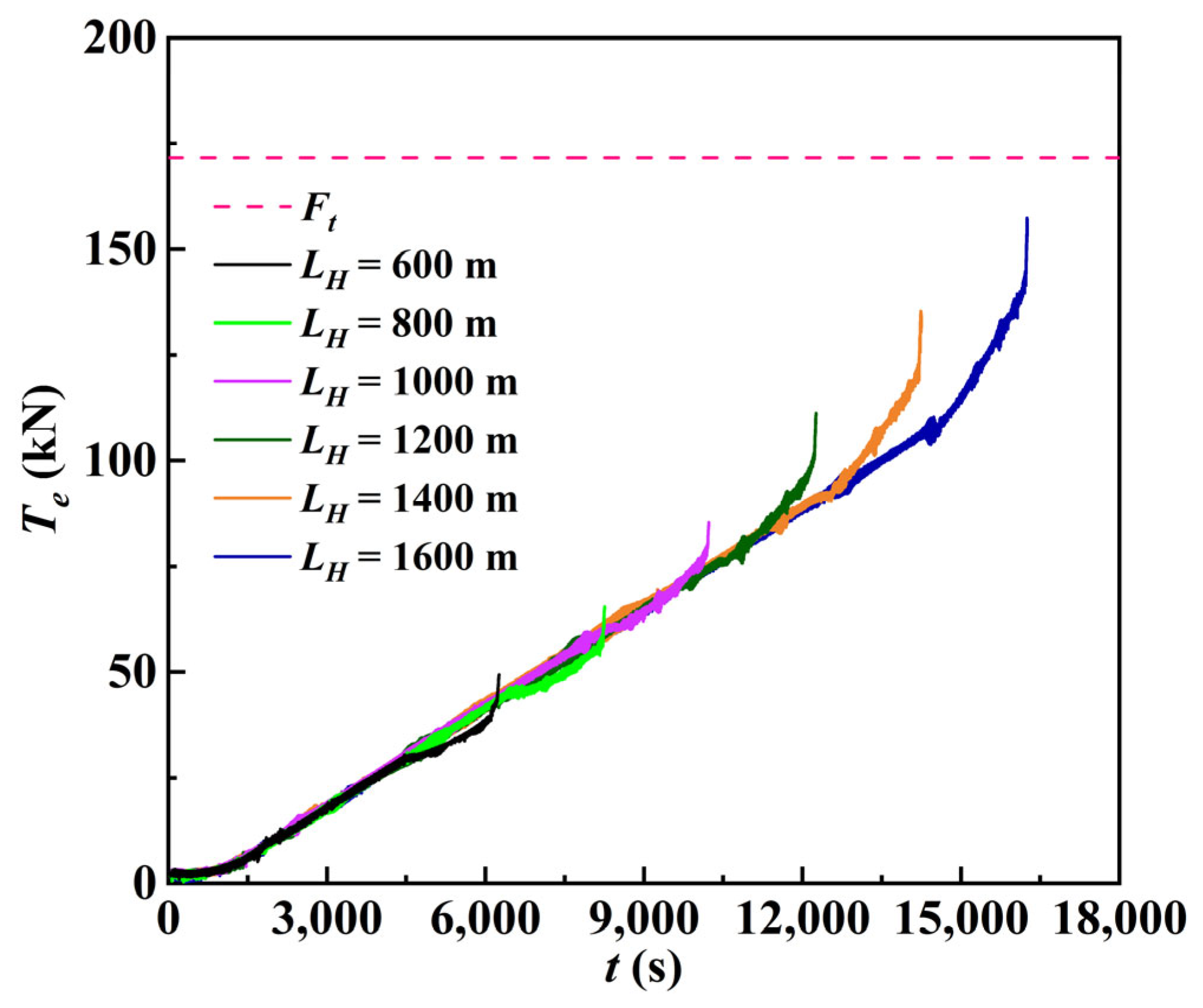
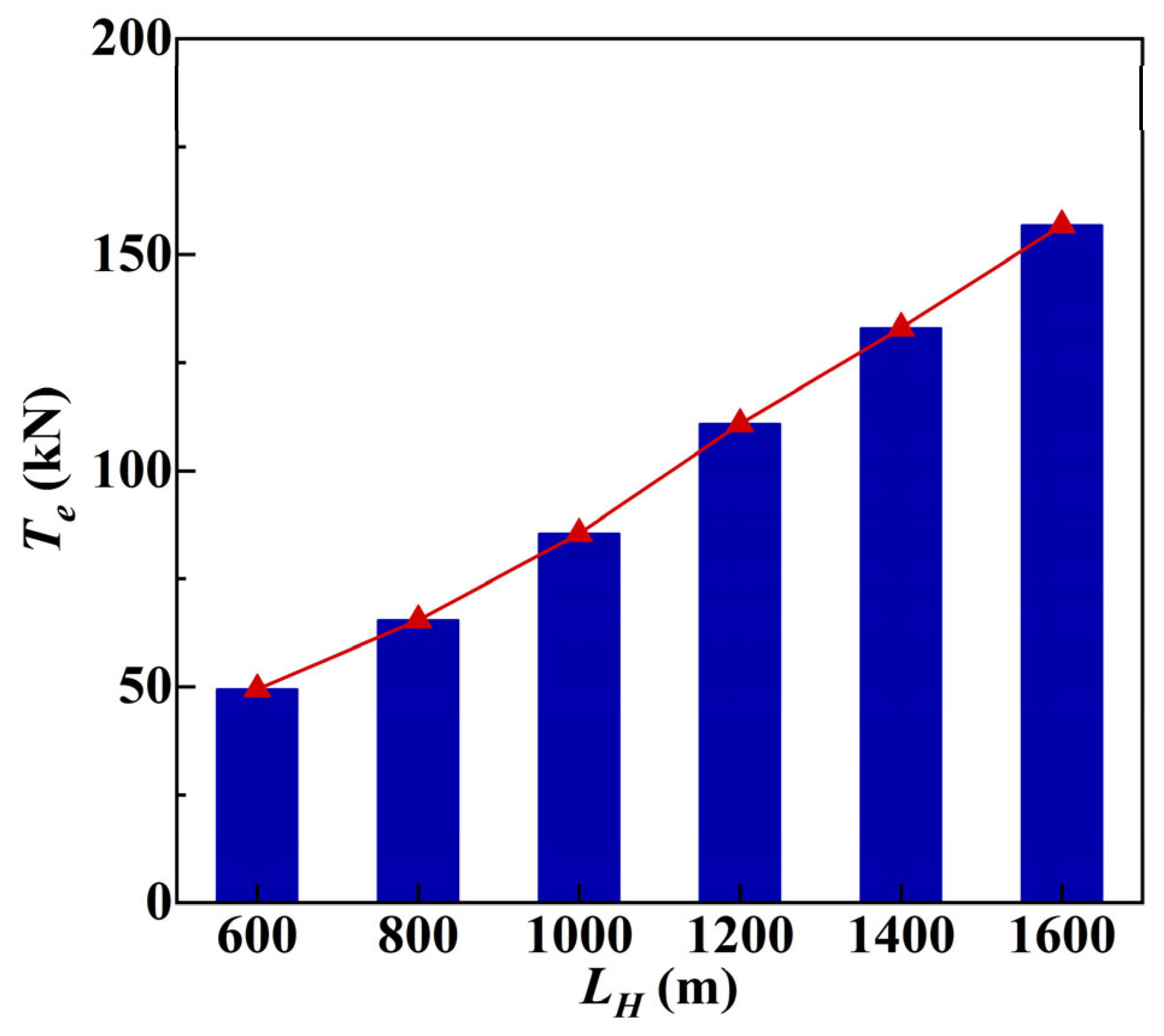
4.1. Effects of the Crossing Length on the Tension in the Cable
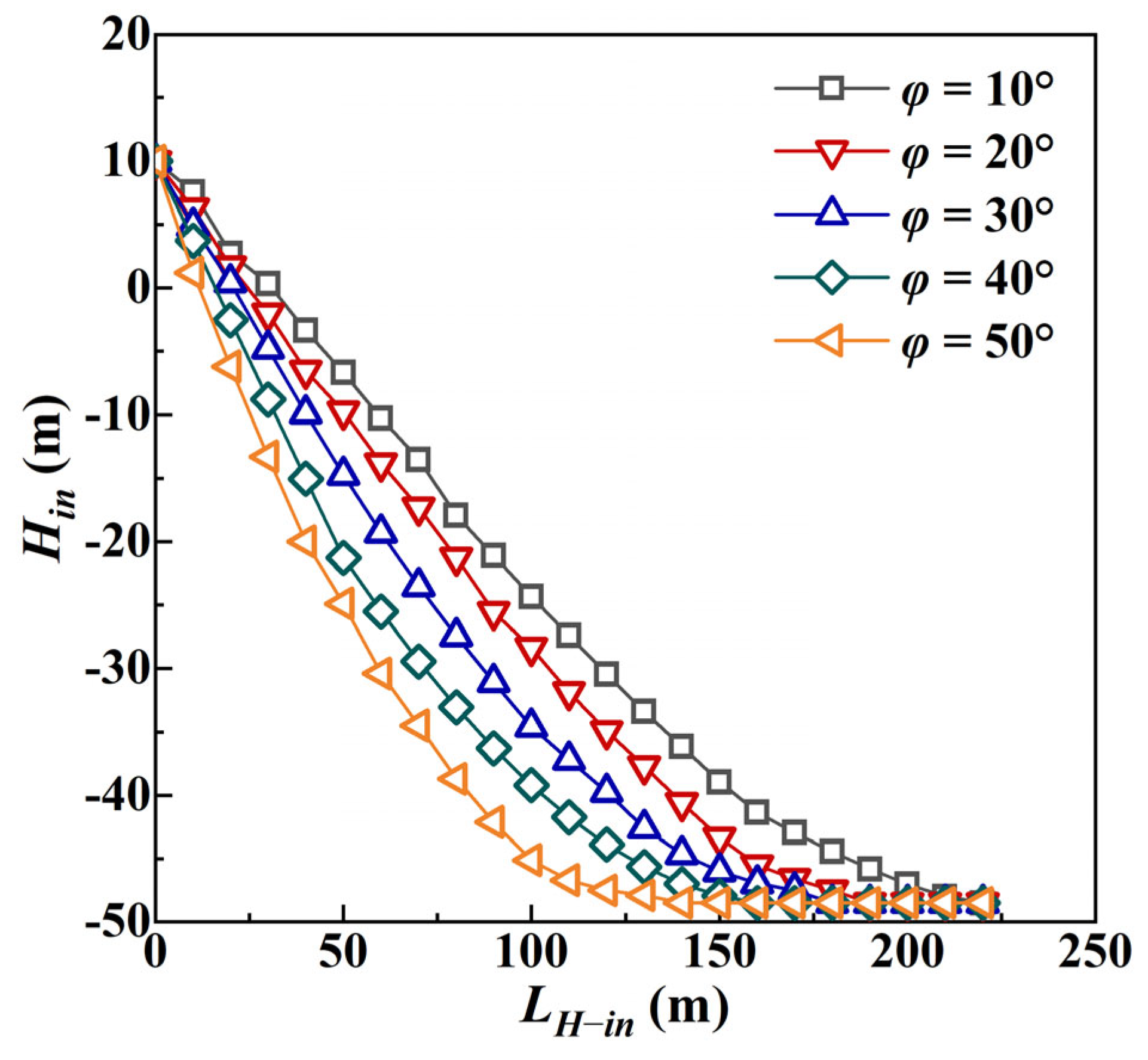
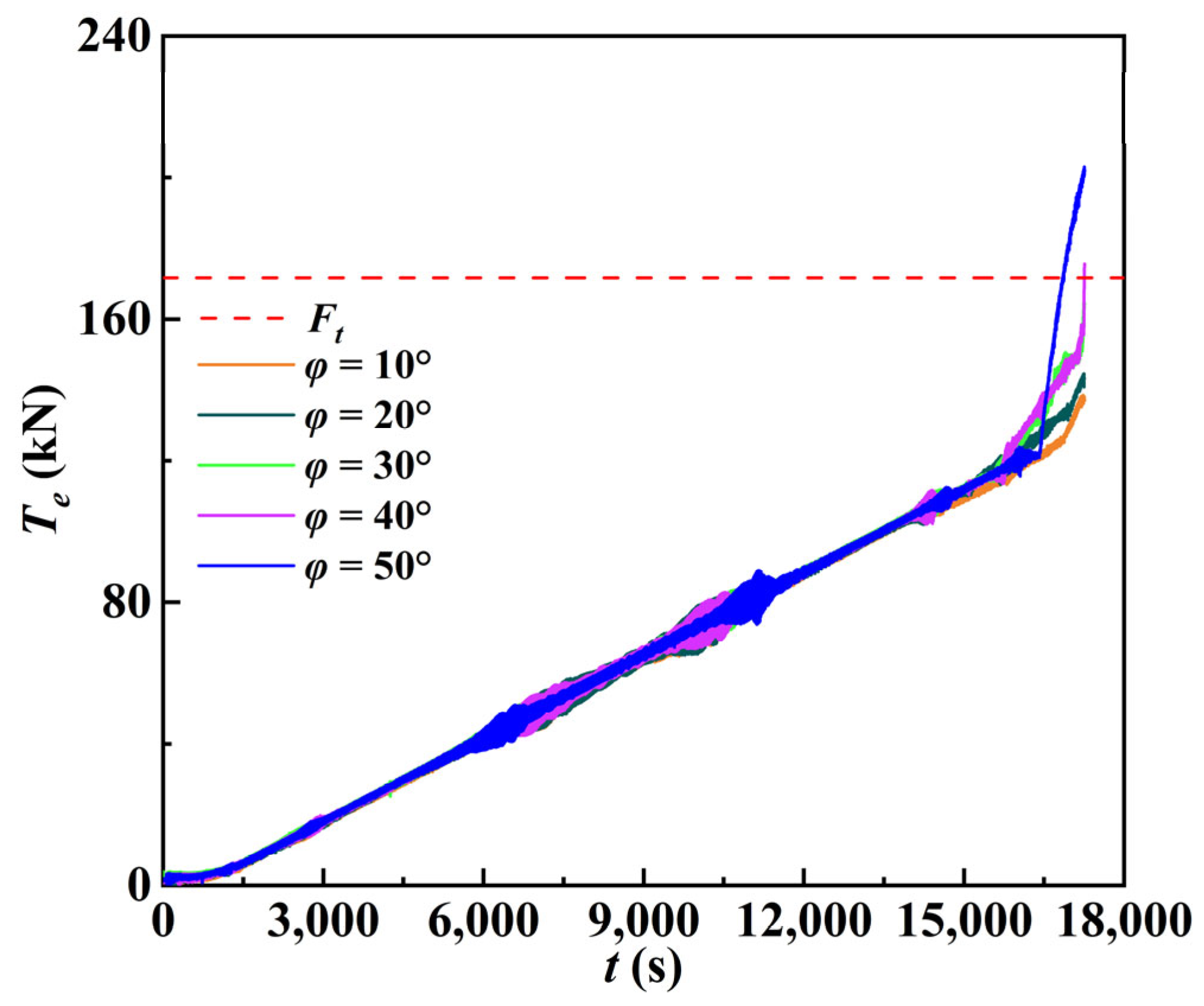
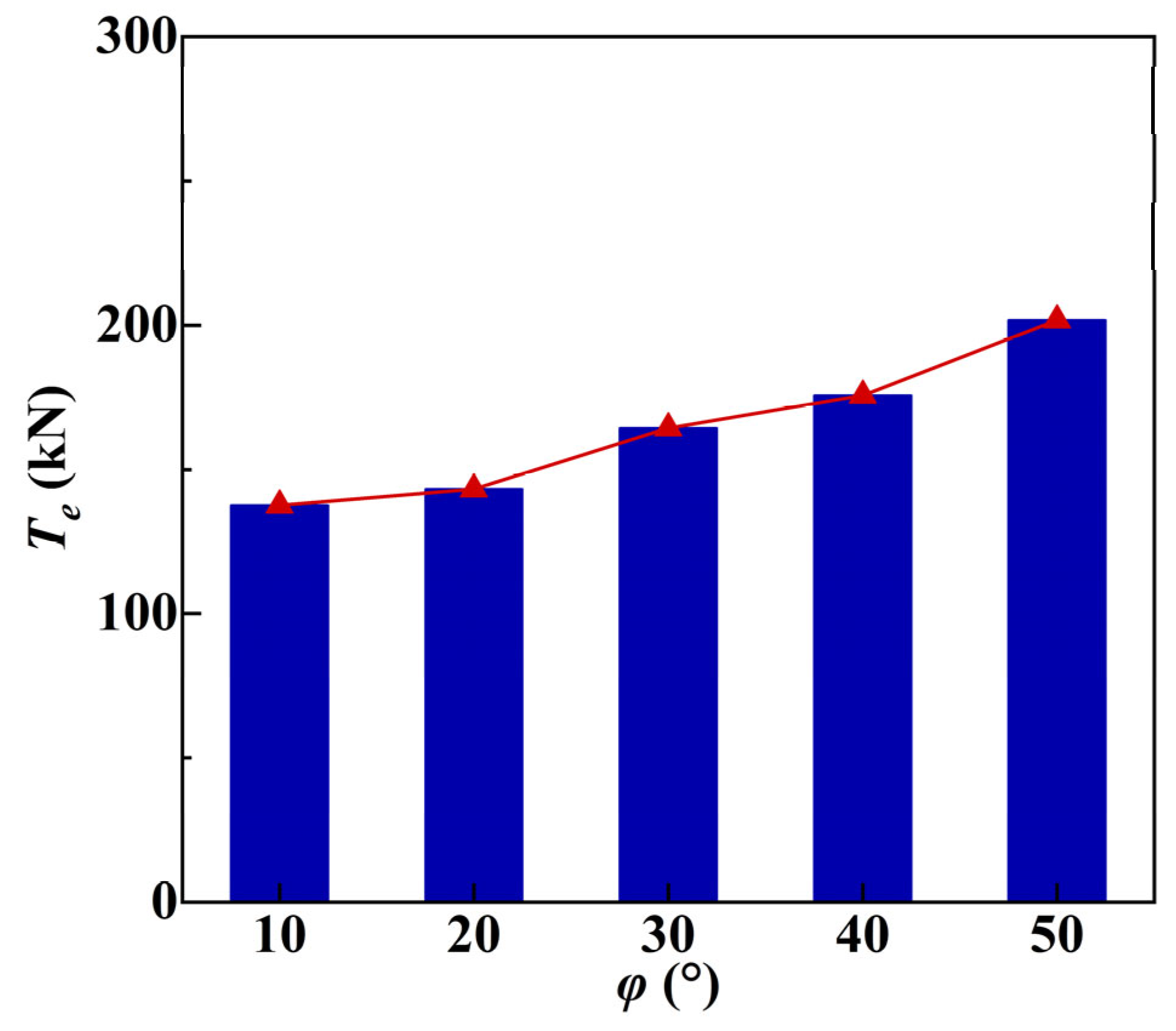
4.2. Effects of the Incident Angle on the Tension in the Cable
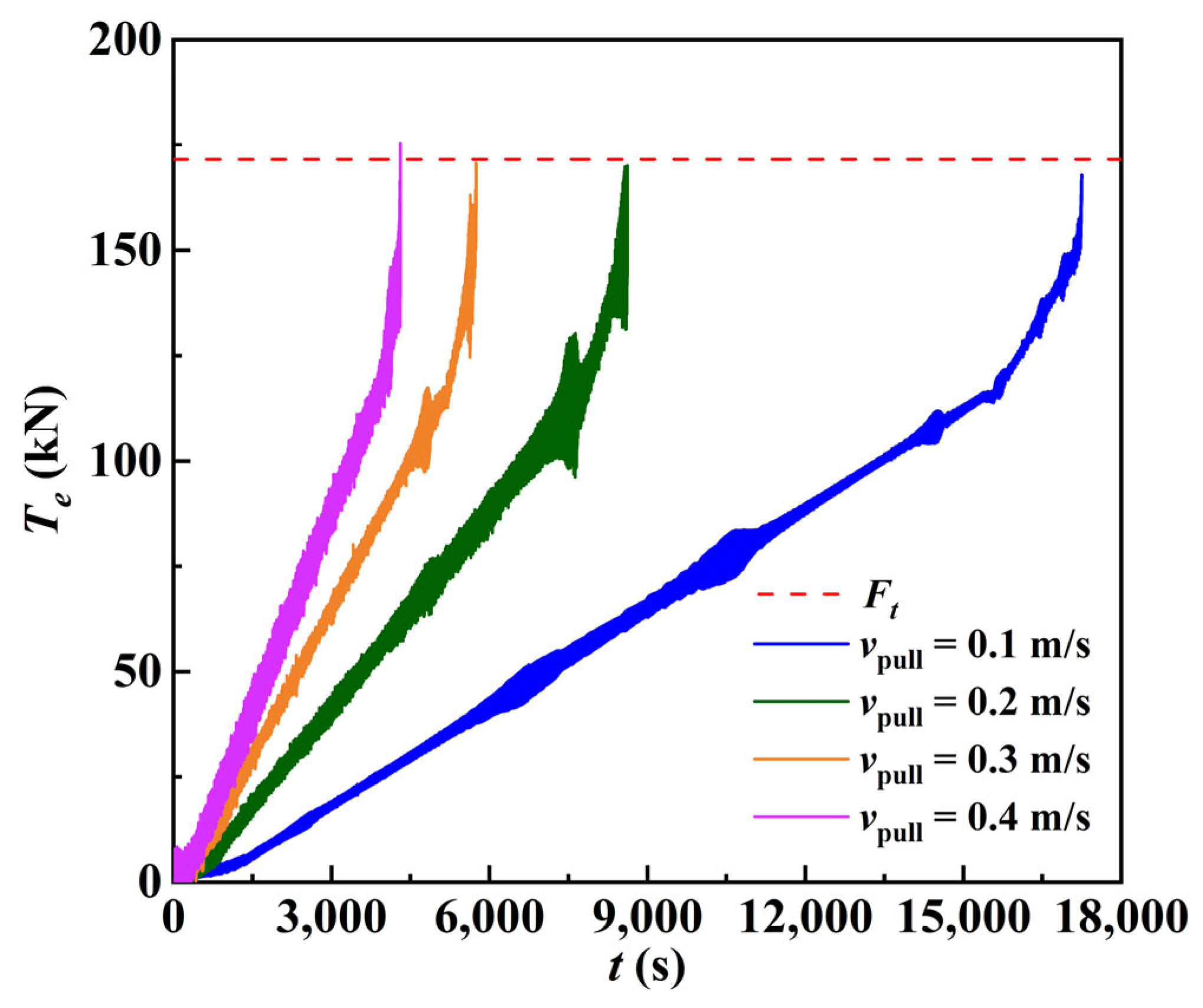
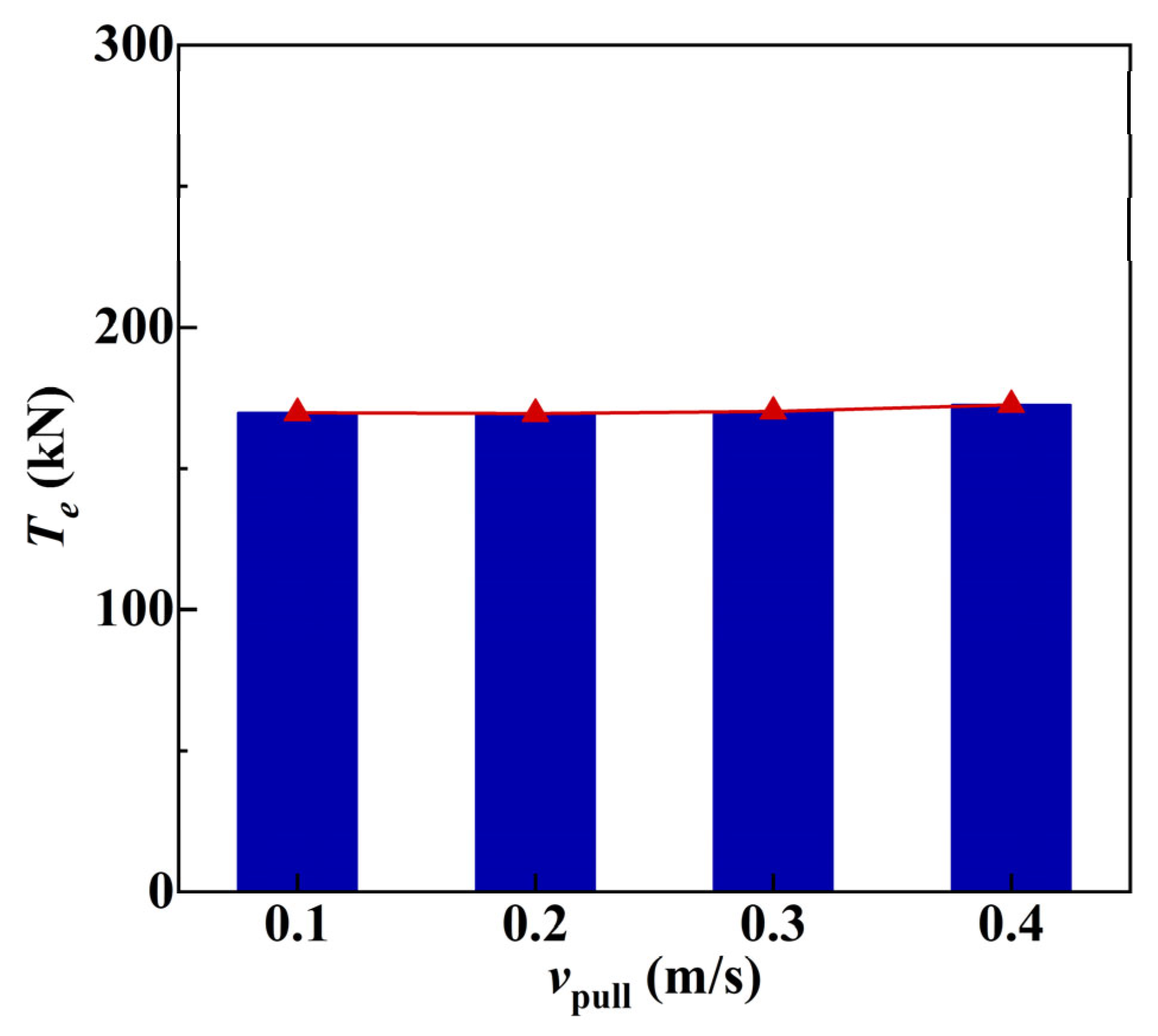
4.3. Effects of the Pullback Velocity on the Tension in the Cable
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Definition |
| a | Contact area |
| a0 | External stress area |
| ai | Internal stress area |
| A | Cross-sectional area of the cable |
| c | Damping coefficient |
| dl/dt | Change rate of the length |
| D | Height from the excavation point to the water surface |
| Dcrit | Deflection |
| E | Effective Young’s modulus |
| EA | Axial stiffness of the cable |
| Fq | Maximum pulling force in the drawing head of the cable |
| Ft | Permissible tension in the cable |
| H | Water depth |
| HB | Height of the buried part of the pipeline |
| k0 | Friction coefficient between the PE pipe and the cable |
| ks | Shear strength |
| ktt | Tension/torque coupling |
| l | Instantaneous length of the segment |
| l0 | Unstretched length of the segment |
| L | Pulling safety distance of the cable |
| LH | Horizontal distance between the entry and exit points |
| LHB | Horizontal length of the buried part of the pipeline |
| p0 | External pressure |
| pi | Internal pressure |
| R | Contact reaction force |
| Sz | Unit vector |
| t | Time |
| T | Pullback force |
| T1 | Initial tension in the cable |
| Te | Effective tension |
| Tw | Wall tension |
| ν | Poisson ratio |
| νpull | Pullback velocity |
| W | Volume weight of the cable |
| φ | Incident angle |
| τ | Twist angle of the segment |
| ε | Total mean axial strain |
| λ | Expansion factor of the segment |
| γ0 | Safety coefficient of the cable load |
| μ | Friction coefficient |
References
- Worzyk, T. Submarine Power Cables: Design, Installation, Repair, Environmental Aspects; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; pp. 136–139. [Google Scholar]
- Bao, S.; Zhang, Z.; Yuan, Z.; Wang, J.; Yu, Q.; Liu, Z. Effects of Floating Airbag on Cable Hydrodynamic Behaviors: An Experimental Study. J. Mar. Sci. Eng. 2022, 10, 402. [Google Scholar] [CrossRef]
- Taormina, B.; Bald, J.; Want, A.; Thouzeau, G.; Lejart, M.; Desroy, N.; Carlier, A. A review of potential impacts of submarine power cables on the marine environment: Knowledge gaps, recommendations and future directions. Renew. Sustain. Energy Rev. 2018, 96, 380–391. [Google Scholar] [CrossRef]
- Tian, Z. The Policy About Submarine Cable Pipeline Project in China. Master’s Thesis, Harbin Engineering University, Harbin, China, 2021. (In Chinese). [Google Scholar]
- Wu, A.; Yuan, Z.; Gong, Y. Overview of construction technology for deep-buried laying of submarine cables in China. Zhejiang Electr. Power 2015, 3, 57–62. (In Chinese) [Google Scholar] [CrossRef]
- Zou, D.; Hu, J. Study on local sediment scour and stress state of submarine cables in offshore wind farms. In Proceedings of the IOP Conference Series: Earth and Environmental Science, 2021 8th International Conference on Coastal and Ocean Engineering, Tokyo, Japan, 3–5 April 2021. [Google Scholar] [CrossRef]
- The Cables Buried in the Seabed Run Out for “Breathability”! Consultation with All Parties to Ensure Winter Electricity Consumption on Chongming Island. Available online: https://baijiahao.baidu.com/s?id=1654575915573352837&wfr=spider&for=pc (accessed on 1 April 2024).
- Osthoff, D.; Heins, E.; Grabe, J. Impact on submarine cables due to ship anchor—Soil interaction. Geotechnik 2017, 40, 265–270. [Google Scholar] [CrossRef]
- Vandals Cut San Francisco Area Fiber Optic Lines for 11th Time in a Year. Available online: https://edition.cnn.com/2015/07/01/tech/california-fiber-optic-cable-cuts/index.html (accessed on 10 April 2024).
- Yan, X.; Ariaratnam, S.T.; Dong, S.; Zeng, C. Horizontal directional drilling: State-of-the-art review of theory and applications. Tunn. Undergr. Space Technol. 2018, 72, 162–173. [Google Scholar] [CrossRef]
- The Distinct Advantages of Horizontal Directional Drilling. Available online: https://www.powrmole.com/blog/the-distinct-advantages-of-horizontal-directional-drilling/ (accessed on 12 April 2024).
- Syms, E.I.B. Horizontal Directional Drilling; Butterworth-Heinemann: Oxford, UK, 2004; pp. 297–326. [Google Scholar]
- Sun, P.; Liu, W.; Yang, H.; Wei, B.; Xia, Y. Progress in research and applications of trenchless horizontal directional drilling equipment and technology in China. Chin. J. Eng. 2022, 44, 122–130. (In Chinese) [Google Scholar] [CrossRef]
- Li, D.; Wang, W.; Lin, Y.; Zhang, Z.; Zhang, X. Exploration and Practice of Land to Sea Directional Drilling and Crossing Technology in Marine Engineering. J. Ocean Technol. 2020, 39, 95–100. (In Chinese) [Google Scholar]
- Tang, P.; Chen, C.; Huang, S.; Huang, D.; Yang, X.; Wei, J.; Jin, L. Research of Land-to-sea Horizontal Directional Drilling Crossing Technology. Pipeline Tech. Equip. 2022, 2, 31–34. (In Chinese) [Google Scholar]
- Black, S.; Cable, B.; Fredrickson, B.; Warren, D. Horizontal directional drilling cable shorelanding at san nicolas island, California. In Proceedings of the Oceans’ 04 MTS/IEEE Techno-Ocean’04 (IEEE Cat. No. 04CH37600), Kobe, Japan, 9–12 November 2004; pp. 2104–2111. [Google Scholar] [CrossRef]
- Bascom, E.C.R.; Rezutko, J. Novel installation of a 138kv pipe-type cable system under water using horizontal directional drilling. In Proceedings of the 2014 IEEE PES T&D Conference and Exposition, Chicago, IL, USA, 14–17 April 2014. [Google Scholar] [CrossRef]
- Jiao, Y.; Meng, J.; Pan, L.; Zhang, Q.; Ku, M. Laying Construction Techniques of 35 kV Submarine Cable in Offshore Wind Farm. Hydropower New Energy 2022, 36, 44–47. (In Chinese) [Google Scholar] [CrossRef]
- Yoshizawa, N.; Yabuta, T. Study on submarine cable tension during laying. IEEE J. Ocean. Eng. 1983, 8, 293–299. [Google Scholar] [CrossRef]
- Nagatomi, O.; Nakamura, M.; Wataru, K. Dynamic simulation and field experiment of submarine cable during laying and recovery. In Proceedings of the International Ocean and Polar Engineering Conference, Kitakyushu, Japan, 26–31 May 2002. [Google Scholar]
- Prpić-Oršić, J.; Nabergoj, R. Nonlinear dynamics of an elastic cable during laying operations in rough sea. Appl. Ocean Res. 2005, 27, 255–264. [Google Scholar] [CrossRef]
- Zhang, T.; Hu, X. Tension analysis in submarine cable laying. Ship Boat 2009, 20, 15–20. (In Chinese) [Google Scholar]
- Yang, N. Tension Analysis of Submarine Cables During Laying Operations. Master’s Thesis, Shanghai Jiao Tong University, Shanghai, China, 2015. (In Chinese). [Google Scholar]
- Feng, Y.; Shang, Q.; Lv, A. Dynamic Finite Element Analysis of Fiber-Optic Composite Submarine Cable Under Wave. Study On. Opt. Commun. 2017, 4, 30–34. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, D.; Bai, Y.; Zhao, W.; Zhu, K. Dynamic analysis of submarine cable during the process of laying back to the seabed. Ships Offshore Struct. 2019, 15, 153–161. [Google Scholar] [CrossRef]
- Chang, H.-C.; Chen, B.-F. Mechanical behavior of submarine cable under coupled tension, torsion and compressive loads. Ocean Eng. 2019, 189, 106272. [Google Scholar] [CrossRef]
- Sun, Y.; Shu, C.; Gao, Z. Analysis of Influencing Factors in the Process of Laying Submarine Optical Cable. In Proceedings of the 2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 11–13 December 2020. [Google Scholar] [CrossRef]
- Okkerstrøm, L. Sensitivity Analysis of Peak Tension Loads on Subsea Power Cables During Laying Operations. Master’s Thesis, Western Norway University of Applied Sciences, Haugesund, Norway, 2021. [Google Scholar]
- Kuang, J.; Chen, G.; Yuan, Z.; Qi, X.; Yu, Q.; Liu, Z. Dynamic Interactions of a Cable-Laying Vessel with a Submarine Cable during Its Landing Process. J. Mar. Sci. Eng. 2022, 10, 774. [Google Scholar] [CrossRef]
- Shen, J.; Liang, Y.; Hong, H.; Chen, J. Numerical Investigation of Burial Depth Effects on Tension of Submarine Power Cables. J. Mar. Sci. Eng. 2024, 12, 1972. [Google Scholar] [CrossRef]
- Peres, M.; Wang, S.; Soares, C.G. Sensitivity analysis of loads on subsea power cables during installation. In Advances in Maritime Technology and Engineering; CRC Press: Boca Raton, FL, USA, 2024; pp. 477–487. [Google Scholar]
- Li, Y.; Jiang, L.; Xie, M.; Yu, J.; Qian, L.; Xu, K.; Chen, M.; Wang, Y. Advancements and Challenges in Power Cable Laying. Energies 2024, 17, 2905. [Google Scholar] [CrossRef]
- Khasanov, R.R.; Pascal, M.A.; Sultanmagomedov, T.; Magomedtagirovich, S.S. Improving the methodology for calculating the thrust force during underwater crossing by directional drilling method. J. Integr. Sci. Technol. 2024, 12, 823. [Google Scholar] [CrossRef]
- Faghih, A.; Goerz, B.; Bayat, A. Stress analysis of steel pipe installation in horizontal directional drilling based on strain monitoring. Tunn. Undergr. Space Technol. 2024, 147, 105673. [Google Scholar] [CrossRef]
- Guo, Z.; Liang, Z. Analysis of the pipeline pull-back load for horizontal directional drilling. KSCE J. Civ. Eng. 2018, 22, 5133–5142. [Google Scholar] [CrossRef]
- Tang, J.; Qin, T.; Zhang, H. Research on influencing factors of cable traction force in horizontal directional drilling. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Sanya, China, 16–18 November 2021. [Google Scholar] [CrossRef]
- Vasilescu, V.-F.; Dinu, D. Installation of submarine cables and pipes in shallow waters and connecting them to the shore by the method of horizontal directional drilling. In Proceedings of the 10th International Conference on Thermal Equipments, Renewable Energy and Rural Development, Bucharest, Romania, 26–27 June 2020. [Google Scholar] [CrossRef]
- Liang, X.-Q.; Hu, D.; Li, Y.-S.; Yang, X.; Jiang, L.; Zhang, Y.-Y. An Improved Model to Calculate Pullback Force of Trenchless Horizontal Directional Drilling Pipeline. Adv. Civ. Eng. 2022, 2022, 1–13. [Google Scholar] [CrossRef]
- Zheng, H. Mechanical response analysis on pipeline during horizontal directional drilling construction and service period. I 2025, 56, 198–204. (In Chinese) [Google Scholar] [CrossRef]
- GB/T 13663.2-2018; Polyethylene (PE) Piping Systems for Water Supple—Part 2 Pipes. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2018.
- Orcaflex11.3b User’s Manual. Available online: https://www.orcina.com/author/heff/page/2/ (accessed on 22 May 2024).
- Liu, X. Mechanics Analysis of Pipeline in Back-Dragging Process of Horizontal Directional Drilling. Doctoral Thesis, Southwest Petroleum University, Chengdu, China, 2017. (In Chinese). [Google Scholar]


| Item | Value (Unit) | Item | Value (Unit) |
|---|---|---|---|
| Outer diameter | 199.2 mm | Mass in the water | 47.9 kg/m |
| Mass in the air | 79.8 kg/m | Permissible tension | 171.7 kN |
| Axial stiffness | 7.0 × 105 N/mm | Bending stiffness | 1.0 × 108 N/mm |
| Item | Value (Unit) | Item | Value (Unit) |
|---|---|---|---|
| Classification | PE 100 | Density | 910.0 kg/m3 |
| Outer diameter | 355.0 mm | Single section length | 12.0 m |
| Thickness | 13.6 mm | Friction coefficient with the cable | 0.35 |
| Axial stiffness | 1.3 × 104 N/mm | Bending stiffness | 2.6 × 1011 N·mm2 |
| Item | Value (Unit) | Item | Value (Unit) |
|---|---|---|---|
| Crossing length | 1970.0 m | Pipe specification | Φ610 × 12.7 mm |
| Pipe length | 2129.0 m | Pipe material density | 7850 kg/m3 |
| Crossing depth | 73.5 m | Mud density | 1200 kg/m3 |
| Incident angle | 16.0° | Unearthed angle | 14° |
| Friction coefficient | 0.3 | Pipeline radius | 0.65 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, G.; Kang, W.; Cong, Y.; Liu, Z. A Numerical Study on the Pullback Process of a Submarine Cable Based on Trenchless Directional Drilling Technology. Water 2025, 17, 1517. https://doi.org/10.3390/w17101517
Qian G, Kang W, Cong Y, Liu Z. A Numerical Study on the Pullback Process of a Submarine Cable Based on Trenchless Directional Drilling Technology. Water. 2025; 17(10):1517. https://doi.org/10.3390/w17101517
Chicago/Turabian StyleQian, Gang, Wei Kang, Yun Cong, and Zhen Liu. 2025. "A Numerical Study on the Pullback Process of a Submarine Cable Based on Trenchless Directional Drilling Technology" Water 17, no. 10: 1517. https://doi.org/10.3390/w17101517
APA StyleQian, G., Kang, W., Cong, Y., & Liu, Z. (2025). A Numerical Study on the Pullback Process of a Submarine Cable Based on Trenchless Directional Drilling Technology. Water, 17(10), 1517. https://doi.org/10.3390/w17101517






