Abstract
The hydrological cycle should be scrutinized and investigated under recent climate change scenarios to ensure global water management and to increase its utilization. Although the FAO proposed the use of the Penman–Monteith (PM) equation worldwide to predict evapotranspiration (ET), which is one of the most crucial components of the hydrological cycle, its complexity and time-consuming nature, have led researchers to examine alternative methods. In this study, the performances of numerous temperature-driven ET methods were examined relative to the PM using daily climatic parameters from central stations in 11 districts of the Kahramanmaras province. Owing to its geographical location and other influencing factors, the city has a degraded Mediterranean climate with varying elevation gradients, while its meteorological patterns (i.e., temperature and precipitation) deviate from those of the main Mediterranean climate. A separate evaluation was performed via ten different statistical metrics, and spatiotemporal ET variability was reported for the districts. This study revealed that factors such as altitude, terrain features, slope, aspect geography, solar radiation, and climatic conditions significantly impact capturing reference values, in addition to temperature. Moreover, an assessment was conducted in the region to evaluate the effect of modified ET formulae on simulations. It can be drawn as a general conclusion that the Hargreaves–Samani and modified Blaney–Criddle techniques can be utilized as alternatives to PM in estimating ET, while the Schendel method exhibited the lowest performance throughout Kahramanmaras.
1. Introduction
Evapotranspiration (ET), a term used in environmental science, hydrology, and agriculture to describe the process by which water is transferred from the Earth’s surface to the atmosphere, has become one of the most complex components of the hydrological cycle as it depends on multi-climatological parameters and their interactions [1,2,3]. This important phenomenon is a component of the Earth’s water cycle, as it influences the movement and distribution of water in the atmosphere, the availability of water resources, and the climate. It is necessary to understand the connections between evapotranspiration and ecosystem type in response to climate change [4,5]. In the long term, the water that is directly available for human consumption and control is what separates evapotranspiration from continental precipitation. Therefore, quantitative ET knowledge is necessary for quantitative assessments of water resources and the impacts of climate and land-use change on these resources [6,7,8].
To better comprehend this complex formation and determine the amount of water lost through ET, definitions have been made based on a variety of assumptions [9,10,11,12,13]. ET approaches can be divided into three categories: hydrological and water balance methods, analytical methods based on climate variables, and empirical methods [14]. The water balance technique and basin hydrology for measuring or indirectly determining the ET value consists of sampling soil water change and lysimeter testing. Since this is primarily a physically based method, its use in climate change assessment is limited to the laboratory [15,16]. The second approach, known as the micrometeorological method, uses a scientific understanding of the physics of evapotranspiration. Mathematical relationships have been developed to describe these processes through two fundamental climatological components: energy balance and mass transport [10,17,18,19]. The third method centers on developing empirical relationships that are often site-specific and based on regional climatological conditions and often used in regression analysis. These techniques are often calibrated by correlating experimental predictions with observed data [20,21,22].
ET can be computed by the aerodynamic approach when energy is unlimited and by the energy balance method when vapor movement (mass transfer) is limitless. Normally, however, both of these factors are limiting; therefore, a combination of the two methods is required [17]. The Penman–Monteith (PM) technique, recommended worldwide by the Food and Agriculture Organization (FAO), is one of the most universally used energy balance and mass transfer-based methods to compute evaporation on terrestrial surfaces [14]. The equation developed by Penman [23] to calculate evaporation from an open water surface was modified by Monteith [24] by including canopy conductance to represent the ET rate from a vegetative surface. In the 1980s, the method was developed and presented in detail by combining the canopy and soil evaporation [25]. Allen et al. [1] updated the PM approach by adapting the ET values to the reference grass plant with constant albedo and surface resistance and proposed it as the FAO-56 Penman–Monteith equation. The PM method, recommended by the FAO for applications worldwide, has been analyzed in various regions for decades and has yielded sufficiently accurate results [26,27,28,29,30].
The fact that the FAO-56 PM equation requires a large number of meteorological data (i.e., temperature, humidity, radiation, and wind speed) makes the solution of the equation difficult, and obtaining such data is not always possible. Although Allen et al. [1] expressed the solvability of the equation using auxiliary formulae based on temperature data for the PM approach, many alternative empirical methods (i.e., temperature-based, radiation-based, and a combination of them) have been investigated for use in cases where sufficient data are not available [31,32,33,34,35]. For instance, Tabari et al. [34] evaluated the performance of thirty-one alternative empirical methods using meteorological data obtained under humid conditions in Northern Iran and the PM method as a reference. Analysis of the data revealed that, in general, the best results were attained with the Blaney–Criddle and Hargreaves methods compared to the PM equation; mass transfer-based approaches underestimated ET, whereas overestimations were more dominant in temperature-based and radiation-based methods. Sarlak and Bagcaci [35] evaluated the performances of six empirical ET approaches, namely Blaney–Criddle, Jensen–Haise, Makking, Turc, Priestley–Taylor, and Hargreaves–Samani, compared to the PM method using daily meteorological data from five stations in Konya Closed Basin. They concluded that in the absence of daily observation data, the Turc, Hargreaves–Samani, and Priestley–Taylor techniques, which require less data, can be used as an alternative to PM. Similarly, Song et al. [36] applied twelve different ET estimation methods relative to the PM method recommended by the FAO in northeast China, which they divided into eight sub-regions according to the climate and land types. In the study, temperature-based (Blaney–Criddle, Thornthwaite, Romanenko-1, and Romanenko-2), radiation-based (Hargreaves–Samani, Turc, Makking, and H-Makking), and combination methods (Linacre, simplified Penman–Monteith, Valiantzas-1, and Valiantzas-2) were employed using data over 126 stations for more than half a century. H-Makking and Valiantzas-2 approaches can be considerable as alternative methods in agricultural areas in northern regions of China, while Valiantzas-2, Romanenko-2, and H-Makking methods are more suitable during crop growth periods. Although the results varied regionally and seasonally, the temperature was the most sensitive parameter for estimating ET values. Furthermore, it is claimed that the Turc approach constantly tends to deviate negatively whereas the Hargreaves–Samani method produces notable biases.
Researchers have performed local calibrations as well as modifications of these empirical methods for use in various regions under differing conditions, even though many of the methods developed for a particular location are widely utilized worldwide. For instance, Cobaner et al. [37] compared the reference evapotranspiration values determined using the PM technique in the Mediterranean region with the values derived using calibrated Hargreaves–Samani equations, which require less data. According to this study, the ET values produced by the Hargreaves–Samani equations calibrated with minimum and maximum temperatures, as well as minimum and maximum humidity data, were close to the values calculated using the PM formula. They concluded that the Hargreaves–Samani equation calibrated with the maximum temperature is better than those calibrated with other meteorological data. Similarly, monthly ET values were computed using the modified Blaney–Criddle and Hargreaves–Samani equations, obtaining data from three stations located in the semi-arid climate regions of Pakistan and compared with PM-driven ET values [38]. Overall, it was stated in the study that both equations overestimated PM-driven ET values, although the findings of the Hargreaves–Samani method were superior to those of the modified Blaney–Criddle method. In another example, the effect of modified approaches on ET was investigated in Eastern Turkiye [14]. Study results showed that the modified Hargreaves–Samani approach formed by the constant values in the Hargreaves–Samani equation revealed better results than the Hargreaves–Samani equation over the region, while altitude-based modified Hargreaves–Samani technique has the lowest correlation results among the other methods in the study. Additionally, they concluded that the modification of the Blaney–Criddle formula increased the performance relative to the Blaney–Criddle equation.
It is necessary to conduct studies to ascertain the suitability and accuracy of empirical techniques for different regions that have emerged from investigations conducted in local areas with soil structure as well as certain climatic and environmental characteristics. Several empirical approaches can be used with varying degrees of success, owing to the unique characteristics of each place and the availability of a limited number of measurable climatic and environmental factors. Hydrological studies are significant for the effective management of water resources in Kahramanmaras, given their considerable water potential. Unfortunately, ET measurements are not available for Turkiye, and these values vary spatiotemporally. However, no comprehensive ET study has been conducted in the city, and a district-based ET study was implemented for the first time in the region. Additionally, the city has complex climate zones, varying vegetation cover, and uneven distribution of elevation gradient.
In this study, the quantitative determination of ET, one of the most significant water losses of the hydrological cycle, can contribute to studies in this field and will also play an important role in various hydrological planning studies, such as agricultural irrigation projects and basin management, to be carried out in the study area. Data-scarce ET time series were assessed utilizing ten climatological-driven ET approaches relative to the PM method over eleven districts of Kahramanmaras region, Turkiye. In this study, the performances of ten empirical evapotranspiration approaches, namely Blaney–Criddle (BC), modified Blaney–Criddle (BCM), Hamon (HM), modified Hamon (HMM), Hargreaves–Samani (HS), Kharrufa (KH), Romanenko (RM), Schendel (SC), Thornthwaite (TH), and Penman–Monteith at 0.5 m (PM0.5), were evaluated at daily and monthly temporal resolution in Kahramanmaras province and its eleven districts and compared to the reference PM method. In addition, the effect of modified techniques on evapotranspiration estimates was investigated over the region.
2. Materials and Methods
The flow diagram used in the methodology is shown in Figure 1. In this study, ET values were simulated using Penman–Monteith at 0.5 m (PM0.5), Blaney–Criddle (BC), modified Blaney–Criddle (BCM), Hamon (HM), modified Hamon (HMM), Hargreaves–Samani (HS), Kharrufa (KH), Schendel (SC) methods, and the reference Penman–Monteith (PM) at daily temporal resolutions, whereas monthly and annual ET values were derived by taking the averages. The Thornthwaite (TH) and Romanenko (RM) techniques were utilized to compute monthly ET values and produce yearly ET values. Days with missing data and ET values equal to zero were excluded from computation.
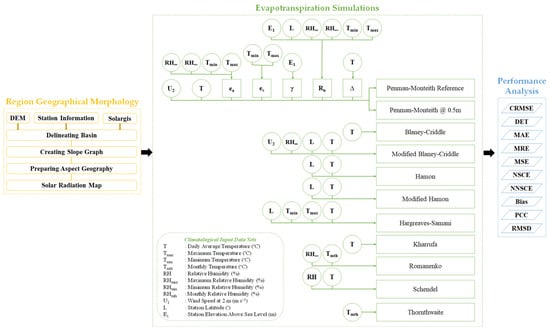
Figure 1.
Flow diagram of the ET analysis methodology over Kahramanmaras.
The following statistical indices were used to assess the performance of the methods: centered root mean square error (CRMSE), determination coefficient (DET), mean absolute error (MAE), mean relative error (MRE), mean squared error (MSE), Nash–Sutcliffe efficiency coefficient (NSCE), normalized Nash–Sutcliffe efficiency (NNSCE), percentage error (Bias), Pearson’s correlation coefficient (PCC), and root mean square error (RMSD).
2.1. Study Area and Data Sets
Kahramanmaras is the eleventh largest city in Turkiye, with a surface area of 14,346 km2, and is situated between 37–39 northern parallels and 36–38 eastern meridians. The province’s northern regions are quite mountainous, with landforms mostly consisting of mountains that are extensions of the Taurus Mountains in the southeast and the depressions that separate them (Figure 2). Digital elevation model (DEM) data for the study area were obtained from the US Geological Survey (USGS) website [39]. After adjusting the required projections and coordinate system as well as delineating the area, the acquired data were examined using the Arc-GIS program, a scalable integrated geographic information system software developed by ESRI. Figure 2 was obtained by processing the coordinate information of the relevant stations shown in Table 1 into the program. As can be seen from the figure, the altitude of the study area ranges from 130 to 3075 m, and the regions where stations S3 and S10 are located have the highest altitude, while the areas where stations S2 and S11 are located have the lowest elevation. Although the altitude values in the territories containing stations S4 and S9 are relatively close to one another, the high-elevation difference between the regions where stations S1 and S3 are located can be seen in Figure 2.
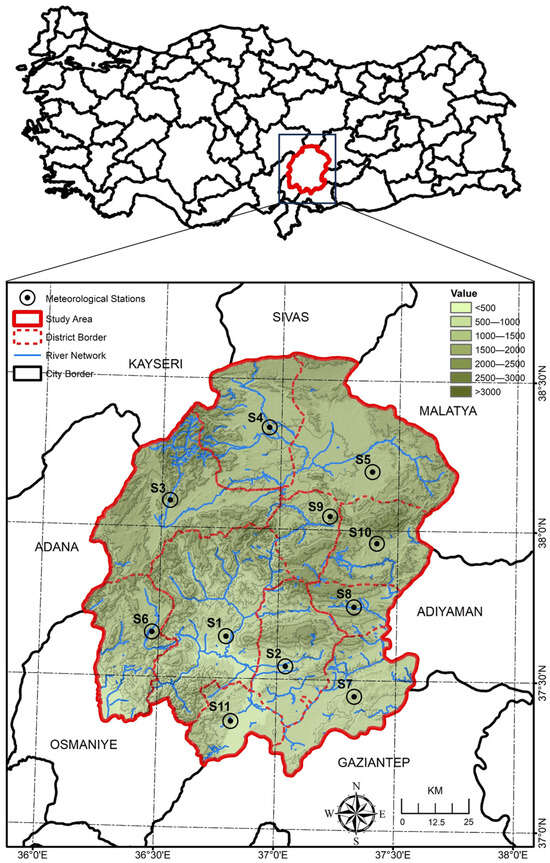
Figure 2.
Map of Kahramanmaras and the location of the MGM meteorological stations.

Table 1.
Details of the weather stations that were utilized in the research.
Kahramanmaras is located at the junction of Eastern Anatolia, Southeastern Anatolia, Central Anatolia, and geographical Mediterranean regions. The city has climate characteristics closer to the “Degraded Mediterranean Climate” due to its geographical location and the influence of other factors. Nevertheless, its temperature and precipitation patterns deviate from those of the main Mediterranean climate. In general, summers in the province are hot and dry, and winters are warm and rainy. The fact that the provincial territory is located in the transition area of the Mediterranean and Southeastern Anatolia regions has caused the climatic conditions in the city to differ. For instance, Andirin district is under the influence of maritime climate, and the Mediterranean climate is more dominant in the southern part of the city, while the northern part of the province experiences a more continental climate [21,40,41,42].
Table 1 displays the details of the stations with data sets from various time periods that were generated using data obtained from the Turkish State Meteorological Service’s (MGM) Meteorological Data Information Presentation and Sales System (MEVBIS). MEVBIS system is a project designed to archive and quickly present all meteorological observation data produced by the MGM after quality control and format conversion [43]. There are a total of 32 meteorological stations within the Kahramanmaras city borders, and some stations measure limited climatological data sets such as only temperature, wind speed, precipitation, or snow. Meteorological measurements have not been made at some stations since 1990 due to the changing city borders; some stations have a history of only a few years, with some regions gaining district status in 2012 with Kahramanmaras becoming a metropolitan city, and some do not have an uninterrupted continuous data set [21,44]. However, ET simulations, especially the Penman–Monteith equation, require numerous data sets, and obtaining such data is not always possible. Within the scope of this study, meteorological stations where the longest-term data were measured in each 11 districts were preferred. Meteorological stations’ properties, such as their names, districts in which they are located, coordinates, and altitudes, are given in detail in Table 1. Using the PM simulations as a reference, the meteorological-driven ET predictions are evaluated for a period of 22 years (2000 through 2021) over the Onikisubat, Goksun, Afsin, and Elbistan regions; 9 years (2013 through 2021) over Andirin and Pazarcik counties; 8 years (2014 through 2021) over Caglayancerit, Ekinozu, Nurhak, and Turkoglu districts; and 5 years (2017 through 2021) over Dulkadiroglu (Table 1). Required data sets, namely average temperature (T, °C), maximum temperature (Tmax, °C), minimum temperature (Tmin, °C), average relative humidity (RH, %), maximum relative humidity (RHmax, %), minimum relative humidity (RHmin, %), average wind speed at 2 m height (, m s−1), and sunshine duration (n, hr) for each station, were acquired from the MEVBIS module at daily temporal resolution within the scope of this study. In this study, multi-paradigm numerical calculation software developed by MathWorks r2006a MATLAB program was utilized in a holistic sense with Microsoft 365 Excel program for manipulations on the obtained data sets, preparation of required time series, ET calculations, and graphing.
2.2. Evapotranspiration Estimation Methods
2.2.1. FAO Penman–Monteith Method (PM)
This study examined the applicability of various empirical approaches in the Kahramanmaras, where the widely known PM method was utilized as a reference in ET quantitative calculations. The method recommended by FAO for use globally is as in Equation (1) in its revised form by adapting the ET values with the reference grass plant with a constant albedo of 0.23, a surface resistance of 70 s m−1, and adequately irrigated at a height of 0.12 m [1,23,24]. The ETPM in the equation expresses the reference evapotranspiration in mm d−1, and Δ (kPa °C−1) denotes the slope of the vapor pressure curve at average air temperature and is calculated using Equations (2) and (3). In these equations, G symbolizes the soil heat flux density (MJ m−2 d−1) and can be considered zero for daily calculations, T is the daily average air temperature (°C), u2 denotes the wind speed at 2 m height (m s−1), es emblematizes the saturated vapor pressure (kPa), ea stands for actual vapor pressure (kPa), γ represents the psychrometric constant (kPa °C−1), and e°(T) indicates the saturated vapor pressure (kPa) at air temperature T (°C).
On the other hand, Rn (MJ m−2 d−1) refers to the net radiation at the crop surface and is equal to the difference between the incoming net shortwave radiation (Rns) and the outgoing net longwave radiation (Rnl). While Rns is also known as net solar radiation and can be calculated using Equation (4), Rs is the part of solar radiation that is not reflected from the surface. The value 0.23 in the equation indicates the albedo coefficient for green grass surfaces. Rs (Solar radiation) can be derived as suggested by Hargreaves–Samani [45] and is shown in Equation (5) when there is no measured data of solar radiation. In the equation, Krs symbolizes the calibration coefficient and can be taken as 0.16, whereas Ra indicates extraterrestrial radiation (MJ m−2 d−1). Tmax and Tmin are the maximum and minimum absolute temperatures over 24 h, respectively. Net outgoing longwave radiation Rnl, the difference between the outgoing and incoming longwave radiation, is computed according to Equation (6).
where σ is the Steffan–Boltzmann constant and has a value of 4.90 10−9 MJ m−2 d−1 K−4. represents the air humidity correction factor and is defined as in Equation (7), while Rso expresses the clear-sky solar radiation (MJ m−2 d−1) and is calculated as shown in Equation (8). In the following equation, E1 represents the station elevation above sea level (m).
In Equation (9), where extraterrestrial radiation is calculated, Gsc is the solar constant and has a value of 0.082 MJ m−2 min−1. dr is the inverse relative distance factor for the Earth–Sun and is unitless (Equation (10)), ws indicates sunset hour angle in radians (Equation (11)), δ refers to solar declination in radians (Equation (12)), ϕ symbolizes station latitude (L) in radians (Equation (13)), and i stands for the Julian day of the year.
The psychrometric constant, γ, which is proportional to the mean atmospheric pressure, can be computed using Equations (14) and (15). While β (kPa) used in the equations indicates atmospheric pressure as a function of altitude, λ refers to the latent heat of vaporization, and its value is 2.45 MJ kg−1. On the other hand, in cases where the u2 data required in Equation (1) are unavailable, the wind speed data measured at various altitudes can be converted to the wind speed at 2 m height using Equation (16). In the equation, zw (m) denotes the height of the measurement location from the ground, while uz (m s−1) indicates the wind speed at height zw. Lastly, the saturated (es) and actual vapor pressures (ea), can be calculated using daily e°(Tmin), e°(Tmax), minimum relative humidity (RHmin), and maximum relative humidity (RHmax) data by Equations (17) and (18), respectively. e°(Tmin) and e°(Tmax) represent the saturation vapor pressure (kPa) at the daily minimum and maximum temperatures, respectively.
To calculate ETPM in cases where the measured climatic parameters are insufficient or missing in the Penman–Monteith method (Equation (1)), which requires various climatic parameters, Hargreaves–Samani [45] and Allen et al. [1] proposed auxiliary equations from Equations (2)–(18) in the FAO Irrigation and Drainage Paper 56. Alternative approaches are being investigated because PM-driven ET and all of these supplementary equations are laborious and time-consuming.
2.2.2. FAO Penman–Monteith 0.5 m Method (PM0.5)
In the standardized reference evapotranspiration method report prepared by the Environmental and Water Resources Institute of the American Society of Civil Engineers [46], the standardized PM0.5 method was recommended for in mm d−1, which will occur on a tall plant-covered surface with a height of approximately 50 cm, as given in Equation (19).
2.2.3. Blaney–Criddle Method (BC)
The BC equation, developed by Blaney and Morin [47] for use in evapotranspiration estimations, was modified by Blaney and Criddle, revised in 1950, and presented as Equation (20) [48,49]. The symbol ETBC denotes Blaney–Criddle-driven ET values in mm d−1 in the equation that uses the daily average air temperature parameter, whereas the symbol p can be used to define the mean daily percentage of annual daylight hours, which varies based on latitude. In the given equation, the seasonal crop coefficient, k, was considered to be 0.85.
2.2.4. Modified Blaney–Criddle Method (BCM)
Climatic conditions would also affect ET, according to Doorenbos and Pruitt’s [31] study, in addition to the crop coefficient in the original Blaney–Criddle equation. Equation (21) was generated by including the adjustment variables a and b, which considered humidity, sunshine duration, and daytime wind speed. Here, stands for evapotranspiration values obtained using the modified Blaney–Criddle technique. Variable a, which can be computed using Equation (22), is a function of RHmin, n (actual sunshine duration), and N (maximum possible sunshine duration), while the b value varies depending on the daily average daytime wind speed (U) (m s−1), in addition to RHmin and n/N ratio (Equation (23)). In cases where daytime wind speed data are unavailable, 1.33 times the average wind speed can be considered for the u value. For the coefficients e0, e1, e2, e3, e4, and e5 employed in Equation (23), the values of 0.81917, −0.0040922, 1.0705, 0.065649, −0.0059684, and −0.0005967 were used, respectively [1,31,50,51].
2.2.5. Hamon Method (HM)
The method for predicting evapotranspiration on a daily scale suggested by Hamon [52] is given in Equation (24), and ETHM symbolizes Hamon-driven ET estimations. The constant C in the equation has a value of 0.0055 and was converted from inches to mm and utilized as 0.1397 in the computations. While D, which indicates the 12 h possible sunshine duration (N/12), is estimated as in Equation (25), Pt is the saturated water vapor density at the daily average temperature and can be calculated using Equation (26).
2.2.6. Modified Hamon Method (HMM)
The approach proposed by Hamon [53] is given by Equation (27). symbol denotes values obtained from modified Hamon-based evapotranspiration simulations. The constant H in the equation, which was converted from inches to millimeters and used as 0.1651 in the calculations, had a value of 0.0065. Equation (28) was used to obtain the Pt values using the modified Hamon technique. After the daily evapotranspiration estimations were determined using the Hamon and modified Hamon techniques, in this study, a local calibration coefficient of 1.2 was set based on the suggestions of previous studies [54,55,56].
2.2.7. Hargreaves–Samani Method (HS)
The technique was developed using 8-year daily lysimeter data representing 8–15 cm grass clipping evapotranspiration in California by Hargreaves [57] and was modified by Hargreaves and Samani [58] (Equation (29)). ETHS denotes evapotranspiration predictions based on the Hargreaves–Samani approach, and the coefficient λ−1 (0.408) was used to convert evapotranspiration values into mm d−1.
2.2.8. Kharrufa Method (KH)
The nonlinear equation based on the relationship between temperature and the average daily percentage of annual daylight hours in the year (p) proposed by Kharrufa [59] is given by Equation (30). The symbol ETKH in the equation represents Kharrufa-driven daily evapotranspiration predictions.
2.2.9. Schendel Method (SC)
While the Schendel [60] method, which uses daily average temperature and relative humidity climatic data, is determined as shown in Equation (31), ETSC symbolizes the evapotranspiration values obtained according to the Schendel technique.
2.2.10. Romenenko Method (RM)
According to Equation (32) developed by Romanenko [61], the ETRM values were derived monthly using temperature (Tmth, °C) and relative humidity (RHmth, %) monthly average climatic data.
2.2.11. Thornthwaite Method (TH)
Thornthwaite [13] defined “potential evapotranspiration” and proposed an equation in his study on climate classification, emphasizing the significance of evapotranspiration value for climate classification (Equation (33)). In Equation (33), derived from the relationship between monthly average temperature and evapotranspiration (ETTH), the ij symbol denotes the monthly temperature index (Equation (34)); the letter I symbolizes the annual temperature index, which is the sum of monthly temperature indices; the coefficient α is determined by the annual temperature index (Equation (35)).
2.3. Statistical Metrics
Eleven distinct evapotranspiration techniques were applied to derive ET estimations for eleven different stations in Kahramanmaras. The performance of eight of these methods—which are computed on a daily time scale—was evaluated using numerous statistical performance assessment indicators compared to the reference PM technique. Performance evaluation indices were computed based on ET values in a daily timeframe to obtain more precise results.
Statistical metrics are widely used to assess model performance in hydrological analyses and applications [62,63,64,65]. BC, BCM, HM, HMM, HS, KH, PM0.5, and SC-driven ET performances were evaluated using CRMSE, PCC, DET, MAE, MRE, MSE, NSCE, NNSCE, Bias, and RMSD statistical indices at a daily temporal resolution. The random error between the simulations and the reference values to the mean reference value was assessed using CRMSE. It can be calculated using Equation (36), and its values vary from 0 to +∞. A lower CRMSE indicates better consistency, whereas a value of zero signifies no random error between the time series [65,66]. PCC is the covariance of the two variables divided by the product of their standard deviations and can be calculated using Equation (37). It measures the strength and direction of the linear relationship between two variables. If PCC is close to 1 (−1), it suggests a strong positive (negative) correlation, while converging to 0 indicates no systematic linear relationship between the estimations and references. However, it is important to note that a zero correlation does not necessarily imply the absence of any relationship between the variables; it simply means that there is no linear relationship [67]. DET quantifies the model’s goodness of fit and can be expressed as shown in Equation (38). It is a statistical metric that determines the proportion of the variance in the dependent variable that is explained by the independent variables in a regression model. Its value ranges from 0 to 1; convergence to 1 indicates that the simulation explains a greater proportion of the variability in the dependent variable [68]. The absolute value of the variation between the simulated ET magnitude and PM was defined as the MAE and calculated using Equation (39). The MAE values vary between 0 and +∞, with a value of 0 denoting perfect predictions. The MRE was utilized to evaluate the average relative difference between the estimated ET values relative to PM (Equation (40)). It is particularly useful for evaluating the accuracy of predictions in simulations in terms of over/under estimations and varies from −∞ to +∞ [64,69]. The MSE was preferred to measure the average squared difference between the estimated ET relative to the PM simulation. Equation (41) can be used to obtain this accuracy metric, and its values range from 0 to +∞. A zero MSE implies that the alternative ET methods perfectly match PM-driven ET values. MAE treats all errors equally, unlike MSE, which squares the errors and may assign more weight to large errors [63,70,71]. The NSCE is a widely used metric for assessing the performance of hydrological applications and can be expressed as shown in Equation (42). NSCE ranges from −∞ to 1, with higher values indicating better model performance and 1 being the ideal simulation [72]. The NNSCE error metric can be obtained by dividing the NSCE by a normalization factor to ensure that it remains between 0 and 1 (Equation (43)). The normalizing process makes the NSCE more interpretable, and the NNSCE is less affected by the scale of the data and is confined to a consistent range. The average tendency of the ET simulations to be larger or smaller than the reference ET can be measured by Bias (Equation (44)), and its values vary from −∞ (underestimation) to +∞ (overestimation) [73]. RMSD describes the difference between model simulations and reference ET in the units of the variable. Its values, which range from 0 to +∞, close to zero imply a perfect fit, while increases indicate an increment in the error in ET predictions [62,64].
As for the terms used in the statistical metrics formulae between Equations (36) and (45), NT indicates the total number of data, ETr,ti denotes the evapotranspiration values obtained based on the PM reference method at tith day, ETp,ti symbolizes the evapotranspiration estimates obtained according to the alternative estimation method at tith day, while and express the mean evapotranspiration values of the prediction and reference methods, respectively.
3. Results
The daily ET values for each station were estimated using the PM, PM0.5, BC, BCM, HM, HMM, HS, KH, and SC techniques, resulting in the box plot shown in Figure 3. A box plot visualizes the five-number summary of the dataset: the minimum, first quartile, median, third quartile, and maximum. The box plot was produced using the fourth-generation programming language MATLAB. Alternative methods are shown on the horizontal axis of the box plot in Figure 3, whereas evapotranspiration values in mm d−1 predicted using these approaches are displayed logarithmically on the vertical axis. As shown in the figure, days with missing data and negative ET values were not evaluated, while the extreme ET values and estimates between these values produced by each approach were presented with values from 0.001 to 100 mm d−1. As can be seen from the figure, PM-driven simulations were overestimated by the PM0.5-based approach over all districts, but the HM method, which displays a symmetrical box plot distribution, consistently underestimates the references in the study area. The positive results of the modifications to the BC method are shown in the graph. For example, the BCM approach yielded more effective outcomes than the BC method, which gave ET values within a narrow range when compared to the reference method over the region. Additionally, at numerous stations, the results acquired by the HMM technique were comparable to those obtained by the reference ETPM values, with higher performance than the HM approach, revealing the importance of modifications made to the HM equation.
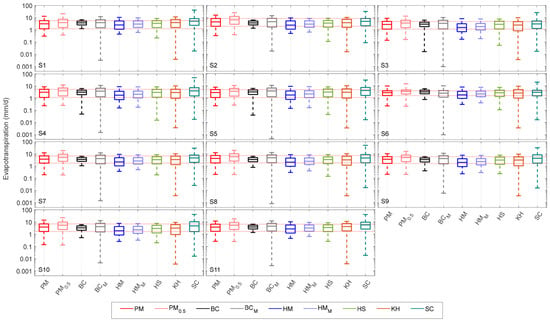
Figure 3.
Box plots of evapotranspiration from the various approaches for the 11 stations at the daily temporal resolution.
The ET values obtained were clustered in the range of 1 to 6 mm d−1 (between the lower and upper quartiles) at Kahramanmaras station (S1), where 22 years of comprehensive data are available, which means that half of all ET values are in this range, considering the PM technique used as reference. The PM0.5 approach results reveal that it slightly overestimates the ET values with respect to the reference PM method. The BC-driven ET values, shown in black, were aggregated in a narrower range at the S1 station relative to the reference method. The BC method simulated the minimum (maximum) ET values with overestimation (underestimation). It can be seen that the methods that give results close to the reference method at the S1 station are the HMM and HS approaches, although there are slight differences in the values of the whiskers. It is clear from the box plot of the HM approach with the best performance, shown in blue, that its quarters are distributed uniformly, and there is no skewness in the data to the PM technique. The upper outlier and interquartile range of the ET simulations produced by the BCM and KH methods—which are represented in gray and orange, respectively—produced similar findings to those of the reference method, but they had a longer minimum outlier owing to the underestimation of the small ET values. Overestimation is dominant in the maxima of SC-based ET predictions, whereas the opposite is true for smaller values less than one.
Additionally, the reference ET values for the S2 station, which had the least amount of accessible climatic data, were concentrated between 2 and 9.5 mm d−1. The BCM and SC techniques yield ET values within a similar range; nevertheless, the values obtained by both methods simulate the minimal ET values with strong underestimation. It can be seen that while the PM0.5 approach produces ET values with a comparable distribution to the reference method, as in the S1 station, it continually produces a slight overestimation. The findings can be made more accurate by multiplying the values by the calibration coefficients to minimize this bias. The BC-based ET values generated for the Dulkadiroglu district were clustered in a narrower range, similar to the results at the S1 station. Although different distributions are attained in the HM, HMM, HS, and KH approaches, where the maximum ET values are estimated to be close to each other, it has been observed that the underestimations are predominant compared with the PM reference method.
Moreover, as can be seen in the box plot of the S3 station, it can be seen that the HS method, shown in green, produces results substantially closer to the reference approach, although it slightly underestimates the minimum outlier. Although the ET values generated by the SC approach remained in the interquartile range compared to the reference method, the absolute values of the extreme ETs were higher. When the PM0.5 technique was examined in terms of distribution, it was observed that it was quite similar to the reference method, although it tended to yield slightly higher ET values compared to the reference method. The convergence of the BC-driven ET time series in the first and third quartiles clearly shows a concentration in a narrower range, similar to those from other stations. It has been noted that the BC, BCM, and KH approaches underestimated the minimum values for quartiles smaller than 0.05 at the S3 station. However, the BCM and KH approaches performed well in the interquartile range and higher whisker values. Although the HM and HMM methods capture ET values with very small variations in a negative way from the reference values, their distributions are similar to those in the PM.
In addition, when looking at the box plot of stations S4 and S5, the extreme ETs were close to one another, and the ET values computed using the reference technique were concentrated in a similar range. It was observed that the ET values acquired by the HS and KH techniques at both stations were concentrated in a similar range and captured the majority of the reference values, although the ET values smaller than the lower quartile were predicted with underestimation. Although the extreme ET values in whiskers simulated with the HM and HMM techniques were close to the reference values, it was observed that both stations estimated ET values with a slight constant underestimation in the interquartile range compared to the reference values. The BCM and SC methods produce overestimation (underestimation) ET values in the upper (lower) whisker compared to the reference method at both stations, while PM0.5-driven ET simulations overestimated ET values in all quartiles.
Additionally, ETPM values, varying between 1.8 and 4 mm d−1 for the interquartile range, were clustered in a narrower range relative to other stations, and they were captured using the HMM, HS, and SC approaches at the S6 station. While the PM0.5 and BC methods produce higher ET values for values between the 25th and 75th percentiles with respect to the PM technique, ETBC values are concentrated in a narrower range. Although it was discovered that the ETHM results were close to the reference for extreme values, these estimations clustered with underestimation until the median. Although BCM-based ET estimates produce values close to the PM, it has been monitored that this method underestimates ET values smaller than the 25th percentile. As can be seen from the figure, the box plot produced by the KH approach has a wider spread with a higher standard deviation, and ETKH values are simulated with a significant degree of bias in comparison to the reference method.
In the box plot of stations S7 and S8, where ETPM values are close to each other, it is seen that the ETBC simulations are similar to the other stations with the clustered in a narrower range. The ET values estimated by these two approaches are close to one another, and their maximum (minimum) values are simulated less (more) than those of the reference method. The PM0.5 model overestimated the reference ET values with a slight difference, similar to the previous six stations. In the Pazarcik and Caglayancerit districts, the formula that yielded the closest results to the reference method was the HS approach. The BCM, KH, and SC approaches, which simulated the minimum ET values up to the first quartiles with a high deviation compared to the reference method, captured the ETPM values at both stations for the values interquartile range. It can also be seen from Figure 3 that the evapotranspiration values obtained via the HM and HMM techniques had a more symmetrical distribution, even though the ET values at both stations underestimated the reference values.
At the S9 station, the interquartile range of reference ET values varies between 1.8 and 6 mm d−1, and the best performance was acquired with the ETHS formula. In the Ekinozu district, although the BCM, KH, and SC approaches underestimated the minimum ET values in the lower whisker with high deviation compared with the reference method, ETPM values were captured between the 25th and 75th percentiles. Underestimation is dominant in HM and HMM-driven predictions, and BC-driven simulations are concentrated in a narrower range with a small standard deviation, whereas KH-based values are spread over a wider range with a high standard deviation. In addition, while the ETBC values are in a narrower range with a small standard deviation in Nurhak and Turkoglu, the PM0.5 technique tends to overestimate evapotranspiration time series compared to the reference method, as in the other stations in general.
When the box plot of the S10 station was examined, while ETKH and ETSC values had high variance compared to ETPM, both methods underestimated evapotranspiration smaller than the median value, and strong overestimation was dominant in ETSC values greater than the median. The BCM approach revealed the most accurate results relative to the reference method at the S10 station (except for the lower whisker), while the best performance was obtained with HS at the S11 station, with insignificant underestimations in the upper whisker. Another result obtained from the figure is that HS, HM, and HMM-based estimates in the Nurhak district have a symmetric distribution and simulate ET values slightly less than the reference values. In the Turkoglu district, ET values in the interquartile range were captured by the BCM, HM, HMM, and KH approaches in addition to the ETHS formula. The graph also shows that the values in the lower than 25th percentile are underestimated by the BCM, KH, and SC techniques.
To investigate the impact of slope on evapotranspiration, its map was prepared using the DEM model via the Arc-GIS program, as seen in Figure 4a. When the slopes of Nurhak and Turkoglu were compared, it was observed that the slope of the district where the S10 station was located was steeper than S11. On the other hand, while low ET values were detected in Nurhak (1368 m) at high altitudes, a positive effect of the slope on ET was observed. Similarly, while the S8 station in Caglayancerit (1001 m) is expected to have lower ET values than the S7 station in Pazarcik (787 m) because of the significant altitude differences, it is believed that the higher slope of Caglayancerit contributes to an increase in ET. In addition, the altitude of the S5 station in Elbistan is 1137 m, and Nurhak ET values are higher than those of S5 and S7 despite the higher altitude. Although the district has a high altitude, its steep slope is predicted to have a directly proportional effect on ET.
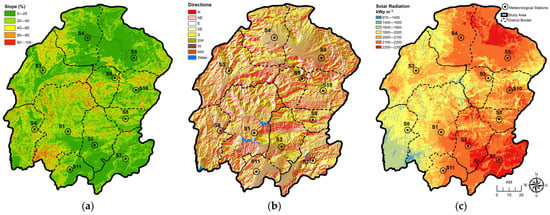
Figure 4.
(a) Kahramanmaras slope map; (b) Kahramanmaras aspect geography map; (c) Kahramanmaras solar radiation map.
While examining the effect of the slope on ET, an aspect geography map over the study area given in Figure 4b was prepared to take into account the direction in which the slope was formed and the angle of receiving sunlight to make more accurate evaluations. To further support and elucidate the aspect map assessments and identify any subtle variations on a station basis, the solar radiation map shown in Figure 4c was generated. The data connected to the prepared map via Arc-GIS were obtained from the internet portal developed by Solargis and financed by the Energy Sector Management Assistance Program (ESMAP) [74]. Larger ETPM values are found in S4, located in Afsin, even though the slopes of the S4 and S5 stations are close to one another when Figure 3 and Figure 4a are examined together. However, it becomes clear from the aspect map in Figure 4b that Afsin has more southern slopes and that these slopes have a positive impact on ET.
Additionally, examining the solar radiation maps of the two stations in Figure 4c, it can be concluded that Elbistan has significantly stronger solar radiation than Afsin; on the other hand, a slight discrepancy occurred in ET values of these stations due to the positive effect of solar radiation on ET. Upon analyzing the aspect (Figure 4b) and solar radiation (Figure 4c) maps of the districts containing the S2 (525 m) and S11 (535 m) stations with similar altitudes (Figure 2) and slopes (Figure 4a), it was observed that Dulkadiroglu had larger ETPM values (Figure 3) than Turkoglu because of the dominance of the southern slopes and high solar radiation. Moreover, when the slopes in Figure 4a of S1 (572 m) and S2 stations with similar heights were examined, it was revealed that the S1 station had a greater slope but exhibited lower ET values. This is because Dulkadiroglu has stronger solar radiation and more southern slopes, as shown in Figure 4b,c, and these two factors have a linear effect on ET.
When the ET values of the S8 (1001 m) and S9 (1246 m) stations, which have close slopes, were compared (Figure 2 and Figure 4a), higher ETs were reached in Caglayancerit because of their lower altitudes (Figure 3). It is also estimated that this may have been triggered because Caglayancerit has more southern slopes (Figure 4b) and higher solar radiation (Figure 4c) than Ekinozu. As another example, as can be seen in Figure 3, ET values in a similar range for S10 (1368 m) and S11 (535 m) stations (Figure 2), which have a high-altitude difference, reveal the importance of the slope (Figure 4a) and the abundance of southern slopes (Figure 4b) in evapotranspiration estimations. On the other hand, even though S5 (1137 m) and S6 (1108 m), whose station altitudes are close to one another, show no discernible differences in their aspect maps (Figure 4b), it is obvious that Andirin has a steeper slope (Figure 4a) and less solar radiation than Elbistan (Figure 4c). Thus, although Elbistan has a flatter land structure, high solar radiation resulted in larger evapotranspiration values in S5.
For the monthly variation analysis of alternative ET methods across Kahramanmaras in a general manner, Thornthwaite and Romanenko methods were added, and the combined ET values of all stations are presented with the scatter plot in Figure 5. The X- and Y-axes of the graph represent the monthly evapotranspiration values in mm d−1 for the reference PM and alternative approaches, respectively. In addition, the calculated monthly correlation value and linear trend line with its formula between the reference PM and other methods are displayed in the plots.
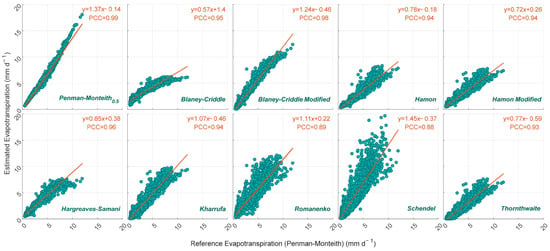
Figure 5.
Scatter plots of evapotranspiration from the various approaches and reference (PM) at the monthly average.
As can be seen from the scatter plot shown in Figure 5, the PM0.5 method has a strong positive correlation with the reference PM method with a PCC value of 0.99, while it estimates high ET values on a monthly basis more so than the references. While the BC-driven simulation revealed a correlation of 0.95, it overestimated (underestimated) low (high) ETPM values. This discrepancy became wider for values greater than 6 mm d−1. On the other hand, a significant improvement is observed in the BCM technique compared to the original method, and it estimates the reference values slightly higher with a strong correlation (0.98). Additionally, the scatter plots of the HM and HMM methods reveal similar results, with a correlation of 0.94 in both methods. Unlike other methods, the two equations, which include water vapor density, tend to underestimate ETPM values.
The HS approach has a PCC value of 0.96, indicating a strong positive relationship with the PM method, whereas it underestimates the maximum extremes in ET estimations relative to the reference values. As can be seen in the box plot in Figure 3, although KH estimated the minimum ET values lower than the references, it is observed that the trend line in the scatter plot in Figure 5, obtained with monthly values with high standard deviation, produces similar results compared to the reference method with 0.94 correlation and yields an approximate slope of 1:1. As can be seen from Figure 5, the RM and SC methods show the highest variance and have correlation values of 0.89 and 0.88, respectively. In general, overestimation is dominant in the RM and SC formulae, and the SC method performs the poorest due to the significantly higher inconsistency in the maximum ET values. The results show that the monthly average temperature-driven ETTH simulation underestimates the reference ETPM values, while it has a lower standard deviation in its distribution compared to the other monthly methods, RM, and a strong PCC value of 0.93.
Figure 6a was obtained to evaluate the CRMSE index of eight different ET estimation methods, which vary between 10.63 and 91.69%, at 11 stations in Kahramanmaras. The BCM-based simulations at the S2 station produced the lowest CRMSE of 10.63% among all values, whereas the HS technique at stations S1, S3, S4, S5, and S9 reached the lowest value. The best results in terms of CRMSE performance are seen to be the KH method, with values of 19.73% and 19.16% at stations S7 and S8, respectively. Moreover, the PM0.5, BCM, and HM methods produced lower CRMSE values than the other methods at stations S6, S10, and S11, respectively. It was also noted that the SC technique, which ranged from 34.94 to 91.69%, showed the worst performance compared with other approaches at all stations.
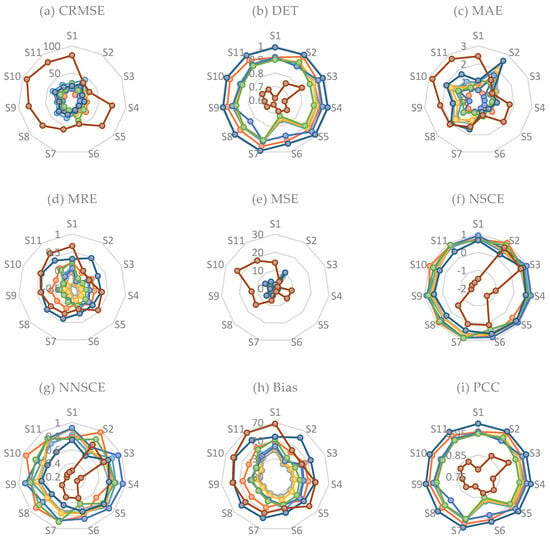
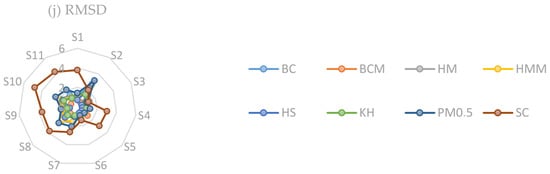
Figure 6.
Variation of statistical metrics. (a) centered root mean square error; (b) determination coefficient; (c) mean absolute error; (d) mean relative error; (e) mean squared error; (f) Nash–Sutcliffe coefficient of efficiency; (g) normalized Nash–Sutcliffe coefficient of efficiency; (h) percent bias; (i) Pearson’s correlation coefficient; (j) root mean square deviation.
Examining Figure 6b, which demonstrates the variation of the determination coefficient, reveals that the PM0.5 approach is the most consistent with the reference method, having the highest DET values (0.94–1) at all stations. On the other hand, the obtained results detect that the SC technique has the lowest DET values ranging from 0.61 to 0.82. The highest DET values, after PM0.5 simulations, were produced with the BC method at the S1 station; the HS method at stations S3, S4, and S5; and the BCM method at the other seven stations.
Additionally, the distribution of the MAE index values, which had the same unit (mm d−1) as evapotranspiration, is shown in Figure 6c. Even though the BCM has the lowest MAE values at S2, S8, and S10, the HS technique is the most successful approach since it shows the least absolute difference at the other eight stations. Although the methods with the highest MAE differ depending on the station, the SC technique has the worst MAE performance at the six stations.
When the results were evaluated according to the MRE index, one of the indices frequently used in performance assessments, BCM showed the best overall result (Figure 6d). The HMM method has the highest accuracy, with an MRE value of 0.0 at station S1, whereas negative MRE values indicate an underestimation tendency at other stations. In general, the PM0.5 and SC (HM and KH) techniques with positive (negative) MRE values overestimated (underestimated) ET compared to the reference method.
The MSE error metric results for the eleven stations are presented in Figure 6e. While the lowest performance is achieved with SC, surprisingly, the PM0.5 values are the highest MSEs after SC. Upon examining the results per station, it is seen that the BCM approach at stations S2, S8, and S10; the KH method at station S7; and the HS technique at the other seven stations have the least error with MSE values closest to zero.
In Figure 6f, the NSCE statistical index is used to evaluate the predictive accuracy of evapotranspiration algorithms. As can be seen from the graph, NSCE values indicated performance higher than 0.5 across stations and methods except for the SC technique, while negative NSCE values were captured for SC methods (except S2 and S3). While the BCM method exhibited the best performance at stations S2, S7, S8, and S10, this method reached the highest NSCE value at station S2 with a value of 0.98. The HS method produced the closest result to the reference values for the other seven stations.
NNSCE is an extension of NSCE and is used as a benchmark metric, allowing for easier comparison and interpretation (Figure 6g). NNSCE performed furthest from the reference method were HM in S3, PM0.5 in S2, and the SC method in the other nine stations. At stations S2, S7, S8, and S10, the BCM method yields accurate results by giving the NNSCE value closest to one, and the KH method converges to 0.9 at station S7. As can be observed from the NNSCE index, the HS technique worked well for the remaining seven stations.
It is observed from Figure 6h that while the BCM, PM0.5, and SC methods, overall, take positive Bias values, indicating a tendency to overestimate, underestimation is more dominant in KH, HM, and HMM approaches with general negative Bias values. Another noteworthy point when the results are examined in terms of the Bias error metric is that the BCM and KH methods have performances closest to zero at the majority of the stations.
The PCC results are given in Figure 6i, and it can be seen that the strongest positive correlation is the PM0.5 method, ranging between 0.97 and 1.00, while the lowest is the SC technique, varying between 0.78 and 0.91.
Figure 6j displays the variation in the RMSD metric at 11 stations, which has the same unit as evapotranspiration as the MAE performance assessment index. As can be seen from the figure, while the BCM method performed better than the other empirical formulae with RMSD values closest to zero at stations S2, S8, and S10, the KH approach showed a successful performance at station S7. The figure indicates that for the other seven stations, the HS method produced RMSD values with a discrepancy of only a maximum of 1 mm d−1. The HS (SC) method achieved the best (worst) performance among all the methods at station S3 (S10) with an RMSD value of 0.49 (4.80) mm d−1.
4. Discussion
As can be seen from the box plot in four equal quartiles, information was obtained regarding the extremes of ET values, the range in which they were clustered, and their distribution. The BCM, KH, and SC-based ET simulations underestimated minimum values smaller than the 25th percentile relative to the ETPM. Saud et al. [75] analyzed the spatiotemporal variation of several methods over Al-Anbar province, western Iraq. They found that the Kharrufa equation tended to underestimate ET values, similar to the above-mentioned finding. On the other hand, the SC method tends to predict maximum extreme ET values larger than the third quartile than the reference method. The performance of the PM0.5 approach was higher for the minimum ET values, which were especially smaller than the lower quartile. However, it produces more ET values, albeit with a slight difference, at larger ET values compared with the reference technique. Additionally, the ETBC values were clustered in a narrower range than the reference ET values with smaller standard deviations. It was concluded that the BCM method produced more successful results than the BC method, showing values close to those of the PM method for values greater than the lower quartile. As a matter of fact, in this sense, the positive effect of the modifications on the BC-based ET equation was observed, as in the previous studies [14,76]. It is also understood that the ET values obtained with the HM and HMM approaches have a more symmetrical distribution; however, the HM method underestimates ETPM at all stations, whereas the modified HM method achieves more successful results than the original HM method. The results of these two modified equations support the importance of adjustment in the original formulae [77,78,79]. For example, Proutsos et al. [19] evaluated 127 ET approaches in Mediterranean urban green sites and concluded that the adjusted models performed more accurate ET simulations overall compared to the original equations. Compared to other techniques, the HS method produces results that are closest to the reference ETPM when examining the box plot of the method at all stations.
The graphs and maps were analyzed to see how altitude, slope, aspect geography, and solar radiation affected the evapotranspiration values. The results showed that evapotranspiration varies proportionally with the impact of altitude on Kahramanmaras. The results support the findings of Lin et al. [80] regarding ET correlation with topography in the Xiliao River Plain, while the outcomes are different from those reported by Ablikim et al. [81], in which ET values rise with the increment in altitude in the Urumqi River Basin. For instance, the reason for the high ET values in S2, which has the lowest altitude of 525 m, is thought to be the adverse effect of altitude on ET. The observation of lower ET values at the S3 station, which has a higher elevation (1344 m) than the S2 station, shows that the same effect occurs. The fact that the S9 station, at an altitude of 1246 m, had lower ET values relative to the S8 station at an altitude of 1001 m supports this effect. As S7 (787 m) exhibited smaller ET values than S2 and S11, which have altitudes of 535 m, it is another example that elevation has an adverse effect on ET. While station S1 (572 m) had smaller ET values relative to the S2 station, indicating the impact of altitude, a larger discrepancy in ET values was observed in response to the minor elevation differences. On the other hand, despite the high-altitude variation between stations S1 and S3 (572 m/1344 m), the difference between the ET values of both stations was lower. Similar results were observed at stations between S10 (1368 m) and S11 (535 m) and between S7 (787 m) and S8 (1001 m). These results reveal that the inverse proportion of altitude on ET may vary depending on altitude and that factors other than elevation may also be effective for ET. For this aim, considering previous studies showing that distributions of slope and aspect may have an effect on evapotranspiration, slope, aspect geography, and solar radiation maps, these were also investigated by correlating with ET [82,83,84]. A strong correlation with ET has been observed on the southern slopes, and solar radiation is another factor controlling ET. Among all the stations, for example, S6, which has a narrow ET distribution with a minor standard deviation and stands out with its low ET values compared to other stations, appears to have the lowest solar radiation. As another example, it is recognized that the S2 station at the lowest altitude exhibits the highest ET values as a result of all these factors, such as the fact that it has a more southern slope compared to other stations and intense solar radiation, in addition to its steeper slope.
Additionally, within the scope of this study, the combined performances of all methods across the city were examined on a monthly basis using a scatter plot. For instance, the Schendel approach produced ET values at some stations that were similar to the reference method, as can be seen from the box plot; on the other hand, the method yielded the lowest performance of all the alternative methods over the entire city when the monthly based scatter plot was examined. Both the BC and TH techniques underestimated ETPM reference values, while an overestimation tendency was observed for the PM0.5 method, although the highest correlation was achieved with it. As stated in the methodology section, the modified Blaney–Criddle approach applies parameters computed using the minimum relative humidity, ratio of actual sunshine to the maximum possible sunshine duration, and daytime wind speed instead of the seasonal crop coefficient used in the original method. This resulted in a significant improvement in the evapotranspiration estimations, as seen from the scatter plot. In the Hamon methods, which tend to underestimate ET, the modified version produced better ET values than the original equation. This graph reveals the importance of modification analysis more clearly and supports the results of previous studies [14,76,77,78]. Another important result obtained from the scatter plot is that the KH method, which tends to predict lower daily ET minimum extremes, showed a high performance in monthly simulations across the city. Additionally, the HS method produced the best result by providing a high correlation, although it underestimated the maximum extreme values.
The performances of the ET approaches on a daily scale were computed and graphed using ten various statistical criteria to enhance the evaluation of the methods to be more detailed and sensitive for each station. As can be seen from the NSCE results, a value higher than 0.5 demonstrates that alternative approaches (except SC) can sufficiently replicate the variability of the ETPM. Conversely, negative NSCE values indicate that for SC-driven simulations at the stations, the mean of the ETPM values is a better predictor than the SC empirical method. The main difference for NNCSE lies in the normalization of the NSCE value, which helps NNSCE to be less sensitive to the variability in the reference data and allows for better comparison across other empirical approaches, regardless of its variance. The highest NSCE and NNSCE values were obtained with BCM-driven simulations in S2, S8, and S10, whereas the best results were yielded with ETHS estimations in S7, and it is the HS method at the other seven stations. The obtained findings were observed more clearly in the NNSCE graph. It is essential to note that while the NSCE is a crucial error metric for measuring predictive accuracy, it has some limitations. For instance, it gives equal weight to both overestimation and underestimation errors, which might not always reflect the true importance of such errors in the direction of discrepancy. In comparison to ETPM, in general, the underestimation is more dominant in Hargreaves–Samani, Kharrufa, and both Hamon equations with negative MRE values, whereas the BCM, PM0.5, and SC techniques overestimated the reference values with positive MRE indices. These results are seen more clearly in the Bias metric. Additionally, overall, HS, BCM, and KH-driven simulations yielded the best MSE, CRMSE, and RMSD results, while the PM0.5 (SC) method had the highest (lowest) value at all stations according to the DET metric. All approaches, excluding SC, have strong positive correlations greater than the PCC value of 0.9 at all stations except for S6. The BC (HS) technique exhibits the highest PCC values in S1 (S3, S4, and S5) after the PM0.5 approach, while the BCM method, in S2 and the six stations between S6 and S11, is secondary in terms of PCC performance.
However, this study has some limitations; for instance, in addition to the aforementioned factors, ET may also be affected by elements such as vegetation cover, soil map, land use, and land cover belonging to the relevant study area, and they were not evaluated within the scope of this study. Despite these limitations, the results of this study can help future studies mitigate the effects of drought and the prejudice of hydrological modeling results over the study area. Furthermore, the findings motivate future studies to analyze how well alternative empirical approaches are performed in other areas with features comparable to the analyzed region.
5. Conclusions
Empirical approaches for calculating ET values hold a significant place in the literature because of their advantages, such as simplicity of use when utilizing meteorological data and obtaining results in a short time. Evapotranspiration may be quantitatively assessed using a variety of techniques. Numerous studies have been conducted to find the most straightforward and accurate method that can be applied in various study regions, and these have been updated in response to evolving circumstances. In this study, evapotranspiration simulations carried out various techniques such as Penman–Monteith, Penman–Monteith at 0.5 m, Blaney–Criddle, modified Blaney–Criddle, Hamon, modified Hamon, Hargreaves–Samani, Kharrufa, Schendel, Romanenko, and Thornthwaite using daily meteorological data from stations in 11 districts of Kahramanmaras province. In evaluating the alternative methods at daily and monthly temporal resolutions, the Penman–Monteith method, recommended by the Food and Agriculture Organization for use worldwide, was considered as a reference.
A box plot was generated using ET values derived from daily scale estimations utilizing the PM, PM0.5, BC, BCM, HM, HMM, HS, and KH, along with SC methods, and assessments were conducted on a station basis. The HM method, which shows a symmetrical box plot distribution, underestimated the ETPM over the region, while the PM0.5 method overestimated the reference ETPM values at all stations. In contrast to the BC method, which produced ET values in a narrow range compared with the reference method in the 11 districts, the BCM method produced more successful results. The HMM method, which has a symmetrical box plot distribution, produced results close to those of the reference method at some of the stations, indicating that the modification of the HM method was positively reflected. Additionally, underestimation is dominant in minimum whisker ET values obtained from BCM, KH, and SC-driven simulations. In the Onikisubat district, the HM, HMM, and HS methods yielded the highest performances among the other methods. Although the BCM, KH, and SC techniques underestimated the minimum extremes, they generally overestimated ET values compared to the reference method. In Dulkadiroglu, where the highest ET values were produced among all stations, the approaches that gave the closest results to the reference method for the interquartile range were the BCM, KH, and SC. In the Goksun district, BCM, HS, KH, and SC-based ET simulations captured ETPM variations greater than the 25th percentile, whereas they predicted the minimum ET values to be lower. It was concluded that the HS and KH approaches, which underestimated the minimum outliers, provided the closest results to the reference method in the districts of Afsin and Elbistan, where similar ET values were achieved. For Andirin, where ET fluctuations were in the lowest range among all stations, the HS and SC methods produced the most accurate results for ETPM values in the interquartile range. The HS method, which slightly underestimated the reference ET values, exhibited the highest accuracy in Pazarcik, Caglayancerit, and Ekinozu districts. In Nurhak, the BCM method was the most successful, slightly underestimating the minimum ETPM outliers, while the second-highest performance belonged to the HS simulations with underestimation relative to the reference method. Finally, in the Turkoglu district, the HMM and HS methods produced results similar to those of the reference method.
To evaluate the statistical performance of the methods on a daily scale, the central square mean error, determination coefficient, mean absolute error, mean relative error, mean squared error, Nash–Sutcliffe efficiency coefficient, normalized NSCE, percentage error, Pearson’s correlation coefficient, and root mean square error metrics were applied. According to the CRMSE index, the HS method had the lowest values in Onikisubat, Goksun, Afsin, Elbistan, and Ekinozu, whereas the BCM approach achieved the highest performance in Dulkadiroglu and Nurhak. Additionally, KH resulted in the smallest CRMSE in Pazarcik and Caglayancerit, whereas PM0.5 and HM were the best in Andirin and Turkoglu, respectively. The PM0.5 approach performed well at all stations based on the DET and PCC metrics because of its similarity with the reference method, although SC-based simulations produced the lowest values. After the PM0.5-driven performance, the methods showing the highest correlations are the HS method at Onikisubat, Goksun, Afsin, and Elbistan, similar to the CRMSE metric, whereas the BCM approach has the highest at other stations. Moreover, the most successful results were obtained via the BCM approach in Dulkadiroglu, Caglayancerit, as well as Nurhak, and the HS method yielded MAE values less than 0.5 mm d−1 at other stations, while the SC and PM0.5 formulae produced strong discrepancy in terms of MAE. An underestimation tendency is observed in the HM, HMM, and KH methods with negative MRE and Bias indices, while the PM0.5 and SC methods overestimated the ETPM values. Additionally, the BCM and HS techniques are generally the ones that are closest to zero, while the methods with the least error vary based on the stations in terms of MRE and Bias metrics. MSE and MRE produced comparable outcomes, and SC-based ET simulations performed the poorest in terms of both statistical indices. The RMSD values more clearly displayed inconsistencies and corroborated those derived from the MSE index. Additionally, the lowest performances were obtained with SC and PM0.5 formulae, while other methods generally received NSCE values greater than 0.7 and BCM, HS as well as KH-driven ET predictions exhibited the best NSCE values. The negative NSCE values in the SC-driven simulations indicated that the model did not capture the variability and patterns present in the reference value. This finding typically means that SC predictions perform poorly and might be less accurate than simply using the mean of the ETPM data as a prediction. NNSCE performances support these results and reveal the variation in accuracy/discrepancy on a station basis more clearly.
In this study, the monthly averages of ET values generated by the TH and RM techniques—which can compute ET on a monthly scale—as well as the daily ET values produced by other methods, were utilized to build a scatter plot. An overestimation tendency is observed for the PM0.5 approach, with the strongest correlation value of 0.99 for the reference among the alternative methodologies. The approach that generates the ET value at a height of 50 cm is likely to have been overestimated as a result of the standardized as a result of coefficient modifications in the original PM equation. The ETBC values were clustered, ranging from 1.82 to 6.15 mm d−1, and the BC model overestimated low ET values, whereas it underestimated high ET values relative to ETPM values. On the other hand, the modified BC version used the “a” and “b” coefficients computed depending on various climatic parameters (i.e., relative humidity, wind speed, and sunshine duration) instead of the “k” seasonal crop coefficient in the formula and yielded significant improvement in the results. After this adjustment, it was concluded that the BCM approach, which has the second highest correlation with a PCC value of 0.98, can be used as an alternative to the PM method over many districts in the region. Although the HM and HMM techniques involving water vapor density underestimated the ETPM values with an identical PCC (0.94), unlike other alternative methods, the modified version produced better results than the original Hamon formula. Furthermore, even though the 1.2 local calibration coefficient improved the results in the equations of both techniques, it is anticipated that regional and seasonal modifications to the included coefficient will improve the accuracy of the ET estimations. In addition, the HS approach produced ET values that were similar to the reference method throughout Kahramanmaraş, demonstrating a successful performance with a low bias between ETPM and ETHS and a high correlation of 0.96 PCC. The KH technique, in which the linear trend line is close to that of the PM method with a PCC value of 0.94, produced accurate ETPM at some stations, although it had higher noise in overall ET estimates. Moreover, the TH method, which underestimates ET values compared to the reference method, showed a high correlation with a PCC value of 0.93. Among all alternative empirical approaches, SC and RM methods generated the highest deviation in the simulations relative to the ETPM values and smallest PCC values of 0.88 and 0.89, respectively. Additionally, both methods tended to overestimate the evapotranspiration time series compared with the reference method. Examining the equations for both methods revealed that ET values were derived only from the average temperature and relative humidity data. However, the majority of other alternative formulae are functions of sunshine duration in addition to the aforementioned parameters, and coefficients derived depending on sunshine duration are also enhanced in the correlation.
Within the scope of this study, where the impact of terrain characteristics and altitude on ET was also assessed, a slope, aspect geography, and solar radiation map of the study area were prepared. It was concluded that altitude has an adverse effect on ET, although the evaluation of altitude alone might not be comprehensive except in rare circumstances. Upon evaluating the aspect, slope, and solar radiation maps in this manner on a station basis, it was observed that the slope positively impacted ET. While the southern slopes of the slope are another factor that increases ET, it has been detected that interconnected solar radiation raises ET. Along with these elements in terrain characteristics, examining the effects of land use and vegetation on ET can motivate future studies.
In light of all examinations and evaluations, it can be concluded that the BCM and HS approaches can be utilized as alternatives to the PM method in estimating evapotranspiration values over Kahramanmaras province. Additionally, the KH technique, which only employs temperature data, can be listed as an alternative for accurately capturing ETs. While the worst results in the region were obtained with SC-driven ET simulations, the PM0.5 method consistently overestimated the ETPM values despite having a high correlation. Investigating the effectiveness of the alternative empirical methodologies assessed in this study in other locations with features comparable to the region is another matter that can attract attention. The obtained ET results will play a significant role in the planning of areas for agriculture and forestry, in determining the usable water potential of dams, in the accurate estimation of water losses in rainfall-runoff simulations, and in hydrometeorological applications such as forecasting drought or flood predictions.
Author Contributions
A.U.: material preparation, data collection, analysis, and manuscript writing. M.O.D.: collecting meteorological data, evaluating analysis, interpretation of the findings, manuscript writing, supervising, editing, and submission. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data of this study are available from the authors upon request.
Acknowledgments
The authors want to thank Kahramanmaras Sutcu Imam University and the Turkish State Meteorological Service for their support and data collection.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization of the UN: Rome, Italy, 1998; Available online: http://www.climasouth.eu/sites/default/files/FAO%2056.pdf (accessed on 23 June 2023).
- Srdic, S.; Srdevic, Z.; Stricevic, R.; Cerekovic, N.; Benka, P.; Rudan, N.; Rajic, M.; Todorovic, M. Assessment of Empirical Methods for Estimating Reference Evapotranspiration in Different Climatic Zones of Bosnia and Herzegovina. Water 2023, 15, 3065. [Google Scholar] [CrossRef]
- Su, Q.; Dai, C.; Zhang, Q.; Zhou, Y. Analysis of Potential Evapotranspiration in Heilongjiang Province. Sustainability 2023, 15, 15374. [Google Scholar] [CrossRef]
- Yang, H.; Luo, P.; Wang, J.; Mou, C.; Mo, L.; Wang, Z.; Fu, Y.; Lin, H.; Yang, Y.; Bhatta, L.D. Ecosystem Evapotranspiration as a Response to Climate and Vegetation Coverage Changes in Northwest Yunnan, China. PLoS ONE 2015, 10, e0134795. [Google Scholar] [CrossRef]
- Yue, P.; Zhang, Q.; Ren, X.; Yang, Z.; Li, H.; Yang, Y. Environmental and biophysical effects of evapotranspiration in semiarid grassland and maize cropland ecosystems over the summer monsoon transition zone of China. Agric. Water Manag. 2022, 264, 107462. [Google Scholar] [CrossRef]
- Dingman, S.L. Physical Hydrology, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002; 646p. [Google Scholar]
- Liu, W.; Zhang, B.; Han, S. Quantitative Analysis of the Impact of Meteorological Factors on Reference Evapotranspiration Changes in Beijing, 1958–2017. Water 2020, 12, 2263. [Google Scholar] [CrossRef]
- Qiu, L.; Wu, Y.; Shi, Z.; Chen, Y.; Zhao, F. Quantifying the Responses of Evapotranspiration and Its Components to Vegetation Restoration and Climate Change on the Loess Plateau of China. Remote Sens. 2021, 13, 2358. [Google Scholar] [CrossRef]
- Penman, H.L. Evaporation: An introductory survey. Neth. J. Agric. Sci. 1956, 4, 9–29. [Google Scholar] [CrossRef]
- Yates, D.; Strzepek, Z. Potential Evapotranspiration Methods and their Impact on the Assessment of River Basin Runoff Under Climate Change; IIASA Working Paper; IIASA: Laxenburg, Austria, 1994; pp. 46–94. Available online: https://pure.iiasa.ac.at/id/eprint/4163/1/WP-94-046.pdf (accessed on 16 June 2023).
- Verstraeten, W.W.; Veroustraete, F.; Feyen, J. Assessment of Evapotranspiration and Soil Moisture Content Across Different Scales of Observation. Sensors 2008, 8, 70–117. [Google Scholar] [CrossRef]
- McMahon, T.A.; Peel, M.C.; Lowe, L.; Srikanthan, R.; McVicar, T.R. Estimating actual, potential, reference crop and pan evaporation using standard meteorological data: A pragmatic synthesis. Hydrol. Earth Syst. Sci. 2013, 17, 1331–1363. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An Approach toward a Rational Classification of Climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Uzunlar, A.; Oz, A.; Dis, M.O. The Effect of Modified Approaches on Evapotranspiration Estimates: Case Study over Van. Cukurova UMFD 2022, 37, 973–988. [Google Scholar] [CrossRef]
- Meissner, R.; Rupp, H.; Haselow, L. Chapter 7—Use of lysimeters for monitoring soil water balance parameters and nutrient leaching. In Climate Change and Soil Interactions; Elsevier: Amsterdam, The Netherlands, 2020; pp. 171–205. [Google Scholar] [CrossRef]
- Brown, S.; Wagner-Riddle, C.; Debruyn, Z.; Jordan, S.; Berg, A.; Ambadan, J.T.; Congreves, K.A.; Machado, P.V.F. Assessing variability of soil water balance components measured at a new lysimeter facility dedicated to the study of soil ecosystem services. J. Hydrol. 2021, 603 Pt C, 127037. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw Hill: Singapore, 1988; 572p. [Google Scholar]
- López-Olivari, R.; Fuentes, S.; Poblete-Echeverría, C.; Quintulen-Ancapi, V.; Medina, L. Site-Specific Evaluation of Canopy Resistance Models for Estimating Evapotranspiration over a Drip-Irrigated Potato Crop in Southern Chile under Water-Limited Conditions. Water 2022, 14, 2041. [Google Scholar] [CrossRef]
- Proutsos, N.; Tigkas, D.; Tsevreni, I.; Alexandris, S.G.; Solomou, A.D.; Bourletsikas, A.; Stefanidis, S.; Nwokolo, S.C. A Thorough Evaluation of 127 Potential Evapotranspiration Models in Two Mediterranean Urban Green Sites. Remote Sens. 2023, 15, 3680. [Google Scholar] [CrossRef]
- Ashour, M.A.; Abdel Nasser, M.S.; Abu-Zaid, T.S. Field Study to Evaluate Water Loss in the Irrigation Canals of Middle Egypt: A Case Study of the Al Maanna Canal and Its Branches, Assiut Governorate. Limnol. Rev. 2023, 23, 70–92. [Google Scholar] [CrossRef]
- Dis, M.O. A New Approach for Completing Missing Data Series in Pan Evaporation Using Multi-Meteorologic Phenomena. Sustainability 2023, 15, 15542. [Google Scholar] [CrossRef]
- Gourgouletis, N.; Gkavrou, M.; Baltas, E. Comparison of Empirical Eto Relationships with ERA5-Land and In Situ Data in Greece. Geographies 2023, 3, 499–521. [Google Scholar] [CrossRef]
- Penman, H.L. Natural Evaporation from Open Water, Bare Soil and Grass. Proc. Math. Phys. Eng. Sci. P Roy Soc. A-Math. Phys. 1948, 193, 120–145. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar]
- Shuttleworth, W.J.; Wallace, J.S. Evaporation from sparse crops-an energy combination theory. Quart. I. R. Met. Soc. 1985, 111, 839–855. [Google Scholar] [CrossRef]
- Calder, I.R. Transpiration observations from a spruce forest and comparisons with predictions from an evaporation model. J. Hydrol. 1978, 38, 33–47. [Google Scholar] [CrossRef]
- Jensen, M.E.; Burman, R.D.; Allen, R.G. Evapotranspiration and Irrigation Water Requirements; ASCE: New York, NY, USA, 1990; 332p. [Google Scholar]
- Lemeur, R.; Zhang, L. Evaluation of three evapotranspiration models in terms of their applicability for an arid region. J. Hydrol. 1990, 114, 395–411. [Google Scholar] [CrossRef]
- Althoff, D.; Santos, R.A.d.; Bazame, H.C.; Cunha, F.F.d.; Filgueiras, R. Improvement of Hargreaves–Samani Reference Evapotranspiration Estimates with Local Calibration. Water 2019, 11, 2272. [Google Scholar] [CrossRef]
- Lin, E.; Qiu, R.; Chen, M.; Xie, H.; Khurshid, B.; Ma, X.; Quzhen, S.; Zheng, S.; Cui, Y.; Luo, Y. Assessing forecasting performance of daily reference evapotranspiration: A comparative analysis of updated temperature penman-monteith and penman-monteith forecast models. J. Hydrol. 2023, 626, 130317. [Google Scholar] [CrossRef]
- Doorenbos, J.; Pruitt, W.O. Crop Water Requirements, FAO Irrigation and Drainage Paper 24; Food and Agriculture Organization of the United Nations, Viale delle Terme di Caracalla: Rome, Italy, 1977; 144p, Available online: https://www.fao.org/3/s8376e/s8376e.pdf (accessed on 23 January 2023).
- Brouwer, C.; Heibloem, H. Irrigation Water Management: Irrigation Water Needs, Irrigation Water Management Training Manual No. 3; Land and Water Development Division FAO Via delle Terme di Caracalla: Rome, Italy, 1986; Available online: https://www.fao.org/3/S2022E/s2022e00.htm (accessed on 23 January 2023).
- Singh, V.; Xu, C. Evaluation and generalization of 13 mass-transfer equations for determining free water Evaporation. Hydrol. Process. 1997, 11, 311–323. [Google Scholar] [CrossRef]
- Tabari, H.; Grismer, M.E.; Trajkovic, S. Comparative analysis of 31 reference evapotranspiration methods under humid conditions. Irrig. Sci. 2011, 31, 107–117. [Google Scholar] [CrossRef]
- Sarlak, N.; Bagcaci, S.C. The Assessment of Empirical Potential Evapotranspiration Methods: A Case Study of Konya Closed Basin. Teknik Dergi 2020, 565, 9755–9772. [Google Scholar] [CrossRef]
- Song, X.; Lu, F.; Xiao, W.; Zhu, K.; Zhou, Y.; Xie, Z. Performance of 12 reference ET estimation method compared with the Penman-Monteith method and the potential influences in northeast China. Meteorol. Appl. 2018, 26, 83–96. [Google Scholar] [CrossRef]
- Cobaner, M.; Citakoglu, H.; Haktanir, T.; Yelkara, F. Determination of optimum Hargreaves-Samani equation for Mediterranean region. DUMF 2016, 7, 181–190. [Google Scholar]
- Hafeez, M.; Chatha, Z.A.; Khan, A.A.; Gulshan, A.B.; Basit, A.; Tahira, F. Comparative Analysis of Reference Evapotranspiration by Hargreaves and Blaney-Criddle Equations in Semi-Arid Climatic Conditions. Curr. Res. Agric. Sci. 2020, 7, 525–557. [Google Scholar] [CrossRef]
- USGS Geographic Information Systems, Digital Elevation Model Data Website. Available online: https://earthexplorer.usgs.gov/ (accessed on 3 May 2023).
- Sarigul, O.; Turoglu, H. Flashflood and Flood Geographical Analysis and Foresight in Kahramanmaraş City. J. Geogr. 2020, 40, 275–293. [Google Scholar] [CrossRef]
- Directorate General of Environmental Impact Assessment, Permit and Inspection. Kahramanmaras City 2021 Year Environmental Status Report. Republic of Turkiye Ministry of Environment, Urbanization and Climate Change. 2021. Available online: https://webdosya.csb.gov.tr/db/ced/icerikler/k.-maras-ilcdr-2021-20220706104818.pdf (accessed on 23 January 2023).
- Cinar, M. Investigation of Mechanical and Physical Features of Cementitious Jet Grout Applications for Various Soil Types. Buildings 2023, 13, 2833. [Google Scholar] [CrossRef]
- MEVBIS, The Meteorological Data Information Presentation and Sales System User’s manuel, the Turkish State Meteorological Service, TC Orman ve Su Isleri Bakanligi, Ankara, Turkiye, 49, March 2017. Available online: https://mevbis.mgm.gov.tr/mevbis/ui/HelpMenu/MEVBIS_Kullanim_Kilavuzu.pdf (accessed on 22 July 2022).
- Ceyhan, Z.N.; Dis, M.O. Determining the Future Population of Kahramanmaras via Multiple Projection Methods. Cukurova UMFD 2022, 37, 1155–1164. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Estimating Potential Evapotranspiration. J. Irrig. Drain. Div. 1982, 108, 225–230. [Google Scholar] [CrossRef]
- ASCE-EWRI. The ASCE Standardized Reference Evapotranspiration Equation; Technical Committee Report to the Environmental and Water Resources Institute of the American Society of Civil Engineers from the Task Committee on Standardization of Reference Evapotranspiration; ASCE-EWRI: Reston, VA, USA, 2005; 173p. [Google Scholar]
- Blaney, H.F.; Morin, K.V. Evaporation and Consumptive Use of Water Empirical Formulas. Trans. Am. Geophys. Union 1942, 23, 76–83. [Google Scholar] [CrossRef]
- Blaney, H.F.; Criddle, W.D. Determining Water Requirements in Irrigation Areas from Climatological and Irrigation Data; United States Department of Agriculture, Soil Conservation Service: Washington, DC, USA, 1950; 48p. Available online: https://ia800300.us.archive.org/4/items/determiningwater96blan/determiningwater96blan.pdf (accessed on 22 July 2022).
- Blaney, H.F.; Criddle, W.D. Determining Consumptive Use and Irrigation Water Requirements; Technical Bulletin No. 1275; United States Department of Agriculture in Cooperation with the Office of Utah State Engineer: Washington, DC, USA, 1962; 59p.
- Frevert, D.K.; Hill, R.W.; Braaten, B.C. Estimation of FAO evapotranspiration coefficients. J. Irrig. Drain. Eng. 1983, 109, 265–270. [Google Scholar] [CrossRef]
- Allen, R.G.; Pruitt, W.O. FAO-24 Reference Evapotranspiration Factors. J. Irrig. Drain. Eng. 1991, 117, 758–772. [Google Scholar] [CrossRef]
- Hamon, W.R. Estimating Potential Evapotranspiration. J. Hydraul. Div. 1961, 87, 107–120. [Google Scholar] [CrossRef]
- Hamon, W.R. Computation of Direct Runoff Amounts from Storm Rainfall; Research Cooperative with the University of Mississippi and Mississippi State University: Starkville, MS, USA, 1963; pp. 52–62. Available online: https://iahs.info/uploads/dms/063006.pdf (accessed on 29 November 2023).
- Lu, J.; Sun, G.; McNulty, S.G.; Amatya, D.M. A comparison of six potential evapotranspiration methods for regional use in the Southeastern United States. JAWRA J. Am. Water Resour. Assoc. 2005, 41, 621–633. [Google Scholar] [CrossRef]
- Xystrakis, F.; Matzarakis, A. Evaluation of 13 Empirical Reference Potential Evapotranspiration Equations on the Island of Crete in Southern Greece. J. Irrig. Drain. Eng. 2011, 137, 211–222. [Google Scholar] [CrossRef]
- Xie, E.; Wang, A. Comparison of Ten Potential Evapotranspiration Models and Their Attribution Analyses for Ten Chinese Drainage Basins. Adv. Atmos. Sci. 2020, 37, 959–974. [Google Scholar] [CrossRef]
- Hargreaves, G.H. Moisture Availability and Crop Production. Trans. ASAE 1975, 18, 980–984. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Ambient Air Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Kharrufa, N. Simplified equation for evapotranspiration in arid regions. Beiträge Zur Hydrol. Sonderh. 1985, 5, 39–47. [Google Scholar]
- Schendel, U. Vegetations Wasserverbrauch Und -Wasserbedarf. Habilit. Kiel 1967, 137, 1–11. [Google Scholar]
- Romanenko, V.A. Computation of the autumn soil moisture using a universal relationship for a large area. Proc. Ukr. Hydrometeorol. Res. Inst. Kiev 1961, 3, 12–25. [Google Scholar]
- Boyle, D.P.; Gupta, H.V.; Sorooshian, S. Toward improved calibration of hydrologic models: Combining the strengths of manual and automatic methods. Water Resour. Res. AGU 2000, 36, 3663–3674. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Dis, M.O.; Anagnostou, E.; Mei, Y. Using high-resolution satellite precipitation for flood frequency analysis: Case study over the Connecticut River Basin. J. Flood Risk Manag. 2018, 11, S514–S526. [Google Scholar] [CrossRef]
- Alpaslan, H.; Akgonen, A.I. Investigation of double tee moment connections under monotonic loading. J. Fac. Eng. Archit. Gazi Univ. 2021, 36, 2271–2286. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation Coefficients: Appropriate Use and Interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef] [PubMed]
- Ozer, D.J. Correlation and the coefficient of determination. Psychol. Bul. 1985, 97, 307–315. [Google Scholar] [CrossRef]
- Kat, C.J.; Els, P.S. Validation metric based on relative error. Math. Comput. Model. Dyn. Syst. 2012, 18, 487–520. [Google Scholar] [CrossRef]
- Willmot, C.J. On the evaluation of model performance in physical geography. In Spatial Statistics and Models; Theory and Decision Library, Gaile, G.L., Willmot, C.J., Eds.; Springer: Dordrecht, The Netherlands, 1984; Volume 40, pp. 443–460. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models: Part 1. A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Global Solar Atlas, Direct Normal Irradiation (DNI) (GeoTIFF), Turkiye Data Website. Available online: https://globalsolaratlas.info/download/turkey (accessed on 16 June 2023).
- Saud, A.; Said, M.A.M.; Abdullah, R.; Hatem, A. Temporal and spatial variability of potential evapotranspiration in semi-Arid Region: Case study the Valleys of Western Region of Iraq. Int. J. Eng. Sci. Technol. 2014, 6, 653. [Google Scholar]
- Heydari, M.M.; Tajamoli, A.; Ghoreishi, S.H.; Darbe-Esfahani, M.K.; Gilasi, H. Evaluation and calibration of Blaney–Criddle equation for estimating reference evapotranspiration in semiarid and arid regions. Environ. Earth. Sci. 2015, 74, 4053–4063. [Google Scholar] [CrossRef]
- McCabe, G.J.; Hay, L.E.; Bock, A.; Markstrom, S.L.; Atkinson, R.D. Inter-annual and spatial variability of Hamon potential evapotranspiration model coefficients. J. Hydrol. 2015, 521, 389–394. [Google Scholar] [CrossRef]
- Okkan, U.; Kiymaz, H. Questioning of Empirically Derived and Locally Calibrated Potential Evapotranspiration Equations for a Lumped Water Balance Model. Water Supply 2020, 20, 1141–1156. [Google Scholar] [CrossRef]
- Usta, S. Development of Jensen Haise Method Reference Evapotranspiration Estimation Equations Suitable for Black Sea Region Climatic Conditions. EJOSAT 2022, 38, 415–427. [Google Scholar] [CrossRef]
- Lin, N.; Jiang, R.Z.; Liu, Q.; Yang, H.; Liu, H.L.; Yang, Q. Quantifying the Spatiotemporal Variation of Evapotranspiration of Different Land Cover Types and the Contribution of Its Associated Factors in the Xiliao River Plain. Remote Sens. 2022, 14, 252. [Google Scholar] [CrossRef]
- Ablikim, K.; Yang, H.; Mamattursun, A. Spatiotemporal Variation of Evapotranspiration and Its Driving Factors in the Urumqi River Basin. Sustainability 2023, 15, 13904. [Google Scholar] [CrossRef]
- Bennie, J.; Huntley, B.; Wiltshire, A.; Hill, M.O.; Baxter, R. Slope, aspect and climate: Spatially explicit and implicit models of topographic microclimate in chalk grassland. Ecol. Modell. 2008, 216, 47–59. [Google Scholar] [CrossRef]
- Tran, A.P.; Rungee, J.; Faybishenko, B.; Dafflon, B.; Hubbard, S.S. Assessment of Spatiotemporal Variability of Evapotranspiration and Its Governing Factors in a Mountainous Watershed. Water 2019, 11, 243. [Google Scholar] [CrossRef]
- Gisolo, D.; Previati, M.; Bevilacqua, I.; Canone, D.; Boetti, M.; Dematteis, N.; Balocco, J.; Ferrari, S.; Gentile, A.; N’Sassila, M.; et al. A calibration free radiation driven model for estimating actual evapotranspiration of mountain grasslands (CLIME-MG). J. Hydrol. 2022, 610, 127948. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).