Seismic Safety Analysis of Interlaminar Rock Mass in the Distributed Underground Reservoir of a Coal Mine
Abstract
1. Introduction
2. Physical Model Experiments
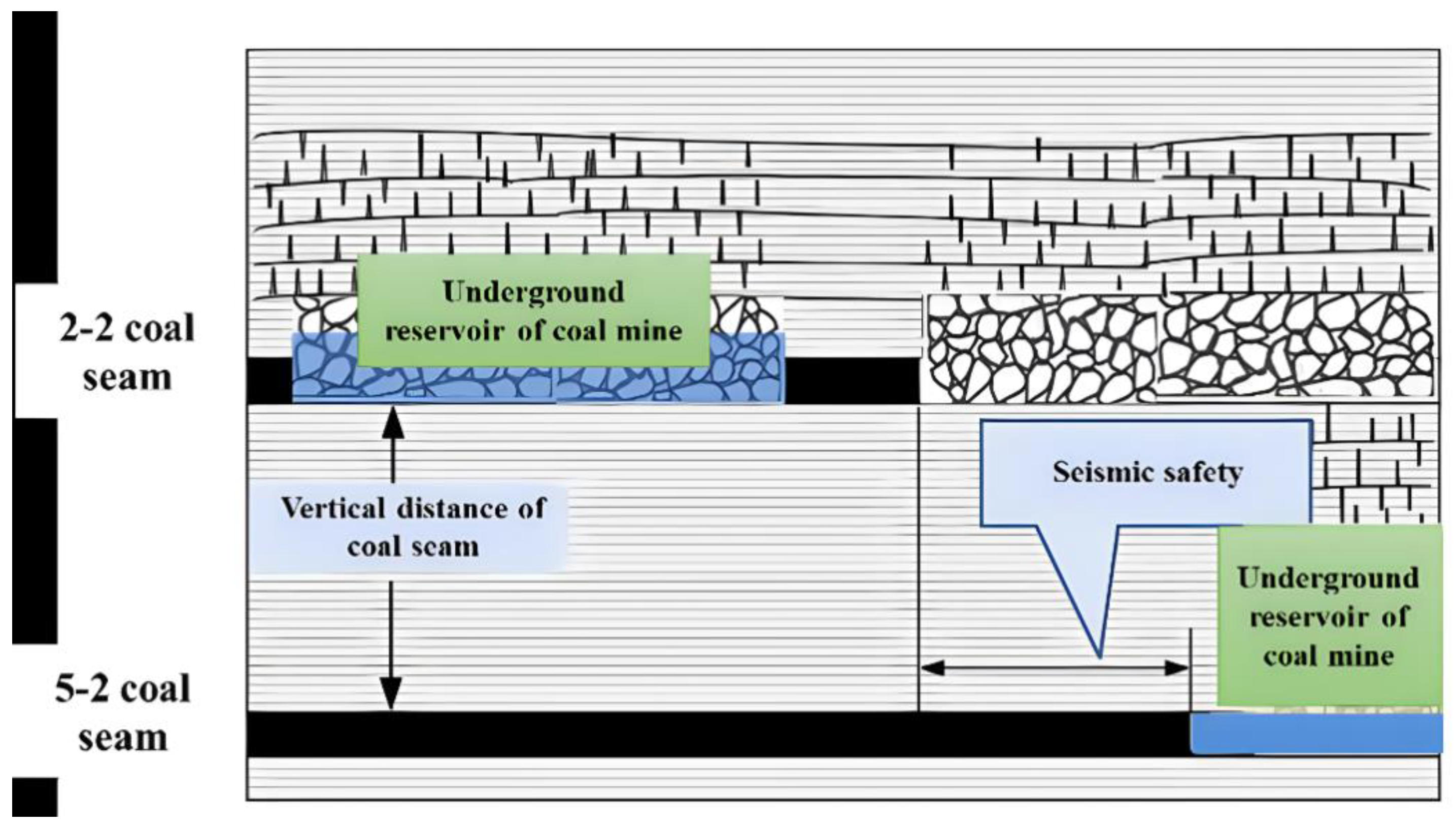
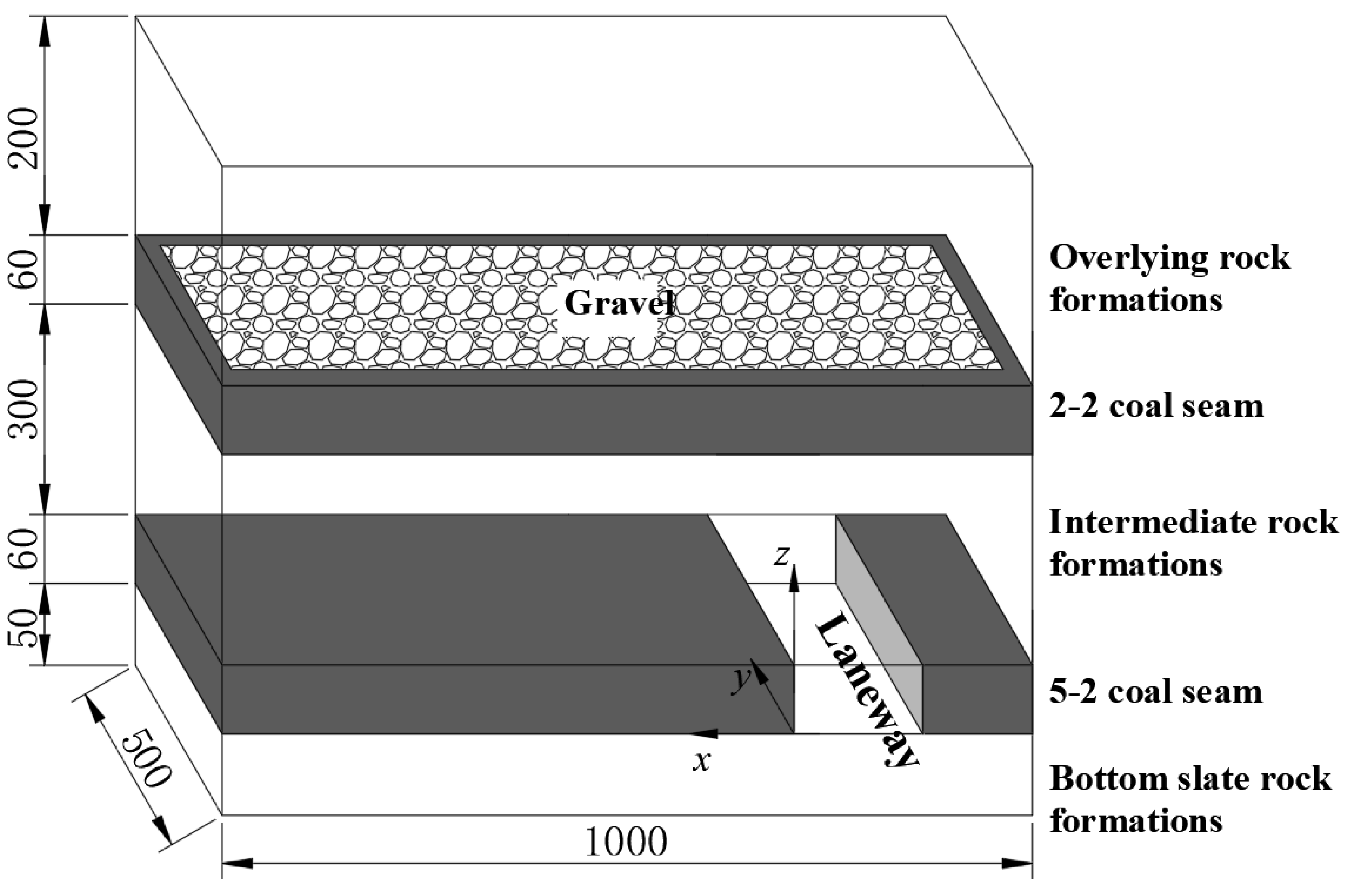
2.1. Engineering Prototype
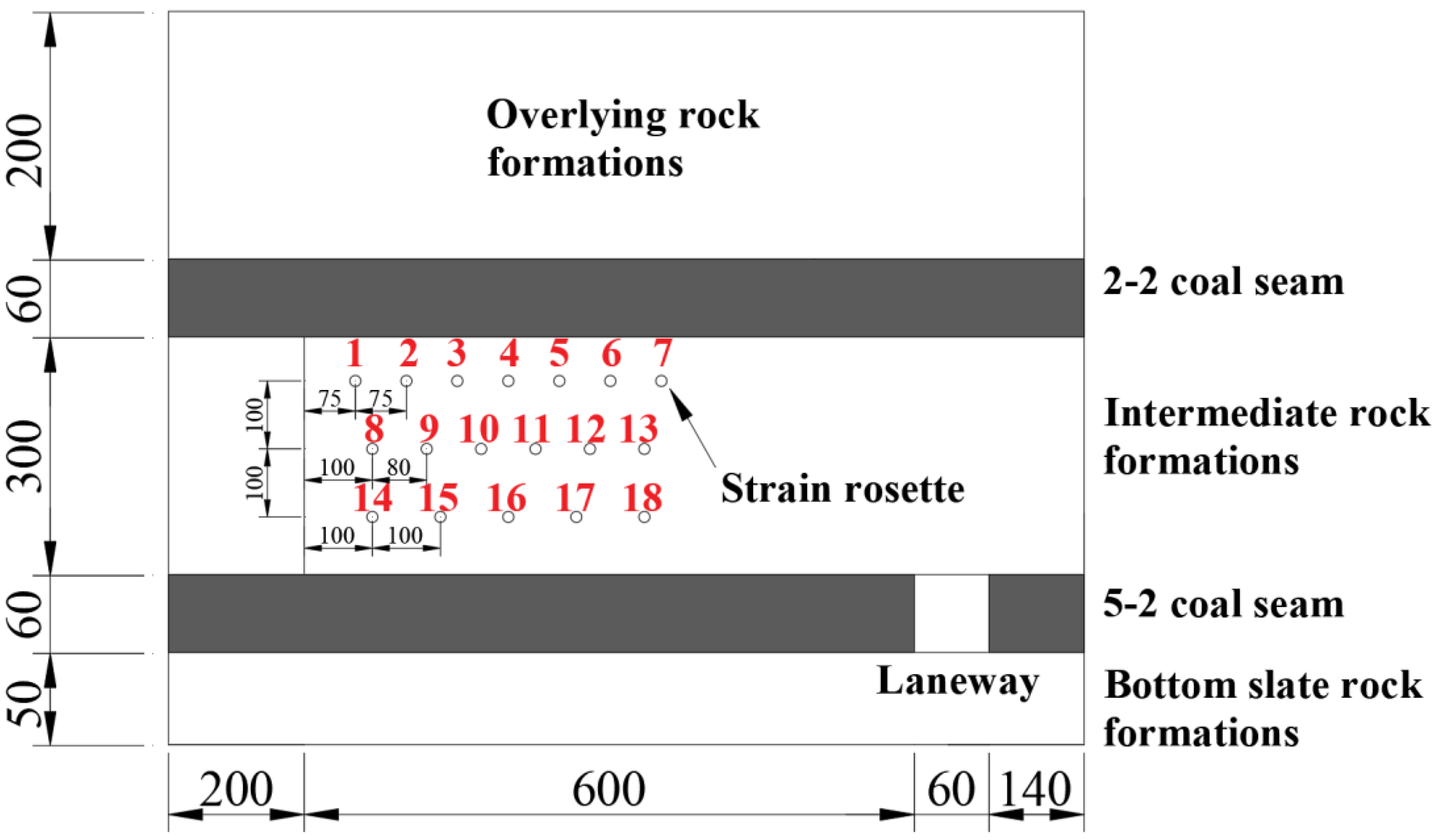
2.2. Experiment Design
2.3. Experiment Process
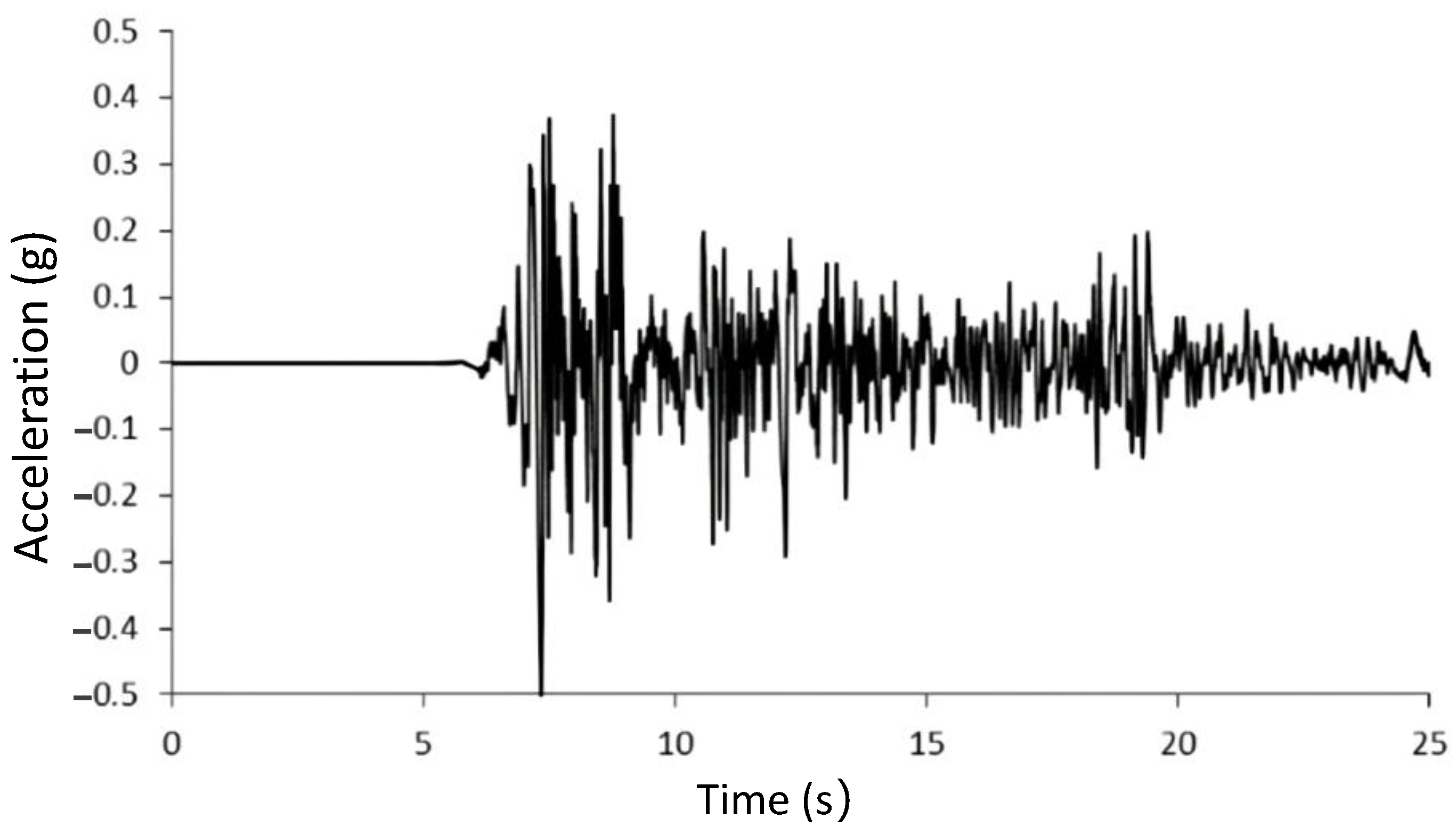
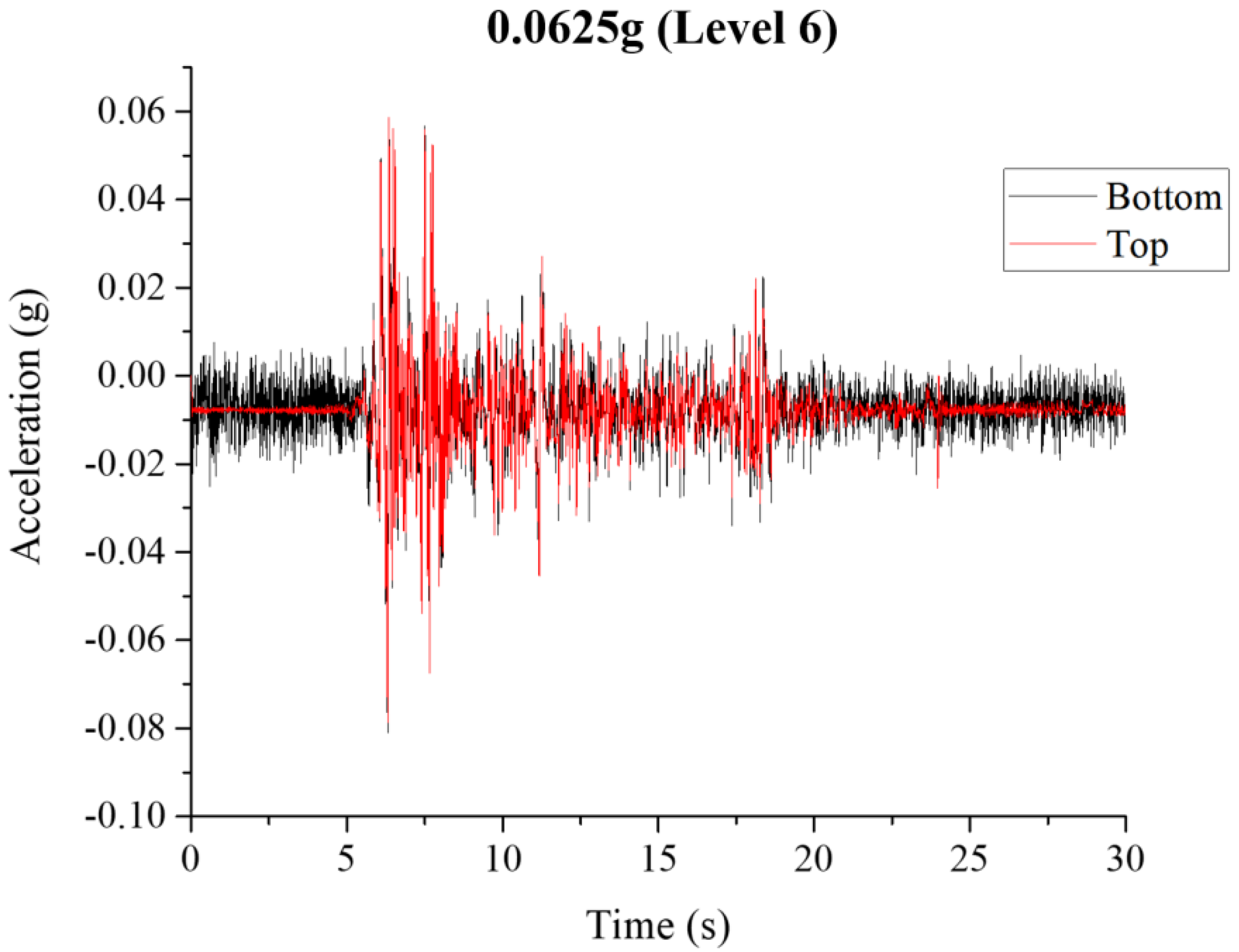
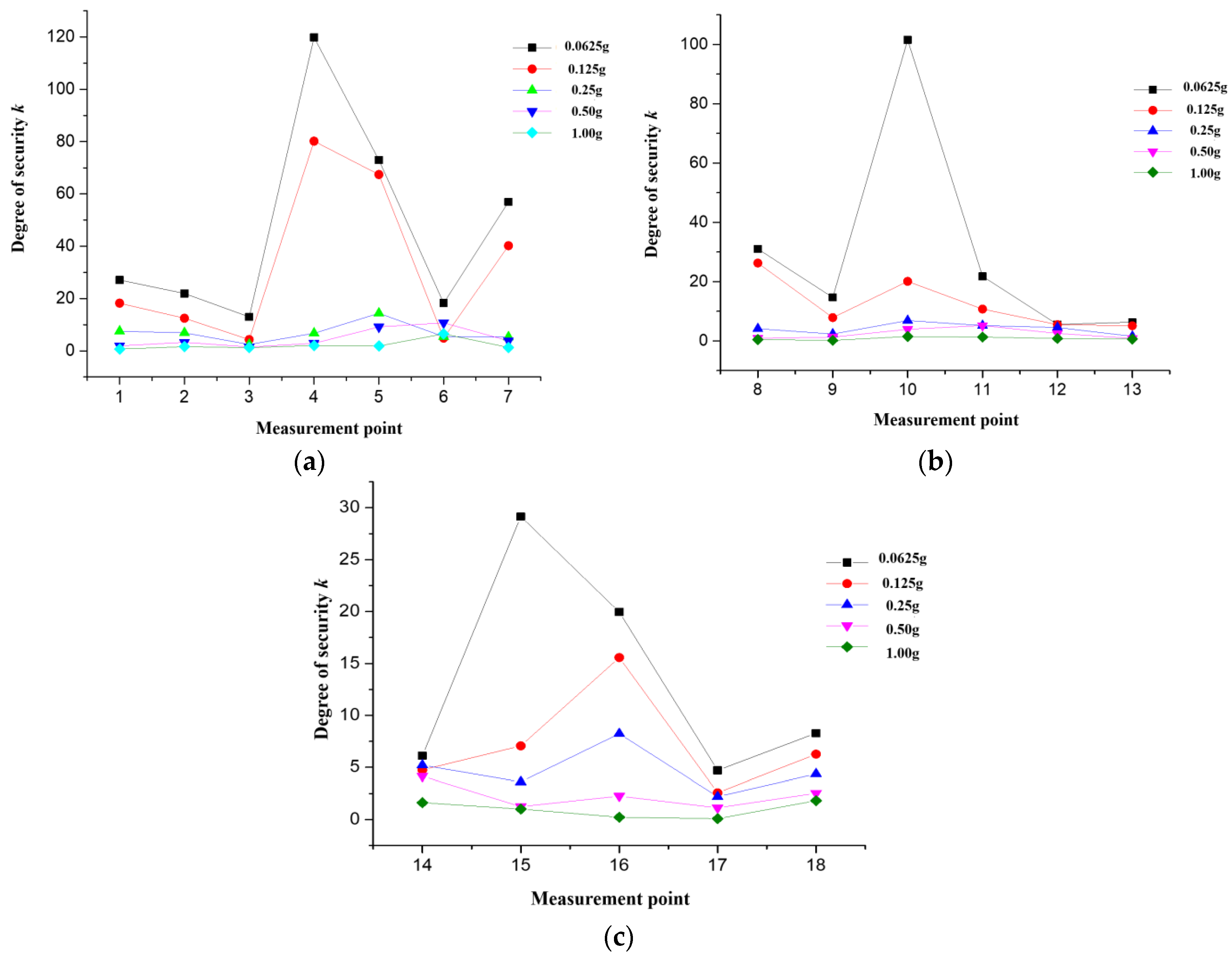
2.4. Experiment Results
3. Numerical Simulation
3.1. Basic Theory
3.1.1. Seismic Dynamic Equation
3.1.2. Dynamic Analysis Equation
3.1.3. Time History Analysis
3.2. Numerical Model
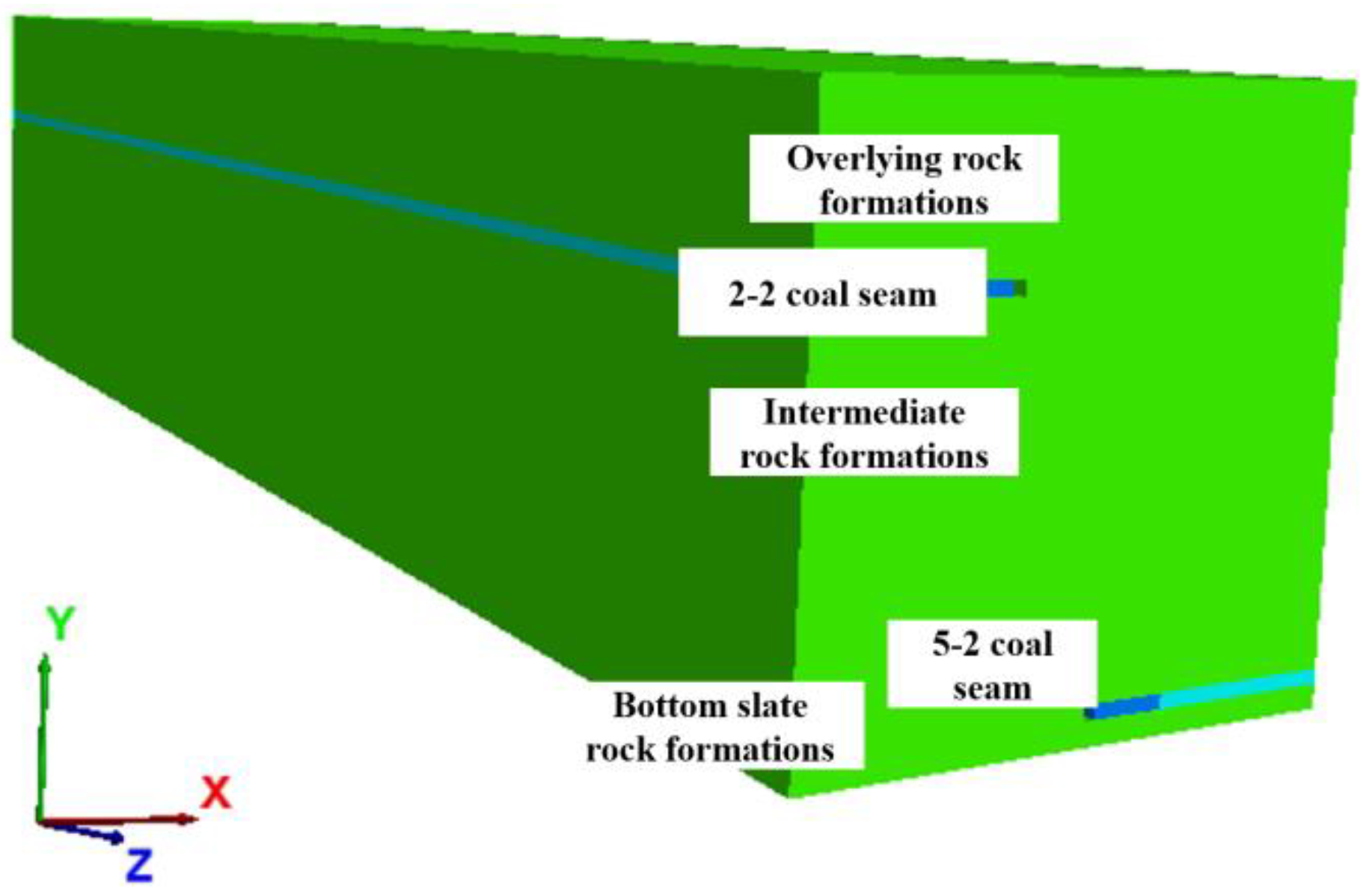
3.2.1. Numerical Model
3.2.2. Boundary Condition
3.2.3. Mechanical Parameters
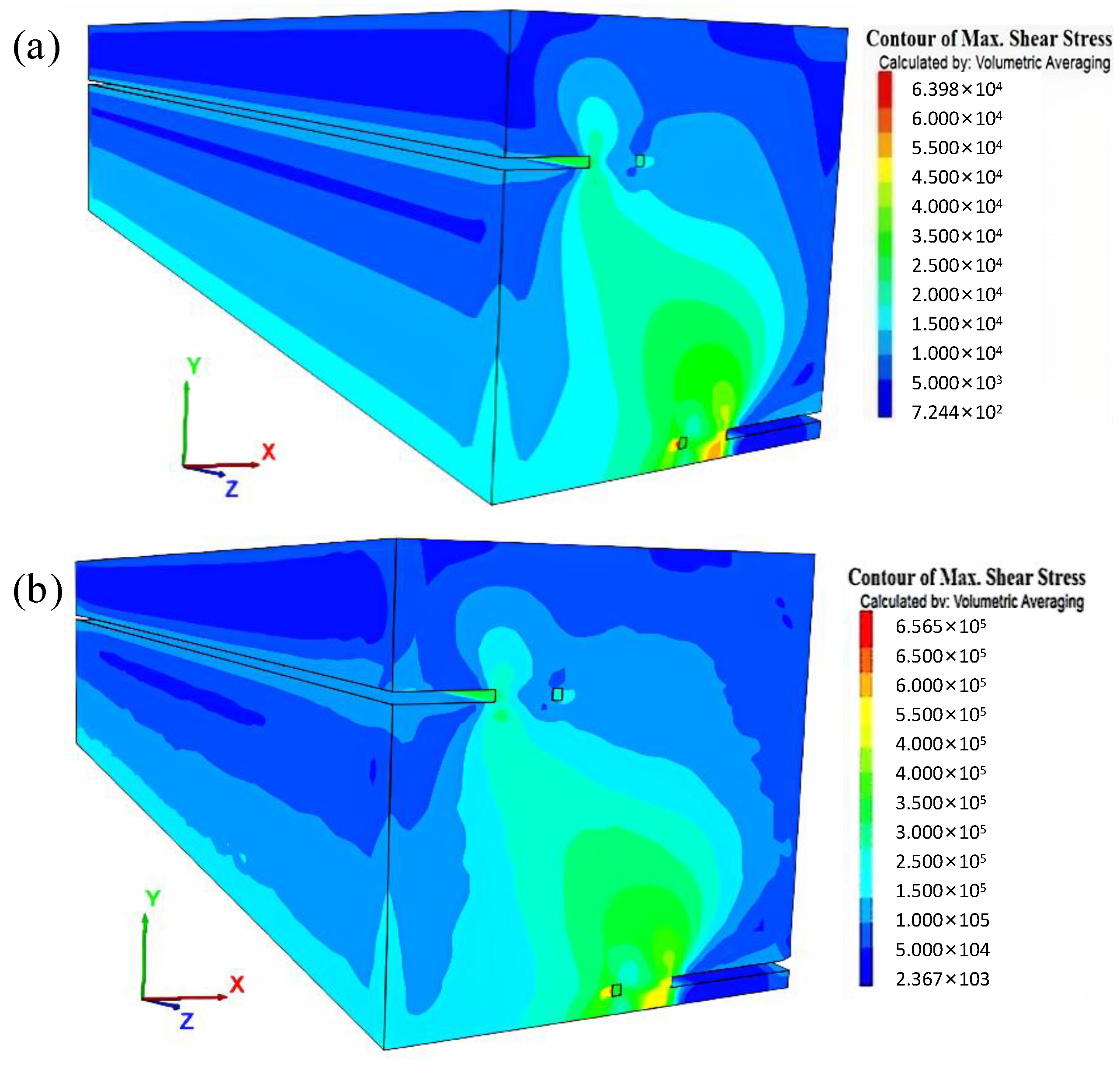
3.2.4. Simulating the Shear Stress Variation with Different Seismic Intensity Conditions
3.2.5. Analyzing the Seismic Safety of the Rock Mass between the Upper and Lower Layers of the Reservoir
3.3. Analysis of Simulation Results
4. Conclusions
- For the seismic safety of the rock mass between the upper and lower layers of the distributed underground reservoir in coal mines, conducting physical model tests alone allows for the analysis of dynamic response behavior at a limited number of monitoring points, which makes it challenging to reflect the overall seismic safety performance of the reservoir. Conversely, conducting dynamic numerical analysis alone poses challenges regarding constitutive relationship and dynamic boundary conditions, making it difficult to evaluate the accuracy and reliability of the simulation results. Therefore, it is essential to undertake comprehensive research using both dynamic model tests and numerical analysis for mutual verification. The study demonstrates that the dynamic response behavior obtained from both methods is relatively consistent.
- The variation trend of the maximum shear stress in the middle rock layer remains consistent under different seismic intensity conditions: the farther away from the lower coal excavation position, the lower the shear stress in the middle rock layer, and the closer to the excavation position, the faster the decrease in shear stress. Therefore, the larger the horizontal safety distance between the upper and lower reservoirs, the smaller the influence between the two reservoirs.
- For the Daliuta Coal Mine, the horizontal safety distance between the upper and lower reservoirs under a seismic load of eight degrees should be greater than 190 m to ensure their safety. Under a seismic load of nine degrees, the horizontal safety distance should be greater than 230 m to ensure their safety. Under a seismic load of 10 degrees, the safety distance between the upper and lower reservoirs should be greater than 270 m to ensure their safety.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gu, D.; Yan, Y.; Zhang, Y. Experimental Study and Numerical Simulation for Dynamic Response of Coal Mine Underground Reservoir. J. China Coal Soc. 2016, 41, 9. [Google Scholar]
- Liu, C.S.; Liang, L.L.; Wang, L.; Zheng, S. Allocation and Utilization of Coal Mine Water for Ecological Protection of Lakes in Semi-Arid Area of China. Sustainability 2022, 14, 9042. [Google Scholar] [CrossRef]
- Peng, S. Coal Resources and Water Resources—A Strategic Study on China Coal Clean, Efficient and Sustainable Development; Science Press: Beijing, China, 2014. [Google Scholar]
- Liu, Q.H.; Xue, Y.B.; Ma, D.; Li, Q. Failure Characteristics of the Water-Resisting Coal Pillar under Stress-Seepage Coupling and Determination of Reasonable Coal Pillar Width. Water 2023, 15, 1002. [Google Scholar] [CrossRef]
- Feng, H.B.; Zhou, J.W.; Chai, B.; Zhou, A.G.; Li, J.Z.; Zhu, H.H.; Chen, H.N.; Su, D.H. Groundwater environmental risk assessment of abandoned coal mine in each phase of the mine life cycle: A case study of Hongshan coal mine, North China. Environ. Sci. Pollut. R 2020, 27, 42001–42021. [Google Scholar] [CrossRef]
- Gu, D.; Zhang, Y.; Cao, Z. Technical progress of water resource protection and utilization by coal mining in China. Coal Sci. Technol. 2016, 44, 7. [Google Scholar]
- Han, P.H.; Zhang, C.; Wang, W. Failure analysis of coal pillars and gateroads in longwall faces under the mining-water invasion coupling effect. Eng. Fail. Anal. 2022, 131, 105912. [Google Scholar] [CrossRef]
- Wang, Q.Q.; Han, Y.B.; Zhao, L.G.; Li, W.P. Water Abundance Evaluation of Aquifer Using GA-SVR-BP: A Case Study in the Hongliulin Coal Mine, China. Water 2023, 15, 3204. [Google Scholar] [CrossRef]
- Chu, Z.; Wu, Z.; Liu, B. Mechanical response of inclined TBM tunnel due to drainage settlement of deep sandstone aquifer. Tunn. Undergr. Space Technol. 2022, 122, 1425144. [Google Scholar] [CrossRef]
- Chu, Z.; Wu, Z.; Liu, Q.; Weng, L.; Xu, X.; Wu, K.; Sun, Z. Viscos-elastic-plastic solution for deep buried tunnels considering tunnel face effect and sequential installation of double linings. Comput. Geotech. 2024, 165, 105930. [Google Scholar] [CrossRef]
- Aksoy, C.O.; Kucuk, K.; Uyar, G.G. Safety pillar design for main galleries in multi-slice longwall top coal caving method. Int. J. Oil Gas Coal Technol. 2015, 9, 329–347. [Google Scholar] [CrossRef]
- Chang, J.Y.; Ahn, S.C.; Lee, J.S.; Kim, J.Y.; Jung, A.R.; Park, J.; Choi, J.W.; Yu, S.D. Exposure assessment for the abandoned metal mine area contaminated by arsenic. Environ. Geochem. Health 2019, 41, 2443–2458. [Google Scholar] [CrossRef] [PubMed]
- Pujades, E.; Willems, T.; Bodeux, S.; Orban, P.; Dassargues, A. Underground pumped storage hydroelectricity using abandoned works (deep mines or open pits) and the impact on groundwater flow. Hydrogeol. J. 2016, 24, 1531–1546. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Guo, Q.; Liu, W. Evaluation of Long-Term Tightness of the Coal Pillar Dam of Underground Reservoir and Protection Countermeasures. Energies 2022, 15, 7229. [Google Scholar] [CrossRef]
- Wang, W.A.; Yao, Q.L.; Xu, Q.; Chen, X.Y.; Liu, H.Y.; Li, X.H. Experimental Study on the Evolution Law of Coal Mine Underground Reservoir Water Storage Space under the Disturbance and Water-Rock Interaction Effect. Minerals 2022, 12, 1491. [Google Scholar] [CrossRef]
- Zhu, W.B.; Yu, S.C.; Xuan, D.Y.; Shan, Z.J.; Xu, J.L. Experimental study on excavating strip coal pillars using caving zone backfill technology. Arab. J. Geosci. 2018, 11, 554. [Google Scholar] [CrossRef]
- Zhu, M.T.; Li, B.; Liu, G. Groundwater risk assessment of abandoned mines based on pressure-state-response-The example of an abandoned mine in southwest China. Energy Rep. 2022, 8, 10728–10740. [Google Scholar] [CrossRef]
- Pitilakis, K.; Tsinidis, G. Performance and Seismic Design of Underground Structures. Earthq. Geotech. Eng. Des. 2014, 28, 279–340. [Google Scholar]
- Rapantova, N.; Licbinska, M.; Babka, O.; Grmela, A.; Pospisil, P. Impact of uranium mines closure and abandonment on groundwater quality. Environ. Sci. Pollut. R 2013, 20, 7590–7602. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.M.; Liu, B.G.; Tannant, D.; Qi, Y. Influence of consolidation settlement on the stability of inclined TBM tunnels in a coal mine. Tunn. Undergr. Space Technol. 2017, 69, 64–71. [Google Scholar] [CrossRef]
- Galav, A.; Singh, G.S.P.; Sharma, S.K. Hydro-Mechanically Coupled Numerical Modelling of Protective Water Barrier Pillars in Underground Coal Mines in India. Mine Water Environ. 2023, 42, 418–440. [Google Scholar] [CrossRef]
- Wu, K.; Zheng, X.M.; Zhao, N.N.; Shao, Z.S. Effect of compressible layer on time-dependent behaviour of soft-rock large deformation tunnels revealed by mathematical analytical method. Appl. Math. Model 2024, 126, 457–481. [Google Scholar] [CrossRef]
- Kumar, R.; Das, A.J.; Mandal, P.K.; Bhattacharjee, R.; Tewari, S. Probabilistic stability analysis of failed and stable cases of coal pillars. Int. J. Rock Mech. Min. Sci. 2021, 144, 104810. [Google Scholar] [CrossRef]
- Kumar, R.; Mandal, P.K.; Ghosh, N.; Das, A.J.; Banerjee, G. Design of Stable Parallelepiped Coal Pillars Considering Geotechnical Uncertainties. Rock Mech. Rock Eng. 2023, 56, 6581–6602. [Google Scholar] [CrossRef]
- Prassetyo, S.H.; Irnawan, M.A.; Simangunsong, G.M.; Wattimena, R.K.; Arif, I.; Rai, M.A. New coal pillar strength formulae considering the effect of interface friction. Int. J. Rock Mech. Min. Sci. 2019, 123, 104102. [Google Scholar] [CrossRef]
- Davoodi, M.; Jafari, M.K.; Sadrolddini, S.M.A. Effect of multi-support excitation on seismic response of embankment dams. Int. J. Civ. Eng. 2013, 11, 19–28. [Google Scholar]
- Moradloo, A.J.; Naiji, A. Effects of rotational components of earthquake on seismic response of arch concrete dams. Earthq. Eng. Eng. Vib. 2020, 19, 349–362. [Google Scholar] [CrossRef]
- Tarinejad, R.; Fatehi, R.; Harichandran, R.S. Response of an arch dam to non-uniform excitation generated by a seismic wave scattering model. Soil Dyn. Earthq. Eng. 2013, 52, 40–54. [Google Scholar] [CrossRef]
- Zhang, J.W.; Li, M.C.; Han, S. Seismic Analysis of Gravity Dam-Layered Foundation System Subjected to Earthquakes with Arbitrary Incident Angles. Int. J. Geomech. 2022, 22, 04021279. [Google Scholar] [CrossRef]
- Jianming, Z.; Xiaosheng, L.; Yusheng, Y. Criteria for seismic safety evaluation and maximum aseismic capability of high concrete face rockfill dams. Chin. J. Geotech. Eng. 2015, 37, 8. [Google Scholar]
- Zhu, F.; Wang, J.T.; Jin, F.; Lu, L.Q. Control performance comparison between tuned liquid damper and tuned liquid column damper using real-time hybrid simulation. Earthq. Eng. Eng. Vib. 2019, 18, 695–701. [Google Scholar]
- Hashash, Y.M.A.; Park, D.; Yao, J.I.C. Ovaling deformations of circular tunnels under seismic loading, an update on seismic design and analysis of underground structures. Tunn. Undergr. Space Technol. 2005, 20, 435–441. [Google Scholar] [CrossRef]
- Shen, X.; Yuan, D.J.; Lin, X.T.; Chen, X.S.; Peng, Y.S. Evaluation and prediction of earth pressure balance shield (EPBS) performance in complex rock strata: A case study in Dalian. J. Rock. Mech. Geotech. 2023, 15, 1491–1505. [Google Scholar] [CrossRef]
- González-Quirós, A.; Fernández-Alvarez, J.P. Conceptualization and finite element groundwater flow modeling of a flooded underground mine reservoir in the Asturian Coal Basin, Spain. J. Hydrol. 2019, 578, 124036. [Google Scholar] [CrossRef]


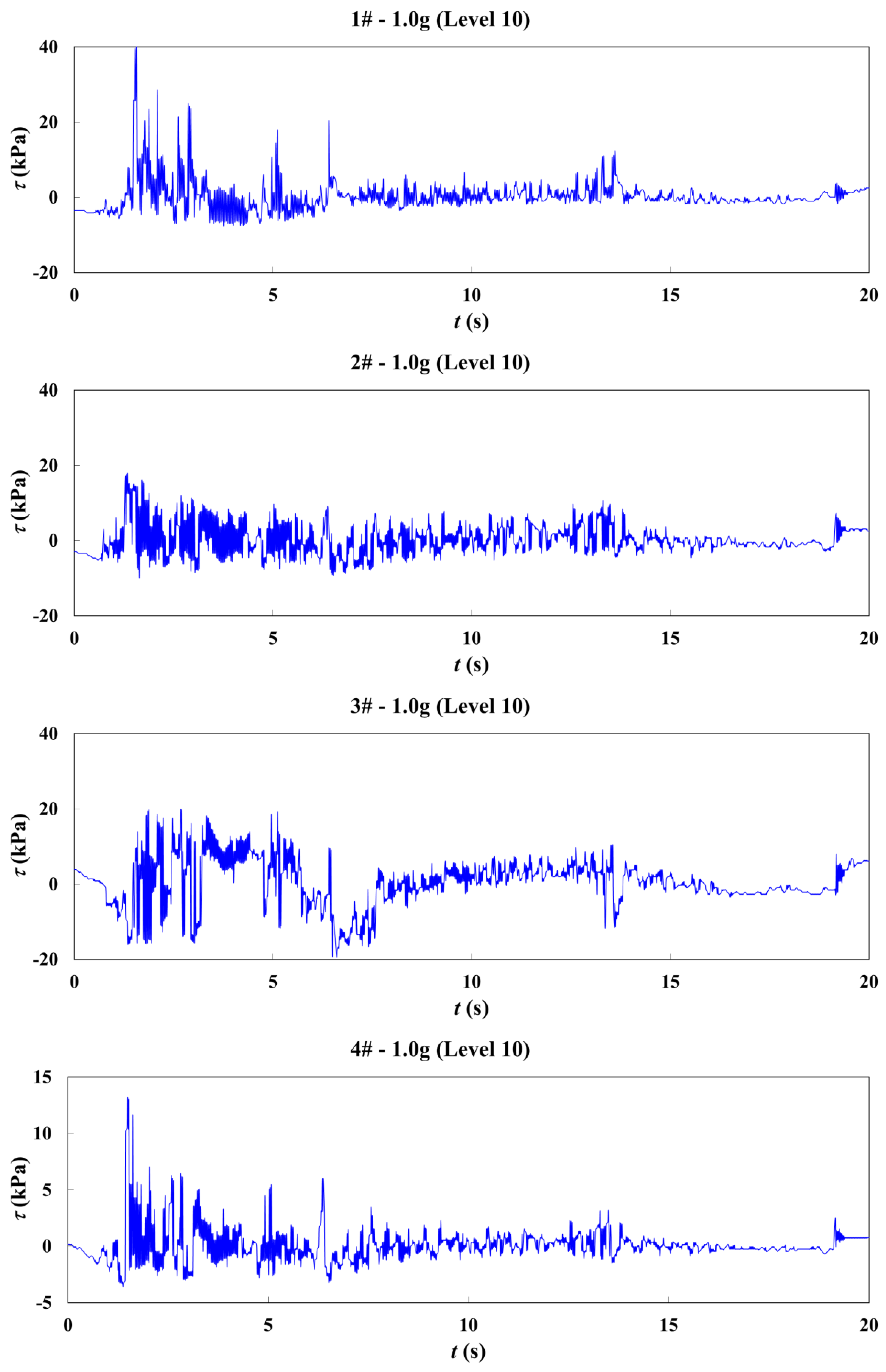
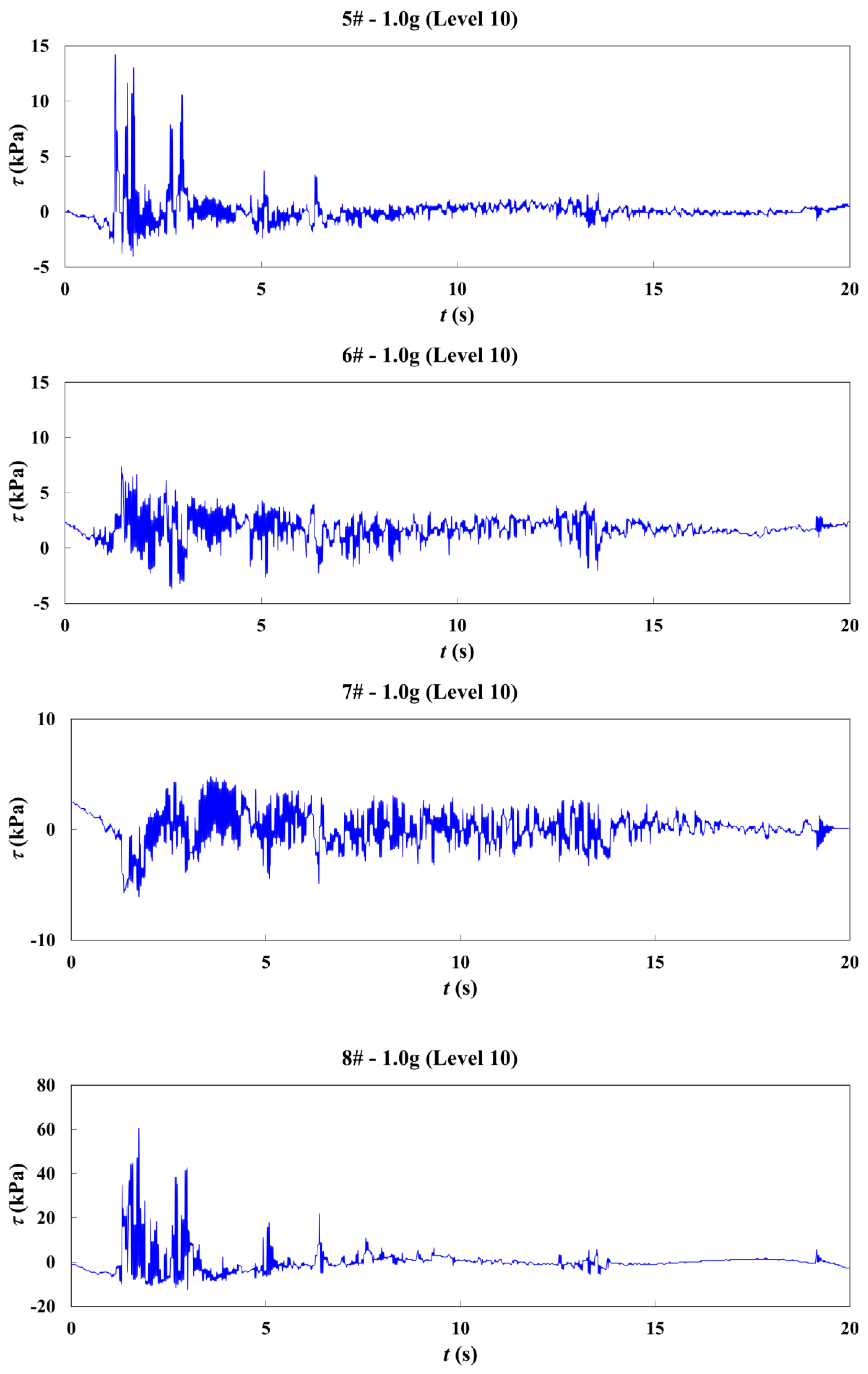
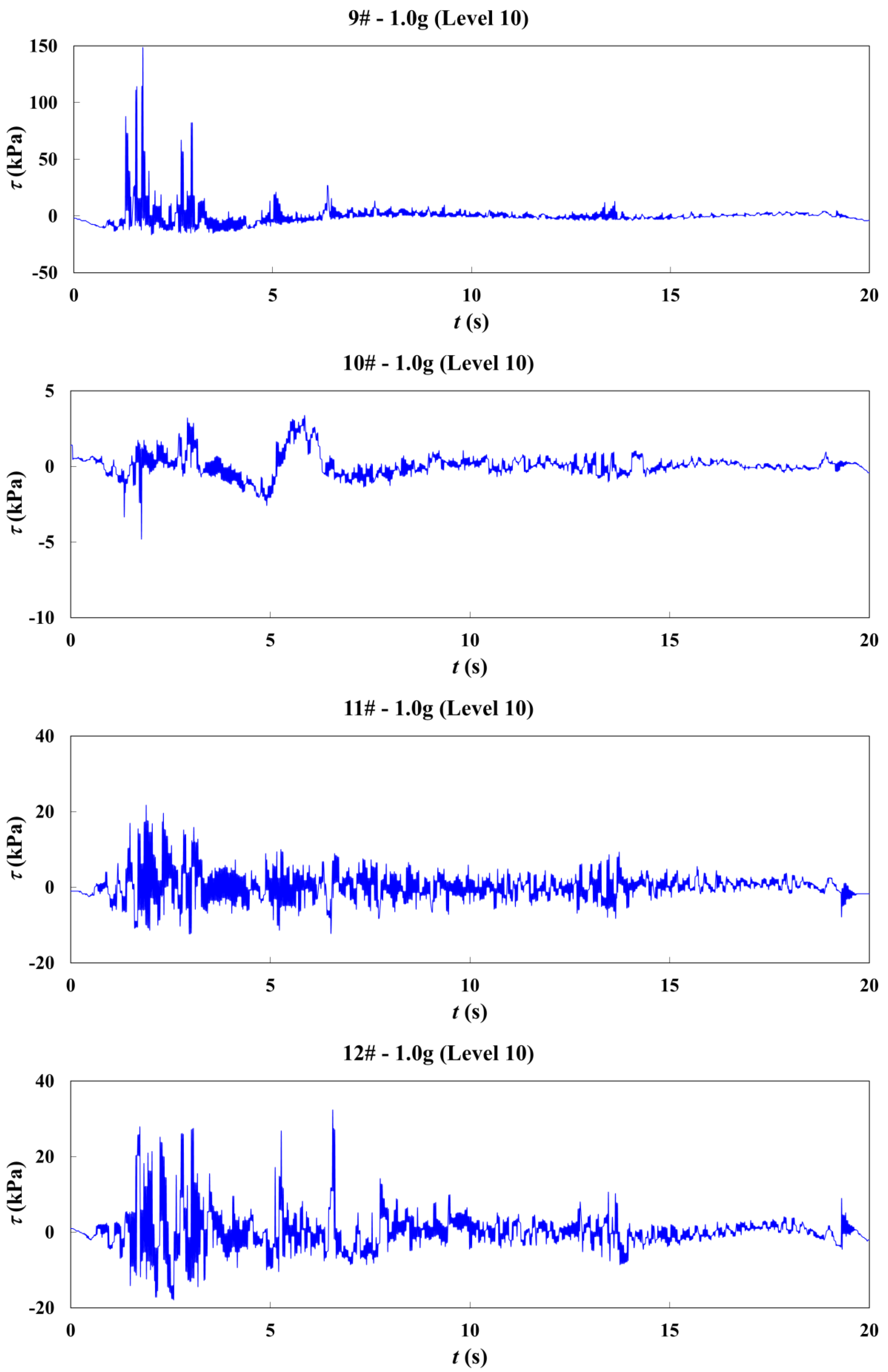
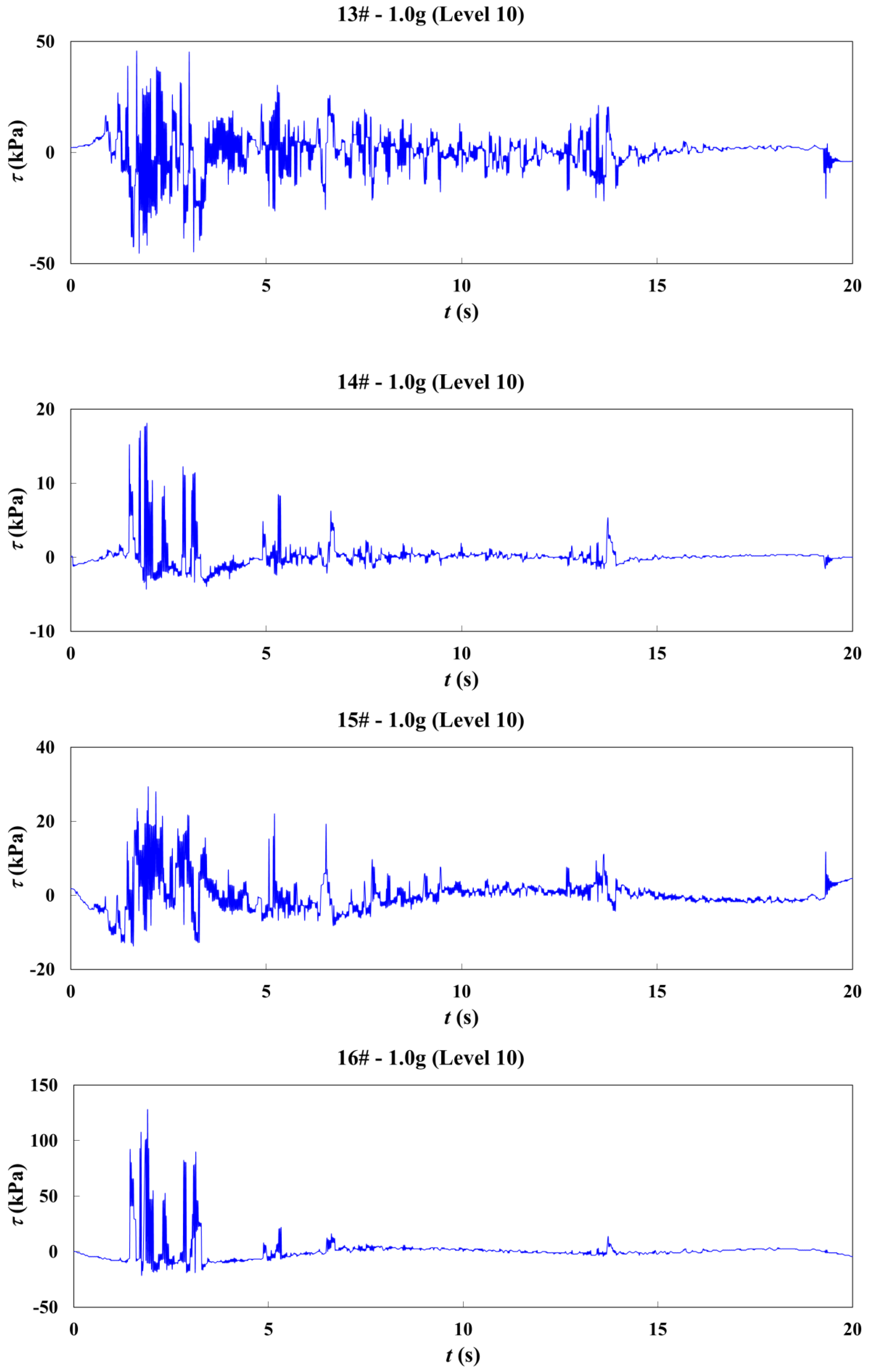

| Rock Type | Density/Kg·m−3 | Compressive Strength/MPa | Cohesion/MPa | Internal Friction/° | Elastic Modulus/GPa | Poisson’s Ratio | Thickness/M |
|---|---|---|---|---|---|---|---|
| wind-blown sand | 1700 | 12 | 0.02 | 20 | 12 | 0.3 | 38 |
| siltstone | 2450 | 41.83 | 7.07 | 38 | 13.2 | 0.18 | 12 |
| fine sandstone | 2410 | 35.04 | 6.46 | 38 | 13.16 | 0.2 | 5 |
| siltstone | 2450 | 41.83 | 7.07 | 38 | 13.2 | 0.18 | 7 |
| fine sandstone | 2410 | 35.04 | 6.46 | 38 | 13.16 | 0.2 | 6 |
| siltstone | 2450 | 41.83 | 7.07 | 38 | 13.2 | 0.18 | 4 |
| fine sandstone | 2410 | 35.04 | 6.46 | 38 | 13.16 | 0.2 | 18 |
| siltstone | 2450 | 41.83 | 7.07 | 38 | 13.2 | 0.18 | 2 |
| 2-2 coal | 1320 | 13.5 | 1 | 30 | 13 | 0.26 | 5 |
| siltstone mudstone | 2450 | 41.83 | 7.07 | 38 | 13.2 | 0.18 | 2 |
| 5-2 coal | 2430 | 45.94 | 5.55 | 29 | 10.09 | 0.15 | 3 |
| wind-blown sand | 1256 | 11.60 | 2.31 | 40.2 | 16.9 | 0.20 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Cao, Z.; Wang, L.; Zha, E.; Li, S.; Chu, Z. Seismic Safety Analysis of Interlaminar Rock Mass in the Distributed Underground Reservoir of a Coal Mine. Water 2024, 16, 366. https://doi.org/10.3390/w16030366
Zhang Y, Cao Z, Wang L, Zha E, Li S, Chu Z. Seismic Safety Analysis of Interlaminar Rock Mass in the Distributed Underground Reservoir of a Coal Mine. Water. 2024; 16(3):366. https://doi.org/10.3390/w16030366
Chicago/Turabian StyleZhang, Yong, Zhiguo Cao, Lujun Wang, Ersheng Zha, Shoubiao Li, and Zhaofei Chu. 2024. "Seismic Safety Analysis of Interlaminar Rock Mass in the Distributed Underground Reservoir of a Coal Mine" Water 16, no. 3: 366. https://doi.org/10.3390/w16030366
APA StyleZhang, Y., Cao, Z., Wang, L., Zha, E., Li, S., & Chu, Z. (2024). Seismic Safety Analysis of Interlaminar Rock Mass in the Distributed Underground Reservoir of a Coal Mine. Water, 16(3), 366. https://doi.org/10.3390/w16030366







