Abstract
The dispersion coefficients are crucial in understanding the spreading of pollutant clouds in river flows, particularly in the context of the depth-averaged two-dimensional (2D) advection–dispersion equation (ADE). Traditionally, the 2D stream-tube routing procedure (2D STRP) has been the predominant method for determining both the longitudinal and transverse dispersion coefficients of the 2D ADE under transient concentration conditions. This study aims to quantitatively analyze and address the limitations of the 2D STRP using hypothetically generated data. The findings of these evaluations revealed that the existing 2D STRP failed to accurately reproduce reliable results when the tracer clouds reached wall boundaries. This limitation prompted the development of the 2D STRP-i, which effectively resolves this drawback. The newly developed routing-based observation method, 2D STRP-i, enables the reliable estimation of dispersion coefficients, considering the effect of the wall boundary. The results indicated that the existing 2D STRP yielded 2D dispersion coefficients with relative errors ranging from 40% to 200%, while 2D STRP-i consistently yielded relative errors of 3% to 5% on average. When applied to tracer test data obtained through remote sensing, the 2D STRP-i demonstrated its ability to accurately observe temporal concentration distributions, even when wall boundaries have a significant impact on contaminant transport.
1. Introduction
Contaminants released to open channels can have a significant impact on the environment and public health. These channels include rivers, streams, canals, and other water bodies that are exposed to the open atmosphere. The type of contaminants and their sources can vary widely depending on the location, industrial activities, and urbanization in the area. When contaminants are instantaneously released into open channels, the resulting contaminant mixing stages can be categorized according to the primary factors governing the dispersion of contaminant clouds, as illustrated in Figure 1. For the simulation of contaminant transport in open-channel flows, it is crucial to employ appropriate modeling approaches, taking into account the characteristics of mixing behaviors. In river flows, which typically exhibit turbulent flow with high Reynolds numbers, the spreading of contaminant plumes in the near-field occurs in a three-dimensional (3D) manner due to turbulent diffusion. During this phase, it is essential to employ 3D numerical models when modeling contaminant transport, requiring a thorough understanding of the turbulent motions of fluid particles. The contaminant mixing in the depth direction is more rapidly completed by vertical turbulent diffusion compared to the spanwise direction, due to the topographical features in rivers characterized by their large aspect ratio (width-to-water-depth ratio). Although this initial phase is quickly completed in the open-channel flows, the computational demands are significantly higher than those of the following phases.
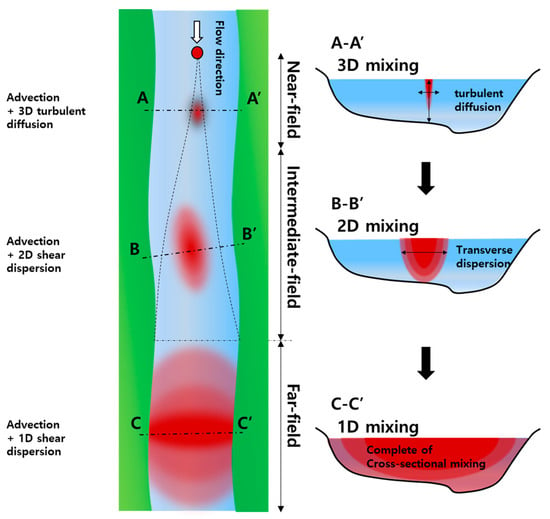
Figure 1.
The contaminant mixing phases in river flows.
Due to this reason, the depth-averaged transport models based on the two-dimensional (2D) advection–dispersion equation (ADE) have commonly been adopted for simulating contaminant transport in riverine environments [1]. In the depth-averaged 2D ADE, dispersion coefficients play a crucial role in accurately representing the spreading behavior of contaminant clouds. This is primarily due to the effects of vertical velocity variations with other associated physical properties, such as turbulent diffusions and channel heterogeneities. Thus, dispersion coefficients of the depth-averaged transport models include numerous attributes characterized by hydraulic, geomorphological, and environmental factors.
The approaches to determine 2D dispersion coefficients in open-channel flows can be divided into two categories: observation-based and estimation-based methods, as shown in Figure 2. In the estimation approach, dispersion coefficients are estimated using theoretical formulas and empirically developed regression models, without the need for concentration distribution. The empirical approaches require a considerable amount of collected data, allowing for the correlation of hydraulic properties with dispersion coefficients under the diverse stream conditions. The effectiveness of these empirical approaches is primarily influenced by the quality of the collected data used for developing regression models. Therefore, it is necessary to collect a substantial amount of dispersion coefficient data through field surveys under various stream conditions in order to establish a reliable empirical relationship between dispersion coefficients and hydraulic properties.
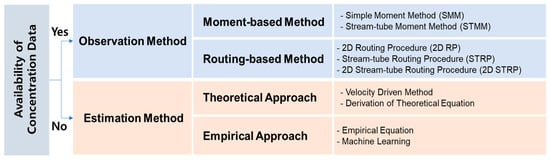
Figure 2.
Available methods for determining 2D dispersion coefficients.
When the concentration profiles, obtained through tracer experiments, are available, the dispersion coefficients can be calculated using the observation-based methods. The tracer experiment is the experimental procedure for measuring the concentration profiles of the tracers released in experimental intervals. Detectable materials such as fluorescent dyes, radioisotopes, and solute solutions are usually chosen as tracer materials [2,3,4,5,6,7,8]. Among the observation methods in Figure 2, The moment-based methods, such as the simple moment method [9] and the stream-tube moment method [10], use concentration data collected under conditions of continuous release for determining the transverse dispersion coefficient (). Thus, the moment-based methods are not feasible to obtain the longitudinal dispersion coefficient () in the condition where tracers are instantaneously released.
To resolve this aforementioned limitation, Baek et al. (2010) [11] developed the 2D stream-tube routing procedure (2D STRP), introducing the routing concept for 2D dispersion analysis. This method enables the simultaneous determination of both and under the transient concentration conditions. Fischer (1968) [12] was the first to introduce the routing concept for the development of the one-dimensional (1D) routing procedure (RP), which allows for the observation of the longitudinal dispersion coefficient of the 1D ADE. The 1D RP inherently requires cross-sectional averaged concentration profiles in the longitudinal space. However, acquiring these spatial profiles in rivers through tracer experiments was technically limited. To overcome this limitation, Fischer (1968) [12] proposed the frozen cloud approximation (FCA) for estimating the concentration profile in longitudinal space using the time-series data of concentration at the measuring locations. The FCA assumes that the spatial distribution of the tracer plume undergoes only minor changes while passing a measuring location [1]. Additionally, it postulates that the centroid of the tracer plume is advected at the velocity identical to the mean velocity of the stream flow [13]. Referring to 1D RP, the 2D STRP also relies on the FCA to estimate the concentration distribution in 2D space based on temporally measured concentration data.
For observing the dispersion coefficients using the 2D STRP, it is necessary to obtain the temporal concentration data of transversely continuous profiles at both upstream and downstream measuring locations. Nevertheless, the spatial acquisition of concentration fields remains problematic in the context of conventional tracer experiments. In the conventional tracer experiment, the concentration is typically measured as temporal data at fixed locations within experimental sections. Because of this technical limitation, many previous studies that employed the 2D STRP interpolated and extrapolated the point-wise measuring concentration data to obtain the transversely continuous concentration profiles [7,11,14,15]. Seo et al. (2016) [7] and Shin et al. (2019) [15] conducted field dispersion studies at five streams and large-scaled experimental channels in South Korea. They employed a 20% fluorescent dye (Rhodamine WT) as a tracer to observe the 2D dispersion coefficients. For measuring the tracer concentration, they installed five fluorometers in the measuring sections. Then, the measured concentrations at discrete lateral points were interpolated referring to the cumulative discharge in the spanwise direction to obtain the continuous concentration curves. Baek and Seo (2010) [11] carried out the tracer tests using a radioisotope as a tracer in the Hongcheon River in South Korea. They measured the concentration of the radioisotope using radiation-detecting equipment at ten points in the lateral direction perpendicular to river flow. To obtain the continuous concentration curves, the kriging method was applied in their study. Baek et al. (2006) [14] performed a dispersion experiment in a meandering channel in a laboratory. They used a salt solution as a tracer, and the concentration of the tracer was measured with six electrode conductivity meters uniformly distributed in the spanwise direction. They also applied interpolation techniques to transversely discrete concentration distributions. These technical limitations and post-processing procedures for obtaining continuous concentration distributions could lead to an unintentional artificial dispersion effect in the measured concentration data.
To resolve the limitations outlined above, it is imperative to employ experimental techniques that enable the detailed observation of the spatial distribution of river mixing. Fischer (1966) [16] pioneered the use of airborne cameras to observe concentration distribution during tracer tests in rivers. However, the spatial distributions were subjectively estimated through human color recognition and were used to comprehend contaminant transport in natural streams. Recently, unmanned aerial vehicles (UAVs) have been widely used to monitor river environments [17,18,19,20,21,22,23,24,25]. Flynn and Chapra (2014) [17] suggested the method for remotely sensing the spatial distribution of submerged aquatic vegetation using the UAVs. Kinzel and Legleiter (2019) [22] explored an experimental method for measuring river discharge with thermal sensors equipped in UAVs. Beak et al. (2019) [21] developed an experimental procedure for tracer tests using UAVs to acquire high-resolution spatiotemporal distributions of tracer clouds in the open-channel flows. More recently, Kwon et al. (2023) [25] investigated the mixing behavior of suspended sediment in a river confluence using the hyperspectral imagery obtained by UAVs. UAVs can offer the advantage of conducting river surveys with high spatial and temporal resolutions. By employing UAVs, researchers can overcome the limitations of previous techniques and obtain detailed and accurate information on the spatial distribution of river mixing. This increased resolution and flexibility in data acquisition will provide valuable insights into the intricate dynamics of mixing processes in rivers.
As previously described, the 2D STRP is currently the only method capable of simultaneously determining 2D dispersion coefficients for the transient concentration distributions. Despite that, the existing 2D STRP could provide inaccurate results in the application of wall-bounded channel flows because this method was derived from infinitely wide channel conditions [11]. However, this limitation was still not considered in previous studies. In this study, we evaluated the performance of the 2D STRP and investigated its drawbacks in wall-bounded open-channel flows. Based on the findings from this evaluation, we developed a new routing method that improves the limitations of the 2D STRP. Moreover, the new routing method developed in this study was applied into spatially and temporally high-resolution concentration data obtained by the remote sensing-based tracer test to verify the performance in the wall-bounded channel flow. Section 2.1 discusses the inherent limitations introduced from the derivation procedure of 2D STRP. Then, in Section 2.2, we introduce a novel routing-based method resolving the limitations of the existing 2D STRP. The results obtained from both the existing and newly developed methods in this study were quantitatively analyzed and addressed, using hypothetically generated data described in Section 2.3. Furthermore, we applied and compared these two methods in tracer experiment, as illustrated in Section 2.4, to assess their applicability in natural environments.
2. Materials and Methods
2.1. D Stream-Tube Routing Procedure (2D STRP)
Baek and Seo (2010) [11] developed the 2D STRP which is a novel approach for the determination of 2D dispersion coefficients using the measured concentration data. Among the existing observation methods, this approach is the predominant one for simultaneously observing both and . Similar to the derivation of 1D RP proposed by Fischer (1968) [12], the spatial routing equation was preferentially obtained from 2D ADE in stream-tube coordinates as presented in Equation (1).
where is the spatial distribution of the predicted concentration at ; is the spatial profile of the measured concentration at ; s and are the longitudinal distance and the normalized cumulative discharge in the stream-tube coordinates; and are the longitudinal dispersion coefficient and the stream-tube dispersion coefficient; and and are dummy distance variables of integration for the longitudinal and transverse direction, respectively. The 2D STRP is a semi-analytical solution for the simplified 2D ADE in stream-tube coordinates. In the derivation process of the 2D STRP, the hydraulic parameters such as flow velocity and water depth in the dispersion terms of 2D ADE are assumed as the reach-averaged values. This assumption leads to the incorporation of into the stream-tube dispersion coefficient, denoted as , as shown in Equation (2).
where is the cross-sectional averaged water depth; and is the dimensionless shape factor defined by Beltaos (1980) [10]. The term in Equation (2) is also called as the bulk dispersion coefficient, [11].
Because it is challenging to obtain the spatial concentration distribution through the tracer experiments, Equation (2) was converted into a routing equation for temporal concentration, introducing the FCA.
where is the temporal profile of the predicted concentration at a downstream section, ; is the temporal profile of the measured concentration at an upstream section, ; and are the times to the centroid of the temporal concentration profiles in sections and ; is the mean velocity of the pollutant cloud; and is a dummy time variable of integration. The derivation procedure for Equations (1) and (3) can be found in detail in Baek and Seo (2010) [11].
The advantage of this method lies in its ability to simultaneously determine both and from tracer test data. Furthermore, by adopting the stream-tube concept, the channel irregularity can be considered. Despite being the only method capable of simultaneously determining 2D dispersion coefficients, this approach has a limitation in that it inherently assumes infinitely wide channels during the derivation process. This limitation prevents it from accurately representing situations where the main flow velocity distribution is strongly skewed in the lateral direction so that the pollutant clouds impinge on the wall boundary. This can lead to significant errors in the calculation of dispersion coefficients using 2D STRP because a portion of the predicted concentration distribution downstream may be calculated beyond the boundaries of the calculation domain, resulting in mass loss.
2.2. Derivation of New 2D Stream-Tube Routing Procedure (2D STRP-i)
To resolve the limitations of the existing 2D STRP, a new routing method, called 2D STRP-i, was developed, which considers the wall reflection conditions of contaminant plumes in finite-width channels [26]. The development of 2D STRP-i is initiated by considering the continuity equation and the mass transport equation in the curvilinear coordinate system [27,28].
where s and n are the longitudinal and transverse curvilinear distance; and are the depth-averaged longitudinal and transverse velocity; is the water depth; and and are metric coefficients which are calculated as follows:
where and represent the incremental distances along the s- and n-axes, respectively.
The curvilinear coordinates are converted into the stream-tube coordinates by applying the concept of cumulative discharge, as expressed in Equation (8).
where is the left endpoint of the riverbank in the transverse direction.
Integrating Equation (4) regarding the lateral direction and substituting this into Equation (8) yields Equation (9).
Then, substituting Equation (9) into Equation (5) and rearranging Equation (5) with chain rules yields the depth-averaged advection–dispersion equation in the stream-tube coordinates [28,29].
Although the quantity in the dispersion terms varies with the transverse direction, previous studies [11,30,31] mentioned that the solution of Equation (10) was insensitive to such variation. Therefore, Equation (10) can be reduced assuming these quantities as the averaged values.
where
Equation (11) represents the 2D ADE in the stream-tube coordinates. The is the scaled longitudinal velocity, while both and represent the factors of longitudinal and transverse dispersion. The mathematical expression of Equation (11) is identical to that of 2D ADE in the Cartesian coordinates, particularly for a straight channel. Therefore, the analytical solution of Equation (11) can be obtained adopting the well-known analytical solution with the method of image to consider the sidewall boundary conditions [32].
where and are the locations of the mass release points. M is the pollutant mass instantaneously released at a specific point . The last term in the right-hand side is the sum of solutions for imaginary sources, which are introduced beyond the calculation domain to achieve the zero-gradient concentration condition at the sidewall. When the mass, M, is released at a specific point, Equation (15) can calculate the spatial concentration distribution at a specific time.
When the mass distribution is expressed by the arbitrary function, , at specific time (t = t1), the initial mass distribution can be represented as a series of discrete slugs [11]. The solution for the given mass distribution can be obtained through the superposition of solutions that are independently calculated for each mass release, as described in Equation (15) [1,31]. The solution for a mass located at a specific point can be expressed as follows:
where the concentration distribution, , can be computed as:
The summation of the solution over the distribution calculated individually for each slug can be represented as:
Assuming that both increments of and are infinitely small, Equation (18) can be expressed as:
Equation (19) represents the newly derived spatial routing method capable of predicting the spatial concentration distribution in downstream regions based on the spatial concentration distribution in upstream regions as input. The solution with the method of image to consider the sidewall boundary conditions can be illustrated as Figure 3.
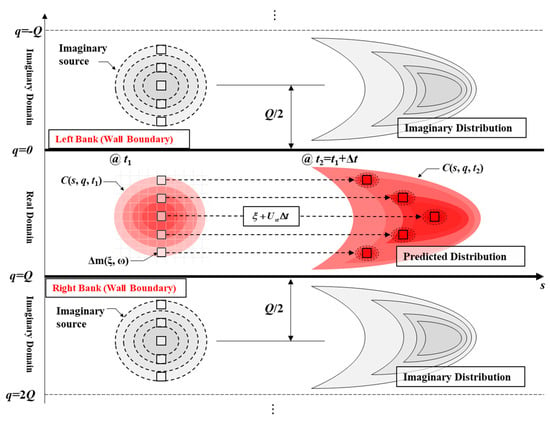
Figure 3.
Conceptual illustration for the application of the method of image to predict spatial concentration distributions in the downstream regions.
However, obtaining the spatial distribution across the entire range of the river reaches is typically challenging. Therefore, applying FCA into Equation (19) is necessary to estimate the spatial distribution from the temporal distribution. Equation (19) can be converted into the temporal routing method by applying Equations (20) to (23).
Applying the FCA into Equation (19), the 2D STRP-i can be finally derived as follows.
By using Equation (24), the temporal concentration at a downstream location, , can be predicted with the averaged dispersion coefficients from the temporal concentration measured upstream, , appropriate hydraulic parameters (, q, and Q), and the factors of dispersions ( and ). The dispersion coefficients in the curvilinear coordinate system can be inversely computed from Equations (13) and (14).
The derivation of both 2D STRP and 2D-STRP-i is based on the concept of the stream-tube. However, the existing 2D STRP does not take into account the metric coefficients ( and ) which represent the irregularities in channel geometry and the meandering nature of streams. Thus, spatial variations in channel geometry cannot be appropriately accounted for in the predictions of concentration distribution at downstream sections. On the other hand, the improved version of 2D STRP, called 2D STRP-i, includes the variation in metric coefficients. Furthermore, because the 2D STRP originates from an analytical solution derived in the condition of infinitely wide channels, it cannot adequately account for the influence of wall boundaries in open channels on contaminant transport. To improve this drawback of 2D STRP, the analytical solution using the method of image was adopted to reflect the impingement of contaminant plumes on wall boundaries.
The optimal dispersion coefficients can be found by selecting the values which yielded the best fit between the calculated and measured temporal concentrations at the downstream locations. The best-fitted distribution was determined when the minimum value of the root mean squared error (RMSE) in the comparison between the predicted and the measured temporal distribution at the downstream section was achieved, as illustrated in Figure 4.
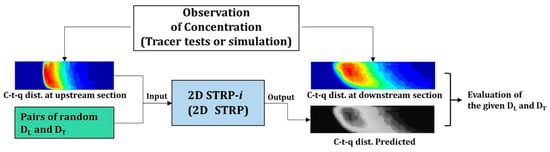
Figure 4.
Illustration of procedure for finding the optimal dispersion coefficient using the routing-based method.
2.3. Evaluation Procedures of the Proposed Routing Method
The discrepancies between the results of 2D STRP and 2D STRP-i in this study were evaluated, using the synthetic data which are the spatial and temporal concentration data. The concentration dataset for the evaluations was produced using the analytic solution described in Equation (15). The evaluation cases were constructed based on the Péclet number, defined as follows.
where represents the mean velocity, while represents the distance at which transverse mixing is fully completed. The complete mixing distance, , can be empirically assumed as follows [32]:
The results provided by Equation (15) were converted to nondimensional variables using the relationship below:
where is the nondimensional longitudinal distance; is the nondimensional transverse distance; is the nondimensional time; is the nondimensional concentration; is the fully mixed concentration; and and are the longitudinal distance and time when the transverse mixing is completed. The nondimensional variables are derived based on the length scale of transverse mixing. When the mass is injected at the center of width, the fully mixed condition in the transverse direction can be observed at .
When the Péclet numbers of the evaluation cases are identical, the nondimensional concentration distributions are identically reproduced, regardless of hydraulic parameters and dispersion coefficients. The Péclet numbers for evaluation cases ranged from 900 to 9000. The detailed values on the 2D dispersion coefficients and hydraulic parameters, used in the generation of synthetic data, are presented in Table 1.

Table 1.
Simulation condition for evaluation of 2D STRP-i.
For each case, ten measuring sections were set as uniform intervals (), as expressed in Figure 5. The concentration data recorded over time were employed as input values in both 2D STRP and 2D STRP-i. The temporal concentration distribution is calculated at the downstream section by inserting the temporal distribution at the upstream section into both 2D STRP and 2D STRP-i. Then, the predicted distribution was matched against that directly measured at the downstream section. The dispersion coefficients were inversely determined as the value which yields the best-fitted distribution. To find the optimal dispersion coefficients, the Latin Hypercube Simulation (LHS) [33,34,35] was applied. The LHS is a kind of stratified Monte Carlo sampling. In this method, the parameter range is partitioned into disjoint intervals. The sample is randomly chosen once from each interval, ensuring the uniform distribution of samples over the parameter range.
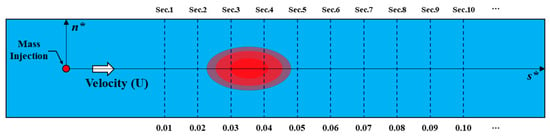
Figure 5.
Locations of the concentration measuring sections for the evaluation procedure. The red dot indicates the tracer mass injection point. The horizontal axis indicates the nondimensional longitudinal distance, while the vertical axis represents the nondimensional transverse distance. The measuring sections were set at uniform intervals ().
2.4. Tracer Tests in Large-Scale Channel
2.4.1. Selection of Experimental Data for Validation of 2D STRP-i
The tracer experiment based on the in situ measurements has generally been conducted to acquire the concentration data for analyzing the contaminant mixing in open-channel flows. The tracer experiments typically produce discrete concentration data at a limited number of points along the experimental intervals. Because of this constraint, prior studies [7,11,14,15] have employed interpolation and extrapolation techniques on the measured concentration data to generate continuous concentration profiles. This approach may result in artificially dispersed concentration profiles, introducing imprecise gradients of the interpolated profiles.
To resolve these limitations, Baek et al. (2019) [21] proposed an experimental framework for remote sensing-based tracer experiments. These techniques enable the observation of tracer concentration with high spatial and temporal resolutions, utilizing the digital imagery data collected by the UAV. They developed experimental procedures and the method for the conversion of RGB digital values to concentration, applying deep learning techniques. Their results showed spatially and temporarily high-resolution tracer concentrations in meandering channels.
The new routing method developed in this study aims to calculate dispersion coefficients more accurately by considering wall reflections of contaminant plumes. Therefore, to validate the performance of the new routing method compared to the existing 2D STRP, experimental methods allowing for concentration measurements near the wall boundaries are required. Thus, the tracer test data observed by Baek et al. (2019) [21] was employed to validate the new routing method in this study.
2.4.2. Experimental Conditions
Tracer tests conducted by Baek et al. (2019) [21] were carried out at the River Experimental Center (REC) of the Korea Institute of Civil Engineering and Building Technology (KICT) in South Korea. The experimental channel was a meandering channel which was artificially constructed to simulate the open-channel flows in the natural river, as shown in Figure 6.
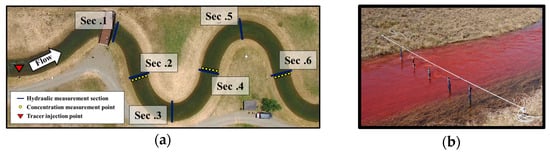
Figure 6.
Experimental channels and measurement sections: (a) The experimental channel and measurement sections for the tracer test; (b) photographic representation of the concentration measurement setup.
The 20% Rhodamine WT solution was used as a tracer. The tracer was instantaneously released at a point upstream of the experimental reach. The hydraulic data, including discharge, velocity distribution, and water depth, were measured at six cross-sections using an Acoustic Doppler Current Profiler (ADCP). The fluorometers were also installed at three cross-sections to measure temporal concentration data. In three sections for measuring temporal concentration profiles, the fluorometers were evenly spaced transversely, as depicted in Figure 6b. In the experimental method for tracer tests based on remote sensing proposed by Beak et al. (2019) [21], deep learning techniques were applied to transform drone-based aerial imagery into high-resolution concentration fields. The deep learning model was trained to establish an empirical relationship between the pixel intensities of each optical band in image data and the concentration of Rhodamine WT was measured by fluorometers. The trained model can generate high-resolution concentration data by applying this established relationship to each pixel in the image data. The detailed description of the experimental conditions and procedures can be found in Baek et al. (2019) [21]. In this study, the EXP-A317 case from Baek et al. (2019) [21] was selected to evaluate both the 2D STRP and 2D STRP-i. The results of hydraulic and concentration measurements, provided from Baek et al. (2019) [21], are summarized in Table 2.

Table 2.
Summary of hydraulic and concentration measurements in tracer test.
2.4.3. Pre-Processing of Tracer Concentration Data
The tracer experiment method based on remote sensing proposed in Baek et al. (2019) [21], as previously mentioned, enables the observation of high-resolution spatiotemporal tracer concentration distributions. The most distinctive advantage of the concentration data produced by this technique is that it allows for the extraction of time-series concentration distributions at any point across the entire experimental section. Figure 7 depicts the spatial distribution of tracer concentration in the EXP-A317 case. The spatial resolution of this spatiotemporal concentration distribution is 5 cm, and the temporal resolution was averaged at 1 s intervals.
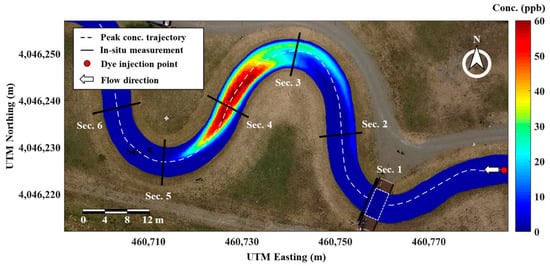
Figure 7.
The observed result of the spatial tracer distribution.
The spatial distribution in the UTM coordinate system was transformed into the stream-tube coordinate system to define the longitudinal direction of streamflow. Previous studies [27,31,36,37] have determined the longitudinal direction based on the hydraulic and geomorphic properties of river flows. As indicated by a dotted line in Figure 7, the path of the maximum concentration at each time was defined as the longitudinal direction in this study to consider the observed path of the tracer plume. The transverse direction was defined as being orthogonal to the longitudinal axes. The longitudinal direction at each transverse point was estimated by tracking the cumulative discharge at each point. The cumulative discharges, as shown in Figure 8, were computed by integrating the local depth-averaged velocity and water depth. Figure 9 presents the spatial concentration distributions that were transformed into the stream-tube coordinates, guided by the trajectory of the maximum concentration. It was observed that the maximum concentration was mainly transported along the center of the channel’s width, while the tracer tails were elongated along the adjacent banks. This elongation can be attributed to the influence of the skewed velocity distribution and the shear effect of wall boundaries. The 2D STRP may encounter challenges when applied to these datasets because of the significant impingement of tracer clouds on the wall boundaries. To verify this limitation, we applied both 2D STRP and 2D STRP-i to determine the 2D dispersion coefficients and compared their results.

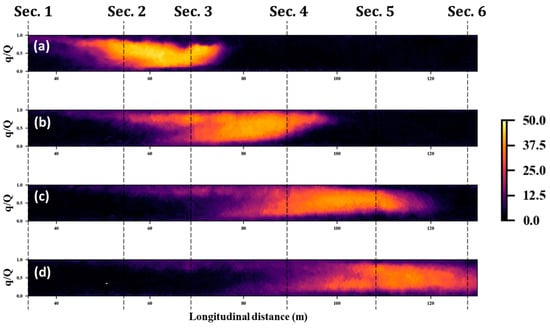
Figure 9.
The spatial concentration distributions in stream-tube coordinates. The horizontal axis indicates the longitudinal distance in meters, while the vertical axis represents the cumulative discharge normalized by total discharge: (a) 90 s after tracer release; (b) 120 s after tracer release; (c) 150 s after tracer release; (d) 175 s after tracer release.
3. Results and Discussion
3.1. Evaluating the Performance of Routing-Based Methods
The performance of both 2D STRP and 2D STRP-i was evaluated in six different cases, with adjustments to the longitudinal dispersion coefficients () controlling the Péclet numbers. Figure 10 and Figure 11 show the representative results from both 2D STRP and 2D STRP-i, which are the temporal concentration distributions of the best fit with the measured distribution for the case of Pe2250. The pollutant clouds reached wall boundaries after Section 4 (s* = 0.08) in Figure 5. Figure 10 shows the prediction of concentration distribution before the pollutant cloud significantly reached the wall boundaries. In this case, both 2D STRP and 2D STRP-i result in identical concentration distributions at the downstream sections. However, in the case corresponding to the concentration distribution after pollutant clouds reached the wall boundaries, 2D STRP provided noticeable inaccuracies, particularly near the wall boundaries. This observation is clearly illustrated in Figure 11. The synthetic data, generated by Equation (15), demonstrated that the gradient of the concentration profile asymptotically approached zero as it neared the wall boundaries, resulting in the concentration curve becoming concave. However, 2D STRP failed to accurately reproduce the mechanism of pollutant clouds impinging on wall boundaries, resulting in the calculation of the concentration distribution outside the intended calculation domain. Consequently, this resulted in a loss in mass in the concentration distribution and a steep gradient, taking the convex shape, for transverse concentration profiles near the wall.
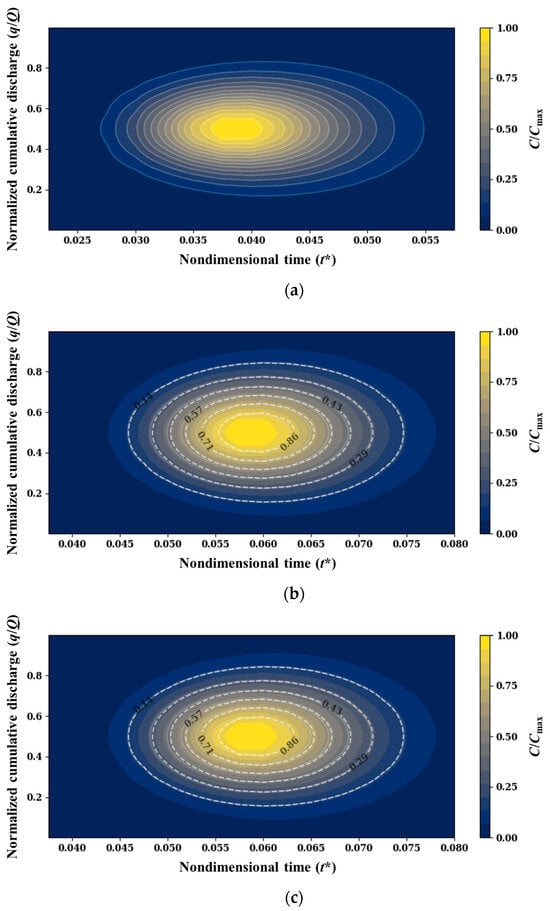
Figure 10.
Predicted concentration distribution for Pe2250 (from Section 2 to Section 3): (a) input distribution observed at Section 2; (b) predicted distribution calculated by 2D STRP at Section 3; (c) predicted distribution calculated by 2D STRP-i at Section 3.
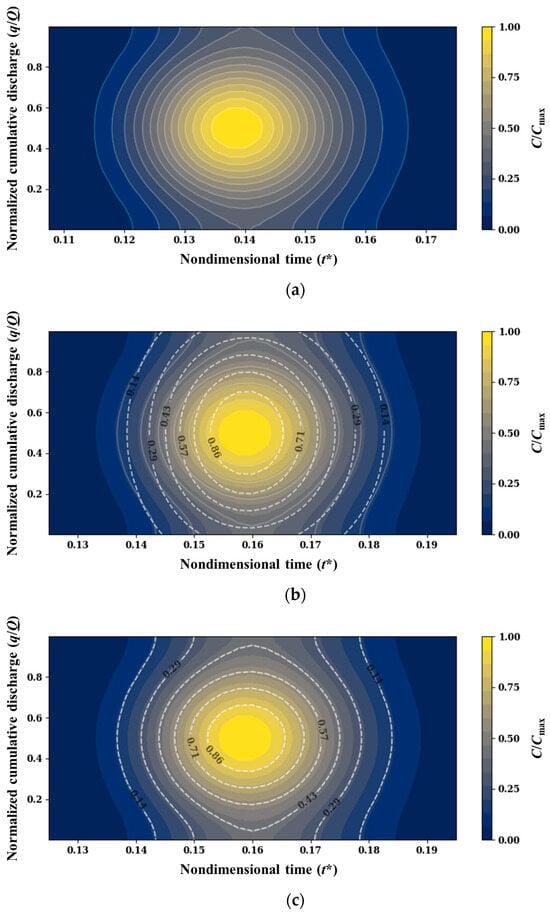
Figure 11.
Predicted concentration distribution for Pe2250 (from Section 7 to Section 8): (a) input distribution observed at Section 7; (b) predicted distribution calculated by 2D STRP at Section 8; (c) predicted distribution calculated by 2D STRP-i at Section 8.
The 2D STRP-i was derived by considering the effects of wall boundaries to compensate for these disadvantages of 2D STRP. As shown in Figure 11c, 2D STRP-i accurately reproduced the shape of the transverse concentration curves, which are concave near the wall boundaries, and the concentration gradient of transverse profiles near the wall boundaries converged to zero like synthetic data.
The dispersion coefficients for both and were also found using the Latin hypercube simulation, as described in Section 2.3. The relative percentage error of the estimated dispersion coefficients were compared to the true values which were used to create the evaluation data as shown in Figure 12.
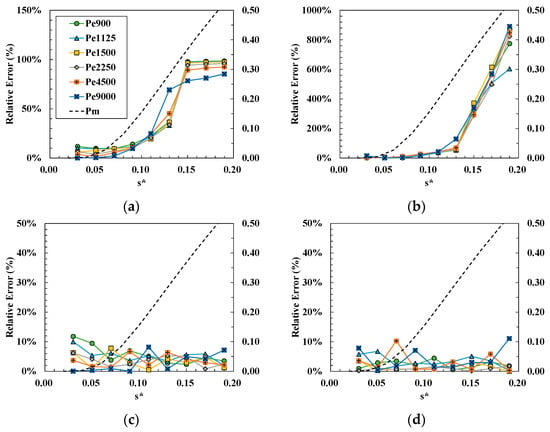
Figure 12.
Relative error of optimal values for both and : (a) longitudinal dispersion coefficients estimated by 2D STRP; (b) transverse dispersion coefficients estimated by 2D STRP; (c) longitudinal dispersion coefficients estimated by 2D STRP-i; (d) transverse dispersion coefficients estimated by 2D STRP-i. The dotted lines indicate the degree of mixing.
The degree of mixing, , was introduced to determine whether the tracer plumes reach the wall boundaries. The values of are defined as [32]:
The degree of mixing initially has a value of zero at the point of mass release. progressively approaches 1 over time. Transverse mixing of the tracer is typically regarded as complete when is close to the value of 0.98. When the peak concentration of tracer plumes approached approximately s* = 0.18, the value of reached 0.5 in this study.
In the results of optimal dispersion coefficients using 2D STRP, the relative errors were generally less than 10% for both and before the pollutant clouds reached the sidewall (). However, when exceeds approximately 0.1, the limitations of 2D STRP become evident, as it fails to incorporate the wall reflection behavior of pollution clouds, leading to a significant overestimation of . Such an overestimation reached up to approximately ten times the actual value in the simulations. Given that 2D STRP aims to simultaneously optimize both and to match the predicted concentration field with the measured concentration field, a substantial increase in the error of invariably impacts as well. The results of 2D STRP-i, which is able to reproduce the wall reflection of pollutant clouds, showed that the relative error was on average less than 5% for and 3% for Thus, the result of evaluations based on synthetic data reveals that 2D STRP-i is capable of determining the optimal dispersion coefficient regardless of the impingement of pollutant clouds on wall boundaries.
3.2. Application to Large-Scale Experiments
The routing-based methods (2D STRP and 2D STRP-i) were applied to the experimental data obtained from tracer tests in large-scale channels outlined in Section 2.4. The tracer experiment data, which were post-processed in this study, enabled the acquisition of continuous concentration profiles across the whole experimental reach without requiring interpolations. The temporal concentration data were transversely collected at 100 points at each section to construct the concentration–time distribution (C-t-q distribution).
The C-t-q distribution at upstream sections was employed as the input distribution for each longitudinal interval. The optimal dispersion coefficients can be determined by finding the optimal values that provide the best-fitted distribution with the measured distribution using appropriate optimization techniques. Piasecki and Katopodes (1999) [38] attempted to find the optimal dispersion coefficients in their contaminant transport models, employing a gradient-based optimization algorithm. They observed that the loss function in their optimization algorithm lost its monotonic convexity, making it challenging to find a unique solution due to uncertainties in concentration data measured in the field surveys. Therefore, the LHS method was employed to find the optimal dispersion coefficients in this study.
The sampling ranges in the LHS were determined based on the range of dimensionless values proposed in previous studies [7,15,32]. The dimensionless longitudinal dispersion coefficient () and the dimensionless transverse dispersion coefficient () were evaluated within the ranges of 1 to 25 and 0.1 to 3.0. The shear velocity, , was determined using the formula for calculating dimensionless values. The bottom slope, S, was assumed to be 0.00125, which corresponds to the design slope of the experimental channels. Within these specified ranges, 5000 pairs of dispersion coefficients were randomly chosen.
The optimal dispersion coefficients were identified as the values that produced the lowest discrepancies between the observed and predicted distributions. The root mean squared error (RMSE) of the lowest discrepancies ranged from 1.89 ppb to 2.85 ppb for 2D STRP-i, while for 2D STRP, the RMSE values were from 1.81 ppb to 2.32 ppb. Because the RMSE of concentration measurements in the tracer experiment was reported as 4 ppb approximately, given this reference point, the optimal dispersion coefficients found in this study can be considered as reasonable values [21].
As illustrated in Figure 13, both the 2D STRP and the 2D STRP-i effectively reproduced the tracer clouds with elongated long tails. However, discrepancies were observed near the wall boundaries in the prediction results between the 2D STRP and 2D STRP-i. In the results obtained using the 2D STRP-i proposed in this study, the concentration gradient adjacent the wall boundaries approached the zero gradient. In contrast, 2D STRP, which did not account for the influence of boundaries, generated steeper gradient distributions adjacent to the side boundaries than the measured distributions.

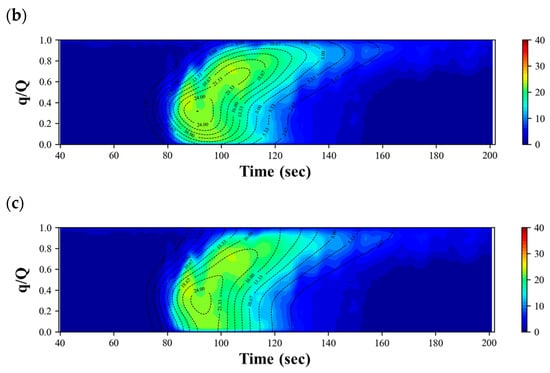
Figure 13.
Predicted temporal concentration distribution (from Section 2 to Section 3); colored region: measured concentration distributions; dashed line: predicted concentration distributions; (a) input concentration distribution at Section 2; (b) concentration distribution predicted by 2D STRP at Section 3; (c) concentration distribution predicted by 2D STRP-i at Section 3.
Therefore, in the optimization procedure for 2D STRP, the transverse dispersion coefficients can be determined to be lower than what might be considered as optimal values, in order to conserve tracer mass. Despite this, calculated by both routing-based methods exhibited similar patterns as shown in Figure 14. As the longitudinal dispersion coefficients are proportional to the longitudinal concentration gradient, their magnitude does not influence mass loss in the 2D STRP model. Therefore, in the existing 2D STRP, the best-fitted distribution tends to be determined with a greater weighting on longitudinal rather than transverse dispersion coefficients.
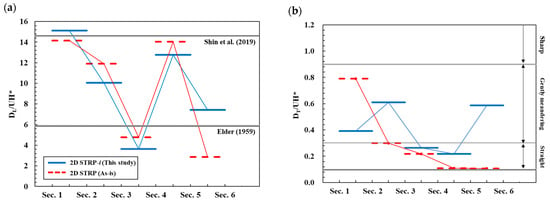
Figure 14.
Results of the nondimensional dispersion coefficients in the large-scale experimental channel; (a) dimensionless longitudinal dispersion coefficients; (b) dimensionless transverse dispersion coefficients; The horizontal solid lines indicate the reference value of nondimensional dispersion coefficients reported by [15,39].
4. Conclusions
In this study, a new routing-based method (2D STRP-i) was developed to resolve the drawbacks of the 2D STRP. The key findings are as follows:
- (i)
- Assessment of the existing 2D STRP:
We quantitatively assessed the accuracy of the results obtained from the 2D STRP by utilizing synthetic data generated through an analytical solution. The 2D STRP demonstrated reasonable performance under the conditions where the contaminant plumes did not significantly approach the wall boundaries. However, the 2D STRP produced inaccurate concentration distributions when the contaminant plumes reached the wall boundaries.
- (ii)
- Assessment of the 2D STRP-i:
The 2D STRP-i effectively considered the influence of wall boundaries on concentration distribution. The results of the 2D STRP-i demonstrated its ability to accurately predict concentration distributions, with less than 5% of relative errors on average, even when contaminant plumes significantly impacted the wall boundaries.
- (iii)
- Application of routing-based method to experimental data
Both 2D STRP and 2D STRP-i were evaluated for their applicability in a large-scale experimental channel. The results showed that the nondimensional longitudinal dispersion coefficient are similarly determined from both 2D STRP and 2D STRP-i, while the nondimensional transverse dispersion coefficients obtained from the 2D STRP were lower than those obtained from 2D STRP-i.
The 2D STRP has been the sole method available to simultaneously observe both and of 2D depth-averaged pollutant transport models. The results of this study indicate that the use of 2D STRP may provide inaccurate dispersion coefficients in the wall-bounded channels due to its inherent functional limitations. The use of 2D STRP-i, developed in this study, is advantageous to estimate accurate dispersion coefficients considering the influence of the boundary effect. Furthermore, the 2D STRP-i can serve as a valuable tool to improve the prediction accuracy of 2D ADE-based numerical models, facilitating the provision of more accurate dispersion parameters.
Author Contributions
Conceptualization, I.W.S.; methodology, D.B.; software, D.B.; validation, D.B. and J.S.K.; formal analysis, S.H.J.; investigation, D.B.; data curation, S.H.J.; writing—original draft preparation, D.B.; writing—review and editing, D.B. and J.S.K.; visualization, S.H.J.; supervision, I.W.S.; funding acquisition, Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (NRF-2021R1C1C2012406).
Data Availability Statement
The data used in this study are available on request from the corresponding author (substantial size of data volume).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fischer, H.B.; List, E.; Koh, R.; Imberger, J.; Brooks, N. Mixing in Inland and Coastal Waters; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- Baek, K.O.; Seo, I.W. On the methods for determining the transverse dispersion coefficient in river mixing. Adv. Water Resour. 2016, 90, 1–9. [Google Scholar] [CrossRef]
- Godfrey, R.G.; Frederick, B.J. Stream Dispersion at Selected Sites; Professional Paper; No. 433-K; U.S. Geological Survey: Denver, CO, USA, 1970.
- Nordin, C.F.; Sabol, G.V. Empirical Data on Longitudinal Dispersion in Rivers; Water-Resources Investigations Report 74–20; U.S. Geological Survey: Denver, CO, USA, 1974.
- Kilpatrick, F.A.; Wilson, J.F. Measurement of Time of Travel in Streams by Dye Tracing; Techniques of Water-Resources Investigation 3-A9; U.S. Geological Survey: Denver, CO, USA, 1989.
- Seo, I.; Baek, K.O.; Jeon, T.M. Analysis of transverse mixing in natural streams under slug tests. J. Hydraul. Res. 2006, 44, 350–362. [Google Scholar] [CrossRef]
- Seo, I.W.; Choi, H.J.; Kim, Y.D.; Han, E.J. Analysis of two-dimensional mixing in natural streams based on transient tracer tests. J. Hydraul. Eng. 2016, 142, 04016020. [Google Scholar] [CrossRef]
- Jung, S.H.; Seo, I.W.; Kim, Y.D.; Park, I. Feasibility of Velocity-Based Method for Transverse Mixing Coefficients in River Mixing Analysis. J. Hydraul. Eng. 2019, 145, 04019040. [Google Scholar] [CrossRef]
- Sayre, W.W. A Laboratory Investigation of Open-Channel Dispersion Processes for Dissolved, Suspended, and Floating Dispersants; US Government Printing Office: Washington, DC, USA, 1968.
- Beltaos, S. Transverse mixing tests in natural streams. J. Hydraul. Div. 1980, 106, 1607–1625. [Google Scholar] [CrossRef]
- Baek, K.O.; Seo, I.W. Routing procedures for observed dispersion coefficients in two-dimensional river mixing. Adv. Water Resour. 2010, 33, 1551–1559. [Google Scholar] [CrossRef]
- Fisher, H.B. Dispersion predictions in natural streams. J. Sanit. Eng. Div. 1968, 94, 927–944. [Google Scholar] [CrossRef]
- Singh, S.K.; Beck, M.B. Dispersion coefficient of streams from tracer experiment data. J. Environ. Eng. 2003, 129, 539–546. [Google Scholar] [CrossRef]
- Baek, K.O.; Seo, I.W.; Jeong, S.J. Evaluation of dispersion coefficients in meandering channels from transient tracer tests. J. Hydraul. Eng. 2006, 132, 1021–1032. [Google Scholar] [CrossRef]
- Shin, J.; Seo, I.W.; Baek, D. Longitudinal and transverse dispersion coefficients of 2D contaminant transport model for mixing analysis in open channels. J. Hydrol. 2019, 583, 124302. [Google Scholar] [CrossRef]
- Fischer, H.B. Longitudinal Dispersion in Laboratory and Natural Streams; Report No. KH-R-12; California Institute of Technology: Pasadena, CA, USA, 1966. [Google Scholar]
- Flynn, K.F.; Chapra, S.C. Remote sensing of submerged aquatic vegetation in a shallow non-turbid river using an unmanned aerial vehicle. Remote Sens. 2014, 6, 12815–12836. [Google Scholar] [CrossRef]
- Tamminga, A.; Hugenholtz, C.; Eaton, B.; Lapointe, M. Hyperspatial remote sensing of channel reach morphology and hydraulic fish habitat using an unmanned aerial vehicle (UAV): A first assessment in the context of river research and management. River Res. Appl. 2015, 31, 379–391. [Google Scholar] [CrossRef]
- Detert, M.; Weitbrecht, V. A low-cost airborne velocimetry system: Proof of concept. J. Hydraul. Res. 2015, 53, 532–539. [Google Scholar] [CrossRef]
- Wigmore, O.; Mark, B.G. Monitoring tropical debris-covered glacier dynamics from high-resolution unmanned aerial vehicle photogrammetry, Cordillera Blanca, Peru. Cryosphere 2017, 11, 2463. [Google Scholar] [CrossRef]
- Baek, D.; Seo, I.W.; Kim, J.S.; Nelson, J.M. UAV-based measurements of spatio-temporal concentration distributions of fluorescent tracers in open channel flows. Adv. Water Resour. 2019, 127, 76–88. [Google Scholar] [CrossRef]
- Kinzel, P.J.; Legleiter, C.J. sUAS-based remote sensing of river discharge using thermal particle image velocimetry and bathymetric lidar. Remote Sens. 2019, 11, 2317. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Sansom, B.J.; Jacobson, R.B. Remote sensing of visible dye concentrations during a tracer experiment on a large, turbid river. Water Resour. Res. 2022, 58, e2021WR031396. [Google Scholar] [CrossRef]
- Kwon, S.; Gwon, Y.; Kim, D.; Seo, I.W.; You, H. Unsupervised Classification of Riverbed Types for Bathymetry Mapping in Shallow Rivers Using UAV-Based Hyperspectral Imagery. Remote Sens. 2023, 15, 2803. [Google Scholar] [CrossRef]
- Kwon, S.; Seo, I.W.; Lyu, S. Investigating mixing patterns of suspended sediment in a river confluence using high-resolution hyperspectral imagery. J. Hydrol. 2023, 620, 129505. [Google Scholar] [CrossRef]
- Baek, D. Routing Method for Two-Dimensional Dispersion Coefficients in Open Channel and Its Application for Remotely Sensed Tracer Tests. Ph.D. Dissertation, Seoul National University, Seoul, Republic of Korea, 2020. [Google Scholar]
- Yotsukura, N.; Sayre, W.W. Transverse mixing in natural channels. Water Resour. Res. 1976, 12, 695–704. [Google Scholar] [CrossRef]
- Shen, H.T. Transient mixing in river channels. J. Environ. Eng. Div. 1978, 104, 445–459. [Google Scholar] [CrossRef]
- Harden, T.O.; Shen, H.T. Numerical simulation of mixing in natural rivers. J. Hydraul. Div. 1979, 105, 393–408. [Google Scholar] [CrossRef]
- Yotsukura, N.; Cobb, E.D. Transverse Diffusion of Solutions in Natural Streams; US Geo. Survey Paper; US Government Printing Office: Washington, DC, USA, 1972; Volume 582.
- Lau, Y.L.; Krishnappan, B.G. Modeling transverse mixing in natural streams. J. Hydraul. Div. 1981, 107, 209–226. [Google Scholar] [CrossRef]
- Rutherford, J.C. River Mixing; John Wiley and Sons: Chichester, UK, 1994; pp. 48–51. [Google Scholar]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. Comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Eglajs, V.; Audze, P. New approach to the design of multifactor experiments. Probl. Dyn. Strengths 1977, 35, 104–107. [Google Scholar]
- Iman, R.L.; Davenport, J.M.; Zeigler, D.K. Latin Hypercube Sampling (Program User’s Guide); [LHC, in FORTRAN] (No. SAND-79–1473); Sandia Labs.: Albuquerque, NM, USA, 1980.
- Carbonneau, P.E.; Lane, S.N.; Bergeron, N. Feature based image processing methods applied to bathymetric measurements from airborne remote sensing in fluvial environments. Earth Surf. Process. Landf. J. Br. Geomorphol. Res. Group 2006, 31, 1413–1423. [Google Scholar] [CrossRef]
- Merwade, V.; Cook, A.; Coonrod, J. GIS techniques for creating river terrain models for hydrodynamic modeling and flood inundation mapping. Environ. Model. Softw. 2008, 23, 1300–1311. [Google Scholar] [CrossRef]
- Piasecki, M.; Katopodes, N.D. Identification of stream dispersion coefficients by adjoint sensitivity method. J. Hydraul. Eng. 1999, 125, 714–724. [Google Scholar] [CrossRef]
- Elder, J. The dispersion of marked fluid in turbulent shear flow. J. Fluid Mech. 1959, 5, 544–560. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).