Prediction Model of Water Abundance of Weakly Cemented Sandstone Aquifer Based on Principal Component Analysis–Back Propagation Neural Network of Grey Correlation Analysis Decision Making
Abstract
1. Introduction
2. Survey of the Research Area
3. The Selection of Influencing Factors to Characterize the Water Abundance of Weakly Cemented Sandstone Aquifers
3.1. Related Factor Indicators
3.1.1. Layers of Sand–Mud Interaction nh
3.1.2. Sand–Mud Ratio nsn
3.1.3. Equivalent Thickness of Sandstone Sdx
3.1.4. Buried Depth of Aquifer H
3.1.5. Core Recovery V
3.1.6. The Average Single-Layer Thickness of Sandstone Sdc
3.1.7. Number of Sandstone Layers nc
3.2. Factor Index Quantification
3.3. Factor Index Screening Based on Grey Correlation Analysis
- Select the target parameter as the reference sequence X0 = (x01, x02, …, x0n), and the control factor as the comparison sequence Xi = (xi1, xi2, …, xin), where n is the number of data groups, i is the i-th control factor, , and m is the number of control factors;
- The initial value method is used to non-dimensionalize the above sequence, and the following is obtained: , ;
- Obtain the grey correlation coefficient () between the above dimensionless reference series and the comparison series:In the formula, is the absolute difference between the reference sequence and each comparison sequence, , Min is the minimum value in , and Max is the maximum value. v is the resolution coefficient, usually v = 0.5;
- Calculate the correlation degree ri:
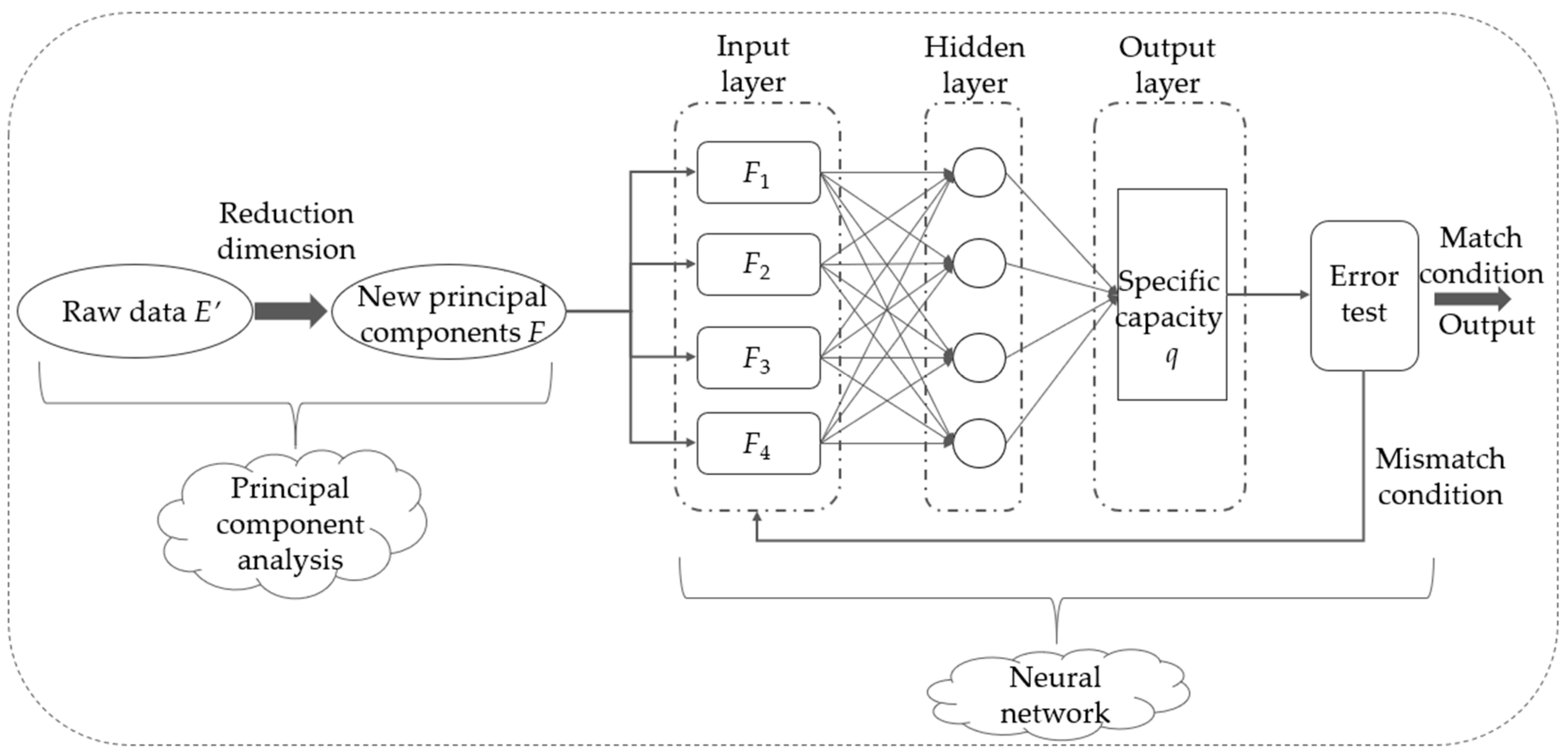
4. Prediction Method for Water Abundance Based on the PCA-BP Neural Network Model
4.1. Principal Component Analysis (PCA)
4.1.1. Principle of Principal Component Analysis
- Generate the variable matrix of each factor index , = (,, …, )T, where and ; m and n represent the number of datasets and the number of factor indicators, respectively.
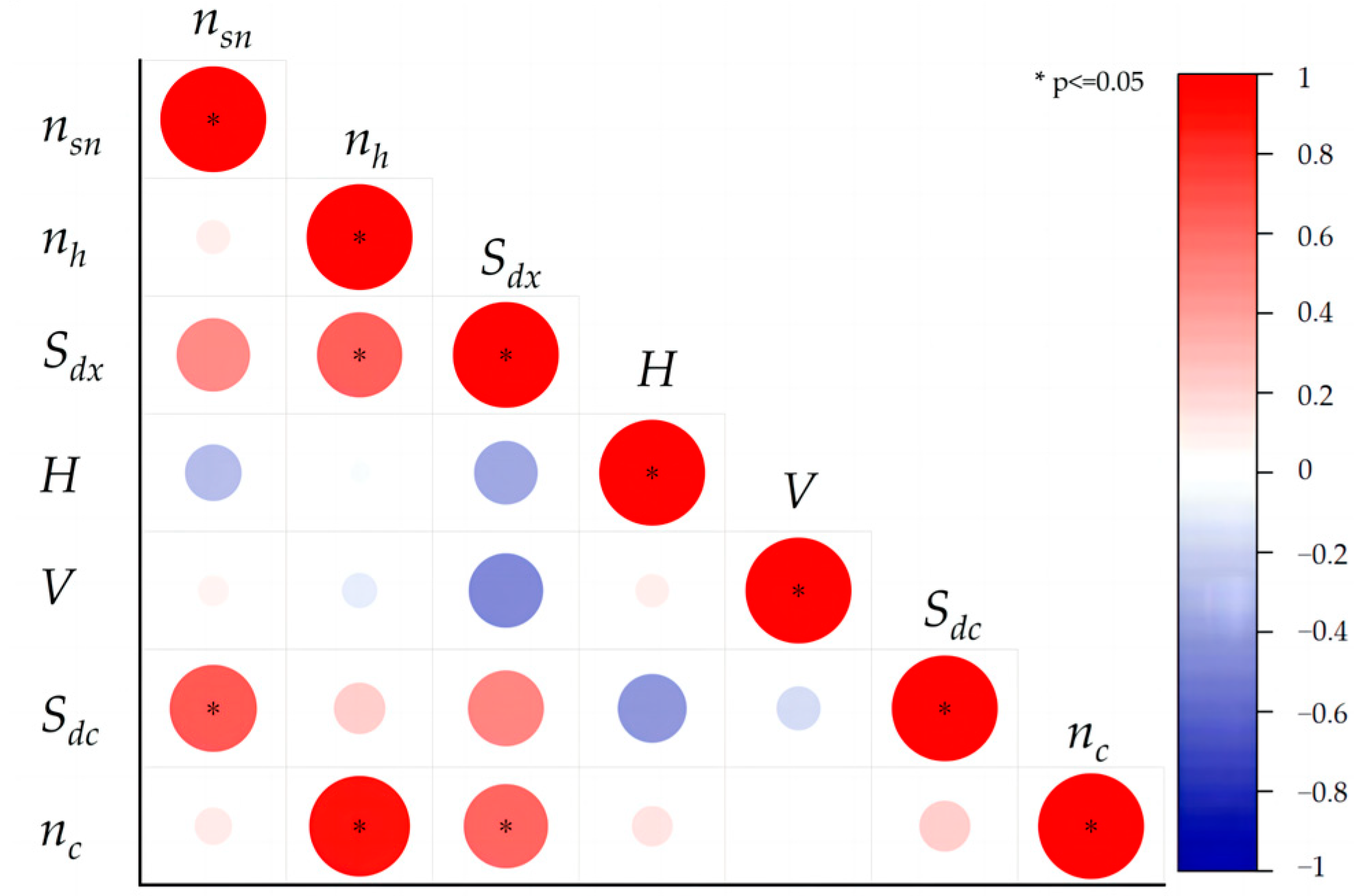
- The correlation analysis is carried out after the above variable matrix is standardized, and the correlation between the influencing factors is preliminarily determined so as to further determine the necessity of principal component analysis.Matrix standardization:In the above formula, is the mean of the column vector, , and is the standard deviation of the column vector, , where and ; m and n represent the number of datasets and the number of factor indicators, respectively.Correlation coefficient calculation:In the formula, and are the a-th column vector and the b-th column vector in the variable matrix , respectively, ; n represents the number of influencing factors.
- Based on the variable correlation matrix, the principal component feature matrix is generated using the PCA algorithm, and the accumulated percentage contribution of each principal component to the influencing factors is calculated.
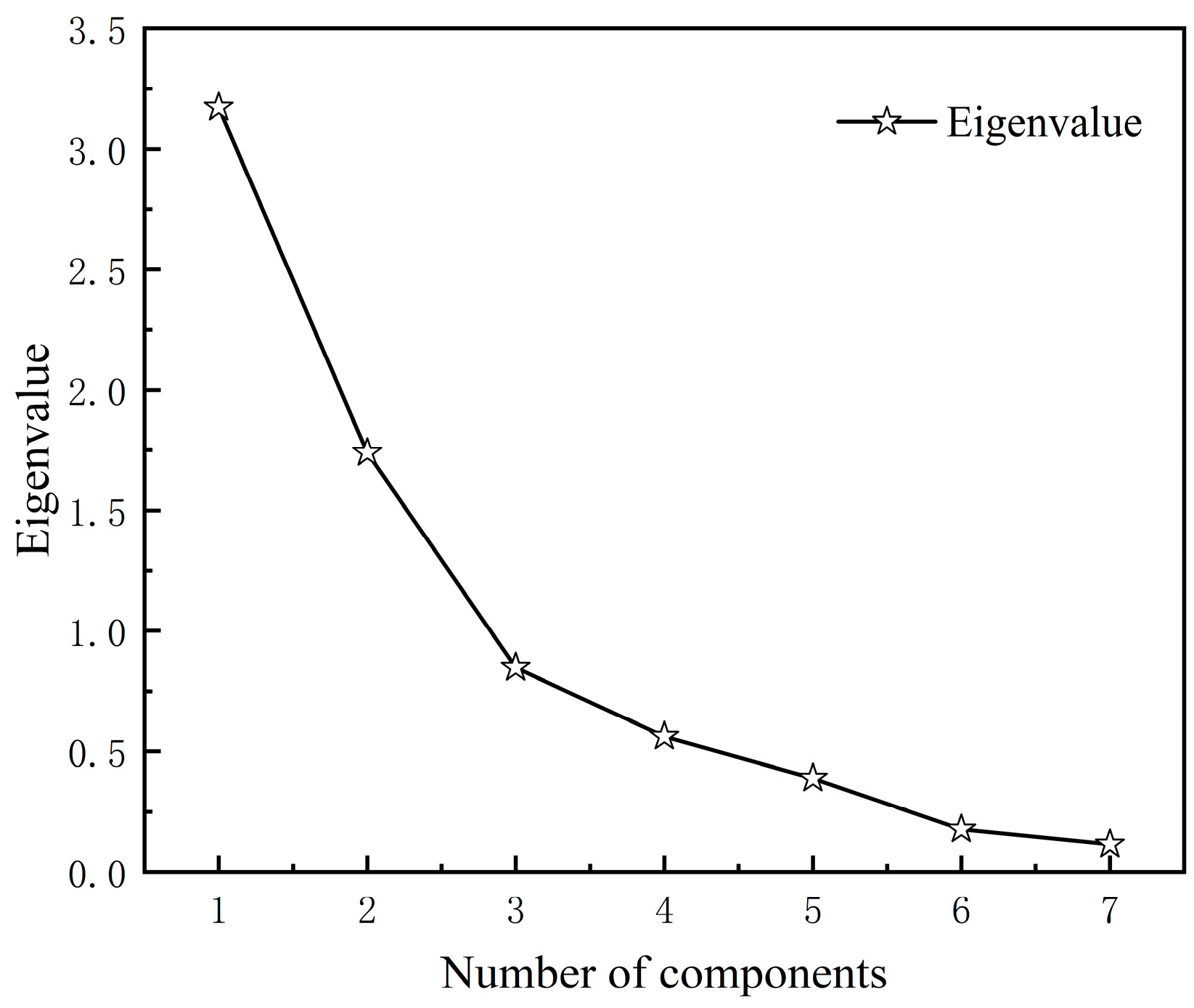
- Analyze the cumulative proportion of principal components to determine whether the accumulating contribution rate meets the information extraction accuracy setting requirements (conventionally set at 80%). If it meets the requirements, the principal components with a cumulative variance contribution of less than 80% are discarded, and the remaining principal components are calculated as follows (see Formula (6)). Generate j () new principal components to ensure that it can represent most of the information of the original variable:Need to meet the conditions:
- ;
- ;
- .
- Constitute the new principal component into the matrix , Fj = (f1j, f2j, …, fmj)T, where fmj represents the value of the j-th new principal component in the m-th set of data.
4.1.2. Construction of the Principal Component Analysis Model
4.2. PCA-BP Neural Network Modeling
5. Discussion and Practical Application
5.1. Comparative Verification of Water-Richness Prediction Models
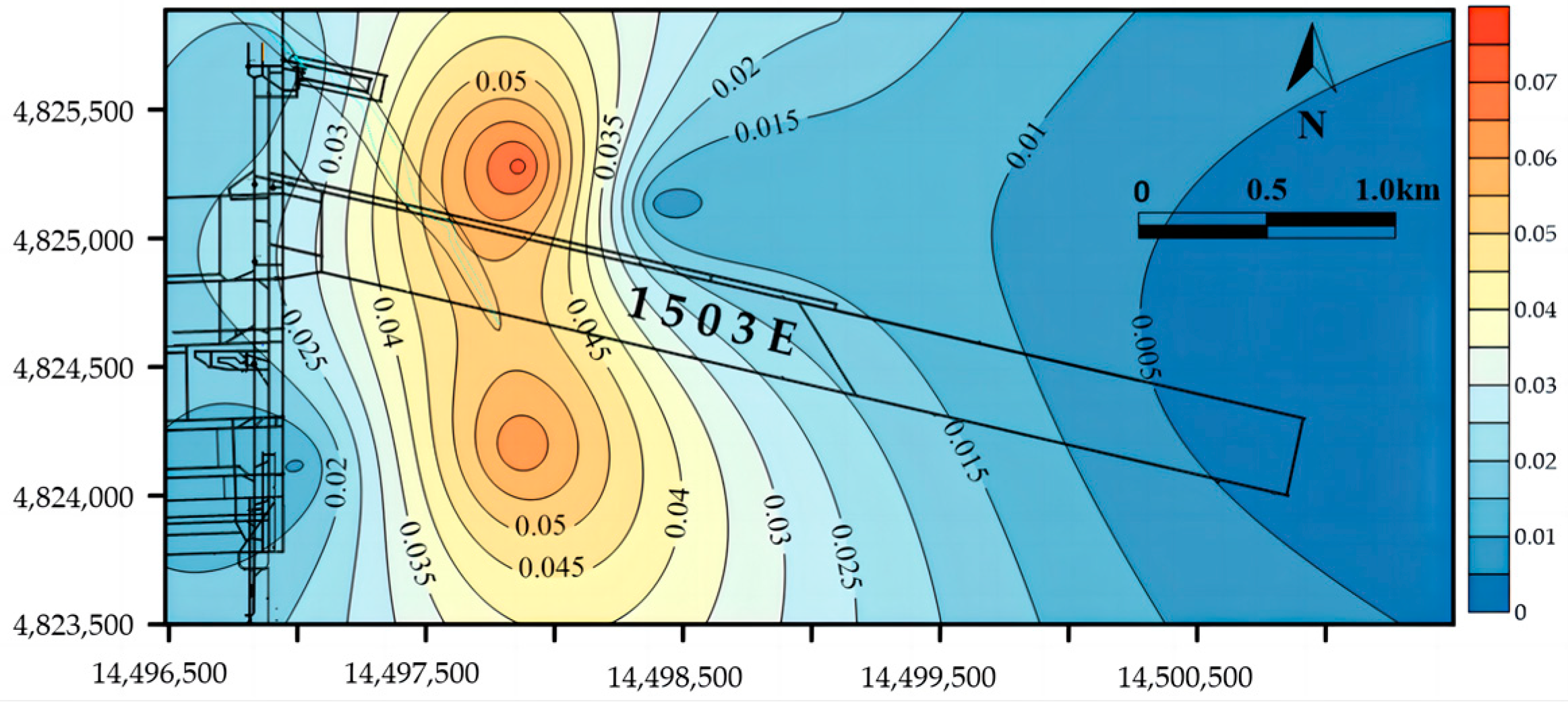
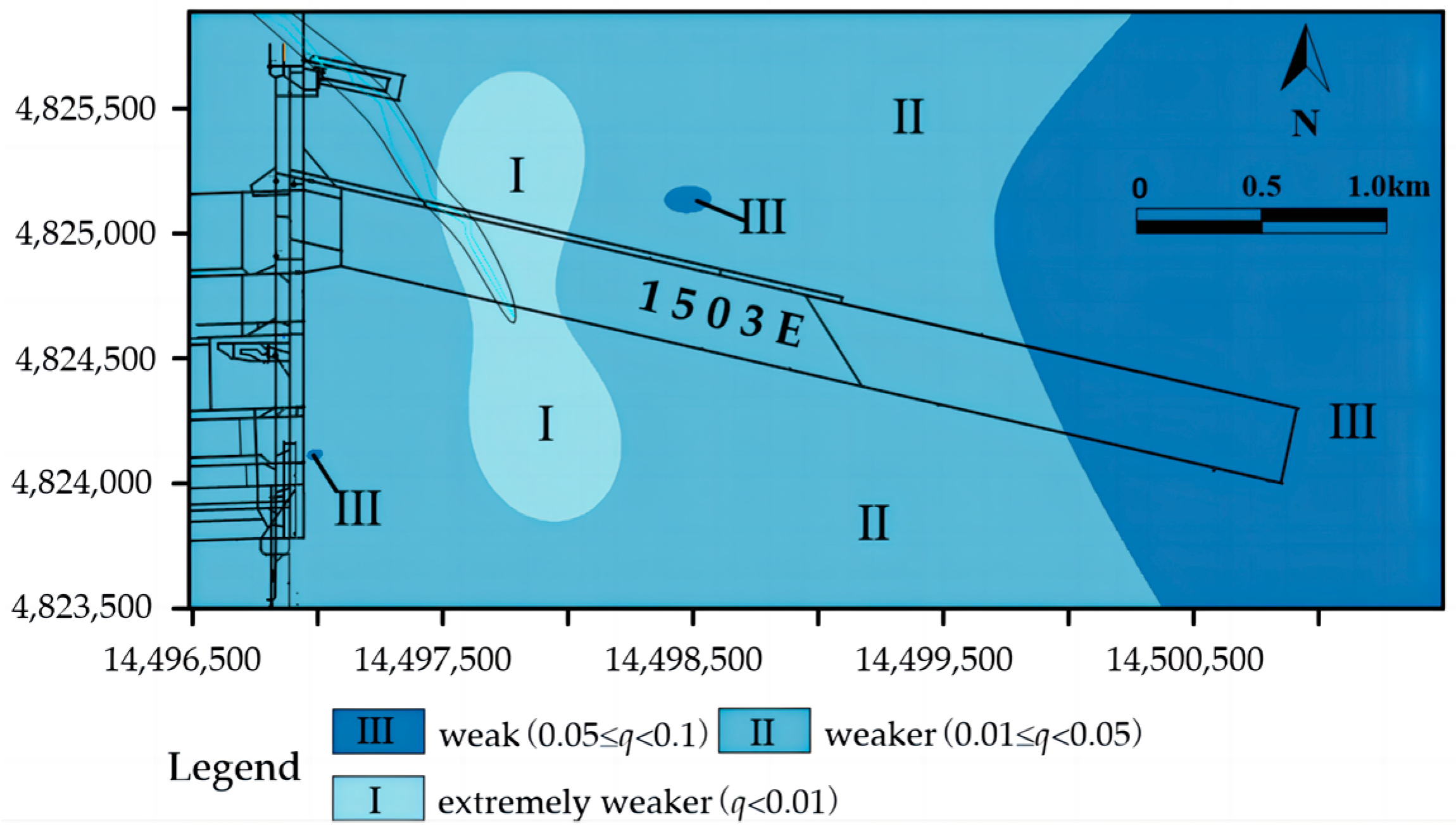
5.2. Evaluation of Water Abundance of Weakly Cemented Sandstone Aquifer in the Study Area
6. Conclusions
- In this paper, the units of water inflow (q) are selected as the predicted value. The grey correlation analysis method (GRA) is used to select the layers of sand–mud interaction nh, the sand–mud ratio nsn, the equivalent thickness of sandstone Sdx, the buried depth of aquifer H, the core recovery V, the average single-layer thickness of sandstone Sdc, and the number of sandstone layers nc, which are more than 0.8 more accurate as the predictive factors of the water richness of weakly cemented sandstone. The higher the degree of closeness between the selected factor index and the predicted value, the more accurate the subsequent prediction results;
- The PCA method is utilized to analyze the correlations among the indicators of the factors, and the influencing factors that are weakly correlated and repeated with the prediction of units of water inflow (q) are eliminated to realize the dimensionality reduction of the original sample input, effectively improve the training efficiency of the whole network, and then enhance the accuracy of predictive modeling of water enrichment in an aquifer with weakly cemented sandstone;
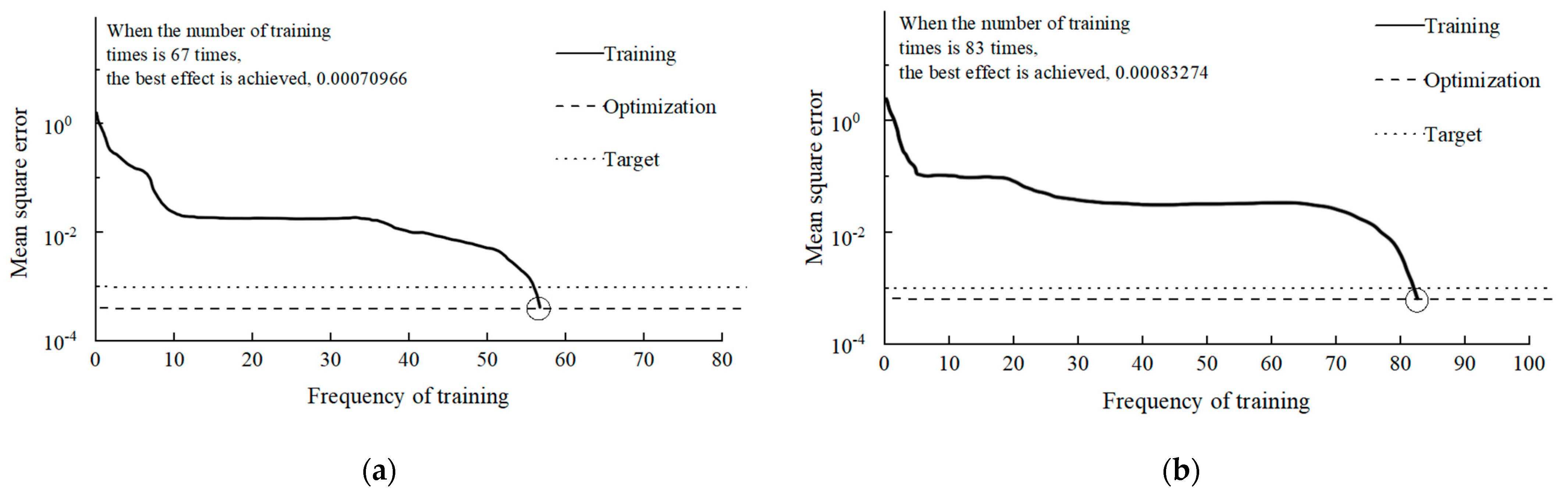
- According to the proportion of 4:1, the samples processed through the principal component analysis and the original samples are categorized into a training dataset and a test dataset, which are input into the PCA-BP neural network of the weakly cemented water-richness prediction model and the single BP network prediction model, respectively, to complete the construction of the corresponding model. Through the comparison of the training process, it is found that the PCA-BP model has fewer iterations and faster convergence speed;
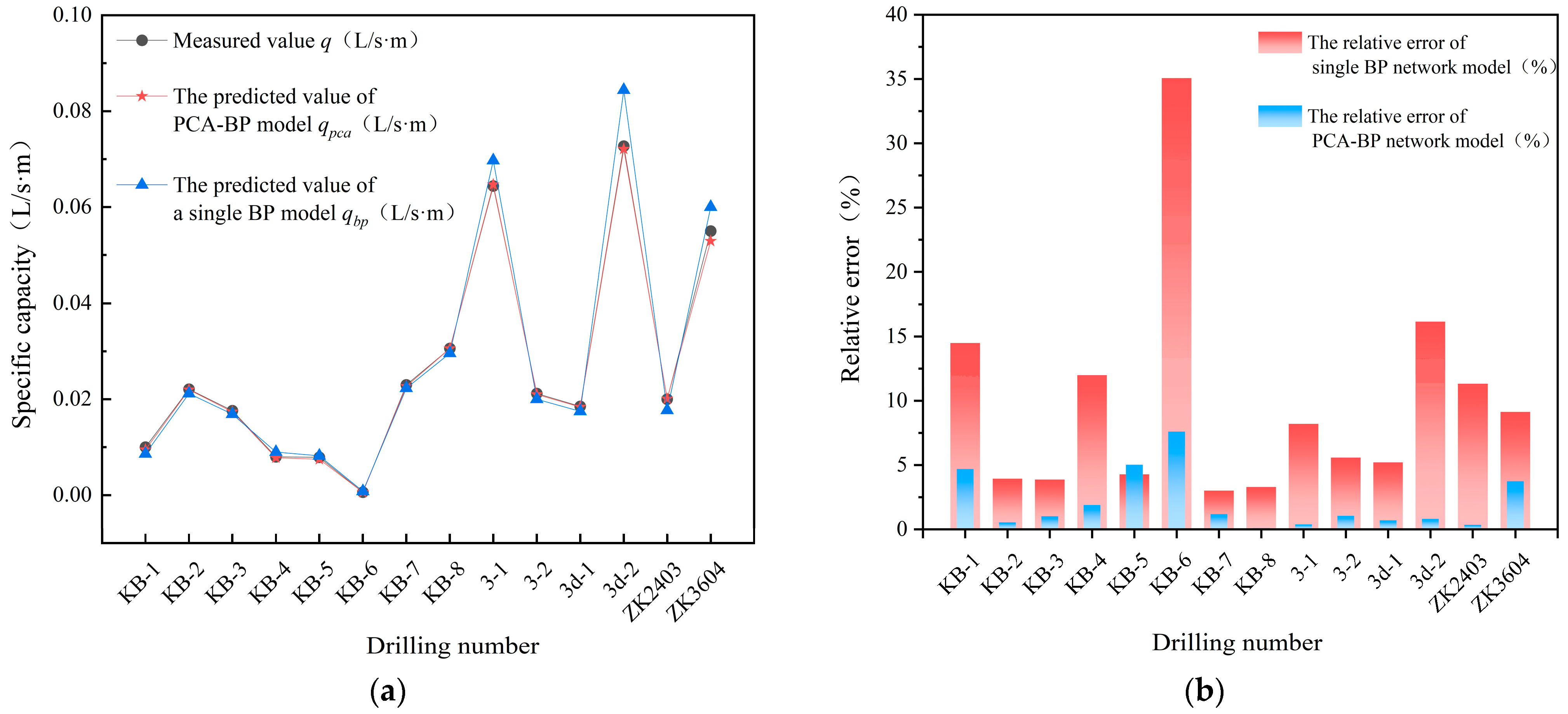
- The borehole data of the weakly cemented sandstone aquifer at the top plate of the No. 3 coal seam within the study area are inputted into the PCA-BP model and the single BP model, respectively. Through comparison, it is found that the average relative error of the PCA-BP model is 2.0794%, and the relative error is relatively stable. The average accuracy reaches 97.9206%, and its prediction accuracy is much greater than that of the single BP network model. In this paper, a PCA-BP prediction model of the water abundance of a cemented sandstone aquifer based on grey correlation analysis and decision making can be obtained through research, which can provide a method to predict the water abundance of a cemented sandstone aquifer with temperature, speed, and high precision;
- The PCA-BP network model is introduced into the practical engineering application of water-richness evaluation of a weakly cemented sandstone aquifer. The prediction results are divided into three grades, namely, extremely weaker water-rich area (q < 0.01 L/s·m), weaker water-rich area (0.01 ≤ q < 0.05 L/s·m), and weak water-rich area (0.05 ≤ q < 0.1 L/s·m).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qian, Z.W.; Jiang, Z.Q.; Cao, L.W.; Sun, Q. Experiment study of penetration grouting model for weakly cemented porous media. Rock Soil Mech. 2013, 34, 139–142, 147. [Google Scholar]
- Wu, R.; Deng, J.G.; Li, M. Study of Macromechanics and Mesomechanics Behavior of Poorly Consolidated Sandstone Using Particle Flow Code; International Field Exploration and Development Conference: Chengdu, China, 2017; p. 12. [Google Scholar]
- Xie, X.Y.; Kang, X.; Zhou, B.; Li, A.Y.; Kang, Y.F. Study on Water-induced Softening Mechanism of Weakly Cemented Sandstone. Build. Constr. 2023, 45, 2359–2362. [Google Scholar]
- Zhu, X.J. Water physical properties of soft rock. Min. Sci. Technol. 1996, 24, 46–50. [Google Scholar]
- Lyu, Y.G.; Xiao, Q.H.; Han, G. Study on Mechanism of High-strength Water-inrush with Sand Caused by Weak Aquifer in Soft Rock Mining Area. Saf. Coal Mines 2019, 50, 38–42, 47. [Google Scholar]
- Lyu, Y.G.; Qi, D.H. Technique based on “double maps” for assessment of water inrush from roof aquifer and its application—With New Shanghai No.1 coal mine at western edge of Ordos basin as example. Coal Geol. Explor. 2016, 44, 108–112. [Google Scholar]
- Lyu, Z.M.; Meng, F.Z.; Lyu, W.M.; Li, L.N. Improved Method for Predicting and Evaluating Water Yield Property. Coal Technol. 2023, 42, 152–155. [Google Scholar]
- Qiu, Z.L.; Chen, W.H.; Bao, D.L.; Liu, Y.H.; Feng, J.W.; Huang, C.M. Combined Detection of Mine Water Disasters with Various Geophysical Prospecting Techniques. Min. Saf. Environ. Prot. 2016, 43, 60–63, 67. [Google Scholar]
- Wu, Q. Progress, problems and prospects of prevention and control technology of mine water and reutilization in China. J. China Coal Soc. 2014, 39, 795–805. [Google Scholar]
- Wu, Q.; Wang, Y.; Zhao, D.K.; Shen, J.J. Water abundance assessment method and application of loose aquifer based on sedimentary characteristics. J. China Univ. Min. Technol. 2017, 46, 460–466. [Google Scholar]
- Yu, J. Research on Aquifer Prediction Method of Coal Seam Roof Sandstone Based on Seismic and Logging Data; China University of Mining and Technology: Xuzhou, China, 2022. [Google Scholar]
- Li, L.N.; Wei, J.C.; Li, L.Y.; Shi, S.Q.; Yin, H.Y. Water yield property prediction model of aquifer based on logging data: A case study from Yingpanhao mine field in Ordos area. China Min. Mag. 2019, 28, 143–147. [Google Scholar]
- Li, Y.T.; Pu, Z.G.; Ding, X.; Wang, Y.; Xie, X.F.; He, X.L. Application of Integrated Geophysical Prospecting in Narin Gol Coalmine No. 2 Sandstone Water Control. Coal Geol. China 2018, 30, 75–79. [Google Scholar]
- Liu, S.C.; Liu, Z.X.; Jiang, Z.H. Application of T EM in Hydrogeological Prospecting of Mining District. J. China Univ. Min. Technol. 2005, 414–417. [Google Scholar]
- Li, Q.; Sui, W.H.; Sun, B.T.; Li, D.L.; Yu, S.B. Application of TOPSIS water abundance comprehensive evaluation method for karst aquifers in a lead zinc mine, China. Earth Sci. Inform. 2022, 15, 397–411. [Google Scholar] [CrossRef]
- Liu, S.Q.; Wu, Q.; Zeng, Y.F.; Gong, H.J.; Li, Z. The Improved AHP Vulnerable Index Method Based on GIS. Earth Sci. 2017, 42, 625–633. [Google Scholar]
- Shi, L.Q.; Huang, J.Y.; Han, J.; Qin, D.X.; Guo, Y.C. PCA-BP model for height prediction of water conducting fracture zone. China Sci. 2019, 14, 471–475. [Google Scholar]
- Detailed Rules for Coal Mine Water Control. National Coal Mine Safety Supervision Bureau Formulated. China, 2018. Available online: https://www.chinamine-safety.gov.cn/xw/zt/2019zt/mkfzszt/gcsy/201906/P020190605471473790006.pdf (accessed on 11 January 2024).
- Li, Z.; Zeng, Y.F.; Liu, S.Q.; Gong, H.J.; Niu, P.K. Application of back propagation artificial neural network in water abundance evaluation. Coal Eng. 2018, 50, 114–118. [Google Scholar]
- Han, Z.; Wang, X.L.; Shi, L.Q. Study on application of PCA-BP neural network in discrimination of karst water inrush source in mine. J. Henan Polytech. Univ. (Nat. Sci.) 2023, 42, 46–53. [Google Scholar]
- Li, Y.Y. Grey correlation analysis of industrial structure and economic growth in Gansu province. Enterp. Econ. 2011, 30, 20–23. [Google Scholar]
- Man, K.; Wu, L.W.; Liu, X.L.; Song, Z.F.; Liu, Z.X.; Liu, R.L.; Cao, Z.X. Rock burst Grade Prediction Based on Grey Correlation Analysis and SSA-RF Mode. Met. Mine 2023, 5, 202–212. [Google Scholar]
- Xu, M.G.; Gao, S.S.; Cao, Y.J.; Lu, Y.N.; Wang, J.J. Forecast of Gas Content Based on Gray Theory and Multiple Regression Analysis. Saf. Coal Mines 2018, 49, 211–214. [Google Scholar]
- Liu, J.; Bai, X.W. Application of Adaptive Neuro-Fuzzy Inference Systems with Principal Component Analysis Model for the Forecasting of Carbonation Depth of Reinforced Concrete Structures. Appl. Sci. 2023, 13, 5824. [Google Scholar] [CrossRef]
- Yuan, H.P.; Ji, S.J.; Liu, G.L.; Xiong, L.J.; Li, H.Z.; Cao, Z.H.; Xia, Z.J. Investigation on Intelligent Early Warning of Rock Burst Disasters Using the PCA-PSO-ELM Model. Appl. Sci. 2023, 13, 8796. [Google Scholar] [CrossRef]
- Duan, Y.F.; Liu, X.J.; Li, X.; Liu, R.; Li, H.W.; Zhao, J. Molten iron yield predicting of blast furnace using PSO-BP model based on PCA decision. China Metall. 2023, 33, 114–126, 137. [Google Scholar]
- Li, Z.H. Damage Detection of Beam Bridge Structure Based on Principal Component analysis And Grey Relational Analysis; Jinan University: Guangzhou, China, 2020. [Google Scholar]
- Lan, T.W.; Guo, X.T.; Zhang, Z.J.; Liu, M.W. Prediction of micro seismic events in rock burst mines based on MEA-BP neural network. Sci. Rep. 2023, 13, 8523. [Google Scholar] [CrossRef] [PubMed]
- Li, W.Y.; Li, B.J.; Ma, W.Y. Prediction of agricultural grey water footprint in Henan Province based on GM (1, N)-BP neural network. Environ. Ecol. Stat. 2023, 30, 335–354. [Google Scholar] [CrossRef]
- Xie, Y.G.; Gao, C.G.; Wang, P.Z.; Zhou, L.; Zhang, C.J.; Qu, X.Q. Research on Vibration Fatigue Damage Locations of Offshore Oil and Gas Pipelines Based on the GA-Improved BP Neural Network. Shock Vib. 2023, 2023, 2530651. [Google Scholar] [CrossRef]

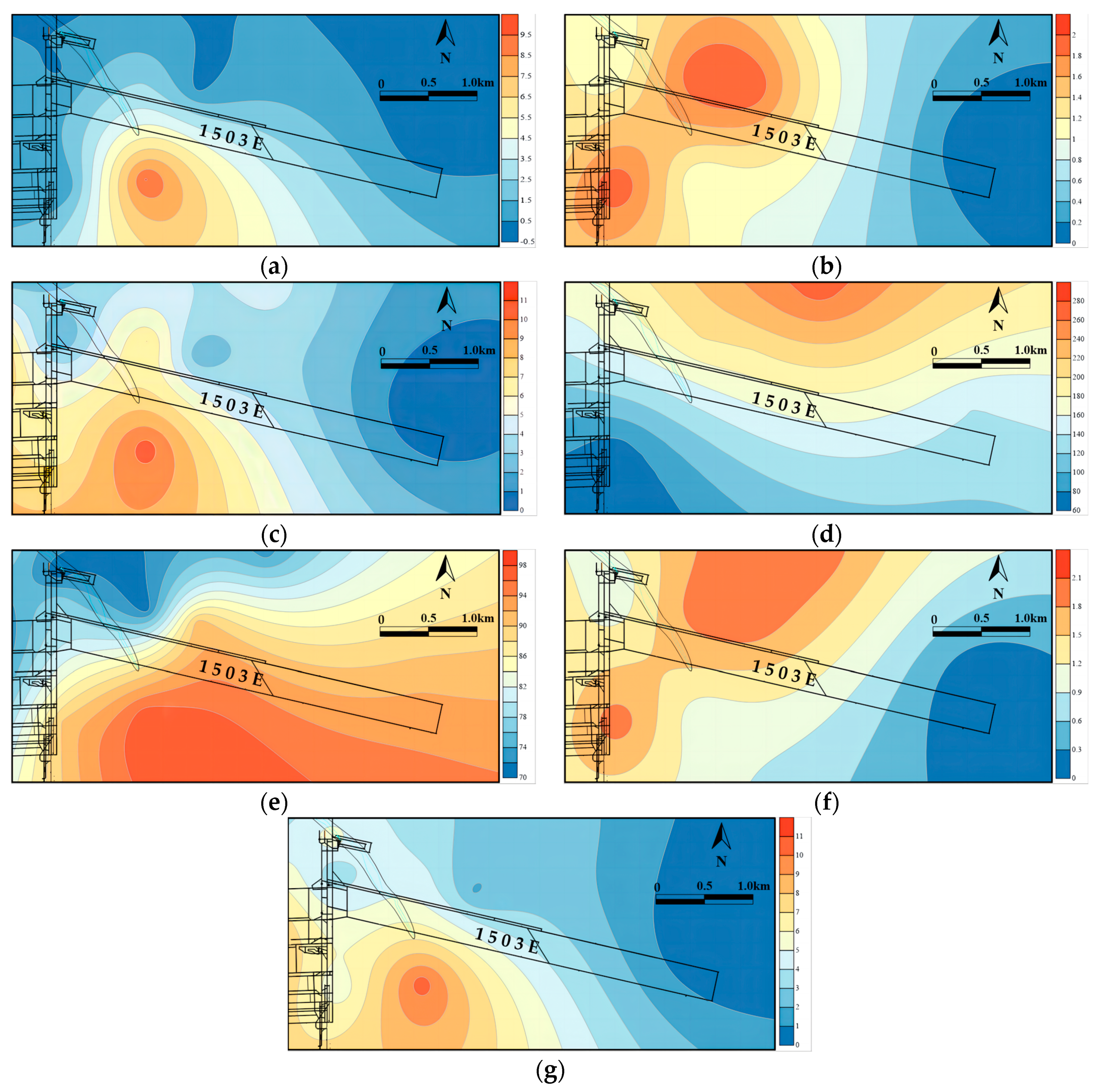
| Drilling Number | Specific Capacity q (L/s·m) | Related Factor Indicators | Coal Seams | ||||||
|---|---|---|---|---|---|---|---|---|---|
| nsn | nh | Sdx | H | V | Sdc | nc | |||
| KB-1 | 0.0100 | 0.5007 | 2.0000 | 6.6640 | 64.9500 | 0.9030 | 5.3200 | 2.0000 | 3-coal |
| KB-2 | 0.0221 | 0.4227 | 1.0000 | 1.9020 | 167.0500 | 0.7804 | 3.1700 | 1.0000 | 3-coal |
| KB-3 | 0.0176 | 0.5489 | 1.0000 | 3.3000 | 169.5500 | 0.7088 | 5.5000 | 1.0000 | 3-coal |
| KB-4-1 | 0.0080 | 0.2632 | 2.0000 | 2.2500 | 195.0500 | 0.9100 | 1.8750 | 2.0000 | 3-coal |
| KB-5 | 0.0079 | 2.2325 | 1.0000 | 6.5100 | 168.9000 | 0.9670 | 1.9500 | 2.0000 | 3-coal |
| KB-6-1 | 0.0006 | 0.0000 | 0.0000 | 0.0000 | 138.7100 | 0.9149 | 0.0000 | 0.0000 | 3-coal |
| KB-7 | 0.0230 | 0.8053 | 1.0000 | 9.1800 | 124.4600 | 0.5466 | 0.0000 | 0.0000 | 3-coal |
| KB-8-1 | 0.0306 | 0.0567 | 1.0000 | 0.4200 | 171.6500 | 0.8763 | 0.7000 | 1.0000 | 3-coal |
| 3-1 | 0.0644 | 9.5909 | 1.0000 | 10.5500 | 112.6000 | 0.9725 | 10.5500 | 1.0000 | 3-coal |
| 3-2 | 0.0212 | 1.2154 | 1.0000 | 7.9440 | 109.5000 | 0.6740 | 9.9300 | 1.0000 | 3-coal |
| 3d-1 | 0.0185 | 4.0941 | 3.0000 | 31.6640 | 104.6600 | 0.5148 | 8.1575 | 4.0000 | 3-coal |
| 3d-2 | 0.0727 | 2.2545 | 2.0000 | 7.0160 | 197.9100 | 0.7109 | 4.3850 | 2.0000 | 3-coal |
| ZK2403 | 0.0200 | 0.7346 | 1.0000 | 4.7020 | 273.8400 | 0.7324 | 2.9750 | 2.0000 | 3-coal |
| ZK3604 | 0.0550 | 0.9630 | 3.0000 | 10.3280 | 193.8000 | 0.9827 | 2.9250 | 4.0000 | 3-coal |
| KB-4-2 | 0.0010 | 0.0000 | 0.0000 | 0.0000 | 272.2600 | 0.8611 | 0.0000 | 0.0000 | 5-coal |
| KB-6-2 | 0.0474 | 9.5758 | 1.0000 | 12.2000 | 218.7000 | 0.9387 | 7.9000 | 2.0000 | 5-coal |
| KB-8-2 | 0.0099 | 2.1967 | 2.0000 | 16.7200 | 240.7500 | 0.7908 | 7.1833 | 3.0000 | 5-coal |
| 5d-1 | 0.2438 | 9.2160 | 1.0000 | 23.5760 | 133.3500 | 0.7124 | 8.6400 | 4.0000 | 5-coal |
| 5d-2 | 0.0033 | 2.0556 | 2.0000 | 5.3600 | 283.0000 | 0.5612 | 3.4040 | 5.0000 | 5-coal |
| ZK3004 | 0.0125 | 2.0468 | 4.0000 | 18.0800 | 257.0000 | 0.5966 | 3.1800 | 6.0000 | 5-coal |
| ZK3602 | 0.0647 | 6.9497 | 3.0000 | 25.2640 | 98.5100 | 0.4058 | 3.4575 | 8.0000 | 5-coal |
| 3-21 | 0.1518 | 2.2653 | 2.0000 | 6.7800 | 130.9000 | 0.7267 | 3.6675 | 4.0000 | 5-coal |
| 5d1-1 | 0.0233 | 1.0769 | 1.0000 | 2.2400 | 105.6000 | 0.9581 | 3.5000 | 1.0000 | 5-coal |
| 5d1-2 | 0.0016 | 2.3778 | 3.0000 | 7.3800 | 229.2500 | 0.6429 | 3.7500 | 4.0000 | 5-coal |
| ZK2401 | 0.0330 | 2.4706 | 1.0000 | 16.4100 | 87.2300 | 0.6887 | 9.1167 | 3.0000 | 5-coal |
| Factor Target | Degree of Association | Ranking of Relevance |
|---|---|---|
| Sdc | 0.8470 | 1 |
| Sdx | 0.8433 | 2 |
| nc | 0.8390 | 3 |
| V | 0.8388 | 4 |
| nh | 0.8372 | 5 |
| H | 0.8243 | 6 |
| nsn | 0.8069 | 7 |
| Factor Target | nsn | nh | Sdx | H | V | Sdc | nc |
|---|---|---|---|---|---|---|---|
| Sdc | 1.000 | 0.085 | 0.607 | −0.181 | −0.084 | 0.620 | 0.356 |
| Sdx | 0.085 | 1.000 | 0.533 | 0.114 | −0.446 | 0.069 | 0.803 |
| nc | 0.607 | 0.533 | 1.000 | −0.260 | −0.546 | 0.541 | 0.669 |
| V | −0.181 | 0.114 | −0.260 | 1.000 | 0.011 | −0.343 | 0.086 |
| nh | −0.084 | −0.446 | −0.546 | 0.011 | 1.000 | −0.082 | −0.569 |
| H | 0.620 | 0.069 | 0.541 | −0.343 | −0.082 | 1.000 | 0.153 |
| nsn | 0.356 | 0.803 | 0.669 | 0.086 | −0.569 | 0.153 | 1.000 |
| Component | Eigenvalue | Contribution Rate (%) | Cumulative Proportion (%) |
|---|---|---|---|
| 1 | 3.172 | 45.319 | 45.319 |
| 2 | 1.739 | 24.841 | 70.160 |
| 3 | 0.848 | 12.114 | 82.274 |
| 4 | 0.562 | 8.035 | 90.309 |
| 5 | 0.388 | 5.542 | 95.851 |
| 6 | 0.176 | 2.518 | 98.369 |
| 7 | 0.114 | 1.631 | 100.000 |
| Drilling Number | Principal Component | Specific Capacity q (L/s·m) | |||
|---|---|---|---|---|---|
| F1 | F2 | F3 | F4 | ||
| KB-1 | −0.44 | 0.76 | −1.14 | 1.41 | 0.010 |
| KB-2 | −1.47 | −0.08 | −0.27 | −0.24 | 0.022 |
| KB-3 | −0.99 | 0.19 | −0.28 | −0.64 | 0.018 |
| KB-4-1 | −1.29 | −0.84 | 0.24 | 0.87 | 0.008 |
| KB-5 | −1.27 | 0.19 | 0.35 | 0.62 | 0.008 |
| KB-6-1 | −2.83 | 0.32 | −0.45 | −0.06 | 0.001 |
| KB-7 | −0.93 | −0.39 | −1.47 | −1.19 | 0.023 |
| KB-8-1 | −2.06 | −0.41 | −0.16 | 0.23 | 0.031 |
| 3-1 | 0.49 | 3.23 | 1.30 | 0.38 | 0.064 |
| 3-2 | −0.03 | 1.45 | −0.77 | −0.63 | 0.021 |
| 3d-1 | 3.47 | 0.37 | −1.18 | −0.15 | 0.019 |
| 3d-2 | −0.09 | −0.46 | 0.19 | −0.18 | 0.073 |
| ZK2403 | −1.10 | −1.05 | 0.86 | −0.93 | 0.020 |
| ZK3604 | 0.11 | −1.03 | 0.42 | 1.86 | 0.055 |
| KB-4-2 | −2.92 | −0.75 | 1.02 | −0.99 | 0.001 |
| KB-6-2 | 0.49 | 1.83 | 2.29 | −0.17 | 0.047 |
| KB-8-2 | 0.77 | −0.21 | 0.93 | −0.07 | 0.010 |
| 5d-1 | 2.34 | 1.98 | 0.53 | −0.62 | 0.244 |
| 5d-2 | 0.61 | −2.01 | 0.63 | −0.93 | 0.003 |
| ZK3004 | 2.37 | −2.58 | 0.26 | 0.46 | 0.013 |
| ZK3602 | 4.16 | −0.85 | −1.47 | −0.13 | 0.065 |
| 3-21 | 0.38 | −0.37 | −0.69 | 0.46 | 0.152 |
| 5d1-1 | −1.64 | 0.83 | −0.45 | 0.84 | 0.023 |
| 5d1-2 | 0.86 | −1.60 | 0.29 | 0.11 | 0.002 |
| ZK2401 | 1.04 | 1.48 | −1.00 | −0.32 | 0.033 |
| Drilling Number | The Measured Value of the Units of Water Inflow q (L/s·m) | PCA-BP Network Model | Single BP Network Model | ||||
|---|---|---|---|---|---|---|---|
| Predicted Value qpca (L/s·m) | Relative Error (%) | Mean Relative Deviation (%) | Predicted Value qbp (L/s·m) | Relative Error (%) | Mean Relative Deviation (%) | ||
| KB-1 | 0.0100 | 0.0095 | 4.6996 | 2.0794 | 0.0086 | 14.4871 | 9.6799 |
| KB-2 | 0.0221 | 0.0220 | 0.5411 | 0.0212 | 3.9416 | ||
| KB-3 | 0.0176 | 0.0174 | 1.0186 | 0.0169 | 3.8645 | ||
| KB-4-1 | 0.0080 | 0.0078 | 1.8899 | 0.0090 | 11.9925 | ||
| KB-5 | 0.0079 | 0.0075 | 5.0265 | 0.0082 | 4.2801 | ||
| KB-6-1 | 0.0006 | 0.0006 | 7.6052 | 0.0008 | 35.0678 | ||
| KB-7 | 0.0230 | 0.0227 | 1.1874 | 0.0223 | 3.0093 | ||
| KB-8-1 | 0.0306 | 0.0306 | 0.0936 | 0.0296 | 3.2901 | ||
| 3-1 | 0.0644 | 0.0647 | 0.3895 | 0.0697 | 8.2038 | ||
| 3-2 | 0.0212 | 0.0210 | 1.0549 | 0.0200 | 5.5790 | ||
| 3d-1 | 0.0185 | 0.0184 | 0.6980 | 0.0175 | 5.2036 | ||
| 3d-2 | 0.0727 | 0.0721 | 0.8100 | 0.0844 | 16.1504 | ||
| ZK2403 | 0.0200 | 0.0201 | 0.3557 | 0.0177 | 11.3198 | ||
| ZK3604 | 0.0550 | 0.0529 | 3.7410 | 0.0600 | 9.1297 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuo, W.; Li, X.; Zhang, Y.; Li, W.; Wang, Q.; Li, L. Prediction Model of Water Abundance of Weakly Cemented Sandstone Aquifer Based on Principal Component Analysis–Back Propagation Neural Network of Grey Correlation Analysis Decision Making. Water 2024, 16, 551. https://doi.org/10.3390/w16040551
Kuo W, Li X, Zhang Y, Li W, Wang Q, Li L. Prediction Model of Water Abundance of Weakly Cemented Sandstone Aquifer Based on Principal Component Analysis–Back Propagation Neural Network of Grey Correlation Analysis Decision Making. Water. 2024; 16(4):551. https://doi.org/10.3390/w16040551
Chicago/Turabian StyleKuo, Wei, Xiaoqin Li, Yuguang Zhang, Wenping Li, Qiqing Wang, and Liangning Li. 2024. "Prediction Model of Water Abundance of Weakly Cemented Sandstone Aquifer Based on Principal Component Analysis–Back Propagation Neural Network of Grey Correlation Analysis Decision Making" Water 16, no. 4: 551. https://doi.org/10.3390/w16040551
APA StyleKuo, W., Li, X., Zhang, Y., Li, W., Wang, Q., & Li, L. (2024). Prediction Model of Water Abundance of Weakly Cemented Sandstone Aquifer Based on Principal Component Analysis–Back Propagation Neural Network of Grey Correlation Analysis Decision Making. Water, 16(4), 551. https://doi.org/10.3390/w16040551







