A Hybrid Model Combined Deep Neural Network and Beluga Whale Optimizer for China Urban Dissolved Oxygen Concentration Forecasting
Abstract
1. Introduction
- (1)
- Firstly, this study considers the impact of various water quality indicators on DOC, constructing a multivariate hybrid model to enhance DOC forecasting accuracy.
- (2)
- Secondly, integrating the VMD and BWO not only addresses the issue of selecting parameters for the CNN-GRU-AM model but also mitigates problems related to white noise and high-frequency signal disruptions, thereby refining the conventional single DOC prediction approach.
- (3)
- Thirdly, this study proposes a more accurate DOC forecasting hybrid method, which can effectively assist in water quality management.
2. Data
2.1. Data Sources
2.2. Data Preprocessing
2.3. Data Description
3. Methodology
3.1. Convolutional Neural Network
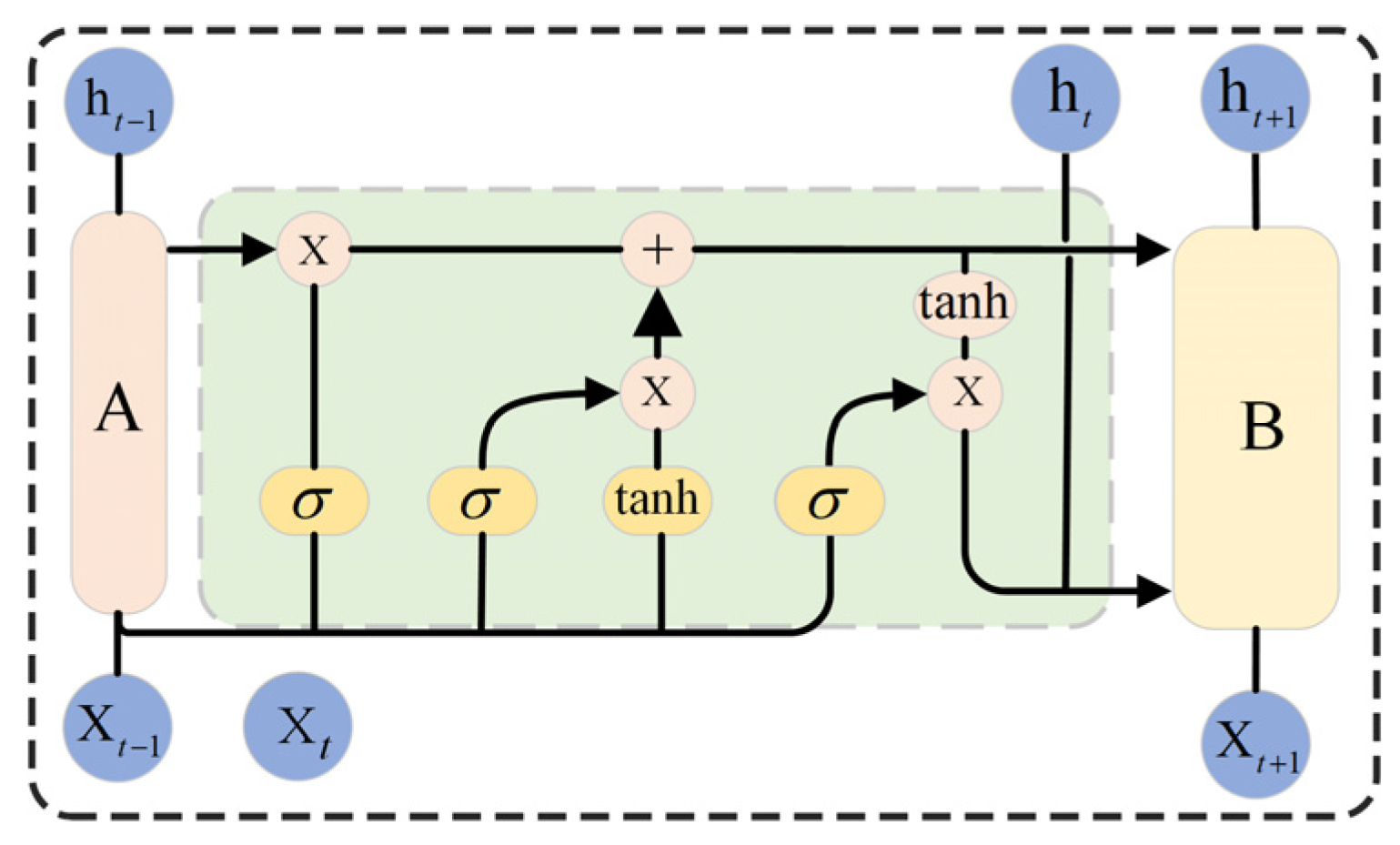
3.2. Gated Recurrent Unit
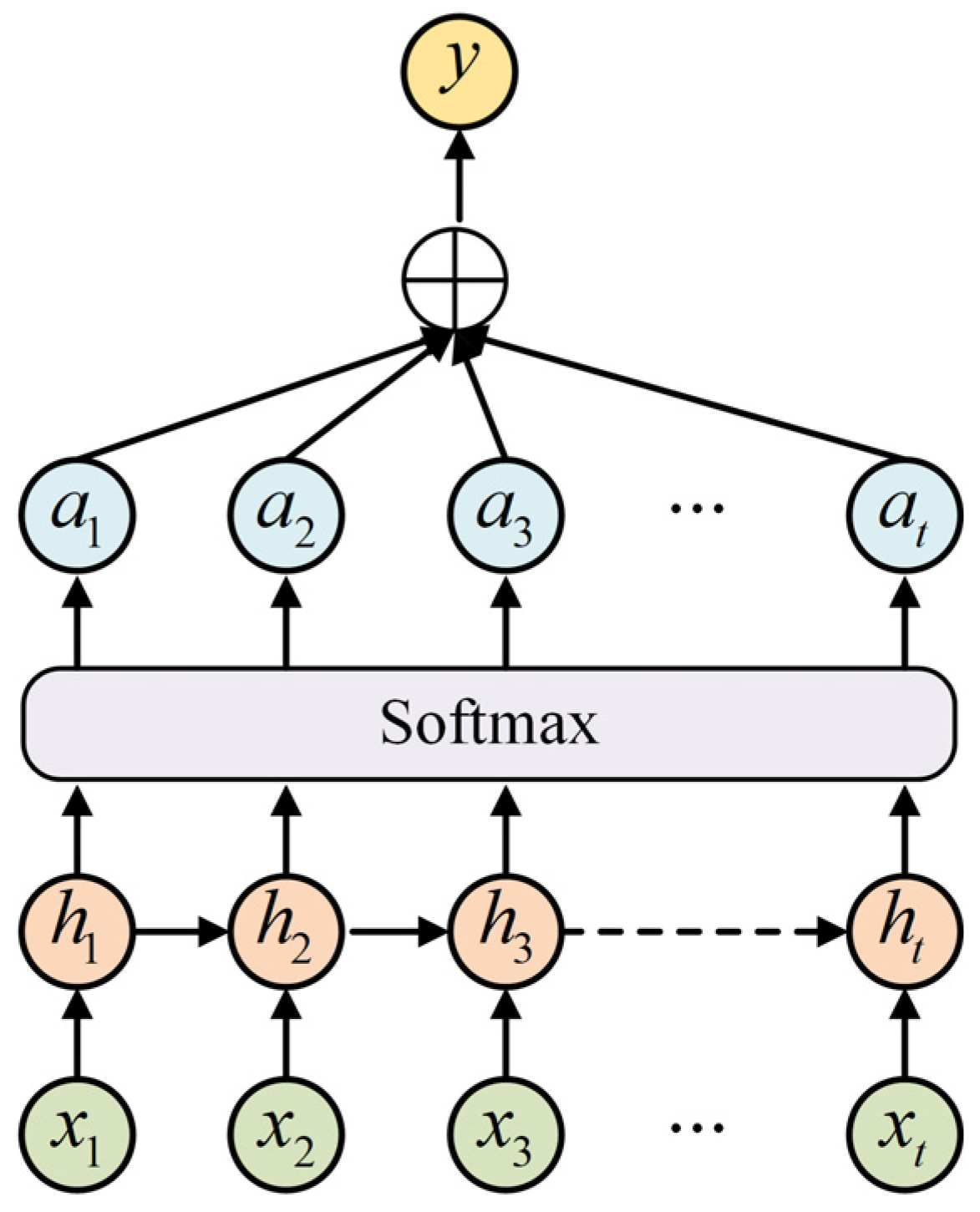
3.3. Attention Mechanism
3.4. Variational Mode Decomposition
3.5. Beluga Whale Optimization
- (1)
- Exploration stage
- (2)
- Development stage
- (3)
- Whale Fall
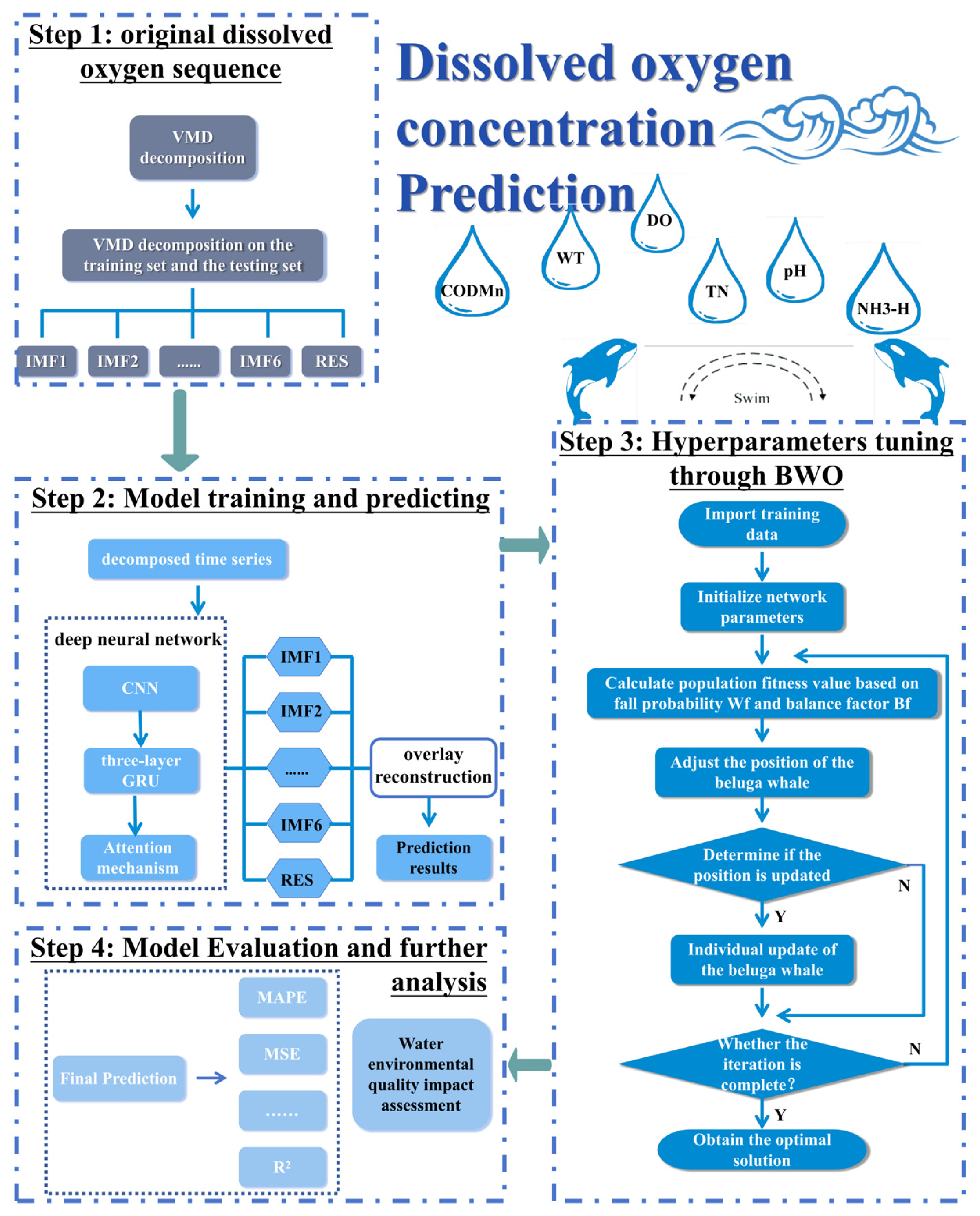
4. Model
4.1. The VMD-BWO-CNN-GRU-AM Model
4.2. Model Evaluation
4.3. Model Parameter Setting
5. Results
5.1. VMD Performance Evaluation
5.2. BWO Performance Evaluation
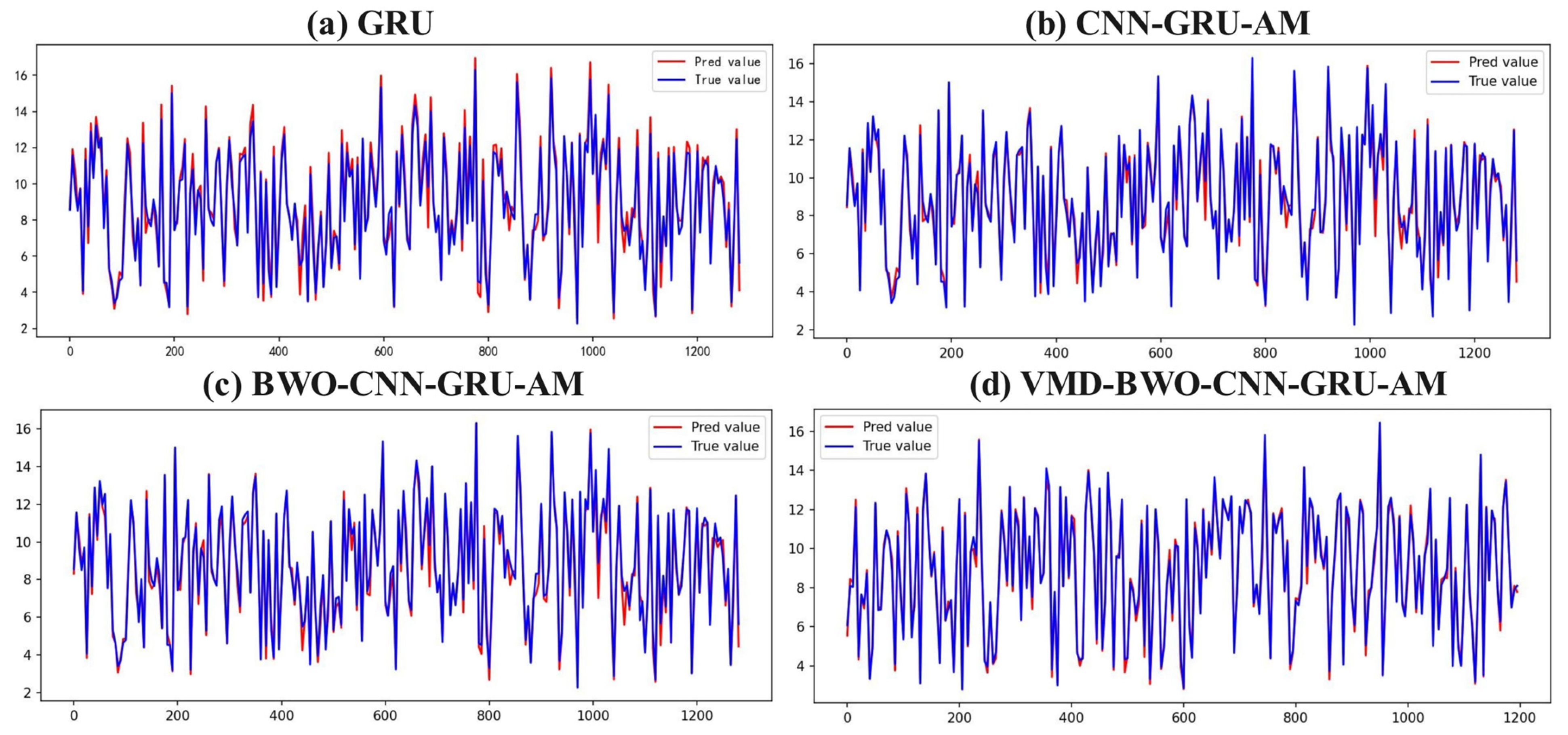
5.3. Model Comparisons
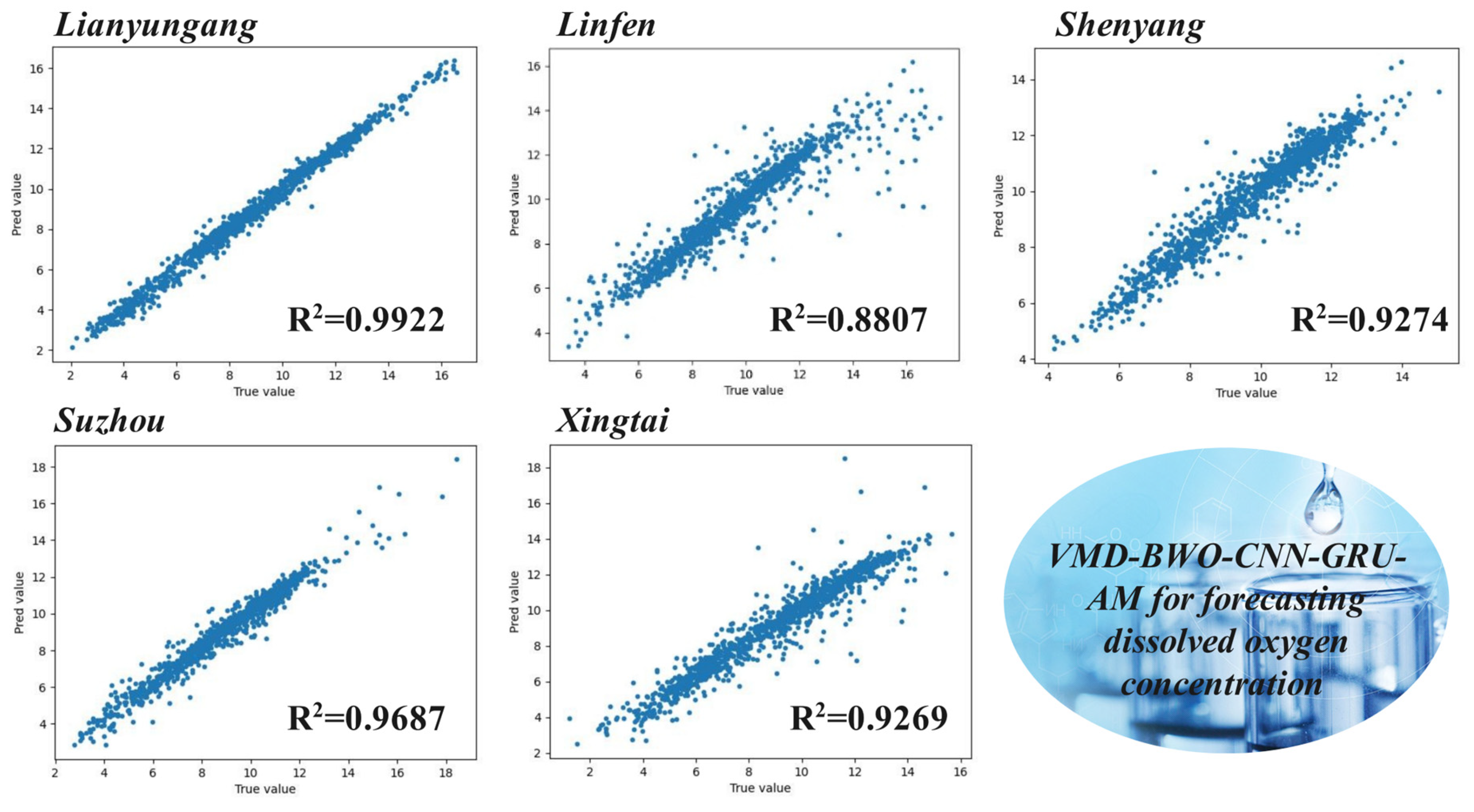
5.4. Contrast Analysis
6. Discussions
- (1)
- This study proposes a hybrid model for predicting urban dissolved oxygen with high accuracy. This study uses urban water quality monitoring data gathered every 4 h from November 2020 to November 2023. The empirical results show that performance indicators such as MSE, RMSE, MAE, and MAPE in VMD-BWO-CNN-GRU-AM are significantly improved when compared to a single model. Taking the Site 1 dataset as an example, these indicators are reduced by 0.2859, 0.3301, 0.2539, and 0.0406, respectively.
- (2)
- The hybrid DOC prediction model can be extended to national surface water quality automatic monitoring stations in different river basins. This study utilized five urban water quality datasets with the worst water quality from different river basins. This method has universal applicability and can effectively improve DOC prediction accuracy in national water control stations, providing a better DOC prediction accuracy forecasting method for other regions to help with water management.
- (3)
- The proposed DOC hybrid forecasting system has good health and social benefits. It can serve as an early warning system of water quality deterioration, especially in cases of organic pollution and eutrophication. Developing accurate predictive models for the key water quality parameter of DOC can assess the effects of disturbances (anthropogenic, such as pollution, or climatic, such as climate change) on the suitability of aquatic habitats and, therefore, on the health of aquatic species.
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ding, F.; Zhang, W.; Cao, S.; Hao, S.; Chen, L.; Xie, X.; Li, W.; Jiang, M. Optimization of water quality index models using machine learning approaches. Water Res. 2023, 243, 120337. [Google Scholar] [CrossRef]
- Wu, J.; Yu, X. Numerical investigation of dissolved oxygen transportation through a coupled SWE and Streeter-Phelps model. Math. Probl. Eng. 2021, 2021, 6663696. [Google Scholar] [CrossRef]
- Du, B.; Huang, S.; Guo, J.; Tang, H.; Wang, L.; Zhou, S. Interval forecasting for urban water demand using PSO optimized KDE distribution and LSTM neural networks. Appl. Soft Comput. 2022, 122, 108875. [Google Scholar] [CrossRef]
- Guo, J.; Sun, H.; Du, B. Multivariable time series forecasting for urban water demand based on temporal convolutional network combining random forest feature selection and discrete wavelet transform. Water Resour. Manag. 2022, 36, 3385–3400. [Google Scholar] [CrossRef]
- Wang, J.; Qian, Y.; Zhang, L.; Wang, K.; Zhang, H. A novel wind power forecasting system integrating time series refining, nonlinear multi-objective optimized deep learning and linear error correction. Energy Convers. Manag. 2024, 299, 117818. [Google Scholar] [CrossRef]
- Stajkowski, S.; Zeynoddin, M.; Farghaly, H.; Gharabaghi, B.; Bonakdari, H. A methodology for forecasting dissolved oxygen in urban streams. Water 2020, 12, 2568. [Google Scholar] [CrossRef]
- Liu, H.; Yang, R.; Duan, Z.; Wu, H. A hybrid neural network model for marine dissolved oxygen concentrations time-series forecasting based on multi-factor analysis and a multi-model ensemble. Engineering 2021, 7, 1751–1765. [Google Scholar] [CrossRef]
- Li, J.; Chen, J.; Chen, Z.; Nie, Y.; Xu, A. Short-term wind power forecasting based on multi-scale receptive field-mixer and conditional mixture copula. Appl. Soft Comput. 2024, 164, 112007. [Google Scholar] [CrossRef]
- Nie, Y.; Li, P.; Wang, J.; Zhang, L. A novel multivariate electrical price bi-forecasting system based on deep learning, a multi-input multi-output structure and an operator combination mechanism. Appl. Energy 2024, 366, 123233. [Google Scholar] [CrossRef]
- Faezeh, M.G.; Taher, R.; Mohammad, K.Z. Decision tree models in predicting water quality parameters of dissolved oxygen and phosphorus in lake water. Sustain. Water Resour. Manag. 2022, 9, 1. [Google Scholar]
- Alnahit, O.A.; Mishra, A.K.; Khan, A.A. Stream water quality prediction using boosted regression tree and random forest models. Stoch. Environ. Res. Risk Assess. 2022, 36, 2661–2680. [Google Scholar] [CrossRef]
- Lu, H.; Ma, X. Hybrid decision tree-based machine learning models for short-term water quality prediction. Chemosphere 2020, 249, 126169. [Google Scholar] [CrossRef]
- Li, W.; Wu, H.; Zhu, N.; Jiang, Y.; Tan, J.; Guo, Y. Prediction of dissolved oxygen in a fishery pond based on gated recurrent unit (GRU). Inf. Process. Agric. 2020, 8, 185–193. [Google Scholar] [CrossRef]
- Wang, X.; Tang, X.; Zhu, M.; Liu, Z.; Wang, G. Predicting abrupt depletion of dissolved oxygen in Chaohu lake using CNN-BiLSTM with improved attention mechanism. Water Res. 2024, 261, 122027. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Q.; Song, L.; Chen, Y. Attention-based recurrent neural networks for accurate short-term and long-term dissolved oxygen prediction. Comput. Electron. Agric. 2019, 165, 104964. [Google Scholar] [CrossRef]
- Peng, L.; Wu, H.; Gao, M.; Yi, H.; Xiong, Q.; Yang, L.; Cheng, S. TLT: Recurrent fine-tuning transfer learning for water quality long-term prediction. Water Res. 2022, 225, 119171. [Google Scholar] [CrossRef]
- Wu, X.; Chen, M.; Zhu, T.; Chen, D.; Xiong, J. Pre-training enhanced spatio-temporal graph neural network for predicting influent water quality and flow rate of wastewater treatment plant: Improvement of forecast accuracy and analysis of related factors. Sci. Total Environ. 2024, 951, 175411. [Google Scholar] [CrossRef]
- Irwan, D.; Ali, M.; Ahmed, A.N.; Jacky, G.; Nurhakim, A.; Ping Han, M.C.; AlDahoul, N.; El-Shafie, A. Predicting water quality with artificial intelligence: A review of methods and applications. Arch. Comput. Methods Eng. 2023, 30, 4633–4652. [Google Scholar] [CrossRef]
- Balahaha Fadi, Z.S.; Latif, S.D.; Ahmed, A.N.; Chow, M.F.; Murti, M.A.; Suhendi, A.; Balahaha Hadi, Z.S.; Wong, J.K.; Birima, A.H.; El-Shafie, A. Machine learning algorithm as a sustainable tool for dissolved oxygen prediction: A case study of Feitsui Reservoir, Taiwan. Sci. Rep. 2022, 12, 3649. [Google Scholar]
- Antanasijević, D.; Pocajt, V.; Perić-Grujić, A.; Ristić, M. Multilevel split of high-dimensional water quality data using artificial neural networks for the prediction of dissolved oxygen in the Danube River. Neural Comput. Appl. 2019, 32, 3957–3966. [Google Scholar] [CrossRef]
- Najwa Mohd Rizal, N.; Hayder, G.; Mnzool, M.; Elnaim, B.M.; Mohammed, A.O.Y.; Khayyat, M.M. Comparison between Regression Models, Support Vector Machine (SVM), and Artificial Neural Network (ANN) in River Water Quality Prediction. Processes 2022, 10, 1652. [Google Scholar] [CrossRef]
- Zhang, Y.; Fitch, P.; Thorburn, J.P. Predicting the Trend of Dissolved Oxygen Based on the kPCA-RNN Model. Water 2020, 12, 585. [Google Scholar] [CrossRef]
- Wang, J.; Qian, Y.; Gao, Y.; Lv, M.; Zhou, Y. A combined prediction system for PM2.5 concentration integrating spatio-temporal correlation extracting, multi-objective optimization weighting and non-parametric estimation. Atmos. Pollut. Res. 2023, 14, 101880. [Google Scholar] [CrossRef]
- Wang, B.; Jin, C.; Zhou, L.; Shen, D.; Jiang, Z. Water quality prediction of Xili Reservoir based on long short-term memory network. J. Yangtze River Acad. Sci. 2023, 40, 64–70. [Google Scholar]
- Kim, J.; Yu, J.; Kang, C.; Ryang, G.; Wei, Y.; Wang, X. A novel hybrid water quality forecast model based on real-time data decomposition and error correction. Process Saf. Environ. Prot. 2022, 162, 553–565. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, J.; Niu, X.; Zeng, B. Combined water quality forecasting system based on multiobjective optimization and improved data decomposition integration strategy. J. Forecast. 2023, 42, 260–287. [Google Scholar] [CrossRef]
- Wang, K.; Liu, Y.; Xing, Q.; Qian, Y.; Wang, J.; Lv, M. An integrated system to significant wave height prediction: Combining feature engineering, multi-criteria decision making, and hybrid kernel density estimation. Expert Syst. Appl. 2024, 241, 122351. [Google Scholar] [CrossRef]
- Jiang, P.; Nie, Y.; Wang, J.; Huang, X. Multivariable short-term electricity price forecasting using artificial intelligence and multi-input multi-output scheme. Energy Econ. 2023, 117, 106471. [Google Scholar] [CrossRef]
- Heydari, S.; Nikoo, M.R.; Mohammadi, A.; Barzegar, R. Two-stage meta-ensembling machine learning model for enhanced water quality forecasting. J. Hydrol. 2024, 641, 131767. [Google Scholar] [CrossRef]
- Wai, K.P.; Chia, M.Y.; Koo, C.H.; Huang, Y.F.; Chong, W.C. Applications of deep learning in water quality management: A state-of-the-art review. J. Hydrol. 2022, 613, 128332. [Google Scholar] [CrossRef]
- Asiri, M.M.; Aldehim, G.; Alotaibi, F.A.; Alnfiai, M.M.; Assiri, M.; Mahmud, A. Short-term load forecasting in smart grids using hybrid deep learning. IEEE Access 2024, 12, 23504–23513. [Google Scholar] [CrossRef]
- Hameed, M.M.; Razali, S.F.M.; Mohtar, W.H.M.W.; Rahman, N.A.; Yaseen, Z.M. Machine learning models development for accurate multi-months ahead drought forecasting: Case study of the Great Lakes, North America. PLoS ONE 2023, 18, e0290891. [Google Scholar] [CrossRef]
- Na, M.; Liu, X.; Tong, Z.; Sudu, B.; Zhang, J.; Wang, R. Analysis of water quality influencing factors under multi-source data fusion based on PLS-SEM model: An example of East-Liao River in China. Sci. Total Environ. 2024, 907, 168126. [Google Scholar] [CrossRef]
- Faraji, H.; Shahryari, A. Estimation of Water Quality Index and Factors Affecting Their Changes in Groundwater Resource and Nitrate and Fluoride Risk Assessment. Water Air Soil Pollut. 2023, 234, 608. [Google Scholar] [CrossRef]
- Interlandi, J.S.; Crockett, S.C. Recent water quality trends in the Schuylkill River, Pennsylvania, USA: A preliminary assessment of the relative influences of climate, river discharge and suburban development. Water Res. 2003, 37, 1737–1748. [Google Scholar] [CrossRef]
- Xu, S.; Li, W.; Zhu, Y.; Xu, A. A novel hybrid model for six main pollutant concentrations forecasting based on improved LSTM neural networks. Sci. Rep. 2022, 12, 14434. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.H.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Vaswani, A. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, I. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Zhong, C.; Li, G.; Meng, Z. Beluga whale optimization: A novel nature-inspired metaheuristic algorithm. Knowl.-Based Syst. 2022, 251, 109215. [Google Scholar] [CrossRef]
- Bastos Filho, C.J.A.; de Lima Neto, F.B.; Lins, A.J.C.C.; Nascimento, A.I.S.; Lima, M.P. A novel search algorithm based on fish school behavior. In Proceedings of the 2008 IEEE International Conference on Systems, Man and Cybernetics, Singapore, 12–15 October 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 2646–2651. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]

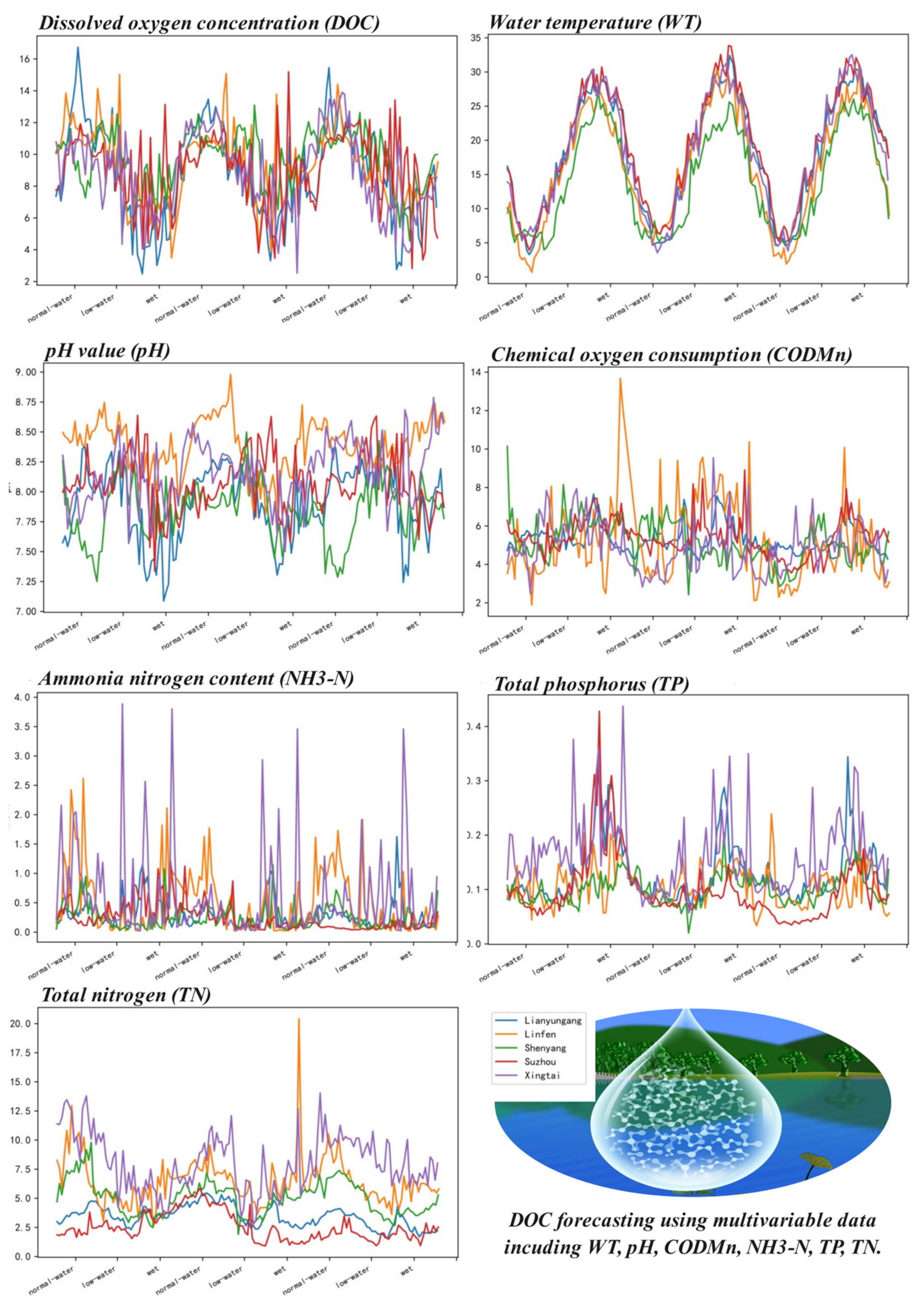
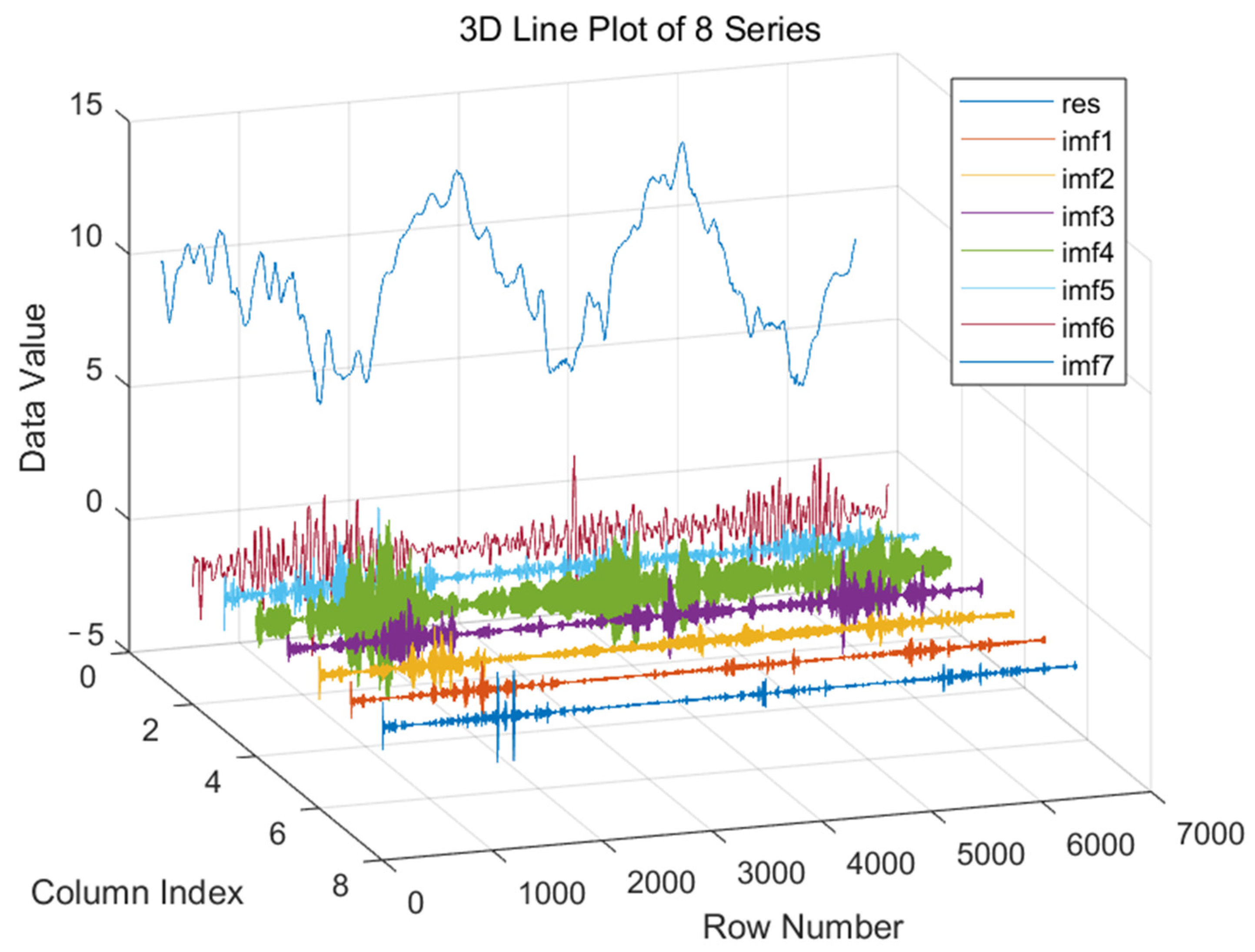
| Dataset | Sampling Frequency | Range | Variables | Samples | Numbers | DOC Statistical Indicators | |||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Min | Max | ||||||
| Lianyungang | 4 h each time | 8 November 2020–11 November 2023 | DOC, pH, NH3-N, TN, WT, CODMn, TP | All | 6588 | 8.8004 | 3.0982 | 1.9346 | 17.2613 |
| Training | 5270 | 9.3010 | 3.0887 | 2.1907 | 17.2614 | ||||
| Validating | 659 | 7.1038 | 2.5465 | 1.9346 | 13.6383 | ||||
| Testing | 659 | 6.4962 | 1.7340 | 2.3959 | 11.1893 | ||||
| Shenyang | 4 h each time | 8 November 2020–11 November 2023 | DOC, pH, NH3-N, TN, WT, CODMn, TP | All | 6588 | 9.7186 | 1.9910 | 3.6453 | 15.5095 |
| Training | 5270 | 9.9893 | 1.8700 | 3.6453 | 15.5095 | ||||
| Validating | 659 | 8.9858 | 2.1984 | 4.1184 | 14.7788 | ||||
| Testing | 659 | 8.2874 | 1.9168 | 3.9901 | 12.6585 | ||||
| Xintai | 4 h each time | 8 November 2020–11 November 2023 | DOC, pH, NH3-N, TN, WT, CODMn, TP | All | 6588 | 8.8607 | 2.6916 | 0.3800 | 20.1115 |
| Training | 5270 | 9.3898 | 2.5796 | 0.3800 | 20.1115 | ||||
| Validating | 659 | 7.1153 | 1.9362 | 2.1620 | 15.8850 | ||||
| Testing | 659 | 6.3755 | 2.0019 | 0.9830 | 10.9100 | ||||
| Linfen | 4 h each time | 8 November 2020–11 November 2023 | DOC, pH, NH3-N, TN, WT, CODMn, TP | All | 6588 | 9.6140 | 2.6219 | 1.7110 | 28.9044 |
| Training | 5270 | 10.0000 | 2.7142 | 1.7110 | 28.9044 | ||||
| Validating | 659 | 8.5213 | 1.5497 | 4.1295 | 16.5814 | ||||
| Testing | 659 | 7.6200 | 1.0254 | 5.3739 | 10.3716 | ||||
| Suzhou | 4 h each time | 8 November 2020–11 November 2023 | DOC, pH, NH3-N, TN, WT, CODMn, TP | All | 6588 | 8.9217 | 2.4038 | 2.2186 | 18.3548 |
| Training | 5270 | 9.0951 | 2.2255 | 2.5726 | 18.3548 | ||||
| Validating | 659 | 8.8640 | 2.7437 | 2.2504 | 17.7152 | ||||
| Testing | 659 | 7.5937 | 2.9401 | 2.2186 | 15.1440 | ||||
| Module | Parameters | Determination Method | Settings |
|---|---|---|---|
| Rolling window size | Window length | Experiment | 42 |
| CNN | Training optimization algorithms | Experiment | Adam |
| Learning rate | Experiment | 0.003 | |
| Number of filters | Experiment | 64 | |
| Kernal Size | Experiment | 5 | |
| Activation function | Experiment | ReLU | |
| GRU | First GRU Layer Neurons | Experiment | (BWO search) |
| Second GRU Layer Neurons | Experiment | (BWO search) | |
| Third GRU Layer Neurons | Experiment | 32 | |
| Forth GRU Layer Neurons | Experiment | 20 | |
| VMD | Number of Modes (K) | Experiment | 8 |
| Alpha | Experience | 2000 | |
| Tolerance | Experiment | 1 × 10−7 | |
| Initial Center Frequencies | Experiment | 1 | |
| DC Component | Experiment | 0 | |
| BWO | Population Size | Experiment | 50 |
| Number of iterations | Experiment | 50 |
| City | Model | MSE | RMSE | MAE | R2 | MAPE |
|---|---|---|---|---|---|---|
| Lianyungang | VMD-BWO-CNN-GRU-AM | 0.0718 | 0.2680 | 0.2029 | 0.9922 | 0.0279 |
| EEMD-BWO-CNN-GRU-AM | 0.1991 | 0.4462 | 0.3150 | 0.9794 | 0.0414 | |
| CEEMDAN-BWO-CNN-GRU-AM | 0.1440 | 0.3794 | 0.2800 | 0.9850 | 0.0386 | |
| Shenyang | VMD-BWO-CNN-GRU-AM | 0.2573 | 0.5073 | 0.3487 | 0.9274 | 0.0365 |
| EEMD-BWO-CNN-GRU-AM | 0.2634 | 0.5132 | 0.3510 | 0.9222 | 0.0370 | |
| CEEMDAN-BWO-CNN-GRU-AM | 0.2616 | 0.5114 | 0.3507 | 0.9223 | 0.0368 | |
| Linfen | VMD-BWO-CNN-GRU-AM | 0.6984 | 0.8357 | 0.4806 | 0.8807 | 0.0524 |
| EEMD-BWO-CNN-GRU-AM | 0.7979 | 0.8933 | 0.5172 | 0.8639 | 0.0556 | |
| CEEMDAN-BWO-CNN-GRU-AM | 0.7768 | 0.8813 | 0.5121 | 0.8670 | 0.0547 | |
| Suzhou | VMD-BWO-CNN-GRU-AM | 0.1648 | 0.4060 | 0.2782 | 0.9687 | 0.0342 |
| EEMD-BWO-CNN-GRU-AM | 0.1794 | 0.4236 | 0.3099 | 0.9611 | 0.0421 | |
| CEEMDAN-BWO-CNN-GRU-AM | 0.1717 | 0.4144 | 0.3168 | 0.9646 | 0.0392 | |
| Xingtai | VMD-BWO-CNN-GRU-AM | 0.5298 | 0.7279 | 0.4647 | 0.9298 | 0.0603 |
| EEMD-BWO-CNN-GRU-AM | 0.5528 | 0.7435 | 0.4866 | 0.9208 | 0.0627 | |
| CEEMDAN-BWO-CNN-GRU-AM | 0.5335 | 0.7304 | 0.4699 | 0.9273 | 0.0605 |
| City | Model | MSE | RMSE | MAE | R2 | MAPE |
|---|---|---|---|---|---|---|
| Lianyungang | VMD-BWO-CNN-GRU-AM | 0.0718 | 0.2680 | 0.2029 | 0.9922 | 0.0279 |
| VMD-FSS-CNN-GRU-AM | 0.1484 | 0.3853 | 0.2876 | 0.9846 | 0.0387 | |
| VMD-PSO-CNN-GRU-AM | 0.1934 | 0.4398 | 0.3199 | 0.9799 | 0.0438 | |
| VMD-WOA-CNN-GRU-AM | 0.2005 | 0.4477 | 0.3242 | 0.9792 | 0.0412 | |
| Shenyang | VMD-BWO-CNN-GRU-AM | 0.2573 | 0.5073 | 0.3487 | 0.9274 | 0.0365 |
| VMD-FSS-CNN-GRU-AM | 0.2655 | 0.5153 | 0.3513 | 0.9220 | 0.0372 | |
| VMD-PSO-CNN-GRU-AM | 0.2710 | 0.5206 | 0.3531 | 0.9217 | 0.0377 | |
| VMD-WOA-CNN-GRU-AM | 0.2718 | 0.5213 | 0.3558 | 0.9214 | 0.0381 | |
| Linfen | VMD-BWO-CNN-GRU-AM | 0.6984 | 0.8357 | 0.4806 | 0.8807 | 0.0524 |
| VMD-FSS-CNN-GRU-AM | 0.7056 | 0.8400 | 0.4907 | 0.8794 | 0.0534 | |
| VMD-PSO-CNN-GRU-AM | 0.7161 | 0.8462 | 0.4959 | 0.8776 | 0.0537 | |
| VMD-WOA-CNN-GRU-AM | 0.7536 | 0.8681 | 0.4980 | 0.8712 | 0.0540 | |
| Suzhou | VMD-BWO-CNN-GRU-AM | 0.1648 | 0.4060 | 0.2782 | 0.9687 | 0.0342 |
| VMD-FSS-CNN-GRU-AM | 0.1684 | 0.4103 | 0.2784 | 0.9680 | 0.0344 | |
| VMD-PSO-CNN-GRU-AM | 0.1704 | 0.4127 | 0.2844 | 0.9677 | 0.0357 | |
| VMD-WOA-CNN-GRU-AM | 0.1708 | 0.4132 | 0.3117 | 0.9676 | 0.0381 | |
| Xingtai | VMD-BWO-CNN-GRU-AM | 0.5298 | 0.7279 | 0.4647 | 0.9298 | 0.0603 |
| VMD-FSS-CNN-GRU-AM | 0.5495 | 0.7413 | 0.4731 | 0.9272 | 0.0606 | |
| VMD-PSO-CNN-GRU-AM | 0.5520 | 0.7430 | 0.4851 | 0.9269 | 0.0626 | |
| VMD-WOA-CNN-GRU-AM | 0.6152 | 0.7843 | 0.4894 | 0.9185 | 0.0632 |
| City | Model | MSE | RMSE | MAE | R2 | MAPE |
|---|---|---|---|---|---|---|
| Lianyungang (Site 1) | SVM | 0.8517 | 0.9229 | 0.7812 | 0.8812 | 0.1183 |
| LSTM | 0.5245 | 0.7071 | 0.5245 | 0.9471 | 0.0708 | |
| BP | 0.9444 | 0.9718 | 0.7350 | 0.9027 | 0.1006 | |
| TCN | 0.5347 | 0.7312 | 0.5686 | 0.9429 | 0.0700 | |
| GRU | 0.3577 | 0.5981 | 0.4568 | 0.9618 | 0.0685 | |
| CNN-GRU | 0.2691 | 0.5187 | 0.3646 | 0.9734 | 0.0485 | |
| CNN-GRU-AM | 0.2440 | 0.4940 | 0.3328 | 0.9757 | 0.0452 | |
| BWO-CNN-GRU-AM | 0.2149 | 0.4635 | 0.3166 | 0.9770 | 0.0423 | |
| VMD-BWO-CNN-GRU-AM | 0.0718 | 0.2680 | 0.2029 | 0.9922 | 0.0279 | |
| Shenyang (Site 2) | SVM | 0.3428 | 0.5855 | 0.4790 | 0.5156 | 0.0728 |
| LSTM | 0.5318 | 0.7282 | 0.5504 | 0.8643 | 0.0591 | |
| BP | 1.0983 | 1.0480 | 0.8346 | 0.7164 | 0.0906 | |
| TCN | 0.4371 | 0.6611 | 0.5031 | 0.8894 | 0.0519 | |
| GRU | 0.3504 | 0.5920 | 0.4312 | 0.9113 | 0.0444 | |
| CNN-GRU | 0.3186 | 0.5649 | 0.3974 | 0.9227 | 0.0426 | |
| CNN-GRU-AM | 0.2867 | 0.5354 | 0.3625 | 0.9304 | 0.0393 | |
| BWO-CNN-GRU-AM | 0.2729 | 0.5224 | 0.3617 | 0.9309 | 0.0384 | |
| VMD-BWO-CNN-GRU-AM | 0.2781 | 0.5273 | 0.3558 | 0.9274 | 0.0381 | |
| Linfen (Site 3) | SVM | 3.1191 | 1.7660 | 1.5460 | 0.1471 | 0.3073 |
| LSTM | 3.0075 | 1.7342 | 1.0137 | 0.5583 | 0.0989 | |
| BP | 3.7728 | 1.9424 | 1.2819 | 0.4522 | 0.1323 | |
| TCN | 2.3375 | 1.5289 | 0.8804 | 0.6598 | 0.0904 | |
| GRU | 2.0800 | 1.4422 | 0.8208 | 0.6973 | 0.0887 | |
| CNN-GRU | 1.5637 | 1.2505 | 0.7411 | 0.7717 | 0.0799 | |
| CNN-GRU-AM | 1.5497 | 1.2449 | 0.6727 | 0.7543 | 0.0730 | |
| BWO-CNN-GRU-AM | 1.4580 | 1.2074 | 0.6674 | 0.7602 | 0.0692 | |
| VMD-BWO-CNN-GRU-AM | 0.6984 | 0.8357 | 0.4806 | 0.8807 | 0.0524 | |
| Suzhou (Site 4) | SVM | 1.3276 | 1.1522 | 0.8678 | 0.6386 | 0.1375 |
| LSTM | 1.0578 | 1.0285 | 0.7218 | 0.8095 | 0.0961 | |
| BP | 2.2151 | 1.4883 | 1.1040 | 0.6053 | 0.1388 | |
| TCN | 0.7262 | 0.8521 | 0.5886 | 0.8692 | 0.0750 | |
| GRU | 0.6179 | 0.7861 | 0.5496 | 0.8887 | 0.0738 | |
| CNN-GRU | 0.6092 | 0.7805 | 0.5404 | 0.8976 | 0.0686 | |
| CNN-GRU-AM | 0.5578 | 0.7469 | 0.4935 | 0.9071 | 0.0645 | |
| BWO-CNN-GRU-AM | 0.5512 | 0.7223 | 0.4848 | 0.9053 | 0.0627 | |
| VMD-BWO-CNN-GRU-AM | 0.1648 | 0.4060 | 0.2782 | 0.9687 | 0.0342 | |
| Xingtai (Site 5) | SVM | 2.4147 | 1.5539 | 1.2504 | 0.3432 | 0.2348 |
| LSTM | 1.0649 | 1.0319 | 0.7198 | 0.8535 | 0.0963 | |
| BP | 2.0370 | 1.4272 | 0.9935 | 0.7267 | 0.1314 | |
| TCN | 0.8451 | 0.9193 | 0.6243 | 0.8837 | 0.0815 | |
| GRU | 0.7379 | 0.8590 | 0.5930 | 0.8985 | 0.0743 | |
| CNN-GRU | 0.7168 | 0.8466 | 0.5391 | 0.8994 | 0.0714 | |
| CNN-GRU-AM | 0.6579 | 0.8111 | 0.5129 | 0.9076 | 0.0665 | |
| BWO-CNN-GRU-AM | 0.6166 | 0.7852 | 0.4897 | 0.9152 | 0.0651 | |
| VMD-BWO-CNN-GRU-AM | 0.5520 | 0.7430 | 0.4851 | 0.9269 | 0.0636 |
| Model | PMAE (100%) | PMAPE (100%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Site | Site 1 | Site 2 | Site 3 | Site 4 | Site 5 | Average | Site 1 | Site 2 | Site 3 | Site 4 | Site 5 | Average |
| SVM | 4.97% | 1.47% | 6.49% | 18.01% | 23.72% | 10.93% | 3.15% | 1.42% | 5.97% | 3.93% | 9.56% | 12.12% |
| LSTM | 26.46% | 23.48% | 18.22% | 25.23% | 31.47% | 24.97% | 27.12% | 25.82% | 12.39% | 26.91% | 33.86% | 24.67% |
| BP | 49.26% | 51.29% | 43.11% | 50.31% | 49.00% | 48.59% | 50.33% | 52.76% | 39.61% | 48.92% | 48.86% | 48.46% |
| TCN | 31.62% | 19.20% | 3.60% | 6.80% | 18.84% | 16.01% | 25.14% | 17.53% | 4.44% | 5.47% | 17.55% | 12.89% |
| GRU | 54.37% | 65.14% | 52.84% | 46.78% | 59.48% | 55.72% | 60.18% | 41.29% | 74.00% | 48.44% | 71.38% | 55.99% |
| SVM-AM | 12.56% | 19.68% | 28.17% | 31.64% | 40.99% | 26.61% | 23.09% | 31.10% | 27.46% | 28.64% | 46.59% | 29.42% |
| LSTM-AM | 58.70% | 78.46% | 59.45% | 64.21% | 88.22% | 69.81% | 62.61% | 35.62% | 28.62% | 57.30% | 33.47% | 72.03% |
| BP-AM | 126.93% | 23.67% | 72.20% | 47.33% | 37.62% | 61.55% | 82.53% | 24.21% | 39.34% | 29.14% | 72.01% | 48.47% |
| TCN-AM | 2.78% | 15.99% | 27.24% | 39.77% | 34.15% | 23.99% | 5.70% | 48.79% | 19.21% | 14.35% | 30.10% | 28.23% |
| GRU-AM | 67.17% | 132.63% | 187.06% | 124.73% | 179.12% | 138.14% | 55.22% | 83.12% | 187.52% | 146.67% | 73.97% | 152.34% |
| CNN-SVM | 14.49% | 40.97% | 45.36% | 28.91% | 30.47% | 32.04% | 30.72% | 67.67% | 34.15% | 13.19% | 48.15% | 35.55% |
| CNN-LSTM | 13.16% | 54.33% | 38.15% | 44.07% | 35.11% | 36.96% | 37.40% | 122.07% | 87.69% | 53.10% | 34.27% | 41.72% |
| CNN-BP | 1.21% | 67.54% | 10.03% | 21.01% | 9.76% | 21.91% | 0.45% | 69.82% | 19.67% | 35.10% | 15.82% | 26.05% |
| CNN-TCN | 2.78% | 14.05% | 6.43% | 3.78% | 5.89% | 6.59% | 0.98% | 19.63% | 7.65% | 3.98% | 5.14% | 7.35% |
| CNN-GRU | 8.54% | 3.54% | 5.60% | 9.76% | 20.10% | 9.51% | 10.43% | 5.10% | 5.78% | 9.08% | 16.31% | 9.70% |
| Proposed model | - | - | - | - | - | - | - | - | - | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Ding, L.; Zhang, D.; Chen, J. A Hybrid Model Combined Deep Neural Network and Beluga Whale Optimizer for China Urban Dissolved Oxygen Concentration Forecasting. Water 2024, 16, 2966. https://doi.org/10.3390/w16202966
Wang T, Ding L, Zhang D, Chen J. A Hybrid Model Combined Deep Neural Network and Beluga Whale Optimizer for China Urban Dissolved Oxygen Concentration Forecasting. Water. 2024; 16(20):2966. https://doi.org/10.3390/w16202966
Chicago/Turabian StyleWang, Tianruo, Linzhi Ding, Danyi Zhang, and Jiapeng Chen. 2024. "A Hybrid Model Combined Deep Neural Network and Beluga Whale Optimizer for China Urban Dissolved Oxygen Concentration Forecasting" Water 16, no. 20: 2966. https://doi.org/10.3390/w16202966
APA StyleWang, T., Ding, L., Zhang, D., & Chen, J. (2024). A Hybrid Model Combined Deep Neural Network and Beluga Whale Optimizer for China Urban Dissolved Oxygen Concentration Forecasting. Water, 16(20), 2966. https://doi.org/10.3390/w16202966






