Optimization of a Groundwater Pollution Monitoring Well Network Using a Backpropagation Neural Network-Based Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Simulation and Optimization of BPNN
2.2.1. Back Propagation Neural Networks-Based Alternative Model
2.2.2. Optimization Model
2.3. Sensitivity Analysis Method
2.4. Groundwater Flow Model
2.5. Fluoride Transport Model
3. Results and Discussion
3.1. Distribution and Simulation of Groundwater Levels and Hydraulic Heads
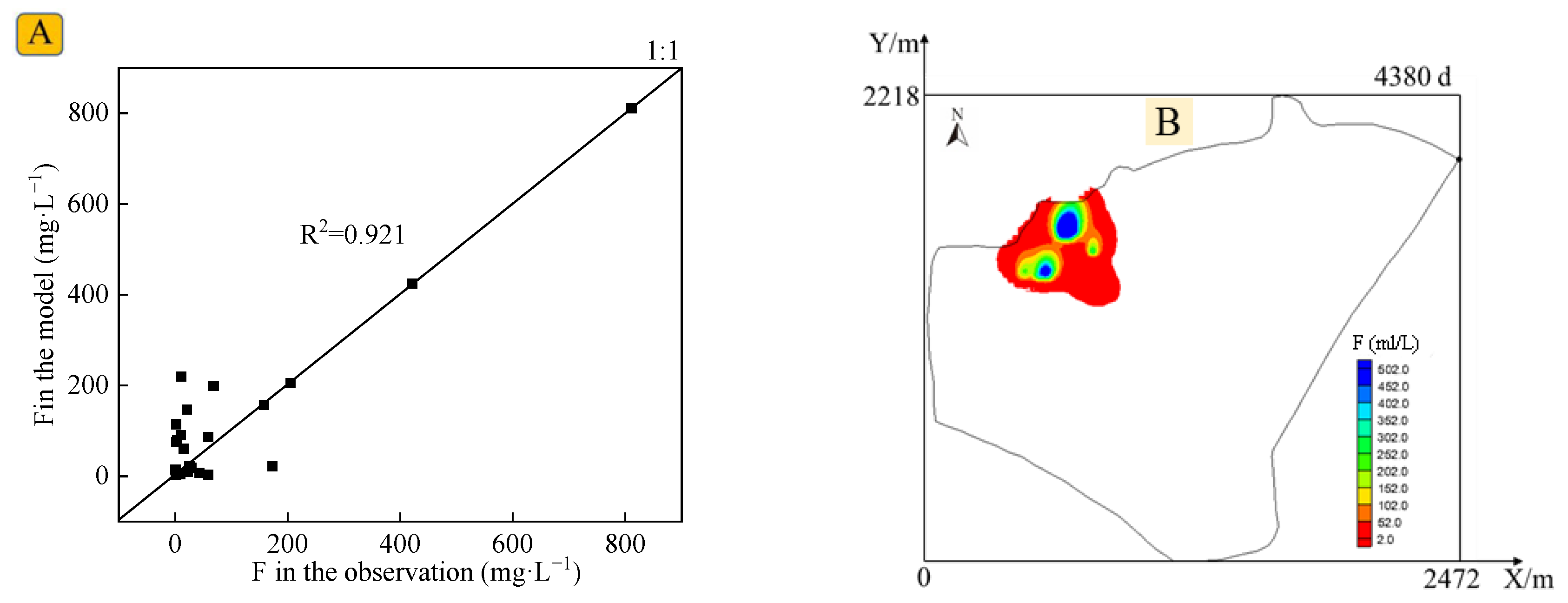
3.2. Solute Transport Modeling
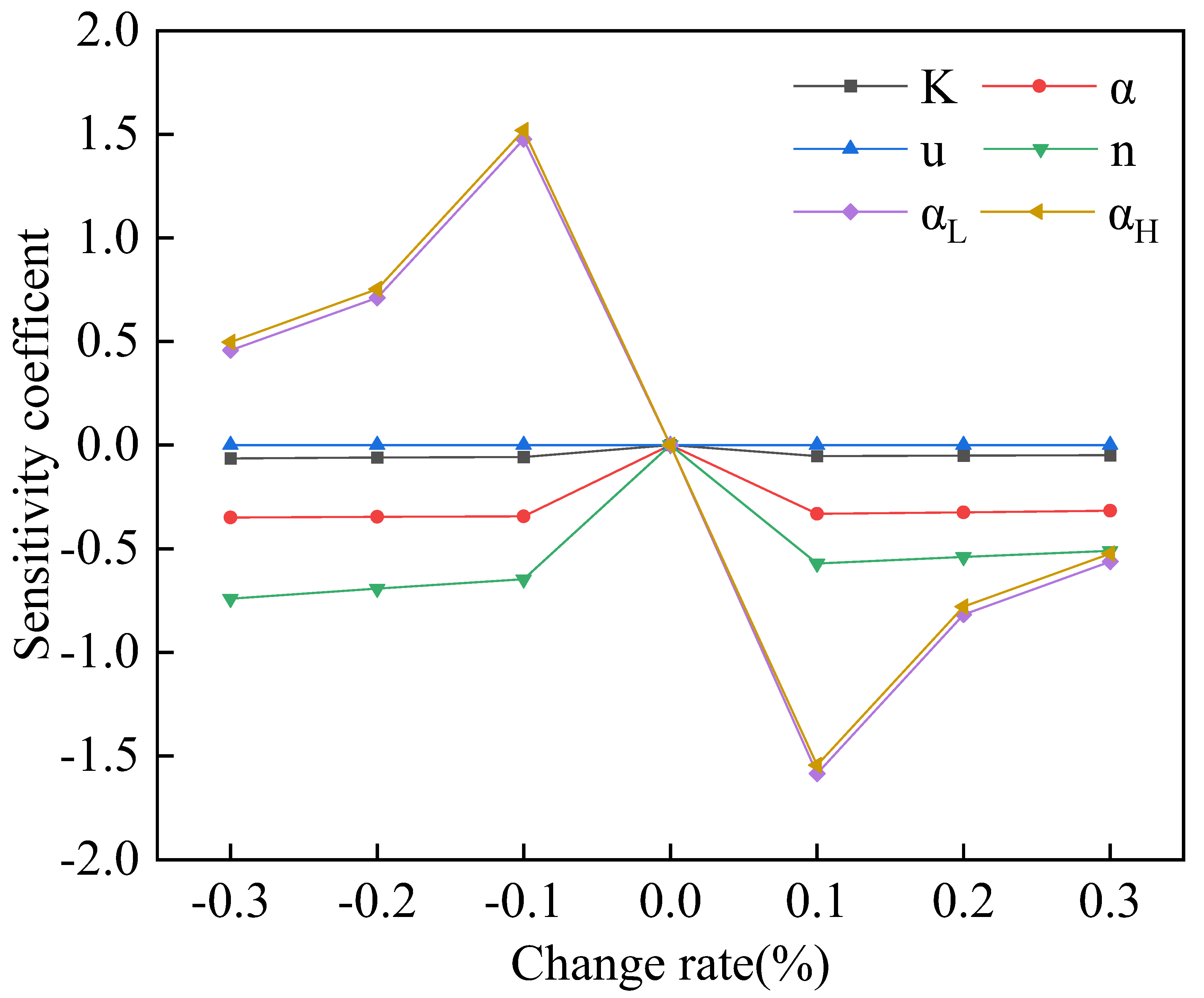
3.3. Sensitivity Analysis
3.4. BPNN-Based Alternative Model
3.5. Optimization Model
3.5.1. Model Construction and Solution
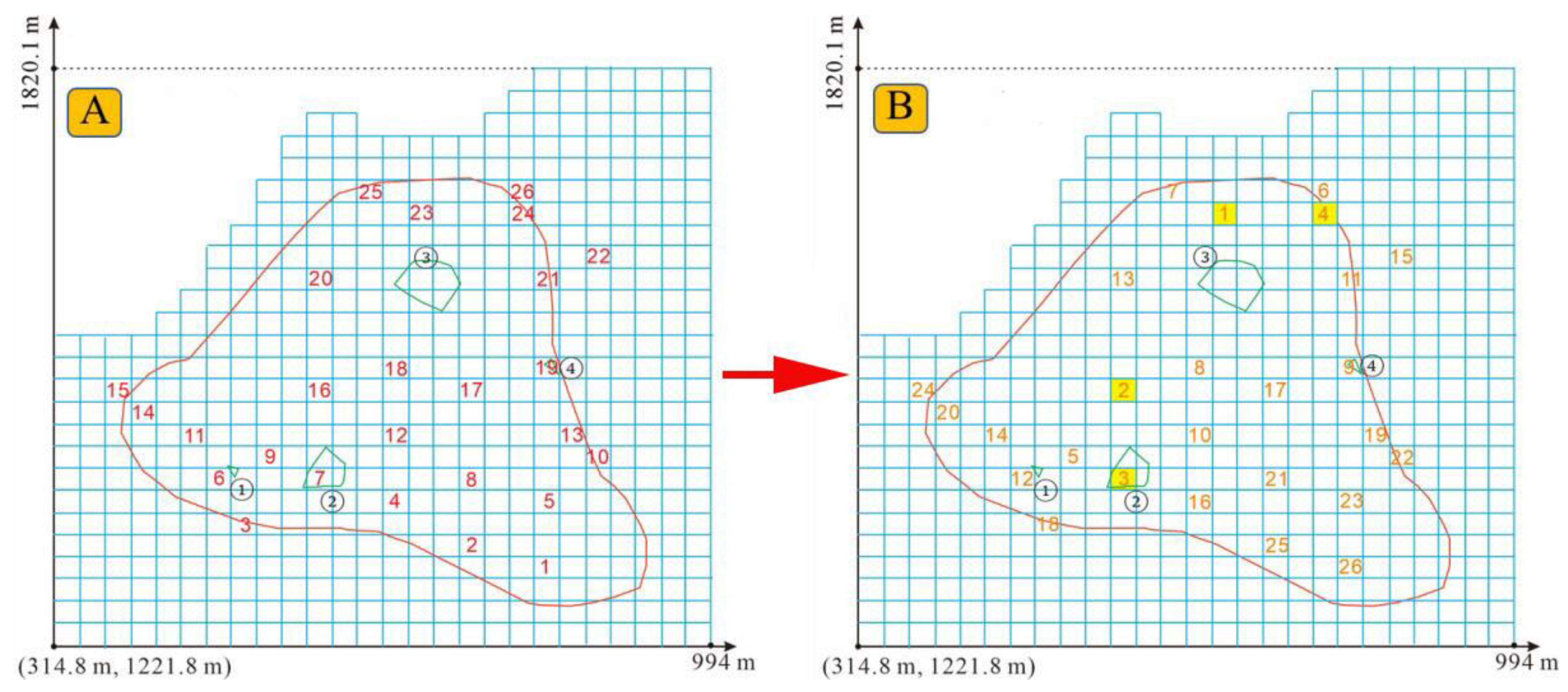
3.5.2. Fluoride Concentration in the Groundwater Monitoring Wells
3.5.3. Test of the Optimization Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Wan, T.; Bai, Y.; Wang, T.; Wei, Z. BPNN-based optimal strategy for dynamic energy optimization with providing proper thermal comfort under the different outdoor air temperatures. Appl. Energy 2022, 313, 118899. [Google Scholar] [CrossRef]
- Durgut, P.G.; Ayvaz, M.T. A novel fully hybrid simulation-optimization approach for enhancing the calibration and verification performance of the TUW hydrological model. J. Hydrol. 2023, 617, 128976. [Google Scholar] [CrossRef]
- Gamage, R.W.; Hettikankanange, P.M.; Lyman, K.D.; Austin, D.E.; Taylor, N.R. Simplified coaxial ion trap: Simulation-based geometry optimization, unidirectional ejection, and trapping conditions. Int. J. Mass Spectrom. 2022, 474, 116801. [Google Scholar] [CrossRef]
- Suthar, D.; Dhaka, M.S. Numerical simulation of CdSe/ZnTe thin film solar cells by SCAPS-1D: Optimization of absorber layer thickness. Solid State Commun. 2023, 371, 115264. [Google Scholar]
- Wang, Y.; Guo, X.; Yin, H.; Zhang, W.; Li, Q. Spatially distributed footprint families-based simulation-optimization approach for agricultural-ecological resources management under uncertainty. J. Hydrol. 2022, 613, 128319. [Google Scholar] [CrossRef]
- Wang, W.; Li, G.; Ye, J.; Li, G.; Tang, Y.; Fang, S. Optimization of Preparation of Cerium-loaded Intercalated Bentonite by Response Surface Method and Genetic Algorithm-back Propagation Neural Network and Its Application in Simultaneous Removal of Ammonia Nitrogen and Phosphorus. Chem. Lett. 2022, 51, 886–890. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, Y.; Wu, J.; Sun, X.; Lin, J.; Wu, J. Multi-objective optimization of the coastal groundwater abstraction for striking the balance among conflicts of resource-environment-economy in Longkou City, China. Water Res. 2022, 211, 118045. [Google Scholar] [CrossRef]
- Van Thieu, N.; Barma, S.D.; Van Lam, T.; Kisi, O.; Mahesha, A. Groundwater level modeling using Augmented Artificial Ecosystem Optimization. J. Hydrol. 2022, 617, 129034. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, Y.; Sun, Y.; Liu, Z.; Zhang, C. A Decision Support Framework for Pollution Source Detection via Coupled Forward-Inverse Optimization and Multi-Information Fusion. Water Resour. Res. 2023, 59, e2022WR032866. [Google Scholar] [CrossRef]
- Akbari, F.; Shourian, M.; Moridi, A. Assessment of the climate change impacts on the watershed-scale optimal crop pattern using a surface-groundwater interaction hydro-agronomic model. Agric. Water Manag. 2022, 265, 107508. [Google Scholar] [CrossRef]
- Anshuman, A.; Eldho, T.I. Entity aware sequence to sequence learning using LSTMs for estimation of groundwater contamination release history and transport parameters. J. Hydrol. 2022, 608, 127662. [Google Scholar] [CrossRef]
- Huang, J.J.; Xiao, M.; Li, Y.; Yan, R.; Zhang, Q.; Sun, Y.; Zhao, T. The optimization of Low Impact Development placement considering life cycle cost using Genetic Algorithm. J. Environ. Manag. 2022, 309, 114700. [Google Scholar] [CrossRef]
- Kumar, H.; Zhu, T.; Sankarasubramanian, A. Understanding the Food-Energy-Water Nexus in Mixed Irrigation Regimes Using a Regional Hydroeconomic Optimization Modeling Framework. Water Resour. Res. 2023, 59, e2022WR033691. [Google Scholar] [CrossRef]
- Kourakos, G.; Brunetti, G.; Bigelow, D.P.; Wallander, S.; Dahlke, H.E. Optimizing Managed Aquifer Recharge Locations in California’s Central Valley Using an Evolutionary Multi-Objective Genetic Algorithm Coupled With a Hydrological Simulation Model. Water Resour. Res. 2023, 59, e2022WR034129. [Google Scholar] [CrossRef]
- Li, W.; Nzeribe, B.N.; Liu, G.R.; Yao, G.; Crimi, M.; Rubasinghe, K.; Divine, C.; Mcdonough, J.; Wang, J. Modeling, simulation and analysis of groundwater flow captured by the horizontal reactive media well using the cell-based smoothed radial point interpolation method. Adv. Water Resour. 2022, 160, 104089. [Google Scholar] [CrossRef]
- Maurício, D.M.; Athayde, G.B.; Fan, F.M.; Garcia, L.H.; Athayde, C.d.V.M. Monitoring groundwater storage in a fractured volcanic aquifer system. Environ. Monit. Assess. 2023, 195, 385. [Google Scholar]
- Katpatal, Y.B.; Singh, C.K. Conjunctive use of flow modelling, entropy, and gis to design the groundwater monitoring network in the complex aquifer system. Int. J. Hydrol. Sci. Technol. 2023, 15, 78–96. [Google Scholar] [CrossRef]
- Fan, Y.; Lu, W.X.; Miao, T.S.; An, Y.K.; Li, J.H.; Luo, J.N. Optimal design of groundwater pollution monitoring network based on the SVR surrogate model under uncertainty. Environ. Sci. Pollut. Res. 2020, 27, 24090–24102. [Google Scholar] [CrossRef]
- Chen, R.J.; Tsay, Y.S.; Ni, S.W. An integrated framework for multi-objective optimization of building performance: Carbon emissions, thermal comfort, and global cost. J. Clean. Prod. 2022, 359, 131978. [Google Scholar] [CrossRef]
- Farlin, J.; Galle, T.; Pittois, D.; Bayerle, M.; Schaul, T. Groundwater quality monitoring network design and optimisation based on measured contaminant concentration and taking solute transit time into account. J. Hydrol. 2019, 573, 516–523. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, X.; Jia, G.; Jiang, J.; Liao, B. Introduction of broadleaf tree species can promote the resource use efficiency and gross primary productivity of pure forests. Plant Cell Environ. 2024, 1–13. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Wei, Z.J.; Jiang. J.; Yu, X.X. Adaptability of tree water use to elevation changes: A case study of a mixed forest in Northern China. J. Hydrol. 2022, 613, 128407. [Google Scholar] [CrossRef]
- Fan, Y.; Lu, W.X.; Miao, T.S.; Li, J.H.; Lin, J. Multi objective optimization of the groundwater exploitation layout in coastal areas based on multiple surrogate models. Environ. Sci. Pollut. Res. 2020, 27, 19561–19576. [Google Scholar] [CrossRef]
- Grbcic, L.; Lucin, I.; Kranjcevic, L.; Druzeta, S. Water supply network pollution source identification by random forest algorithm. J. Hydroinformatics 2020, 22, 1521–1535. [Google Scholar] [CrossRef]
- Reuss, M.; Oswald, S.E.; Kumke, M.M.U. Optical In Situ Monitoring of Acid Mine Drainage Remediation: Laboratory and Model Investigation. Ground Water Monit. Remediat. 2023, 43, 67–81. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Xiong, Y.; Luo, J.N.; Liu, X.; Liu, Y.; Xin, X.; Wang, S.Y. Machine learning-based optimal design of groundwater pollution monitoring network. Environ. Res. 2022, 211, 113022. [Google Scholar] [CrossRef]
- Qiu, R.J.; Wang, Y.K.; Wang, D.; Qiu, W.J.; Wu, J.C.; Tao, Y.W. Water temperature forecasting based on modified artificial neural network methods: Two cases of the Yangtze River. Sci. Total Environ. 2020, 737, 139729. [Google Scholar] [CrossRef]
- Golden, H.E.; Evenson, G.R.; Christensen, J.R.; Lane, C.R. Advancing Watershed Legacy Nitrogen Modeling to Improve Global Water Quality. Environ. Sci. Technol. 2023, 57, 2691–2697. [Google Scholar] [CrossRef]
- Taupega-Satau, S.; Amosa, P.; Leauga, A.; Nunufolau, J.; Yan, T.V.N. Macroinvertebrate Community Index (MCI) and Quantitative Macroinvertebrate Community Index (QMCI) Analysis: A Comparative Study between Le Afe and Mulivaifagatoloa Rivers, Upolu Island, Samoa. J. Geosci. Environ. Prot. 2024, 12, 149–167. [Google Scholar] [CrossRef]
- Roukerd, F.R.; Rajabi, M.M. Anomaly detection in groundwater monitoring data using LSTM-Autoencoder neural networks. Environ. Monit. Assess. 2024, 196, 692. [Google Scholar] [CrossRef]
- Zhang, S.M.; Wang, X.D.; Huang, Z.W.; Bao, Y.T.; Jiang, J.; Liu, Z.Q. Quercus acutissima exhibits more adaptable water uptake patterns in response to seasonal changes compared to Pinus massoniana. For. Ecosyst. 2025, 12, 2197–5620. [Google Scholar] [CrossRef]





| Test Items | Detection Limit | Minimum | Maximum | Groundwater Class IV | Water Quality Assessment score |
|---|---|---|---|---|---|
| Arsenic (μg/L) | 0.3 | 0.4 | 1690 | 50 | 33.8 |
| Cadmium (mg/L) | 0.005 | 0 | 0.023 | 0.01 | 2.3 |
| Total hardness (calculated as CaCO3) (mg/L) | 5 | 122 | 2860 | 650 | 4.4 |
| Total dissolved solids (mg/L) | 4 | 1230 | 8700 | 2000 | 4.35 |
| Volatile phenol (mg/L) | 0.0003 | 0 | 0.0175 | 0.01 | 1.748 |
| Dissolved oxygen (mg/L) | 0.5 | 1.7 | 103 | 10 | 10.3 |
| Ammonium nitrogen (mg/L) | 0.025 | 0.688 | 2.06 | 1.5 | 1.372 |
| Sulfate (mg/L) | 0.018 | 151 | 3800 | 350 | 10.857 |
| Chloride (mg/L) | 0.007 | 0.00 | 988 | 350 | 2.822 |
| Fluoride (mg/L) | 0.006 | 0.50 | 811 | 2 | 405.475 |
| Partition | Permeability Coefficient (m/d) | Precipitation Recharge Rate (m/d) | Specific Yield | Porosity |
|---|---|---|---|---|
| Western region | 0.8 | 8.0 × 10−5 | 0.02 | 0.25 |
| Eastern region | 1.0 | 6.0 × 10−5 | 0.03 | 0.22 |
| Random Variables | Probability Distributions | Average Values | Value Ranges |
|---|---|---|---|
| S1 (mg/d) | Normal distribution | 439 | 307.3~570.7 |
| S2 (mg/d) | Normal distribution | 1132 | 792.4~1471.6 |
| S3 (mg/d) | Normal distribution | 1330 | 931~1729 |
| S4 (mg/d) | Normal distribution | 1600 | 1120~2080 |
| Vertical dispersion αL (m) | Lognormal distribution | 15 | 10.5~19.5 |
| Horizontal dispersion αH (m) | Lognormal distribution | 12 | 8.4~15.6 |
| Integer Programming Model | Numbers of the Monitoring Wells | Fluoride Pollution Rates (%) | Average Pollution Rates (%) | |||
|---|---|---|---|---|---|---|
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | |||
| Optimization | 7, 16, 23, and 24 | 100 | 100 | 93.75 | 100 | 98.44 |
| Random 1 | 9, 12, 17, and 23 | 75 | 75 | 66.67 | 72.92 | 72.40 |
| Random 2 | 4, 11, 19, and 24 | 64.58 | 75 | 60.42 | 68.75 | 67.19 |
| Random 3 | 10, 14, 18, and 20 | 41.67 | 43.75 | 29.17 | 35.42 | 37.50 |
| Random 4 | 5, 16, 20, and 26 | 66.67 | 68.75 | 50 | 56.25 | 60.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Huang, X.; Wang, B.; Zhang, X.; Zhao, C.; Ying, R.; Feng, Y.; Hu, Z. Optimization of a Groundwater Pollution Monitoring Well Network Using a Backpropagation Neural Network-Based Model. Water 2024, 16, 2965. https://doi.org/10.3390/w16202965
Wang H, Huang X, Wang B, Zhang X, Zhao C, Ying R, Feng Y, Hu Z. Optimization of a Groundwater Pollution Monitoring Well Network Using a Backpropagation Neural Network-Based Model. Water. 2024; 16(20):2965. https://doi.org/10.3390/w16202965
Chicago/Turabian StyleWang, Heng, Xu Huang, Bing Wang, Xiaoyu Zhang, Caiyi Zhao, Rongrong Ying, Yanhong Feng, and Zhewei Hu. 2024. "Optimization of a Groundwater Pollution Monitoring Well Network Using a Backpropagation Neural Network-Based Model" Water 16, no. 20: 2965. https://doi.org/10.3390/w16202965
APA StyleWang, H., Huang, X., Wang, B., Zhang, X., Zhao, C., Ying, R., Feng, Y., & Hu, Z. (2024). Optimization of a Groundwater Pollution Monitoring Well Network Using a Backpropagation Neural Network-Based Model. Water, 16(20), 2965. https://doi.org/10.3390/w16202965







