Abstract
Modeling agricultural systems, from the point of view of saving and optimizing water, is a challenging task, because it may require multiple soil physical and hydraulic measurements to investigate the entire crop cycle. The Beerkan method was proposed as a quick and easy approach to estimate the saturated soil hydraulic conductivity, Ks. In this study, a new complete three-dimensional model for Beerkan experiments recently proposed was used. It consists of thirteen different calculation approaches that differ in estimating the macroscopic capillary length, initial (θi) and saturated (θs) soil water contents, use transient or steady-state infiltration data, and different fitting methods to transient data. A steady-state version of the simplified method based on a Beerkan infiltration run (SSBI) was used as the benchmark. Measurements were carried out on five sampling dates during a single growing season (from November to June) in a long-term experiment in which two soil management systems were compared, i.e., minimum tillage (MT) and no tillage (NT). The objectives of this work were (i) to test the proposed new model and calculation approaches under real field conditions, (ii) investigate the impact of MT and NT on soil properties, and (iii) obtain information on the seasonal variability of Ks and other main soil physical properties (θi, soil bulk density, ρb, and water retention curve) under MT and NT. The results showed that the model always overestimated Ks compared to SSBI. Indeed, the estimated Ks differed by a factor of 11 when the most data demanding (A1) approach was considered by a factor of 4–8, depending on the transient or steady-state phase use, when A3 was considered and by a practically negligible factor of 1.0–1.9 with A4. A relatively higher seasonal variability was detected for θi at the MT than NT system. Under both MT and NT, ρb did not change between November and April but increased significantly until the end of the season. The selected calculation approaches provided substantially coherent information on Ks seasonal evolution. Regardless of the approach, the results showed a temporal stability of Ks at least from early April to June under NT; conversely, the MT system was, overall, more affected by temporal changes with a relative stability at the beginning and middle of the season. These findings suggest that a common sampling time for determining Ks could be set at early spring. Soil management affected the soil properties, because the NT system was significantly wetter and more compact than MT on four out of five dates. However, only NT showed a significantly increasing correlation between Ks and the modal pore diameter, suggesting the presence of a relatively smaller and better interconnected pore network in the no-tilled soil. This study confirms the need to test infiltration models under real field conditions to evaluate their pros and cons. The Beerkan method was effective for intensive soil sampling and accurate field investigations on the temporal variability of Ks.
1. Introduction
The knowledge of soil properties is crucial for modeling hydrological processes of agricultural systems [1]. Among the many soil properties of interest, the field-saturated hydraulic conductivity, Ks, represents a key soil parameter, because it is a measure of a soil’s ability to transmit water when it is fully saturated [2]. As Ks is also an indicator of the structural characteristics of the porous medium, accounting for the effects of soil spatial arrangement of solids and pores [3,4], it is potentially usable to evaluate optimal or not optimal soil conditions for crops growth [5,6]. As a practical example, references in the literature suggest that Ks might be suitable for detecting low-yielding zones in agricultural fields, because, due to relatively high degree of soil compaction or reduced water and air permeability (i.e., due to a degraded soil structure), a reduction in crop yield may be expected [7,8]. Moreover, accurate modeling of agricultural systems needs repeated determinations of the soil’s physical and hydraulic properties to assess their temporal variability over the whole crop cycle [1,9,10].
It is well known that soil structure, and, consequently, Ks, can change over time [11,12,13], mainly due to soil tillage, agricultural rotations [14], or, more generally, due to changes induced by cropping systems [15,16,17]. At the cropping season scale, the soil structure may also be subject to changes in the short (or very short) term [10,18], since it is also specifically dependent on several soil and environmental conditions, including the soil water content at the time of measurements [17], amount and intensity of rainfall [19,20], as well as the wet–dry and freeze–thaw cycles [21,22]; however, a preeminent factor is due to the time elapsed since the last intensive soil tillage [11]. Parvin et al. [4] recently reiterated that quantitative analysis of post-tillage changes in the soil structure and related hydraulic properties are necessary for evaluating, and improving, soil hydrological models. In a recent meta-analysis, Blanchy et al. [23] quantified the effects of soil management practices on saturated and near-saturated soil hydraulic conductivity. They confirmed that, when a comparison “shortly after tillage vs. consolidated soil” was carried out, tillage initially determines an increase in Ks, but they also showed that the subsequent soil consolidation mainly disconnects the largest macropores (Figure 11 of their paper). Consequently, saturated or near-saturated hydraulic conductivity is reduced more strongly compared to markedly unsaturated soil conditions [23].
Several studies have investigated the effects of soil structure, consolidation, and surface sealing by measuring temporal changes in the soil hydraulic properties during one or a few growing seasons [12,15,17,24], but little information exists on the seasonal variability of such properties from post-tillage to harvest, e.g., [25,26,27]. For instance, Bormann and Klaasen [25] investigated the seasonal variability of some soil physical and hydraulic properties, including soil water content, bulk density, and unsaturated and saturated soil hydraulic conductivity, on four different dates of a cropping season from March to October. They reported that, for all investigated soil hydraulic properties, seasonal variability was detected, although it was statistically significant for the minority of the investigated variables, i.e., saturated hydraulic conductivity and field capacity [25]. Therefore, although the detected seasonal changes were not highly significant (p < 0.1), they concluded that the soil hydraulic properties were not constant over time, as assumed in most hydrological models. Kool et al. [24] detected changes in soil water retention and Ks as a consequence of soil bulk density (ρb) that increased dynamically with time following tillage. After modeling the relationship between water retention and ρb, they used a soil bulk density “matching point” to discriminate adequate (or not adequate) structural soil conditions to investigate the Ks evolution. They pointed out that, although no clear relationship between Ks and ρb was obtained under unstructured soil, i.e., for ρb < 1.06 g cm−3, Ks decreased markedly and significantly at increasing ρb above the observed matching point (ρb = 1.06 g cm−3) up to a value of about 1.5 g cm−3.
Several efforts have recently been made to test simple, fast enough, and accurate Ks measurement techniques, e.g., [8,28,29]. The Beerkan method [30] involves the determination of the three-dimensional cumulative infiltration resulting from the application of a slightly positive, and not strictly constant, water pressure head (approximately 1 cm) over a circular source delimited by a cylinder inserted shallowly into the soil [30]. The soil hydrodynamic parameters are then estimated by applying the physically based infiltration model proposed by Haverkamp et al. [31] to the field data. Due to the simplicity of application in the field, the relatively short execution times of experiments, and the possibility of analyzing both the quasi-steady and transient phases of the infiltration process, the Beerkan method has received increasing attention from hydrologists and practitioners [29,32]. In a recent numerical investigation, Bagarello et al. [33] demonstrated the acceptable correspondence between theoretical and practical Beerkan experiments in most of the considered circumstances, further emphasizing the practical interest in the method.
Stewart and Abou Najm [34,35] developed a new comprehensive model for single-ring infiltration that considered (i) four different approaches for estimating Ks values from both transient and steady-state single-ring infiltration data, (ii) four approaches in which the macroscopic capillary length and the initial and saturated soil water contents may be constrained, and (iii) different fitting linearization methods applied to transient data [28,36]. Furthermore, it considers a more complete calculation approach that makes use of the macroscopic capillary length estimated from measured soil water retention. The model is interesting, because it allows different estimates of Ks from Beerkan-type field infiltration experiments, depending on the available experimental information [28,36].
Di Prima et al. [36] first applied and validated the Stewart and Abou Najm model, selecting four soils with contrasting soil textures. The field-saturated soil hydraulic conductivity was estimated by four different approaches that differed by the way they constrain the macroscopic capillary length (λ) and the initial (θi) and saturated (θs) soil water contents. For validation purposes, the model was compared to Ks estimations obtained from the steady-state version of the simplified method based on a Beerkan infiltration run (SSBI method) and by numerical inverse modeling with Hydrus-2D/3D. The reliability of the Ks data, which was also checked through a comparison with unsaturated hydraulic conductivity measurements obtained from evaporation experiments, suggested that this new comprehensive model for single-ring infiltration data may represent a flexible tool for analyzing both transient and steady-state infiltration data. However, since the model has not been tested yet under complex agronomic field conditions, further application is needed to evaluate the pros and cons.
Testing hydraulic models during a crop season and under different soil management systems may be influenced by different soil conditions, including water content at the time of sampling, bulk density, and porosity (size, number, and connectivity), that vary during the season but also from one year to another. To exclude the influence of long-term temporal variability, case studies considering relatively stable soil conditions should be considered as long-term no-tilled or conservation tillage experiments [37,38,39,40,41]. Indeed, after a transition time from the last main tillage (variable from five to ten years), a steady-state condition is reached in which both improved soil structure and stabilized crop yields may be assumed [40,41,42].
Although the temporal variability of soil hydraulic properties topic has been generally well investigated, to our knowledge, little information is available on Ks evolution, as well as on the ability of different hydraulic models (e.g., simplified or more physically based) to provide coherent information on the temporal variability under contrasting management systems. It could be hypothesized that, regardless of the used hydraulic model for estimating the soil hydraulic conductivity, coherent information on its temporal variability should be obtained, but there is no experimental evidence supporting this hypothesis.
The general objective of this work was to investigate the temporal variability of the physical and hydraulic properties of two contrasting soil management systems, i.e., minimum tillage and no tillage, during a wheat crop cycle in southern Italy. For this aim, we applied the infiltration model proposed by Stewart and Abou Najm [34]. Specific goals were intended to provide information on (i) the applicability of the model, and calculation approaches, under real field conditions, (ii) the temporal variability of Ks and ancillary soil variables, obtained with the applied approaches (more or less data demanding), and (iii) the impact of minimum tillage and no tillage on the physical and hydraulic properties of the soil.
2. The Comprehensive Infiltration Model by Stewart and Abou Najm
The Stewart and Abou Najm [34] model describes the three-dimensional cumulative infiltration, I (L) from a surface circular source, and under a positive pressure head, using the following explicit relationships for transient (1a) and steady-state (1b) conditions:
where t (T) is the time, τcrit (T) is the maximum time for which, under transient condition of water flow, the relationship (1a) can be considered valid, θs (L3L−3) is the saturated soil water content, θi (L3L−3) is the initial volumetric soil water content, hsource (L) is the established ponding depth of the water, λ (L) is the macroscopic capillary length of the soil, Ks (L T−1) is the field-saturated soil hydraulic conductivity, a and b are dimensionless constants equal to 0.45 and 0.55, respectively, and f is a correction factor that depends on soil initial and boundary conditions and ring geometry:
where G* (L) is equal to
in which rd (L) is the radius of the ring, and d (L) is its depth insertion into the soil.
We discriminated the transient and steady-state conditions of cumulative infiltration data using the procedure proposed by Bagarello et al. [43]. We assumed that steady-state conditions were reached at the end of the infiltration process, then we performed a linear regression analysis for the last three I vs. t data points. The time until steady-state conditions, τcrit, was determined as the first value for which
where Ireg(t) was estimated from the regression analysis, and E defines a given threshold to check linearity. Equation (4) was applied from the start of the experiment until finding the first data point that fits the condition E* ≤ E. A value of E = 2% was considered in this investigation [36]. Therefore, transient infiltration conditions occur from time 0 until τcrit (i.e., when E* > 2%), while steady-state conditions exist for all data points that exceed τcrit (E* ≤ 2%).
Equation (1) is usually simplified as follows [44]:
where the intercept, C3 (L), and the slope, C4 (L T−1), are estimated by linear regression analysis of the I vs. t plot, and the infiltration coefficients C1 (L T−0.5) and C2 (L T−1) can be determined according to the fitting methods referred to as cumulative infiltration (CI, Zhang [45]), cumulative linearization (CL, Smiles and Knight [46]), and differential linearization (DL, Vandervaere et al. [47]).
Following Di Prima et al. [36]’s suggestions, all three fitting linearization methods (CI, CL, and DL) were considered in this investigation, because each of the above methods has advantages (i.e., to check for the adequacy of the infiltration model and detect possible soil heterogeneities) [48]. Therefore, fourteen calculation approaches for Ks estimation were adopted in this investigation that differed by the use of the transient or stationary part of infiltration curve; the fitting linearization method (CI, CL, or DL); or the way in which λ, θi, and θs were constrained for obtaining Ks. The five calculation approaches (i.e., A1 to A5) proposed by Stewart and Abou Najm [34,35] were thus labeled by a subscript that identifies the fitting methods to analyze the transient (CI, CL, or DL) or the steady-state (SS) data.
Approach 1 (A1) estimates Ks by constraining the parameters λ, θi, and θs and fitting Equation (1) to cumulative infiltration. Stewart and Abou Najm [35] proposed to estimate λ from water retention data. According to this approach, when the soil is relatively dry at the beginning of the infiltration experiment, λ tends towards a maximum value, λmax (L):
where η (-) is the pore size index, and hb (L) represents the pressure head scale parameter of the Brooks and Corey [49,50] (BC) model. The A1 approach also requires determining θi and θs in the field.
Approach 2 (A2) only requires estimates for θi and θs. For the transient-state data, only C1 and C2 coefficients need to be determined, and Ks and λ are calculated as follows:
Conversely, for the steady-state data, λ and Ks are calculated as
Approach 3 (A3) allows the estimation of Ks using only λ, estimated by Equation (6), and C2 or C4 determined from the infiltration experiment. For transient and steady-state data, Ks is calculated, respectively, by the following equations:
Approach 4 (A4) uses Equations (11) and (12) in conjunction with a λ value of first approximation. According to Stewart and Abou Najm [34,35] and Di Prima et al. [36], a value of λ = 150 mm was selected.
Approach 5 (A5) coincides with the steady-state version of the simplified method based on a Beerkan infiltration run (SSBI) proposed by Bagarello et al. [51]. The SSBI method is widely applied, because it stands out for some advantages, including that it does not need additional information to estimate Ks, such as soil water content at the time of measurement and at saturation, particle size distribution, or bulk density [29]. The SSBI estimates Ks by the following equation:
Note that, in Equation (13), λ is considered as the reciprocal of the sorptive number, α* (L−1), which expresses the relative importance of gravity and capillary forces during a ponding infiltration process [28,29].
The selected approaches need different inputs and, consequently, are expected to differ in terms of prediction accuracy. For example, A1 is the most data demanding, as it requires the estimation of λ from water retention data and θi and θs from soil samples, while A4 is the most simplified one, requiring only the measurement of the infiltration curve.
3. Materials and Methods
3.1. Long-Term Experiment Field and Lab Measurements
The experiment was conducted during the crop season 2015–2016 at the experimental farm of the Council for Agricultural Research and Economics (CREA-AA), Foggia (41°27′03″ N, 15°30′06″ E). The site is under a long-term field experiment performed on a monoculture of durum wheat [27] that started in 2002 to compare the effect of minimum tillage (MT) and sod-seeding (i.e., no tillage, NT) on crop yields. According to USDA classification, the soil texture is clay, with 42.7% clay and 27.7% silt, and it is classified by Soil Taxonomy–USDA as fine, mesic, Typic Chromoxerert [52]. The experimental design was a completely randomized block design with three replicates and unit plots of 500 m2 each. For both treatments (MT and NT), wheat straw was chopped into 10–15-cm lengths and spread back on the plot in early September. Depending on the seasonal outcome, after 1 month, a chemical weed control was performed. MT consists of a two-layer soil tillage at 40 cm deep (i.e., a chisel and rotary tiller combination) performed in early November. Fertilization and sowing followed after 1 or 2 days. More information on plot management and the main soil properties can be found in Castellini et al. [27].
Five sampling dates between November 2015 and June 2016 were carried out both under MT and NT plots (Figure 1) with the aim of monitoring the entire crop cycle, and the soil water retention curve, soil bulk density, soil water content at the time of sampling, and cumulative infiltration were determined. Specifically, for each soil management system and sampling date, 5–12 soil cores (8 cm inner diameter and 5 cm height; 250 cm3) were collected at randomly selected points into stainless steel rings to determine selected points of the soil water retention curve at high pressure heads (h = −5, −10, −20, −40, −70, and −100 cm); a disturbed soil sample was also collected at each sampling point to determine the water retention curve at low pressure heads (h = −330, −1,030, −3,060, and −15,300 cm). The Brooks and Corey [49] model was used to fit the measured soil water retention data, as required by the Stewart and Abou Najm [35] model.
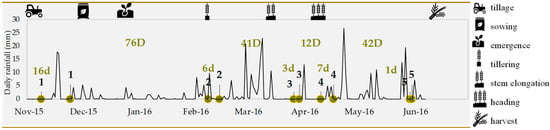
Figure 1.
Timeline of the field measurements (i.e., Beerkan infiltration tests and soil sampling) carried out under minimum tillage (MT) and no tillage (NT) plots in the 5 sampling dates (i.e., from 1 to 5). Numbers marked with lowercase or uppercase green letters represent the number of days elapsed between the beginning and the end of a single sampling date (d) and the time between two successive sampling dates (D). The daily rainfall was reported as a black continuous line.
At each sampling point five to eight infiltration experiments of Beerkan type were performed in the surface layer of the soil. To do this, a steel ring with a sharp edge and an inner diameter of 8.5 cm was shallowly inserted into the soil (i.e., about 1 cm) to conduct infiltration experiments, and the cumulative infiltration, I(t), was built using 15 water volumes of 60 mL each. In close proximity to each site for infiltration tests, two undisturbed soil cores (5 cm inner diameter and 5 cm height; 98 cm3) were collected at the 0 to 5 cm and 5 to 10 cm depths to determine the soil water content at the time of sampling, θi, and the soil dry bulk density, ρb.
All determinations were made in the row (i.e., between the plants) to avoid the areas that could have been compacted by the transit of agricultural machinery and always excluding the surfaces with visible superficial cracks.
3.2. Data Analysis
As reported by Stewart and Abou Najm [34], the application of the infiltration model requires a preliminary analysis of the infiltration curves to check that an apparent steady-state flow condition was reached. For this aim, we firstly determined the time to steady state, τcrit, the corresponding infiltrated depth, I(τcrit), and the total duration of the infiltration test, tend (T). Consequently, infiltration curves that met the restrictions of the model (Equation (1)) were considered [36].
Soil water retention data were averaged for each sampling date and soil management and parameterized with the BC model, obtaining a representative mean water retention curve. With reference to calculation approaches A1 and A3, λ values estimated from the mean water retention curves collected at the different sampling dates (1 to 5) were averaged to obtain a representative value soil management system (MT and NT). Similarly, a single mean value of θi and ρb was used for each sampling date and soil management [36]. As usual for similar applications, θs was estimated from ρb data, assuming a mean soil particle density of 2650 kg m−3 [36,50].
To assess the ability of the model to give reliable estimations of Ks (i.e., positive values), the ratio between valid Ks values and the sample size was calculated. For the purpose of the model evaluation, comparing the Ks values obtained with the 14 calculation approaches, we merged the whole set of infiltration data (MT + NT). However, only a “minimum dataset” (N = 44) was used for this aim, and the water infiltration experiments that simultaneously provided a valid Ks estimation with all calculation approaches were considered. We performed a first analysis of the Ks data using the distribution-free overlapping method [53,54]. The overlapping method, which can be defined as the area intersected by two or more probability density functions, is suggested to quantify the similarity among samples that are described in terms of distributions [53]. Consequently, a more stringent approach than those based on the comparison of mean values can be considered. The R software package was used for this analysis [54], and both the graphical representation of the overlapping area and the corresponding matrix of overlap percentages were analyzed. A threshold of 75% of the overlapping areas was considered in this investigation to properly discriminate among calculation approaches, according to references in the literature [55,56] and suggestions from hands-on experience.
A further comparison was carried on the minimum dataset to compare the mean values of Ks obtained with the different approaches. Specifically, the paired differences of Ks values (e.g., A1−A2CI, A1−A2CL, A1−A2DL, A1−A2SS, …, A1−A5, …, A4SS−A5) obtained from considered calculation approaches were determined, and the hypothesis of normal distribution of the differences was checked by the Kolmogorov–Smirnov test. Therefore, when the data were normally distributed, a paired t-test (p < 0.05) was used to test the mean differences between paired observations; conversely, a Wilcoxon signed rank test (p < 0.05) was used for non-normally distributed data [36].
The temporal variability of the physical and hydraulic properties (i.e., θi, ρb, Ks, and Brooks and Corey model parameters) under MT and NT was investigated using all available experimental information by the Tukey’s Honestly Significant Difference (THSD) test, whereas the statistical significance between MT and NT for a given sampling date was evaluated according to a two-tailed t-test. A significance level of α = 0.05 was always assumed.
4. Results
4.1. Sampling Dates and Temporal Changes of θi and ρb
Figure 1 shows sampling dates, time elapsed between the start and the end of each sampling campaign, time elapsed between two successive soil samplings, and the observed daily rainfalls. Sampling dates 1, 2, and 4 lasted longer due to the occurrence of some rainfall events. Consequently, a few days (i.e., 16, 6, and 7, respectively) had to pass before the soil reached the near-optimal conditions in terms of initial soil water content to avoid soil over-compaction during sampling. However, in the remaining cases, soil sampling was carried out in no more than three days (Figure 1).
Regardless of soil management (MT or NT), the soil water content at the time of measurements (θi) decreased over time (Figure 2). On all dates, θi was higher under NT than MT; these differences in θi values were always significant, except for the second sampling date. The temporal variability of the soil water content was detectable under MT, because, according to the THSD test, the differences in θi values between different sampling dates were always significant, except for three cases (1 vs. 2, 3 vs. 4, and 4 vs. 5). Conversely, a similar impact of temporal variability on θi was not detected under NT, because the soil water content was statistically different only between the first and the last date (Figure 2).
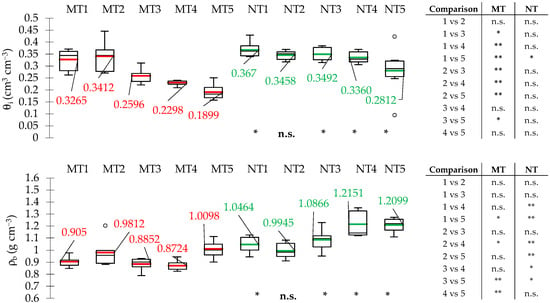
Figure 2.
Box plots of soil water content at the time of sampling (θi) and soil bulk density (ρb) carried out for each sampling date (1 to 5) under minimum tillage (MT) and no tillage (NT). The thick red–green line within each box represents the mean value (the fine black line, the median); for improved interpretation, mean values are also reported by numbers. Circles represent outliers. For a given soil management, inferences of the THSD-test between dates (i.e., x vs. y) are summarized on the right (* p < 0.05; ** p < 0.01; n.s. not significant). For a given sampling date, inferences of the two tailed t-test between MT and NT were reported under the NT boxes (* p < 0.05; n.s. not significant).
Overall, soil bulk density (ρb) increased over time as expected, but this trend was not always significant (Figure 2). Indeed, the correlation between ρb and the time (namely, the time elapsed between the last tillage and the sampling dates) revealed only a weak significance for the NT system (p < 0.10) and no correlation for the MT one. The bulk density of the soil surface layer was always higher under NT than MT; the differences between soil management systems were always significant, except for the second sampling date. For the MT plot, the ρb at the end of the crop season (June, MT5) was significantly higher than the values of the beginning (MT1, MT3, and MT4); a higher ρb value was found for MT2, due to a soil sampling carried out under relatively wetter soil conditions (Figure 1). For the NT plot, the ρb values of the last two dates (NT4 and NT5) were significantly higher than those measured in the first three dates (NT1, NT2, and NT3) (Figure 2).
4.2. Soil Water Retention Curve: Model Parametrization and Temporal Changes
The measured soil water retention curves showed a relatively low variability, since the observed coefficients of variation, CV, of water retention corresponding to the applied pressure head values were in the range of 5.2–12.8%.
The mean values of the measured water contents were always lower in MT than in NT soils. They decreased during the growing season, as the differences in water contents were higher in the winter season (∆ = 7–8%) and decrease in spring (∆ = 6–4%, respectively, beginning and end of April) and the summer season (∆ = 2% in June).
The BC model better fitted the MT than NT data (Figure 3), and the standard error between the estimated and measured water retention data was generally low (<0.003 cm3 cm−3), resulting in being five times higher under NT than MT (Table 1). The worse fit of the BC model for NT was mainly due to the discontinuity of the two data series, i.e., a decoupling of the water retention data obtained on undisturbed (h ≥ −100 cm) and sieved (h < −100 cm) soil samples. This represents an event that, although it did not substantially affect the quality of the fit in our case, can occur when analyzing soil water retention data from both undisturbed and repacked soil samples. Bittelli and Flury [57], for example, coupling measured soil water retention curves determined by pressure plates and dew point potential methods for both undisturbed cores and repacked samples, showed higher theta values for the undisturbed samples and lower values for disturbed ones at a given soil pressure head. A similar result was reported by Schelle et al. [58] when, for a clay loam soil, water retention data from evaporation experiments and the dew point method were considered.
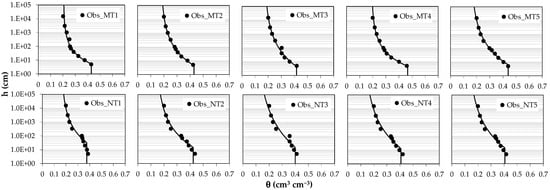
Figure 3.
Mean values of the measured soil water retention data (Obs) for each sampling time (1 to 5) for minimum tillage (MT) and no tillage (NT) systems. The Brooks and Corey (BC) fitting curve (lines) are also reported (sample size, N, was between 5 and 12).

Table 1.
Parameters of the Brooks and Corey model and associated standard error (SE), corresponding to mean soil water retention curves obtained for each soil management (MT and NT), and sampling date (1 to 5) (sample size, N was between 5 and 12).
The estimated saturated soil water content (θs) of MT soil increased from approximately 0.41–042 cm3 cm−3 in the first part of the season (MT1–MT3) to 0.44–0.46 cm3 cm−3 in the second one (M4–MT5) (Table 1); on the other hand, the θs of the NT soil started from 0.37 cm3 cm−3 in November and remained quite stable, in the range of 0.40–0.42 cm3 cm−3, throughout the season (NT2–NT5). The estimated air entry pressure (hb) was lower and quite stable during the growing season for MT, whereas it changed for NT where it started from relatively higher values (hb = 32 cm) decreased, and then remained stable in the range 13–15 cm throughout the season (NT2–NT5) (Table 1).
4.3. Cumulative Infiltration
Figure 4 shows the entire dataset of the cumulative infiltration curves measured under MT and NT over the five sampling dates. Overall, the curves exhibit the expected shape, with a downward concave part corresponding to the transient state and a linear part at the end of infiltration that is related to the steady state. A general view would suggest greater variability for first and third sampling dates, as a broad range of infiltration curves was obtained. The parameters that account for the steady-state flow conditions (e.g., time to steady state) suggest a higher variability in the third and fourth sampling dates (for the latter especially under the NT), as relatively higher CV values were observed (Table S1). Excluding some discrepancies in the early season (NT2 and MT3), the τcrit overall increased over time for MT and decreased for NT. The infiltrated depth at the equilibration time, I(τcrit), was 75% of the total infiltrated depth (Itot = 170 mm) for MT and 73% of Itot for NT; this suggests that quasi-steady-state conditions were always recognized before the end of infiltration experiments. Differences in the soil structure and associated bulk densities affected the duration of infiltrations (tend) that, on average, was halved between NT (1540 s) and MT (691 s) (Table S1).
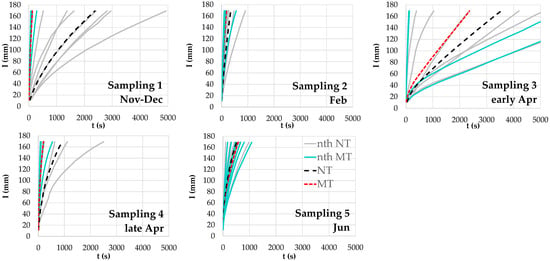
Figure 4.
Cumulative infiltration carried out under minimum tillage and no tillage plots (MT and NT) during the five sampling dates. Note that mean curves were represented with black-red dashed lines.
4.4. Saturated Hydraulic Conductivity: Models Evaluation and Comparison
The fourteen calculation approaches applied showed a different ability to return physically valid saturated hydraulic conductivity estimations (Figure 5). Overall, A1 and approaches that used the steady-state information (e.g., A3SS, A4SS, and A5), never failed and returned 100% of the Ks estimations both under MT and NT (i.e., 34 valid values out of 34 infiltration tests). On the other hand, A2 was more deficient, with a sample size that, regardless of transient or steady-state data analysis, never exceeded 5% of the valid Ks estimations. Approaches A3 and A4, applied with transient data, returned 73% valid Ks estimations. Moreover, when the fitting linearization methods were considered, the CI, CL, and DL methods returned 59, 49, and 44% valid Ks estimations. However, regardless of the considered criterion, it seems that data analysis was affected also by soil management, because no Ks estimation was obtained in 43% and 35% of cases under NT and MT, respectively. Given the small sample size obtained with A2, calculation approaches from A2CI to A2SS were excluded from the subsequent data analysis and comparisons.
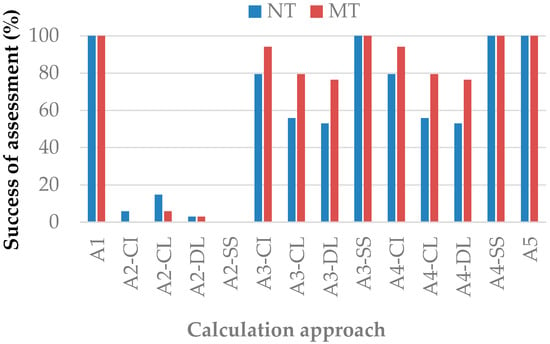
Figure 5.
Success percentage of saturated hydraulic conductivity estimation obtained with the five calculation approaches (A1 to A5). The acronyms CI, CL, and DL refer to fitting methods used to analyze the transient-state data (i.e., cumulative infiltration, cumulative linearization, and differential linearization, respectively), while SS refers to steady-state data. A1 to A4 refer to the Stewart and Abou Najm [35] model, while A5 refers to the SSBI method (Bagarello et al. [51]). Note that, for each soil management, the sample size N = 34 refers to the sum of the five sampling dates.
For the minimum dataset (N = 44; NT = 18 + MT = 26), i.e., the water infiltration experiments that simultaneously provided a valid Ks estimation with all calculation approaches considered, the saturated soil hydraulic conductivity, Ks estimates from the calculation approaches were compared both in terms of cumulative empirical frequency distributions (Figure 6) and mean values (Table 2). The lowest values were obtained using A4SS and A5 criteria, while the highest ones were obtained when A1 was adopted (Figure 6). The distribution-free overlapping method applied to Ks pairs revealed a satisfactory agreement based on the adopted criterion (overlapping areas equal to or greater than 75%), because six calculation approaches showed a relatively higher similarity in frequency distributions as follows: A4SS vs. A5 (96.3%), A3CI vs. A3CL (81.5%), A4CI vs. A4CL (81.1%), A3DL vs. A3SS (78.4%), A4DL vs. A4SS, and A4SS vs. A5 (>76.5%) (Figure 6). This result suggests that (i) the most data demanding criterion A1 for Ks estimation was always different as compared to the other approaches, and (ii) regardless of the A3 or A4 approaches, similarity in the Ks frequency distributions were detected when using CI and CL or DL and SS. Similar results were obtained when mean values of Ks were considered (Table 2). Overestimation of the Ks value obtained by A1, as evaluated from the ratio between mean Ks values obtained by A1 and those with the remaining criteria (i.e., A1/A3CI, …, A1/A5) fall in the ranges 1.5–2.9 (for A1/A3CI and A1/A3SS), 5.8–11.6 (for A1/A4CL and A1/A4SS), and 11.3 for A1/A5.
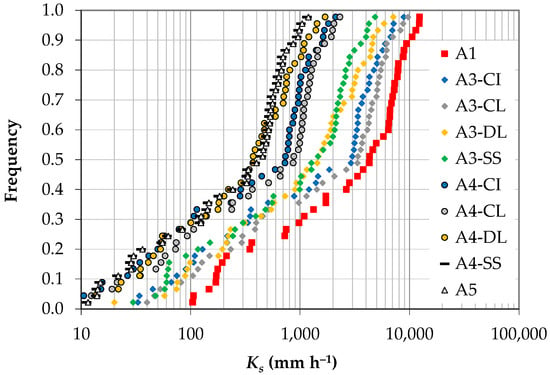
Figure 6.
Empirical cumulative frequency distribution of the saturated hydraulic conductivity (Ks) obtained from different calculation criteria and considering the minimum dataset (N = 44).

Table 2.
Sample size (N), minimum (Min), maximum (Max), mean, median, and coefficient of variation (CV, in %) of the saturated soil hydraulic conductivity Ks (mm h−1) values obtained by the different calculation approaches (N = 44).
For comparison purposes, the A5 approach, namely, the steady-state version of the simplified method based on a Beerkan infiltration run (SSBI), was compared to the remaining approaches, and the ratio between them (A1/A5, A3/A5, and A4/A5) considered. The SSBI method is reported to be reliable, because it receives exhaustive validation using synthetic and real data [51,59]. In the latter, for example, the SSBI was compared to several methods for Ks estimation, including BEST-steady [60], one-ponding depth method by Reynolds and Elrick [61], method 2 by Wu et al. [62], or approach 4 by Stewart and Abou Najm [34]. The results showed that the SSBI always overestimated Ks, but the differences were negligible from a practical point of view and included at most within a factor of 1.2 [59]. Overall, and regardless of the fitting linearization method, the approaches A1 and A3 returned similar Ks values, as well as similarities between A4 and A5 were observed. Specifically, discrepancies of about 1 order of magnitude (a factor of 11.3) were detected between A1 and A5, while they were within the range of 3.9–7.7 between A3 and A5 and lower than a factor 2 (1.4 as the mean) when A4 was considered. The correlation analysis showed that Ks data were always significantly correlated, but the regression line never coincided with identity one, according to the calculated 95% confidence intervals for the intercept and the slope, except for the A4SS-A5 comparison for which a substantial match between Ks estimations (differences of a factor of 1.03) was found, as expected (Figure 7).
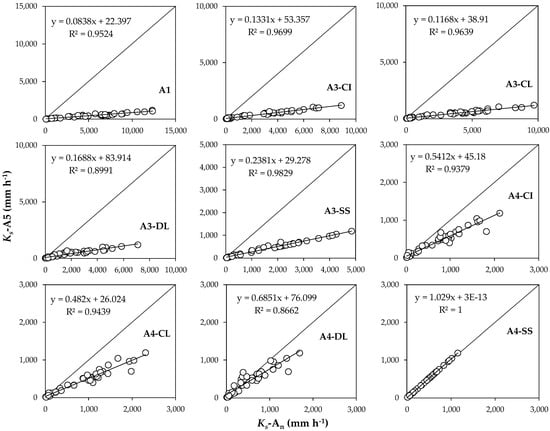
Figure 7.
Comparison between estimated Ks values obtained with A5 criterion (Ks–A5) against the calculation criteria A1, A3, and A4 and different fitting methods CI, CL, and DL (Ks–An) using the minimum dataset (N = 44).
4.5. Temporal Changes of Ks
A sample size lower than the minimum of N = 5 was obtained for MT4 and NT3 and NT4 and NT5 when approaches A3 and A4 were applied. Consequently, the temporal variability of Ks was investigated using only estimates from A1, the steady-state method A3SS and A5, which is the SSBI method (Figure 8). Approach A4SS was not considered for the temporal analysis due to substantial equivalence with the SSBI (Figure 7).
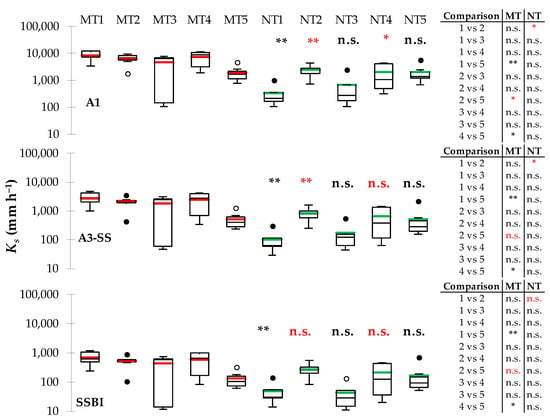
Figure 8.
Box plots of saturated hydraulic conductivity (Ks) at different sampling dates for minimum tillage (MT) and no tillage (NT) management systems conducted using the A1, A3SS, and A5 (SSBI) approaches. For a given soil management, inferences of the THSD test between dates (i.e., x vs. y) are summarized on the right (* p < 0.05; ** p < 0.01; n.s. not significant). For a given sampling date, inferences of the two tailed t-test between MT and NT were reported near NT boxes (* p < 0.05; n.s. not significant). For the general interpretation on box plots, please refer to the captions in Figure 2. Note that the discrepancies regarding the statistical significances among the three calculation criteria are shown with red character.
Overall, the evolution of Ks over time was different (opposite) between the two soil management systems, because, starting from November, it was decreasing under MT and increasing under NT. Furthermore, the two soil management systems showed an identical behavior when A1 and A3SS approaches were considered. According to the THSD test, comparable information on the temporal variability of Ks was generally obtained for MT regardless of the considered approach, because significantly lower Ks values were always detected between the first sampling date and the last one (i.e., MT1 > MT5) and between the last two (MT4 > MT5) (Figure 8). Under NT, significantly different Ks values were detected between the first and second sampling dates only when A1 and A3SS approaches were considered. Therefore, although the calculation approaches for Ks estimation were not fully equivalent for studying the temporal variability, especially when NT was considered, the THSD test gave the same response in 9 out of 10 cases, regardless of soil management and the comparisons considered (Figure 8).
The considered calculation approaches slightly affected the comparison between alternative soil management systems of the second sampling date (i.e., different results when using A1–A3SS were obtained and not different results when the SSBI was considered), but, in general, A3SS and SSBI approaches returned the same information, suggesting comparable Ks values between MT and NT from April onwards (Figure 8).
5. Discussion
5.1. Usability of the Stewart and Abou Najm Model and Ks Differences Among Approaches
The capability of the Stewart and Abou Najm [34] model to return valid estimations of Ks for statistical analysis and evaluations was tested under real field conditions, namely, during the crop cycle of durum wheat and under minimum or no tillage soil management in a clay soil of south Italy. This allowed to explore medium-high soil water contents (average range, 0.19–0.37 cm3 cm−3) and medium-low values of soil bulk density (0.87–1.22 g cm−3).
Approach A1 may be considered the most data demanding, because it needs to know site representative values of λ, θi, and θs, as well as η and hb parameters of Equation (6), which can be estimated from the measured retention data. In that respect, A1 was found to be an efficient approach, as it always returned a valid estimate of Ks. In general, the literature suggests that Ks estimates may be acceptable when Equation (1) is directly fitted to experimental data, and A1 yielded Ks estimates not significantly different from the Ks modeled by Hydrus [36,63]. Similarly, the best performances were obtained with A1 also by Stewart and Abou Najm [34] for five soils that ranged from coarse (sand) to fine (silt or little clay) soils, since the estimated Ks values differed from those modeled not more than 20% and less than 1% on average. Approach A2, which estimates λ and Ks from the infiltration data, was the most limiting for research, because too often (>85% of cases) returned negative estimates for the mentioned parameters. Consequently, this approach proved to be unreliable under our experimental conditions. A similar model response was obtained by Stewart and Abou Najm [35] and Di Prima et al. [36], as they detected inaccurate λ and Ks estimations or that A2 failed to give valid estimations at all. Therefore, the poor results obtained from this approach suggested neglecting it in the present investigation. Approaches A3 and A4 showed similar performances. Depending on the fitting linearization methods (CI, CL, or DL) or steady-state approach (SS) adopted, A3 and A4 proved to be quite efficient, as they returned Ks estimates in 53–100% of field tests. Approach A5 always returned a valid Ks estimate (100% of the field tests). Among fitting linearization methods to analyze the transient part of the infiltration curve, however, some differences were detected, as CI was more efficient in returning Ks estimations compared to CL or DL (i.e., 87, 68, and 65% on average, respectively) when A3 and A4 were considered. From a practical point of view, using steady-state approaches was more profitable than transient ones, as largely suggested in the literature, e.g., [28]. This result may be linked to the specific soil condition that was relatively wet at the time of infiltration, thus preventing an accurate analysis of the early stage of the infiltration process. In general, the single-ring method can be expected to yield more accurate estimates of Ks in coarse-textured soils than in fine-textured ones and, for the latter soil texture, if the transient method is used instead of the steady-state [28,29]. The soils of the Capitanata Plain and Foggia district are deep fine-textured soils. Therefore, ideal soil conditions (i.e., uniformly dry soil profile) to properly apply transient methods, may be reached only between late summer and early autumn. Otherwise, the analysis of the transient phase of the infiltration curve can be difficult and the estimates of soil sorptivity uncertain or impossible to obtain [59]; consequently, negative Ks values may be obtained.
Regarding the Ks differences among the approaches, our results showed that A1, A3, and A4 generally overestimated the saturated hydraulic conductivity compared to the reference approach A5 (i.e., SSBI method). In particular, one order of magnitude overestimation was observed for the most data demanding approach (A1) given the ratio between the two mean Ks values was equal to 11.3. Regardless of the considered transient or steady-state phases (CI, CL, DL, or SS), differences were relatively smaller for A3 (ratio equal to 5.7 on average) and negligible for A4 (ratio equal to 1.4 on average).
Two points needed further analysis: (i) the generally estimated high values of Ks and (ii) the unexpected discrepancies of some approaches compared to the literature findings. Regarding the first point, a comparison with data obtained in the past for the same soil using different field and laboratory methods showed that the mean Ks values were in the ranges of 60–110 and 95–310 mm h−1 under near-saturated or saturated soil conditions, respectively [64,65]. Therefore, former Ks values did not differ much from the results obtained with approaches A4SS or A5 (Table 2). For the same site, Ks values up to about 2220 mm h−1 were recorded using the simplified falling head method and up to about 1120 mm h−1 using the BEST method [42], which, however, remain widely lower than those obtained with A1 (Table 2). Regarding the second point, Di Prima et al. [36] reported that approach A1 yielded generally lower Ks values than the remaining calculation approaches, and for the rare cases in which overestimations of Ks were detected, they were at most equal to a factor 1.6.
To further investigate the unexpected discrepancies in Ks values obtained in this study, the A1 and A5 (i.e., SSBI) results were compared. Figure 9a shows the direct (and highly significant) correlation between the ratio Ks-A1/Ks-SSBI as a function of ERFIT, namely, the relative error of the fitting of the considered infiltration model (Equation (1)) to the experimental data. Figure 9b–d also show three illustrative examples of fitting accuracy for the minimum, intermedium, and maximum ERFIT values, accounting for A1 overestimates between a factor of 9.6 and 23.8 (Figure 9a). The markedly concave shape of the infiltration curve in Figure 9d can typically be associated with heterogeneity in the soil profile, for example, an infiltration process that evolves into a layered porous medium characterized by a relatively less permeable lower layer. Alternatively, it could be linked to a high tortuosity of the conductive pore system, which is therefore poorly interconnected [66,67]. Our data seem to confirm the latter interpretation, because the fitting accuracy seems to be dependent on the soil management given that the mean overestimation was higher under MT than NT. The plots under study also showed this behavior in past investigations, as NT was occasionally more compact and more conductive as compared to MT [42]. However, since the MT plot was more prone to dryness in the surface layers than NT, the first hypothesis may also be plausible, as a concave shape can also occur when stratifications in the soil profile are associated with differences in soil water contents (a dry layer over a wetter one). Other possible factors, including air entrapment or soil sealing at the surface from repeated water applications, also seem plausible for our experimental conditions in some randomly distributed points [36].
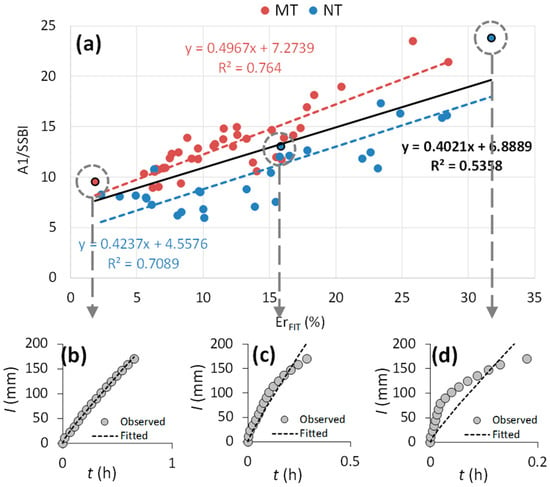
Figure 9.
Ratio of saturated hydraulic conductivity obtained with approaches A1 and A5 (SSBI) against the relative error of the fitting of the functional relationships to the experimental data (a), and examples of fitting accuracy for the minimum (ErFIT = 1.8%; experiment MT1-SD3) (b), intermediate (ErFIT = 15.8%; NT1-SD3) (c), and maximum (ErFIT = 31.7%; NT5-SD5) (d) values, as labeled in subpanel (a) (black-edged points). The black continuous regression line corresponds to the whole set of data.
5.2. Temporal Variability of Soil Physical and Hydraulic Properties
With reference to the temporal variability of basic soil physical properties, only the volumetric soil water content (θi) under NT showed a clear temporal stability resulting in relatively high and not significantly different values for the first four sampling dates (from mid-November to end-April). Since, for this time interval, the measured mean differences between θi and the field capacity were negligible (about 0.35 and 0.34 cm3 cm−3, respectively), the soil water status matched the maximum water reserve for plant growth. Such information might be considered valuable for modeling studies simulating crop growth. Conversely, a relatively higher temporal variability was found in the tilled (MT) soil, where the soil water content significantly decreased from April (MT3) to June (MT5).
Soil bulk density showed a generally increasing trend for both management systems, but the differences between two consecutive sampling dates were difficult to interpret. In particular, ρb experienced significant increases only after the third or the fourth epoch of measure. Since such a result was obtained regardless of the soil management, we hypothesized that the sampling dates were too close each other to adequately investigate this physical property of the soil. An alternative evaluation on the temporal variability of ρb was therefore conducted by considering more spaced measures that included only the first, third, and last dates. The results showed a common pattern between the two management systems, as the soil bulk density did not change significantly between the first sampling date (early season) and third sampling date (middle season) while increasing significantly in the late season (fifth sampling date).
Several seasonal trends for ρb were reported in the literature, e.g., [15,25]. Alletto and Coquet [15], for example, considered three sampling dates between May and November, which were interspaced by one or three months. The results showed that most of the variations occurred between May and June, i.e., respectively, 10 and 51 days after seedbed preparation. They pointed out that the timing of tillage events relative to the measurements has a strong effect on soil properties. In fact, the soil porosity induced by tillage was unstable, and after a few weeks, the benefits in soil porosity gained by tillage were lost due to the cumulative effects of gravity and rainfall. They concluded that temporal changes appeared to be one of the main sources of variability for ρb (and Ks) under conventional tillage and MT; for such reasons, short-term tillage effects are difficult to capture [15]. Bormann and Klaassen [25] studied the seasonal changes of some physical and hydraulic properties during four dates between March and October. They reported that ρb firstly decreases between spring and summer, and afterwards, it again increases in late summer or stays constant in autumn, depending on the considered soil. This behavior was linked to tillage effects and the increased activity of soil fauna during the summer [25].
Evaluation of the temporal variability of Ks was possible only applying A1 and the steady-state approaches (A3SS, A4SS, and A5), namely, the criteria capable of returning valid estimations while preserving the sample size collected. Regardless of the four approaches considered, information on the temporal variability of Ks under NT was quite clear, showing an overall lack of temporal variability. This confirms that the NT soil management system is quite stable, and most of the variability is that induced during sowing, i.e., from NT1 to NT2. On the other hand, although the MT system was more affected by spatial variability (mainly in April), the considered approaches made it possible to identify a broad time window (indicatively between November and end of April) in which Ks mean values were stable and comparable, followed by a Ks decrease at the end of the growing season (MT5). It is worth noting that the results could be informative for the case study and affected by the specific climatic conditions of the year considered (Figure 1) and thus, similarly to other studies [12,13,15,16,26], are hardly generalizable. However, the specific information obtained for the site could be useful to better interpret the long-term behavior of the crop system considered. In fact, our results show that, apart from the seasonal temporal variability, an optimal sampling window could be indicated in April, both under NT and MT, during which relatively stable Ks values (i.e., stable soil structure conditions) can be expected. Therefore, for the aim to study the long-term effect of management systems on the soil physical and hydraulic properties, it could be recommended to concentrate intensive soil sampling during this time interval.
5.3. Impact of Minimum Tillage and No Tillage on the Physical and Hydraulic Properties of the Soil
Soil management affected the soil physical and hydraulic properties, as the soil water content and bulk density were significantly higher under NT than MT in four out of five sampling dates. This result was expected, as widely reported in the literature (e.g., Strudley et al. [11], among others), but this check was the prerequisite to verify the basic reliability of the measurements obtained.
The higher soil compaction detected under NT did not always lead to a reduction in soil permeability, since, for two out of five sampling dates (i.e., third and fifth), the saturated hydraulic conductivity in NT was not significantly different from MT. Regardless of the approach considered, significant differences in Ks values were detected between MT and NT only in the first sampling date (i.e., MT1 > NT1). In other words, our results showed that, at the end of the wheat crop cycle, NT was significantly more compact but no less conductive than MT.
To investigate the discrepancies in the soil pores diameter, the modal diameters of the pore distribution curves estimated from the measured water retention curves were compared [7]. The modal diameter, dmode, was selected, because it represents an indicator of the pore diameter that, implicitly, also provides information on the so-called S-index [68] that discriminates the non-capillary from capillary porosity. The comparison in terms of normalized pore volume distributions between MT and NT at the start and end of the investigation (i.e., first and fifth sampling dates) showed that (i) dmode increased by a factor 1.7 under NT and remained practically constant under MT (i.e., differed by a factor 1.1), and consequently, (ii) the ratio of the modal diameters in the two management systems (MT/NT) decreased over time by a factor ranging from eight to five (Figure 10a). The differences between the two alternative soil management systems were further evident, as the saturated hydraulic conductivity was found to be significantly correlated with the pores diameter only under NT (Figure 10b). The limited sources in the literature available for clay soils confirm the direct relationship between Ks and dmode [69,70]. Park and Smucker [71] suggested that, under conventional tillage (CT), the water flow could be limited to inter-aggregate macropores, while greater portions of the water flow may be observed under NT, due to the flow within intra-aggregate porosity. They observed a power relationship between Ks and total porosity for NT soil aggregates but not for CT soil aggregates [71]. Our results seem to confirm this finding (Figure 10b) with independently obtained soil information, i.e., field hydrodynamic measurements (Ks) and lab hydrostatic measurements (water retention curve).
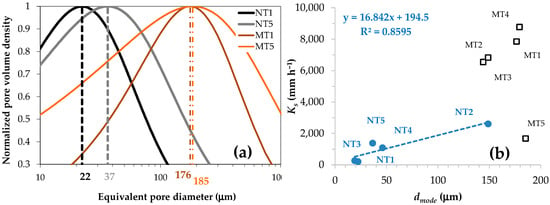
Figure 10.
Normalized pore volume distributions and corresponding modal diameters (continuous and dotted lines, respectively) for the first (1) and last (5) sampling dates under no tillage, NT, and minimum tillage, MT (a), and a correlation between the saturated hydraulic conductivity (Ks) and modal pores diameter (dmode) for all sampling dates (b). Note that the Ks values refer to the medians obtained with Approach 5 (SSBI).
6. Summary and Conclusions
In this study, we applied the comprehensive model by Stewart and Abou Najm for single-ring infiltration data that includes thirteen calculation approaches for Ks determination, together with the SSBI method that provided the fourteenth calculation approach used as a benchmark for comparison. The considered approaches differed by the way they derive Ks and constrain λ, θi, and θs; the use of transient or steady-state data; and the fitting linearization methods applied to transient data (CI, CL, and DL). A field experiment aimed at investigating the long-term effects of two alternative soil management systems, MT and NT, was selected to study the seasonal variability of Ks during a wheat crop cycle, and the ability of the selected hydraulic models to provide consistent information on Ks temporal changes (from November to June) was assessed.
For the first time, the performance of the Stewart and Abou Najm model has been checked under agronomic conditions, and its pros and cons have been evaluated under real field conditions. Among the different calculation approaches, A1 and the steady-state approaches (A3SS, A4SS, and A5) always provided valid Ks estimations, while the transient approaches were comparatively less applicable, also due to the relatively high soil water content at the time of sampling. Regarding the criteria that used transient data, cumulative infiltration (CI) was more efficient compared to cumulative linearization (CL) and differential linearization (DL). However, approach A1 greatly overestimated Ks compared to past investigations conducted in the same site.
The approaches that proved to be usable for the temporal analysis of Ks (A1, A3SS, A4SS, and A5), agreed to detecting a stability in this soil property in the NT system at least from early April onwards. Conversely, the MT system was more affected by temporal changes and showed temporal stability only at the beginning of the season. The considered approaches agreed on identifying a seasonal window where the Ks mean values were stable and comparable from February to late April. Consequently, for the aim of monitoring the long-term experiment, a common time for determining Ks might be set for early spring.
The long-term soil management has evidently changed the physical and hydraulic properties of the soil. At the end of the wheat crop cycle, NT was significantly more compact but no less conductive than MT. Regardless of the approach considered, significant differences in Ks values were detected under MT and NT only after tillage (i.e., MT > NT), while the two managing systems yielded similar Ks estimates (MT ≈ NT) at the end of the cropping season (June). Comparison of the pore volume distributions at the beginning and at the end of investigation showed that (i) modal pore diameters were higher in MT than in NT by an average factor of two, and (ii) the modal pore diameters increased over time under NT, while they remained stable under MT. However, Ks was found to be significantly correlated with pore diameters only for NT.
The practical result of such changes in the physical and hydraulic properties was a significant increase in water retention under NT, at least from April onwards. Our work both confirmed the well-known literature results and provided original information on the temporal dynamics of the soil properties. In conclusion, since NT offers clear environmental benefits compared to MT, our results could be important, because they have identified quite stable and comparable physical and hydraulic properties between the two management systems in April. This time frame is relevant for the simulation of winter durum wheat, because it coincides with the heading and ripening phases until harvest.
Other models and approaches that only require cumulative infiltration and some ancillary soil variables, like the BEST procedure proposed by Lassabatere et al. [50], could easily be applied to validate our predictions. Anyway, this multi-model approach represents a promising tool to better investigate the spatiotemporal variability of the soil hydraulic conductivity of agro-environments. Finally, some signals of a good correspondence between lab (dmode) and field (Ks) measurements were detected that encourage future investigations on the always little explored relationship between hydraulic conductivity and soil porosity.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/w16202950/s1: Table S1. Sample size (N), minimum (Min), maximum (Max), mean, and coefficient of variation (CV%) of the equilibration time, ts (s), infiltrated depth at the equilibration time, I(ts) (mm), and total duration, tend (s) for the infiltration runs.
Author Contributions
Conceptualization, M.C., S.D.P. and M.I.; methodology, M.C., S.D.P. and M.I.; formal analysis, M.C., S.D.P. and M.I.; investigation, M.C. and L.G.; resources, M.C. and M.R.; data curation, M.C., L.G., V.A. and D.A.; writing—original draft preparation, M.C.; writing—review and editing, M.C., S.D.P., R.L., V.A., D.A., M.R. and M.I.; funding acquisition, M.C. and M.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The dataset is available on request from the authors.
Acknowledgments
The work was supported by the PRIMA Foundation, call 2019-Section 1–GA no. 1912 “Re-search-based participatory approaches for adopting Conservation Agriculture in the Mediterranean Area—CAMA” project. This work is part of the side activities of the GENFORAGRIS project “Fenotipizzazione di genotipi di olivo resistenti a Xylella fastidiosa e messa a punto di un modello di gestione agronomica ad elevata sostenibilità”, funded by MASAF, D.M. n. 664538 del 28/12/2022. We also thank Alessandro Vittorio Vonella for managing the experimental field device and Eman-uele Barca for the valuable suggestions on the distribution-free overlapping method.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Jarvis, N.; Larsbo, M.; Lewan, E.; Garré, S. Improved descriptions of soil hydrology in crop models: The elephant in the room? Agric. Syst. 2022, 202, 103477. [Google Scholar] [CrossRef]
- Amoozegar, A.; Warrick, A.W. Hydraulic Conductivity of Saturated Soils: Field Methods. In Methods of Soil Analysis; Klute, A., Ed.; American Society of Agronomy, Inc. & Soil Science Society of America, Inc.: Madison, WI, USA, 1986. [Google Scholar] [CrossRef]
- Hillel, D. Environmental Soil Physics; Academic Press: San Diego, CA, USA, 1998; p. 771. [Google Scholar]
- Parvin, N.; Sandin, M.; Larsbo, M. Seedbed consolidation and surface sealing for soils of different texture and soil organic carbon contents. Soil Tillage Res. 2021, 206, 104849. [Google Scholar] [CrossRef]
- Passioura, J.B. Soil structure and plant growth. Aust. J. Soil Res. 1991, 29, 717–728. [Google Scholar] [CrossRef]
- Horton, R.; Ankeny, M.D.; Allmaras, R.R. Effects of compaction on soil hydraulic properties. In Soil Compaction in Crop Production; Soane, B.D., van Ouwerkerk, C., Eds.; Elsevier: Amsterdam, The Netherlands, 1994; pp. 141–165. [Google Scholar]
- Reynolds, W.D.; Drury, C.F.; Tan, C.S.; Fox, C.A.; Yang, X.M. Use of indicators and pore volume-function characteristics to quantify soil physical quality. Geoderma 2009, 152, 252–263. [Google Scholar] [CrossRef]
- Keller, T.; Sutter, J.A.; Nisse, K.; Rydberg, T. Using field measurement of saturated soil hydraulic conductivity to detect low-yielding zones in three Swedish fields. Soil Till. Res. 2012, 124, 68–77. [Google Scholar] [CrossRef]
- Drewry, J.J.; McNeill, S.J.; Carrick, S.; Lynn, I.H.; Eger, A.; Payne, J.; Rogers, G.; Thomas, S.M. Temporal trends in soil physical properties under cropping with intensive till and no-till management. N. Z. J. Agric. Res. 2019, 64, 223–244. [Google Scholar] [CrossRef]
- Geris, J.; Verrot, L.; Gao, L.; Peng, X.; Oyesiku-Blakemore, J.; Smith, J.U.; Hodson, M.E.; McKenzie, B.M.; Zhang, G.; Hallett, P.D. Importance of short-term temporal variability in soil physical properties for soil water modelling under different tillage practices. Soil Tillage Res. 2021, 213, 105132. [Google Scholar] [CrossRef]
- Strudley, M.W.; Green, T.R.; Ascough, J.C., II. Tillage effects on soil hydraulic properties in space and time: State of the science. Soil Tillage Res. 2008, 99, 4–48. [Google Scholar] [CrossRef]
- Schwen, A.; Bodner, G.; Scholl, P.; Buchan, G.D.; Loiskandl, W. Temporal dynamics of soil hydraulic properties and the water-conducting porosity under different tillage. Soil Tillage Res. 2011, 113, 89–98. [Google Scholar] [CrossRef]
- Bodner, G.; Scholl, P.; Loiskandl, W.; Kaul, H.P. Environmental and management influences on temporal variability of near saturated soil hydraulic properties. Geoderma 2013, 204–205, 120–129. [Google Scholar] [CrossRef]
- Lacolla, G.; Caranfa, D.; De Corato, U.; Cucci, G.; Mastro, M.A.; Stellacci, A.M. Maize Yield Response, Root Distribution and Soil Desiccation Crack Features as Affected by Row Spacing. Plants 2023, 12, 1380. [Google Scholar] [CrossRef] [PubMed]
- Alletto, L.; Coquet, Y. Temporal and spatial variability of soil bulk density and near-saturated hydraulic conductivity under two contrasted tillage management systems. Geoderma 2009, 152, 85–94. [Google Scholar] [CrossRef]
- Kreiselmeier, J.; Chandrasekhar, P.; Weninger, T.; Schwen, A.; Julich, S.; Feger, K.-H.; Schwärzel, K. Temporal variations of the hydraulic conductivity characteristic under conventional and conservation tillage. Geoderma 2020, 362, 114127. [Google Scholar] [CrossRef]
- Popolizio, S.; Stellacci, A.M.; Giglio, L.; Barca, E.; Spagnuolo, M.; Castellini, M. Seasonal and Soil Use Dependent Variability of Physical and Hydraulic Properties: An Assessment under Minimum Tillage and No-Tillage in a Long-Term Experiment in Southern Italy. Agronomy 2022, 12, 3142. [Google Scholar] [CrossRef]
- Hu, W.; Tabley, F.; Beare, M.; Tregurtha, C.; Gillespie, R.; Qiu, W.; Gosden, P. Short-term dynamics of soil physical properties as affected by compaction and tillage in a silt loam soil. Vadose Zone J. 2018, 17, 180115. [Google Scholar] [CrossRef]
- Rousseva, S.; Torri, D.; Pagliai, M. Effect of rain on the macroporosity at the soil surface. Eur. J. Soil Sci. 2002, 53, 83–94. [Google Scholar] [CrossRef]
- Castellini, M.; Iovino, M.; Bagarello, V. Testing the hydrodynamic behavior of a loam soil by beerkan infiltration runs with six heights of water pouring. J. Hydrol. 2024, 630, 130697. [Google Scholar] [CrossRef]
- Angulo-Jaramillo, R.; Moreno, F.; Clothier, B.E.; Thony, J.L.; Vachaud, G.; Fernandez-Boy, E.; Cayuela, J.A. Seasonal variation of hydraulic properties of soils measured using a tension disk infiltrometer. Soil Sci. Soc. Am. J. 1997, 61, 27–32. [Google Scholar] [CrossRef]
- Peng, X.; Horn, R.; Smucker, A. Pore shrinkage dependency of inorganic and organic soils on wetting and drying cycles. Soil Sci. Soc. Am. J. 2007, 71, 1095–1103. [Google Scholar] [CrossRef]
- Blanchy, G.; Albrecht, L.; Bragato, G.; Garré, S.; Jarvis, N.; and Koestel, J. Impacts of soil management and climate on saturated and near-saturated hydraulic conductivity: Analyses of the Open Tension-disk Infiltrometer Meta-database (OTIM). EGUsphere 2022, preprint. [Google Scholar] [CrossRef]
- Kool, D.; Tong, B.; Tian, Z.; Heitman, J.L.; Saur, T.J.; Horton, R. Soil water retention and hydraulic conductivity dynamics following tillage. Soil Tillage Res. 2019, 193, 95–100. [Google Scholar] [CrossRef]
- Bormann, H.; Klaassen, K. Seasonal and land use dependent variability of soil hydraulic and soil hydrological properties of two Northern German soils. Geoderma 2008, 145, 295–302. [Google Scholar] [CrossRef]
- Jirků, V.; Kodešová, R.; Nikodem, A.; Mühlhanselová, M.; Žigová, A. Temporal variability of structure and hydraulic properties of topsoil of three soil types. Geoderma 2013, 204–205, 43–58. [Google Scholar] [CrossRef]
- Castellini, M.; Stellacci, A.M.; Barca, E.; Iovino, M. Application of multivariate analysis techniques for selecting soil physical quality indicators: A case study in long-term field experiments in Apulia (southern Italy). Soil Sci. Soc. Am. J. 2019, 83, 707–720. [Google Scholar] [CrossRef]
- Iovino, M.; Abou Najm, M.R.; Angulo-Jaramillo, R.; Bagarello, V.; Castellini, M.; Concialdi, P.; Di Prima, S.; Lassabatere, L.; Stewart, R.D. Parameterization of a comprehensive explicit model for single-ring infiltration. J. Hydrol. 2021, 601, 126801. [Google Scholar] [CrossRef]
- Castellini, M.; Di Prima, S.; Moret-Fernández, D.; Lassabatere, L. Rapid and accurate measurement methods for determining soil hydraulic properties: A review. J. Hydrol. Hydromech. 2021, 69, 1–19. [Google Scholar] [CrossRef]
- Braud, I.; De Condappa, D.; Soria, J.M.; Haverkamp, R.; Angulo-Jaramillo, R.; Galle, S.; Vauclin, M. Use of scaled forms of the infiltration equation for the estimation of unsaturated soil hydraulic properties (the Beerkan method). Eur. J. Soil Sci. 2005, 56, 361–374. [Google Scholar] [CrossRef]
- Haverkamp, R.; Ross, P.J.; Smettem, K.R.J.; Parlange, J.Y. 3-dimensional analysis of infiltration from the disc infiltrometer. 2. Physically-based infiltration equation. Water Resour. Res. 1994, 30, 2931–2935. [Google Scholar] [CrossRef]
- Angulo-Jaramillo, R.; Bagarello, V.; Di Prima, S.; Gosset, A.; Iovino, M.; Lassabatere, L. Beerkan Estimation of Soil Transfer parameters (BEST) across soils and scales. J. Hydrol. 2019, 576, 239–261. [Google Scholar] [CrossRef]
- Bagarello, V.; Dohnal, M.; Iovino, M.; Lai, J. Correspondence between theory and practice of a Beerkan infiltration experiment. Vadose Zone J. 2022, 21, e20220. [Google Scholar] [CrossRef]
- Stewart, R.D.; Abou Najm, M.R. A Comprehensive model for single ring infiltration I: Initial water content and soil hydraulic properties. Soil Sci. Soc. Am. J. 2018, 82, 548–557. [Google Scholar] [CrossRef]
- Stewart, R.D.; Abou Najm, M.R. A Comprehensive model for single ring infiltration II: Estimating field-saturated hydraulic conductivity. Soil Sci. Soc. Am. J. 2018, 82, 558–567. [Google Scholar] [CrossRef]
- Di Prima, S.; Castellini, M.; Abou Najm, M.R.; Stewart, R.D.; Angulo-Jaramillo, R.; Winiarski, T.; Lassabatere, L. Experimental Assessment of a New Comprehensive Model for Single Ring Infiltration Data. J. Hydrol. 2019, 573, 937–951. [Google Scholar] [CrossRef]
- Körschens, M. The importance of long-term field experiments for soil science and environmental research—A review. Plant Soil Environ. 2006, 52, 1–8. [Google Scholar]
- Peterson, G.A.; Lyon, D.J.; Fenster, C.R. Valuing long-term field experiments: Quantifying the scientific contribution of a long-term tillage experiment. Soil Sci. Soc. Am. J. 2012, 76, 757–765. [Google Scholar] [CrossRef]
- Stellacci, A.M.; Castellini, M.; Diacono, M.; Rossi, R.; Gattullo, C.E. Assessment of Soil Quality under Different Soil Management Strategies: Combined Use of Statistical Approaches to Select the Most Informative Soil Physico-Chemical Indicators. Appl. Sci. 2021, 11, 5099. [Google Scholar] [CrossRef]
- Reichert, J.M.; Rosa, V.T.; Vogelmann, E.S.; Rosa, D.P.; Horn, R.; Reinert, D.J.; Sattler, A.; Denardin, J.E. Conceptual framework for capacity and intensity physical soil properties affected by short and long-term (14 years) continuous no-tillage and controlled traffic. Soil Tillage Res. 2016, 158, 123–136. [Google Scholar] [CrossRef]
- Mathers, C.; Heitman, J.; Huseth, A.; Locke, A.; Osmond, D.; Woodley, A. No-till imparts yield stability and greater cumulative yield under variable weather conditions in the southeastern USA piedmont. Field Crops Res. 2023, 292, 108811. [Google Scholar] [CrossRef]
- Castellini, M.; Vonella, A.V.; Ventrella, D.; Rinaldi, M.; Baiamonte, G. Determining soil hydraulic properties using infiltrometer techniques: An assessment of temporal variability in a long-term experiment under minimum- and no-tillage soil management. Sustainability 2020, 12, 5019. [Google Scholar] [CrossRef]
- Bagarello, V.; Iovino, M.; Reynolds, W. Measuring hydraulic conductivity in a cracking clay soil using the Guelph permeameter. Trans. ASAE 1999, 42, 957–964. [Google Scholar] [CrossRef]
- Philip, J. The theory of infiltration: 4. Sorptivity and algebraic infiltration equations. Soil Sci. 1957, 84, 257–264. [Google Scholar] [CrossRef]
- Zhang, R. Determination of soil sorptivity and hydraulic conductivity from the disk infiltrometer. Soil Sci. Soc. Am. J. 1997, 61, 1024. [Google Scholar] [CrossRef]
- Smiles, D.; Knight, J. A note on the use of the Philip infiltration equation. Soil Res. 1976, 14, 103–108. [Google Scholar] [CrossRef]
- Vandervaere, J.-P.; Peugeot, C.; Vauclin, M.; Angulo Jaramillo, R.; Lebel, T. Estimating hydraulic conductivity of crusted soils using disc infiltrometers and minitensiometers. J. Hydrol. HAPEX-Sahel 1997, 188–189, 203–223. [Google Scholar] [CrossRef]
- Vandervaere, J.-P.; Vauclin, M.; Elrick, D.E. Transient flow from tension infiltrometers I. The two-parameter equation. Soil Sci. Soc. Am. J. 2000, 64, 1263–1272. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, T. Hydraulic Properties of Porous Media; Colorado State University: Fort Collins, CO, USA, 1964; Hydrology Papers 3. [Google Scholar]
- Lassabatere, L.; Angulo-Jaramillo, R.; Soria Ugalde, J.M.; Cuenca, R.; Braud, I.; Haverkamp, R. Beerkan estimation of soil transfer parameters through infiltration experiments—BEST. Soil Sci. Soc. Am. J. 2006, 70, 521. [Google Scholar] [CrossRef]
- Bagarello, V.; Di Prima, S.; Iovino, M. Estimating saturated soil hydraulic conductivity by the near steady-state phase of a Beerkan infiltration test. Geoderma 2017, 303, 70–77. [Google Scholar] [CrossRef]
- Soil Survey Staff. Keys to Soil Taxonomy, 11th ed.; USDA–NRCS: Washington, DC, USA, 2010. [Google Scholar]
- Pastore, M.; Calcagnì, A. Measuring distribution similarities between samples: A distribution-free overlapping index. Front. Psychol. 2019, 10, 1089. [Google Scholar] [CrossRef]
- Pastore, M. Overlapping: A R package for Estimating Overlapping in Empirical Distributions. J. Open Source Softw 2018, 3, 1023. [Google Scholar] [CrossRef]
- Srisomkiew, S.; Kawahigashi, M.; Limtong, P.; Yuttum, O. Digital soil assessment of soil fertility for Thai jasmine rice in the Thung Kula Ronghai region, Thailand. Geoderma 2022, 409, 115597. [Google Scholar] [CrossRef]
- Nardi, D.; Marini, L. Role of abandoned grasslands in the conservation of spider communities across heterogeneous mountain landscapes. Agric. Ecosyst. Environ. 2021, 319, 107526. [Google Scholar] [CrossRef]
- Bittelli, M.; Flury, M. Errors in Water Retention Curves Determined with Pressure Plates. Soil Sci. Soc. Am. J. 2009, 73, 1453–1460. [Google Scholar] [CrossRef]
- Schelle, H.; Heise, L.; Janicke, K.; Durner, W. Water retention characteristics of soils over the whole moisture range: A comparison of laboratory methods. Eur. J. Soil Sci. 2013, 64, 814–821. [Google Scholar] [CrossRef]
- Di Prima, S.; Stewart, R.D.; Castellini, M.; Bagarello, V.; Abou Najm, M.R.; Pirastru, M.; Giadrossich, F.; Iovino, M.; Angulo-Jaramillo, R.; Lassabatere, L. Estimating the macroscopic capillary length from Beerkan infiltration experiments and its impact on saturated soil hydraulic conductivity predictions. J. Hydrol. 2020, 589, 125159. [Google Scholar] [CrossRef]
- Bagarello, V.; Di Prima, S.; Iovino, M. Comparing alternative algorithms to analyze the beerkan infiltration experiment. Soil Sci. Soc. Am. J. 2014, 78, 724. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Elrick, D.E. Ponded infiltration from a single ring: I. analysis of steady flow. Soil Sci. Soc. Am. J. 1990, 54, 1233–1241. [Google Scholar] [CrossRef]
- Wu, L.; Pan, L.; Mitchell, J.; Sanden, B. Measuring saturated hydraulic conductivity using a generalized solution for single-ring infiltrometers. Soil Sci. Soc. Am. J. 1999, 63, 788. [Google Scholar] [CrossRef]
- Ghazouani, H.; M’Hamdi, B.D.; Autovino, D.; Bel Haj, A.M.; Rallo, G.; Provenzano, G.; Boujelben, A. Optimizing subsurface dripline installation depth with Hydrus 2D/3D to improve irrigation water use efficiency in the central Tunisia. Int. J. Metrol. Qual. Eng. 2015, 6, 402. [Google Scholar] [CrossRef]
- Castellini, M.; Ventrella, D. Impact of conventional and minimum tillage on soil hydraulic conductivity in typical cropping system in southern Italy. Soil Tillage Res. 2012, 124, 47–56. [Google Scholar] [CrossRef]
- Castellini, M.; Niedda, M.; Pirastru, M.; Ventrella, D. Temporal changes of soil physical quality under two residue management systems. Soil Use Manag. 2014, 30, 423–434. [Google Scholar] [CrossRef]
- Katuwal, S.; Arthur, E.; Tuller, M.; Moldrup, P.; de Jonge, L.W. Quantification of soil pore network complexity with X-ray computed tomography and gas transport measurements. Soil Sci. Soc. Am. J. 2015, 79, 1577–1589. [Google Scholar] [CrossRef]
- Dhaliwal, J.K.; Anderson, S.H.; Lee, J.; Jagadamma, S.; Saha, D. Computed tomography scanning revealed macropore-controlled N2O emissions under long-term tillage and cover cropping practices. Sci. Total Environ. 2024, 926, 171782. [Google Scholar] [CrossRef]
- Dexter, A.R.; Czyz, E.A. Applications of S-theory in the study of soil physical degradation and its consequences. Land Degrad. Dev. 2007, 18, 369–381. [Google Scholar] [CrossRef]
- Turek, M.E.; Armindo, R.A.; Wendroth, O. Hydraulic-energy indices reveals spatial dependence in a subtropical soil under maize crop in southern Brazil. Pedosphere 2021, 31, 771–782. [Google Scholar] [CrossRef]
- Castellini, M.; Diacono, M.; Preite, A.; Montemurro, F. Short- and Medium-Term Effects of On-Farm Compost Addition on the Physical and Hydraulic Properties of a Clay Soil. Agronomy 2022, 12, 1446. [Google Scholar] [CrossRef]
- Park, E.J.; Smucker, A.J.M. Saturated hydraulic conductivity and porosity within macroaggregates modified by tillage. Soil Sci. Soc. Am. J. 2005, 69, 38–45. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).