Abstract
River flood routing computes changes in the shape of a flood wave over time as it travels downstream along a river. Conventional flood routing models, especially hydrodynamic models, require a high quality and quantity of input data, such as measured hydrologic time series, geometric data, hydraulic structures, and hydrological parameters. Unlike physically based models, machine learning algorithms, which are data-driven models, do not require much knowledge about underlying physical processes and can identify complex nonlinearity between inputs and outputs. Due to their higher performance, lower complexity, and low computation cost, researchers introduced novel machine learning methods as a single application or hybrid application to achieve more accurate and efficient flood routing. This paper reviews the recent application of machine learning methods in river flood routing.
1. Introduction
Floods are one of the most devastating disasters that cause damage to human lives, society, and ecosystems. Accurate simulation of flood flow is significantly important for flood control and the reduction of flood losses. Physically based models and data-driven models are two main categories of existing flood routing models. Physically based models can be divided into hydraulic and hydrologic flood routing models constructed based on empirical or theoretical governing equations describing the propagation of a flood wave along a river to estimate the changes in streamflow (depth and discharge) with time. Various physical characteristics and boundary conditions are required to be determined to construct physically based models, which require in-depth (extensive) knowledge of the physical process. Widely used physically based models involve the Muskingum model [1,2,3] and the hydrodynamic model based on Saint-Venant equations, which are solved by various numerical methods [4,5,6,7,8,9,10].
Data-driven models map relationships between hydrological variables to describe hydrological processes without requiring extensive knowledge of underlying physical principles. Simple data-driven models based on linear assumptions for regression fitting include the auto-regressive moving average (ARMA) model [11] and the autoregressive integrated moving average (ARIMA) model [12]. In recent decades, machine learning (ML) methods have gained popularity along with the development of artificial intelligence. ML methods can deal with more complex hydrological processes by mapping nonlinear relationships between hydrological variables. Commonly applied ML methods in river flood routing computation include support vector regression (SVR) [13,14], artificial neural networks (ANNs) [15,16], multilayer perceptron (MLP) [14], gated recurrent units (GRUs) [14,17], long short-term memory (LSTM) [14,18], and so on. Machine learning methods have been widely applied in hydrological fields such as rainfall-runoff models and flood forecasting. However, the applications for river flood routing are relatively limited.
As a flood wave moves down a channel, the change in the shape of the wave is affected by various factors, including channel resistance and lateral withdrawal or addition of flow. For the river reach without lateral inflow, the peaks of flood waves gradually decrease as the waves travel downstream due to friction. If there is lateral inflow, the attenuation of flood waves can be reduced, or flood waves can even be amplified. By applying flood routing methods, a flood wave entering a river from an upstream section is traced along the river channel, and the flow hydrograph at any downstream location can be calculated. This information is significant for assessing flood effects and designing structures for flood control, such as reservoirs and levees. In addition, flood routing can also be applied to predict the change in hydrograph shape at a downstream section of a river if the river channel undergoes changes over time or hydraulic structures are constructed in the river. It should be noted that flood routing models, including physically-based models and ML models developed for the previous river environment, are not applicable to the changed river environment and should be changed or reconstructed adaptively.
This paper mainly reviews the single application and hybrid application of ML methods for river flood routing, as shown in Figure 1. The hybrid application of ML methods is divided into two categories: one is for optimization of a physically based flood routing model, and the other is for combined usage with a physically based flood routing model to improve prediction accuracy.
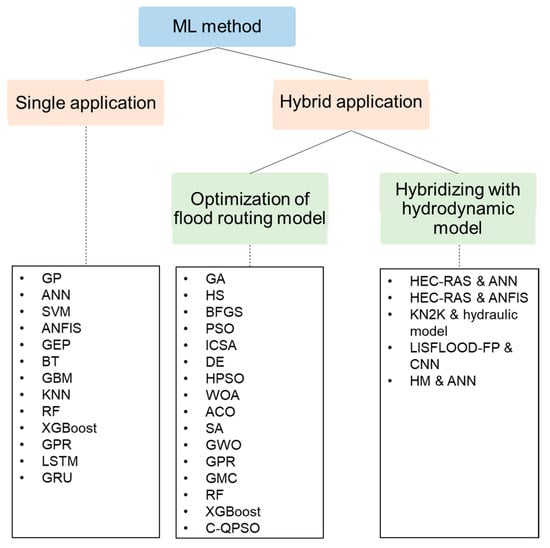
Figure 1.
Application of ML methods for river flood routing.
2. ML Methods
2.1. Single Application
Numerous studies have applied ML models for flood routing simulation. Physically based models require physical parameters and river geometry data, while machine learning methods only use the time series data from upstream gauging stations to estimate the water level or discharge at the downstream locations of a river. Reviewed papers regarding the single application of ML methods for flood routing computation are presented in Table 1.

Table 1.
Single applications of ML method for flood routing simulation.
2.1.1. Support Vector Regression (SVR)
SVR is a machine learning technique based on structural risk minimization theory and statistical learning hypotheses [29]. The idea of SVR is that an entire sample set can be characterized by a small number of support vectors [30]. In SVR, a kernel function is used to create a linearly divisible space by converting the sample space, and then predictive analysis on the new samples is performed using the hyperplane with the largest margin and support vectors [14]. The learning ability of a SVR model is highly affected by the selected kernel function. The widely used kernel functions are the linear kernel, precomputed kernel, polynomial kernel, and radial basis function kernel. Karahan et al. [13] used SVM for three different flood routing problems. In this study, the dynamics of the studied floods were captured by applying the SVM to observed data, and the model showed good performance for flood routing modeling. Katipoglu and Sarigol [27] compared the performance of various ML models, including SVM, for flood routing prediction in Eskisehir, Sivas, and Ankara, and Zhou and Kang [14] used a linear kernel in a SVR for flood routing in the Yangtze River.
2.1.2. Artificial Neural Network (ANN)
ANN is a nonlinear modeling approach that mimics human brain function [31]. The nonlinear input-output relationship in an ANN model is estimated by neurons, weights, and biases. In an ANN, it is important to properly determine the activation function, number of hidden neurons, and number of hidden layers. Coulibaly et al. [32] showed that an ANN with only one hidden layer is appropriate to solve hydrological problems. Therefore, many studies in the hydrological field used one hidden layer to estimate the nonlinear relationships [10,30]. The number of hidden nodes is usually defined by performing a trial-and-error method [30]. However, Huang [33] proposed that the number of hidden nodes could be determined based on the sample size. The most widely used training method for ANNs is the Levenberg–Marquardt (LM) algorithm, as it converges fast and is the most efficient technique [34].
In the last few years, ANN has been applied to river flood routing problems, including estimation at ungauged sites. Panda et al. [15] compared the performance of a MIKE11 hydrodynamic model and the ANN technique and found that the trained ANN model performs much better than MIKE11HD results. In this study, an ANN with one hidden layer and 8 hidden neurons was applied to predict downstream water levels using measured hourly water level data at upstream gauging stations as inputs.
Elsafi [16] used an ANN to simulate flows at a downstream location of the Nile in Sudan based on flows measured at upstream locations. This study examined four scenarios in which data from different stations were used as input and compared their performance in flood forecasting.
Tayfur et al. [23] trained an ANN to predict the downstream hydrograph, and the ANN results were compared to the results of nonlinear Muskingum models optimized by ant colony optimization (ACO), genetic algorithm (GA), and particle swarm optimization (PSO), and numerical solutions of Saint-Venant equations. The results of this study demonstrated that the performance of flood routing using machine learning algorithms is as good as that of the Saint-Venant model.
ANNs, combined with meta-heuristic algorithms, have been investigated by many researchers. Nikoo et al. [21] presented an ANN optimized by a social-based algorithm (SBA) to simulate flood routing. SBA is one of the meta-heuristic approaches that combines the evolutionary algorithm (EA) and the imperialist competitive algorithm (ICA) [35]. This paper showed that the hybrid optimization approach can achieve better results in efficiency and performance. In addition, Hassanvand et al. [22] optimized the ANN flood routing model with ICA and the Bat algorithm (BA), and their results showed that the ANN-ICA predicts more accurately.
The multilayer perceptron (MLP) is one of the ANNs that is the most widely used feedforward model. A MLP consists of one input and output layer and at least one hidden layer, and the layers of a MLP are fully connected [36]. Latt [20] investigated feedforward ANNs to solve the complex nonlinear problems of Muskingum flood routing for a natural river in Myanmar. A feed-forward multilayer perceptron (FMLP) structure was designed in this study based on the Muskingum routing equations. Therefore, the FMLP has the same input and output variables as a Muskingum routing approach. This study showed that the feedforward ANN is a promising alternative in Muskingum routing after comparing the FMLP to the nonlinear Muskingum models using other reported methods such as GA [37], nelder-mead simplex (NMS) algorithm [38], and broyden-fletcher-goldfarb-shanno (BFGS) method [39] in solving the parameter estimation. In addition, Zhou and Kang [14] applied a MLP with one hidden layer, including 100 hidden neurons, for the flood routing.
2.1.3. Recurrent Neural Network (RNN)
RNN is a neural network that originated from the idea that cognition in humans is based on past memory and experience [17]. The main difference compared to the MLP is that RNN can consider the previous inputs and involve a memory function of the previous information. Commonly used hidden layer neurons are RNN, LSTM, and GRU.
LSTM is a recurrent neural network that uses gated memory units to control input, memory, output, and other information so that the problem of gradient disappearance and explosion of the RNN for long sequence data are solved [40]. Vizi et al. [18] applied a LSTM for water level prediction using daily water levels observed at 12 stream gauges. The LSTM model was compared to the discrete linear cascade model (DLCM) in this research, and it was concluded that the LSTM model has better performance than the DLCM. This study noted that the encoder-decoder architecture of the LSTM is effective for dealing with multi-horizon forecasting problems.
GRU is a recurrent neural network that is similar to the structure of LSTM, but the number of gates used in the construction of the two models is different. It has been reported that GRU is simpler than LSTM but has similar learning abilities regarding long-term dependencies in time series data [17]. Zhou and Kang [14] constructed a GRU model for flood routing in the Yangtze River and compared the performance of the GRU with other machine learning models such as SVR, gaussian process regression (GRP), MLP, random forest regression (RFR), and LSTM. It was demonstrated that the GRU model showed superior performance compared to other models. Ren et al. [17] adopted MLP and RNNs, including LSTM and GRU, to predict the water level of cascaded channels by mining the high-dimensional correlated hydrodynamic features, considering the spatial and temporal window. This study compared the RNN-based prediction models with various methods, such as the MLP-based prediction model, ANN, SVM, and RF, and demonstrated that the RNN-based prediction model is more suitable for the water level prediction of cascade channels.
2.1.4. Random Forest Regression (RFR)
RFR is an ensemble machine learning approach proposed by Breiman [41]. It is based on the idea of integrated learning and the definition of several independent trees. The results from randomized and de-correlated decision trees are aggregated to obtain predictions [42]. The most important hyper-parameters of the RFR are the number of trees and randomly selected features. Zhou and Kang [14] and Katipoglu and Sarigol [27] used the RFR for flood routing and compared the performance of the RFR to other various machine learning models. Zhou and Kang [14] noted that the RFR model showed overfitting for inflow hydrograph prediction of the Three Georges Reservoir.
2.1.5. K-Nearest Neighbor (KNN)
KNN is a non-parametric classification and regression algorithm [27]. It stores all of the available cases and creates new clusters by classifying them based on their similarity measure. The KNN finds the nearest neighbor using Euclidean distance and performs classification. Katipoglu and Sarigol [27] investigated the performance of the KNN algorithm compared with kernel-based and tree-based algorithms for flood routing prediction and concluded that the KNN can produce successful outputs for flood forecasting in Ankara.
2.1.6. Adaptive Neuro-Fuzzy Inference System (ANFIS)
ANFIS was first introduced by Jang et al. [43] based on a first-order Sugeno system. It is a neural network integrating ANNs learning ability and fuzzy reasoning [44]. The main advantage of applying ANFIS is that fuzzy rules are extracted from expert knowledge or numerical data, and a rule base is constructed adaptively [45]. The main limitation of ANFIS is the time-consuming process of training structure [46]. Hassanvand et al. [22] combined GA and PSO with ANFIS in river flood routing, and this study showed that the time required to optimize the model decreased significantly. Chu [47] designed an ANFIS based on the Muskingum formula for describing the relationship between inflows and outflows and demonstrated that the proposed approach shows good predictions for outflows.
2.1.7. Gradient-Boosted Machine (GBM)
GBM was introduced by Friedman [48] and has been widely used in many studies for classification and regression purposes. It is an ensemble-based method that generates a strong learner (or decision tree) by integrating individual weak learners [49]. For each iteration, a new decision tree is added to the previous model by minimizing the loss function [50]. Katipoglu and Sarigol [27] compared the performance of various ML algorithms, including GBM, in flood routing prediction and demonstrated that the optimized GBM shows better performance than other algorithms such as SVM and RF. Katipoglu and Sarigol [27] noted that the advantage of applying GBM is the flexibility to optimize different loss functions.
2.1.8. Genetic Programming (GP)
The genetic programming (GP) was derived from Darwin’s principle of natural evolution. GP operates on parse trees to describe the input-output relationship [19]. Control parameters have to be set before applying the GP algorithm, such as population size, maximum number of generations, and crossover and mutation probability. Sivapragasam et al. [19] proposed a GP model as an alternative to the non-linear Muskingum model. This study demonstrated that the GP model can route complex flood hydrographs in natural channels and perform better than the non-linear Muskingum model.
2.1.9. Other ML Methods
Pashazadeh and Javan [24] applied ANN and gene expression programming (GEP) as alternatives to the Muskingum model to predict the downstream outflow hydrograph. This study investigated inflow hydrographs at different time steps for GEP and ANN models. The results showed that the GEP model presents better performance compared with the ANN and Muskingum models for multiple inflows system. Chen et al. [25] developed a new model applying ensemble empirical mode decomposition (EEMD) and stepwise regression for water level forecasting in a tidal river. Only water level data were used in the proposed model, and it was found that the model is simple and highly accurate. Other machine learning methods applied for flood routing include GPR [14], bagged tree (BT) [27], and extreme gradient boosting (XGBoost) [27].
Machine learning methods have been combined with mathematical techniques such as wavelet packet decomposition [51], which divides an input time series into two components: detail and approximation. Seo and Kim [51] applied the hybrid models named wavelet packet-based adaptive neuro-fuzzy inference system (WPANFIS) and wavelet packet-based artificial neural network (WPANN) to forecast the downstream river stage using the upstream observed river stage and lags. The results of this study indicated that the ANN and ANFIS models for water level forecasting improved after integrating wavelet packet decomposition. A hybrid approach applying empirical model decomposition (EMD) and neural networks was proposed by Katipoglu and Sarigol [28] for flood routing prediction. This study hybridized the EMD signal decomposition technique with the cascade forward backpropagation neural network (CFBNN) and feed-forward backpropagation neural network (FFBNN) algorithms. The results of this study showed that the EMD signal decomposition technique can improve the performance of ML models, and the EMD-FFBNN model was the most successful algorithm in flood routing computation. In addition, hybrid machine learning models including least squares support vector machine (LSSVM), EMD-LSSVM, PSO-LSSVM, Wavelet-LSSVM, and variational model decomposition (VMD)-LSSVM were investigated by Katipoglu and Sarigo [26]. This research compared the performance of the five flood routing methods and showed that the PSO-LSSVM is the best model.
2.2. Hybrid Application
2.2.1. ML-Based Optimization Technique
Optimization can be divided into traditional optimization methods and meta-heuristic optimization methods. Traditional methods such as linear programming [52], non-linear programming [53], and dynamic programming [54] can rapidly converge to local optima [55]. However, these methods require strict constraints and make it difficult to achieve a global optimal solution for problems with complicated search spaces and large dimensions [56]. To overcome the limitations of traditional optimization methods, intelligent optimization algorithms have become popular due to their flexibility, simplicity of use, effective handling of discrete problems, lack of need for differentiation, and ability to find global optima [57]. Muskingum routing, which is a hydrological method developed by McCarthy [58], has been widely used for river flood routing with parameter estimation for linear and nonlinear forms [20]. To improve the performance of the Muskingum model, numerous meta-heuristic algorithms have been applied in the optimization of the model parameters, whose results have been reported to be more accurate than the outputs of conventional methods such as the Lagrange multiplier (LMM) and segmented least squares method (S-LSM) [59]. The inspiration for meta-heuristic algorithms originated from natural concepts. For example, GA was proposed based on Darwin’s “survival of the fittest”, PSO simulates the collective behavior of birds, and the clonal selection algorithm (CSA) comes from cuckoo nesting behavior. Table 2 shows the machine learning methods used for the estimation of parameters in Muskingum models.

Table 2.
ML methods used for the parameter estimation of Muskingum models.
Mohan [37] applied the GA and found that GA is efficient in determining the parameters of nonlinear Muskingum routing models. Kim et al. [60] used a heuristic algorithm, harmony search (HS), and demonstrated that HS performs better in the parameter determination of the nonlinear Muskingum model than GA. The GA approach creates a new vector from only two vectors, while a new vector is originated from every single existing vector in the HS algorithm, which allows the HS to find better solutions with greater flexibility [60]. Chu and Chang [61] compared the PSO algorithm to the GA and HS and showed that the HS algorithm produces the most precise results. An improved backtracking search algorithm (BSA) introduced by Yuan et al. [1] was demonstrated to outperform PSO, GA, and differential evolution (DE) [64] for parameter identification in the nonlinear Muskingum model. Other algorithms such as immune Nelder-Mead simplex (NMS) algorithm [38], immune clonal selection algorithm (ICSA) [62], parameter setting free-harmony search (PSF-HS) algorithm [63], harmony search-broyden-fletcher-goldfarb-shanno (HS-BFGS) algorithm [65], and modified honey-bee mating optimization (MHBMO) algorithm [71] have been proposed due to their efficiency and fast convergence.
Mai et al. [77] proposed a hybrid cuckoo quantum-behavior particle swarm optimization (C-QPSO) and demonstrated the global optimization ability of the algorithm in its application to the estimation of parameters for a nonlinear Muskingum model. Other hybrid optimization algorithms combining two approaches include HS-BFGS [65], SFLA-NMS [67], and MHBMO-GRG [71]. These hybrid techniques can provide appropriate initial guesses for Muskingum parameters and reduce the uncertainties, resulting in different results for different runs [71]. Ouyang et al. [66] presented a hybrid particle swarm optimization (HPSO) by combining PSO with the NMS method to estimate the Muskingum model parameters. This study first used the PSO algorithm to conduct the global optimization, then applied the NMS method to perform the local search for optimal. Similarly, Ehteram et al. [72] developed the hybrid bat-swarm algorithm (HBSA) by integrating the bat algorithm (BA) and the PSO algorithm for the optimization of four parameters of the Muskingum model so that a global optimum can be searched without trapping in the local minimums. Another attempt to find a global solution was made by Okkan and Kirdemir [76] using a hybrid PSO-LM algorithm for calibrating a nonlinear Muskingum model.
Efforts were also made to determine the parameters of modified forms of nonlinear Muskingum models by applying meta-heuristic optimization techniques. Niazkar and Afzali [71] proposed MHBMO-GRG for a six-parameter Muskingum model. Hamedi et al. [69] applied the weed optimization algorithm (WOA) in the estimation of parameters for an extended nonlinear Muskingum model by introducing a parameterized initial storage condition. Moghaddam et al. [70] and Farahani et al. [73] implemented the PSO algorithm and the Shark algorithm, respectively, for four-parameter non-linear Muskingum models. Akbari and Hessami-Kermani [59] used the Grey Wolf Optimizer (GWO) algorithm to estimate the parameters of two nonlinear Muskingum models with three and four constant parameters.
Zhao et al. [78] applied ML techniques to the parameter calibration of the Routing Application for Parallel Computation of Discharge (RAPID) model without requiring measured streamflow. The RAPID model uses a linear Muskingum routing algorithm. This study explored four ML architectures, including GPR, gaussian mixture copula (GMC), XGBoost, and random forest (RF), to learn the relationship between river features and model parameters. The first two methods perform probabilistic predictions, while XGBoost and RF yield single-point predictions. It was shown that XGBoost performs best, followed by GPR, RF, and GMC.
2.2.2. Hybrid Application of a Hydraulic Model and the ML Method
A number of simplifications and assumptions are involved in physically based river flood routing models. Hydrologic and hydraulic methods are two main classes of conventional flood routing methods. Hydrological models such as the Muskingum model solve the storage and continuity equations to estimate the downstream flow hydrograph. Examples of hydraulic models include kinematic wave models and models based on Saint-Venant equations. The efficiency of hydraulic models can be restricted due to the high demands on computer resources and the quality and quantity of inputs [20]. In addition, a high resolution in space and a small calculation time step lead to quite high computational efforts [79], which restricts the application of a hydrodynamic model in real-time operation. Therefore, methodologies combining artificial intelligence and hydrodynamic models have been proposed by many studies due to their robustness and speed. Table 3 shows the studies on the hybrid application of a hydraulic model and a ML method for flood routing prediction.

Table 3.
Hybrid applications of a hydraulic model and ML method.
Shrestha et al. [80] integrated flows computed from a one-dimensional hydrodynamic numerical model at a river section where measured data are not available for ANN training and validation. In this study, the studied river reach was divided into sub-reaches, and different ANN blocks were used for individual sub-reaches. The integration of observations and results of the numerical model into the ANN model training enhanced the overall model performance. This study used a hydrodynamic numerical model only to generate data for historical flood events. Peters et al. [79] applied the HEC-RAS, which simulates one-dimensional hydrodynamic flow by numerically solving the Saint-Venant equations, to generate training data for a multilayer-feedforward network (MLFN) covering possible extreme flood events instead of only considering recorded floods. By combining the HEC-RAS and an ANN, this study tried to overcome both the high computational demands regarding the application of a hydrodynamic model and the restricted extrapolation abilities of ANNs. Similarly, Razavi and Karamouz [81] trained an adaptive ANN model for river flood routing using synthetic data generated by the HEC-RAS model. They applied a MLP, a RNN, a time-delay neural network (TDNN), and a time-delay recurrent neural network (TDRNN) and found that the dynamic networks, i.e., TDNN and TDRNN, show better performance than the static MLP network. Ghalkhani et al. [82] used ANN and an adaptive neuro-fuzzy inference system (ANFIS) for flood routing. These two models were trained using the upstream hydrographs generated by HEC-1 and the routed hydrographs generated by HEC-RAS at the downstream end. The two models used data from up to 10 previous time intervals (approximately 2.5 h) as inputs. This study showed that the results of the ANN and ANFIS models coincided with the results of the HEC-RAS and suggested the application of the two machine learning models due to their stability and high speed. In addition, Tawfik [85] performed sensitivity analysis by applying HEC-RAS to identify effective parameters on the peak discharge from river reach and the shape of the downstream hydrograph. Then, the HEC-RAS was used to generate synthetic data for training, validating, and testing the ANNs to estimate peak discharge from river reach and the downstream outflow hydrograph. The first ANN was trained to predict the peak discharge based on the peak and base time of the upstream inflow hydrograph, reach length, channel bed slope, and Manning’s coefficient of the channel. The second ANN was trained to predict the outflow hydrograph from the upstream inflow hydrograph. The ANN showed better performance compared to the Muskingum method in the prediction of the outflow hydrograph.
Liu et al. [83] presented KN2K, which is a real-time updating approach for a one-dimensional hydraulic model by combining the k-nearest neighbor (KNN) procedure and the Kalman filter (KF). This study used the KNN procedure to improve the robustness and accuracy of the KF. The updating performance of KN2K was compared to that of the KF method, and it turned out that the KN2K method is more reliable than the KF method.
Kabir et al. [84] applied a deep convolutional neural network (CNN) model to rapidly predict fluvial flood inundation. The modeling approach based on a CNN method was proposed to solve the problem of the high computational demand of two-dimensional (2D) hydraulic models in real-time applications. The inputs of the CNN include discharge time series with lags and observation time, and the outputs of the model are water depths. The inputs of the CNN are generated from the LISFLOOD-FP, which is a 2D hydraulic model. The results of this study showed high accuracy in capturing flooded cells and that the CNN model performs better than the SVR method.
Li and Jun [10] hybridized a hydrodynamic model based on the Saint-Venant equations with ANNs to improve the accuracy of flood forecasting for the Han River, South Korea. This study applied ANNs to correct the errors of the hydrodynamic model using the observed discharge and water levels, and outputs of the hydrodynamic model. When the lead time of flood forecasting increases, the hybrid model shows improved accuracy compared to a single ANN model, which indicates that the hybrid approach presents less deterioration in forecasting accuracy at higher lead times. The computational results of this study showed that the hybridized approach presents better performance than the single application of the hydrodynamic model or an ANN model in flood forecasting.
3. Conclusions
This paper provides a comprehensive review of the application of ML techniques for river flood routing prediction. The application of ML methods demonstrated outstanding performance in flood routing modeling with high accuracy. The advancement of novel ML methods is determined by properly designing learning algorithms, and the performance of ML models could be improved through coupling with other physically-based models, ML methods, and soft computing techniques. Such hybrid applications were demonstrated to provide more efficient and robust models that can effectively learn more complex flood routing predictions. In real-time applications, ML models can overcome the problems of stability and long computational time of conventional flood routing models, such as hydrodynamic models. The difficulties of applying hydrodynamic models in real-time operations were discussed by [79], who overcame such problems by using ANNs. However, one of the main limitations of ML models is that the trained models are difficult to generalize due to their limited prediction ability when the inputs of the model go beyond the data used to train them. ML models can be highly sensitive to the input data [10,14]. The effects of training data on the performance of ML models have not been fully studied, as mentioned by [86].
Author Contributions
Conceptualization, L.L. and K.S.J.; investigation, L.L. and K.S.J.; resources, L.L. and K.S.J.; writing—original draft preparation, L.L.; writing—review and editing, K.S.J.; supervision, K.S.J.; funding acquisition, K.S.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Korea Environmental Industry and Technology Institute (KEITI) through R&D Program for Innovative Flood Protection Technologies against Climate Crisis, funded by Korea Ministry of Environment (MOE) (Grant number: 2022003460001).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| ACO | Ant colony optimization |
| ANFIS | Adaptive neuro-fuzzy inference system |
| ANN | Artificial neural network |
| ANSE | Arithmetic mean |
| ARIMA | Auto-regressive integrated moving average |
| ARMA | Auto-regressive moving average |
| BA | Bat algorithm |
| BFGS | Broyden-fletcher-goldfarb-shanno |
| BSA | Backtracking search algorithm |
| BT | Bagged tree |
| CC | Coefficient of correlation |
| CE | Coefficient of efficiency |
| CFBNN | Cascade forward backpropagation neural network |
| CNN | Convolutional neural network |
| C-QPSO | Cuckoo quantum-behavior particle swarm optimization |
| CSA | Clonal selection algorithm |
| DE | Differential evolution |
| DE | Differential evolution |
| DLCM | Discrete linear cascade model |
| DP | Difference in peak |
| DPF | Difference in peak flow |
| EA | Evolutionary algorithm |
| EEMD | Ensemble empirical mode decomposition |
| EMD | Empirical model decomposition |
| EQp | Error of peak discharge |
| ETp | Error of time to peak |
| FFBNN | Feed-forward backpropagation neural network |
| FMLP | Feed forward multilayer perceptron |
| GA | Genetic algorithm |
| GBM | Gradient-boosted machine |
| GEP | Gene expression programming |
| GMC | Gaussian mixture copula |
| GP | Genetic programming |
| GPR | Gaussian process regression |
| GRG | Generalized reduced gradient |
| GRP | Gaussian process regression |
| GRU | Gated recurrent unit |
| GWO | Grey wolf optimizer |
| HBSA | Hybrid bat-swarm algorithm |
| HPSO | Hybrid particle swarm optimization |
| HS | Harmony search |
| ICA | Imperialist competitive algorithm |
| ICSA | Immune clonal selection algorithm |
| IOA | Index of agreement |
| KF | Kalman filter |
| KGE | Kling–Gupta efficiency |
| KN2K | KNN-KF |
| KNN | K-nearest neighbor |
| LM | Levenberg–Marquardt |
| LMM | Lagrange multiplier |
| LSSVM | Least squares support vector machine |
| LSTM | Long short-term memory |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| MBE | Mean bias error |
| MHBMO | Modified honeybee mating optimization |
| ML | Mahine Learning |
| MLFN | Multilayer-feedforward network |
| MLP | Multilayer perceptron |
| MRE | Mean relative error |
| MSE | Mean square error |
| MWLP | MLP-based water level prediction |
| NMM | Nonlinear Muskingum model |
| NMS | Nelder-mead simplex |
| NSE | Nash-Sutcliffe Coefficient |
| PCC | Pearson correlation coefficient |
| PI | Persistence index |
| PSF-HS | Parameter setting free-harmony search |
| PSO | Particle swarm optimization |
| PWRMSE | Peak-weighted root mean square error |
| R2 | Coefficient of determination |
| RAPID | Routing application for parallel computation of discharge |
| RCM | Rating curve method |
| RF | Random forest |
| RFR | Random forest regression |
| RMSE | Root mean square error |
| RNN | Recurrent neural network |
| RWLP | RNN-based water level prediction |
| SA | Shark algorithm |
| SBA | Social-based algorithm |
| SDE | Standard deviation of the NSE |
| SFLA | Shuffled frog leaping algorithm |
| SI | Scatter index |
| S-LSM | Segmented least square method |
| SSE | Sum of squared error |
| SSQ | Sum of the square of the deviations between the observed and routed outflows |
| SVM | Support vector machine |
| SVR | Support vector regression |
| TDNN | Time delay neural network |
| TDRNN | Time delay recurrent neural network |
| TSS | Taylor skill score |
| VMD | Variational model decomposition |
| WI | Willmott’s index of agreement |
| WOA | Weed optimization algorithm |
| WPANFIS | Wavelet packet-based adaptive neuro-fuzzy inference system |
| WPANN | Wavelet packet-based artificial neural network |
| XGBoost | Extreme gradient boosting |
References
- Yuan, X.; Wu, X.; Tian, H.; Yuan, Y.; Adnan, R.M. Parameter identification of nonlinear Muskingum model with Backtracking Search Algorithm. Water Resour. Manag. 2016, 30, 2767–2783. [Google Scholar] [CrossRef]
- Gong, Y.; Liu, P.; Cheng, L.; Chen, G.; Zhou, Y.; Zhang, X.; Xu, W. Determining dynamic water level control boundaries for a multi-reservoir system during flood seasons with considering channel storage. J. Flood Risk Manag. 2020, 13, e12586. [Google Scholar] [CrossRef]
- Chao, L.; Zhang, K.; Yang, Z.-L.; Wang, J.; Lin, P.; Liang, J.; Li, Z.; Gu, Z. Improving flood simulation capability of the WRF-Hydro-RAPID model using a multi-source precipitation merging method. J. Hydrol. 2021, 592, 125814. [Google Scholar] [CrossRef]
- Dhote, P.R.; Thakur, P.K.; Domeneghetti, A.; Chouksey, A.; Garg, V.; Aggarwal, S.P.; Chauhan, P. The use of SARAL/AltiKa altimeter measurements for multi-site hydrodynamic model validation and rating curves estimation: An application to Brahmaputra River. Adv. Space Res. 2021, 68, 691–702. [Google Scholar] [CrossRef]
- Singh, R.K.; Kumar Villuri, V.G.; Pasupuleti, S.; Nune, R. Hydrodynamic modeling for identifying flood vulnerability zones in lower Damodar River of eastern India. Ain Shams Eng. J. 2020, 11, 1035–1046. [Google Scholar] [CrossRef]
- Chatterjee, C.; Förster, S.; Bronstert, A. Comparison of hydrodynamic models of different complexities to model floods with emergency storage areas. Hydrol. Process. 2008, 22, 4695–4709. [Google Scholar] [CrossRef]
- Fang, P.; Li, J.; Liu, Q. Flood routing models in confluent and dividing channels. Appl. Math. Mech. 2004, 25, 1333–1343. [Google Scholar]
- Wang, K.; Wang, Z.; Liu, K.; Cheng, L.; Bai, Y.; Jin, G. Optimizing flood diversion siting and its control strategy of detention basins: A case study of the Yangtze River, China. J. Hydrol. 2021, 597, 126201. [Google Scholar] [CrossRef]
- Li, L.; Jun, K.S. Distributed parameter unsteady flow model for the Han River. J. Hydro-Environ. Res. 2018, 21, 86–95. [Google Scholar] [CrossRef]
- Li, L.; Jun, K.S. A hybrid approach to improve flood forecasting by combining a hydrodynamic flow model and artificial neural networks. Water 2022, 14, 1393. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, H.; Fang, H. Component-based Reconstruction Prediction of Runoff at Multi-time Scales in the Source Area of the Yellow River Based on the ARMA Model. Water Resour. Manag. 2022, 36, 433–448. [Google Scholar] [CrossRef]
- Yan, B.; Mu, R.; Guo, J.; Liu, Y.; Tang, J.; Wang, H. Flood risk analysis of reservoirs based on full-series ARIMA model under climate change. J. Hydrol. 2022, 610, 127979. [Google Scholar] [CrossRef]
- Karahan, H.; Iplikci, S.; Yasar, M.; Gurarslan, G. River flow estimation from upstream flow records using support vector machines. J. Appl. Math. 2014, 2014, 714213. [Google Scholar] [CrossRef]
- Zhou, L.; Kang, L. Comparative analysis of multiple machine learning methods for flood routing in the Yangtze River. Water 2023, 15, 1556. [Google Scholar] [CrossRef]
- Panda, R.K.; Pramanik, N.; Bala, B. Simulation of river stage using artificial neural network and MIKE 11 hydrodynamic model. Comput. Geosci. 2010, 36, 735–745. [Google Scholar] [CrossRef]
- Elsafi, S.H. Artificial neural networks (ANNs) for flood forecasting at Dongola Station in the River Nile, Sudan. Alex. Eng. J. 2014, 53, 655–662. [Google Scholar] [CrossRef]
- Ren, T.; Liu, X.; Niu, J.; Lei, X.; Zhang, Z. Real-time water level prediction of cascaded channels based on multilayer perception and recurrent neural network. J. Hydrol. 2020, 585, 124783. [Google Scholar] [CrossRef]
- Vizi, Z.; Batki, B.; Ratki, L.; Szalanczi, S.; Rehevary, I.; Kozak, P.; Kiss, T. Water level prediction using long short-term memory neural network model for a lowland river: A case study on the Tisza River, Central Europe. Environ. Sci. Eur. 2023, 35, 92. [Google Scholar] [CrossRef]
- Sivapragasam, C.; Maheswaran, R.; Venkatesh, V. Genetic programming approach for flood routing in natural channels. Hydrol. Process. 2008, 22, 623–628. [Google Scholar] [CrossRef]
- Latt, Z.Z. Application of feedforward artificial neural network in Muskingum flood routing: A black-box forecasting approach for a natural river system. Water Resour. Manag. 2015, 29, 4995–5014. [Google Scholar] [CrossRef]
- Nikoo, M.; Ramezani, F.; Hadzima-Nyarko, M.; Nyarko, E.K.; Nikoo, M. Flood-routing modeling with neural network optimized by social-based algorithm. Nat. Hazards. 2016, 82, 1–24. [Google Scholar] [CrossRef]
- Hassanvand, M.R.; Karami, H.; Mousavi, S.-F. Investigation of neural network and fuzzy inference neural network and their optimization using meta-algorithms in river flood routing. Nat. Hazards 2018, 94, 1057–1080. [Google Scholar] [CrossRef]
- Tayfur, G.; Singh, V.P.; Moramarco, T.; Barbetta, S. Flood hydrograph prediction using machine learning methods. Water 2018, 10, 968. [Google Scholar] [CrossRef]
- Pashazadeh, A.; Javan, M. Comparison of the gene expression programming, artificial neural network (ANN), and equivalent Muskingum inflow models in the flood routing of multiple branched rivers. Theor. Appl. Climatol. 2020, 139, 1349–1362. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Yeh, H.-C.; Kao, S.-P.; Wei, C.; Su, P.-Y. Water level forecasting in tidal rivers during typhoon periods through ensemble empirical model decomposition. Hydrology 2023, 10, 47. [Google Scholar] [CrossRef]
- Katipoglu, O.M.; Sarigo, M. Coupling machine learning with signal process techniques and particle swarm optimization for forecasting flood routing calculations in the Eastern Black Sea Basin, Turkiye. Environ. Sci. Pollut. Res. 2023, 30, 46074–46091. [Google Scholar] [CrossRef] [PubMed]
- Katipoglu, O.M.; Sarigol, M. Prediction of flood routing results in the Central Anatolian region of Turkiye with various machine learning models. Stoch. Environ. Res. Risk Assess. 2023, 37, 2205–2224. [Google Scholar] [CrossRef]
- Katipoglu, O.M.; Sarigol, M. Boosting flood routing prediction performance through a hybrid approach using empirical model decomposition and neural networks: A case of the Mera River in Ankara. Water Supply 2023, 23, 4403–4415. [Google Scholar] [CrossRef]
- Safavi, H.R.; Esmikhani, M. Conjunctive use of surface water and groundwater: Application of support vector machines (SVMs) and generic algorithms. Water Resour. Manag. 2013, 27, 2623–2644. [Google Scholar] [CrossRef]
- Rahbar, A.; Mirarabi, A.; Nakhaei, M.; Talkhabi, M.; Jamali, M. A Comparative Analysis of Data-Driven Models (SVR, ANFIS, and ANNs) for Daily Karst Spring Discharge Prediction. Water Resour. Manag. 2022, 36, 589–609. [Google Scholar] [CrossRef]
- Mokhtarzad, M.; Eskandari, F.; Vanjani, N.J.; Arabasadi, A. Drought forecasting by ANN, ANFIS and SVM and comparison of the models. Environ. Earth Sci. 2017, 76, 729. [Google Scholar] [CrossRef]
- Coulibaly, P.; Anctil, F.; Rasmussen, P.; Bobee, B. A recurrent neural networks approach using indices of low-frequency climatic variability to forecast regional annual runoff. Hydrol. Process. 2000, 14, 2755–2777. [Google Scholar] [CrossRef]
- Huang, G.-B. Learning capability and storage capacity of two-hidden-layer feedforward networks. IEEE Trans. Neural Netw. 2003, 14, 274–281. [Google Scholar] [CrossRef] [PubMed]
- Maiti, S.; Tiwari, R.K. A comparative study of artificial neural networks Bayesian neural networks and adaptive neuro-fuzzy inference system in groundwater level prediction. Environ. Earth Sci. 2013, 71, 3147–3160. [Google Scholar] [CrossRef]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 4661–4666. [Google Scholar]
- Rumelhart, D.E.; McClelland, J.L.; James, L. Parallel Distribution Processing: Exploration in the Microstructure of Cognition; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Mohan, S. Parameter estimation of nonlinear Muskingum models using genetic algorithm. J. Hydraul. Eng. 1997, 123, 137–142. [Google Scholar] [CrossRef]
- Barati, R. Parameter estimation of nonlinear Muskingum models using the Nelder-Mead simplex algorithm. J. Hydrol. Eng. 2011, 16, 946–954. [Google Scholar] [CrossRef]
- Geem, Z.W. Parameter estimation for the nonlinear Muskingum model using the BFGS techniques. J. Irrig. Drain. Eng. 2006, 132, 474–478. [Google Scholar] [CrossRef]
- Li, Z.; Kang, L.; Zhou, L.; Zhu, M. Deep Learning Framework with Time Series Analysis Methods for Runoff Prediction. Water 2021, 13, 575. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Svetnik, V.; Liaw, A.; Tong, C.; Culberson, J.C.; Sheridan, R.P.; Feuston, B.P. Random forest: A classification and regression tool for compound classification and QSAR modeling. J. Chem. Inf. Comput. Sci. 2003, 43, 1947–1958. [Google Scholar] [CrossRef]
- Jang, J.S.R.; Sun, C.T.; Mizutani, E. Neuro-Fuzzy and Soft Computing; Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Dolatabadi, M.; Mehrabpour, M.; Esfandyari, M.; Alidadi, H.; Davoudi, M. Modeling of simultaneous adsorption of dye and metal ion by sawdust from aqueous solution using of ANN and ANFIS. Chemom. Intell. Lab. Syst. 2018, 181, 72–78. [Google Scholar] [CrossRef]
- Firat, M.; Gungor, M. River flow estimation using adaptive neuro fuzzy inference system. Math. Comput. Simul. 2007, 75, 87–96. [Google Scholar] [CrossRef]
- Mwaura, A.M.; Liu, Y.-K. Adaptive neuro-fuzzy inference system (ANFIS) based modelling of incipient steam generator tube rupture diagnosis. Ann. Nucl. Energy 2021, 147, 108262. [Google Scholar] [CrossRef]
- Chu, H.-J. The Muskingum flood routing model using a neuro-fuzzy approach. KSCE J. Civ. Eng. 2009, 13, 371–376. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: Berlin/Heidelberg, Germany, 2013; Volume 26, pp. 203–206. [Google Scholar]
- Park, S.; Jung, S.; Lee, J.; Hur, J. A short-term forecasting of wind power outputs based on gradient boosting regression tree algorithms. Energies 2023, 16, 1132. [Google Scholar] [CrossRef]
- Seo, Y.; Kim, S. River stage forecasting using wavelet packet decomposition and data-driven models. Procedia Eng. 2016, 154, 1225–1230. [Google Scholar] [CrossRef]
- Dantzig, G.B. Linear programming. Oper. Res. 2002, 50, 42–47. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Nonlinear Programming. J. Oper. Res. Soc. 1997, 48, 334. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef]
- Nassef, A.M.; Abdelkareem, M.A.; Maghrabie, H.M.; Baroutaji, A. Review of Metaheuristic Optimization Algorithms for Power Systems Problems. Sustainability 2023, 15, 9434. [Google Scholar] [CrossRef]
- Salgotra, R.; Sharma, P.; Raju, S.; Gandomi, A.H. A Contemporary Systematic Review on Meta-heuristic Optimization Algorithms with Their MATLAB and Python Code Reference. In Archives of Computational Methods in Engineering; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Kumar, N.; Shaikh, A.A.; Mahato, S.K.; Bhunia, A.K. Applications of new hybrid algorithm based on advanced cuckoo search and adaptive Gaussian quantum behaved particle swarm optimization in solving ordinary differential equations. Expert Syst. Appl. 2021, 172, 114646. [Google Scholar] [CrossRef]
- McCarthy, G.T. The Unit Hydrograph and Flood Routing. In Proceedings of Conference of the North Atlantic Division; U.S. Army Corps of Engineers: New London, CT, USA, 1938. [Google Scholar]
- Akbari, K.; Hessami-kermani, M.-R. Parameter estimation of Muskingum model using grey wolf optimizer algorithm. MethodsX 2021, 8, 101589. [Google Scholar] [CrossRef]
- Kim, J.H.; Geem, Z.W.; Kim, E.S. Parameter estimation of the nonlinear Muskingum model using harmony search. J. Am. Water Resour. Assoc. 2001, 37, 1131–1138. [Google Scholar] [CrossRef]
- Chu, H.J.; Chang, L.C. Applying particle swarm optimization to parameter estimation of the nonlinear Muskingum model. J. Hydrol. Eng. 2009, 14, 1024–1027. [Google Scholar] [CrossRef]
- Luo, J.; Xie, J. Parameter estimation for nonlinear Muskingum model based on immune clonal selection algorithm. J. Hydrol. Eng. 2010, 15, 844–851. [Google Scholar] [CrossRef]
- Geem, Z.W. Parameter estimation of the nonlinear Muskingum model using parameter-setting-free harmony search. J. Hydrol. Eng. 2011, 16, 684–688. [Google Scholar] [CrossRef]
- Xu, D.M.; Qiu, L.; Chen, S.Y. Estimation of nonlinear Muskingum model parameter using Differential Evolution. J. Hydrol. Eng. 2012, 17, 348–353. [Google Scholar] [CrossRef]
- Karahan, H.; Gurarslan, G.; Geem, Z.W. Parameter estimation of the nonlinear Muskingum flood-routing model using a hybrid harmony search algorithm. J. Hydro. Eng. 2013, 18, 352–360. [Google Scholar] [CrossRef]
- Ouyang, A.; Li, K.; Truong, T.K.; Sallam, A.; Sha, E.H.M. Hybrid particle swarm optimization for parameter estimation of Muskingum model. Neural Comput. Appl. 2014, 25, 1785–1799. [Google Scholar] [CrossRef]
- Haddad, O.B.; Hamedi, F.; Fallah-Mehdipour, E.; Orouji, H.; Marino, M.A. Application of a hybrid optimization method in Muskingum parameter estimation. Irrig. Drain. Eng. 2015, 141, 482–489. [Google Scholar] [CrossRef]
- Niazkar, M.; Afzali, S.H. Assessment of modified honey bee mating optimization for parameter estimation of nonlinear Muskingum models. J. Hydrol. Eng. 2015, 20, 04014055. [Google Scholar] [CrossRef]
- Hamedi, F.; Bozorg-Haddad, O.; Pazoki, M.; Asgari, H.R.; Parsa, M.; Loaiciga, H.A. Parameter estimation of extended nonlinear Muskingum models with the weed optimization algorithm. J. Irrig. Drain. Eng. 2016, 142, 04016059. [Google Scholar] [CrossRef]
- Moghaddam, A.; Behmanesh, J.; Farsijani, A. Parameter estimation for the new four-parameter nonlinear Muskingum model using the particle swarm optimization. Water Resour. Manag. 2016, 30, 2143–2160. [Google Scholar] [CrossRef]
- Niazkar, M.; Afzali, S.H. Application of new hybrid optimization technique for parameter estimation of new improved version of Muskingum model. Water Resour. Manag. 2016, 30, 4713–4730. [Google Scholar] [CrossRef]
- Ehteram, M.; Othman, F.B.; Yaseen, Z.M.; Afan, H.A.; Allawi, M.F.; Malek, M.B.A.; Ahmed, A.N.; Shahid, S.; Singh, V.P.; EI-Shafie, A. Improving the Muskingum flood routing method using a hybrid of particle swarm optimization and bat algorithm. Water 2018, 1, 807. [Google Scholar] [CrossRef]
- Farahani, N.; Karami, H.; Farzin, S.; Ehteram, M.; Kisi, O.; El Shafie, A. A new method for flood routing utilizing four-parameter nonlinear Muskingum an Shark algorithm. Water Resour. Manag. 2019, 33, 4879–4893. [Google Scholar] [CrossRef]
- Akbari, R.; Hessami-Kermani, M.R.; Shojaee, S. Flood routing: Improving outflow using a new nonlinear muskingum model with four variable parameters coupled with PSO-GA algorithm. Water Resour. Manag. 2020, 34, 3219–3316. [Google Scholar] [CrossRef]
- Norouzi, H.; Bazargan, J. Effects of uncertainty in determining the parameters of the linear Muskingum method using the particle swarm optimization (PSO) algorithm. J. Water Clim. Change 2021, 12, 2055–2067. [Google Scholar] [CrossRef]
- Okkan, U.; Kirdemir, U. Locally tuned hybridized particle swarm optimization for the calibration of the nonlinear Muskingum flood routing model. J. Water Clim. Change 2020, 11 (Suppl. S1), 343–358. [Google Scholar] [CrossRef]
- Mai, X.; Liu, H.-B.; Liu, L.-B. A new hybrid cuckoo quantum-behavior particle swarm optimization algorithm and its application in Muskingum model. Neural Process. Lett. 2023, 55, 8309–8337. [Google Scholar] [CrossRef]
- Zhao, Y.; Chadha, M.; Olsen, N.; Yeates, E.; Turner, J.; Gugaratshan, G.; Qian, G.; Todd, M.D.; Hu, Z. Machine learning-enabled calibration of river routing model parameters. J. Hydroinform. 2023, 25, 1799. [Google Scholar] [CrossRef]
- Peters, R.; Schmitz, G.; Cullmann, J. Flood routing modelling with Artificial Neural Network. Adv. Geosci. 2006, 9, 131–136. [Google Scholar] [CrossRef]
- Shrestha, R.R.; Theobald, S.; Nestmann, F. Simulation of flood flow in a river system using artificial neural networks. Hydrol. Earth Syst. Sci. 2005, 9, 313–321. [Google Scholar] [CrossRef]
- Razavi, S.; Karamouz, M. Adaptive neural networks for flood routing in river systems. Water Int. 2007, 32, 360–375. [Google Scholar] [CrossRef]
- Ghalkhani, H.; Golian, S.; Saghafian, B.; Farokhnia, A.; Shamseldin, A. Application of surrogate artificial intelligent models for real-time flood routing. Water Environ. J. 2013, 27, 535–548. [Google Scholar] [CrossRef]
- Liu, K.; Li, Z.; Yao, C.; Chen, J.; Zhang, K.; Saifullah, M. Coupling the k-nearest neighbor procedure with the Kalman filter for real-time updating of the hydraulic model in flood forecasting. Int. J. Sediment Res. 2016, 31, 146–158. [Google Scholar] [CrossRef]
- Kabir, S.; Patidar, S.; Xia, X.; Liang, Q.; Neal, J.; Pender, G. A deep convolutional neural network model for rapid prediction of fluvial flood inundation. J. Hydrol. 2020, 590, 125481. [Google Scholar] [CrossRef]
- Tawfik, A.M. River flood routing using artificial neural networks. Ain Shams Eng. J. 2023, 14, 101904. [Google Scholar] [CrossRef]
- Peng, A.; Zhang, X.; Xu, W.; Tian, Y. Effects of Training Data on the Learning Performance of LSTM Network for Runoff Simulation. Water Resour. Manag. 2022, 36, 2381–2394. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).