Back-Calculation of Manning’s Roughness Coefficient by 2D Flow Simulation and Influence of In-Channel Physical Parameters in a Mountain River, Japan
Abstract
1. Introduction
2. Materials and Methods
2.1. Summary of Methods
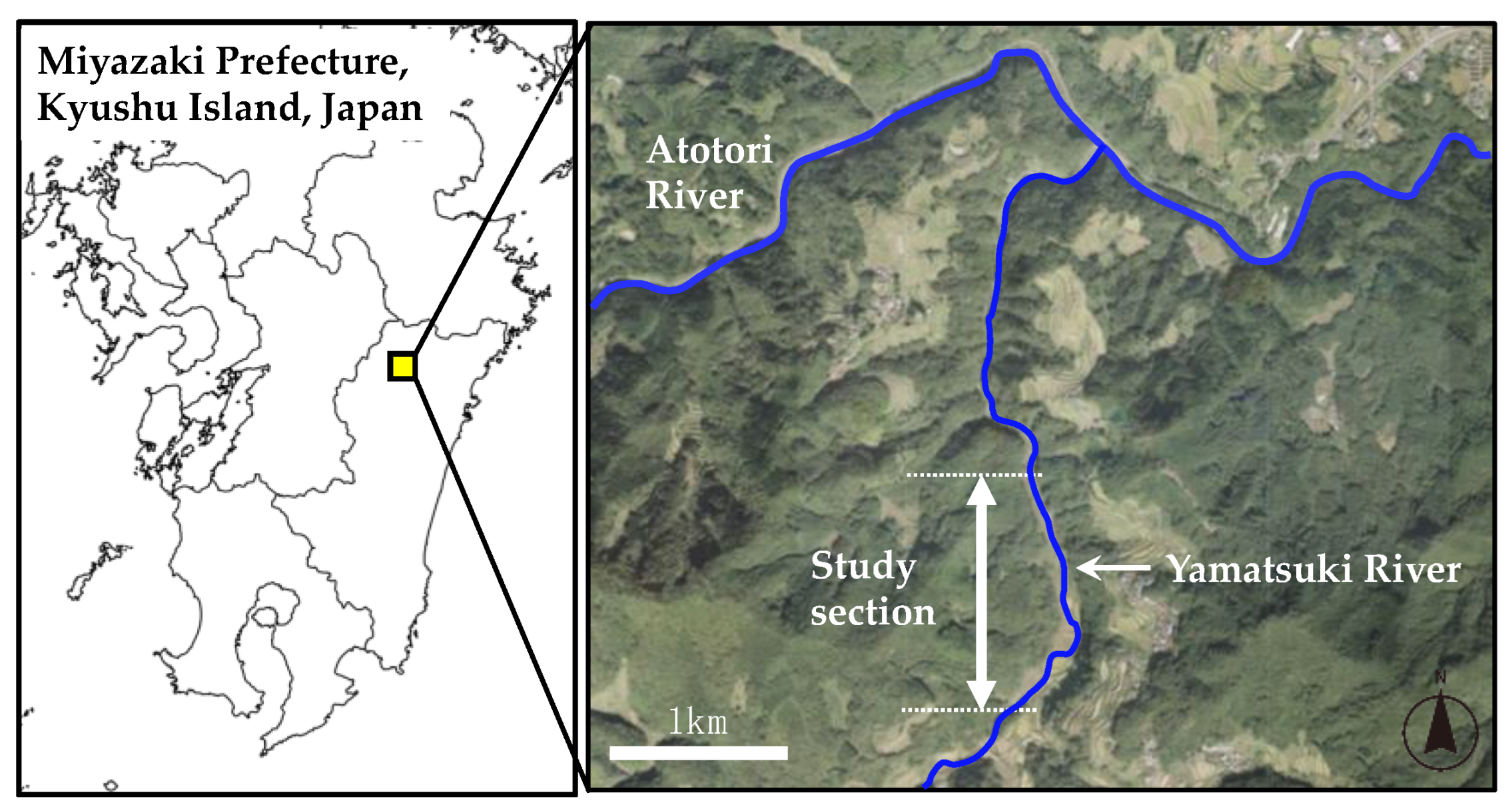
2.2. Study Field
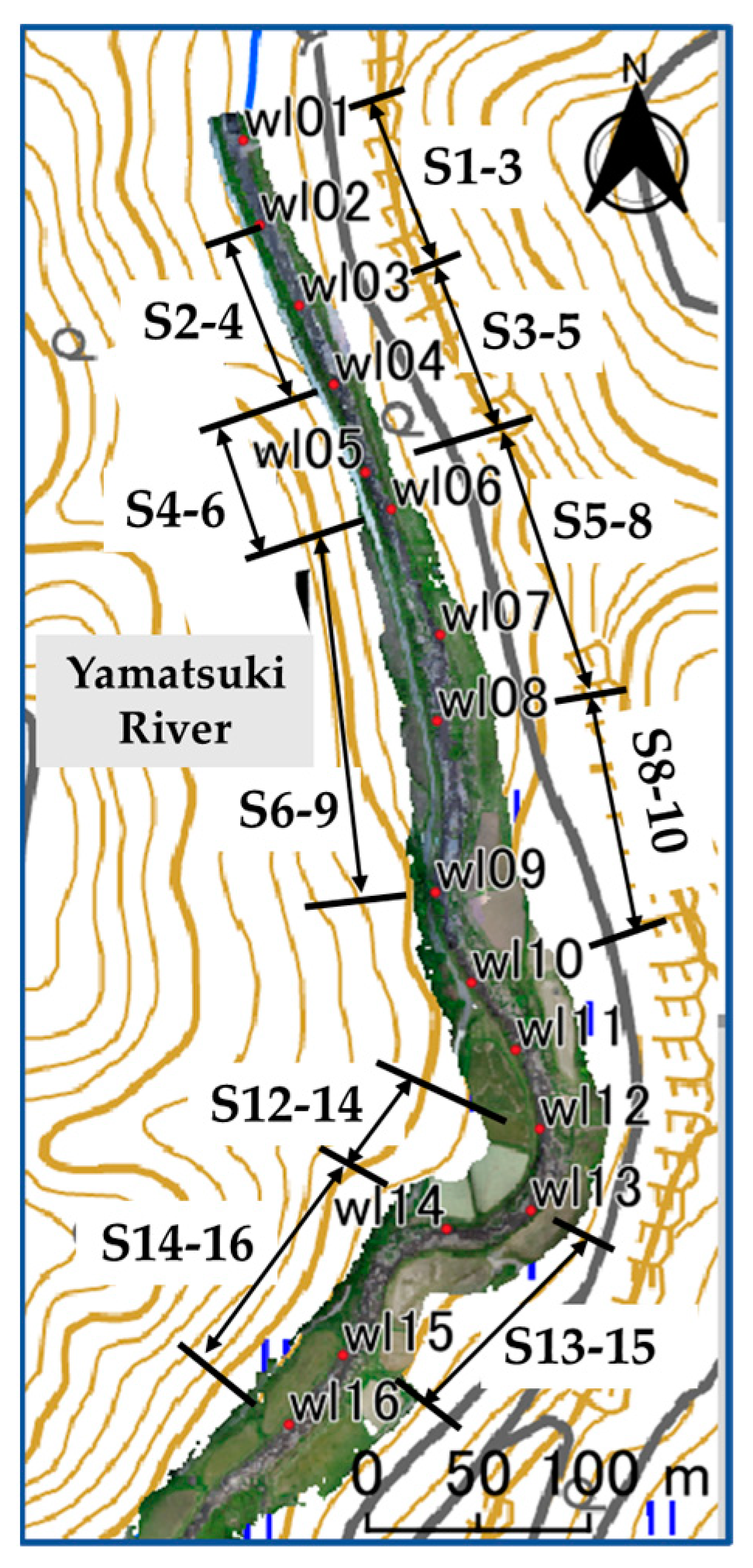
2.3. Field Observations
2.4. Analysis Method
2.4.1. Preparation of Data Set for Unsteady Two-Dimensional Flow Calculations
2.4.2. Two-Dimensional Flow Calculation Method
- (1)
- Overview of the software (Nays2DH)
- (2)
- Calculation conditions
- (3)
- Boundary conditions
- (4)
- Back-calculation of Manning’s roughness coefficient
- (5)
- Accuracy verification
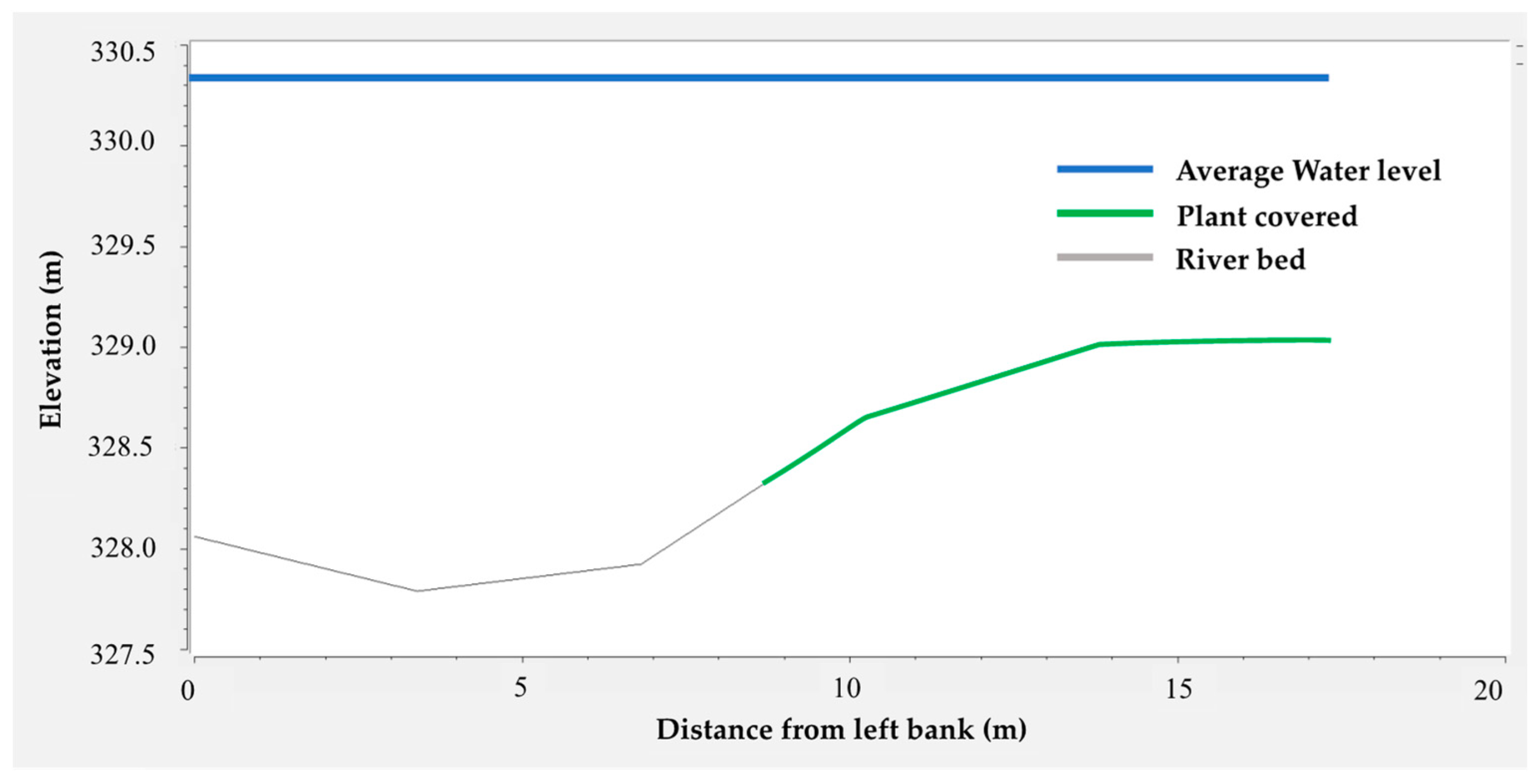
2.4.3. In-Channel Physical Parameters Related to the Roughness Coefficient
2.4.4. Regression Analysis to Examine In-Channel Physical Parameters Most Strongly Affecting the Roughness Coefficient
3. Results and Discussion
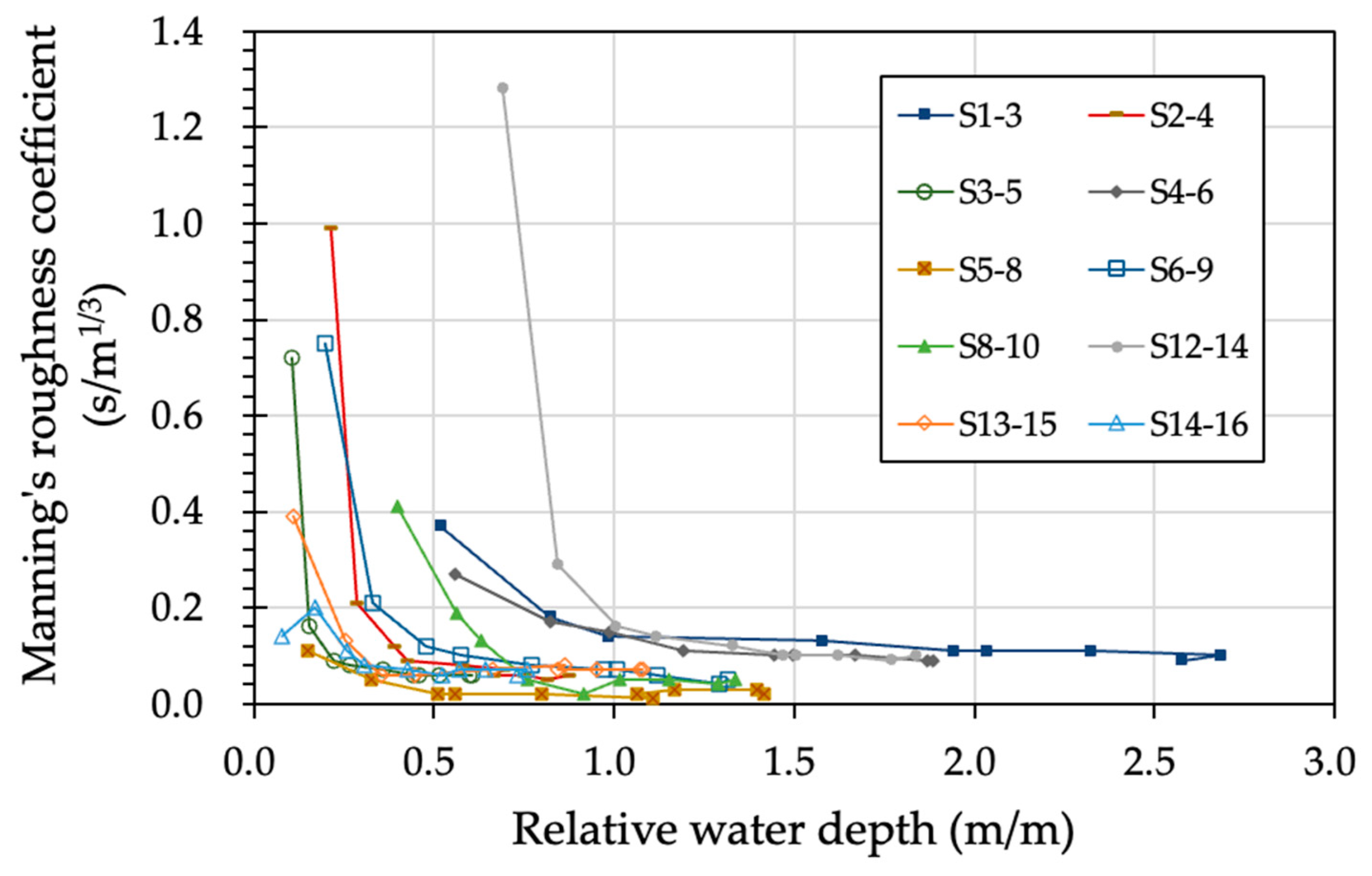
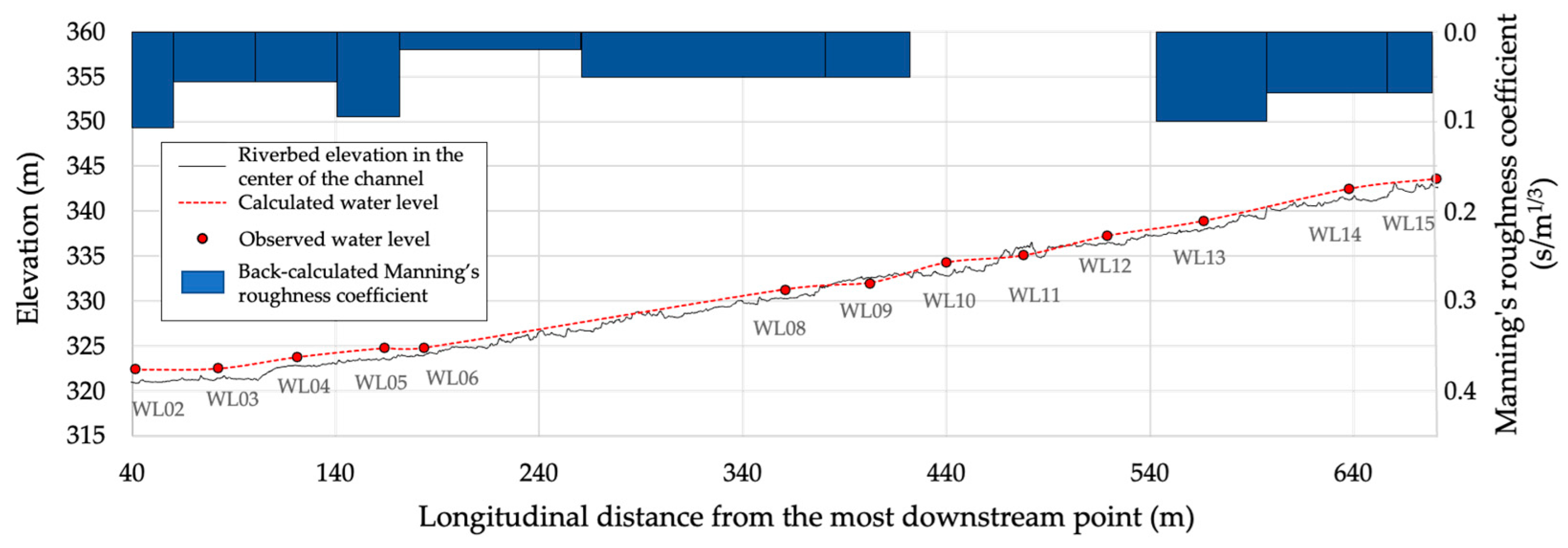
3.1. The Back-Calculated Manning’s Roughness Coefficients and Their Relationship with the Relative Water Depth
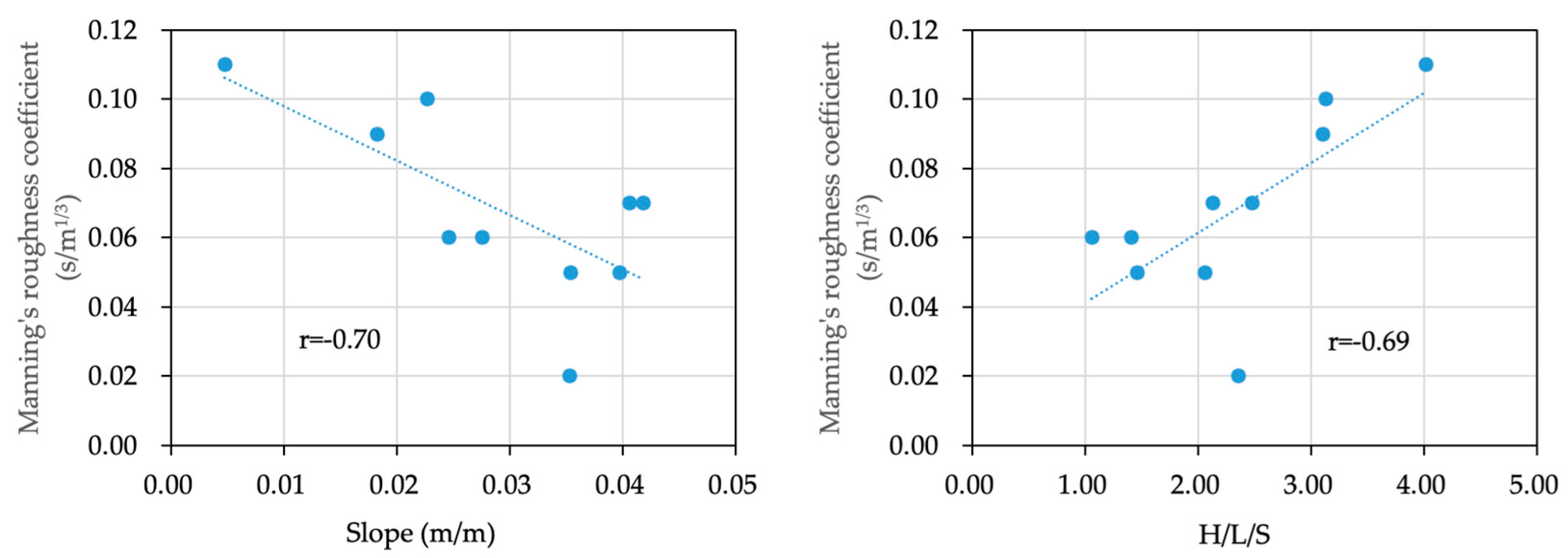
3.2. Effects of In-Channel Physical Parameters on the Roughness Coefficient
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Milliman, J.D.; Syvitski, J.P.M. Geomorphic/Tectonic Control of Sediment Discharge to the Ocean: The Importance of Small Mountainous Rivers. J. Geol. 1992, 100, 525–544. [Google Scholar] [CrossRef]
- Reid, L.M. Research and Cumulative Watershed Effects. In General Technical Report; US Department of Agriculture, Forest Service, Pacific Southwest Research Station: Berkeley, CA, USA, 1993; Volume 141, 118p. [Google Scholar] [CrossRef]
- Nehlsen, W.; Williams, J.E.; Lichatowich, J.A. Pacific Salmon at the Crossroads: Stocks at Risk from California, Oregon, Idaho, and Washington. Fisheries 1991, 16, 4–21. [Google Scholar] [CrossRef]
- Frissell, C.A. Topology of Extinction and Endangerment of Native Fishes in the Pacific Northwest and California (U.S.A.). Conserv. Biol. 1993, 7, 342–354. [Google Scholar] [CrossRef]
- Asano, Y.; Uchida, T.; Nishiguchi, Y. Measured Channel Resistance at Mountain Rivers during Flood. Jpn. Soc. Eros. Control Eng. 2018, 70, 12–23. [Google Scholar]
- Comiti, F.; Mao, L.; Wilcox, A.; Wohl, E.E.; Lenzi, M.A. Field-Derived Relationships for Flow Velocity and Resistance in High-Gradient Streams. J. Hydrol. 2007, 340, 48–62. [Google Scholar] [CrossRef]
- David, G.C.L.; Wohl, E.; Yochum, S.E.; Bledsoe, B.P. Controls on Spatial Variations in Flow Resistance along Steep Mountain Streams. Water Resources Research 2010, 46, W03513. [Google Scholar] [CrossRef]
- Reid, D.E.; Hickin, E.J. Flow Resistance in Steep Mountain Streams. Earth Surf. Process. Landf. 2008, 33, 2211–2240. [Google Scholar] [CrossRef]
- Rickenmann, D.; Recking, A. Evaluation of Flow Resistance in Gravel-Bed Rivers through a Large Field Data Set. Water Resour. Res. 2011, 47, W0758. [Google Scholar] [CrossRef]
- Yochum, S.E.; Comiti, F.; Wohl, E.; David, G.C.L.; Mao, L. Photographic Guidance for Selecting Flow Resistance Coefficients in High-Gradient Channels. In General Technical Report RMRS-GTR; GTR-323; USDA Forest Service: Washington, DC, USA, 2014; pp. 1–91. [Google Scholar]
- Marcus, W.A.; Roberts, K.; Harvey, L.; Tackman, G. An Evaluation of Methods for Estimating Manning’s n in Small Mountain Streams. Mt. Res. Dev. 1992, 12, 227–239. [Google Scholar] [CrossRef]
- Montgomery, D.R.; Buffington, J.M. Channel-Reach Morphology in Mountain Drainage Basins. Geol. Soc. Am. Bull. 1997, 109, 596–611. [Google Scholar] [CrossRef]
- Barnes, H.H., Jr. Roughness Characteristics of Natural Channels. In U.S. Geological Survey Water-Supply Paper; US Government Printing Office: Washington, DC, USA, 1967. [Google Scholar]
- Yarahmadi, M.B.; Parsaie, A.; Shafai-Bejestan, M.; Heydari, M.; Badzanchin, M. Estimation of Manning Roughness Coefficient in Alluvial Rivers with Bed Forms Using Soft Computing Models. Water Resour. Manage. 2023, 37, 3563–3584. [Google Scholar] [CrossRef]
- Takemura, Y.; Nigo, S.; Ohno, J.; Fukuoka, S. Problem of Conventional 2D Analysis Method for Flood Flows in Mountain Streams with Boulders and Proposal of a New Analysis Method. Adv. River Eng. 2019, 25, 267–272. [Google Scholar]
- Liu, Y.; Shimatani, Y.; Yamashita, T.; Sato, T.; Ikematsu, S. Stepped-Bed Morphology Changes in Restoredmountain Stream Inuced by Flood. Adv. River Eng. 2012, 18, 83–88. [Google Scholar]
- Shimizu, Y.; Takebayashi, H.; Inoue, T.; Hamaki, M.; Iwasaki, T.; Nabi, M. Nays2DH_SolverManual_Japanese_v4.Pdf. Available online: https://i-ric.org/webadmin/wp-content/uploads/2023/06/Nays2DH_SolverManual_Japanese_v4.pdf (accessed on 1 December 2023).
- Ministry of Land, Infrastructure, Transport and Tourism Civil Engineering Work Design Guidelines Part II River Edition Chapter 4 Sabo Facilities. Available online: https://www.qsr.mlit.go.jp/site_files/file/s_top/h22doboku/kasen/2-05.pdf (accessed on 15 December 2023).
- Asano, Y.; Uchida, T. Detailed Documentation of Dynamic Changes in Flow Depth and Surface Velocity during a Large Flood in a Steep Mountain Stream. J. Hydrol. 2016, 541, 127–135. [Google Scholar] [CrossRef]
- Abrahams, A.D.; Li, G.; Atkinson, J.F. Step-pool Streams: Adjustment to Maximum Flow Resistance. Water Resour. Res. 1995, 31, 2593–2602. [Google Scholar] [CrossRef]
- Shawn, M.; Chartrand, P.J.W. Alluvial Architecture in Headwater Streams with Special Emphasis on Step–Pool Topography. Earth Surf. Process. Landf. 2000, 25, 583–600. [Google Scholar]
- Hasegawa, K.; Kanbayashi, S. Formation Mechanism of Step-Pool Systems in Steep Rivers and Guide Lines for the Design of Construction. Proc. Hydraulic. Eng. 1996, 40, 893–900. [Google Scholar] [CrossRef][Green Version]
- Fukuoka, S.; Shimatani, Y.; Tamura, H.; Tomari, K.; Nakayama, M.; Takase, A.; Iuch, T. Field Experiments on Reed Deformation and Falling and Roughness Coefficient on Floodchannel by Flows. Adv. River Eng. 2003, 9, 49–54. [Google Scholar]
- Ashida, K.; Egashira, S.; Takayuki, N. Structure and friction law of flow over a step-pool bed form. Disaster Prev. Res. Inst. Annu. 1986, 29, 391–403. [Google Scholar]
- Wilcox, A.C.; Wohl, E.E.; Comiti, F.; Mao, L. Hydraulics, Morphology, and Energy Dissipation in an Alpine Step-Pool Channel. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]

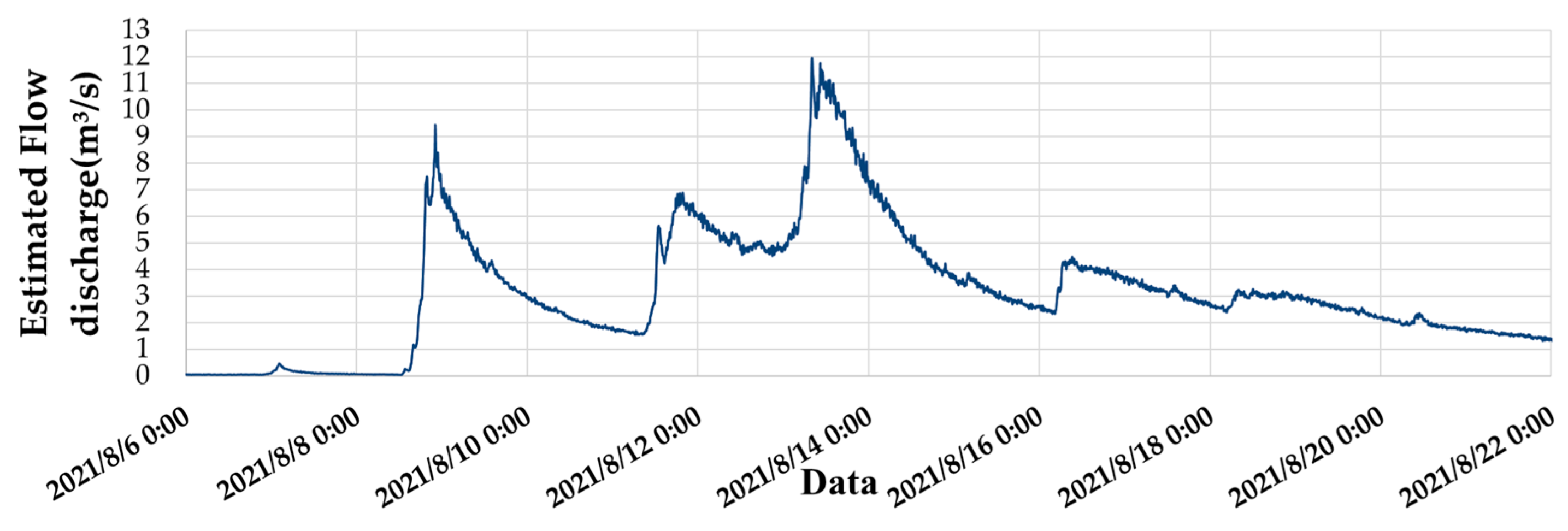

| Date and Time | Estimated Discharge at wl04 (m³/s) |
|---|---|
| 8 August 2021 13:00 | 0.062 |
| 8 August 2021 15:20 | 0.416 |
| 8 August 2021 17:00 | 1.261 |
| 8 August 2021 17:20 | 1.876 |
| 8 August 2021 18:40 | 3.611 |
| 8 August 2021 19:10 | 5.617 |
| 8 August 2021 21:00 | 6.754 |
| 8 August 2021 22:20 | 8.056 |
| 13 August 2021 7:50 | 9.894 |
| 13 August 2021 8:20 | 11.519 |
| Section Name | Mean Squared Error |
|---|---|
| S1–3 | 0.00017 |
| S2–4 | 0.00031 |
| S3–5 | 0.00003 |
| S4–6 | 0.00008 |
| S5–8 | 0.00023 |
| S6–9 | 0.00048 |
| S8–10 | 0.00183 |
| S12–14 | 0.00012 |
| S13–15 | 0.00021 |
| S14–16 | 0.00003 |
| Cal. Section Name | Manning’s Roughness Coefficient (s/m1/3) | Ratio of Width to Depth (m/m) | Slope (m/m) | D84 (m) | Relative Depth (m/m) | Ratio of Plant (m2/m2) | Step (%) | Riffle (%) | Rapid (%) | Pool (%) | H/L/S |
|---|---|---|---|---|---|---|---|---|---|---|---|
| S1–3 | 0.11 | 6.46 | 0.005 | 0.40 | 2.32 | 0.00 | 3.07 | 36.87 | 2.90 | 1.50 | 4.02 |
| S2–4 | 0.06 | 4.94 | 0.025 | 1.25 | 0.87 | 0.00 | 3.38 | 22.70 | 3.83 | 3.04 | 1.06 |
| S3–5 | 0.06 | 6.95 | 0.028 | 1.45 | 0.61 | 0.00 | 3.22 | 21.87 | 2.22 | 6.34 | 1.41 |
| S4–6 | 0.09 | 6.51 | 0.018 | 0.55 | 1.88 | 0.01 | 3.79 | 31.39 | 0.82 | 5.80 | 3.11 |
| S5–8 | 0.02 | 9.00 | 0.035 | 0.60 | 1.42 | 0.22 | 7.08 | 16.04 | 3.18 | 5.77 | 2.36 |
| S6–9 | 0.05 | 10.29 | 0.035 | 0.75 | 1.31 | 0.39 | 5.84 | 20.04 | 2.35 | 4.71 | 2.06 |
| S8–10 | 0.05 | 18.23 | 0.040 | 0.55 | 1.34 | 0.63 | 4.24 | 24.62 | 2.26 | 2.32 | 1.46 |
| S12–14 | 0.10 | 9.44 | 0.023 | 0.70 | 1.84 | 0.30 | 6.96 | 17.45 | 2.02 | 8.06 | 3.13 |
| S13–15 | 0.07 | 11.47 | 0.042 | 0.90 | 1.08 | 0.20 | 9.02 | 18.32 | 3.18 | 4.65 | 2.13 |
| S14–16 | 0.07 | 12.39 | 0.041 | 1.05 | 0.76 | 0.14 | 9.03 | 16.88 | 3.95 | 7.27 | 2.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takata, H.; Obata, S.; Sato, T.; Shimatani, Y. Back-Calculation of Manning’s Roughness Coefficient by 2D Flow Simulation and Influence of In-Channel Physical Parameters in a Mountain River, Japan. Water 2024, 16, 320. https://doi.org/10.3390/w16020320
Takata H, Obata S, Sato T, Shimatani Y. Back-Calculation of Manning’s Roughness Coefficient by 2D Flow Simulation and Influence of In-Channel Physical Parameters in a Mountain River, Japan. Water. 2024; 16(2):320. https://doi.org/10.3390/w16020320
Chicago/Turabian StyleTakata, Hiroshi, Shogo Obata, Tatsuro Sato, and Yukihiro Shimatani. 2024. "Back-Calculation of Manning’s Roughness Coefficient by 2D Flow Simulation and Influence of In-Channel Physical Parameters in a Mountain River, Japan" Water 16, no. 2: 320. https://doi.org/10.3390/w16020320
APA StyleTakata, H., Obata, S., Sato, T., & Shimatani, Y. (2024). Back-Calculation of Manning’s Roughness Coefficient by 2D Flow Simulation and Influence of In-Channel Physical Parameters in a Mountain River, Japan. Water, 16(2), 320. https://doi.org/10.3390/w16020320








