Abstract
The soil water retention curve (SWRC) is a vital soil property used to evaluate the soil’s water holding capacity, a critical factor in various applications such as determining soil water availability for plants, soil conservation and management, climate change adaptation, and mitigation of flood risks. Estimating SWRC directly in the field and laboratory is a time-consuming and laborious process and requires numerous instruments and measurements at a specific location. In this context, various estimation approaches have been developed, including pedotransfer functions (PTFs), over the past three decades to estimate soil water retention and its associated properties. Despite the efficiencies, PTFs and semi-physical approach-based models often have several limitations, particularly in the dry range of the SWRC. PTFs-based modeling has become a key research topic due to readily available soil data and cost-effective methods for deriving essential soil parameters, which enable more efficient decision-making in sustainable land-use management. Therefore, advancement and adjustment are necessary for reliable estimations of the SWRC from readily available data. This article reviews the evaluation of the current and past PTFs for estimating the SWRC. This study aims to evaluate PTF techniques and semi-physical approaches based on soil texture, bulk density, porosity, and other related factors. Additionally, it also assesses the performance and limitations of various common semi-physical models proposed and developed by Arya and Paris, Haverkamp and Parlange, the Modified Kovács model by Aubertin et al., Chang and Cheng, Meskini-Vishkaee et al., Vidler et al., and Zhai et al. This assessment will be effective for researchers in this field and provide valuable insight into the importance of new PTFs for modeling SWRC.
1. Introduction
The hydraulic characterization of unsaturated soil is crucial for several reasons, as it provides valuable insights into soil properties and the behavior of soil under unsaturated or partially saturated conditions [1]. Since the last century, the scientific community has made significant strides in understanding unsaturated soil behavior and developing straightforward methods for prediction. Throughout this period, numerous models and theories have been formulated to address various soil water flow-related issues, such as fluxes, mass storage, and energy dynamics within the soil and plant-based ecosystems [2].
However, accurately characterizing unsaturated hydraulics remains a challenge, as it involves measurement and quantification of parameters such as the soil-water retention curve (SWRC), the hydraulic conductivity function, and soil-water diffusivity. These characterizations of soil and water are essential in various fields, including agriculture, hydrology, environmental science, and geotechnical engineering [3,4]. The application of these hydraulic properties encompasses the calculation of water movement, the estimation of water availability for plants, the assessment of the potential for groundwater contaminant transport, the design of irrigation systems, and the evaluation of slope and embankment stability [5,6]. However, characterizing unsaturated soil properties poses challenges due to the inherent complexity arising from incomplete soil saturation. This complexity is influenced by many factors, including bulk density, organic matter content, soil texture, structure, and temperature [7,8,9]. Therefore, a conceptual understanding of unsaturated soil properties is essential for sustainable land use and management.
The occurrence and retention of moisture in the unsaturated media primarily result from two principal forces, adhesion, and cohesion, along with meniscus phenomena, as shown in Figure 1. Adhesive forces are hygroscopic interactions in which molecules attract water and soil particles [10], while cohesive forces are attractive interactions between water molecules that enable them to stick together, forming a continuous column of water within the soil pores [11]. Menisci form between adjacent soil particles as water adheres to the soil, creating a continuous water layer with a meniscus on both the upper and lower sides. Typically, in wet soil, the meniscus is less curved; however, as the soil dries, the curvature increases, strengthening the forces that make water less available to plants. This higher energy level requires greater efforts from gravity or plant roots to overcome these forces and extract water [12,13]. The soil water retention at a particular suction level is primarily influenced by many factors, such as pore space shape and size distribution, soil particle size, mineralogy, and surface activity [11,14]. Figure 1 illustrates how water is retained within the soil matrix and how the processes of adsorption, absorption, and varying water potential (both low and high) influence the release or retention of water in the soil.
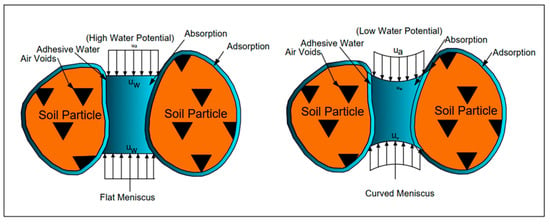
Figure 1.
Mechanisms of water retention in unsaturated soil: The roles of adhesion, cohesion, and meniscus formation.
Following previous research findings, the SWRC plays a crucial role in estimating unsaturated soil’s hydraulic and mechanical properties [15]. It provides a comprehensive understanding of how water interacts with the soil, offering insights into water-holding capacity, drainage characteristics, and moisture retention under wetting and drying conditions [16]. Moreover, the SWRC is instrumental in determining key parameters, including characteristic length, saturated and unsaturated hydraulic conductivity, available water content, capillary head at the wetting front, infiltration capacity, and time to ponding [17]. These parameters are essential for understanding soil water flow storage, and they are typically derived from a combination of laboratory tests and field data [18,19]. Additionally, estimating the SWRC is pivotal for understanding soil permeability, water storage, shear strength, soil water contamination, and thermal properties [20,21,22].
The SWRC describes a fundamental relationship between soil suction and volumetric water content or degree of saturation [23]. Soil suction is the sum of matric suction and osmotic suction. While the significance of matric suction in unsaturated soils has been extensively studied, there has been relatively limited focus on comprehending the impact of osmotic suction and its effects on the properties of unsaturated soil [23]. The sigmoidal shape of SWRC is divided into three zones: the capillary or boundary effect zone, the transitional or two-phase zone, and the residual or dry zone, as shown in Figure 2. It is typically represented on a semi-logarithmic scale to show a family of curves for various soil conditions [12]. The maximum amount of moisture held in the soil pores is represented by the saturated water content (θs), and the moisture moves slowly toward the residual and dry end of the soil suction. The soil’s moisture release or entry rate varies depending on the range of pore sizes in the soil matrix. The moisture rate in soil with a narrow pore size distribution, such as in sandy soils, is faster than in clay soils. The slope of the dry portion of the curve is influenced by the air entry value (AEV), which represents the suction at which higher saturation levels begin to decline [24,25]. Initially, as the soil dries, the moisture retention curve remains relatively flat until it reaches the air-entry value. During this stage, the pores remain saturated due to increased suction. Once the suction exceeds the AEV, air enters the larger pores, forming a continuous network of air-filled and water-filled pores. As water evaporates, saturation decreases, resulting in a partially saturated state [25,26]. The inflection points, AEV, and residual suction are crucial for determining the soil’s water retention properties.
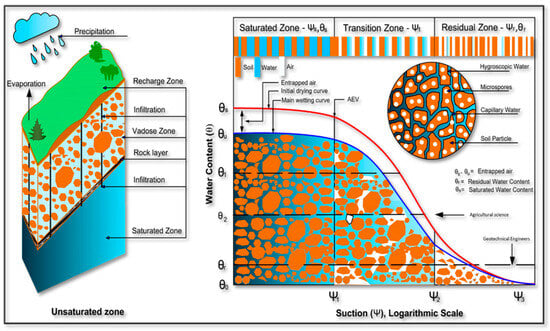
Figure 2.
Schematic representation of SWRC showing zones of degree of saturation, where θS, saturated moisture content θr, residual moisture content, AEV, air entry value).
The SWRC can be determined in the laboratory and filed using various methods, including a sandbox, pressure plates, hanging cups, gamma radiation, electromagnetic-based sensors, tensiometers tension disc-infiltrometers, and the Beerkan Estimation of Soil Transfer (BEST) method [19,27,28,29]. Both laboratory and field experiments have their advantages and limitations. While these measurement methods assist in determining the SWRC, they can be expensive, time-consuming, and often inadequate for studies requiring temporal and spatial scale analysis [30]. The alternative to the experimental measurement is the utilization of pedotransfer functions (PTFs), a technique adopted by various soil scientists and researchers [30,31]. Estimating various hydraulic properties using PTFs method has been a premier focus for soil scientists and researchers since the last century [32]. When direct measurements are challenging or costly, PTFs estimate soil hydraulic properties from basic soil texture and other physical attributes [33]. PTFs typically predict the hydraulic properties of soil, including thermal, mechanical, and physical characteristics, which are essential in many fields of science and engineering [6,34]. However, PTFs face several challenges in soil science and engineering when evaluating the SWRC of unsaturated soil [35]. It is essential to understand that the accuracy of PTFs is contingent upon the specific input data soil properties and the range of soil conditions being analyzed. The use of empirical parameters significantly influences the accuracy of PTFs in predicting hydraulic functions [36,37]. As a result, continuous pursuit of improvement is needed to validate these empirical parameters on a global scale to enhance the estimation capabilities of PTFs [38].
Although all the developed PTFs are helpful for further improvement, their accuracy and reliability are generally unsatisfactory, and they are still applied in the numerical simulation of water and solute transport in the unsaturated zone [39,40]. Many researchers and soil scientists prioritize the development and improvement of both new and existing PTFs [37,38]. Therefore, it is crucial to emphasize that existing PTF models should be used carefully, and their results should be validated against field measurements whenever possible [41]. However, no recent review or software program can fully adjust PTFs based on semi-physical methods to align them with experimental data. Consequently, this study aims to review various common semi-physical and analytical-based models to evaluate their performance and assess the challenges and limitations of the commonly used SWRC models based on semi-physical methods.
This study considered the models proposed by Arya and Paris [42], Haverkamp and Parlange [43], the Modified Kovács model by Aubertin et al.[11], Chang and Cheng [44], Meskini-Vishkaee et al. [45], Vidler et al. [46] and Zhai et al. [47], as shown in Figure 3. Furthermore, this study quantifies and assesses the main uncertainties in these models to devise a direction for future research. This study highlights the need for more robust, physically based models to address the shortcomings of existing approaches, considering the complexities introduced by variations in soil composition, structure, and local environmental conditions. The ultimate goal is to contribute to the development of accurate and widely applicable PTFs for improved SWRC estimation in diverse soil types and geographical regions.
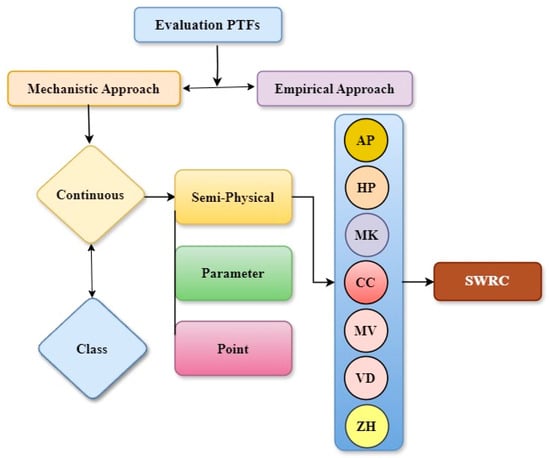
Figure 3.
PTFs-based seven semi-physical approaches for estimation of SWRC; AP: Arya and Paris [42]; HP: Haverkamp and Parlange [43]; MK: Modified Kovács model by Aubertin et al. [11]; CC: Chang and Cheng [44]; MV: Meskini-Vishkaee et al. [45]; Vidler: Vidler et al. [46]; Zhai: Zhai et al. [47].
2. Materials and Methods
2.1. Evaluation of Pedotransfer Functions (PTFs)
Based on soil properties, PTFs can be categorized into two main approaches: mechanistic and empirical. The mechanistic approach is based on the physical principles governing soil water movement, derived from measurements of basic soil data. It involves translating readily measurable soil properties such as texture, particle size distribution (PSD), bulk density (BD), and particle density into a pore-size distribution model (PoSD). This model is then linked to water content at various soil water matric potential heads, and the models can be applied either analytically or numerically. Many models are attributed to this approach, including the primary and prominent physical empirical model that was developed, which emphasizes the resemblance in shape between the water retention curve and cumulative particle size distribution [48]. For estimating the SWRC, the PSD data are initially transformed into the PoSD model and then into other pore volume parameters. This technique is helpful for homogeneous soils, while for heterogeneous soils, it requires more detailed soil information and may be computationally intensive. However, it is valuable for providing insights into the underlying systems and is more transferrable across multiple scenarios and conditions. The empirical approach, often called the data-driven approach, relies on statistical relationships derived from measured soil data. It involves fitting correlation functions between predictor and response variables [9]. The two most commonly used empirical approaches are statistical regressions and data mining techniques, such as regression trees, artificial neural networks, and group data handling methods [49]. The outcomes of the empirical approach based on PTFs can be numeric values or characteristic classes. However, it is important to note that most PTFs are developed for specific local or regional climatic conditions and are not universally transferable [9]. Empirical PTFs generally require large datasets containing measurements of soil properties and relevant soil features or environmental factors. However, empirical approaches are simpler and computationally less intensive than mechanistic models. Still, they are limited to specific conditions, and data ranges do not capture the full range of soil variability, which may be less accurate than mechanistic PTFs [50,51,52].
In addition, PTFs can be further categorized into two main types based on soil textures: class PTFs and continuous PTFs, which consider soil texture and properties in their respective classifications [31,53]. A class of PTFs predicts the hydraulic properties of soil that exist in similar groups of soil particles, such as sand and loam, as well as similar intervals of organic matter content or bulk density. Based on the prediction class PTFs are comparatively inexpensive and less time-consuming; however, the accuracy is relatively low due to only one average value of hydraulic properties. Class PTFs are suitable for calculating the parameters of the Van Genuchten and Brook and Corey models [42,54,55,56]. Continuous PTFs exist without similar grouping, constantly changing the soil hydraulic properties such as silt and clay and organic matter content, and many PTFs are deployed in this category [57,58].
Further classification of PTFs based on estimates is point-based, parameter-based, and semi-physical-based [59]. Point-based PTFs estimate the SWRC properties at some specific chosen matric potentials [8]. The model is calibrated to a specific soil, and the input parameters are based on laboratory or field measurements of soil properties. Point-based PTFs may be accurate for specific soil and properties but may not be transferable to other soils or regions. An example of point estimation is estimated by statistical approach at selected water potentials or specific points, i.e., −10, −33 is field capacity, and −1500 kpa is permanent wilting point [3,48]. The parameter-based PTF approach involves fitting analytical or empirical models and usually depends on the experimentally measured soil properties. Water retention at any potential point can be measured using a parametric technique in a continuous yield function in all these models, e.g., Brook and Corey (BC), Campbell, and Van Genuchten models (VG) [55,56,57,58]. Parameter-based PTFs estimate a desired soil attribute by using statistical models that incorporate different soil factors or characteristics. Parameter-based PTFs are more versatile than point-based PTFs because they can be applied to a broader range of soils but still require much information and may not be more accurate than point-based PTFs.
The semi-physical-based model integrates physical principles such as PSD, PoSD, and capillary action, with theoretical insights of soil behavior derived from empirical correlations. The study conducted by Arya and Haverkamp [42,43] contributed to the development of the original method and subsequently adaptations, improving its application in various mathematical models. The primary objective of this approach is to balance accuracy and simplicity when estimating the SWRC, particularly for soils that exhibit unique characteristics or when limited data are available. The concept of similarity enables the translation of PSD data into PoSD on a volume basis. The PSD and PoSD are fundamental components of this semi-physical approach [44,46]. The PSD data provide information about the mass percentage of particle fractions, which can be determined through laboratory tests or on-site measurements. Based on earlier studies, the semi-physical method for estimating SWRC is particularly effective for sandy soils and can generate more reliable results. However, its effectiveness and precision might be reduced in clay and loam soils because these types of soils have a complex pore structure and intricate interactions between particles [41]. By applying the semi-physical approach, the method can be optimized to more effectively evaluate SWRC on different soil types [51].
2.2. Analytical-Based Models
Analytical PTFs-based models derive soil-water retention equations from fundamental physical concepts and theories. These equations often incorporate mathematical functions that demonstrate the relationship between soil water content and soil water potential. Analytical PTFs are commonly calculated by solving the governing equations of water flow in unsaturated soils. In recent decades, numerous conventional models have been proposed to predict the SWRC [60]. Many of these conventional models are modified from existing approaches that use empirical or analytical curve fitting equations with at least two or more fitting parameters [60]. These models contain shape curve parameters known as hydraulic parameters, which are usually obtained from experimental data [61]. The most common and well-known of these models are in (Table 1) are Van Genuchten [56], Brooks and Corey [55], and Fredlund and Xing [62]. These models are helpful because they provide continuous analytical functions for the SWRC, which can be integrated into various PTF-based models. Notably, the Brooks Corey and Van Genuchten models are widely implemented in semi-physical models [55,56,63]. Their parameters are obtained by optimizing the models to fit the measured SWRCs [64,65]. However, specific parameters within these models are difficult to estimate, time-consuming to obtain, confronting limitations, and confusing, especially at the saturation and dryness points.
Additionally, these models are based on simple equations and have limited theoretical background, which usually underestimates the water content. These equations consist of scaling parameters (α, n, and m) and field survey data, both of which are usually complex and time-consuming to acquire. Moreover, the estimation of SWRC can vary among different models for the same soil. Hence, many alternative approaches have been proposed by researchers that can be easily incorporated into the SWRC modeling [62,66].

Table 1.
Common analytical equations corresponding to fitting parameters, where θ is volumetric water content (cm3/cm3); ψ is suction head or pressure head (cm or any pressure unit); θr is residual water content (cm3/cm3); θs is saturated water content (cm3/cm3); and α, n, m are the empirical shape parameters, where m is (dimensionless) parameter often set to = 1 − 1/n saturation. In Brooks and Corey equation, hd represents the air entry suction (cm).
Table 1.
Common analytical equations corresponding to fitting parameters, where θ is volumetric water content (cm3/cm3); ψ is suction head or pressure head (cm or any pressure unit); θr is residual water content (cm3/cm3); θs is saturated water content (cm3/cm3); and α, n, m are the empirical shape parameters, where m is (dimensionless) parameter often set to = 1 − 1/n saturation. In Brooks and Corey equation, hd represents the air entry suction (cm).
| Model | Function | Parameters | Source |
|---|---|---|---|
| Van Genuchten (1980) | [56,67] | ||
| Fredlund and Xing (1994) | [62,68] | ||
| Brooks and Corey (1964) | [55,69] |
3. Results and Discussion
3.1. Semi-Physical-Based Models
3.1.1. Arya and Paris (AP) Model
The pioneer of the PSD models is the AP model, commonly used in various studies to improve the SWRC estimation [42]. The theory of this model is based on fundamental soil properties like bulk density, particle density, and texture, along with a linear relationship between the mean pore radius, mean particle radius, and empirical scaling parameters. The AP model first translates PSD data into pore sizes, considering the soil particles as a pack for calculating the PoSD. It introduces a shape coefficient to represent complex pore structures and address tortuous pore lengths. Initially, AP assumed that all soil particles are spherical and that the scaling parameter α is an empirical constant, typically ranging from 1.35 to 1.40 for all soil types. Subsequently, this study evaluated and enhanced the scaling parameter of the SWRC and explored three different approaches for determining the α scaling parameter. The most effective method for fitting the measured and estimated SWRC was the non-linear α approach, followed by the linear process, with the constant α approach performing the least effectively [70]. Using the linear and constant methods often leads to underestimating the water content in the dry range (high tension region) and overestimating it in the wet range (low tension region) [71]. These discrepancies are particularly noticeable near points where the SWRC curve experienced sharp changes. The changes in SWRC may be attributed to the limitations of soil texture and the capillary theory [12,72]. The findings in [44] revealed that the AP model was more effective and efficient when using the non-linear and linear α methods for calculating the scale parameter α [73]. As a result, the volumetric water content estimate is obtained from the pore volume, which is assumed to be filled with water, while the suction head is calculated using the capillary equation [74]. Subsequently, the models were applied to various materials, including glass beds, coal minerals, and organic matter, to estimate SWRC. However, the model eliminates organic water content, with hysteresis volume changing and contact angle influencing the SWRC. Despite these limitations, many practitioners consider the AP model better suited for enhancement due to its similarity in shape to the SWRC [75] The water content corresponding to each interval ith can be calculated using Equation (1).
where volumetric water content (cm3 cm−3); is the total porosity of the sample is the ratio of measured saturated water content to theoretical porosity; is the solid mass friction of particles in the specific interval of diameter (g g−1); is particle density (g cm−3); is bulk density (g cm−3); ri is the pore radius in the considered interval (cm); ψ is the pressure head (cm); is the surface tension (g s−2); is water density (g cm−3); g is the acceleration due to gravity (m s−2); is the pore radius of ith friction, and Θ is the contact angle which is typically considered zero in the AP model [42,54,71].
3.1.2. Haverkamp and Parlange (HP) Model
Like the AP model, Haverkamp and Parlange [43] developed a model to describe the water retention properties of sandy soil. Their model is based on the assumption of shape similarity where the volumetric water content (θ) is considered equal to the cumulative particle size distribution function F(d) and the saturated water content (θs), with ‘d’ representing the particle diameter. The analytical expression uses the Brooks and Corey model to account for the influence of air entrainment and hysteresis. The hysteresis was introduced in this model and to develop a model that needs to parameterize natural saturated water content and dry bulk density. The advantage of the HP model is its ability to accurately predict water content at low pressures from saturated water content and particle density () while capturing the effects of soil structure on water retention [43]. The HP model provides reliable estimates for sandy soils with complex pore structures and aggregation, but its applicability is limited to specific fields and soils. Like the AP models, the HP models exhibit some drawbacks, such as trapped air, linear relationship between pore radius (R), particle diameter (D), and contact angle, which influence the SWRC. Additionally, the concept of hysteresis is introduced; its application is complicated, difficult to follow, and less user-friendly. In conclusion, the HP model helps understand hysteresis and the complexity of pore structure, contributing to further prediction of the SWRC model [76].
3.1.3. Modified Kovács (MK) Model
The Aubertin et al. [11] derived a comprehensive and well-established SWRC from the Kovács model [77]. The modified Kovács (MK) model predicted the parameters from the basic properties of soil, such as grain size distribution, porosity, and the use of specific surface area. In this regard, a set of equations was developed to predict three parameters (i.e., m, ac, and ψr) for full saturation to correlate with the SWRC. Important geotechnical properties were identified with the help of statistical analysis. The two major components, capillarity and adhesiveness, contributed to both low and high suctions. Granular (sand, silt) and fine-grained materials were used for improved model efficiency. The parameter estimation of fine-grained material was in a relatively low range of liquid limit and porosity values [11]. Better results were observed in granular and fine-grained materials, while pure clay and silt soil required further improvement. The MK model accurately predicted the SWRC for various soil types, accounting for the basic soil properties [11]. The MK model has limited applicability and is restricted to specific soil types and geotechnical properties. Its accuracy and reliability may vary when applied to soils with specific characteristics or heterogeneous soil conditions. Consequently, this model requires further validation and refinement to ensure its effectiveness in diverse soil types and conditions. Compared to other semi-physical-based models, the MK model’s parameters can be easily determined in a laboratory for the entire project. Moreover, the MK model is considered user-friendly and has great potential for further improvement due to its robust explanation of parameters and simplicity.
The MK model incorporates several parameters for calculating the volumetric water content in Equation (5), where Sr is the degree of saturation; θ is the volumetric water content; n is the total porosity; Sc and Sa correspond to the capillary and adhesive components [11].
3.1.4. Chang and Cheng (CC) Model
The Chang and Cheng model [44] introduced an improved model for a high suction head based on the AP model by incorporating PSD data for normalized circles and silt-shaped pore spaces. Earlier research studies have emphasized the significance of the non-linear relationship between PSD and PoSD for accurately estimating SWRC [11,43]. However, utilizing the non-linear PoSD derived from PSD remains challenging and can lead to errors in predicting the SWRC. The key enhancement lies in the CC model’s conceptualization of pore space, featuring larger circle-shaped pores interconnected by narrower silt-shaped spaces. The smaller silt-shaped pore spaces are included as part of the larger pores by employing geometric relationships.
Consequently, the CC model described the PSD and PoSD as lognormal distributions. The model assumes the lognormal PoSD, characterized by two parameters: the mean pore size and the standard deviation of pore size distribution. These parameters are associated with the SWRC through equations that account for capillary forces and air-entry pressure. One advantage of the CC model is that it requires only two fitting parameters, which can be obtained from the basic soil data, enabling the estimation of soil-water content from saturated to oven-dry conditions. In addition, the use of α and β values, which are essential parameters for estimating the volume fractions of silt-shaped spaces, can significantly influence the dry range of the SWRC [78]. The CC model recognizes that the volume fraction of each unit cell, specifically the central pore that connects two silt-shaped spaces, is equal to the corresponding particle mass fraction. Therefore, pore volume fractions of different sizes can be readily obtained. This assumption implies that the ratio of the volume occupied by the unit cell to the total volume is the same as the ratio of the mass of particles within the unit cell to the total mass. By integrating pore structure into the CC model, water content estimation in the dry range of suction is improved. When estimating the PoSD with a pore model, the CC model considers silt-shaped pore spaces, which may increase the pore volume fraction at the minimum pore diameter range.
A research study found that the non-linear relationship between the PSD and PoSD in the CC model is more appropriate than the linear relationship used in the AP model. However, the CC approach provides a relatively better estimation of the relationship between soil water content and soil water potential for sandy soil [7,44]. According to the CC results, the scaling approach and traditional method underestimated the SWRC, while the improved method showed the best relationship with measured data. To obtain the α and β values, an expression that relates both parameters to the specific surface area (SSA) was applied in Equation (6). The water content associated with different pore-filling stages can be estimated by Equation (7), and the pore size and the corresponding suction head could be calculated using Equation (8). The SWRC can ultimately be obtained using the calculated suction heads and water contents.
where SSA is the specific surface area (m2 g−1), the α parameter is obtained from (Table 2), and the β value from Equation (6). The fraction of the cumulative pore volume fraction of the ith fraction is equal to the total porosity ; in Equation (7) is the saturated water content (cm3 cm−3); is the cumulative pore volume corresponding to the solid friction of the jth particle friction. In addition, di is equivalent to the pore diameter (µm), and Di is the mean particle diameter of the ith fraction utilized in the PSD data to calculate the pore diameters. These are sequentially balanced with corresponding pore volume fractions to obtain the calculated PoSD.

Table 2.
The estimated values of α for various soil textures [44].
3.1.5. Meskini Vishkaee (MV) Model
The Meskini Vishkaee (MV) model [79] presented a conceptual scaling factor approach, following the continuous form of the PSD and bulk density data. This approach uses a packing density-scaling factor approach to predict and improve the dry range of SWRC. The MV model results were obtained from 82 soil samples from the UNSODA database. The model results showed that the proposed method effectively predicts the SWRC for all soil types. The MV model study concluded with the findings that the scaled PSD curve resulted in more precise SWRC estimation than obtained using unscaled PSD data. However, the MV model relies on the assumption of soil particle’s packing behavior. This model adjusts sand, silt, and clay to maintain the continuous form of the SWRC. In their study, the efficiency of the MV model was assessed across various soil classes, and the model outputs displayed a strong correlation with fine and medium-textured soils.
Furthermore, the scaling approach utilized in the MV study was found to provide a more accurate estimation compared to the MV-VG model and the ROSETTA program [80]. Overall, this approach provides a simple and practical SWRC prediction method. However, it should be noted that this approach relies on the assumption of the soil particle packing behavior and may not accurately reflect the complex interactions as those found in heterogeneous soil types. Therefore, to ensure accuracy and fitness for a particular soil, it is essential to validate the predicted curves using experimental data [79]. The MV model calculated volumetric water content using Equation (9) and Suction using Equation (10).
In the above Equation (10), is equal to Equation (11) and the suction head ψi is associated with the radius of a particle of the ith fraction and subsequently follows the scaling approach.
3.1.6. Vidler et al. (VD) Model
Vidler et al. [46] presented a model to predict the drying path of SWRC for various materials, including soil, mine waste, and coal for Plant Available Water (PAW). Experiments were conducted on the topsoil of Hunter Valley, New South Wales, Australia. This model’s input parameters included PSD and saturated water content without requiring laboratory calibration. This model highlighted the importance of mono-sized particles (i.e., 3 to 60 µm) in calculating the adhesive forces. This study assumed that the pore diameter was linked to 30% of particle size, considered spherical in shape and uniform in size. However, it was acknowledged that this assumption might not be suitable for large or very small pores, as it might neglect pore-filling spaces. The VD approach employed an apollonian gasket procedure to assess the level of pore filling for each primary pore size. The filling degree for each set of primary pores was determined. Following apollonian geometry, it was redistributed into a greater number of smaller pores to create the final pore size distribution. This redistribution process involved converting each pore size into an equivalent circular pore area with drainage suction, forming the ultimate PoSD.
This model was tested against sand and coal and compared with several existing PSD-based models, such as MV, AP CC, and MK models. The MV model demonstrated good agreement and consistent prediction for volumetric water content in mining materials. It was found that the model was useful for topsoil and other tailing materials when the calibration with existing data was not feasible. Compared to similar PSD models as shown in (Table 3) about the MV, AP CC, and MK models, the main improvement in the VD model was achieved by utilizing an apollonian gasket for each primary pore size to assess the level of pore filling. However, this filling occurred only under certain criteria, which considered the size ratio and fraction of smaller particles. This model is suitable for similar particle sizes and has shown promising results for varying particle sizes. In addition, the topsoil and tailings measured had little organic matter. However, if the materials have higher organic matter contents, it is possible to improve the accuracy of the proposed model by adding a regression parameter for organic matter content. However, the procedure is complicated difficult to follow, and less user-friendly. The VD model estimates volumetric water content using Equation (12) and suction using Equation (13).
where the volumetric water content θi is equals the soil’s porosity; Aik refers to the area of the kth sub-pore within the ith particle size bin; Ai represents the total pore area in the pore space of the ith size fraction, which is the sum of all Aik values in the ith particle size bin; θi is the volumetric water content related to the ith particle size bin; ψi is the suction for each sub-pore; γ represents the surface tension of water; rik is the circular radius of the kth sub-pore within the pore space of the ith size fraction, and αi indicates the receding contact angle of the water-solid interface for the particles linked to the ith size fraction.

Table 3.
Comparison and evaluation of different semi-physical models concerning efficiency for proposed soil models.
3.1.7. Zhai et al. (ZH) Model
In their study, Zhai et al. [47] proposed a method to estimate the SWRC from coarse-grained soils based on their grain size distribution. Their model is based on the mathematical relationship between the meniscus radii equations and the diameter of soil particles. This model aimed to improve the capillary barrier system (CBS) for coarse-grained soil. This approach uses soil void ratio and specific surface area derived from the grain size distribution (GSD) data to fit these parameters into empirical equations. The value for air entry was determined using the discrete theorem of circles. Subsequently, the mathematical equations were correlated to the meniscus radii with the soil particles comprising different diameters, assuming that soil particles are simplified as spheres in a 2D plane and a rigid soil skeleton. The positive aspect of this model is the use of contact angle and the geometrical relationship of radii spherical particles, which improves the SWRC for coarse-grained soil. It should be noted that the suggested approach is only appropriate for soils where capillary water predominates, making it suitable for barrier layers in a CBS, which are usually constructed from coarse-grain soil. This approach provides a practical way to estimate the SWRC from coarse-grained soils, but its accuracy may depend on the assumptions and empirical equations used in the ZH model. The ZH model estimates volumetric water content using Equation (14).
where S is the degree of saturation; Am is the total water area in all the representative elemental triangles; Atotal is the total water area in all the representative elemental triangles at fully saturated conditions; is the total void area in the ith element of the triangle; is the total area of voids in the soil element and N is the total number of element of triangles [47].
4. Discussion
The traditional approach to estimating the SWRC involves conducting various laboratory tests and field experiments. However, this process is time-consuming and expensive, and inaccuracies can be introduced due to errors in tools or by humans, resulting in variations in the measurement of water potentials and their associated water content. Moreover, the estimation of SWRC relies on small soil samples tested in the laboratory, which might not fully encompass the complexities of real field conditions. Hence, researchers and scientists prioritize a semi-physical approach that relies on PTF techniques due to their simplicity and similarity. This study presents a contemporary survey of semi-physical and analytical-based models commonly used in the last four decades. Several previous theories and models have been published to estimate the SWRC based on semi-physical approaches. This literature review was conducted primarily for two reasons. Firstly, we quantified and assessed the performance and evaluation of various PSD-based models. Secondly, we assessed and quantified the main uncertainties in the models. Several PTFs-based models, such as CC, MK, and MV, demonstrate superior performance with specific soil types or under particular environmental conditions. However, owing to the larger-scale soil variability, uncertainties have arisen in many models, including HP, VD, and ZH models. Therefore, it is necessary to understand and evaluate the performance of PTFs before applying them to specific conditions.
Applying a PSD-based model on a larger scale presents several challenges and limitations. Analyzing various articles, we have identified several common challenges, such as temperature, hysteresis, adhesion, contact angle, and the linear relationship between the mean pore and particle radius, which are frequently present but often overlooked in these models. As a result, these common challenges lead to underestimating the dry range of the SWRC. Additionally, using empirical scaling parameters can result in an imbalance between the dry and wet ranges of the SWRC. The HP model only partially addresses incorporating hysteresis over sandy soil [43]. Specific models require minor improvements, while many others are deemed unrealistic due to omitting various factors, including contact angle, hysteresis, organic content, soil adhesion, and cohesion properties. According to the literature, none of the models has been validated comprehensively on a large scale.
Some PSD-based models have also been tested on various scales, regions, and soils. For example, Arya and Paris [42] developed a PSD-based model for SWRC and tested it on various soil types. Similarly, Haverkamp and Parlange [43] and Modified Kovács developed PTFs for estimating SWRC, which are widely used in soil science research. The MK model was tested in various soils, and comparatively good performance was observed in finer soils; however, the models’ effectiveness was limited to specific soil types. The efficiency and performance of the seven PTFs-based models (Table 3) regarding their capability and suitability to perform effectively with clay, loam, and sand are assessed. Their results are presented for input and output parameters accordingly. The predicted results of all seven models revealed a strong correlation in sandy soils, whereas they relatively underperformed for clay and loam soils. Soil heterogeneity was one of the limiting factors associated with underestimating clay and loam soils.
Furthermore, the predictability of PSD-based models for the employed PTFs techniques can be vulnerable to soil variability and climate variations. These factors can potentially affect the accuracy and predictions of SWRC. The main issue observed in the PSD-based models is the characterization of soil particles with a non-linear distribution of pore space. However, the CC model [44,46] assumes a non-linear relationship between the PSD and PoSD particles to calculate silt pore distribution to enhance the dry range of SWRC. Many studies have suggested that considering non-linear pore space is essential for attaining higher accuracy and more reliable model predictions [46,78]. Therefore, recent studies such as CC and VD incorporated a non-linear relationship between pore radius and mean particle radius of pore space in the modeling frameworks. The pore filling needs to consider several factors, such as the size ratio between particles, the relative composition of coarse and fine particles, the overall particle size, and the geometry of particles. The least common approach predicts particle packing for the spherically natural grains. None of the SWRC models have been implemented sufficiently to account for the pore-filling process. Vidler [46] introduced the pore-filling GSD SWRC technique in their model, which is appropriate for mining data from spherical granular media with particle packing.
Studies show that the shape of SWRC in sandy soils is significantly affected by the presence of fine particles (<0.125 mm) [28]. However, some researchers have modified previous approaches and achieved satisfactory outcomes for clay, loam, and sandy soils. However, a non-linear distribution of pore spaces partially improves the accuracy and reliability of soil properties in both homogeneous and heterogeneous conditions. To fill this gap and improve accuracy and reliability, it is necessary to effectively address soil heterogeneity and comprehend its influence on water flow modeling. In addition, the models’ equilibrium may be unbalanced by overlooking large-scale scenarios. Measuring the contact angle between the water and the soil surfaces is an essential factor that governs the drainage suction of a pore according to the capillarity law. Most soils are hydrophilic, exhibiting relatively low contact angles. To overcome this, assuming the contact angle of zero has shown promising results for various types of soils, as reported from several studies, e.g., in [46,47,81]. Using the contact angle based on the sessile drop technique [82], the prediction accuracy can be further enhanced for sand, coal, and other mineral particles.
The integration of temperature components in the modeling framework is crucial when utilizing PTFs to estimate the SWRC under different temperature conditions. Various studies have accounted for temperature, as in [7,72], it was found that temperature could significantly affect the movement and availability of water in the soil. Temperature change significantly affects soil properties such as hydraulic conductivity, water saturation, and pore size distribution. Increasing temperatures influence the evaporation rates, the viscosity of water, soil structure, and PoSD [72]. Decreased temperatures affect soil properties through the freezing and thawing cycles, which can change pore structure and hydraulic properties. Neglecting the temperature-dependent variations can lead to a prediction deviation from actual behavior. Moreover, the SWRC models are limited in considering the microscopic water that forms a thin film on soil particles. However, this study [82] showed that considering microscopic water could improve the accuracy and depict a good representation of the soil water content in fine soil.
Furthermore, soil–water interactions can exhibit complexity due to non-linear connections, such as the soil structure, mineralogy, and the amount of organic matter present [83]. The SWRC can be underestimated if the assumption of a linear relationship is not correctly applied to a particular type of soil. Several studies argue that incorporating isotropic or anisotropic behavior into the SWRC modeling also significantly impacts outputs [84]. Due to the complexity of soil structure and the required degree of accuracy, no single study has fully utilized such conditions. Collectively addressing these challenges can lead to precise and reliable predictions of soil water retention for all soil types.
5. Conclusions
The SWRC is a crucial hydraulic property of soil influenced by many environmental factors such as soil behavior, infiltration, water movement, drainage mechanisms, and inherent soil variability. Therefore, this study reviewed and examined current and past PTFs techniques to assess their efficiency and reliability for estimating SWRC. This review focuses mainly on the most common PSD-based models to identify proficiency and basic input parameters, as well as their effect on SWRC. This study summarizes that PTFs relying on empirical relationships may not fully capture the complexities of specific soil conditions or contexts. Variations in the soil composition, structure, and local environmental conditions can introduce uncertainties into the PTFs predictions. As a result, the accuracy of PTFs varies across different soil types and geographical regions. Furthermore, the analysis exhibits that each model has at least one limitation, and many of these models fail to consider crucial soil behaviors, such as volume change and hysteresis. Furthermore, the findings of this study indicate that none of the PTF models accurately represented SWRC in the higher suction range. However, the Modified Kovács (MK) and Chang and Cheng (CC) models performed relatively better in the high range, where the influence of adsorbed water was pronounced. Although several PTFs-based models can be found in the existing literature, it is important to note that no single function has been universally identified as applicable to describe the water retention characteristics in all soil types. Therefore, further research is needed to develop more advanced PTFs-based models that explicitly differentiate between capillary and adsorption theory water across all soil types and conditions. Future research should extend beyond specific materials and stress conditions to include soil structures that more accurately reflect in situ states. The developed model should be rigorously validated in arid and semi-arid climates to optimize its performance and expand its applicability.
Author Contributions
All authors contributed to writing the manuscript; U.F. contributed to the literature survey and the writing of the original manuscript; M.A. contributed to a review of methods of PTFs evaluation, discussion of Section 3 and Section 4, and refinement of the manuscript; S.L. and J.Y. contributed to the review of this manuscript and writing; S.U. contributed to critical review application and manuscript writing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
This review article is based on an analysis of the existing literature. We did not generate any original data or models for this study.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this article.
Abbreviations/Nomenclature
| Symbols and Notation | |
| Symbols | Description |
| θ | Volumetric water content |
| ωi | Soil mass friction |
| Bulk density | |
| e | Void ratio |
| ψ | Pressure head |
| Water density | |
| ri | Pore radius |
| θr | Residual water |
| Ai | Total pore area |
| Cumulative pore volume | |
| Di | Mean diameter |
| Ri | Particle radius |
| Aik | Area kth sub-pore |
| γ | Surface tension |
| rik | Circular radius |
| αi | Receding angle |
| θS | Saturated water |
| S | Degree of saturation |
| Pore volume | |
| particle density | |
| Length of the pore | |
| Surface tension | |
| g | Gravity |
| Porosity | |
| di | Pore diameter |
| Abbreviations and their full name | |
| Abbreviation | Elaboration |
| SWRC | Soil-Water Retention Curve |
| PTFs | Pedotransfer Functions |
| BC | Brooks and Corey |
| VG | Van Genuchten |
| SSA | Specific Surface Area |
| AEV | Air-Entry Value |
| PoSD | Pore Size Distribution |
| AP | Arya and Paris |
| HP | Haverkamp and Parlange |
| MK | Modified Kovács |
| CC | Chang and Cheng |
| MV | Meskini-Vishkaee |
| VD | Vidler |
| ZH | Zhai |
References
- Ghavidelfar, S.; Shamseldin, A.Y.; Melville, B.W. Estimation of Soil Hydraulic Properties and Their Uncertainty through the Beerkan Infiltration Experiment. Hydrol. Process. 2015, 29, 3699–3713. [Google Scholar] [CrossRef]
- Shein, E.V. Physically Based Mathematical Models in Soil Science: History, Current State, Problems, and Outlook (Analytical Review). Eurasian Soil Sci. 2015, 48, 712–718. [Google Scholar] [CrossRef]
- Botula, Y.D.; Cornelis, W.M.; Baert, G.; Van Ranst, E. Evaluation of Pedotransfer Functions for Predicting Water Retention of Soils in Lower Congo (D.R. Congo). Agric. Water Manag. 2012, 111, 1–10. [Google Scholar] [CrossRef]
- Farooq, U.; Taha Bakheit Taha, A.; Tian, F.; Yuan, X.; Ajmal, M.; Ullah, I.; Ahmad, M. Flood Modelling and Risk Analysis of Cinan Feizuo Flood Protection Area, Huaihe River Basin. Atmosphere 2023, 14, 678. [Google Scholar] [CrossRef]
- Alves, R.; Gitirana, G. de F.N.; Vanapalli, S.K. Effect of the Particle-Size Distribution Variability on the SWCC Predictions of Coarse-Grained Materials. MATEC Web Conf. 2021, 337, 02010. [Google Scholar] [CrossRef]
- Too, V.K.; Omuto, C.T.; Biamah, E.K.; Obiero, J.P.; Too, V.K.; Omuto, C.T.; Biamah, E.K.; Obiero, J.P. Review of Soil Water Retention Characteristic (SWRC) Models between Saturation and Oven Dryness. Open J. Mod. Hydrol. 2014, 4, 173–182. [Google Scholar] [CrossRef]
- Pham, T.A.; Hashemi, A.; Sutman, M.; Medero, G.M. Effect of Temperature on the Soil-Water Retention Phenomena in Unsaturated Soils: Analytical and Experimental Models. SSRN Electron. J. 2022, 63, 101301. [Google Scholar] [CrossRef]
- Latorre, B.; Moret-Fernández, D.; Lassabatere, L.; Rahmati, M.; López, M.V.; Angulo-Jaramillo, R.; Sorando, R.; Comín, F.; Jiménez, J.J. Influence of the β Parameter of the Haverkamp Model on the Transient Soil Water Infiltration Curve. J. Hydrol. 2018, 564, 222–229. [Google Scholar] [CrossRef]
- Perreault, S.; El Alem, A.; Chokmani, K.; Cambouris, A.N. Development of Pedotransfer Functions to Predict Soil Physical Properties in Southern Quebec (Canada). Agronomy 2022, 12, 526. [Google Scholar] [CrossRef]
- Aubertin, M.; Mbonimpa, M.; Buissière, B.; Chapuis, R.P.; Development of a Model to Predict the Water Retention Curve Using Basic Geotechnical Properties. Document En Libre Accès Dans PolyPublie DEVELO. 2003. Available online: https://publications.polymtl.ca/2604/ (accessed on 28 August 2024).
- Aubertin, M.; Mbonimpa, M.; Bussière, B.; Chapuis, R.P. A Model to Predict the Water Retention Curve from Basic Geotechnical Properties. Can. Geotech. J. 2003, 40, 1104–1122. [Google Scholar] [CrossRef]
- Fredlund, D.G. Relationship between the Laboratory SWCCs and Field Stress State. In Unsaturated Soil Mechanics—From Theory to Practice, Proceedings of the 6th Asia Pacific Conference on Unsaturated Soils, Guilin, China, 23–26 October 2015; CRC Press: Boca Raton, FL, USA, 2015; pp. 3–14. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.; Lin, Y.; Jiang, T. A Simple and Practical Method for Predicting Soil Water Characteristic Curve Based on Grading Parameters. Jpn. Geotech. Soc. Spec. Publ. 2019, 7, 293–296. [Google Scholar] [CrossRef]
- Su, M.; Liu, C.; Wang, L.P.; Zheng, W. Prediction of Saturated Hydraulic Conductivity of Sandy Soil Using Sauter Mean Diameter of Soil Particles. Eur. J. Soil Sci. 2022, 73, 1–10. [Google Scholar] [CrossRef]
- He, H.; Aogu, K.; Li, M.; Xu, J.; Sheng, W.; Jones, S.B.; González-Teruel, J.D.; Robinson, D.A.; Horton, R.; Bristow, K.; et al. A Review of Time Domain Reflectometry (TDR) Applications in Porous Media. Adv. Agron. 2021, 168, 83–155. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; John Wiley & Sons: New York, NY, USA, 1993; p. 517. [Google Scholar]
- Assouline, S. What Can We Learn From the Water Retention Characteristic of a Soil Regarding Its Hydrological and Agricultural Functions? Review and Analysis of Actual Knowledge. Water Resour. Res. 2021, 57, 1–16. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Taslimitehrani, V.; Dong, G.; Pachepsky, Y.A. Sample Dimensions Effect on Prediction of Soil Water Retention Curve and Saturated Hydraulic Conductivity. J. Hydrol. 2015, 528, 127–137. [Google Scholar] [CrossRef]
- Haghverdi, A.; Öztürk, H.S.; Durner, W. Measurement and Estimation of the Soil Water Retention Curve Using the Evaporation Method and the Pseudo Continuous Pedotransfer Function. J. Hydrol. 2018, 563, 251–259. [Google Scholar] [CrossRef]
- Choudhury, C.; Tadikonda, B.V. Soil-Water Characteristic Curve Models for Clays. In Proceedings of the Indian Geotechnical Conference IGC 2014, Kakinada, India, 18–20 December 2014; p. 10. [Google Scholar]
- Fallah, M.; Shabanpor, M.; Zakerinia, M.; Ebrahimi, S. Risk Assessment of Gas Oil and Kerosene Contamination on Some Properties of Silty Clay Soil. Environ. Monit. Assess. 2015, 187, 1–13. [Google Scholar] [CrossRef]
- Noreen, A.; Hussain, S.; Farooq, U.; Younas, T.; Khan, R.; Elsehrawy, M.G. Determination of Heavy Metals Concentration in Water and Soil at Various Locations in Lahore and Their Harmful Impacts on Human and Plants Life. Pak. J. Med. Health Sci. 2022, 16, 1578–1581. [Google Scholar] [CrossRef]
- Onyelowe, K.C.; Mojtahedi, F.F.; Azizi, S.; Mahdi, H.A.; Sujatha, E.R.; Ebid, A.M.; Darzi, A.G.; Aneke, F.I. Innovative Overview of SWRC Application in Modeling Geotechnical Engineering Problems. Designs 2022, 6, 69. [Google Scholar] [CrossRef]
- Arairo, W.; Prunier, F.; Djeran-Maigre, I. Water Retention in Unsaturated Soils Subjected to Wetting and Drying Cycles. In Proceedings of the IV International Conference on Computational Methods for Coupled Problems in Science and Engineering (COUPLED 2011), Kos, Greece, 20–22 June 2011; pp. 767–778. [Google Scholar]
- Wijaya, M.; Leong, E.C.; Rahardjo, H. Effect of Shrinkage on Air-Entry Value of Soils. Soils Found. 2015, 55, 166–180. [Google Scholar] [CrossRef]
- Es-haghi, M.S.; Rezania, M.; Bagheri, M. Machine Learning-Based Estimation of Soil’s True Air-Entry Value from GSD Curves. Gondwana Res. 2023, 123, 280–292. [Google Scholar] [CrossRef]
- Kargas, G.; Koka, D.; Londra, P.A. Evaluation of Soil Hydraulic Parameters Calculation Methods Using a Tension Infiltrometer. Soil Syst. 2022, 6, 63. [Google Scholar] [CrossRef]
- Farooq, U.; Gorczewska-Langner, W.; Szymkiewicz, A. Water Retention Curves of Sandy Soils Obtained from Direct Measurements, Particle Size Distribution, and Infiltration Experiments. Vadose Zone J. 2024, 23, e20364. [Google Scholar] [CrossRef]
- Lee, K.S.; Lee, D.S.; Jung, H.G.; Lee, S.P.; Ryu, J.H.; Choi, W.J.; Yang, J.E.; Chung, D.Y. Evaluation of Pedotransfer Functions for Estimating Soil Water Retention Curve of Ap Horizon Soils for Various Soil Series of Reclaimed Tidal Flat Soil. Agronomy 2022, 12, 1507. [Google Scholar] [CrossRef]
- Mbayaki, C.W.; Karuku, G.N. Soil Hydraulic Properties of a Chromic Luvisol in Katumani, Kenya. Trop. Subtrop. Agroecosystems 2022, 25. [Google Scholar] [CrossRef]
- Botula, Y.-D.; Van Ranst, E.; Cornelis, W.M. Pedotransfer Functions to Predict Water Retention for Soils of the Humid Tropics: A Review. Rev. Bras. Ciência do Solo 2014, 38, 679–698. [Google Scholar] [CrossRef]
- Hwang, S., II; Choi, S., II. Use of a Lognormal Distribution Model for Estimating Soil Water Retention Curves from Particle-Size Distribution Data. J. Hydrol. 2006, 323, 325–334. [Google Scholar] [CrossRef]
- Mcbratney, A.B.; Minasny, B.; Cattle, S.R.; Vervoort, R.W. From Pedotransfer Functions to Soil Inference Systems. Geoderma 2001, 109, 41–73. [Google Scholar] [CrossRef]
- Van Looy, K.; Bouma, J.; Herbst, M.; Koestel, J.; Minasny, B.; Mishra, U.; Montzka, C.; Nemes, A.; Pachepsky, Y.A.; Padarian, J.; et al. Pedotransfer Functions in Earth System Science: Challenges and Perspectives. Rev. Geophys. 2017, 55, 1199–1256. [Google Scholar] [CrossRef]
- Rahmati, M.; Vanderborght, J.; Šimůnek, J.; Vrugt, J.A.; Moret-Fernández, D.; Latorre, B.; Lassabatere, L.; Vereecken, H. Soil Hydraulic Properties Estimation from One-Dimensional Infiltration Experiments Using Characteristic Time Concept. Vadose Zone J. 2020, 19, e20068. [Google Scholar] [CrossRef]
- Mohammadi, M.H.; Meskini-Vishkaee, F. Predicting the Film and Lens Water Volume between Soil Particles Using Particle Size Distribution Data. J. Hydrol. 2012, 475, 403–414. [Google Scholar] [CrossRef]
- Tóth, B.; Weynants, M.; Nemes, A.; Makó, A.; Bilas, G.; Tóth, G. New Generation of Hydraulic Pedotransfer Functions for Europe. Eur. J. Soil Sci. 2015, 66, 226–238. [Google Scholar] [CrossRef] [PubMed]
- Wösten, J.H.M.; Lilly, A.; Nemes, A.; Le Bas, C. Development and Use of a Database of Hydraulic Properties of European Soils. Geoderma 1999, 90, 169–185. [Google Scholar] [CrossRef]
- Romano, N.; Palladino, M. Prediction of Soil Water Retention Using Soil Physical Data and Terrain Attributes. J. Hydrol. 2002, 265, 56–75. [Google Scholar] [CrossRef]
- Rastgou, M.; Bayat, H.; Mansoorizadeh, M.; Gregory, A.S. Estimating Soil Water Retention Curve by Extreme Learning Machine, Radial Basis Function, M5 Tree and Modified Group Method of Data Handling Approaches. Water Resour. Res. 2022, 58, 1–26. [Google Scholar] [CrossRef]
- Patil, N.G.; Singh, S.K. Pedotransfer Functions for Estimating Soil Hydraulic Properties: A Review. Pedosphere 2016, 26, 417–430. [Google Scholar] [CrossRef]
- Arya, L.M.; Paris, J.F. A Physicoempirical Model to Predict the Soil Moisture Characteristic from Particle-Size Distribution and Bulk Density Data. Soil Sci. Soc. Am. J. 1981, 45, 1023–1030. [Google Scholar] [CrossRef]
- Haverkamp, R.; Parlange, J.-Y. Predicting the Water-Retention Curve from Particle-Size Distribution 1. Sandy Soils without Organic Matter. Soil Sci. 1986, 142, 325–339. [Google Scholar] [CrossRef]
- Chang, C.C.; Cheng, D.H. Predicting the Soil Water Retention Curve from the Particle Size Distribution Based on a Pore Space Geometry Containing Slit-Shaped Spaces. Hydrol. Earth Syst. Sci. 2018, 22, 4621–4632. [Google Scholar] [CrossRef]
- Meskini-Vishkaee, F.; Mohammadi, M.H.; Vanclooster, M. A Scaling Approach, Predicting the Continuous Form of Soil Moisture Characteristics Curve, from Soil Particle Size Distribution and Bulk Density Data. Hydrol. Earth Syst. Sci. Discuss. 2013, 10, 14305–14329. [Google Scholar] [CrossRef]
- Vidler, A.; Buzzi, O.; Fityus, S. A Simple Water Retention Model Based on Grain Size Distribution. Appl. Sci. 2021, 11, 9452. [Google Scholar] [CrossRef]
- Zhai, Q.; Rahardjo, H.; Satyanaga, A.; Dai, G. Estimation of the Soil-Water Characteristic Curve from the Grain Size Distribution of Coarse-Grained Soils. Eng. Geol. 2020, 267, 105502. [Google Scholar] [CrossRef]
- Matula, S.; Mojrová, M.; Špongrová, K. Estimation of the Soil Water Retention Curve (SWRC) Using Pedotransfer Functions (PTFs). Soil Water Res. 2007, 2, 113–122. [Google Scholar] [CrossRef]
- Nguyen, P.M.; Haghverdi, A.; de Pue, J.; Botula, Y.D.; Le, K.V.; Waegeman, W.; Cornelis, W.M. Comparison of Statistical Regression and Data-Mining Techniques in Estimating Soil Water Retention of Tropical Delta Soils. Biosyst. Eng. 2017, 153, 12–27. [Google Scholar] [CrossRef]
- Chapuis, R.P. Analyzing Grain Size Distributions with the Modal Decomposition Method: Literature Review and Procedures. Bull. Eng. Geol. Environ. 2021, 80, 6649–6666. [Google Scholar] [CrossRef]
- Ghanbarian-Alavijeh, B.; Millán, H.; Huang, G. A Review of Fractal, Prefractal and Pore-Solid-Fractal Models for Parameterizing the Soil Water Retention Curve. Can. J. Soil Sci. 2011, 91, 1–14. [Google Scholar] [CrossRef]
- Khlosi, M.; Alhamdoosh, M.; Douaik, A.; Gabriels, D.; Cornelis, W.M. Enhanced Pedotransfer Functions with Support Vector Machines to Predict Water Retention of Calcareous Soil. Eur. J. Soil Sci. 2016, 67, 276–284. [Google Scholar] [CrossRef]
- Román Dobarco, M.; Cousin, I.; Le Bas, C.; Martin, M.P. Pedotransfer Functions for Predicting Available Water Capacity in French Soils, Their Applicability Domain and Associated Uncertainty. Geoderma 2019, 336, 81–95. [Google Scholar] [CrossRef]
- Arya, L.M.; Leij, F.J.; Shouse, P.J. Scaling Parameter to Predict the Soil Water Characteristic from Particle-Size Distribution Data. Soil Sci. Soc. Am. J. 1999, 63, 510–519. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Hydraulic Properties of Porous Media and Their Relation to Drainage Design. Trans. ASAE 1964, 7, 26–28. [Google Scholar] [CrossRef]
- Van Genuchten, M.A. Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Baker, L. Development of Class Pedotransfer Functions of Soil Water Retention-A Refinement. Geoderma 2007, 144, 225–230. [Google Scholar] [CrossRef]
- Campbell, G.S. A Simple Method for Determining Unsaturated Conductivity from Moisture Retention Data. Soil Sci. 1974, 117, 311–314. [Google Scholar] [CrossRef]
- Wang, J.-P.; Hu, N.; Françoise, B.; Lambert, P. Unsaturated Sandy Soils From Basic Soil Gradation Parameters. Water Resour. Res. 2017, 53, 6069–6088. [Google Scholar] [CrossRef]
- Ghanbarian-Alavijeh, B.; Liaghat, A.; Huang, G.H.; Van Genuchten, M.T. Estimation of the van Genuchten Soil Water Retention Properties from Soil Textural Data. Pedosphere 2010, 20, 456–465. [Google Scholar] [CrossRef]
- Kargas, G.; Koka, D.; Londra, P.A. Determination of Soil Hydraulic Properties from Infiltration Data Using Various Methods. Land 2022, 11, 779. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Xing, A. Equations for the Soil-Water Characteristic Curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Merdun, H. Pedotransfer Functions for Point and Parametric Estimations of Soil Water Retention Curve. Plant, Soil Environ. 2006, 52, 321–327. [Google Scholar] [CrossRef]
- Rahimi, A.; Rahardjo, H.; Leong, E.C. Effect of Range of Soil-Water Characteristic Curve Measurements on Estimation of Permeability Function. Eng. Geol. 2015, 185, 96–104. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Luo, X. Parameter Estimation for Soil Water Retention Curve Using the Salp Swarm Algorithm. Water 2018, 10, 815. [Google Scholar] [CrossRef]
- Kosugi, K. Lognormal Distribution Model for Unsaturated Soil Hydraulic Properties. Water Resour. Res. 1996, 32, 2697–2703. [Google Scholar] [CrossRef]
- Van Genuchten, M.; Leij, F.; Yates, S. The RETC Code for Quantifying the Hydraulic Functions of Unsaturated Soils. 1991. Available online: https://www.pc-progress.com/Documents/programs/retc.pdf (accessed on 28 August 2024).
- Andrabi, S.G.; Ghazanfari, E.; Vahedifard, F. An Empirical Relationship between Brooks–Corey and Fredlund–Xing Soil Water Retention Models. J. Porous Media 2019, 22, 1423–1437. [Google Scholar] [CrossRef]
- Wang, Q.; Horton, R.; Shao, M. Horizontal Infiltration Method for Determining Brooks-Corey Model Parameters. Soil Sci. Soc. Am. J. 2002, 66, 1733–1739. [Google Scholar] [CrossRef]
- Zhao, Y.Q.; Wang, W.K.; Wang, Z.F.; Li, L.C. Physico-Empirical Methods for Estimating Soil Water Characteristic Curve under Different Particle Size. IOP Conf. Ser. Earth Environ. Sci. 2018, 191, 012018. [Google Scholar] [CrossRef]
- Rezaee, L.; Shabanpour, M.; Davatgar, N. Estimating the Soil Water Retention Curve from Soil Particle Size Distribution Using the Arya and Paris Model for Iranian Soils. Turkish J. Agric. For. 2011, 35, 649–657. [Google Scholar] [CrossRef]
- Qiao, X.; Ma, S.; Pan, G.; Liu, G. Effects of Temperature Change on the Soil Water Characteristic Curve and a Prediction Model for the Mu Us Bottomland, Northern China. Water 2019, 11, 1235. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, W.; Chen, F. Bayesian Approach for Predicting Soil-Water Characteristic Curve from Particle-Size Distribution Data. Energies 2019, 14, 2992. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, C.; Chen, C.; Chen, H. Calculation of Capillary Rise Height of Soils by SWCC Model. Adv. Civ. Eng. 2018, 2018, 5190354. [Google Scholar] [CrossRef]
- Toyohara, T.; Akiyama, Y.; Suzuki, T.; Takeuchi, Y.; Mishima, E.; Tanemoto, M.; Momose, A.; Toki, N.; Sato, H.; Nakayama, M.; et al. A Physicoempirical Model to Predict the Soil Moisture Characteristic from Particle-Size Distribution and Bulk Density Data 1 LALIT M. ARYA AND JACK F. PARIS. Sangre Saragossa 2010, 45, 944–952. [Google Scholar]
- Braddock, R.D.; Parlange, J.Y.; Lee, H. Application of a Soil Water Hysteresis Model to Simple Water Retention Curves. Transp. Porous Media 2001, 44, 407–420. [Google Scholar] [CrossRef]
- Kovács, B.G. Seepage Hydraulics; Elsevier Science Publishers: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Chang, C.-C.; Cheng, D.-H.; Qiao, X.-Y.-C.; Cheng, D.-H.; Qiao, X.-Y. Improving Estimation of Pore Size Distribution to Predict the Soil Water Retention Curve from Its Particle Size Distribution. Geoderma 2019, 340, 206–212. [Google Scholar] [CrossRef]
- Meskini-Vishkaee, F.; Mohammadi, M.H.; Vanclooster, M. Predicting the Soil Moisture Retention Curve, from Soil Particle Size Distribution and Bulk Density Data Using a Packing Density Scaling Factor. Hydrol. Earth Syst. Sci. 2014, 18, 4053–4063. [Google Scholar] [CrossRef][Green Version]
- Mohammadi, M.H.; Meskini-Vishkaee, F. Predicting Soil Moisture Characteristic Curves from Continuous Particle-Size Distribution Data. Pedosphere 2013, 23, 70–80. [Google Scholar] [CrossRef]
- Tomasella, J.; Pachepsky, Y.; Crestana, S.; Rawls, W.J. Comparison of Two Techniques to Develop Pedotransfer Functions for Water Retention. Soil Sci. Soc. Am. J. 2003, 67, 1085–1092. [Google Scholar] [CrossRef]
- Vidler, A.; Buzzi, O.; Fityus, S. The Significance of Hydrophobicity for the Water Retention Properties of Sand and Coal. Appl. Sci. 2021, 11, 5966. [Google Scholar] [CrossRef]
- Yerro, A.; Ceccato, F. Soil–Water–Structure Interactions. Geotechnics 2023, 3, 301–305. [Google Scholar] [CrossRef]
- Zhou, C.; Chen, R. Modelling the Water Retention Behaviour of Anisotropic Soils. J. Hydrol. 2021, 599, 126361. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).