Interpreting Controls of Stomatal Conductance across Different Vegetation Types via Machine Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Flux and Meteorological Observations
2.1.1. FLUXNET Data
2.1.2. Transpiration Data Acquisition
2.2. Calculation of Stomatal Conductance
2.3. Leaf Area Index
2.4. Data Analysis
2.4.1. Data Reprocessing
2.4.2. Random Forest Model
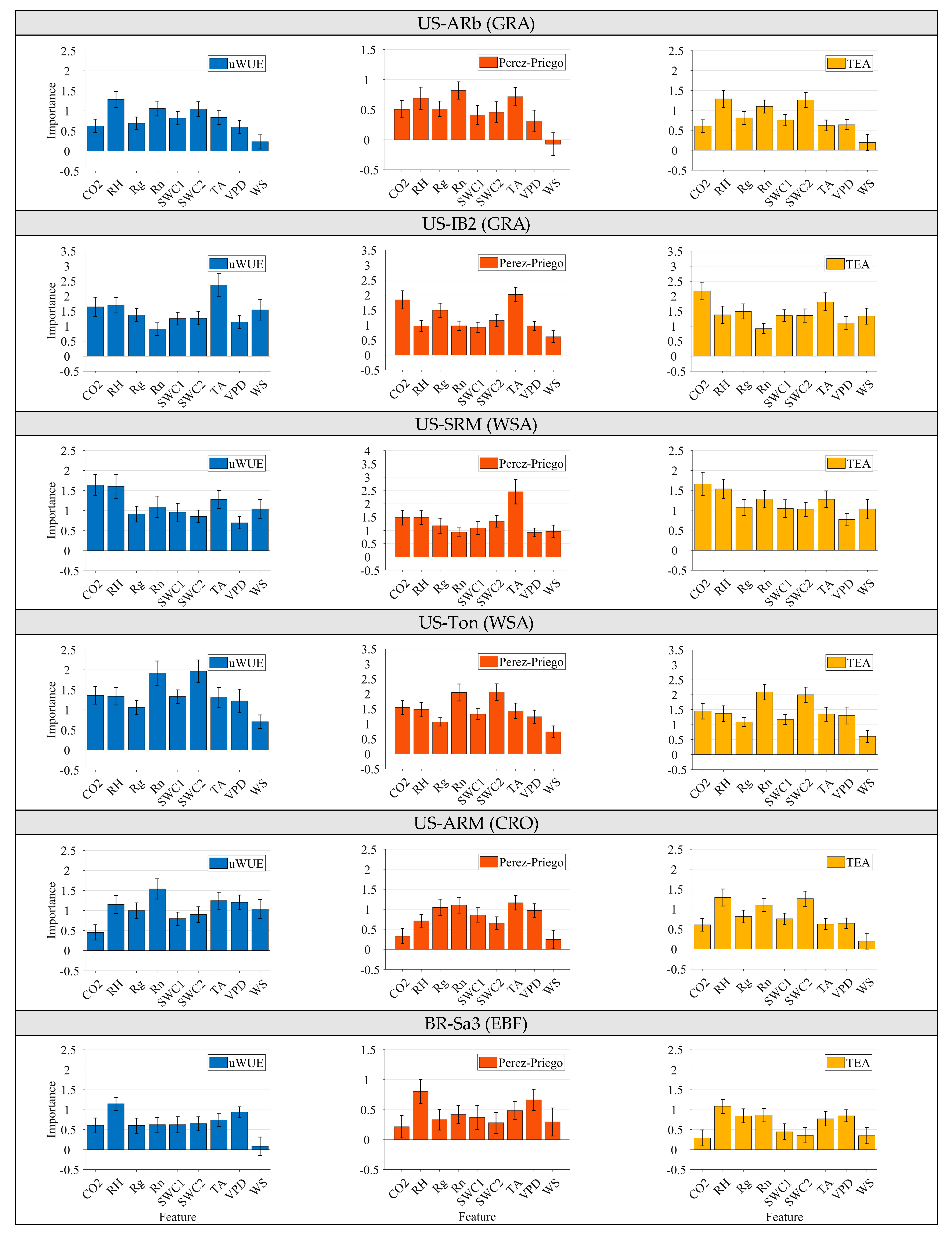
2.4.3. Feature Importance Analysis
3. Results and Discussion
3.1. Differences in Hydrometeorological Effects on Gs in Different Biomes
3.2. Consistency of Factors Influencing Gs across Similar Vegetation and Climate
3.3. Effects of Environmental Elements at Different Vegetation Fertility Stages
3.4. Effect of LAI on Stomatal Conductance Prediction Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Site ID | Sow (YYYY-MM-DD) | Harvest (YYYY-MM-DD) |
|---|---|---|
| US-ARM | 2002-09-28 | 2003-07-25 |
| 2003-09-28 | 2004-05-19 | |
| 2005-10-26 | 2006-06-21 | |
| 2006-11-14 | 2007-07-07 | |
| 2008-09-28 | 2009-06-18 | |
| 2009-09-29 | 2010-06-22 | |
| 2011-10-25 | 2012-05-21 | |
| 2012-10-10 | 2013-06-21 |
Appendix B


References
- Hetherington, A.M.; Woodward, F.I. The role of stomata in sensing and driving environmental change. Nature 2003, 424, 901–908. [Google Scholar] [CrossRef] [PubMed]
- Katul, G.G.; Palmroth, S.; Oren, R. Leaf stomatal responses to vapour pressure deficit under current and CO2-enriched atmosphere explained by the economics of gas exchange. Plant Cell Environ. 2009, 32, 968–979. [Google Scholar] [CrossRef] [PubMed]
- Sperry, J.S.; Venturas, M.D.; Anderegg, W.R.; Mencuccini, M.; Mackay, D.S.; Wang, Y.; Love, D.M. Predicting stomatal responses to the environment from the optimization of photosynthetic gain and hydraulic cost. Plant Cell Environ. 2017, 40, 816–830. [Google Scholar] [CrossRef] [PubMed]
- Betts, R.A.; Cox, P.M.; Lee, S.E.; Woodward, F.I. Contrasting physiological and structural vegetation feedbacks in climate change simulations. Nature 1997, 387, 796–799. [Google Scholar] [CrossRef]
- Betts, R.A.; Boucher, O.; Collins, M.; Cox, P.M.; Falloon, P.D.; Gedney, N.; Hemming, D.L.; Huntingford, C.; Jones, C.D.; Sexton, D.M. Projected increase in continental runoff due to plant responses to increasing carbon dioxide. Nature 2007, 448, 1037–1041. [Google Scholar] [CrossRef] [PubMed]
- Lemordant, L.; Gentine, P.; Swann, A.S.; Cook, B.I.; Scheff, J. Critical impact of vegetation physiology on the continental hydrologic cycle in response to increasing CO2. Proc. Natl. Acad. Sci. USA 2018, 115, 4093–4098. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Liu, S.; Abdul-Aziz, O.I. Hydrological effects of the increased CO2 and climate change in the Upper Mississippi River Basin using a modified SWAT. Clim. Chang. 2012, 110, 977–1003. [Google Scholar] [CrossRef]
- Zhao, J.; Feng, H.; Xu, T.; Xiao, J.; Guerrieri, R.; Liu, S.; Wu, X.; He, X.; He, X. Physiological and environmental control on ecosystem water use efficiency in response to drought across the northern hemisphere. Sci. Total Environ. 2021, 758, 143599. [Google Scholar] [CrossRef] [PubMed]
- Kannenberg, S.A.; Anderegg, W.R.; Barnes, M.L.; Dannenberg, M.P.; Knapp, A.K. Dominant role of soil moisture in mediating carbon and water fluxes in dryland ecosystems. Nat. Geosci. 2024, 17, 38–43. [Google Scholar] [CrossRef]
- Mencuccini, M.; Manzoni, S.; Christoffersen, B. Modelling water fluxes in plants: From tissues to biosphere. New Phytol. 2019, 222, 1207–1222. [Google Scholar] [CrossRef]
- Wu, J.; Serbin, S.P.; Ely, K.S.; Wolfe, B.T.; Dickman, L.T.; Grossiord, C.; Michaletz, S.T.; Collins, A.D.; Detto, M.; McDowell, N.G. The response of stomatal conductance to seasonal drought in tropical forests. Glob. Chang. Biol. 2020, 26, 823–839. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Liu, Z.; Guo, J.; Wang, Y.; Ma, J.; Yu, S.; Yu, P.; Xu, L. Estimate canopy transpiration in larch plantations via the interactions among reference evapotranspiration, leaf area index, and soil moisture. For. Ecol. Manag. 2021, 481, 118749. [Google Scholar] [CrossRef]
- Du, J.; Dai, X.; Huo, Z.; Wang, X.; Wang, S.; Wang, C.; Zhang, C.; Huang, G. Stand transpiration and canopy conductance dynamics of Populus popularis under varying water availability in an arid area. Sci. Total Environ. 2023, 892, 164397. [Google Scholar] [CrossRef] [PubMed]
- Stoy, P.C.; El-Madany, T.S.; Fisher, J.B.; Gentine, P.; Gerken, T.; Good, S.P.; Klosterhalfen, A.; Liu, S.; Miralles, D.G.; Perez-Priego, O. Reviews and syntheses: Turning the challenges of partitioning ecosystem evaporation and transpiration into opportunities. Biogeosciences 2019, 16, 3747–3775. [Google Scholar] [CrossRef]
- Wang, S.; Ibrom, A.; Bauer-Gottwein, P.; Garcia, M. Incorporating diffuse radiation into a light use efficiency and evapotranspiration model: An 11-year study in a high latitude deciduous forest. Agric. For. Meteorol. 2018, 248, 479–493. [Google Scholar] [CrossRef]
- Celis, J.; Xiao, X.; Basara, J.; Wagle, P.; McCarthy, H. Simple and Innovative Methods to Estimate Gross Primary Production and Transpiration of Crops: A Review. Digit. Ecosyst. Innov. Agric. 2023, 121, 125–156. [Google Scholar]
- Nelson, J.A.; Pérez-Priego, O.; Zhou, S.; Poyatos, R.; Zhang, Y.; Blanken, P.D.; Gimeno, T.E.; Wohlfahrt, G.; Desai, A.R.; Gioli, B. Ecosystem transpiration and evaporation: Insights from three water flux partitioning methods across FLUXNET sites. Glob. Chang. Biol. 2020, 26, 6916–6930. [Google Scholar] [CrossRef]
- Zhou, S.; Yu, B.; Zhang, Y.; Huang, Y.; Wang, G. Partitioning evapotranspiration based on the concept of underlying water use efficiency. Water Resour. Res. 2016, 52, 1160–1175. [Google Scholar] [CrossRef]
- Perez-Priego, O.; Katul, G.; Reichstein, M.; El-Madany, T.S.; Ahrens, B.; Carrara, A.; Scanlon, T.M.; Migliavacca, M. Partitioning eddy covariance water flux components using physiological and micrometeorological approaches. J. Geophys. Res. Biogeosci. 2018, 123, 3353–3370. [Google Scholar] [CrossRef]
- Nelson, J.A.; Carvalhais, N.; Cuntz, M.; Delpierre, N.; Knauer, J.; Ogée, J.; Migliavacca, M.; Reichstein, M.; Jung, M. Coupling water and carbon fluxes to constrain estimates of transpiration: The TEA algorithm. J. Geophys. Res. Biogeosci. 2018, 123, 3617–3632. [Google Scholar] [CrossRef]
- Pastorello, G.; Trotta, C.; Canfora, E.; Chu, H.; Christianson, D.; Cheah, Y.-W.; Poindexter, C.; Chen, J.; Elbashandy, A.; Humphrey, M. The FLUXNET2015 dataset and the ONEFlux processing pipeline for eddy covariance data. Sci. Data 2020, 7, 225. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Zhou, S.; Zhao, X.; Gao, X.; Jiang, K.; Zhang, B.; Cheng, L.; Song, X.; Siddique, K.H. Evapotranspiration partitioning based on leaf and ecosystem water use efficiency. Water Resour. Res. 2022, 58, e2021WR030629. [Google Scholar] [CrossRef]
- Zhou, S.; Yu, B.; Huang, Y.; Wang, G. Daily underlying water use efficiency for AmeriFlux sites. J. Geophys. Res. Biogeosci. 2015, 120, 887–902. [Google Scholar] [CrossRef]
- Wu, G.; Hu, Z.; Keenan, T.F.; Li, S.; Zhao, W.; Cao, R.C.; Li, Y.; Guo, Q.; Sun, X. Incorporating spatial variations in parameters for improvements of an evapotranspiration model. J. Geophys. Res. Biogeosci. 2020, 125, e2019JG005504. [Google Scholar] [CrossRef]
- Monteith, J.; Unsworth, M. Principles of Environmental Physics: Plants, Animals, and the Atmosphere; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Diefendorf, A.F.; Mueller, K.E.; Wing, S.L.; Koch, P.L.; Freeman, K.H. Global patterns in leaf 13C discrimination and implications for studies of past and future climate. Proc. Natl. Acad. Sci. USA 2010, 107, 5738–5743. [Google Scholar] [CrossRef] [PubMed]
- Buckley, T.N. How do stomata respond to water status? New Phytol. 2019, 224, 21–36. [Google Scholar] [CrossRef] [PubMed]
- Ficklin, D.L.; Novick, K.A. Historic and projected changes in vapor pressure deficit suggest a continental-scale drying of the United States atmosphere. J. Geophys. Res. Atmos. 2017, 122, 2061–2079. [Google Scholar] [CrossRef]
- Urban, J.; Ingwers, M.W.; McGuire, M.A.; Teskey, R.O. Increase in leaf temperature opens stomata and decouples net photosynthesis from stomatal conductance in Pinus taeda and Populus deltoides x nigra. J. Exp. Bot. 2017, 68, 1757–1767. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Gao, Y.; Yuan, X.; Yuan, M.; Huang, L.; Wang, S.; Liu, C.E.; Duan, C. Effects of heavy metals on stomata in plants: A review. Int. J. Mol. Sci. 2023, 24, 9302. [Google Scholar] [CrossRef]
- Driesen, E.; Van den Ende, W.; De Proft, M.; Saeys, W. Influence of environmental factors light, CO2, temperature, and relative humidity on stomatal opening and development: A review. Agronomy 2020, 10, 1975. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, F. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Sarker, I.H. Machine learning: Algorithms, real-world applications and research directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, W.W. Evolution of machine learning in environmental science—A perspective. Environ. Data Sci. 2022, 1, e3. [Google Scholar] [CrossRef]
- Ellsäßer, F.; Röll, A.; Ahongshangbam, J.; Waite, P.-A.; Schuldt, B.; Hölscher, D. Predicting tree sap flux and stomatal conductance from drone-recorded surface temperatures in a mixed agroforestry system—A machine learning approach. Remote Sens. 2020, 12, 4070. [Google Scholar] [CrossRef]
- Vitrack-Tamam, S.; Holtzman, L.; Dagan, R.; Levi, S.; Tadmor, Y.; Azizi, T.; Rabinovitz, O.; Naor, A.; Liran, O. Random forest algorithm improves detection of physiological activity embedded within reflectance spectra using stomatal conductance as a test case. Remote Sens. 2020, 12, 2213. [Google Scholar] [CrossRef]
- Houshmandfar, A.; O’Leary, G.; Fitzgerald, G.J.; Chen, Y.; Tausz-Posch, S.; Benke, K.; Uddin, S.; Tausz, M. Machine learning produces higher prediction accuracy than the Jarvis-type model of climatic control on stomatal conductance in a dryland wheat agro-ecosystem. Agric. For. Meteorol. 2021, 304, 108423. [Google Scholar] [CrossRef]
- Saunders, A.; Drew, D.M.; Brink, W. Machine learning models perform better than traditional empirical models for stomatal conductance when applied to multiple tree species across different forest biomes. Trees For. People 2021, 6, 100139. [Google Scholar] [CrossRef]
- Gaur, S.; Drewry, D.T. Explainable machine learning for predicting stomatal conductance across multiple plant functional types. Agric. For. Meteorol. 2024, 350, 109955. [Google Scholar] [CrossRef]
- Rubel, F.; Kottek, M. Observed and projected climate shifts 1901–2100 depicted by world maps of the Köppen-Geiger climate classification. Meteorol. Z. 2010, 19, 135. [Google Scholar] [CrossRef]
- Goulden, M. FLUXNET2015 BR-Sa3 Santarem-Km83-Logged Forest; FluxNet; University of California-Irvine: Irvine, CA, USA, 2016. [Google Scholar]
- Billesbach, D.; Bradford, J.; Torn, M. FLUXNET2015 US-AR1 ARM USDA UNL OSU Woodward Switchgrass 1; FluxNet; Lawerence Berkeley National Lab, US Department of Agriculture (USDA): Berkeley, CA, USA, 2016. [Google Scholar]
- Billesbach, D.; Bradford, J.; Torn, M. AmeriFlux FLUXNET-1F US-AR2 ARM USDA UNL OSU Woodward Switchgrass 2; Lawrence Berkeley National Laboratory (LBNL): Berkeley, CA, USA, 2023. [Google Scholar]
- Torn, M. FLUXNET2015 US-ARb ARM Southern Great Plains Burn Site-Lamont; FluxNet; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2016. [Google Scholar]
- Biraud, S.; Fischer, M.; Chan, S.; Torn, M. AmeriFlux FLUXNET-1F US-ARM ARM Southern Great Plains Site-Lamont; AmeriFlux; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2022. [Google Scholar]
- Matamala, R. FLUXNET2015 US-IB2 Fermi National Accelerator Laboratory-Batavia (Prairie Site); FluxNet; Argonne National Lab. (ANL): Argonne, IL, USA, 2016. [Google Scholar]
- Scott, R. AmeriFlux AmeriFlux US-SRM Santa Rita Mesquite; Lawrence Berkeley National Laboratory (LBNL): Berkeley, CA, USA, 2016. [Google Scholar]
- Ma, S.; Xu, L.; Verfaillie, J.; Baldocchi, D. AmeriFlux FLUXNET-1F US-Ton Tonzi Ranch; Lawrence Berkeley National Laboratory (LBNL): Berkeley, CA, USA, 2023. [Google Scholar]
- Zhang, K.; Zhu, G.; Ma, J.; Yang, Y.; Shang, S.; Gu, C. Parameter analysis and estimates for the MODIS evapotranspiration algorithm and multiscale verification. Water Resour. Res. 2019, 55, 2211–2231. [Google Scholar] [CrossRef]
- Jin, J.; Yan, T.; Wang, H.; Ma, X.; He, M.; Wang, Y.; Wang, W.; Guo, F.; Cai, Y.; Zhu, Q. Improved modeling of canopy transpiration for temperate forests by incorporating a LAI-based dynamic parametrization scheme of stomatal slope. Agric. For. Meteorol. 2022, 326, 109157. [Google Scholar] [CrossRef]
- BADM: Biological, Ancillary, Disturbance, and Metadata. Available online: https://ameriflux.lbl.gov/data/badm/ (accessed on 16 April 2024).
- Nelson, J. Jnelson18/Ecosystem-Transpiration: Additional Installation Instructions (v1.1). 2020. Available online: https://zenodo.org/records/3921923 (accessed on 1 January 2023). [CrossRef]
- Smith, M.; Allen, R.; Periera, L.; Raes, D. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Myneni, R.; Knyazikhin, Y.; Park, T. MODIS/Terra+Aqua Leaf Area Index/FPAR 4-Day L4 Global 500m SIN Grid V061; USGS: Sioux Falls, SD, USA, 2021. [CrossRef]
- Croft, H.; Chen, J.M.; Luo, X.; Bartlett, P.; Chen, B.; Staebler, R.M. Leaf chlorophyll content as a proxy for leaf photosynthetic capacity. Glob. Chang. Biol. 2017, 23, 3513–3524. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Zhu, R.; Zeng, D.; Kosorok, M.R. Reinforcement learning trees. J. Am. Stat. Assoc. 2015, 110, 1770–1784. [Google Scholar] [CrossRef] [PubMed]
- Zeppel, M.J.; Lewis, J.D.; Chaszar, B.; Smith, R.A.; Medlyn, B.E.; Huxman, T.E.; Tissue, D.T. Nocturnal stomatal conductance responses to rising [CO2], temperature and drought. New Phytol. 2012, 193, 929–938. [Google Scholar] [CrossRef] [PubMed]
- Chandra, S.P.; Adiga, V.; Chinmaya, P.; Kikkeri, V.V.; Senapati, S. Modulation of stomatal conductance in response to changes in external factors for plants grown in the tropical climate. J. High Sch. Sci. 2023, 7, 1–17. [Google Scholar]
- Kimm, H.; Guan, K.; Gentine, P.; Wu, J.; Bernacchi, C.J.; Sulman, B.N.; Griffis, T.J.; Lin, C. Redefining droughts for the US Corn Belt: The dominant role of atmospheric vapor pressure deficit over soil moisture in regulating stomatal behavior of Maize and Soybean. Agric. For. Meteorol. 2020, 287, 107930. [Google Scholar] [CrossRef]
- Rana, M.S.; Rath, J.R.; Reddy, C.V.; Pelzang, S.; Shelke, R.G.; Patel, S. Ecotypic adaptation of plants and the role of microbiota in ameliorating the environmental extremes using contemporary approaches. In Rhizobiome; Elsevier: Amsterdam, The Netherlands, 2023; pp. 377–402. [Google Scholar]
- Xu, J.; Wu, B.; Ryu, D.; Yan, N.; Zhu, W.; Ma, Z. Quantifying the contribution of biophysical and environmental factors in uncertainty of modeling canopy conductance. J. Hydrol. 2021, 592, 125612. [Google Scholar] [CrossRef]
- Hao, Z.; Geng, X.; Wang, F.; Zheng, J. Impacts of climate change on agrometeorological indices at winter wheat overwintering stage in Northern China during 2021–2050. Int. J. Climatol. 2018, 38, 5576–5588. [Google Scholar] [CrossRef]
- Feng, X.; Liu, H.; Feng, D.; Tang, X.; Li, L.; Chang, J.; Tanny, J.; Liu, R. Quantifying winter wheat evapotranspiration and crop coefficients under sprinkler irrigation using eddy covariance technology in the North China Plain. Agric. Water Manag. 2023, 277, 108131. [Google Scholar] [CrossRef]
- Bishop, C. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Wu, B.-J.; Chow, W.S.; Liu, Y.-J.; Shi, L.; Jiang, C.-D. Effects of stomatal development on stomatal conductance and on stomatal limitation of photosynthesis in Syringa oblata and Euonymus japonicus Thunb. Plant Sci. 2014, 229, 23–31. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Ma, X.; Dou, X.; Zhu, J.; Zhao, C. Impacts of climate change on vegetation phenology and net primary productivity in arid Central Asia. Sci. Total Environ. 2021, 796, 149055. [Google Scholar] [CrossRef] [PubMed]
- Launiainen, S.; Katul, G.G.; Kolari, P.; Lindroth, A.; Lohila, A.; Aurela, M.; Varlagin, A.; Grelle, A.; Vesala, T. Do the energy fluxes and surface conductance of boreal coniferous forests in Europe scale with leaf area? Glob. Chang. Biol. 2016, 22, 4096–4113. [Google Scholar] [CrossRef] [PubMed]
- Roberts, J. Forest transpiration: A conservative hydrological process? J. Hydrol. 1983, 66, 133–141. [Google Scholar] [CrossRef]
- Fang, H.; Wei, S.; Jiang, C. Intercomparison and uncertainty analysis of global MODIS, cyclopes, and GLOBCARBON LAI products. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 5959–5962. [Google Scholar]



| Site ID | Latitude (°N) | Longitude (°E) | Climate Type | Plant Functional Type | Measurement Height (Z, m) | Depths1 (cm) | Depth2 (cm) | Temporal Cover |
|---|---|---|---|---|---|---|---|---|
| BR-Sa3 [41] | −3.0180 | −54.9714 | Am | EBF | 64 | 10 | 20 | 2000–2004 |
| US-AR1 [42] | 36.4267 | −99.4200 | Dsa | GRA | 2.84 | 10 | 30 | 2009–2012 |
| US-AR2 [43] | 36.6358 | −99.5975 | Dsa | GRA | 2.95 | 10 | 30 | 2009–2012 |
| US-Arb [44] | 35.5497 | −98.0402 | Cfa | GRA | 3.45 | 10 | 30 | 2005–2006 |
| US-ARM [45] | 36.6058 | −97.4888 | Cfa | CRO | 4.28 | 10 (5 before 13 April 2005) | 20 (25 before 13 April 2005) | 2002–2013 |
| US-IB2 [46] | 41.8406 | −88.2410 | Dfa | GRA | 3.76 | 2.5 | 10 | 2004–2011 |
| US-SRM [47] | 31.8214 | −110.8661 | BSk | WSA | 7.82 | 2.5 | 12.5 | 2004–2014 |
| US-Ton [48] | 38.4309 | −120.9660 | Csa | WSA | 23 | surface | 20 | 2001–2014 |
| Period | Method | SWC1 | SWC2 | VPD | TA | RH | WS | CO2 | Rn | Rg |
|---|---|---|---|---|---|---|---|---|---|---|
| Growing | uWUE | 0.8116 | 1.1922 | 1.0090 | 1.1558 | 1.2629 | 0.8127 | 0.4957 | 1.1381 | 0.9938 |
| Perez-Priego | 0.9903 | 0.8785 | 0.8077 | 1.2641 | 0.5956 | 0.1992 | 0.4172 | 1.0697 | 0.8140 | |
| TEA | 1.1261 | 1.0491 | 1.2467 | 1.1335 | 0.9460 | 0.8015 | 0.5262 | 1.4220 | 1.0293 | |
| Overwintering | uWUE | 0.1521 | 0.2328 | 0.3372 | 0.2324 | 0.2226 | 0.6757 | 0.4982 | −0.0184 | −0.0024 |
| Perez-Priego | 0.3937 | 0.2208 | 0.5302 | 0.5693 | 0.1855 | −0.0222 | 0.1035 | 0.0186 | 0.1759 | |
| TEA | 0.2525 | 0.3437 | 0.5123 | 0.5632 | 0.3119 | 0.7706 | 0.3355 | 0.2498 | 0.4221 |
| Period | Data Set | R2 | RMSE (mm/s) | ||||
|---|---|---|---|---|---|---|---|
| uWUE | Perez-Priego | TEA | uWUE | Perez-Priego | TEA | ||
| Growing | Train | 0.7478 | 0.7691 | 0.7781 | 0.4186 | 0.1503 | 0.4278 |
| Test | 0.5173 | 0.6106 | 0.5738 | 0.5644 | 0.2020 | 0.6077 | |
| Overwintering | Train | 0.5863 | 0.6680 | 0.6397 | 0.1317 | 0.0479 | 0.1832 |
| Test | 0.3114 | 0.6444 | 0.3415 | 0.1708 | 0.4896 | 0.2963 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, R.; Zuo, W.; Zheng, Z.; Han, Q.; Shi, J.; Zhang, Y.; Qiu, J.; Wang, S.; Zhu, Y.; Cao, W.; et al. Interpreting Controls of Stomatal Conductance across Different Vegetation Types via Machine Learning. Water 2024, 16, 2251. https://doi.org/10.3390/w16162251
Xue R, Zuo W, Zheng Z, Han Q, Shi J, Zhang Y, Qiu J, Wang S, Zhu Y, Cao W, et al. Interpreting Controls of Stomatal Conductance across Different Vegetation Types via Machine Learning. Water. 2024; 16(16):2251. https://doi.org/10.3390/w16162251
Chicago/Turabian StyleXue, Runjia, Wenjun Zuo, Zhaowen Zheng, Qin Han, Jingyan Shi, Yao Zhang, Jianxiu Qiu, Sheng Wang, Yan Zhu, Weixing Cao, and et al. 2024. "Interpreting Controls of Stomatal Conductance across Different Vegetation Types via Machine Learning" Water 16, no. 16: 2251. https://doi.org/10.3390/w16162251
APA StyleXue, R., Zuo, W., Zheng, Z., Han, Q., Shi, J., Zhang, Y., Qiu, J., Wang, S., Zhu, Y., Cao, W., & Zhang, X. (2024). Interpreting Controls of Stomatal Conductance across Different Vegetation Types via Machine Learning. Water, 16(16), 2251. https://doi.org/10.3390/w16162251








