Numerical Simulation Analysis of the Correlation between Hydrodynamic Noise of Hydraulic Turbines and Defects in Runner Blades

Abstract

To investigate the hydrodynamic noise characterization of hydraulic turbines with runner blade defects, this article establishes the intact machine model and three kinds of models with runner blade defects. Using the Computational Fluid Dynamic (CFD) and Computational Acoustic (CA) hybrid simulation computational methods, the hydrodynamic noise field of the hydraulic turbine is numerically simulated, and the results of the acoustic near field and acoustic far field are shown. 1. The double-row leaf grille and the runner are the primary sound source areas of the hydraulic turbine, and the intensity of sound radiation from these areas is positively correlated with the degree of runner blade defects. 2. As the runner blade defects develop, the sound power level (SWL) increases more significantly in the guide vanes near the nose of the spiral case in the double-row leaf grille. The most pronounced increase in the SWL is observed at the defective craters on the runner blades. 3. The frequency of the defective noise signal is primarily concentrated in the low-frequency band. The dominant frequency amplitude associated with runner blade defects increases and rises after the occurrence of defects. Secondary frequency changes are also observed, and the location of these changes varies at different receiving points.

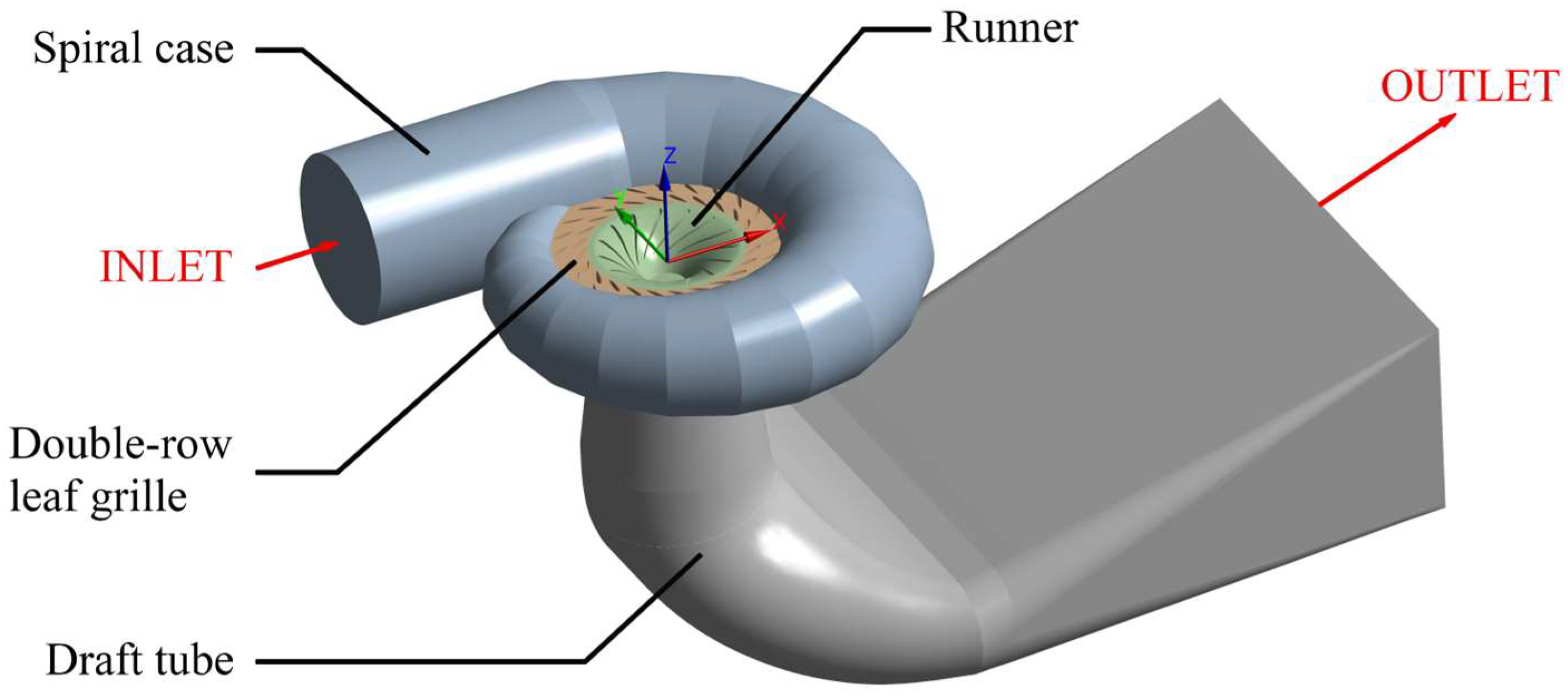
1. Introduction

Factors affecting the operation of hydraulic turbines mainly include overspeed, vibration, cavitation, sediment abrasion, etc., and in serious cases, they will lead to structural defects in the machine. As the runner is the main rotating power output component of the hydraulic turbine, its structural defect will not only reduce the power generation efficiency but also affect the operation stability of the hydraulic turbine. In practice, runner defects are mainly caused by abrasion and cavitation phenomenon [1]; sediment and other impurities of excessive water flow will cause serious abrasion on the surface of the runner blades, and cavitation formed by the collapse of the vacuole will also cause erosion of the overflow surface, which will result in the formation of defects of varying sizes and shapes of the form. The defects on the overflow surface of the Francis turbine generally occur in the lower half of the suction surface of the runner blade at the water outlet side, and the specific characteristics are shown in Figure 1 [2,3]. The local area with pockmarks and pits on the surface of the runner blade due to the defects seriously reduces the smoothness of the fluid flow. In addition to defects in the structure of the turbine machine set, the phenomena of wear and cavitation will greatly increase the noise generated during operation, which will have a serious impact on the physical and mental health of the power station personnel [4].

Abnormal noise in hydraulic turbines usually signals the occurrence of malfunction, so the research of hydraulic turbine hydrodynamic noise has a broad application prospect. Noise in hydraulic turbines is mainly radiated noise induced by fluid–solid interactions, as well as by interactions between fluid molecules [5], the former of which is also known as flow-induced noise. Wang [6] et al. used different numbers of blades as the research variable and conducted numerical calculations of the sound field in a centrifugal pump using a hybrid simulation method combining Computational Fluid Dynamics (CFD) and Computational Acoustics (CA). The results showed that the vane tongue is the main noise source of the centrifugal pump. The sound pressure level of the model pump decreased first and then increased as the number of blades increased. It reached its minimum value at six blades and was verified by noise experimental tests to confirm the accuracy of the combined calculation method. Dang [7] et al. predicted the noise induced by pressure fluctuations on the surface of the turbine blades by combining the Large Eddy Simulation (LES) with the Ffowcs, Williams, and Hawkings acoustic analogy formulae, and compared the power coefficients with the experimental results, which achieved good consistency and verified the reliability of this simulation and computation method. Li [8] et al. numerically simulated the noise induced by an underwater submarine and found that the streaming noise at the same frequency is higher than the flow noise, and the acoustic monitoring point closer to the solid boundary has a higher acoustic signal intensity. Yang [9] et al. used a combination of CFD and CA to numerically solve the flow field and internal acoustic field in a pump unit and found that the runner is the main source of hydrodynamic noise inside the pump. Ren [10] et al. numerically calculated the structural vibration noise of underwater vehicles and found that the hydrodynamic noise is mainly generated by the turbulent fluctuating pressure excitation, the dominant frequency is mainly concentrated in the low-frequency range, and the radiation intensity of the noise is in line with the intrinsic vibration characteristics of the machinery. Yang [11] et al. analyzed and compared the contribution of the spiral case, guide vane, and runner to the internal noise of the mixed-flow pump through hybrid simulation calculations of CFD and CA. The study shows that the runner is the main noise source of the mixed-flow pump, and the internal noise is mainly in the low-frequency range. Wang [12] et al. carried out acoustic numerical simulation of hydraulic turbine based on the Ffowcs, Williams, and Hawkings integral method, and through the study of its acoustic distribution, acoustic spectrum, and acoustic directivity, it was found that the noise signal was mainly caused by the passing frequency of the blades, especially the first-order frequency, which had a low frequency and broad band, and the noise radiation from blades has distinct dipole properties in the flow direction.Yu [13] et al. simulated the far-field noise of an autonomous underwater vehicle, and the results showed that the irregular vibration of the propeller triggers a small increase in noise, which shows that the unsteady operation of the machinery is a non-negligible factor in the study of the variation of the flow noise characteristics. Zhang [14] et al. explored the causes and specific locations of the flow noise in a Francis turbine through acoustic numerical simulation based on the sound power level assessment method by comparing the experimental and simulated values. Overall, the noise is strongest at the edge of the blade inlet in the flow channel, and the flow noise in the draft tube is strongest in relation to the rotating flow. He [15] et al. studied the flow characteristics and hydrodynamic noise characteristics inside the centrifugal pump in depth after simulation calculations and found that the radiation of hydrodynamic noise mainly originates from the pressure fluctuation of the inner wall of the pump. Xu [16] et al. found through acoustic numerical simulations of axial flow pumps that the radiated noise of the axial flow pump exhibits dipole characteristics under the blade frequency in all flow conditions and the sound pressure level increases with the increase in the flow rate. Si [17] et al. simulated the centrifugal pump noise, and the results show that the centrifugal pump noise radiation has significant dipole characteristics, and with the change in the flow rate in the flow field, the intensity and directivity of the sound source also changed accordingly. Mao [18] et al. simulated and solved the flow-induced noise of the pump turbine and found that the sound source radiation of the acoustic field is highly consistent with the internal flow characteristics of the flow field; its radiation intensity is affected by the pressure pulsation frequency and the unit’s intrinsic frequency, and the distribution of the radiation of the acoustic source can also reflect the development of the flow field. It can be seen that the research on hydrodynamic noise has become more and more perfect, and most studies use numerical simulation methods to explore the cause and development law of hydrodynamic noise inside hydraulic machinery. However, most of the research objects are pumps and model machines, and the research on the hydrodynamic noise of prototype turbines is still relatively lacking, which needs to be supplemented to provide more practical and feasible engineering guidance for hydropower stations. Meanwhile, with the change in turbine flow conditions, the main noise signals are located in the low-frequency band, and the corresponding spectral change characteristics also lack a more detailed study. This aspect should be supplemented, and the captured change pattern of the signals will be of great benefit to the condition monitoring of the hydraulic turbine.

In addition, for the faults existing in the hydraulic turbine operation, the power station usually carries out regular maintenance, but this cannot find the faults in time and eliminate them, and scholars have found that the hydraulic turbine has been running in a faulty state for a long time long before the maintenance period [19,20]. In order to be able to give timely information about faults, the monitoring of turbine faults using noise signals has received more and more attention in recent years [21]; moreover, acoustic monitoring methods have significant advantages in practical engineering due to their simplicity. Power stations do not need to use expensive, high-quality vibration sensors, and the acoustic sensors themselves do not need to be installed and calibrated, which greatly saves O&M costs [22]. However, structural defects occurring inside the turbine are difficult to observe, and often, the defects are already very serious when they are detected, so in practice, it is difficult to extract the abnormal noise in the defective state, especially the noise signals corresponding to the different stages in the development of the defects. Based on this, this article concludes that the numerical simulation of hydraulic turbines in different defective states is a feasible means to study the hydrodynamic noise characteristics corresponding to different defective degrees.

Therefore, in this paper, with reference to the parts and shapes of runner blade defects in Figure 1, we establish three kinds of runner blade defect models, carry out acoustic numerical simulations together with the intact model, compare and analyze the change rule of the hydrodynamic noise characteristics corresponding to different defects of the runner blades, and monitor the change characteristics of the noise signals with the deepening of the runner defects so as to discover the defect failures of the turbine and reduce the overhauling cost. In this way, defective turbine faults can be detected in a timely manner, thus reducing maintenance costs and ensuring power generation efficiency.

2. Numerical Simulation Modeling

2.1. Modeling of Hydraulic Turbine Integrity

Referring to the HLA855a-LJ-250 Francis turbine for calculation modeling, the rated output of the turbine is 44.3 MW and the installation elevation is 2081.8 m. The number of stay vanes and guide vanes is 24, and the rated opening of guide vanes is 128.34 mm. The diameter of the runner inlet is 2500 mm, the diameter of the runner outlet is 2353 mm, the number of blades is 15, the width of the runner blades is 1.014 m at the hub, 1.023 m in the center, and 1.032 m at the blade rows, the height of the inlet side of the runner blades is 0.638 m, the height of the outlet side is 0.989 m, and the surface area of the individual blades is 1.537 m², of which the suction surface is 0.794 m². The top view of the runner rotates in a clockwise direction. The rated operating conditions of the unit were selected for the simulation, and the corresponding turbine operating parameters are shown in

Table 1. Operating parameters of hydraulic turbines at rated operating conditions.

Parameter	Rated Head (Hr)	Rated Runner Speed (nr)	Inlet Flow Velocity (v)
Value	106 m2	300 r/min	7.436 m/s

.

The numerical simulation domain is the flow area of the fluid in the turbine and is divided into four parts, namely, the spiral case, the double-row leaf grille (including the stay vane and the guide vane), the runner, and the draft tube. The 3D modeling of the hydraulic turbine was carried out using SolidWorks; the model dimensions were basically the same as the actual dimensions of the hydraulic turbine, and the modeling is shown in Figure 2.

2.2. Modeling of Runner Blade Defect States

Name the intact model as M1. Based on the hydraulic turbine field maintenance example in Figure 1, with reference to the occurrence parts and area of the defective damage of the runner blades and the pattern of development of deficiencies, the defective damage occurring in the runner blades is divided into three different stages, which corresponds to the establishment of 3 different defective states of the runner blade model, and according to the degree of the defect, from low to high, the defective model will be named M2, M3, and M4. The runner blade defect parameters in the 4 models used for simulation are shown in

Table 2. Runner blade defect parameters in each model.

Models	Total Defect Area	Percentage of Defect Area on Suction Surface	Maximum Defect Depth
M1	0 m2	0%	0 mm
M2	0.093 m2	0.78%	5.0 mm
M3	0.219 m2	1.84%	7.5 mm
M4	0.289 m2	2.43%	10.0 mm

Note: The total area of the suction surface of the runner blades is 11.91 m².

. In Table 2, it can be seen that from M1 to M4, the defective area of the runner blades is gradually increasing, and the depth is also gradually deepening.

The data in Table 2 are reference data for the modeling of the runner defective blades. Referring to the previous overhaul examples and related studies, it can be seen that, in this study, the defects in the model were mainly in the form of pits, located on the outflow edge of the suction surface of the rotor blades, while the rest of the model remained in the same and intact condition. The defects of the runner blades in the model are shown in Figure 3, and it can be seen that there is no defect damage in M1, while the degree of defects increases in M2, M3, and M4 in that order. The number of defect pits also gradually increased, and the pits gradually connected to form a larger defect area on the blade.

2.3. Mesh-Independent Verification

Ansys Meshing was used to mesh each of the 4 models separately, using tetrahedral unstructured mesh drawing and ensuring that the mesh size of each model was the same. The turbine components are meshed individually, the internal interfaces share topology, and the mesh is encrypted for defective craters, vanes, and runner blades to capture finer turbulent motions and ensure the accuracy of the acoustic calculation results. The computational domain meshing is shown in Figure 4.

The selection of actual operating parameters for the rated condition of the turbine, mesh-independent verification is carried out using the area-weighted average of the surface sound power level of the runner as a metric, as shown in Figure 5. When the number of meshes of M1, M2, M3, and M4 reached 6.63 million, 6.45 million, 6.55 million, and 6.72 million, respectively, with the continued increase in the number of meshes, the maximum value of the change in the sound power level of the four models did not exceed 0.10%, and the change tended to be stable. Following the principle of maximally utilizing computational resources and saving solution time, it is considered that the mesh-independence requirement has been met at this point.

The modeling and calculation conditions in this paper are selected with reference to the relevant data of hydraulic turbines in reality, and the calculation results of the model that has passed the mesh-independence validation will also be used for analysis in the latter part of this paper to ensure the accuracy and reliability of the simulation calculation results. The computational mesh selection for each model is shown in

Table 3. Calculation mesh selection.

Models	Mesh Quantity	Number of Mesh Nodes	Average Orthogonal Mass
M1	6,639,143	1,232,114	0.87
M2	6,458,123	1,201,798	0.87
M3	6,552,869	1,219,586	0.86
M4	6,721,478	1,242,735	0.85

, and for the four models, the mesh cell size set in the software was 0.14 m for the spiral case, 0.07 m for the double-row leaf grille, 0.035 m for the runner, and 0.14 m for the draft tube.

3. Numerical Simulation Methods

The simulations used Fluent with the CFD and CA hybrid simulation computational methods. The steady solution is carried out first, and after obtaining the stable flow field calculation result, the transient solution is carried out again using this result as the initial condition. The steady-state calculations are performed using the Realizable k − ε turbulence model, which imposes some constraints on the positive stress terms as a way of making the calculations more accurate and applicable to a wider range of flow types for the case of large time-averaged strain rates. The transport equations for the model are expressed as follows:

$$\rho \frac{\partial k}{\partial t}+\rho \frac{\partial (k{u}_i)}{\partial x_i}=\frac{\partial }{\partial x_j}\left[\left(u+\frac{u_t}{{\sigma }_k}\right)\frac{\partial k}{\partial x_j}\right]+G_k-\rho \epsilon$$

(1)

$$\rho \frac{\partial \epsilon }{\partial t}+\rho \frac{\partial (\epsilon u_i)}{\partial x_i}=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{u_t}{{\sigma }_{\epsilon }}\right)\frac{\partial \epsilon }{\partial x_j}\right]+\rho C_{1}E\epsilon -\rho C_2\frac{{\epsilon }^2}{k+\sqrt{v\epsilon }}$$

(2)

$$G_k={\nu }_t\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)\frac{\partial u_i}{\partial x_j}$$

(3)

$${\nu }_t=\rho C_{\mu }\frac{k^2}{\epsilon }$$

(4)

In the formula, ρ is the density of the fluid; k is the turbulent kinetic energy; ε is the turbulent dissipation rate; t is time; x_i and x_j are the coordinate tensors (i, j = 1, 2, 3, …); u is the flow velocity; u_i and u_j are the flow velocity tensors; G_k is the turbulent kinetic energy generated by the velocity gradient; ν_t is the turbulent eddy viscosity coefficient; C_μ = 0.09; σ_k and σ_ε are the turbulent Prandtl numbers for k and ε, respectively, and σ_k = 1.0, σ_ε = 1.3; C₁ = max(0.43, η/η + 5); C₂ = 1.9.

Steady calculations were performed while using a Broadband Noise Source model to solve for the turbine near-sound field. The Broadband Noise Source model is derived based on the acoustic analog equation; the most classical form of the acoustic analog is as follows:

$$\frac{{\partial }^2}{\partial t^2}\left(\rho -{\rho }_0\right)-c_0^2\frac{{\partial }^2}{\partial x_i\partial x_j}\left(\rho -{\rho }_0\right)=\frac{{\partial }^2{T}_{ij}}{\partial x_i\partial x_j}$$

(5)

In the formula, (ρ − ρ₀) is the value of fluid density change; c₀ is the speed of sound; and T_ij is the Lighthill tensor, which is defined as follows:

$$T_{ij}=\rho u_i{u}_j+\left[\left(p-p_0\right)-c_0^2\left(\rho -{\rho }_0\right)\right]{\delta }_{ij}-{\tau }_{ij}$$

(6)

In the formula, (p − p₀) is the value of fluid pressure change; τ_ij is the viscous stress term (ignoring the Reynolds stress); and δ_ij is the Kronecker function, δ_ij = [1 (i = j), 0 (i ≠ j)].

Based on the acoustic analogy theory, in the Broadband Noise Source model, the sound power generated per unit volume in the sound field can be expressed by the following formula:

$$W=\alpha {\rho }_0\left(\frac{u^3}{l}\right)\frac{u^5}{c_0^5}$$

(7)

In the formula, α is the model constant and l is the feature-length scale.

The acoustic energy in the turbulent flow field of the hydraulic turbine satisfies the continuous distribution condition in a wide frequency range, so the Broadband Noise Source model can be used for the near-field noise calculation of the machine, and the sound power level (SWL) is used to judge the main source radiation area in the model and the size of its source radiation capacity. The SWL indicates the size of the sound energy radiated by the sound source per unit of time, which is not affected by the distance, location, and environment of the sound source, and the larger the SWL is, the stronger the ability of the sound source to emit sound. The SWL is calculated by the following formula:

$$\mathrm{SWL}=10\lg \frac{W}{W_0}$$

(8)

In the formula, W is the actual effective sound power measured and W₀ is the reference sound power; in the present study, take 10⁻¹² W. The sound power level in the following text is also expressed uniformly in terms of the SWL.

After the steady solutions, the near-field sound source results are extracted and replaced with a new turbulence model and acoustic model for the transient solutions. The turbulence model was replaced with the Large Eddy Simulation (LES) model, and the control formulae are as follows:

$$\frac{\partial \overline{u_i}}{\partial t}+\frac{\partial \overline{u_i}\overline{u_j}}{\partial x_i}=-\frac{1}{\rho }\frac{\partial \overline{p}}{\partial x_i}+v\frac{{\partial }^2{u}_i}{\partial x_i{x}_j}+\frac{\partial {\tau }_{ij}}{\partial x_j}$$

(9)

In the formula, $\overline{u_i}$ and $\overline{u_j}$ are the time-averaged flow velocities; $\overline{p}$ is the time-averaged pressure; and τ_ij is the sublattice stress mathematical model. In this study, the Smargorinsky–Lilly model was used with the following formula:

$${\tau }_{ij}=2V_{t}T\overline{S_{ij}}+\frac{1}{3}{\delta }_{ij}{\tau }_{ij}$$

(10)

$$V_t=C_S{\Delta }^2{\left(2\overline{S_{ij}}\cdot \overline{S_{ij}}\right)}^{0.5}$$

(11)

$$\overline{S_{ij}}=0.5\left[\left(\frac{\partial \overline{u_i}}{\partial x_i}\right)+\left(\frac{\partial \overline{u_j}}{\partial x_i}\right)\right]$$

(12)

In the formula, C_S is the constant, usually taken as 0.18. By substituting the expression of the sublattice stress term into Formula (9), the sublattice stress term is closed, and thus the LES control equation with the sublattice stress term used in this simulation can be obtained. The LES is a numerical simulation method between the Direct Numerical Simulation (DNS) and Reynolds averaging, which requires less computational resources than the DNS and gives more accurate results than Reynolds averaging. The acoustic model used for the transient solution is the Ffowcs, Williams, and Hawkings (FW-H) equations, which are controlled by the following equations:

$$\frac{1}{c_0^2}\frac{{\partial }^2}{\partial t^2}\left[pH\left(f\right)\right]-{\nabla }^2\left[pH\left(f\right)\right]=\frac{\partial }{\partial t}\left[{\rho }_0{V}_i\frac{\partial f}{\partial x_i}\delta \left(f\right)\right]-\frac{\partial }{\partial x_i}\left[p_{ij}\frac{\partial f}{\partial x_j}\delta \left(f\right)\right]+\frac{{\partial }^2}{\partial x_i\partial x_j}\left[H\left(f\right)T_{ij}\right]$$

(13)

The FW-H equation can be applied in the presence of solid boundary flows and is the most widely used form of acoustic analogy. In the formula $p=c_0^2{\rho }^{\prime }$, H(f) is the Heaviside generalization function and ∇ is the laplace operator. The FW-H equations are suitable for solving most sound fields, especially turbine sound fields undergoing rotational motion. The sound pressure level (SPL) is used as the evaluation index of the far-field acoustic signal obtained from the transient solution, and the SPL calculation formula is as follows:

$$\mathrm{SPL}=20\lg \frac{p}{p_0}$$

(14)

In the formula, p is the actual effective sound pressure measured and p₀ is the reference sound pressure; in the present study, take 2 × 10⁻⁵ Pa. The sound pressure levels in the following text are also expressed uniformly in terms of the SPL.

Therefore, the specific steps of numerical simulation in this paper are, firstly, using the Realizable k − ε turbulence model for steady calculations. Then, turn on the Scalable Wall Functions (SWF) and, using the Broadband Noise Source Model, set the velocity inlet and the pressure outlet. The steady residual convergence criterion is 0.001, and the pressure–velocity coupling methods use SIMPLE; the spatial discrete formats are all second order. Perform transient calculations by switching to the FW-H acoustic model, setting the runner blades as the sound source area, and the signal is written out at a frequency of 1 Hz. Switching to the LES model with the Smagorinsky–Lilly subgrid scale model, the transient residual convergence criterion is 0.00001, and the pressure–velocity coupling methods use PISO. Set the second-order time term format, where the time step is taken as 0.00005 s, the total time step is 20,000, the total computation time is 1 s, and the maximum frequency of the acoustic signal is 10,000 Hz.

4. Near-Field Sound Source Characterization

Extract the SWL radiated by each overcurrent component on the x-coordinate axis, as shown in Figure 6. The SWL of the double-row leaf grille and the runner is significantly higher than the other components, followed by the draft tube, and the spiral case is the lowest. The water flow in the spiral case to the inlet of the double-row leaf grille shows a significant increase in the SWL, which shows that the increase in flow field resistance is one of the reasons for the increase in the SWL. The generation of defective pits makes the surface of the runner blades more and more uneven, and the protruding and concave parts exacerbate the collision between the water flow and the foliage surface, which is an important reason for the increase in the resistance of the flow field in this study.

There is some overlap in the distribution of the SWL of the double-row leaf grille and the runner in each model, as shown in Figure 6a (M1). With the deepening of the runner blade defects, the SWL peaks at some locations, and the runner showed a sudden increase. The higher the defects of the runner blades were, the more serious the sudden change in the SWL peaks. The x-coordinate intervals of the higher SWL in the draft tube correspond to the straight cone part versus the elbow part area, and it is evident that the flow produces a higher SWL on the downstream side and a lower SWL after flowing out of the elbow part. Therefore, the narrowing of the flow path is also a cause of the elevated SWL.

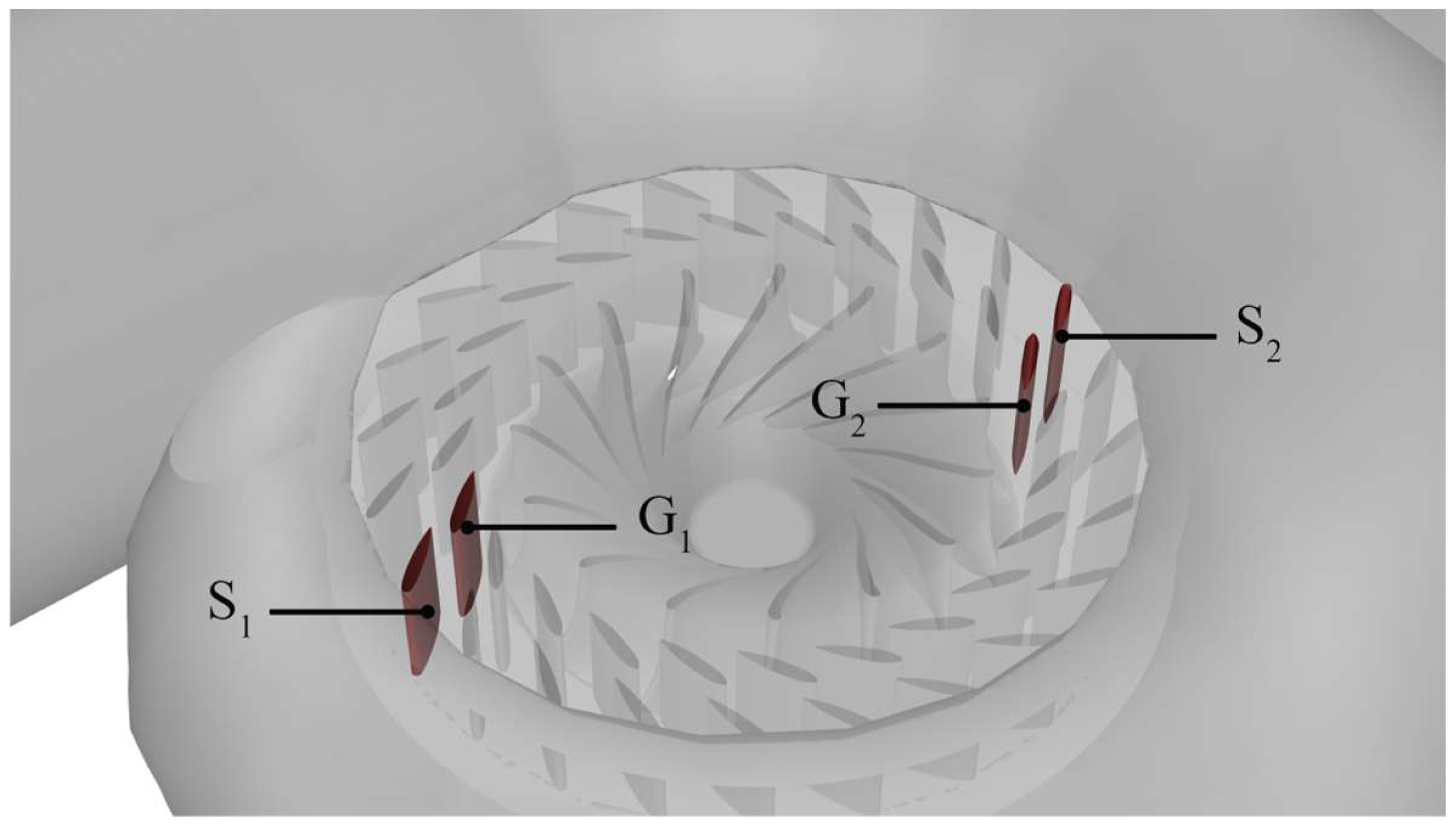
The narrow flow channel at the nose of the spiral case can likewise have an impact on water flow. As illustrated in Figure 7, the stay vane S₁ and the guide vane G₁ are marked in the double-row leaf grille near the nose of the spiral case and labeled S₂ and G₂, respectively, in opposite directions around their circumferences, and the extraction method is consistent in each model.

The distribution of the SWL on the leaf surface of S₁ and S₂ is shown in Figure 8. The SWL distribution between the pressure and suction surfaces of the stay vane is not significantly different, and the SWL is higher at the water inlet side. From the top, the SWL grows first, decreases to the middle of the leaf surface, grows again later, and decreases again to the bottom, and the overall presentation is symmetrically distributed along the horizontal centerline of the leaf surface, with distinct dipole source features. The intensity of SWL radiation in S₁ is significantly higher than that in S₂, and with the gradual increase in model deficiencies, the SWL of S₁ grows in parallel, and the radiation of the sound source shows a positive correlation with the deficiencies; in contrast, the SWL changes in S₂ are very weak.

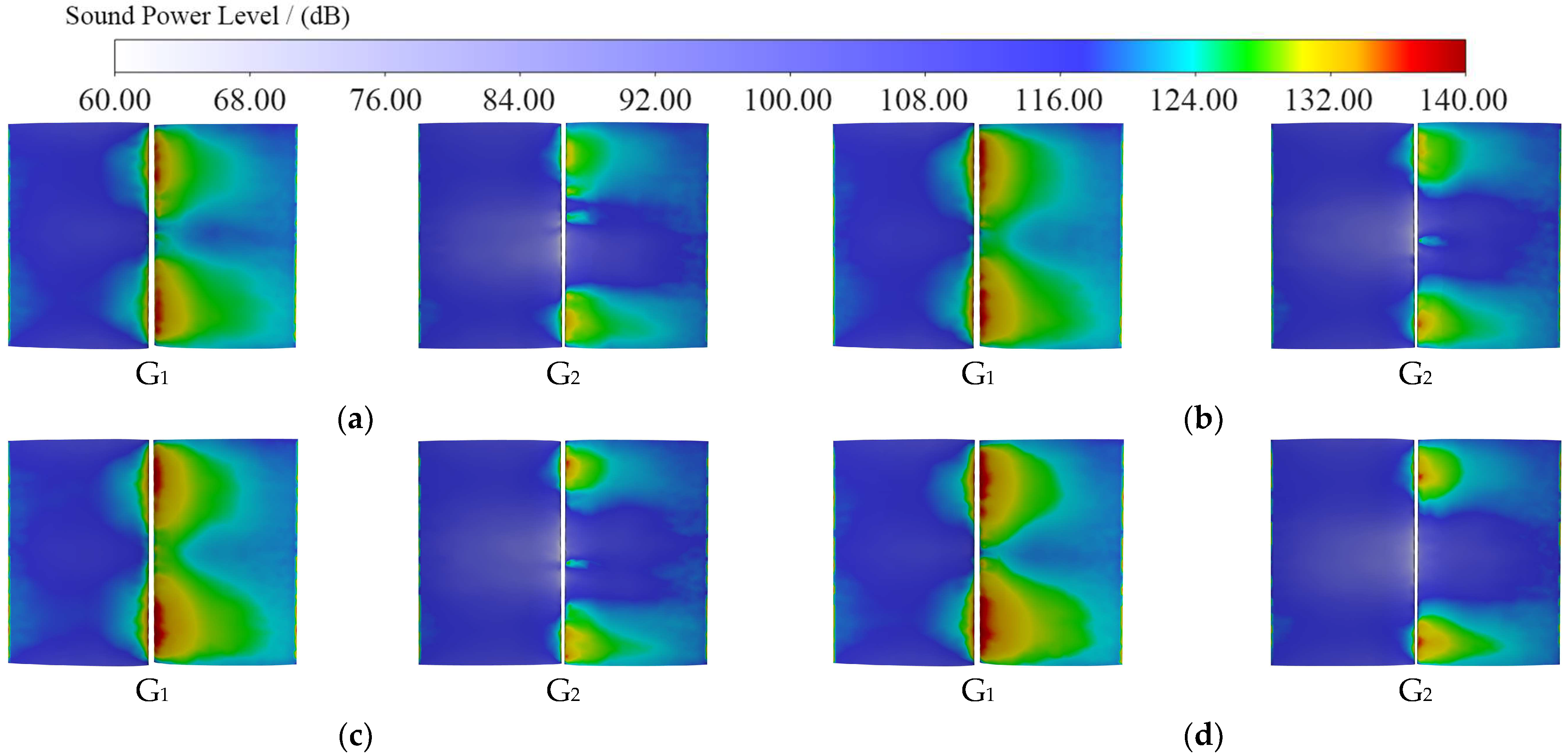
Then, the SWL distribution on the leaf surface of the guide vanes G₁ and G₂ was extracted, as illustrated in Figure 9. The SWL distribution of the guide vane is roughly the same as the stay vane; however, the SWL intensity of the suction side of the guide vane was significantly higher than that of the pressure side, and the overall source intensity of the guide vane was higher than that of the stay vane; the SWL strength of G₁ near the nose of the spiral case is higher than the SWL strength of G₂ opposite its circumference. Moving from M1 to M4, the radiation of the SWL on the surface of the guide vane is enhanced, and the guide vane is more pronounced than the stay vane. Consequently, during the development of the runner blade defects, the strongest and most pronounced changes in the sound source were observed in the double-row leaf grille in the guide vane, especially close to the region of the nose of the spiral case.

The magnitude of change in the SWL in the double-row leaf grille region was not large in the different models. This may be due to the fact that the defects are mainly located in the runner region, and the increase in flow resistance in the flow field can hardly affect the double-row leaf grille region located upstream. However, the inlet side of the movable guide vane still produces corresponding changes, so it can be seen that the defective runner blade still induces some degree of changes in the acoustic near-field characteristics of other components.

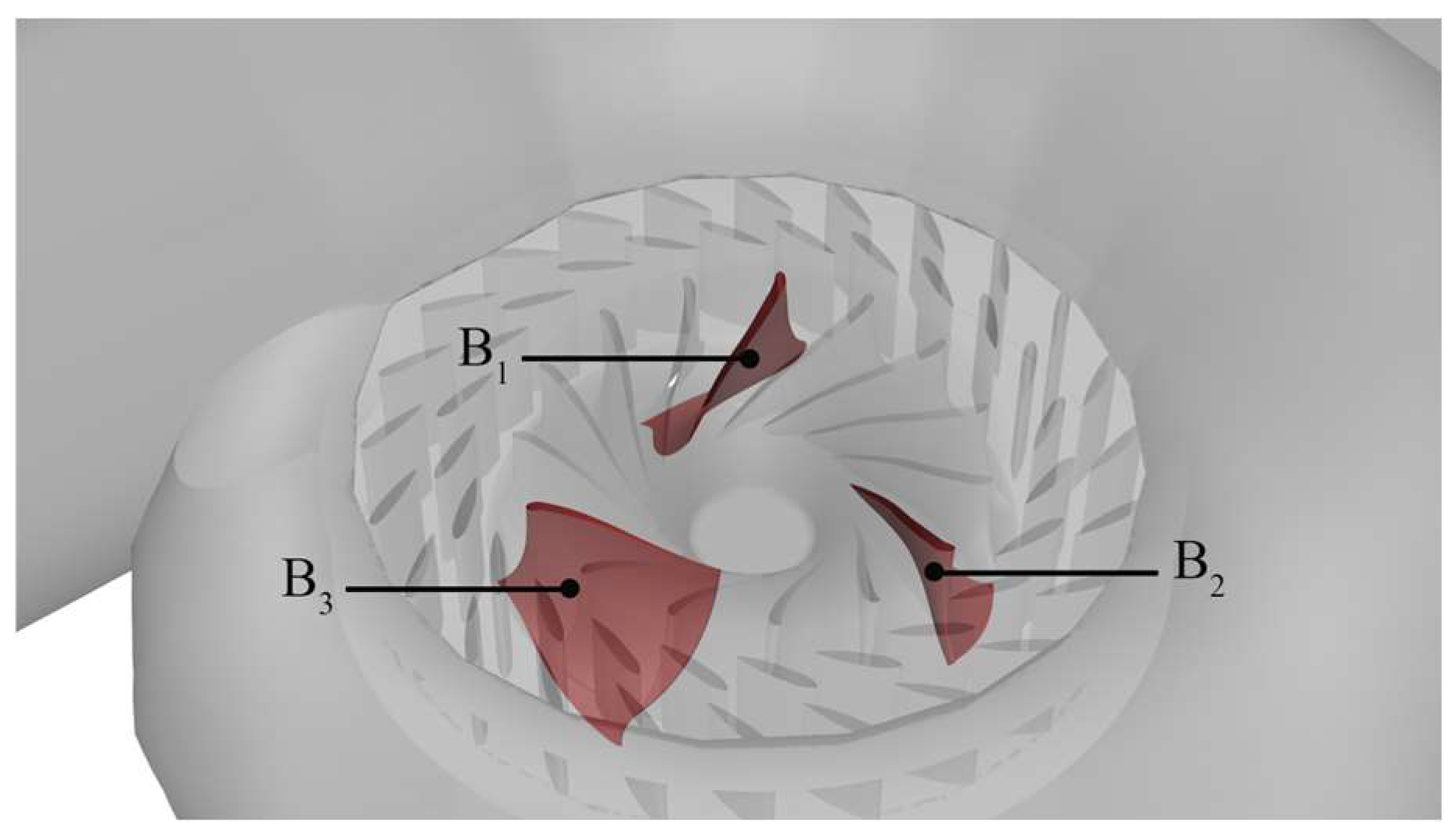
Mark the three feature blades in the runner as illustrated in Figure 10. Firstly, blade B₁ was taken near the inlet section of the spiral case, and then featured blades were taken every four blades in a clockwise direction, noted as blade B₂ and blade B₃, where B₃ was closer to the nose of the spiral case.

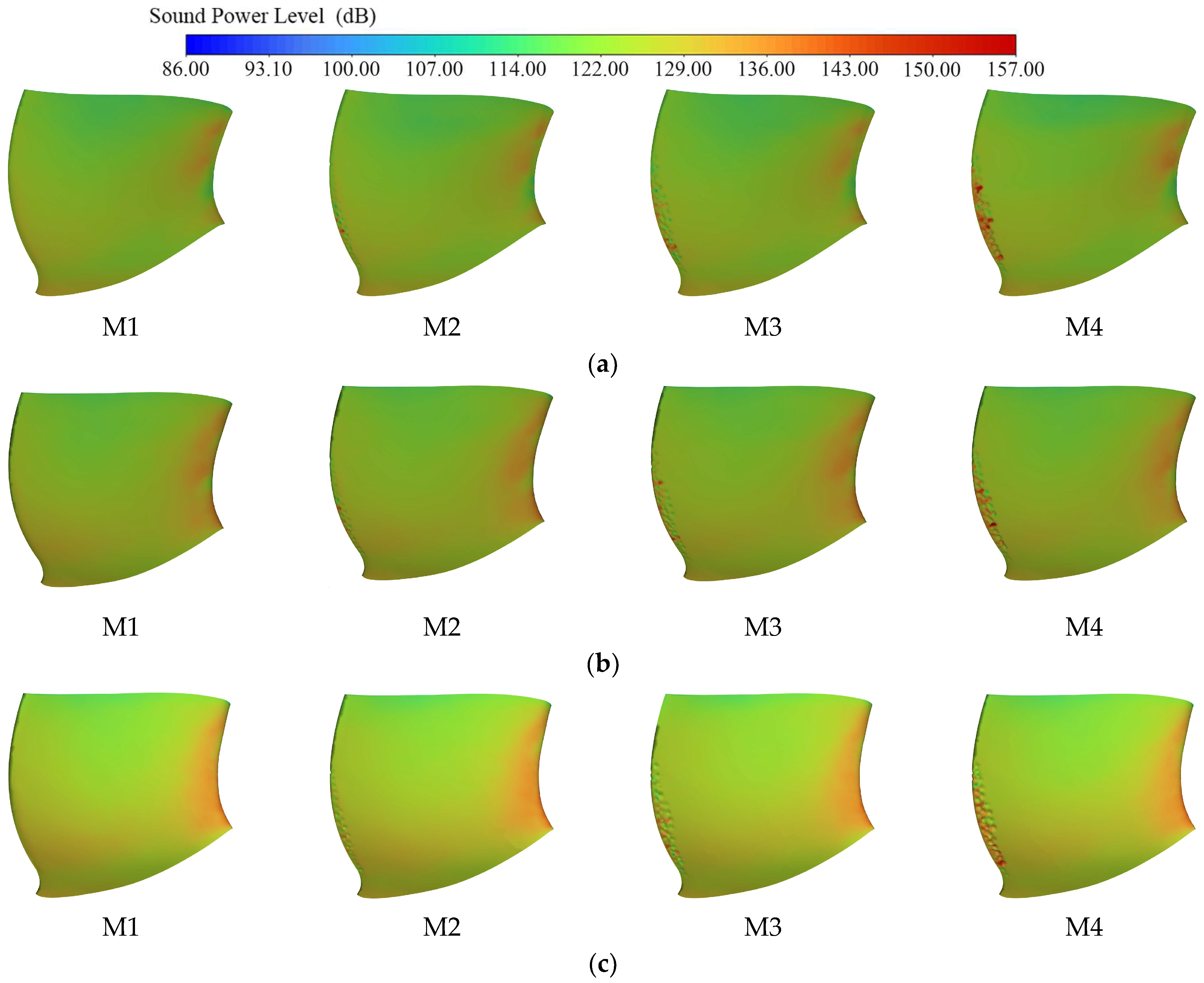
The SWL distribution on the suction surface of runner blades B₁, B₂, and B₃ is extracted, as illustrated in Figure 11. Because of the presence of the defective crater, highly significant SWL differences arise on the suction surface of the runner blades in different models. The SWL was higher on the water inlet side and outlet side of the blade, whereas the SWL was more evenly distributed on the M1 leaf surface and was higher on the water inlet side. In the rest of the models, the outflow edge (mainly at the defect crater) produces a significant area of a high SWL, with stronger sound source radiation as the defect damage deepens, which is most evident in M4. However, in M1, M2, and even M3, the SWL distribution of their different positions of the blades did not reflect a large difference, except in M4, and the high SWL radiation area at the water outlet edge of B₂ is slightly smaller than that of B₁ and B₃, which can be seen because only when the defect of the runner blades reaches a certain degree will the runner blades near the nose end of the spiral case produce a higher SWL than the other blades.

The effect of defects on the distribution of the SWL at the water outlet side of the suction surface of the runner blades was the most significant. Because the defective crater increases the resistance to flow at the blade surface, the collisions between fluid molecules and between the fluid and solid boundaries are more intense, the kinetic energy of the molecules is further converted into internal energy, and the Brownian motion is intensified, resulting in more complex and chaotic flow lines, faster fluid velocity, and a higher Reynolds number. Therefore, with the deepening of the damage of the runner blade defects, the water flow pattern is also more turbulent, and the impact of the fluid acting on the surface of the blade at the defective crater is stronger, corresponding to the SWL gradually increasing, and the sound source radiation range is also wider.

5. Far-Field Acoustic Signal Characterization

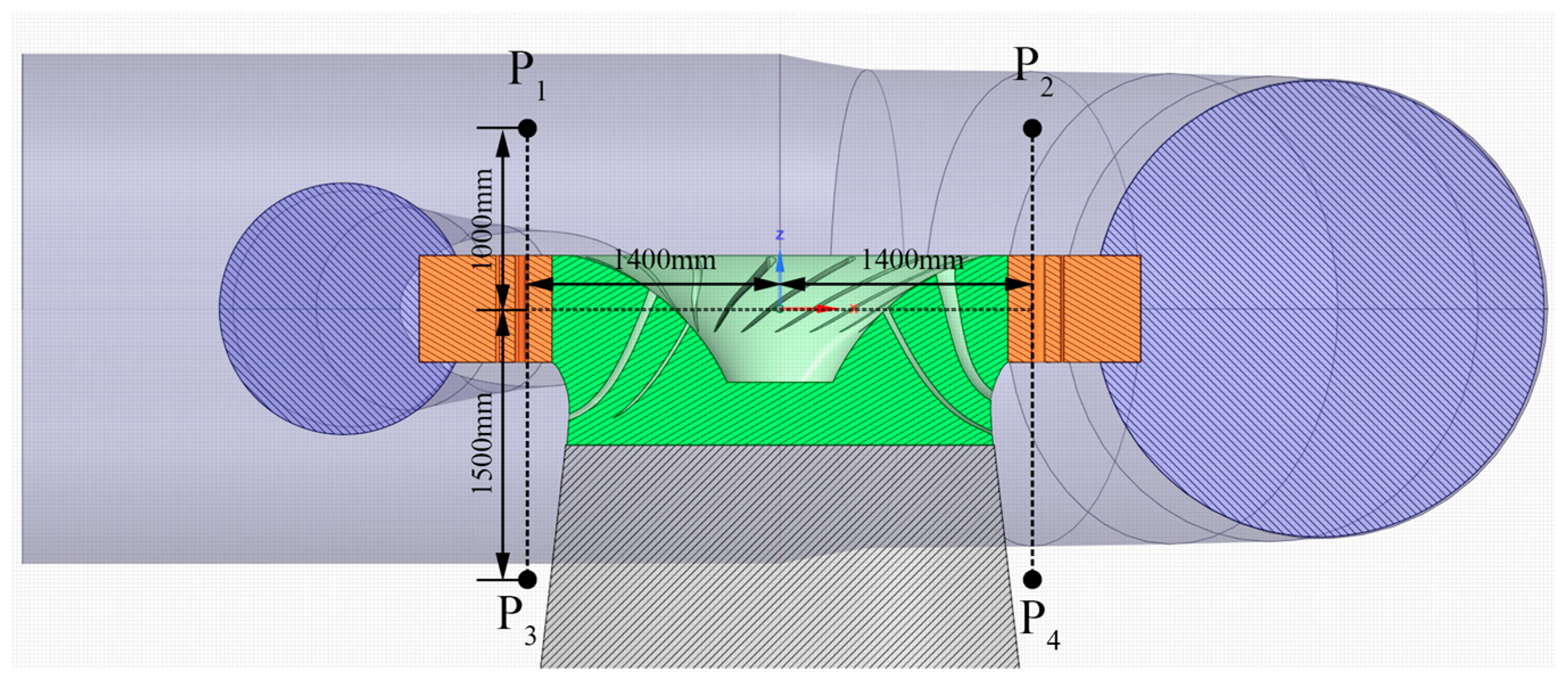
An acoustic signal receiver is required to solve for the acoustic far field using the FW-H equation. The location of the receiving point and the wall need to exist at a certain distance to ensure that the received sound waves have been fully developed. In practice, the main locations on the turbine where sensors can be placed include above the receiver (above the guide vane), inside the turbine (above the center of rotation of the runner), near the straight cone part of the draft tube, and so on.

The results of the acoustic near-field analysis of this turbine reveal that the intensity of the sound source is higher near the nose of the spiral case, and the change with the deepening of the defect of the runner blades is more obvious. Under comprehensive consideration, four signal reception points for acoustic far-field analysis were marked on the xz section of the model (y = 0). The side close to the nose of the spiral case above the guide vane was marked P₁, below the guide vane, i.e., on the upstream side of the draft tube, was marked P₃, and on the opposite side of its circumference, P₂ and P₄, respectively, were marked. The spatial location of the signal reception point is shown in Figure 12, and its spatial coordinates are shown in

Table 4. Acoustic signal receiving point’s spatial coordinates.

Receiving Point	x Coordinate	y Coordinate	z Coordinate
P1	−1400 (mm)	0 (mm)	1000 (mm)
P2	1400 (mm)	0 (mm)	1000 (mm)
P3	−1400 (mm)	0 (mm)	−1500 (mm)
P4	1400 (mm)	0 (mm)	−1500 (mm)

.

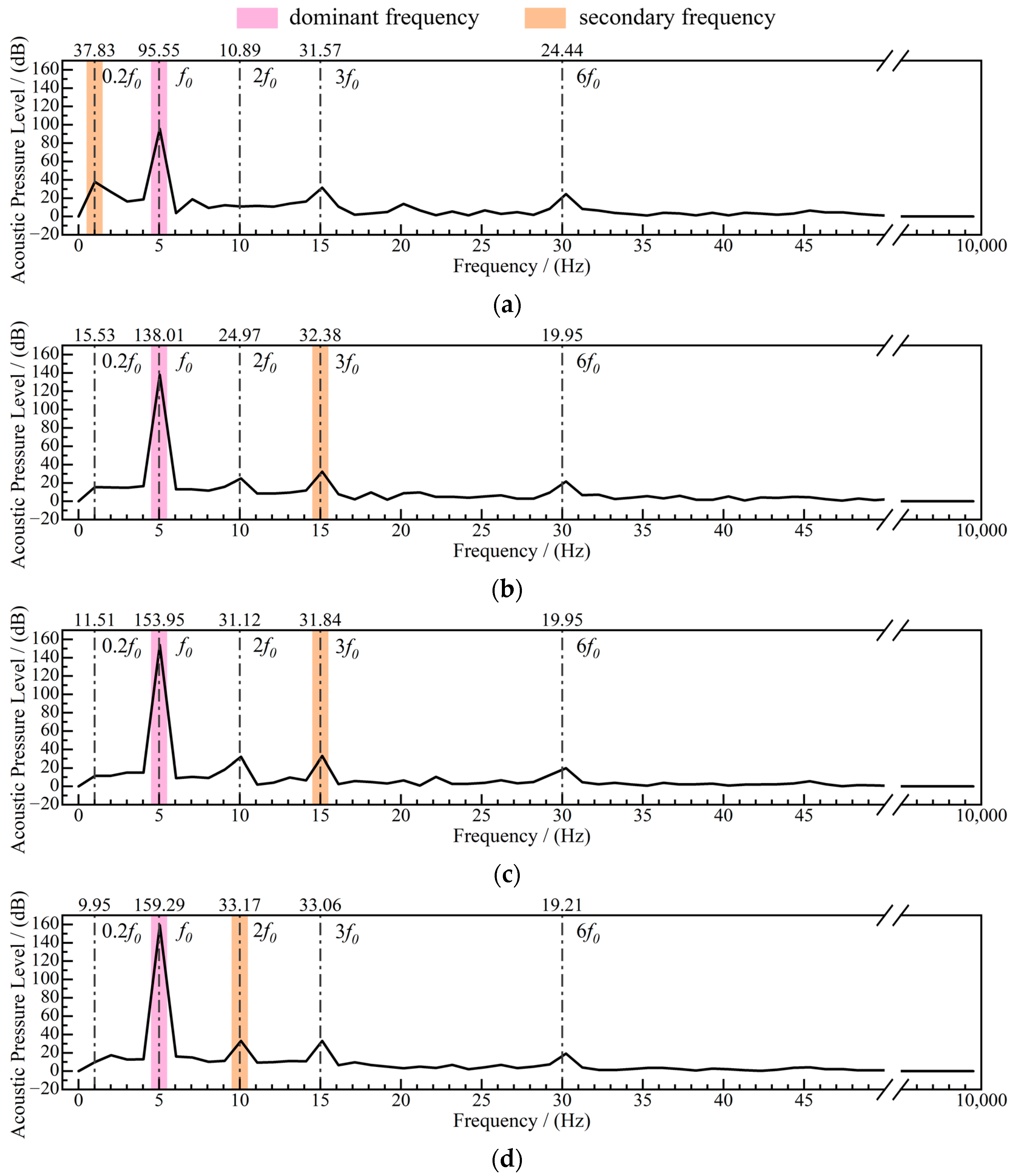
The turbine’s basic frequency f₀ is 5 Hz. The acoustic signals are processed by FFT, and the spectrograms of the signals at each monitoring point in different models are obtained. The main high amplitude frequencies of the acoustic signals are concentrated in the low-frequency band, so the spectrograms are uniformly processed with breakpoints in order to analyze the characteristics of the low-frequency band of the acoustic far-field signals in a more detailed way.

Figure 13 demonstrates the SPL spectral curves of each model in P₁. The dominant frequency of each signal is f₀, and the corresponding SPL of the dominant frequencies from M1 to M4 are 95.55 dB, 138.01 dB, 153.95 dB, and 159.29 dB in order, which shows that the amplitude of the dominant frequency shows a sharp positive correlation with the degree of defects in the runner blades. The presence of defects causes a large increase in the SPL of the dominant frequency, but in the model where defects are already present, the increase in SPL with the deepening of the defects is gradually decreasing. The 0.2f₀, 2f₀, 3f₀, and 6f₀ in the frequency domain also produce higher amplitudes, which shows that more signal frequency components are included in P₁. The secondary frequency of M1 is located at 0.2f₀, which corresponds to an SPL of 37.83 dB, at which time the signal frequency is more concentrated in the 0~5 Hz band. The amplitude of 2f₀ is still undeveloped. The secondary frequency in M2 becomes 3f₀, corresponding to an SPL of 32.38 dB. The amplitude of 0.2f₀ is no longer prominent due to the decrease, the development in the subsequent model also tends to level off, and the amplitude of 2f₀ begins to develop. The SPL of 3f₀ in M3 decreases to 31.84 dB, but the SPL of 2f₀ rises to 31.12 dB, which is already very close to 3f₀. In M4, the amplitude of 2f₀ exceeds 3f₀ and becomes the secondary frequency, and the SPL of 2f₀ is 33.17 dB.

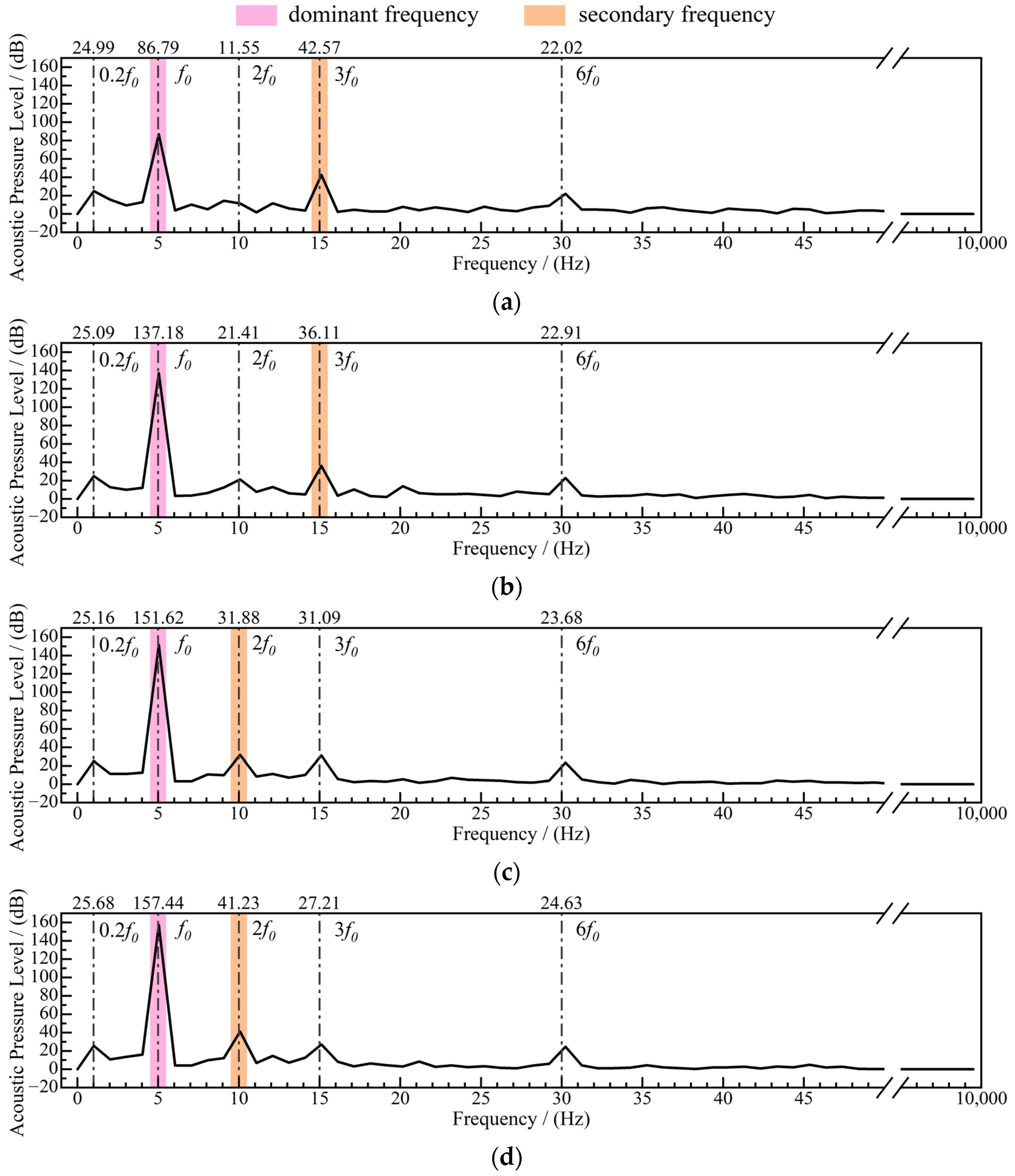
The spectral curves of the acoustic signals of each model in P₂ are shown in Figure 14. Also, the dominant frequency of the signal of each model is f₀, and the SPL corresponding to the dominant frequencies from M1 to M4 are 86.79 dB, 137.18 dB, 151.62 dB, and 157.44 dB in order, and the SPL corresponding to the amplitude also grows with deepening of the runner blade defect, but the amplitude is lower than that of P₁. The secondary frequencies of M1 to M4 are located at 3f₀, 3f₀, 2f₀, and 2f₀, and the SPL corresponding to the amplitudes are 42.57 dB, 36.11 dB, 31.09 dB, and 27.21 dB, respectively. 2f₀ is not the most important SPL in M1. The amplitude is not highlighted in M1 and then starts to grow after the model develops a defect, and the amplitude of 3f₀ gradually decreases during the development of the defect and is surpassed by 2f₀ in M3, which is no longer a secondary frequency of P₂.

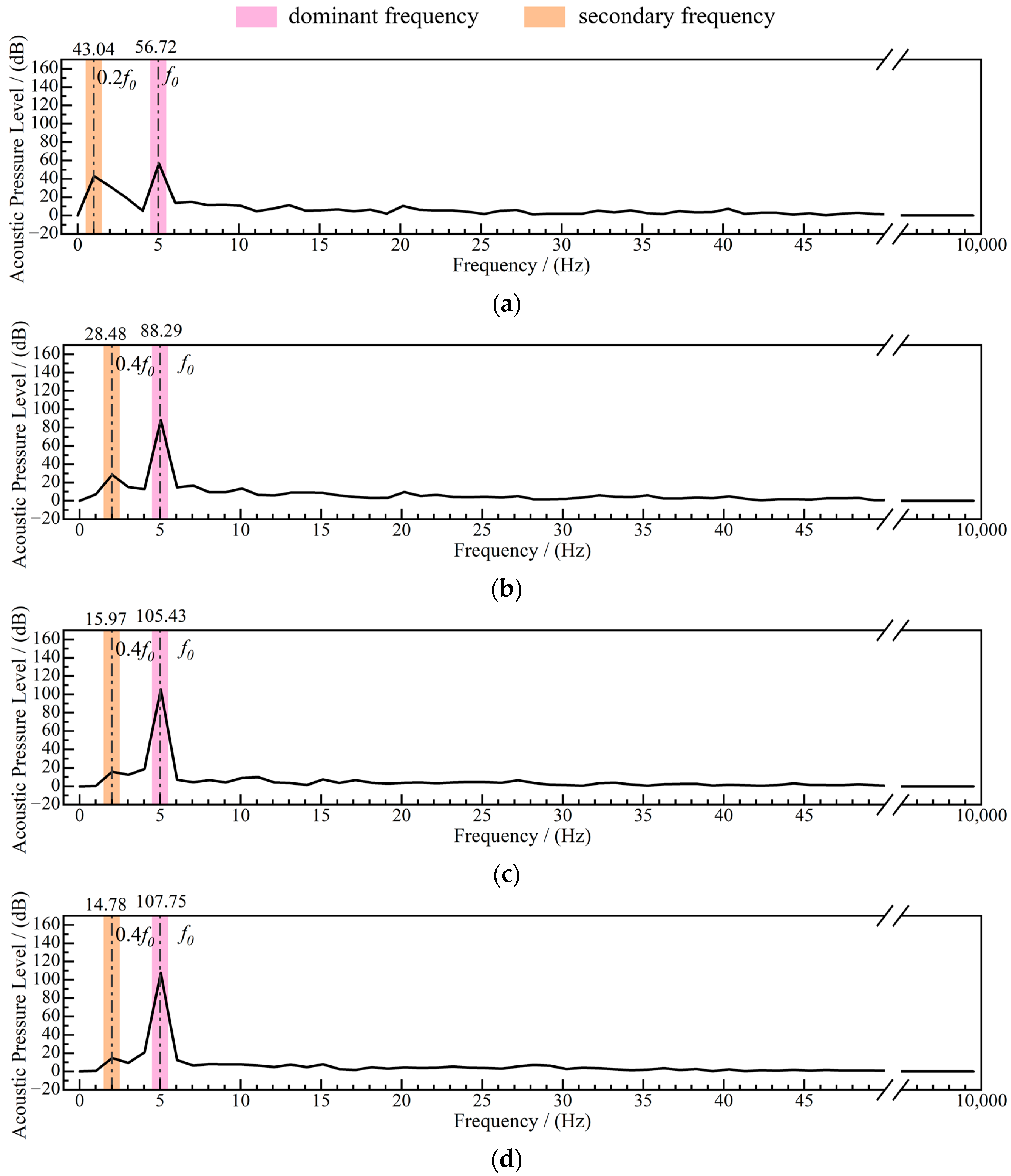
The signal frequency components of P₃ shown in Figure 15 are significantly less than those of P₁ and P₂. The dominant frequency of the signals of each model is still f₀, and the SPL corresponding to the dominant frequency amplitudes of M1 to M4 increases at values of 56.72 dB, 88.29 dB, 105.43 dB, and 107.75 dB. It can be seen that the lack of runner blades causes a large increase in the dominant frequency amplitude of P₃, and the increase in dominant frequency amplitudes from M1 to M2 (31.57 dB) is approximately two times that from M2 to M3 (17.14 dB). The secondary frequency of M1 is located at 0.2f₀, corresponding to an SPL of 43.04 dB, which is a higher and more concentrated amplitude around the band, and the secondary frequencies of M2, M3, and M4 are at 0.4f₀, with SPLs of 28.48 dB, 15.97 dB, and 14.78 dB, in order. The amplitude at 0.2f₀ is greatly weakened, and the effect on the signal spectrum gradually disappears. In the model with the presence of the defect, the signal spectrum shows a certain narrow-band feature near the dominant frequency, indicating that the frequency of P₃ is more concentrated at the fundamental frequency and more concentrated with the side of <f₀.

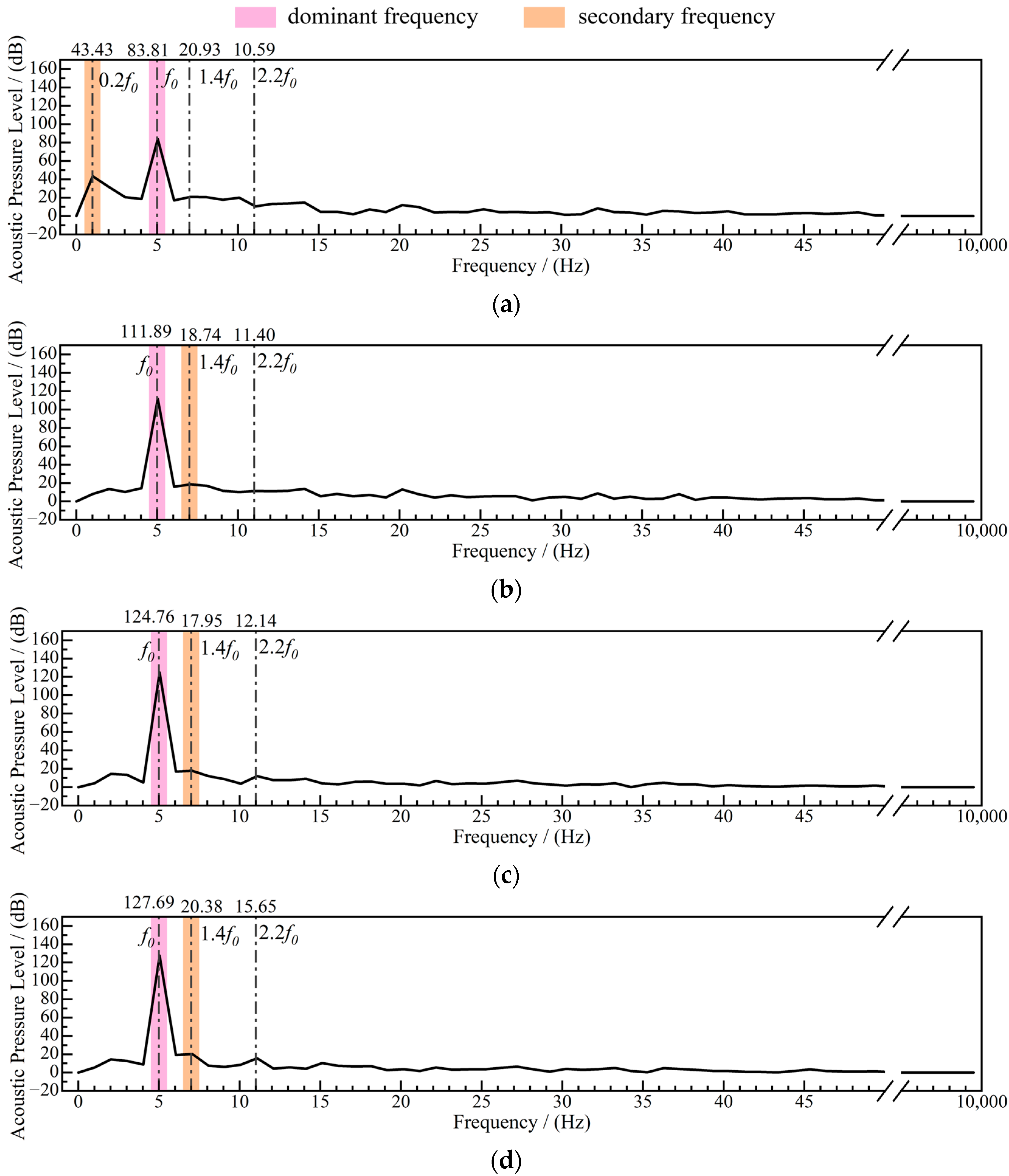
The spectral characteristics of the SPL of each model in P₄ are shown in Figure 16. Compared with P₃, the dominant frequency components are added to 1.4f₀ and 2.2f₀. The dominant frequency of each model is still f₀, and the SPL of the dominant frequency increases from M1 to M4 at values of 83.81 dB, 111.89 dB, 124.76 dB, and 127.69 dB, respectively, which are obviously positively correlated with the deficiency degree of the model. The amplitude is higher than that of P₃, and the model located at the downstream side of P₄ is additionally exposed to acoustic radiation from the diffusion section of the draft tube compared with P₃ located at the upstream side. The secondary frequency of M1 is located at 0.2f₀, which corresponds to an SPL of 43.43 dB, and the frequency is more concentrated in the band from 0 to 5 Hz. But, the amplitudes of 0.2f₀ in M2, M3, and M4 are very low. The secondary frequencies of M2, M3, and M4 are 1.4f₀, corresponding to SPLs of 18.74 dB, 17.95 dB, and 20.38 dB, in order, with very small fluctuations. It can be seen that the frequency development of P₄ under the defective model is more concentrated on the side of >f₀.

The dominant frequency of the acoustic signal at each receiving point of each model is located at f₀, and the magnitude of its dominant frequency amplitude depends on the magnitude of the defect in the model. The dominant frequency amplitudes of the receiver points near the nose of the spiral case and on the downstream side of the draft tube (P₁, P₄) are higher than those of the opposite receiver points (P₂, P₃). The receiving points located above the defective crater (P₁, P₂) have more frequency components in their spectra and higher SPLs than the monitoring points located below the defective pit (P₃, P₄), which means that there are more distinctive feature frequencies to be recognized. In P₁ and P₂, the secondary frequencies in the models with defects are 2f₀ and 3f₀, and the amplitude of 2f₀ exceeds 3f₀ with the continuation of deepening defects followed by the development of secondary frequencies, but the nodes of the defect degree that cause the secondary frequency change are different, and the secondary frequency change occurs earlier in P₂. In P₃ and P₄, the secondary frequencies in the models with defects are 0.4f₀ and 1.4f₀, respectively, and the development of the frequencies tends to be in the lower frequency band around the dominant frequency. P₃ concentrates on the side of <f₀, and P₄ concentrates on the side of >f₀.

6. Conclusions

The main acoustic source area of the hydraulic turbine is the double-row leaf grille and runner in the acoustic near field, and when the runner blade is defective, its acoustic source becomes stronger, and the intensity of acoustic radiation is positively correlated with the degree of defect. The far-field acoustic signals predominantly feature frequencies in the low-frequency band. The dominant frequencies are all the turbine basic frequencies f₀ (5 Hz), and the amplitudes of the dominant frequencies all rise with the deepening of the runner blade defect. When the runner blade defect occurs, the secondary frequencies of the signals at most of the receiving points change, and they are different from their secondary frequencies in the intact M1. Receiving points located above the guide vane have more signal components, with more secondary frequencies of 2f₀ and 3f₀, and the secondary frequency changes from 3f₀ to 2f₀ during the development of the defect, whereas receiving points located below the active guide vane have fewer signal components and correspondingly lower secondary frequencies.

In general, the frequency composition of acoustic signals at different locations of the reception points is different, and their signal secondary frequencies and development laws in different models have unique characteristics of change. Therefore, during the operation of the hydraulic turbine, attention should be paid to the abnormal noise signals from the double-row leaf grille and runner, especially in the area near the nose of the spiral case. With reference to the identified defective noise spectral characteristics, timely warning information can be issued to prevent the hydraulic turbine from working with disease for a long time, reduce the maintenance cost, and further provide guidance for the determination of the defective degree of the hydraulic turbine. It is important to note that this study is based on the rated operating conditions of the turbine, and only the initial condition that was artificially altered for the calculations between the different models is the degree of deficiency of the runner blades. Therefore, the above conclusions are applicable to the rated operating conditions of the turbine and need to be satisfied simultaneously with the degree of runner blade defects as the only variable studied. Moreover, the actual defect shape of the turbine adopted in this paper may not be applicable to other turbines, so the actual reference needs to confirm the real defect state of the turbine, and the hydrodynamic noise characteristics caused by different defect shapes may be different. Nevertheless, this study can also provide guidance for the numerical simulation of hydrodynamic noise in other working conditions of this turbine so as to obtain more research results with reference significance for practical engineering.