Application of Oversampling Techniques for Enhanced Transverse Dispersion Coefficient Estimation Performance Using Machine Learning Regression
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset Explanations
2.2. Estimation of DT
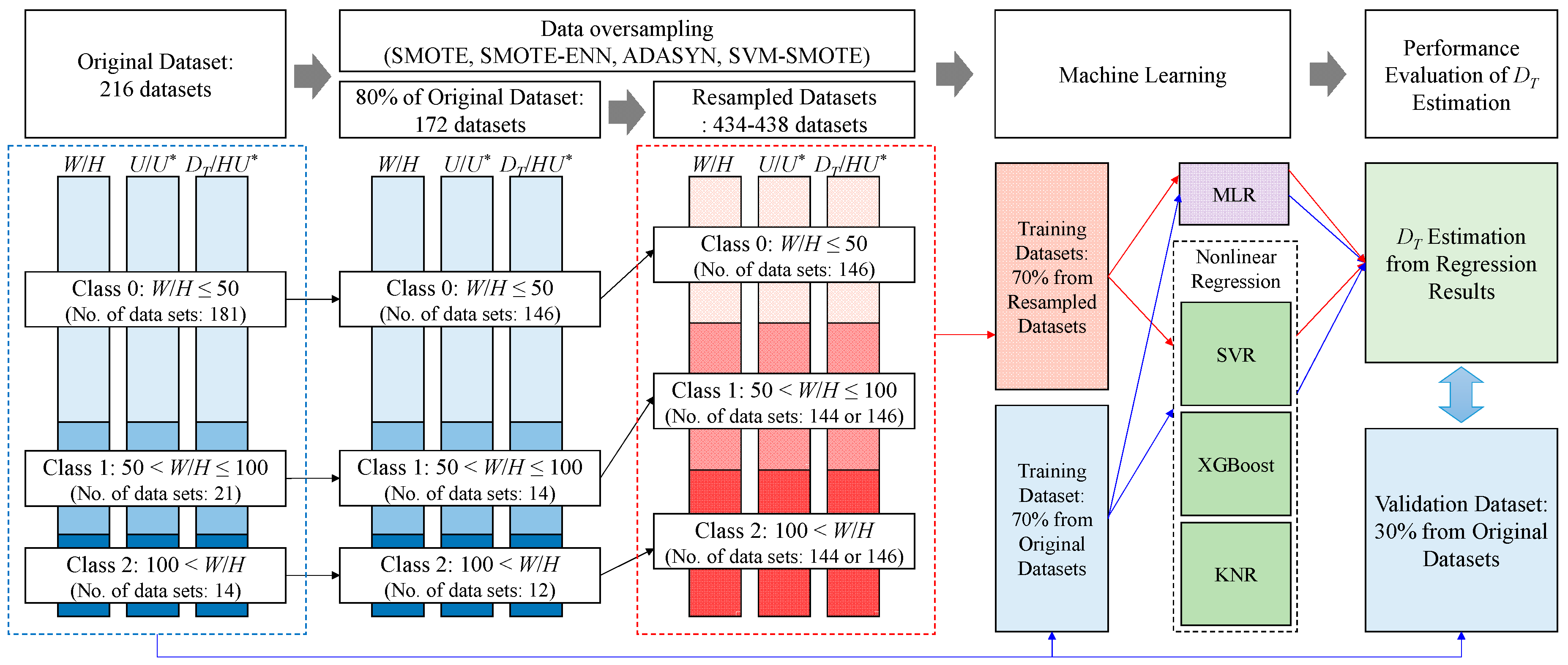
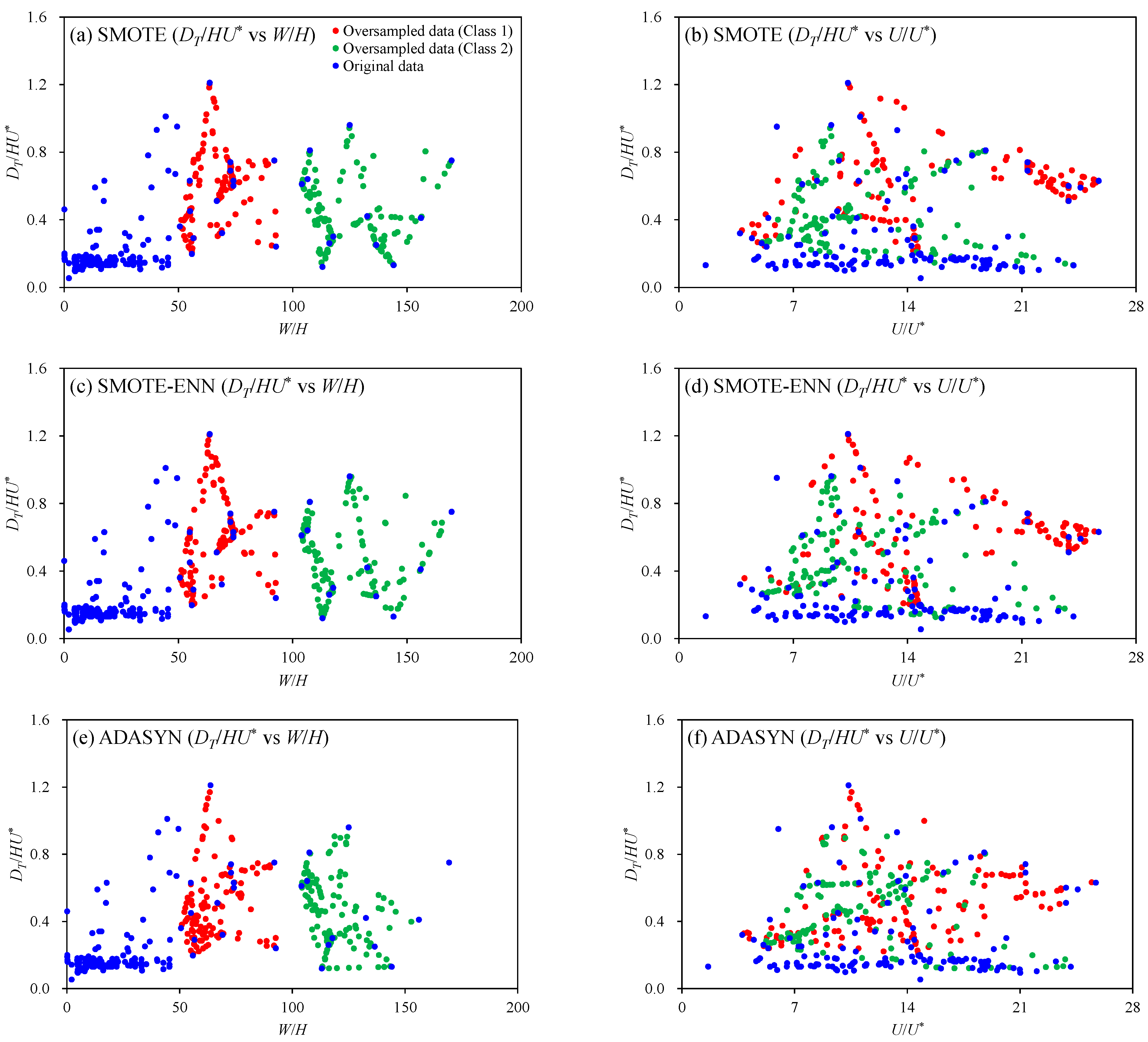
2.3. Data Oversampling
2.4. Machine Learning Regression Methods
2.4.1. Support Vector Machine Regression (SVR) Model
2.4.2. eXtream Gradient Boosting Regression (XGBoost) Model
2.4.3. k–Nearest Neighbors Regression (KNR) Model
3. Results
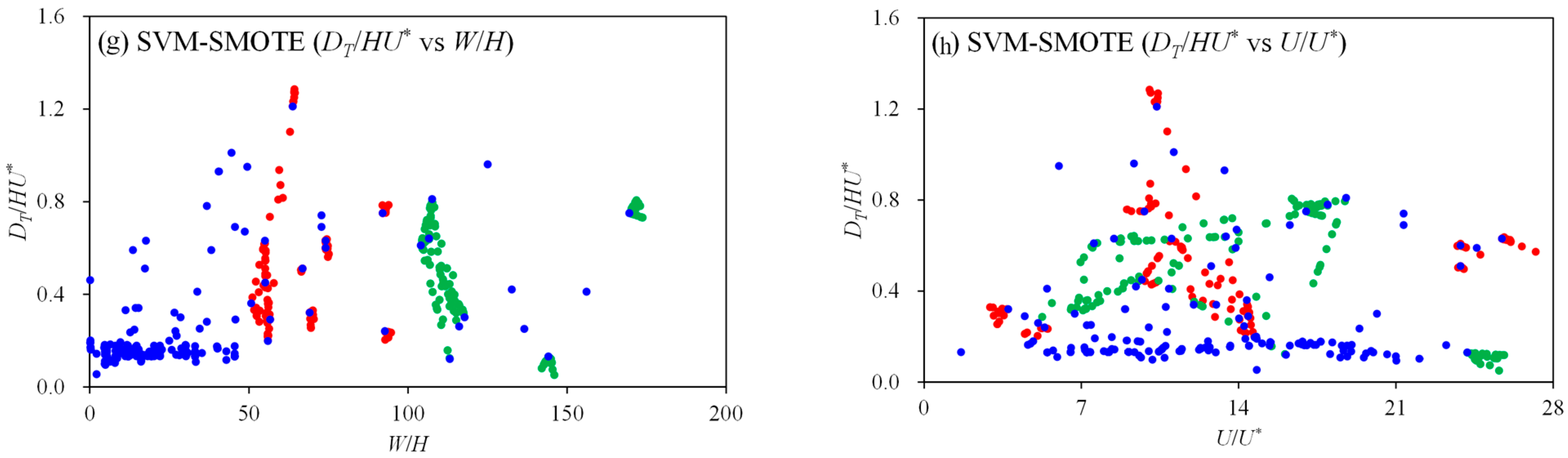
3.1. Oversampling Results and Performance Evaluations
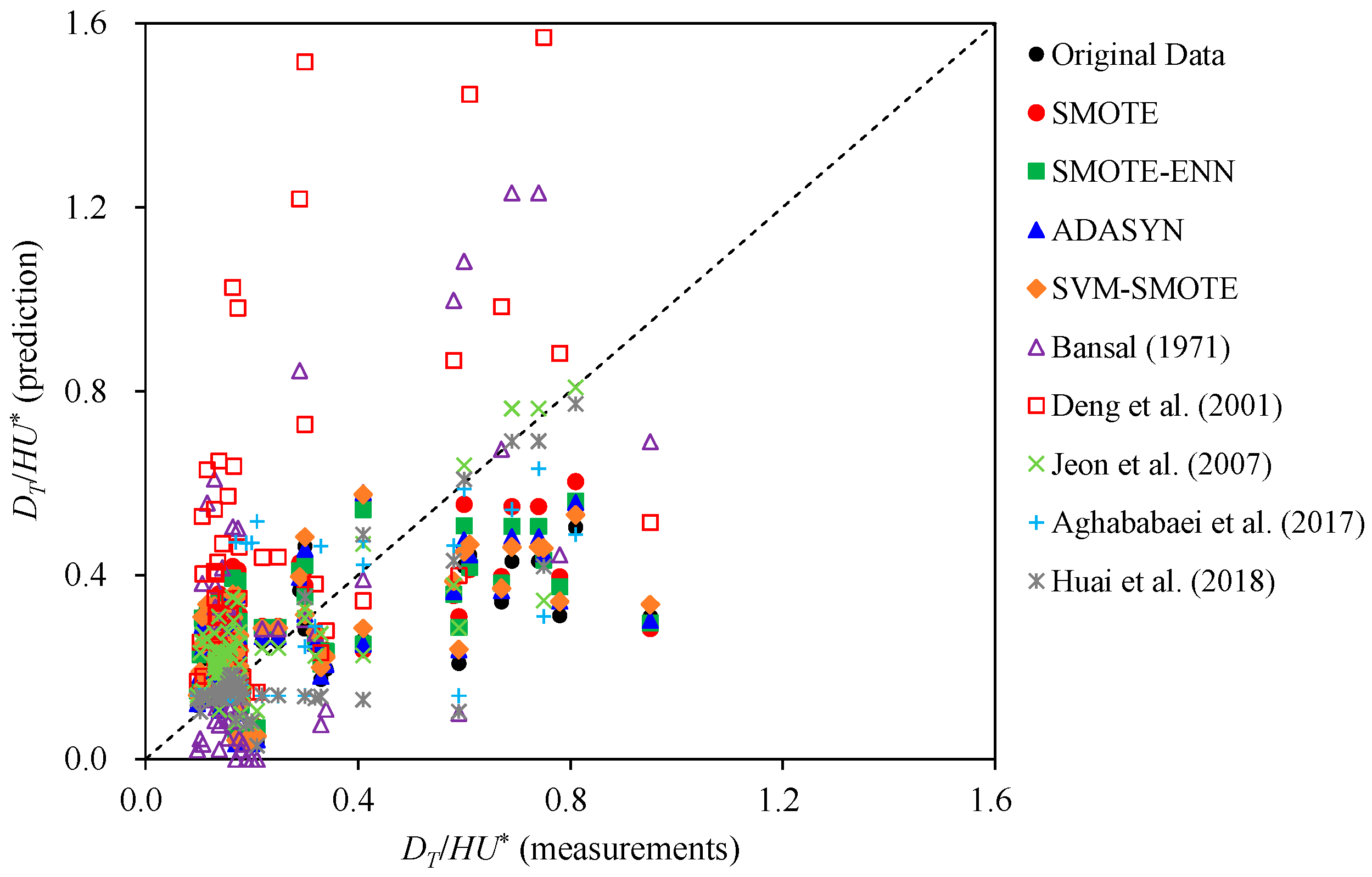
3.2. DT Predictions Using MLR
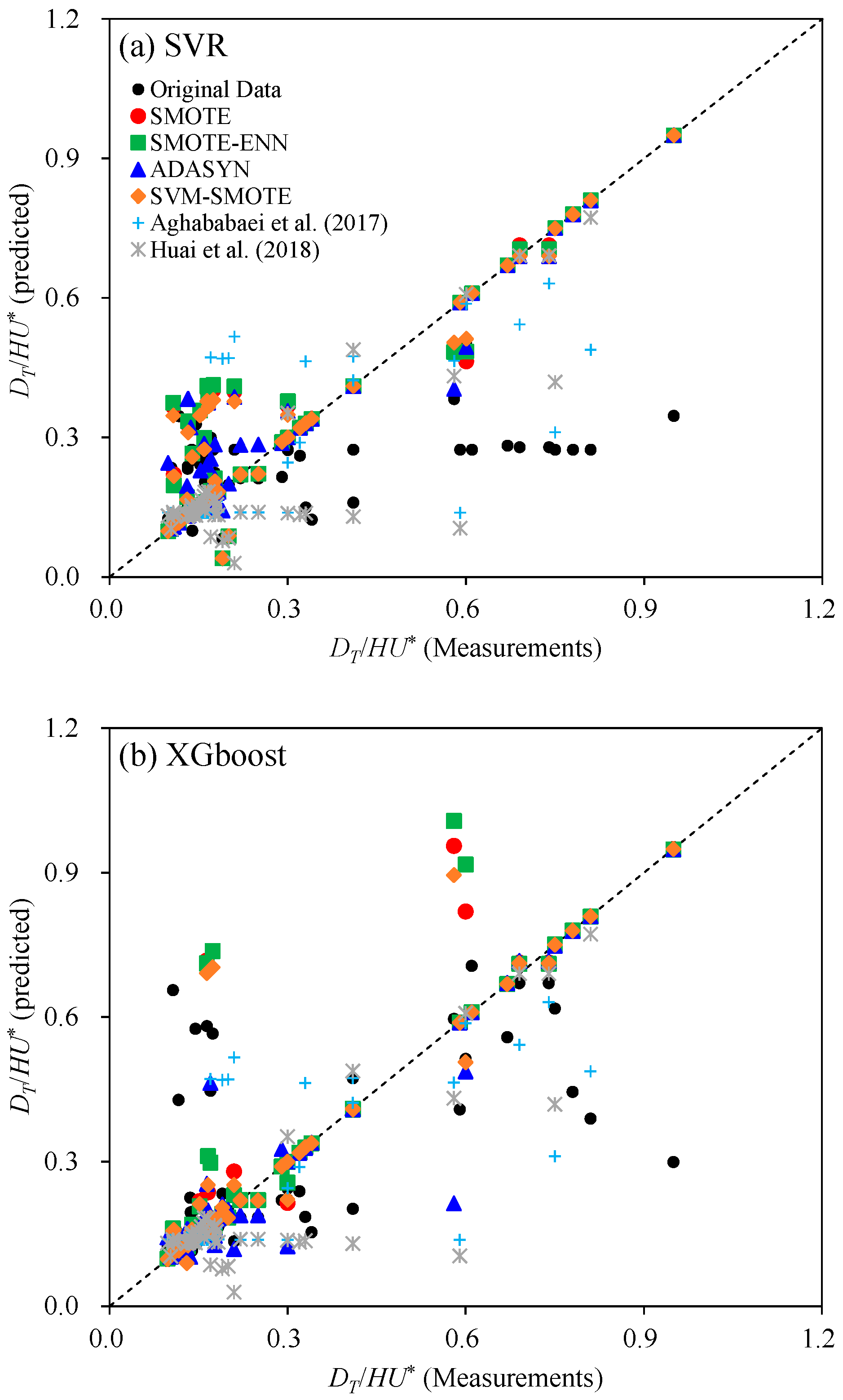
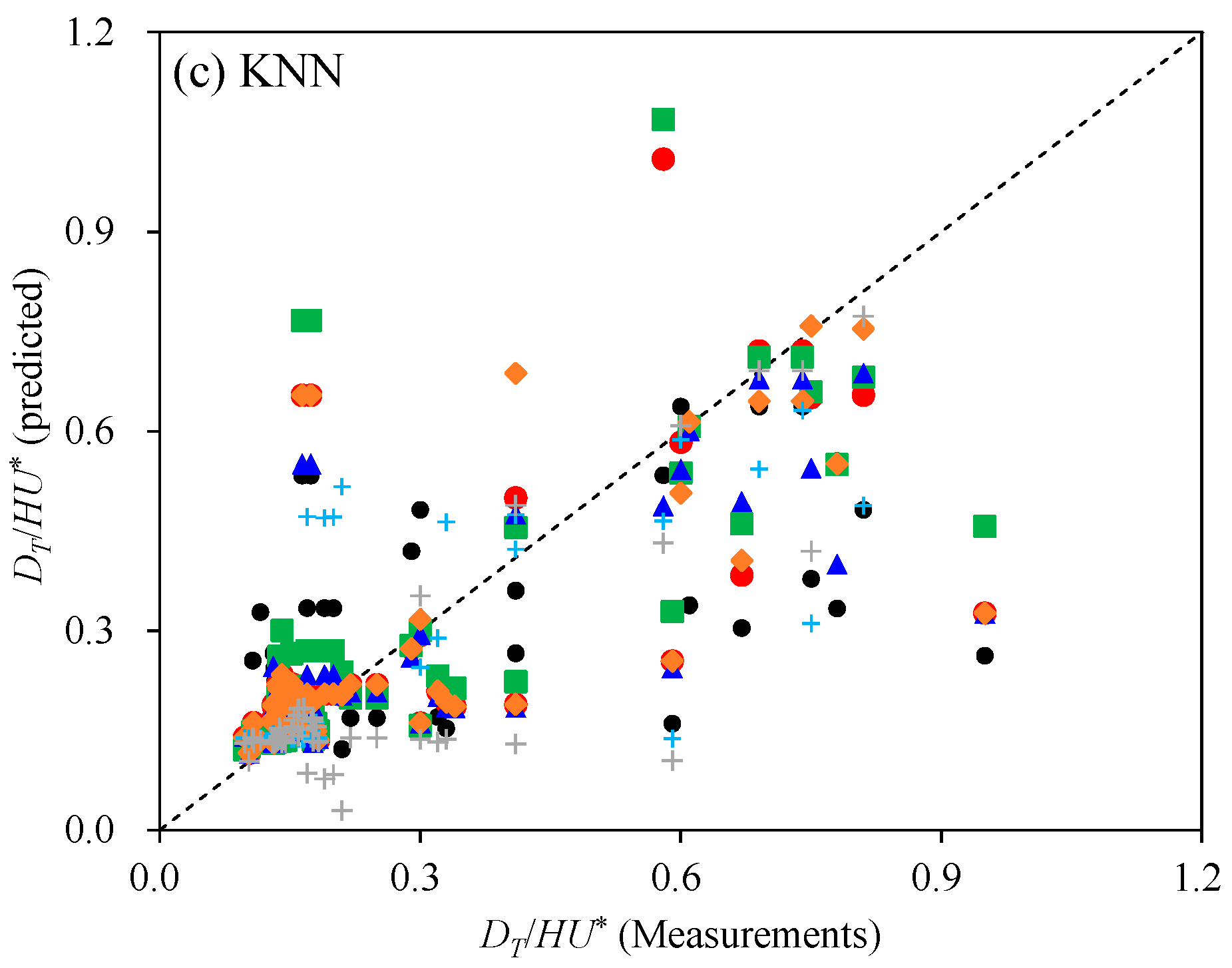
3.3. DT Predictions Using Nonlinear Regression Methods
4. Discussion
4.1. DT Estimation Performance Using MLR through Data Augmentation
4.2. Comparisons of DT Estimation Results Using MLR and Nonlinear Regression Methods
4.3. The Feasibility of Two Variables for DT Estimation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shin, J.; Seo, I.W.; Baek, D. Longitudinal and transverse dispersion coefficients of 2D contaminant transport model for mixing analysis in open channels. J. Hydrol. 2020, 583, 124302. [Google Scholar] [CrossRef]
- Piasecki, M.; Katopodes, N.D. Identification of stream dispersion coefficients by adjoint sensitivity method. J. Hydraul. Eng. 1999, 125, 714–724. [Google Scholar] [CrossRef]
- King, I.; Letter, J.V.; Donnel, B.P. RMA4 Users Guide 4.5x; US Army, Engineer Research and Development Center, WES, CHL: Vicksburg, MI, USA, 2008. [Google Scholar]
- Lee, M.E.; Seo, I.W. Analysis of pollutant transport in the Han River with tidal current using a 2D finite element model. J. Hydro-environ. Res. 2007, 1, 30–42. [Google Scholar] [CrossRef]
- Park, I.; Seo, I.W.; Shin, J.; Song, C.G. Experimental and numerical investigations of spatially-varying dispersion tensors based on vertical velocity profile and depth-averaged flow field. Adv. Water Res. 2020, 142, 103606. [Google Scholar] [CrossRef]
- Baek, K.O.; Seo, I.W.; Jeong, S.J. Evaluation of dispersion coefficients in meandering channels from transient tracer tests. J. Hydraul. Eng. 2006, 132, 1003–1119. [Google Scholar] [CrossRef]
- Seo, I.W.; Lee, M.E.; Baek, K.O. 2D modeling of heterogeneous dispersion in meandering channels. J. Hydraul. Res. 2008, 44, 350–362. [Google Scholar] [CrossRef]
- Tabatabaei, S.H.; Heidarpour, M.; Ghasemi, M.; Hoseinipour, E.Z. Transverse mixing coefficient on dunes with vegetation on a channel wall. In Proceedings of the World Environmental and Water Resources Congress 2013: Showcasing the Future, Cincinnati, OH, USA, 19–23 May 2013; pp. 1903–1911. [Google Scholar]
- Beltaos, S. Transverse mixing tests in natural streams. J. Hydraul. Div. 1980, 106, 1607–1625. [Google Scholar] [CrossRef]
- Jeon, T.M.; Baek, K.O.; Seo, I.W. Development of an empirical equation for the transverse dispersion coefficient in natural streams. Environ. Fluid Mech. 2007, 7, 317–329. [Google Scholar] [CrossRef]
- Seo, I.W.; Choi, H.J.; Kim, Y.D.; Han, E.J. Analysis of two-dimensional mixing in natural streams based on transient tracer tests. J. Hydraul. Eng. 2016, 142, 04016020. [Google Scholar] [CrossRef]
- Gond, L.; Mignot, E.; Le Coz, J.; Kateb, L. Transverse mixing in rivers with longitudinally varied morphology. Water Resour. Res. 2020, 57, e2020WR029478. [Google Scholar] [CrossRef]
- Jung, S.H.; Seo, I.W.; Kim, Y.D.; Park, I. Feasibility of velocity-based method for transverse mixing coefficients in river mixing analysis. J. Hydraul. Eng. 2019, 145, 04019040. [Google Scholar] [CrossRef]
- Fischer, H.B.; List, J.E.; Koh, R.C.Y.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters, 2nd ed.; Academic Press: San Diego, CA, USA, 1979; pp. 80–147. [Google Scholar]
- Rutherford, J.C. River Mixing; John Wiley and Sons: London, UK, 1994; pp. 62–63. [Google Scholar]
- Gharbi, S.; Verrette, J.L. Relation between longitudinal and transversal mixing coefficients in natural streams. J. Hydraul. Res. 1998, 36, 43–54. [Google Scholar] [CrossRef]
- Deng, Z.Q.; Singh, V.P.; Bengtsson, L. Longitudinal dispersion coefficient in straight rivers. J. Hydraul. Eng. 2001, 127, 919–927. [Google Scholar] [CrossRef]
- Baek, K.O.; Seo, I.W. Empirical equation for transverse dispersion coefficient based on theoretical background in river bends. Environ. Fluid Mech. 2013, 13, 465–477. [Google Scholar] [CrossRef]
- Aghababaei, M.; Etemad-Shahidi, A.; Jabbari, E.; Taghipour, M. Estimation of transverse mixing coefficient in straight and meandering streams. Water Resour. Manag. 2017, 31, 3809–3827. [Google Scholar] [CrossRef]
- Baek, K.O.; Lee, D.Y. Development of simple formula for transverse dispersion coefficient in meandering rivers. Water 2023, 15, 3120. [Google Scholar] [CrossRef]
- Tao, H.; Al-Khafaji, Z.S.; Qi, C.; Yassen, Z.M. Artificial intelligence models for suspended river sediment prediction: State-of-the art, modeling framework appraisal, and proposed future research directions. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1585–1612. [Google Scholar] [CrossRef]
- Tayfur, G.; Singh, V.P. Predicting longitudinal dispersion coefficient in natural streams by artificial neural network. J. Hydraul. Eng. 2005, 131, 991–1000. [Google Scholar] [CrossRef]
- Noori, R.; Karbassi, A.; Farokhnia, A.; Dehghani, M. Predicting the longitudinal dispersion coefficient using support vector machine and adaptive neuro-fuzzy inference system techniques. Environ. Eng. Sci. 2009, 26, 1503–1510. [Google Scholar] [CrossRef]
- Sattar, A.M.A.; Gharabaghi, B. Gene expression models for prediction of longitudinal dispersion coefficient in streams. J. Hydrol. 2015, 524, 587–596. [Google Scholar] [CrossRef]
- Seifi, A.; Riahi-Madvar, H. Improving one-dimensional pollution dispersion modeling in rivers using ANFIS and ANN-based GA optimized models. Environ. Sci. Pollut. Res. 2019, 26, 867–885. [Google Scholar] [CrossRef]
- Azar, N.A.; Milan, S.G.; Kayhomayoon, Z. The prediction of longitudinal dispersion coefficient in natural streams using LS-SVM and ANFIS optimized by Harris hawk optimization algorithm. J. Contam. Hydrol. 2021, 240, 103781. [Google Scholar] [CrossRef] [PubMed]
- Ghiasi, B.; Noori, R.; Sheikhian, H.; Zeynolabedin, A.; Sun, Y.; Jun, C.; Hamouda, M.; Bateni, S.M.; Abolfathi, S. Uncertainty quantification of granular computing-neural network model for prediction of pollutant longitudinal dispersion coefficient in aquatic streams. Sci. Rep. 2022, 12, 4610. [Google Scholar] [CrossRef] [PubMed]
- Ohadi, S.; Monfared, S.A.H.; Moghaddam, M.A.; Givehchi, M. Feasibility of a novel predictive model based on multilayer perceptron optimized with Harris hawk optimization for estimating of the longitudinal dispersion coefficient in rivers. Neural Comp. Appl. 2023, 35, 7081–7105. [Google Scholar] [CrossRef]
- Azamathulla, H.M.; Ahmad, Z. Gene-expression programming for transverse mixing coefficient. J. Hydrol. 2012, 434–435, 142–148. [Google Scholar] [CrossRef]
- Huai, W.; Shi, H.; Yang, Z.; Zeng, Y. Estimating the transverse mixing coefficient in laboratory flumes and natural rivers. Water Air Soil Pollut. 2018, 229, 252. [Google Scholar] [CrossRef]
- Zahiri, J.; Nezaratian, H. Estimation of transverse mixing coefficient in streams using M5, MARS, GA, and PSO approaches. Environ. Sci. Pollut. Res. 2020, 27, 14553–14566. [Google Scholar] [CrossRef] [PubMed]
- Nezaratian, H.; Zahiri, J.; Peykani, M.F.; Haghiabi, A.; Parsaie, A. A genetic algorithm-based support vector machine to estimate the transverse mixing coefficient in streams. Water Qual. Res. J. 2021, 56, 128. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Noori, R.; Afroozi, D.; Ghiasi, B.; Hosseini-Moghari, S.M.; Mirchi, A.; Haghighi, A.T.; Kløve, B. A comprehensive uncertainty analysis of model-estimated longitudinal and lateral dispersion coefficients in open channels. J. Hydrol. 2021, 603, 126850. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Huang, R.; Ma, C.; Ma, J.; Huangfu, X.; He, Q. Machine learning in natural and engineered water systems. Water Res. 2021, 205, 117666. [Google Scholar] [CrossRef]
- Xu, T.; Coco, G.; Neale, M. A predictive model of recreational water quality based on adaptive synthetic sampling algorithms and machine learning. Water Res. 2020, 177, 115788. [Google Scholar] [CrossRef]
- Bourel, M.; Segura, A.M.; Crisci, C.; López, G.; Sampognaro, L.; Vidal, V.; Kruk, C.; Piccini, C.; Perera, G. Machine learning methods for imbalanced data set for prediction of faecal contamination in beach waters. Water Res. 2021, 202, 117450. [Google Scholar] [CrossRef]
- Prasad, D.V.V.; Kumar, P.S.; Venkataramana, L.Y.; Prasannamedha, G.; Harshana, S.; Srividya, S.J.; Harrinei, K.; Indraganti, S. Automating water quality analysis using ML and auto ML techniques. Environ. Res. 2021, 202, 111720. [Google Scholar] [CrossRef]
- Snieder, E.; Abogadil, K.; Khan, U.T. Resampling and ensemble techniques for improving ANN-based high-flow forecast accuracy. Hydrol. Earth Syst. Sci. 2021, 25, 2543–2566. [Google Scholar] [CrossRef]
- Nasir, N.; Kansal, A.; Alshaltone, O.; Barneih, F.; Sameer, M.; Shanableh, A.; Al-Shamma’a, A. Water quality classification using machine learning algorithms. J. Water Proc. Eng. 2022, 48, 102920. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1 June 2008. [Google Scholar]
- Batista, G.E.; Prati, R.C.; Monard, M.C. A study of the behavior of several methods for balancing machine learning training data. ACM SIGKDD Explor. Newsl. 2004, 6, 20–29. [Google Scholar] [CrossRef]
- Zhou, H.; Dong, X.; Xia, S.; Wang, G. Weighted oversampling algorithms for imbalanced problems and application in prediction of streamflow. Knowl.-Based Syst. 2021, 229, 107306. [Google Scholar] [CrossRef]
- Rahman, M.A.; Akter, A.; Richi, F.S.; Shoud, A.; Ahmed, T. A comparative study of undersampling and oversampling methods for flood forecasting in Bangladesh using machine learning. In Proceedings of the 2023 IEEE 14th International Conference on Computing Communication and Networking Technologies (ICCCNT), Delhi, India, 6–8 July 2023. [Google Scholar]
- Hasan, M.A.; Rouf, N.T.; Hossain, M.S. A location-independent flood prediction model for Bangladesh’s rivers. In Proceedings of the 2023 IEEE 35th International Conference on Tools with Artificial Intelligence (ICTAI), Atlanta, GA, USA, 6–8 November 2023. [Google Scholar]
- Kalinske, A.A.; Pien, C.L. Eddy diffusion. Ind. Eng. Chem. 1944, 36, 220–223. [Google Scholar] [CrossRef]
- Elder, J.W. The dispersion of marked fluid in turbulent shear flow. J. Fluid Mech. 1959, 5, 544–560. [Google Scholar] [CrossRef]
- Sayre, W.W.; Chang, F.M. A Laboratory Investigation of Open-Channel Dispersion Processes for Dissolved, Suspended, and Floating Dispersants; Professional Paper, No. 433-E; U.S. Geological Survey: Washington, DC, USA, 1968; pp. 37–71.
- Sullivan, P.J. Dispersion in a Turbulent Shear Flow. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 1968. [Google Scholar]
- Bansal, M.K. Dispersion and Reaeration in Natural Stream. Ph.D. Thesis, Universite de Kansas Laurence, Lawrence, KS, USA, 1970. [Google Scholar]
- Okoye, J.K. Characteristics of Transverse Mixing in Open-Channel Flows. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1971. [Google Scholar]
- Prych, E.A. Effects of Density Differences on Lateral Mixing in Open-Channel Flows. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1970. [Google Scholar]
- Yotsukura, N.; Fischer, H.B.; Sayre, W.W. Measurement of Mixing Characteristics of the Missouri River between Sioux City, Iowa, and Plattsmouth, Nebraska; Water Supply Paper. No. 1899-G; U.S. Geological Survey: Washington, DC, USA, 1970; pp. 11–26.
- Holly, E.R. Transverse Mixing in Rivers; Report No. S132; Delft Hydraulics Laboratory: Delft, The Netherlands, 1971; pp. 34–84. [Google Scholar]
- Yotsukura, N.; Cobb, E.D. Transverse Diffusion of Solutes in Natural Streams; U.S. Geological Survey: Washington, DC, USA, 1972; pp. 2–19.
- Fischer, H.B. Longitudinal dispersion and turbulent mixing in open-channel flow. Annu. Rev. Fluid Mech. 1973, 5, 59–78. [Google Scholar] [CrossRef]
- Holley, E.R.; Abraham, G. Laboratory studies on transverse mixing in rivers. J. Hydraul. Res. 1973, 11, 219–253. [Google Scholar] [CrossRef]
- Sayre, W.W.; Yeh, T. Transverse Mixing Characteristics of the Missouri River Downstream from the Cooper Nuclear Station; Rep. No.145; Iowa Institute of Hydraulic Research: Iowa City, IA, USA, 1973; pp. 1–46. [Google Scholar]
- Engmann, J.E.O. Transverse Mixing Characteristics of Open and Ice-Covered Channel Flows. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 1974. [Google Scholar]
- Miller, A.C.; Richardson, E.V. Diffusion and dispersion in open channel flow. J. Hydraul. Div. 1974, 100, 159–171. [Google Scholar] [CrossRef]
- Lau, Y.L.; Krishnappan, B.G. Transverse dispersion in rectangular channels. J. Hydraul. Div. 1977, 103, 1173–1189. [Google Scholar] [CrossRef]
- Beltaos, S.; Day, T.J. A field study of longitudinal dispersion. Can. J. Civ. Eng. 1978, 5, 572–585. [Google Scholar] [CrossRef]
- Sayre, W.W.; Caro-Cordero, R. Shore-Attached Thermal Plumes in Rivers. Modelling in Rivers; Wiley-Interscience: London, UK, 1979; pp. 15.1–15.44. [Google Scholar]
- Lau, Y.L.; Krishnappan, B.G. Modelling transverse mixing in natural streams. J. Hydraul. Div. 1981, 107, 209–226. [Google Scholar] [CrossRef]
- Holly, F.M.; Nerat, G. Field calibration of stream-tube dispersion model. J. Hydraul. Eng. 1983, 109, 1455–1470. [Google Scholar] [CrossRef]
- Webel, G.; Schatzmann, M. Transverse mixing in open channel flow. J. Hydraul. Eng. 1984, 110, 423–435. [Google Scholar] [CrossRef]
- Long, T.; Guo, J.; Feng, Y.; Huo, G. Modulus of transverse diffuse simulation based on artificial neural network. Chongqing Environ. Sci. 2002, 24, 25–28. (In Chinese) [Google Scholar]
- Seo, I.W.; Baek, K.O.; Jeon, T.M. Analysis of transverse mixing in natural streams under slug tests. J. Hydraul. Res. 2006, 44, 350–362. [Google Scholar] [CrossRef]
- Fischer, H.B. The effect of bends on dispersion in streams. Water Resour. Res. 1969, 5, 496–506. [Google Scholar] [CrossRef]
- Yotsukura, N.; Sayre, W.W. Transverse mixing in natural channels. Water Resour. Res. 1976, 12, 695–704. [Google Scholar] [CrossRef]
- Baek, K.O.; Seo, I.W. Estimation of transverse dispersion coefficient for two-dimensional mixing in natural streams. J. Hydro-environ. Res. 2017, 15, 67–74. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Zhou, W.; Yan, Z.; Zhang, L. A comparative study of 11 non-linear regression models highlighting autoencoder, DBN, and SVR, enhanced by SHAP importance analysis in soybean branching prediction. Sci. Rep. 2024, 14, 5905. [Google Scholar] [CrossRef] [PubMed]
- Taunk, K.; De, S.; Verma, S.; Swetapadma, A. A brief review of nearest neighbor algorithm for learning and classification. In Proceedings of the International Conference on Intelligent Computing and Control Systems (ICICCS 2019), Madurai, India, 15–17 May 2019. [Google Scholar]
- Jeatrakul, P.; Wong, K.; Fung, C. Classification of imbalanced data by combining the complementary neural network and SMOTE algorithm. In Proceedings of the Neural Information Processing Models and Applications: 17th International Conference, ICONIP 2010, Sydney, Australia, 22–25 November 2010. [Google Scholar]
- Rastogi, A.K.; Narang, N.; Siddiqui, Z.A. Imbalanced big bata classification: A distributed implementation of SMOTE. In Proceedings of the Workshop Program of the 19th International Conference on Distributed Computing and Networking, ACM, 14, Varanasi, India, 4–7 January 2018. [Google Scholar]
- Pedregosa, F.; Grise, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; Vanderplas, J.; Passos, A.; Cournapeau, D.; Brucher, M.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Nguyen, H.M.; Cooper, E.W.; Kamei, K. Borderline oversampling for imbalanced data classification. Int. J. Knowl. Eng. Soft Data Paradig. 2011, 3, 4–21. [Google Scholar] [CrossRef]
- Winson, D.L. Asymptotic properties of nearest neighbor rules using edited data. IEEE Trans. Syst. Man Cybern. 1972, SMC-2, 408–421. [Google Scholar]
- Lemaitre, G.; Nogueira, F.; Aridas, C.K. Imbalanced-learn: A Python Toolbox to Tackle the Curse of Imbalanced Datasets in Machine Learning. J. Mach. Learn. Res. 2017, 18, 1–5. [Google Scholar]
- Hodges, J.L. The significance probability of the Smirnov two-sample test. Ark. Mat. 1958, 3, 469–486. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inform. Process. Syst. 1996, 9, 155–161. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Altman, N.S. An introduction to kernel and nearest neighbor nonparametric regression. Am. Stat. 1992, 46, 175–185. [Google Scholar]
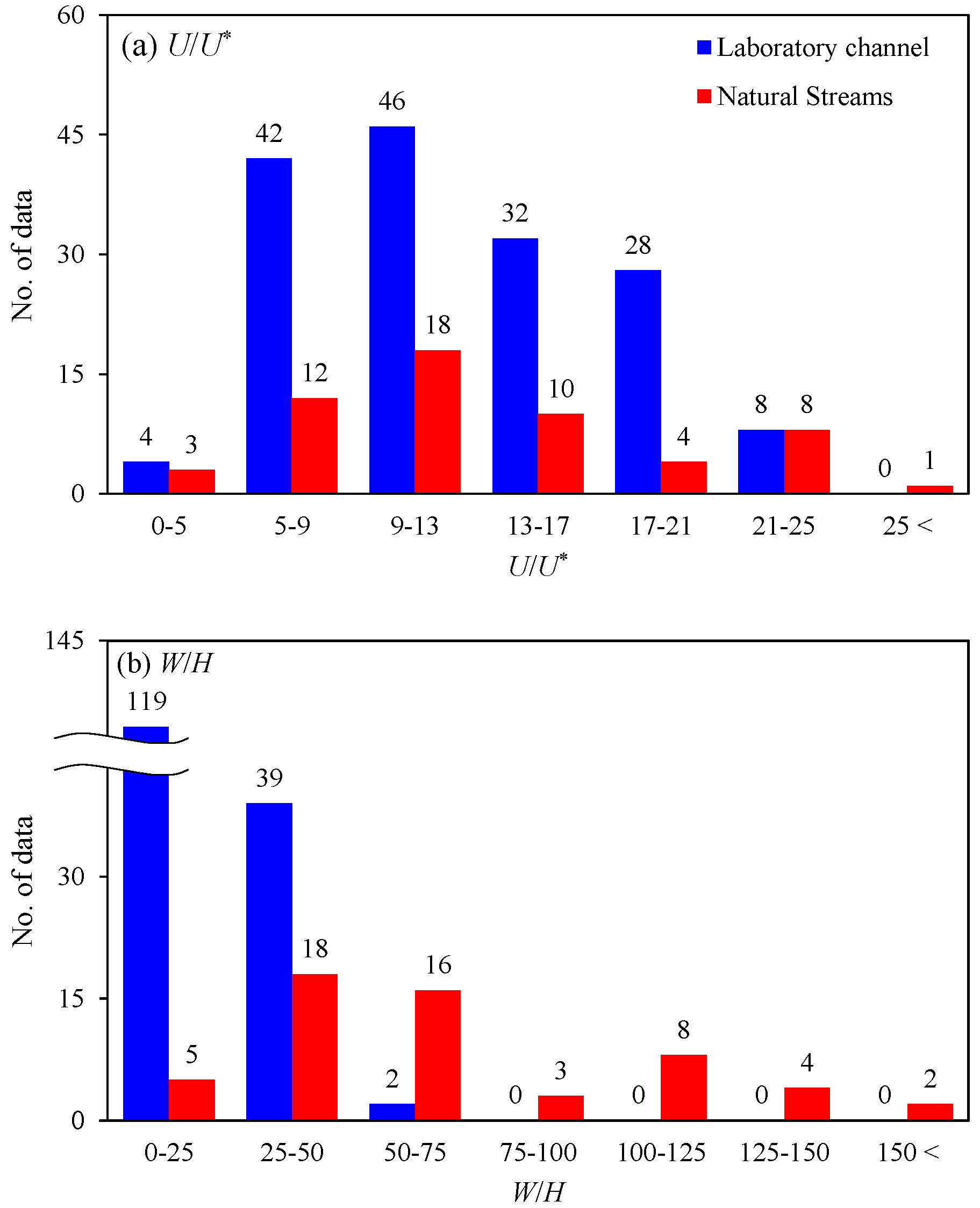
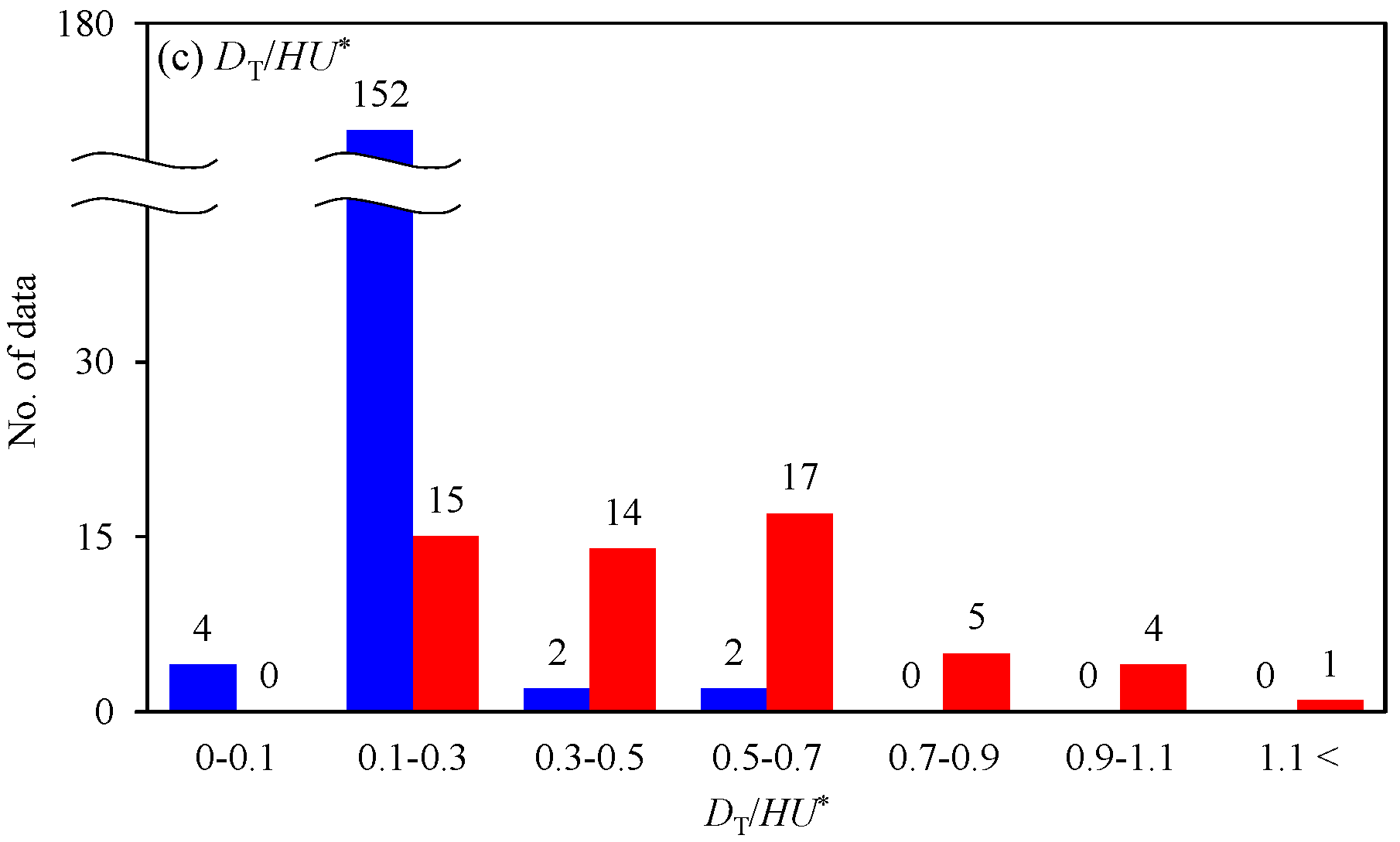
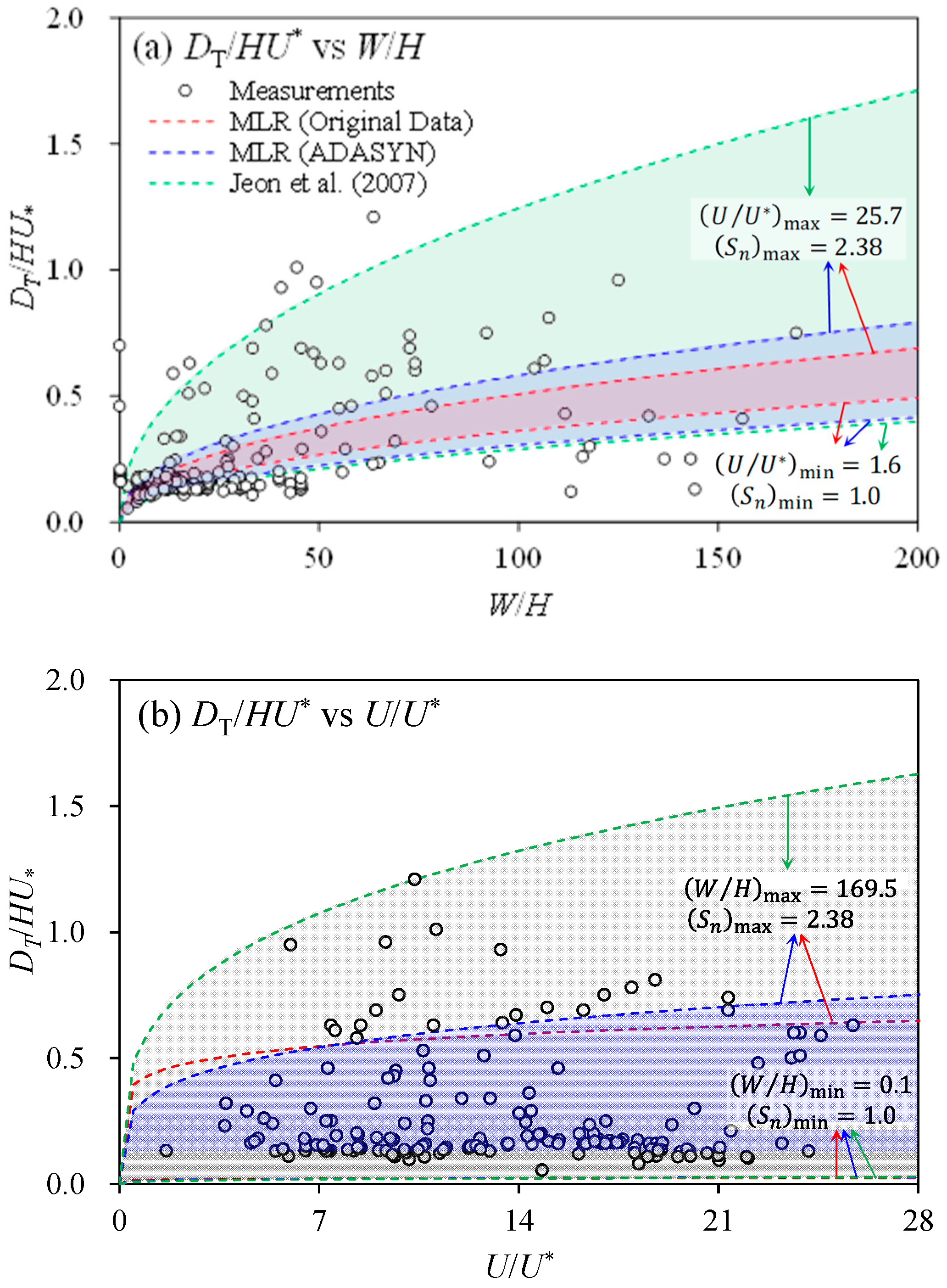
| Laboratory Channels (No. of Datasets = 160) | Natural Streams (No. of Datasets = 56) | |||||
|---|---|---|---|---|---|---|
| Max | 65.1 | 24.6 | 0.70 | 169.5 | 25.7 | 1.21 |
| Min | 0.1 | 1.6 | 0.05 | 14.4 | 3.7 | 0.12 |
| Average | 17.7 | 12.5 | 0.16 | 67.9 | 12.8 | 0.51 |
| Median | 14.7 | 11.9 | 0.14 | 57.4 | 11.0 | 0.49 |
| Standard Deviation | 12.8 | 4.9 | 0.07 | 40.3 | 6.0 | 0.24 |
| References | Empirical Formulas | Method |
|---|---|---|
| Yotsukura and Sayre [70] | MLR | |
| Bansal [50] | ||
| Deng et al. [17] | ||
| Jeon et al. [10] | ||
| Baek and Seo [18] | , | |
| Gond et al. [12] | , , : flow nonuniformity parameter | |
| Aghababaei et al. [19] | Genetic-programming-based symbolic regression (GP-SR) | |
| Huai et al. [30] | (straight flume) (natural streams) | Genetic programming (GP) |
| Technique | Data Resampling | Pros | Cons | Reference |
|---|---|---|---|---|
| SMOTE | Generates synthetic samples near minority instances | Mitigates class imbalance | Sensitive to noisy data | Chawla et al. [34] |
| SMOTE-ENN | Applies Edited Nearest Neighbor (ENN) for noise reduction | Effective in handling noisy data | Possible to discard informative instances during undersampling | Batista et al. [42] |
| ADASYN | Utilizes density distribution for minority class data synthesis | Adapts to data density variations | Possible to introduce noise due to adaptability | He et al. [41] |
| SVM-SMOTE | Integrates with support vector machine (SVM) for minority data synthesis | Generates samples in the feature space of minority class | Computationally expensive and sensitive to SVM parameters | Nguyen et al. [78] |
| Oversampling | Classification Performance Indicators | Kolmogorov–Smirnov Test: p-Value | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Accuracy (Equation (8)) | Precision (Equation (9)) | Recall (Equation (10)) | F1 (Equation (11)) | AUC * | Average | ||||
| SMOTE | 0.826 | 0.937 | 0.884 | 0.910 | 0.983 | 0.992 | 0.988 | 0.979 | 0.986 |
| SMOTE-ENN | 0.820 | 0.939 | 0.874 | 0.905 | 0.983 | 0.988 | 0.960 | 0.994 | 0.981 |
| ADASYN | 0.749 | 0.931 | 0.806 | 0.864 | 0.971 | 0.889 | 0.595 | 0.783 | 0.756 |
| SVM-SMOTE | 0.763 | 0.937 | 0.815 | 0.872 | 0.969 | 0.846 | 0.833 | 0.954 | 0.878 |
| Data | Coefficients | ||
|---|---|---|---|
| a | b | c | |
| Original | 0.0443 | 0.4430 | 0.1228 |
| SMOTE | 0.0323 | 0.3648 | 0.4055 |
| SMOTE-ENN | 0.0408 | 0.3652 | 0.3118 |
| ADASYN | 0.0352 | 0.4437 | 0.2348 |
| SVM-SMOTE | 0.0558 | 0.4021 | 0.1273 |
| This Study | Previous Studies | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Original Data | SMOTE | SMOTE-ENN | ADASYN | SVM-SMOTE | Bansal [50] | Deng et al. [17] | Jeon et al. [10] | Aghababaei et al. [19] | Huai et al. [30] | |
| MAPE (%) | 53.4 | 67.3 | 65.7 | 57.2 | 63.0 | 108.8 | 155.4 | 51.2 | 27.0 | 15.0 |
| MAPE (%) () | 56.4 | 73.8 | 71.6 | 61.2 | 67.9 | 80.8 | 131.7 | 55.5 | 27.7 | 15.0 |
| MAPE (%) () | 37.1 | 31.2 | 33.0 | 35.0 | 36.4 | 262.5 | 285.5 | 23.9 | 22.2 | 14.9 |
| Data | Data Range | MAPE (%) | Average | Rank | ||
|---|---|---|---|---|---|---|
| SVR | XGBoost | KNR | ||||
| Original Data | Total | 44.1 | 44.3 | 42.2 | 43.6 | 5 |
| 50 | 44.4 | 49.2 | 44.2 | 46.0 | ||
| 50 < | 42.5 | 17.3 | 31.3 | 30.4 | ||
| SMOTE | Total | 24.3 | 18.0 | 31.6 | 24.6 | 3 |
| 50 | 27.9 | 19.3 | 32.7 | 26.7 | ||
| 50 < | 4.5 | 10.9 | 25.0 | 13.5 | ||
| SMOTE-ENN | Total | 24.8 | 18.2 | 33.4 | 25.5 | 4 |
| 50 | 28.5 | 19.1 | 34.4 | 27.3 | ||
| 50 < | 4.3 | 13.4 | 28.0 | 15.2 | ||
| ADASYN | Total | 21.5 | 10.9 | 30.2 | 20.9 | 1 |
| 50 | 24.4 | 11.0 | 31.6 | 22.4 | ||
| 50 < | 5.6 | 10.2 | 22.4 | 12.7 | ||
| SVM-SMOTE | Total | 22.5 | 16.5 | 32.9 | 23.9 | 2 |
| 50 | 25.9 | 18.1 | 34.1 | 26.1 | ||
| 50 < | 3.5 | 7.7 | 25.9 | 12.4 | ||
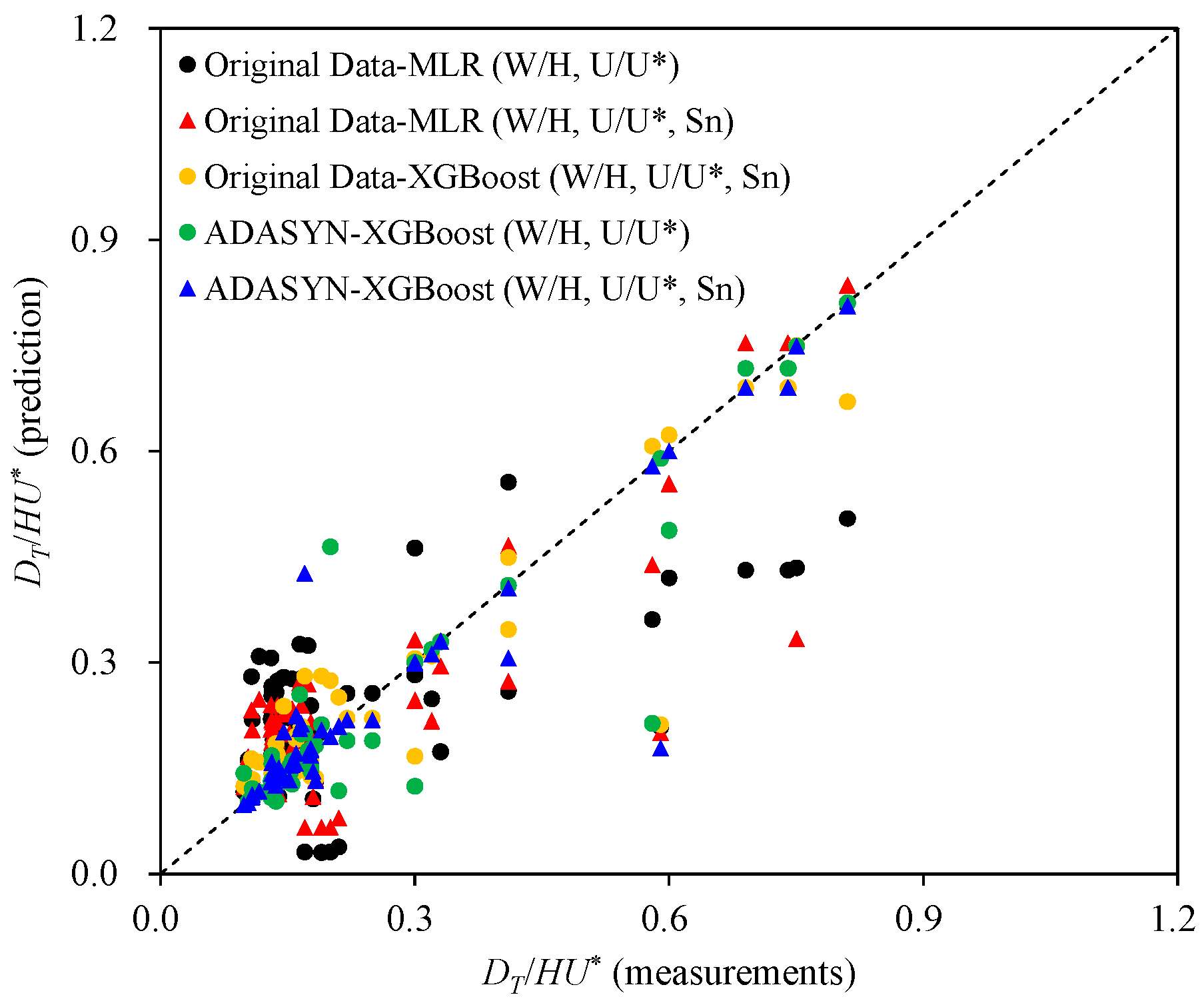
| Original Data—MLR | Original Data—XGBoost | ADASYN—XGBoost | |||
|---|---|---|---|---|---|
| MAPE (%) | 54.2 | 38.0 | 15.7 | 12.4 | 9.5 |
| Performance Improvement (%) | - | 29.8 | 71.1 | 77.1 | 82.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Park, I. Application of Oversampling Techniques for Enhanced Transverse Dispersion Coefficient Estimation Performance Using Machine Learning Regression. Water 2024, 16, 1359. https://doi.org/10.3390/w16101359
Lee S, Park I. Application of Oversampling Techniques for Enhanced Transverse Dispersion Coefficient Estimation Performance Using Machine Learning Regression. Water. 2024; 16(10):1359. https://doi.org/10.3390/w16101359
Chicago/Turabian StyleLee, Sunmi, and Inhwan Park. 2024. "Application of Oversampling Techniques for Enhanced Transverse Dispersion Coefficient Estimation Performance Using Machine Learning Regression" Water 16, no. 10: 1359. https://doi.org/10.3390/w16101359
APA StyleLee, S., & Park, I. (2024). Application of Oversampling Techniques for Enhanced Transverse Dispersion Coefficient Estimation Performance Using Machine Learning Regression. Water, 16(10), 1359. https://doi.org/10.3390/w16101359





