Quantitative Analysis of the Uncertainty of Drought Process Simulation Based on Atmospheric–Hydrological Coupling in Different Climate Zones
Abstract
:1. Introduction
2. Data and Methodology
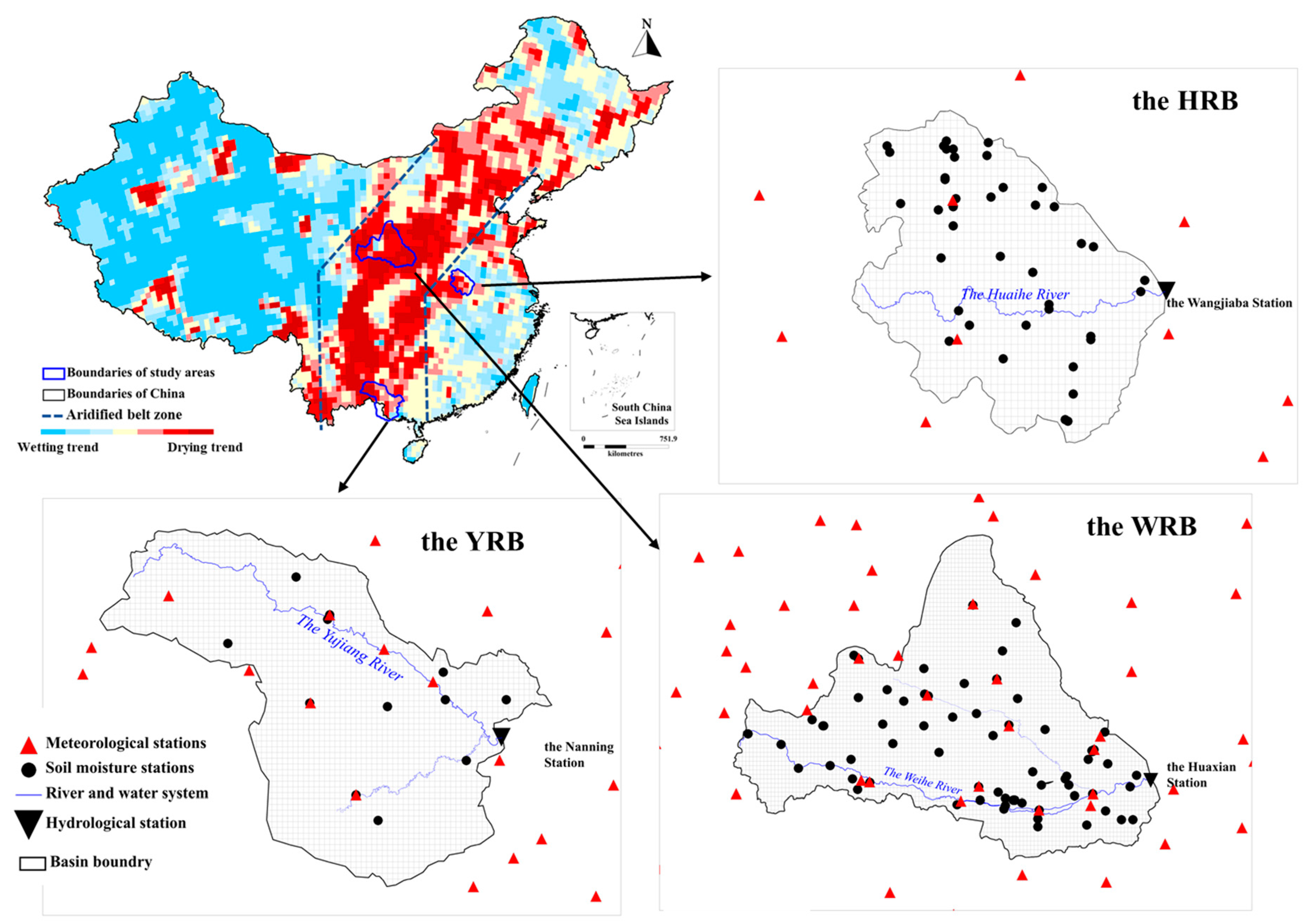
2.1. Study Areas
2.2. Hydrological Model
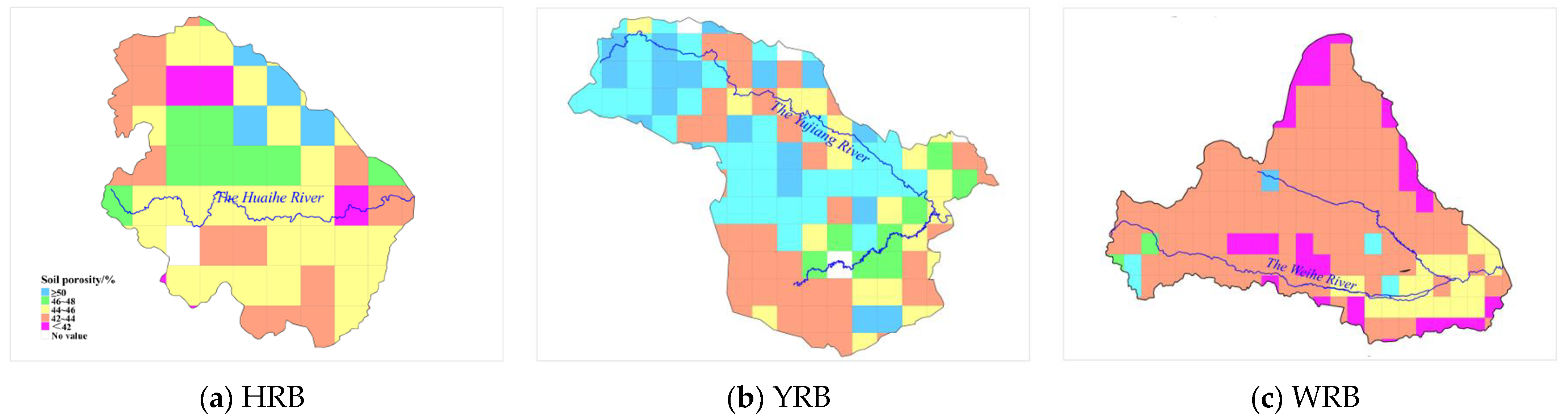
2.3. Data
2.4. Method
2.4.1. Drought Process Identification Based on Soil Moisture
2.4.2. Uncertainty Construction of Drought Process Simulation
3. Results
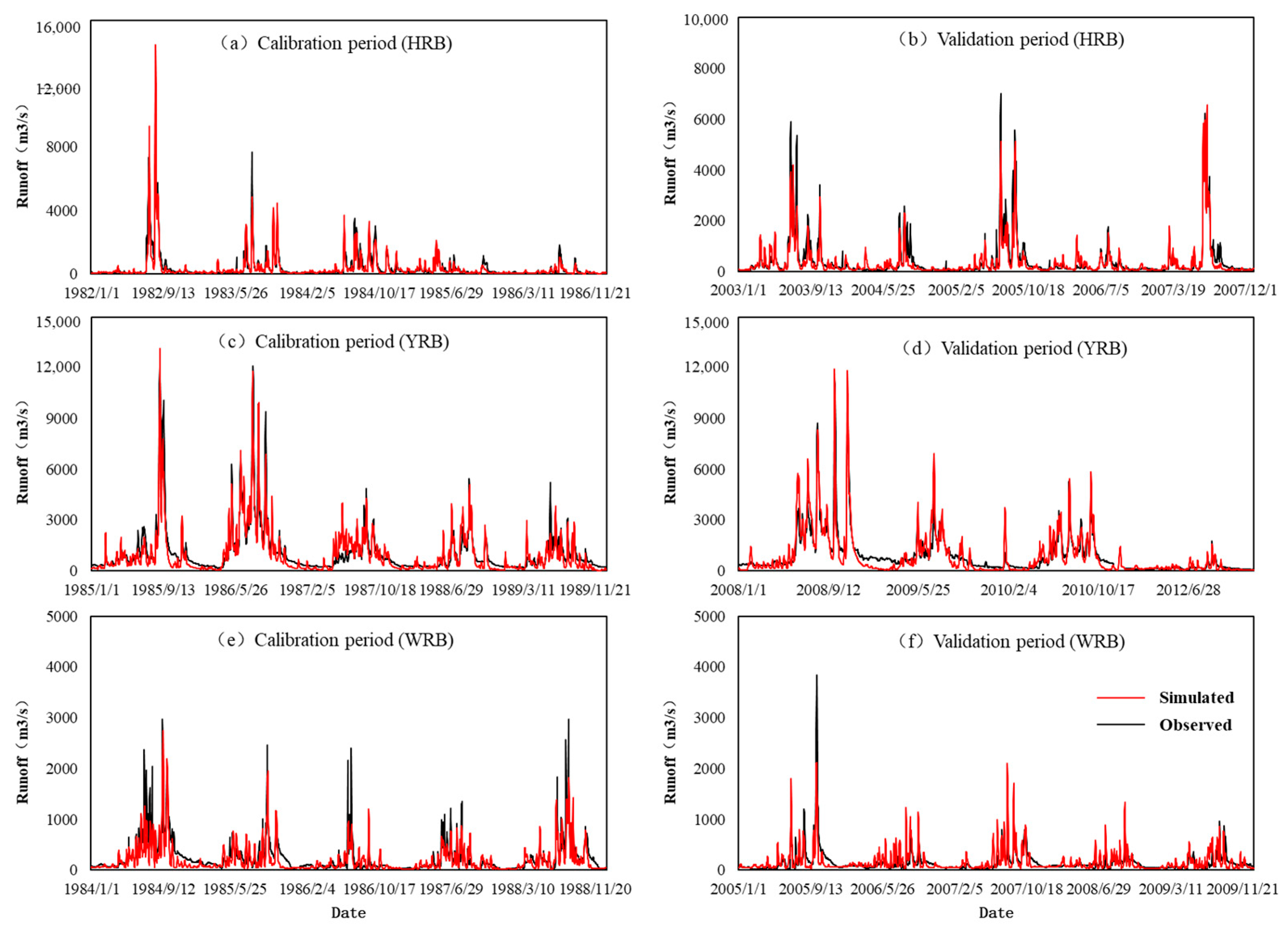
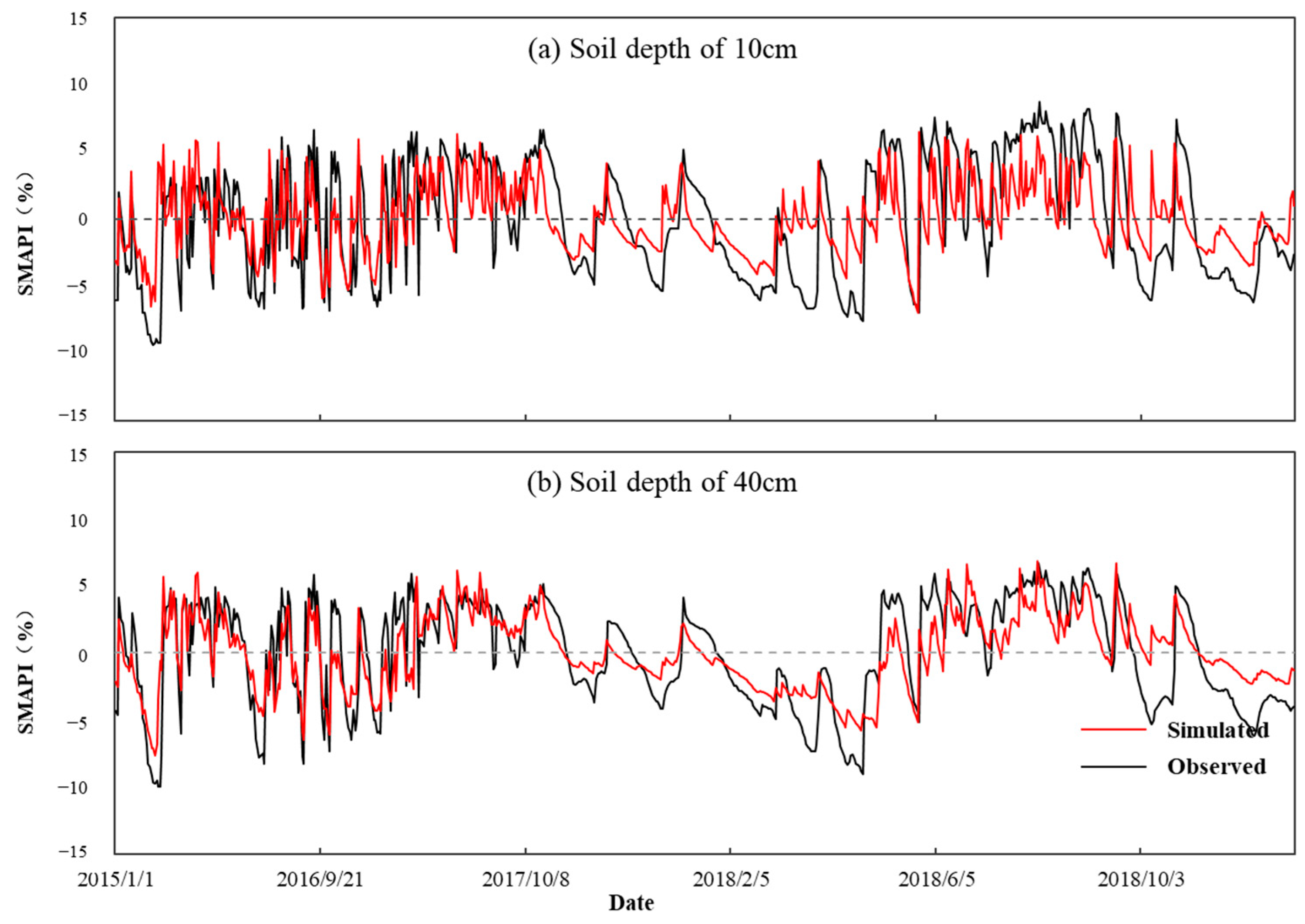
3.1. Simulation Results of the VIC Model
3.1.1. Validation of Runoff
3.1.2. Validation of Soil Moisture
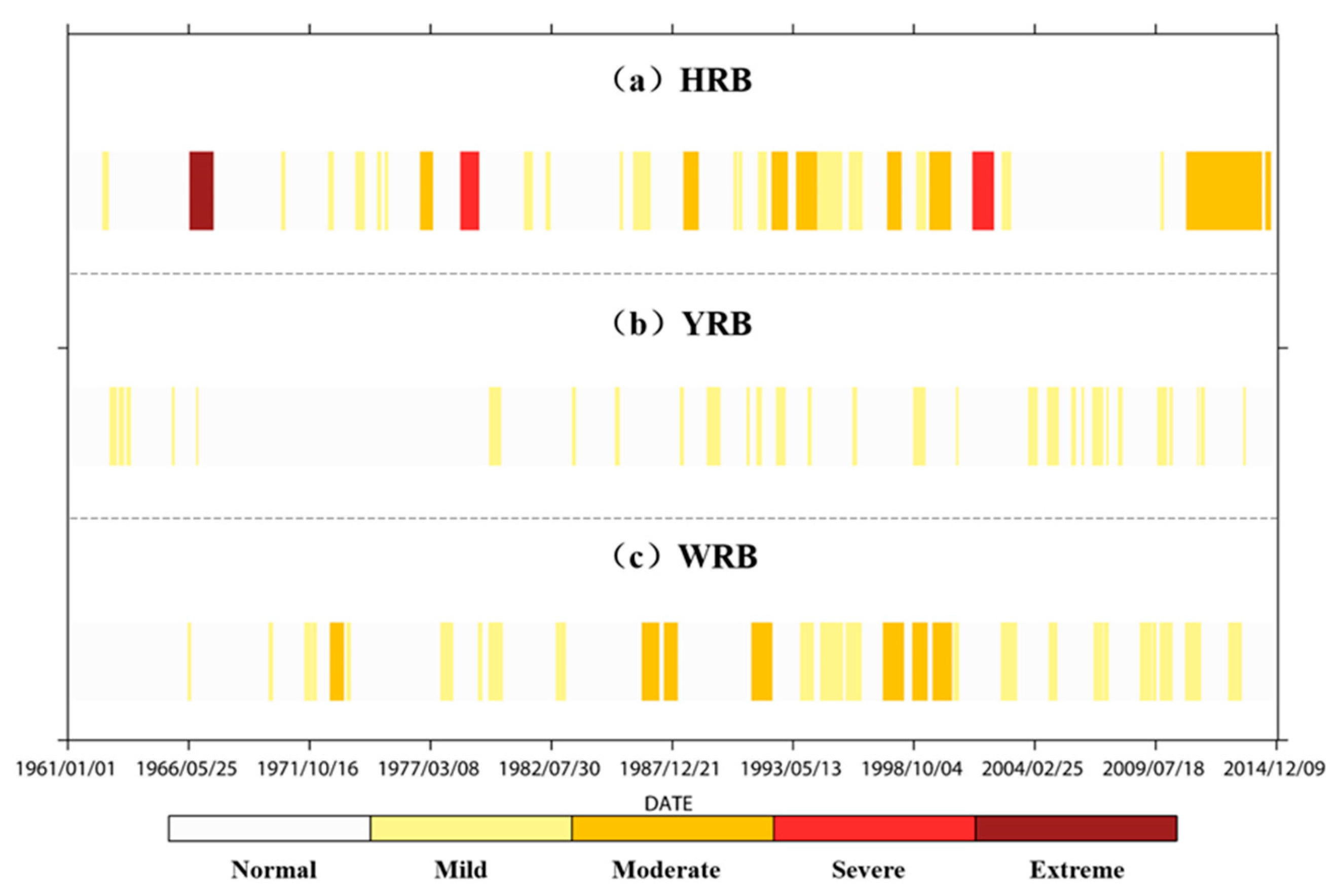
3.2. Identified Historical Drought Events
3.3. Drought Processes Based on Different Initial Conditions
3.4. Uncertainty Characteristics of the Impact of Different Initial Soil States on Drought Processes
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Parmesan, C.; Morecroft, M.D.; Trisurat, Y. Climate Change 2022—Impacts, Adaptation and Vulnerability; GIEC: Geneva, Switzerland, 2023. [Google Scholar]
- Zhang, A.; Zhang, C.; Fu, G.; Wang, B.; Bao, Z.; Zheng, H. Assessments of Impacts of Climate Change and Human Activities on Runoff with SWAT for the Huifa River Basin, Northeast China. Water Resour. Manag. 2012, 26, 2199–2217. [Google Scholar] [CrossRef]
- Song, S.; Nie, Z.; Geng, X.; Shen, X.; Wang, Z.; Zhu, P. Response of runoff to climate change in the area of runoff yield in upstream Shiyang River Basin, Northwest China: A case study of the Xiying River. J. Groundw. Sci. Eng. 2023, 11, 89–96. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, Y.; Zhao, Y.; Long, Y. Using SWAT Model to Assess the Impacts of Land Use and Climate Changes on Flood in the Upper Weihe River, China. Water 2022, 14, 2098. [Google Scholar] [CrossRef]
- Satoh, Y.; Yoshimura, K.; Pokhrel, Y.; Kim, H.; Shiogama, H.; Yokohata, T.; Hanasaki, N.; Wada, Y.; Burek, P.; Byers, E.; et al. The timing of unprecedented hydrological drought under climate change. Nat. Commun. 2022, 13, 3287. [Google Scholar] [CrossRef] [PubMed]
- Yang, P.; Zhang, S.; Xia, J.; Zhan, C.; Cai, W.; Wang, W.; Luo, X.; Chen, N.; Li, J. Analysis of drought and flood alternation and its driving factors in the Yangtze River Basin under climate change. Atmos. Res. 2022, 270, 106087. [Google Scholar] [CrossRef]
- Zhang, G.; Gan, T.Y.; Su, X. Twenty-first century drought analysis across China under climate change. Clim. Dyn. 2021, 59, 1665–1685. [Google Scholar] [CrossRef]
- Chen, L.; Wang, G.; Miao, L.; Gnyawali, K.R.; Li, S.; Amankwah, S.O.Y.; Huang, J.; Lu, J.; Zhan, M. Future drought in CMIP6 projections and the socioeconomic impacts in China. Int. J. Climatol. 2021, 41, 4151–4170. [Google Scholar] [CrossRef]
- Song, Z.; Xia, J.; She, D.; Li, L.; Hu, C.; Hong, S. Assessment of meteorological drought change in the 21st century based on CMIP6 multi-model ensemble projections over mainland China. J. Hydrol. 2021, 601, 126643. [Google Scholar] [CrossRef]
- Zhang, G.; Su, X.; Singh, V.P.; Ayantobo, O.O. Appraising standardized moisture anomaly index (SZI) in drought projection across China under CMIP6 forcing scenarios. J. Hydrol. Reg. Stud. 2021, 37, 100898. [Google Scholar] [CrossRef]
- Huang, T.; Wu, Z.; Xiao, P.; Sun, Z.; Liu, Y.; Wang, J.; Wang, Z. Possible Future Climate Change Impacts on the Meteorological and Hydrological Drought Characteristics in the Jinghe River Basin, China. Remote Sens. 2023, 15, 1297. [Google Scholar] [CrossRef]
- Lin, Q.; Wu, Z.; Zhang, Y.; Peng, T.; Chang, W.; Guo, J. Propagation from meteorological to hydrological drought and its application to drought prediction in the Xijiang River basin, South China. J. Hydrol. 2023, 617, 128889. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, Z.; Shao, Q.; He, H.; Guo, X. From meteorological to agricultural drought: Propagation time and probabilistic linkages. J. Hydrol. Reg. Stud. 2023, 46, 101329. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Glantz, M.H. Understanding: The drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Kiem, A.S.; Johnson, F.; Westra, S.; van Dijk, A.; Evans, J.P.; O’Donnell, A.; Rouillard, A.; Barr, C.; Tyler, J.; Thyer, M.; et al. Natural hazards in Australia: Droughts. Clim. Chang. 2016, 139, 37–54. [Google Scholar] [CrossRef]
- Zhang, Y.; You, Q.; Chen, C.; Ge, J.; Adnan, M. Evaluation of Downscaled CMIP5 Coupled with VIC Model for Flash Drought Simulation in a Humid Subtropical Basin, China. J. Clim. 2018, 31, 1075–1090. [Google Scholar] [CrossRef]
- Luo, L.; Wood, E.F. Monitoring and predicting the 2007 U.S. drought. Geophys. Res. Lett. 2007, 34, L22702. [Google Scholar] [CrossRef]
- Yuan, X.; Wood, E.F.; Luo, L.; Pan, M. A first look at Climate Forecast System version 2 (CFSv2) for hydrological seasonal prediction. Geophys. Res. Lett. 2011, 38, L13402. [Google Scholar] [CrossRef]
- WU, Z.; LU, G.; GUO, H.; KUANG, Y. Drought monitoring technology based on simulation of soil moisture. J. Hohai Univ. (Nat. Sci.) 2012, 40, 28–32. [Google Scholar]
- Yuan, X.; Wood, E.F.; Ma, Z. A review on climate-model-based seasonal hydrologic forecasting: Physical understanding and system development. WIREs Water 2015, 2, 523–536. [Google Scholar] [CrossRef]
- Yuan, X.; Ma, F.; Wang, L.; Zheng, Z.; Ma, Z.; Ye, A.; Peng, S. An experimental seasonal hydrological forecasting system over the Yellow River basin—Part 1: Understanding the role of initial hydrological conditions. Hydrol. Earth Syst. Sci. 2016, 20, 2437–2451. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, Z.; Xiao, H.; Wu, H. Spatio-Temporal Analysis of Drought Events in the Upper Reaches of Yangtze River Basin Based on Simulation of Soil Moisture. Resour. Environ. Yangtze Basin 2018, 27, 176–184. [Google Scholar]
- Boeing, F.; Rakovec, O.; Kumar, R.; Samaniego, L.; Schrön, M.; Hildebrandt, A.; Rebmann, C.; Thober, S.; Müller, S.; Zacharias, S.; et al. High-resolution drought simulations and comparison to soil moisture observations in Germany. Hydrol. Earth Syst. Sci. 2022, 26, 5137–5161. [Google Scholar] [CrossRef]
- Golden, H.E.; Lane, C.R.; Adnan, R.; Qiusheng, W. Improving global flood and drought predictions: Integrating non-floodplain wetlands into watershed hydrologic models. Environ. Res. Lett. 2021, 16, 1–5. [Google Scholar] [CrossRef]
- Chan, S.S.; Seidenfaden, I.K.; Jensen, K.H.; Sonnenborg, T.O. Climate change impacts and uncertainty on spatiotemporal variations of drought indices for an irrigated catchment. J. Hydrol. 2021, 601, 126814. [Google Scholar] [CrossRef]
- De Luca, D.L.; Apollonio, C.; Petroselli, A. The Benefit of Continuous Hydrological Modelling for Drought Hazard Assessment in Small and Coastal Ungauged Basins: A Case Study in Southern Italy. Climate 2022, 10, 34. [Google Scholar] [CrossRef]
- Lin, Q.; Wu, Z.; Liu, J.; Singh, V.P.; Zuo, Z. Hydrological drought dynamics and its teleconnections with large-scale climate indices in the Xijiang River basin, South China. Theor. Appl. Climatol. 2022, 150, 229–249. [Google Scholar] [CrossRef]
- Xing, Z.; Ma, M.; Su, Z.; Lv, J.; Yi, P.; Song, W. A review of the adaptability of hydrological models for drought forecasting. Proc. Int. Assoc. Hydrol. Sci. 2020, 383, 261–266. [Google Scholar] [CrossRef]
- Brigode, P.; Oudin, L.; Perrin, C. Hydrological model parameter instability: A source of additional uncertainty in estimating the hydrological impacts of climate change? J. Hydrol. 2013, 476, 410–425. [Google Scholar] [CrossRef]
- Shen, M.; Chen, J.; Zhuan, M.; Chen, H.; Xu, C.; Xiong, L. Estimating uncertainty and its temporal variation related to global climate models in quantifying climate change impacts on hydrology. J. Hydrol. 2018, 556, 10–24. [Google Scholar] [CrossRef]
- Anderson, G.J.; Lucas, D.D.; Bonfils, C. Uncertainty Analysis of Simulations of the Turn-of-the-Century Drought in the Western United States. J. Geophys. Res. Atmos. 2018, 123, 13219–13237. [Google Scholar] [CrossRef]
- Chaney, N.W.; Herman, J.D.; Reed, P.M.; Wood, E.F. Flood and drought hydrologic monitoring: The role of model parameter uncertainty. Hydrol. Earth Syst. Sci. 2015, 19, 3239–3251. [Google Scholar] [CrossRef]
- DeChant, C.M.; Moradkhani, H. Analyzing the sensitivity of drought recovery forecasts to land surface initial conditions. J. Hydrol. 2015, 526, 89–100. [Google Scholar] [CrossRef]
- Shi, X.; Yang, Z.; Xu, Z.; Li, Y. Effect of Uncertainty in Rainfall Input on Distributed Watershed Hydrological Simulation: A Case Study of Wuliehe River Basin. J. China Hydrol. 2014, 34, 26–32. [Google Scholar]
- Meresa, H.; Tischbein, B.; Mendela, J.; Demoz, R.; Abreha, T.; Weldemichael, M.; Ogbu, K. The role of input and hydrological parameters uncertainties in extreme hydrological simulations. Nat. Resour. Model. 2021, 35, e12320. [Google Scholar] [CrossRef]
- Smith, K.A.; Barker, L.J.; Tanguy, M.; Parry, S.; Harrigan, S.; Legg, T.P.; Prudhomme, C.; Hannaford, J. A multi-objective ensemble approach to hydrological modelling in the UK: An application to historic drought reconstruction. Hydrol. Earth Syst. Sci. 2019, 23, 3247–3268. [Google Scholar] [CrossRef]
- Samaniego, L.; Kumar, R.; Breuer, L.; Chamorro, A.; Flörke, M.; Pechlivanidis, I.G.; Schäfer, D.; Shah, H.; Vetter, T.; Wortmann, M.; et al. Propagation of forcing and model uncertainties on to hydrological drought characteristics in a multi-model century-long experiment in large river basins. Clim. Chang. 2016, 141, 435–449. [Google Scholar] [CrossRef]
- Ahmadalipour, A.; Moradkhani, H. Analyzing the uncertainty of ensemble-based gridded observations in land surface simulations and drought assessment. J. Hydrol. 2017, 555, 557–568. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Krysanova, V.; Benestad, R.E.; Hov, Ø.; Piniewski, M.; Otto, I.M. Uncertainty in climate change impacts on water resources. Environ. Sci. Policy 2018, 79, 1–8. [Google Scholar] [CrossRef]
- Nearing, G.S.; Tian, Y.; Gupta, H.V.; Clark, M.P.; Harrison, K.W.; Weijs, S.V. A philosophical basis for hydrological uncertainty. Hydrol. Sci. J. 2016, 61, 1666–1678. [Google Scholar] [CrossRef]
- Staudinger, M.; Seibert, J. Predictability of low flow—An assessment with simulation experiments. J. Hydrol. 2014, 519, 1383–1393. [Google Scholar] [CrossRef]
- Koster, R.D.; Suarez, M.J.; Heiser, M. Variance and Predictability of Precipitation at Seasonal-to-Interannual Timescales. J. Hydrometeorol. 2000, 1, 26–46. [Google Scholar] [CrossRef]
- Li, H.; Luo, L.; Wood, E.F.; Schaake, J. The role of initial conditions and forcing uncertainties in seasonal hydrologic forecasting. J. Geophys. Res. 2009, 114, D04114. [Google Scholar] [CrossRef]
- Wood, A.W.; Lettenmaier, D.P. An ensemble approach for attribution of hydrologic prediction uncertainty. Geophys. Res. Lett. 2008, 35, L14401. [Google Scholar] [CrossRef]
- Shukla, S.; Lettenmaier, D.P. Seasonal hydrologic prediction in the United States: Understanding the role of initial hydrologic conditions and seasonal climate forecast skill. Hydrol. Earth Syst. Sci. 2011, 15, 3529–3538. [Google Scholar] [CrossRef]
- Shukla, S.; Sheffield, J.; Wood, E.F.; Lettenmaier, D.P. On the sources of global land surface hydrologic predictability. Hydrol. Earth Syst. Sci. Discuss. 2013, 17, 2781–2796. [Google Scholar] [CrossRef]
- Yuan, X.; Wood, E.F.; Roundy, J.K.; Pan, M. CFSv2-Based Seasonal Hydroclimatic Forecasts over the Conterminous United States. J. Clim. 2013, 26, 4828–4847. [Google Scholar] [CrossRef]
- Sinha, T.; Sankarasubramanian, A. Role of climate forecasts and initial conditions in developing streamflow and soil moisture forecasts in a rainfall–runoff regime. Hydrol. Earth Syst. Sci. 2013, 17, 721–733. [Google Scholar] [CrossRef]
- Mo, K.C.; Lettenmaier, D.P. Hydrologic Prediction over the Conterminous United States Using the National Multi-Model Ensemble. J. Hydrometeorol. 2014, 15, 1457–1472. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P.; Xia, Y. Seasonal Drought Prediction: Advances, Challenges, and Future Prospects. Rev. Geophys. 2018, 56, 108–141. [Google Scholar] [CrossRef]
- Wood, A.W.; Hopson, T.; Newman, A.; Brekke, L.; Arnold, J.; Clark, M. Quantifying Streamflow Forecast Skill Elasticity to Initial Condition and Climate Prediction Skill. J. Hydrometeorol. 2016, 17, 651–668. [Google Scholar] [CrossRef]
- Lu, G.; Yan, G.; Wu, Z.; He, H. Analysis on aridification within last 50 years in China. Water Resour. Hydropower Eng. 2010, 41, 78–82. [Google Scholar]
- Jiashuai, G.; Qiongfang, L.; Mingyuan, N.; Qihui, C.; Pengfei, H.; Zhengmo, Z.; Tianshan, Z.; Yao, D.; Yun, S.; Xingye, H. An Analysis of Meteorological Drought Characteristics in the Upper Reaches of Huaihe River Based on Multidimensional Copula Function. China Rural Water Hydropower 2019, 8, 83–87, 92. [Google Scholar]
- Wei, Z.; Yi, L.; Qiongfang, L.; Liliang, R.; Tao, C. Drought Evaluation for Upper Reaches of the Huaihe River. J. China Hydrol. 2009, 29, 69–72. [Google Scholar]
- Hui, L.; Jingcai, W.; Jinbai, H.; Chenjuan, J. Comparative study on spatial and temporal distribution characteristics of meteorological drought in the upper and middle reaches of Huai River Basin based on SPI and SPEI. J. Water Resour. Water Eng. 2019, 39, 59–67. [Google Scholar]
- Lijie, Z.; Jian, L. Spatiotemporal change of drought at various time scales indicated by SPEI and SPI in Xijiang river basin. Plateau Meteorol. 2018, 37, 560–567. [Google Scholar]
- Rongjie, F.; Chaohua, J.; Lili, S.; Chunqing, G. An Analysis of Change Law of Runoff Sequences in Xijiang River Basin. China Rural Water Hydropower 2020, 1, 111–115, 124. [Google Scholar]
- Ruirui, X.; Peng, G.; Xingmin, M.; Xueke, C.; Chaojun, G. Dynamic of Streamflow and Sediment Load and Its Response to Human Activities in the Weihe River Basin. Yellow River 2020, 42, 17–24. [Google Scholar]
- Zhaoxia, J.; Jun, X.; Yang, K.; Dunxian, S.; Qiang, W. Spatial and Temporal Patterns of Droughts in Weihe River Basin Based on CI Drought Index. Yellow River 2017, 39, 86–91, 95. [Google Scholar]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. Atmos. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F. Characteristics of global and regional drought, 1950–2000: Analysis of soil moisture data from off-line simulation of the terrestrial hydrologic cycle. J. Geophys. Res. 2007, 112, D17115. [Google Scholar] [CrossRef]
- Rosenbrock, H.H. An Automatic Method for Finding the Greatest or Least Value of a Function. Comput. J. 1960, 3, 175–184. [Google Scholar] [CrossRef]
- Wu, Z.; Lu, G.; Wen, L.; Lin, C.A. Reconstructing and analyzing China’s fifty-nine year (1951–2009) drought history using hydrological model simulation. Hydrol. Earth Syst. Sci. 2011, 15, 2881–2894. [Google Scholar] [CrossRef]
- Yao, M.; Yuan, X. Evaluation of summer drought ensemble prediction over the Yellow River basin. Atmos. Ocean. Sci. Lett. 2018, 11, 314–321. [Google Scholar] [CrossRef]
- Mao, Y.; Wu, Z.; He, H.; Lu, G.; Xu, H.; Lin, Q. Spatio-temporal analysis of drought in a typical plain region based on the soil moisture anomaly percentage index. Sci. Total Environ. 2017, 576, 752–765. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Dong, Z.; Qiaoqian, L.; Zhengquan, C. Real-Time Performance Evaluation of Numerical Weather Prediction Models Using Uncertainty Index. Meteorol. Sci. Technol. 2007, 35, 322–326. [Google Scholar]
- Fan, J.; Xu, F.; Sun, X.; Dong, W.; Ma, X.; Liu, G.; Cheng, Y.; Wang, H. Construction and Application of Hydrometeorological Comprehensive Drought Index in Weihe River. Atmosphere 2022, 13, 610. [Google Scholar] [CrossRef]
- Yanjun, L.; Xiaodong, Z.; Fan, L.; Jing, M. Analysis of Drought Evolvement Characteristics Based on Standardized Precipitation Index in the Huaihe River Basin. Procedia Eng. 2012, 28, 434–437. [Google Scholar] [CrossRef]
- Te, Z.; Ji, L.; Rong, W.; Wenjuan, C.; Xiaohua, D.; Zhouliang, S. Response of Vegetation to Meteorological Drought in Upper Huaihe River Basin. Res. Soil Water Conserv. 2020, 27, 213–219. [Google Scholar]
- Shen, H.; Yuan, F.; Ren, L.; Ma, M.; Kong, H.; Tong, R. Regional drought assessment using a distributed hydrological model coupled with Standardized Runoff Index. Proc. Int. Assoc. Hydrol. Sci. 2015, 368, 397–402. [Google Scholar] [CrossRef]
- Xiaoffen, C.; Zaimin, W.; Jun, H.; Zhenlong, W. Analysis of Drought Characteristics in the Huaihe River Basin in Recent 60 Years. South-to-North Water Transf. Water Sci. Technol. 2015, 11, 20–24. [Google Scholar]
- Zhang, Q.; Xiao, M.; Singh, V.P.; Chen, X. Copula-based risk evaluation of droughts across the Pearl River basin, China. Theor. Appl. Climatol. 2012, 111, 119–131. [Google Scholar] [CrossRef]
- Qiu, J.; Wang, Y.; Xiao, J. Spatiotemporal Distribution of Droughts in the Xijiang River Basin, China and Its Responses to Global Climatic Events. Water 2017, 9, 265. [Google Scholar] [CrossRef]
- Jingjing, F.; Shibo, W.; Fanfan, X.; Chenyu, W.; Dengfeng, L.; Tianling, Q.; Guanpeng, L.; Yao, C. Impact of ENSO events on meteorological drought in the Weihe River basin, China. Front. Earth Sci. 2023, 11, 1093632. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, H.; Wang, W.; Fu, G. From meteorological droughts to hydrological droughts A case study of the Weihe River Basin, China. Arab. J. Geosci. 2019, 12, 364. [Google Scholar] [CrossRef]
- Zhao, G.; Mu, X.; Tian, P.; Wang, F.; Gao, P. Climate changes and their impacts on water resources in semiarid regions: A case study of the Wei River basin, China. Hydrol. Process. 2013, 27, 3852–3863. [Google Scholar] [CrossRef]
- Zhuguo, M.; Congbin, F.; Li, X.; Wenhai, C.; Shuwang, T. Some problems in the study on the relationship between soil moisture and climatic chagne. Adv. Earth Sci. 2001, 16, 563–566. [Google Scholar]
- Renhe, Z.; Li, L.; Zhiyan, Z. Variations of soil moisture over China and their influences on Chinese climate. Chin. J. Nat. 2016, 38, 313–319. [Google Scholar]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Li, M.; Ma, Z.; Niu, G.-Y. Modeling spatial and temporal variations in soil moisture in China. Chin. Sci. Bull. 2011, 56, 1809–1820. [Google Scholar] [CrossRef]
- Chenghu, S.; Weijing, L.; Zuqiang, Z.; Jinhai, H. Distribution and variation feathers of soil humudity anomaly in Huaihe River Basin and its Relationship with climatic anomaly. J. Appl. Meteorol. Sci. 2005, 16, 129–138. [Google Scholar]
- Niu, J.; Chen, J.; Sun, L. Exploration of drought evolution using numerical simulations over the Xijiang (West River) basin in South China. J. Hydrol. 2015, 526, 68–77. [Google Scholar] [CrossRef]
- Reynolds, C.A.; Jackson, T.J.; Rawls, W.J. Estimating soil water-holding capacities by linking the Food and Agriculture Organization Soil map of the world with global pedon databases and continuous pedotransfer functions. Water Resour. Res. 2000, 36, 3653–3662. [Google Scholar] [CrossRef]
- Noor, S.; Singh, A.; Chitra, R.; Gupta, M. Effect of Clay Content on Permeability and Compaction Parameters of Sand. Int. J. Latest Trends Eng. Technol. 2015, 5, 197–201. [Google Scholar]
- Saxton, K.E.; Rawls, W.J. Soil Water Characteristic Estimates by Texture and Organic Matter for Hydrologic Solutions. Soil Sci. Soc. Am. J. 2006, 70, 1569–1578. [Google Scholar] [CrossRef]
- Hansen, M.; DeFries, R.; Townshend, J.R.; Sohlberg, R. Global land cover classification at 1km resolution using a decision tree classifier. Int. J. Remote Sens. 2000, 21, 1331–1365. [Google Scholar] [CrossRef]











| SMAPI | Drought Classification |
|---|---|
| ≤ −25% | Extreme |
| −25% < ≤ −20% | Severe |
| −20% < ≤ −15% | Moderate |
| −15% < ≤−5% | Mild |
| −5% < ≤ 5% | Normal |
| Parameters (Units) | Description | HRB | YRB | WRB |
|---|---|---|---|---|
| the shape parameter of saturation capacity curve | 0.1 | 0.28 | 0.12 | |
| (mm) | maximum velocity of baseflow | 0.008 | 0.05 | 0.163 |
| the fraction of where non-linear baseflow begins | 31.5 | 8 | 1 | |
| the fraction of maximum soil moisture where non-linear baseflow occurs | 1 | 0.7 | 1 | |
| (m) | the thickness of the first soil layer | 0.1 | 0.1 | 0.1 |
| (m) | the thickness of the second soil layer | 0.5 | 0.58 | 0.725 |
| (m) | the thickness of the third soil layer | 0.63 | 0.99 | 0.225 |
| Basin | Period | Year | Daily RE (%) | Daily NSE |
|---|---|---|---|---|
| HRB | Calibration | 1966~1990 | −7.9 | 0.68 |
| Validation | 1996~2007 | −8.5 | 0.83 | |
| YRB | Calibration | 1981~1995 | −6.0 | 0.84 |
| Validation | 2002~2010 | 0.7 | 0.72 | |
| WRB | Calibration | 1980~1990 | −12.8 | 0.65 |
| Validation | 2003~2012 | 0.2 | 0.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Wu, Z.; He, H.; Chen, R.; Wu, X. Quantitative Analysis of the Uncertainty of Drought Process Simulation Based on Atmospheric–Hydrological Coupling in Different Climate Zones. Water 2023, 15, 3286. https://doi.org/10.3390/w15183286
Xu H, Wu Z, He H, Chen R, Wu X. Quantitative Analysis of the Uncertainty of Drought Process Simulation Based on Atmospheric–Hydrological Coupling in Different Climate Zones. Water. 2023; 15(18):3286. https://doi.org/10.3390/w15183286
Chicago/Turabian StyleXu, Huating, Zhiyong Wu, Hai He, Ruifang Chen, and Xiaotao Wu. 2023. "Quantitative Analysis of the Uncertainty of Drought Process Simulation Based on Atmospheric–Hydrological Coupling in Different Climate Zones" Water 15, no. 18: 3286. https://doi.org/10.3390/w15183286






