Construction and Application of a Water Resources Spatial Equilibrium Model: A Case Study in the Yangtze River Economic Belt
Abstract
:1. Introduction
2. Materials and Methods
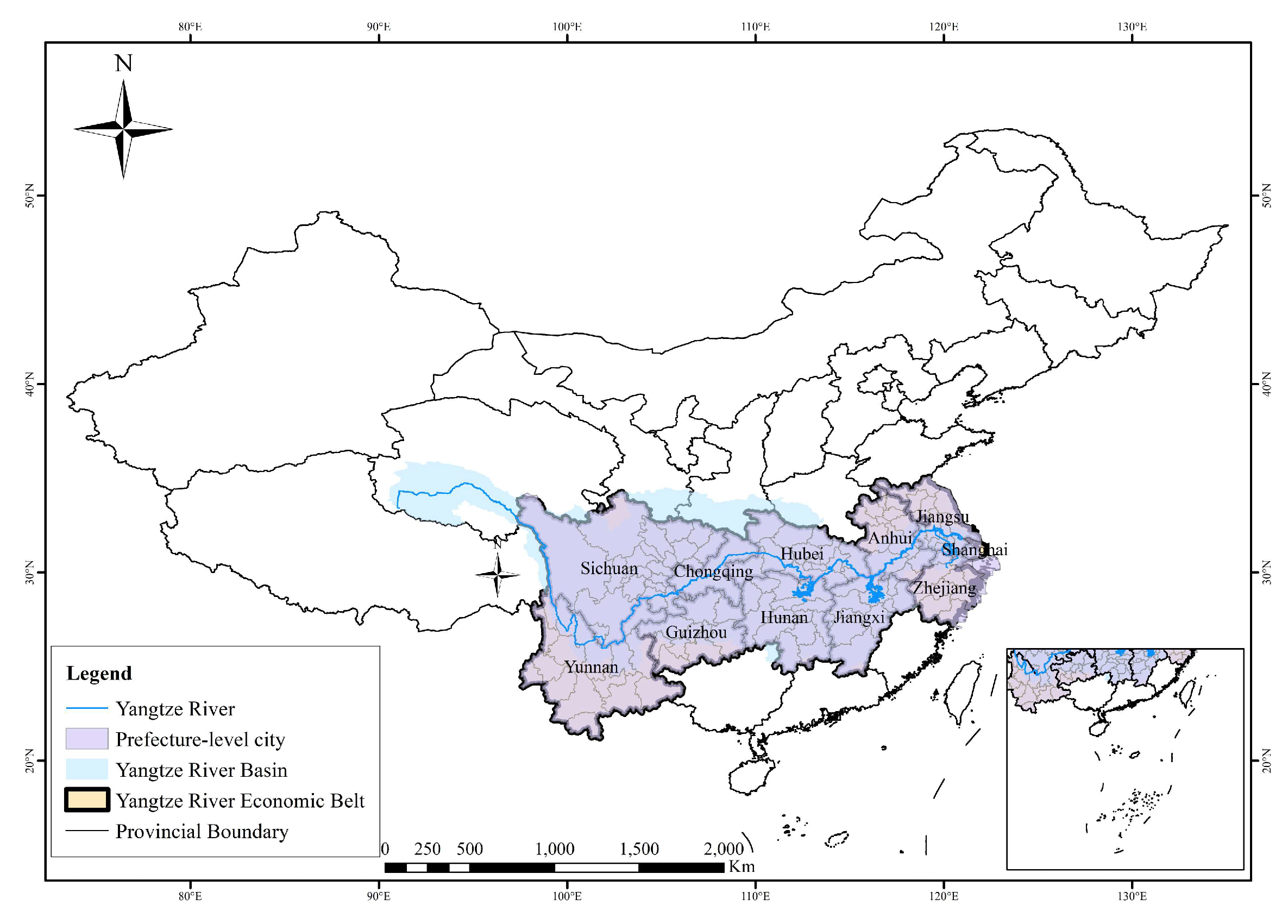
2.1. Study Area and Data
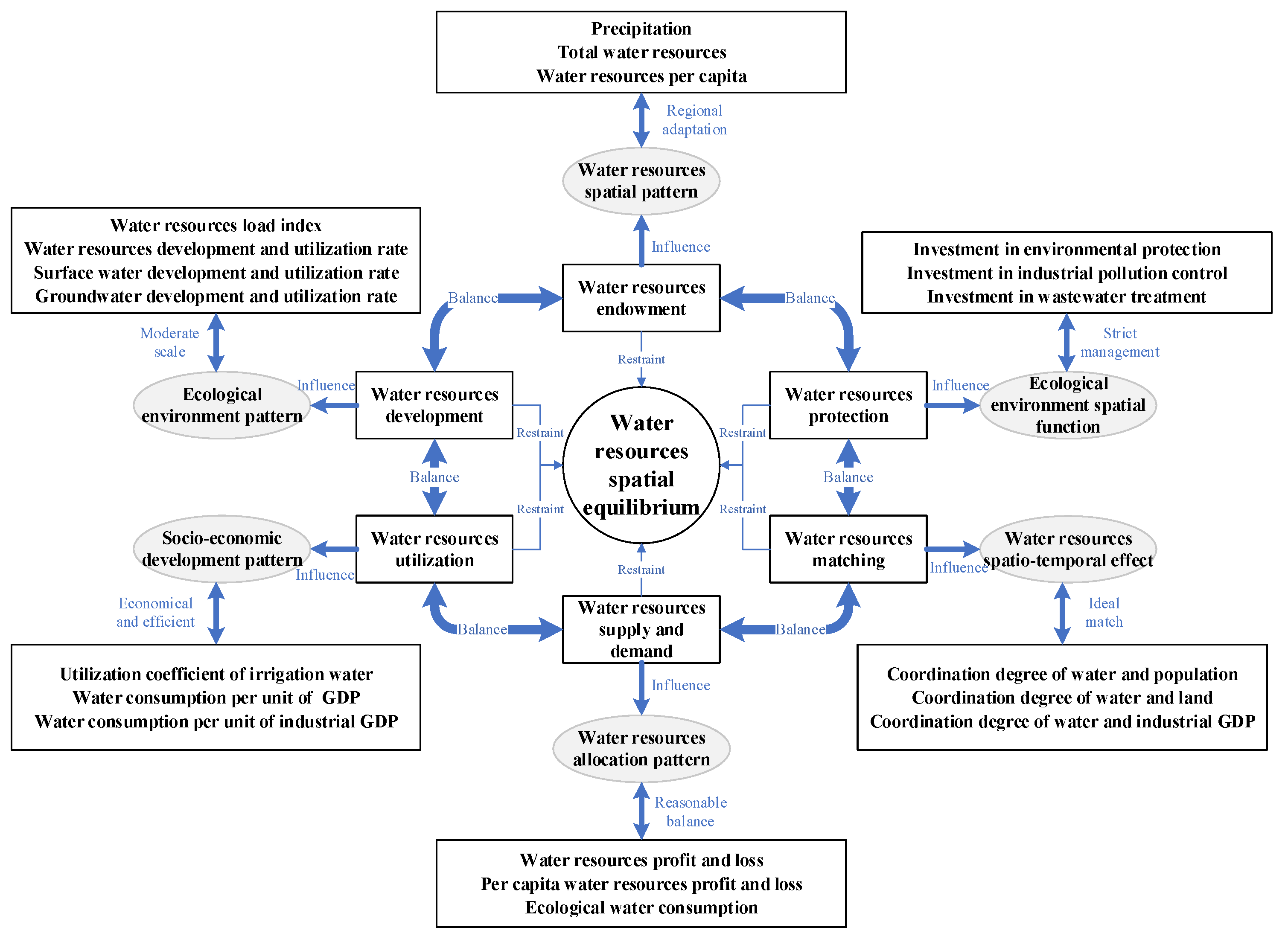
2.2. Conceptual Definition
2.3. Calculation Method
2.3.1. Gini Coefficient
2.3.2. Variable Set
2.3.3. Set Pair and Partial Connection Number
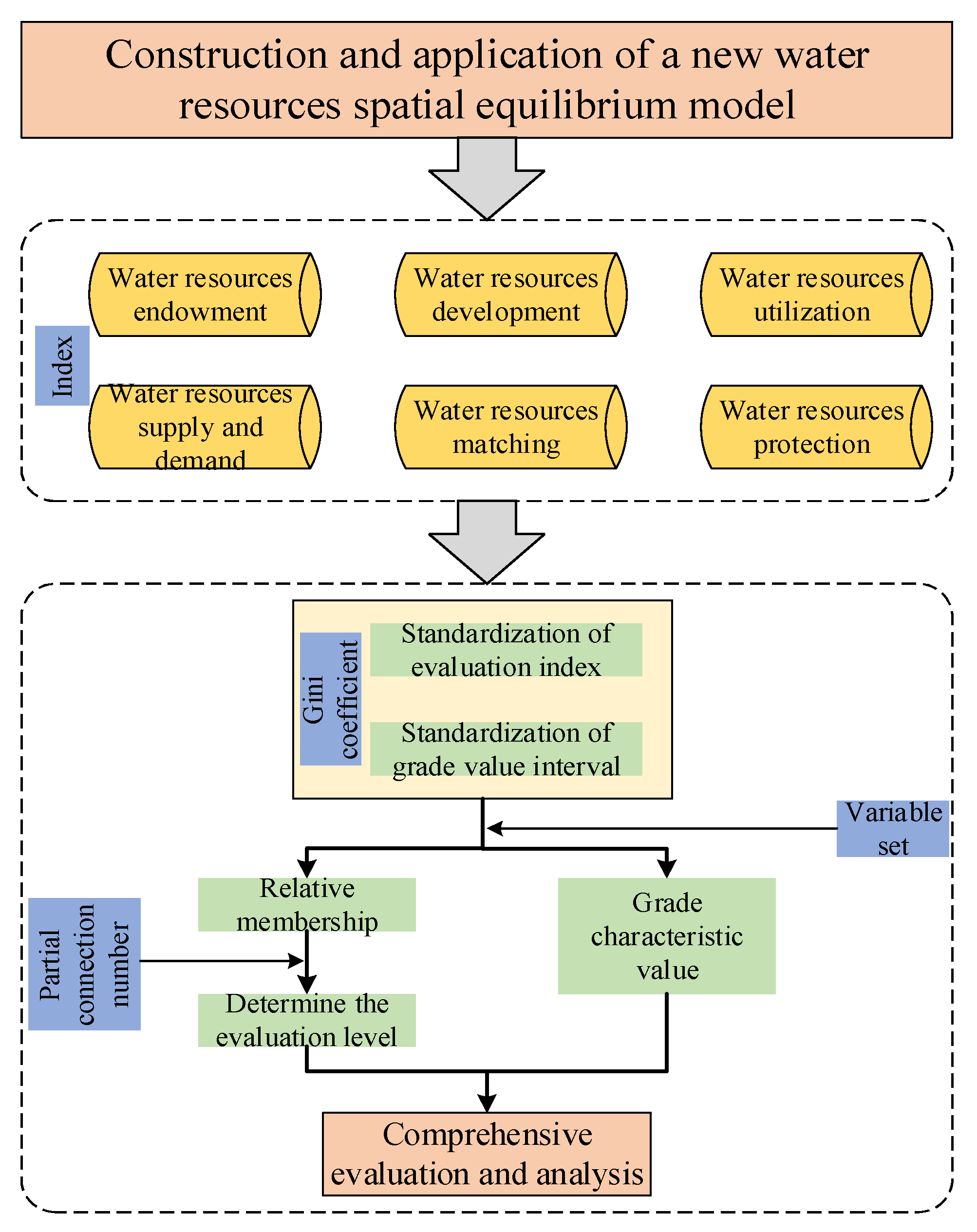
2.3.4. Technology Roadmap
3. Model Application
3.1. Calculation of the Grade Characteristic Values Based on the Variable Set
3.2. Determination of the Evaluation Grade Based on Partial Connection Number
4. Results
4.1. Provinces
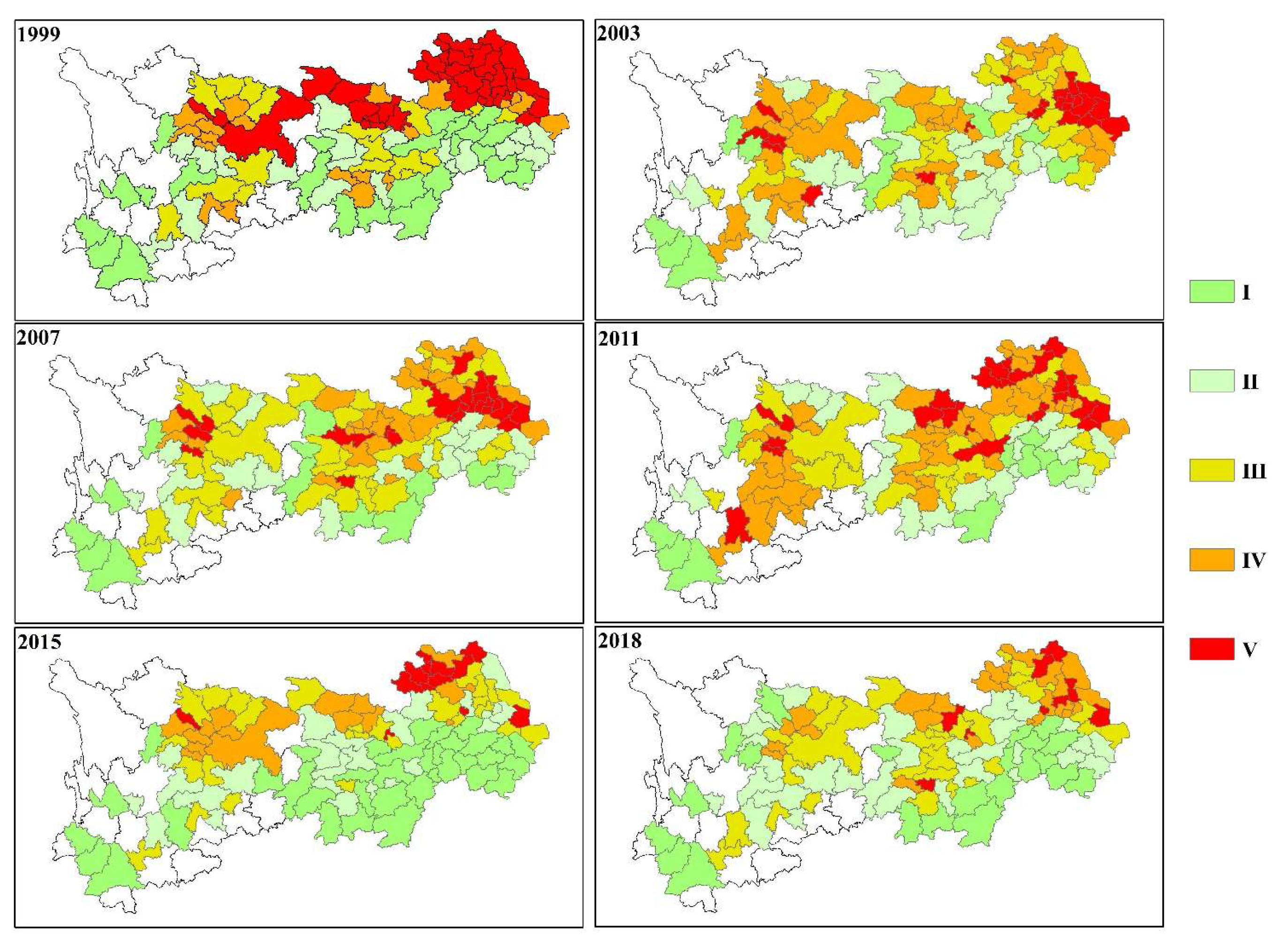
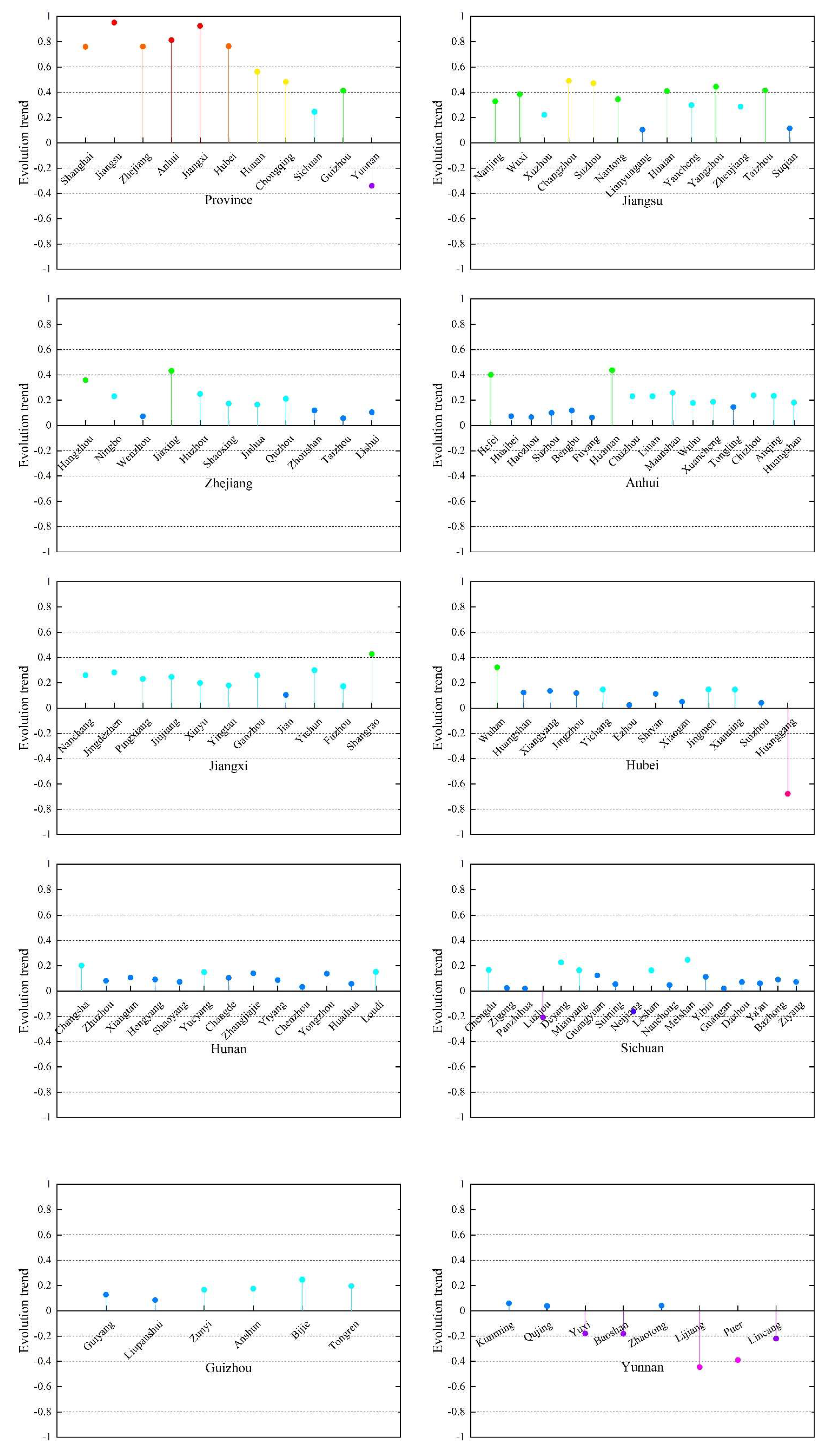
4.2. Cities
5. Discussion
5.1. Calculation Method of Water Resource Spatial Equilibrium
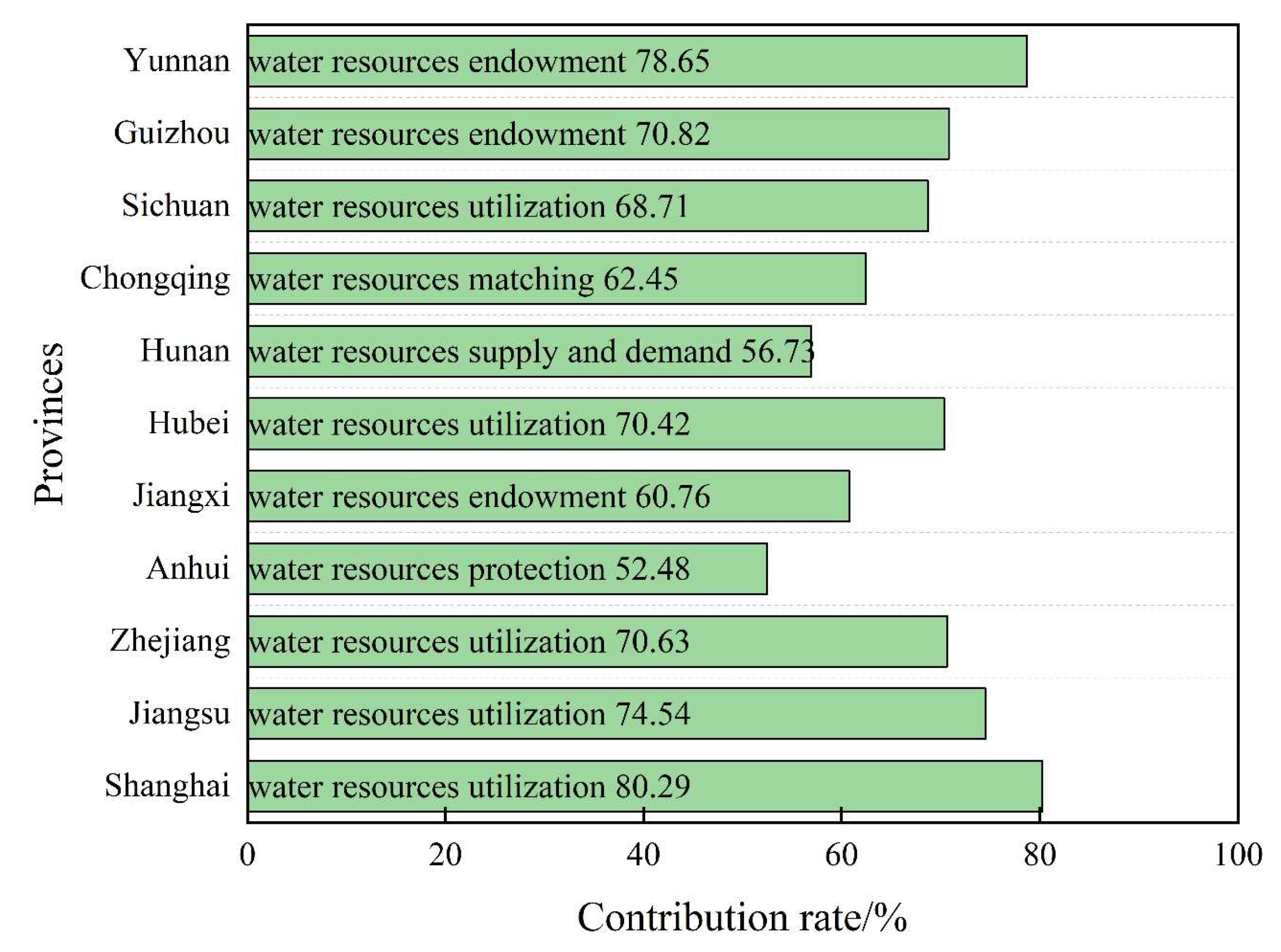
5.2. Factors That Influence Water Resource Spatial Equilibrium
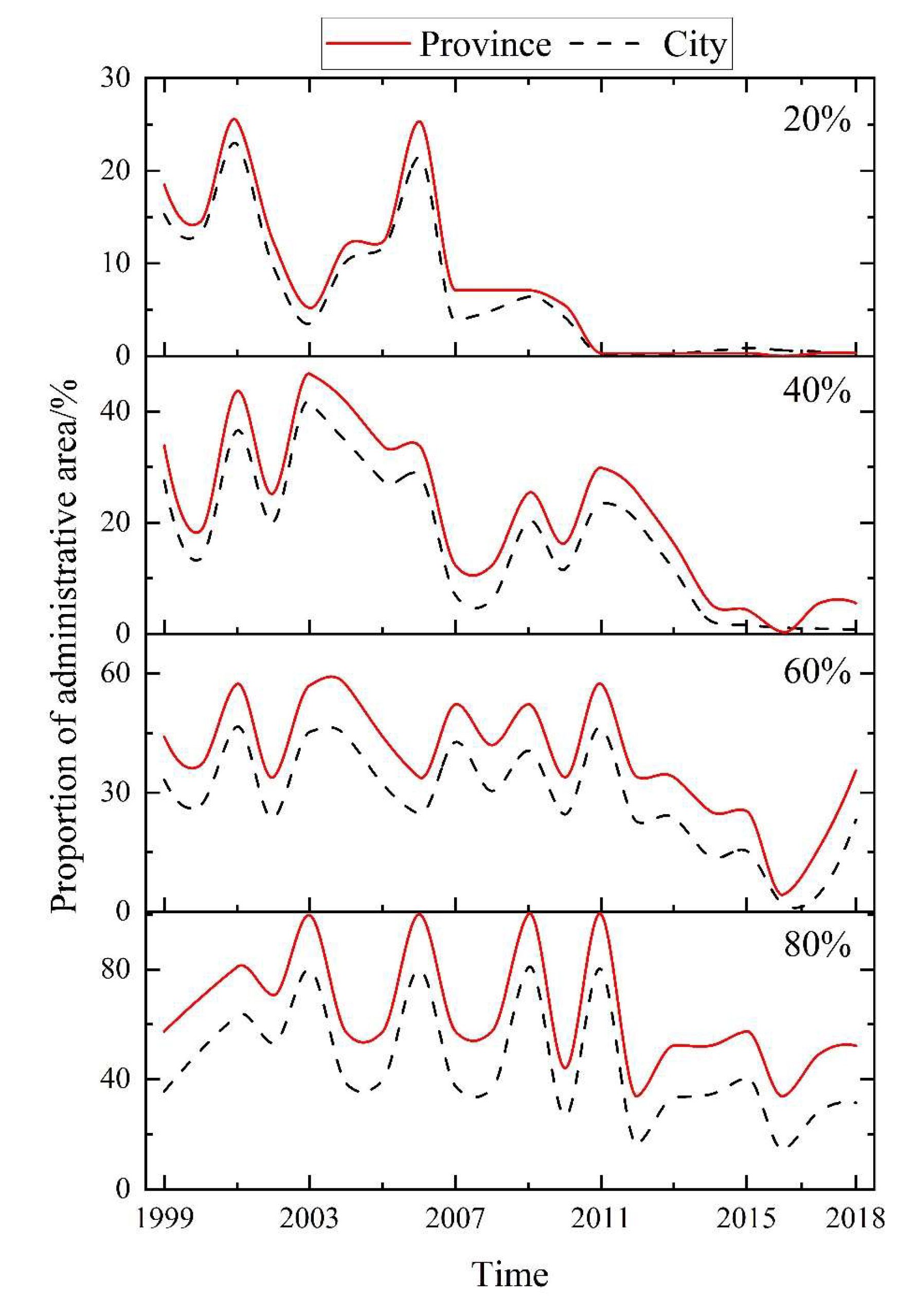
5.3. Scale Characteristics of Water Resource Spatial Equilibrium
6. Conclusions
- (1)
- The water resource spatial equilibrium is used to coordinate the relationship between supply and demand of water resource to achieve the sustainable development.
- (2)
- In the 11 provinces of the study area, the water resource spatial equilibrium gradually improved over time. In terms of the spatial trend, the south was better than the north and the west was better than the east. The water resource spatial equilibrium in the 11 provinces was sorted as follows: Yunnan > Sichuan > Zhejiang > Jiangxi > Hunan Province > Guizhou > Hubei > Chongqing > Anhui > Jiangsu > Shanghai.
- (3)
- In the 110 cities in the study area, the water resource spatial equilibrium showed that the spatial trend of the three major urban agglomerations was much better than that of the other regions. The temporal trend could be divided into two stages, namely, a stable fluctuation stage from 1999 to 2011 and an improvement stage from 2012 to 2018. The evolutionary trend of water resource spatial equilibrium increased in all cities except Huanggang, Luzhou, Neijiang, Yuxi, Baoshan, Lijiang, Pu’er, and Lincang.
- (4)
- Compared with the provincial scale, city-scale research on the water resource spatial equilibrium can more effectively identify and optimize the control area. When the control targets were set to 20%, 40%, 60%, and 80%, the proportion of administrative area based on the city scale decreased by 1.20%, 4.99%, 10.52%, and 19.05%, respectively.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zuo, Q.; Han, C.; Ma, J. Application Rules and Quantification Methods of Water Resources Spatial Equilibrium Theory. Hydro-Sci. Eng. 2019, 6, 50–58. [Google Scholar]
- Zhao, Z.; Wang, H.; Zhang, L.; Liu, X.; Zhao, Y. Construction and application of resilience evaluation model of water resource-water environment-social economy complex system in the Yangtze River Economic Belt. Adv. Water Sci. 2022, 33, 705–717. [Google Scholar]
- Yang, Y.; Gong, S.; Wang, H.; Zhao, Z.; Yang, B. New model for water resources spatial equilibrium evaluation and its application. Adv. Water Sci. 2021, 32, 33–44. [Google Scholar]
- Fox, K.A. A Spatial Equilibrium Model of the Livestock-Feed Economy in the United States. Econ. J. Econ. Soc. 1953, 21, 547–566. [Google Scholar] [CrossRef]
- Glaeser, E.L.; Gottlieb, J.D. The Wealth of Cities: Agglomeration Economies and Spatial Equilibrium in the United States. J. Econ. Lit. 2009, 47, 983–1028. [Google Scholar] [CrossRef]
- Kawaguchi, T.; Suzuki, N.; Kaiser, H.M. A Spatial Equilibrium Model for Imperfectly Competitive Milk Markets. Am. J. Agric. Econ. 1997, 79, 851–859. [Google Scholar] [CrossRef]
- Killingback, T.; Doebeli, M. Spatial Evolutionary Game Theory: Hawks and Doves Revisited. Proc. R. Soc. London. Ser. B Biol. Sci. 1996, 263, 1135–1144. [Google Scholar]
- Roca, C.P.; Cuesta, J.A.; Sánchez, A. Evolutionary Game Theory: Temporal and Spatial Effects beyond Replicator Dynamics. Phys. Life Rev. 2009, 6, 208–249. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Maiti, T.; Petrie, D. General Equilibrium Effects of Spatial Structure: Health Outcomes and Health Behaviours in Scotland. Reg. Sci. Urban Econ. 2014, 49, 286–297. [Google Scholar] [CrossRef]
- Wang, J.; Jiao, J.; Chao, D.U.; Hao, H.U. Competition of Spatial Service Hinterlands between High-Speed Rail and Air Transport in China: Present and Future Trends. J. Geogr. Sci. 2015, 25, 1137–1152. [Google Scholar] [CrossRef]
- Fan, X.; Ying, C.; Ming, D.; Yuping, H. Calculation method and application of spatial equilibrium coefficient of water resources. Water Resour. Prot. 2020, 36, 52–57. [Google Scholar]
- Chao, C.; Shaoyu, T.; Haiying, P.; Shaokai, Y. Ecological carrying capacity of water resources in the central Yunnan urban agglomeration area. Resour. Sci. 2016, 38, 1561–1571. [Google Scholar] [CrossRef]
- Dai, J.; Ji, C. An Competition Equilibrium Model on the Diverse-Source Water Supply Market Created by Interbasin Water Transfer. In Proceedings of the 2006 International Conference on Management Science and Engineering, Lille, France, 5–7 October 2006; Zhang, H., Zhao, R.M., Chen, L., Eds.; Curran Associates, Inc.: New York, NY, USA, 2006; pp. 995–1000. [Google Scholar]
- Wang, J.F.; Liu, C.M.; Wang, Z.Y.; Yu, J.J. A Marginal Revenue Equilibrium Model for Spatial Water Allocation. Sci. China Ser. D-Earth Sci. 2002, 45, 201–210. [Google Scholar] [CrossRef]
- Shi, W.; Yu, X.; Liao, W.; Wang, Y.; Jia, B. Spatial and Temporal Variability of Daily Precipitation Concentration in the Lancang River Basin, China. J. Hydrol. 2013, 495, 197–207. [Google Scholar] [CrossRef]
- De, L.M.; González-Hidalgo, J.C.; Brunetti, M.; Longares, L.A. Precipitation Concentration Changes in Spain 1946–2005. Nat. Hazards Earth Syst. Sci. 2011, 11, 1259–1265. [Google Scholar] [CrossRef]
- Coscarelli, R.; Caloiero, T. Analysis of Daily and Monthly Rainfall Concentration in Southern Italy (Calabria Region). J. Hydrol. 2012, 416–417, 145–156. [Google Scholar] [CrossRef]
- Vyshkvarkova, E.; Voskresenskaya, E.; Martin-Vide, J. Spatial Distribution of the Daily Precipitation Concentration Index in Southern Russia. Atmos. Res. 2018, 203, 36–43. [Google Scholar] [CrossRef]
- Monjo, R.; Martin-Vide, J. Daily Precipitation Concentration around the World According to Several Indices. Int. J. Climatol. 2016, 36, 3828–3838. [Google Scholar] [CrossRef]
- Zhou, R.; Jin, J.; Cui, Y.; Ning, S.; Zhou, L.; Zhang, L.; Wu, C.; Zhou, Y. Spatial Equilibrium Evaluation of Regional Water Resources Carrying Capacity based on Dynamic Weight Method and Gagum Gini Coefficient. Front. Earth Sci. 2022, 9, 790349. [Google Scholar] [CrossRef]
- Xingmin, S.; Wenjuan, W. Gini Coefficient of Ecological Security of Shaanxi Based on Water Resources. Agric. Res. Arid Areas 2010, 28, 233–236. [Google Scholar]
- Xiaoya, Z.; Shilun, Y. Climatic and Anthropogenic Impacts on Water Discharge in the Yangtze River Over the Last 56 Years (1956–2011). Resour. Environ. Yangtze Basin 2014, 23, 1729–1739. [Google Scholar]
- Liu, B.; Jiang, T.; Ren, G.; Fraedrich, K. Projected Surface Water Resource of the Yangtze River Basin Before 2050. Clim. Chang. Res. 2007, 3, 145–150. [Google Scholar]
- Peng, M.; Xu, H.; Qu, C.; Xu, J.; Chen, L.; Duan, L.; Hao, J. Understanding China’s Largest Sustainability Experiment: At-mospheric and Climate Governance in the Yangtze River Economic Belt as a Lens. J. Clean. Prod. 2021, 290, 125760. [Google Scholar] [CrossRef]
- Kong, Y.; He, W.; Yuan, L.; Zhang, Z.; Gao, X.; Zhao, Y.; Degefu, D.M. Decoupling Economic Growth from Water Consumption in the Yangtze River Economic Belt, China. Ecol. Indic. 2021, 123, 107344. [Google Scholar] [CrossRef]
- Zuo, Q.; Han, C.; Ma, J.; Wang, X. Theoretical Method and Applied Research Framework of Water Resources Spatial Equilib-rium. Yellow River 2019, 41, 113–118. [Google Scholar]
- Wang, H.; Liu, J. Collaboration of National Water Resources with Eco-Social System in China. China Water Resour. 2016, 17, 7–9. [Google Scholar]
- Jin, J.; Li, J.; Wu, C. Research Progress on Spatial Equilibrium of Water Resources. J. North China Univ. Water Resour. Electr. Power (Nat. Sci. Ed.) 2019, 40, 47–60. [Google Scholar]
- Wang, J. Implement “Spatial Equilibrium” to Strengthen the Rigid Constraints of Carrying Capacity. Water Resour. Dev. Res. 2018, 18, 20–21. [Google Scholar]
- Li, J.; Wang, P.; He, J.; Guo, X. Study on Theory Methodology and Countermeasures about Water Resources Spatial Equilibrium. China Water Resour. 2019, 23, 23–25. [Google Scholar]
- Flinn, J.; Guise, J. An Application of Spatial Equilibrium Analysis to Water Resource Allocation. Water Resour. Res. 1970, 6, 398. [Google Scholar] [CrossRef]
- Chen, S. Theory and Model of Engineering Variable Fuzzy Set—Mathematical Basis for Fuzzy Hydrology and Water Re-sources. J. Dalian Univ. Technol. 2005, 2, 308–312. [Google Scholar]
- Liu, X.; Zhao, K. Multiple Attribute Decision Making and Its Applications Based on Complex Number Arithmetic Operation of Connection Number with Interval Numbers. Math. Pract. Theory 2008, 38, 57–64. [Google Scholar]
- Hong, S.; Song, Z.; Cheng, T.; Wang, H. Spatial Matching Analysis of Water Resources in the Intake Area of South-North Water Transfer Project Based on Gini Coefficient. J. Beijing Norm. Univ. (Nat. Sci.) 2017, 53, 175–179. [Google Scholar]
- Deng, C.; Wang, H.; Gong, S.; Zhang, J.; Yang, B.; Zhao, Z. Effects of Urbanization on Food-Energy-Water Systems in Mega-Urban Regions: A Case Study of the Bohai MUR, China. Environ. Res. Lett. 2020, 15, 044014. [Google Scholar] [CrossRef]
- Wei, G.; Huaicheng, G.; Xikang, H. Evaluating City-Scale Net Anthropogenic Nitrogen Input (NANI) in Mainland China. Acta Sci. Nat. Univ. Pekin. 2014, 50, 951–959. [Google Scholar]

| Scholar | Definition |
|---|---|
| Wang [27] | Coordinated development among water resource carrying capacity, socioeconomic systems, and different regions. |
| Zuo [26] | A relatively stable and balanced state of development, utilization, and protection of water resource in space. |
| Jin [28] | The water resource spatial equilibrium is a dual balance of supply and demand of water resources, which is coordinated and matched in time and space among the water resource spatial distribution, social economy, and ecological environment. |
| Wang [29] | The population and economy is balanced with the water resource carrying capacity, in which people and water live in harmony. |
| Li [30] | The population, economic, and social development of a river basin or a certain area is balanced with water resources. |
| Grade | Gini Coefficient Interval | Income Distribution | Water Resource Spatial Equilibrium |
|---|---|---|---|
| I | 0–0.2 | Absolute average | Absolute equilibrium |
| II | 0.2–0.3 | General fairness | General equilibrium |
| III | 0.3–0.4 | Relative reasonable | Relative equilibrium |
| IV | 0.4–0.5 | General gap | General disequilibrium |
| V | 0.5–1 | Great disparity | Serious disequilibrium |
| District | Relative Membership Degree | Grade Characteristic Values | ||||
|---|---|---|---|---|---|---|
| I | II | III | IV | V | ||
| Shanghai | 0 | 0.06 | 0.09 | 0.16 | 0.69 | 4.54 |
| Jiangsu | 0 | 0.05 | 0.11 | 0.74 | 0.20 | 3.67 |
| Chongqing | 0 | 0.06 | 0.58 | 0.28 | 0.08 | 3.25 |
| Hubei | 0.02 | 0.15 | 0.46 | 0.37 | 0 | 3.19 |
| Anhui | 0.04 | 0.20 | 0.52 | 0.24 | 0 | 2.94 |
| Guizhou | 0 | 0.19 | 0.62 | 0.19 | 0 | 2.88 |
| Hunan | 0.02 | 0.15 | 0.70 | 0.13 | 0 | 2.86 |
| Jiangxi | 0 | 0.24 | 0.76 | 0 | 0 | 2.82 |
| Zhejiang | 0 | 0.79 | 0.21 | 0 | 0 | 2.21 |
| Sichuan | 0.08 | 0.75 | 0.17 | 0 | 0 | 2.07 |
| Yunnan | 0.32 | 0.65 | 0.03 | 0 | 0 | 1.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Cai, Y.; Yang, Y. Construction and Application of a Water Resources Spatial Equilibrium Model: A Case Study in the Yangtze River Economic Belt. Water 2023, 15, 2984. https://doi.org/10.3390/w15162984
Zhao Z, Cai Y, Yang Y. Construction and Application of a Water Resources Spatial Equilibrium Model: A Case Study in the Yangtze River Economic Belt. Water. 2023; 15(16):2984. https://doi.org/10.3390/w15162984
Chicago/Turabian StyleZhao, Ziyang, Yihui Cai, and Yafeng Yang. 2023. "Construction and Application of a Water Resources Spatial Equilibrium Model: A Case Study in the Yangtze River Economic Belt" Water 15, no. 16: 2984. https://doi.org/10.3390/w15162984
APA StyleZhao, Z., Cai, Y., & Yang, Y. (2023). Construction and Application of a Water Resources Spatial Equilibrium Model: A Case Study in the Yangtze River Economic Belt. Water, 15(16), 2984. https://doi.org/10.3390/w15162984







