Flow Field and Gas Field Distribution of Non-Submerged Cavitation Water Jet Based on Dual-Nozzle with Concentric Configuration
Abstract
:1. Introduction
2. Numerical Simulation
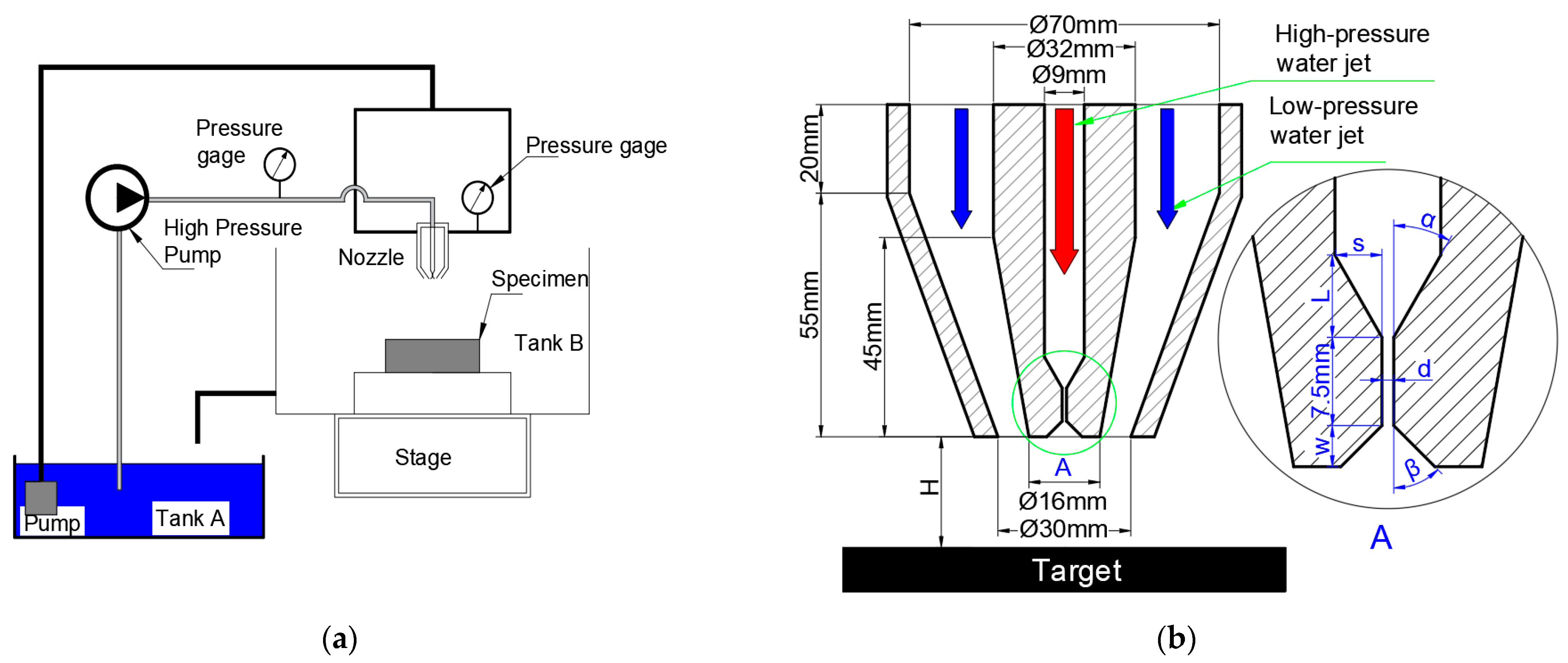
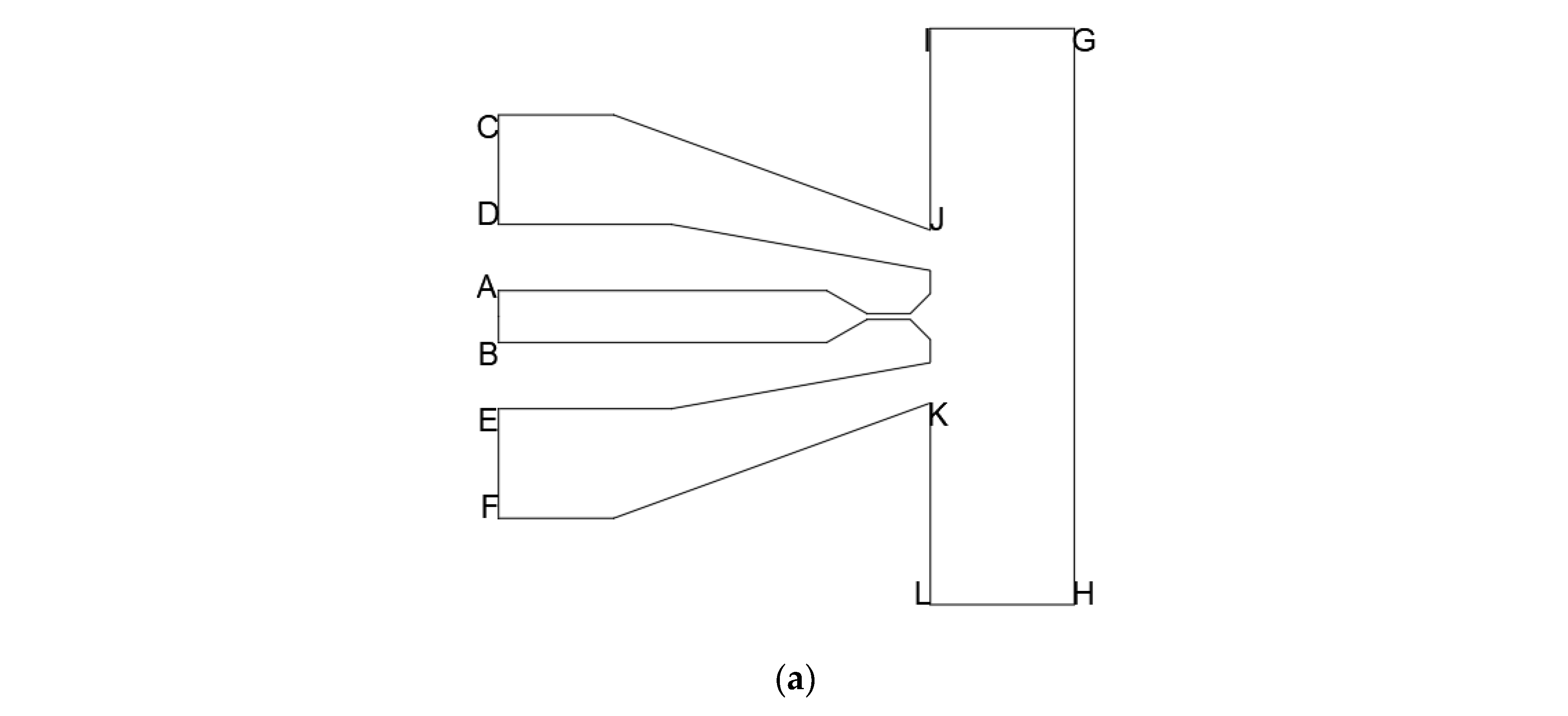
2.1. Geometric Model
2.2. Meshing and Boundary Condition
2.3. Control Equation
2.3.1. Multiphase Flow Model
2.3.2. Turbulence Model
2.3.3. Cavitation Model
- = vapor phase;
- = vapor volume fraction;
- = vapor density;
- = vapor phase velocity;
- = mass transfer source terms connected to the growth and collapse of the vapor bubbles, respectively.
- = vapor volume fraction;
- = vapor density;
- = bubble radius;
- = bubble surface pressure;
- = local far-field pressure;
- = liquid density.
- = saturation vapor pressure;
- (evaporation coefficient) = 50;
- (volume fraction of gas nuclei) = 5 × 10−4;
- = vapor density;
- (bubble radius) = 1 × 10−6 m;
- = local far-field pressure;
- = liquid density;
- (condensation coefficient) = 0.01.
2.4. Mesh Refinement Analysis
2.5. Model Experimental Validation
3. Results and Discussions
3.1. Analysis of Flow Field Characteristics
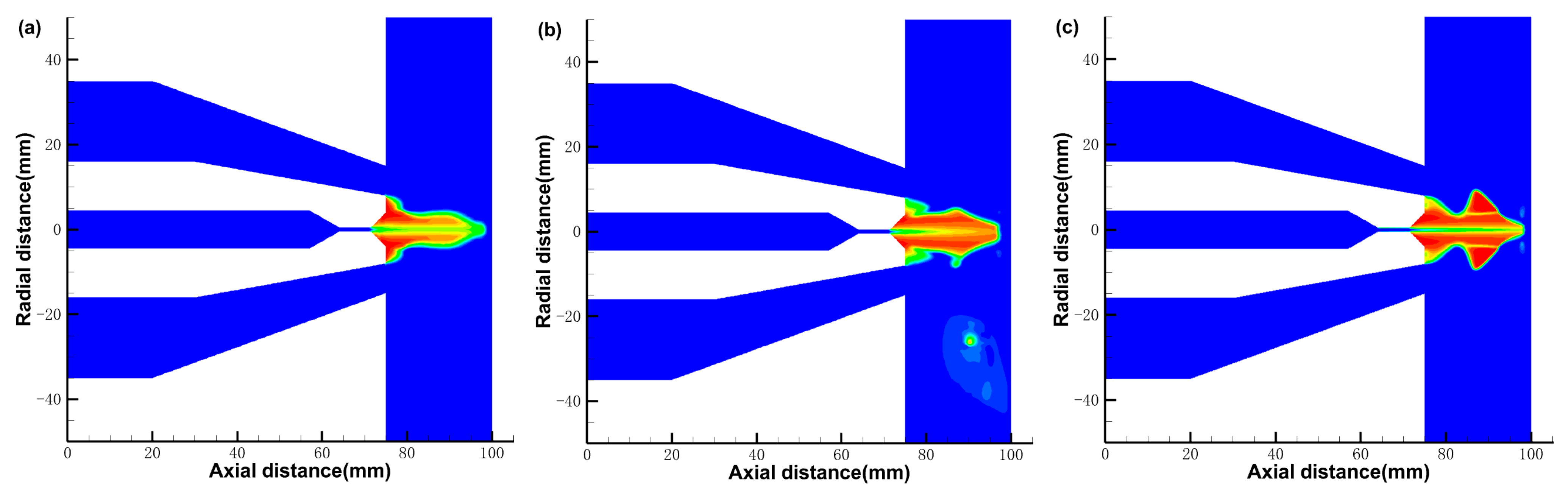
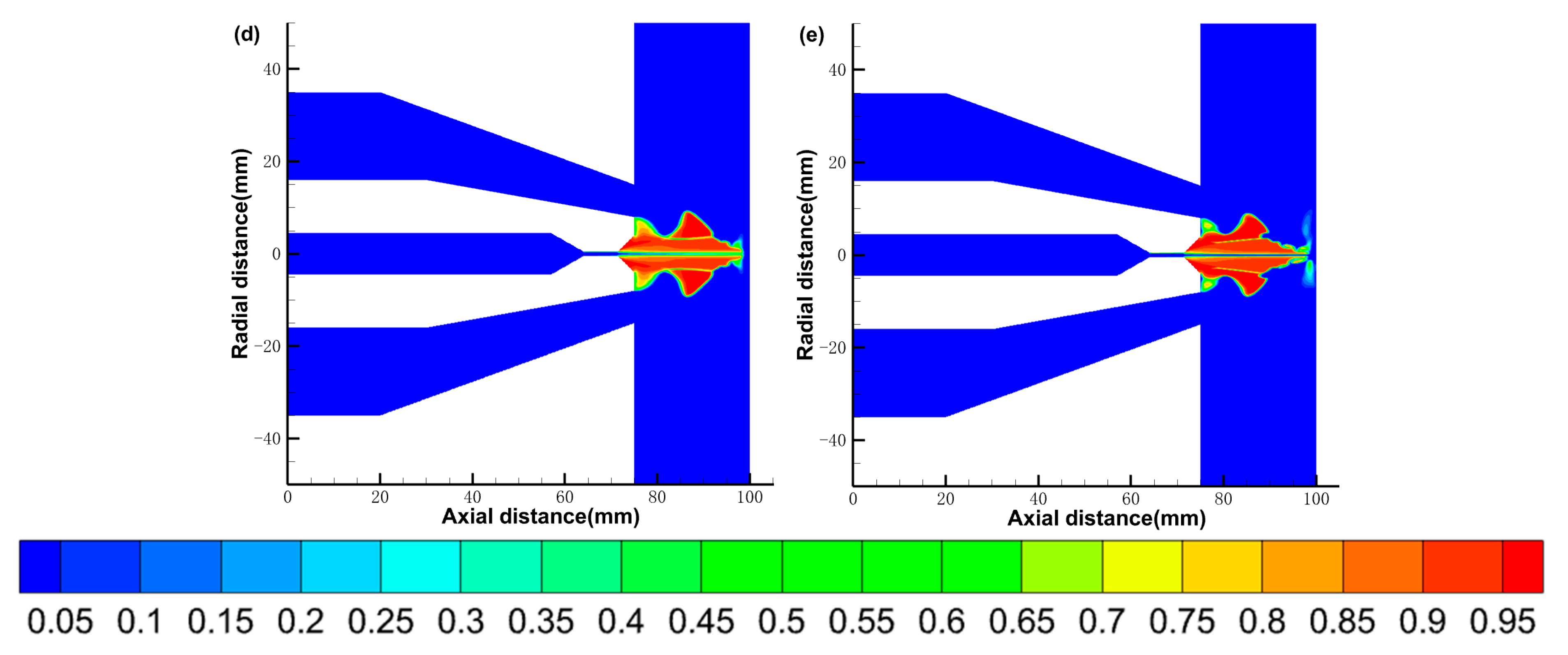
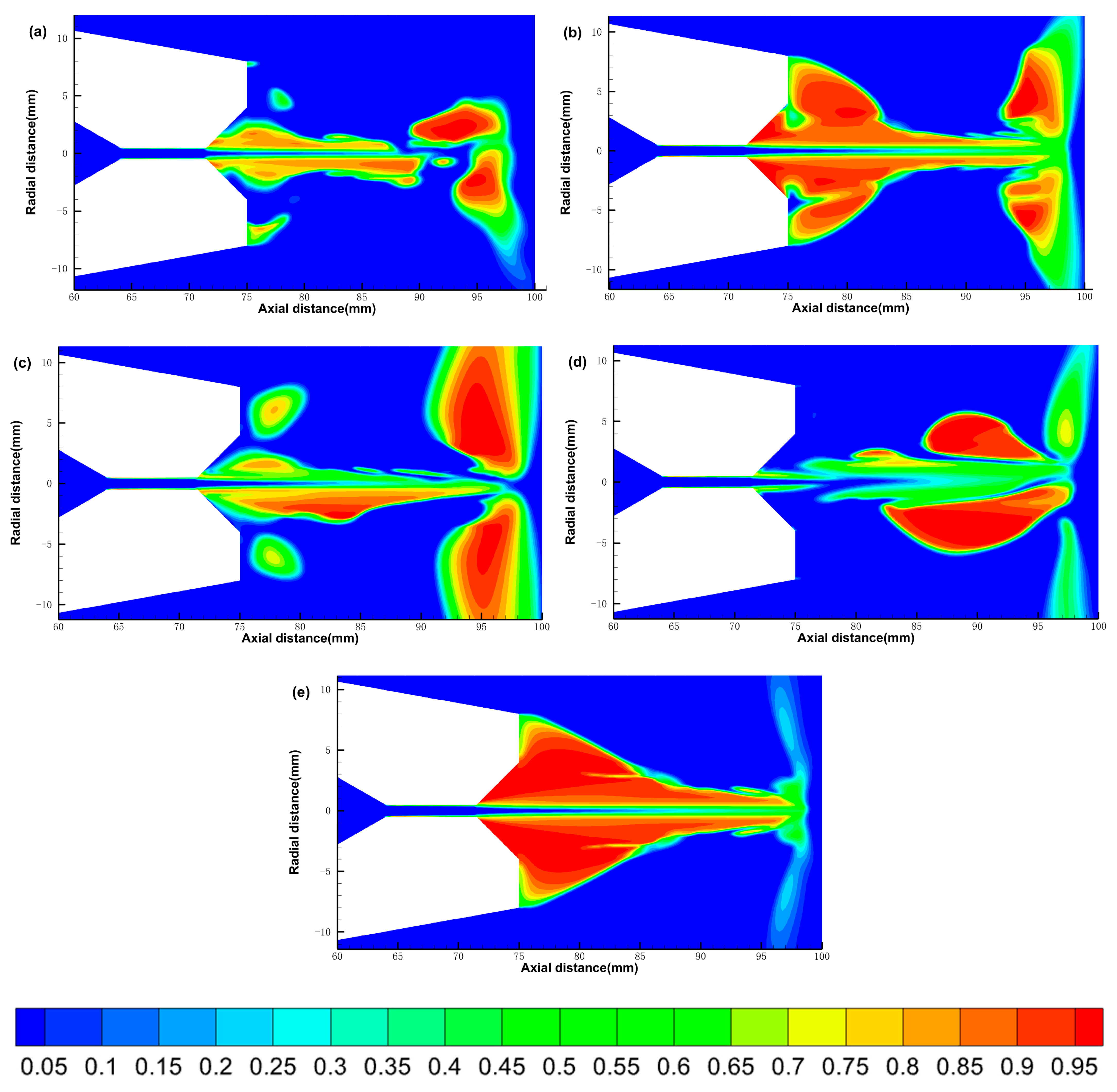
3.1.1. The Gas Phase Distribution
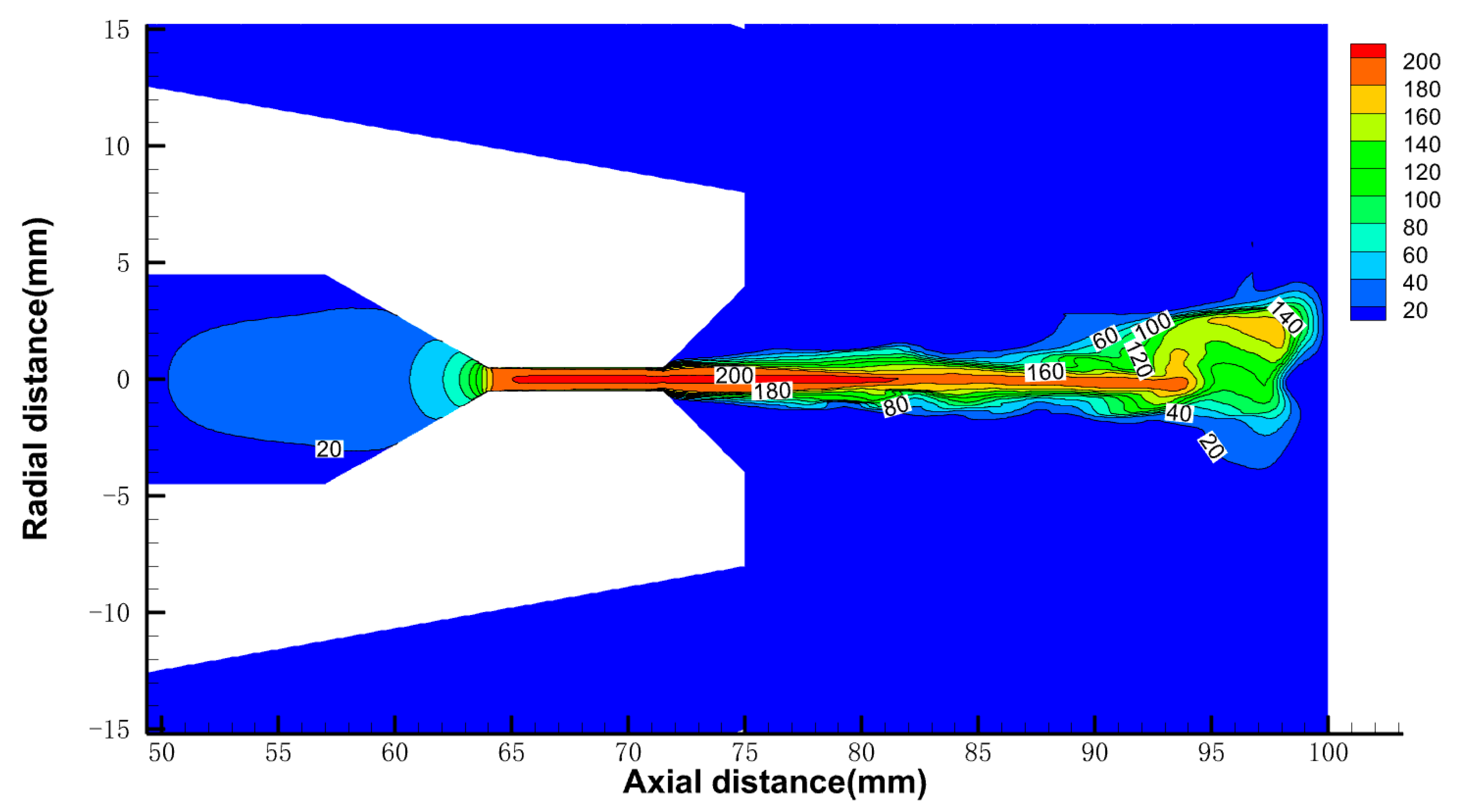
3.1.2. The Velocity Distribution
3.1.3. The Pressure Distribution
3.2. Effects of Geometric Parameters of Inner Nozzle
3.2.1. The Gas Phase Distribution
3.2.2. The Velocity Distribution
3.2.3. The Pressure Distribution
3.3. Effects of Pressure Ratio of Inner Nozzle to External Nozzle
3.3.1. The Gas Phase Distribution
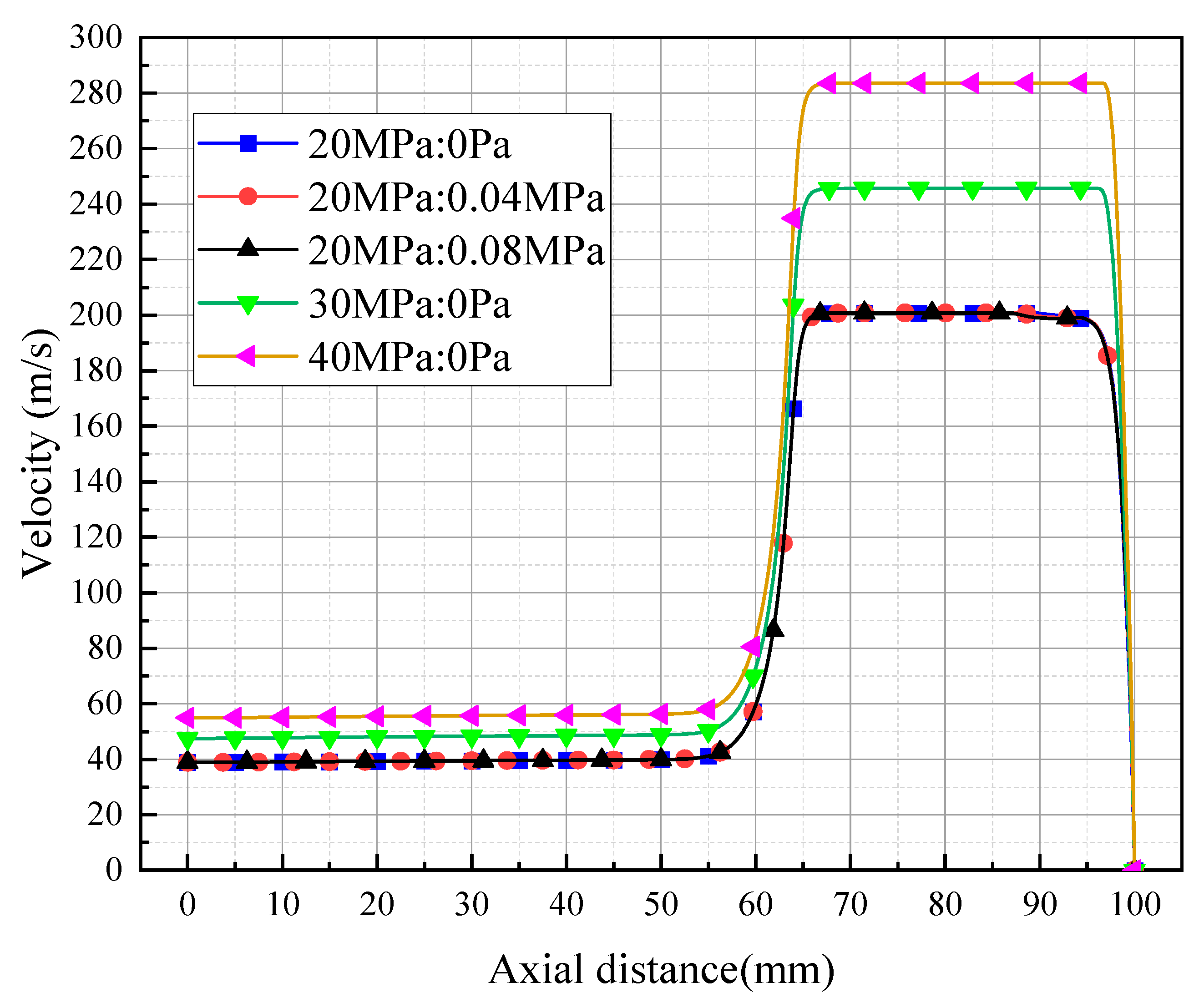
3.3.2. The Velocity Distribution
3.3.3. The Pressure Distribution
3.4. Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Q.; Shi, Z.; Shi, W.; Xie, Z.; Tan, L.; Yang, Y. Research on Flow Field Characteristics in Water Jet Nozzle and Surface Damage Caused by Target Impact. Sustainability 2022, 14, 9074. [Google Scholar] [CrossRef]
- Chlupová, A.; Hloch, S.; Nag, A.; Šulák, I.; Kruml, T. Effect of pulsating water jet processing on erosion grooves and microstructure in the subsurface layer of 25CrMo4 (EA4T) steel. Wear 2023, 524, 204774. [Google Scholar] [CrossRef]
- Natarajan, Y.; Murugesan, P.K.; Mohan, M.; Khan, S.A.L.A. Abrasive Water Jet Machining process: A state of art of review. J. Manuf. Process. 2020, 49, 271–322. [Google Scholar] [CrossRef]
- Zhao, H.; Jiang, H.; Warisawa, S.; Li, H. Numerical study of abrasive water jet rotational slits in hard rock using a coupled SPH-FEM method. Powder Technol. 2023, 426, 118622. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, Z.; Liu, K.; Zhao, S.; Wang, Y. Coupled CEL-FDEM modeling of rock failure induced by high-pressure water jet. Eng. Fract. Mech. 2023, 277, 108958. [Google Scholar] [CrossRef]
- Luo, X.; Zhang, J.; Yang, F.; He, F.; Xia, Y. Research on the hard rock cutting characteristics of disc cutter under front-mounted water jet precutting kerf conditions. Eng. Fract. Mech. 2023, 287, 109330. [Google Scholar] [CrossRef]
- Nadolny, K.; Romanowski, M.; Sutowski, P. Assessing the technological quality of abrasive water jet and laser cutting processes by geometrical errors and a multiplicative indicator. Measurement 2023, 217, 113060. [Google Scholar] [CrossRef]
- Winter, S.; Smith, A.; Lappin, D.; McDonagh, G.; Kirk, B. Failure of non-vacuum steam sterilization processes for dental handpieces. J. Hosp. Infect. 2017, 97, 343–347. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.F.; Shi, W.D.; Li, W.; Chen, S.P.; Zhang, W.Q.; Pan, B. Experimental study on the surface property changes of aluminum alloy and stainless steel after impingement with submerged cavitation jet. Strength Mater. 2021, 53, 353–363. [Google Scholar] [CrossRef]
- Murugesan, P.; Jung, S.; Lee, H. Inner surface peening for long and narrow helical pipe using acoustic cavitation. Mater. Des. 2023, 229, 111906. [Google Scholar] [CrossRef]
- Dong, W.; Yao, L.; Luo, W. Numerical Simulation of Flow Field of Submerged Angular Cavitation Nozzle. Appl. Sci. 2023, 13, 613. [Google Scholar] [CrossRef]
- Ge, M.; Manikkam, P.; Ghossein, J.; Subramanian, R.K.; Coutier-Delgosha, O.; Zhang, G. Dynamic mode decomposition to classify cavitating flow regimes induced by thermodynamic effects. Energy 2022, 254, 124426. [Google Scholar] [CrossRef]
- Ge, M.; Petkovšek, M.; Zhang, G.; Jacobs, D.; Coutier-Delgosha, O. Cavitation dynamics and thermodynamic effects at elevated temperatures in a small Venturi channel. Int. J. Heat Mass Transf. 2021, 170, 120970. [Google Scholar] [CrossRef]
- Enomoto, K.; Hirano, K.; Mochizuki, M.; Kurosawa, K.; Saito, H.; Hayashi, E. Improvement of residual stress on material surface by water jet peening; Water jet peening ni yoru zairyo hyomen no zanryu oryoku kaizen koka no kento. Zair. J. Soc. Mater. Sci. Jpn. 1996, 45, 734–739. [Google Scholar] [CrossRef]
- Giorgetti, V.; Santos, E.A.D.; Marcomini, J.B.; Sordi, V.L. Stress corrosion cracking and fatigue crack growth of an API 5L X70 welded joint in an ethanol environment. Int. J. Press. Vessel. Pip. 2019, 169, 223–229. [Google Scholar] [CrossRef]
- Ryakhovskikh, I.V.; Bogdanov, R.I. Model of stress corrosion cracking and practical guidelines for pipe-lines operation. Eng. Fail. Anal. 2021, 121, 105134. [Google Scholar] [CrossRef]
- Shakeri, I.; Shahani, A.R.; Rans, C.D. Fatigue crack growth of butt welded joints subjected to mixed mode loading and overloading. Eng. Fract. Mech. 2021, 241, 107376. [Google Scholar] [CrossRef]
- Xu, S.; Wang, C.; Wang, W. Failure analysis of stress corrosion cracking in heat exchanger tubes during start-up operation. Eng. Fail. Anal. 2015, 51, 1–8. [Google Scholar] [CrossRef]
- Lv, F.; Hu, X.; Ma, C.; Yang, B.; Luo, Y. Failure analysis on cracking of backing plate of lifting lug for air preheater. Eng. Fail. Anal. 2020, 109, 104395. [Google Scholar] [CrossRef]
- Soyama, H. Introduction of compressive residual stress using a cavitating jet in air. J. Eng. Mater. Technol. 2004, 126, 123–128. [Google Scholar] [CrossRef]
- Soyama, H. Improvement of fatigue strength by using cavitating jets in air and water. J. Mater. Sci. 2007, 42, 6638–6641. [Google Scholar] [CrossRef]
- Soyama, H.; Chighizola, C.R.; Hill, M.R. Effect of compressive residual stress introduced by cavitation peening and shot peening on the improvement of fatigue strength of stainless steel. J. Mater. Process. Technol. 2021, 288, 116877. [Google Scholar] [CrossRef]
- Soyama, H.; Hoshino, J. Enhancing the aggressive intensity of hydrodynamic cavitation through a Venturi tube by increasing the pressure in the region where the bubbles collapse. AIP Adv. 2016, 6, 045113. [Google Scholar] [CrossRef] [Green Version]
- Nakashima, K.; Ebi, Y.; Shibasaki-Kitakawa, N.; Soyama, H.; Yonemoto, T. Hydrodynamic cavitation reac-tor for efficient pretreatment of lignocellulosic biomass. Ind. Eng. Chem. Res. 2016, 55, 1866–1871. [Google Scholar] [CrossRef]
- Soyama, H. Enhancing the aggressive intensity of a cavitating jet by means of the nozzle outlet geometry. J. Fluids Eng. 2011, 133, 101301. [Google Scholar] [CrossRef]
- Soyama, H. Comparison between the improvements made to the fatigue strength of stainless steel by cavitation peening, water jet peening, shot peening and laser peening. J. Mater. Process. Technol. 2019, 269, 65–78. [Google Scholar] [CrossRef]
- Soyama, H. Cavitation peening: A review. Metals 2020, 10, 270. [Google Scholar] [CrossRef] [Green Version]
- Yamauchi, Y.; Soyama, H.; Adachi, Y.; Sato, K.; Shindo, T.; Oba, R.; Oshima, R.; Yamabe, M. Suitable region of high-speed submerged water jets for cutting and peening. JSME Int. J. Ser. B Fluids Therm. Eng. 1995, 38, 31–38. [Google Scholar] [CrossRef] [Green Version]
- Marcon, A.; Melkote, S.N.; Castle, J.; Sanders, D.G.; Yoda, M. Effect of jet velocity in co-flow water cavita-tion jet peening. Wear 2016, 360, 38–50. [Google Scholar] [CrossRef]
- Marcon, A.; Melkote, S.N.; Yoda, M. Effect of nozzle size scaling in co-flow water cavitation jet peening. J. Manuf. Process. 2018, 31, 372–381. [Google Scholar] [CrossRef]
- Zhu, R.; Zhu, H.; Zhang, X. Numerical investigation about the unsteady behavior of a free submerged cavitation jet using the SBES approach. Ocean. Eng. 2023, 281, 115010. [Google Scholar] [CrossRef]
- Liu, M.; Li, W.; Li, H.; Xu, X.; Tian, F.; Agarwal, R.K.; Ji, L. Numerical simulation of cryogenic cavitating flow by an extended transport-based cavitation model with thermal effects. Cryogenics 2023, 133, 103697. [Google Scholar] [CrossRef]
- Zwart, P.J.; Gerber, A.G.; Belamri, T. A two-phase flow model for predicting cavitation dynamics. In Proceedings of the Fifth International Conference on Multiphase Flow, Yokohama, Japan, 30 May–3 June 2004. [Google Scholar]
- Yang, Y.F. Research on the Mechanism of Submerged High-Pressure Water Cavitation Jet and Hollow Bubble Shock Wave Strengthening Metal Properties. Ph.D. Thesis, Jiangsu University, Zhenjiang, China, 2020. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CDFDLAST2021&filename=1020758544.nh (accessed on 20 June 2020).
- Zhang, H.; Han, B.; Yu, X.G.; Ju, D.Y. Numerical and experimental studies of cavitation behavior in water-jet cavitation peening processing. Shock Vib. 2013, 20, 895–905. [Google Scholar] [CrossRef]











| Mesh-1 | Mesh-2 | Mesh-3 | Mesh-4 | Mesh-5 | |
|---|---|---|---|---|---|
| Number of grids | 14,860 | 22,200 | 79,200 | 122,840 | 245,400 |
| Contraction Segment | Expansion Segment | Throat Diameter d | Target Distance H | |
|---|---|---|---|---|
| Nozzle A | L = 7 mm, s = 4 mm (α = 30°) | w = 3.5 mm, β = 45° | 1 mm | 25 mm |
| Nozzle B | L = 6.125 mm, s = 3.5 mm (α = 30°) | w = 3.5 mm, β = 45° | 2 mm | 25 mm |
| Nozzle C | L = 12 mm, s = 4 mm (α = 18°) | w = 3.5 mm, β = 45° | 1 mm | 25 mm |
| Nozzle D | L = 7 mm, s = 4 mm (α = 30°) | No expansion segment | 1 mm | 25 mm |
| Nozzle E | No contraction segment | No expansion segment | 1 mm | 25 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Zang, J.; Zheng, H. Flow Field and Gas Field Distribution of Non-Submerged Cavitation Water Jet Based on Dual-Nozzle with Concentric Configuration. Water 2023, 15, 2904. https://doi.org/10.3390/w15162904
Luo Y, Zang J, Zheng H. Flow Field and Gas Field Distribution of Non-Submerged Cavitation Water Jet Based on Dual-Nozzle with Concentric Configuration. Water. 2023; 15(16):2904. https://doi.org/10.3390/w15162904
Chicago/Turabian StyleLuo, Yun, Jingyu Zang, and Hongxiang Zheng. 2023. "Flow Field and Gas Field Distribution of Non-Submerged Cavitation Water Jet Based on Dual-Nozzle with Concentric Configuration" Water 15, no. 16: 2904. https://doi.org/10.3390/w15162904





