Influence of Multi-Cross Structures on the Flood Discharge Capacity of Mountain Rivers in the Yellow River Basin
Abstract
:1. Introduction
2. Methodology
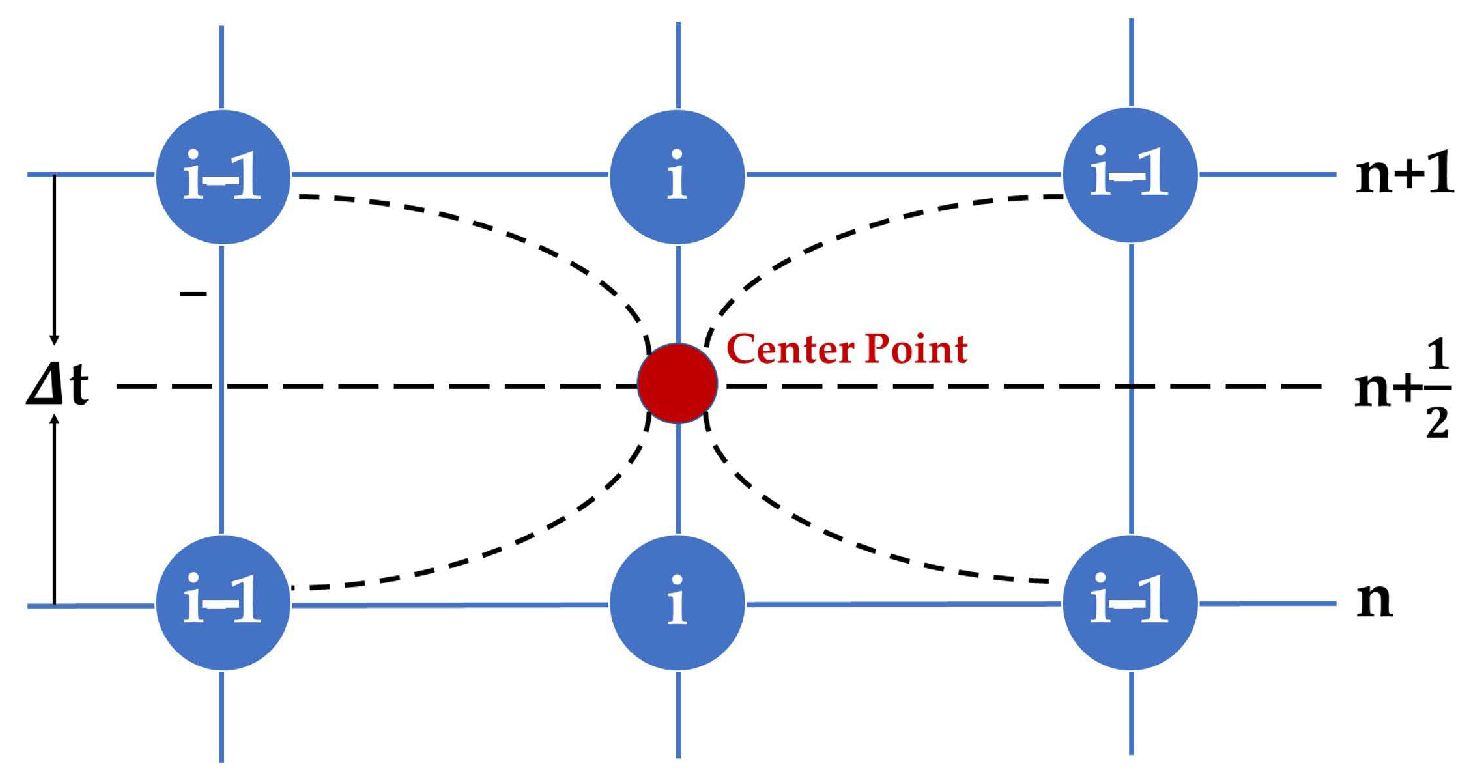
2.1. Mathematical Model
2.2. Model Solution
3. Case Analysis and Results
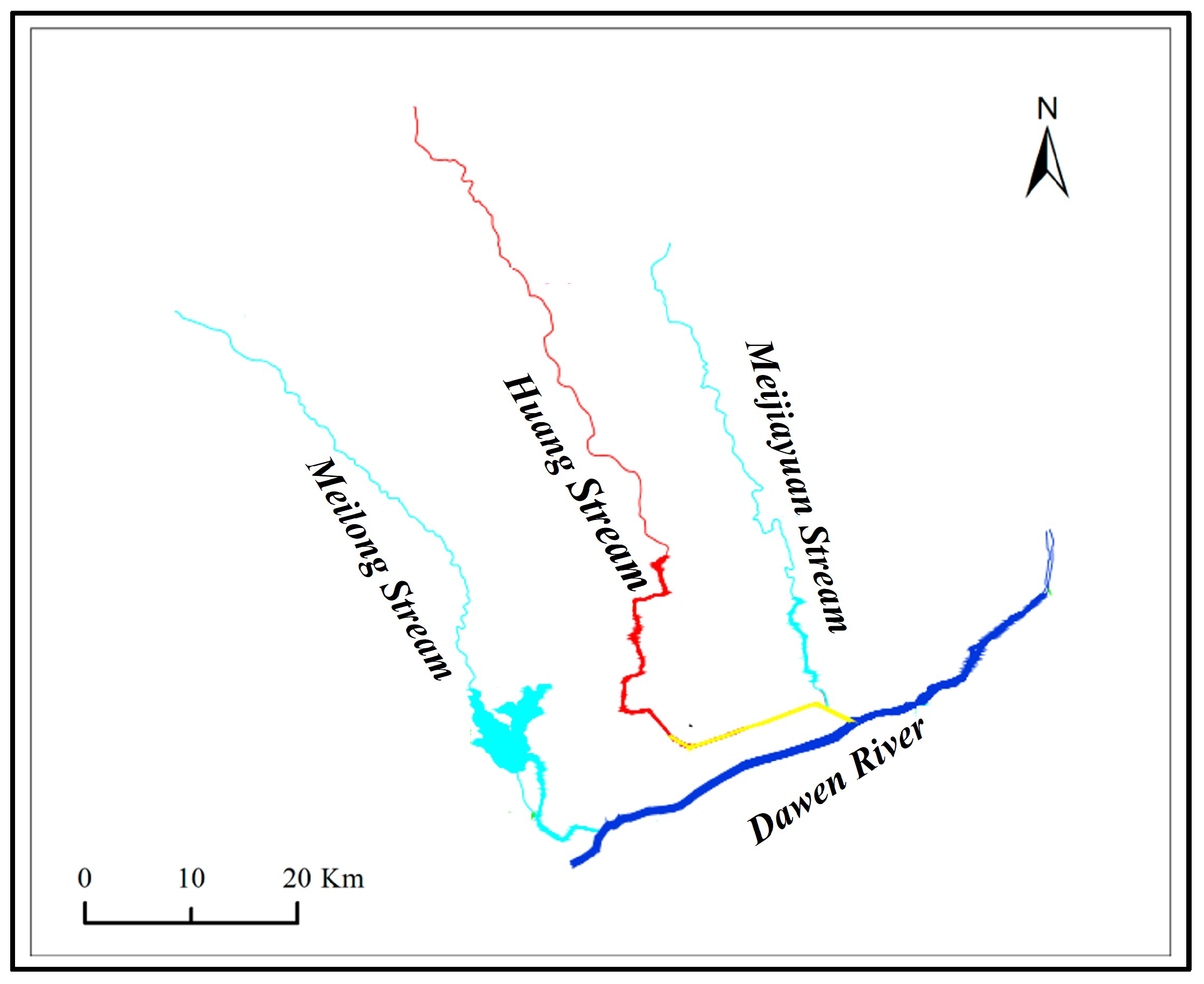
3.1. Overview of the Research Area
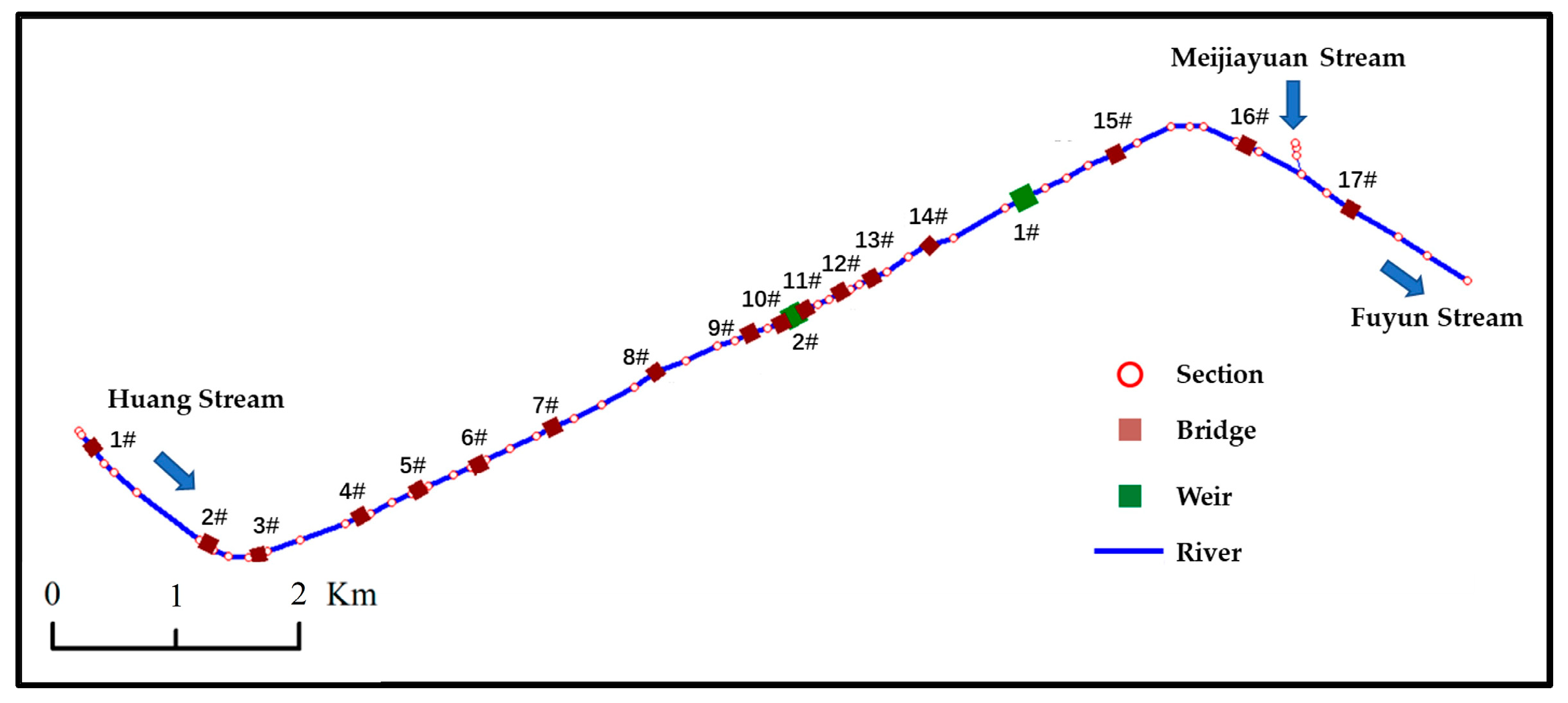
3.2. River Simplification
3.3. Hydraulic Calculation Boundary Conditions
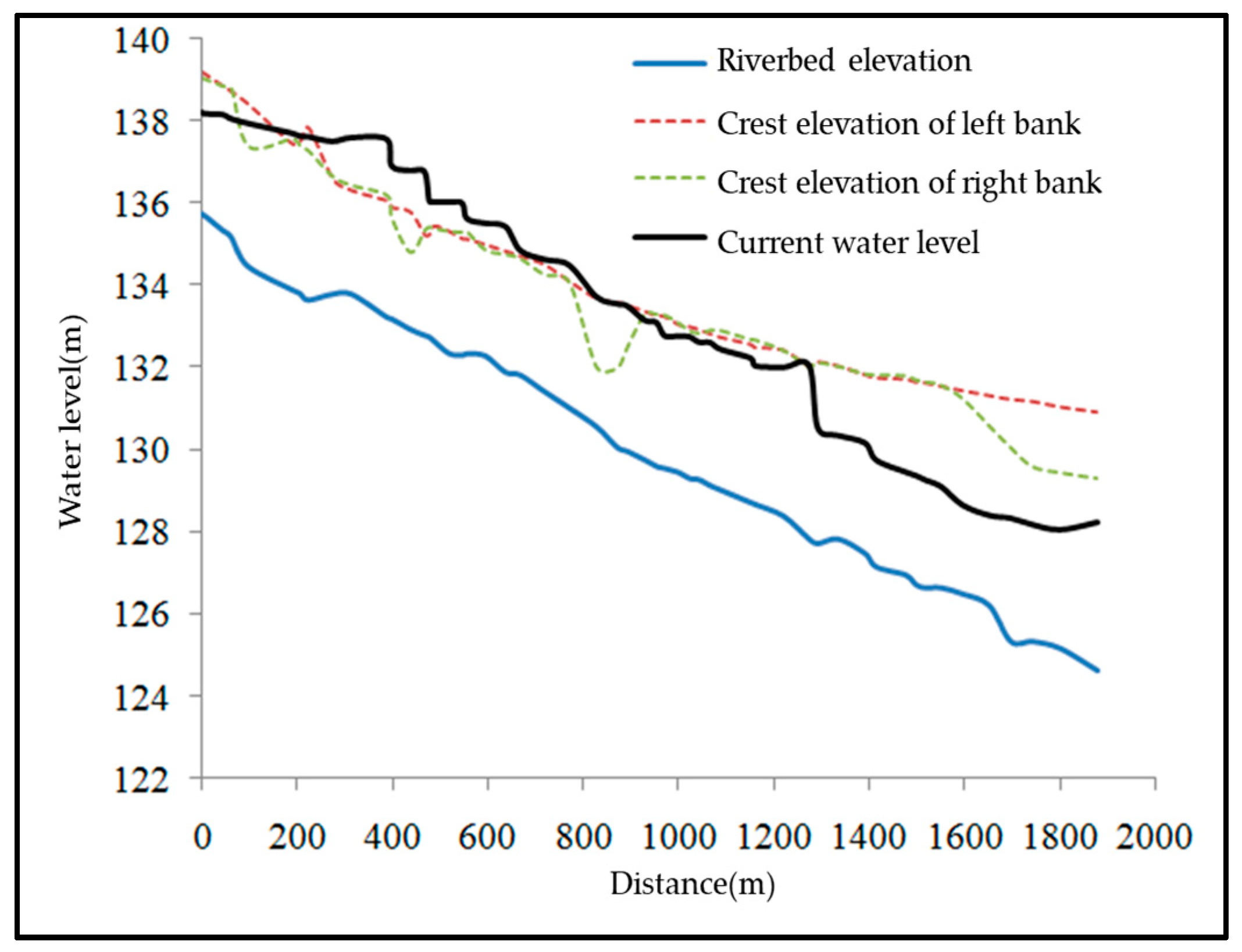
3.4. Flood Discharge Capacity under Current Conditions
3.5. Analysis of the Influence of Weirs on the Flood Discharge Capacity
3.6. Analysis of the Influence of Bridges on the Flood Discharge Capacity
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shih, D.S.; Yeh, G.T. Studying Inertia Effects in Open Channel Flow Using Saint-Venant Equations. Water 2018, 10, 1652. [Google Scholar] [CrossRef] [Green Version]
- Wu, G.; Yang, F.; Huang, M. Study on seasonal channel flood routing model coupled with leakage term. S-to-N Water Trfs. Water Sci. Technol. 2018, 16, 33–37. [Google Scholar]
- Reggiani, P.; Todini, E.; Meißner, D. On mass and momentum conservation in the variable-parameter Muskingum method. J. Hydrol. 2016, 543, 562–576. [Google Scholar] [CrossRef]
- Kalinin, G.P.; Milyukov, P.I. On the computation of unsteady flow in open channels. Met. Gidrol. 1957, 10, 10–18. [Google Scholar]
- Montes, N.; Aranda, J.Á.; García-Bartual, R. Real Time Flow Forecasting in a Mountain River Catchment Using Conceptual Models with Simple Error Correction Scheme. Water 2020, 12, 1484. [Google Scholar] [CrossRef]
- Lee, E.H. Development of a New 8-Parameter Muskingum Flood Routing Model with Modified Inflows. Water 2021, 13, 3170. [Google Scholar] [CrossRef]
- Li, Z.; He, M.; Yan, F.; Hu, Y.; Liu, Z.; Tong, B. Applications of channel flood routing methods in middle part of Huaihe River and Hutuo River. J. Hohai. Univ. Nat. Sci. 2020, 48, 95–101. [Google Scholar]
- Fenton, J.D. Flood routing methods. J. Hydrol. 2019, 570, 251–264. [Google Scholar] [CrossRef]
- Saeed, M.; Li, H.; Ullah, S.; Rahman, A.U.; Ali, A.; Khan, R.; Hassan, W.; Munir, I.; Alam, S. Flood Hazard Zonation Using an Artificial Neural Network Model: A Case Study of Kabul River Basin, Pakistan. Sustainability 2021, 13, 13953. [Google Scholar] [CrossRef]
- Tamiru, H.; Dinka, M.O. Application of ANN and HEC-RAS model for flood inundation mapping in lower Baro Akobo River Basin, Ethiopia. J. Hydrol. Reg. Stud. 2021, 36, 100855. [Google Scholar] [CrossRef]
- Liu, Z.; Feng, S.; Lan, F.; Chen, S.; Liang, H.; Fei, K. Regulation scheme of Shegong River based on watershed flood hazard analysis. Water Res. Prot. 2018, 34, 38–43+64. [Google Scholar]
- Bulti, A.T. The Influence of Dam Construction on the Catchment Hydrologic Behavior and its Effects on a Discharge Forecast in Hydrological Models. Water Resour. Manag. 2021, 35, 2023–2037. [Google Scholar] [CrossRef]
- Wang, Q.; Peng, W.; Dong, F.; Liu, X.; Ou, N. Simulating Flow of An Urban River Course with Complex Cross Sections Based on the MIKE21 FM Model. Water 2020, 12, 761. [Google Scholar] [CrossRef] [Green Version]
- Karymbalis, E.; Andreou, M.; Batzakis, D.V.; Tsanakas, K.; Karalis, S. Integration of GIS-Based Multicriteria Decision Analysis and Analytic Hierarchy Process for Flood-Hazard Assessment in the Megalo Rema River Catchment (East Attica, Greece). Sustainability 2021, 13, 10232. [Google Scholar] [CrossRef]
- Liu, Q.; Qin, Y.; Zhang, Y.; Li, Z. A coupled 1D–2D hydrodynamic model for flood simulation in flood detention basin. Nat. Hazard. 2015, 75, 1303–1325. [Google Scholar] [CrossRef]
- Liu, J.; Wang, J.; Xiong, J.; Cheng, W.; Cui, X.; He, W.; He, Y.; Duan, Y.; Yang, G.; Wang, N. Dynamic Assessment of the Flood Risk at Basin Scale under Simulation of Land-Use Scenarios and Spatialization Technology of Factor. Water 2021, 13, 3239. [Google Scholar] [CrossRef]
- He, C.; Wei, J.; Song, Y.; Luo, J.-J. Seasonal Prediction of Summer Precipitation in the Middle and Lower Reaches of the Yangtze River Valley: Comparison of Machine Learning and Climate Model Predictions. Water 2021, 13, 3294. [Google Scholar] [CrossRef]
- Liu, L.; Wu, Z.; Li, Q. Overtopping Risk Analysis of Earth Dams Considering Effects of Failure Duration of Release Structures. Complexity 2020, 2020, 3528350. [Google Scholar] [CrossRef]
- Malik, R.; Setia, B. Interference between pier models and its effects on scour depth. SN Appl. Sci. 2019, 2, 68. [Google Scholar] [CrossRef] [Green Version]
- Subedi, A.; Sharma, S.; Islam, A.; Lamichhane, N. Quantification of the Effect of Bridge Pier Encasement on Headwater Elevation Using HEC-RAS. Hydrology 2019, 6, 25. [Google Scholar] [CrossRef] [Green Version]
- Ren, M.; Xu, Z.; Su, G. Comparative analysis on bridge backwater depths estimated using 2-D hydrodynamic model and empirical formulas. J. Hydroelectr. Eng. 2017, 36, 78–87. [Google Scholar]
- Vaheddoost, B.; Safari, M.J.S.; Ilkhanipour, Z.R. Discharge coefficient for vertical sluice gate under submerged condition using contraction and energy loss coefficients. Flow Meas. Instrum. 2021, 80, 102007. [Google Scholar] [CrossRef]
- Mohamed, I.M.; Abdelhaleem, F.S. Flow Downstream Sluice Gate with Orifice. KSCE J. Civ. Eng. 2020, 24, 3692–3702. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, L.; Zhang, F.; Zhang, C.; Wu, M.; Tang, H.; Zhu, H. Launch condition and flood diversion effect of flood diversion area named Garden Lake. J. Hohai. Univ. Nat. Sci. 2020, 48, 209–214. [Google Scholar]
- Baird, D.C.; Abban, B.; Scurlock, S.M.; Abt, S.B.; Thornton, C.I. Two-Dimensional Numerical Modeling of Flow in Physical Models of Rock Vane and Bendway Weir Configurations. Water 2021, 13, 458. [Google Scholar] [CrossRef]
- Seyedjavad, M.; Naeeni, S.O.; Saneie, M. Flow velocity pattern around trapezoidal piano key side weirs. Flow Meas. Instrum. 2020, 76, 101847. [Google Scholar] [CrossRef]
- Li, G.; Li, S.; Hu, Y. The effect of the inlet/outlet width ratio on the discharge of piano key weirs. J. Hydraul. Res. 2020, 58, 594–604. [Google Scholar] [CrossRef]
- Atashi, V.; Bejestan, M.S.; Lim, Y.H. Flow Pattern and Erosion in a 90-Degrees Sharp Bend around a W−Weir. Water 2023, 15, 11. [Google Scholar] [CrossRef]
- Skilodimou, H.D.; Bathrellos, G.D.; Alexakis, D.E. Flood Hazard Assessment Mapping in Burned and Urban Areas. Sustainability 2021, 13, 4455. [Google Scholar] [CrossRef]
- Salehi, S.; Azimi, A.H. Discharge Characteristics of Weir-Orifice and Weir-Gate Structures. J. Irrig. Drain. Eng. 2019, 145, 04019025. [Google Scholar] [CrossRef]




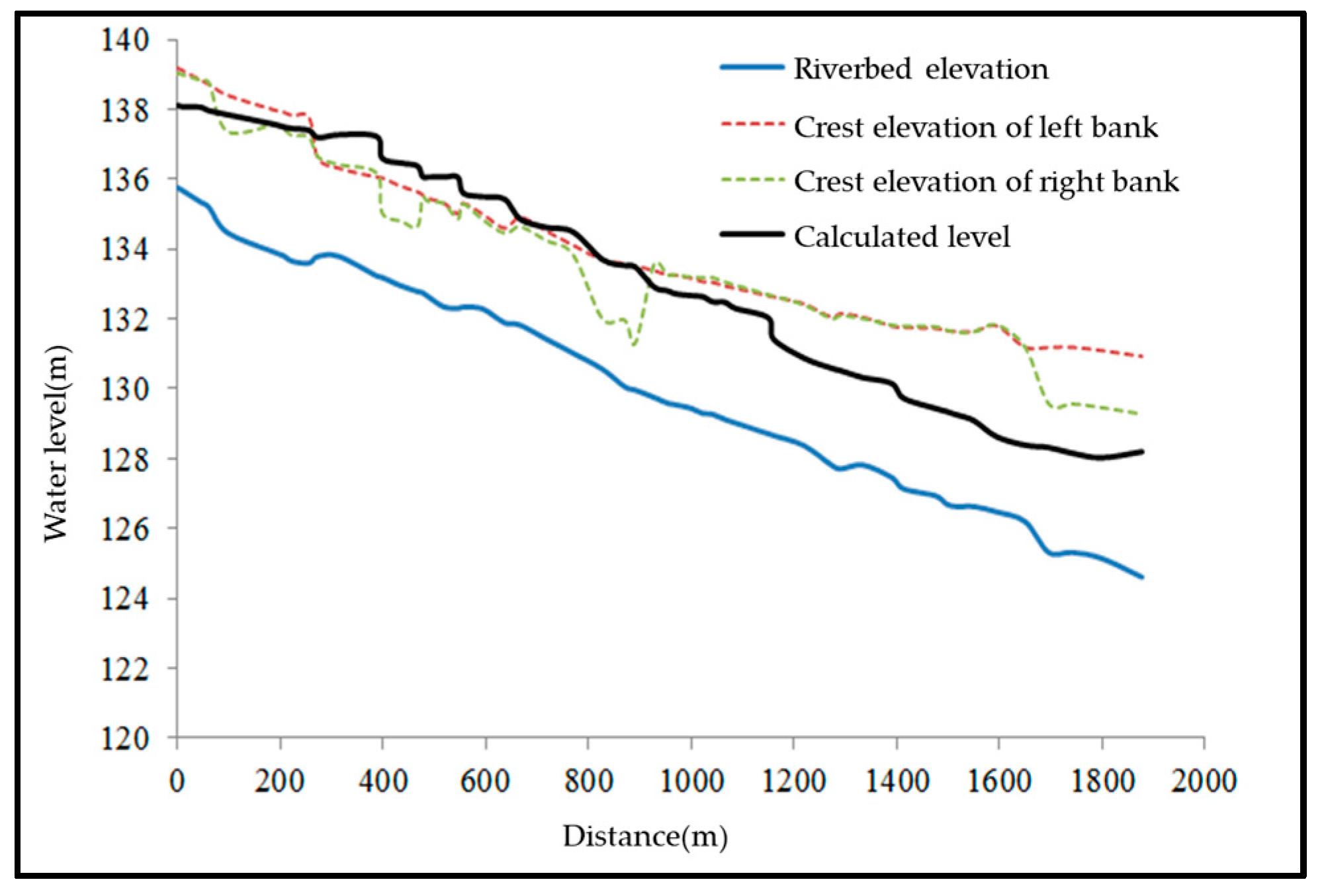
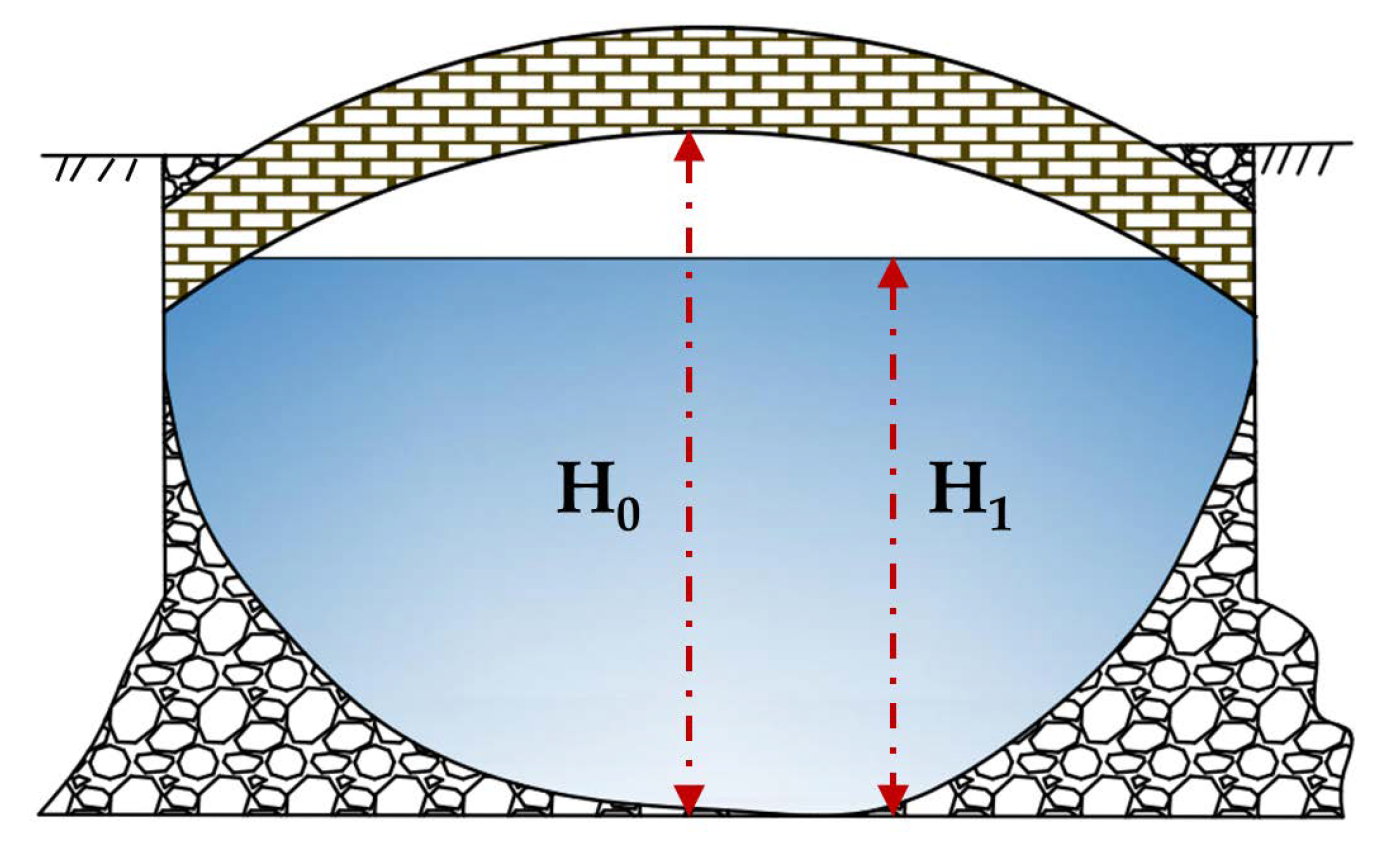
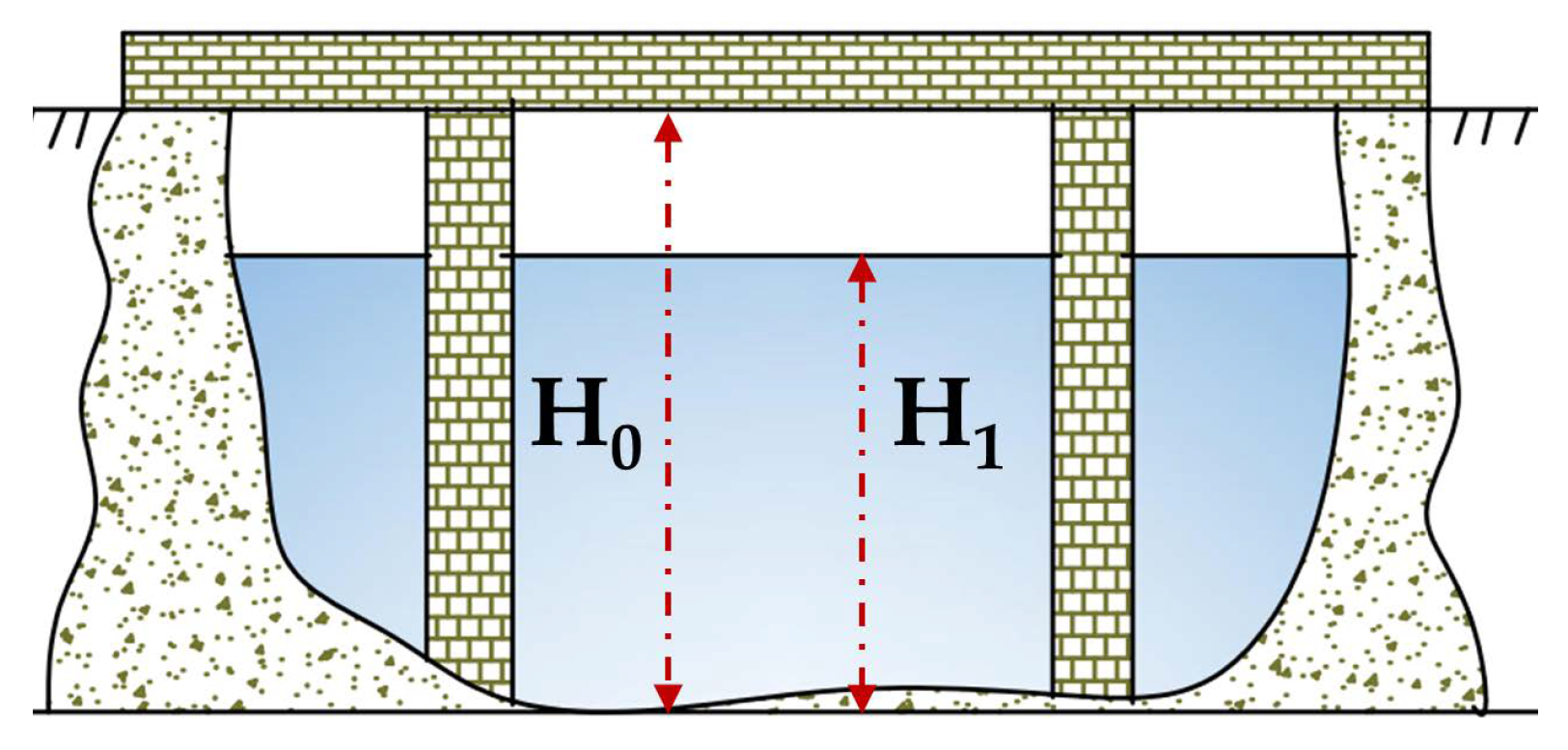
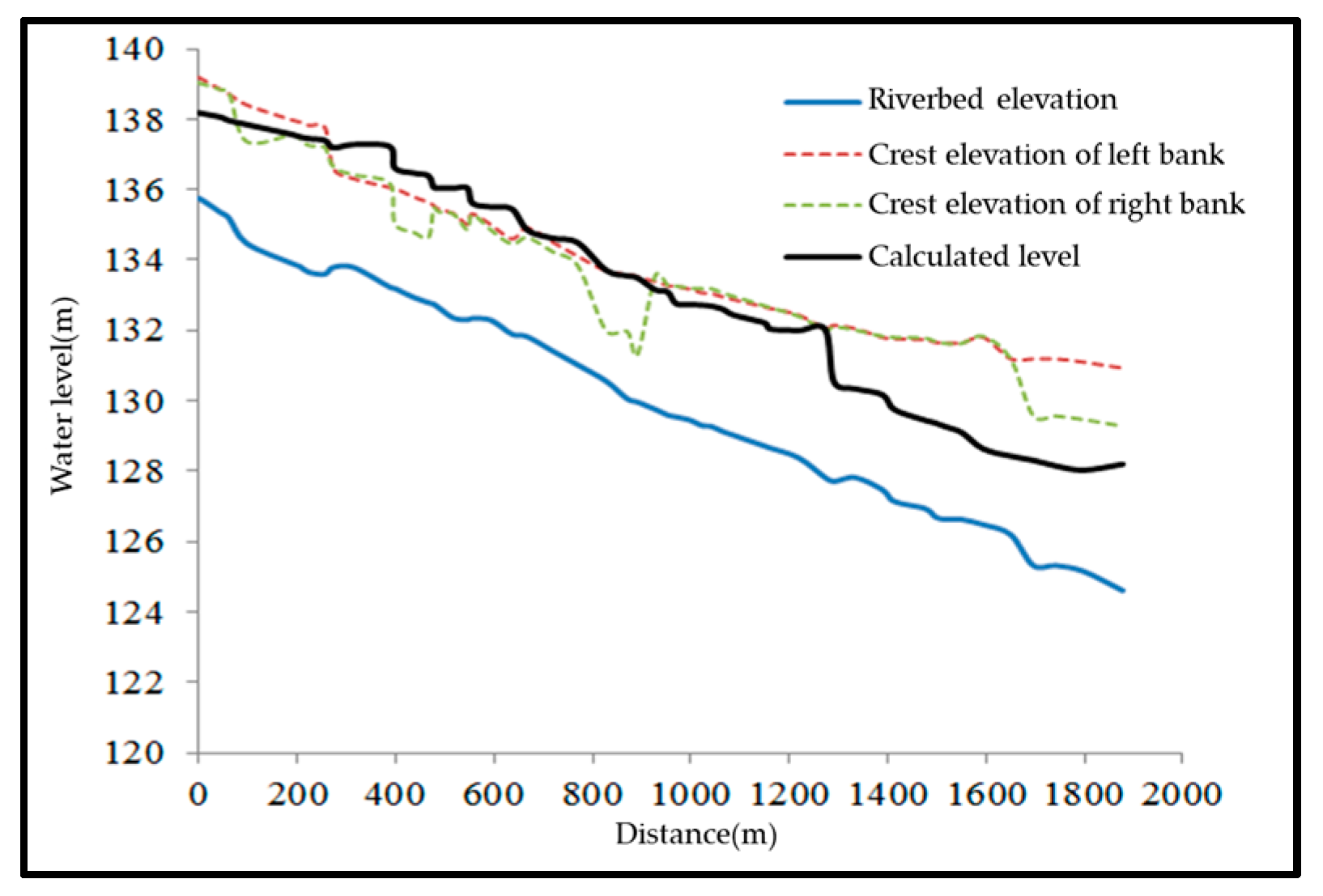
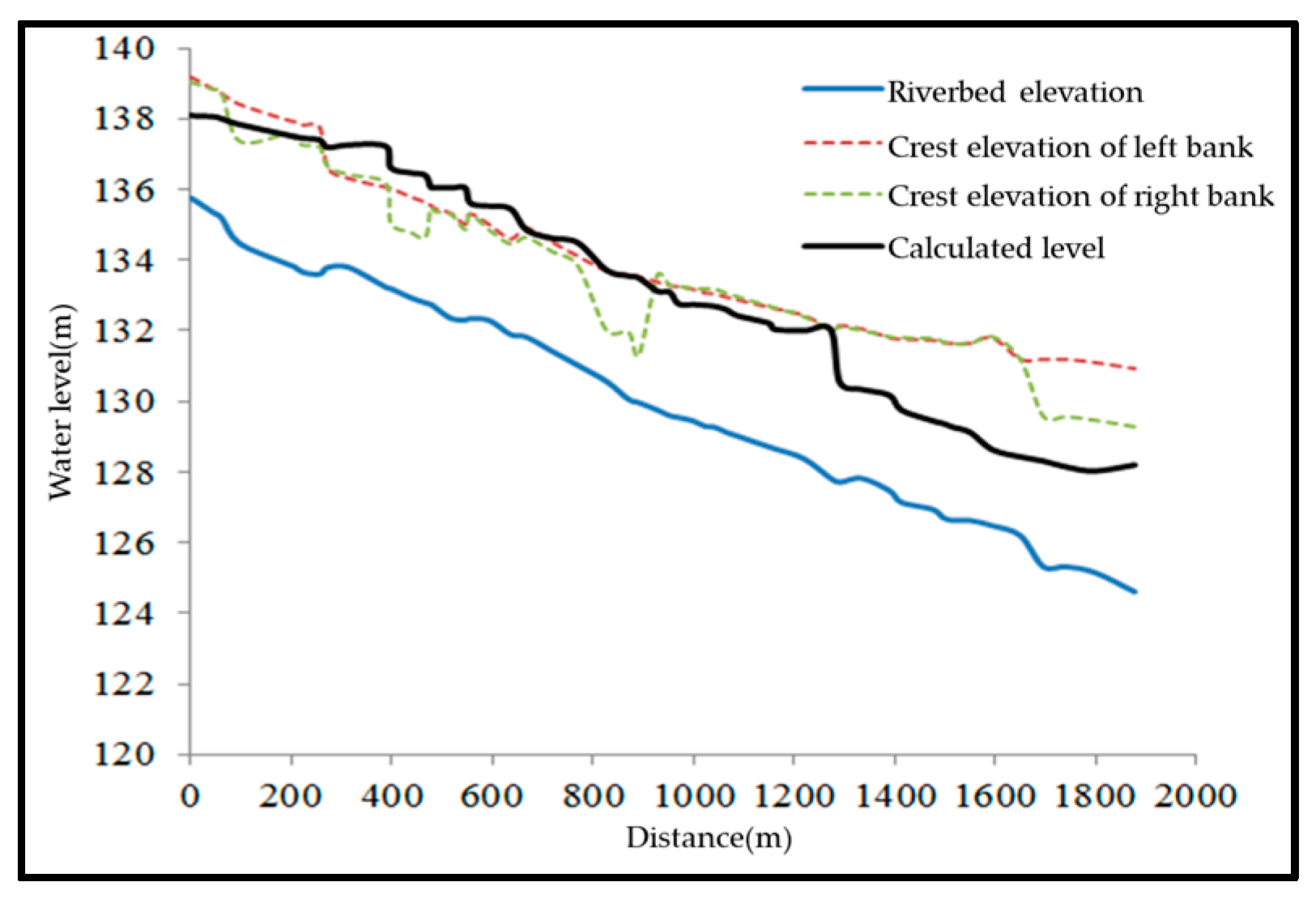

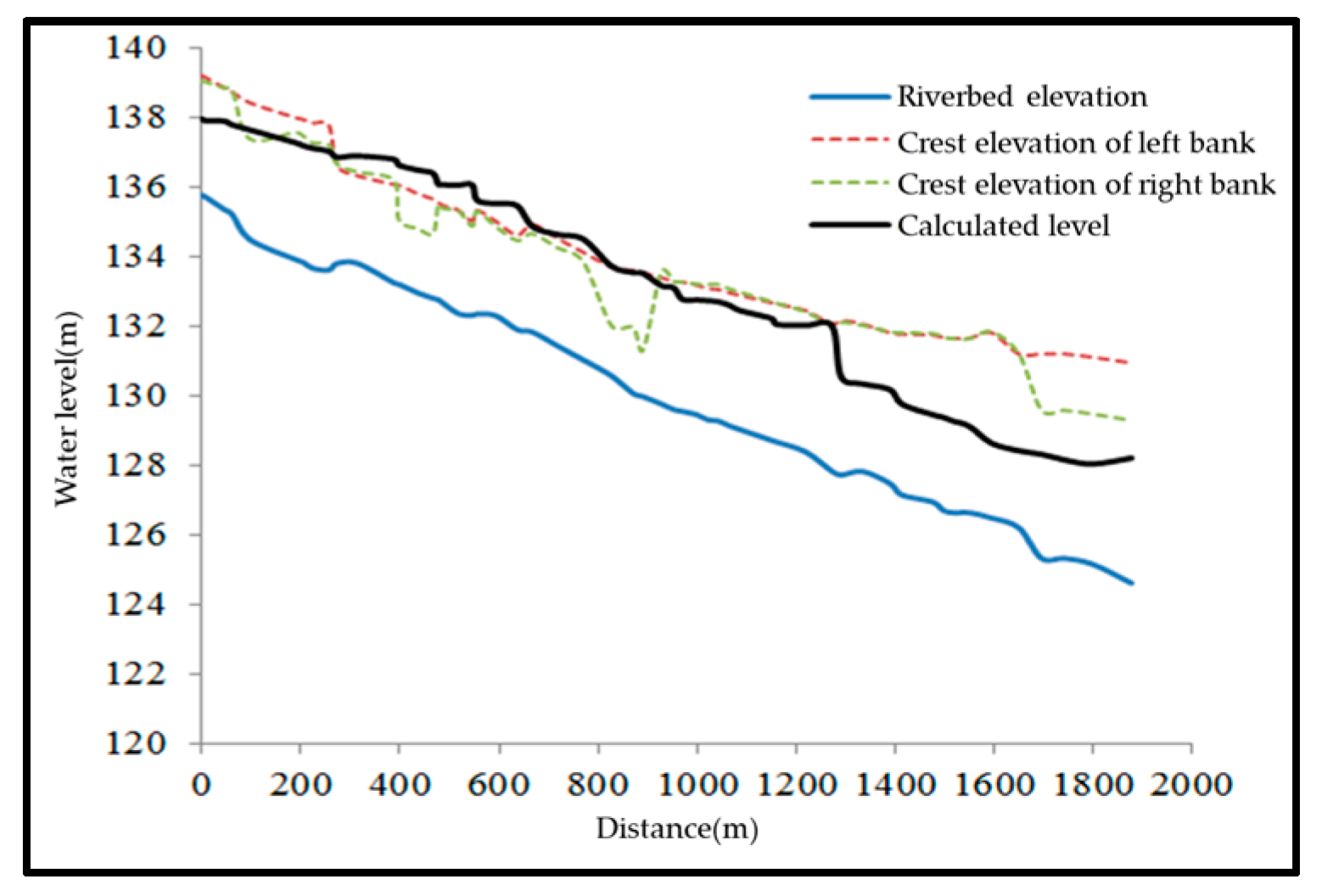
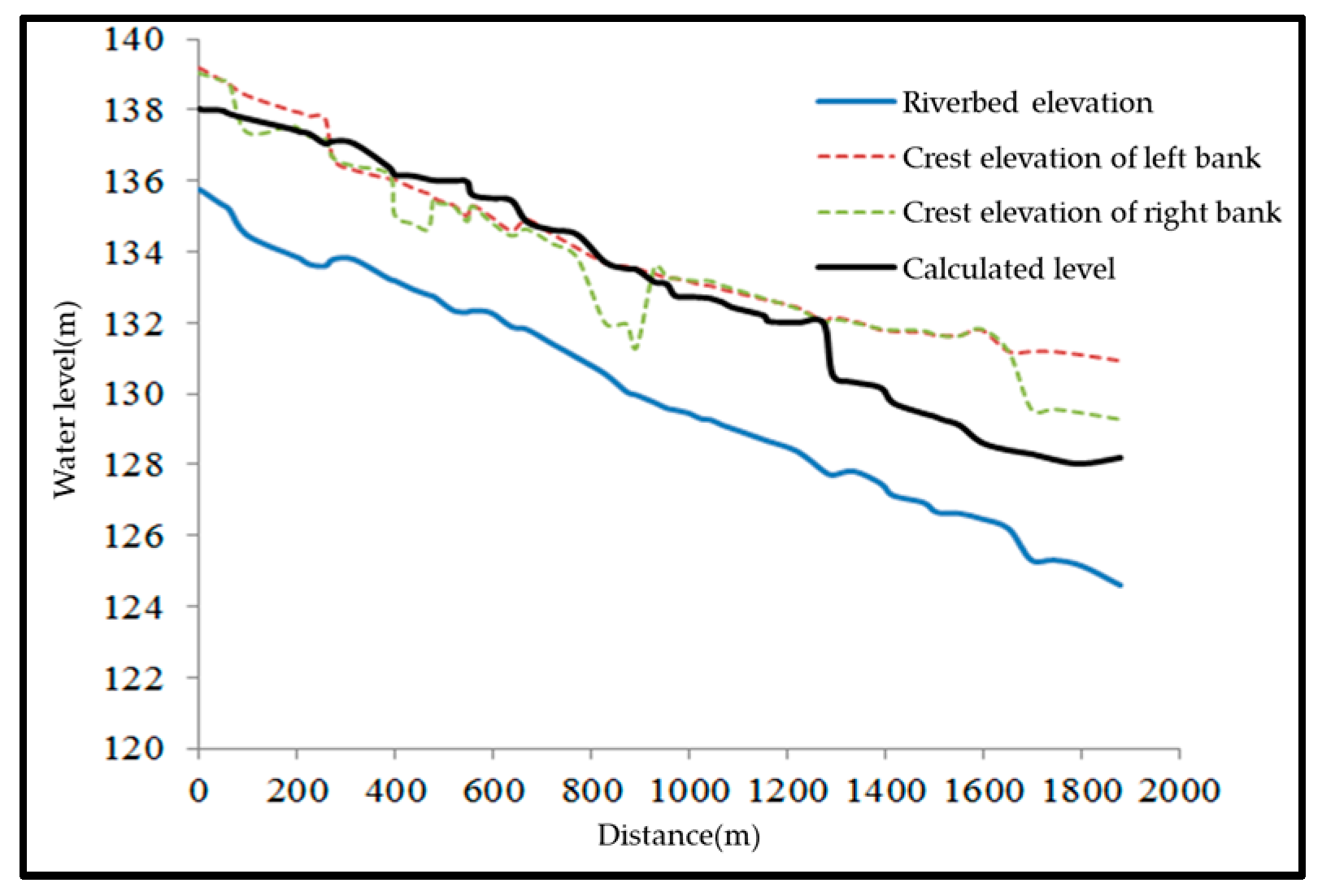
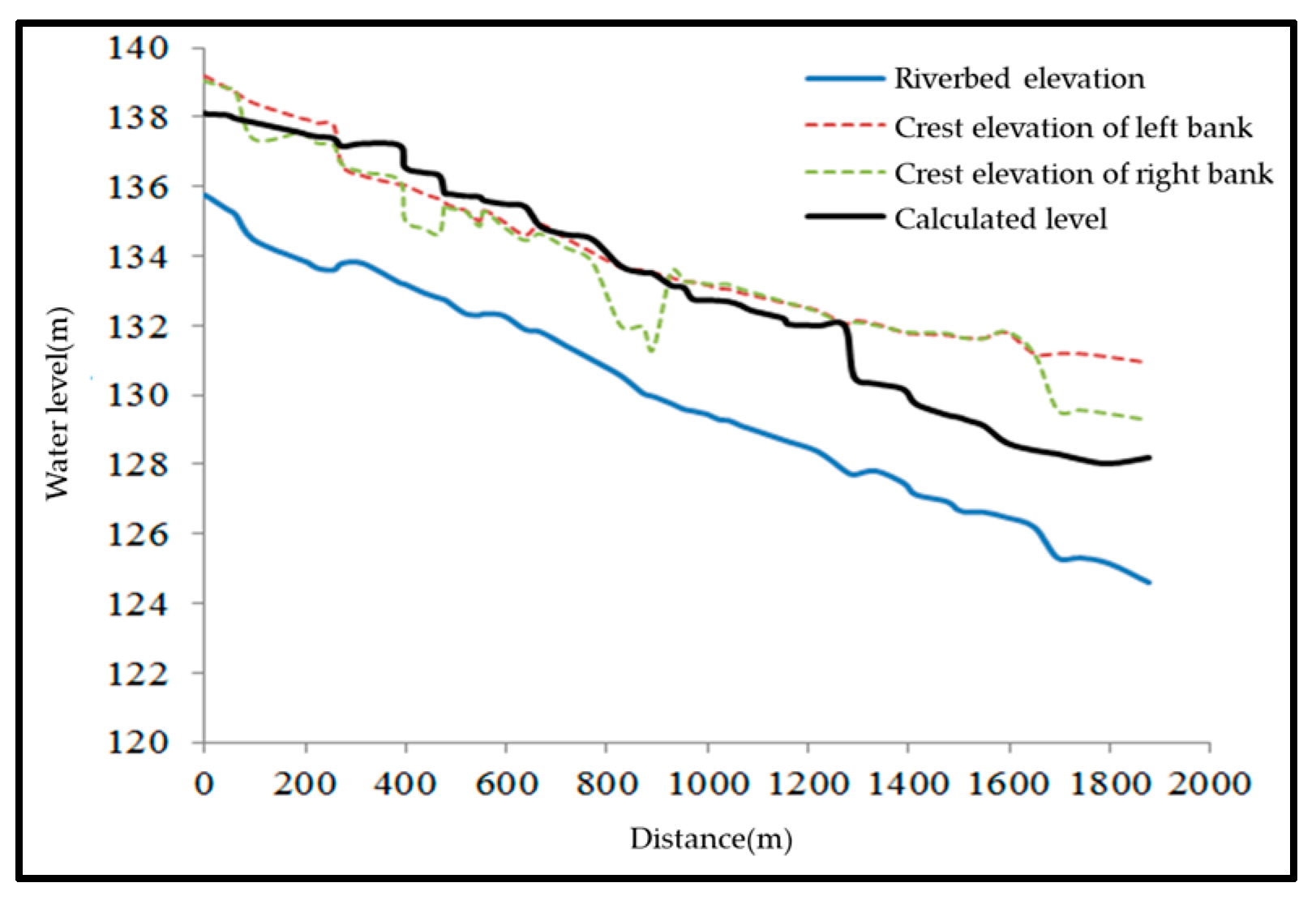
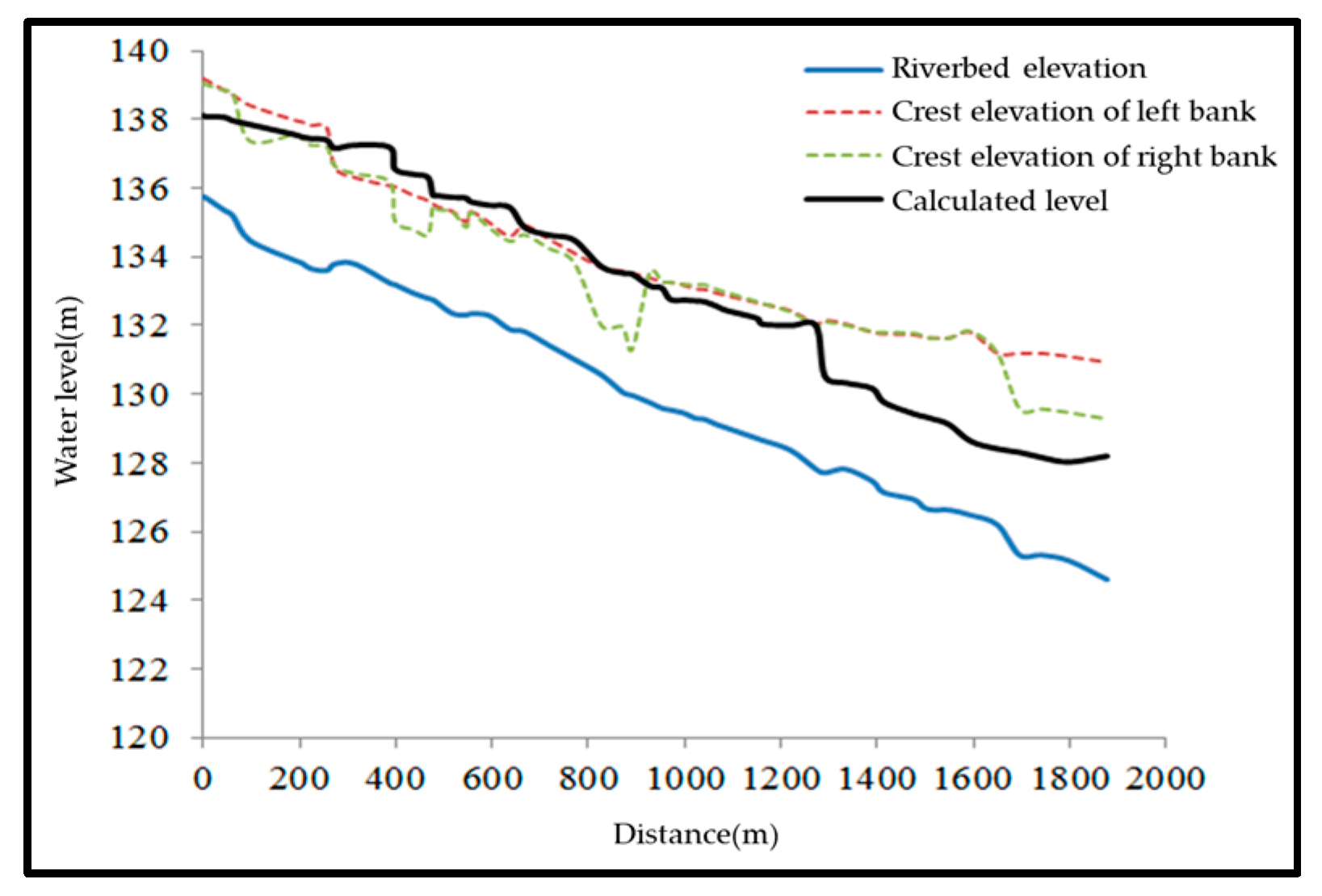
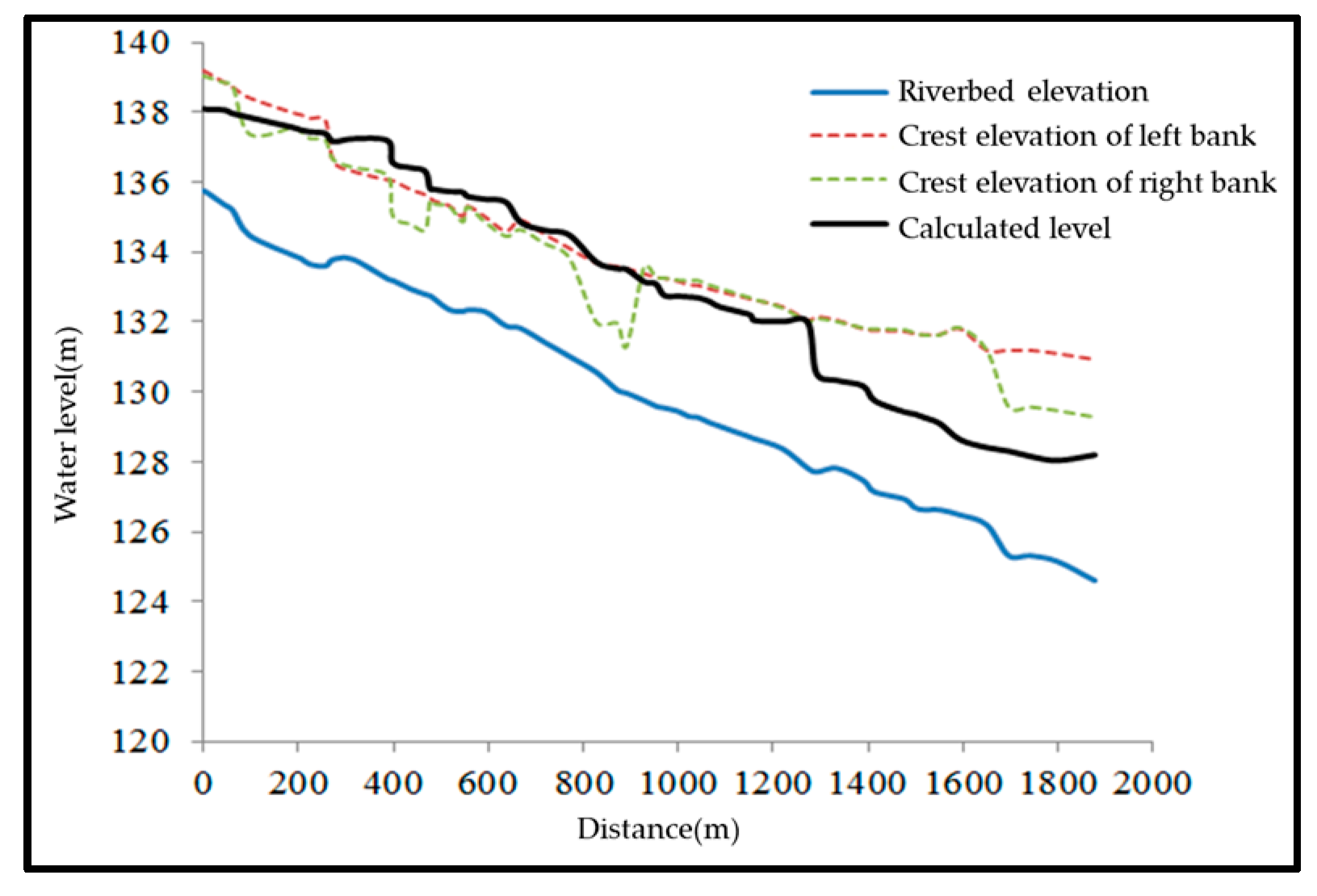


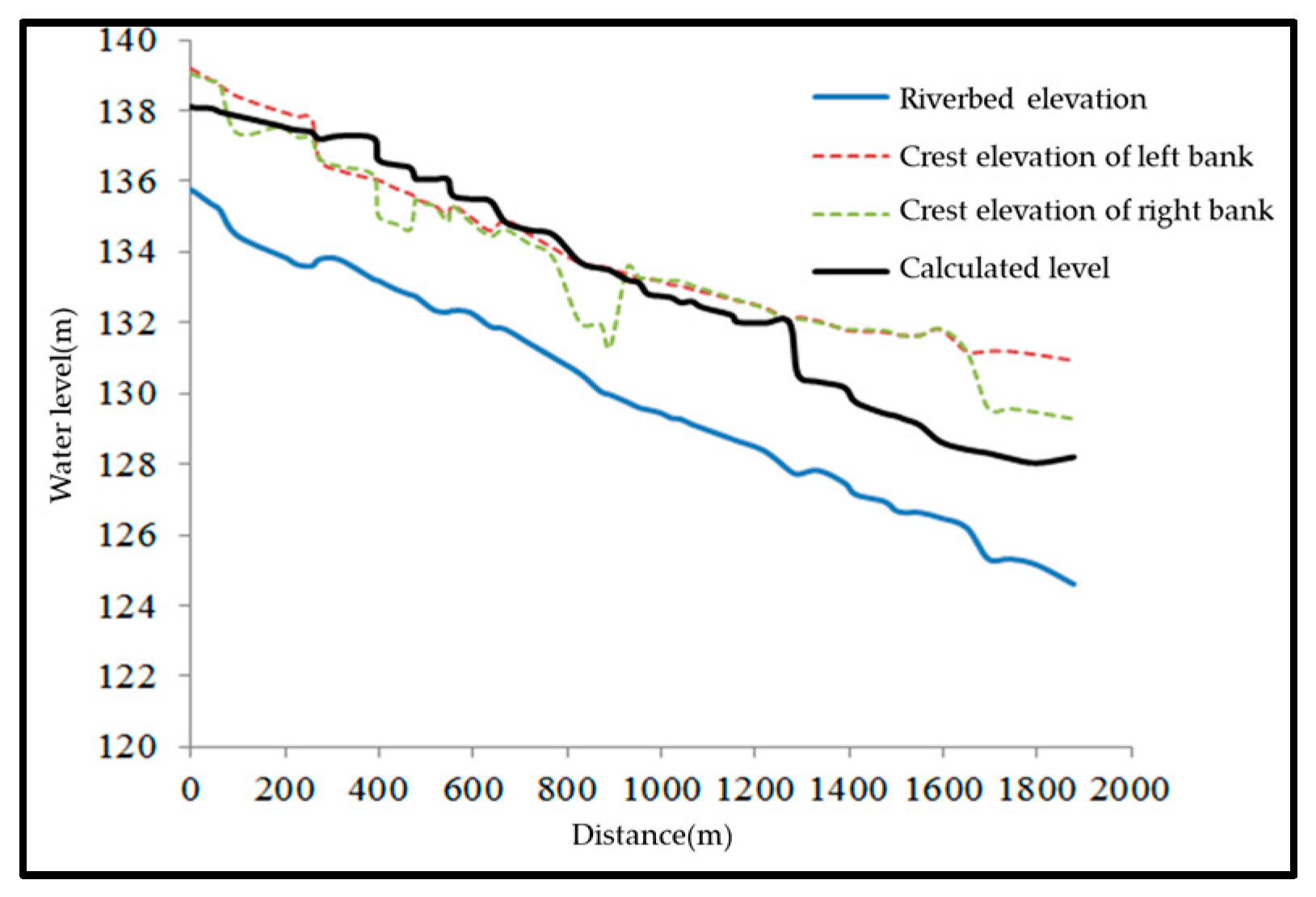
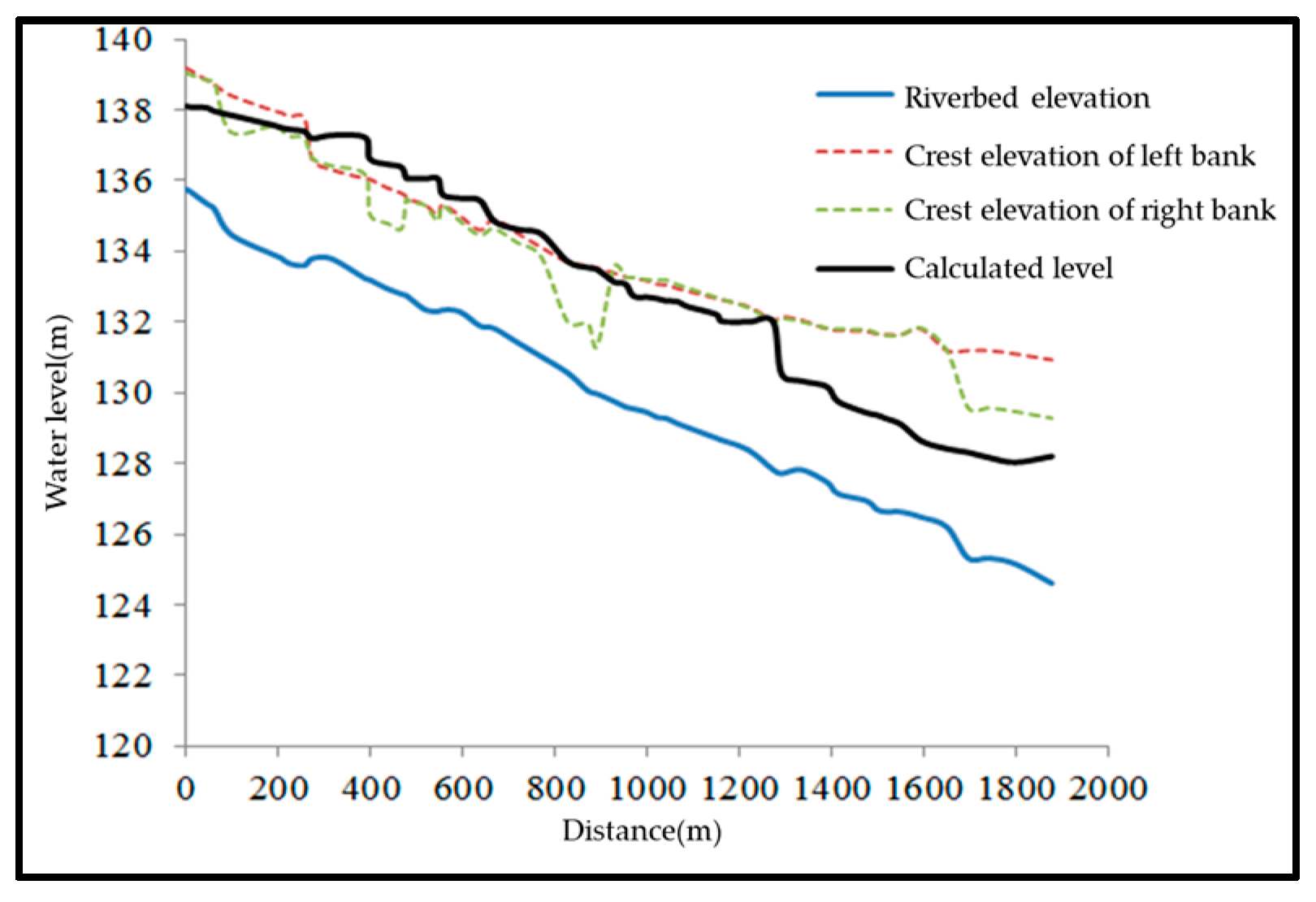
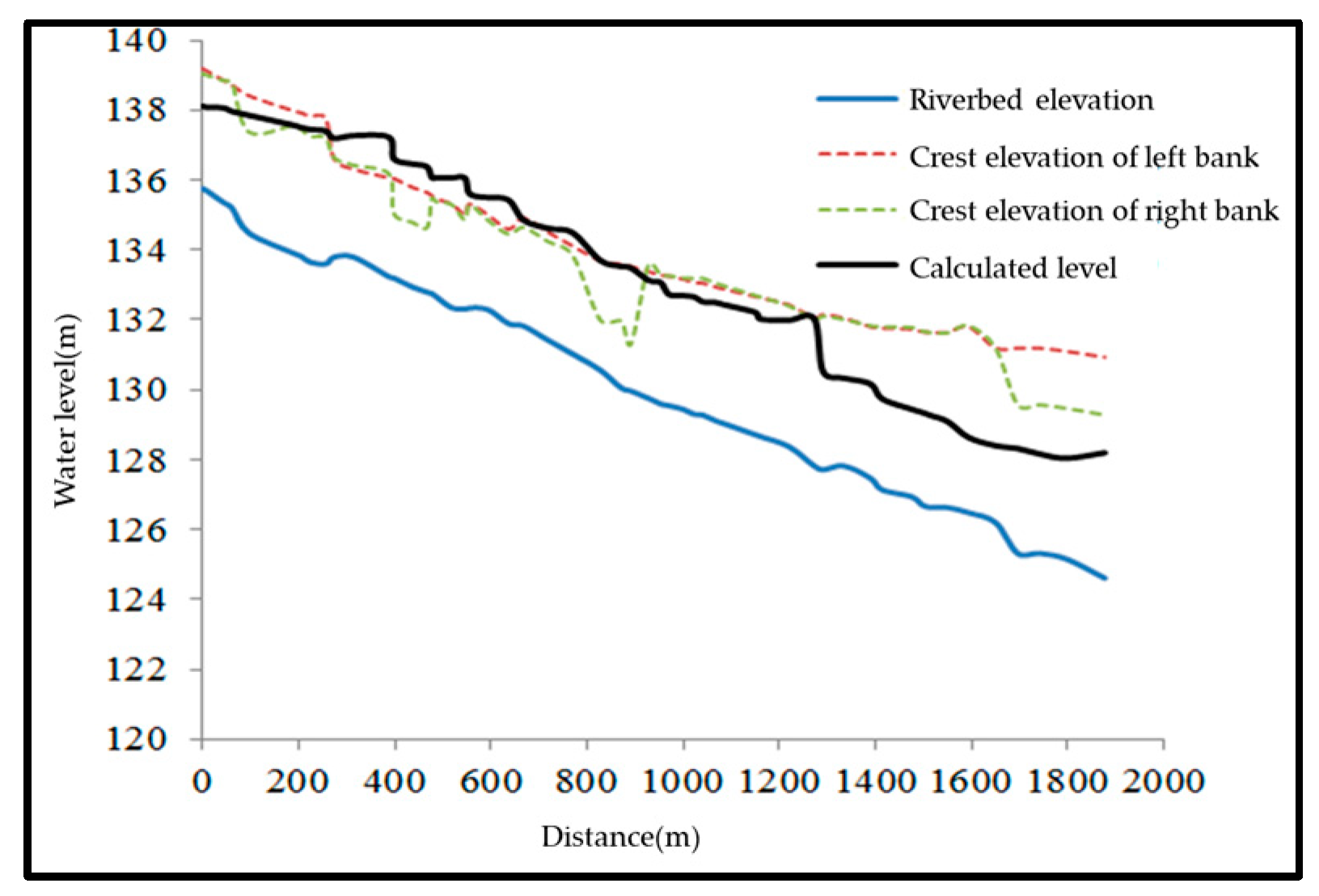

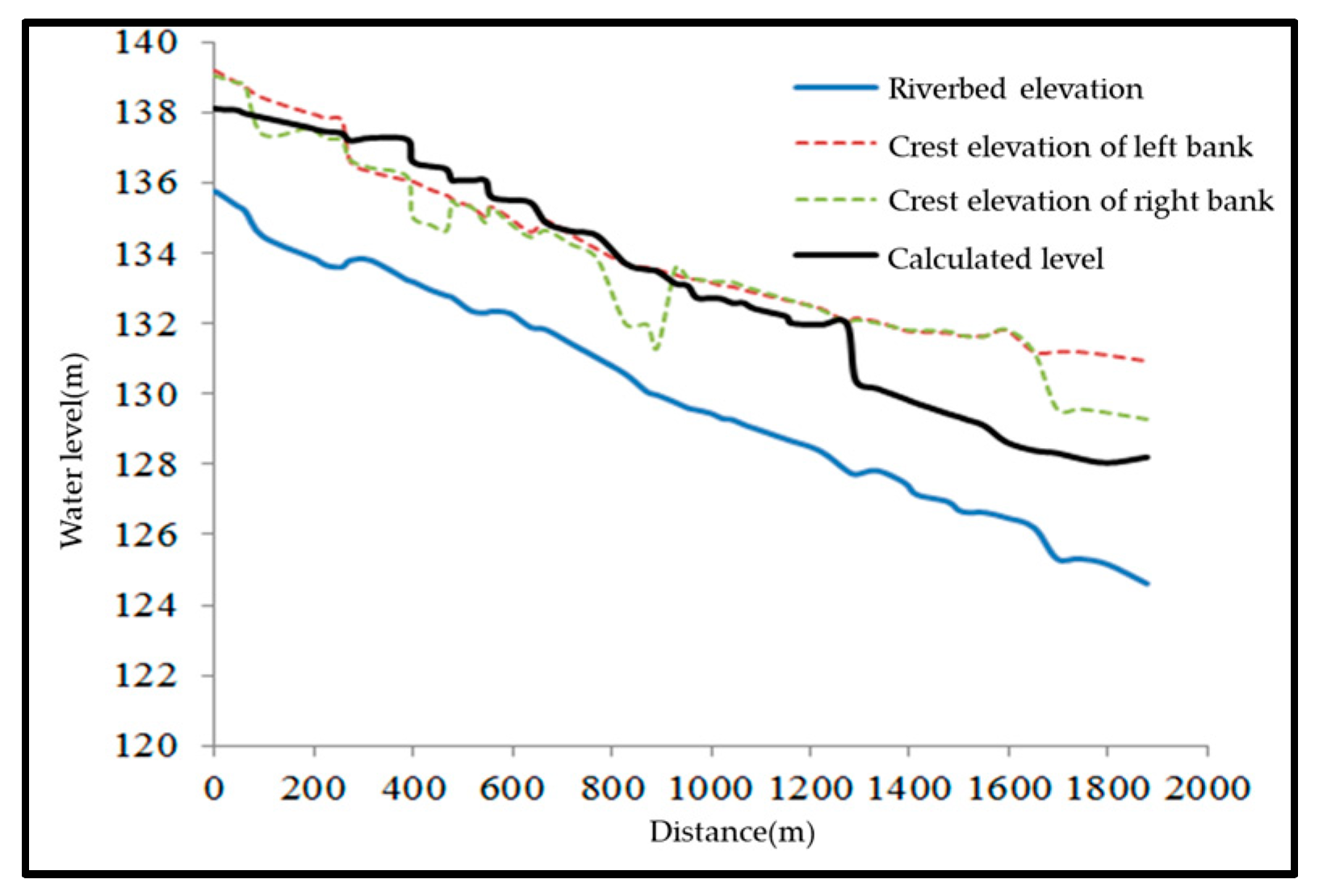
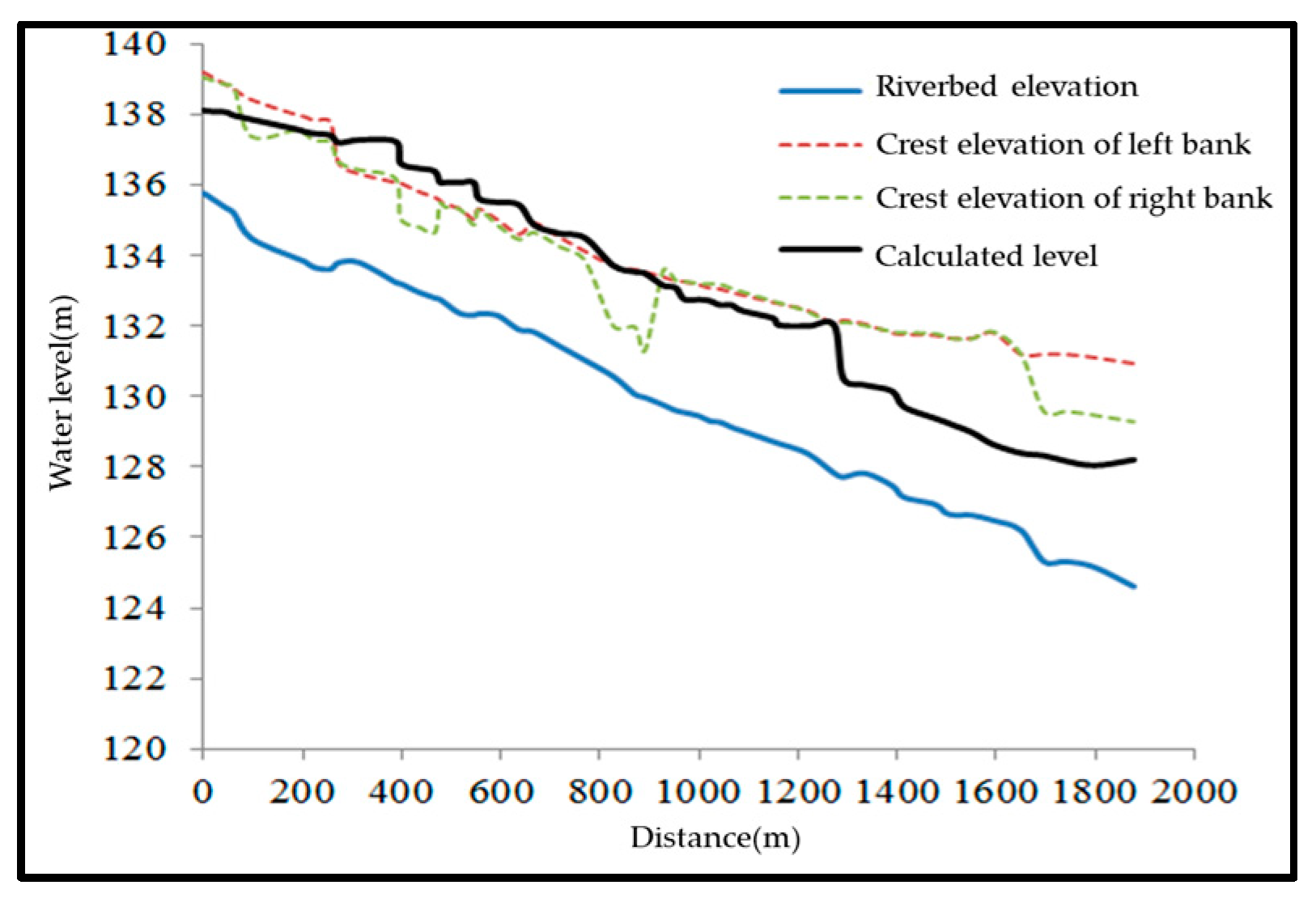

| Condition | #1 Weir Height | #2 Weir Height | Backwater Range | Maximum Backwater Height | Impact |
|---|---|---|---|---|---|
| 1 | 2.00 | 0.75 | [928.09, 1283.00] | 1.33 | No |
| 2 | 0.00 | 0.75 | [1255.14, 1283.00] | 0.19 | No |
| 3 | 2.00 | 0.00 | [891.53, 962.43] | 0.24 | No |
| 4 | 0.00 | 0.00 | 0.00 | 0.00 | No |
| Bridge Number | Location | Type | N | H0 | H1 | |||
|---|---|---|---|---|---|---|---|---|
| Without Bridge | With Bridge | |||||||
| 1# | 25.37 | Flat slab | 1 | 138.80 | 138.14 | 138.14 | 0.00 | −0.66 |
| 2# | 195.82 | Flat slab | 2 | 137.42 | 137.53 | 137.64 | 0.11 | 0.22 |
| 3# | 261.84 | Flat slab | 2 | 136.41 | 137.2 | 137.50 | 0.30 | 1.09 |
| 4# | 392.89 | Flat slab | 3 | 135.63 | 136.7 | 137.21 | 0.51 | 1.58 |
| 5# | 471.74 | Flat slab | 2 | 135.42 | 136.02 | 136.39 | 0.37 | 0.97 |
| 6# | 550.25 | Flat slab | 1 | 134.62 | 135.65 | 135.79 | 0.14 | 1.17 |
| 7# | 652.04 | Flat slab | 1 | 134.83 | 134.95 | 135.12 | 0.17 | 0.29 |
| 8# | 790.29 | Flat slab | 1 | 133.38 | 133.88 | 134.09 | 0.21 | 0.71 |
| 9# | 912.53 | Flat slab | 2 | 132.98 | 133.11 | 133.3 | 0.19 | 0.32 |
| 10# | 955.64 | Flat slab | 3 | 132.90 | 132.7 | 132.92 | 0.22 | 0.02 |
| 11# | 979.22 | Flat slab | 2 | 133.06 | 132.56 | 132.75 | 0.19 | −0.31 |
| 12# | 1032.00 | Arch | 1 | 132.19 | 132.5 | 132.67 | 0.17 | 0.48 |
| 13# | 1076.39 | Arch | 1 | 133.16 | 132.38 | 132.51 | 0.13 | −0.65 |
| 14# | 1155.53 | Flat slab | 2 | 131.85 | 132.05 | 132.15 | 0.10 | 0.30 |
| 15# | 1401.87 | Flat slab | 1 | 131.31 | 129.94 | 129.94 | 0.00 | −1.37 |
| 16# | 1572.66 | Flat slab | 1 | 131.03 | 128.86 | 128.86 | 0.00 | −2.17 |
| 17# | 1719.09 | Flat slab | 1 | 130.50 | 128.28 | 128.28 | 0.00 | −2.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Shen, H.; Zhang, J.; Meng, Z.; Zhang, Y.; Han, W. Influence of Multi-Cross Structures on the Flood Discharge Capacity of Mountain Rivers in the Yellow River Basin. Water 2023, 15, 2719. https://doi.org/10.3390/w15152719
Hu J, Shen H, Zhang J, Meng Z, Zhang Y, Han W. Influence of Multi-Cross Structures on the Flood Discharge Capacity of Mountain Rivers in the Yellow River Basin. Water. 2023; 15(15):2719. https://doi.org/10.3390/w15152719
Chicago/Turabian StyleHu, Jianyong, Hui Shen, Jinxin Zhang, Zhenzhu Meng, Yuzhou Zhang, and Wei Han. 2023. "Influence of Multi-Cross Structures on the Flood Discharge Capacity of Mountain Rivers in the Yellow River Basin" Water 15, no. 15: 2719. https://doi.org/10.3390/w15152719
APA StyleHu, J., Shen, H., Zhang, J., Meng, Z., Zhang, Y., & Han, W. (2023). Influence of Multi-Cross Structures on the Flood Discharge Capacity of Mountain Rivers in the Yellow River Basin. Water, 15(15), 2719. https://doi.org/10.3390/w15152719






