Prediction of the Height of Fractured Water-Conducting Zone: Significant Factors and Model Optimization
Abstract
:1. Introduction
2. Overview of the Study Area
2.1. Physiographic Conditions
2.2. The Spatial Distribution Characteristics of Main Coal Seams
3. Methodology
3.1. Research Technical Route
3.2. Calculation Principle of Grey Entropy Correlation Analysis
3.3. Analysis of the Applicability of Regression Model Construction Methods
- (1)
- Single-factor regression model construction method
- (2)
- Multi-factor regression model construction method
4. Regression Model Construction for the Height of FWCZ
4.1. Initial Selection and Quantification of Influencing Factors
4.2. Construction of Single-Factor Regression Models
4.3. Multi-Factor Regression Models Constructed
- (1)
- Multiple stepwise regression (MSR) model
- (2)
- GA-BP neural network model
- (3)
- GA-CatBoost regression model
5. Reliability Verification and Basic Application of the Best Predictive Model
5.1. Optimization of Regression Models
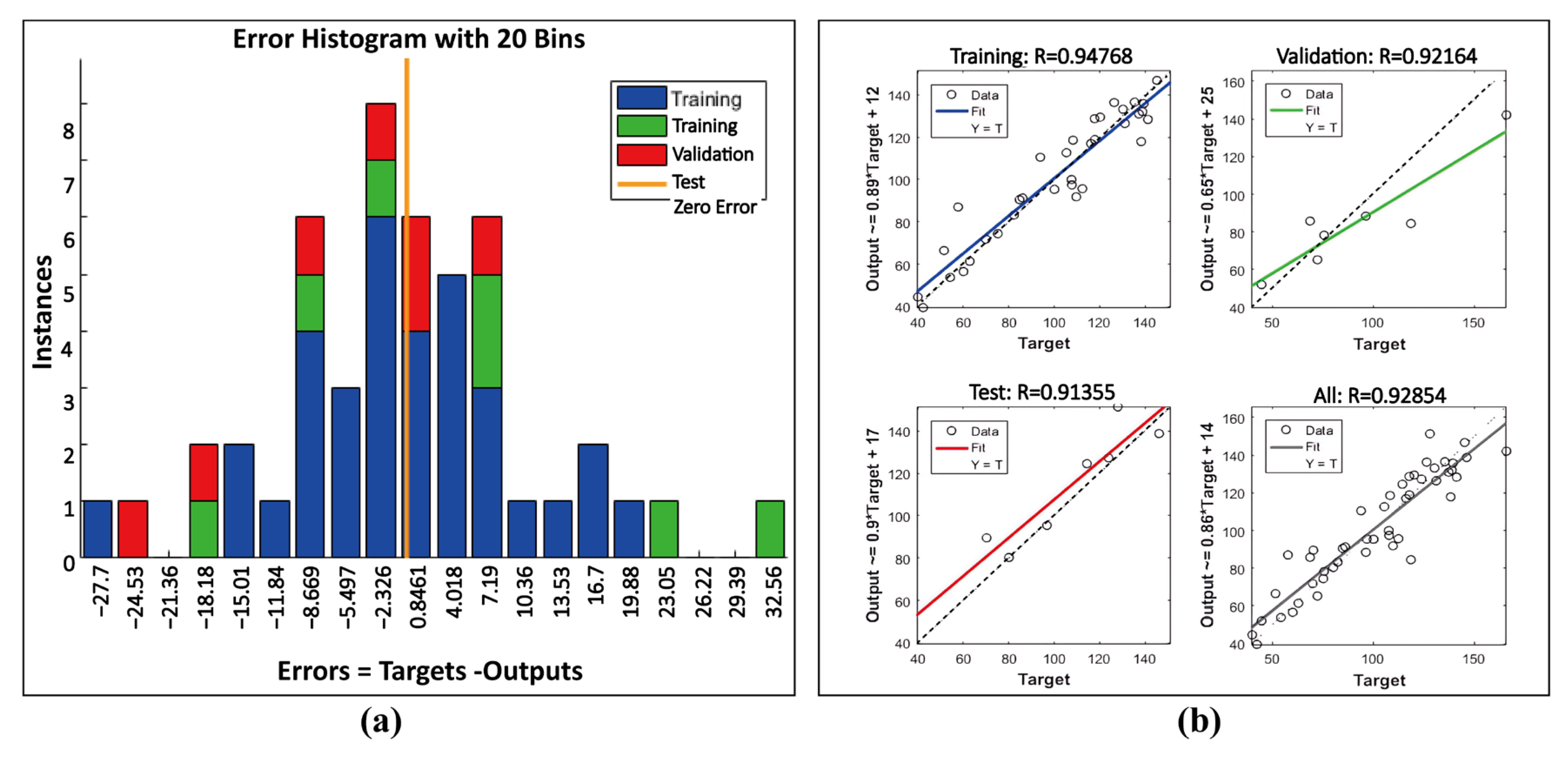
5.2. Reliability Validation of the Best Predictive Model
5.3. Determination of the Limiting Mining Height under Conditions of Water-Preserved Mining
- (1)
- When the depth of a coal seam is less than 100 m, and the base-load ratio is below 1.5, the limiting mining height should not exceed 1 m. If the practical mining height exceeds 1 m, there is a high risk of water loss during coal mining. The eastern part of the study area has poor water yield and recharge properties. There are no engineering requirements for water preservation in mining. However, the development of coal resources must be accompanied by measures to prevent and control secondary surface hazards in arid mining regions. The northeastern region of the study area is characterized by a lack of water resources. Coal mining in this area poses a significant threat to water bodies, and the damage caused by mining activities is often irreversible. Therefore, it is recommended to restrict or avoid coal seam mining in water-preserve and restricted mining regions.
- (2)
- When the depth of a coal seam is less than 150 m, and the bedrock–soil ratio is 1–3, the limiting mining height should be 1–3 m. The corresponding fully mechanized coal faces are mainly located in the southeastern regions of the Yushen I and II planning areas. These areas are classified as water-preserve and restricted mining regions because they pose a greater risk of water body damage due to coal mining. However, despite the impact of coal mining, the abundance of surface diving water provides an opportunity for ecological restoration techniques to revitalize the mining area’s ecology in the short term.
- (3)
- When a coal seam is at a depth of 150–250 m, and the bedrock–soil ratio is 4–6, the limiting mining height should be 3–6 m. In such cases, the bedrock–soil ratio of the overburden typically ranges from 18.0–30.5. To extract coal seams, mining techniques such as limited height and stratification mining, coordinated mining, and filling mining are suitable for application in controllably water-preserved mining regions.
- (4)
- When the coal seam depth exceeds 250 m and the bedrock–soil ratio is 0.25, the limiting mining height exceeds 6.0 m. At present, the longwall mining method, which involves mining the full thickness at once, does not cause damage to the surface ecology or water levels. This method is considered to be used in natural water-preserved mining regions.
5.4. Discussion
6. Conclusions
- (1)
- We have identified the reason why the prediction of the height of FWCZ in the Yushenfu mining area exhibits obvious gray characteristics. On the one hand, there are significant spatial heterogeneity characteristics in the main coal seams. From a spatial distribution perspective, the burial depth of coal seams is generally shallow in the east and deep in the west. The distribution range of shallow coal seams is relatively wide. Meanwhile, there is significant variability in the vertical distribution of the main coal seams due to sedimentation and tectonic activity. On the other hand, the complex and variable geological conditions of coal seams result in a variety of mining methods, while the selection of technical parameters is also influenced by subjective factors. In brief, the complex and constantly changing geological and hydrogeological conditions of coal seam occurrence are important factors contributing to significant uncertainty and inaccuracy in predicting the height of the FWCZ.
- (2)
- A modeling approach has been proposed for predicting the height of FWCZ. This method is based on the analysis of significant factors and the multi-level evaluation of the selected prediction models. This modeling method has significant advantages in ensuring the objective and reasonable selection of indicators, as well as ensuring a high level of model reliability. Through the grey entropy correlation analysis method, we can conclude that the descending order of correlation between the height of FWCZ and its significant influencing factors is as follows: comprehensive hardness of the overlying rock, the average thickness of sandstone, mining depth, and mining height. The multi-level evaluation consists of the comparison of the goodness of fit, validation of typical examples, and analysis of parameter inversion. The calculation results of the analysis of parameter inversion indicate that the fractured/mining height ratio of the main coal seams is mainly concentrated between 20.45 and 30.59 within the mining height range of 2.5–5.5 m, with an average ratio of 25.52. Through the application of a multi-level evaluation method, we can conclude that under the condition of small sample data sets with high quality, the GA-CatBoost algorithm has better prediction accuracy compared to SFR, MSR, and GA-BP algorithms. Thus, the GA-CatBoost regression model is the best predictive model.
- (3)
- We have proposed a prediction method for determining the limiting mining height by considering water conservation in coal mining. Based on theoretical criteria for setting waterproof coal–rock pillars, this method utilizes the best predictive model to predict the optimal mining height, thereby helping to prevent incidents of underground roof water inrush. Furthermore, by comprehensively applying the principles of water conservation, classifying coal mining areas, and using the prediction method for determining the maximum mining height, we can identify the typical characteristics of coal seam occurrence in each mining area and establish appropriate mining principles. Relevant research results can provide a fundamental theoretical guarantee for ensuring underground safety production and protecting groundwater in mining areas.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.X.; Tu, S.H.; Bai, Q.S.; Li, J.J. Overburden fracture evolution laws and water-controlling technologies in mining very thick coal seam under water-rich roof. Int. J. Min. Sci. Technol. 2013, 23, 693–700. [Google Scholar] [CrossRef]
- Wang, G.; Wu, M.M.; Wang, R.; Xu, H.; Song, X. Height of the mining-induced fractured zone above a coal face. Eng. Geol. 2017, 216, 140–152. [Google Scholar] [CrossRef]
- Teng, Y.H.; Yi, S.H.; Zhu, W.; Jing, S.Q. Development patterns of fractured water-conducting zones under fully mechanized mining in wet-collapsible loess area. Water 2023, 15, 22. [Google Scholar] [CrossRef]
- Zhou, Y.; Yu, X.Y. Study of the evolution of water-conducting fracture zones in overlying rock of a fully mechanized caving face in gently inclined extra-thick coal seams. Appl. Sci. 2022, 12, 9057. [Google Scholar] [CrossRef]
- Xu, S.Y.; Zhang, Y.B.; Shi, H.; Wang, K.; Geng, Y.P.; Chen, J.F. Physical simulation of strata failure and its impact on overlying unconsolidated aquifer at various mining depths. Water 2018, 10, 650. [Google Scholar] [CrossRef] [Green Version]
- Du, W.G.; Chai, J.; Zhang, D.D.; Lei, W.L. The study of water-resistant key strata stability detected by optic fiber sensing in shallow-buried coal seam. Int. J. Rock Mech. Min. Sci. 2021, 141, 104604. [Google Scholar] [CrossRef]
- Wang, X.Z.; Zhu, W.B.; Xie, J.L.; Han, H.K.; Xu, J.M.; Tang, Z.Y.; Xu, J.L. Borehole-Based monitoring of mining-induced movement in ultrathick-and-hard sandstone strata of the Luohe formation. Minerals 2021, 11, 1157. [Google Scholar] [CrossRef]
- Hou, E.K.; Yuan, F.; Wang, S.M.; Xie, X.S.; Wu, B.H. Seismic identification and development characteristics of water conducting fissure zone in goaf. J. China Coal Soc. 2023, 48, 414–429. (In Chinese) [Google Scholar] [CrossRef]
- Guo, W.B.; Zhao, G.B.; Lou, G.Z.; Wang, S.R. Height of fractured zone inside overlying strata under high-intensity mining in China. Int. J. Min. Sci. Technol. 2019, 29, 45–49. [Google Scholar] [CrossRef]
- He, J.H.; Li, W.P.; Fan, K.F.; Qiao, W.; Wang, Q.Q.; Li, L.N. A method for predicting the water-flowing fractured zone height based on an improved key stratum theory. Int. J. Min. Sci. Technol. 2023, 33, 61–71. [Google Scholar] [CrossRef]
- Ning, J.G.; Wang, J.; Tan, Y.L.; Xu, Q. Mechanical mechanism of overlying strata breaking and development of fractured zone during close-distance coal seam group mining. Int. J. Min. Sci. Technol. 2020, 30, 207–215. [Google Scholar] [CrossRef]
- State Bureau of Technical Supervision. Exploration Specification of Hydrogeology and Engineering Geology in Mining Areas; Coal Industry Publish House: Beijing, China, 2021; p. 30. [Google Scholar]
- Wu, Q.; Shen, J.J.; Liu, W.T.; Wang, Y. A RBFNN-based method for the prediction of the developed height of a water-conductive fractured zone for fully mechanized mining with sublevel caving. Arab. J. Geosci. 2017, 10, 172. [Google Scholar] [CrossRef]
- Zheng, Q.S.; Wang, C.F.; Liu, W.T.; Pang, L.F. Evaluation on Development height of water-conduted fractures on overburden roof based on nonlinear algorithm. Water 2022, 14, 3853. [Google Scholar] [CrossRef]
- Zhao, D.K.; Wu, Q. An approach to predict the height of fractured water-conducting zone of coal roof strata using random forest regression. Sci. Rep. 2018, 8, 10986. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rasouli, H.; Shahriar, K.; Madani, S.H. Prediction of the height of fracturing via gene expression programming in Australian longwall panels: A comparative study. Rudarsko-Geološko-Naftni Zbornik 2022, 37, 91–104. [Google Scholar] [CrossRef]
- Miao, L.T.; Xia, Y.C.; Duan, Z.H.; Sun, X.Y.; Du, R.J. Coupling characteristics and intelligent integration technology of coal-overlying rock-groundwater-ecological environment in Yu-Shen-Fu mining area in the middle reaches of the Yellow River. J. China Coal Soc. 2021, 46, 1521–1531. (In Chinese) [Google Scholar] [CrossRef]
- Wang, S.M.; Huang, Q.X.; Fan, L.M.; Wang, W.K.; Yu, X.Y.; Wang, G.Z.; Yang, Z.Y.; Hou, E.K.; Shen, T.; Fen, Q.K.; et al. Coal Mining and Ecological Water Level Protection in Ecologically Fragile Areas, 1st ed.; Science Press: Beijing, China, 2010; pp. 1–195. [Google Scholar]
- Miao, L.T. Study on Hosting Pattern and Influence of the Seam Exploitation on Water Recourses in the Main Seam of Yushenfu Deposit. Master’s Thesis, Xi’an University of Science and Technology, Xi’an, China, 2008. (In Chinese). [Google Scholar]
- Li, Z.X.; Shen, X.L.; Li, M.P.; Wang, H.S. Occurrence regularity of uppermost minable coal seams and their harmful level of mining in Yushen mining area. Coal Geol. Explor. 2019, 47, 130–139. (In Chinese) [Google Scholar] [CrossRef]
- Li, H.H.; Chen, D.Y.; Arzaghi, E.; Abbassi, R.; Xu, B.B.; Patelli, E.; Tolo, S. Safety assessment of hydro-generating units using experiments and grey-entropy correlation analysis. Energy 2018, 165, 222–234. [Google Scholar] [CrossRef] [Green Version]
- Guo, W.B.; Wang, Y.G. The definition of high-intensity mining based on green coal mining and its index system. J. Min. Saf. Eng. 2017, 34, 616–623. (In Chinese) [Google Scholar] [CrossRef]
- Verma, A.K.; Sirvaiya, A. Comparative analysis of intelligent models for prediction of Langmuir constants for CO2 adsorption of Gondwana coals in India. Geomech. Geophys. Geo-Energy Geo-Resour. 2016, 2, 97–109. [Google Scholar] [CrossRef] [Green Version]
- Singh, T.N.; Kanchan, R.; Verma, A.K. Prediction of blast induced ground vibration and frequency using an artificial intelligent technique. Noise Vib. World 2004, 35, 7–15. [Google Scholar] [CrossRef]
- Lu, C.G.; Zhang, S.A.; Xue, D.; Xiao, F.C.; Liu, C. Improved estimation of coalbed methane content using the revised estimate of depth and CatBoost algorithm: A case study from southern Sichuan Basin, China. Comput. Geosci. 2022, 158, 104973. [Google Scholar] [CrossRef]
- Wang, X.; Yin, S.X.; Xu, B.; Cao, M.; Zhang, R.G.; Tang, Z.Y.; Huang, W.X.; Li, W.L. Study on height optimization prediction model of overburden water-conducting fracture zone under fully mechanized mining. Coal Sci. Technol. 2022, 1–13. (In Chinese) [Google Scholar] [CrossRef]
- Singh, J.; Verma, A.K.; Banka, H.; Singh, T.N.; Maheshwar, S. A study of soft computing models for prediction of longitudinal wave velocity. Arab. J. Geosci. 2016, 9, 224. [Google Scholar] [CrossRef]
- Hancock, J.T.; Khoshgoftaar, T.M. CatBoost for big data: An interdisciplinary review. J. Big Data 2020, 7, 94. [Google Scholar] [CrossRef]
- Song, S.J. Study on the Stratification Transfer Prediction Method of the Mining Subsidence Based on the Key Geological and Mining Factors. Ph.D. Thesis, Xi’an University of Science and Technology, Xi’an, China, 2008. (In Chinese). [Google Scholar]
- Liu, G. A formula for calculating the development height of water flowing fractured zone. Int. Core. J. Eng. 2022, 8, 511–522. [Google Scholar] [CrossRef]
- Wang, S.M.; Shen, Y.J.; Sun, Q.; Hou, E.K. Scientific issues of coal detraction mining geological assurance and their technology expectations in ecologically fragile mining areas of Western China. J. Min. Strata Control 2020, 2, 5–19. (In Chinese) [Google Scholar] [CrossRef]
- Rudakov, D.; Westermann, S. Analytical modeling of mine water rebound: Three case studies in closed hard-coal mines in Germany. Min. Miner. Depos. 2021, 15, 22–30. [Google Scholar] [CrossRef]
- Bazaluk, O.; Sadovenko, I.; Zahrytsenko, A.; Saik, P.; Lozynskyi, V.; Dychkovskyi, R. Forecasting Underground Water Dynamics within the Technogenic Environment of a Mine Field: Case Study. Sustainability 2021, 13, 7161. [Google Scholar] [CrossRef]







| Coal Seam | Areal Range | Minable Area (km2) | Burial Depth (m) | Thickness (m) | Texture | Stability |
|---|---|---|---|---|---|---|
| 5−2 | Shenfu mining area | 5040 | 8.11–280.75 133.43 | 0.53–6.66 3.00 | Simple/ Relatively simple | Relatively stable |
| Yushen II and IV planning areas | 46.81–198.80 123.43 | 0.80–2.06 1.00 | Simple/ Relatively simple | Relatively stable | ||
| 4−3 | Yushen III and IV planning areas | 3995 | 50.61–179.86 113.22 | 0.30–3.68 2.00 | Simple | Relatively stable |
| 3−1 | Yushen III and IV planning areas | 7175 | 43.23–267.53 107.24 | 0.50–12.19 2.50 | Simple | Stable |
| 2−2 | Yushen I, III, and IV planning areas | >6012 | 51.80–555.75 261.15 | 0.53–12.58 5.00 | Simple | Stable |
| 1−2 | Yushen III and IV planning areas | 6084 | 173.13–588.21 416.35 | 0–11.27 8.00 | Simple/ Relatively simple | Relatively stable |
| No. | Drilling Hole | Coal Mine | X1 (m) | X2 (m) | X3 (m) | X4 | X5 | X6 | X7 | X8 | X0 (m) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | L1 | Liuxiang | 266.5 | 7.9 | 150 | 1.54 | 0.94 | 0.93 | 8.22 | 2.48 | 117.84 |
| 2 | ZK2-5 | Daliuta | 90.3 | 3.0 | 230 | 2.47 | 0.99 | 0.71 | 7.02 | 2.31 | 60.09 |
| 3 | ZK2-6 | Ningtiaota | 95.5 | 3.5 | 250 | 0.95 | 0.99 | 0.64 | 6.88 | 2.30 | 72.31 |
| 4 | 6 | Ningtiaota | 188.9 | 5.5 | 300 | 2.80 | 0.86 | 0.82 | 11.16 | 2.98 | 145.23 |
| 5 | ZK2-7 | Zhangjiamao | 142.1 | 3.0 | 300 | 6.89 | 0.72 | 0.87 | 3.52 | 2.28 | 68.66 |
| 6 | ZK13 | Zhangjiamao | 87.0 | 3.0 | 300 | 2.14 | 1.00 | 0.91 | 5.77 | 2.83 | 75.20 |
| 7 | ZK15 | Zhangjiamao | 77.1 | 3.0 | 300 | 2.30 | 0.98 | 0.89 | 6.72 | 2.98 | 75.60 |
| 8 | 9 | Zhangjiamao | 165.9 | 5.6 | 300 | 1.80 | 0.96 | 0.92 | 9.45 | 3.00 | 165.90 |
| 9 | ZK2-8 | Hongliulin | 169.2 | 3.0 | 350 | 7.22 | 0.73 | 0.89 | 3.81 | 2.26 | 70.28 |
| 10 | ZK2-9 | Jinjie | 167.4 | 5.0 | 250 | 7.11 | 0.70 | 0.85 | 4.51 | 2.33 | 131.13 |
| 11 | ZK2-10 | Liangshujing | 101.8 | 5.0 | 290 | 8.23 | 0.70 | 0.80 | 4.63 | 2.42 | 86.07 |
| 12 | ZK2-11 | Liangshujing | 194.6 | 5.0 | 290 | 8.55 | 0.89 | 0.77 | 4.58 | 2.51 | 141.26 |
| 13 | ZK2-12 | Liangshujing | 161.1 | 5.0 | 290 | 7.14 | 0.88 | 0.89 | 5.21 | 2.09 | 130.29 |
| 14 | ZK2-13 | Liangshujing | 35.5 | 5.0 | 290 | 0.64 | 0.96 | 1.00 | 3.06 | 2.03 | 54.22 |
| 15 | ZK2-14 | Liangshujing | 242.6 | 5.0 | 290 | 6.66 | 0.92 | 0.90 | 5.84 | 2.50 | 139.45 |
| 16 | ZK3-1 | Liangshujing | 327.1 | 5.5 | 290 | 3.67 | 0.79 | 0.99 | 10.22 | 2.55 | 105.40 |
| 17 | ZK3-2 | Liangshujing | 389.9 | 5.5 | 290 | 4.57 | 0.80 | 0.97 | 12.10 | 2.61 | 96.82 |
| 18 | ZK3-3 | Liangshujing | 383.6 | 5.5 | 290 | 2.39 | 0.77 | 0.98 | 11.09 | 2.58 | 100.11 |
| 19 | ZK3-4 | Xiaobaodang | 243.4 | 4.5 | 290 | 2.00 | 0.98 | 0.97 | 5.89 | 2.44 | 108.30 |
| 20 | ZK3-5 | Yushuwan | 242.2 | 4.5 | 295 | 1.88 | 0.96 | 0.91 | 7.58 | 2.45 | 114.40 |
| 21 | Y3 | Yushuwan | 278.5 | 5.5 | 255 | 1.31 | 0.96 | 0.91 | 7.25 | 2.59 | 128.00 |
| 22 | Y4 | Yushuwan | 280.5 | 5.5 | 297 | 1.35 | 0.96 | 0.93 | 6.17 | 2.92 | 138.30 |
| 23 | Y5 | Yushuwan | 287.5 | 5.5 | 255 | 1.29 | 0.99 | 0.94 | 10.02 | 2.88 | 135.40 |
| 24 | Y6 | Yushuwan | 265.5 | 5.5 | 255 | 0.92 | 0.98 | 0.96 | 5.41 | 3.03 | 118.60 |
| 25 | Y7 | Yushuwan | 272.8 | 5.0 | 250 | 1.58 | 0.88 | 0.89 | 6.58 | 2.97 | 57.71 |
| 26 | ZK3-6 | Yushuwan | 242.9 | 4.5 | 300 | 1.84 | 0.91 | 0.84 | 5.30 | 2.82 | 107.63 |
| 27 | ZK3-7 | Yushuwan | 279.3 | 5.0 | 300 | 1.33 | 0.96 | 0.93 | 6.17 | 2.56 | 137.3 |
| 28 | ZK3-8 | Yushuwan | 286.9 | 5.0 | 300 | 1.40 | 0.99 | 0.89 | 10.02 | 2.57 | 138.9 |
| 29 | ZK3-9 | Yushuwan | 275.5 | 5.0 | 300 | 1.04 | 0.99 | 0.92 | 5.89 | 2.61 | 117.80 |
| 30 | H3 | Yushuwan | 244.2 | 5.0 | 300 | 1.78 | 0.98 | 0.97 | 5.54 | 2.98 | 112.44 |
| 31 | H4 | Hanglaiwan | 244.8 | 5.0 | 300 | 1.90 | 0.96 | 0.91 | 7.58 | 2.98 | 116.20 |
| 32 | H5 | Hanglaiwan | 249.9 | 4.5 | 300 | 1.82 | 0.91 | 0.84 | 5.30 | 2.82 | 107.80 |
| 33 | H7 | Hanglaiwan | 233.4 | 4.5 | 300 | 2.13 | 0.97 | 0.86 | 5.92 | 2.71 | 93.90 |
| 34 | JT4 | Jinjitan | 241.8 | 5.5 | 300 | 3.00 | 0.96 | 0.93 | 4.68 | 2.83 | 126.40 |
| 35 | JT5 | Jinjitan | 240.6 | 5.5 | 300 | 3.00 | 0.93 | 0.87 | 4.85 | 2.82 | 146.18 |
| 36 | JT6 | Jinjitan | 241.6 | 5.5 | 300 | 3.29 | 0.95 | 0.91 | 4.25 | 2.86 | 120.25 |
| 37 | JSD1 | Jinjitan | 263.6 | 5.5 | 300 | 3.27 | 0.96 | 0.93 | 4.56 | 3.03 | 51.52 |
| 38 | JSD2 | Jinjitan | 260.6 | 5.5 | 300 | 3.37 | 0.93 | 0.87 | 5.08 | 3.01 | 109.72 |
| 39 | JSD3 | Jinjitan | 261.7 | 5.5 | 300 | 3.68 | 0.94 | 0.91 | 4.28 | 3.01 | 69.94 |
| 40 | ZP1 | Yuyang | 195.2 | 3.5 | 200 | 3.11 | 0.85 | 0.90 | 5.68 | 2.81 | 96.30 |
| 41 | ZP2 | Yuyang | 188.3 | 3.5 | 200 | 3.07 | 0.89 | 0.92 | 5.05 | 2.88 | 84.80 |
| 42 | ZK1-1 | Yujialiang | 40.1 | 1.5 | 300 | 1.44 | 0.99 | 0.96 | 6.28 | 2.11 | 42.33 |
| 43 | ZK1-2 | Yujialiang | 52.6 | 1.5 | 300 | 1.21 | 0.98 | 0.99 | 4.12 | 2.02 | 44.64 |
| 44 | ZK1-3 | Yujialiang | 45.2 | 1.5 | 300 | 1.39 | 0.98 | 0.93 | 5.33 | 2.08 | 40.02 |
| 45 | ZK2-1 | Yujialiang | 77.3 | 3.5 | 360 | 0.56 | 1.00 | 0.70 | 4.33 | 2.01 | 62.86 |
| 46 | ZK2-2 | Yujialiang | 179.1 | 5.0 | 400 | 7.14 | 0.99 | 0.88 | 7.19 | 2.89 | 123.89 |
| 47 | ZK2-3 | Yujialiang | 129.1 | 3.5 | 360 | 0.79 | 0.98 | 0.88 | 6.01 | 2.22 | 82.37 |
| 48 | ZK2-4 | Yujialiang | 106.9 | 3.5 | 360 | 3.65 | 0.99 | 0.99 | 8.62 | 2.12 | 80.11 |
| Influencing Factors | Correlation Coefficient | p-Value | Significance |
|---|---|---|---|
| X1 | 0.544 ** | 0.000 | Significant |
| X2 | 0.674 ** | 0.000 | Significant |
| X3 | −0.058 | 0.696 | Not significant |
| X4 | 0.155 | 0.294 | Not significant |
| X5 | −0.027 | 0.857 | Not significant |
| X6 | 0.030 | 0.838 | Not significant |
| X7 | 0.333 * | 0.021 | Significant |
| X8 | 0.421 ** | 0.003 | Significant |
| Influencing Factors | Entropy Value Ei | Weight Coefficient ωi |
|---|---|---|
| X8 | 0.915 | 0.43100 |
| X7 | 0.948 | 0.26125 |
| X1 | 0.968 | 0.15932 |
| X2 | 0.971 | 0.14843 |
| Indicators | MSE | RMSE | MAE | MAPE | R² |
|---|---|---|---|---|---|
| Training set | 0.169 | 0.405 | 0.340 | 0.402% | 1 |
| Test set | 135.103 | 11.623 | 9.032 | 9.37% | 0.872 |
| Working Face | Coal Mine | Ming Depth (m) | Ming Height (m) | Average Thickness of Sandstone (m) | Comprehensive Hardness of Cover Rock (MPa) | The Height of FWCZ | ||
|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X7 | X8 | Predictive Value (m) | True Value (m) | Error (%) | ||
| 14202 | Zhangjiamao | 87.1 | 3.0 | 6.21 | 2.66 | 74.63 | 75.60 | −1.28 |
| 12-2 upper 0101 | Jinjitan | 256.8 | 5.5 | 5.35 | 2.87 | 116.49 | 111.49 | 4.48 |
| 122106 | Caojiatan | 286.3 | 6.0 | 7.93 | 2.93 | 132.47 | 139.15 | −4.80 |
| 2207 | Wulanmulun | 97.5 | 2.2 | 9.89 | 3.09 | 101.77 | 97.50 | −4.38 |
| 2305 | Hanjiawan | 105.0 | 4.4 | 9.65 | 3.02 | 109.15 | 110.11 | −0.87 |
| No. | X1 (m) | X2 (m) | X7 (m) | X8 (MPa) | Ratio | No. | X1 (m) | X2 (m) | X7 (m) | X8 (MPa) | Ratio |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 98.2 | 2.5 | 3 | 2.00 | 24.12 | 33 | 98.2 | 2.5 | 9 | 2.00 | 31.90 |
| 2 | 98.2 | 2.5 | 3 | 2.35 | 27.13 | 34 | 98.2 | 2.5 | 9 | 2.35 | 30.64 |
| 3 | 98.2 | 2.5 | 3 | 2.70 | 30.55 | 35 | 98.2 | 2.5 | 9 | 2.70 | 34.60 |
| 4 | 98.2 | 2.5 | 3 | 3.05 | 35.75 | 36 | 98.2 | 2.5 | 9 | 3.05 | 39.62 |
| 5 | 149.2 | 3.5 | 3 | 2.00 | 21.39 | 37 | 149.2 | 3.5 | 9 | 2.00 | 26.71 |
| 6 | 149.2 | 3.5 | 3 | 2.35 | 22.96 | 38 | 149.2 | 3.5 | 9 | 2.35 | 26.17 |
| 7 | 149.2 | 3.5 | 3 | 2.70 | 23.82 | 39 | 149.2 | 3.5 | 9 | 2.70 | 27.02 |
| 8 | 149.2 | 3.5 | 3 | 3.05 | 25.30 | 40 | 149.2 | 3.5 | 9 | 3.05 | 29.62 |
| 9 | 200.2 | 4.5 | 3 | 2.00 | 21.66 | 41 | 200.2 | 4.5 | 9 | 2.00 | 24.39 |
| 10 | 200.2 | 4.5 | 3 | 2.35 | 23.39 | 42 | 200.2 | 4.5 | 9 | 2.35 | 24.40 |
| 11 | 200.2 | 4.5 | 3 | 2.70 | 23.07 | 43 | 200.2 | 4.5 | 9 | 2.70 | 23.72 |
| 12 | 200.2 | 4.5 | 3 | 3.05 | 20.93 | 44 | 200.2 | 4.5 | 9 | 3.05 | 25.57 |
| 13 | 251.2 | 5.5 | 3 | 2.00 | 19.73 | 45 | 251.2 | 5.5 | 9 | 2.00 | 20.56 |
| 14 | 251.2 | 5.5 | 3 | 2.35 | 20.71 | 46 | 251.2 | 5.5 | 9 | 2.35 | 21.44 |
| 15 | 251.2 | 5.5 | 3 | 2.70 | 20.02 | 47 | 251.2 | 5.5 | 9 | 2.70 | 21.77 |
| 16 | 251.2 | 5.5 | 3 | 3.05 | 13.78 | 48 | 251.2 | 5.5 | 9 | 3.05 | 23.07 |
| 17 | 98.2 | 2.5 | 6 | 2.00 | 26.35 | 49 | 98.2 | 2.5 | 12 | 2.00 | 33.27 |
| 18 | 98.2 | 2.5 | 6 | 2.35 | 27.46 | 50 | 98.2 | 2.5 | 12 | 2.35 | 32.6 |
| 19 | 98.2 | 2.5 | 6 | 2.70 | 30.75 | 51 | 98.2 | 2.5 | 12 | 2.70 | 35.82 |
| 20 | 98.2 | 2.5 | 6 | 3.05 | 36.03 | 52 | 98.2 | 2.5 | 12 | 3.05 | 39.61 |
| 21 | 149.2 | 3.5 | 6 | 2.00 | 24.94 | 53 | 149.2 | 3.5 | 12 | 2.00 | 26.54 |
| 22 | 149.2 | 3.5 | 6 | 2.35 | 24.95 | 54 | 149.2 | 3.5 | 12 | 2.35 | 26.00 |
| 23 | 149.2 | 3.5 | 6 | 2.70 | 24.35 | 55 | 149.2 | 3.5 | 12 | 2.70 | 27.20 |
| 24 | 149.2 | 3.5 | 6 | 3.05 | 26.66 | 56 | 149.2 | 3.5 | 12 | 3.05 | 28.99 |
| 25 | 200.2 | 4.5 | 6 | 2.00 | 23.66 | 57 | 200.2 | 4.5 | 12 | 2.00 | 24.03 |
| 26 | 200.2 | 4.5 | 6 | 2.35 | 23.25 | 58 | 200.2 | 4.5 | 12 | 2.35 | 24.05 |
| 27 | 200.2 | 4.5 | 6 | 2.70 | 21.33 | 59 | 200.2 | 4.5 | 12 | 2.70 | 23.81 |
| 28 | 200.2 | 4.5 | 6 | 3.05 | 22.64 | 60 | 200.2 | 4.5 | 12 | 3.05 | 24.69 |
| 29 | 251.2 | 5.5 | 6 | 2.00 | 20.54 | 61 | 251.2 | 5.5 | 12 | 2.00 | 20.40 |
| 30 | 251.2 | 5.5 | 6 | 2.35 | 21.36 | 62 | 251.2 | 5.5 | 12 | 2.35 | 21.28 |
| 31 | 251.2 | 5.5 | 6 | 2.70 | 20.85 | 63 | 251.2 | 5.5 | 12 | 2.70 | 21.68 |
| 32 | 251.2 | 5.5 | 6 | 3.05 | 20.79 | 64 | 251.2 | 5.5 | 12 | 3.05 | 22.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, L.; Shen, Y.; Wang, N.; Kou, H.; Song, S. Prediction of the Height of Fractured Water-Conducting Zone: Significant Factors and Model Optimization. Water 2023, 15, 2720. https://doi.org/10.3390/w15152720
Gu L, Shen Y, Wang N, Kou H, Song S. Prediction of the Height of Fractured Water-Conducting Zone: Significant Factors and Model Optimization. Water. 2023; 15(15):2720. https://doi.org/10.3390/w15152720
Chicago/Turabian StyleGu, Linjun, Yanjun Shen, Nianqin Wang, Haibo Kou, and Shijie Song. 2023. "Prediction of the Height of Fractured Water-Conducting Zone: Significant Factors and Model Optimization" Water 15, no. 15: 2720. https://doi.org/10.3390/w15152720
APA StyleGu, L., Shen, Y., Wang, N., Kou, H., & Song, S. (2023). Prediction of the Height of Fractured Water-Conducting Zone: Significant Factors and Model Optimization. Water, 15(15), 2720. https://doi.org/10.3390/w15152720






