Fundamental Study on the Development of an Inexpensive Velocity Meter for River Floods Using Stagnation Points
Abstract
:1. Introduction
2. Purpose of the Study
2.1. Afflux by Poles during Flooding
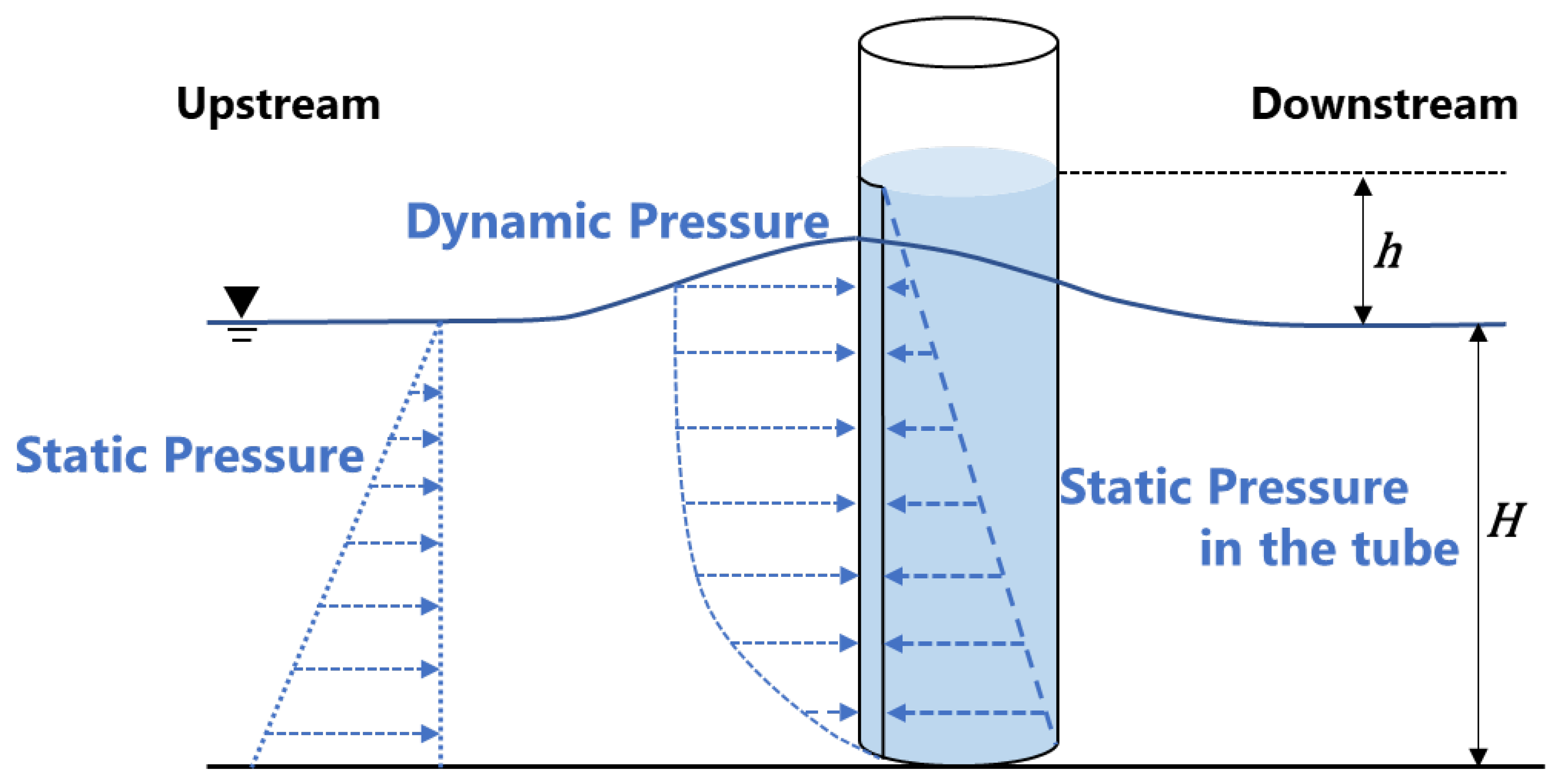
2.2. Large Pitot Tube
2.3. Slit Pitot Tube
3. Afflux by Poles, Piers, etc., during Flooding
3.1. Verification Methods
3.2. Results
4. Large Pitot Tube
4.1. Velocity Meter Based on Pitot Tube Principle
4.2. Creation of Large Pitot Tube Velocity Meters
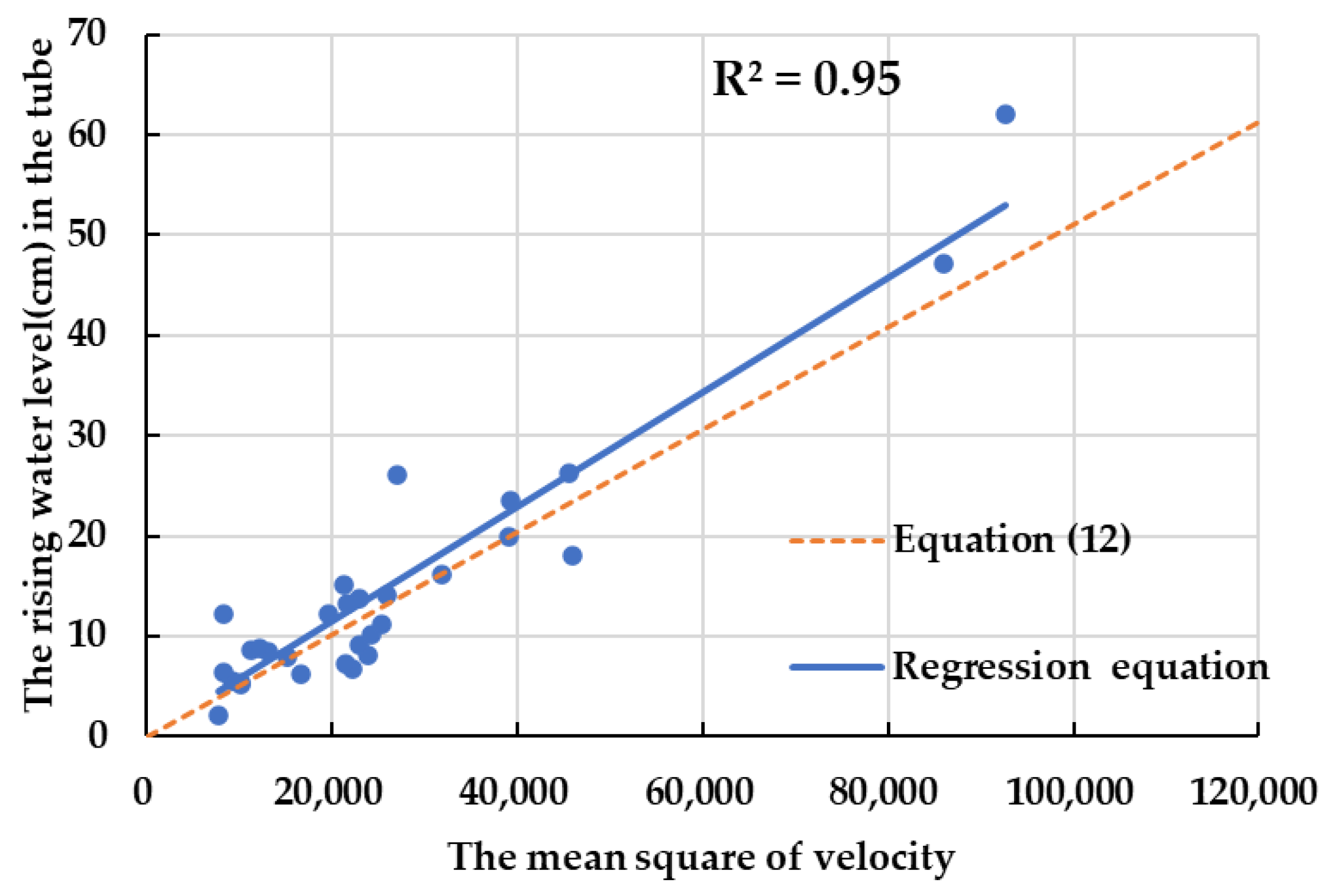
4.3. Verification Methods
4.4. Result
5. Slit-Type Pitot Tube Velocity Meter
5.1. Idea and Principle
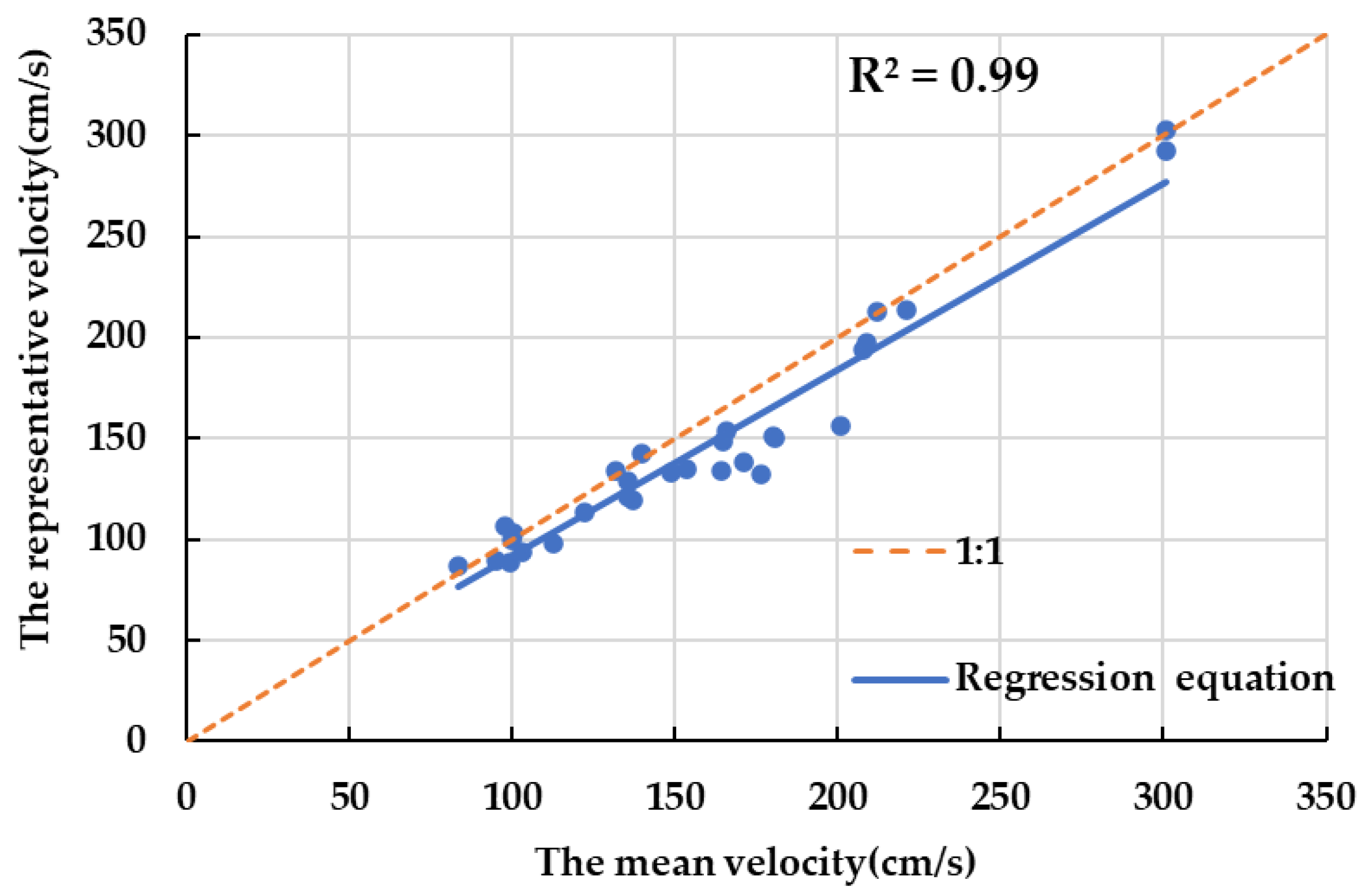
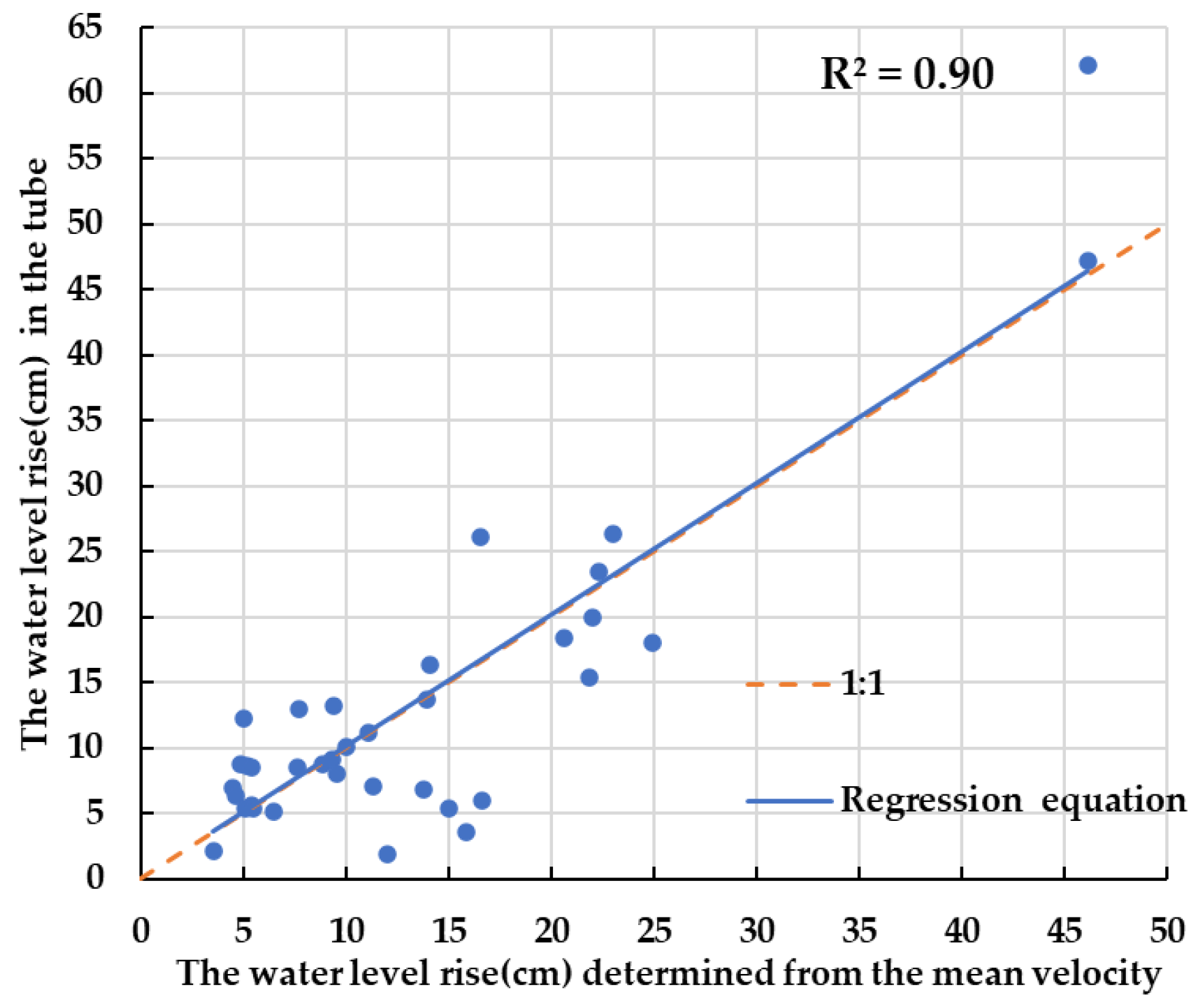
5.2. Verification Method
5.3. Result
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- AR6 Climate Change 2021: The Physical Science Basis IPCC. Available online: https://www.ipcc.ch/report/sixthassessment-report-working-group-i/ (accessed on 15 November 2022).
- 09_kikouhendounoeikyou.pdf. Available online: https://www.mlit.go.jp/river/shinngikai_blog/shaseishin/kasenbunkakai/shouiinkai/kikouhendou_suigai/1/pdf/09_kikouhendounoeikyou.pdf (accessed on 20 February 2022).
- 03_honbun.pdf. Available online: https://www.mlit.go.jp/river/shinngikai_blog/shaseishin/kasenbunkakai/shouiinkai/kikouhendou_suigai/pdf/03_honbun.pdf (accessed on 20 February 2022).
- Estrella, M.; Saalismaa, N. Ecosystem-based disaster risk reduction (Eco-DRR): An overview. In The Role of Ecosystems in Disaster Risk Reduction; United Nations University Press: Tokyo, Japan, 2013; Volume 332. [Google Scholar]
- Nature-Based Solutions for Climate. Available online: https://www.iucn.org/our-work/topic/nature-based-solutions-climate (accessed on 12 January 2023).
- North-West-NFM-handbook. Available online: https://thefloodhub.co.uk/wp-content/uploads/2018/11/North-West-NFM-handbook.pdf (accessed on 16 December 2022).
- Gunawan, B.; Sun, X.; Sterling, M.; Shiono, K.; Tsubaki, R.; Rameshwaran, P.; Knight, D.W.; Chandler, J.H.; Tang, X.; Fujita, I. The application of LS-PIV to a small irregular river for inbank and overbank flows. Flow Meas. Instrum. 2012, 24, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Le Coz, J.; Camenen, B.; Peyrard, X.; Dramais, G. Uncertainty in open-channel discharges measured with the velocity-area method (vol 26, pg 18, 2012). Flow Meas. Instrum. 2015, 46, 18–29. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.D.; Lee, H.J.; Oh, B.D. Investigation on Application of Parshall Flume for Flow Measurement of Low-Flow Season in Korea. Meas. Sci. Rev. 2010, 10, 111–115. [Google Scholar] [CrossRef]
- Cheng, N.S. Power-law index for velocity profiles in open channel flows. Adv. Water Resour. 2007, 30, 1775–1784. [Google Scholar] [CrossRef]
- Herschy, R. The velocity-area method. Flow Meas. Instrum. 1993, 4, 7–10. [Google Scholar] [CrossRef]
- Chen, F.W.; Liu, C.W. Assessing the applicability of flow measurement by using non-contact observation methods in open channels. Environ. Monit. Assess. 2020, 192, 289. [Google Scholar] [CrossRef]
- Muste, M.; Yu, K.; Spasojevic, M. Practical aspects of ADCP data use for quantification of mean river flow characteristics; part I: Moving-vessel measurements. Flow Meas. Instrum. 2004, 15, 1–16. [Google Scholar] [CrossRef]
- Moradi, G.; Vermeulen, B.; Rennie, C.D.; Cardot, R.; Lane, S.N. Evaluation of aDcp processing options for secondary flow identification at river junctions. Earth Surf. Process. Landf. 2019, 44, 2903–2921. [Google Scholar] [CrossRef] [Green Version]
- Figuerez, J.A.; Gonzalez, J.; Galan, A. Accurate Open Channel Flowrate Estimation Using 2D RANS Modelization and ADCP Measurements. Water 2021, 13, 1772. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Niizato, K. Flood discharge observation using radio current meter. Doboku Gakkai Ronbunshu 1994, 1994, 41–50. [Google Scholar] [CrossRef]
- Plant, W.J.; Keller, W.C.; Hayes, K. Measurement of river surface currents with coherent microwave systems. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1242–1257. [Google Scholar] [CrossRef]
- Miyamura, E.; Nakajima, Y.; Yoshimura, A. Full-scale Commercialized Microwave Doppler Current Meter-Fixed Doppler Current Meter & RYUKAN. New Era River Disch. Meas. 2012, 3, 55–60. [Google Scholar]
- Dal Sasso, S.F.; Pizarro, A.; Samela, C.; Mita, L.; Manfreda, S. Exploring the optimal experimental setup for surface flow velocity measurements using PTV. Environ. Monit. Assess. 2018, 190, 460. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.C.; Young, C.C.; Liu, W.C. Application of an Automated Discharge Imaging System and LSPIV during Typhoon Events in Taiwan. Water 2018, 10, 280. [Google Scholar] [CrossRef] [Green Version]
- Fujita, I.; Notoya, Y.; Tani, K.; Tateguchi, S. Efficient and accurate estimation of water surface velocity in STIV. Environ. Fluid Mech. 2019, 19, 1363–1378. [Google Scholar] [CrossRef] [Green Version]
- Eltner, A.; Sardemann, H.; Grundmann, J. Technical Note: Flow velocity and discharge measurement in rivers using terrestrial and unmanned-aerial-vehicle imagery. Hydrol. Earth Syst. Sci. 2020, 24, 1429–1445. [Google Scholar] [CrossRef] [Green Version]
- Bandini, F.; Frias, M.C.; Liu, J.; Simkus, K.; Karagkiolidou, S.; Bauer-Gottwein, P. Challenges with Regard to Unmanned Aerial Systems (UASs) Measurement of River Surface Velocity Using Doppler Radar. Remote Sens. 2022, 14, 1277. [Google Scholar] [CrossRef]
- Harada, Y.; Nihei, Y.; Sakai, T.; Kimizu, A. Undamental Study on Measuring Accuracy for Flood Discharge with Floats. Proc. Hydraul. Eng. 2007, 51, 1081–1086. [Google Scholar] [CrossRef] [Green Version]
- Fukuoka, S.; Watanabe, A.; Takatsugu, W.; Sakamoto, H. Effect of Plan and Cross Sectional Shapes on Accuracy of Discharge Measurement by Means of Floats. Proc. Hydraul. Eng. 2002, 46, 803–808. [Google Scholar] [CrossRef] [Green Version]
- Nihei, Y.; Irokawa, Y.; Ide, K.; Takamura, T. Study on River-Discharge Measurements using Accoustic Doppler Current Profilers. J. Hydraul. Coast. Environ. Eng. 2008, 64, 99–114. [Google Scholar]
- Leyland, J.; Hackney, C.R.; Darby, S.E.; Parsons, D.R.; Best, J.L.; Nicholas, A.P.; Aalto, R.; Lague, D. Extreme flood-driven fluvial bank erosion and sediment loads: Direct process measurements using integrated Mobile Laser Scanning (MLS) and hydro-acoustic techniques. Earth Surf. Process. Landf. 2017, 42, 334–346. [Google Scholar] [CrossRef]
- Le Coz, J.; Hauet, A.; Pierrefeu, G.; Dramais, G.; Camenen, B. Performance of image-based velocimetry (LSPIV) applied to flash-flood discharge measurements in Mediterranean rivers. J. Hydrol. 2010, 394, 42–52. [Google Scholar] [CrossRef] [Green Version]
- Nakano, K.; Hayashi, H.; Shimatani, Y. Flood Flow Velocity Estimation Method Using Movies Taken by Residents. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2018, 74, I_601–I_606. [Google Scholar] [CrossRef] [PubMed]
- Chaplin, J.R.; Teigen, P. Steady flow past a vertical surface-piercing circular cylinder. J. Fluids Struct. 2003, 18, 271–285. [Google Scholar] [CrossRef]
- Unger, J.; Hager, W.H. Down-flow and horseshoe vortex characteristics of sediment embedded bridge piers. Exp. Fluids 2007, 42, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.R.; Yang, Q.P.; Xiao, H. CFD modeling of scale effects on turbulence flow and scour around bridge piers. Comput. Fluids 2009, 38, 1050–1058. [Google Scholar] [CrossRef]
- Watanabe, G.; Akamatsu, Y.; Irie, T.; Ono, Y. The Evluation of Dynamic Water Pressure to Existing Bridge Pier in a River at a Flood. J. Jpn. Soc. Civ. Eng. Ser. A2 (Appl. Mech. (AM)) 2015, 71, I_359–I_368. [Google Scholar] [CrossRef]
- Yokoi, Y. The aspect of the flow around a circular cylinder in a free surface water flow. In Proceedings of the EPJ Web of Conferences, Františkovy Lázně, Czech Republic, 19–22 November 2022; p. 01070. [Google Scholar]
- Matsutomi, H.; Okamoto, K.; Sato, K. Basic examination on the simplified method for estimating velocity of inundated flow with inundation traces. Proc. Hydraul. Eng. 2008, 52, 673–678. [Google Scholar] [CrossRef] [Green Version]
- Pitot Tube Working and Principle. Available online: https://www.hkdivedi.com/2018/06/pitot-tube-working-and-principle.html (accessed on 24 December 2022).

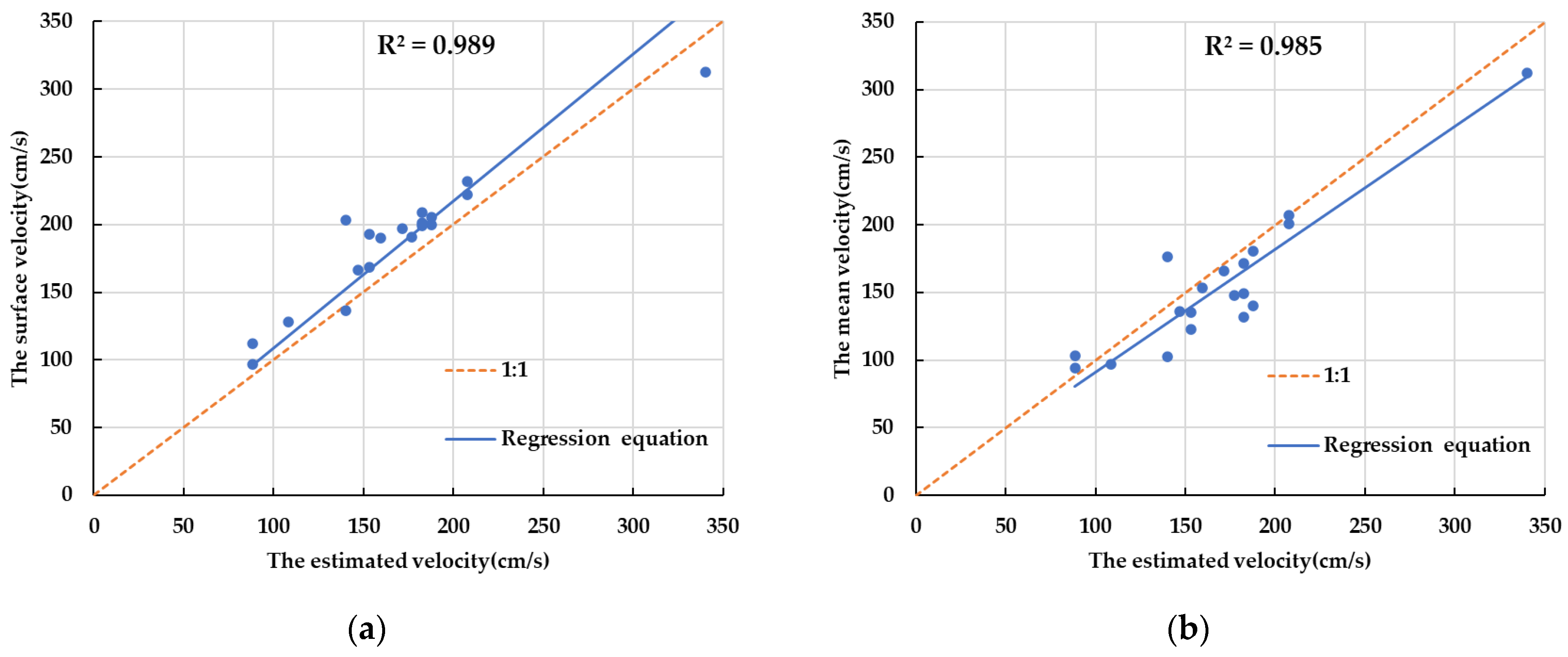
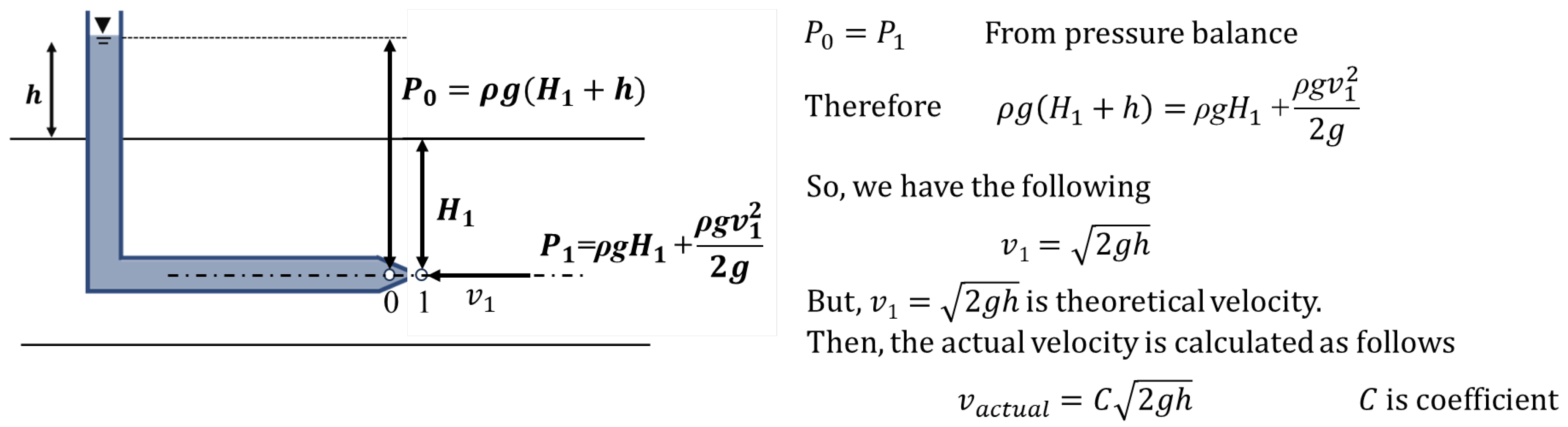

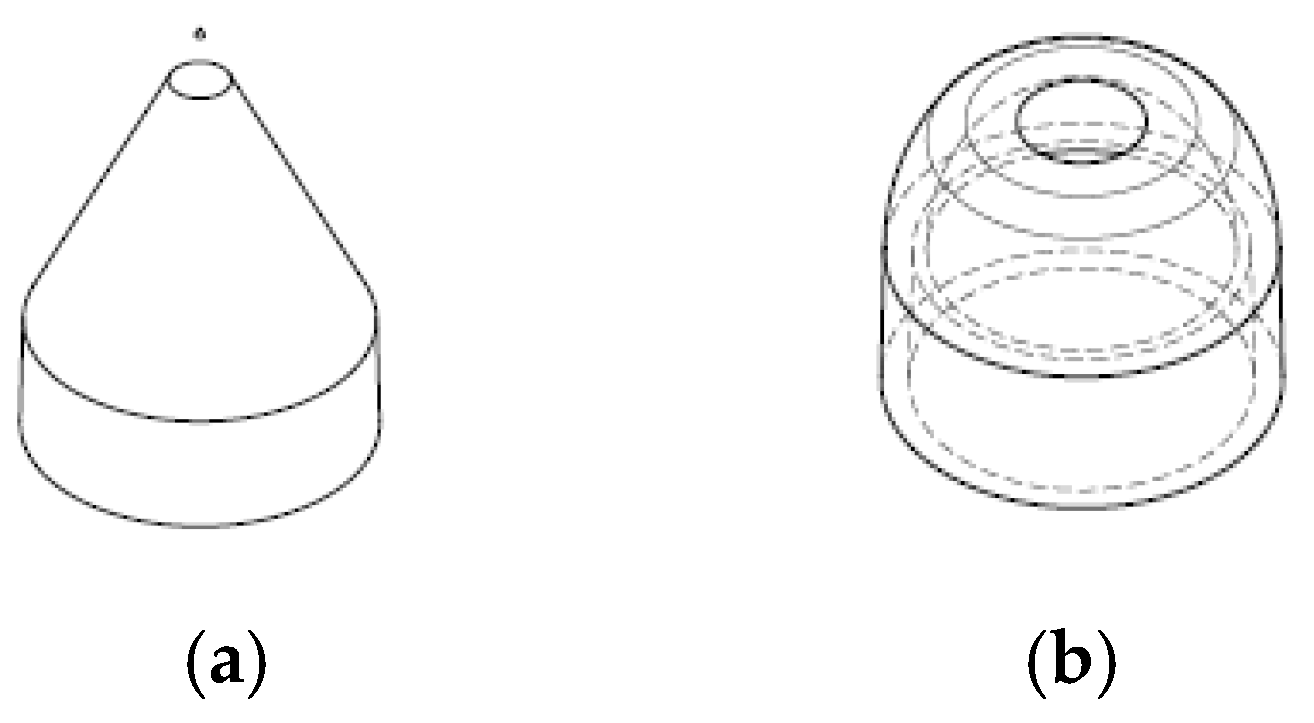

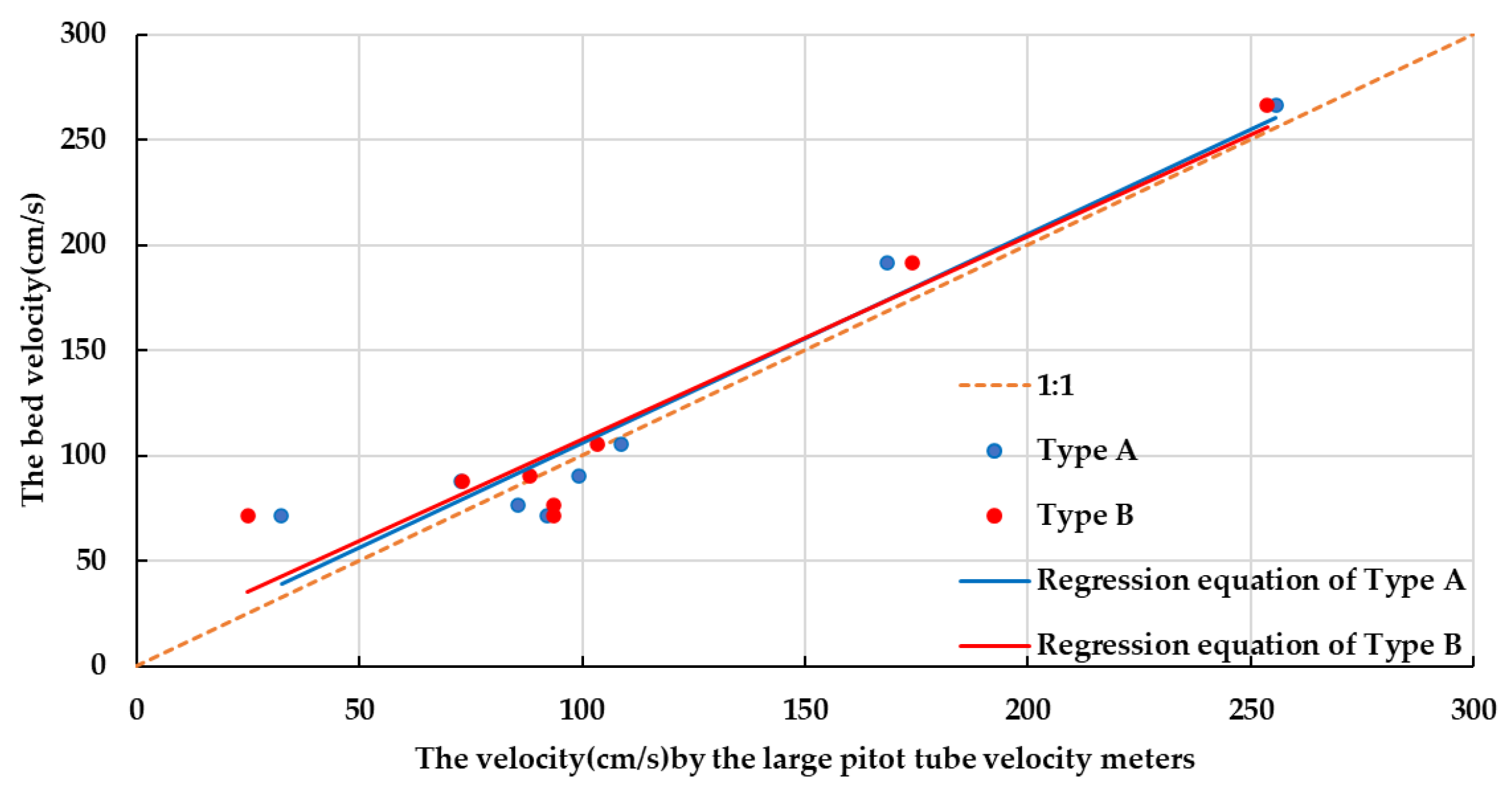



| Diameter (mm) | 40 | 120 | 200 |
| Estimated velocity (cm/s) | 146.8 | 171.5 | 177.1 |
| Surface | 20% Depth | 40% Depth | Mean | 20% Depth | Bed |
|---|---|---|---|---|---|
| 166.4 | 166.7 | 157.5 | 135.7 | 100.0 | 62.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouchi, A.; Shimatani, Y.; Takata, H.; Minagawa, T. Fundamental Study on the Development of an Inexpensive Velocity Meter for River Floods Using Stagnation Points. Water 2023, 15, 2625. https://doi.org/10.3390/w15142625
Ouchi A, Shimatani Y, Takata H, Minagawa T. Fundamental Study on the Development of an Inexpensive Velocity Meter for River Floods Using Stagnation Points. Water. 2023; 15(14):2625. https://doi.org/10.3390/w15142625
Chicago/Turabian StyleOuchi, Akito, Yukihiro Shimatani, Hiroshi Takata, and Tomoko Minagawa. 2023. "Fundamental Study on the Development of an Inexpensive Velocity Meter for River Floods Using Stagnation Points" Water 15, no. 14: 2625. https://doi.org/10.3390/w15142625




