Advanced Machine Learning Techniques to Improve Hydrological Prediction: A Comparative Analysis of Streamflow Prediction Models
Abstract
:1. Introduction
1.1. Literature Review
1.1.1. Traditional Methods for River Inflow Prediction
1.1.2. Machine Learning Approaches for River Inflow Prediction
- Comparative Evaluation: the study provides a comprehensive comparative evaluation of multiple machine learning models for predicting river inflow. While previous studies have explored individual models, this research systematically compares the performance of CatBoost, ElasticNet, KNN, Lasso, LGBM, Linear Regression, MLP, Random Forest, Ridge, SGD, and XGBoost. Such a comprehensive comparative analysis is novel in the context of river inflow prediction.
- Time Series Analysis: the study specifically focuses on time series analysis for river inflow prediction. Time series data present unique challenges, due to temporal dependencies. By applying different machine learning techniques to this specific domain, the research contributes to the advancement of time series prediction methodologies in the context of water resource management.
- Application to River Inflow Prediction: while machine learning models have been applied in various domains, their application to river inflow prediction is of significant importance for water resource management. Predicting river inflow accurately is crucial for making informed decisions regarding water allocation, flood management, and hydropower generation.
- Performance Evaluation on Multiple Datasets: the study evaluates the performance of the models on multiple datasets, including training, validation, and testing data. This comprehensive evaluation provides a robust assessment of the models’ performance and their ability to generalize to unseen data, contributing to the understanding of their efficacy in real-world scenarios.
1.2. Objectives of the Study
2. Methodology and Methods
2.1. CatBoostRegressor Algorithm
2.2. k-Nearest Neighbors
- Prepare the training data with input features and target values.
- Determine the value of k, the number of nearest neighbors to consider.
- Calculate the distance between the new data point and the training data points.
- Select the k nearest neighbors, based on the distances.
- Calculate the target values’ average among the k closest neighbors. Use the average value as the new data point’s estimated goal value.
2.3. Light Gradient-Boosting Machine Regressor (LGBM)
2.4. Linear Regression (LR)
2.5. Multilayer Perceptron
- (a)
- Assign random weights to the connections between the neurons as part of the initialization process.
- (b)
- The input layer: Take in input data and send them to the top-most hidden layer.
- (c)
- Hidden layers: Each hidden layer neuron computes the weighted sum of its inputs using the current weights and then applies an activation function (such as a sigmoid) to the sum.
- (d)
- Output layer: The neurons in the output layer compute the same activation function and weighted sum as the neurons in the hidden layers.
- (e)
- The MLP’s final output is derived from the neurons in the output layer.
2.6. Random Forest
- Random Subset Selection: a random subset of data points is chosen from the training set. This subset typically contains a fraction of the total data points, denoted by ‘p’.
- Construction of a Decision Tree: using the subset of data points that was chosen, a decision tree is built. This procedure is repeated using various subsets of the data for a total of ‘N’ trees.
- Prediction Aggregation: each of the ‘N’ decision trees predicts the value of the target variable for a new data point. The outcomes of all the predictions from the trees are averaged to provide the final forecast.
2.7. Lasso
2.8. Ridge
2.9. ElasticNet
2.10. Stochastic Gradient Descent (SGD) Regressor
2.11. Extreme Gradient-Boosting Regression Model (XGBoost)
- Choosing the XGBoost model’s parameters, such as the learning rate, the number of trees, the maximum depth, and the feature fraction, is the step-one process. These variables can be altered to improve performance and regulate how the model behaves.
- Create the model and train it: the XGBoost model is produced by the construction of several decision trees. A gradient-based optimization technique that minimizes the loss function is used to build each tree. The ensemble of trees is continuously expanded throughout the training phase, and predictions are updated in line with gradients in the loss function.
- After model training, the model may be used to make predictions about fresh data points. The XGBoost method incorporates the predictions from each tree in the ensemble to obtain the final regression prediction. The particular method for combining the predictions is determined by the loss function that is used.
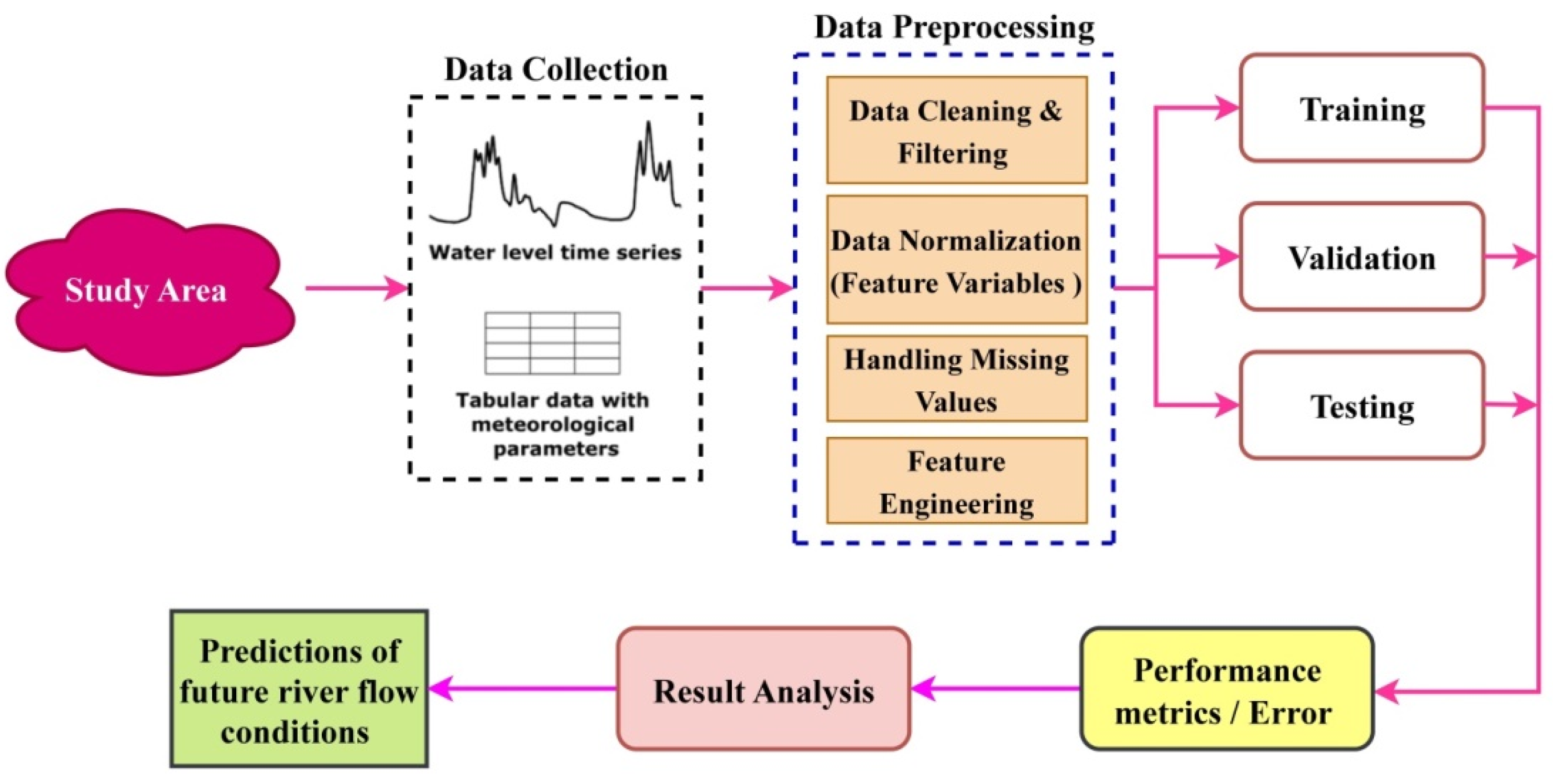
3. Model Training and Validation
- Data Split: a training set, a validation set, and a test set are each provided as separate datasets. The model is trained using the training set. The validation set is used to fine-tune the model and assess model performance throughout training, whereas the test set is used to measure the trained model’s final performance on unseen data.
- Model Selection: select the most effective model architecture or machine learning technique for the particular job. The kind of data, the task (classification, regression, etc.), and the resources available are all factors in the model selection process.
- Model Training: develop the selected model using the training dataset. During the training phase, the model parameters are frequently repeatedly improved in order to minimize a chosen loss or error function. In order to do this, training data are fed into the model, predictions are generated and compared to actual values, and model parameters are updated, depending on computed errors. This procedure continues until a convergence requirement is satisfied, after a certain number of epochs.
- Model Evaluation: using the validation dataset, evaluate how well the trained model performed. The validation data is used to generate predictions, which are then compared to the actual results. There are several assessment measures employed, including mean squared error (MSE), mean absolute error (MAE), root mean square error (RMSE), root mean square percent error (RMSPE), and R-squared (R2) [75].
- 5.
- Iterative Refinement: to enhance performance, modify the model architecture or data preparation stages based on the evaluation findings. Until a suitable performance is attained, this iterative procedure is continued.
- 6.
- Final Assessment: after the model has been adjusted, its performance is evaluated using the test dataset, which simulates unseen data. This offers a neutral assessment of how well the model performs in realistic situations.
4. Study Area, Data Collection and Preprocessing
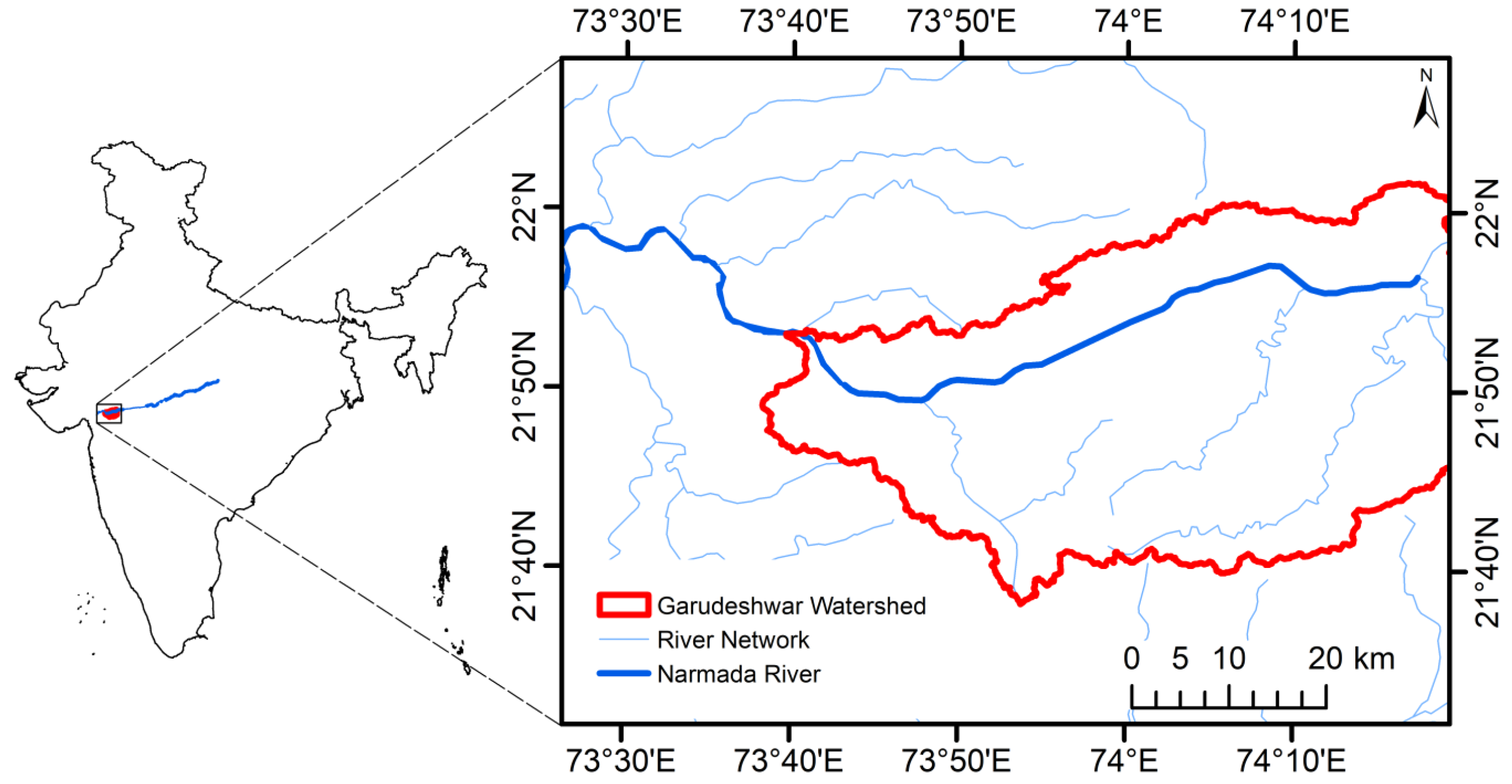
4.1. Study Area
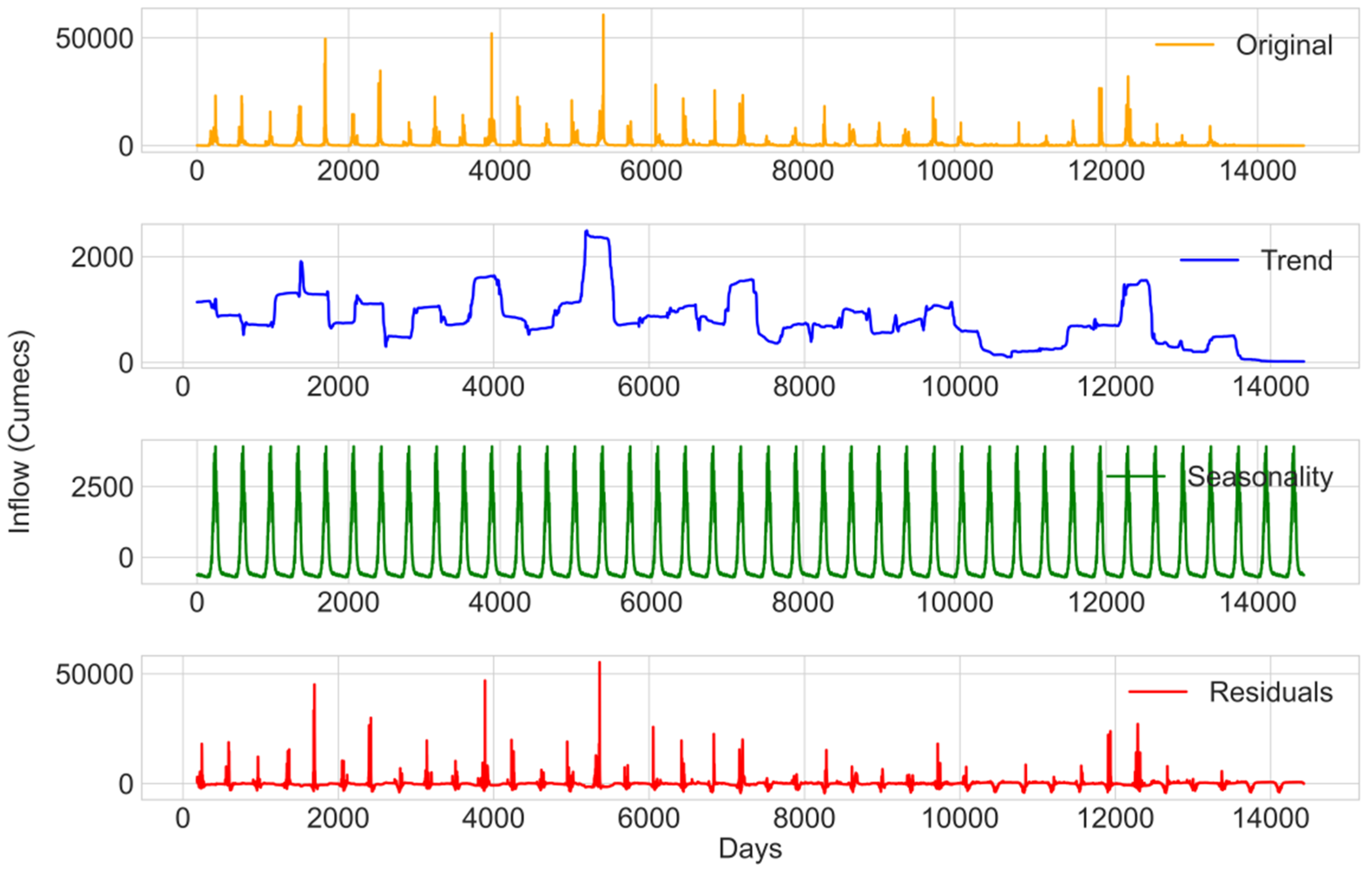
4.2. Data Collection
4.3. Techniques for Preprocessing Data
4.3.1. Creating Lagged Features
4.3.2. Date Feature Engineering
4.3.3. One-Hot Encoding
5. Model Preparation
6. Results and Discussion
6.1. Performance Metrics of Training Data
6.2. Performance Metrics of Validation Data
6.3. Performance Metrics of Testing Data
6.4. Comparison of the Models
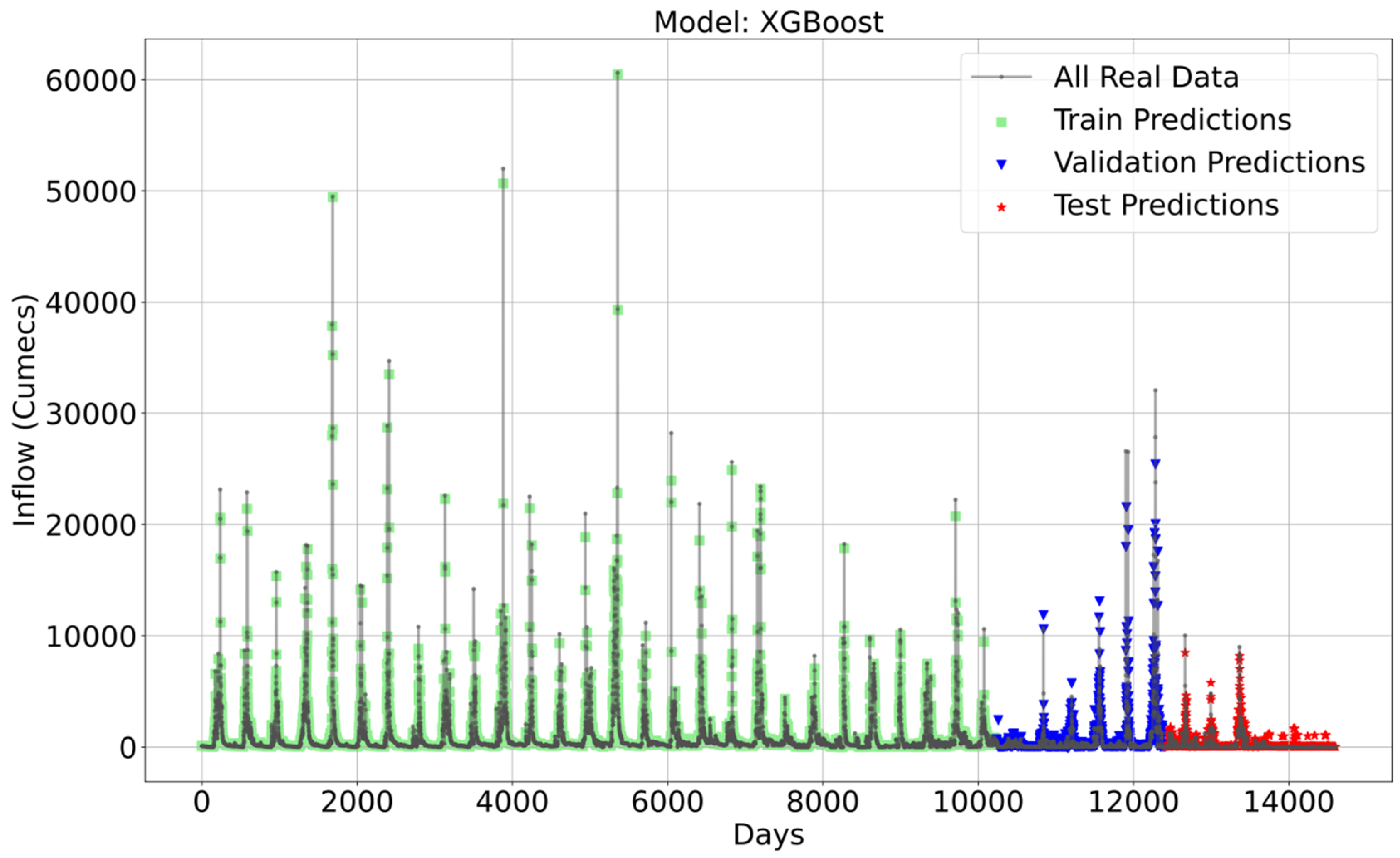
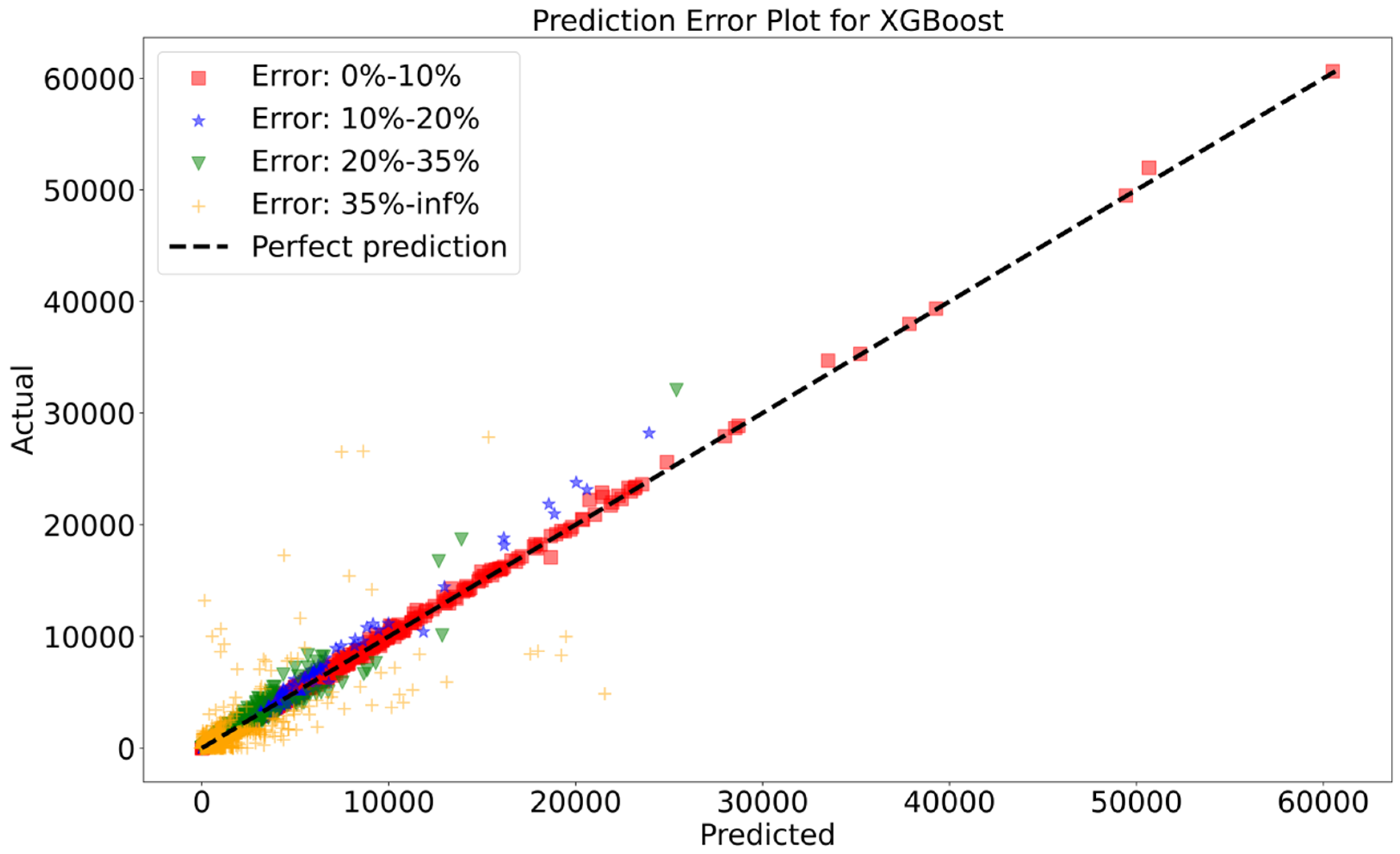
- Training Data: XGBoost has the highest R2 and the lowest MAE, MSE, RMSE, and RMSPE values, indicating the best performance on the training data. The time series prediction for XGBoost is shown in Figure 5, where predicted streamflow inflows are depicted alongside the actual data. The fundamental patterns and fluctuations in streamflow across the dataset are largely captured by the XGBoost model, as can be seen in this figure.
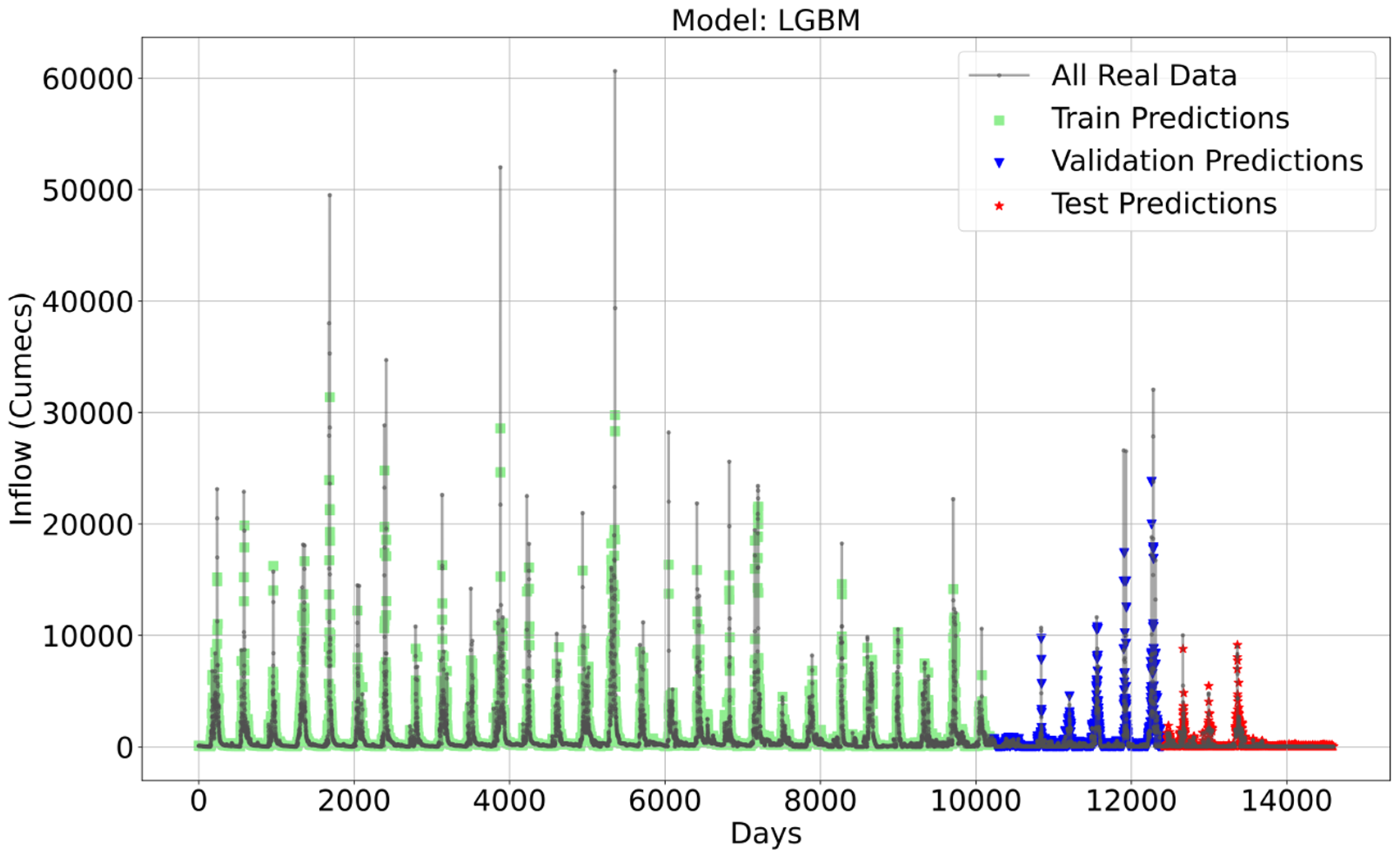
- Validation Data: the LGBM model has the highest R2 and the lowest MAE, MSE, RMSE, and RMSPE values, demonstrating the best performance on the validation data. The time series prediction for LGBM against the actual data is shown in Figure 6.
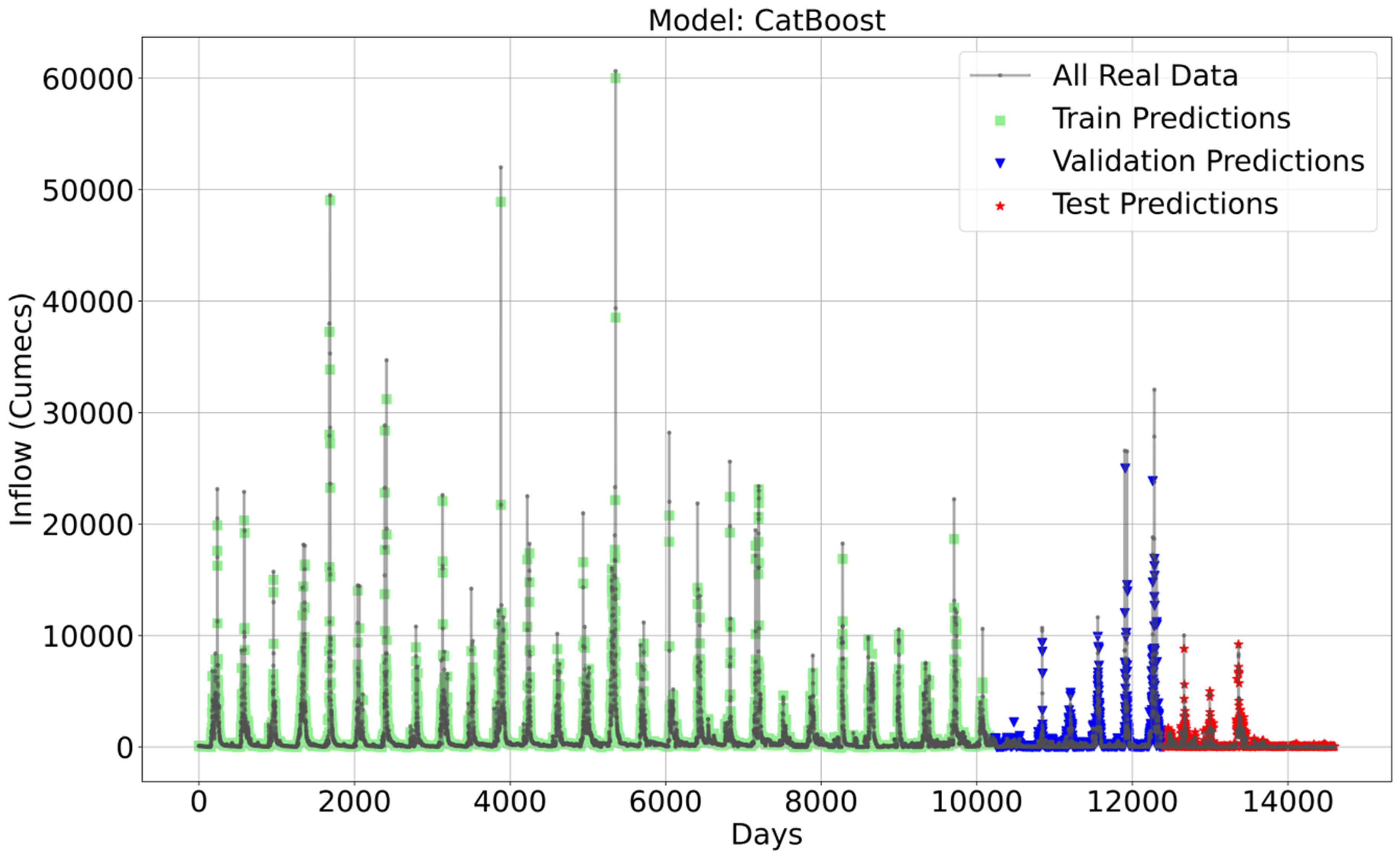
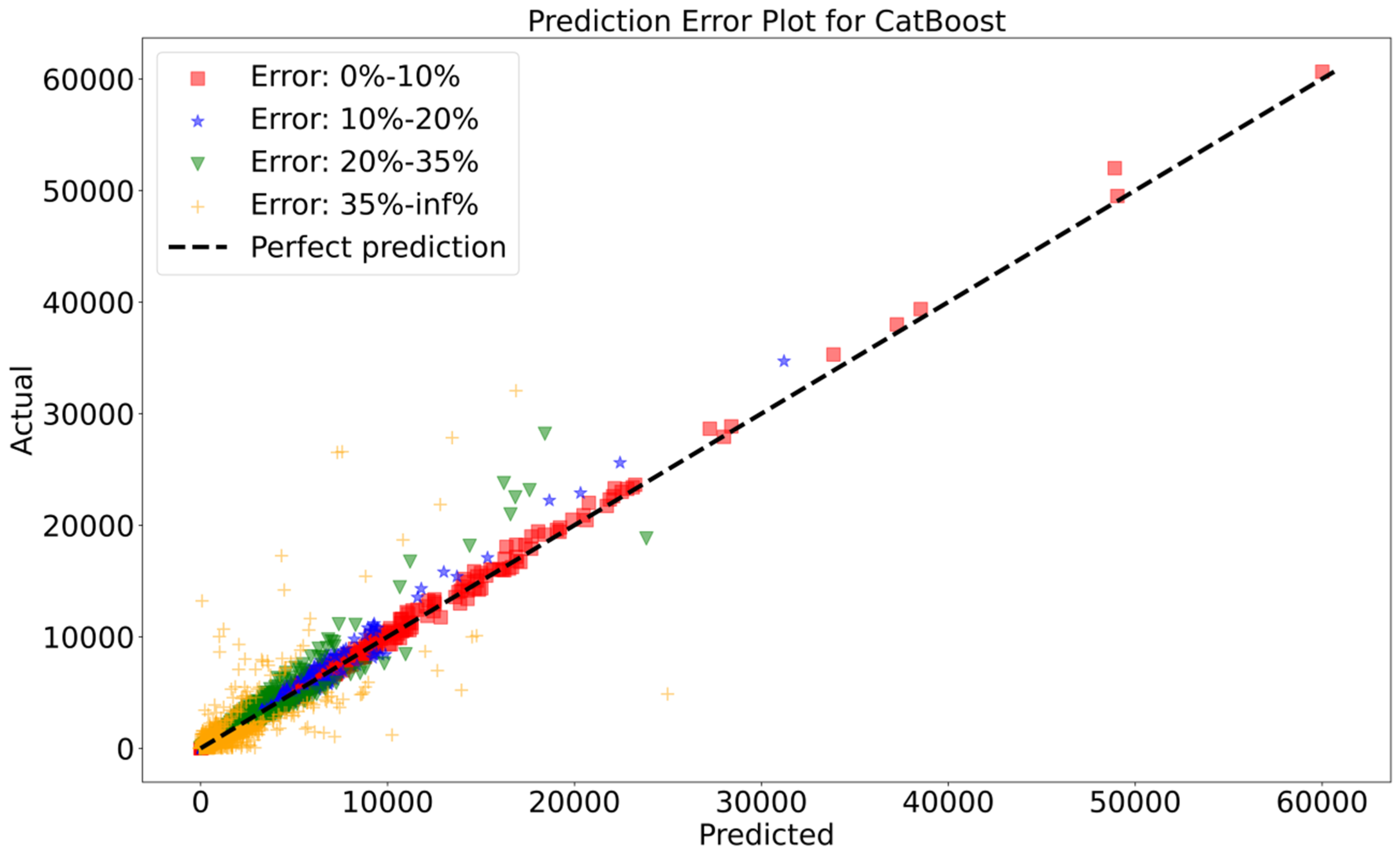
- Testing Data: LGBM has the highest R2 and the lowest MAE, MSE, and RMSE values, showing the best performance on the testing data.
6.5. Limitations of the Study
- (a)
- One limitation of our research is the reliance on a specific dataset from the Garudeshwar gauging station. The generalizability of the findings may be limited to this particular location, and may not directly apply to other river systems. Future studies should consider incorporating data from multiple gauging stations or rivers to validate the performance of the models across different regions.
- (b)
- Another limitation is the time frame of the dataset used in the study, which spans from 1980 to 2019. Although this provides a substantial historical perspective, it may not capture recent changes or evolving patterns in river inflow. Incorporating more up-to-date data would enhance the accuracy and relevance of the predictions.
- (c)
- Additionally, the study focused primarily on machine learning models and did not consider other factors that could influence river inflow, such as climate change, land use changes, or anthropogenic activities. Incorporating these factors into the modeling process may provide a more comprehensive understanding of the dynamics of river inflow.
- (d)
- Lastly, the performance of the models may be influenced by the quality and completeness of the data. Data quality issues, such as measurement errors, could impact the accuracy of the predictions. It is crucial for future research to address data preprocessing and quality control techniques to mitigate such limitations.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- El-Shafie, A.; Taha, M.R.; Noureldin, A. A neuro-fuzzy model for inflow forecasting of the Nile river at Aswan high dam. Water Resour. Manag. 2007, 21, 533–556. [Google Scholar] [CrossRef]
- Stakhiv, E.; Stewart, B. Needs for Climate Information in Support of Decision-Making in the Water Sector. Procedia Environ. Sci. 2010, 1, 102–119. [Google Scholar] [CrossRef] [Green Version]
- Kumar, V.; Yadav, S.M. Multi-objective reservoir operation of the Ukai reservoir system using an improved Jaya algorithm. Water Supply 2022, 22, 2287–2310. [Google Scholar] [CrossRef]
- Chabokpour, J.; Chaplot, B.; Dasineh, M.; Ghaderi, A.; Azamathulla, H.M. Functioning of the multilinear lag-cascade flood routing model as a means of transporting pollutants in the river. Water Supply 2020, 20, 2845–2857. [Google Scholar] [CrossRef]
- Venkataraman, K.; Tummuri, S.; Medina, A.; Perry, J. 21st century drought outlook for major climate divisions of Texas based on CMIP5 multimodel ensemble: Implications for water resource management. J. Hydrol. 2016, 534, 300–316. [Google Scholar] [CrossRef] [Green Version]
- Hanak, E.; Lund, J.R. Adapting California’s water management to climate change. Clim. Chang. 2012, 111, 17–44. [Google Scholar] [CrossRef]
- Sharma, K.V.; Kumar, V.; Singh, K.; Mehta, D.J. LANDSAT 8 LST Pan sharpening using novel principal component based downscaling model. Remote Sens. Appl. Soc. Environ. 2023, 30, 100963. [Google Scholar] [CrossRef]
- Cho, K.; Kim, Y. Improving streamflow prediction in the WRF-Hydro model with LSTM networks. J. Hydrol. 2022, 605, 127297. [Google Scholar] [CrossRef]
- Nearing, G.S.; Kratzert, F.; Sampson, A.K.; Pelissier, C.S.; Klotz, D.; Frame, J.M.; Prieto, C.; Gupta, H.V. What Role Does Hydrological Science Play in the Age of Machine Learning? Water Resour. Res. 2021, 57, e2020WR028091. [Google Scholar] [CrossRef]
- Liang, J.; Li, W.; Bradford, S.; Šimůnek, J. Physics-Informed Data-Driven Models to Predict Surface Runoff Water Quantity and Quality in Agricultural Fields. Water 2019, 11, 200. [Google Scholar] [CrossRef] [Green Version]
- Dinic, F.; Singh, K.; Dong, T.; Rezazadeh, M.; Wang, Z.; Khosrozadeh, A.; Yuan, T.; Voznyy, O. Applied Machine Learning for Developing Next-Generation Functional Materials. Adv. Funct. Mater. 2021, 31, 2104195. [Google Scholar] [CrossRef]
- Clark, M.P.; Fan, Y.; Lawrence, D.M.; Adam, J.C.; Bolster, D.; Gochis, D.J.; Hooper, R.P.; Kumar, M.; Leung, L.R.; Mackay, D.S.; et al. Improving the representation of hydrologic processes in Earth System Models. Water Resour. Res. 2015, 51, 5929–5956. [Google Scholar] [CrossRef]
- Legesse, D.; Vallet-Coulomb, C.; Gasse, F. Hydrological response of a catchment to climate and land use changes in Tropical Africa: Case study South Central Ethiopia. J. Hydrol. 2003, 275, 67–85. [Google Scholar] [CrossRef]
- Yang, S.; Wan, M.P.; Chen, W.; Ng, B.F.; Dubey, S. Model predictive control with adaptive machine-learning-based model for building energy efficiency and comfort optimization. Appl. Energy 2020, 271, 115147. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, W.; Liu, Q.; Zhao, Y.; Liu, P.; Wu, D.; Banu, M.; Chen, L. Data-driven modeling of process, structure and property in additive manufacturing: A review and future directions. J. Manuf. Process. 2022, 77, 13–31. [Google Scholar] [CrossRef]
- Hernández-Rojas, L.F.; Abrego-Perez, A.L.; Lozano Martínez, F.E.; Valencia-Arboleda, C.F.; Diaz-Jimenez, M.C.; Pacheco-Carvajal, N.; Garcia-Cardenas, J.J. The Role of Data-Driven Methodologies in Weather Index Insurance. Appl. Sci. 2023, 13, 4785. [Google Scholar] [CrossRef]
- Feng, D.; Lawson, K.; Shen, C. Mitigating Prediction Error of Deep Learning Streamflow Models in Large Data-Sparse Regions With Ensemble Modeling and Soft Data. Geophys. Res. Lett. 2021, 48, e2021GL092999. [Google Scholar] [CrossRef]
- San, O.; Rasheed, A.; Kvamsdal, T. Hybrid analysis and modeling, eclecticism, and multifidelity computing toward digital twin revolution. GAMM-Mitt. 2021, 44, e202100007. [Google Scholar] [CrossRef]
- Aliashrafi, A.; Zhang, Y.; Groenewegen, H.; Peleato, N.M. A review of data-driven modelling in drinking water treatment. Rev. Environ. Sci. Bio/Technol. 2021, 20, 985–1009. [Google Scholar] [CrossRef]
- Singh, K.; Singh, B.; Sihag, P.; Kumar, V.; Sharma, K.V. Development and application of modeling techniques to estimate the unsaturated hydraulic conductivity. Model. Earth Syst. Environ. 2023. [Google Scholar] [CrossRef]
- Yang, D.; Chen, K.; Yang, M.; Zhao, X. Urban rail transit passenger flow forecast based on LSTM with enhanced long-term features. IET Intell. Transp. Syst. 2019, 13, 1475–1482. [Google Scholar] [CrossRef]
- Nagar, U.P.; Patel, H.M. Development of Short-Term Reservoir Level Forecasting Models: A Case Study of Ajwa-Pratappura Reservoir System of Vishwamitri River Basin of Central Gujarat. In Hydrology and Hydrologic Modelling—HYDRO 2021; Timbadiya, P.V., Patel, P.L., Singh, V.P., Sharma, P.J., Eds.; Springer: Singapore, 2023; pp. 261–269. [Google Scholar] [CrossRef]
- Mehta, D.J.; Eslamian, S.; Prajapati, K. Flood modelling for a data-scare semi-arid region using 1-D hydrodynamic model: A case study of Navsari Region. Model. Earth Syst. Environ. 2022, 8, 2675–2685. [Google Scholar] [CrossRef]
- Gangani, P.; Mangukiya, N.K.; Mehta, D.J.; Muttil, N.; Rathnayake, U. Evaluating the Efficacy of Different DEMs for Application in Flood Frequency and Risk Mapping of the Indian Coastal River Basin. Climate 2023, 11, 114. [Google Scholar] [CrossRef]
- Omukuti, J.; Wanzala, M.A.; Ngaina, J.; Ganola, P. Develop medium- to long-term climate information services to enhance comprehensive climate risk management in Africa. Clim. Resil. Sustain. 2023, 2, e247. [Google Scholar] [CrossRef]
- Kumar, V.; Yadav, S.M. A state-of-the-Art review of heuristic and metaheuristic optimization techniques for the management of water resources. Water Supply 2022, 22, 3702–3728. [Google Scholar] [CrossRef]
- Rivera-González, L.; Bolonio, D.; Mazadiego, L.F.; Valencia-Chapi, R. Long-Term Electricity Supply and Demand Forecast (2018–2040): A LEAP Model Application towards a Sustainable Power Generation System in Ecuador. Sustainability 2019, 11, 5316. [Google Scholar] [CrossRef] [Green Version]
- Singh, D.; Vardhan, M.; Sahu, R.; Chatterjee, D.; Chauhan, P.; Liu, S. Machine-learning- and deep-learning-based streamflow prediction in a hilly catchment for future scenarios using CMIP6 GCM data. Hydrol. Earth Syst. Sci. 2023, 27, 1047–1075. [Google Scholar] [CrossRef]
- Mohammadi, B. A review on the applications of machine learning for runoff modeling. Sustain. Water Resour. Manag. 2021, 7, 98. [Google Scholar] [CrossRef]
- Ibrahim, K.S.M.H.; Huang, Y.F.; Ahmed, A.N.; Koo, C.H.; El-Shafie, A. Forecasting multi-step-ahead reservoir monthly and daily inflow using machine learning models based on different scenarios. Appl. Intell. 2023, 53, 10893–10916. [Google Scholar] [CrossRef]
- Rajesh, M.; Anishka, S.; Viksit, P.S.; Arohi, S.; Rehana, S. Improving Short-range Reservoir Inflow Forecasts with Machine Learning Model Combination. Water Resour. Manag. 2023, 37, 75–90. [Google Scholar] [CrossRef]
- Cai, H.; Liu, S.; Shi, H.; Zhou, Z.; Jiang, S.; Babovic, V. Toward improved lumped groundwater level predictions at catchment scale: Mutual integration of water balance mechanism and deep learning method. J. Hydrol. 2022, 613, 128495. [Google Scholar] [CrossRef]
- Jiang, S.; Zheng, Y.; Wang, C.; Babovic, V. Uncovering Flooding Mechanisms Across the Contiguous United States Through Interpretive Deep Learning on Representative Catchments. Water Resour. Res. 2022, 58, e2021WR030185. [Google Scholar] [CrossRef]
- Herath, H.M.V.V.; Chadalawada, J.; Babovic, V. Hydrologically informed machine learning for rainfall–runoff modelling: Towards distributed modelling. Hydrol. Earth Syst. Sci. 2021, 25, 4373–4401. [Google Scholar] [CrossRef]
- Chadalawada, J.; Herath, H.M.V.V.; Babovic, V. Hydrologically Informed Machine Learning for Rainfall-Runoff Modeling: A Genetic Programming-Based Toolkit for Automatic Model Induction. Water Resour. Res. 2020, 56, e2019WR026933. [Google Scholar] [CrossRef]
- Lima, C.H.R.; Lall, U. Spatial scaling in a changing climate: A hierarchical bayesian model for non-stationary multi-site annual maximum and monthly streamflow. J. Hydrol. 2010, 383, 307–318. [Google Scholar] [CrossRef]
- Turner, S.W.D.; Marlow, D.; Ekström, M.; Rhodes, B.G.; Kularathna, U.; Jeffrey, P.J. Linking climate projections to performance: A yield-based decision scaling assessment of a large urban water resources system. Water Resour. Res. 2014, 50, 3553–3567. [Google Scholar] [CrossRef]
- Ab Razak, N.H.; Aris, A.Z.; Ramli, M.F.; Looi, L.J.; Juahir, H. Temporal flood incidence forecasting for Segamat River (Malaysia) using autoregressive integrated moving average modelling. J. Flood Risk Manag. 2018, 11, S794–S804. [Google Scholar] [CrossRef]
- Banihabib, M.E.; Bandari, R.; Valipour, M. Improving Daily Peak Flow Forecasts Using Hybrid Fourier-Series Autoregressive Integrated Moving Average and Recurrent Artificial Neural Network Models. AI 2020, 1, 263–275. [Google Scholar] [CrossRef]
- Demirel, M.C.; Venancio, A.; Kahya, E. Flow forecast by SWAT model and ANN in Pracana basin, Portugal. Adv. Eng. Softw. 2009, 40, 467–473. [Google Scholar] [CrossRef]
- Chen, J.; Wu, Y. Advancing representation of hydrologic processes in the Soil and Water Assessment Tool (SWAT) through integration of the TOPographic MODEL (TOPMODEL) features. J. Hydrol. 2012, 420–421, 319–328. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; El-shafie, A.; Jaafar, O.; Afan, H.A.; Sayl, K.N. Artificial intelligence based models for stream-flow forecasting: 2000–2015. J. Hydrol. 2015, 530, 829–844. [Google Scholar] [CrossRef]
- Dong, N.; Guan, W.; Cao, J.; Zou, Y.; Yang, M.; Wei, J.; Chen, L.; Wang, H. A hybrid hydrologic modelling framework with data-driven and conceptual reservoir operation schemes for reservoir impact assessment and predictions. J. Hydrol. 2023, 619, 129246. [Google Scholar] [CrossRef]
- Kumar, V.; Sharma, K.V.; Caloiero, T.; Mehta, D.J.; Singh, K. Comprehensive Overview of Flood Modeling Approaches: A Review of Recent Advances. Hydrology 2023, 10, 141. [Google Scholar] [CrossRef]
- Ikram, R.M.A.; Ewees, A.A.; Parmar, K.S.; Yaseen, Z.M.; Shahid, S.; Kisi, O. The viability of extended marine predators algorithm-based artificial neural networks for streamflow prediction. Appl. Soft Comput. 2022, 131, 109739. [Google Scholar] [CrossRef]
- Ni, L.; Wang, D.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J.; Liu, J. Streamflow forecasting using extreme gradient boosting model coupled with Gaussian mixture model. J. Hydrol. 2020, 586, 124901. [Google Scholar] [CrossRef]
- Meresa, H. Modelling of river flow in ungauged catchment using remote sensing data: Application of the empirical (SCS-CN), Artificial Neural Network (ANN) and Hydrological Model (HEC-HMS). Model. Earth Syst. Environ. 2019, 5, 257–273. [Google Scholar] [CrossRef]
- Adnan, R.M.; Kisi, O.; Mostafa, R.R.; Ahmed, A.N.; El-Shafie, A. The potential of a novel support vector machine trained with modified mayfly optimization algorithm for streamflow prediction. Hydrol. Sci. J. 2022, 67, 161–174. [Google Scholar] [CrossRef]
- Meng, E.; Huang, S.; Huang, Q.; Fang, W.; Wu, L.; Wang, L. A robust method for non-stationary streamflow prediction based on improved EMD-SVM model. J. Hydrol. 2019, 568, 462–478. [Google Scholar] [CrossRef]
- Noori, R.; Karbassi, A.R.; Moghaddamnia, A.; Han, D.; Zokaei-Ashtiani, M.H.; Farokhnia, A.; Gousheh, M.G. Assessment of input variables determination on the SVM model performance using PCA, Gamma test, and forward selection techniques for monthly stream flow prediction. J. Hydrol. 2011, 401, 177–189. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A Brief Review of Random Forests for Water Scientists and Practitioners and Their Recent History in Water Resources. Water 2019, 11, 910. [Google Scholar] [CrossRef] [Green Version]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. Super ensemble learning for daily streamflow forecasting: Large-scale demonstration and comparison with multiple machine learning algorithms. Neural Comput. Appl. 2021, 33, 3053–3068. [Google Scholar] [CrossRef]
- Song, Z.; Xia, J.; Wang, G.; She, D.; Hu, C.; Hong, S. Regionalization of hydrological model parameters using gradient boosting machine. Hydrol. Earth Syst. Sci. 2022, 26, 505–524. [Google Scholar] [CrossRef]
- Akbarian, M.; Saghafian, B.; Golian, S. Monthly streamflow forecasting by machine learning methods using dynamic weather prediction model outputs over Iran. J. Hydrol. 2023, 620, 129480. [Google Scholar] [CrossRef]
- Luo, P.; Luo, M.; Li, F.; Qi, X.; Huo, A.; Wang, Z.; He, B.; Takara, K.; Nover, D.; Wang, Y. Urban flood numerical simulation: Research, methods and future perspectives. Environ. Model. Softw. 2022, 156, 105478. [Google Scholar] [CrossRef]
- Kumar, V.; Azamathulla, H.M.; Sharma, K.V.; Mehta, D.J.; Maharaj, K.T. The State of the Art in Deep Learning Applications, Challenges, and Future Prospects: A Comprehensive Review of Flood Forecasting and Management. Sustainability 2023, 15, 10543. [Google Scholar] [CrossRef]
- Niu, W.; Feng, Z. Evaluating the performances of several artificial intelligence methods in forecasting daily streamflow time series for sustainable water resources management. Sustain. Cities Soc. 2021, 64, 102562. [Google Scholar] [CrossRef]
- Bhasme, P.; Vagadiya, J.; Bhatia, U. Enhancing predictive skills in physically-consistent way: Physics Informed Machine Learning for Hydrological Processes. arXiv 2021, arXiv:2104.11009. [Google Scholar] [CrossRef]
- Souza, D.P.M.; Martinho, A.D.; Rocha, C.C.; da S. Christo, E.; Goliatt, L. Hybrid particle swarm optimization and group method of data handling for short-term prediction of natural daily streamflows. Model. Earth Syst. Environ. 2022, 8, 5743–5759. [Google Scholar] [CrossRef]
- Martinho, A.D.; Saporetti, C.M.; Goliatt, L. Approaches for the short-term prediction of natural daily streamflows using hybrid machine learning enhanced with grey wolf optimization. Hydrol. Sci. J. 2023, 68, 16–33. [Google Scholar] [CrossRef]
- Haznedar, B.; Kilinc, H.C.; Ozkan, F.; Yurtsever, A. Streamflow forecasting using a hybrid LSTM-PSO approach: The case of Seyhan Basin. Nat. Hazards 2023, 117, 681–701. [Google Scholar] [CrossRef]
- Hao, R.; Bai, Z. Comparative Study for Daily Streamflow Simulation with Different Machine Learning Methods. Water 2023, 15, 1179. [Google Scholar] [CrossRef]
- Bakhshi Ostadkalayeh, F.; Moradi, S.; Asadi, A.; Moghaddam Nia, A.; Taheri, S. Performance Improvement of LSTM-based Deep Learning Model for Streamflow Forecasting Using Kalman Filtering. Water Resour. Manag. 2023, 37, 3111–3127. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. Catboost: Unbiased boosting with categorical features. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 2–8 December 2018; Volume 31, pp. 6638–6648. [Google Scholar]
- Kramer, O. K-Nearest Neighbors. In Dimensionality Reduction with Unsupervised Nearest Neighbors; Springer: Berlin/Heidelberg, Germany, 2013; Volume 51, pp. 13–23. [Google Scholar] [CrossRef]
- Fan, J.; Ma, X.; Wu, L.; Zhang, F.; Yu, X.; Zeng, W. Light Gradient Boosting Machine: An efficient soft computing model for estimating daily reference evapotranspiration with local and external meteorological data. Agric. Water Manag. 2019, 225, 105758. [Google Scholar] [CrossRef]
- Su, X.; Yan, X.; Tsai, C.-L. Linear regression. Wiley Interdiscip. Rev. Comput. Stat. 2012, 4, 275–294. [Google Scholar] [CrossRef]
- Gardner, M.; Dorling, S. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Biau, G.; Scornet, E. A random forest guided tour. TEST 2016, 25, 197–227. [Google Scholar] [CrossRef] [Green Version]
- Luo, X.; Chang, X.; Ban, X. Regression and classification using extreme learning machine based on L1-norm and L2-norm. Neurocomputing 2016, 174, 179–186. [Google Scholar] [CrossRef]
- McDonald, G.C. Ridge regression. Wiley Interdiscip. Rev. Comput. Stat. 2009, 1, 93–100. [Google Scholar] [CrossRef]
- Ryali, S.; Chen, T.; Supekar, K.; Menon, V. Estimation of functional connectivity in fMRI data using stability selection-based sparse partial correlation with elastic net penalty. Neuroimage 2012, 59, 3852–3861. [Google Scholar] [CrossRef] [Green Version]
- Song, S.; Chaudhuri, K.; Sarwate, A.D. Stochastic gradient descent with differentially private updates. In Proceedings of the 2013 IEEE Global Conference on Signal and Information Processing, Austin, TX, USA, 3–5 December 2013; pp. 245–248. [Google Scholar] [CrossRef] [Green Version]
- Sheridan, R.P.; Wang, W.M.; Liaw, A.; Ma, J.; Gifford, E.M. Extreme Gradient Boosting as a Method for Quantitative Structure–Activity Relationships. J. Chem. Inf. Model. 2016, 56, 2353–2360. [Google Scholar] [CrossRef]
- Chadalawada, J.; Babovic, V. Review and comparison of performance indices for automatic model induction. J. Hydroinform. 2019, 21, 13–31. [Google Scholar] [CrossRef] [Green Version]


| Flow | |
|---|---|
| Mean | 784.8985221 |
| Standard Error | 18.28637548 |
| Median | 184.0000428 |
| Mode | 23.19005239 |
| Standard Deviation | 2210.307722 |
| Sample Variance | 4,885,460.225 |
| Kurtosis | 128.7110287 |
| Skewness | 8.786730848 |
| Range | 60,640.72647 |
| Minimum | 1.270052203 |
| Maximum | 60,641.99652 |
| Sr No. | Model | MAE_Train | MSE_Train | RMSE_Train | RMSPE_Train | R2_Train |
|---|---|---|---|---|---|---|
| 1 | CatBoost | 124.89 | 131,672.45 | 362.87 | 150.28 | 0.98 |
| 2 | ElasticNet | 414.90 | 2,304,350.42 | 1518.01 | 853.11 | 0.61 |
| 3 | KNN | 320.95 | 1,773,732.98 | 1331.82 | 310.48 | 0.70 |
| 4 | Lasso | 327.18 | 1,923,781.45 | 1387.00 | 568.25 | 0.67 |
| 5 | LGBM | 215.89 | 863,329.16 | 929.16 | 256.82 | 0.85 |
| 6 | LR | 434.94 | 1,979,323.29 | 1406.88 | 1005.55 | 0.67 |
| 7 | MLP | 298.63 | 1,599,712.13 | 1264.80 | 276.29 | 0.73 |
| 8 | RF | 117.58 | 332,086.13 | 576.27 | 295.72 | 0.94 |
| 9 | Ridge | 330.27 | 1,923,316.06 | 1386.84 | 584.78 | 0.68 |
| 10 | SGD | 366.52 | 1,973,385.04 | 1404.77 | 980.74 | 0.67 |
| 11 | XGBoost | 75.04 | 38,693.90 | 196.71 | 142.99 | 0.99 |
| Sr No. | Model | MAE_Val | MSE_Val | RMSE_Val | RMSPE_Val | R2_Val |
|---|---|---|---|---|---|---|
| 1 | CatBoost | 261.90 | 1,430,686.30 | 1196.11 | 346.56 | 0.65 |
| 2 | ElasticNet | 385.08 | 1,555,769.49 | 1247.30 | 778.53 | 0.61 |
| 3 | KNN | 329.22 | 1,960,894.83 | 1400.32 | 446.31 | 0.51 |
| 4 | Lasso | 293.32 | 1,156,911.27 | 1075.60 | 538.62 | 0.71 |
| 5 | LGBM | 243.10 | 1,181,938.31 | 1087.17 | 287.91 | 0.71 |
| 6 | LR | 393.23 | 1,194,250.83 | 1092.82 | 992.99 | 0.70 |
| 7 | MLP | 249.45 | 1,069,732.66 | 1034.28 | 307.27 | 0.73 |
| 8 | RF | 259.75 | 1,386,585.60 | 1177.53 | 368.38 | 0.66 |
| 9 | Ridge | 296.56 | 1,157,972.15 | 1076.09 | 579.68 | 0.71 |
| 10 | SGD | 345.98 | 1,183,130.23 | 1087.72 | 908.38 | 0.71 |
| 11 | XGBoost | 264.54 | 1,349,874.60 | 1161.84 | 419.95 | 0.67 |
| Sr No. | Model | MAE_Test | MSE_Test | RMSE_Test | RMSPE_Test | R2_Test |
|---|---|---|---|---|---|---|
| 1 | CatBoost | 108.24 | 135,853.97 | 368.58 | 327.13 | 0.66 |
| 2 | ElasticNet | 267.84 | 195,282.23 | 441.91 | 1308.04 | 0.52 |
| 3 | KNN | 163.42 | 257,940.28 | 507.88 | 1067.24 | 0.36 |
| 4 | Lasso | 183.20 | 141,977.14 | 376.80 | 959.14 | 0.65 |
| 5 | LGBM | 105.68 | 115,456.65 | 339.79 | 332.76 | 0.71 |
| 6 | LR | 292.27 | 209,780.42 | 458.02 | 1424.00 | 0.48 |
| 7 | MLP | 131.03 | 123,120.76 | 350.89 | 466.30 | 0.69 |
| 8 | RF | 123.84 | 152,710.94 | 390.78 | 831.76 | 0.62 |
| 9 | Ridge | 187.82 | 146,634.81 | 382.93 | 996.15 | 0.64 |
| 10 | SGD | 252.24 | 195,665.92 | 442.34 | 1451.56 | 0.51 |
| 11 | XGBoost | 129.03 | 171,242.26 | 413.81 | 1102.39 | 0.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, V.; Kedam, N.; Sharma, K.V.; Mehta, D.J.; Caloiero, T. Advanced Machine Learning Techniques to Improve Hydrological Prediction: A Comparative Analysis of Streamflow Prediction Models. Water 2023, 15, 2572. https://doi.org/10.3390/w15142572
Kumar V, Kedam N, Sharma KV, Mehta DJ, Caloiero T. Advanced Machine Learning Techniques to Improve Hydrological Prediction: A Comparative Analysis of Streamflow Prediction Models. Water. 2023; 15(14):2572. https://doi.org/10.3390/w15142572
Chicago/Turabian StyleKumar, Vijendra, Naresh Kedam, Kul Vaibhav Sharma, Darshan J. Mehta, and Tommaso Caloiero. 2023. "Advanced Machine Learning Techniques to Improve Hydrological Prediction: A Comparative Analysis of Streamflow Prediction Models" Water 15, no. 14: 2572. https://doi.org/10.3390/w15142572






