Regression Tree Ensemble Rainfall–Runoff Forecasting Model and Its Application to Xiangxi River, China
Abstract
:1. Introduction
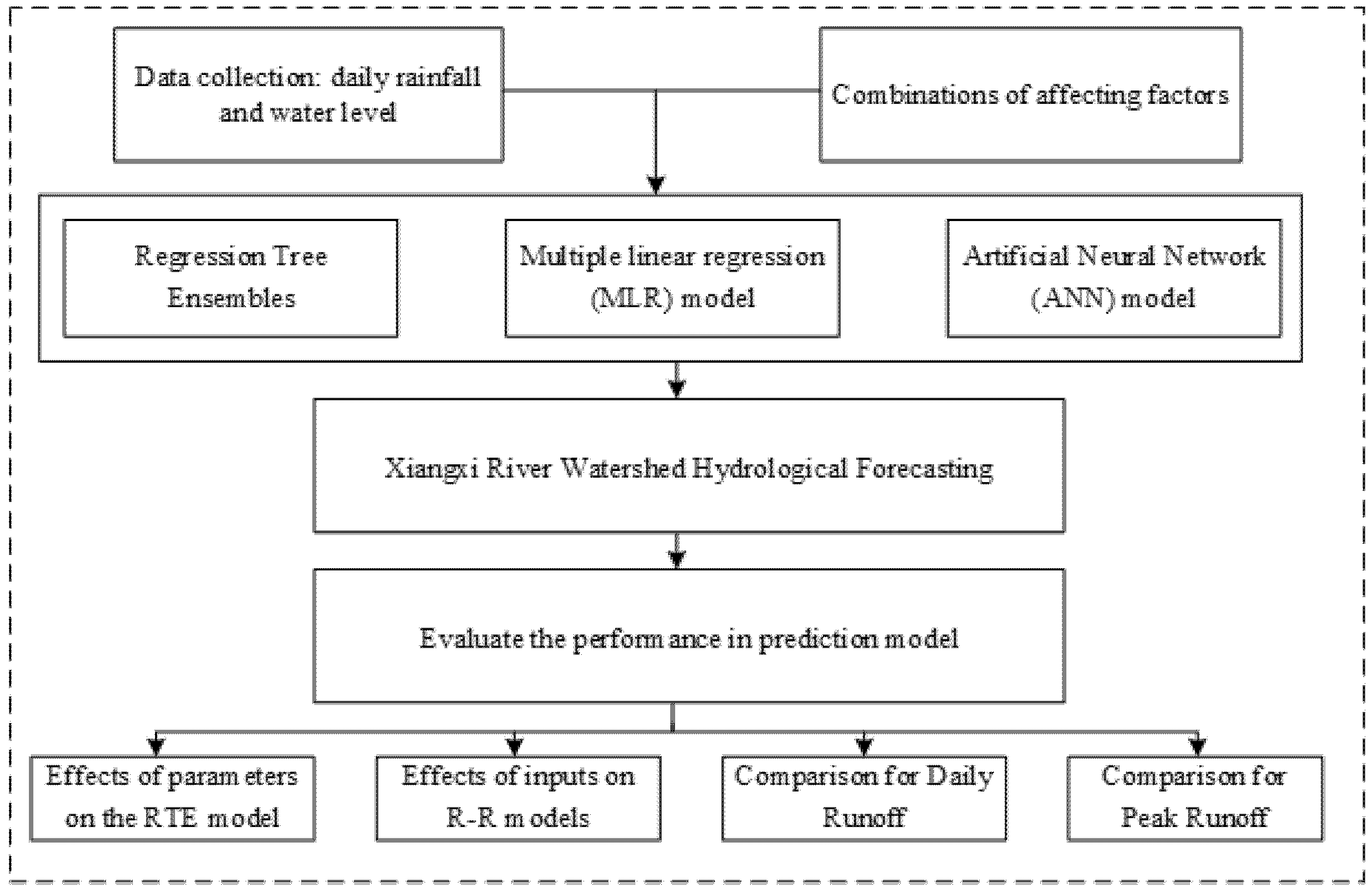
2. Materials and Methods
2.1. Regression Tree Ensemble (RTE)
2.2. Multiple Linear Regression (MLR) Model
2.3. Artificial Neural Network (ANN) Model
2.4. Performance Indices
3. Case Study
3.1. Study Area
3.2. Hydrological Forecasting for Xiangxi River Watershed
4. Results Analysis
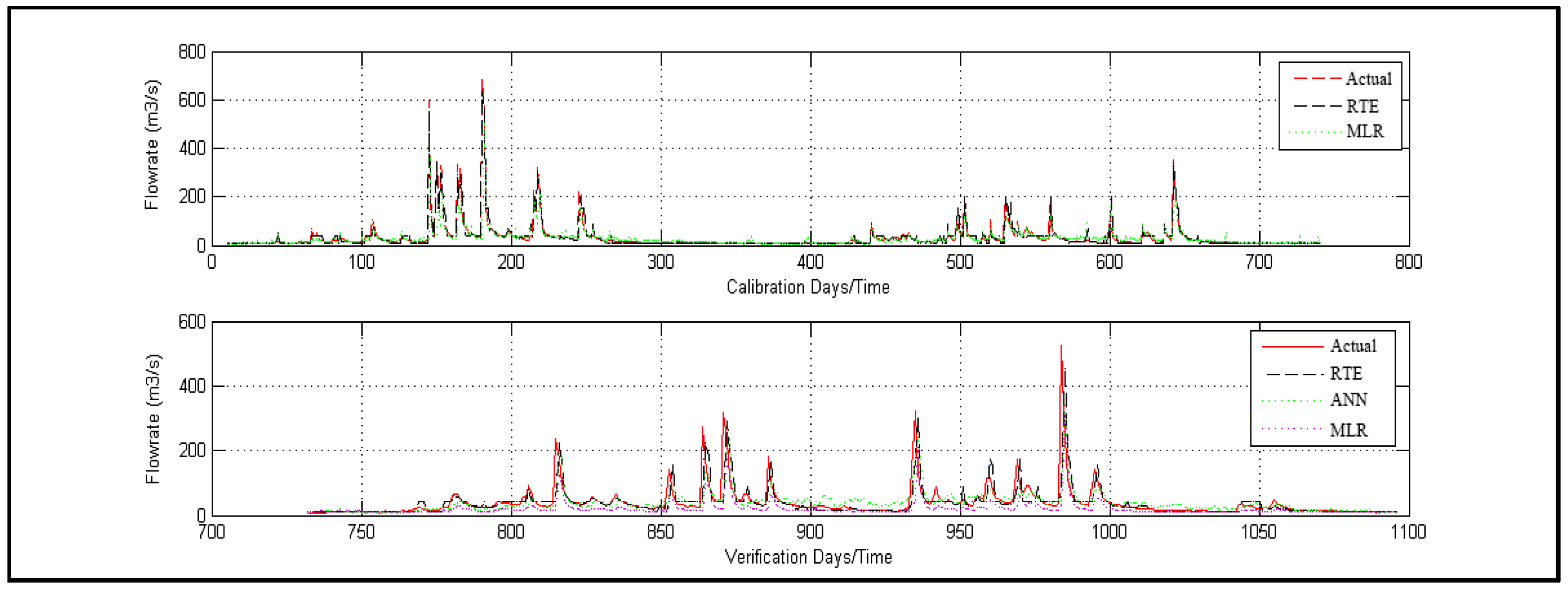
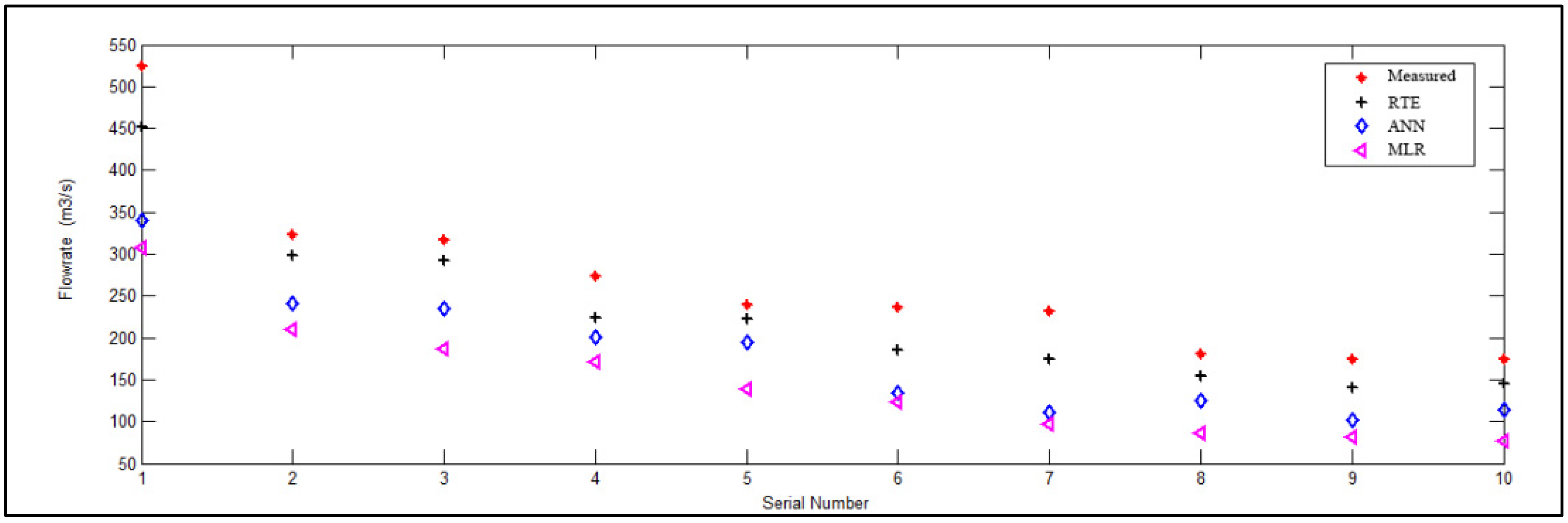
4.1. Comparison of Models
- (1)
- The prediction accuracy and generalization ability were significantly improved compared to the single model and the network in an ideal state, indicating that the ensemble model established for discharge forecasting is feasible and effective. The ensemble model integrated the advantages of each single model, effectively avoiding the errors of the single model being too large and having unstable defects. It had the characteristics of high-precision forecasting, strong generalization ability, and error smoothening.
- (2)
- According to the predicted results from the comparison of each single model, the prediction accuracy of the ANN model was better than that of the MLR model. However, according to the fitting results of the training samples, the fitting effect of the MLR model was equivalent to that of the ANN model. Furthermore, according to the forecast values of the test samples, the generalization ability of both the MLR model and the ANN model was poor.
- (3)
- As a whole, as a single model, the absolute value of the average relative error of prediction was less than 15% for both the MLR and the ANN model, and the absolute value of the maximum relative error was less than 29.55%, which can meet the precision requirement of discharge forecasting to some extent. However, their accuracy was inferior to that of the RTE.
4.2. Comparison of Daily Runoff
4.3. Comparison of Peak Runoff
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schirmer, M.; Leschik, S.; Musolff, A. Current research in urban hydrogeology—A review. Adv. Water Resour. 2013, 51, 280–291. [Google Scholar] [CrossRef]
- Fletcher, T.; Andrieu, H.; Hamel, P. Understanding, management and modelling of urban hydrology and its consequences for receiving waters: A state of the art. Adv. Water Resour. 2013, 51, 261–279. [Google Scholar] [CrossRef]
- Montanari, A. Uncertainty of Hydrological Predictions. In Treatise on Water Science; Elsevier: Berlin, Germany, 2011; Volume 2, pp. 459–478. [Google Scholar]
- Shoaib, M.; Shamseldin, A.Y.; Khan, S.; Sultan, M.; Ahmad, F.; Sultan, T.; Dahri, Z.H.; Ali, I. Input Selection of Wavelet-Coupled Neural Network Models for Rainfall-Runoff Modelling. Water Resour. Manag. 2018, 33, 955–973. [Google Scholar] [CrossRef]
- Wang, Q.J.; Schepen, A.; Robertson, D. Merging Seasonal Rainfall Forecasts from Multiple Statistical Models through Bayesian Model Averaging. J. Clim. 2012, 25, 5524–5537. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Wagener, T. Hydrological Modeling. In Treatise on Water Science; Elsevier: Berlin, Germany, 2011; Volume 2, pp. 435–457. [Google Scholar]
- Nguyen, P.K.-T.; Chua, L.H.-C. The data-driven approach as an operational real-time flood forecasting model. Hydrol. Process. 2012, 26, 2878–2893. [Google Scholar] [CrossRef]
- Vermeulen, L.C.; Hofstra, N. Influence of climate variables on the concentration of Escherichia coli in the Rhine, Meuse, and Drentse Aa during 1985–2010. Reg. Environ. Chang. 2014, 14, 307–319. [Google Scholar] [CrossRef]
- Deo, R.C.; Şahin, M. Application of the Artificial Neural Network model for prediction of monthly Standardized Precipitation and Evapotranspiration Index using hydrometeorological parameters and climate indices in eastern Australia. Atmospheric Res. 2015, 161, 65–81. [Google Scholar] [CrossRef]
- Kuriqi, A.; Ardiclioglu, M. Investigation of hydraulic regime at middle part of the Loire River in context of floods and low flow events. Pollack Period. 2018, 13, 145–156. [Google Scholar] [CrossRef]
- Kuriqi, A.; Ardiçlioglu, M.; Muceku, Y. Investigation of seepage effect on river dike’s stability under steady state and transient conditions. Pollack Period. 2016, 11, 87–104. [Google Scholar] [CrossRef] [Green Version]
- Najafzadeh, M.; Niazmardi, S. A Novel Multiple-Kernel Support Vector Regression Algorithm for Estimation of Water Quality Parameters. Nonrenewable Resour. 2021, 30, 3761–3775. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Homaei, F.; Farhadi, H. Reliability assessment of water quality index based on guidelines of national sanitation foundation in natural streams: Integration of remote sensing and data-driven models. Artif. Intell. Rev. 2021, 54, 4619–4651. [Google Scholar] [CrossRef]
- Schaake, J.; Franz, K.; Bradley, A.; Buizza, R. The Hydrological Ensemble Prediction Experiment. Hydrol. Earth Syst. Sci. Discuss. 2006, 3, 3321–3332. [Google Scholar] [CrossRef]
- Coustau, M.; Rousset-Regimbeau, F.; Thirel, G.; Habets, F.; Janet, B.; Martin, E.; de Saint-Aubin, C.; Soubeyroux, J.-M. Impact of improved meteorological forcing, profile of soil hydraulic conductivity and data assimilation on an operational Hydrological Ensemble Forecast System over France. J. Hydrol. 2015, 525, 781–792. [Google Scholar] [CrossRef]
- Buizza, R.; Hollingsworth, A.; Lalaurette, F.; Ghelli, A. Probabilistic Predictions of Precipitation Using the ECMWF Ensemble Prediction System. Weather Forecast. 1999, 14, 168–189. [Google Scholar] [CrossRef]
- Bowler, N.E.; Arribas, A.; Mylne, K.R.; Robertson, K.B.; Beare, S.E. The MOGREPS short-range ensemble prediction system. Q. J. R. Meteorol. Soc. 2008, 134, 703–722. [Google Scholar] [CrossRef]
- Hamill, T.M.; Hagedorn, R.; Whitaker, J.S. Probabilistic forecast calibration using ECMWF and GFS ensemble reforecasts. Part II: Precipitation. Mon. Weather. Rev. 2008, 136, 2620–2632. [Google Scholar] [CrossRef] [Green Version]
- Dietterich, T.G. Ensemble methods in machine learning. In Proceedings of the First International Workshop, MCS 2000, Cagliari, Italy, 21–23 June 2000; pp. 1–15. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Freund, Y.; Schapiro, R.E. Experiments with a new boosting algorithm. In Proceedings of the Thirteenth International Conference on International Conference on Machine Learning, Bari, Italy, 3–6 July 1996; pp. 148–156. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Dietterich, T.G. Ensemble learning to appear. In The Handbook of Brain Theory and Networks, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Segal, M.R. Machine Learning Benchmarks and Random Forest Regression; Center for Bioinformatics and Molecular Biostatistics, University of California: San Francisco, CA, USA, 2003. [Google Scholar]
- Rezaeianzadeh, M.; Tabari, H.; Yazdi, A.A.; Isik, S.; Kalin, L. Flood flow forecasting using ANN, ANFIS and regression models. Neural Comput. Appl. 2014, 25, 25–37. [Google Scholar] [CrossRef]
- Huang, Z.X.; Jin, X.P. Basic hydrological Climate Prediction Theory and Application Technology; China Water Power Press: Beijing, China, 2005. (In Chinese) [Google Scholar]
- Supriya, P.; Krishnaveni, M.; Subbulakshmi, M. Regression Analysis of Annual Maximum Daily Rainfall and Stream Flow for Flood Forecasting in Vellar River Basin. Aquat. Procedia 2015, 4, 957–963. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef] [Green Version]
- French, M.N.; Krajewski, W.F.; Cuykendall, R.R. Rainfall forecasting in space and time using a neural network. J. Hydrol. 1992, 137, L-31. [Google Scholar] [CrossRef]
- Jain, A.; Kumar, A.M. Hybrid neural network models for hydrologic time series forecasting. Appl. Soft Comput. 2007, 7, 585–592. [Google Scholar] [CrossRef]
- Sarkara, A.; Pandey, P. River Water Quality Modelling Using Artificial Neural Network Technique. Aquat. Procedia 2015, 4, 1070–1077. [Google Scholar] [CrossRef]
- Kasiviswanathan, K.S.; Cibin, R.; Sudheer, K.P.; Chaubey, I. Constructing prediction interval for artificial neural network rainfall runoff models based on ensemble simulations. J. Hydrol. 2013, 499, 275–288. [Google Scholar] [CrossRef]
- Dawson, C.W.; Wilby, R. Hydrological modeling using artificial neural networks. Prog. Phys. Geogr. 2001, 25, 80–108. [Google Scholar] [CrossRef]
- O’Connell, P.E.; Nash, J.E.; Farrell, J.P. River flow forecasting through conceptual models part II—The Brosna catchment at Ferbane. J. Hydrol. 1970, 10, 317–329. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. Original. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Karunanithi, N.; Grenney, W.J.; Whitley, D.; Bovee, K. Neural Networks for River Flow Prediction. J. Comput. Civ. Eng. 1994, 8, 201–220. [Google Scholar] [CrossRef]
- Hu, T.S.; Lam, K.C.; Ng, S.T. River flow time series prediction with a range-dependent neural network. Hydrol. Sci. J. 2001, 46, 729–745. [Google Scholar] [CrossRef] [Green Version]
- Şahin, M.; Kaya, Y.; Uyar, M. Comparison of ANN and MLR models for estimating solar radiation in Turkey using NOAA/AVHRR data. Adv. Space Res. 2013, 51, 891–904. [Google Scholar] [CrossRef]
- Marla, C.; Soyoung, M.; Kim, L.H. Multiple linear regression models of urban runoff pollutant load and event, mean concentration considering rainfall variables. J. Environ. Sci. 2010, 22, 946–952. [Google Scholar]
- Anctil, F.; Tape, D.G. An exploration of artificial neural network rainfall-runoff forecasting combined with wavelet decomposition. J. Environ. Eng. Sci. 2004, 3, S121–S128. [Google Scholar] [CrossRef]
- Sinha, J.; Sahu, R.K.; Agarwal, A.; Pali, A.K.; Sinha, B.L. Rainfall-Runoff Modelling using Multi-Layer Perceptron Technique—A Case Study of the Upper Kharun Catchment in Chhattisgarh. J. Agric. Eng. 2013, 68, 132–140. [Google Scholar]
- Kim, Y.O.; Jeong, D.I.; Ko, I.H. Combining Rainfall-Runoff Model Outputs for Improving Ensemble Streamflow Prediction. J. Hydrol. Eng. 2006, 11, 578–588. [Google Scholar] [CrossRef]
- Viney, N.R.; Vaze, J.; Chiew, F.H.S.; Perraud, J.; Post, D.A.; Teng, J. Comparison of multi-model and multi-donor ensembles for regionalisation of runoff generation using five lumped rainfall-runoff models. In Proceedings of the 18th World IMACS Congress and MODSIM09 International Congress on Modelling and Simulation: Interfacing Modelling and Simulation with Mathematical and Computationalences, Cairns, Australia, 13–17 July 2009; Volume 1, pp. 3428–3434. [Google Scholar]

| Statistical Parameters | Daily Precipitation | Daily Evaporation | Daily Discharge | Daily High Temperature | Daily Low Temperature | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1991–1992 | 1993 | 1991–1992 | 1993 | 1991–1992 | 1993 | 1991–1992 | 1993 | 1991–1992 | 1993 | |
| Maximum | 119.9 | 81.8 | 12 | 12 | 684 | 525 | 41.6 | 40.1 | 27.3 | 26.7 |
| Minimum | 0 | 0 | 0 | 0 | 7.99 | 8.75 | 0.6 | 2.7 | −6.9 | −2.8 |
| Average | 2.484 | 2.793 | 3.591 | 3.021 | 33.129 | 39.144 | 22.785 | 21.951 | 12.545 | 12.351 |
| Standard deviation | 7.903 | 7.801 | 2.617 | 2.362 | 57.747 | 48.490 | 9.076 | 8.919 | 7.645 | 7.585 |
| Days in Advance | Daily Precipitation | Daily Evaporation | Daily Max Temperature | Daily Min Temperature | Daily Discharge |
|---|---|---|---|---|---|
| 1 | 0.6363 | 0.4617 | 0.6136 | 0.7239 | 0.8179 |
| 2 | 0.4023 | 0.6429 | 0.6355 | 0.6972 | 0.7031 |
| 3 | 0.4334 | 0.6551 | 0.6702 | 0.6459 | 0.6417 |
| 4 | 0.4120 | 0.7099 | 0.6572 | 0.6520 | 0.6654 |
| 5 | 0.3833 | 0.6929 | 0.5896 | 0.6261 | 0.6378 |
| 6 | 0.2968 | 0.6156 | 0.6430 | 0.7014 | 0.6069 |
| 7 | 0.4349 | 0.5853 | 0.6143 | 0.6652 | 0.6348 |
| 8 | 0.5257 | 0.7120 | 0.6215 | 0.7838 | 0.6557 |
| 9 | 0.4513 | 0.6944 | 0.5908 | 0.6674 | 0.6716 |
| 10 | 0.2847 | 0.5730 | 0.6954 | 0.6659 | 0.6994 |
| Models | Calibration | Verification | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Z | R2 | NE | RMSE | Z | R2 | NE | RMSE | ||
| Five factors | RTE | 0.6293 | 0.5562 | 0.5963 | 42.30 | 0.6028 | 0.3650 | 0.3450 | 40.76 |
| MLR | 0.5893 | 0.5210 | 0.4580 | 48.90 | 0.5536 | 0.2463 | 0.2891 | 41.25 | |
| ANN | 0.5900 | 0.5223 | 0.4230 | 46.65 | 0.5645 | 0.2866 | 0.2923 | 41.02 | |
| Four factors | RTE | 0.7273 | 0.6752 | 0.6725 | 32.96 | 0.6146 | 0.3777 | 0.3624 | 38.36 |
| MLR | 0.6608 | 0.4367 | 0.4325 | 43.40 | 0.5272 | 0.2780 | 0.2576 | 41.32 | |
| ANN | 0.6721 | 0.5036 | 0.4420 | 40.27 | 0.5341 | 0.2853 | 0.2840 | 41.11 | |
| Two factors | RTE | 0.7096 | 0.5031 | 0.5035 | 40.75 | 0.5429 | 0.2948 | 0.2894 | 40.83 |
| MLR | 0.6560 | 0.4303 | 0.4303 | 43.65 | 0.5229 | 0.2734 | 0.2704 | 41.45 | |
| ANN | 0.6691 | 0.4829 | 0.4351 | 40.30 | 0.5070 | 0.2571 | 0.2500 | 41.91 | |
| Daily precipitation | RTE | 0.6106 | 0.3728 | 0.3724 | 45.80 | 0.5569 | 0.3102 | 0.2931 | 40.38 |
| MLR | 0.5273 | 0.2780 | 0.2780 | 49.14 | 0.5590 | 0.3125 | 0.2983 | 43.32 | |
| ANN | 0.5368 | 0.2974 | 0.2891 | 46.29 | 0.5260 | 0.2767 | 0.2860 | 41.35 | |
| Daily discharge | RTE | 0.6936 | 0.4811 | 0.4807 | 41.65 | 0.5709 | 0.3259 | 0.3343 | 39.92 |
| MLR | 0.6263 | 0.3922 | 0.3299 | 45.08 | 0.5710 | 0.3261 | 0.3213 | 39.92 | |
| ANN | 0.6201 | 0.4065 | 0.3091 | 45.28 | 0.5716 | 0.3269 | 0.2967 | 39.90 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, A.; Fan, G.; Ding, X.; Huang, G. Regression Tree Ensemble Rainfall–Runoff Forecasting Model and Its Application to Xiangxi River, China. Water 2022, 14, 463. https://doi.org/10.3390/w14030463
Zhai A, Fan G, Ding X, Huang G. Regression Tree Ensemble Rainfall–Runoff Forecasting Model and Its Application to Xiangxi River, China. Water. 2022; 14(3):463. https://doi.org/10.3390/w14030463
Chicago/Turabian StyleZhai, Aifeng, Guohua Fan, Xiaowen Ding, and Guohe Huang. 2022. "Regression Tree Ensemble Rainfall–Runoff Forecasting Model and Its Application to Xiangxi River, China" Water 14, no. 3: 463. https://doi.org/10.3390/w14030463
APA StyleZhai, A., Fan, G., Ding, X., & Huang, G. (2022). Regression Tree Ensemble Rainfall–Runoff Forecasting Model and Its Application to Xiangxi River, China. Water, 14(3), 463. https://doi.org/10.3390/w14030463






