Abstract
Mathematical models have become an excellent tool to evaluate the characteristics and performance of Constructed Wetlands (CWs). They help to characterize the dynamics of pollutant removal in these systems. The aim of this research was to evaluate the kinetics of organic matter removal in CWs using two models: (i) the conventional first order model and (ii) the sigmoidal or k-n model. For this purpose, data from 41 CWs where domestic sewage is treated were used. The cluster analysis was performed to identify similar groups of CWs based on the estimation of model coefficients. According to the results obtained, the model that provides a better fit for the removal of organic matter in CWs is the sigmoidal-type. However, its “n” coefficient, which would represent an increase in resistance to degradation, remains a not totally explained variable. The sigmoidal or k-n model is promising, presenting good adjustment indices.
1. Introduction
Municipal sewerage produces a high amount of wastewater that has high concentrations of solids, organic substances, and nutrients. The disposal of this wastewater without the use of proper treating methods may cause contamination of fresh water bodies. Constructed wetlands (CWs) systems are a simple and low-cost alternative to treat wastewater and improve water quality [1,2,3,4,5].
CWs are nature-based wastewater treatment systems in which physical, chemical, and biological processes are carried out in parallel and simultaneously, and influence each other. Altogether, these processes assist in the removal of organic and inorganic contaminants present in wastewaters. Moreover, the microorganisms and aquatic macrophytes involved can remove and absorb pollutants and, as a result, obtain a substantial improvement in the removal efficiency of these systems [6,7,8,9].
One of the most commonly used types of CWs is the horizontal subsurface flow (HSSF) constructed wetland, because of advantages such as continuous feeding, and the decrease of contact by animals and insects with the wastewater, making it a poor environment for the proliferation of mosquitoes. Furthermore, when well-operated, they do not present a bad smell [10].
In order to understand the biological and chemical transformation and degradation that occurs in CWs, mathematical modeling can be utilized. Therefore, reliable mathematical models can be applied to evaluate and improve current knowledge. In order to obtain a desired organic matter concentration established by the laws and standards for wastewater discharge, the use of organic matter decay prediction equations has been widely adopted [11].
The use of numerical models to evaluate the CWs performance helps to understand the dynamics of the processes and the mechanisms to remove the contaminants involved in these systems. The more frequent models used in CWs design projects are based on first order equations. They predict an exponential decay between the inlet and outlet concentrations under permanent conditions of resident fluid, time, volume, and surface area necessary to achieve efficiency [12,13].
However, traditional first-order models are correlated with idealized theoretical hydrodynamics. They do not appropriately portray liquid behavior in the treatment system because they cannot effectively simulate flow anomalies. Moreover, these models do not reproduce the decrease in the biodegradability of the effluent throughout the treatment, do not take into account the fraction of the recalcitrant or non-removable residual effluent, and ignore the influence of factors such as evapotranspiration and precipitation [14].
In order to make the first order models represent reality, Brasil et al. [15] proposed a sigmoidal equation model in which the empirical coefficient (n) is added. According to these authors, although the coefficient (n) is a power of the hydraulic retention time (t), its inclusion is due to the need to consider the increased resistance to the degradation of organic material, and this varies according to the system configuration, the support media, and the type of wastewater to be treated [15].
Although new models have been developed to predict the removal of organic matter in CWs, the use of different empirical parameters can lead to inefficient practical results, since these variations cause different solutions in CW design projects. Different models applied to similar conditions give different configurations, which raises the question on whether there is a model that can accurately represent what occurs in these systems, and which one it is.
In order to validate these models, they must be evaluated with a large amount of CWs data [16]. Therefore, the aim of this research was to verify the kinetic study of first order models of organic matter removal from municipal wastewater in constructed wetlands systems.
2. Materials and Methods
For the development of this research, information from 41 horizontal subsurface flow constructed wetlands treating domestic sewage, operated in different countries, was used. The influent COD in these CWs ranged from 88 to 598 mg L−1. The characteristics analyzed for each system were: the season in which the experiment was conducted; type of influent sewage (raw or treated at primary level); vegetation (present or absent); total organic loading rate (OLR); hydraulic retention time (t); wetland length (L); length/width ratio (L/W); influent COD concentration (Co); type of porous substrate (gravel, crushed stone, river sand, steel slag); and treatment efficiency, represented by the remaining relative fraction (C⁄Co). Data from studies of these 41 CWs were published by nine different teams of authors [11,15,16,17,18,19,20,21,22,23]. When data were not directly available, the Digitizer tool from OriginPro software was used to obtain C or C/Co and t values throughout the profiles presented.
Two kinetic equations were used in this study: (a) the conventional first order equation and (b) the sigmoidal equation proposed by Brasil et al. [15]. The first order degradation kinetics (Equation (1)) described below represents the basic option for modeling CWs. The sigmoidal-type equation (Equation (2)) was used to correct the probable inadequacies of the first order model.
where: C is the resident liquid COD concentration at time “t”, Co is the influent COD concentration, k is the organic matter removal coefficient and t is the hydraulic retention time.
where: n is the dimensionless coefficient that represents the increase in resistance of the remaining organic material and the other variables were previously defined.
C/Co = exp(−k·t)
C/Co = exp(−k·tn)
The data obtained from C/Co along with the hydraulic retention time were used to obtain the organic matter removal coefficient (k) and the representative coefficient of the increase in the organic matter degradation resistance (n). The settings were performed in the OriginPro software with the generalized least squares method for non-linear regression models using Levenberg–Maquardt’s algorithm [24]. This algorithm provides a numerical solution for the problem of minimizing the non-linear function and it is dependent on several variables.
The cluster analysis was performed with the identification of groups of similar CWs based on the estimation of kinetic coefficients, applied OLR and HRT characteristics. Based on the cluster analysis, model comparisons were carried out in order to define which model fitted best for each group. These comparisons were made using the Akaike Information Criterion and standard error of the regression (SE) as a measure of how well the model fits the data. For the SE estimator, smaller values indicate that the observations are better, since they are closer to the adjusted line. The coefficients R² and adjusted R², despite having been obtained, were not considered in the present study, since Spiess and Neumeyer [25], found through simulations that these values are an unfavorable measure for describing the validity of a non-linear adjustment.
The values of the coefficients of the model that obtained the best fit according to AIC and SE were plotted and the trend lines were adjusted in order to assist in the identification of the behavior of the coefficients according to the variables. For these trends, no statistical analysis was performed due to the data showing wide variability.
3. Results and Discussion
3.1. Determining the Best Model
Table 1 shows the cluster analysis results as well as the respective OLR range and the number of elements in each group.

Table 1.
Cluster analysis results, OLR range and the number of elements in each group.
It can be seen from Table 1 that the cluster analysis resulted in five clusters divided according to their average OLR. For example, group 1 has an average OLR between 4~43 g m−3 d−1, presenting 14 CWs with similar characteristics to each other. Using the SE, we determined, within each group, the model (first order or sigmoidal) that showed the best fit (Table 2).

Table 2.
Best model for each group according to the standard errors of regression (SE) and their ranges.
The model that presented a better fit for most CWs was the sigmoidal-type model. Brasil et al. [15], using this model, concluded that the n coefficient circumvents inconveniences such as change of degradability over the CWs. This coefficient also provides for changes in hydrodynamics due to factors such as formation of dead zones near to the root zone of the plant, effect of the pollutants’ velocity and dispersion of pollutants into the wastewater [14]. The magnitude of n is a function of both variations of recalcitrant organic material and the degree of dispersion hydraulic system [15].
To understand better how the n coefficient relates to other CWs characteristics such as organic loading rate (OLR), volumetric rate decay coefficient (k), theoretical dispersion number (d), influent concentration (Co) and others, we performed a study using the information available in this work database. The characteristics that have identifiable relation with the n coefficient were OLR and Co, which are discussed below. Trend graphs of the n coefficient and these characteristics were made. Although for group 1, the first order model presented smaller SE ranges (Table 2), the values of the sigmoidal-type model fittings were also used for comparison with other four groups.
3.2. Relation between n Coeficcient and Organic Loading Rate (OLR)
Table 3 shows the ranges of n coefficient values and its respective means, geometric means and medians.

Table 3.
Ranges of n coefficient and its respective means, geometric means and medians.
According to Table 3, it is observed that for all groups formed, the median values of the coefficient n varied between 0.29 to 0.54, thus corroborating the values found by Hom et al. [26] and in the literature regarding the sigmoidal-type model, which are located in the same range, showing the tendency of this coefficient to be between 0 and 1. Figure 1 shows the association between the n coefficient and OLR.
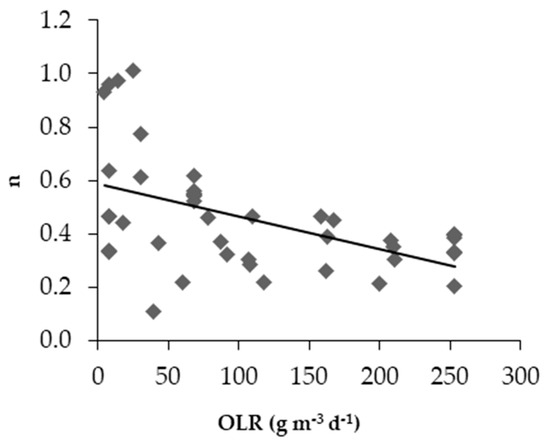
Figure 1.
Association (trend) between the n coefficient and total organic loading rate (as COD).
It can be observed from Figure 1 a slight tendency for the n coefficient to decrease as OLR increases, which also can be seen in Table 1, where for the group 5 (the highest values of OLR) n ranges are narrower when compared to group 1 (smaller OLR values). Chagas et al. [18] evaluated the kinetics of organic matter removal in HSSF constructed wetlands cultivated with yellow lilies submitted to different OLR and found n values from, 0.107 up to 0.448. Matos et al. [14] found n coefficients varying between 0.420~0.830 for different CWS with varying dimensions and widths. For these authors, the sigmoidal-type model, due to its simplicity and improvements in the representation of real behavior, should be the preferred model to describe the decay of organic matter from wastewater treated in HSSF CWs [14].
The tendency between the n coefficient and the OLR is inversely proportional. It shows that the increase of the influent loadings changes the environmental conditions, causing the microorganisms—which were initially considered in abundance—to become a limiting factor, while the organic material, a limiting factor for low organic loadings, begins to be in excess in the environment. Thus, it is believed that there will be an optimal organic loading rate value in which the CW will present a maximum efficiency. For OLR higher than this value, the efficiency of the CW will be reduced, since the microorganisms will be insufficient to degrade all the material present in the system. Factors such as influent concentration and climatic conditions will influence this optimum organic loading rate value. Finally, Fia et al. [27] also observed a reduction in the n value with the increase of OLR.
3.3. Association between n Coefficient and Inffluent COD Concentration (Co)
The initial hypotheses were: (i) the higher the influent concentration of sewage (Co), the higher its degradability, so, the n coefficient would not influence the decay profile, being close to 1.0; (ii) likewise, for low influent concentrations, degradability would be low, so the wastewater would be more recalcitrant, being the n coefficient low.
As noted in Figure 2, the association (trend) between the n coefficient and the influent COD concentration is inversely proportional, refuting the initial hypotheses. This may be due to the fact that, the higher the initial concentration, the higher the variety of substances (lipids, carbohydrates, proteins) with different values of k, highlighting the importance of the n coefficient, which in this case is low.
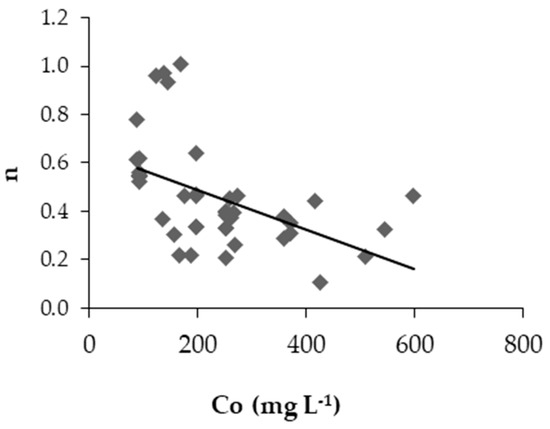
Figure 2.
Association (trend) between the n coefficient and Co (as chemical oxygen demand).
Likewise, for low initial concentrations, the degradability would be smaller and the organic material more recalcitrant. This would characterize the conditions of a pre-treated sewage (primary, secondary or tertiary effluent), in which there is remaining material that is more difficult to degrade, i.e., having a k value smaller and more uniform. For constant k values, the strength of n coefficient is smaller, since it does not have the need for large corrections for the k values, so, for these conditions, n approaches to the unit (1.0).
Matos et al. [28] observed graphically and using Pearson’s coefficient (−0.985) that the value of (n) is strongly associated with the deterioration grade of organic matter (OM). In summary, the greater the magnitude of variation in OM concentrations at the beginning of CWs, the lower the value of n.
3.4. Evaluation of Sigmoidal-Type Model
Hom et al. [26], Cerf [29], and Marugán et al. [30] used a model, similar to the sigmoidal-type model presented here, to study the kinetics of chlorine disinfection in the environment. They considered the existence of a factor that, over time, reduced the chlorine performance in the bacterial disinfection and, in the equation of Brasil et al. [15], this reduction occurs in the degradation of organic material present in the wastewater.
In studies conducted by Hom et al. [26], the equivalent values of n coefficient found ranged from 0.207 to 0.757. These values and the values found in literature for sigmoidal-type model are in the same range, showing the tendency of the n coefficient display a value between 0 and 1 (see Table 3).
Marugán et al. [30] cited the model of Hom et al. [26] presenting it as the sigmoidal-type model, and concludes that, for the case that n = 1, the equation is simplified, becoming the first order model. For n > 1, the model plays a concave curve (shoulder type behavior); while for n < 1, the graph reproduces a convex curve (tailing-off type behavior) (Figure 3).
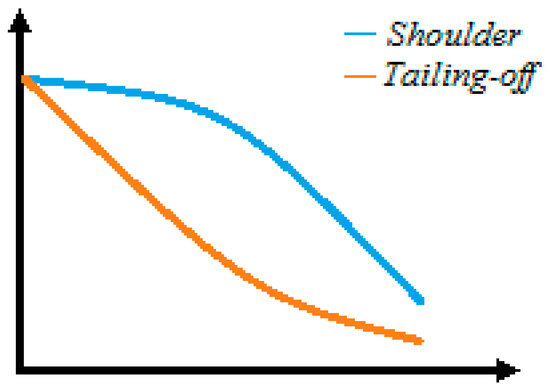
Figure 3.
Behavior of “shoulder” type and “tailing-off” type graphics according to n values.
Among those 41 CWs studied, only one (belonging to group 1) showed an n value slightly higher to a unit (1.01) (Table 3). The outlier labeling technique was used to see if this value would be an outlier, which did not occur, thus it cannot be ruled out. All other CWs presented n < 1, as the values obtained by Hom et al. [26]. Thus, the graph style that reflects this situation is the tailing-off (n < 1—concave curve), wherein the degradation is rapid initially, followed by a reduction in the rate which is influenced by the n coefficient, yielding a plateau. It demonstrates that, contrary to expectations, this model is not represented by a true sigmoidal decay curve, but a modified exponential decay curve. In fact, it would be sigmoidal in case the graph had presented both styles shoulder and tailing-off type.
Cerf [29] explained that, for the case where n < 1, the inactivation curve of microorganism by chorine can be explained by the hypothesis that the individuals of a population are not identical and that the distribution of their resistance is permanently (time-independent), or by the mechanistic concept. A similar analogy can be made for the case of the organic matter decay in CWs, since it is the degradation of various organic compounds (proteins, carbohydrates, lipids, persistent organic) which have a distinct resistance to decomposition.
Although in the beginning the least resistant substances are degraded with a higher rate and the recalcitrant compounds remain, this rate will reduce until it becomes zero. The global equations set for each of the groups are shown in Figure 4.
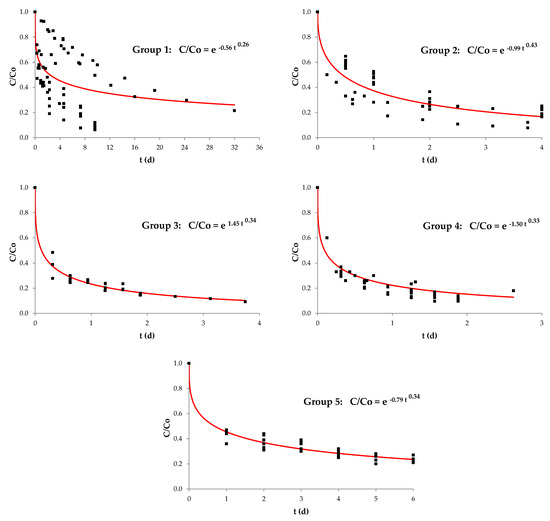
Figure 4.
Common equations for sigmoidal-type model for each group.
As shown in Figure 4, it appears that all groups clustered obtained a good global fit, since the estimated values are close to the line of trend. However, it is noted that group 1 was the least adequate when compared with the other groups formed.
4. Conclusions
The mathematical model with the best fit for removing organic matter in constructed wetlands systems is the k-n model, also known as the sigmoidal-type. This model has a coefficient whose nature has not yet been determined. However, the analyses indicated that there is a slight tendency of the n coefficient to decrease as OLR increases and that the higher the influent COD concentration on the CW, the smaller the value of the n coefficient. Due to the good fit indices, the k-n model can be considered as promising for use in constructed wetland systems.
Author Contributions
Conceptualization, A.C.B. and A.T.d.M.; data curation, B.S.S. and R.B.G.B.; investigation, B.S.S., A.C.B. and R.B.G.B.; methodology, A.C.B. and B.S.S.; resources, A.C.B.; supervision, A.C.B.; validation, A.T.d.M., F.F.e.S. and A.C.B.; writing—original draft, B.S.S. and R.B.G.B.; writing—review and editing, A.C.B., A.T.d.M. and F.F.e.S. All authors have read and agreed to the published version of the manuscript.
Funding
We acknowledge the Coordination for the Improvement of Higher Education Personnel (CAPES Finance Code 001) for funding this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, H.; Tang, W.; Wang, W.; Yin, W.; Liu, H.; Ma, X.; Zhou, Y.; Lei, P.; Wei, D.; Zhang, L.; et al. A Review on China’s Constructed Wetlands in Recent Three Decades: Application and Practice. J. Environ. Sci. 2021, 104, 53–68. [Google Scholar] [CrossRef] [PubMed]
- Ergaieg, K.; Ben Miled, T. Full-Scale Hybrid Constructed Wetlands Monitoring for Decentralized Tertiary Treatment of Municipal Wastewater. Arab. J. Geosci. 2021, 14, 1407. [Google Scholar] [CrossRef]
- Jiang, L.; Chui, T.F.M. A Review of the Application of Constructed Wetlands (CWs) and Their Hydraulic, Water Quality and Biological Responses to Changing Hydrological Conditions. Ecol. Eng. 2022, 174, 106459. [Google Scholar] [CrossRef]
- Sharma, R.; Malaviya, P. Constructed wetlands for textile wastewater remediation: A review on concept, pollutant removal mechanisms, and integrated technologies for efficiency enhancement. Chemosphere 2022, 290, 133358. [Google Scholar] [CrossRef] [PubMed]
- Parde, D.; Patwa, A.; Shukla, A.; Vijay, R.; Killedar, D.J.; Kumar, R. A review of constructed wetland on type, treatment and technology of wastewater. Environ. Technol. Innov. 2021, 21, 101261. [Google Scholar] [CrossRef]
- Fernandez-Gatell, M.; Corbella, C.; Sanchez-Vila, X.; Puigagut, J. Microbial activity enhancement in constructed wetlands operated as bioelectrochemical systems. Chemosphere 2022, 287, 132383. [Google Scholar] [CrossRef]
- Caselles-Osorio, A.; Vega, H.; Lancheros, J.C.; Casierra-Martínez, H.A.; Mosquera, J.E. Horizontal Subsurface-Flow Constructed Wetland Removal Efficiency Using Cyperus articulatus L. Ecol. Eng. 2017, 99, 479–485. [Google Scholar] [CrossRef]
- Türker, O.C.; Yakar, A. A Hybrid Constructed Wetland Combined with Microbial Fuel Cell for Boron (B) Removal and Bioelectric Production. Ecol. Eng. 2017, 102, 411–421. [Google Scholar] [CrossRef]
- Nivala, J.; Boog, J.; Headley, T.; Aubron, T.; Wallace, S.; Brix, H.; Mothes, S.; van Afferden, M.; Müller, R.A. Side-By-Side Comparison of 15 Pilot-Scale Conventional and Intensified Subsurface Flow Wetlands for Treatment of Domestic Wastewater. Sci. Total Environ. 2019, 658, 1500–1513. [Google Scholar] [CrossRef]
- Matos, A.T.; Matos, M.P. Disposição de Águas Residuárias no Solo e em Sistemas Alagados Construídos; Editora UFV: Viçosa, Brazil, 2017. [Google Scholar]
- Von Sperling, M.; de Paoli, A.C. First-Order COD Decay Coefficients Associated with Different Hydraulic Models Applied to Planted and Unplanted Horizontal Subsurface-Flow Constructed Wetlands. Ecol. Eng. 2013, 57, 205–209. [Google Scholar] [CrossRef]
- Ferreira, A.G.; Borges, A.C.; Rosa, A.P. Comparison of First-Order Kinetic Models for Sewage Treatment in Horizontal Subsurface-Flow Constructed Wetlands. Environ. Technol. 2020, 42, 4511–4518. [Google Scholar] [CrossRef] [PubMed]
- Ventura, D.; Rapisarda, R.; Sciuto, L.; Milani, M.; Consoli, S.; Cirelli, G.L.; Licciardello, F. Application of First-Order Kinetic Removal Models on Constructed Wetlands under Mediterranean Climatic Conditions. Ecol. Eng. 2022, 175, 106500. [Google Scholar] [CrossRef]
- Matos, A.T.; Matos, M.P.; Costa, R.A.; von Sperling, M. Influence of the Geometric Configuration of Unplanted Horizontal Subsurface Flow Constructed Wetlands in the Adjustment of Parameters of Organic Matter Decay Models. J. Water Process Eng. 2018, 22, 123–130. [Google Scholar] [CrossRef]
- Brasil, M.D.S.; Matos, A.T.; Silva, C.M.; Cecon, P.R.; Soares, A.A. Modeling of Pollution Removal in Constructed Wetlands with Horizontal Subsurface Flow. Agrartech. Forsch. (Agric. Eng. Res.) 2007, 13, 48–56. [Google Scholar]
- Giraldi, D.; de Michieli Vitturi, M.; Iannelli, R. Fitovert: A Dynamic Numerical Model of Subsurface Vertical Flow Constructed Wetlands. Environ. Model. Softw. 2010, 25, 633–640. [Google Scholar] [CrossRef]
- Villaseñor, J.; Mena, J.; Fernández, F.J.; Gómez, R.; de Lucas, A. Kinetics of Domestic Wastewater COD Removal by Subsurface Flow Constructed Wetlands Using Different Plant Species in Temperate Period. Int. J. Environ. Anal. Chem. 2011, 91, 693–707. [Google Scholar] [CrossRef]
- Chagas, R.C.; Matos, A.T.; Cecon, P.R.; Lo Monaco, P.A.V.; França, L.G.F. Cinética de Remoção de Matéria Orgânica em Sistemas Alagados Construídos Cultivados com Lírio Amarelo. Rev. Bras. Eng. Agrícola E Ambient. 2011, 15, 1186–1192. [Google Scholar] [CrossRef]
- Konnerup, D.; Koottatep, T.; Brix, H. Treatment of Domestic Wastewater in Tropical, Subsurface Flow Constructed Wetlands Planted with Canna and Heliconia. Ecol. Eng. 2009, 35, 248–257. [Google Scholar] [CrossRef]
- Trang, N.T.D.; Konnerup, D.; Schierup, H.-H.; Chiem, N.H.; Tuan, L.A.; Brix, H. Kinetics of Pollutant Removal from Domestic Wastewater in a Tropical Horizontal Subsurface Flow Constructed Wetland System: Effects of Hydraulic Loading Rate. Ecol. Eng. 2010, 36, 527–535. [Google Scholar] [CrossRef]
- Valentim, M.A.A. Desempenho de Leitos Cultivados (“Constructed Wetland”) para Tratamento de Esgoto: Contribuições para Concepção e Operação. Ph.D. Thesis, State University of Campinas, Campinas, Brazil, 2003. [Google Scholar]
- Sandoval-Cobo, J.J.; Peña, M.R. Análisis del Desempeño de un Humedal Artificial de Flujo Sub-Superficial en Zonas Tropicales Basado en Modelos Hidráulicos y una Cinética de Primer Orden. In Proceedings of the Seminario Manejo Integral de Aguas Residuales Domésticas—Conferencia Latino Americana (LATINOSAN), Cali, Colombia, 12–16 November 2007. [Google Scholar]
- Eustáquio Júnior, V.; Matos, A.T.; Lo Monaco, P.A.V.; Campos, L.C.; Borges, A.C. Efficiency of Constructed Wetland Systems Cultivated with Black Oats Treatment of Domestic Sewage. Acta Sci. Technol. 2012, 34, 391–398. [Google Scholar] [CrossRef]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. Anal. Lect. Notes Math. 1978, 630, 105–116. [Google Scholar] [CrossRef]
- Spiess, A.-N.; Neumeyer, N. An Evaluation of R2 as an Inadequate Measure for Nonlinear Models in Pharmacological and Biochemical Research: A Monte Carlo Approach. BMC Pharmacol. 2010, 10, 6. [Google Scholar] [CrossRef]
- Hom, L.W. Kinetics of Chlorine Disinfection in an Ecosystem. J. Sanit. Eng. Div. 1972, 98, 183–194. [Google Scholar] [CrossRef]
- Fia, F.R.L.; Matos, A.T.; Fia, R.; Borges, A.C.; Teixeira, D.L. Remoção de Matéria Orgânica e Determinação de Parâmetros Cinéticos em Sistemas Alagados Construídos em Escala Laboratorial. Acta Sci. Technol. 2012, 34, 149–156. [Google Scholar] [CrossRef][Green Version]
- Matos, A.T.; Matos, M.P.; Costa, R.A.; von Sperling, M. Influence Factors in the Adjustment of Parameters of the Modified First-Order Kinetics Equation Used to Model Constructed Wetland Systems. Acta Sci. Technol. 2019, 41, 36709. [Google Scholar] [CrossRef]
- Cerf, O. Tailing of Survival Curves of Bacterial Spores. J. Appl. Bacteriol. 1977, 42, 1–19. [Google Scholar] [CrossRef]
- Marugán, J.; van Grieken, R.; Sordo, C.; Cruz, C. Kinetics of the Photocatalytic Disinfection of Escherichia Coli Suspensions. Appl. Catal. B Environ. 2008, 82, 27–36. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).