Water Temperature Evolution Driven by Solar Radiation in an Ice-Covered Lake: A Numerical Study and Observational Data
Abstract
:1. Introduction
2. Observational Study
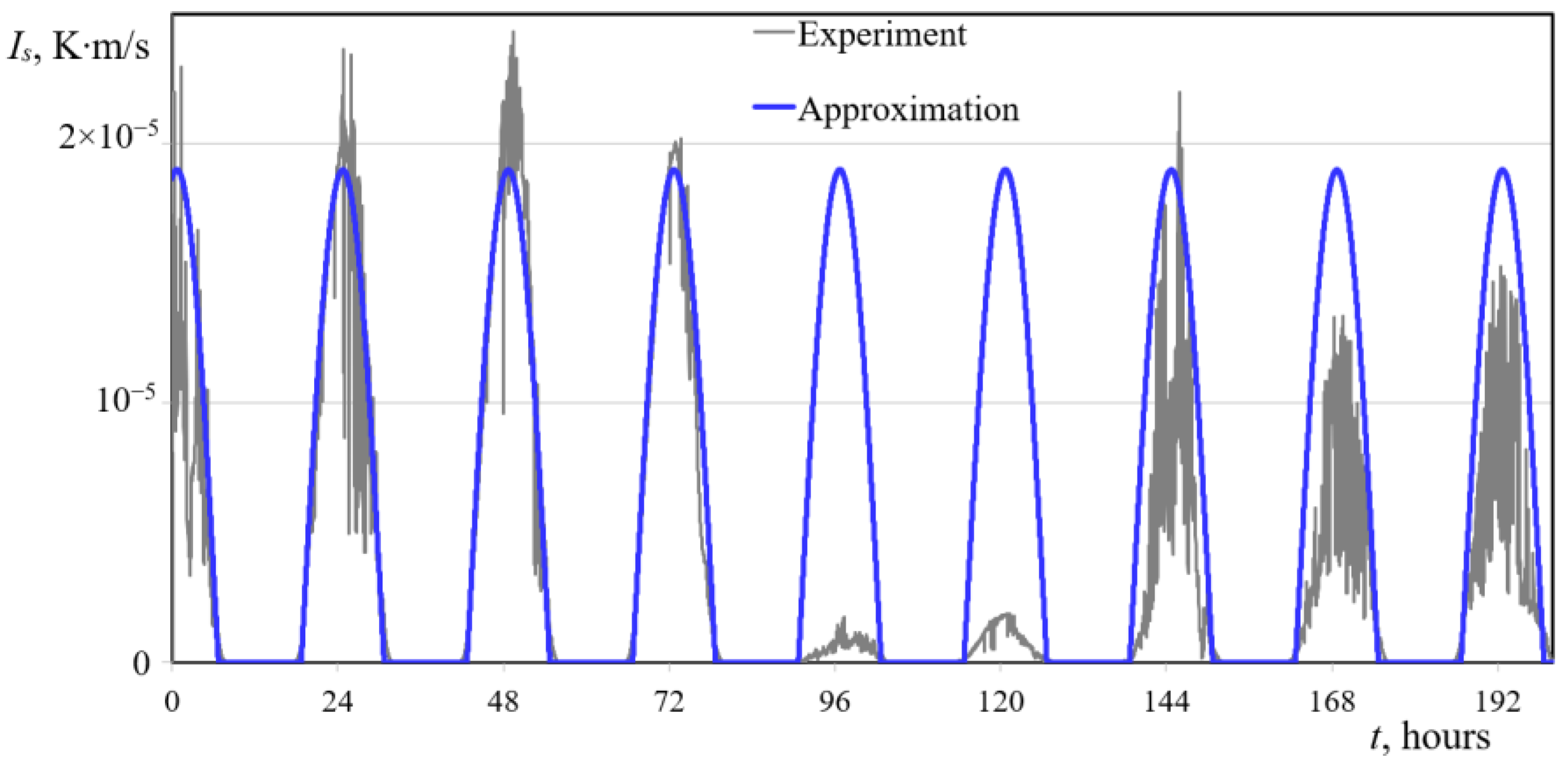
Field Measurements of Water Temperature and Solar Radiation
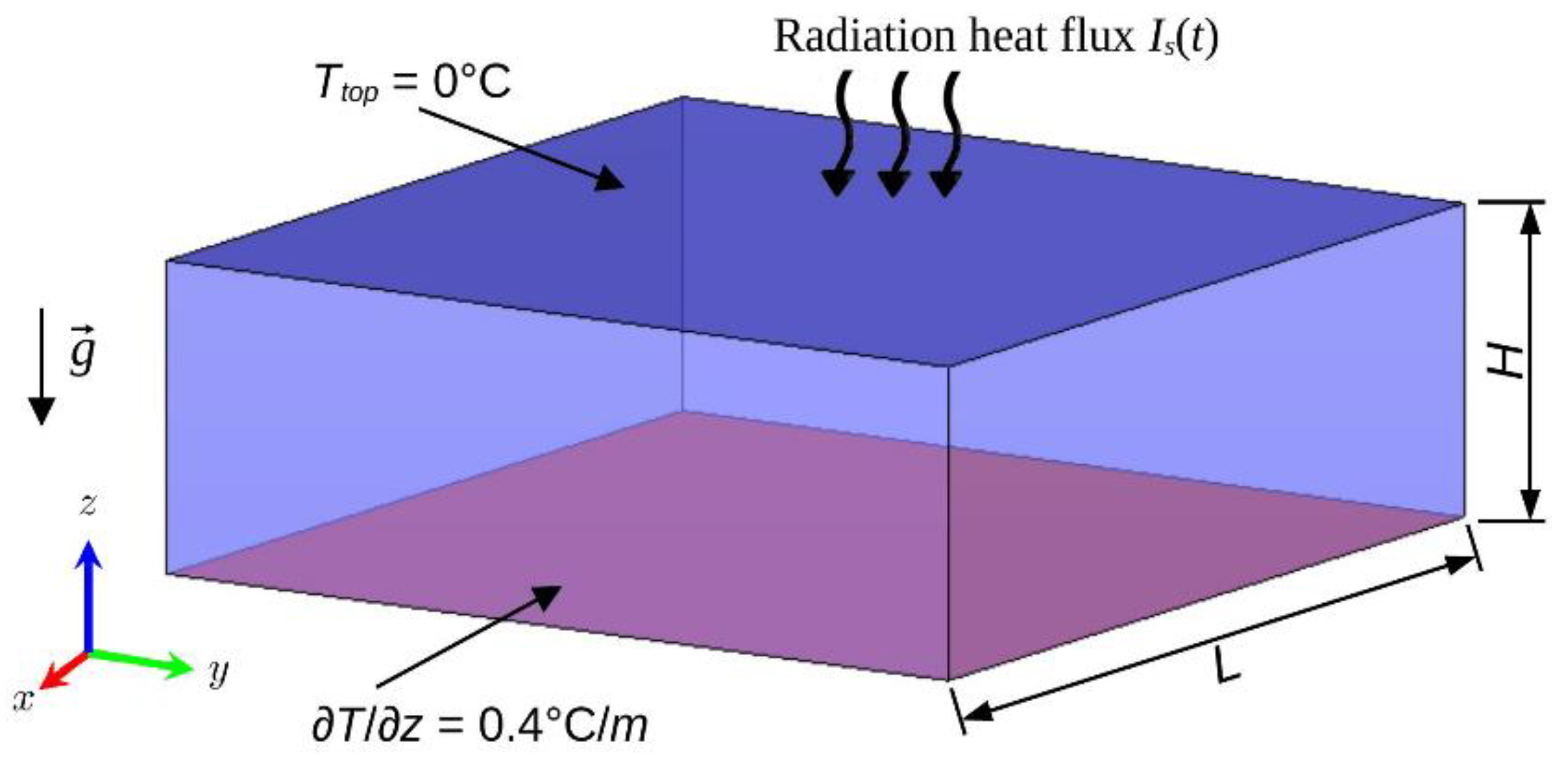
3. Computational Problem Definition
4. Computational Aspects
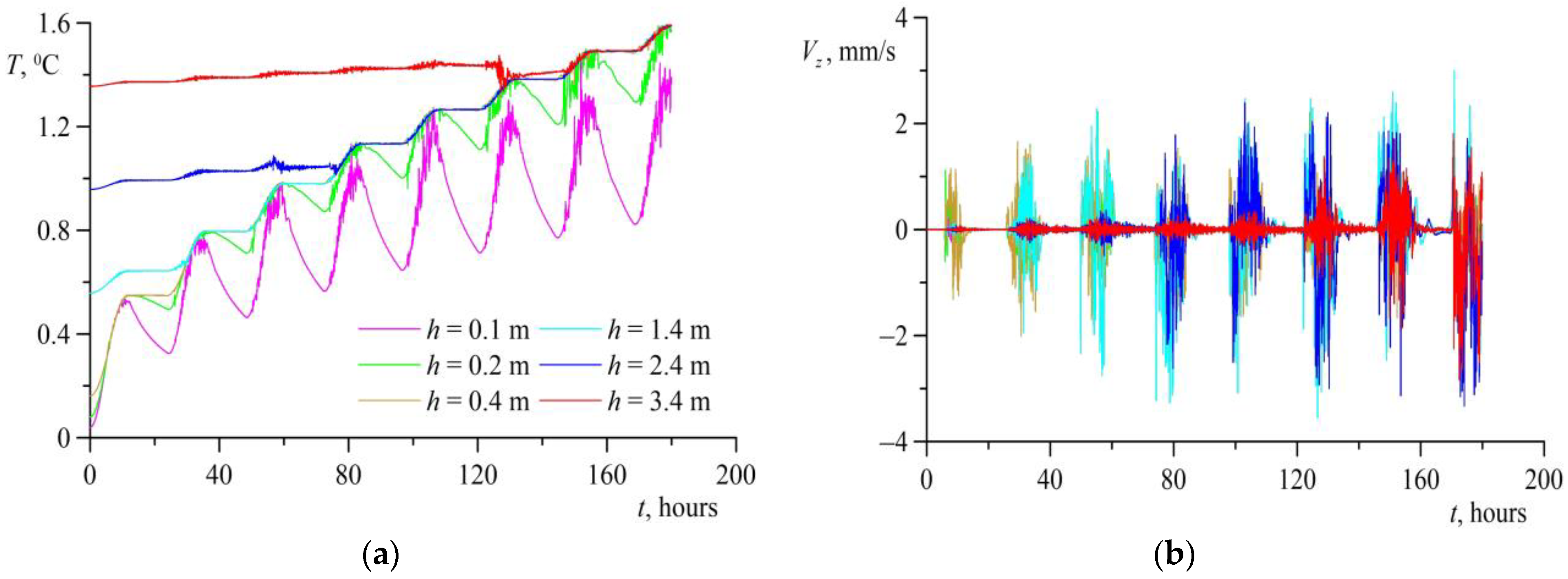
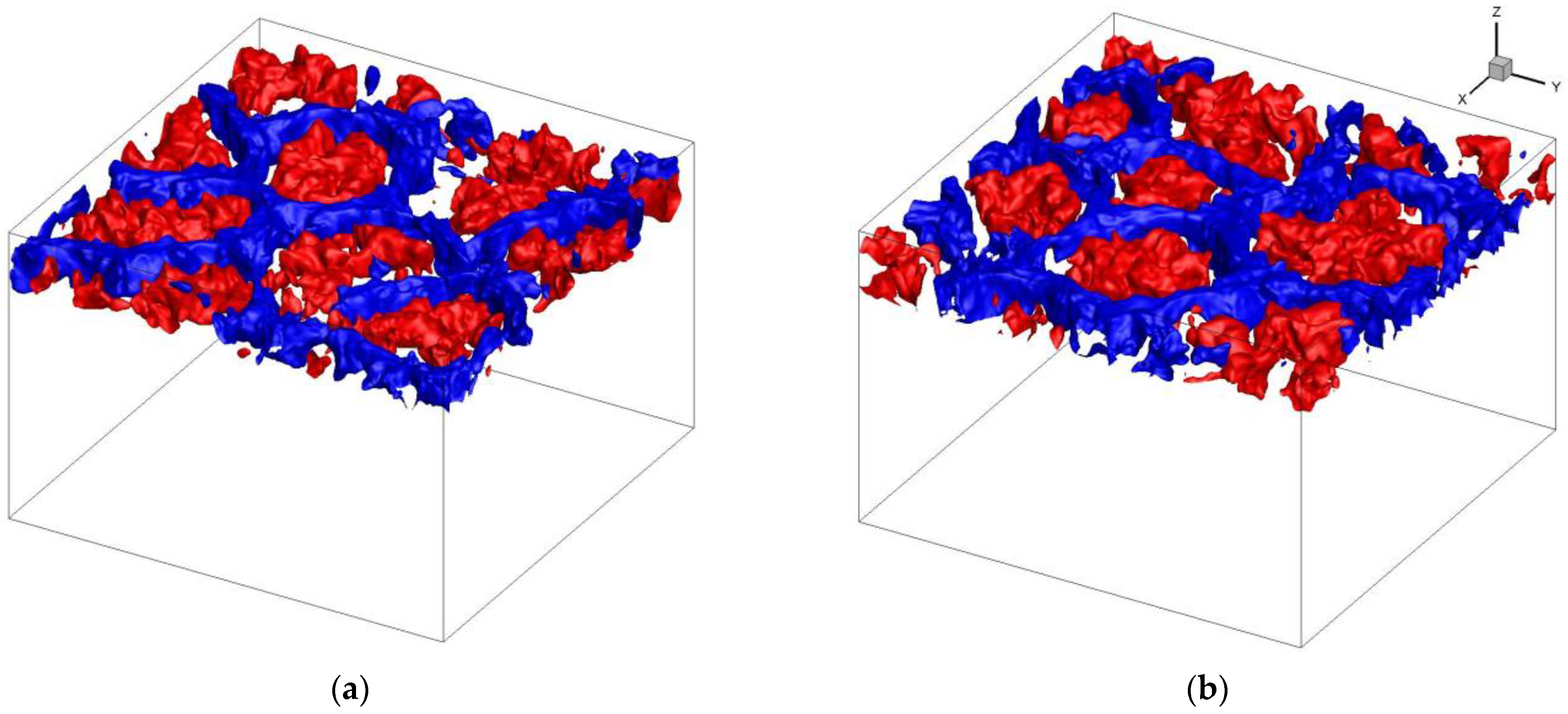
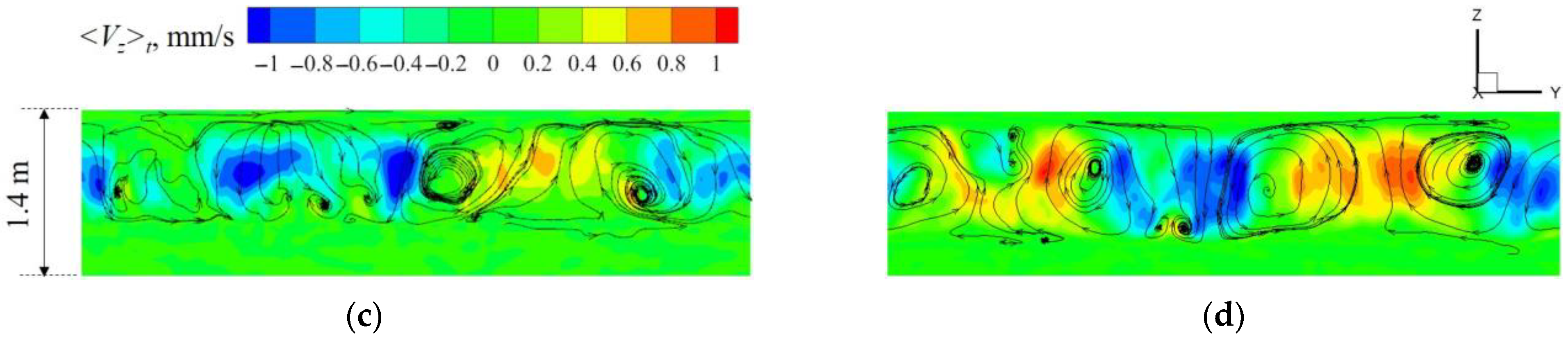
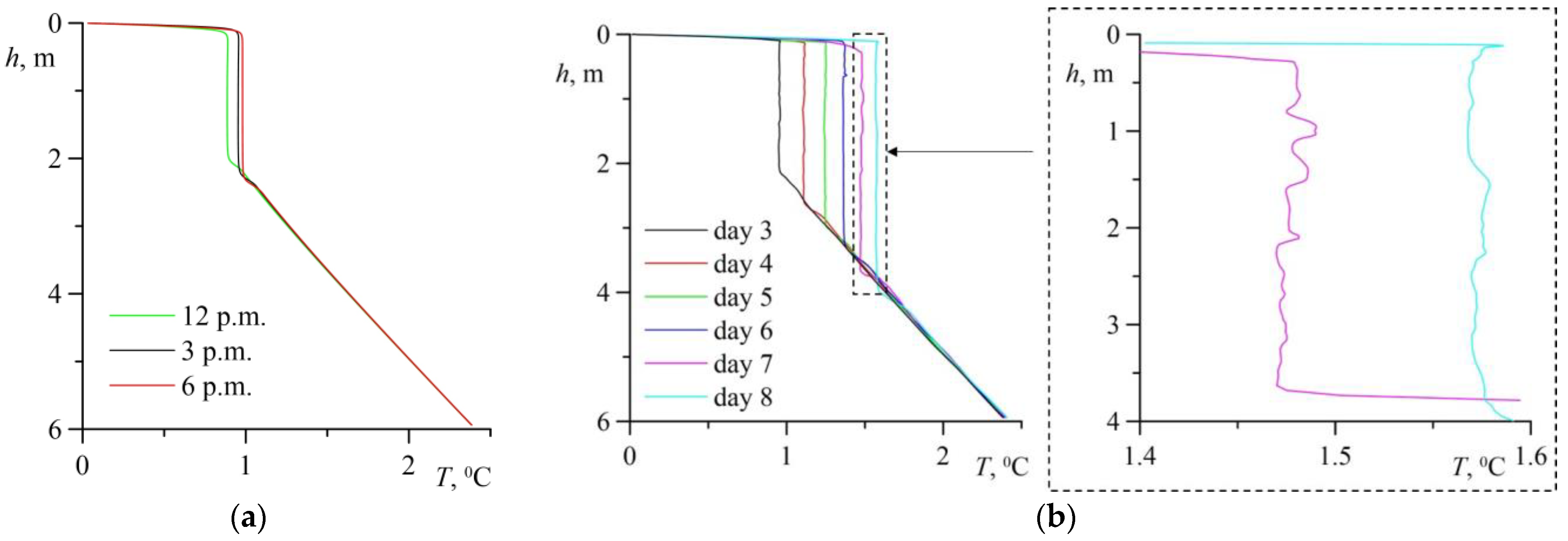
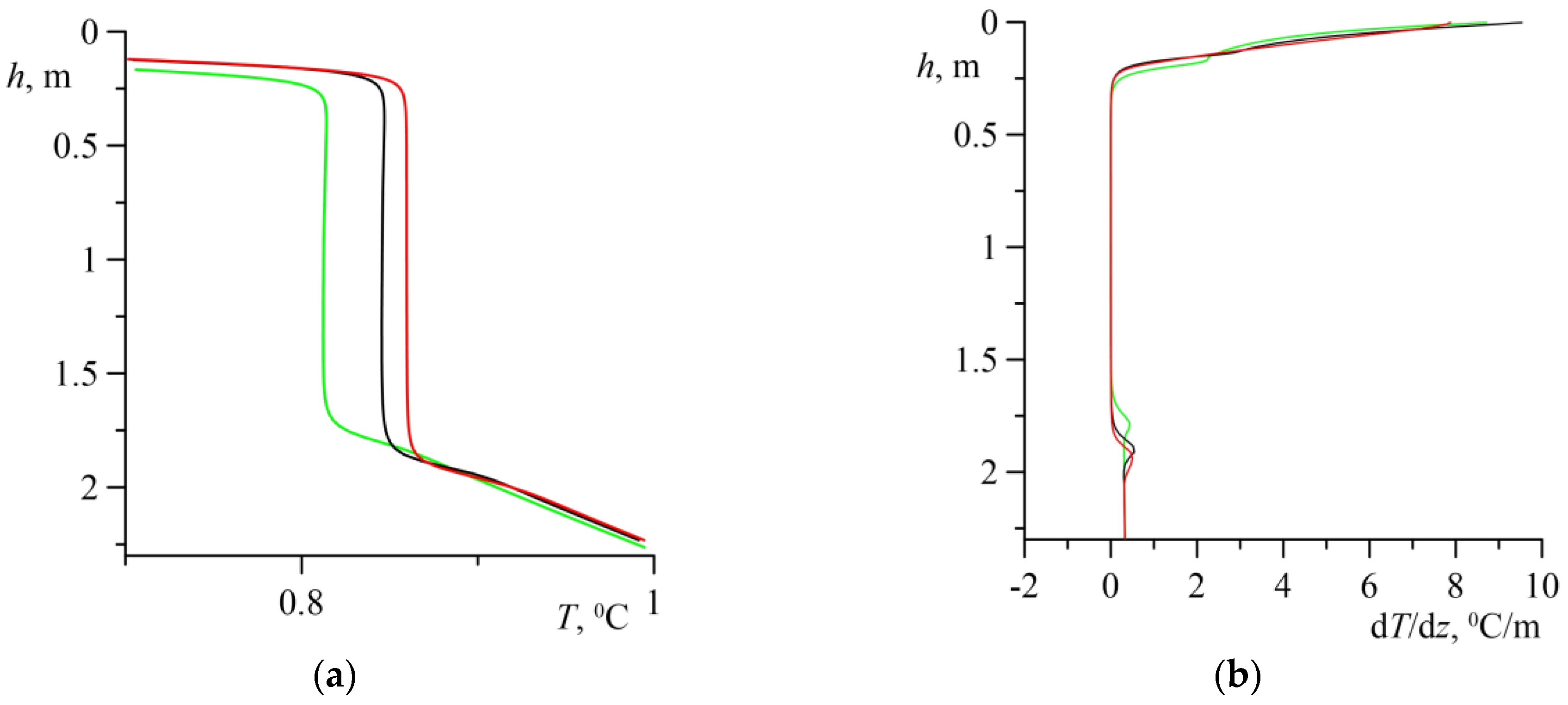
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kirillin, G.; Leppäranta, M.; Terzhevik, A.; Granin, N.; Bernhardt, J.; Engelhardt, C.; Efremova, T.; Golosov, S.; Palshin, N.; Sherstyankin, P.; et al. Physics of seasonally ice-covered lakes: A review. Aquat. Sci. 2012, 74, 659–682. [Google Scholar] [CrossRef]
- Bouffard, D.; Wüest, A. Convection in lakes. Annu. Rev. Fluid Mech. 2019, 51, 189–215. [Google Scholar] [CrossRef]
- Ozersky, T.; Bramburger, A.J.; Elgin, A.K.; Vanderploeg, H.A.; Wang, J.; Austin, J.A.; Carrick, H.J.; Chavarie, L.; Depew, D.C.; Fisk, A.T.; et al. The changing face of winter: Lessons and questions from the Laurentian Great Lakes. Geophys. Res. Biogeosci. 2021, 126, e2021JG006247. [Google Scholar] [CrossRef]
- Hampton, S.E.; Galloway, A.W.E.; Powers, S.M.; Ozersky, T.; Woo, K.H.; Batt, R.D.; Labou, S.G.; O’Reilly, C.M.; Sharma, S.; Lottig, N.R.; et al. Ecology under lake ice. Ecol. Lett. 2017, 20, 98–111. [Google Scholar] [CrossRef]
- Jansen, J.; MacIntyre, S.; Barrett, D.C.; Chin, Y.-P.; Cortés, A.; Forrest, A.L.; Hrycik, A.R.; Martin, R.; McMeans, B.C.; Rautio, M.; et al. Winter limnology: How do hydrodynamics and biogeochemistry shape ecosystems under ice? Geophys. Res. Biogeosci. 2021, 126, e2020JG006237. [Google Scholar] [CrossRef]
- Bengtsson, L.; Malm, J.; Terzhevik, A.; Petrov, M.; Boyarinov, P.; Glinsky, A.; Palshin, N. Field investigation of winter thermo- and hydrodynamics in a small Karelian lake. Limnol. Oceanogr. 1996, 41, 1502–1513. [Google Scholar] [CrossRef]
- Petrov, M.P.; Terzhevik, A.Y.; Zdorovennov, R.E.; Zdorovennova, G.E. Motion of water in an ice-covered shallow lake. Water Resour. 2007, 34, 113–122. [Google Scholar] [CrossRef]
- Forrest, A.L.; Laval, B.E.; Pieters, R.; Lim, D.S.S. Convectively driven transport in temperate lakes. Limnol. Oceanogr. 2008, 53, 2321–2332. [Google Scholar] [CrossRef] [Green Version]
- Kirillin, G.; Engelhardt, C.; Golosov, S.; Hintze, T. Basin-scale internal waves in the bottom boundary layer of ice-covered Lake Müggelsee, Germany. Aquat. Ecol. 2009, 43, 641–651. [Google Scholar] [CrossRef]
- Kirillin, G.B.; Forrest, A.L.; Graves, K.E.; Fischer, A.; Engelhardt, C.; Laval, B.E. Axisymmetric circulation driven by marginal heating in ice-covered lakes. Geophys. Res. Lett. 2015, 42, 2893–2900. [Google Scholar] [CrossRef]
- Ulloa, H.N.; Winters, K.B.; Wüest, A.; Bouffard, D. Differential heating drives downslope flows that accelerate mixed-layer warming in ice-covered waters. Geophys. Res. Lett. 2019, 46, 13872–13882. [Google Scholar] [CrossRef] [Green Version]
- Cortés, A.; MacIntyre, S. Mixing processes in small arctic lakes during spring. Limnol. Oceanogr. 2020, 65, 260–288. [Google Scholar] [CrossRef]
- Volkov, S.Y.; Bogdanov, S.R.; Zdorovennov, R.E.; Palshin, N.I.; Zdorovennova, G.E.; Efremova, T.V.; Gavrilenko, G.G.; Terzhevik, A.Y. Resonance Generation of Short Internal Waves by the Barotropic Seiches in an Ice-Covered Shallow Lake. Phys. Oceanogr. 2020, 27, 374–389. [Google Scholar] [CrossRef]
- Ramón, C.L.; Ulloa, H.N.; Doda, T.; Winters, K.B.; Bouffard, D. Bathymetry and latitude modify lake warming under ice. Hydrol. Earth Syst. Sci. 2021, 25, 1813–1825. [Google Scholar] [CrossRef]
- Castendyk, D.N.; Dugan, H.A.; Gallagher, H.A.; Pujara, N.; Doran, P.T.; Priscu, J.C.; Lyons, W.B. Barotropic seiches in a perennially ice-covered lake, East Antarctica. Limnol. Oceanogr. Lett. 2022, 7, 26–33. [Google Scholar] [CrossRef]
- Kelley, D. Convection in ice-covered lakes: Effects on algal suspension. J. Plankton Res. 1997, 19, 1859–1880. [Google Scholar] [CrossRef]
- Kiili, M.; Pulkkanen, M.; Salonen, K. Distribution and development of under-ice phytoplankton in 90-m deep water column of Lake Päijänne (Finland) during spring convection. Aquat. Ecol. 2009, 43, 707–713. [Google Scholar] [CrossRef]
- Vehmaa, A.; Salonen, K. Development of phytoplankton in Lake Pääjärvi (Finland) during under-ice convective mixing period. Aquat. Ecol. 2009, 43, 693–705. [Google Scholar] [CrossRef]
- Pernica, P.; North, R.L.; Baulch, H.M. In the cold light of day: The potential importance of under-ice convective mixed layers to primary producers. Inland Waters 2017, 7, 138–150. [Google Scholar] [CrossRef]
- Palshin, N.; Zdorovennova, G.; Zdorovennov, R.; Efremova, T.; Gavrilenko, G.; Terzhevik, A. Effect of Under-Ice Light Intensity and Convective Mixing on Chlorophyll a Distribution in a Small Mesotrophic Lake. Water Resour. 2019, 46, 384–394. [Google Scholar] [CrossRef]
- Terzhevik, A.; Palshin, N.; Golosov, S.; Zdorovennov, R.; Zdorovennova, G.; Mitrokhov, A.; Potakhin, M.; Shipunova, E.; Zverev, I. Hydrophysical aspects of oxygen regime formation in a shallow ice-covered lake. Water Resour. 2010, 37, 662–673. [Google Scholar] [CrossRef]
- Salmi, P.; Salonen, K. Regular build-up of the spring phytoplankton maximum before ice-break in a boreal lake. Limnol. Oceanogr. 2016, 61, 240–253. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.; Wells, M.G.; Li, J.; Young, J. Mixing, stratification, and plankton under lake-ice during winter in a large lake: Implications for spring dissolved oxygen levels. Limnol. Oceanogr. 2020, 65, 2713–2729. [Google Scholar] [CrossRef]
- Kirillin, G.; Shatwell, T.; Wen, L. Ice-covered lakes of Tibetan Plateau as solar heat collectors. Geophys. Res. Lett. 2021, 48, e2021GL093429. [Google Scholar] [CrossRef]
- Kirillin, G.; Aslamov, I.; Leppäranta, M.; Lindgren, E. Turbulent mixing and heat fluxes under lake ice: The role of seiche oscillations. Hydrol. Earth Syst. Sci. 2018, 22, 6493–6504. [Google Scholar] [CrossRef] [Green Version]
- Kirillin, G.; Aslamov, I.; Kozlov, V.; Zdorovennov, R.; Granin, N. Turbulence in the stratified boundary layer under ice: Observations from Lake Baikal and a new similarity model. Hydrol. Earth Syst. Sci. 2020, 24, 1691–1708. [Google Scholar] [CrossRef] [Green Version]
- Winters, K.B.; Ulloa, H.N.; Wüest, A.; Bouffard, D. Energetics of radiatively heated ice-covered lakes. Geophys. Res. Lett. 2019, 46, 8913–8925. [Google Scholar] [CrossRef]
- Kouraev, A.V.; Zakharova, E.A.; Rémy, F.; Kostianoy, A.G.; Shimaraev, M.N.; Hall, N.M.J.; Zdorovennov, R.E.; Suknev, A.Y. Giant ice rings on lakes and field observations of lens-like eddies in the Middle Baikal (2016–2017). Limnol. Oceanogr. 2019, 64, 2738–2754. [Google Scholar] [CrossRef]
- Farmer, D.M. Penetrative convection in the absence of mean shear. Q. J. R. Meteorol. Soc. 1975, 101, 869–891. [Google Scholar] [CrossRef]
- Mironov, D.V.; Terzhevik, A.Y. Spring Convection in Ice-Covered Freshwater Lakes. Izv. Atmos. Ocean. Phys. 2000, 36, 627–634. [Google Scholar]
- Mironov, D.; Terzhevik, A.; Kirillin, G.; Jonas, T.; Malm, J.; Farmer, D. Radiatively driven convection in ice-covered lakes: Observations, scaling, and a mixed layer model. J. Geophys. Res. 2002, 107, 7-1–7-16. [Google Scholar] [CrossRef]
- Jonas, T.; Terzhevik, A.Y.; Mironov, D.V.; Wüest, A. Radiatively driven convection in an ice-covered lake investigated by using temperature microstructure technique. J. Geophys. Res. 2003, 108, 3183. [Google Scholar] [CrossRef] [Green Version]
- Salonen, K.; Pulkkanen, M.; Salmi, P.; Griffiths, R. Interannual variability of circulation under spring ice in a boreal lake. Limnol. Oceanogr. 2014, 59, 2121–2132. [Google Scholar] [CrossRef]
- Zdorovennova, G.; Palshin, N.; Golosov, S.; Efremova, T.; Belashev, B.; Bogdanov, S.; Fedorova, I.; Zverev, I.; Zdorovennov, R.; Terzhevik, A. Dissolved Oxygen in a Shallow Ice-Covered Lake in Winter: Effect of Changes in Light, Thermal and Ice Regimes. Water 2021, 13, 2435. [Google Scholar] [CrossRef]
- Jewson, D.; Granin, N.; Zhdanov, A.; Gnatovsky, R. Effect of snow depth on under-ice irradiance and growth of Aulacoseira baicalensis in Lake Baikal. Aquat. Ecol. 2009, 43, 673–679. [Google Scholar] [CrossRef]
- Dombrovsky, L.A.; Kokhanovsky, A.A. Solar heating of icecovered lake and ice melting. J. Quant. Spectrosc. Radiat. Transf. 2023, 294, 108391. [Google Scholar] [CrossRef]
- Weyhenmeyer, G.A.; Obertegger, U.; Rudebeck, H.; Jakobsson, E.; Jansen, J.; Zdorovennova, G.; Bansal, S.; Block, B.D.; Carey, C.C.; Doubek, J.P.; et al. Towards critical white ice conditions in lakes under global warming. Nat. Commun. 2022, 13, 4974. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, Z.; Li, Z.; Leppäranta, M.; Arvola, L.; Song, S.; Huotari, J.; Lin, Z. Under-ice dissolved oxygen and metabolism dynamics in a shallow lake: The critical role of ice and snow. Water Resour. Res. 2021, 57, e2020WR027990. [Google Scholar] [CrossRef]
- Huang, W.; Zhao, W.; Zhang, C.; Leppäranta, M.; Li, Z.; Li, R.; Lin, Z. Sunlight penetration dominates the thermal regime and energetics of a shallow ice-covered lake in arid climate. Cryosphere 2022, 16, 1793–1806. [Google Scholar] [CrossRef]
- Kirillin, G.; Terzhevik, A. Thermal instability in freshwater lakes under ice: Effect of salt gradients or solar radiation? Cold Reg. Sci. Technol. 2011, 65, 184–190. [Google Scholar] [CrossRef]
- Yang, B.; Wells, M.G.; McMeans, B.C.; Dugan, H.A.; Rusak, J.A.; Weyhenmeyer, G.A.; Brentrup, J.A.; Hrycik, A.R.; Laas, A.R.; Pilla, M.; et al. A new thermal categorization of ice-covered lakes. Geophys. Res. Lett. 2021, 48, e2020GL091374. [Google Scholar] [CrossRef]
- Bouffard, D.; Zdorovennova, G.; Bogdanov, S.; Efremova, T.; Lavanchy, S.; Palshin, N.; Terzhevik, A.; Råman Vinnå, L.; Volkov, S.; Wüest, A.; et al. Under-ice convection dynamics in a boreal lake. Inland Waters 2019, 9, 142–161. [Google Scholar] [CrossRef] [Green Version]
- Bai, Q.; Li, R.; Li, Z.; Lepparanta, M.; Arvola, L.; Li, M. Time-series analyses of water temperature and dissolved oxygen concentration in Lake Valkea-Kotinen (Finland) during ice season. Ecol. Inform. 2016, 36, 181–189. [Google Scholar] [CrossRef]
- Block, B.D.; Denfeld, B.A.; Stockwell, J.D.; Flaim, G.; Grossart, H.-P.F.; Knoll, L.B.; Maier, D.B.; North, R.L.; Rautio, M.; Rusak, J.A.; et al. The unique methodological challenges of winter limnology. Limnol. Oceanogr. Methods 2019, 17, 42–57. [Google Scholar] [CrossRef] [Green Version]
- Mironov, D.V.; Danilov, S.D.; Olbers, D.J. Large-eddy simulation of radiatively-driven convection in ice covered lakes. In Proceedings of the Sixth Workshop on Physical Processes in Natural Waters; Casamitjana, X., Ed.; University of Girona: Girona, Spain, 2001; pp. 71–75. [Google Scholar]
- Smirnov, S.; Smirnovsky, A.; Bogdanov, S.; Zdorovennov, R.; Palshin, N.; Efremova, T.; Terzhevik, A.; Zdorovennova, G. The radiatively-driven turbulent convection in ice-covered lake: Numerical and observational study. In Proceedings of the EGU General Assembly 2022, Vienna, Austria, 23–27 May 2022. EGU22-9182. [Google Scholar] [CrossRef]
- Malm, J.; Terzhevik, A.; Bengtsson, L.; Boyarinov, P.; Glinsky, A.; Palshin, N.; Petrov, M. Temperature and salt content regimes in three shallow ice-covered lakes: 1. Temperature, salt content, and density structure. Nordic Hydrol. 1997, 28, 99–128. [Google Scholar] [CrossRef]
- Malm, J.; Terzhevik, A.; Bengtsson, L.; Boyarinov, P.; Glinsky, A.; Palshin, N.; Petrov, M. Temperature and salt content regimes in three shallow ice-covered lakes: 2. Heat and mass fluxes. Nordic Hydrol. 1997, 28, 129–152. [Google Scholar] [CrossRef]
- Volkov, S.; Bogdanov, S.; Zdorovennov, R.; Zdorovennova, G.; Terzhevik, A.; Palshin, N.; Bouffard, D.; Kirillin, G. Fine scale structure of convective mixed layer in ice-covered lake. Environ. Fluid Mech. 2019, 19, 751–764. [Google Scholar] [CrossRef] [Green Version]
- Zdorovennov, R.E.; Gavrilenko, G.G.; Zdorovennova, G.E.; Palshin, N.I.; Efremova, T.V.; Golosov, S.D.; Terzhevik, A.Y. Optical properties of Lake Vendyurskoe. Geogr. Environ. Sustain. 2016, 9, 74–87. [Google Scholar] [CrossRef]
- Bogdanov, S.R.; Zdorovennov, R.E.; Palshin, N.I.; Zdorovennova, G.E.; Terzhevik, A.Y.; Gavrilenko, G.G.; Volkov, S.Y.; Efremova, T.V.; Kuldin, N.A.; Kirillin, G.B. Deriving of Turbulent Stresses in a Convectively Mixed Layer in a Shallow Lake Under Ice by Coupling Two ADCPs. Fundam. Prikl. Gidrofiz. 2021, 14, 17–28. [Google Scholar] [CrossRef]
- Bogdanov, S.; Zdorovennov, R.; Palshin, N.; Zdorovennova, G. Deriving Six Components of Reynolds Stress Tensor from Single-ADCP Data. Water 2021, 13, 2389. [Google Scholar] [CrossRef]
- Bouffard, D.; Zdorovennov, R.; Zdorovennova, G.; Pasche, N.; Wüest, A.; Terzhevik, A. Ice-covered Lake Onega: Effects of radiation on convection and internal waves. Hydrobiologia 2016, 780, 21–36. [Google Scholar] [CrossRef]
- Bogdanov, S.; Zdorovennova, G.; Volkov, S.; Zdorovennov, R.; Palshin, N.; Efremova, T.; Terzhevik, A.; Bouffard, D. Structure and dynamics of convective mixing in Lake Onego under ice-covered conditions. Inland Waters 2019, 9, 177–192. [Google Scholar] [CrossRef] [Green Version]
- Couston, L.; Nandaha, J.; Favier, B. Competition between Rayleigh–Bénard and horizontal convection. J. Fluid Mech. 2022, 947, A13. [Google Scholar] [CrossRef]
- Smirnov, S.; Smirnovsky, A.; Bogdanov, S. The Emergence and Identification of Large-Scale Coherent Structures in Free Convective Flows of the Rayleigh-Bénard Type. Fluids 2021, 6, 431. [Google Scholar] [CrossRef]
- Volkov, S.Y.; Bogdanov, S.R.; Zdorovennova, G.E.; Zdorovennov, R.E.; Palshin, N.I.; Terzhevik, A.Y. Large-scale structure of convectively-mixed layer in a shallow ice-covered lake. Fundam. Prikl. Gidrofiz. 2019, 12, 30–39. [Google Scholar] [CrossRef]
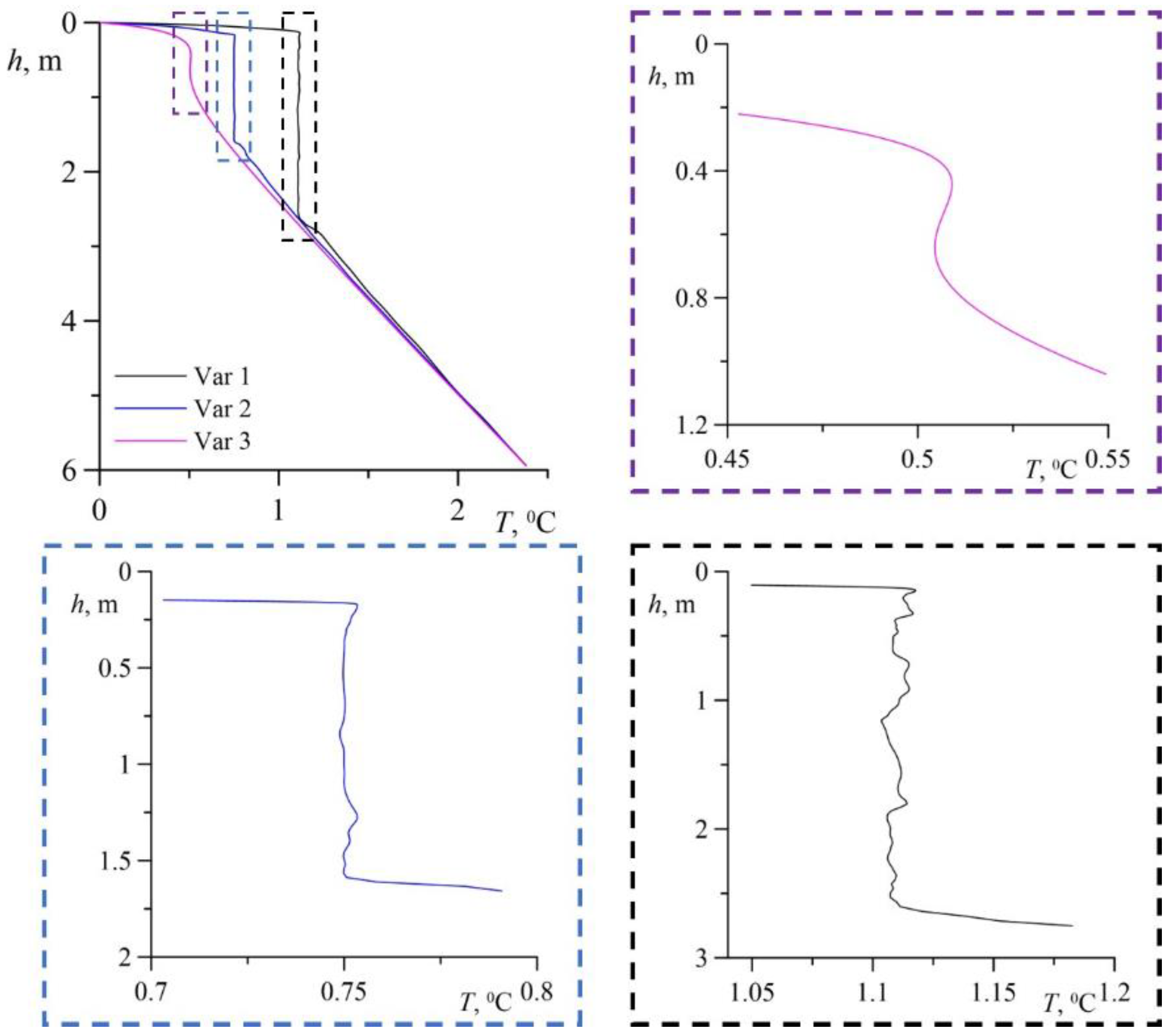


| Cases | I0, K·m/s |
|---|---|
| Variant 1 (initial) | 1.9 × 10−5 |
| Variant 2 | 0.95 × 10−5 |
| Variant 3 | 0.475 × 10−5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smirnov, S.; Smirnovsky, A.; Zdorovennova, G.; Zdorovennov, R.; Palshin, N.; Novikova, I.; Terzhevik, A.; Bogdanov, S. Water Temperature Evolution Driven by Solar Radiation in an Ice-Covered Lake: A Numerical Study and Observational Data. Water 2022, 14, 4078. https://doi.org/10.3390/w14244078
Smirnov S, Smirnovsky A, Zdorovennova G, Zdorovennov R, Palshin N, Novikova I, Terzhevik A, Bogdanov S. Water Temperature Evolution Driven by Solar Radiation in an Ice-Covered Lake: A Numerical Study and Observational Data. Water. 2022; 14(24):4078. https://doi.org/10.3390/w14244078
Chicago/Turabian StyleSmirnov, Sergei, Alexander Smirnovsky, Galina Zdorovennova, Roman Zdorovennov, Nikolay Palshin, Iuliia Novikova, Arkady Terzhevik, and Sergey Bogdanov. 2022. "Water Temperature Evolution Driven by Solar Radiation in an Ice-Covered Lake: A Numerical Study and Observational Data" Water 14, no. 24: 4078. https://doi.org/10.3390/w14244078





