Towards i5 Ecohydraulics: Field Determination of Manning’s Roughness Coefficient, Drag Force, and Macroinvertebrate Habitat Suitability for Various Stream Vegetation Types
Abstract
:1. Introduction
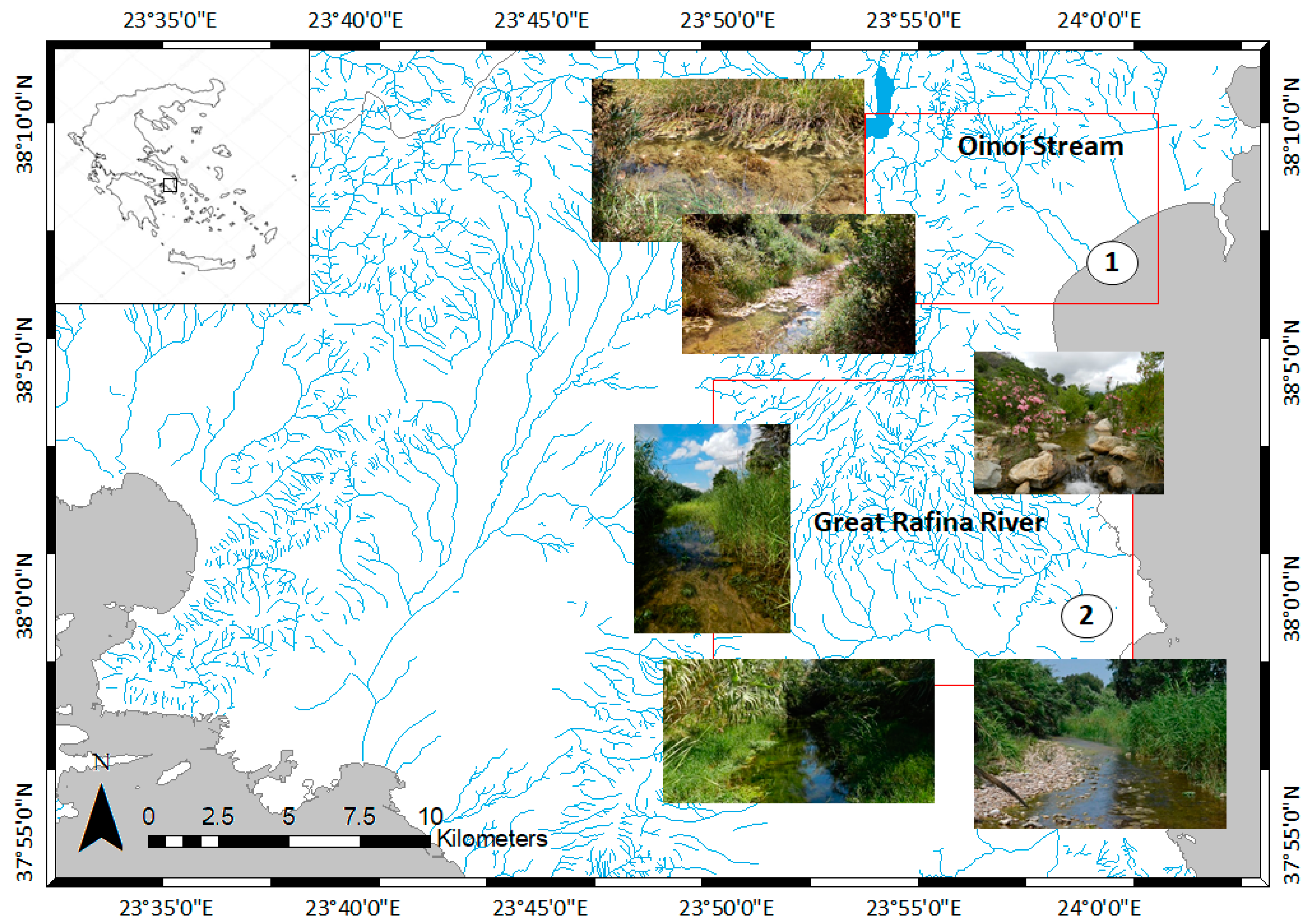
2. Materials and Methods
2.1. Presampling
2.2. Sampling
2.3. Postsampling Analysis
2.3.1. Manning’s Roughness Coefficients and Drag Force
2.3.2. Habitat Suitability
3. Results
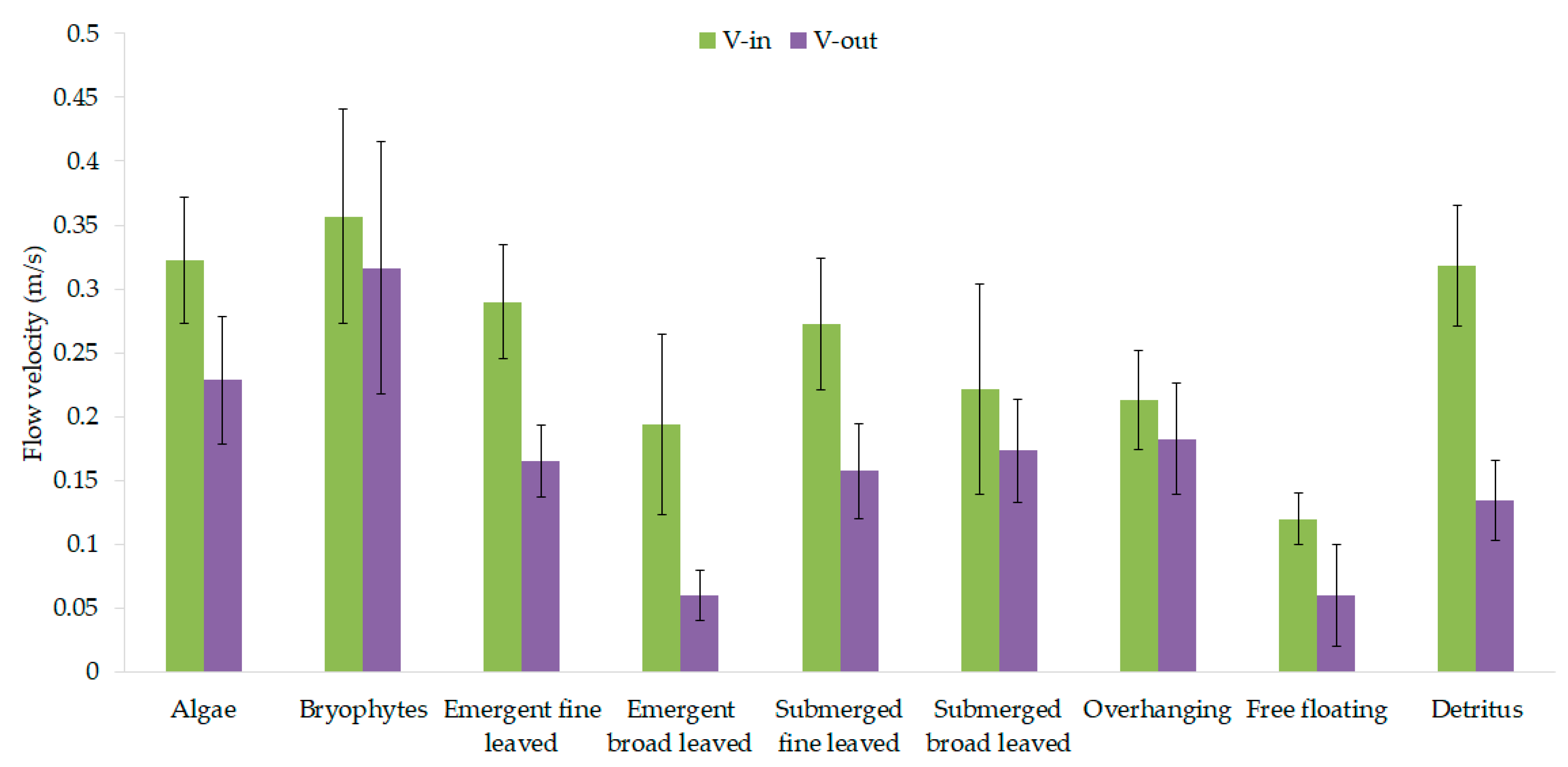
3.1. Vegetation-Adapted Manning’s Roughness Coefficients and Drag Force
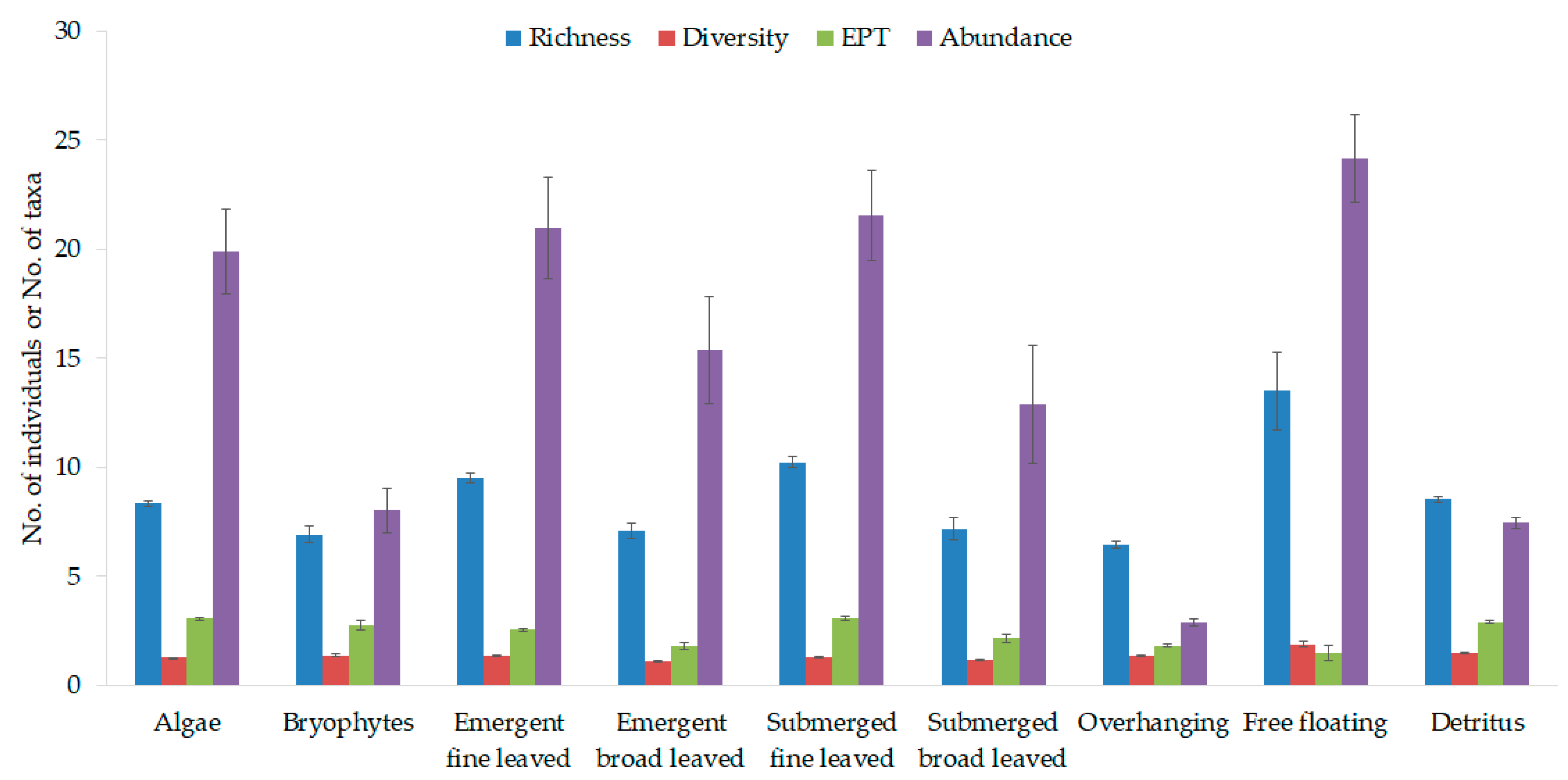
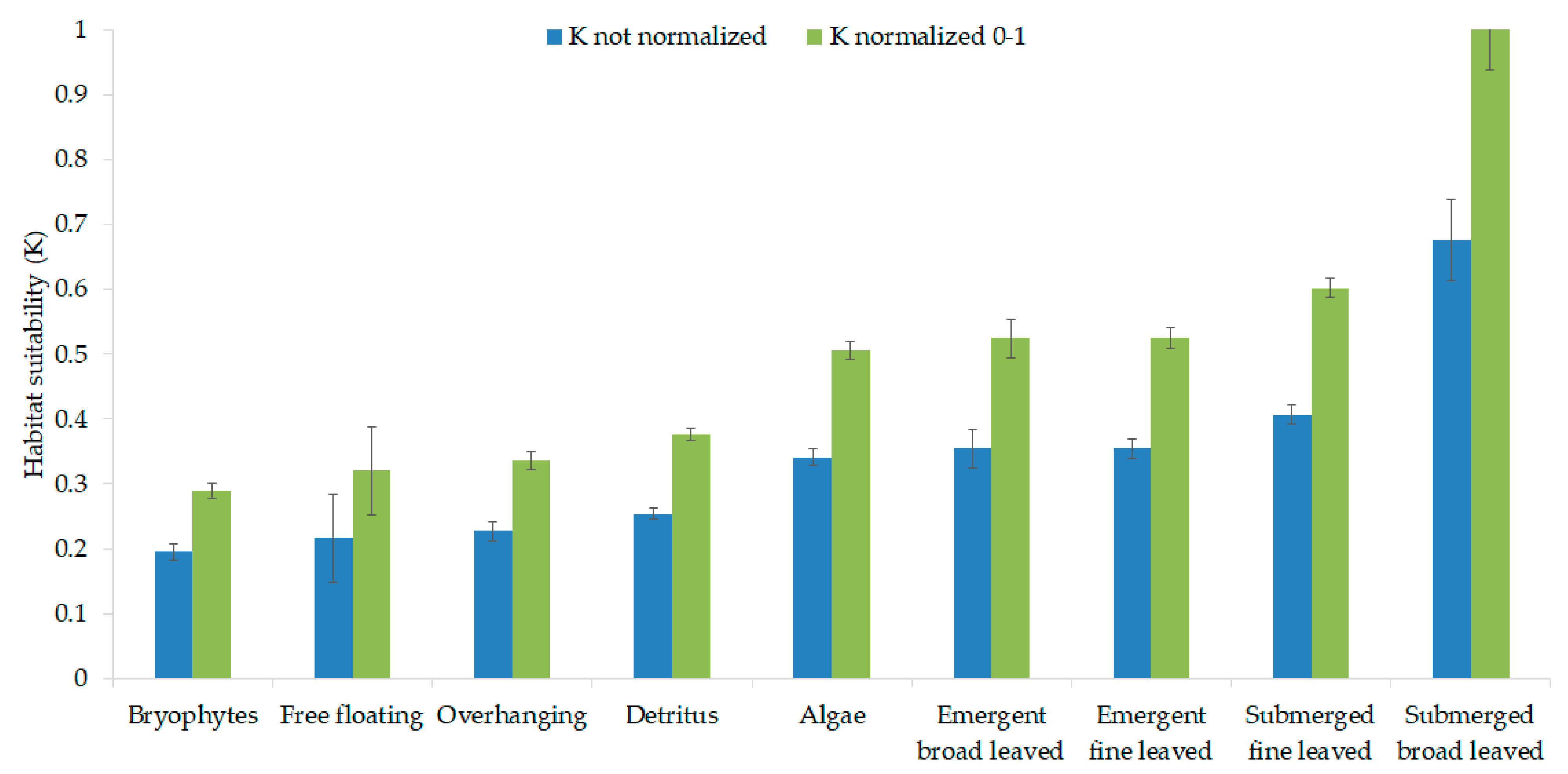
3.2. Macroinvertebrate Habitat Suitability of Various Stream Vegetation Types
4. Discussion
4.1. Parsimony and the Importance of Including Stream Vegetation in Ecohydraulic Models
4.2. How to Include Stream Vegetation in the Hydraulic Module
4.3. How to Include Stream Vegetation in the Habitat Module
4.4. i5 Ecohydraulics: Implications and Future Research
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Harlow, F.H. Fluid dynamics in Group T-3 Los Alamos National Laboratory (LA-UR-03-3852). J. Comput. Phys. 2004, 195, 414–433. [Google Scholar] [CrossRef] [Green Version]
- Theodoropoulos, C.; Skoulikidis, N.; Rutschmann, P.; Stamou, A. Ecosystem-based environmental flow assessment in a Greek regulated river with the use of 2D hydrodynamic habitat modelling. River Res. Appl. 2018, 34, 538–547. [Google Scholar] [CrossRef]
- Stuart, I.G.; Sharpe, C.P. Ecohydraulic model for designing environmental flows supports recovery of imperiled Murray cod (Maccullochella peelii) in the Lower Darling–Baaka River following catastrophic fish kills. Mar. Freshw. Res. 2021, 73, 247–258. [Google Scholar] [CrossRef]
- Hardy, T.; Kollaus, K.; Tolman, K.; Heard, T.; Howard, M. Ecohydraulics in applied river restoration: A case study in the San Marcos River, Texas, USA. J. Appl. Water Eng. Res. 2016, 4, 2–10. [Google Scholar] [CrossRef]
- Theodoropoulos, C.; Stamou, A.; Vardakas, L.; Papadaki, C.; Dimitriou, E.; Skoulikidis, N.; Kalogianni, E. River restoration is prone to failure unless pre-optimized within a mechanistic ecological framework|Insights from a model-based case study. Water Res. 2020, 173, 115550. [Google Scholar] [CrossRef] [PubMed]
- Vowles, A.; Eakins, L.R.; Piper, A.T.; Kerr, J.; Kemp, P.S. Developing realistic fish passage criteria: An ecohydraulics approach. In Ecohydraulics: An Integrated Approach; Maddock, I., Harby, A., Kemp, P., Wood, P.J., Eds.; Wiley-Blackwell: Chichester, UK, 2013; pp. 143–156. [Google Scholar]
- Mitsopoulos, G.; Theodoropoulos, C.; Papadaki, C.; Dimitriou, E.; Santos, J.M.; Zogaris, S.; Stamou, A. Model-based ecological optimization of vertical slot fishways using macroinvertebrates and multispecies fish indicators. Ecol. Eng. 2020, 158, 106081. [Google Scholar] [CrossRef]
- Maddock, I.; Harby, A.; Kemp, P.; Wood, P.J. Ecohydraulics: An Integrated Approach; Wiley and Sons: Chichester, UK, 2013. [Google Scholar]
- Zeiringer, B.; Seliger, C.; Greimel, F.; Schmutz, S. River hydrology, flow alteration, and environmental flow. In Riverine Ecosystem Management; Schmutz, S., Sendzimir, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 67–89. [Google Scholar]
- Acreman, M.C.; Dunbar, M.J. Defining environmental river flow requirements: A review. Hydrol. Earth Syst. Sci. 2004, 8, 861–876. [Google Scholar] [CrossRef]
- Gopal, B. Methodologies for the assessment of environmental flows. In Environmental Flows: An Introduction for Water Resources Managers; Gopal, B., Ed.; National Institute of Ecology: New Delhi, India, 2012. [Google Scholar]
- Vargas-Luna, A.; Crosato, A.; Uijttewaal, W.S.J. Effects of vegetation on flow and sediment transport: Comparative analyses and validation of predicting models. Earth Surf. Process. Landf. 2015, 40, 157–176. [Google Scholar] [CrossRef]
- Huttunen, K.L.; Mykrä, H.; Oksanen, J.; Astorga, A.; Paavola, R.; Muotka, T. Habitat connectivity and in-stream vegetation control temporal variability of benthic invertebrate communities. Sci. Rep. 2017, 7, 1448. [Google Scholar] [CrossRef] [Green Version]
- Tessier, C.; Cattaneo, A.; Pinel-Alloul, B.; Galanti, G.; Morabito, G. Biomass, composition and size structure of invertebrate communities associated to different types of aquatic vegetation during summer in Lago di Candia (Italy). J. Limnol. 2004, 63, 190–198. [Google Scholar] [CrossRef]
- Sun, X.; Shiono, K.; Rameshwaran, P.; Chandler, J.H. Modelling vegetation effects in irregular meandering river. J. Hydraul. Res. 2010, 48, 775–783. [Google Scholar] [CrossRef]
- Benifei, R.; Solari, L.; Vargas-Luna, A.; Geerling, G.; Van Oorschot, M. Effect of vegetation on floods: The case of river Magra. In Proceedings of the 36th IAHR World Congress, The Hague, The Netherlands, 28 June–3 July 2015. [Google Scholar]
- Theodoropoulos, C.; Syrmou, E.; Karaouzas, I.; Gritzalis, K.; Stamou, A. Simulated effects of streambed vegetation on river hydraulics and the habitat suitability of freshwater macroinvertebrates. In Proceedings of the 17th International Conference on Environmental Science and Technology, Athens, Greece, 1–4 September 2021. [Google Scholar]
- Lama, G.F.C.; Errico, A.; Francalanci, S.; Solari, L.; Chirico, G.B.; Preti, F. Hydraulic modeling of field experiments in a drainage channel under different riparian vegetation scenarios. In Innovative Biosystems Engineering for Sustainable Agriculture, Forestry and Food Production; Coppola, A., Di Renzo, G., Altieri, G., D’Antonio, P., Eds.; Springer: Cham, Switzerland, 2020; pp. 69–77. [Google Scholar]
- Lama, G.F.C.; Crimaldi, M.; Pasquino, V.; Padulano, R.; Chirico, G.B. Bulk drag predictions of riparian Arundo donax stands through UAV-acquired multispectral images. Water 2021, 13, 1333. [Google Scholar] [CrossRef]
- Lama, G.F.C.; Errico, A.; Pasquino, V.; Mirzaei, S.; Preti, F.; Chirico, G.B. Velocity uncertainty quantification based on riparian vegetation indices in open channels colonized by Phragmites australis. J. Ecohydraulics 2022, 7, 71–76. [Google Scholar] [CrossRef]
- Errico, A.; Lama, G.F.C.; Francalanci, S.; Chirico, G.B.; Solari, L.; Preti, F. Flow dynamics and turbulence patterns in a drainage channel colonized by common reed (Phragmites australis) under different scenarios of vegetation management. Ecol. Eng. 2019, 133, 39–52. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, H.; Jing, Y.; Wang, Z.; Ji, C.; Zhang, H. A study on Manning’s coefficient of rigid unsubmerged vegetation under open channel constant gradual flow condition. In Proceedings of the ASME 2010 International Mechanical Engineering Congress and Exposition, ASMEDC, Vancouver, BC, Canada, 12–18 November 2010. [Google Scholar]
- Fathi-Moghadam, M.; Kashefipour, M.; Ebrahimi, N.; Emamgholizadeh, S. Physical and numerical modeling of submerged vegetation roughness in rivers and flood plains. J. Hydrol. Eng. 2011, 16, 858–864. [Google Scholar] [CrossRef]
- Aberle, J.; Järvelä, J. Flow resistance of emergent rigid and flexible floodplain vegetation. J. Hydraul. Res. 2013, 51, 33–45. [Google Scholar] [CrossRef]
- Petryk, S.; Bosmajian, G. Analysis of flow through vegetation. J. Hydraul. Div. 1975, 101, 871–884. [Google Scholar] [CrossRef]
- Cantisani, A.; Giosa, L.; Mancusi, L.; Sole, A. FLORA-2D: A new model to simulate the inundation in areas covered by flexible and rigid vegetation. Int. J. Eng. Innov. Technol. 2014, 3, 179–186. [Google Scholar]
- Shields, F.D.; Coulton, K.G.; Nepf, H. Representation of Vegetation in Two-Dimensional Hydrodynamic Models. J. Hydraul. Eng. 2017, 143, 02517002. [Google Scholar] [CrossRef] [Green Version]
- Lama, G.F.C.; Errico, A.; Francalanci, S.; Solari, L.; Preti, F.; Chirico, G.B. Evaluation of flow resistance models based on field experiments in a partly vegetated reclamation channel. Geosciences 2020, 10, 47. [Google Scholar] [CrossRef] [Green Version]
- Lama, G.F.C.; Giovannini, R.M.; Errico, A.; Mirzaei, S.; Padulano, R.; Chirico, G.B.; Preti, F. Hydraulic efficiency of green-blue flood control scenarios for vegetated rivers: 1D and 2D unsteady simulations. Water 2021, 13, 2620. [Google Scholar] [CrossRef]
- Box, W.; Järvelä, J.; Västilä, K. Flow resistance of floodplain vegetation mixtures for modelling river flows. J. Hydrol. 2021, 601, 110467. [Google Scholar] [CrossRef]
- Lama, G.F.C.; Sadeghifar, T.; Azad, M.T.; Sihag, P.; Kisi, O. On the indirect estimation of wind wave heights over the southern coasts of Caspian Sea: A comparative analysis. Water 2022, 4, 843. [Google Scholar] [CrossRef]
- Sadeghifar, T.; Lama, G.F.C.; Sihag, P.; Bayram, A.; Kisi, O. Wave height predictions in complex sea flows through soft computing models: Case study of Persian Gulf. Ocean. Eng. 2022, 245, 110467. [Google Scholar] [CrossRef]
- Marjoribanks, T.I.; Hard, R.J.; Lane, S.N.; Tancock, M.J. Patch-scale representation of vegetation within hydraulic models. Earth Surf. Process. Landf. 2017, 42, 699–710. [Google Scholar] [CrossRef] [Green Version]
- Bovee, Κ.D. Development and Evaluation of Habitat Suitability Criteria for Use in the Instream Flow Incremental Methodology; Instream Flow Information Paper #21 FWS/OBS-86/7; USDI Fish and Wildlife Service: Washington, DC, USA, 1986.
- Muñoz-Mas, R.; Martínez-Capel, F.; Schneider, M.; Mouton, A.N. Assessment of brown trout habitat suitability in the Jucar River Basin (SPAIN): Comparison of data-driven approaches with fuzzy-logic models and univariate suitability curves. Sci. Total Environ. 2012, 440, 123–131. [Google Scholar] [CrossRef] [Green Version]
- Theodoropoulos, C.; Vourka, A.; Skoulikidis, N.; Rutschmann, P.; Stamou, A. Evaluating the performance of habitat models for predicting the environmental flow requirements of benthic macroinvertebrates. J. Ecohydraulics 2018, 3, 30–44. [Google Scholar] [CrossRef]
- Campaioli, S.; Ghetti, P.F.; Minelli, A. Manuale per il Riconoscimento dei Macroinvertebrati Delle Acque Dolci Italiane. Provincia Autonoma di Trento: Trento, Italy, 1994. [Google Scholar]
- Tachet, H.; Richoux, P.; Bournaud, M.; Usseglio-Polatera, P. Invertebres d’eau Douche: Systematique, Biologie, Ecologie; CNRS: Paris, France, 2010. [Google Scholar]
- Patsia, A.; Lazaridou, M. Water Quality through the Directive 2000/60 E.C.: Guide for Benthic Invertebrates of Running Waters of Greece; ION: Athens, Greece, 2011. [Google Scholar]
- Chow, V.T. Open Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Stamou, A.; Papadonikolaki, G.; Gkesouli, A. Modeling the flow in an experimental flume with submerged rigid elements. In Proceedings of the 2nd IAHR Europe Congress, Munich, Germany, 27–29 June 2012. [Google Scholar]
- Freeman, G.E.; Rahmeyer, W.; Copeland, R.R. Determination of Resistance Due to Shrubs and Woody Vegetation; ERDC/CHL TR-00-25, U.S. Army Engineer; Coastal and hydraulics Laboratory: Vicksburg, MS, USA, 2000. [Google Scholar]
- Hervouet, J.M. Hydrodynamics of Free Surface Flows: Modelling with the Finite Element Method; John Wiley & Sons Ltd.: Chichester, UK, 2007. [Google Scholar]
- Englund, G.; Malmqvist, B. Effects of flow regulation, habitat area and isolation on the macroinvertebrate fauna of rapids in North Swedish Rivers. Regul. Rivers Res. Manag. 1996, 12, 433–445. [Google Scholar] [CrossRef]
- Monk, W.A.; Wood, P.J.; Hannah, D.M.; Wilson, D.A.; Extence, C.A.; Chadd, R.P. Flow variability and macroinvertebrate community response within riverine systems. River Res. Appl. 2006, 22, 595–615. [Google Scholar] [CrossRef] [Green Version]
- Waddle, T.J.; Holmquist, J.G. Macroinvertebrate response to flow changes in a subalpine stream: Predictions from two-dimensional hydrodynamic models. River Res. Appl. 2011, 29, 366–379. [Google Scholar] [CrossRef] [Green Version]
- Holmquist, J.G.; Schmidt-Gengenbach, J.; Roche, J.W. Stream macroinvertebrates and habitat below and above two wilderness fords used by mules, horses, and hikers in Yosemite National Park. W. N. Am. Nat. 2015, 75, 311–324. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Paradis, E.; Blomberg, S.; Bolker, B.; Brown, J.; Claramunt, S.; Claude, J.; Cuong, H.S.; Desper, R.; Didier, G.; Durand, B.; et al. Ape: Analyses of Phylogenetics and Evolution. R package v5.6-2. Available online: https://cran.r-project.org/web/packages/ape/index.html (accessed on 11 October 2022).
- de Leeuw, J. Model selection in multinomial experiments. In On Model Uncertainty and Its Statistical Implications. Lecture Notes in Economics and Mathematical Systems; Dijkstra, T.K., Ed.; Springer Verlag: New York, NY, USA, 1988; pp. 118–138. [Google Scholar]
- Koutsoyiannis, D. Seeking parsimony in hydrology and water resources technology. European Geosciences Union General Assembly, Vienna, Austria. Geophys. Res. Abstr. 2009, 11, 11469. [Google Scholar]
- Dunbar, M.J.; Pedersen, M.L.; Cadman, D.; Extence, C.; Waddingham, J.; Chadd, R.; Larsen, S.E. River discharge and local-scale physical habitat influence macroinvertebrate LIFE scores. Freshw. Biol. 2010, 55, 226–242. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, L.; Bandini, F.; Kittel, C.M.M.; Balbarini, N.; Hansted, N.G.; Grosen, H.; Bauer-Gottwein, P. Spatio-temporally varying Strickler coefficient: A calibration approach applied to a Danish river using in-situ water surface elevation and UAS altimetry. J. Hydrol. 2022, 613, 128443. [Google Scholar] [CrossRef]
- Kittel, C.M.M.; Hatchard, S.; Neal, J.C.; Nielsen, K.; Bates, P.D.; Bauer-Gottwein, P. Hydraulic model calibration using CryoSat-2 observations in the Zambezi catchment. Water Resour. Res. 2021, 57, e2020WR029261. [Google Scholar] [CrossRef]
- Theodoropoulos, C.; Georgalas, S.; Mamassis, N.; Stamou, A.; Skoulikidis, N. Comparing environmental flow scenarios from hydrological methods, legislation guidelines and hydrodynamic habitat models downstream of the Marathon Dam (Attica, Greece). Ecohydrology 2018, 11, e2019. [Google Scholar] [CrossRef]
- Cowan, W.L. Estimating hydraulic roughness coefficients. Agric. Eng. 1956, 37, 473–475. [Google Scholar]
- Theodoropoulos, C.; Skoulikidis, N.; Stamou, A. Habfuzz: A tool to calculate the instream hydraulic habitat suitability using fuzzy logic and fuzzy Bayesian inference. J. Open Source Softw. 2016, 1, 82. [Google Scholar] [CrossRef]
- Díaz, R.G. Analysis of Manning coefficient for small-depth flows on vegetated beds. Hydrol. Process. 2005, 19, 3221–3233. [Google Scholar] [CrossRef]
- Ree, W.O.; Palmer, V.J. Flow of Water in Channels Protected by Vegetative Linings; Technical Bulletin; US Soil Conservation Service: Washington DC, USA, 1949; p. 119. [Google Scholar]
- Einstein, H.A.; Banks, R.B. Fluid resistance of composite roughness. Eos Trans. Am. Geophys. Union 1950, 31, 603–610. [Google Scholar] [CrossRef]
- Sayer, W.W. Roughness spacing in rigid open channels. J. Hydraul. Div. 1961, 87, 121–150. [Google Scholar] [CrossRef]

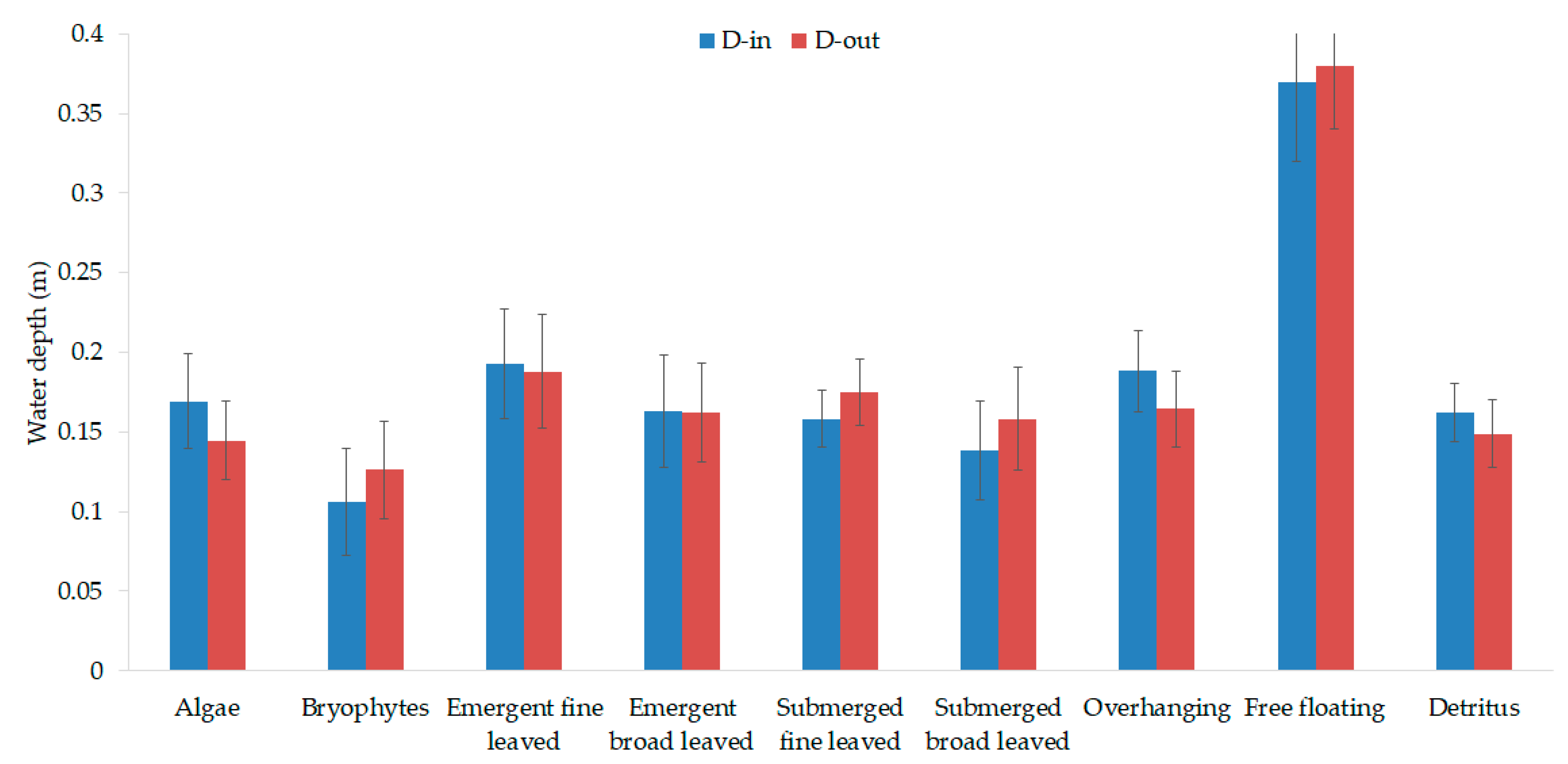
| Vegetation-Adapted Manning’s Roughness Coefficients (n) | |||||
|---|---|---|---|---|---|
| Veg. Type|Veg. Density | Dense (80% < d ≤ 100%) | Moderate (50% < d ≤ 80%) | Sparse (0% < d ≤ 50%) | Average | |
| Algae | n/a | n/a | n/a | n/a | |
| Group 1: Emergent vegetation | Emergent fine-leaved | 0.042 (6) | 0.042 (6) | 0.034 (6) | 0.038 (12) |
| Emergent broad-leaved | 0.052 (1) | 0.048 (2) | 0.034 (4) | 0.039 (6) | |
| Overhanging | 0.047 (5) | 0.045 (9) | 0.036 (7) | 0.041 (16) | |
| Group 1 average | 0.047 (12) | 0.045 (17) | 0.035 (17) | 0.039 (34) | |
| Group 2: Submerged vegetation | Submerged fine-leaved | 0.052 (7) | 0.049 (9) | 0.046 (6) | 0.048 (15) |
| Submerged broad-leaved | 0.049 (1) | 0.049 (1) | 0.038 (4) | 0.040 (5) | |
| Bryophytes | 0.032 (5) | 0.031 (6) | 0.028 (4) | 0.029 (10) | |
| Group 2 average | 0.044 (13) | 0.043 (16) | 0.037 (14) | 0.039 (30) | |
| Free-floating | n/a | n/a | n/a | n/a | |
| Detritus | n/a | n/a | n/a | n/a | |
| Vegetation-Adapted Drag Force (FD) | |||||
|---|---|---|---|---|---|
| Veg. Type | Veg. Density | Dense (80% < d ≤ 100%) | Moderate (50% < d ≤ 80%) | Sparse (0% < d ≤ 50%) | Average | |
| Algae | n/a | n/a | n/a | n/a | |
| Group 1: Emergent vegetation | Emergent fine-leaved | 0.707 (6) | 0.707 (6) | 0.412 (6) | 0.559 (12) |
| Emergent broad-leaved | n/a | 0.144 (2) | 0.141 (4) | 0.142 (6) | |
| Overhanging | 0.252 (5) | 0.252 (9) | 0.352 (7) | 0.302 (16) | |
| Group 1 average | 0.478 (11) | 0.367 (17) | 0.301 (17) | 0.334 (34) | |
| Group 2: Submerged vegetation | Submerged fine-leaved | 0.783 (7) | 0.760 (9) | 0.251 (6) | 0.505 (15) |
| Submerged broad-leaved | 0.016 (1) | 0.016 (1) | 0.045 (4) | 0.030 (5) | |
| Bryophytes | 0.592 (5) | 0.339 (6) | 0.385 (4) | 0.029 (10) | |
| Group 2 average | 0.463 (13) | 0.371 (16) | 0.227 (14) | 0.362 (30) | |
| Free-floating | n/a | n/a | n/a | n/a | |
| Detritus | n/a | n/a | n/a | n/a | |
| Vegetation-Adapted Macroinvertebrate Habit Suitability | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Veg. Type | Unvegetated | Algae | Bryophytes | SFL | SBL | EFL | EBL | Overhanging | Free-Floating | Detritus | |
| Substrate | |||||||||||
| Silt | 0.30 | 0.64 | 0.50 | 0.71 | 0.98 | 0.65 | 0.65 | 0.53 | 0.52 | 0.55 | |
| Sand | 0.45 | 0.79 | 0.64 | 0.85 | 1.00 | 0.80 | 0.80 | 0.67 | 0.66 | 0.70 | |
| Fine gravel | 0.37 | 0.71 | 0.57 | 0.78 | 1.00 | 0.72 | 0.72 | 0.60 | 0.59 | 0.62 | |
| Medium gravel | 0.54 | 0.88 | 0.74 | 0.95 | 1.00 | 0.90 | 0.90 | 0.77 | 0.76 | 0.80 | |
| Large gravel | 0.66 | 1.00 | 0.85 | 1.00 | 1.00 | 1.00 | 1.00 | 0.88 | 0.87 | 0.91 | |
| Small stones | 0.65 | 0.99 | 0.84 | 1.00 | 1.00 | 1.00 | 1.00 | 0.88 | 0.87 | 0.90 | |
| Large stones | 0.62 | 0.96 | 0.82 | 1.00 | 1.00 | 0.98 | 0.98 | 0.85 | 0.84 | 0.88 | |
| Boulders | 0.63 | 0.97 | 0.82 | 1.00 | 1.00 | 0.98 | 0.98 | 0.86 | 0.85 | 0.88 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Theodoropoulos, C.; Vagenas, G.; Katsogiannou, I.; Gritzalis, K.; Stamou, A. Towards i5 Ecohydraulics: Field Determination of Manning’s Roughness Coefficient, Drag Force, and Macroinvertebrate Habitat Suitability for Various Stream Vegetation Types. Water 2022, 14, 3727. https://doi.org/10.3390/w14223727
Theodoropoulos C, Vagenas G, Katsogiannou I, Gritzalis K, Stamou A. Towards i5 Ecohydraulics: Field Determination of Manning’s Roughness Coefficient, Drag Force, and Macroinvertebrate Habitat Suitability for Various Stream Vegetation Types. Water. 2022; 14(22):3727. https://doi.org/10.3390/w14223727
Chicago/Turabian StyleTheodoropoulos, Christos, Georgios Vagenas, Ioanna Katsogiannou, Konstantinos Gritzalis, and Anastasios Stamou. 2022. "Towards i5 Ecohydraulics: Field Determination of Manning’s Roughness Coefficient, Drag Force, and Macroinvertebrate Habitat Suitability for Various Stream Vegetation Types" Water 14, no. 22: 3727. https://doi.org/10.3390/w14223727








