Modification of the Water Quality Index (WQI) Process for Simple Calculation Using the Multi-Criteria Decision-Making (MCDM) Method: A Review
Abstract
1. Introduction
2. Overview and Purposes of Developing Water Quality Index (WQI)
2.1. Comparison of WQI
2.2. Importance of WQI
- Scientific research: indices can be used to minimize a large number of data into a process that provide insight into research and perform an analysis of many of these environmental programs.
- Public information: indices can be applied to educate the public on environmental conditions.
- Trend analysis: indices can be utilized for environmental information, at various time periods, to evaluate changes in environmental quality that have taken place over the period.
- Standard enforcement: indices can be applied to particular areas to evaluate the extent to which legislature standards and existing criteria are fulfilled or exceeded.
- Resource assignment: the location ranking, by evaluating the environmental conditions at various places or geographical regions.
- Specific indices: the water classification in this category is based on the type of use and requirement (drinking, irrigation, industries, bathing, etc.), which is defined by OWQI, CCME, etc.
- Public indices: the type of water used in the assessment process, such as NSFWQI, (Horton 1965), are ignored in this category.
- Statistical indices: the statistical approaches are used in these indices and personal opinions are not included.
- Planning indices: this step includes an instrument tool that facilitates decision-making and makes a plan for managing water quality projects.
2.3. Background History and Concept of WQI
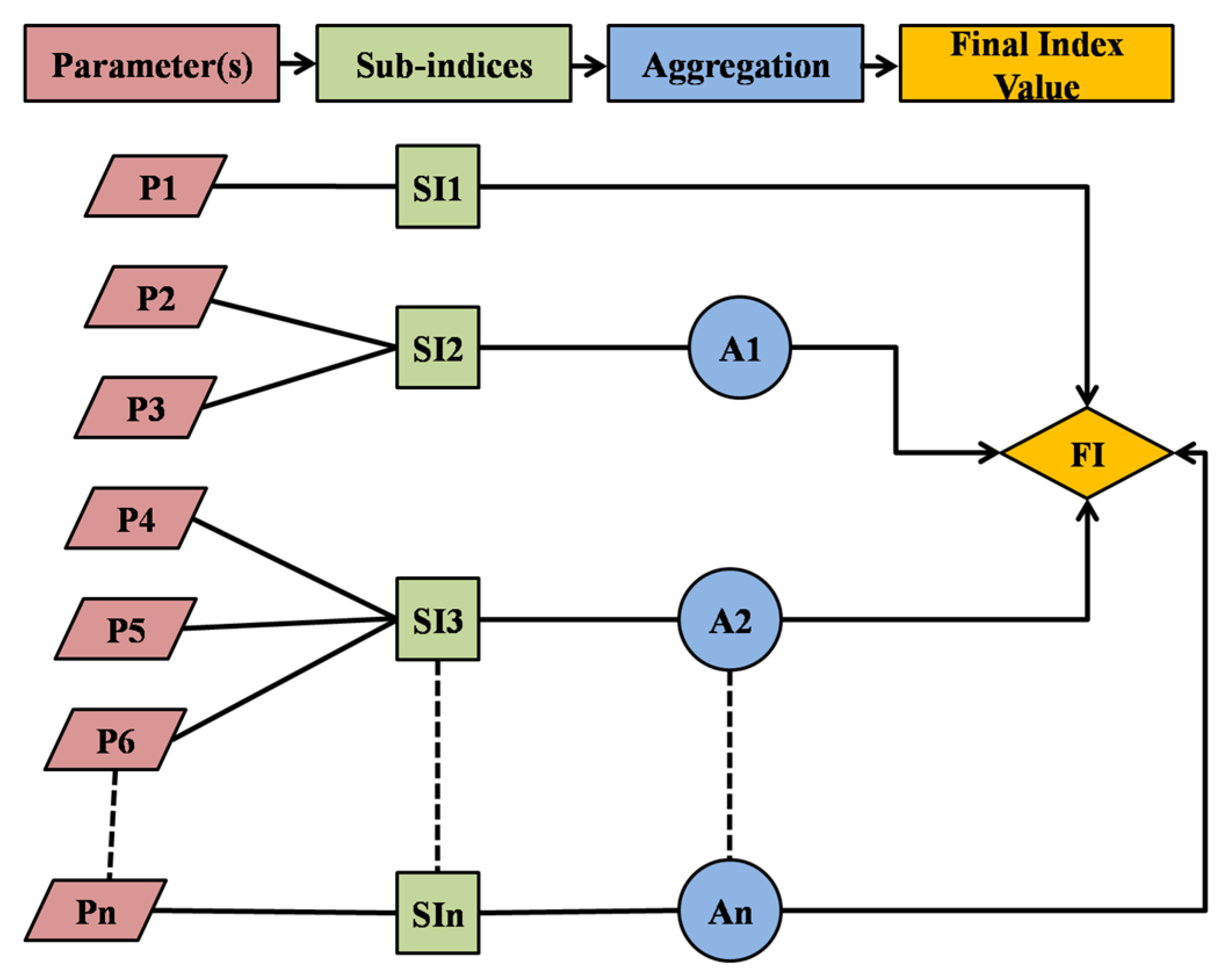
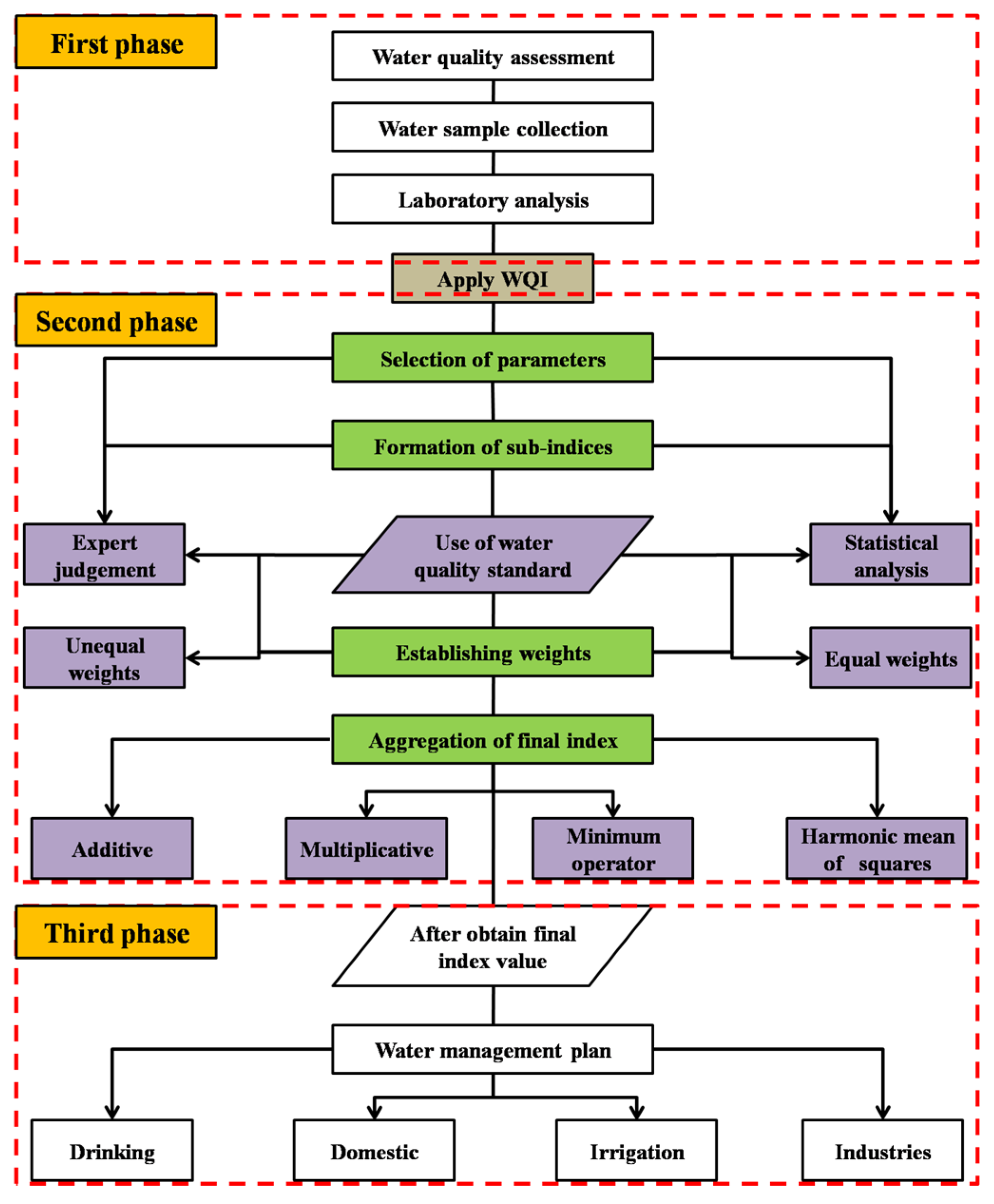
3. Common Steps for Developing Water Quality Index (WQI)
- Selection of parameters;
- Obtaining the sub-index value;
- Establishing of weights;
- Sub-index aggregation to get the value of the final index [7]
3.1. Selections of Parameters
3.1.1. Fixed System
3.1.2. Open System
3.1.3. Mixed System
3.2. Formation of Sub-Indices
- Expert opinion or judgment can be performed individually or as a group.
- Statistical methods.
- Use of water quality standards.
3.2.1. Expert Judgement
3.2.2. Statistical Techniques
3.2.3. Factor Analysis (FA)
3.2.4. Cluster Analysis (CA)
3.3. Use of Water Quality Standards
3.4. Establishing Weights
3.5. Aggregation of Sub-Indices
3.5.1. Additive Method
3.5.2. Multiplicative Method
3.5.3. Minimum Operator
3.5.4. Harmonic Mean of Squares Method
4. Multi-Criteria Decision-Making (MCDM)
4.1. Measuring Attractiveness by a Categorical Based Evaluation Technique (MACBETH) Method
4.2. Analytical Hierarchical Process (AHP) Method
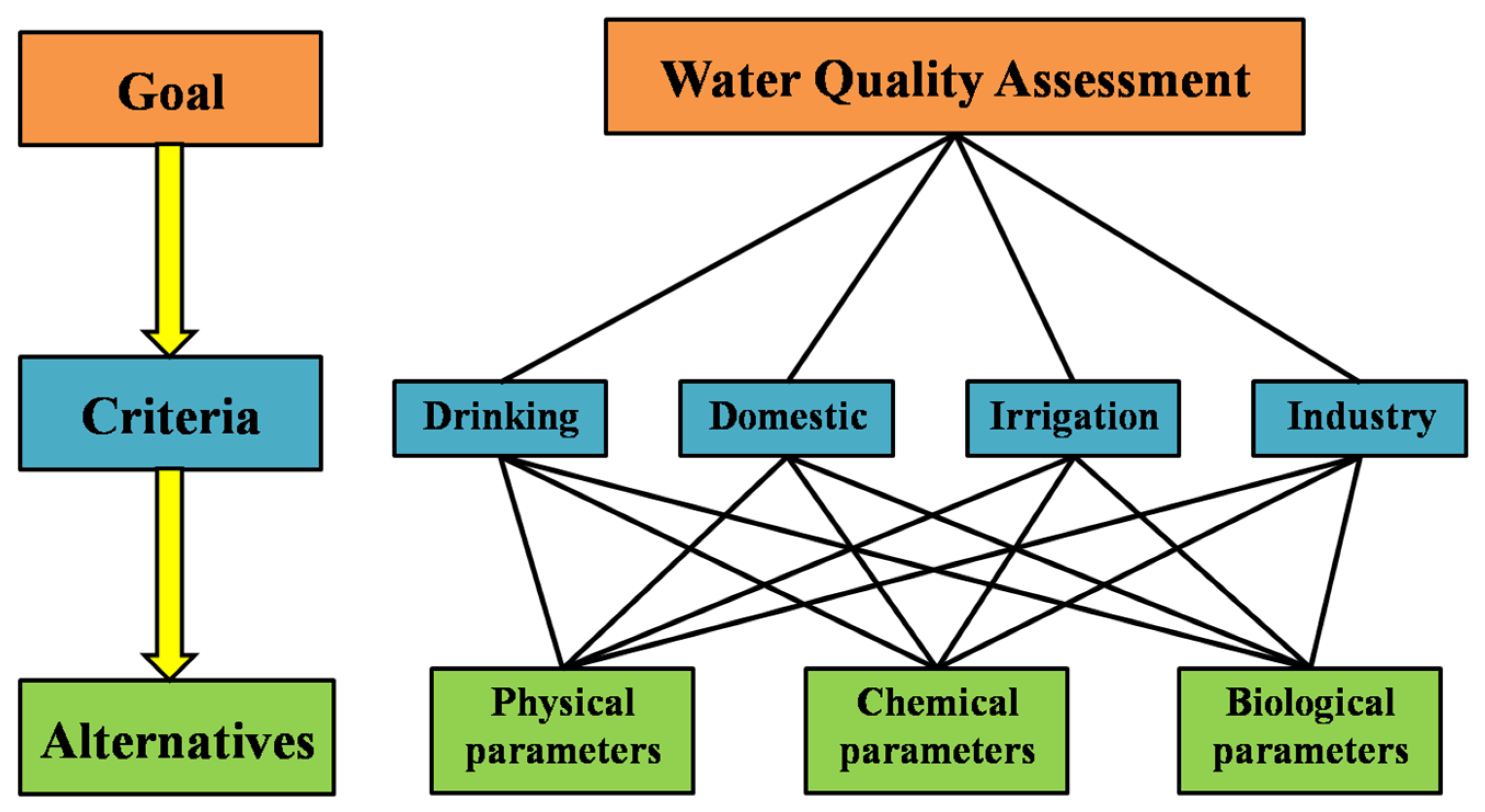
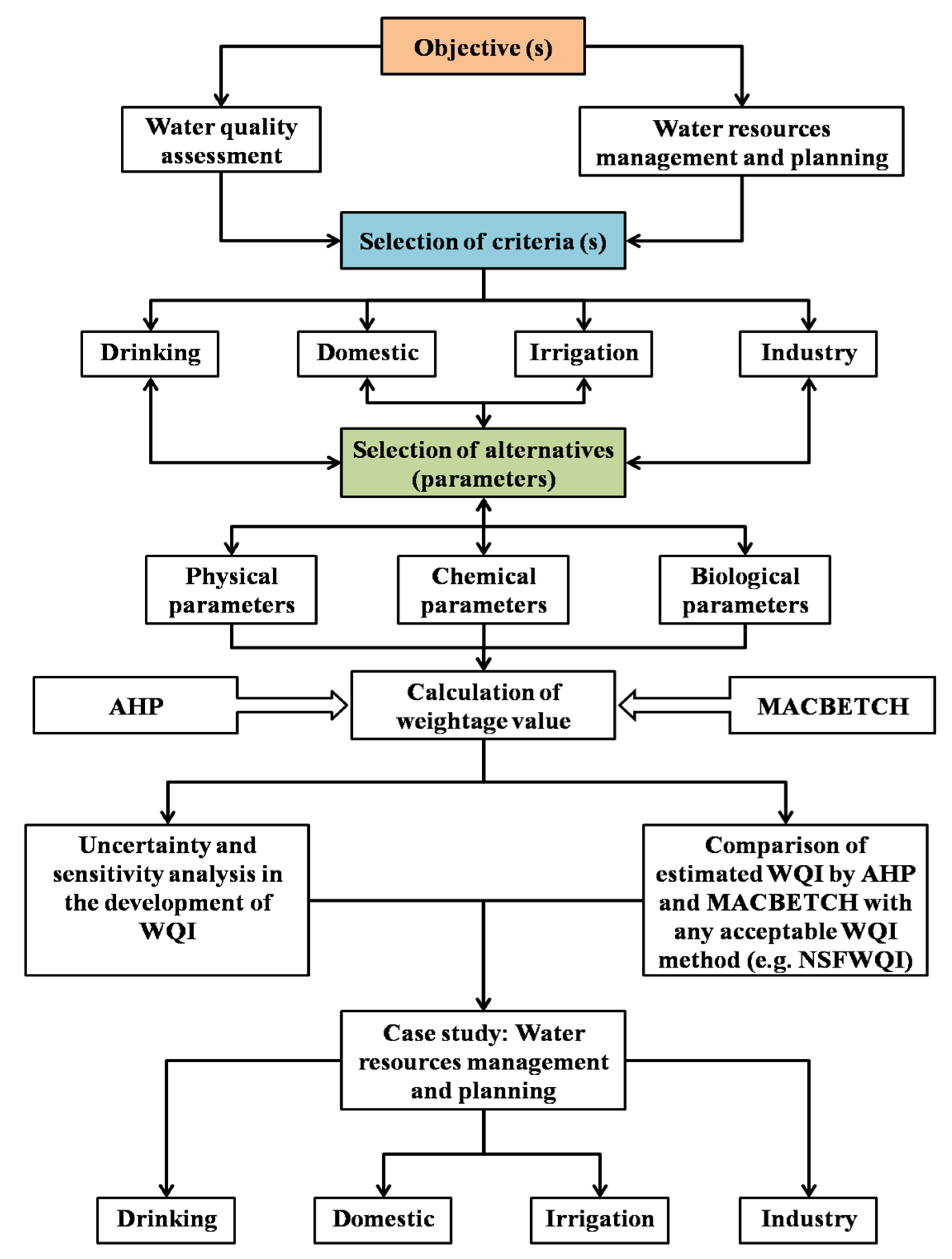
4.2.1. Selection of Criteria
4.2.2. Selection of Alternatives
4.2.3. Aggregation of AHP and MACBETH Methods for Parameters Weights
4.2.4. Comparison with WQI Estimated by AHP/MACBETH and Developed Index (NFSWQI, OWQI, BMWQI and WAWQI)
4.2.5. Uncertainty and Senstivity Analysis in the Development of WQI
5. Future Developments
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jha, M.K.; Shekhar, A.; Jenifer, M.A. Assessing Groundwater Quality for Drinking Water Supply Using Hybrid Fuzzy-GIS-Based Water Quality Index. Water Res. 2020, 179, 1–16. [Google Scholar] [CrossRef]
- Akhtar, N.; Syakir, M.I.; Rai, S.P.; Saini, R.; Pant, N.; Anees, M.T.; Qadir, A.; Khan, U. Multivariate Investigation of Heavy Metals in the Groundwater for Irrigation and Drinking in Garautha Tehsil, Jhansi District, India. Anal. Lett. 2020, 53, 774–794. [Google Scholar] [CrossRef]
- Akhtar, N.; Syakir, M.I.; Anees, M.T.; Qadir, A.; Yusuff, M.S. Characteristics and Assessment of Groundwater. In Groundwater; Chapter 3; IntechOpen: London, UK, 2020; pp. 1–20. [Google Scholar]
- Sutadian, A.D.; Muttil, N.; Yilmaz, A.; Perera, C. Development of River Water Quality Indices—A Review. Environ. Monit. Assess. 2016, 188, 1–33. [Google Scholar] [CrossRef] [PubMed]
- Lumb, A.; Sharma, T.C.; Bibeault, J.F. A Review of Genesis and Evolution of Water Quality Index (WQI) and Some Future Directions. Water Qual. Expo. Health 2011, 3, 11–24. [Google Scholar] [CrossRef]
- Banda, T.D.; Kumarasamy, M. A Review of the Existing Water Quality Indices (WQIs). J. Phys. Opt. 2020, 2, 1–19. [Google Scholar]
- Abbasi, T.; Abbasi, S.A. Water Quality Indices; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Horton, R.K. An Index Number System for Rating Water Quality. J. Water Pollut. Control Fed. 1965, 37, 300–306. [Google Scholar]
- Brown, R.M.; McClelland, N.I.; Deininger, R.A.; Tozer, R.G. A Water Quality Index—Do We Dare? Water Sew. Works 1970, 117, 339–343. [Google Scholar]
- Scottish Research Development Department (SRDD). Development of a Water Quality Index; Engineering Division: Edinburg, UK, 1976.
- Liou, S.M.; Lo, S.L.; Wang, S.H. A Generalized Water Quality Index for Taiwan. Environ. Monit. Assess. 2004, 96, 35–52. [Google Scholar] [CrossRef]
- Canadian Council of Ministers of the Environment (CCME). Canadian Water Quality Index 1.0 Technical Report and User’s Manual; Canadian Environmental Quality Guidelines Water Quality Index Technical Subcommittee: Gatineau, QC, Canada, 2001.
- Zandbergen, P.A.; Hall, K.J. Analysis of the British Columbia Water Quality Index for Watershed Managers: A Case Study of Two Small Watersheds. Water Qual. Res. J. 1998, 33, 519–549. [Google Scholar] [CrossRef]
- Sargaonkar, A.; Deshpande, V. Development of an Overall Index of Pollution for Surface Water Based on a General Classification Scheme in Indian Context. Environ. Monit. Assess. 2003, 89, 43–67. [Google Scholar] [CrossRef] [PubMed]
- Cude, C.G. Oregon Water Quality Index a Tool for Evaluating Water Quality Management Effectiveness. J. Am. Water Resour. Assoc. 2001, 37, 125–137. [Google Scholar] [CrossRef]
- Bhargave, D.S. Expression for Drinking Water Supply Standards. J. Environ. Eng. 1985, 111, 304–310. [Google Scholar] [CrossRef]
- Shuhaimi-Othman, M.; Lim, E.C.; Mushrifah, I. Water Quality Changes in Chini Lake, Pahang, West Malaysia. Environ. Monit. Assess. 2007, 131, 279–292. [Google Scholar] [CrossRef]
- Nemerow, N.L. Benefits of Water Quality Enhancement; Environmental Protection Agency, Water Quality Office, US Government: Washington, DC, USA, 1971.
- Banda, T.D. Developing an Equitable Raw Water Pricing Model: The Vaal Case Study. Master’s Thesis, Tshwane University of Technology, Pretoria, South Africa, 2015. [Google Scholar]
- Banda, T.D.; Kumarasamy, M. Aggregation Techniques Applied in Water Quality Indices (WQIs). Pollut. Res. 2020, 39, 400–441. [Google Scholar]
- Qu, X.; Chen, Y.; Liu, H.; Xia, W.; Lu, Y.; Gang, D.D.; Lin, L.S. A Holistic Assessment of Water Quality Condition and Spatiotemporal Patterns in Impounded Lakes along the Eastern Route of China’s South-to-North Water Diversion Project. Water Res. 2020, 185, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Li, H.; Ye, Z.; Wen, J.; Hu, Y.; Liu, Y. Application of Modified Water Quality Index (WQI) in the Assessment of Coastal Water Quality in Main Aquaculture Areas of Dalian, China. Mar. Pollut. Bull. 2020, 157, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Nong, X.; Shao, D.; Zhong, H.; Liang, J. Evaluation of Water Quality in the South-to-North Water Diversion Project of China Using the Water Quality Index (WQI) Method. Water Res. 2020, 178, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Şener, Ş.; Şener, E.; Davraz, A. Evaluation of Water Quality Using Water Quality Index (WQI) Method and GIS in Aksu River (SW-Turkey). Sci. Total Environ. 2017, 584–585, 131–144. [Google Scholar] [CrossRef] [PubMed]
- Hurley, T.; Sadiq, R.; Mazumder, A. Adaptation and Evaluation of the Canadian Council of Ministers of the Environment Water Quality Index (CCME WQI) for Use as an Effective Tool to Characterize Drinking Source Water Quality. Water Res. 2012, 46, 3544–3552. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, X.; Chen, Y.; Cai, Y.; Deng, J. Assessing River Water Quality Using Water Quality Index in Lake Taihu Basin, China. Sci. Total Environ. 2018, 612, 914–922. [Google Scholar] [CrossRef]
- Effendi, H.; Romanto; Wardiatno, Y. Water Quality Status of Ciambulawung River, Banten Province, Based on Pollution Index and NSF-WQI. Procedia Environ. Sci. 2015, 24, 228–237. [Google Scholar] [CrossRef]
- De Oliveira, M.D.; de Rezende, O.L.T.; de Fonseca, J.F.R.; Libânio, M. Evaluating the Surface Water Quality Index Fuzzy and Its Influence on Water Treatment. J. Water Process. Eng. 2019, 32, 100890. [Google Scholar] [CrossRef]
- Ghimire, S.; Flury, M.; Scheenstra, E.J.; Miles, C.A. Spatio-Temporal Variation of WQI, Scaling and Corrosion Indices, and Principal Component Analysis in Rural Areas of Marand, Iran. Sci. Total Environ. 2019, 11, 1–09. [Google Scholar] [CrossRef]
- Seifi, A.; Dehghani, M.; Singh, V.P. Uncertainty Analysis of Water Quality Index (WQI) for Groundwater Quality Evaluation: Application of Monte-Carlo Method for Weight Allocation. Ecol. Indic. 2020, 117, 106653. [Google Scholar] [CrossRef]
- Sahoo, S.; Khaoash, S. Impact Assessment of Coal Mining on Groundwater Chemistry and Its Quality from Brajrajnagar Coal Mining Area Using Indexing Models. J. Geochem. Explor. 2020, 215, 1–17. [Google Scholar] [CrossRef]
- Adimalla, N.; Qian, H. Groundwater Quality Evaluation Using Water Quality Index (WQI) for Drinking Purposes and Human Health Risk (HHR) Assessment in an Agricultural Region of Nanganur, South India. Ecotoxicol. Environ. Saf. 2019, 176, 153–161. [Google Scholar] [CrossRef] [PubMed]
- Yousefi, H.; Zahedi, S.; Niksokhan, M.H. Modifying the Analysis Made by Water Quality Index Using Multi-Criteria Decision Making Methods. J. Afr. Earth Sci. 2018, 138, 309–318. [Google Scholar] [CrossRef]
- Sutadian, A.D.; Muttil, N.; Yilmaz, A.G.; Perera, B.J.C. Using the Analytic Hierarchy Process to Identify Parameter Weights for Developing a Water Quality Index. Ecol. Indic. 2017, 75, 220–233. [Google Scholar] [CrossRef]
- Yan, F.; Qiao, D.; Qian, B.; Ma, L.; Xing, X.; Zhang, Y.; Wang, X. Improvement of CCME WQI Using Grey Relational Method. J. Hydrol. 2016, 543, 316–323. [Google Scholar] [CrossRef]
- Mohebbi, M.R.; Saeedi, R.; Montazeri, A.; Vaghefi, K.A.; Labbafi, S.; Oktaie, S.; Abtahi, M.; Mohagheghian, A. Assessment of Water Quality in Groundwater Resources of Iran Using a Modified Drinking Water Quality Index (DWQI). Ecol. Indic. 2013, 30, 28–34. [Google Scholar] [CrossRef]
- Fathi, P.; Ebrahimi, E.; Mirghafarry, M.; Esmaeili Ofogh, A. Water Quality Assessment in Choghakhor Wetland Using Water Quality Index (WQI). Iran. J. Fish. Sci. 2016, 15, 508–523. [Google Scholar]
- Bassi, N.; Kumar, M.D. Water Quality Index as a Tool for Wetland Restoration. Water Policy. 2017, 19, 390–403. [Google Scholar] [CrossRef][Green Version]
- Al-Musawi, N.O.; Al-Obaidi, S.K.; Al-Rubaie, F.M. Evaluating Water Quality Index of Al Hammar Marsh, South of Iraq with the Application of GIS Technique. J. Eng. Sci. Technol. 2018, 13, 4118–4130. [Google Scholar]
- Singh, A.K.; Sathya, M.; Verma, S.; Jayakumar, S. Spatiotemporal Variation of Water Quality Index in Kanwar Wetland, Begusarai, India. Sustain. Water Resour. Manag. 2020, 6, 1–8. [Google Scholar] [CrossRef]
- Hong, Z.; Zhao, Q.; Chang, J.; Peng, L.; Wang, S.; Hong, Y.; Liu, G.; Ding, S. Evaluation of Water Quality and Heavy Metals in Wetlands along the Yellow River in Henan Province. Sustainability 2020, 12, 1300. [Google Scholar] [CrossRef]
- Ghorbani, A.; Mohammadi, M.; Mohammadi, Z. Water Quality Evaluation of Torghabeh River of Mashhad Using Combination of NSFWQI Index and Geographic Information System. Int. J. Adv. Biol. Biomed. Res. 2014, 2, 2416–2430. [Google Scholar]
- Mladenović-Ranisavljević, I.I.; Takić, L.; Nikolić, Đ. Water Quality Assessment Based on Combined Multi-Criteria Decision-Making Method with Index Method. Water Resour. Manag. 2018, 32, 2261–2276. [Google Scholar] [CrossRef]
- Sarkar, K.; Majumder, M. Application of AHP-Based Water Quality Index for Quality Monitoring of Peri-Urban Watershed. Environ. Dev. Sustain. 2021, 23, 1780–1798. [Google Scholar] [CrossRef]
- Chung, E.S.; Kim, S.U.; Park, K.S.; Lee, K.S. Integrated Watershed Management Using Multicriteria Decision Making Techniques; International Water Resources Association (IWRA): Cancun, Quintana Roo, Mexico, 2017; pp. 1–12. [Google Scholar]
- Jakeman, A.J.; Giupponi, C.; Karssenberg, D.; Hare, M.P.; Fassio, A.; Letcher, R.A. Integrated Management of Water Resources: Concepts, Approaches and Challenges. In Sustainable Management of Water Resources: An Integrated Approach; Edward Elgar: Northampton, MA, USA, 2006. [Google Scholar] [CrossRef]
- Talukder, B.; Blay-Palmer, A.; Hipel, K.W.; VanLoon, G.W. Elimination Method of Multi-Criteria Decision Analysis (MCDA): A Simple Methodological Approach for Assessing Agricultural Sustainability. Sustainability 2017, 9, 287. [Google Scholar] [CrossRef]
- Soltani, A.; Hewage, K.; Reza, B.; Sadiq, R. Multiple Stakeholders in Multi-Criteria Decision-Making in the Context of Municipal Solid Waste Management: A Review. Waste Manag. 2015, 35, 318–328. [Google Scholar] [CrossRef] [PubMed]
- Oztaysi, B. A Decision Model for Information Technology Selection Using AHP Integrated TOPSIS-Grey: The Case of Content Management Systems. Knowl. Based Syst. 2014, 70, 44–54. [Google Scholar] [CrossRef]
- Ilangkumaran, M.; Karthikeyan, M.; Ramachandran, T.; Boopathiraja, M.; Kirubakaran, B. Risk Analysis and Warning Rate of Hot Environment for Foundry Industry Using Hybrid MCDM Technique. Saf. Sci. 2014, 72, 133–143. [Google Scholar] [CrossRef]
- Yilmaz, B.; Harmancioglu, N.B. Multi-Criteria Decision Making for Water Resource Management: A Case Study of the Gediz River Basin, Turkey. Water SA 2010, 36, 563–576. [Google Scholar] [CrossRef]
- Alamanos, A.; Mylopoulos, N.; Loukas, A.; Gaitanaros, D. An Integrated Multicriteria Analysis Tool for Evaluating Water Resource Management Strategies. Water 2018, 10, 1795. [Google Scholar] [CrossRef]
- Wang, H.; Cai, Y.; Tan, Q.; Zeng, Y. Evaluation of Groundwater Remediation Technologies Based on Fuzzy Multi-Criteria Decision Analysis Approaches. Water 2017, 9, 443. [Google Scholar] [CrossRef]
- Chung, E.S.; Lee, K.S. Identification of Spatial Ranking of Hydrological Vulnerability Using Multi-Criteria Decision Making Techniques: Case Study of Korea. Water Resour. Manag. 2009, 23, 2395–2416. [Google Scholar] [CrossRef]
- Ceballos, B.; Lamata, M.T.; Pelta, D.A. A Comparative Analysis of Multi-Criteria Decision-Making Methods. Prog. Artif. Intell. 2016, 5, 315–322. [Google Scholar] [CrossRef]
- Brown, R.M.; McClelland, N.I.; Deininger, R.A.; Landwehr, J.M. Validating the WQI. In Proceedings of the National Meeting of American Society of Civil Engineers on Water Resources Engineering, Washington, DC, USA, 29 January–2 February 1973. [Google Scholar]
- Ott, W.R. Environmental Indices: Theory and Practice; Ann Arbor Science Publishers: Ann Arbor, MI, USA, 1978. [Google Scholar]
- Steinhart, C.E.; Schierow, L.J.; Chesters, G. A Review of Water Quality and Related Indices. Great Lakes Environmental Planning Study Contribution No. 38; Water Resources Center, University of Wisconsin: Madison, WI, USA, 1981. [Google Scholar]
- Cooper, J.A.G.; Ramm, A.E.L.; Harrison, T.D. The estuarine health index: A new approach to scientific information transfer. Ocean Coast. Manag. 1994, 25, 103–141. [Google Scholar] [CrossRef]
- Richardson, A.M. Development of an Estuarine Water Quality Index (eWQI) for New South Wales; The University of Sydney: Sydney, Australia, 1997. [Google Scholar]
- Van Helmond, C.; Breukel, R. Physico-Chemical water quality indices. In Proceedings of the International Works on Information Strategies in Water Management, Nunspeet, The Netherlands, 9–12 September 1996; Volume 7, pp. 475–479. [Google Scholar]
- Pesce, S.F.; Wunderlin, D.A. Use of water quality indices to verify the impact of Córdoba City (Argentina) on Suquía River. Water Res. 2000, 34, 2915–2926. [Google Scholar] [CrossRef]
- Ŝtambuk-Giljanović, N. Comparison of Dalmatian Water Evaluation Indices. Water Environ. Res. 2003, 75, 388–405. [Google Scholar] [CrossRef]
- Kim, A.G.; Cardone, C.R. Scatterscore: A reconnaissance method to evaluate changes in water quality. Environ. Monit. Assess. 2005, 111, 277–295. [Google Scholar] [CrossRef] [PubMed]
- Tsegaye, T.; Sheppard, D.; Islam, K.R.; Tadesse, W.; Atalay, A.; Marzen, L. Development of chemical index as a measure of in-stream water quality in response to land-use and land cover changes. Water Air Soil Pollut. 2006, 174, 161–179. [Google Scholar] [CrossRef]
- Prescott-Allen, R. The Wellbeing of Nations: A Country-by-Country Index of Quality of Life and the Environment; Island Press: Washington, DC, USA, 2001. [Google Scholar]
- Esty, D.C.; Levy, M.A.; Srebotnjak, T.; Sherbinin, A.; Kim, C.H.; Anderson, B. Pilot 2006 Environmental Performance Index; Yale Center for Environmental Law & Policy: New Haven, CT, USA; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Bharti, N.; Katyal, D. Water Quality Indices Used for Surface Water Vulnerability Assessment. Int. J. Environ. Sci. 2011, 2, 154–173. [Google Scholar]
- Wendling, Z.A.; Emerson, J.W.; Esty, D.C.; Levy, M.A.; Sherbinin, A. Environmental Performance Index; Yale Center for Environmental Law & Policy, Yale University: New Haven, CT, USA, 2018; Available online: https://epi.yale.edu/ (accessed on 1 February 2021).
- Kolkwitz, R.; Marsson, M. Ökologie Der Tierischen Saprobien. Beiträge Zur Lehre von Der Biologischen Gewässerbeurteilung (Ecology of Animal Saprobias. Contributions to the Teaching of Biological Water Assessment). Int. Rev. Hydrobiol. Hydrogr. 1909, 2, 126–152. [Google Scholar] [CrossRef]
- Jamshidzadeh, Z.; Barzi, M.T. Wastewater Quality Index (WWQI) as an Assessment Tool of Treated Wastewater Quality for Agriculture: A Case of North Wastewater Treatment Plant Effluent of Isfahan. Environ. Sci. Pollut. Res. 2020, 27, 7366–7378. [Google Scholar] [CrossRef] [PubMed]
- Ladson, A.R.; White, L.J.; Doolan, J.A.; Finlayson, B.L.; Hart, B.T.; Lake, P.S.; Tilleard, J.W. Development and Testing of an Index of Stream Condition for Waterway Management in Australia. Freshw. Biol. 1999, 41, 453–468. [Google Scholar] [CrossRef]
- Yale Center for Environmental Law & Policy, Yale University; Center for International Earth Science Information Network (CIESIN), Columbia University. EPI.Environmental Performance Index; Yale Center for Environmental Law & Policy, Yale University: New Haven, CT, USA, 2010. [Google Scholar]
- Sarkar, C.; Abbasi, S.A. Qualidex—A New Software for Generating Water Quality Indice. Environ. Monit. Assess. 2006, 119, 201–231. [Google Scholar] [CrossRef]
- Ocampo-Duque, W.; Ferre-Huguet, N.; Domingo, J.L.; Schuhmacher, M. Assessing Water Quality in Rivers with Fuzzy Inference Systems: A Case Study. Environ. Int. 2006, 32, 733–742. [Google Scholar] [CrossRef] [PubMed]
- Swamee, P.K.; Tyagi, A. Improved Method for Aggregation of Water Quality Subindices. J. Environ. Eng. 2007, 133, 220–225. [Google Scholar] [CrossRef]
- Said, A.; Stevens, D.K.; Sehlke, G. An Innovative Index for Evaluating Water Quality in Streams. Environ. Manag. 2004, 34, 406–414. [Google Scholar] [CrossRef]
- Kannel, P.R.; Lee, S.; Lee, Y.S.; Kanel, S.R.; Khan, S.P. Application of Water Quality Indices and Dissolved Oxygen as Indicators for River Water Classification and Urban Impact Assessment. Environ. Monit. Assess. 2007, 132, 93–110. [Google Scholar] [CrossRef] [PubMed]
- Dunnette, D.A. A Geographically Variable Water Quality Index Used in Oregon. J. Water Pollut. Control Fed. 1979, 51, 53–61. [Google Scholar]
- Hanh, P.T.M.; Sthiannopkao, S.; Ba, D.T.; Kim, K.W. Development of Water Quality Indexes to Identify Pollutants in Vietnam’s Surface Water. J. Environ. Eng. 2011, 137, 273–283. [Google Scholar] [CrossRef]
- Prati, L.; Pavanello, R.; Pesarin, F. Assessment of Surface Water Quality by a Single Index of Pollution. Water Res. 1971, 5, 741–751. [Google Scholar] [CrossRef]
- Smith, D.G. A Better Water Quality Indexing System for Rivers and Streams. Water Res. 1990, 24, 1237–1244. [Google Scholar] [CrossRef]
- Stoner, J.D. Water-Quality Indices for Specific Water Uses; Geological Survey Circular: Arlington, VA, USA, 1978. [Google Scholar] [CrossRef]
- WHO. Guidelines for Drinking Water Quality, 4th ed.; World Health Organization: Geneva, Switzerland, 2017. [Google Scholar]
- Banda, T.D.; Kumarasamy, M.V. Development of Water Quality Indices (WQIs): A Review. Pol. J. Environ. Stud. 2020, 29, 2011–2021. [Google Scholar] [CrossRef]
- Meyer, M.A.; Booker, J.M. Eliciting and Analyzing Expert Judgment: A Practical Guide; Nuclear Regulatory Commission, Division of Systems Research: Washington, DC, USA; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2001.
- Steurer, J. The Delphi Method: Techniques and Applications. Skelet. Radiol. 2011, 40, 959–961. [Google Scholar] [CrossRef]
- Deininger, R.A. A Water Quality Index for Rivers. Water Int. 1980, 5, 16–21. [Google Scholar] [CrossRef]
- Ghesquière, O.; Walter, J.; Chesnaux, R.; Rouleau, A. Scenarios of Groundwater Chemical Evolution in a Region of the Canadian Shield Based on Multivariate Statistical Analysis. J. Hydrol. Reg. Stud. 2015, 4, 246–266. [Google Scholar] [CrossRef]
- Nagaraju, A.; Thejaswi, A.; Sreedhar, Y. Assessment of Groundwater Quality of Udayagiri Area, Nellore District, Andhra Pradesh, South India Using Multivariate Statistical Techniques. Earth Sci. Res. J. 2016, 20, 1. [Google Scholar] [CrossRef]
- Hou, D.; O’Connor, D.; Nathanail, P.; Tian, L.; Ma, Y. Integrated GIS and Multivariate Statistical Analysis for Regional Scale Assessment of Heavy Metal Soil Contamination: A Critical Review. Environ. Pollut. 2017, 231, 1188–1200. [Google Scholar] [CrossRef] [PubMed]
- Rehman, F.; Cheema, T.; Lisa, M.; Azeem, T.; Ali, N.A.; Khan, Z.; Rehman, F.; Rehman, S.U. Statistical Analysis Tools for the Assessment of Groundwater Chemical Variations in Wadi Bani Malik Area, Saudi Arabia. Glob. Nest J. 2018, 20, 355–362. [Google Scholar] [CrossRef]
- Bu, H.; Song, X.; Zhang, Y. Using Multivariate Statistical Analyses to Identify and Evaluate the Main Sources of Contamination in a Polluted River near to the Liaodong Bay in Northeast China. Environ. Pollut. 2019, 245, 1058–1070. [Google Scholar] [CrossRef] [PubMed]
- Busico, G.; Kazakis, N.; Cuoco, E.; Colombani, N.; Tedesco, D.; Voudouris, K.; Mastrocicco, M. A Novel Hybrid Method of Specific Vulnerability to Anthropogenic Pollution Using Multivariate Statistical and Regression Analyses. Water Res. 2020, 171, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Hallock, D. AWater Quality Index for Ecology’s Stream Monitoring Program; Washington State Department of Ecology: Olympia, WA, USA, 2002.
- Behera, B.; Das, M. Application of Multivariate Statistical Techniques for the Characterization of Groundwater Quality of Bacheli and Kirandul Area, Dantewada District, Chattisgarh. J. Geol. Soc. India 2018, 91, 76–80. [Google Scholar] [CrossRef]
- Gulgundi, M.S.; Shetty, A. Groundwater quality assessment of urban Bengaluru using multivariate statistical techniques. Appl. Water Sci. 2018, 8, 1–15. [Google Scholar] [CrossRef]
- Muangthong, S.; Shrestha, S. Assessment of Surface Water Quality Using Multivariate Statistical Techniques: Case Study of the Nampong River and Songkhram River, Thailand. Environ. Monit. Assess. 2015, 187, 1–12. [Google Scholar] [CrossRef]
- Daughney, C.J.; Raiber, M.; Moreau-Fournier, M.; Morgenstern, U.; Raaij, R.V.D. Use of Hierarchical Cluster Analysis to Assess the Representativeness of a Baseline Groundwater Quality Monitoring Network: Comparison of New Zealand’s National and Regional Groundwater Monitoring Programs. Hydrogeol. J. 2012, 20, 185–200. [Google Scholar] [CrossRef]
- Trabelsi, R.; Zouari, K. Coupled Geochemical Modeling and Multivariate Statistical Analysis Approach for the Assessment of Groundwater Quality in Irrigated Areas: A Study from North Eastern of Tunisia. Groundw.Sustain. Dev. 2019, 8, 413–427. [Google Scholar] [CrossRef]
- Ponsadailakshmi, S.; Sankari, S.G.; Prasanna, S.M.; Madhurambal, G. Evaluation of Water Quality Suitability for Drinking Using Drinking Water Quality Index in Nagapattinam District, Tamil Nadu in Southern India. Groundw.Sustain. Dev. 2018, 6, 43–49. [Google Scholar] [CrossRef]
- House, M.A. A Water Quality Index for River Management. Water Environ. J. 1989, 3, 336–344. [Google Scholar] [CrossRef]
- Bascaron, M. Establishment of a Methodology for the Determination of Water Quality. Bol. Inf. Medio Ambient. 1979, 9, 30–51. [Google Scholar]
- BIS. Indian Standards Drinking Water Specifications IS 10500:2012; Bahadur Shah Zafar Marg: New Delhi, India, 2012. [Google Scholar]
- USEPA. 2018 Edition of the Drinking Water Standards and Health Advisories Tables; U.S. Environmental Protection Agency: Washington, DC, USA, 2018.
- INWQS. Interim National Water Quality Standard; Ministry of Environment And Water, Department of Environment (DOE): Putrajaya, Malaysia, 2008.
- APHA. Standard Methods for the Examination of Water and Wastewater, 23rd ed.; American Public Health Association: Washington, DC, USA, 2017. [Google Scholar]
- Almeida, C.; González, S.O.; Mallea, M.; González, P. A Recreational Water Quality Index Using Chemical, Physical and Microbiological Parameters. Environ. Sci. Pollut. Res. 2012, 19, 3400–3411. [Google Scholar] [CrossRef] [PubMed]
- Deininger, R.A.; Maciunas, J.J. A Water Quality Index for Public Water Supplies; Department of Environmental and Industrial Health, School of Public Health, University of Michigan: Ann Arbor, MI, USA, 1971. [Google Scholar]
- Tyson, J.M.; House, M.A. The Application of a Water Quality Index to River Management. Water Sci. Technol. 1989, 21, 1149–1159. [Google Scholar] [CrossRef]
- Dojlido, J.A.N.; Raniszewski, J.; Woyciechowska, J. Water Quality Index Applied to Rivers in the Vistula River Basin in Poland. Environ. Monit. Assess. 1994, 33, 33–42. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets, Fuzzy Logic and Fuzzy Systems; World Scientific: Singapore, 1996. [Google Scholar] [CrossRef]
- Brown, R.M.; McClelland, N.I.; Deininger, R.A.; O’Connor, M.F. A Water Quality Index—Crashing the Psychological Barrier. In Indicators of Environmental Quality, Environmental Science Research; Thomas, W.A., Ed.; Springer: Boston, MA, USA, 1972; Volume 1. [Google Scholar] [CrossRef]
- Walski, T.M.; Parker, F.L. Consumers Water Quality Index. J. Environ. Eng. Div. 1974, 100, 593–611. [Google Scholar] [CrossRef]
- Harkins, R.D. An Objective Water Quality Index. J. Water Pollut. Control Fed. 1974, 7, 588–591. [Google Scholar]
- Ross, S.L. An Index System for Classifying River Water Quality. Water Pollut. Control 1977, 76, 113–132. [Google Scholar]
- Canter, L.W. The Guidance of Water Quality Status in Indonesia. Decree No 115/20032003; Environmental Impact Assessment; University of Oklahoma, Macgraw-Hill: New York, NY, USA, 1977. [Google Scholar]
- Tiwari, T.N.; Mishra, M.A. A Preliminary Assignment of Water Quality Index of Major Indian Rivers. Indian J. Environ. Prot. 1985, 5, 276–279. [Google Scholar]
- Dinius, S.H. Design of an Index of Water Quality. JAWRA J. Am. Water Resour. Assoc. 1987, 23, 833–843. [Google Scholar] [CrossRef]
- Sharifi, M. Assessment of Surface Water Quality by an Index System in Anzali Basin. Hydrol. Basis Water Resour. Manag. 1990, 197, 163–171. [Google Scholar]
- Rocchini, R.; Swain, L.G. The British Columbia Water Quality Index. Water Quality Branch; British Columbia Ministry of Environment, Land and Parks: Victoria, BC, Australia, 1995; Volume 13.
- Wepener, V.; Van Vuren, J.H.J.; Preez, H.H.D.U. The Implementation of an Aquatic Toxicity Index as a Water Quality Monitoring Tool in the Olifants River (Kruger National Park). Koedoe 1999, 42, 85–96. [Google Scholar] [CrossRef]
- Nagels, J.W.; Davies-Colley, R.J.; Smith, D.G. A Water Quality Index for Contact Recreation in New Zealand. Water Sci. Technol. 2001, 43, 285–292. [Google Scholar] [CrossRef] [PubMed]
- Kaurish, F.W.; Younos, T. Developing a Standardized Water Quality Index for Evaluating Surface Water Quality. J. Am. Water Resour. Assoc. 2007, 43, 533–545. [Google Scholar] [CrossRef]
- Schiff, R.; Benoit, G. Effects of Impervious Cover at Multiple Spatial Scales on Coastal Watershed Streams. J. Am. Water Resour. Assoc. 2007, 43, 712–730. [Google Scholar] [CrossRef]
- Boyacioglu, H. Development of a Water Quality Index Based on a European Classification Scheme. Water SA 2007, 33, 101–106. [Google Scholar] [CrossRef]
- Ocampo Duque, W.A. On the Development of Decision-Making Systems Based on Fuzzy Models to Assess Water Quality in Rivers. Ph.D. Thesis, Department of Chemical Engineering, Universitat Rovira i Virgil, Tarragona, Spain, 2008. [Google Scholar]
- Islam, N.; Sadiq, R.; Rodriguez, M.J. Optimizing Booster Chlorination in Water Distribution Networks: A Water Quality Index Approach. Environ. Monit. Assess. 2013, 185, 8035–8050. [Google Scholar] [CrossRef] [PubMed]
- Wanda, E.M.M.; Mamba, B.B.; Msagati, T.A.M. Determination of the Water Quality Index Ratings of Water in the Mpumalanga and North West Provinces, South Africa. Phys. Chem. Earth 2016, 92, 70–78. [Google Scholar] [CrossRef]
- Medeiros, A.C.; Faial, K.R.F.; Faial, K.D.C.F.; Lopes, I.D.S.; Lima, M.D.O.; Guimarães, R.M.; Mendonça, N.M. Quality Index of the Surface Water of Amazonian Rivers in Industrial Areas in Pará Brazil. Mar. Pollut. Bull. 2017, 123, 156–164. [Google Scholar] [CrossRef]
- García-Ávila, F.; Ramos-Fernández, L.; Pauta, D.; Quezada, D. Evaluation of Water Quality and Stability in the Drinking Water Distribution Network in the Azogues City, Ecuador. Data Br. 2018, 18, 111–123. [Google Scholar] [CrossRef] [PubMed]
- Sutadian, A.; Muttil, N.; Yilmaz, A.G.; Perera, B.J.C. Development of a Water Quality Index for Rivers in West Java Province, Indonesia. Ecol. Indic. 2018, 85, 966–982. [Google Scholar] [CrossRef]
- Mojahedi, S.A.; Attari, J. A comparative study of water quality Indices for Karun river. Proc. World Environ. Water Resour. Congr. GT Rivers 2009, 342, 2444–2452. [Google Scholar] [CrossRef]
- Chaturvedi, A.; Bhattacharjee, S.; Mondal, G.C.; Kumar, V.; Singh, P.K.; Singh, A.K. Exploring new correlation between hazard index and heavy metal pollution index in groundwater. Ecol. Indic. 2019, 97, 239–246. [Google Scholar] [CrossRef]
- Lumb, A.A.; Halliwell, D.; Sharma, T. Application of CCME water quality index to monitor water quality: A case of the Mackenzie River Basin, Canada. Environ. Monit. Assess. 2006, 113, 411–429. [Google Scholar] [CrossRef] [PubMed]
- Khan, F.; Husain, T.; Lumb, A. Water quality evaluation and trend analysis in selected watersheds of the Atlantic region of Canada. Environ. Monit. Assess. 2003, 88, 221–248. [Google Scholar] [CrossRef] [PubMed]
- Terrado, M.; Barceló, D.; Tauler, R.; Borrell, E.; Campos, S.D. Surface-water-quality indices for the analysis of data generated by automated sampling networks. TrAC Trends Anal. Chem. 2010, 29, 40–52. [Google Scholar] [CrossRef]
- Gade, P.K.; Osuri, M. Evaluation of Multi Criteria Decision Making Methods for Potential Use in Application Security; Blekinge Institute of Technology: Karlskrona, Sweden, 2014. [Google Scholar]
- Hajkowicz, S.; Collins, K. A Review of Multiple Criteria Analysis for Water Resource Planning and Management. WaterResour. Manag. 2007, 21, 1553–1566. [Google Scholar] [CrossRef]
- Amorocho-Daza, H.; Cabrales, S.; Santos, R.; Saldarriaga, J. A New Multi-Criteria Decision Analysis Methodology for the Selection of New Water Supply Infrastructure. Water 2019, 11, 805. [Google Scholar] [CrossRef]
- Bana e Costa, C.A.; De Corte, J.M.; Vansnick, J.C. MACBETH (Measuring Attractiveness by a Categorical Based Evaluation Technique). In Wiley Encyclopedia of Operations Research and Management Science; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 2945–2950. [Google Scholar]
- Joerin, F.; Cool, G.; Rodriguez, M.J.; Gignac, M.; Bouchard, C. Using Multi-Criteria Decision Analysis to Assess the Vulnerability of Drinking Water Utilities. Environ. Monit. Assess. 2010, 166, 313–330. [Google Scholar] [CrossRef] [PubMed]
- Lavoie, R.; Joerin, F.; Vansnick, J.C.; Rodriguez, M.J. Integrating Groundwater into Land Planning: A Risk Assessment Methodology. J. Environ. Manag. 2015, 154, 358–371. [Google Scholar] [CrossRef] [PubMed]
- Lavoie, R.; Deslandes, J.; Proulx, F. Assessing the Ecological Value of Wetlands Using the MACBETH Approach in Quebec City. J. Nat. Conserv. 2016, 30, 67–75. [Google Scholar] [CrossRef]
- De Carvalho, B.E.; Marques, R.C.; Netto, O.C. Rethinking Brasília’s Water Services: ‘New Targets’ Using the Regulatory Impact Assessment (RIA) Tool. J. WaterSanit. Hyg. Dev. 2019, 9, 7–18. [Google Scholar] [CrossRef]
- Demesouka, O.E.; Vavatsikos, A.P.; Anagnostopoulos, K.P. Using MACBETH Multicriteria Technique for GIS-Based Landfill Suitability Analysis. J. Environ. Eng. 2016, 142. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Estimating Technological Coefficients by the Analytic Hierarchy Process. Socio-Econ.Plann. Sci. 1979, 13, 333–336. [Google Scholar] [CrossRef]
- Lai, V.S.; Trueblood, R.P.; Wong, B.K. Software Selection: A Case Study of the Application of the Analytical Hierarchical Process to the Selection of a Multimedia Authoring System. Inf. Manag. 1999, 36, 221–232. [Google Scholar] [CrossRef]
- Forman, E.H.; Gass, S.I. The Analytic Hierarchy Process—An Exposition. Oper. Res. 2001, 49, 469–486. [Google Scholar] [CrossRef]
- Ishizaka, A.; Labib, A. Analytic Hierarchy Process and Expert Choice: Benefits and Limitations. Oper. Res. Insight 2009, 22, 201–220. [Google Scholar] [CrossRef]
- Carbajal-Hernández, J.J.; Sánchez-Fernández, L.P.; Villa-Vargas, L.A.; Carrasco-Ochoa, J.A.; Martínez-Trinidad, J.F. Water quality assessment in shrimp culture using an analytical hierarchical process. Ecol. Indic. 2013, 29, 148–158. [Google Scholar] [CrossRef]
- Delgado-Galván, X.; Pérez-García, R.; Izquierdo, J.; Mora-Rodríguez, J. An analytic hierarchy process for assessing externalities in water leakage management. Math. Comput. Model. 2010, 52, 1194–1202. [Google Scholar] [CrossRef]
- Dar, T.; Rai, N.; Bhat, A. Delineation of Potential Groundwater Recharge Zones Using Analytical Hierarchy Process (AHP). Geol. Ecol. Landsc. 2020, 1, 1–16. [Google Scholar] [CrossRef]
- Kazakis, N.; Busico, G.; Colombani, N.; Mastrocicco, M.; Pavlou, A.; Voudouris, K. GALDIT-SUSI a Modified Method to Account for Surface Water Bodies in the Assessment of Aquifer Vulnerability to Seawater Intrusion. J. Environ. Manag. 2019, 235, 257–265. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Xiang, M.; Yang, J.; Fan, W.; Yi, Y. Distributed Hierarchical Evaluation and Carrying Capacity Models for Water Resources Based on Optimal Water Cycle Theory. Ecol. Indic. 2019, 101, 432–443. [Google Scholar] [CrossRef]
- Alobaidy, A.H.M.J.; Abid, H.S.; Maulood, B.K. Application of Water Quality Index for Assessment of Dokan Lake Ecosystem, Kurdistan Region, Iraq. J. Water Resour. Prot. 2010, 2, 792–798. [Google Scholar] [CrossRef]
- Zotou, I.; Tsihrintzis, V.A.; Gikas, G.D. Comparative Assessment of Various Water Quality Indices (WQIs) in Polyphytos Reservoir-Aliakmon River, Greece. Proceedings 2018, 2, 611. [Google Scholar] [CrossRef]
- Madalina, P.; Gabriela, B.I. Water Quality Index—An Instrument for Water Resources. Air Water Compon. Environ. 2014, 1, 391–398. [Google Scholar] [CrossRef]
- Satyanarayana, E.; Ratnakar, D.; Muralidhar, M. Major Ion Chemistry of Groundwater and Surface Water in Parts of Mulugu-Venkatapur Mandal, Warangal District, Telangana State, India. J. Waste Water Treat. Anal. 2016, 7. [Google Scholar] [CrossRef]
- Shrestha, S.; Kazama, F. Assessment of Surface Water Quality Using Multivariate Statistical Techniques: A Case Study of the Fuji River Basin, Japan. Environ. Model. Softw. 2007, 22, 464–475. [Google Scholar] [CrossRef]
- Juahir, H.; Zain, S.M.; Yusoff, M.K.; Hanidza, T.I.T.; Armi, A.S.M.; Toriman, M.E.; Mokhtar, M. Spatial Water Quality Assessment of Langat River Basin (Malaysia) Using Environmetric Techniques. Environ. Monit. Assess. 2011, 173, 625–641. [Google Scholar] [CrossRef] [PubMed]
- Njuguna, S.M.; Onyango, J.A.; Githaiga, K.B.; Gituru, R.W.; Yan, X. Application of Multivariate Statistical Analysis and Water Quality Index in Health Risk Assessment by Domestic Use of River Water. Case Study of Tana River in Kenya. Process Saf. Environ. Prot. 2020, 133, 149–158. [Google Scholar] [CrossRef]
- Jena, V.K.; Sinha, D. Ground Water Quality Assessment by Multivariate Factor Analysis. Res. J. Chem. Environ. 2017, 21, 21–25. [Google Scholar]
- Khalil, B.; Ou, C.; Proulx-Mcinnis, S.; St-Hilaire, A.; Zanacic, E. Statistical Assessment of the Surface Water Quality Monitoring Network in Saskatchewan. WaterAir Soil Pollut. 2014, 225, 1–22. [Google Scholar] [CrossRef]
- Khalil, B.; Ouarda, T.B.M.J.; St-Hilaire, A.; Chebana, F. A Statistical Approach for the Rationalization of Water Quality Indicators in Surface Water Quality Monitoring Networks. J. Hydrol. 2010, 386, 173–185. [Google Scholar] [CrossRef]
- Zahedi, S. Modification of expected conflicts between Drinking Water Quality Index and Irrigation Water Quality Index in water quality ranking of shared extraction wells using Multi Criteria Decision Making techniques. Ecol. Indic. 2017, 83, 368–379. [Google Scholar] [CrossRef]
- Meireles, A.C.M.; Andrade, E.M.; Chaves, L.C.G.; Frischkorn, H.; Crisostomo, L.A. A new proposal of the classification of irrigation water. Revista Ciência Agronômica 2010, 41, 349–357. [Google Scholar] [CrossRef]
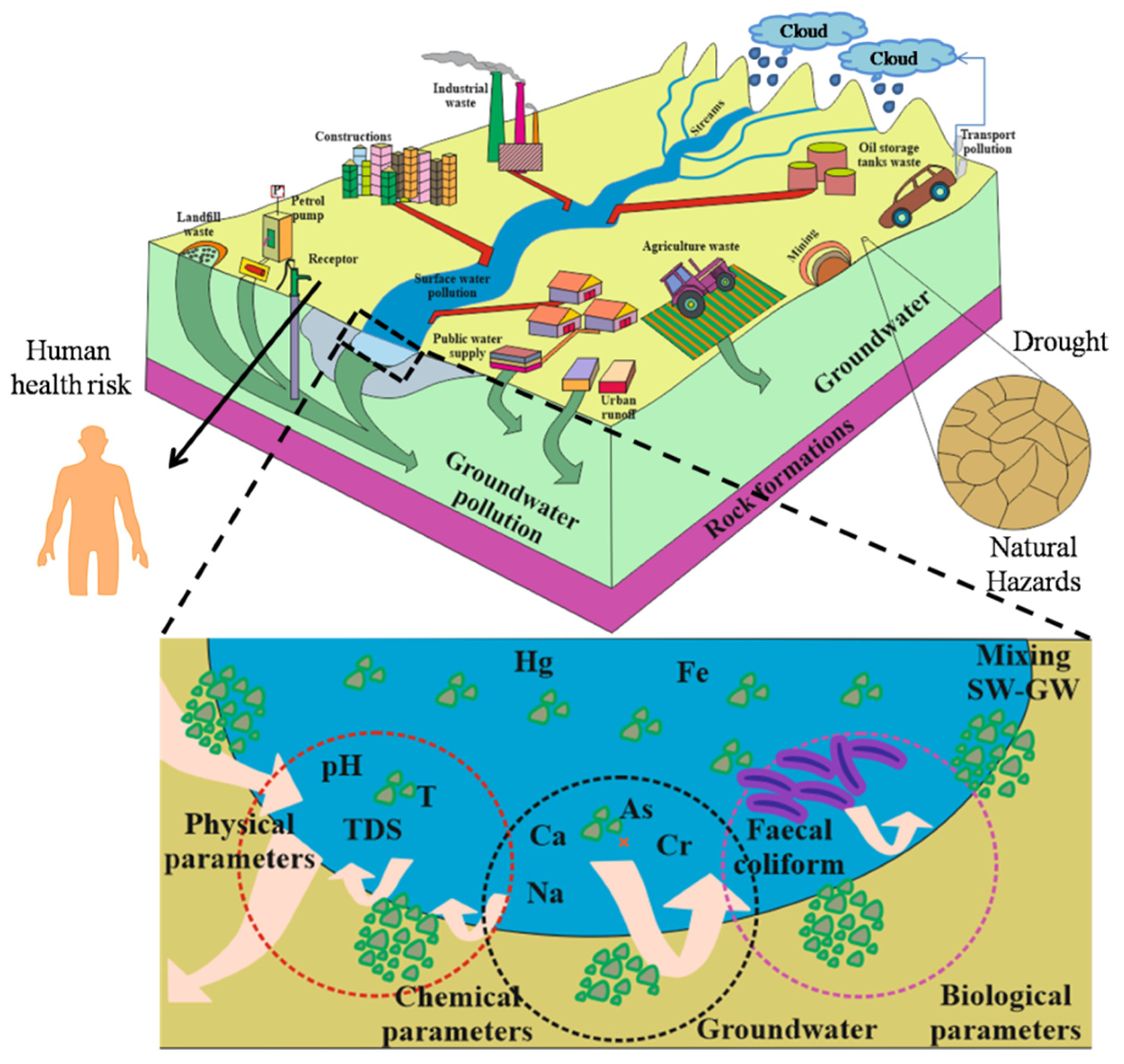
| Index (Author) | Method | Objectives |
|---|---|---|
| Water quality index for freshwater life [12] | Evaluate water quality for freshwater life against guidelines. | Inland water |
| The well–being of nations [66] | Evaluate inhabitants indices against ecosystem indices. | Human and ecosystem |
| Overall index of pollution [14] | Evaluating and categorising a range of water quality parameters in comparison with the Bureau of Indian Standards (BIS) and other recognized guidelines such as World health organization (WHO). | Stream/river health |
| Index of river water quality [11] | Using the multiplicative aggregate process for a variety of water quality parameters as standardized scores. | Stream/river health |
| The Scatterscore [64] | Evaluate decreases or incraeses in parameters over space and time. | Water quality |
| Chemical water quality index [65] | Evaluate a range of parameters by standardizing the maximum concentration of each measurement to every parameter. | Lake basin |
| Environmental performance index [67] | Using a targeted proximity calculation for 16 indexes classified into six policy goals. | Environmental health and ecosystem vitality |
| Water Quality Parameters | Parameters (Units) | Usage of Parameters | WHO [84] | BIS [104] | USEPA [105] | INWQS [106] | Method | Equipment and Analytical Techniques |
|---|---|---|---|---|---|---|---|---|
| Physical Parameters | Color (TCU) | D | 15 | 5–15 | - | 15 | Solution by (Pt-Co) | Spectrophotometer |
| Taste and Odor (TON) | D | - | - | - | - | ASTM D-1292 triangle | Attitude taste Scale (ATS) | |
| Temperature (°C) | D | - | - | - | - | KM 3002 | Digital Thermometer | |
| EC (µS/cm) | D, I, H, A | 250 | 250 | - | 1000 | Electrometric | Conductivity meter—Hach | |
| TDS (mg/L) | D, I, H, A | - | 500–2000 | - | 500–1000 | Gravimetric Method | Hach potable meters | |
| Turbidity (NTU) | D, A | - | 1–5 | - | 5 | Turbidimeter | Hach Turbidimeter | |
| Salinity (ppt) | D, I | - | - | - | 0.5 | Filtration | SHKY Conductivly meter | |
| Chemical Parameters | pH | D, I, H, A | - | 6.5–8.5 | 6.5–8.5 | 6.5–8.5 | Electrometric | pH meter—Hach |
| Hardness (mg/L) | D, I, H, A | 200 | 200–600 | - | 250 | Titration | Digital Burette | |
| DO (mg/L) | D | - | 6 | - | >7 | Colorimetric | Portable meter | |
| BOD (mg/L) | D, A | - | 2 | - | 1 | Titration | UV Visible Spectrophotometer | |
| COD (mg/L) | D | - | - | - | 10 | Titration | ||
| TOC (mg/L) | D | - | - | - | - | Titration | ||
| DOC (mg/L) | D | - | - | - | - | Titration by H2SO4 | ||
| Alkalinity (mg/L) | D, I, H, A | - | 200–600 | - | - | Titration by H2SO4 | pH meter | |
| Acidity (mg/L) | D, I, H, A | - | - | - | - | Titration by H2SO4 | ||
| Biological parameters | Total coliform (100 ml) | D | - | - | - | - | Maximum probable number (MPN) | Bacteriological Incubator |
| Fecal coliform (10 ml) | D | - | - | - | - | |||
| Anions | Carbonate (mg/L) | D, I, H, A | - | - | - | - | Titration by H2SO4 | Digital Burette |
| Bicarbonate (mg/L) | D, I, H, A | - | 600 | - | - | Titration by H2SO4 | ||
| Chloride (mg/L) | D, I, H, A | 250 | 250–1000 | 250 | 200 | Argentometric Method | Ion Chromatograph,Dionex (ICS 5000),ICP-MS, flame photometer, UV–Vis Spectrophotometer | |
| Fluoride (mg/L) | D, I, H, A | 1.5 | 1–1.5 | 4 | 1.5 | SPADNS colorimetric | ||
| Nitrate (mg/L) | D, I, H, A | 45 | 45–NR | 10 | 7 | Phenol disulphonic acid | ||
| Sulfate (mg/L) | D, I, H, A | 500 | 200–400 | - | 250 | Gravimetric | ||
| Cations | Calcium (mg/L) | D, I, H, A | - | 75–200 | - | - | Conductivity | Ion Chromatograph,Dionex (ICS 5000),ICP-MS, flame photometer, Atomic fluorescence spectrometry (AFS) |
| Magnesium (mg/L) | D, I, H, A | - | 0.1–0.3 | - | - | Conductivity | ||
| Sodium (mg/L) | D, I, H, A | 20 | - | - | - | Conductivity | ||
| Potassium (mg/L) | D, I, H, A | - | - | - | - | Conductivity | ||
| Heavy Metals | Arsenic (mg/L) | D | 0.01 | 0.01–0.05 | 0.01 | 0.05 | American Public Health Association [107] | Atomic fluorescence spectrometry (AFS), Inductively Coupled Plasma Mass Spectrometry (ICP-MS), Atomic absorption spectrometer (AAS), Inductively Coupled Plasma Optical emission spectroscopy (ICP-OES), X-ray fluorescence (XRF) |
| Aluminium (mg/L) | D | 0.1 | 0.03–0.2 | - | - | |||
| Chromium (mg/L) | D | 0.05 | 0.05–NR | 0.1 | 0.05 | |||
| Copper (mg/L) | D | 2 | 0.5–1.5 | 1.3 | 0.02 | |||
| Iron (mg/L) | D | 0.5 | 0.30–NR | - | 1 | |||
| Lead (mg/L) | D | 0.01 | 0.01–NR | - | 0.05 | |||
| Manganese (mg/L) | D | 0.10 | 0.1–0.3 | - | 0.1 | |||
| Cobalt (mg/L) | D | - | - | - | ||||
| Cadmium (mg/L) | D | 0.003 | 0.003–NR | 0.005 | 0.01 | |||
| Nickel (mg/L) | D | 0.07 | 0.02–NR | - | 0.05 | |||
| Zinc (mg/L) | D | 3 | 5–15 | - | 5 | |||
| Mercury (mg/L) | D | 0.006 | 0.001–NR | 0.002 | 0.001 |
| Serial No. | Index (References) | No of Selection Parameters | Formation of Sub-Indices | Establish Weights | Aggregation Method |
|---|---|---|---|---|---|
| 1 | Horton Index [8] | 8 | ✓ | ✓ | ✓ |
| 2 | Fuzzy Index [112] | No guidelines | Fuzzy logic | ✓ | Fuzzy logic |
| 3 | National Sanitation Foundation (NSFWQI) [9] | 11 | ✓ | ✓ | ✓ |
| 4 | Prati Index [81] | 13 | ✓ | ✓ | ✓ |
| 5 | Water Contamination Index [18] | 6 | ✓ | * | ✓ |
| 6 | Weighted Arithmetic Index (AW-WQI) [113] | 2 | ✓ | ✓ | ✓ |
| 7 | Walski and Parker Index [114] | 10 | ✓ | ✓ | ✓ |
| 8 | Harkins Index [115] | No guidelines | ✓ | ✓ | ✓ |
| 9 | SRDD Index [10] | 10 | ✓ | ✓ | ✓ |
| 10 | Ross Index [116] | 4 | ✓ | ✓ | ✓ |
| 11 | Storet Index [117] | No guidelines | ✓ | ✓ | ✓ |
| 12 | Stoner Index [83] | 13 | ✓ | ✓ | ✓ |
| 13 | Bascarón Index [103] | 23 | ✓ | ✓ | ✓ |
| 14 | Deininger Index [88] | 11 | ✓ | ✓ | ✓ |
| 15 | Tiwari and Mishra Index [118] | 14 | ✓ | ✓ | ✓ |
| 16 | Bhargava Index [16] | 4 | ✓ | ✓ | ✓ |
| 17 | Dinius Index [119] | 12 | ✓ | ✓ | ✓ |
| 18 | House Index [102] | 9 | ✓ | ✓ | ✓ |
| 19 | Smith Index [82] | 7 | ✓ | ✓ | ✓ |
| 20 | Anzali Index [120] | 9 | ✓ | ✓ | ✓ |
| 21 | Dojlido Index [111] | 7 | ✓ | * | ✓ |
| 22 | British Columbia Index [13,121] | 4 | * | * | * |
| 23 | Aquatic toxicity Index [122] | 12 | ✓ | ✓ | ✓ |
| 24 | Oregon Index [15] | 8 | ✓ | ✓ | ✓ |
| 25 | Canadian Index (CCMEWQI) [12] | 4 | * | * | * |
| 26 | Contact Recreation Index [123] | 8 | ✓ | * | ✓ |
| 27 | Hallock Index [95] | 8 | ✓ | * | ✓ |
| 28 | Dalmatian Index [63] | 9 | ✓ | ✓ | ✓ |
| 29 | Overall Index of Pollution [14] | 8 | ✓ | ✓ | ✓ |
| 30 | River Status Index [11] | 13 | ✓ | * | ✓ |
| 31 | Kaurish Index [124] | 9 | ✓ | * | ✓ |
| 32 | Schiff Index [125] | 9 | ✓ | * | ✓ |
| 33 | Universal Index [126] | 12 | ✓ | ✓ | ✓ |
| 34 | Malaysia Index [17] | 6 | ✓ | ✓ | ✓ |
| 35 | Catalan Index [127] | 5 | ✓ | ✓ | ✓ |
| 36 | Hanh Index [80] | 11 | ✓ | * | ✓ |
| 37 | Almeida Index [108] | 9 | ✓ | ✓ | ✓ |
| 38 | Ved Prakash Index [7] | 4 | ✓ | ✓ | ✓ |
| 39 | Modified Canadian Index (MCWQI) [128] | 4 | * | * | * |
| 40 | Vaal Index [19] | 15 | ✓ | ✓ | ✓ |
| 41 | Wanda Index [129] | 7 | ✓ | ✓ | ✓ |
| 42 | Medeiros Index [130] | 11 | ✓ | ✓ | ✓ |
| 43 | Garcia-Ávila Index [131] | 13 | ✓ | ✓ | ✓ |
| 44 | West Java Index [132] | 17 | ✓ | ✓ | ✓ |
| 45 | Drinking Water Quality Index [101] | 17 | ✓ | ✓ | ✓ |
| 46 | Wastewater Water Quality Index [71] | 23 | ✓ | ✓ | ✓ |
| Index (References) | WQI Applications Reviewed by Government Agencies Allowed | WQI Applications Reported and Applied in Country | Advantages | Disadvantages |
|---|---|---|---|---|
| National Sanitation Foundation (NSFWQI) [9] | Maharashtra Pollution Control Board (15 May 2014). Compilation of Water Quality Data Recorded by MPCB 2011-12. 〈http://mpcb.gov.in/ereports/pdf/Water_Quality_Report_2011-12_TERI.pdf〉 12 March 2020 Central Pollution Control Board, Government of India (2003). 〈http://mpcb.gov.in/images/pdf/WaterQuality0709/Chapter3_WQ.pdf〉 5 April 2020. USEPA (1974). Water Quality Index Application in Kansas River Basin. 〈http://nepis.epa.gov/Exe/ZyPDF.cgi/20008TH7.PDF?Dockey=20008TH7.PDF〉 19 June 2020. | USA, India [9,133] | The data can be obtained in a single index value with a goal, quick and compete more effectively. Assessment of changes in water quality in multiple regions. Index values refer to the possible utilisation of water. | It is not a particular use of water since it describes a general quality of water. Some data are lost during manipulation. |
| Weighted Arithmetic Index (AW-WQI) [113] | Not Applicable | India [134] | It comprises the values of different physical-chemical water quality parameters in a mathematical calculation demonstrating the environmental status of the water. It represents the importance of each parameter in water quality assessment and management. It can be applied to characterise the suitability of water for human usage. | This index may not give adequate details on the real water quality situation. This index does not contain all variables that can characterise water quality. This index measures only the direct impact of pollution on the water body. |
| Oregon Index [15] | Oregon Department of Water Quality. (2014). 〈http://www.deq.state.or.us/lab/wqm/docs/wqiAnnualRep2014.pdf〉 16 January 2021. Oregon Department of Environmental Quality. (1993). 〈http://www.oregondeq.com/lab/wqm/wqindex/malowy3.htm〉 2 June 2020. Idaho Department of Environmental Quality (2002). 〈https://www.deq.idaho.gov/media/457032-assessment_river_entire.pdf〉 6 January 2020. | Oregon, USA Idahu, USA [15,74,79] | Through use of weighted harmonics to aggregate sub-indexes allows the OWQI to control the most affected parameters. The formulation is sensitive to environmental conditions and has major effects on the quality of water. | It does not give conclusive information on changes in habitat, toxicity, or biology concentrations. It is unable to assess all health toxicity (bacteria, elements, toxics). |
| Canadian Index (CCMEWQI) [12] | Water Quality results for New Brunswick watersheds. http://www2.gnb.ca/content/gnb/en/departments/elg/environment/content/water/content/watersheds.html〉 15 September 2020. CCME Water Quality Index 1.0 User’s Manual. http://www.ccme.ca/files/Resources/calculators/WQI%20User’s%20Manual%20(en).pdf〉 24 December 2020. The British Columbia Water Quality Index. 〈http://www.env.gov.bc.ca/wat/wq/BCguidelines/indexreport.html〉 9 October 2020. | Spain, Canada [135,136,137] | Simple to measure. It has low sensitivity for missing data. High adaptability to various water consumption. The analysis of data from automatic sampling is sufficient. | In determining the index, all parameters are of equal significance. The quality of the water is only partially defined. It cannot be combined with other biological data or indicators. F1 doesn’t operate effectively if there are too few parameters taking into account. |
| Malaysian Index [17] | DoE Malaysia (2002). Malaysia environmental quality report 2001. Putrajaya, Malaysia: Department of Environment, Ministry of Science, Technology, and Environment | Malaysia [17] | Some basic water quality parameters are comprised. The width of each parameter is specified to estimate the effect of the database. | TThe use of water is not taken into account. There are no biological parameters. |
| Fuzzy Index [112] | Not Applicable | Spain [75] | Natural language simple to interpret May deal with a vague and complicated situation Can explain several nonlinear connections by simple rules Will provide a mathematically transparent model Can address missing information without affecting the WQI value Free of uncertainty and with careful selection of parameters can reflect different water quality purposes Can account for interconnection between parameters (interdependencies) | Simple to manage or can be biassed because of people subjectivity To some degree rigidity (alert parameter selection can decreases it) Not free of eclipsing, but trial and error mechanism can be done Cannot include water quality parameters recommendations |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akhtar, N.; Ishak, M.I.S.; Ahmad, M.I.; Umar, K.; Md Yusuff, M.S.; Anees, M.T.; Qadir, A.; Ali Almanasir, Y.K. Modification of the Water Quality Index (WQI) Process for Simple Calculation Using the Multi-Criteria Decision-Making (MCDM) Method: A Review. Water 2021, 13, 905. https://doi.org/10.3390/w13070905
Akhtar N, Ishak MIS, Ahmad MI, Umar K, Md Yusuff MS, Anees MT, Qadir A, Ali Almanasir YK. Modification of the Water Quality Index (WQI) Process for Simple Calculation Using the Multi-Criteria Decision-Making (MCDM) Method: A Review. Water. 2021; 13(7):905. https://doi.org/10.3390/w13070905
Chicago/Turabian StyleAkhtar, Naseem, Muhammad Izzuddin Syakir Ishak, Mardiana Idayu Ahmad, Khalid Umar, Mohamad Shaiful Md Yusuff, Mohd Talha Anees, Abdul Qadir, and Yazan Khalaf Ali Almanasir. 2021. "Modification of the Water Quality Index (WQI) Process for Simple Calculation Using the Multi-Criteria Decision-Making (MCDM) Method: A Review" Water 13, no. 7: 905. https://doi.org/10.3390/w13070905
APA StyleAkhtar, N., Ishak, M. I. S., Ahmad, M. I., Umar, K., Md Yusuff, M. S., Anees, M. T., Qadir, A., & Ali Almanasir, Y. K. (2021). Modification of the Water Quality Index (WQI) Process for Simple Calculation Using the Multi-Criteria Decision-Making (MCDM) Method: A Review. Water, 13(7), 905. https://doi.org/10.3390/w13070905









