Modeling Bacterial Regrowth and Trihalomethane Formation in Water Distribution Systems
Abstract
1. Introduction
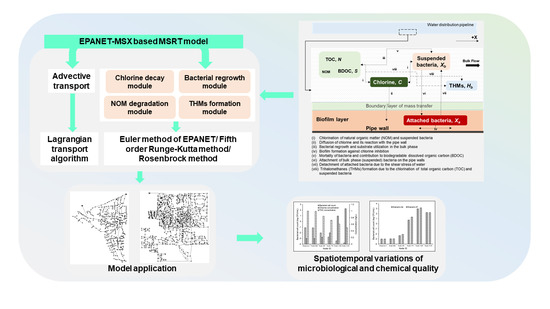
2. Model Development
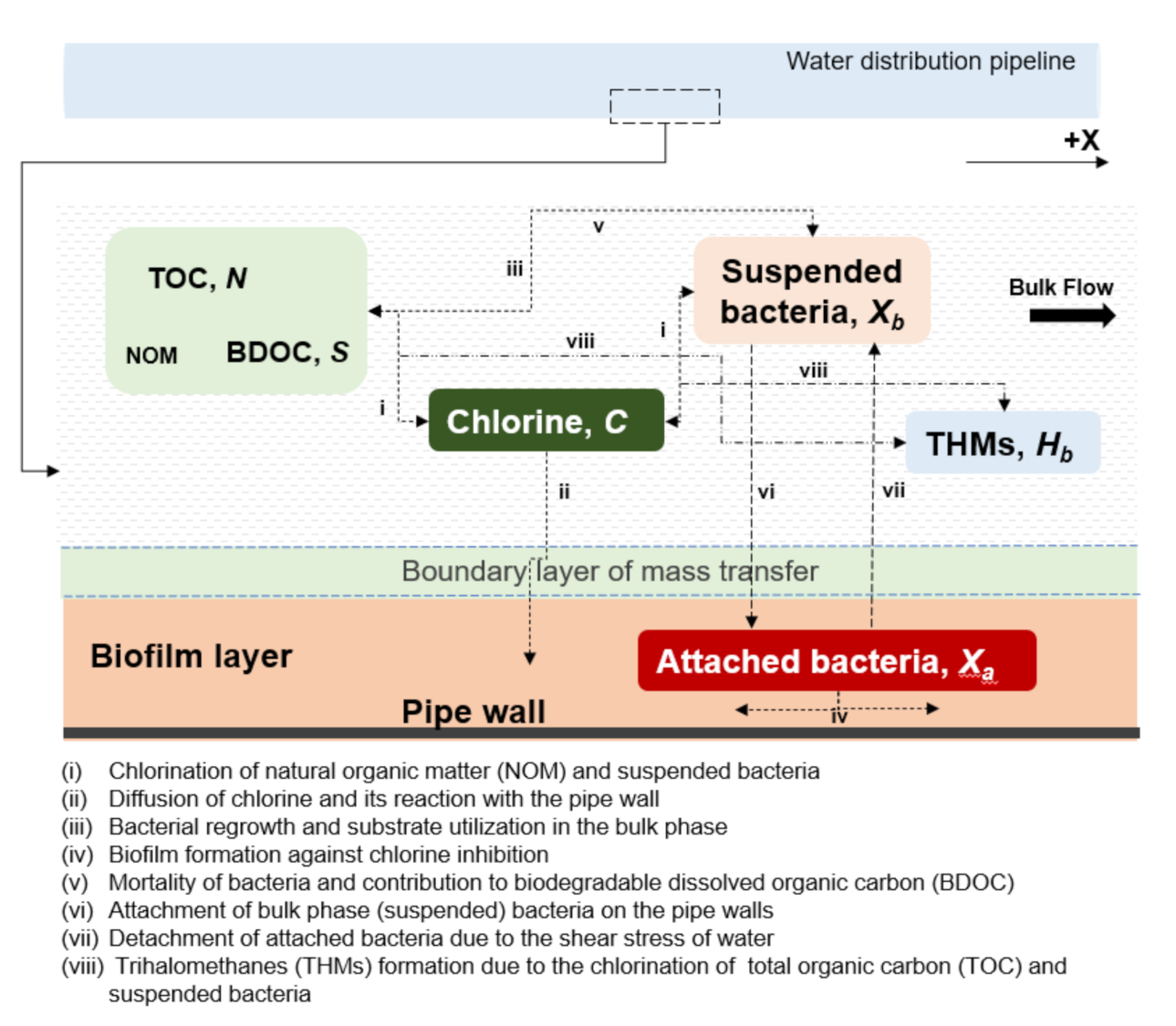
2.1. Conceptual Model
2.2. Multispecies Interactions
2.3. Numerical Model
2.4. Model Implementation
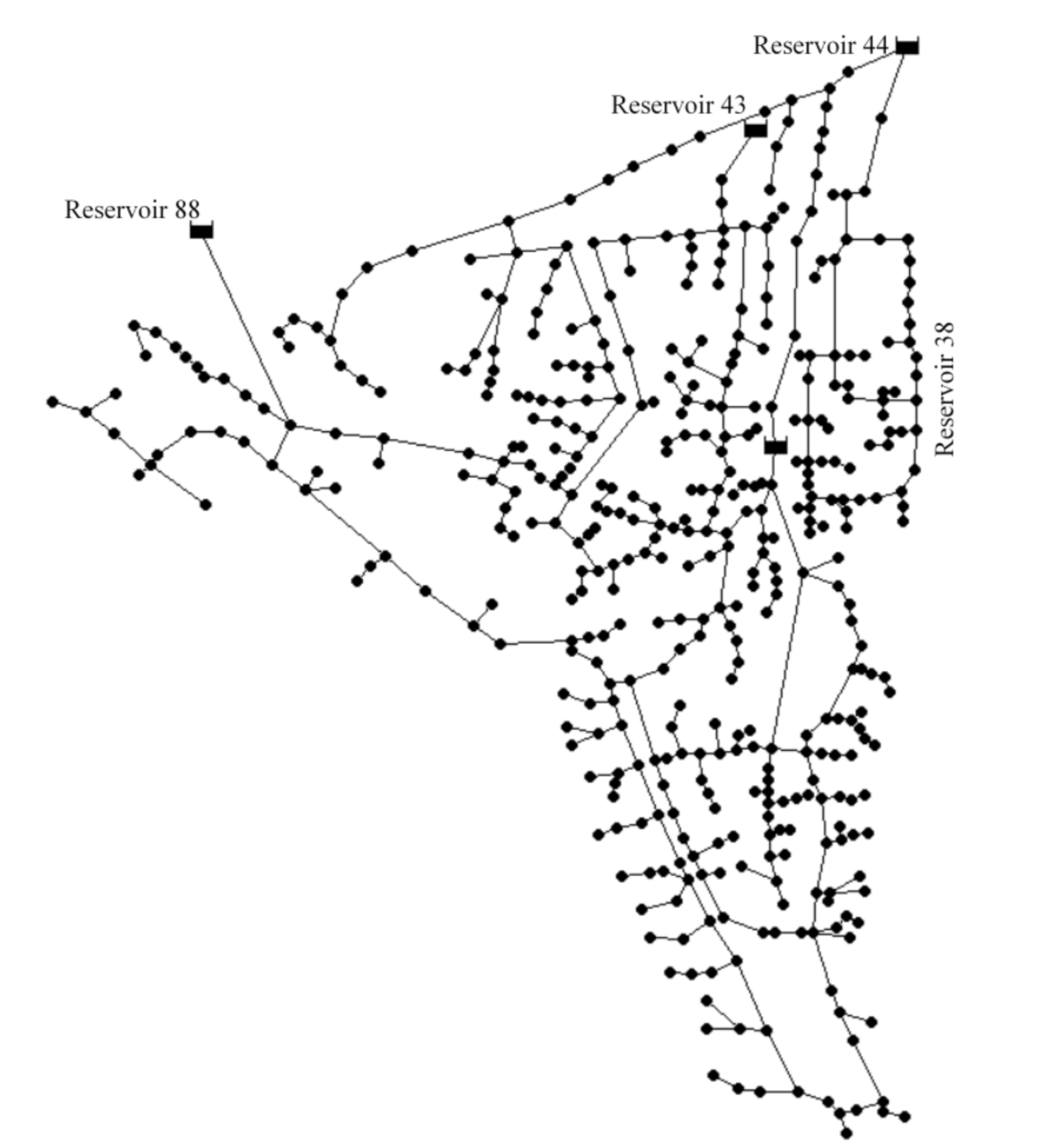
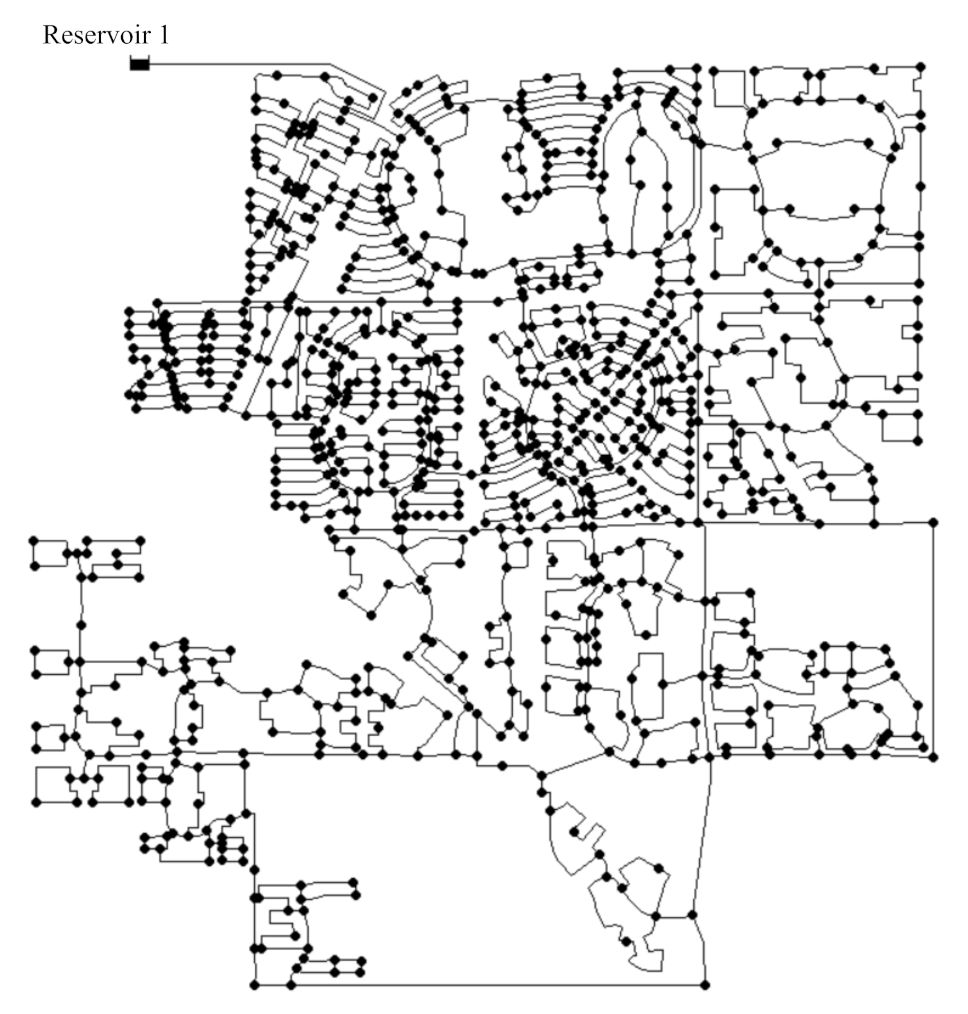
3. Model Application
3.1. Test Problems
3.2. Test Conditions
3.3. Results and Discussion
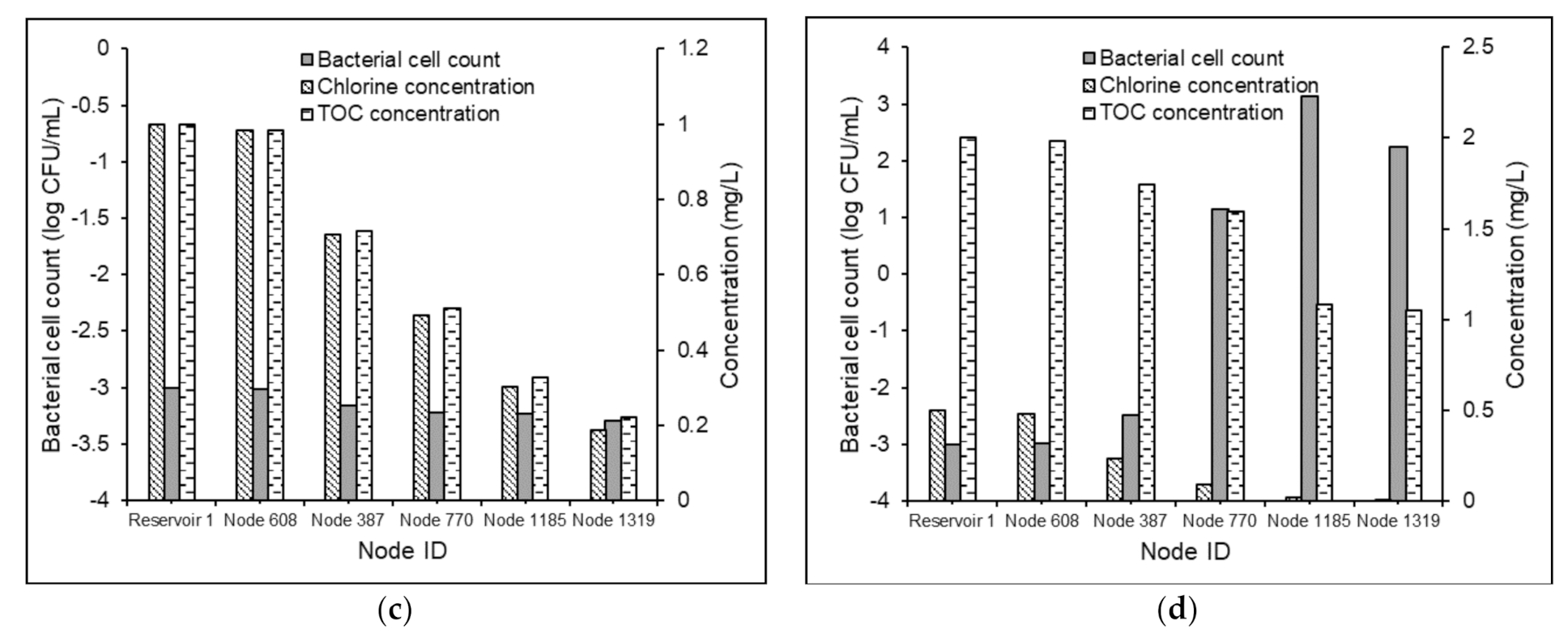
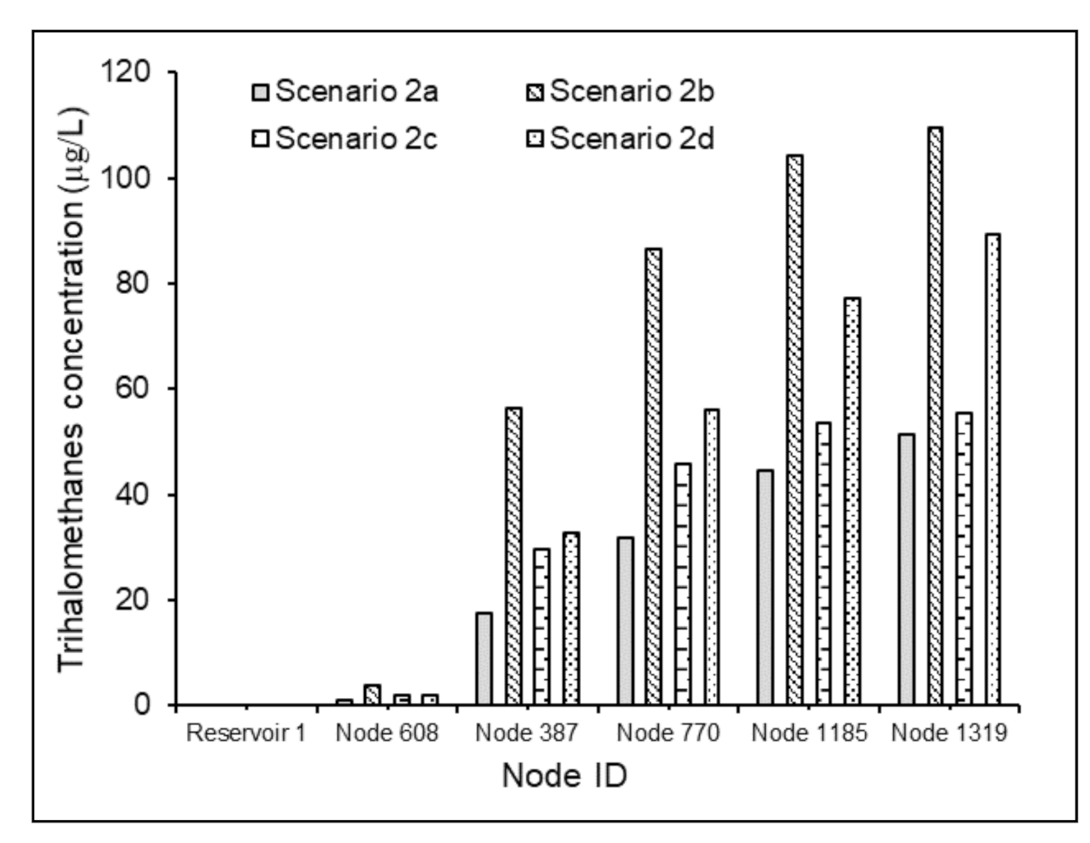
3.3.1. Effects of Source Water Characteristics
3.3.2. Effects of Water Residence Times
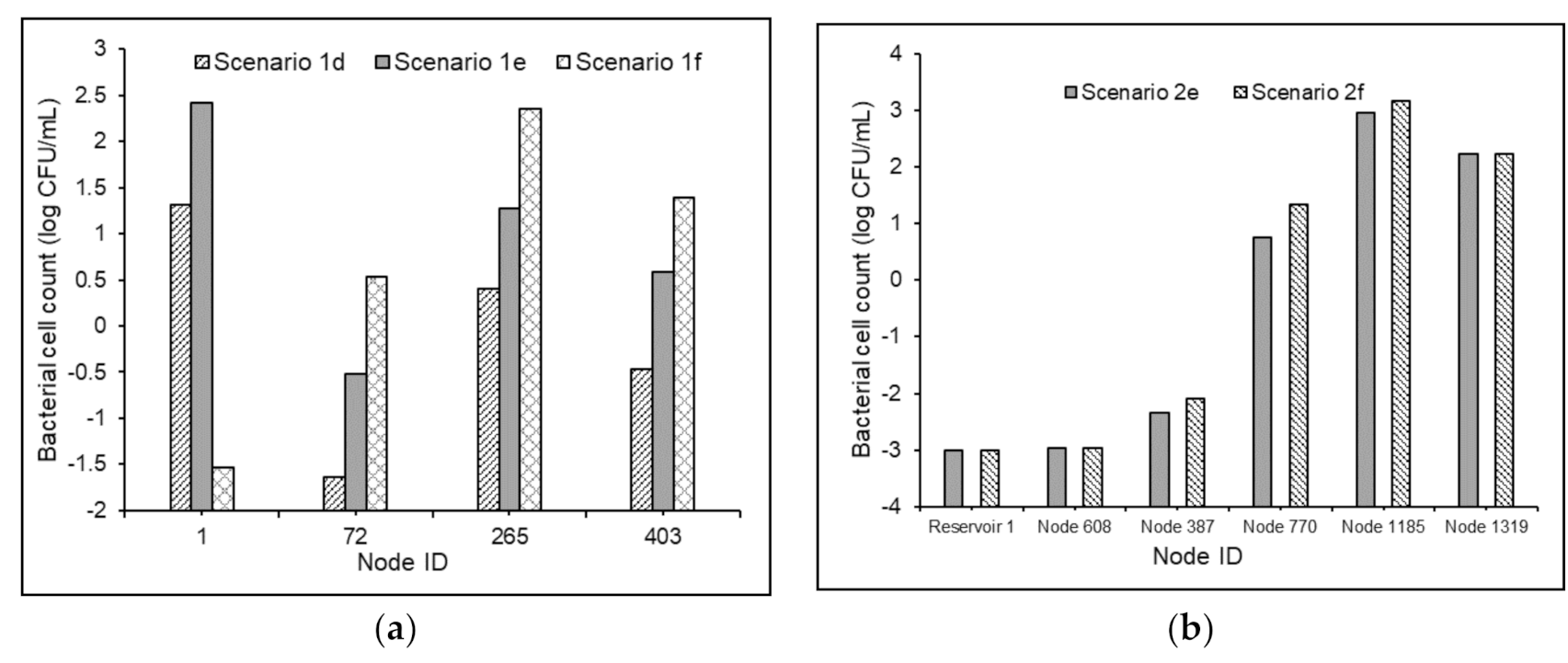
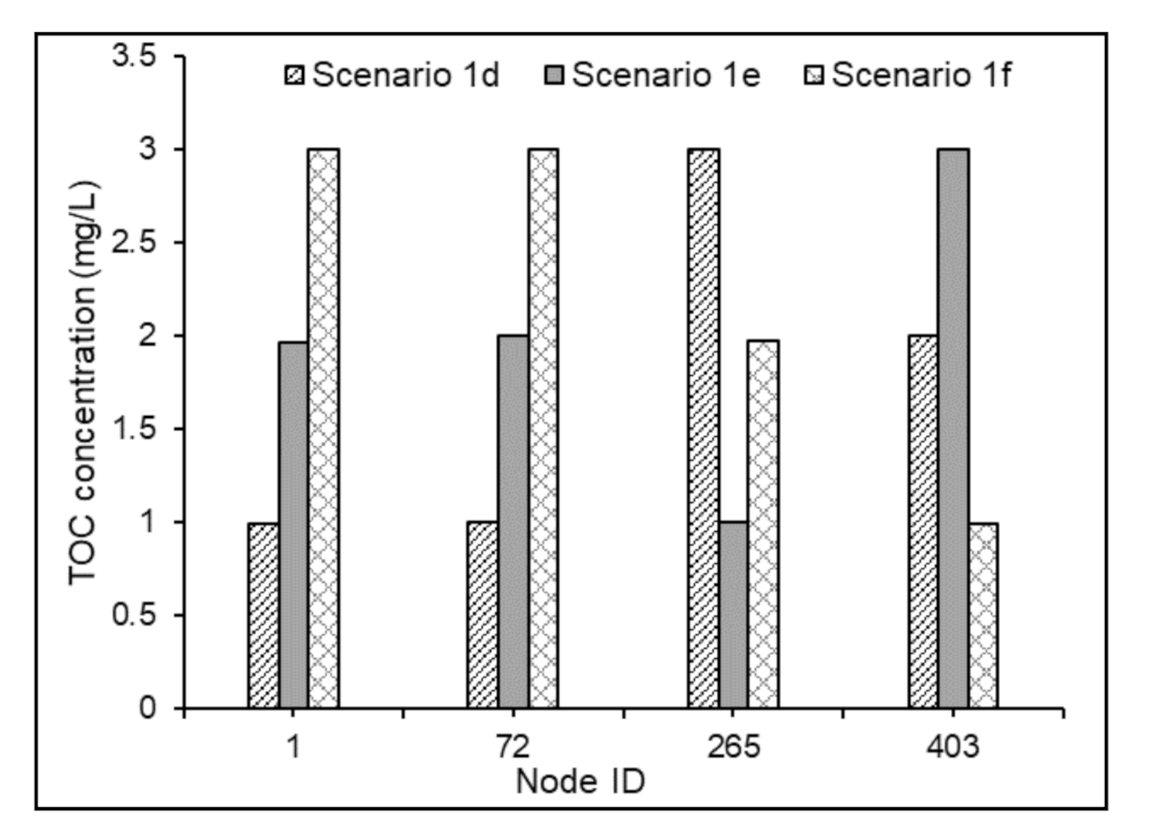
3.3.3. Water Quality Modeling in Non-chlorinated Systems
4. Parameter Sensitivity Analysis
4.1. Deterministic Sensitivity Analysis Procedure
4.2. Sensitivity of Model Parameters
4.2.1. Parameter Sensitivity on Bacterial Regrowth Module Outputs
4.2.2. Parameter Sensitivity on Chlorine Decay Module Outputs
4.2.3. Parameter Sensitivity on THM Formation Module Outputs
4.3. Parameter Sensitivity under Non-chlorinated Conditions
5. Limitations of the Study and Future Scope
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, L.; Xing, X.; Hu, C.; Wang, H. One-year survey of opportunistic premise plumbing pathogens and free-living amoebae in the tap-water of one northern city of China. J. Environ. Sci. 2019, 77, 20–31. [Google Scholar] [CrossRef] [PubMed]
- Albert, M.; Hijnen, W.; Van Vossen, J.; Blokker, M. Modelling Bacterial Biomass in a Non-chlorinated Drinking Water Distribution System. Procedia Eng. 2017, 186, 127–134. [Google Scholar] [CrossRef]
- Lu, C.; Biswas, P.; Clark, R.M. Simultaneous transport of substrates, disinfectants and microorganisms in water pipes. Water Res. 1995, 29, 881–884. [Google Scholar] [CrossRef]
- Servais, P.; Laurent, P.; Billen, G.; Gatel, D. Development of a Model of BDOC and Bacterial Biomass Fluctuations in Distribution Systems. Rev. Sci. Eau 1995, 8, 427–462. [Google Scholar]
- Dukan, S.; Levi, Y.; Piriou, P.; Guyon, F.; Villon, P. Dynamic modelling of bacterial growth in drinking water networks. Water Res. 1996, 30, 1991–2002. [Google Scholar]
- Munavalli, G.R.; MohanKumar, M.S. Dynamic simulation of multicomponent reaction transport in water distribution systems. Water Res. 2004, 38, 1971–1988. [Google Scholar] [CrossRef] [PubMed]
- Horn, H.; Reiff, H.; Morgenroth, E. Simulation of growth and detachment in biofilm systems under defined hydrodynamic conditions. Biotechnol. Bioeng. 2003, 81, 607–617. [Google Scholar] [CrossRef]
- Zhang, W.; Miller, C.T.; DiGiano, F.A. Bacterial Regrowth Model for Water Distribution Systems Incorporating Alternating Split-Operator Solution Technique. J. Environ. Eng. 2004, 130, 932–941. [Google Scholar] [CrossRef]
- Monteiro, L.; Carneiro, J.; Covas, D.I.C. Modelling chlorine wall decay in a full-scale water supply system. Urban Water J. 2020, 17, 754–762. [Google Scholar] [CrossRef]
- Abokifa, A.A.; Yang, Y.J.; Lo, C.S.; Biswas, P. Investigating the role of biofilms in trihalomethane formation in water distribution systems with a multicomponent model. Water Res. 2016, 104, 208–219. [Google Scholar] [CrossRef]
- Abhijith, G.R.; Mohan, S. Cellular Automata-based Mechanistic Model for Analyzing Microbial Regrowth and Trihalomethanes Formation in Water Distribution Systems. J. Environ. Eng. 2021, 147, 04020145. [Google Scholar] [CrossRef]
- Digiano, F.A.; Zhang, W. Uncertainty analysis in a mechanistic model of bacterial regrowth in distribution systems. Environ. Sci. Technol. 2004, 38, 5925–5931. [Google Scholar] [CrossRef] [PubMed]
- Shang, F.; Uber, J.G.; Rossman, L.A. EPANET Multi-Species Extension User’s Manual; Risk Reduction Engineering Laboratory, US Environmental Protection Agency: Cincinnati, OH, USA, 2007; p. 115. [Google Scholar]
- Rossman, L.A. EPANET 2: Users Manual; National Risk Management Research Laboratory, US Environmental Protection Agency: Cincinnati, OH, USA, 2000. [Google Scholar]
- Naser, G.; Karney, B.W. A 2-D transient multicomponent simulation model: Application to pipe wall corrosion. J. Hydro-Environ. Res. 2007, 1, 56–69. [Google Scholar] [CrossRef]
- Huck, P.M. Measurement of biodegradable organic matter and bacterial growth potential in drinking water. J. Am. Water Work. Assoc. 1990, 82, 78–86. [Google Scholar] [CrossRef]
- Escobar, I.C.; Randall, A.A.; Taylor, J.S. Bacterial growth in distribution systems: Effect of assimilable organic carbon and biodegradable dissolved organic carbon. Environ. Sci. Technol. 2001, 35, 3442–3447. [Google Scholar] [CrossRef]
- Kim, D.; Chung, S.; Lee, S.; Choi, J. Relation of microbial biomass to counting units for Pseudomonas aeruginosa. Afr. J. Microbiol. Res. 2012, 6, 4620–4622. [Google Scholar] [CrossRef]
- Picioreanu, C.; Van Loosdrecht, M.C.M.; Heijnen, J.J. Two-Dimensional Model of Biofilm Detachment Caused by Internal Stress from Liquid Flow. Biotechnol. Bioeng. 2001, 70, 205–218. [Google Scholar] [CrossRef]
- Nieuwenhuijsen, M.J.; Toledano, M.B.; Eaton, N.E.; Fawell, J.; Toledano, B.; Eaton, E.; Elliott, P.; Nieuwenhuijsen, J. Chlorination Disinfection Byproducts in Water and Their Association with Adverse Reproductive Outcomes: A Review. Occup. Environ. Med. 2000, 57, 73–85. [Google Scholar] [CrossRef] [PubMed]
- Sohn, J.; Amy, G.; Cho, J.; Lee, Y.; Yoon, Y. Disinfectant decay and disinfection by-products formation model development: Chlorination and ozonation by-products. Water Res. 2004, 38, 2461–2478. [Google Scholar] [CrossRef]
- Wang, J.; Liu, X.; Wai, T.; Xiao, J.; Chow, A.T.; Keung, P. Disinfection byproduct formation from chlorination of pure bacterial cells and pipeline biofilms. Water Res. 2013, 47, 2701–2709. [Google Scholar] [CrossRef]
- Domínguez-Tello, A.; Arias-Borrego, A.; García-Barrera, T.; Gómez-Ariza, J.L. A two-stage predictive model to simultaneous control of trihalomethanes in water treatment plants and distribution systems: Adaptability to treatment processes. Environ. Sci. Pollut. Res. 2017, 24, 22631–22648. [Google Scholar] [CrossRef]
- Clark, R.M.; Sivaganesan, M. Predicting Chlorine Residuals in Drinking Water: Second Order Model. J. Water Resour. Plan. Manag. 2002, 128, 152–161. [Google Scholar] [CrossRef]
- Chen, X.; Stewart, P.S. Chlorine penetration into artificial biofilm is limited by a reaction-diffusion interaction. Environ. Sci. Technol. 1996, 30, 2078–2083. [Google Scholar] [CrossRef]
- Bois, F.Y.; Fahmy, T.; Block, J.C.; Gatel, D. Dynamic modeling of bacteria in a pilot drinking-water distribution system. Water Res. 1997, 31, 3146–3156. [Google Scholar] [CrossRef]
- Schrottenbaum, I.; Uber, J.; Ashbolt, N.; Murray, R.; Janke, R.; Szabo, J.; Boccelli, D. Simple Model of Attachment and Detachment of Pathogens in Water Distribution System Biofilms. In Proceedings of the World Environmental and Water Resources Congress 2009, Kansas City, MO, USA, 17–21 May 2009; ASCE: Reston, VA, USA; pp. 145–157. [Google Scholar]
- Clark, R.M.; Sivaganesan, M. Predicting Chlorine Residuals and Formation of TTHMs in Drinking Water. J. Environ. Eng. 2002, 124, 1203–1210. [Google Scholar] [CrossRef]
- Kiéné, L.; Lu, W.; Lévi, Y. Relative importance of the phenomena responsible for chlorine decay in drinking water distribution systems. Water Sci. Technol. 1998, 38, 219–227. [Google Scholar] [CrossRef]
- Abhijith, G.R.; Mohan, S. Random Walk Particle Tracking embedded Cellular Automata model for predicting temporospatial variations of chlorine in water distribution systems. Environ. Process. 2020, 7, 271–296. [Google Scholar] [CrossRef]
- Camper, A.K. Factors Limiting Microbial Growth in Distribution Systems: Laboratory and Pilot-Scale Experiments; American Water Works Association: Denver, CO, USA, 1996. [Google Scholar]
- Billen, G.; Servais, P.; Bouillot, P.; Ventresque, C. Functioning of biological filters used in drinking-water treatment—the Chabrol model. J. Water Supply Res. Technol. 1992, 41, 231–241. [Google Scholar]
- Characklis, W.G.; Marshall, K.C. Biofilms; Wiley: New York, NY, USA, 1990; ISBN 0-471-82663-4. [Google Scholar]
- Clark, R.M. Chlorine demand and TTHM formation kinetics: A second-order model. J. Environ. Eng. 1998, 124, 16–24. [Google Scholar] [CrossRef]
- Hernandez-Lopez, R.D.; Tzatchkov, V.G.; Martin-Dominguez, A.; Alcocer-Yamanaka, V.H. Study of hydraulics and mixing in roof tanks used in intermittent water supply. J. Water Sanit. Hyg. Dev. 2016, 6, 547–554. [Google Scholar] [CrossRef]
- Eliades, D.G.; Kyriakou, M.; Vrachimis, S.G.; Polycarpou, M.M. EPANET-MATLAB Toolkit: An Open-Source Software for Interfacing EPANET with MATLAB. In Proceedings of the Computing and Control for the Water Industry (CCWI) 2016, Amsterdam, The Netherlands, 4 August 2016; pp. 1–8. [Google Scholar]
- Reca, J.; Martínez, J. Genetic algorithms for the design of looped irrigation water distribution networks. Water Resour. Res. 2006, 42, 1–9. [Google Scholar] [CrossRef]
- Bi, W.; Dandy, G.C.; Maier, H.R. Improved genetic algorithm optimization of water distribution system design by incorporating domain knowledge. Environ. Model. Softw. 2015, 69, 370–381. [Google Scholar] [CrossRef]
- Kang, D.; Lansey, K. Revisiting Optimal Water-Distribution System Design: Issues and a Heuristic Hierarchical Approach. J. Water Resour. Plan. Manag. 2012, 138, 208–217. [Google Scholar] [CrossRef]
- Hozalski, R.M.; Bouwer, E.J.; Goel, S. Removal of natural organic matter (NOM) from drinking water supplies by ozone-biofiltration. Water Sci. Technol. 1999, 40, 157–163. [Google Scholar] [CrossRef]
- Loucks, D.P.; Beek, E. Van Water Resources Systems Planning and Management: An Introduction to Methods, Models And Applications, 1st ed.; UNESCO: Paris, France, 2005; ISBN 9231039989. [Google Scholar]
- Lele, U.N.; Watve, M.G. Bacterial growth rate and growth yield: Is there a relationship? Proc. Indian Natl. Sci. Acad. 2014, 80, 537–546. [Google Scholar] [CrossRef]


| Parameter | Value/Formula | Unit | Reference | Base Value Selected |
|---|---|---|---|---|
| L/mg-C.s | [29] | - | ||
| L/CFU.s | [10] | - | ||
| 1.04 × 10−7–1.43 × 10−5 | m/s | [30] | 1.04 × 10−7 m/s | |
| 0.0072 | mg/m2.s | [12] | ||
| 1.39 × 10−5–4.2 × 10−4 | 1/s | [6,31] | 4.2 × 10−4 1/s | |
| 7.2 × 10−16–6.1 × 10−10 | mg-C/CFU.s | [26] | 8.6 × 10−7 1/s | |
| 0.05–1.20 | mg-C/L | [32,33] | 0.195 mg-C/L | |
| 0.007–1.50 | mg-C/mg-C | [26] | 0.007 × 106 CFU/mg-C | |
| 0.05–5.0 | L/mg-Cl | [6,10,26] | 0.35 L/mg-Cl | |
| 37 | °C | [12] | 37 °C | |
| 7 | °C | [12] | 7 °C | |
| 0.59 ± 0.15 | mg-C/mg-Cl | [26] | 0.34 × 106 CFU/mL | |
| 0.4–4.88 | mg-C/mg-Cl | [34] | 0.98 mg-C/mg-Cl | |
| a | 0.3 | - | [5] | 0.3 |
| 9 × 10−7–1.8 × 10−5 | 1/s | [6,26] | 6.3 × 10−5 1/s | |
| 5.5 × 10−6–4.2 × 10−4 | 1/s | [26] | ||
| 4 × 10−4 | 1/s | [6] | 6.618 × 10−7 m.s/g | |
| 6.618 × 10−7 | m.s/g | [27] | ||
| Blasius equation | g.m/s2 | [7] | Temperature effects on water dynamic viscosity | |
| 3–3000 | - | [26] | 100 | |
| 5.68–188.20 | µg-THM /mg-Cl | [28,34] | 118.435 µg-THM /mg-Cl | |
| 4.487 | µg-THM /mg-Cl | [10] | 4.487 µg-THM /mg-Cl |
| Scenario ID | Reservoir ID 38 | Reservoir ID 43 | Reservoir ID 44 | Reservoir ID 88 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C0 * | Xb0 * | N0 * | C0 | Xb0 | N0 | C0 | Xb0 | N0 | C0 | Xb0 | N0 | |
| Scenario 1a | 0.5 | 0.01 | 1.0 | 1.0 | 0.1 | 2.0 | 2.0 | 1 | 3.0 | 0.5 | 10 | 1.0 |
| Scenario 1b | 1.0 | 0.1 | 2.0 | 2.0 | 1 | 3.0 | 0.5 | 10 | 1.0 | 1.0 | 100 | 2.0 |
| Scenario 1c | 2.0 | 1 | 3.0 | 0.5 | 10 | 1.0 | 1.0 | 100 | 2.0 | 2.0 | 0.01 | 3.0 |
| Scenario 1d | - | 0.01 | 1.0 | - | 0.1 | 2.0 | - | 1 | 3.0 | - | 10 | 1.0 |
| Scenario 1e | - | 0.1 | 2.0 | - | 1 | 3.0 | - | 10 | 1.0 | - | 100 | 2.0 |
| Scenario 1f | - | 1 | 3.0 | - | 10 | 1.0 | - | 100 | 2.0 | - | 0.01 | 3.0 |
| Scenario ID | Water Quality Characteristics in the Reservoir ID 1 | |
|---|---|---|
| Scenario 2a | 0.5 | 1.0 |
| Scenario 2b | 1.0 | 2.0 |
| Scenario 2c | 0.5 | 2.0 |
| Scenario 2d | 1.0 | 1.0 |
| Scenario 2e | - | 1.0 |
| Scenario 2f | - | 2.0 |
| Parameter | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Bacterial Regrowth Module | Chlorine Decay Module | THM Formation Module | |||||||
| Scenario 1a | Scenario 1b | Scenario 1c | Scenario 1a | Scenario 1b | Scenario 1c | Scenario 1a | Scenario 1b | Scenario 1c | |
| 0.435 | 0.952 | 0.882 | −0.488 | −0.583 | −0.543 | 0.995 | 0.995 | 0.996 | |
| −1.116 | −1.747 | −1.749 | - | −0.001 | - | - | - | - | |
| 0.022 | 0.005 | 0.003 | −0.018 | −0.017 | −0.015 | −0.001 | −0.001 | −0.002 | |
| 2.433 | 2.148 | 2.145 | - | 0.002 | 0.002 | - | - | - | |
| 0.002 | 0.001 | 0.001 | - | - | - | - | - | - | |
| −0.689 | −0.542 | −0.906 | - | −0.001 | −0.001 | - | - | - | |
| 0.002 | 0.011 | 0.016 | - | −0.003 | −0.002 | - | - | - | |
| −0.551 | −0.833 | −0.821 | - | −0.001 | −0.001 | - | - | - | |
| −1.116 | −1.747 | −1.749 | - | - | - | - | - | - | |
| −0.194 | −0.437 | −0.357 | 0.101 | 0.141 | 0.126 | −0.014 | −0.017 | −0.008 | |
| a | - | - | - | - | - | - | - | - | - |
| −0.080 | −0.077 | −0.082 | - | - | - | - | - | - | |
| . | −1.184 | −0.567 | −0.499 | - | - | - | - | - | - |
| 0.003 | 002 | 0.003 | - | - | - | - | - | - | |
| 0.003 | 0.005 | 0.003 | - | - | - | - | - | - | |
| - | - | - | - | - | - | 1.000 | 1.000 | 1.000 | |
| - | - | - | - | - | - | - | - | - | |
| Parameter | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bacterial Regrowth Module | Chlorine Decay Module | THM Formation Module | ||||||||||
| Scenario 2a | Scenario 2b | Scenario 2c | Scenario 2d | Scenario 2a | Scenario 2b | Scenario 2c | Scenario 2d | Scenario 2a | Scenario 2b | Scenario 2c | Scenario 2d | |
| 1.831 | 3.211 | 3.658 | 0.474 | −2.121 | −3.483 | −5.217 | −0.835 | 0.996 | 0.993 | 0.994 | 0.995 | |
| −3.837 | −2.942 | −2.563 | −5.099 | −0.066 | −0.198 | −0.055 | - | 0.006 | 0.006 | 0.001 | - | |
| 0.183 | 0.105 | 0.061 | 0.280 | −0.086 | −0.083 | −0.080 | −0.092 | −0.015 | −0.009 | −0.008 | −0.012 | |
| 35.327 | 24.195 | 43.618 | 10.610 | 0.646 | 1.964 | 0.987 | - | −0.056 | −0.060 | −0.038 | - | |
| - | - | - | - | - | - | - | - | - | - | - | - | |
| −14.172 | −7.627 | −10.193 | −6.091 | −0.287 | −0.828 | −0.317 | - | - | 0.024 | 0.015 | - | |
| 2.102 | 1.850 | 1.916 | - | −0.026 | −0.097 | −0.055 | - | 0.002 | 0.002 | −0.001 | - | |
| −1.522 | −1.427 | −1.420 | −1.469 | −0.026 | −0.091 | −0.022 | - | 0.002 | 0.003 | 0.001 | - | |
| −3.837 | −2.942 | −2.563 | −5.099 | −0.065 | −0.188 | −0.041 | - | 0.006 | 0.006 | 0.002 | - | |
| −8.576 | −6.580 | −3.000 | −10.282 | 1.173 | 2.028 | 1.373 | 1.588 | −0.128 | −0.127 | −0.058 | −0.378 | |
| a | - | 0.001 | 0.001 | - | - | - | - | - | - | - | - | - |
| −1.103 | −0.628 | −0.935 | −0.553 | −0.021 | −0.059 | −0.031 | - | 0.002 | 0.002 | 0.001 | - | |
| −9.367 | −5.445 | −8.017 | −4.799 | −0.183 | −0.533 | −0.273 | - | 0.016 | 0.016 | 0.011 | - | |
| 0.008 | 0.007 | 0.007 | 0.001 | - | - | - | - | - | - | - | - | |
| - | - | - | - | - | - | - | - | - | - | - | - | |
| - | - | - | - | - | - | - | - | 1.000 | 1.000 | 1.000 | 1.000 | |
| - | - | - | - | - | - | - | - | - | - | - | - | |
| Parameter | |||||
|---|---|---|---|---|---|
| Test Problem 1 | Test Problem 2 | ||||
| Scenario 1d | Scenario 1e | Scenario 1f | Scenario 2e | Scenario 2f | |
| - | - | - | - | - | |
| - | - | - | - | ||
| - | - | - | - | - | |
| 2.727 | 2.726 | 2.711 | 33.359 | 32.105 | |
| - | - | - | - | - | |
| −0.674 | −0.743 | −0.773 | −10.730 | −6.736 | |
| 0.002 | 0.001 | 0.013 | 2.002 | 1.843 | |
| - | - | - | - | - | |
| - | - | - | - | - | |
| - | - | - | - | - | |
| a | - | - | - | - | - |
| −0.062 | −0.062 | −0.062 | −0.839 | −0.641 | |
| −0.552 | −0.552 | −0.551 | −7.194 | −5.554 | |
| 0.002 | 0.001 | 0.001 | 0.001 | 0.001 | |
| - | - | - | - | - | |
| - | - | - | - | - | |
| - | - | - | - | - | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abhijith, G.R.; Kadinski, L.; Ostfeld, A. Modeling Bacterial Regrowth and Trihalomethane Formation in Water Distribution Systems. Water 2021, 13, 463. https://doi.org/10.3390/w13040463
Abhijith GR, Kadinski L, Ostfeld A. Modeling Bacterial Regrowth and Trihalomethane Formation in Water Distribution Systems. Water. 2021; 13(4):463. https://doi.org/10.3390/w13040463
Chicago/Turabian StyleAbhijith, Gopinathan R., Leonid Kadinski, and Avi Ostfeld. 2021. "Modeling Bacterial Regrowth and Trihalomethane Formation in Water Distribution Systems" Water 13, no. 4: 463. https://doi.org/10.3390/w13040463
APA StyleAbhijith, G. R., Kadinski, L., & Ostfeld, A. (2021). Modeling Bacterial Regrowth and Trihalomethane Formation in Water Distribution Systems. Water, 13(4), 463. https://doi.org/10.3390/w13040463