Abstract
2,4,6-trichloroanisole (2,4,6-TCA) formation is often reported as a cause of taste and odor (T&O) problems in water distribution systems (WDSs). The biosynthesis via microbial O-methylation of 2,4,6-trichlorophenol (2,4,6-TCP) is the dominant formation pathway in distribution pipes. This paper attempted to utilize the reported data on the microbial O-methylation process to formulate deterministic kinetic models for explaining 2,4,6-TCA formation dynamics in WDSs. The pipe material’s critical role in stimulating O-methyltransferases enzymatic activity and regulating 2,4,6-TCP bioconversion in water was established. The kinetic expressions formulated were later applied to develop a novel EPANET-MSX-based multi-species reactive-transport (MSRT) model. The effects of operating conditions and temperature in directing the microbiological, chemical, and organoleptic quality variations in WDSs were analyzed using the MSRT model on two benchmark systems. The simulation results specified chlorine application’s implication in maintaining 2,4,6-TCA levels within its perception limit (4 ng/L). In addition, the temperature sensitivity of O-methyltransferases enzymatic activity was described, and the effect of temperature increase from 10 to 25 °C in accelerating the 2,4,6-TCA formation rate in WDSs was explained. Controlling source water 2,4,6-TCP concentration by accepting appropriate treatment techniques was recommended as the primary strategy for regulating the T&O problems in WDSs.
1. Introduction
The propagation of water parcels through water distribution systems (WDSs) alters its physical, chemical, and biological characteristics. Thus, the main task during WDS operation is to distribute microbiologically and chemically safe and aesthetically pleasing drinking water. Globally, water with color (turbidity) and off-flavor is considered unhealthy, and taste and odor (T&O) perception in the water is a common symptom of water quality failure. In addition, the discoloration and T&O problems may mask the graver concerns related to microbiological and chemical quality failures. To this end, many countries have executed non-mandatory (secondary) standards to guide the aesthetic and organoleptic quality of drinking water [1]. A recent study found out that the traditional characterization measures and the prevailing secondary standards [2] for some chemical contaminants are insufficient to minimize the T&O issues in WDSs [3]. These findings are linked with the increased demand for drinking water quality with improved human living standards. Incidentally, understanding the causes and mechanisms of the formation of T&O problems in WDSs gains significance.
The T&O problems in the delivered drinking water may be caused by the ubiquitous presence of off-flavor compounds in the source water [4]. However, studies conducted in different parts of the globe support the argument that the T&O problems in the delivered water have their principal origin inside the distribution pipe networks [5]. The abiogenic T&O issues in WDSs, caused by leaching from pipes [6] and the formation of disinfection by-products (DBPs) [7], could be sufficiently resolved by pipe material replacing and/or by reducing organic matter content. However, the biogenic T&O issues in WDSs are challenging to control due to their low molecular weights [1]. This necessitates critical investigation on the crucial role of biofilm growth and planktonic microbial regrowth in causing the WDS T&O problems.
As a definite sensory process, out of T&O, taste is seldom a problem in WDSs, and most “tastes” are concerned almost exclusively with odors [8,9]. Nonetheless, in the vernacular concerning drinking water, the terms “taste” and “odor” are generally combined. The definition of T&O problems in WDSs and the evaluation methods are detailed in Supplementary Materials Section 1. The human olfactory system can recognize various T&O and distinguish the different chemicals in the water [10]. The T&O recognized by the water consumers are commonly described as earthy, musty, chlorinous, grassy, swampy, septic, sulfide, hay-like, manure, geranium, fishy, moldy, paint-like, woody, marshy, iodoform-like, medicinal, phenol, aromatic, and petroleum [5,8]. Out of the above, the T&O problem most frequently reported in WDSs is “earthy-musty flavor” and is known to be caused predominantly by the presence of geosmin (GSM, earthy) [11], 2-methylisoborneol (2-MIB, musty) [4], and 2,4,6-trichloroanisole (2,4,6-TCA, musty) [6] in water. The olfactory threshold of 2,4,6-TCA is very low (30 ng/L) compared to that of GSM (4 ng/L) and 2-MIB (9 ng/L) [12]. Interestingly, 2,4,6-TCA concentrations as high as 122.3 ng/L have been detected in a WDS of China [13]. A more recent survey conducted by [14] in 11 Chinese cities revealed a very high detection frequency of haloanisoles (including 2,4,6-TCA), ranging between 78 and 100%, in the tap water. The water quality investigation conducted in France by [12] discovered the individual or combined presence of 2,4,6-TCA in causing earthy–musty odor problems in >75% of the tap water, untreated groundwater, and untreated surface water samples tested. Likewise, a study conducted in Sweden also reported the detection of 2,4,6-TCA with concentrations varying between 0.5 and 2.0 ng/L in a lake water source [15].
Although 2,4,6-TCA is frequently detected and induces serious organoleptic effects, its formation pathways in WDSs were not well-explored compared to GSM and 2-MIB until lately. Recent research identified two independent pathways for 2,4,6-TCA formation [16]: chlorination of anisole in natural organic matter (NOM); microbial O-methylation of precursor 2,4,6-trichlorophenol (2,4,6-TCP). The formation of 2,4,6-TCA via para-position substitution by chlorine reactions with anisole occurs only at very acidic conditions (pH = 4) [17]. Hence, biomethylation is regarded as its dominant formation pathway in WDSs [18].
The precursor for 2,4,6-TCA formation by bioconversion, 2,4,6-TCP, is a toxic environmental pollutant and is commonly detected in drinking water sources [19]. During the microbial O-methylation process, the microorganisms, utilizing chlorophenol O-methyltransferases (CPOMTs) enzyme, transfer a methyl group from donors to the hydroxyl group of 2,4,6-TCP [20]. This is similar to the SN2 reaction where the nucleophile attacks the substrate, donates an electron pair to the new bond, and replaces the leaving group (a substitution). CPOMTs is a category of methyltransferases, a mix of enzymes, of which over 95% uses S-adenosyl methionine (SAM) as the methyl donor [21]. Apart from SAM, the other methyl donors include methanol, methylamines, and methanethiol, which are amply present as NOM in the natural waters [20]. Since 2,4,6-TCA is less toxic than its precursor 2,4,6-TCP, the microbial O-methylation process could be regarded as a detoxification mechanism [22].
Recently, [16] investigated the formation of 2,4,6-TCA by the microbial O-methylation process in a pilot-scale WDS by conducting “long column-type” experiments. From the experimental dataset, they proposed a pseudo-first-order kinetic model to explain 2,4,6-TCA formation kinetics. However, their model (kinetic parameters) did not incorporate the effects of microbial quantity, 2,4,6-TCP concentration, temperature, flow velocity, pipe material, and free chlorine in the formation of 2,4,6-TCA. Likewise, due to the empirical nature of this model, its extension for predicting 2,4,6-TCA formation in real-world WDSs becomes impracticable. This paper specifically addresses this issue by developing a mechanistic multi-species reactive-transport (MSRT) model allowing deterministic investigations of the occurrence of T&O issues due to 2,4,6-TCA formation in WDSs.
The present study attempted to conceptualize the biosynthesis of 2,4,6-TCP via microbial O-methylation process based on the inferences reported by [16,20]. The reaction kinetics pertaining to 2,4,6-TCP degradation and 2,4,6-TCA formation was transformed into deterministic kinetic model equations based on scientific knowledge. The data extracted from [16] were applied to calibrate the developed kinetic models, and the role and influence of microbial density and temperature on the bioconversion of 2,4,6-TCP to 2,4,6-TCA were deterministically evaluated. The kinetic models depicting the relationship between the microbial density and 2,4,6-TCP degradation and/or 2,4,6-TCA formation were integrated with the governing equations of the existing microbial regrowth model by [23], and an MSRT model capable of predicting microbiological and organoleptic quality variations in WDSs was developed. The MSRT model, implemented using the multi-species extension of EPANET (EPANET-MSX) [24], considers the advective transport and reactions of chlorine, NOM, microorganisms, and 2,4,6-TCP in WDSs. Simulations were conducted within two benchmark systems, and the resulted output includes concentrations of the relevant biotic and abiotic parameters signifying the physicochemical and biological interactions in WDSs. The simulations presented herein are of the natural occurrence of T&O issues in WDSs, as the outcome of the interactions between the microbiota and 2,4,6-TCP, under operating conditions relevant to WDSs all over the world.
The proposed MSRT model was developed as a simulation engine to aid in the design of WDSs, specifically to meet the microbiological and organoleptic quality constraints of drinking water. The model is generic, and due to this reason, any configuration of the WDS could be incorporated into the model in discerning the T&O variations of the delivered water at different locations. In addition, the paper aims to set a potential base for future elaboration in applying the model to pilot or real-world systems. In this regard, the simulation results may help future research to conduct experimental/field investigation to understand and control the various factors that affect the T&O problems in WDSs. The precision in measuring quality parameters such as microbial cell counts, chlorine, NOM, 2,4,6-TCP, and 2,4,6-TCA will become pertinent then. Measuring minor variations in these parameters poses a challenge. Nonetheless, highly accurate and sensitive analytical methods have already been developed and can be applied in the context of WDSs.
The remainder of the paper is systematized as follows: Section 2 explains the derivation of deterministic kinetic expressions to define the 2,4,6-TCP degradation and 2,4,6-TCA formation, utilizing the dataset reported by [16]. Section 3 presents the conceptual and numerical details of the proposed MSRT model. Section 4 features the MSRT model application on two WDSs to demonstrate the spatial distribution of microbiological, chemical, and T&O issues under different operating and temperature conditions. Limitations and conclusions of the present study are summarized in Section 5 and Section 6, respectively.
2. Reaction Kinetics of Microbial O-Methylation Process
2.1. Modeling 2,4,6-TCP Degradation and 2,4,6-TCA Formation
It is postulated that the detoxification of 2,4,6-TCP and biosynthesis of 2,4,6-TCA by microbial O-methylation are performed by the planktonic microorganisms present in WDSs. Thus, a first-order model (Equation (1)) was developed to simulate 2,4,6-TCP degradation based on the assumption that the planktonic microbial density governs the reaction kinetics and the bulk phase 2,4,6-TCP concentration limits the reaction rate.
where is the 2,4,6-TCP concentration (mg/L); is time (h); is the effective 2,4,6-TCP degradation constant (1/h). The value of the kinetic constant, depends on the concentration of planktonic microbial cell count in water.
The formation of 2,4,6-TCA is presumed to have the same rate as that of the degradation of 2,4,6-TCP. Thus, a yield coefficient [25] was applied to simulate the 2,4,6-TCA formation, as shown in Equation (2).
where is the 2,4,6-TCA concentration (ng/L) and is the effective yield coefficient corresponding to 2,4,6-TCA formation (ng/mg). It is assumed that the 2,4,6-TCA formation yield has first-order dependence on the planktonic microbial density and zero-order dependence on both CPOMT enzymatic synthesis and methyl donor distribution in the bulk water. These assumptions were accepted to accommodate the knowledge gap in comprehending the effects of CPOMTs on non-SAM methyl donors in WDSs [20].
For a closed system with no continuous flow of reactants entering the system or products leaving the system, the previous equations (Equations (1) and (2)) were analytically solved to obtain the temporal distribution of 2,4,6-TCP and 2,4,6-TCA.
where and are the initial concentrations of 2,4,6-TCP (mg/L) and 2,4,6-TCA (ng/L), respectively.
2.2. Selection and Extraction of Literature Data
The model equations (Equations (3) and (4)) were applied to the experimental dataset of [16] for 2,4,6-TCA formation due to microbial O-methylation at different residence times in a pilot-scale reactor. The experimental setup consisted of three closed loops made of polyethylene (PE), stainless steel (SS), and ductile iron (DI) pipes of 150 mm diameter. The pipes used were approximately 80 m long. The reported dataset corresponds to the experiments conducted, using tap water spiked with 2,4,6-TCP concentration as 0.2 mg/L, at three flow velocities (0.1, 0.6, and 1.4 m/s) in two different water temperatures (20 and 30 °C). The other basic parameters of the tap water used were: total organic matter (TOC) = 1.5 ± 0.2 mg/L; conductivity = 35–80 mS/cm; pH = 7.2 ± 0.1; residual chlorine ≤0.05 mg/L. The authors of [16] described the effects of temperature, flow velocity, pipe material, free chlorine, composition, and microbial community diversity on the biosynthesis of 2,4,6-TCA under the test conditions described above. They have also calibrated the kinetic parameters of a pseudo-first-order kinetic model, (ng/L) and (1/h), describing maximum formation concentration of 2,4,6-TCA and rate constant of 2,4,6-TCA formation, respectively, using the experimental dataset. Ideally, the pilot-scale long-column experiments by [16] are comparable to batch-scale closed-system experiments. Hence, the model parameters (Equations (3) and (4)) were related with the and . was equaled with and was related with the ratio of and .
2.3. Estimation of Planktonic Microbial Cell Count
Due to the continuous circulation of the water under substrate-limiting conditions, the steady-state assumption is presumed for planktonic microbial concentration inside the long-column reactor [16]. Thus, Equation (5) was formulated to determine the planktonic microbial cell counts inside the closed loops of the pilot-scale reactor under non-chlorinated conditions.
where is the planktonic microbial cell count (CFU/mL); is the biofilm detachment coefficient (m. h/g); is the shear stress induced by the flow velocity (g. m/h2); is the biofilm concentration (CFU/cm2); is the hydraulic mean radius (m); is the microbial deposition coefficient (1/h); is the natural mortality constant (1/h). The values of , , and were selected as 1.838 × 10−10 m. h/g [26], 0.20 1/h [27], and 0.27 1/h [28], respectively. The Blasius equation [29] (Table S1) defined the flow-induced shear stress at the pipe walls.
To account for the uncertainties associated with the mechanisms defined in Equation (5), a diverse set of estimations (total 27 in number) were made by making ±10% changes to the above-mentioned values of the parameters , , and , and by varying the values of between (3.74 ± 0.65) × 104, (2.22 ± 0.41) × 105, and (3.50 ± 0.51) × 105 CFU/cm2 for PE, SS, and DI pipe loops, respectively [16]. The steady-state model was applied to the long-column experimental cases reported for PE, SS, and DI pipe loops. The estimated planktonic microbial cell counts under 20 °C and non-chlorinated conditions are given in Table 1. The wide disparities in the values of the planktonic microbial cell counts validate the direct effects of the flow velocity in the biofilm layers’ detachment and enhancement of the planktonic microbial density in the bulk water.

Table 1.
Estimated planktonic microbial cell counts inside the pipe loops at 20 °C under non-chlorinated conditions.
2.4. Relationship between Model Parameters and Planktonic Microbial Cell Count
It was postulated that a logarithmic function (Equation (6)) defines the relationship between the kinetics of 2,4,6-TCP degradation due to microbial O-methylation and the planktonic microorganisms (Table 1).
where is the 2,4,6-TCP degradation constant (1/h) and is the empirical microbial activation constant (mL/CFU). The values ( values reported by [16]) were fitted using the proposed logarithmic model, and the values of the parameters and were estimated using linear regression (Microsoft Office Excel 2016 Solver). The best-fitting value of was estimated as 0.002 1/h, and the value of was obtained as 1.37 × 109 mL/CFU, 2.87 × 106 mL/CFU, and 2.15 × 108 mL/CFU for PE, SS, and DI pipe loops, respectively. The obtained values could be considered to infer that the influence of the planktonic microorganisms in 2,4,6-TCP degradation is maximum in the PE pipes and minimum in the SS pipes. Nonetheless, based on the least-squares method, the value of was determined as 5.5 × 107 mL/CFU. The goodness of fit between the predicted and reported values is given in Figure 1a. The R2, p-value ( = 0.05), and F-value (Fcritical = 4.494) for the predictions were obtained as 0.681, 0.684, and 0.172, respectively. Thus, it may be inferred that the model predictions are approximately identical to the experimental data. Furthermore, it would be naïve not to stress the significance of pipe material on the kinetics of 2,4,6-TCP degradation in WDSs. However, the available dataset is insufficient to pursue further in this direction, and hence, additional investigations are recommended.
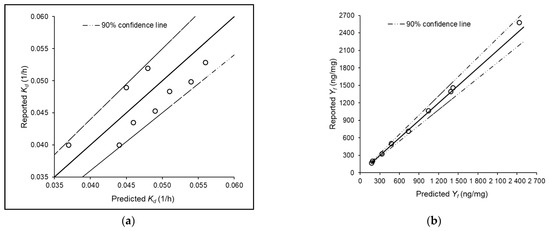
Figure 1.
Goodness of fit between predicted and experimentally derived values of (a) and (b) . The open circle symbol represents the experimentally derived value. The continuous solid line symbolizes the perfect fitting and the dashed line represents 90% confidence line.
As mentioned before, a first-order dependence (Equation (7)) of the planktonic microbial cell count is approximated to the yield of formation of 2,4,6-TCA during the microbial O-methylation of 2,4,6-TCP.
where is the yield coefficient corresponding to 2,4,6-TCA formation by microbial O-methylation (ng.mL/mg.CFU) and is the pipe material-dependent yield coefficient (ng/mg). The value of was determined as 0.429 ng.mL/mg. CFU using linear regression. Remarkably, the values (Table 2) for SS and DI pipe loops were approximately 3 and 6.4 times greater than that of the PE pipe loop. These obvious distinctions in the yield coefficient value could be attributed to the existence of Mn2+ and Mg2+ ions in water, possibly due to leaching from SS and DI pipes, that are reported to enhance the 2,4,6-TCA formation [20] by stimulating O-methyltransferases enzymatic activity [30] in WDSs. However, due to data paucity, the role of metal ions is not verified in the present paper, and further research is suggested. Figure 1b shows the goodness of fit between the model predicted and experimentally derived values. The results confirmed that the predictions of the linear model (Equation (6)) are statistically significant (R2 = 0.999, p-value = 0.950, and F-value = 0.004), and are well-replicating the experimental observations.

Table 2.
Estimated values of pipe-material-dependent yield coefficient and temperature coefficients.
2.5. Effects of Temperature on Model Parameters
The reported dataset corresponding to 20 and 30 °C [16] indicated the critical effects of water temperature on the kinetics of degradation of 2,4,6-TCP and subsequent formation of 2,4,6-TCA. Therefore, a temperature-dependent model (Equations (8) and (9)), derived from the Arrhenius equation, was developed to comprehend the direct role of temperature in enhancing the planktonic microbial activity in the bioconversion of 2,4,6-TCA from 2,4,6-TCP by CPOMTs.
where and are the effective 2,4,6-TCP degradation constant (1/h), and and are the effective yield coefficients corresponding to 2,4,6-TCA formation (ng/mg) at T °C and 20 °C, respectively. and are the temperature coefficient corresponding to and , respectively. The temperature coefficient is defined as the ratio of the activation energy and the average kinetic energy at 20 °C.
Wide variations were observed in the estimated values of and for PE, SS, and DI pipe loops (Table 2). Temperature influence on the reaction kinetic parameters determining 2,4,6-TCP degradation and 2,4,6-TCA formation was obtained to be maximum for the PE pipes and minimum for the SS pipes. Concerning the 2,4,6-TCP degradation kinetic parameter, the value of the temperature coefficient for DI was almost 2.2 times that for SS. In comparison, the same corresponding to 2,4,6-TCA formation yield for DI was almost 1.4 times of SS. Yet, a logical relationship between the temperature coefficient values and the pipe material could not be derived due to the lack of sufficient data. Further investigation might be vital in unmasking the effects of water temperature on the planktonic microbial activity in the biosynthesis of 2,4,6-TCA in WDSs.
3. Development of MSRT Model
3.1. Conceptual Model Development
The conventional MSRT models, investigating the microbiological and chemical quality in WDSs, incorporates the biotic and abiotic reactions between chlorine, NOM, and microbial biomass [23,28,31,32,33]. Nevertheless, a mechanistic model integrating the biological processes relating to 2,4,6-TCP detoxification and 2,4,6-TCA formation with the regrowth dynamics of planktonic microorganisms in WDSs has not been developed to date. The present MSRT model’s novelty hinges on predicting the spatiotemporal distributions of 2,4,6-TCA causing T&O issues in WDSs.
The proposed one-dimensional mechanistic MSRT model integrates the propagation (via advection) and reactions of the following seven species in WDSs: chlorine, total organic carbon (TOC), biodegradable dissolved organic carbon (BDOC), microorganisms (planktonic and biofilm), trihalomethanes (THMs), 2,4,6-TCP, and 2,4,6-TCA (Figure 2). Chlorine is considered the primary disinfectant chemical. TOC indicated the mass of the total organic material, and BDOC signified the biodegradable fraction of NOM utilizable as substrate by the microorganisms in WDSs. The equivalent organic carbon content of the planktonic and biofilm microorganism cells was approximated as 10−9 mg/CFU [34]. THMs were considered the surrogate parameter for DBPs in WDSs [32].
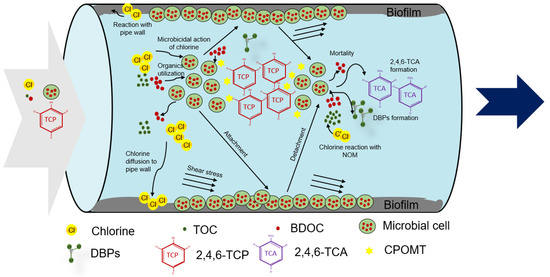
Figure 2.
Schematic representation of multi-species reactive-transport (MSRT) model domain.
The existing scientific knowledge was applied during the model development to define chlorine decay, NOM degradation, planktonic microbial regrowth, biofilm dynamics, and THM formation inside the distribution pipes. For minimizing the interdependent parameters, the mechanisms that cannot be experimentally investigated were omitted. The microbial O-methylation mechanism was abstracted using the model equations defined in the previous section (Section 2). The Monod equation represented the substrate utilization and regrowth of planktonic microbiota, while a simple first-order model denoted the biofilm growth. The direct effects of chlorine and temperature on microbial activity were incorporated via empirical expressions [28,31]. The second-order kinetics was assumed for chlorine reactions with NOM and microbial biomass [35]. Yield coefficients were selected to represent THMs formation by chlorine reactions with NOM [25] and planktonic microorganisms [36]. The natural mortality of microorganisms was modeled using first-order kinetics, and 30% of the dead microbes were assumed to be later contributing as BDOC [37]. A detailed explanation of the multi-species interactions considered in the model formulation is included in Supplementary Materials Section 2.
3.2. Numerical Model Development
The mass balances of all seven species in the distribution pipes are represented using partial and ordinary differential equations of the following form:
The notations denote: = concentration of reactive-species (mg/L); = bulk phase; = wall phase; = distance (m); = number of reactions; = reaction of species . For microorganisms, both the planktonic (bulk phase) and biofilm (wall phase) distribution was considered, while only the bulk phase concentrations were selected for the remaining six reactive species. The bulk phase is the dynamic portion of the pipe in which the advection mechanism controls the axial distribution of the seven model species. On the other hand, the wall phase was approximated as a static portion uniformly distributed over the inner pipe surface. The partial differential equations (Equation (10)) defined the spatiotemporal distributions of the species considered in the bulk phase, and an ordinary differential equation (Equation (11)) represented the biofilm regrowth. The eight governing advective-reactive (AR) equations of the model are defined in the Supplementary Materials Section 3. The values of the kinetic parameters used, and their corresponding literature sources are provided in Table S1.
The mass balance equations of all seven species at the nodes/junctions where two or more pipes meet (Equation (12)) are formulated by assuming that the mixing of the water parcels is complete and instantaneous at the mixing points. The flow-weighted average of concentrations coming from the incoming pipes is assigned as the water parcels’ concentration leaving these nodes after mixing. Accordingly, the concentration of any bulk phase species leaving any node at any time can be expressed as follows:
where = concentration of any bulk phase species at node (mg/L); = number of incoming pipes at node ; = flow rate in pipe (L/s); = concentration of any bulk phase species inside pipe (mg/L); = length of pipe (m); = external source flow rate into node (L/s); = external source concentration of any bulk phase species at node (mg/L); = total number of nodes in the network.
For applying the mass balance equations in the storage tanks, the complete mixing model [38] is selected by assuming that the water parcels entering a tank are completely mixed instantaneously with the previously present water parcels. The complete mixing model is relatively simple, and it requires no extra parameters. Furthermore, the model is suitable to model the storage components operated in a fill-and-draw manner.
3.3. Model Implementation
The concentrations of the seven species at different and values can be derived by solving the model governing equations (Equations (10)–(12) and Equations (S1)–(S8)). In the present study, the AR equations were applied using the EPNET-MATLAB interface [39] to generate .msx files and were solved using the EPANET-MSX dynamic link library (DLL) for Windows. The advection parts of the AR equations were solved with the default Lagrangian transport algorithm, and the reaction parts were solved utilizing the fifth-order Runge–Kutta method with automatic time step control. The EPANET 2.0 [38] DLL for Windows was applied for performing hydraulic analysis.
4. Application of MSRT Model
4.1. Test Networks
The proposed MSRT model was applied to two benchmark problems: the Balerma network [40] and the KLmod network [41]. The schematics of the two test networks are shown in Figures S1 and S2. The Balerma network with four reservoirs, 443 demand nodes, and 454 pipes is an adaptation of the irrigation network in the province of Almeria (Spain). The KLmod network is a single-sourced network consisting of 935 demand nodes and 1274 pipes, meeting the average demand of 29.1 million liters/day. Both the test networks considered were applied in the recent work of [23] to examine the microbial regrowth and DBP formation in WDSs. Balerma and KLmod networks are distinct from each other in terms of configuration and hydraulic characteristics. Hence, the model application in these two test networks would help discern the role of network characteristics in influencing the organoleptic quality variations of the delivered water at different locations and prove the generality of the proposed model. The results presented in Section 2 exhibit the direct influence of the pipe material on microbial O-methylation kinetics in WDSs. Apparently, due to the lack of exact information on the pipe material used in Balerma and KLmod networks, PE was considered as the pipe material. Furthermore, the selection of PE as the pipe material enabled the usage of the kinetic parameters, derived in Section 2, in the MSRT model application without any necessary correction for pipe material.
4.2. Test Conditions
Different test conditions applicable to the normal operation of WDSs worldwide were chosen to elucidate the influence of system operating conditions and source water quality characteristics in determining the microbiological, chemical, and T&O issues in WDSs (Table 3). The water delivered through the two test networks was assumed to be pretreated by processes representing characteristic drinking-water physicochemical treatment processes, including alum coagulation, dynamic settling, and dual media filtration (sand and anthracite) [42]. Chlorine residual is typically maintained in WDSs to prevent microbial regrowth and accidental contamination. Considering the recent drift towards non-chlorinated operation [43], both non-chlorinated and chlorinated ( = 0.5 and 1.0 mg/L) conditions were considered for the simulations. The post disinfection of the pretreated water was supposed to be carried out using sodium hypochlorite under chlorinated conditions.

Table 3.
Test conditions considered for conducting simulations.
BDOC is the fraction of NOM in the delivered water in WDSs that can be assimilated and/or mineralized by the heterotrophic microbial community residing in WDSs [44]. Thus, the BDOC loading of the treated drinking water in the reservoirs was presumed as the determinative factor for the delivered water’s biological stability in WDSs [45]. For the Balerma network simulations, the was varied as 0.01, 0.1, and 0.3 mg/L conforming to substrate-limiting, substrate-well-off, and substrate-rich conditions in WDSs to represent different degrees of biological stability of the delivered water [46]. However, for the KLmod network simulations, the was selected as 0.01 mg/L to signify a biologically stable condition. The values were varied as 0.01, 0.05, 0.1, and 0.2 mg/L for the Balerma network, and for the KLmod network, the same was varied as 0.01 and 0.2 mg/L. The values reflected the fluctuating extent of the 2,4,6-TCP pollution of the source water. The was varied as 10 and 25 °C to corroborate the seasonal variations in the T&O problems in WDSs [16]. The pH of the delivered water was fixed as 7.2 ± 0.1, confirming the USEPA guidelines for drinking water [47].
The water quality analyses of the Balerma network were conducted under two scenarios (Scenarios I and II) corresponding to hydraulic characteristics. The demand-driven hydraulic analysis was performed using EPANET 2.0 DLL. Scenario I corresponded to the condition in which the variations in the pipe flow velocity, water age, and residual pressure at the demand nodes were 0.07–3.38 (average = 0.89) m/s, 0.1–2.63 (average = 1.15 h), and 20–68.46 (average = 32.57) m, respectively. Under Scenario II, the variations in the pipe flow velocity, water age, and residual pressure at the nodes were obtained as 0.01–0.92 (average = 0.23) m/s, 0.1–8.91 (average = 3.04 h), and 22.95–111.21 (average = 60.85) m, respectively. For the KLmod network, the variations in the pipe flow velocity, water age, and residual pressure at the nodes were calculated as 0–2.35 (average = 0.19) m/s, 0.1–24 (average = 6.93) h, 28.35–59.60 (average = 40.08) m, respectively. The distribution of flow velocities, water age, and residual pressure in the pipes and demand nodes of Balerma network (under Scenarios I and II) and KLmod network are schematically depicted in Figures S3–S5. Due to the comparatively lower water age in the Balerma network, the planktonic microbial cell count () value of 0.1 CFU/mL in the source water was used to demonstrate the microbial activity effects on the bioconversion of 2,4,6-TCP. For the KLmod network, = 0.01 CFU/mL was selected to represent the treated water meeting the bacteriological quality requirements for direct human consumption. The simulations of both the test problems were performed with a time step 300 s until a 0.1% convergence in the values of all the reactive species (steady-state condition) was achieved in the nodes.
4.3. Reliability Indices
In the water quality context, reliability can be defined as the probability that the chemical species concentration stays in a safe and standard domain [48]. In this study, the reliability indices were used to compare the effects of the test conditions in managing the microbial regrowth, THM formation, and 2,4,6-TCA formation in WDSs. In this regard, planktonic microbial colony count, THM concentration, and 2,4,6-TCA concentration were considered in determining reliability values, and dedicated functions were formulated to evaluate the indices based on their temporal variations in the demand nodes.
The dedicated evaluation function for 2,4,6-TCA concentration at the demand node at time was defined as follows:
where is the evaluation function for 2,4,6-TCA and is perception threshold concentration for 2,4,6-TCA (ng/L). The value of was selected as 4.0 ng/L [49], and a linear variation of from 1 to 0 was assumed for an increase of the 2,4,6-TCA concentration from 0 to 4.0 ng/L (Equation (13)).
The evaluation functions proposed for microbial biomass () and THM concentrations () are defined in Equations (14) and (15), respectively.
where and are the threshold values for planktonic microbial colony count (CFU/mL) and THM concentration (µg/L), respectively. The values of and were selected as 0.1 CFU/mL and 80 µg THMs/L [50], respectively. The dedicated evaluation functions for 2,4,6-TCA, microbial biomass, and THMs are illustrated in Figure S6.
The proposed water quality reliability indices (, = 1, 2, 3) (Equation (16)) described the temporal variations of 2,4,6-TCA, planktonic microbial biomass, and THMs in the demand nodes ( in number) over the time period .
where is the maximum/desirable value of , i.e., 1. The value of = 0 indicated that the 2,4,6-TCA concentration exceeded 4.0 ng/L at all demand nodes over the considered time period. The second () and third () reliability indices evaluated the feasibility of the WDS operation practice in controlling the microbial regrowth and THM formation, respectively.
4.4. Results and Discussion
Figure 3 and Figure S7 compare the model predicted distribution of 2,4,6-TCA under the non-chlorinated condition in the Balerma network at T = 25 and 10 °C, respectively. The 2,4,6-TCA distribution for the Balerma network with Po = 0.2 mg/L and the KLmod network with Po = 0.01 and 0.2 mg/L are shown in Figure 4 and Figure 5, Figures S8 and S9, respectively. Figure 6 and Figure 7 illustrate the temperature influence on the 2,4,6-TCA distribution under Po = 0.2 mg/L and So = 0.01 mg/L in the Balerma network and KLmod network, respectively. The simulation results obtained on microbiological, chemical, and organoleptic quality under all the test conditions considered are detailed in Table 4 and Table 5, Tables S2 and S3.
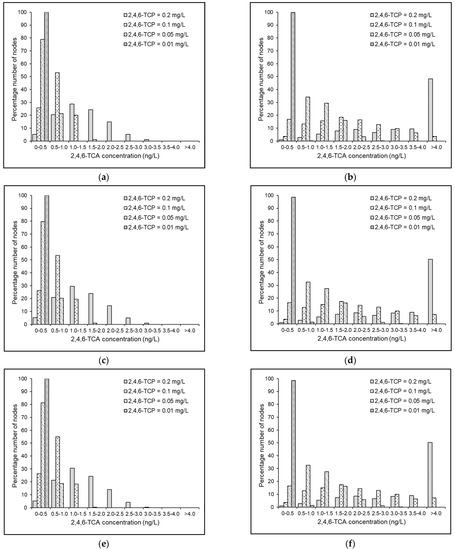
Figure 3.
Predicted distribution of 2,4,6-TCA in the Balerma network under = 25 °C, = (a,b) 0.01, (c,d) 0.1, and (e,f) 0.3 mg/L, Scenario (a,c,e) I and (b,d,f) II, and under non-chlorinated condition.
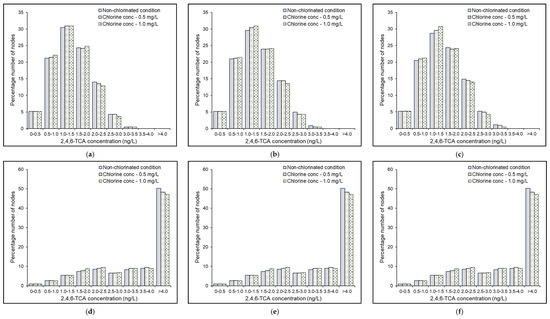
Figure 4.
Predicted distribution of 2,4,6-TCA in the Balerma network under = 25 °C, = 0.2 mg/L, = (a,d) 0.01, (b,e) 0.1, and (c,f) 0.3 mg/L, and Scenarios (a–ca; b; c; ) I and (d–f) II.
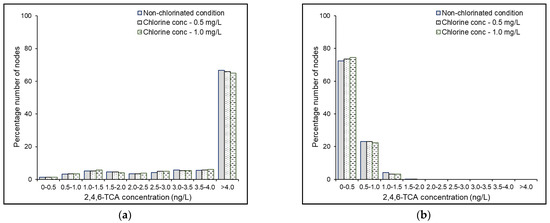
Figure 5.
Predicted distribution of 2,4,6-TCA in the KLmod network under = 25 °C, and = (a) 0.2 and (b) 0.01 mg/L.
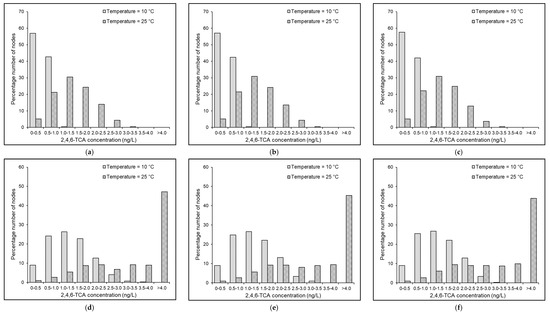
Figure 6.
Predicted distribution of 2,4,6-TCA in the Balerma network under = 0.2 mg/L, = 0.01 mg/L, = (a,d) 0, (b,e) 0.5, and (c,f) 1.0 mg/L, and Scenarios (a–c) I and (d–f) II.
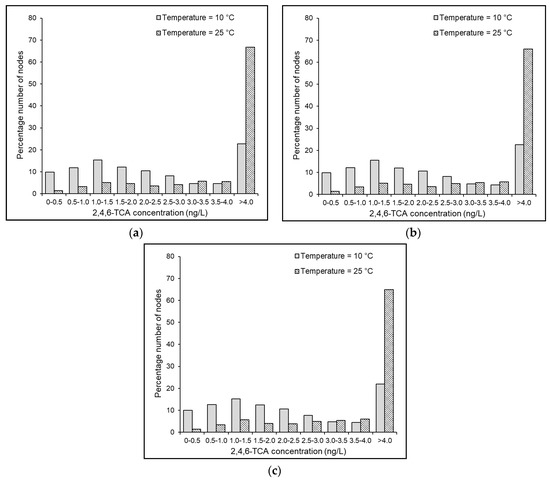
Figure 7.
Predicted distribution of 2,4,6-TCA in the KLmod network under = 0.2 mg/L, (a) non-chlorinated condition and = (a) 0, (b) 0.5, and (c) 1.0 mg/L.

Table 4.
Balerma network simulation results under = 25 °C

Table 5.
Balerma network simulation results under T = 10 °C and Po = 0.2 mg/L.
4.5. Effects of Source 2,4,6-TCP Concentration
For the Balerma network, under the substrate-rich condition and Scenario I, the upsurge in the concentration of 2,4,6-TCP in the source water from 0.01 mg/L to 0.2 mg/L effectuated in increasing the average concentration of 2,4,6-TCA in the demand nodes from 0.07 ng/L to 1.43 ng/L. Under Scenario II, the equivalent increase was from 0.22 ng/L to 4.33 ng/L. For the KLmod network under T = 25 °C, the similar increase in the source concentration of 2,4,6-TCP resulted in increasing the average 2,4,6-TCA concentration from 0.38 ng/L to 7.5 ng/L and increasing the number of demand nodes exceeding the 2,4,6-TCA perception threshold from zero to 624 (out of 935). Thus, it can be inferred that under similar settings concerning biomass density, an increase in the source concentration of 2,4,6-TCP directly affects the 2,4,6-TCA formation inside WDSs [1] (Figure 3 and Figure S7 and Table 4 and Table 5, Tables S2 and S3).
Whilst 2,4,6-TCP has been shown to influence the 2,4,6-TCA formation directly; it is essential to note the effect of water age and the system pressure head in influencing its formation rate. Under substrate-rich condition and Po = 0.2 mg/L, the α1 value under Scenario I was obtained as 0.633. In addition, the T&O at all the demand nodes was lower than its perception threshold (Figure 3e). However, under Scenario II, the α1 value declined to 0.188, and the 2,4,6-TCA concentration exceeded Athres value in 223 (out of 443) demand nodes. Such a greater formation rate of 2,4,6-TCA estimated with the increase in the water age and operating pressure head could be largely attributed to the rise in the planktonic microbial cell count (from 0.182 to 1.818 CFU/mL) and its direct impacts on the kinetics of the microbial O-methylation process (Equations (6) and (7)) in WDSs. Though, it may be argued that 2,4,6-TCP, being toxic, could hinder microbiota activity inside WDSs [51]. Nevertheless, this inhibitory mechanism was not explicitly included in the model formulation. Hence, the apparent decline in the planktonic and biofilm growth rate and its subsequent impact on 2,4,6-TCA formation under high concentrations of 2,4,6-TCP were not reflected in the model predictions (Table 4 and Table 5 and Table S2).
Nonetheless, it is interesting to appraise the comparative significance of 2,4,6-TCP and planktonic microbial density in influencing the bioconversion of 2,4,6-TCP in WDSs. Under the case with very high level of 2,4,6-TCP in the source water ( = 0.2 mg/L) and very rich substrate content ( = 0.3 mg/L), 223 demand nodes were found to exceed the value ( = 0.188) under Scenario II. However, under reduced substrate concentration ( = 0.01 mg/L) and the same source 2,4,6-TCP concentration, the number of demand nodes exceeding the value reduced to 209 ( = 0.195). It was observed that under a drop in the substrate availability in the source water ( from 0.3 to 0.01 mg/L), the average planktonic microbial cell count value in the Balerma network, under Scenario II, reduced from 1.818 to 0.064 CFU/mL. Surprisingly, the number of demand nodes exceeding the T&O perception threshold under the substrate-limiting condition and substrate-rich condition was found almost equal (3.2% difference) (Figure 3). This could be attributed to the response of the planktonic microbial density on the microbial O-methylation process kinetics. At = 25 °C, the 88% reduction in the planktonic microbial activity inside the distribution pipes resulted in declining the scale of the effective 2,4,6-TCP degradation kinetic rate constant and effective 2,4,6-TCA formation yield coefficient only by 12.9% and 0.4%, respectively. The obtained results seem to confirm that compared with the planktonic microbial density, 2,4,6-TCP concentration in the source water is the dominant factor for causing T&O issues in WDSs (Table 4 and Table 5 and Table S2). Hence, based on the simulation outputs, it may be argued that the primary strategy for regulating 2,4,6-TCA formation in WDSs should be to control the levels of its precursor 2,4,6-TCP by accepting appropriate treatment techniques.
4.6. Effects of Source Chlorine Concentration
It has been reported that chlorine can oxidize/chlorinate 2,4,6-TCP and slow down the 2,4,6-TCA formation rate inside WDSs [1,16]. Nevertheless, the mechanisms concerning the chlorination of 2,4,6-TCP were not specifically included in the 2,4,6-TCP degradation module of the MSRT model. Hence, the probable influence of chlorine in suppressing the biosynthesis of 2,4,6-TCA formation via oxidation of 2,4,6-TCP was not replicated in the simulation outputs.
In the Balerma network under the substrate-rich condition at = 25 °C, the diminution in the planktonic microbial cell count by chlorination ( = 0.5 and 1.0 mg/L) under Scenarios I and II was obtained as 34% and 54% and 80% and 96%, respectively (Table 4). For the KLmod network, the corresponding reduction in the planktonic microbial activity via chlorination was estimated at 38% and 59% (Table S2). As anticipated, the chlorination brought out a noticeable impact in controlling the microbial activity in WDSs. Subsequently, the planktonic microbial inactivity slowed down the microbial O-methylation kinetics and declined the formation rate of 2,4,6-TCA inside the system (Figure 4 and Figure 5 and Figures S8 and S9). Hence, it may be inferred that under similar settings concerning the biological stability of water and 2,4,6-TCP concentration, an increase in the chlorine concentration directly suppresses the biosynthesis of 2,4,6-TCA in WDSs.
In this context, it is appropriate to elucidate the impacts of the delivered water’s biological stability in determining the chlorine influence towards directing the organoleptic quality. Under Scenario II in the Balerma network at = 25 °C, the average planktonic microbial cell count and the value under the substrate-rich condition and = 0.5 mg/L were obtained as 0.354 CFU/mL and 0.188, respectively. However, the corresponding values under non-chlorinated conditions were found as 0.222 and 0.195 and 0.064 and 0.208 for substrate-well-off and substrate-limiting conditions. These values seem to validate the importance of the relative concentrations of residual chlorine and substrate availability in determining the microbiological activity [32], and subsequently, the T&O issues inside WDSs. Hence, it may be reasoned that for the Balerma network, improving the biological stability/reducing the substrate loading is more beneficial than inducing chlorination to control 2,4,6-TCA formation (Table 4 and Table 5).
An interesting remark from the simulation results is that the faster planktonic microbial regrowth in the distribution pipes caused by the increased influent concentration of BDOC does not necessarily contribute towards residual chlorine consumption nor THMs formation inside the WDSs (Table 4 and Table 5 and Table S2). Compared with the planktonic microbiota, the significant share of chlorine consumption inside the bulk phase of WDSs was caused by its reactions with TOC (=1.0 mg/L). Correspondingly, the contribution of microbial biomass to the THMS formation was obtained to be subservient compared to that by NOM [33]. This is mainly attributable to the relative values of the second-order kinetic parameters governing the chlorine reactions between NOM and microbial biomass used in the model for the simulations.
4.7. Effects of Temperature
Temperature is known to be an imperative factor affecting the rate and extent of chlorine decay, NOM degradation, planktonic microbial activity, DBP formation, and 2,4,6-TCP degradation in WDSs [20,52]. Due to this reason, the model employed empirical expressions for defining the temperature influence of the reaction kinetics of chlorine (Table S1), planktonic regrowth (Equations (S2)–(S4)), and the microbial O-methylation process (Equations (7) and (8)). For a temperature increase from 10 to 25 °C, the model estimated an almost two-fold (193%) increase in the values of the kinetic rate constants defining the chlorine reactions in the bulk phase. The equivalent increase in the kinetic rate constant defining the planktonic microbial regrowth was 92%. Due to the temperature sensitivity of the CPOMT enzymatic synthesis by the microbiota [20], the increase in the parameter values defining 2,4,6-TCP degradation kinetics and 2,4,6-TCA formation yield for a similar temperature increase was obtained as 70% and 78%, respectively.
Under similar settings concerning planktonic biomass density, a reduced rate of 2,4,6-TCA formation occurred at 10 °C compared to the same at 25 °C (Figure 6 and Figure 7) due to the inferior biosynthetic activity on 2,4,6-TCP at lower temperatures. However, due to the reduced response of the planktonic microbial density on the microbial O-methylation process kinetics at lower temperatures, the planktonic microbial cell count reduction has shown subservient effects over 2,4,6-TCA formation inhibition at = 10 °C than at = 25 °C. As expected, a slower rate for planktonic microbial regrowth, specifically under non-chlorinated conditions, was observed in both the Balerma and KLmod networks under = 10 °C than under = 25 °C (Table 4 and Table 5 and Table S2). Interestingly, a conflicting picture arose when the results corresponding to chlorine application were considered. The average planktonic microbial cell count in the Balerma network under = 0.01 mg/L, = 1.0 mg/L and Scenario II was obtained as 0.038 and 0.022 CFU/mL at = 10 and 25 °C, respectively. At an equivalent chlorine dose and temperature increase, the average planktonic microbial cell count in the KLmod network was obtained as 0.018 and 0.014 CFU/mL. Even though these differences were trivial, they revealed the obvious influence of temperature in shaping the chlorine inhibitory effects on the planktonic microbial activity. Hence, from the obtained results, it may be inferred that even with high chlorine levels, the reduction in the planktonic microbial cell count at lower temperatures is caused primarily by the slower rate of substrate utilization by the microbiota due to the subservient inhibitory effect of chlorine on planktonic microbial activity. Thus, it may be argued that reducing the organic content of the source water is more advantageous than chlorine application in controlling the microbial activity, THM formation, and 2,4,6-TCA formation simultaneously.
4.8. Controlling 2,4,6-TCP Levels in the Source Water
The proposed mechanistic model’s application on the two benchmark problems shed light on the effects of temperature and the levels of 2,4,6-TCP, chlorine, and organic matter in the 2,4,6-TCA formation in WDSs. Out of all factors analyzed, 2,4,6-TCP concentration in the source water was identified as the principal factor influencing the kinetics of microbial O-methylation mechanism leading to the biosynthesis of 2,4,6-TCA. More importantly, microbial regrowth is ubiquitous in drinking water distribution pipes, and the water delivered via WDSs is far from sterile [53]. Regulating the 2,4,6-TCP levels in the source water can thus be regarded as the prime approach for controlling the 2,4,6-TCA formation and subsequent T&O problems. Application of several biological and physicochemical treatment methods such as biodegradation, aquatic phytoremediation, adsorption, membrane separation, ion exchange, solvent extraction, ozonation, and electrochemical oxidation, etc., to remove phenolic pollutants including 2,4,6-TCP from the aqueous environments can be found in the literature [54,55,56].
Among several advanced treatment technologies, adsorption has been proven to be an effective technology for removing 2,4,6-TCP [57]. Some of the natural and synthetic adsorbents, such as biochar derived from macroalgae [58], bentonite modified by exchanging Na+ ions with the cationic surfactant [57], biomass prepared from an agricultural solid waste in the form of Acacia leucocephala bark [59], biomass prepared from Azolla filiculoides [60], biochar prepared from water hyacinth [61], untreated agricultural waste pine cone powder [62], powdered activated carbon [56], have been reported to be useful. However, the difficulty in preparing and characterizing the same hinders their application towards 2,4,6-TCP removal from water [55]. Extensive research on 2,4,6-TCP removal from water continues, and the interest is slowly changing from methods such as adsorption to new technologies such as enzymatic treatment [54,63]. Improvements in the treatment techniques are expected to increase the efficiency of removing phenolic compounds in water, eliminating 2,4,6-TCP in the drinking water sources.
5. Limitations of the Study and Future Scope
The paper developed kinetic models to define the bioconversion of 2,4,6-TCP and simultaneous formation of 2,4,6-TCA in WDSs. Nevertheless, due to data paucity, a detailed examination of the effects of pipe material, metal ions (Mn2+ and Mg2+), and temperature in the microbial O-methylation kinetics were not attempted. Additionally, the present study neglected the effects of CPOMT enzymatic synthesis and methyl donor distribution in the water on 2,4,6-TCA formation. Further investigations are hence required in this direction. The proposed MSRT model applied the computing environment of EPANET-MSX, and so, the simulation results were affected by the numerical constraints of the default Lagrangian transport algorithm. Moreover, the MSRT model utilized the existing scientific knowledge and reported values from the literature to define the interactions between chlorine, NOM, and microbiota inside the WDSs. Nevertheless, the biological and physicochemical reactions may get determined by the pH, water chemistry, and hydraulic conditions to a great extent. The proposed kinetic models applied for microbial regrowth, chlorine decay, NOM degradation, and 2,4,6-TCP bioconversion to 2,4,6-TCA assume the influence of pH, iron, and bromide concentration, ammonia, and phosphate content on the bulk phase reactions is negligible. A detailed experimental investigation may assess the relative significance of all the biotic and biotic factors in controlling the microbiological and organoleptic quality of the delivered water. Thus, a comprehensive experimental/field study may be vital in fine-tuning the model parameters. Therefore, future work intends to calibrate and validate the MSRT model.
6. Conclusions
The long-column experimental dataset by [11] regarding 2,4,6-TCA formation was applied to derive a deterministic model for defining the kinetics of microbial O-methylation process in WDSs. The planktonic microorganisms were found to influence the 2,4,6-TCP degradation kinetics logarithmically, while a linear relationship was established between the 2,4,6-TCA formation yield and the planktonic microbial density. The rate and extent of the bioconversion process were found to be critically influenced by the pipe material, plausibly due to its role in contributing Mn2+ and Mg2+ ions in water and its ensuing impact on stimulating O-methyltransferases enzymatic activity.
The first-ever MSRT model, integrating the biological processes relating to 2,4,6-TCA formation with the regrowth dynamics of planktonic microorganisms, was developed for predicting the spatiotemporal variations of T&O issues in WDSs. The effects of temperature and the levels of 2,4,6-TCP, chlorine, and organic matter in the 2,4,6-TCA formulation were analyzed by applying the MSRT model on two well-tested systems: Balerma and KLmod networks. The simulation results indicated that, under similar settings concerning biomass density, the concentration of 2,4,6-TCP in the source water directly impacts the 2,4,6-TCA formation inside WDSs. Out of all factors, 2,4,6-TCP concentration in WDSs was categorized as the predominant factor influencing the 2,4,6-TCA biosynthesis. Hence, regulating its levels in the source water was recommended as the principal strategy for T&O problem control. Increasing the chlorine levels of the delivered water displayed an evident impact in slowing down the microbial O-methylation kinetics and declining the formation rate of 2,4,6-TCA. However, chlorination was found less effective, specifically at lower temperatures, due to the greater temperature sensitivity of chlorine reactivity. In addition, improved biological stability of source water brought out more significant control of planktonic microbial regrowth and 2,4,6-TCA formation than chlorine addition. Thus, the results corroborated the benefits of BDOC reduction in the source water over inducing chlorination in controlling disinfection by-products and 2,4,6-TCA formation in WDSs.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4441/13/5/638/s1, Figure S1: Schematic of Balerma network, Figure S2: Schematic of KLmod network, Figure S3: Distribution of pipe flow velocity in the Balerma network ((a) Scenario I and (b) Scenario II) and KLmod network, Figure S4: Distribution of water age in the nodes of Balerma network ((a) Scenario I and (b) Scenario II) and KLmod network, Figure S5: Distribution of residual pressure in the nodes of the Balerma network ((a) Scenario I and (b) Scenario II) and KLmod network, Figure S6: Dedicated evaluation functions for the determination of reliability in terms of (a) 2,4,6-TCA, (b) microbial biomass, and (c) THMs, Figure S7: Predicted distribution of 2,4,6-TCA in the Balerma network under = 25 °C, = 0.2 mg/L, = (a,b) 0.01, (c,d) 0.1, and (e,f) 0.3 mg/L, and Scenarios (a,c,e) I and (b,d,f) II, and under non-chlorinated condition, Figure S8: Predicted distribution of 2,4,6-TCA in the Balerma network under = 10 °C, = 0.2 mg/L, = (a,d) 0.01, (b,e) 0.1, and (c,f) 0.3 mg/L, and Scenarios (a–c) I and (d–f) II, Figure S9: Predicted distribution of 2,4,6-TCA in the KLmod network under = 25 °C, and = (a) 0.2 and (b) 0.01 mg/L, Table S1: Values and literature sources of the model parameters used, Table S2: Results of KLmod network simulations, Table S3: Average 2,4,6-TCA concentrations at the nodes and values for the Balerma network under = 10 °C.
Author Contributions
Conceptualization, G.R.A. and A.O.; methodology, G.R.A. and A.O.; investigation, G.R.A.; writing—original draft preparation, G.R.A.; writing—review and editing, A.O.; supervision, A.O.; project administration, A.O.; funding acquisition, A.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by a grant from the Ministry of Science & Technology of the State of Israel and Federal Ministry of Education and Research (BMBF), Germany.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhou, X.; Zhang, K.; Zhang, T.; Li, C.; Mao, X. An ignored and potential source of taste and odor (T&O) issues—Biofilms in drinking water distribution system (DWDS). Appl. Microbiol. Biotechnol. 2017, 101, 3537–3550. [Google Scholar] [CrossRef]
- USEPA. National Secondary Drinking Water Regulations EPA 570/9-76-000; USEPA: Washington, DC, USA, 1979.
- Dietrich, A.M.; Burlingame, G.A. Critical Review and Rethinking of USEPA Secondary Standards for Maintaining Organoleptic Quality of Drinking Water. Environ. Sci. Technol. 2015, 49, 708–720. [Google Scholar] [CrossRef] [PubMed]
- Zuo, Y.; Li, L.; Wu, Z.; Song, L. Isolation, identification and odour-producing abilities of geosmin/2-MIB in actinomycetes from sediments in Lake Lotus, China. J. Water Supply Res. Technol. 2009, 58, 552–561. [Google Scholar] [CrossRef]
- Suffet, I.H.; Corado, A.; Chou, D.; McGuire, M.J.; Butterworth, S. AWWA taste and odor survey. J. Am. Water Work. Assoc. 1996, 88, 168–180. [Google Scholar] [CrossRef]
- Peter, A.; Von Gunten, U. Taste and odour problems generated in distribution systems: A case study on the formation of 2,4,6-trichloroanisole. J. Water Supply Res. Technol. 2009, 58, 386–394. [Google Scholar] [CrossRef]
- Khiari, D.; Bruchet, A.; Gittelman, T.; Matia, L.; Barrett, S.; Suffet, I.H.; Hund, R. Distribution-generated taste-and-odor phenomena. Water Sci. Technol. 1999, 40, 129–133. [Google Scholar] [CrossRef]
- Lin, S.D. Tastes and Odors in Water Supplies—A Review; Illinois State Water Survey: Urbana, IL, USA, 1977. [Google Scholar]
- Baker, R.A. Examination of Present Knowledge. J. Am. Water Work. Assoc. 1966, 58, 695–699. [Google Scholar]
- NCHS. CDC Taste and Smell Examination Component Manual; NCHS: Atlanta, GA, USA, 2013.
- Jensen, S.; Anders, C.; Goatcher, L.; Perley, T.; Kenefick, S.; Hrudey, S. Actinomycetes as a factor in odour problems affecting drinking water from the North Saskatchewan River. Water Res. 1994, 28, 1393–1401. [Google Scholar] [CrossRef]
- Malleret, L.; Bruchet, A.; Hennion, M.-C. Picogram Determination of “Earthy-Musty” Odorous Compounds in Water Using Modified Closed Loop Stripping Analysis and Large Volume Injection GC/MS. Anal. Chem. 2001, 73, 1485–1490. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Luo, Q.; Yuan, S.; Wei, Z.; Song, H.; Wang, N.; Wang, Z. Simultaneous determination of ten taste and odor compounds in drinking water by solid-phase microextraction combined with gas chromatography-mass spectrometry. J. Environ. Sci. 2013, 25, 2313–2323. [Google Scholar] [CrossRef]
- Zhang, N.; Xu, B.; Qi, F.; Kumirska, J. The occurrence of haloanisoles as an emerging odorant in municipal tap water of typical cities in China. Water Res. 2016, 98, 242–249. [Google Scholar] [CrossRef]
- Nyström, A.; Grimvall, A.; Krantz-Rüilcker, C.; Sävenhed, R.; Åkerstrand, K. Drinking Water Off-Flavour Caused by 2,4,6-Trichloroanisole. Water Sci. Technol. 1992, 25, 241–249. [Google Scholar] [CrossRef]
- Zhang, K.; Cao, C.; Zhou, X.; Zheng, F.; Sun, Y.; Cai, Z.; Fu, J. Pilot investigation on formation of 2,4,6-trichloroanisole via microbial O-methylation of 2,4,6-trichlorophenol in drinking water distribution system: An insight into microbial mechanism. Water Res. 2018, 131, 11–21. [Google Scholar] [CrossRef]
- Zhang, K.; Zhou, X.; Zhang, T.; Mao, M.; Li, L.; Liao, W. Kinetics and mechanisms of formation of earthy and musty odor compounds: Chloroanisoles during water chlorination. Chemosphere 2016, 163, 366–372. [Google Scholar] [CrossRef]
- Zhang, K.; San, Y.; Cao, C.; Zhang, T.; Cen, C.; Li, Z.; Fu, J. Kinetic and mechanistic investigation into odorant haloanisoles degradation process by peracetic acid combined with UV irradiation. J. Hazard. Mater. 2021, 401, 123356. [Google Scholar] [CrossRef]
- Richardson, S.D.; DeMarini, D.M.; Kogevinas, M.; Fernandez, P.; Marco, E.; Lourencetti, C.; Ballesté, C.; Heederik, D.; Meliefste, K.; McKague, A.B.; et al. What’s in the Pool? A Comprehensive Identification of Disinfection By-products and Assessment of Mutagenicity of Chlorinated and Brominated Swimming Pool Water. Environ. Heal. Perspect. 2010, 118, 1523–1530. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Luo, Z.; Zhang, T.; Mao, M.; Fu, J. Study on formation of 2,4,6-trichloroanisole by microbial O-methylation of 2,4,6-trichlorophenol in lake water. Environ. Pollut. 2016, 219, 228–234. [Google Scholar] [CrossRef]
- Lennard, L. Methyltransferases. In Comprehensive Toxicology; McQueen, C.A., Ed.; Elsevier: Oxford, UK, 2010; pp. 435–457. ISBN 978-0-08-046884-6. [Google Scholar]
- Maggi, L.; Mazzoleni, V.; Fumi, M.; Salinas, M.R. Transformation ability of fungi isolated from cork and grape to produce 2,4,6-trichloroanisole from 2,4,6-trichlorophenol. Food Addit. Contam. Part A 2008, 25, 265–269. [Google Scholar] [CrossRef] [PubMed]
- Abhijith, G.; Kadinski, L.; Ostfeld, A. Modeling Bacterial Regrowth and Trihalomethane Formation in Water Distribution Systems. Water 2021, 13, 463. [Google Scholar] [CrossRef]
- Shang, F.; Uber, J.G.; Rossman, L.A. EPANET Multi-Species Extension User’s Manual; National Risk Management Research Laboratory US Environmental Protection Agency: Cincinatti, OH, USA, 2007.
- Clark, R.M.; Sivaganesan, M. Predicting Chlorine Residuals and Formation of TTHMs in Drinking Water. J. Environ. Eng. 1998, 124, 1203–1210. [Google Scholar] [CrossRef]
- Schrottenbaum, I.; Uber, J.; Ashbolt, N.; Murray, R.; Janke, R.; Szabo, J.; Boccelli, D. Simple Model of Attachment and Detachment of Pathogens in Water Distribution System Biofilms. In Proceedings of the World Environmental and Water Resources Congress 2009, Kansas City, MI, USA, 17–21 May 2009; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2009; pp. 145–157. [Google Scholar]
- Bois, F.Y.; Fahmy, T.; Block, J.-C.; Gatel, D. Dynamic modeling of bacteria in a pilot drinking-water distribution system. Water Res. 1997, 31, 3146–3156. [Google Scholar] [CrossRef]
- Munavalli, G.; Kumar, M.S.M.S.M. Dynamic simulation of multicomponent reaction transport in water distribution systems. Water Res. 2004, 38, 1971–1988. [Google Scholar] [CrossRef] [PubMed]
- Horn, H.; Reiff, H.; Morgenroth, E. Simulation of growth and detachment in biofilm systems under defined hydrodynamic conditions. Biotechnol. Bioeng. 2003, 81, 607–617. [Google Scholar] [CrossRef] [PubMed]
- Ibdah, M.; Zhang, X.-H.; Schmidt, J.; Vogt, T. A Novel Mg2+-dependent O-Methyltransferase in the Phenylpropanoid Metabolism of Mesembryanthemum crystallinum. J. Biol. Chem. 2003, 278, 43961–43972. [Google Scholar] [CrossRef]
- Zhang, W.; Miller, C.T.; DiGiano, F.A. Bacterial Regrowth Model for Water Distribution Systems Incorporating Alternating Split-Operator Solution Technique. J. Environ. Eng. 2004, 130, 932–941. [Google Scholar] [CrossRef]
- Abokifa, A.A.; Yang, Y.J.; Lo, C.S.; Biswas, P. Investigating the role of biofilms in trihalomethane formation in water distribution systems with a multicomponent model. Water Res. 2016, 104, 208–219. [Google Scholar] [CrossRef]
- Abhijith, G.R.; Mohan, S.; Abhijith, G.R. Cellular Automata-Based Mechanistic Model for Analyzing Microbial Regrowth and Trihalomethanes Formation in Water Distribution Systems. J. Environ. Eng. 2021, 147, 04020145. [Google Scholar] [CrossRef]
- Kim, N.-J. Relation of microbial biomass to counting units for Pseudomonas aeruginosa. Afr. J. Microbiol. Res. 2012, 6, 4620–4622. [Google Scholar] [CrossRef]
- Boccelli, D.L.; Tryby, M.E.; Uber, J.G.; Summers, R. A reactive species model for chlorine decay and THM formation under rechlorination conditions. Water Res. 2003, 37, 2654–2666. [Google Scholar] [CrossRef]
- Wang, J.-J.; Liu, X.; Ng, T.W.; Xiao, J.-W.; Chow, A.T.; Wong, P.K. Disinfection byproduct formation from chlorination of pure bacterial cells and pipeline biofilms. Water Res. 2013, 47, 2701–2709. [Google Scholar] [CrossRef]
- Dukan, S.; Levi, Y.; Piriou, P.; Guyon, F.; Villon, P. Dynamic modelling of bacterial growth in drinking water networks. Water Res. 1996, 30, 1991–2002. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET 2: Users Manual; National Risk Management Research Laboratory US Environmental Protection Agency: Cincinatti, OH, USA, 2000.
- Eliades, D.G.; Kyriakou, M.; Vrachimis, S.G.; Polycarpou, M.M. EPANET-MATLAB Toolkit: An Open-Source Software for Interfacing EPANET with MATLAB. In Proceedings of the Computing and Control for the Water Industry CCWI 2016, Amsterdam, The Netherlands, 7–9 November 2016; pp. 1–8. [Google Scholar]
- Reca, J.; Martínez, J. Genetic algorithms for the design of looped irrigation water distribution networks. Water Resour. Res. 2006, 42, 1–9. [Google Scholar] [CrossRef]
- Bi, W.; Dandy, G.; Maier, H. Improved genetic algorithm optimization of water distribution system design by incorporating domain knowledge. Environ. Model. Softw. 2015, 69, 370–381. [Google Scholar] [CrossRef]
- Prévost, M.; Rompré, A.; Coallier, J.; Servais, P.; Laurent, P.; Clément, B.; Lafrance, P. Suspended bacterial biomass and activity in full-scale drinking water distribution systems: Impact of water treatment. Water Res. 1998, 32, 1393–1406. [Google Scholar] [CrossRef]
- Rosario-ortiz, B.F.; Rose, J.; Speight, V.; Von Gunten, U.; Schnoor, J. How do you like your tap water? Science 2016, 351, 912–914. [Google Scholar] [CrossRef] [PubMed]
- Huck, P.M. Measurement of Biodegradable Organic Matter and Bacterial Growth Potential in Drinking Water. J. Am. Water Work. Assoc. 1990, 82, 78–86. [Google Scholar] [CrossRef]
- Escobar, I.C.; Randall, A.A.; Taylor, J.S. Bacterial Growth in Distribution Systems: Effect of Assimilable Organic Carbon and Biodegradable Dissolved Organic Carbon. Environ. Sci. Technol. 2001, 35, 3442–3447. [Google Scholar] [CrossRef]
- Prest, E.I.; Ehammes, F.; Van Loosdrecht, M.C.M.; Vrouwenvelder, J.S. Biological Stability of Drinking Water: Controlling Factors, Methods, and Challenges. Front. Microbiol. 2016, 7, 45. [Google Scholar] [CrossRef]
- USEPA National Primary Drinking Water Guidelines. Available online: https://www.epa.gov/sites/production/files/2016-06/documents/npwdr_complete_table.pdf (accessed on 22 February 2021).
- Gheisi, A.; Forsyth, M.; Naser, G. Water Distribution Systems Reliability: A Review of Research Literature. J. Water Resour. Plan. Manag. 2016, 142, 04016047. [Google Scholar] [CrossRef]
- Benanou, D.; Acobas, F.; De Roubin, M.R.; David, F.; Sandra, P. Analysis of off-flavors in the aquatic environment by stir bar sorptive extraction–thermal desorption–capillary GC/MS/olfactometry. Anal. Bioanal. Chem. 2003, 376, 69–77. [Google Scholar] [CrossRef]
- USEPA. National Primary Drinking Water Regulations: Stage 2 Disinfectants and Disinfection Byproducts Rule; Office of Ground Water and Drinking Water, Environmental Protection Agency: Washington, DC, USA, 2006; Volume 71.
- Gowda, T.H.; Lock, J.; Kurtz, R. A comprehensive study of risk assessment for a hazardous compound of public health concern. Water Air Soil Pollut. 1985, 24, 189–190. [Google Scholar] [CrossRef]
- Blokker, E.M.; Pieterse-Quirijns, E. Modeling temperature in the drinking water distribution system. J. Am. Water Work. Assoc. 2013, 105, E19–E28. [Google Scholar] [CrossRef]
- Douterelo, I.; Boxall, J.B.; Deines, P.; Sekar, R.; Fish, K.E.; Biggs, C.A. Methodological approaches for studying the microbial ecology of drinking water distribution systems. Water Res. 2014, 65, 134–156. [Google Scholar] [CrossRef]
- Villegas, L.G.C.; Mashhadi, N.; Chen, M.; Mukherjee, D.; Taylor, K.E.; Biswas, N. A Short Review of Techniques for Phenol Removal from Wastewater. Curr. Pollut. Rep. 2016, 2, 157–167. [Google Scholar] [CrossRef]
- Enyoh, C.E.; Isiuku, B.O. 2,4,6-Trichlorophenol (TCP) removal from aqueous solution using Canna indica L.: Kinetic, isotherm and Thermodynamic studies. Chem. Ecol. 2021, 37, 64–82. [Google Scholar] [CrossRef]
- Najm, I.N.; Snoeyink, V.L.; Richard, Y. Removal of 2,4,6-trichlorophenol and natural organic matter from water supplies using PAC in floc-blanket reactors. Water Res. 1993, 27, 551–560. [Google Scholar] [CrossRef]
- Anirudhan, T.; Ramachandran, M. Removal of 2,4,6-trichlorophenol from water and petroleum refinery industry effluents by surfactant-modified bentonite. J. Water Process. Eng. 2014, 1, 46–53. [Google Scholar] [CrossRef]
- Nazal, M.K.; Gijjapu, D.; Abuzaid, N. Study on adsorption performance of 2,4,6-trichlorophenol from aqueous solution onto biochar derived from macroalgae as an efficient adsorbent. Sep. Sci. Technol. 2020, 1–11. [Google Scholar] [CrossRef]
- Kumar, N.S.; Woo, H.-S.; Min, K. Equilibrium and kinetic studies on biosorption of 2,4,6-trichlorophenol from aqueous solutions by Acacia leucocephala bark. Colloids Surfaces B Biointerfaces 2012, 94, 125–132. [Google Scholar] [CrossRef]
- Zazouli, M.A.; Balarak, D.; Mahdavi, Y. Application of Azolla for 2,4,6-Trichlorophenol (TCP) Removal from Aqueous Solutions. Arch. Hyg. Sci. 2013, 2, 143–149. [Google Scholar]
- Islam, M.S.; Abedin, M.Z. Adsorption of phenol from aqueous solution by water hyacinth ash. ARPN J. Eng. Appl. Sci. 2007, 2, 11–17. [Google Scholar]
- Kumar, N.S.; Asif, M.; Poulose, A.M.; Suguna, M.; Al-Hazza, M.I. Equilibrium and Kinetic Studies of Biosorptive Removal of 2,4,6-Trichlorophenol from Aqueous Solutions Using Untreated Agro-Waste Pine Cone Biomass. Processes 2019, 7, 757. [Google Scholar] [CrossRef]
- Xu, D.-Y.; Yang, Z. Cross-linked tyrosinase aggregates for elimination of phenolic compounds from wastewater. Chemosphere 2013, 92, 391–398. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).